A Hardware Realization Framework for Fuzzy Inference System Optimization

The effectiveness of Fuzzy Inference Systems (FISs) in manipulating uncertainty and nonlinearity makes them a subject of significant interest for decision-making in embedded systems. Accordingly, optimizing FIS hardware improves its performance, efficiency, and capabilities, leading to a better user experience, increased productivity, and cost savings. To be compatible with the limited power budget in most embedded systems, this paper presents a framework to realize ultra-low power FIS hardware. It supports optimizations for both conventional arithmetic as well as MSDF-computing to be highly consistent with MSDF-based sensors. In MSDF-computing FIS all the processes of fuzzification, inference, and defuzzification are done on serially coming data bits. To demonstrate the efficiency of the proposed framework, we utilized Matlab, Chisel3, and Vivado to implement it from high-level descriptions of FIS to hardware synthesis. We also developed a Scala library in Chisel3 to establish a connection between these tools, bridging the gap, and facilitating design space exploration at the arithmetic level. Furthermore, we realized an FIS for the navigation of autonomous mobile robots in unknown environments. Synthesis results show the superiority of the output of our suggested design framework in terms of resource usage as well as power and energy consumption compared to the Matlab HDL code generator output.

Keywords:

Subject: Computer Science and Mathematics - Hardware and Architecture

1. Introduction

Fuzzy inference systems have emerged as a crucial component of contemporary technology, serving as a class of computational models proficient in addressing uncertainties inherent in modeling and data [1,2]. FISs find applications in diverse domains, such as information fusion [3], pattern recognition [4], prediction [5], decision-making [6,7], and control systems [8]. Their ability to handle uncertain and imprecise information makes them particularly useful in these areas, where the input data often contain noise, errors, or missing values. FISs can help to identify patterns in complex datasets, make accurate predictions based on historical data, and make informed decisions in uncertain and dynamic environments [9,10]. Furthermore, FISs can be integrated into control systems to regulate the behavior of complex systems, such as robots, vehicles, or industrial processes [5,11,12]. In addition, FISs are utilized in financial applications to predict stock prices and to analyze market trends, and in medical diagnosis systems to help doctors interpret medical test results and to make informed treatment decisions [13,14]. Consequently, the pivotal role and extensive utilization of FISs dictate the need to augment their design for greater efficiency and sustainability.

The pursuit of higher efficiency and diminished processing demands and power consumption via hardware redesign is widely embraced as a strategy for optimizing systems in the context of sustainable computing [15]. On the other hand, as the need for high-speed computing intensifies, FISs have migrated to VLSI, leading to a substantial improvement in their processing speed [16]. Nonetheless, the considerable expenses associated with VLSI chip redesign or modification have necessitated the adoption of Field Programmable Gate Arrays (FPGAs) [17,18]. Therefore, FPGAs have emerged as a favorable choice for implementing FISs owing to their cost-effectiveness and flexibility in hardware design modifications. This trend has been favorably received by research aimed at optimizing the implementation of target hardware on FPGA.

To optimize hardware through its high-level description, a range of optimization techniques can be employed across different levels of granularity, from coarse-grained levels such as task graphs to fine-grained levels such as data flow graphs [19,20]. Computer arithmetic provides a suite of efficient methods and tools for minimizing the processing requirements of specific tasks, particularly at the fine-grained level [21,22,23]. The MSDF data processing technique is one such example that enables early termination of computation and the utilization of compact processing elements to handle data sequentially and at the bit level [24,25,26].

MSDF computing leverages the significance of digits in data to minimize the number of processing components and operations required for computation [27,28]. The technique processes data hierarchically, beginning with the most significant digit and advancing toward the least significant digit. By prioritizing the most significant digits, certain computations, such as comparison, can be terminated early [24,25,26,28]. Moreover, because the data bits are processed serially, the effect of early termination can be propagated back to the processing elements that are computing the next set of bits, resulting in reduced processing time and power consumption.

This paper introduces a hardware realization framework that leverages both conventional arithmetic and MSDF computing techniques to conduct hyper-exploration on the design space and optimize FISs for sustainable computing. In addition, the proposed framework serves as a connection between high-level FIS description tools, such as Matlab, and hardware synthesis tools, such as Synopsys Design Compiler and Xilinx Vivado Design Suite. The framework proposed in this study is implemented and tested by realizing FIS for a robot navigation case study.

The remainder of this paper is structured as follows. Section 2 provides an overview of the necessary background information and foundational concepts related to FIS and MSDF computing. The proposed framework is detailed in Section 3. Section 4 outlines the experimental design and case study utilized to evaluate the framework’s effectiveness. Section 5 presents the experimental results and corresponding discussions. Finally, Section 6 concludes the paper.

2. Background and Preliminaries

2.1. Fuzzy Set Theory

Fuzzy sets are an extension of the classical notion of the set that each element has a degree of membership in

[0, 1]

Definition 1.

Let X be the universe of discourse. Then, a fuzzy set A on X is characterized by membership function

μ_{A} : X \to [0, 1]

Definition 2.

Let A and B be two fuzzy sets defined on set X. The standard form of the set operations intersection and union calculate the membership of each

x \in X

by Equation (1) and (2), respectively.

μ_{A \cap B} (x) = m i n {μ_{A} (x), μ_{B} (x)} .

(1)

μ_{A \cup B} (x) = m a x {μ_{A} (x), μ_{B} (x)} .

(2)

2.2. Fuzzy Inference System (FIS)

A FIS is an artificial intelligence framework that utilizes fuzzy logic for inference. A FIS consists of three main building blocks namely, fuzzification, inference, and defuzzification.

Fuzzification is the process of associating each crisp input value with a set of fuzzy values based on the corresponding linguistic terms defined for that input.

By inference, the fuzzy set operations are used to evaluate predefined rules that specify how the input variables should be combined to generate the output. Each rule is a combination of antecedent (if) and consequent (then) clauses, where the antecedent specifies the conditions under which the rule applies, and the consequent specifies the action to be taken. In the inference, the process of composing fuzzy relations is generally accomplished using either max-min or max-product compositions.

The process of defuzzification involves the conversion of each fuzzy output to a crisp numerical value. This numerical value is then sent to the control system, where it is used to adjust the system’s behavior. There are several defuzzification methods available to accomplish this task, including the centroid method, the max or mean-max membership principles, and the weighted average method.

2.3. MSDF Computing

In MSDF arithmetic, also known as Left to Right Arithmetic, the computation commences from the Most Significant Digit (MSD) for all arithmetic operations, unlike conventional arithmetic where addition and multiplication are performed from the least significant digit to the most significant positions. As a result, in the serial fashion of MSDF (also referred to as Online arithmetic), the result digits can be generated upon receiving a limited number of digits from the operands, even as the remaining input digits are being received. This computational approach offers advantages in terms of lower latency and power consumption by terminating unnecessary computations. The serial nature of MSDF computing further contributes to a reduced area for the arithmetic unit, resulting in a smaller memory footprint and fewer interconnects. Furthermore, dependent operations can be executed nearly simultaneously by considering a delay parameter.

By employing MSDF arithmetic, computations can be terminated once the desired precision is achieved, eliminating the need for additional computations [24,29]. In contrast, conventional arithmetic requires the generation of the least significant part of the result, which is subsequently discarded based on the required precision. Furthermore, in specific operations, such as finding the maximum and minimum values, the result becomes evident upon encountering the first unequal digits among the operands.

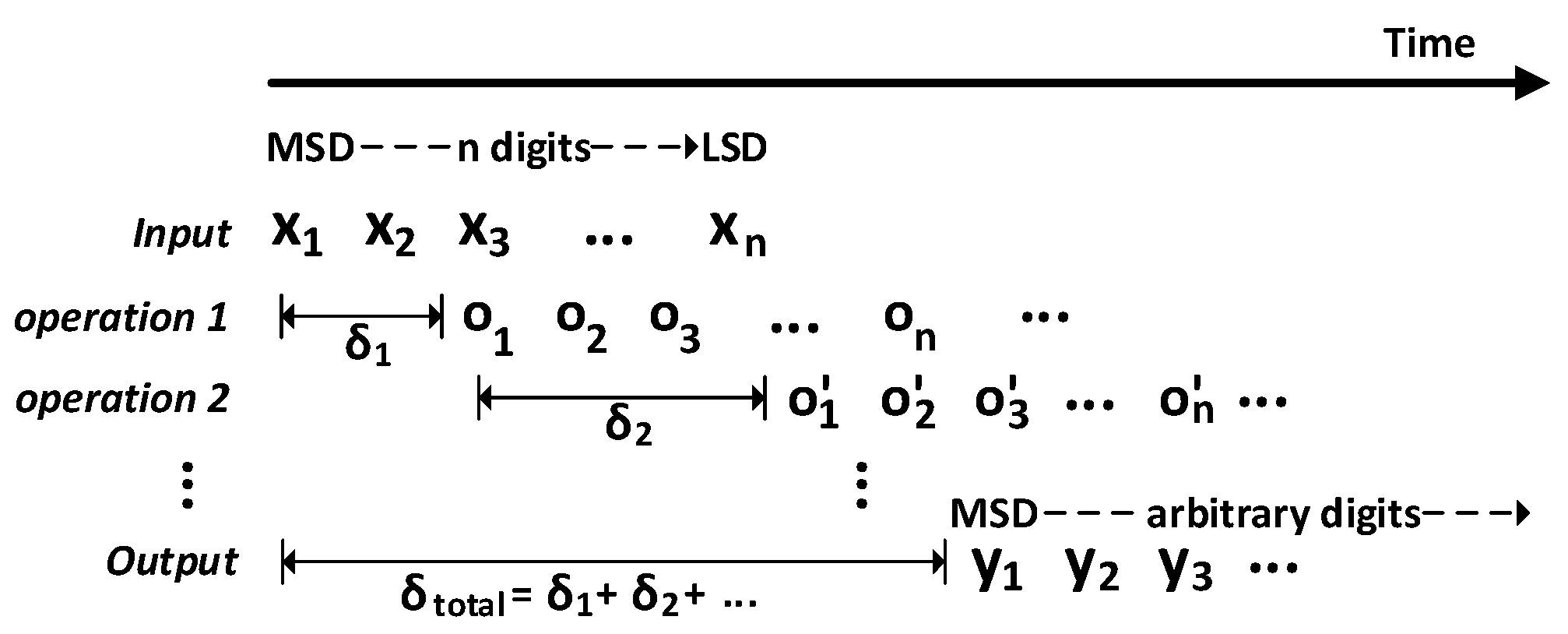
In the context of MSDF computing, the online delay is defined as the time interval required for generating the output digits while the input digits are sequentially received. It signifies the duration between the arrival of input data and the corresponding production of output digits in a serial fashion. Due to the prioritization of the most significant digits in MSDF computing, result digits are generated only after receiving a limited number of operand digits. Consequently, there is a gradual accumulation of delay until the final result is achieved. This characteristic is crucial to consider when assessing the computational efficiency and performance of MSDF computing. Figure 1 depicts the progressive accumulation of online delay in MSDF computing. In this context, each operation i contributes an online delay

δ_{i}

to the overall online delay

δ_{t o t a l}

of the chained operations.

3. Proposed Framework

Hardware design space exploration can be conducted across various dimensions such as architecture, memory hierarchy, data path and pipeline, communication interfaces, arithmetic, and optimization metrics. The proposed framework aligns with the productivity approach of diverse Computer Arithmetic systems, aiming to optimize the final product in terms of power and area goals. Moreover, it effectively utilizes available tools from high-level descriptions of FIS to hardware synthesis. 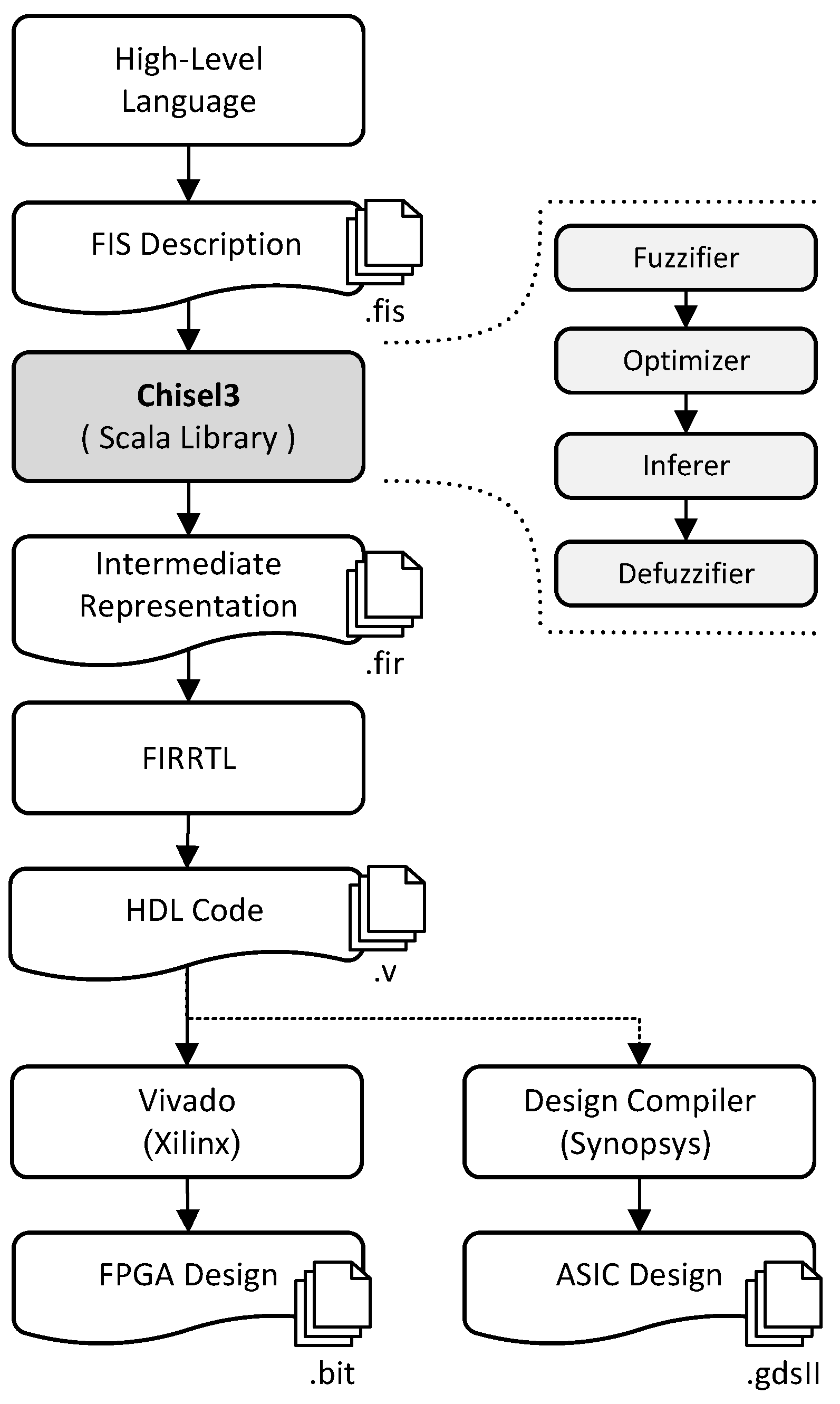Figure 2 depicts the overarching structure of this framework, showcasing the processes involved and their corresponding outputs, spanning from the high-level description of FIS to its hardware representation. Additionally, a Scala library is developed in Chisel3 to establish a connection between these tools, bridging the gap. It facilitates design space exploration encompassing both conventional arithmetic and MSDF computing. Also, it comprises four primary modules to construct a FIS, namely the Fuzzifier, Optimizer, Inferer, and Defuzzifier.

3.1. Fuzzifier

The Fuzzifier module incorporates a collection of procedures designed to represent membership functions within the structure of a FIS. Also, to facilitate support for MSDF computing as well as data processing in a serial bit arrangement, there are potential options available for implementing membership functions. These options include the utilization of Lookup Tables (LUT) or adopting unconventional methods such as online arithmetic. The LUT-based implementations on FPGAs provide a favorable equilibrium among flexibility, efficiency, programmability, and speed, rendering them a highly recommended option for function implementation on FPGA platforms [30,31].

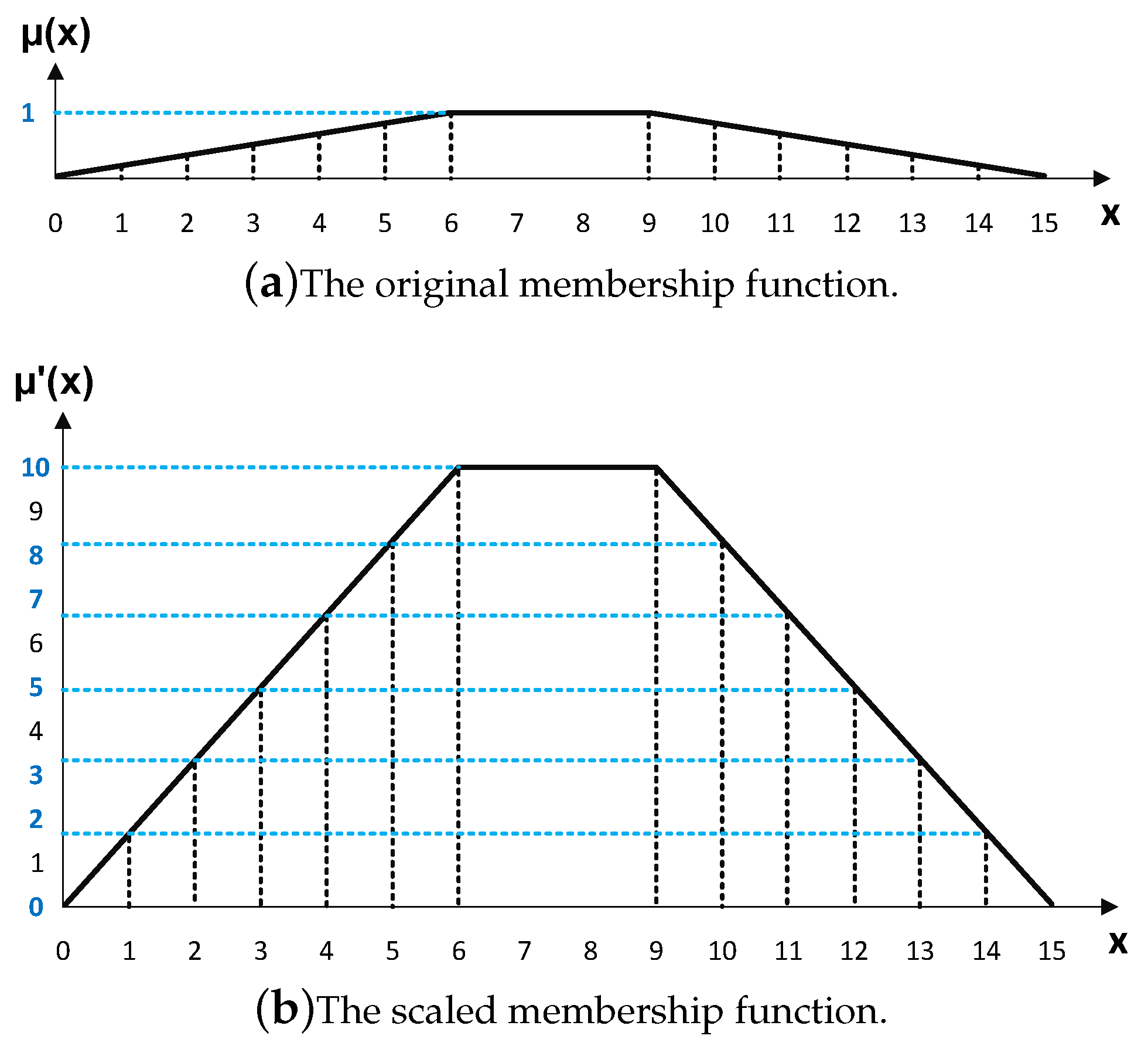
As hardware platforms typically have finite precision arithmetic capabilities, the quantization and scaling techniques are applied to represent the fuzzy values and intermediate computations accurately within the hardware constraints. Here, the output value of membership functions can be scaled using an S factor. A higher value of S corresponds to increased precision, necessitating a greater number of bits for the membership function output. Figure 3a illustrates a trapezoidal membership function, while Figure 3b depicts the same function scaled with a factor of

S = 10

, resulting in a precision of

0.1

. Also, the value of

\tilde{μ} (x)

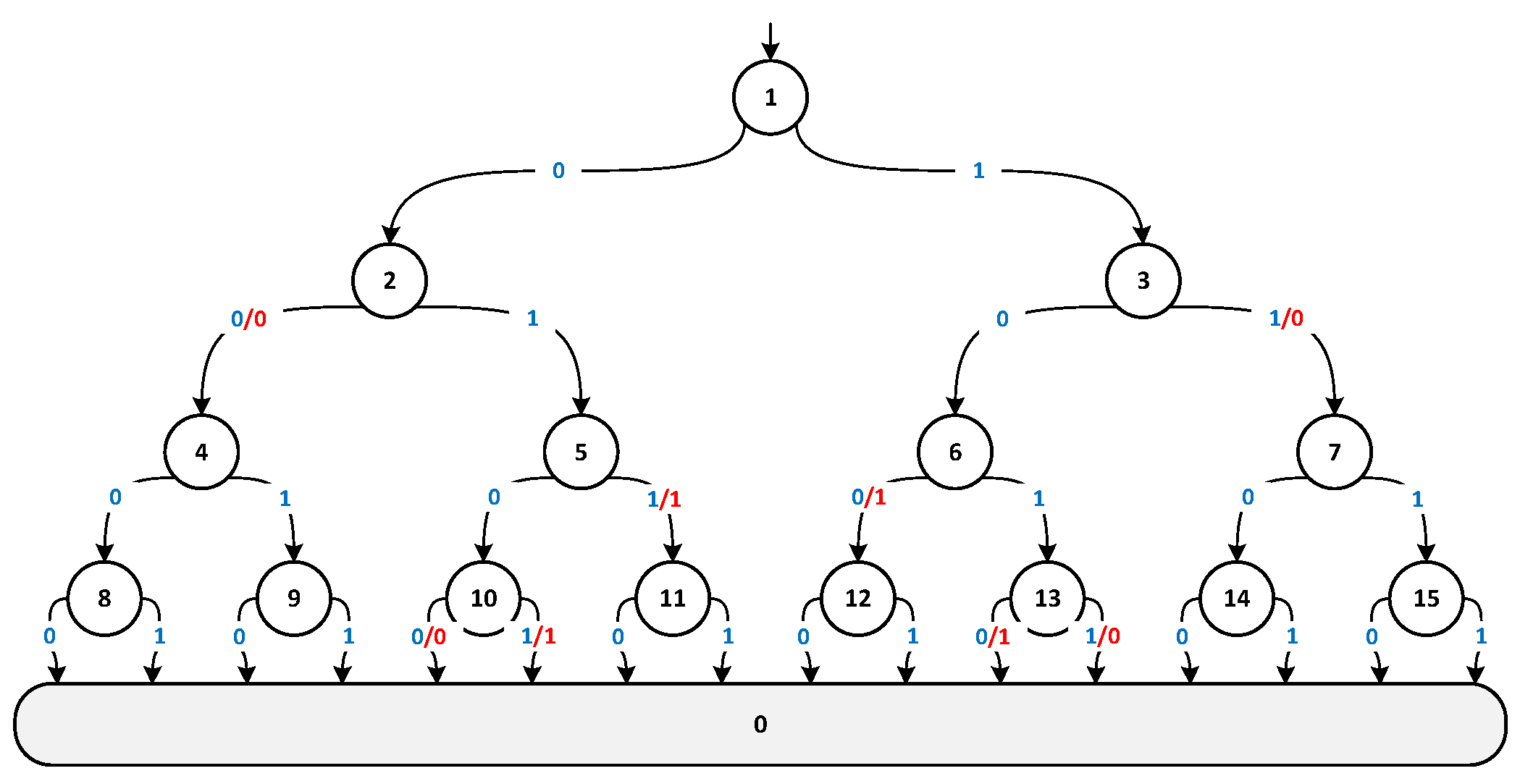
is rounded to the nearest value indicated by the blue numbers on the vertical axis. Table 1 presents the corresponding truth table, which could be used for deriving the equivalent Finite State Machine (FSM) as well as calculating the online delay

δ

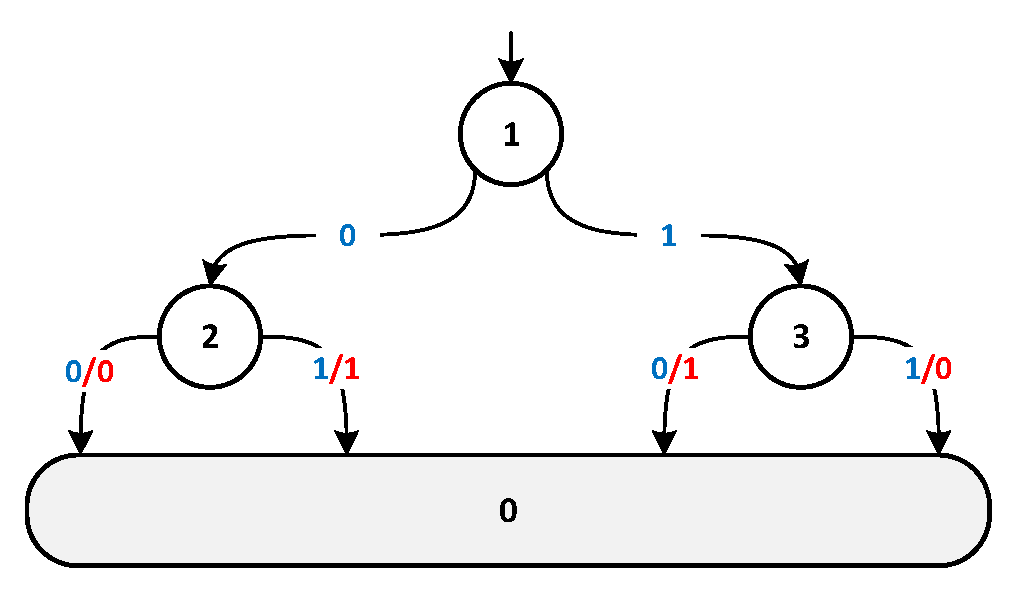
Figure 4 presents the mealy FSM corresponding to the most significant digit of the output. This pseudo-tree structure is the same for all outputs and only the output on the edges related to the transition rules are different. Furthermore, the online delay

δ

is 4, indicating that the determination of the output’s fourth bit from the left directly corresponds to the determination of the value of

y_{1}

Also, if the number of input bits is n, the considered FSM has

2^{n}

states, where we define the initial state as 1, and the state change formula is based on Equation (3).

S_{t + 1} = \{\begin{matrix} 2 S_{t} + x_{i} & 0 < S_{t} < 2^{n} \\ 0 & o . w . \end{matrix} .

(3)

3.2. Optimizer

In this research, we have devised an approximate computing approach to manipulate specific bits within the LUTs systematically. This technique effectively reduces the online delay

δ

associated with serial processing in MSDF computing. For example, if the controller is tolerant enough so that we can increase the value of the membership function

\tilde{μ}

for

X = 4

and

X = 11

0.1

, it results in Table 2. In this table,

δ

of producing MSD is reduced to 2.

Figure 5 presents the mealy FSM corresponding to

y_{1}^{'}

which is MSD of the output for the optimized LUT.

3.3. Inferer

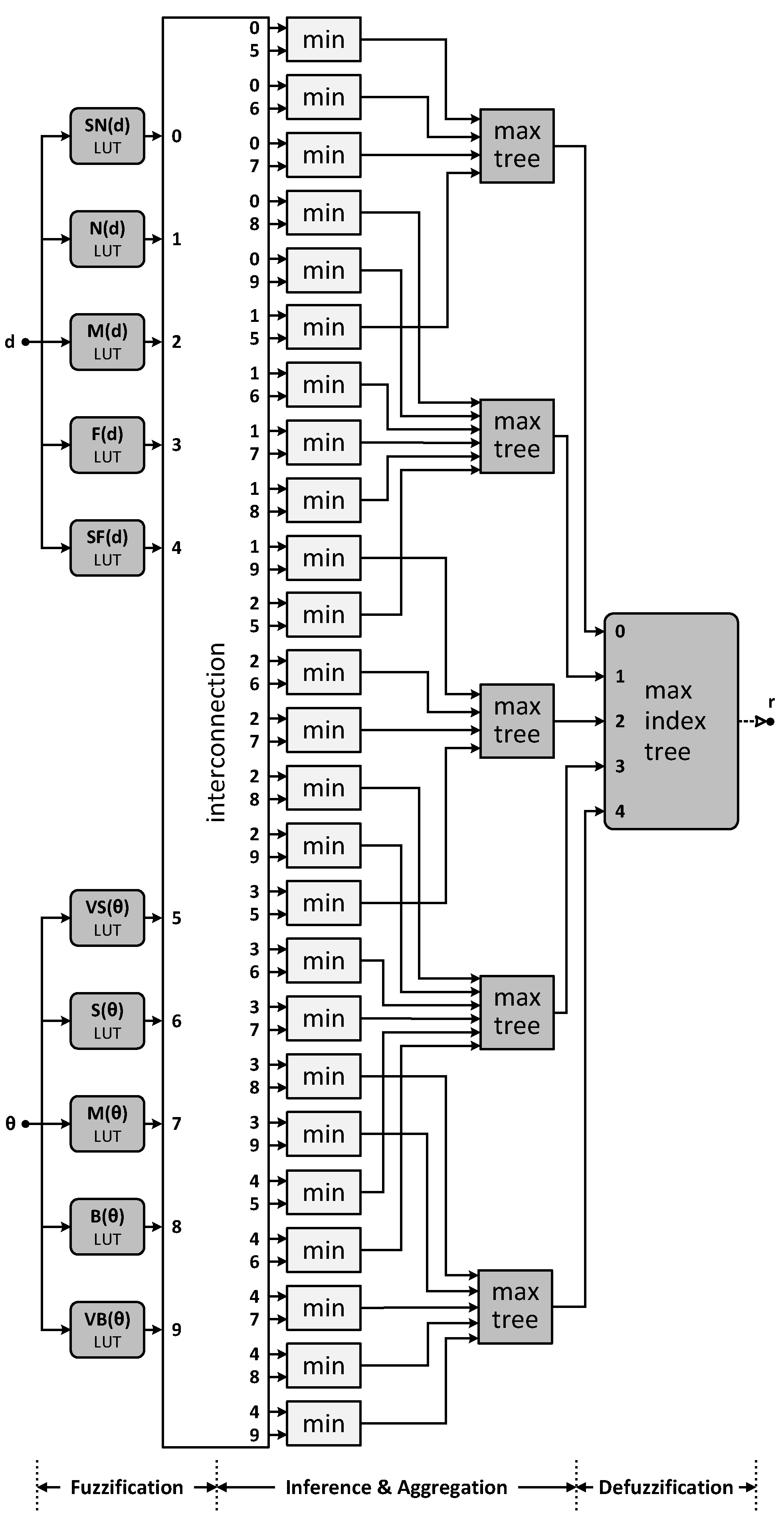
The Inferer module encompasses the implementation of specific reductions necessary for min-max operations associated with FIS rules. Additionally, it handles the aggregation of rules that possess output with the same linguistic value.

3.4. Defuzzifier

In this research, our focus is on evaluating the efficiency of MSDF computing using conventional number representation. Therefore, we implemented the Maximum Membership defuzzification method, identifying the fuzzy set with the highest membership degree. This fuzzy set represents the strongest influence on the output. The crisp output value is then determined based on the representative value of the selected fuzzy set, considering the shape and characteristics of its membership function. This crisp output value, obtained through defuzzification, provides a definitive and usable value for further processing, decision-making, or control actions.

4. Evaluation Methodology

4.1. Case Study

Path planning of mobile robots in unknown environments is one of the most common problems for robot navigation. The extent of the desired environment is assumed as a rectangle, where several obstacles are located inside it. The problem is that a robot has to move from a starting point to a target point by avoiding obstacles. The fact that the environment is unknown to the robot means that it is unfamiliar with its surroundings, it can solely detect obstacles within its visual range. 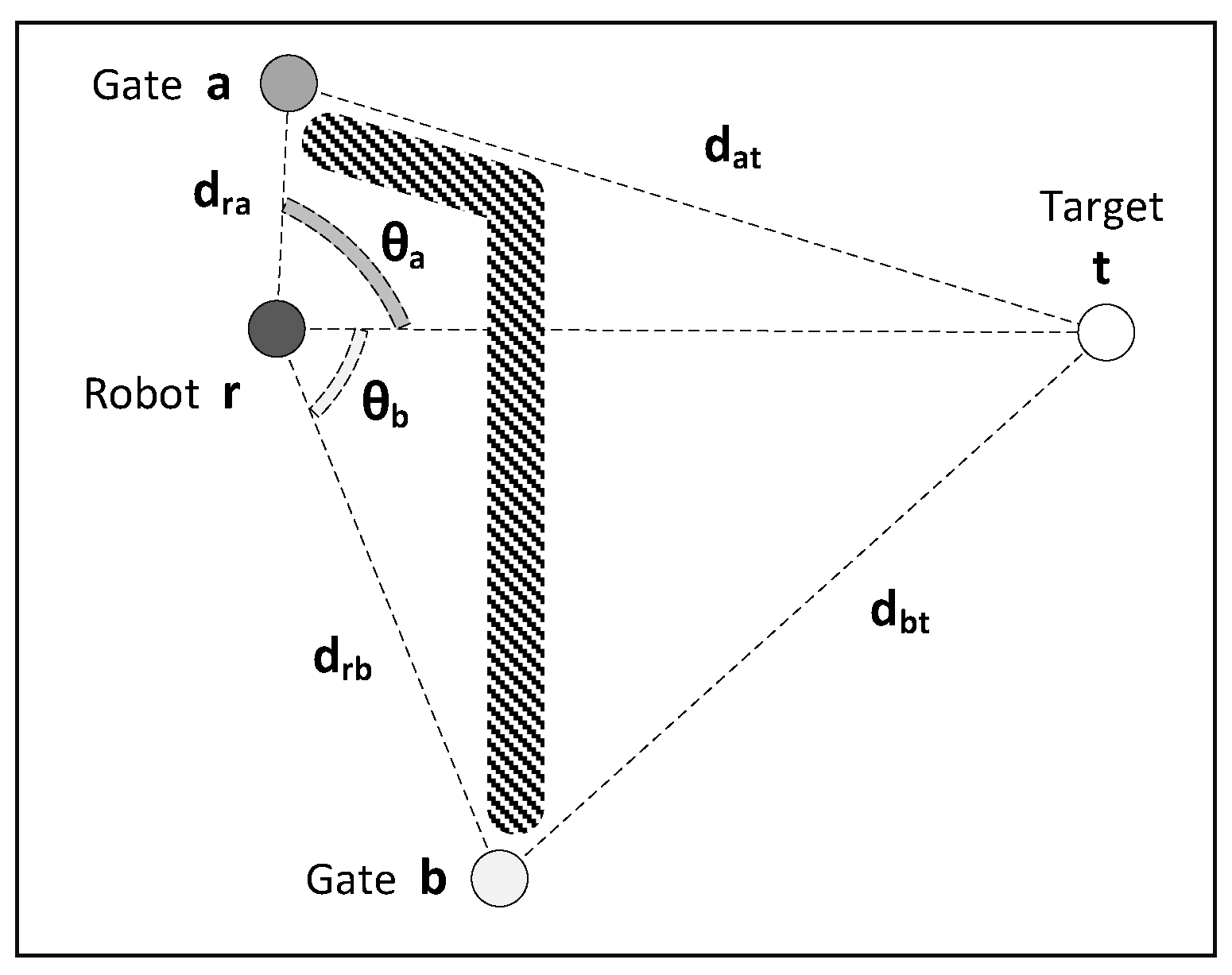Figure 6 illustrates an environment including a robot, an obstacle, and two gates to move the robot to the target point. Here, the robot confronts an obstacle that obstructs its direct path toward the destination. Consequently, it is presented with two alternatives; either passing through gate a or gate b. In this situation, FIS calculates a rank value r for each gate, and the gate with the lowest r value is selected to pass. Since the space behind the obstacle is unknown to the robot, the robot assumes that there is no obstacle behind it and considers the promising distance values

d_{a} = d_{r a} + d_{a t}

and

d_{b} = d_{r b} + d_{b t}

for gates a and b, respectively. Then, it sends the values of

(d_{a}, θ_{a})

and

(d_{b}, θ_{b})

to the FIS to calculate the rank of the corresponding gates.

4.2. Experimental Design

In this section, the experimental design of a FIS is described in two steps. The first step demonstrates the desired robot navigation algorithm, as well as the components of the corresponding FIS. The second step presents the hardware realization of the proposed FIS that supports MSDF computing.

4.2.1. Step 1 (Software Implementation)

A simple FIS-based algorithm is developed for the navigation of a robot in an unknown environment. We implemented it in MATLAB, where the input contains information about the start points and target points of the robots as well as the specification of the environment and the obstacles inside it. Algorithm 1 presents the navigation subroutine for a robot. The main loop is repeated until the robot reaches the target point. In each iteration, the robot scans all the visible gates and calculates their ranks. In this stage, an FIS calculates the rank of each gate. Then, the gate with the best (least) rank is selected for passing.

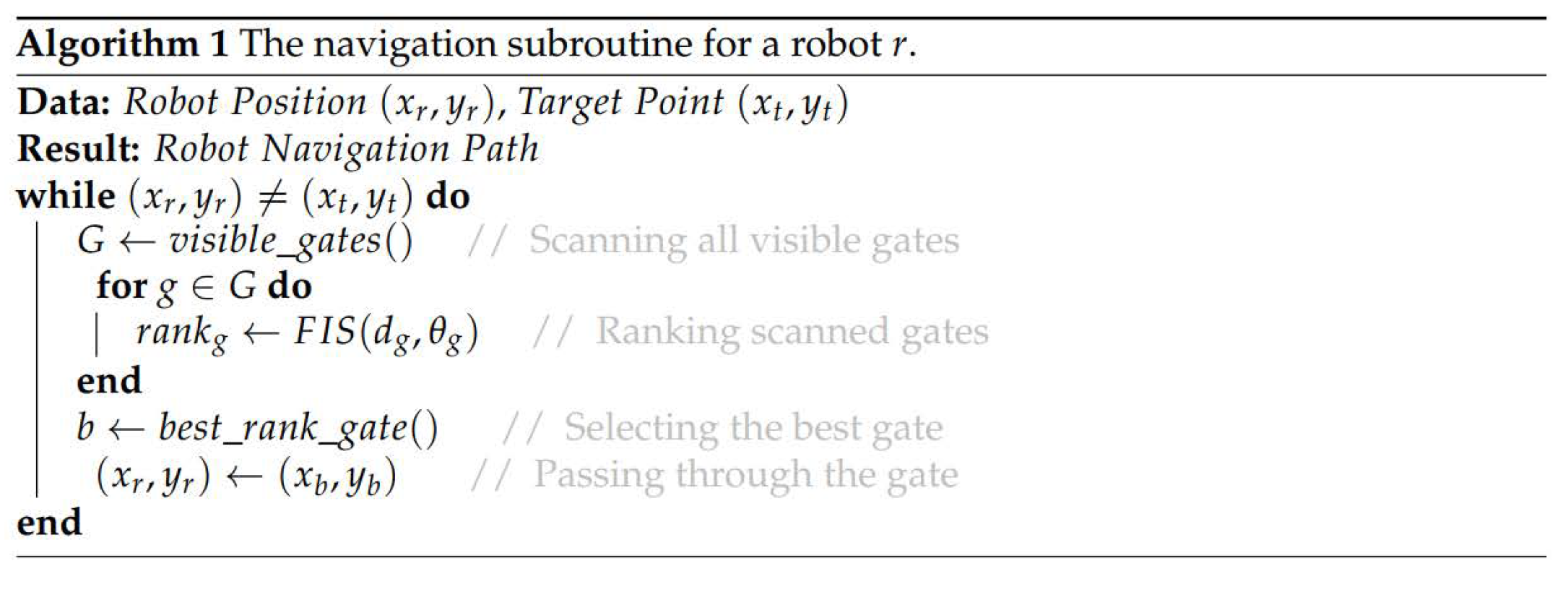
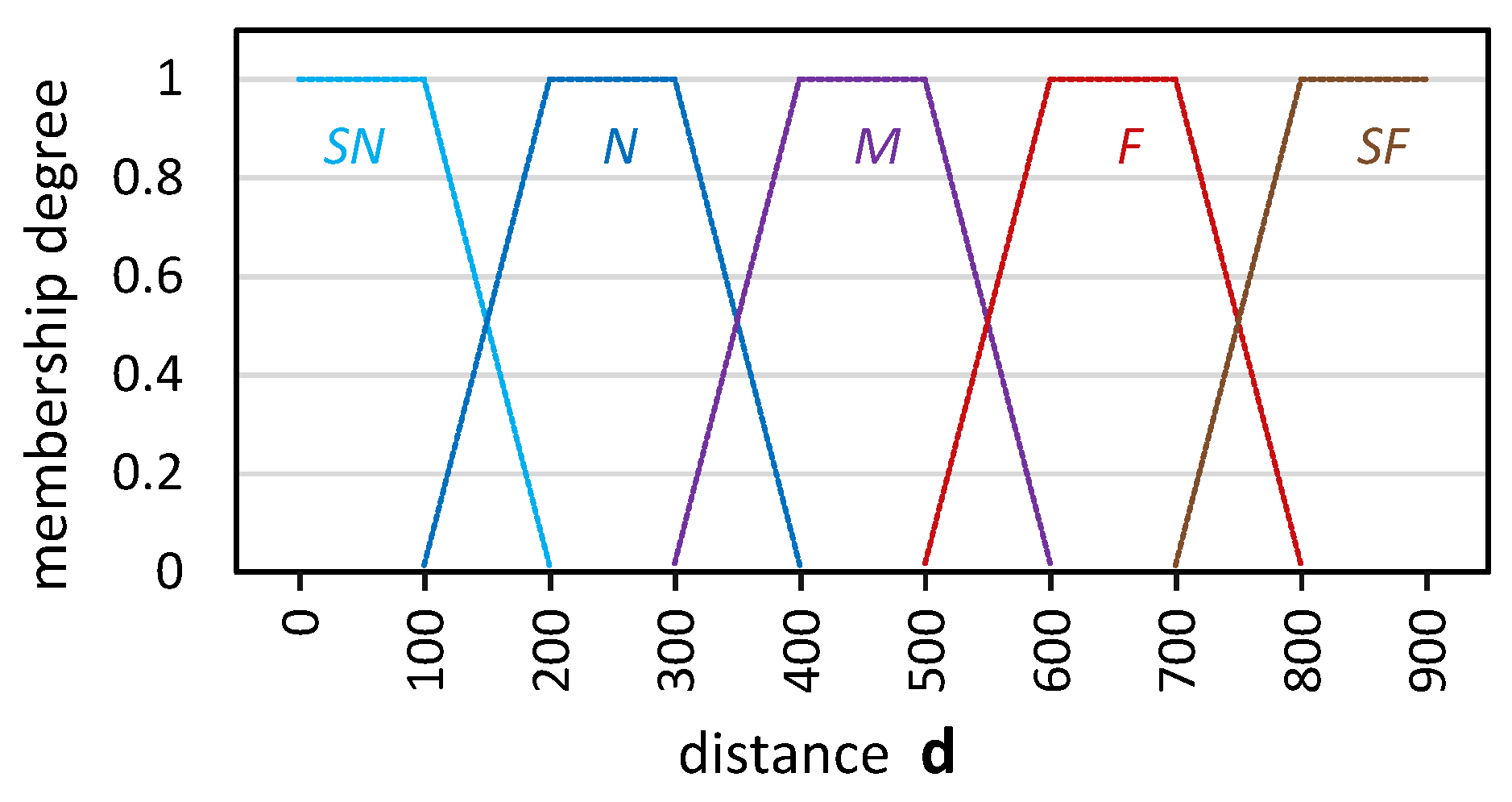
The FIS ranked each gate according to two input parameters; the promising distance d in meters, and the deviation angle

θ

in degrees. The distance parameter d indicates the (promising) distance of the robot to the target point by passing through the desired gate. Since the most promising distance in the defined environment is related to moving from one corner to the opposite corner from the path close to the sides, this parameter can be in the range of

[0, 1023]

for a

700 \times 700

rectangular environment. Also, five linguistic values of So Near (SN), Near (N), Medium (M), Far (F) and So Far (SF) are defined for the fuzzification of this parameter. Figure 7 shows the trapezoidal membership functions of these linguistic values.

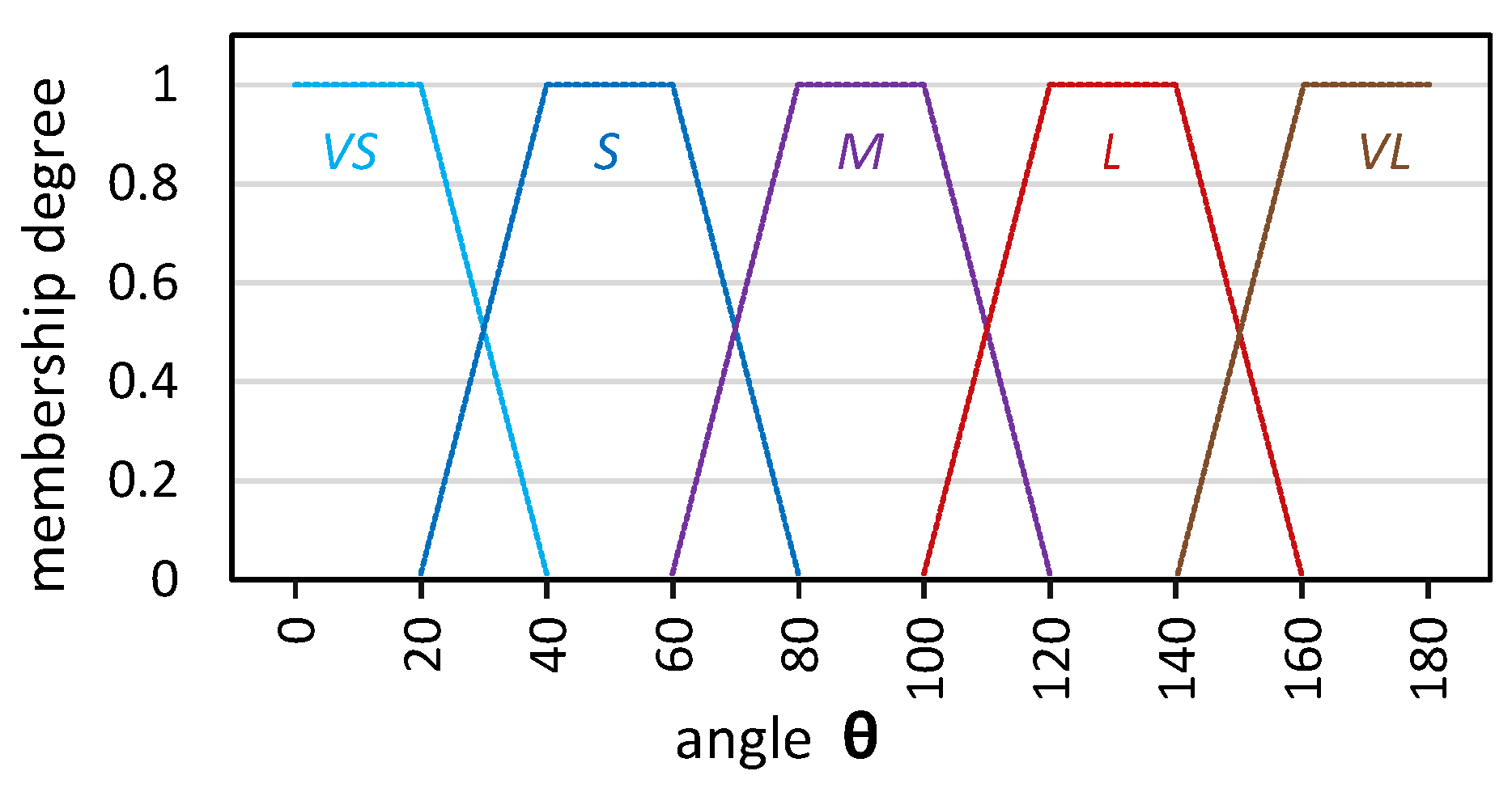
The angle parameter

θ

indicates the deviation (to the right or left) of the robot from the straight path to the target point. This deviation can be in the range of

[0, 180]

degrees. Also, five linguistic values of Very Small (VS), Small (S), Medium (M), Large (L) and Very Large (VL) are defined for the fuzzification of the angle parameter. Figure 8 displays the trapezoidal membership functions of these linguistic values.

The FIS inference component maps the fuzzified input values to fuzzy rank values according to predefined IF-THEN rules. Table 3 presents the set of 25 defined inference rules. Here, each column indicates the set of rules on an angle linguistic value and each column indicates the set of rules on a distance linguistic value, where the output is a rank value

r \in {0, 1, 2, 3, 4}

pointed in the junction. For example, the rule (IF angle IS Very-Large AND distance IS So-Far THEN rank IS 4) is presented by the cell placed in the junction of the last column and last row. It should be stated that the order of ranks from best to worst is 0, 1, 2, 3, and 4. Therefore, when the angle is

V e r y S m a l l

and the distance is

M e d i u m

or less, and also when the angle is

S m a l l

and the distance is

S o N e a r

, the rank is 0 (the best possible rank). Also, inference rules with similar output are aggregated together using the

m a x

operator.

As well, the SOM (smallest value for which the output fuzzy set is maximum) is used for the defuzzification. In other words, the output rank value is the best rank with the maximum degree of membership.

4.2.2. Step 2 (Hardware Realization)

Figure 9 illustrates the structure of the fuzzy inference system described in the previous section. In the fuzzification component, membership functions are implemented as lookup tables and map the two inputs d and

θ

to values in the integer interval

[0, 100]

5. Experimental Results

In this section, we elaborate on the experimental results of hardware design using the proposed framework (conventional arithmetic and MSDF computing) with MATLAB’s HDL coder (conventional arithmetic).

5.1. Experiment and Evaluation Method

Since for the design of FIS hardware, we have discretized it and adopted the lookup table approach, at first we compared it with the continuous implementation approach to show the equivalence of the outputs. Therefore, we applied the Monte Carlo approach for validation.

For hardware evaluation, the experiments were conducted on a standard Avnet ZedBoard 7020 baseboard with a Zynq-7000 All Programmable SoC XC7Z020-CLG484-1. We evaluated our design using the Xilinx Vivado design suite and downloaded the synthesized bitstream to the target board. Furthermore, we undertook a comprehensive evaluation by focusing on the assessment of Worst Negative Slack (WNS), Maximum Clock Frequency, resource utilization, and power consumption across identical benchmarks.

It is imperative to emphasize that WNS, as the maximum allowable delay by which a signal can be extended without infringing upon the circuit’s specified clock period, holds paramount significance. Ensuring that WNS remains within predefined tolerances serves as a pivotal safeguard against potential timing violations, the ramifications of which could manifest as critical inaccuracies in circuit operation.

5.2. Availability

The source code of the proposed Fuzzy Inference System (FIS) along with generated verilog codes (Chisel) and files for each of the phases (Fuzzification, Inference, Defuzzification) for both conventional and MSDF-based computing systems as well as MATLAB Simulink models for HDL code generation and Monte Carlo simulation are available at:

https://github.com/cslab-chosun/online-fuzzy-chisel

5.3. Validation

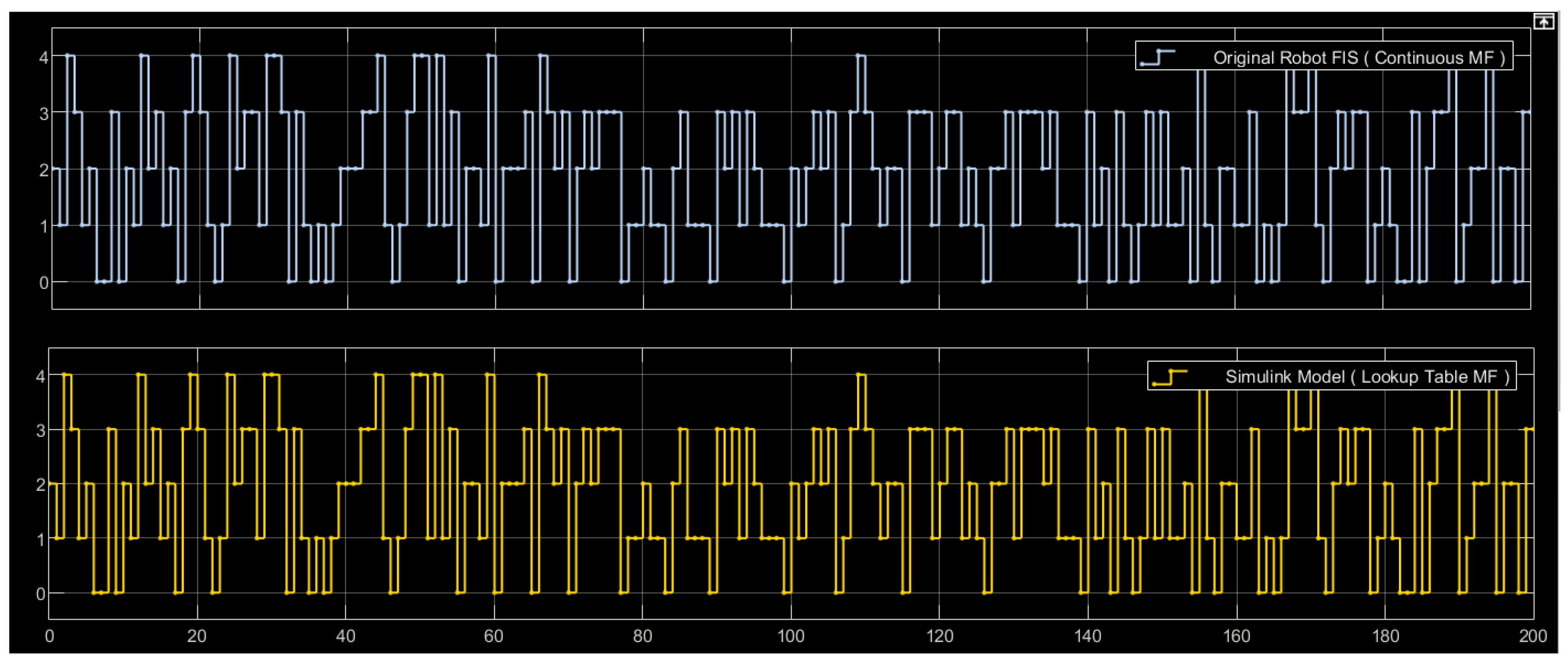
We initiated a Monte Carlo simulation involving the generation of

100, 000

random inputs to validate the functionality of the modified FIS model. This allowed us to perform a comparative analysis between the outputs of the hardware model, where the membership functions are implemented using LUT, and the original FIS software implementation, characterized by continuous membership functions. Remarkably, throughout this experiment, the outputs of both models remained identical for all input scenarios. Figure 10 illustrates the output graphs of both models using a subset of 200 randomly selected input samples. In this context, both graphs are identical, demonstrating consistent FIS output across two implementations, the first one utilizes continuous function membership functions, and the other employs their discrete counterparts.

5.4. Discussion

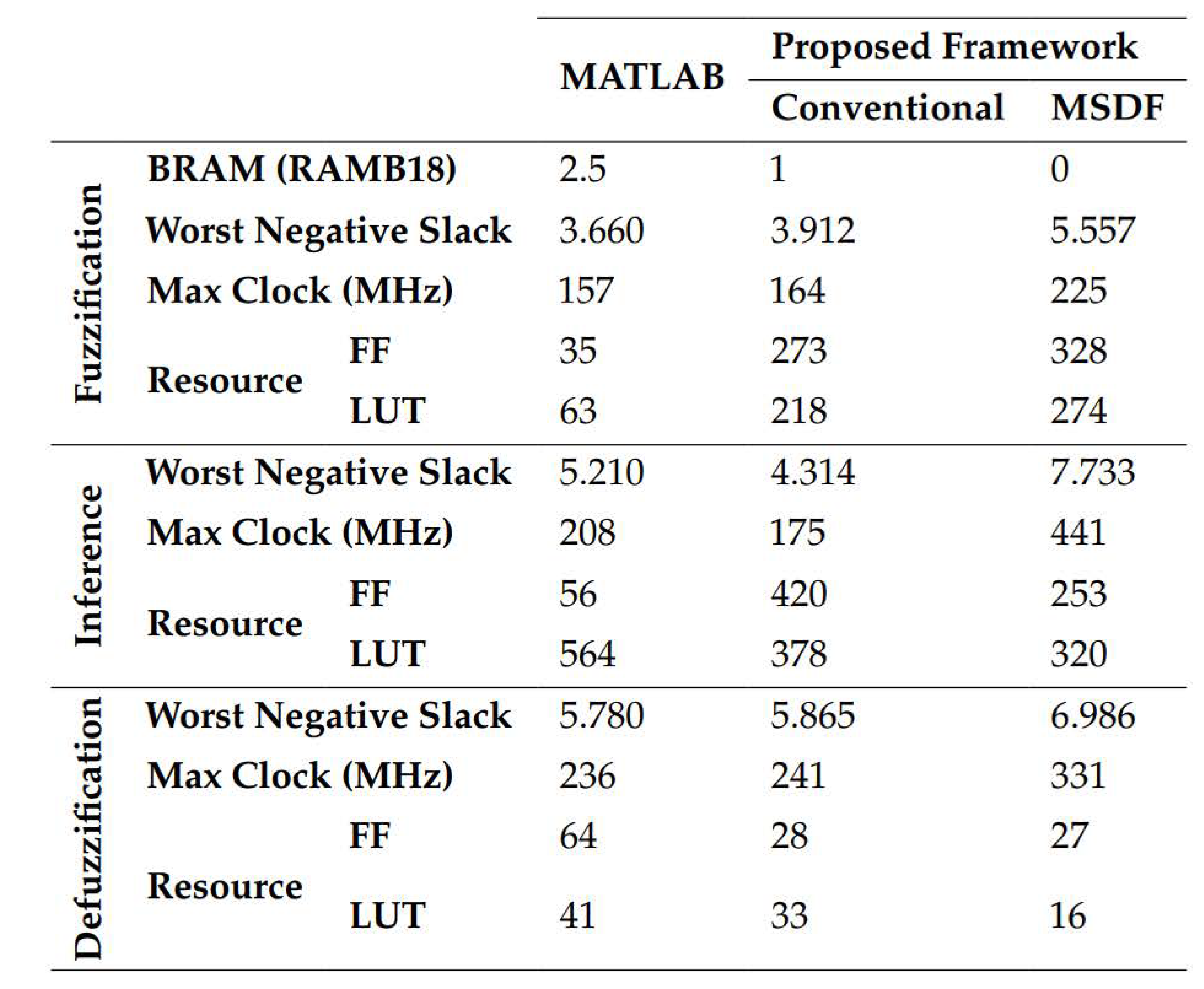
In this section, our initial focus is on the discrete examination of the outcomes of the primary subsystems within the fuzzy inference system. Table 4 presents the distinct results associated with the Fuzzification, Inference, and Defuzzification subsystems.

In the Fuzzification subsystem, the WNS in both the conventional and MSDF-based designs of the proposed framework demonstrates substantial improvements. Specifically, the WNS values in these configurations are

7 %

and

52 %

superior, respectively, in comparison to the MATLAB design. Moreover, the maximum clock frequencies in both the conventional and MSDF-based designs within the proposed framework exhibit notable advancements. Specifically, these clock frequencies demonstrate improvements of

4 %

and

43 %

, respectively, in contrast to the corresponding MATLAB design. In terms of resource consumption, the designs within the proposed framework make efficient use of Flip Flops and LUTs, resulting in a net gain in performance when compared to the corresponding MATLAB design, which consumes

2.5

blocks of RAM. Furthermore, in the MSDF-based design mode, the proposed framework excels in inferring LUTs and Flip-Flops, outperforming the conventional design mode, which necessitates the inclusion of an entire Block RAM (RAMB18) for LUT formation. As a result, the collective utilization of LUTs and Flip Flops in the MSDF-based design remains lower than that in the conventional design, all while preserving the advantageous reduction of block RAM usage. This optimized resource allocation highlights the effectiveness of the proposed framework in achieving enhanced efficiency and performance in the Fuzzification subsystem.

Within the Inference subsystem, the WNS in the conventional design configuration lags by

17 %

, while the MSDF-based design excels by

48 %

when compared to the MATLAB design. Also, the maximum clock frequencies in the conventional design exhibit a

16 %

decrement in performance, whereas the MSDF-based design showcases a noteworthy

112 %

improvement in comparison to the MATLAB design. Regarding the allocation of essential resources, it is noteworthy that in the proposed framework designs, there is an increased count of inferred Flip-Flops, while the quantity of LUTs is reduced when compared to the MATLAB design. Additionally, the count of both FFs and LUTs in the MSDF-based design is notably diminished in contrast to the conventional design. These outcomes unequivocally demonstrate the superior performance of the MSDF-based design.

In the defuzzification subsystem, a comprehensive evaluation across all compared criteria affirms that our conventional design surpasses the hardware generated by MATLAB, and notably, the MSDF-based design excels over both of these alternatives.

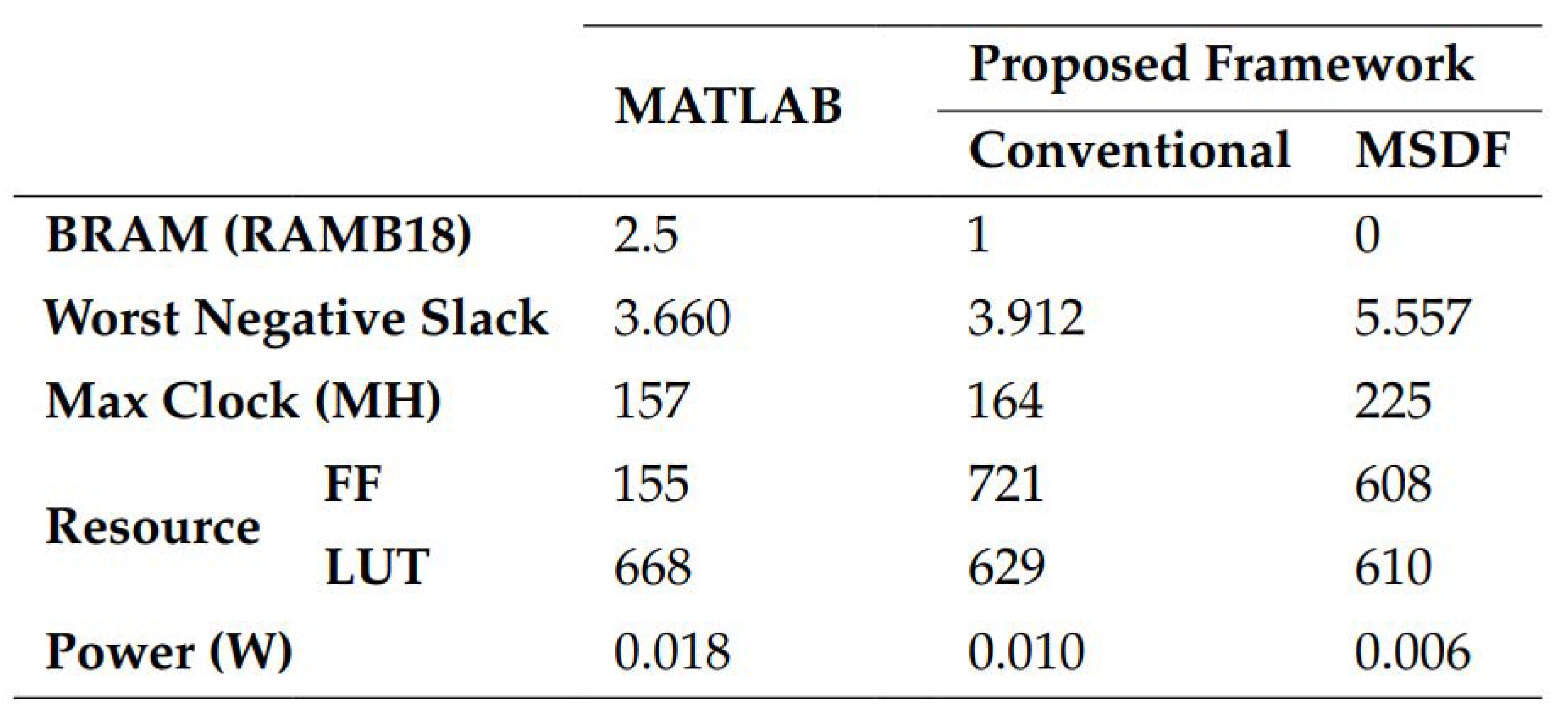
Table 5 provides a comprehensive overview of the comparative assessment between the fuzzy inference system hardware designed by MATLAB and the framework proposed in this study. It demonstrates a higher clock speed and lower WNS path as well as reduced resource and block RAM consumption for the proposed framework. It is worth noting that the integration of all three FIS subsystems in a cohesive manner holds the potential for enhanced results. This integration not only offers greater optimization opportunities but also ensures the accurate interpretation of interconnections within the subsystems categorized as I/O, leading to improved outcomes. Furthermore, when compared to MATLAB HDL Coder, our conventional and MSDF approaches exhibit a substantial reduction in power consumption, with figures of

44 %

and

67 %

, respectively. These results underscore the remarkable advancements in power efficiency achieved through our design methodology.

6. Conclusions and Future Work

The proposed method exhibited exceptional compatibility with MSDF-based sensors, facilitating the execution of fuzzification, inference, and defuzzification processes on serially arriving data bits. Leveraging the MSDF approach enabled early decision-making for Max and Min operations, leading to improved performance and decreased power consumption by eliminating unnecessary computations at an early stage. Additionally, the adoption of serial computation resulted in reduced area requirements and a diminished memory footprint, further enhancing the overall efficiency of the approach. To assess the efficacy of the proposed framework, an FIS was implemented for autonomous mobile robot navigation in unknown environments. The synthesis results provided compelling evidence of the superior performance of the design suggested by our framework with

67 %

improvement in power consumption, compared with the hardware generated by MATLAB HDL coder. Also, this research showcased the potential of leveraging MSDF computing for achieving low-power FIS hardware in embedded systems. Future work could explore further optimizations and applications of the proposed approach in different domains and scenarios.

References

Gholamizadeh, K.; Zarei, E.; Omidvar, M.; Yazdi, M. Fuzzy sets theory and human reliability: Review, applications, and contributions. Linguist. Methods Under Fuzzy Inf. Syst. Saf. Reliab. Anal.
Ma, Z.M.; Yan, L. A Literature Overview of Fuzzy Conceptual Data Modeling. J. Inf. Sci. Eng. 2010, 26, 427–441. [Google Scholar]
Zhang, Y.; Wang, G.; Zhou, T.; Huang, X.; Lam, S.; Sheng, J.; Choi, K.S.; Cai, J.; Ding, W. Takagi-Sugeno-Kang fuzzy system fusion: A survey at hierarchical, wide and stacked levels. Inf. Fusion 2024, 101, 101977. [Google Scholar] [CrossRef]
Ejegwa, P.A.; Ahemen, S. Enhanced intuitionistic fuzzy similarity operators with applications in emergency management and pattern recognition. Granul. Comput. 2023, 8, 361–372. [Google Scholar] [CrossRef]
Sharma, R.P.; Dharavath, R.; Edla, D.R. IoFT-FIS: Internet of farm things based prediction for crop pest infestation using optimized fuzzy inference system. Internet Things 2023, 21, 100658. [Google Scholar] [CrossRef]
Özkan, B.; Dengiz, O.; Turan, İ.D. Site suitability analysis for potential agricultural land with spatial fuzzy multi-criteria decision analysis in regional scale under semi-arid terrestrial ecosystem. Sci. Rep. 2020, 10, 22074. [Google Scholar] [CrossRef] [PubMed]
Ragab, M.; Ashary, E.B.; Aljedaibi, W.H.; Alzahrani, I.R.; Kumar, A.; Gupta, D.; Mansour, R.F. A novel metaheuristics with adaptive neuro-fuzzy inference system for decision making on autonomous unmanned aerial vehicle systems. ISA Trans. 2023, 132, 16–23. [Google Scholar] [CrossRef] [PubMed]
Karatop, B.; Taşkan, B.; Adar, E.; Kubat, C. Decision analysis related to the renewable energy investments in Turkey based on a Fuzzy AHP-EDAS-Fuzzy FMEA approach. Comput. Ind. Eng. 2021, 151, 106958. [Google Scholar] [CrossRef]
Liu, S.; Huang, S.; Xu, X.; Lloret, J.; Muhammad, K. Efficient Visual Tracking Based on Fuzzy Inference for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2023. [Google Scholar] [CrossRef]
Teferra, D.M.; Ngoo, L.M.; Nyakoe, G.N. Fuzzy-based prediction of solar PV and wind power generation for microgrid modeling using particle swarm optimization. Heliyon, 1280. [Google Scholar]
Guzman-Urbina, A.; Ouchi, K.; Ohno, H.; Fukushima, Y. FIEMA, a system of fuzzy inference and emission analytics for sustainability-oriented chemical process design. Appl. Soft Comput. 2022, 126, 109295. [Google Scholar] [CrossRef]
Rodriguez, R.; Trovão, J.P.F.; Solano, J. Fuzzy logic-model predictive control energy management strategy for a dual-mode locomotive. Energy Convers. Manag. 2022, 253, 115111. [Google Scholar] [CrossRef]
Moghari, S.; Ghorani, M. A symbiosis between cellular automata and dynamic weighted multigraph with application on virus spread modeling. Chaos Solitons Fractals 2022, 155, 111660. [Google Scholar] [CrossRef] [PubMed]
Yolcu, O.C.; Yolcu, U. A novel intuitionistic fuzzy time series prediction model with cascaded structure for financial time series. Expert Syst. Appl. 2023, 215, 119336. [Google Scholar] [CrossRef]
Awasthi, K.; Awasthi, S. Green Computing: A Sustainable and Eco-friendly Approach for Conservation of Energy (A Contribution to Save Environment). In Sustainable Computing: Transforming Industry 4.0 to Society 5.0; Springer, 2023; pp. 319–333.
Selvachandran, G.; Quek, S.G.; Lan, L.T.H.; Giang, N.L.; Ding, W.; Abdel-Basset, M.; De Albuquerque, V.H.C.; others. A new design of mamdani complex fuzzy inference system for multiattribute decision making problems. IEEE Trans. Fuzzy Syst. 2019, 29, 716–730. [Google Scholar] [CrossRef]
eddine LACHOURI, C.; Mansouri, K.; Belmeguenai, A.; mourad LAFIFI, M. FPGA Implementation of adaptive neuro-fuzzy inference systems controller for greenhouse climate. Int. J. Adv. Comput. Sci. Appl. 2016, 7. [Google Scholar]
Indira, P.B.; Krishna, R.D. Optimized adaptive neuro fuzzy inference system (OANFIS) based EEG signal analysis for seizure recognition on FPGA. Biomed. Signal Process. Control 2021, 66, 102484. [Google Scholar] [CrossRef]
Mirhosseini, M.; Fazlali, M.; Fallah, M.K.; Lee, J.A. A fast MILP solver for high-level synthesis based on heuristic model reduction and enhanced branch and bound algorithm. J. Supercomput.
Zacharopoulos, G.; Ejjeh, A.; Jing, Y.; Yang, E.Y.; Jia, T.; Brumar, I.; Intan, J.; Huzaifa, M.; Adve, S.; Adve, V.; others. Trireme: Exploration of Hierarchical Multi-Level Parallelism for Hardware Acceleration. ACM Trans. Embed. Comput. Syst. 2023. [Google Scholar] [CrossRef]
Givaki, K.; Khonsari, A.; Gholamrezaei, M.; Gorgin, S.; Najafi, M.H. A generalized residue number system design approach for ultra-low power arithmetic circuits based on deterministic bit-streams. IEEE Trans. -Comput.-Aided Des. Integr. Circuits Syst.
Leitersdorf, O.; Leitersdorf, D.; Gal, J.; Dahan, M.; Ronen, R.; Kvatinsky, S. AritPIM: High-throughput in-memory arithmetic. IEEE Trans. Emerg. Top. Comput. 2023. [Google Scholar] [CrossRef]
Mohamed, N.A.; Cavallaro, J.R. A Unified Parallel CORDIC-based Hardware Architecture for LSTM Network Acceleration. IEEE Trans. Comput. 2023. [Google Scholar] [CrossRef]
Gorgin, S.; Gholamrezaei, M.; Javaheri, D.; Lee, J.A. kNN-MSDF: A Hardware Accelerator for k-Nearest Neighbors Using Most Significant Digit First Computation. 2022 IEEE 35th International System-on-Chip Conference (SOCC). IEEE, 2022, pp. 1–6.
Gorgin, S.; Gholamrezaei, M.; Javaheri, D.; Lee, J.A. An Energy-Efficient K-means Clustering FPGA Accelerator via Most-Significant Digit First Arithmetic. 2022 International Conference on Field-Programmable Technology (ICFPT). IEEE, 2022, pp. 1–4.
Gorgin, S.; Gholamrezaei, M.H.; Javaheri, D.; Lee, J.A. An Efficient FPGA Implementation of k-Nearest Neighbors via Online Arithmetic. 2022 IEEE 30th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM). IEEE, 2022, pp. 1–2.
Valls, J.; Kuhlmann, M.; Parhi, K.K. Evaluation of CORDIC algorithms for FPGA design. J. VLSI Signal Process. Syst. Signal, Image Video Technol. 2002, 32, 207–222. [Google Scholar] [CrossRef]
Arifeen, T.; Gorgin, S.; Gholamrezaei, M.H.; Hassan, A.S.; Ercegovac, M.D.; Lee, J.A. Low Latency and High Throughput Pipelined Online Adder for Streaming Inner Product. J. Signal Process. Syst.
Hassan, A.S.; Arifeen, T.; Lee, J.A. Data footprint reduction in DNN inference by sensitivity-controlled approximations with online arithmetic. 2020 23rd Euromicro Conference on Digital System Design (DSD). IEEE, 2020, pp. 534–541.
Abideen, Z.U.; Perez, T.D.; Martins, M.; Pagliarini, S. A Security-aware and LUT-based CAD Flow for the Physical Synthesis of hASICs. IEEE Trans. -Comput.-Aided Des. Integr. Circuits Syst.
Nikolić, S.; Zgheib, G.; Ienne, P. Detailed Placement for Dedicated LUT-Level FPGA Interconnect. ACM Trans. Reconfigurable Technol. Syst. 2022, 15, 1–33. [Google Scholar] [CrossRef]

Figure 1. The progressive accumulation of online delay (

δ

) in chained operations.

Figure 1. The progressive accumulation of online delay (

δ

) in chained operations.

Figure 2. The proposed hardware realization framework for fuzzy inference systems.

Figure 3. A sample trapezoidal membership function and its discretized counterpart with a scale factor of S=10.

Figure 4. The FSM corresponds to

y_{1}

(the MSD of

\tilde{μ} (x)

Figure 4. The FSM corresponds to

y_{1}

(the MSD of

\tilde{μ} (x)

Figure 5. The optimized FSM corresponds to

y_{1}^{'}

Figure 5. The optimized FSM corresponds to

y_{1}^{'}

Figure 6. A simple problem with one obstacle.

Figure 7. The fuzzy membership functions for distance d.

Figure 8. The fuzzy membership functions for angle

θ

Figure 8. The fuzzy membership functions for angle

θ

Figure 9. Architecture of the fuzzy inference system.

Figure 10. Monte Carlo simulation results with

T = 200

for comparing the original robot FIS (trapezoidal membership functions) and the synthesized FIS (lookup table membership functions with a scale factor of

S = 100

Figure 10. Monte Carlo simulation results with

T = 200

for comparing the original robot FIS (trapezoidal membership functions) and the synthesized FIS (lookup table membership functions with a scale factor of

S = 100

Table 1. The LUT corresponding to Figure 3b.

x					$\tilde{μ} (x)$
X	$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	$y_{1}$	$y_{2}$	$y_{3}$	$y_{4}$	Y
0	0	0	0	0	0	0	0	0	0
1	0	0	0	1	0	0	1	0	2
2	0	0	1	0	0	0	1	1	3
3	0	0	1	1	0	1	0	1	5
4	0	1	0	0	0	1	1	1	7
5	0	1	0	1	1	0	0	0	8
6	0	1	1	0	1	0	1	0	10
7	0	1	1	1	1	0	1	0	10
8	1	0	0	0	1	0	1	0	10
9	1	0	0	1	1	0	1	0	10
10	1	0	1	0	1	0	0	0	8
11	1	0	1	1	0	1	1	1	7
12	1	1	0	0	0	1	0	1	5
13	1	1	0	1	0	0	1	1	3
14	1	1	1	0	0	0	1	0	2
15	1	1	1	1	0	0	0	0	0

Table 2. The

y_{1}

-optimized LUT corresponding to Table 1.

Table 2. The

y_{1}

-optimized LUT corresponding to Table 1.

x					$\tilde{μ} (x)$
X	$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	$y_{1}^{'}$	$y_{2}^{'}$	$y_{3}^{'}$	$y_{4}^{'}$	Y’
0	0	0	0	0	0	0	0	0	0
1	0	0	0	1	0	0	1	0	2
2	0	0	1	0	0	0	1	1	3
3	0	0	1	1	0	1	0	1	5
4	0	1	0	0	1	0	0	0	8
5	0	1	0	1	1	0	0	0	8
6	0	1	1	0	1	0	1	0	10
7	0	1	1	1	1	0	1	0	10
8	1	0	0	0	1	0	1	0	10
9	1	0	0	1	1	0	1	0	10
10	1	0	1	0	1	0	0	0	8
11	1	0	1	1	1	0	0	0	8
12	1	1	0	0	0	1	0	1	5
13	1	1	0	1	0	0	1	1	3
14	1	1	1	0	0	0	1	0	2
15	1	1	1	1	0	0	0	0	0

Table 3. The FIS inference rules.

		angle $θ$
		VS	S	M	L	VL
distance $d$	SN	0	0	1	2	3
	N	0	1	2	3	3
	M	0	1	2	3	4
	F	1	1	3	4	4
	SF	1	2	3	4	4

Table 4. Comparing hardware components designed by MATLAB versus the proposed framework.

Table 5. The overall comparison of FIS hardware designed by MATLAB versus the proposed framework.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer