1. Introduction
Several countries around the world have large territories characterized by the presence of buildings not designed according to seismic codes and therefore unsuitable to resist possible earthquakes. A crucial aspect lies therefore in the assessment of the seismic vulnerability of existing buildings which can be performed by means of detailed individual models or simplified methods at urban scale. The seismic vulnerability assessment of single buildings requires a deep knowledge of the structure and involves the construction of accurate numerical models. Since the task is very demanding, several simplified models of buildings have been analyzed in the last decades [
1,
2]. Although simplified, these approaches involve the execution of difficult calculations and therefore cannot be applied at urban scale where a great number of buildings must be analyzed and a fast, although reliable, vulnerability assessment is crucial in identifying the areas most exposed to seismic risk in which to intervene as a priority.
With this aim, many simplified methods for seismic vulnerability assessment at urban scale have been presented in the scientific literature. For example, the Rapid Visual Screening (RVS) is a qualitative estimation procedure which can be used to classify the vulnerability of the structures by means of observations made from the building exterior, without taking into consideration the building inside [
3]. This visual survey can be considered as the first step in the vulnerability assessment for determining the risk priorities for buildings before going into further details and classifying them according to their construction materials and their structural systems. Other methodologies, called vulnerability index methods (VIM), are based on the estimation of some characteristic indexes. These approaches rely on the knowledge of a large number of damages survey data and structural information in order to investigate the influence of different parameters on the seismic vulnerability of the building [
4,
5]. For instance, they have been applied to seven European cities [
6]. The macro-seismic approach combines the vulnerability index method with an analytical function which expresses the expected damage for given earthquake intensity [
7,
8,
9,
10]. Another popular method is based on the Damage Probability Matrix [
11,
12,
13], which returns an estimate of vulnerability in numeric form; in particular, it expresses the likelihood of a certain level of damage for each seismic intensity. This method provides the seismic vulnerability as an estimation of the probability of occurrence of damage in buildings in terms of the intensity of the earthquake.
Since seismic assessment at urban scale involves the use of a great number of data, many of which are repeated for similar buildings, an interesting and promising approach is nowadays based on Machine Learning Algorithms (MLA). These algorithms allow to produce reliable results through a learning process applied to opportune training datasets, then making precise predictions about new data. MLA, formerly of specific interest of computer scientist, have been largely developed in the last decades and applied to several engineering research fields. In recent years they have found a wide range of applications also in structural engineering, since they are useful in dealing with problems associated with uncertainties due to their effectiveness and robustness in dealing with noise.
Several applications of MLA to seismic vulnerability analyses at urban scale have been developed. For example, applications of an Artificial Neural Network (ANN) Model [
14] and of a SWOT-Quantitative Strategic Planning Matrix (QSPM) [
15] have been recently developed for the evaluation of seismic vulnerability in different municipalities in Iran. Other studies evaluated the seismic vulnerability of large sets of buildings in urban environments through a procedure based on the fast calculation of capacity curves of low-rise reinforced concrete buildings using neural networks [
16]. Building capacity curves for 256 reinforced concrete buildings with between 4 and 7 floors have been also obtained in [
17], where the influence of the structural parameters on the seismic performance has been quantified using a set of Artificial Neural Network algorithms. In [
18] the assessment of the vulnerability of urban blocks to earthquakes using an artificial neural network—multi-layer perceptron (ANN-MLP) has been presented. To train the neural network and compute earthquake vulnerability maps, a combined Multi-Criteria Decision Analysis (MCDA) process has been adopted. A combination of artificial neural network-based predictive models and decision-making methods based on a hierarchy process with the aim of improving the earthquake risk assessment has been presented in [
19,
20] and applied to a city in Indonesia. They identified the major indicators needed to create reliable vulnerability maps in seismic risk assessment. In particular, in [
20] artificial neural networks, have been also used to train and optimize a database of 145 damaged buildings from the Haiti earthquake. The comparison between the performances of artificial neural networks and traditional regression models in the evaluation of the seismic vulnerability of a large set of buildings have been presented in [
21]. A hybrid approach of machine learning (random forest) and hierarchical analysis (Saaty matrix) has been used for seismic risk assessment of the peruvian city of Pisco [
22] and a double-entry table relating hazard and vulnerability levels has been presented. Frequency ratio (FR), decision tree (DT), and random forest (RF) methods have been also applied to seismic data for Gyeongju, South Korea, in [
23].
In this paper our main goal is to calculate, through an opportune combination of a simple fully connected ANN and a Random Forest Classifier, a seismic vulnerability score for the buildings in a specific urban area based on a dataset reporting the damages produced by multiple seismic events. In particular, the region around the city of L’Aquila, in Italy, has been considered, in relation to the devastating sequence of earthquakes occurred in April 2009. Our approach can be considered as an inverse problem, according to which the a-posteriori vulnerability of the buildings is inferred from the observed damages. Several building’s features (such as for example date of construction, construction material, number of floors, floor area) have been identified and a thorough analysis of the contribution of each feature to overall vulnerability is performed.
A further comparison with another vulnerability score, built according with the main construction features of the buildings available in the chosen dataset, and thus denoted as a-priori, will be performed. From the comparison between these two scores, we can deduce some general trends which allow to improve and enrich the estimate of the seismic vulnerability of buildings at urban scale. As a whole, the proposed procedure can represent a flexible, feature-focused tool applicable to seismic vulnerability assessment of different urbanized territories and could be extremely useful in planning appropriate measures for risk management, in particular if combined with further information regarding road infrastructures, when available.
2. Buildings Dataset and a-priori seismic vulnerability estimation
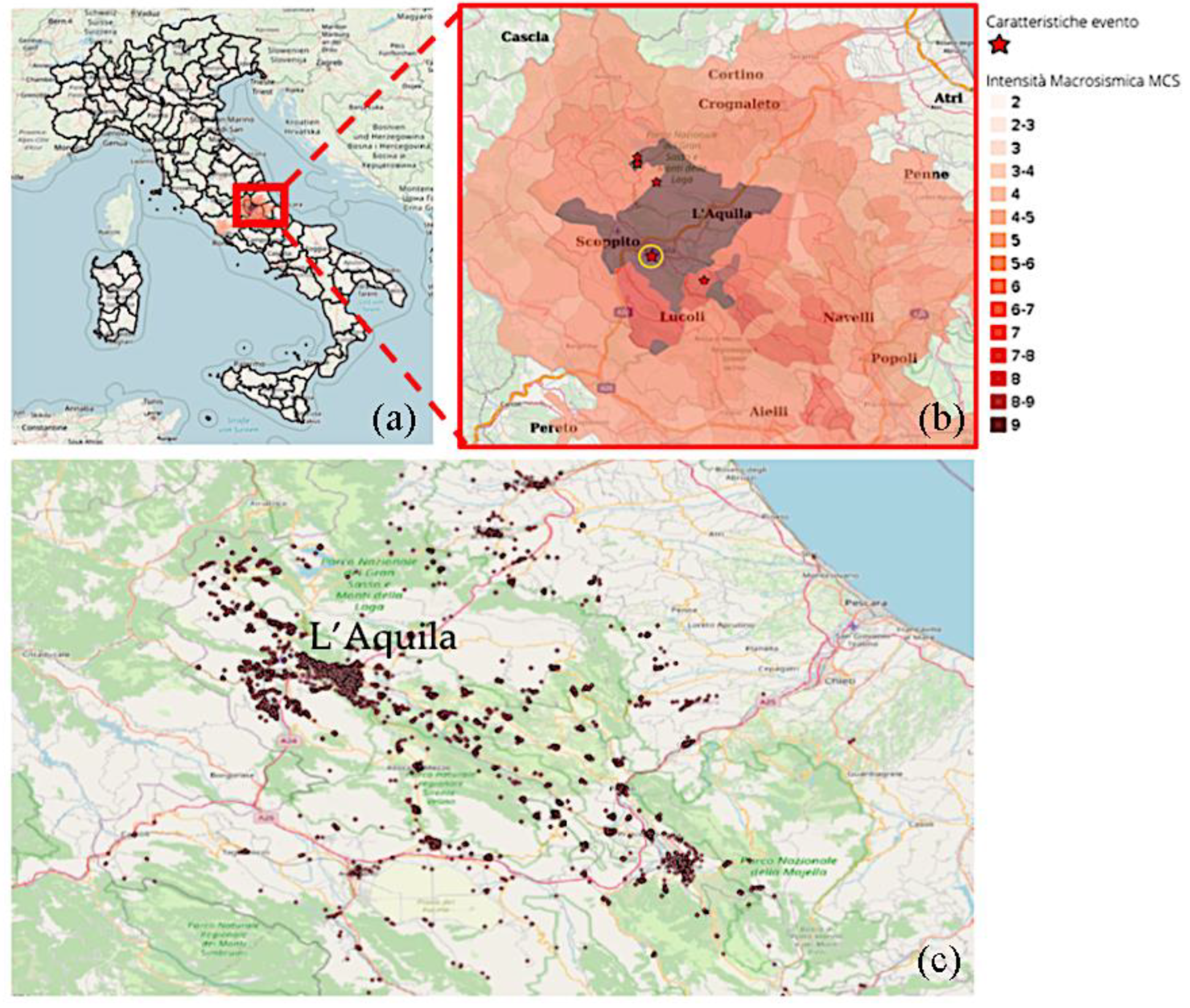
In 2009 a long sequence of seismic events occurred in the Abruzzo region of central Italy (see panels (a) and (b) of
Figure 1), attributed to its complex tectonic setting. In fact, this region is characterized by the convergence of the African and Eurasian plates that, accompanied by the extension of the Apennine Mountain range, generates a significant seismic activity. The considered sequence started on December 2008 and culminated on April 6
th, 2009, with a main shock of magnitude Mw 6.3 registered at 3:32 AM local time and followed by several aftershocks. This earthquake had an epicenter located near the city of L’Aquila, the capital of the Abruzzo region, and occurred at a shallow depth of approximately 8.8 kilometers, a detail which contributed to the significant damage experienced in the region.
In our analysis we utilize the extensive Da.D.O. dataset [
24], which includes a comprehensive record of 58,140 buildings in the proximity of L’Aquila. This dataset encompasses
pre-event characteristics such as age, construction material, and geometry of the buildings, as well as
post-event damage assessments following a series of the five most significant earthquakes, each with a magnitude greater than 5 ML, that occurred between April 6th and 9th, 2009. The epicenters of these earthquakes are represented as red star symbols in panel (b) of Figure 1, while the main event of magnitude Mw 6.3 is also marked with a circle. The geographical positions of the buildings present in the dataset are depicted in panel (c) of the same figure, highlighting their distribution in the affected area. Additionally, the data have been georeferenced and converted into shapefile format for effective analyses.
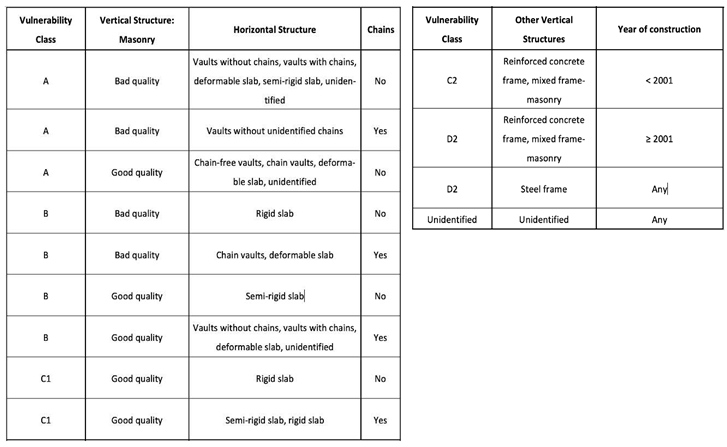
Based on the information reported on Da.D.O. dataset, an
a-priori vulnerability score for each building in the considered area can be calculated based on the appropriate structural features, as shown in
Table 1. This is a categorical score ranging from the maximum level A (highest vulnerability) to the minimum level D2 (lowest vulnerability). This
a-priori score will be later compared with an
a-posteriori one, evaluated on the basis of the observed damages as explained in the next sections.
3. Machine learning models and Dataset pre-processing
The aim of our work is to use the information reported on the dataset for assessing the correlations of building features with damage levels and to propose a new vulnerability score for each building evaluated a-posteriori on the basis of the observed damage. In this respect, we approach the problem of seismic vulnerability assessment as a multi-class classification task which employs machine learning algorithms.
3.1. ANN and Random Forest algorithms
We have chosen to focus our study on a classification approach involving two machine learning models: a Random Forest Classifier (RFC) and a custom-designed Artificial Neural Network (ANN).
Random Forest Classifier (RFC): this model is an ensemble learning technique, well-regarded for its robustness and accuracy in various applications. The main key strength of Random Forest algorithms lies in their ability to prevent overfitting, a common challenge in machine learning models. This is achieved through its ensemble nature (see Figure 2), where multiple trees, each trained on subsets of the data with randomized feature selection, contribute to the final classification thus ensuring a very reliable performance.
Artificial Neural Network (ANN): This is a computational model inspired by the way biological neural networks in the human brain process information. It consists of interconnected layers of nodes, or neurons, where each node is a simple processor. The input data is fed into the network and passes through multiple layers of these neurons, each transforming the input in a specific way. The power of ANNs comes from their ability to learn complex patterns and relationships in data by adjusting the weights of connections between neurons through a process known as backpropagation. Our custom ANN has been tailored to best capture the underlying relations encoded in the data (see Figure 3).
Figure 3.
Architecture of the ANN used in our work (numbers in <brackets> record the size of each component): the input is a vector of 81 values encoding the position and features of buildings. This vector is normalized and passed to a series of General Matrix Multiplications (Gemm). We use the Relu activation function to introduce non-linearity in the model. The last layer is a Softmax function that normalizes the output to represent a probability distribution across the 4 damage classes.
Figure 3.
Architecture of the ANN used in our work (numbers in <brackets> record the size of each component): the input is a vector of 81 values encoding the position and features of buildings. This vector is normalized and passed to a series of General Matrix Multiplications (Gemm). We use the Relu activation function to introduce non-linearity in the model. The last layer is a Softmax function that normalizes the output to represent a probability distribution across the 4 damage classes.
We also employed the One-hot Encoding technique for representing categorical data within these machine learning models. This method converts categorical variables into a form that can be provided to ML algorithms to do a better job in prediction. It involves expanding each categorical class into a new binary column, which increases the efficiency of the process. This step is critical in ensuring that categorical data, such as building types or construction materials, are effectively incorporated into our vulnerability assessment models.
3.2. Data Pre-Processing
In order to ensure the compatibility of data with the analysis pipeline, we have to opportunely pre-process them. Beside usual normalization and data cleaning, the main steps are the following two:
Since the original dataset employs a highly detailed damage categorization some simplification is necessary. First of all, we will only refer to damage occurred in vertical structures. The level of damage is originally classified according to what is proposed in the European Macroseismic Scale EMS-98, namely: D1 (light damage), D2 (moderate damage), D3 (extensive damage), D4 (total damage), and D5 (collapse). The zero damage class D0 is also added to the previous ones for completeness. Since in the database damages are reported for different portions of each building, the different combinations results in a complex matrix of 26 distinct damage classes with non-homogeneous number of elements. To circumvent this issue, we condensed these classes assuming for each building the highest level of damage sustained by any of its portions. Finally, merging the 3 highest damage classes (D3, D4, D5) into a macro class representing general ‘high damage’ reduces the classification to four ordinal damage categories, ranging from D0 to D3. Alternative strategies, like assigning a numerical score to each of the 26 categories for regression analysis or experimenting with different class counts, have been explored but did not enhance the model’s performance. This optimized approach is both efficient and practical, ensuring a more balanced and manageable dataset for analysis.
Then, specific columns from the original dataset are selected for analysis, including geographic, structural, and damage-related information. The considered structural characteristics of the buildings concern: horizontal and vertical structures, floors, stairs, roofing, infils. Our goal is to understand how different features influence various models’ decisions, particularly in classifying various levels of damage, in order to see if we can streamline these features.
To select the top predictive features, preliminary models were trained, utilizing the Shapley Additive exPlanations (SHAP) Model for both neural network and random forest . This model, initially introduced by Lloyd Shapley [
25], employs
game theory to explain the outputs of machine learning models. The core idea of SHAP is based on Shapley values which calculate the contribution of each subset of features (from a total of ‘m’ features) to the model’s predictions [
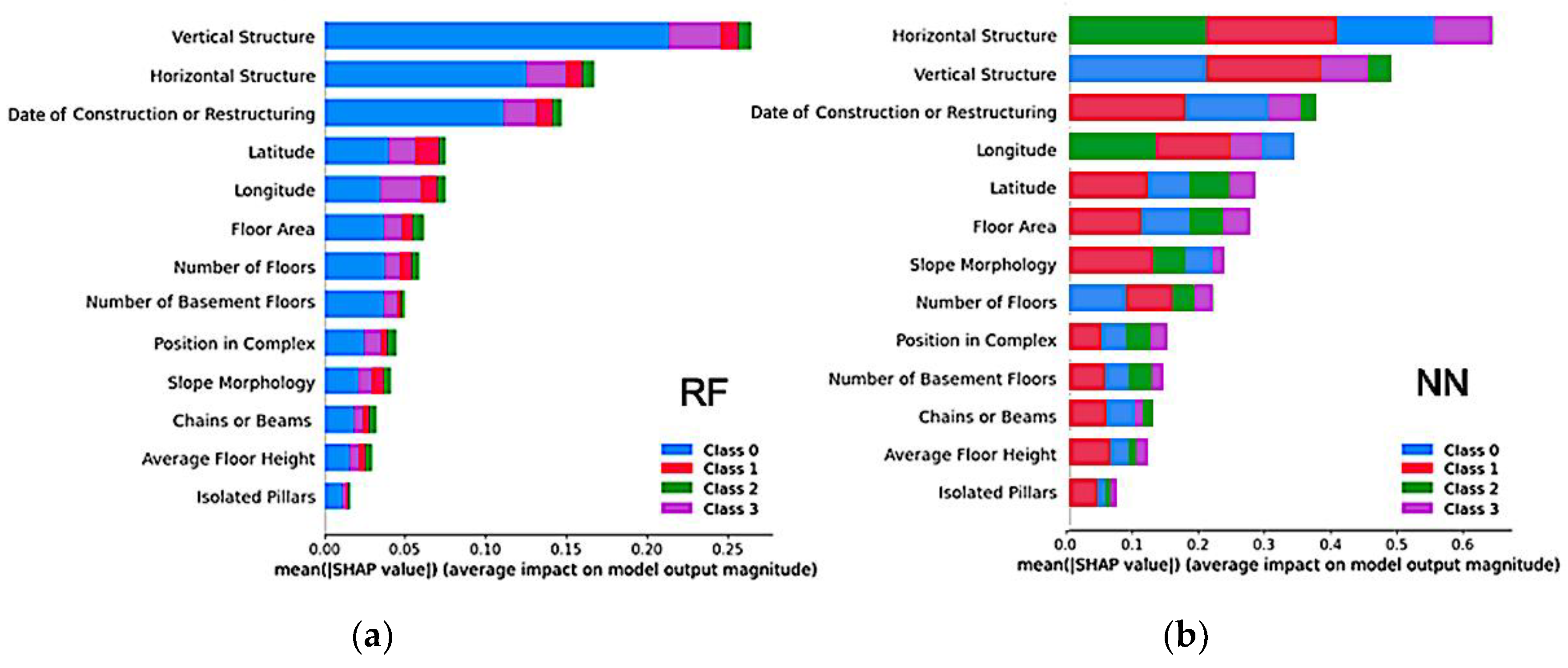
26]. Specifically, the impact of the ‘i-th’ feature is determined by comparing the predictions of the original model with those of a model trained without the ‘i-th’ feature. Since removing a feature can also affect others, this comparison must be done for every possible subset of features excluding the ‘i-th’ one. The Shapley value is then the average of these comparison scores. The output of this process is the bar plot shown in Figure 4 where the overall impact of each feature on the prediction task is split into colors representing the contribution to each damage class in the dataset. Thus SHAP was used to gain insight into which features are linked with specific damage levels, according to our data dataset and models.
Figure 4.
Impact of input features to the output of the proposed models, (a) random forest (RF) and (b) neural network (NN), expressed by the mean of their Shap values. The output classes are reported in the legend from the one associated with the lower damage level (D0) to that associated with the highest one (D3). For each row (feature) in the bar graph, the classes are ordered from the one which, overall, has been mostly predicted from the model to the one which has been predicted the least amount of time.
Figure 4.
Impact of input features to the output of the proposed models, (a) random forest (RF) and (b) neural network (NN), expressed by the mean of their Shap values. The output classes are reported in the legend from the one associated with the lower damage level (D0) to that associated with the highest one (D3). For each row (feature) in the bar graph, the classes are ordered from the one which, overall, has been mostly predicted from the model to the one which has been predicted the least amount of time.
From these graphs, it’s evident that the random forest model tends to predict a lower level of damage compared to the neural network. Despite some differences in the importance ranking of features, which is expected due to the distinct nature of the two models, the top six influential features are the same for both. These significant features are mainly structural, like the type of vertical and horizontal structures and the construction year, aligning with the predefined vulnerability classes. Contrarily, features like “Chains or Beams,” “Average Floor Height,” and “Isolated Pillars,” though part of the predefined vulnerability classes, are not influential in our models.
These three less influential features are consistent across both models, allowing us to reduce the total number of input parameters from 13 to 10. Further reduction to 8 is possible by excluding building location (latitude and longitude) from the vulnerability assessment.
4. A-posteriori seismic vulnerability estimation and numerical results
As already anticipated, the core of our analysis is the evaluation, on the basis of the observed damage levels, of an a-posteriori vulnerability score for each feature present in the dataset, and by extension, for each building. This score is derived from the neural network and random forest models, with an average over the two models’ results taken to mitigate model-specific biases.
The initial task simply involves training these models to predict the damage based on the available dataset information, dividing the data into training and validation sets, and reporting the performance of both models on the validation set (20% of the data).
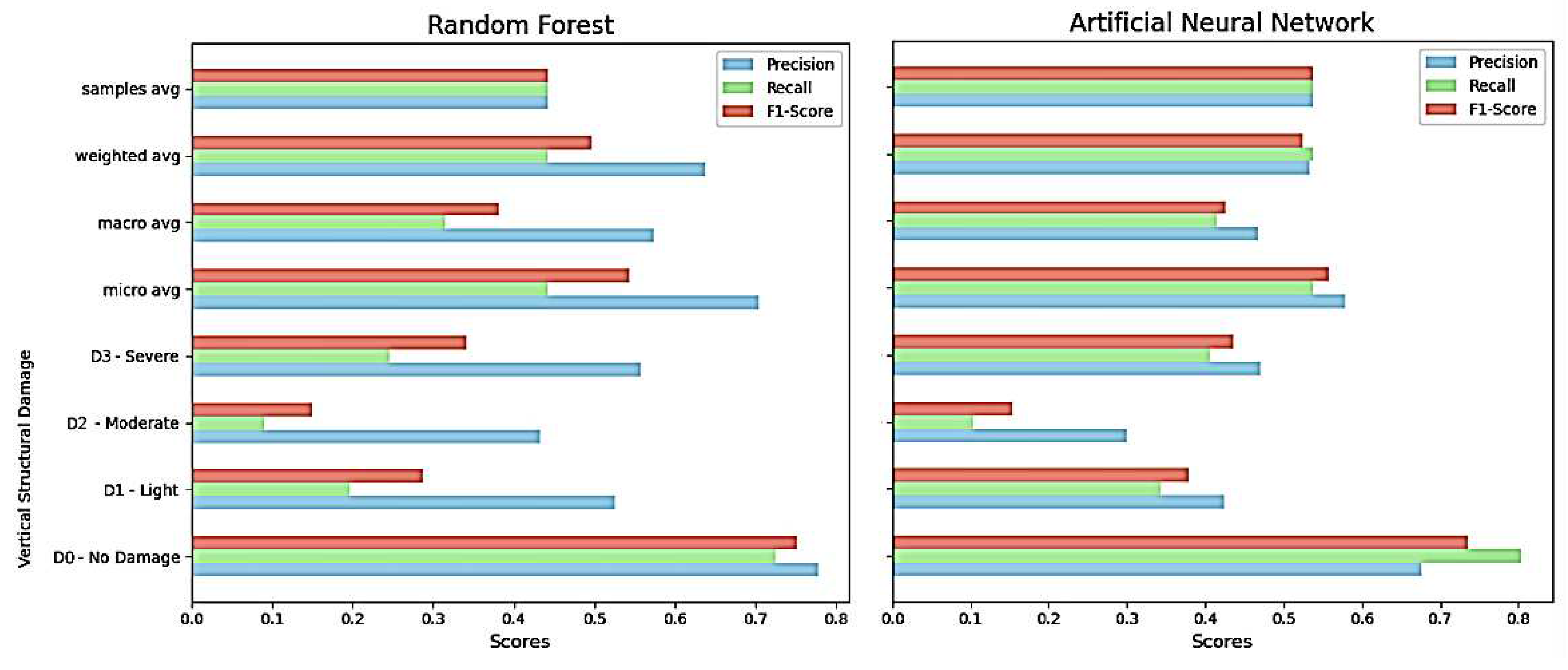
The results reported in Figure 5 show the performance of both models when tested on the validation dataset, that is, on new data the models have not seen during training. One can see that the ANN achieves higher precision and recall on all classes, being especially capable of identifying the highest damage class (D3 – Severe Damage) when compared to the Random Forest.
The second step is dedicated to evaluating the predictive power of our models and establishing the advantages of our vulnerability scoring method. In particular, we introduce an innovative technique to derive an a-posteriori vulnerability score for each structural feature of the buildings in our dataset. In the following we show how it works:
Figure 5.
Performances on validation data: we evaluate the standard metrics of precision, recall and their geometric average, usually named F1 score; precision evaluates the percentage of true positives in classification, while recall is the percentage of buildings of any given class that were identified as such. We evaluate performance on each class and report various weighted averages.
Figure 5.
Performances on validation data: we evaluate the standard metrics of precision, recall and their geometric average, usually named F1 score; precision evaluates the percentage of true positives in classification, while recall is the percentage of buildings of any given class that were identified as such. We evaluate performance on each class and report various weighted averages.
Creation of Dummy Buildings: these are not real buildings, but virtual ones created only for the analysis. Each dummy building mirrors the actual buildings in all respects except for one chosen feature, which is held constant across the entire set. For instance, we might simulate a group of buildings all having exactly two floors, regardless of their original design.
Model Predictions: we then input these dummy buildings into our pre-trained machine learning models—the Neural Network and the Random Forest. The models assess each building and output a damage prediction, treating the fixed feature as a variable of interest.
A-posteriori Vulnerability Score Derivation: by analyzing the predicted damage across all dummy buildings with the fixed feature, we calculate an average predicted damage value. This average becomes a numerical representation—a score—of the vulnerability contributed by that specific feature (e.g., having two floors).
Comprehensive Feature Analysis: this procedure is methodically applied to each categorical feature within our dataset. As a result, we establish a continuous a-posteriori vulnerability score for every characteristic examined.
Score Averaging for Robustness: to ensure our findings are not skewed by the idiosyncrasies of a single model, we further average the results of the a-posteriori vulnerability scores obtained with both the Neural Network and the Random Forest models. This step enhances the reliability of our results, yielding a more balanced and comprehensive a-posteriori vulnerability score for each building feature.
By systematically applying this method, we not only assign a quantifiable score to the elements that contribute to building vulnerability but also provide a scalable approach to assess any number of features.
4.1. Demonstrating Spatial Independence in Seismic Vulnerability Prediction
As first application we show that this method can be extended to continuous input features, such as building coordinates, by ‘placing’ dummy buildings across a virtual geographical grid and evaluating their average damage for each location, thus interpolating a continuous vulnerability map that highlights the impact of the seismic events within the urban area. The core of this methodology lies in the model's capacity to differentiate between the inherent vulnerability of individual buildings and the spatial dependency typically associated with seismic risk.
One possible approach is centered on training the models without giving as input any information about the location of earthquake epicenters. This method is strategically designed to test the models’ ability in identifying areas of high vulnerability without prior knowledge of the location of the epicenters. Successfully discerning such patterns solely from the spatial distribution of building damages would significantly affirm the models’ capability to intuitively understand and interpret the underlying seismic phenomena.
Another approach exploits the distance of each building from the five main earthquake epicenters, thus providing a more comprehensive analysis. By correlating the observed damages with the buildings’ proximity to the epicenters, this approach enhances the accuracy of our vulnerability assessment and validates the findings of the first approach, establishing a more robust and reliable analysis framework.
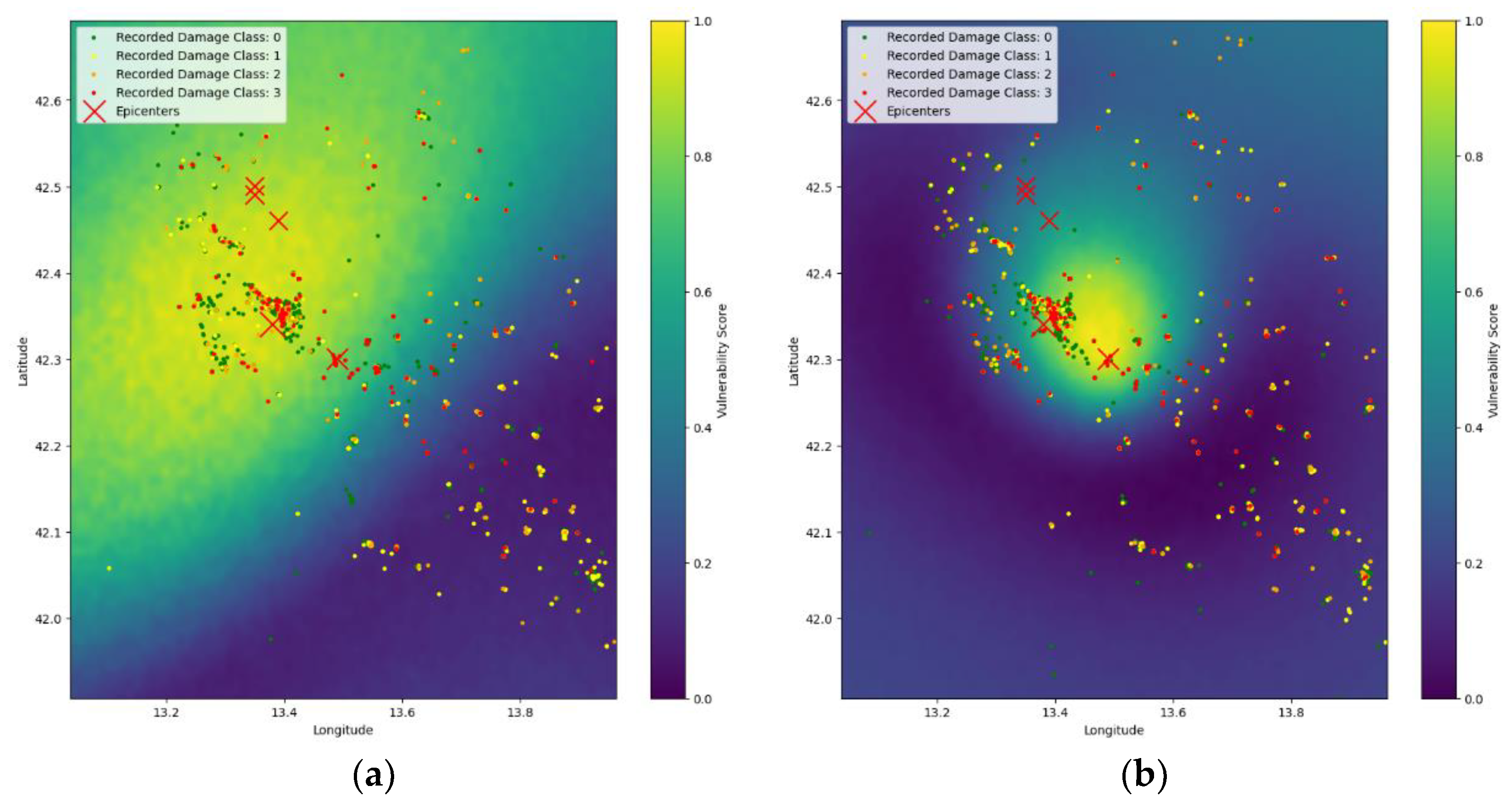
A comparison between the two approaches is shown in Figure 6.
In Figure 6 (a), obtained using a Neural Network which operates without any information about the location of epicenters, we show how well our model autonomously clearly identifies as zones of high vulnerability those close to the epicenters.
Figure 6.
(a): neural network's independent identification of high vulnerability zones without earthquake epicenter data, demonstrating the model's capability to discern seismic risk using resulting damage data. (b): epicenter-aware model's detailed vulnerability landscape, emphasizing its ability to enhance prediction accuracy by incorporating distances to major earthquake epicenters. See text for further details.
Figure 6.
(a): neural network's independent identification of high vulnerability zones without earthquake epicenter data, demonstrating the model's capability to discern seismic risk using resulting damage data. (b): epicenter-aware model's detailed vulnerability landscape, emphasizing its ability to enhance prediction accuracy by incorporating distances to major earthquake epicenters. See text for further details.
This capability is critical, since it confirms that the model is able to use geographic coordinates as a bias to discern risk based on structural attributes only, regardless of the spatial clustering of seismic events.
The second image, reported in Figure 6 (b) and interpolated by an epicenter-aware model, exploits the distance from major earthquake epicenters to enhance prediction accuracy and affords a more detailed vulnerability landscape. The evident correspondence between plots (a) and (b) confirms the robustness of our methodology, ensuring that the model's predictions are not confounded by the proximity to seismic events but are instead a true reflection of the buildings' vulnerability.
4.2. Feature analysis and a-posteriori vulnerability score
By leveraging the model’s ability to separate spatial dependencies from building vulnerability, we can now finally evaluate a new continuous vulnerability score for each building which does not depend on its position with respect to the epicenters but exploits the information about observed damages. This point is critical because it allows such a-posteriori vulnerability score to be potentially useful outside of the location and the events considered in the present study.
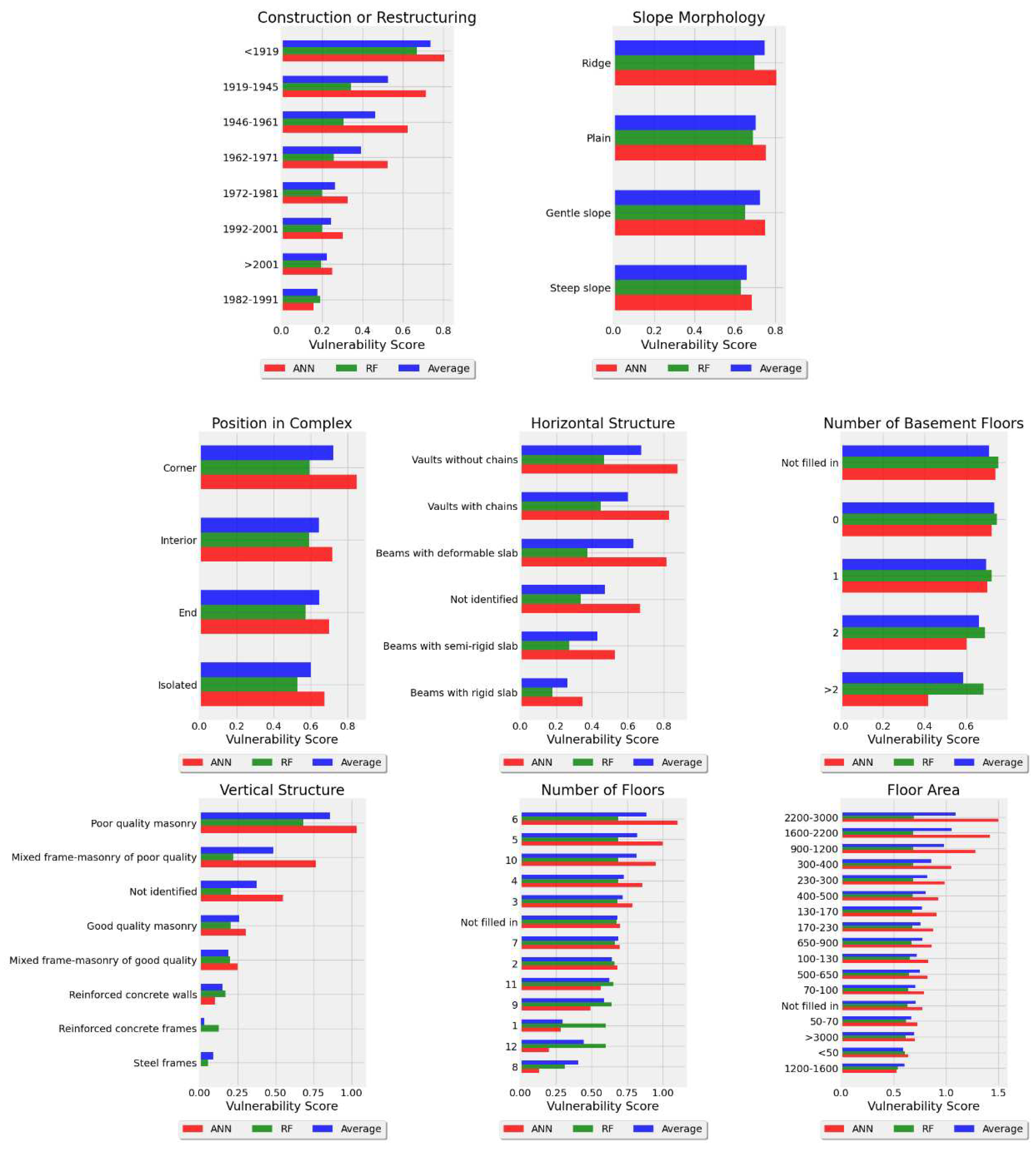
As already explained, our approach consists in using virtual (dummy) buildings in order to to extrapolate the impact of each feature for the prediction of damage. We do this by focusing on one feature at a time and averaging the prediction over a large sample of different buildings with different characteristics and positions, but with the same chosen feature. Figure 7 provides a detailed view of the a-posteriori vulnerability scores for each feature calculated by both the random forest (green bars) and the neural network (red bars) algorithms, alongside their average (blue bars).
This analysis is instrumental in isolating the contribution of individual building attributes—ranging from year of construction to employed materials—towards the overall vulnerability. By comparing the scores between models, we can evaluate the consistency of our predictive features, ensuring that our vulnerability assessment is both accurate and reliable.
Figure 7.
A-posteriori Vulnerability scores for the 8 considered building features, calculated by both random forest (RF, green bars) and artificial neural network (ANN, red bars) models, highlighting the impact of specific attributes on overall building vulnerability. For each feature, the average score of the two models is also reported (blue bars), representing a more reliable measure of the true features’ vulnerability.
Figure 7.
A-posteriori Vulnerability scores for the 8 considered building features, calculated by both random forest (RF, green bars) and artificial neural network (ANN, red bars) models, highlighting the impact of specific attributes on overall building vulnerability. For each feature, the average score of the two models is also reported (blue bars), representing a more reliable measure of the true features’ vulnerability.
4.3. Correlation analysis at fixed distance
We aim to analyze the correlation between various vulnerability metrics and observed damage. To achieve this, we focus on a subset of 13,678 buildings located within 6 km of the five major epicenters. We compare our continuous a-posteriori vulnerability score with the a-priori one, which categorizes buildings into five levels of vulnerability, scaled from the maximum level A (highest vulnerability) to the minimum level D2 (lowest vulnerability). This analysis is presented through separated graphical representations, due to the different nature (respectively continuous and categorized) of the two vulnerability scores.
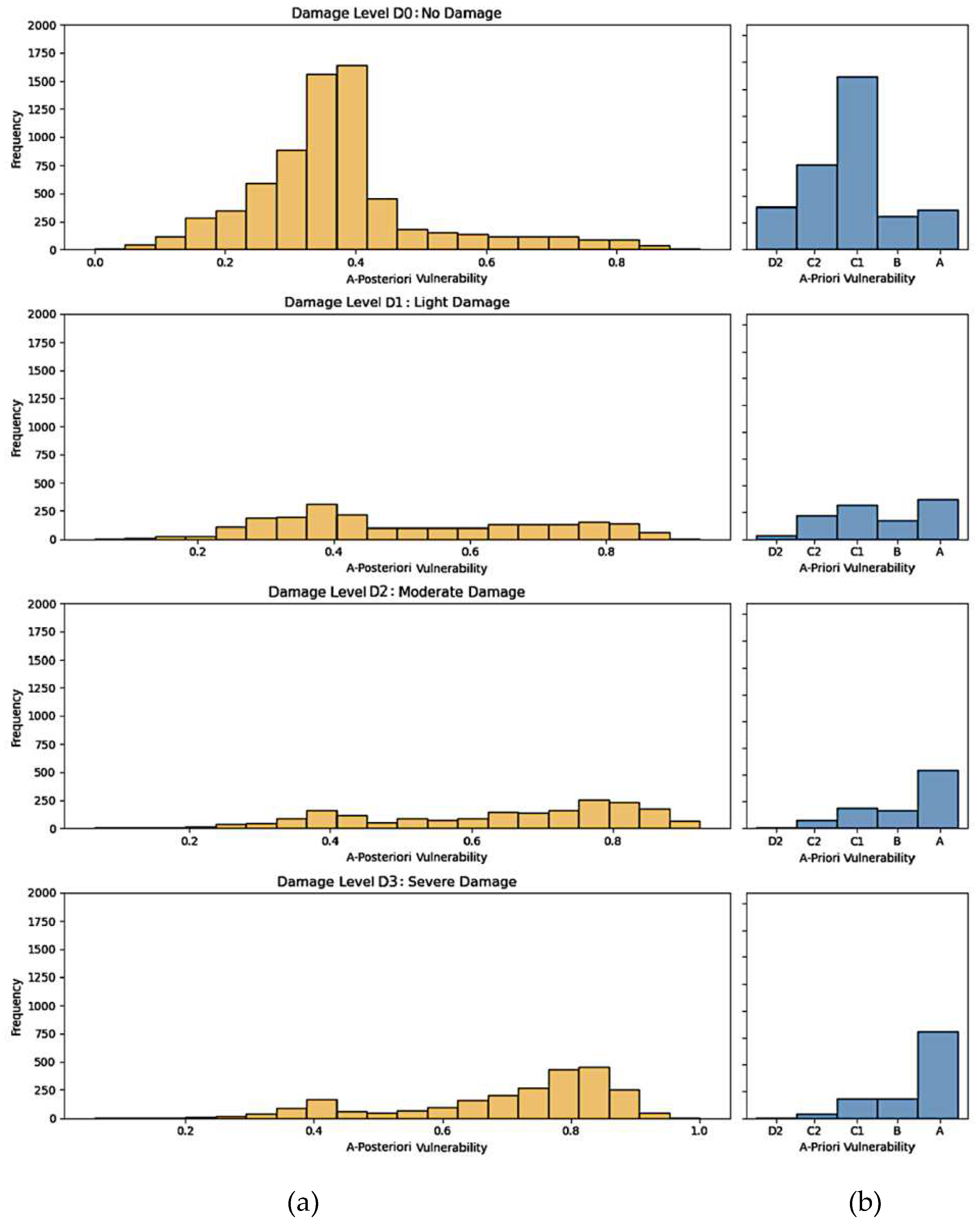
In the bar chart distributions of Figure 8, the frequency of buildings for each damage level is plotted against both our derived a-posteriori vulnerability score (a) and the a-priori vulnerability one (b), which can be considered as a benchmark. The a-posteriori vulnerability score typically exhibits a continuous distribution that is more closely aligned with the actual damage levels. This alignment is especially pronounced for the extremes of the damage spectrum (Damage Levels D0 and D3), showing our method's enhanced capability in differentiating between the most and least vulnerable structures.
Figure 8.
Distribution bar chart comparing our continuous a-posteriori vulnerability score (a) with the established categorical a-priori classification method (b) for the four levels of damage, with a focus on 13678 buildings within a distance of 6 km from the major epicenters.
Figure 8.
Distribution bar chart comparing our continuous a-posteriori vulnerability score (a) with the established categorical a-priori classification method (b) for the four levels of damage, with a focus on 13678 buildings within a distance of 6 km from the major epicenters.
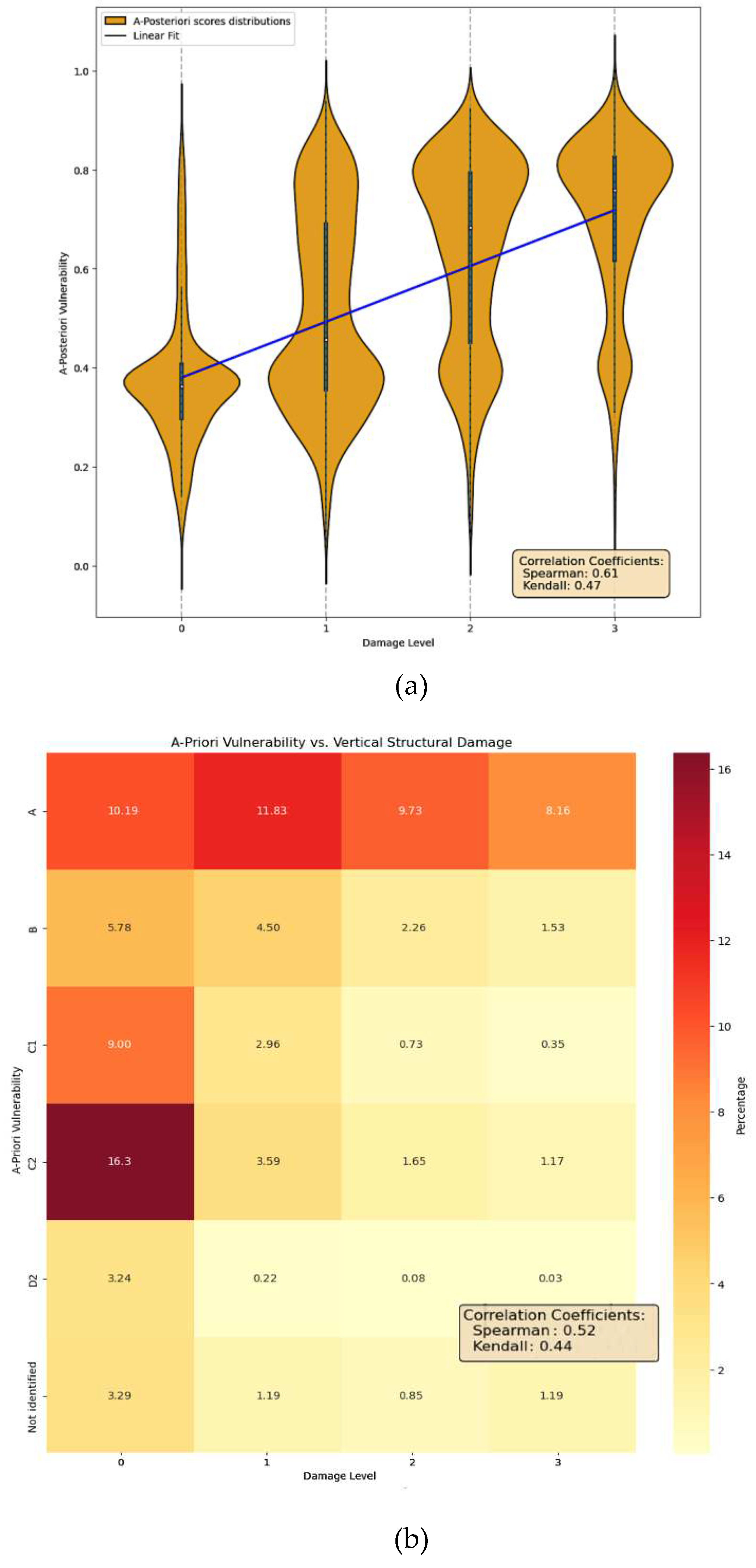
In Figure 9 we try to compare in a more quantitative way the predictive power of the two methods. In panel (a) a violin plot allows to appreciate the good linear correlation between the a-posteriori vulnerability distributions and the observed damage classes, confirmed by the values of both the Spearman and Kendall coefficients reported in the box. On the other hand, in panel (b), the contingency matrix for the a-priori vulnerability, where the color gradient of each cell reflects the corresponding percentage of buildings in the dataset is reported. The matrix shows a less evident correlation with the observed damage, confirmed again by the lower values of the considered coefficients with respect to the a-posteriori ones. This result further identifies the a-posteriori vulnerability score as a better predictor of damage, particularly at higher damage levels.
Figure 9.
(a) A violin plot which shows the linear correlation between the a-posteriori vulnerability scores and the observed damage, with good values for both Spearman (0.61) and Kendall (0.47) coefficients. (b) A less evident correlation with the damage emerges from the contingency matrix of the a-priori vulnerability score, where darker colors indicate a higher percentage of buildings: lower values of Spearman (0.52) and Kendall (0.44) confirms the worse predictive power of this score with respect to the a-posteriori one.
Figure 9.
(a) A violin plot which shows the linear correlation between the a-posteriori vulnerability scores and the observed damage, with good values for both Spearman (0.61) and Kendall (0.47) coefficients. (b) A less evident correlation with the damage emerges from the contingency matrix of the a-priori vulnerability score, where darker colors indicate a higher percentage of buildings: lower values of Spearman (0.52) and Kendall (0.44) confirms the worse predictive power of this score with respect to the a-posteriori one.
4.4. Correlation Analysis over Distance
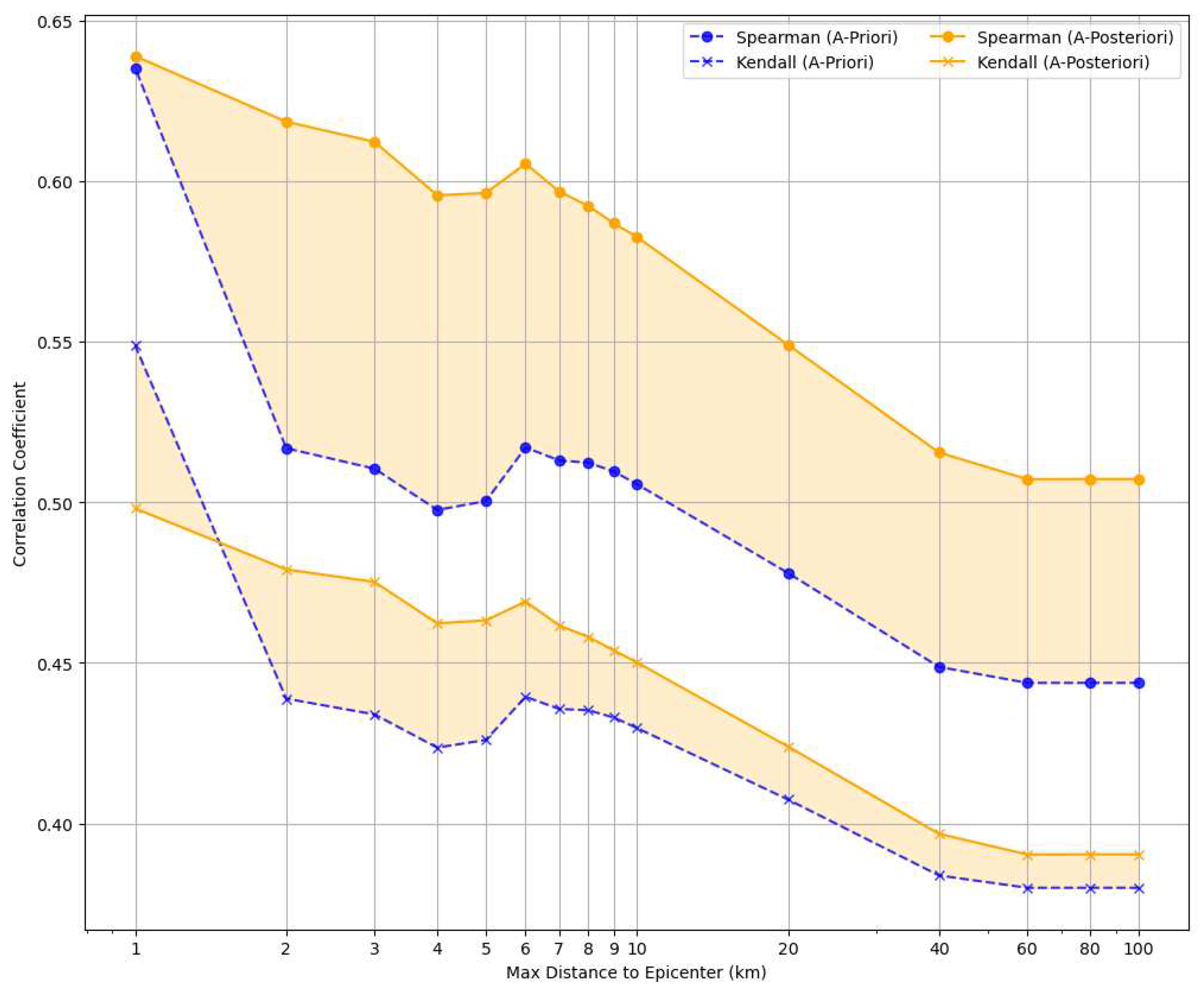
In contrast to the previous section, where we focused on buildings within a 6 km radius of any epicenter, let us now explore the impact of varying this maximum distance. By plotting in Figure 10 the Spearman and Kendall correlation coefficients as function of increasing distances from the epicenters, we effectively illustrate the enhanced accuracy of our vulnerability scoring system.
Looking at the figure, both the a-priori scores and the derived a-posteriori ones exhibit a predictable correlation decrease with the increases of the distance from the epicenter, aligning with the expected lower impact of the earthquake. However, our a-posteriori vulnerability score consistently maintains a notably higher correlation with the damage level, even at large distances. This trend not only underlines the robustness of our approach but also highlights its predictive power in assessing earthquake vulnerability across varying proximities to epicenters.
Figure 10.
Spearman and Kendall correlation coefficients plotted against increasing distances from the main earthquakes’ epicenters, illustrating the robustness and accuracy of our a-posteriori vulnerability scoring system (orange continuous lines) over different proximities, also compared with the a-priori scores (blue dashed lines).
Figure 10.
Spearman and Kendall correlation coefficients plotted against increasing distances from the main earthquakes’ epicenters, illustrating the robustness and accuracy of our a-posteriori vulnerability scoring system (orange continuous lines) over different proximities, also compared with the a-priori scores (blue dashed lines).
5. Discussion and conclusions
Our methodology, as explained in detail in the previous sections, offers a novel and promising approach to seismic vulnerability assessment of buildings in urban areas. The procedure has been developed on the basis of the results obtained considering a large dataset reporting the damage occurred in the buildings in the region around L’Aquila (Italy) after the devastating sequence of earthquakes occurred in April 2009. By focusing on the generation of an a-posteriori vulnerability score based on the observed damage for each building we have developed a more refined and adaptable tool for seismic vulnerability assessment.
The core of our method lies in the use of machine learning models, specifically a Neural Network and a Random Forest Classifier, to predict damage based on building features. This approach relies on the introduction of virtual dummy buildings able to assess the impact of individual features on the overall vulnerability, ensuring a spatial independence and a broad applicability across diverse locations. After a preliminary training of the models with the observed damage data, where geographical information has been used as bias for separating spatial dependency from building feature analysis, we introduced our a-posteriori scoring system through the analysis of simulated buildings over various distances from any epicenter. Such an approach showed an improved performance with respect to a more traditional a-priori method, which assigns categorical vulnerability scores based only on building’s characteristics. On the contrary, our a-posteriori method assigns continuous numerical scores to each building, thus allowing for a more detailed and dynamic representation of vulnerability.
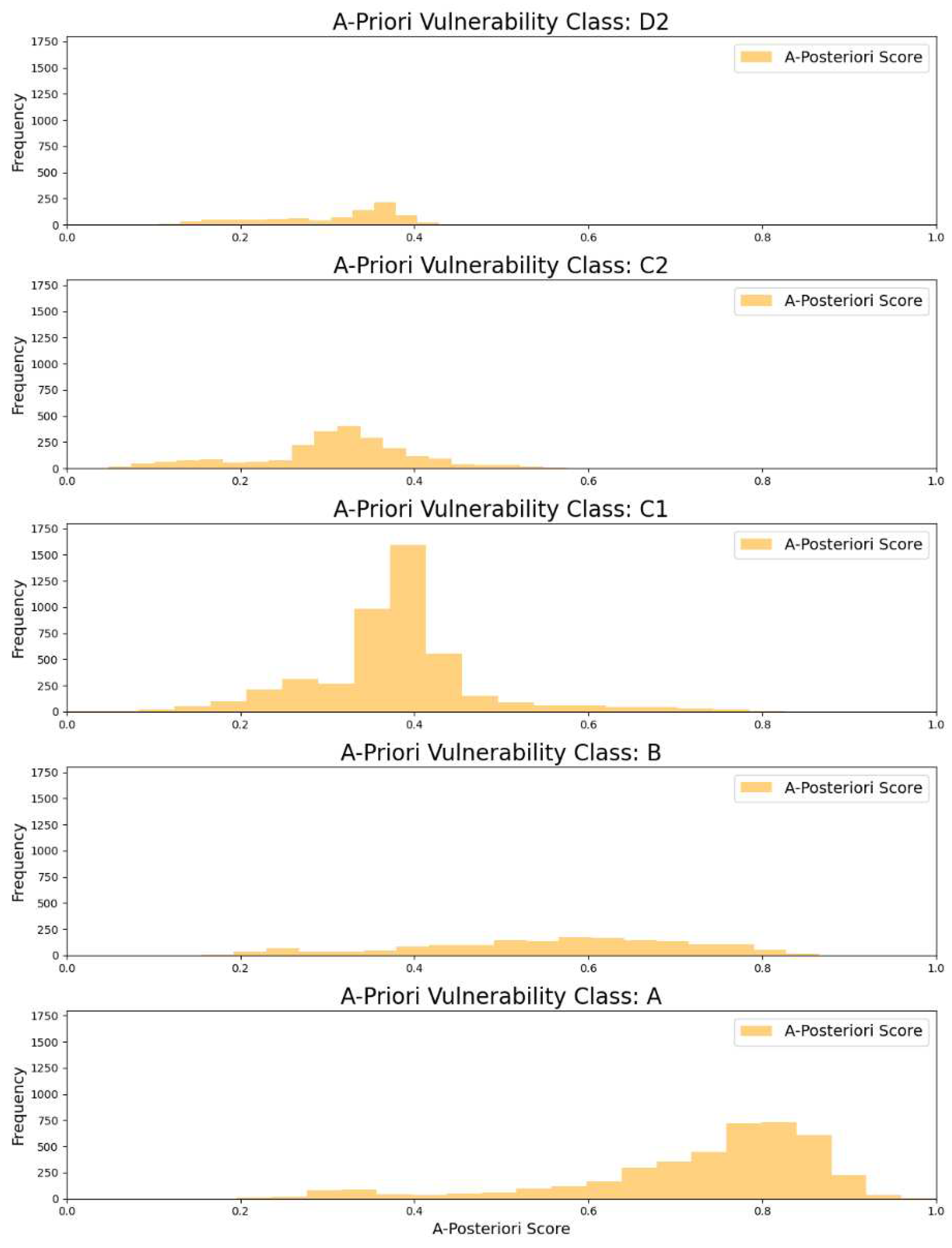
Finally, to better appreciate the difference between the two approaches, in
Figure 11 we plot the distribution of our
a-posteriori vulnerability score within each
a-priori vulnerability class, from the less vulnerable (D2) to the more vulnerable (A). This visual data representation enables us to discern the considerable improvement in both the quality and the quantity of information yield by our novel scoring system.
Figure 11.
The distribution of the a-posteriori vulnerability score is reported for each predefined a-priori vulnerability category. Here, we clearly observe a wide spectrum of a-posteriori scores for each a-priori vulnerability one. This pattern indicates that the a-priori classification may lack the granularity inherent to the different building features, which could reflect different degrees of seismic resilience.
Figure 11.
The distribution of the a-posteriori vulnerability score is reported for each predefined a-priori vulnerability category. Here, we clearly observe a wide spectrum of a-posteriori scores for each a-priori vulnerability one. This pattern indicates that the a-priori classification may lack the granularity inherent to the different building features, which could reflect different degrees of seismic resilience.
In fact, looking at the various panels, it becomes evident that a significant number of buildings classified as highly vulnerable based on their categorical a-priori score (see classes A, B and C1) can be identified as slightly vulnerable by our continuous a-posteriori score, which always shows a broad distribution of values, and vice-versa (see classes D2 and C2).
In conclusion, the flexibility of our approach, which focuses on building features rather than specific geographic locations, makes it highly transferable to various urban settings with different building typologies and seismic histories. Once trained with our dataset, the presented machine learning algorithms could be applied to other urbanized contexts where information about seismic damages are not available, thus helping urban planners and policymakers to develop effective vulnerability management strategies in the corresponding regions.
Author Contributions
Conceptualization: Greco, Pluchino and Rapisarda; methodology: Ferranti; software: Ferranti; validation: Ferranti and Scibilia; feature selection: Scibilia and Ferranti; formal analysis: all authors; investigation: Ferranti; resources: Greco, Pluchino and Rapisarda; data curation: Ferranti and Scibilia; writing—original draft preparation, all authors; writing—review and editing: all authors; visualization: all authors; supervision: Greco, Pluchino and Rapisarda; Project administration: Greco, Pluchino and Rapisarda; Funding acquisition: Greco, Pluchino and Rapisarda. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Italian Ministry of University and Research (MUR) with the projects “PRIN2017 linea Sud: Stochastic forecasting in complex systems” and PRIN2020 #20209F3A37.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Greco, A.; Caddemi, S.; Caliò, I.; Fiore, I. A Review of Simplified Numerical Beam-like Models of Multi-Storey Framed Buildings. Buildings 2022, 12, 1397. [CrossRef]
- Greco, A.; Fiore, I.; Occhipinti, G.; Caddemi, S.; Spina, D. ; Caliò, I. An Equivalent Non-Uniform Beam-Like Model for Dynamic Analysis of Multi-Storey Irregular Buildings. Applied Sciences, 2020 vol. 10, p. 3212. [CrossRef]
- Perrone, D.; Aiello, MA; Pecce, M; Rossi, F. Rapid visual screening for seismic evaluation of RC hospital buildings. Structures 2015. Vol. 3 p. 57–70. [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull Earthquake Eng, 2006, 4, 415–443. [CrossRef]
- Benedetti, D; Benzoni, G; Parisi, MA. Seismic vulnerability and risk evaluation for old urban nuclei. Earthquake Eng Struct Dyn 1988; 16:183–201. [CrossRef]
- Mourous, P; Le Brun, B. Risk-UE project: an advanced approach to earthquake risk scenarios with application to different European towns. In: Oliveira, C.S., Roca, A., Goula, X. (eds) Assessing and Managing Earthquake Risk. Geotechnical, Geological And Earthquake Engineering, 2008 vol 2. Springer, Dordrecht. [CrossRef]
- Bernardini, A; Giovinazzi, S; Lagomarsino, S; Parodi ,S. Vulnerabilità e previsione di danno a scala territoriale secondo una metodologia macrosismica coerente con la scala EMS-98. In Proceedings of the 12th Italian Conference on Earthquake Engineering Pisa, Italy:, June, 2007.
- Vicente, R; Parodi, S; Lagomarsino, S; Varum, H; Silva, J.A.R.M. Seismic vulnerability and risk assessment: Case study of the historic city centre of Coimbra, Portugal. Bulletin of Earthquake Engineering. 2011, 9 (4), pp. 1067. [CrossRef]
- Greco, A.; Pluchino, A.; Barbarossa, L.; Barreca, G.; Caliò, I.; Martinico, F.; Rapisarda, A. A New Agent-Based Methodology for the Seismic Vulnerability Assessment of Urban Areas. ISPRS Int. J. Geo-Inf. 2019, 8, 274. [CrossRef]
- Fischer, E; Barreca, G; Greco, A; Martinico, F.; Pluchino, A.; Rapisarda, A. Seismic risk assessment of a large metropolitan area by means of simulated earthquakes. Nat Hazards 2023 118, 117–153. [CrossRef]
- Eleftheriadou, A. K; Karabinis, A. I. Evaluation of damage probability matrices from observational seismic damage data. Earthquakes and Structures, 2013 4(3), 299–324.
- Mitesh Surana; Abdelghani Meslem; Yogendra Singh; Dominik H. Lang. Analytical evaluation of damage probability matrices for hill-side RC buildings using different seismic intensity measures, Engineering Structures, 2020 Vol 207, 110254. [CrossRef]
- Si Qi Li;Yong Sheng Chen. Analysis of the probability matrix model for the seismic damage vulnerability of empirical structures. Natural Hazards 2020 104:705–730. [CrossRef]
- Alizadeh, M; Ngah, I; Hashim, M; Pradhan, B; Pour, A.B. A hybrid analytic network process and artificial neural network (ANP-ANN) model for urban earthquake vulnerability assessment. Remote Sens. 2018, 10, 975. [CrossRef]
- Alizadeh, M; Zabihi, H; Rezaie, F; Asadzadeh, A; Wolf, I.D; Langat, P.K; Khosravi, I; Beiranvand Pour, A; Mohammad Nataj, M; Pradhan, B. Earthquake Vulnerability Assessment for Urban Areas Using an ANN and Hybrid SWOT-QSPM Model. Remote Sens. 2021, 13, 4519. [CrossRef]
- de-Miguel-Rodríguez, J.; Morales-Esteban, A.; Requena-García-Cruz, M.-V.; Zapico-Blanco, B.; Segovia-Verjel, M.-L.; Romero-Sánchez, E.; Carvalho-Estêvão, J.M. Fast Seismic Assessment of Built Urban Areas with the Accuracy of Mechanical Methods Using a Feedforward Neural Network. Sustainability 2022, 14, 5274. [CrossRef]
- Arslan, M.H. An evaluation of effective design parameters on earthquake performance of RC buildings using neural networks. Eng. Struct. 2010, 32, 1888–1898. [CrossRef]
- Afsari, R.; Nadizadeh Shorabeh, S.; Bakhshi Lomer, A.R.; Homaee, M.; Arsanjani, J.J. Using Artificial Neural Networks to Assess Earthquake Vulnerability in Urban Blocks of Tehran. Remote Sens. 2023, 15, 1248.8. [CrossRef]
- Jena, R.; Pradhan, B. Integrated ANN-cross-validation and AHP-TOPSIS model to improve earthquake risk assessment. Int. J.Disaster Risk Reduct. 2020, 50, 101723. [CrossRef]
- Harirchian, E.; Lahmer, T. Improved Rapid Assessment of Earthquake Hazard Safety of Structures via Artificial Neural Networks. IOP Conf. Ser. Mater. Sci. Eng. 2020, 897, 012014. [CrossRef]
- Kalakonas, P.; Silva, V. Seismic vulnerability modelling of building portfolios using artificial neural networks. Earthq. Eng. Struct. Dyn. 2022, 51, 310–327. [CrossRef]
- Luis Izquierdo-Horna, Jose Zevallos, Yustin Yepez, An integrated approach to seismic risk assessment using random forest and hierarchical analysis: Pisco Peru. Heliyon,Volume 8, Issue 10, 2022,. [CrossRef]
- Han, J.; Kim, J.; Park, S.; Son, S.; Ryu, M. Seismic Vulnerability Assessment and Mapping of Gyeongju, South Korea Using Frequency Ratio, Decision Tree, and Random Forest. Sustainability 2020, 12, 7787. [CrossRef]
- dataset developed by Eucentre (European Center for Training and Research in Seismic Engineering, http://egeos.eucentre.it/danno_osservato/web/danno_osservato).
- Shapley, Lloyd S. A value for n-person games,1953, 307-317, Princeton University Press. [CrossRef]
- W. E. Marcílio and D. M. Eler, From explanations to feature selection: assessing SHAP values as feature selection mechanism, 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 2020, pp. 340-347. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).