Submitted:
08 December 2023
Posted:
12 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
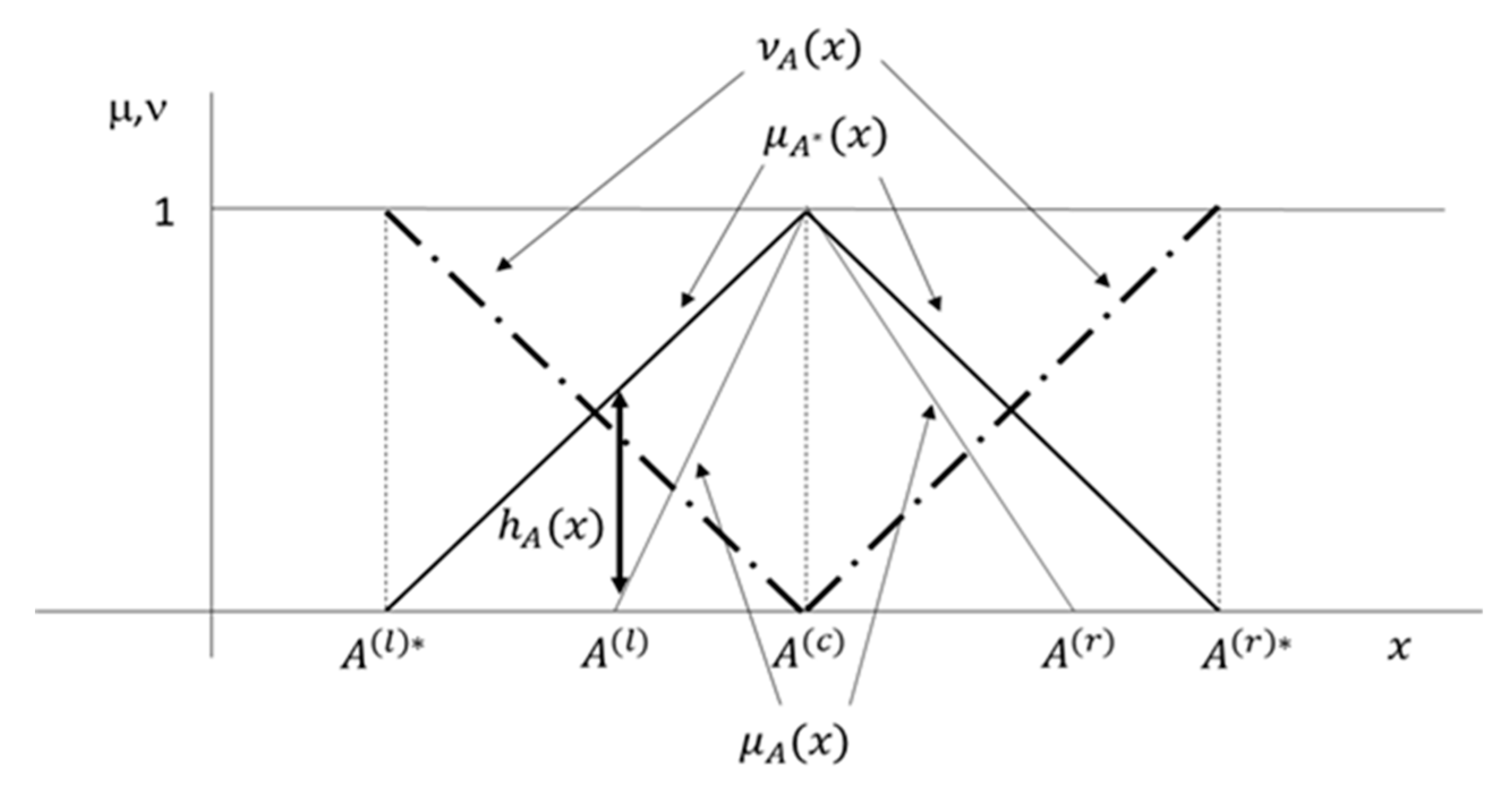
2. Intuitionistic fuzzy numbers
2.1. Fuzzy numbers and intuitionistic fuzzy numbers
- i. is normal, i.e.,
- ii. is convex, i.e.,
- ,
- It is normal, i.e.,
- is convex,
- and is concave:
2.2. Intuitionistic fuzzy number arithmetic
- are the local optima at internal points where . Thus, is negative semidefinite if is obtained at and positive semidefinite for .
- If there are no local optima in , the argument that optimizes is found at the vertex of the domain .
3. An intuitionistic fuzzy framework to evaluate life contingencies for heterogeneous life expectancies
3.1. Modelling one-year death probabilities with intuitionistic fuzzy numbers
- A widely used method for determining is the numerical rating system (Kita, 1988), which is particularly prevalent in the life settlement market (Xu, 2020). With this method, , where represents a percentage increase in the death probability associated with the jth factor, that is, it is a so-called debit. Conversely, implies a decrease in the death probability as the factor increases LE, that is, it is a credit. The debits and credits can be precisely estimated (Werth, 1995) or expressed imprecisely using fluctuation bands instead of clear values; in this last case, IFNs could be suitable to model them. According to Xu and Hoesch (2018), medical underwriting for life settlements is inherently imprecise due to several factors. Base mortality tables inherited from the life insurance market introduce inaccuracies in mortality rates for elderly populations because data for these age groups are scarce (Braun & Xu, 2020). Other factors also contribute to biased and imprecise information fitting for debits and credit. These include false application of information, lack of critical information, and incorporation of irrelevant and false information. These factors emphasize the need to assess life settlement prices by introducing variability bands in mortality multipliers when calculating LS prices of LSs (Xu & Hoesch, 2018).
- Lim and Shyamalkumar (2022) indicate that to fit the mortality multiplier, unreported deaths must be considered, whose knowledge is inherently vague because data on this issue in practice are incomplete. They outline that a commonly agreed estimate is "approximately 5%" and seniors ranging from "5-7%,". Note that these statements are vague and imprecise and are therefore susceptible to being modelled with a TIFN whose base TFN may be (5%, 5,5%, 7%).
- Goodwin et al. (2004) recommend that, in tariffing involving older people with impairments, seeking the judgment of a professional gerontologist is advisable. Fuzzy-set instruments can naturally model subjective information from experts (Shapiro, 2004).
- Evaluating not only central values but also extreme mortality scenarios is common practice in insurance markets. Richards (2008) provided an example in the context of life annuities, and Xu and Boesch (2018) expressed extreme scenarios in the 5th and 95th percentiles. In Andrés-Sánchez and González-Vila (2023), the use of a fuzzy triangular number is justified to shape the mortality multiplier that can be considered "most reliable" and two extreme scenarios below and above this central value. The use of TIFNs generalizes the use of TFNs involving a central scenario and two pairs of extreme scenarios, below and above this central value. In these pairs, while one scenario might be factually extreme (e.g., percentiles 10 and 90), the other could be potentially extreme (e.g., comparable to percentiles 0.5 and 99.5).
- In the life settlement market, reliable values of life expectancy and, consequently, the mortality multiplier are typically expressed not by a crisp parameter but with a set of crisp estimates. This is because the LE of the insured is often reported by at least two independent medical underwriters (Xu, 2020). Therefore, for a given policy, if the set of multipliers by LE providers is , it seems reliable to give a fuzzy quantification to the mortality multiplier, as “it must be approximately and it may fluctuate in margins depending on (Andrés-Sánchez & González-Vila, 2023).
- The derivation of the sensitivity of death probability to risk factors through regression methods, as developed by Meyricke and Sherris (2013), assumes that the estimation of death probabilities and coefficients involves probabilistic confidence intervals. The results of Couso et al. (2001), Dubois et al. (2004), and Sfiris and Papadopoulos (2014) facilitate the inference of fuzzy numbers using probabilistic confidence intervals. These findings were employed in a regression framework by Adjenughwure and Papadopoulos (2020) and Al-Kandari et al. (2021), where the variables of interest were predicted by fuzzy numbers induced from probabilistic confidence interval estimates derived from statistical regression. From Remark 6, we can induce a TIFN from the estimated TFN.
- Of course, fuzzy one-year standard mortality probabilities may consider an impairment cause common to a wide proportion of the population, for which the evaluator has developed mortality tables ad hoc (Drinkwater et al., 2006). An example of this is the mortality tables for smokers. If a person has no other cause of impairment,
3.2. Modelling the probabilities of survival and the curtate life expectancy with intuitionistic fuzzy numbers
3.3. Pricing immediate whole life annuities and immediate whole life insurances with intuitionistic fuzzy parameters
4. Pricing special rate annuities and life settlements with intuitionistic fuzzy parameters
4.1. Obtaining the periodical payment of a substandard annuity with intuitionistic fuzzy number parameters
4.2. Pricing life settlements with intuitionistic fuzzy number parameters
5. Conclusions and further research
Author Contributions
Funding
Data Availability Statement
Ethics Statement
Conflicts of Interest
References
- Aalaei, M. (2022). Pricing life settlements in the secondary market using fuzzy internal rate of return. Journal of Mathematics and Modelling in Finance, 2(2), 53-62. [CrossRef]
- AA-Partners Ltd. (2017). AAP Life Settlement Valuation. Available online: https://www.aa-partners.ch/fileadmin/files/Valuation/AAP_Life_Settlement_Valuation_-_Manual_V6.0.pdf (accessed on 10 September 2022).
- Adjenughwure, K.; Papadopoulos, B. Fuzzy-statistical prediction intervals from crisp regression models. Evol. Syst. 2020, 11, 201–213. [Google Scholar] [CrossRef]
- Al-Kandari, M.; Adjenughwure, K.; Papadopoulos, K. A Fuzzy-Statistical Tolerance Interval from Residuals of Crisp Linear Regression Models. Mathematics 2020, 8, 1422. [Google Scholar] [CrossRef]
- Anderton, W. N., & Robb, G. H. (1998). Impaired Lives Annuities. In Medical Selection of Life Risks (pp. 169-171). London: Palgrave Macmillan UK.
- Andrés Sánchez, J. D., & Gonzalez-Vila, L. (2019). A fuzzy-random extension of the Lee-Carter mortality prediction model. International Journal Of Computational Intelligence Systems, 12, 2, 775-794. [CrossRef]
- Andrés-Sanchez, J., & Gómez, A.T. (2003). Applications of fuzzy regression in actuarial analysis. Journal of Risk and Insurance, 70(4), 665-699. [CrossRef]
- Andrés-Sanchez, D., & Gonzalez-Vila, L. (2017a). Some computational results for the fuzzy random value of life actuarial liabilities. Iranian Journal of Fuzzy Systems, 14(4), 1-25. [CrossRef]
- Andrés-Sánchez, J., & Gonzalez-Vila, L. G. V. (2017b). The valuation of life contingencies: A symmetrical triangular fuzzy approximation. Insurance: Mathematics and Economics, 72, 83-94. [CrossRef]
- Andrés-Sánchez, J. (2012). Claim reserving with fuzzy regression and the two ways of ANOVA. Applied Soft Computing, 12(8), 2435-2441. [CrossRef]
- Andrés-Sánchez, J. (2014). Fuzzy claim reserving in nonlife insurance. Comput. Sci. Inf. Syst., 11(2), 825-838. [CrossRef]
- Andrés-Sánchez, J. D. (2023). Fuzzy Random Option Pricing in Continuous Time: A Systematic Review and an Extension of Vasicek’s Equilibrium Model of the Term Structure. Mathematics, 11(11), 2455. [CrossRef]
- Andrés-Sánchez, J., & Puchades, L. G. V. (2012). Using fuzzy random variables in life annuities pricing. Fuzzy sets and Systems, 188(1), 27-44. [CrossRef]
- Andrés-Sánchez, J., & Puchades, L. G. V. (2023). Life settlement pricing with fuzzy parameters. Applied Soft Computing, 148, 110924. [CrossRef]
- Andrés-Sánchez, J., Puchades, L. G. V., & Zhang, A. (2020). Incorporating fuzzy information in pricing substandard annuities. Computers & Industrial Engineering, 145, 106475. [CrossRef]
- Anzilli, L., & Facchinetti, G. (2017). New definitions of mean value and variance of fuzzy numbers: An application to the pricing of life insurance policies and real options. International Journal of Approximate Reasoning, 91, 96–113. [CrossRef]
- Anzilli, L., Facchinetti, G., & Pirotti, T. (2018). Pricing of minimum guarantees in life insurance contracts with fuzzy volatility. Information Sciences, 460, 578–593. [CrossRef]
- Apaydin A. and Baser, F. (2010). Hybrid fuzzy least-squares regression analysis in claims reserving with geometric separation method. Insur. Math. Econ., 47, 113–122. [CrossRef]
- Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy sets and Systems, 20(1), 87-96. [CrossRef]
- Atanassov, K. T. (1989). More on intuitionistic fuzzy sets. Fuzzy sets and systems, 33(1), 37-45. [CrossRef]
- Atanassova, L. (2006). On intuitionistic fuzzy versions of L. Zadeh’s extension principle. Notes on Intuitionistic Fuzzy Sets, 13(3), 33-36. Available online: https://ifigenia.org/images/b/bc/NIFS-13-3-33-36.pdf.
- Bauer, D., Russ, J., & Zhu, N. (2020). Asymmetric information in secondary insurance markets: Evidence from the life settlements market. Quantitative Economics, 11(3), 1143-1175. [CrossRef]
- Bayeg, S., & Mert, R. (2021). On intuitionistic fuzzy version of Zadeh’s extension principle. Notes on Intuitionistic Fuzzy Sets. 27, 3, 9-17. [CrossRef]
- Betzuen, A., López, M. J., & Rivas, J. A. (1997). Actuarial mathematics with fuzzy parameters: An application to collective pension plans. Fuzzy economic review, 2(2), 4. [CrossRef]
- Bhaumik, A., Roy, S.K., & Li, D.F. (2017). Analysis of triangular intuitionistic fuzzy matrix games using robust ranking. Journal of Intelligent & Fuzzy Systems, 33(1), 327-336. [CrossRef]
- Boltürk, E., & Kahraman, C. (2022). Interval-valued and circular intuitionistic fuzzy present worth analyses. Informatica, 33(4), 693-711. [CrossRef]
- Braun, A., Xu, J. (2020). Fair value measurement in the life settlement market. The Journal of Fixed Income, 29 (4), 100-123. [CrossRef]
- Brockett, P.L., Chuang, S.-L., Deng, Y., MacMinn, R.D. (2013). Incorporating longevity risk and medical information into life settlement pricing. Journal of Risk and Insurance, 80 (3), 799-826. [CrossRef]
- Buckley, J. J. (1987). The fuzzy mathematics of finance. Fuzzy sets and systems, 21(3), 257-273. [CrossRef]
- Buckley, J. J. (1992). Solving fuzzy equations in economics and finance. Fuzzy Sets and Systems, 48(3), 289-296. [CrossRef]
- Buckley, J.J., & Qu, Y. (1990). On using α-cuts to evaluate fuzzy equations. Fuzzy Sets and Systems, 38, 3, 309–312. [CrossRef]
- Bundock, G. (2006). Application Processing. In: Brackenridge, R.D.C., Croxson, R.S., MacKenzie, R. (eds) Brackenridge’s Medical Selection of Life Risks. Palgrave Macmillan, London. [CrossRef]
- Burillo, P., & Bustince, H. (1996). Construction theorems for intuitionistic fuzzy sets. Fuzzy Sets and Systems, 84(3), 271-281. [CrossRef]
- Cassú C., Planas, P., Ferrer, J. C., & Bonet, J. (1996). Accumulated capital for the retirement plans in fuzzy finance mathematics. Fuzzy economic review, 1(1), 5. [CrossRef]
- Couso, I.; Montes, S.; Gil, P. The necessity of the strong α-cuts of a fuzzy set. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2001, 9, 249–262. [Google Scholar] [CrossRef]
- Cummins, D.J., & Derrig, R. A. (1997). Fuzzy financial pricing of property-liability insurance. North American Actuarial Journal, 1(4), 21-40. [CrossRef]
- Dębicka, J., Heilpern, S., & Marciniuk, A. (2022). Modelling Marital Reverse Annuity Contract in a Stochastic Economic Environment. Statistika: Statistics & Economy Journal, 102(3). [CrossRef]
- Derrig, R. A., & Ostaszewski, K. M. (1997). Managing the tax liability of a property-liability insurance company. Journal of Risk and Insurance, 695-711. [CrossRef]
- Devolder, P. (1988). Le taux d'actualization en assurance. Geneva Papers on Risk and Insurance, 13, 265-272. Available online: https://link.springer.com/content/pdf/10.1057/gpp.1988.20.pdf.
- Dong, W., & Shah, H. C. (1987). Vertex method for computing functions of fuzzy variables. Fuzzy sets and Systems, 24(1), 65-78. [CrossRef]
- Dong, M. G., & Li, S. Y. (2016). Project investment decision making with fuzzy information: A literature review of methodologies based on taxonomy. Journal of Intelligent & Fuzzy Systems, 30(6), 3239-3252. [CrossRef]
- Dubois, D., & Prade, H. (1993). Fuzzy numbers: an overview. Readings in Fuzzy Sets for Intelligent Systems, 112-148.
- Dubois, D., & Prade, H. (2012). Gradualness, uncertainty and bipolarity: making sense of fuzzy sets. Fuzzy sets and Systems, 192, 3-24. [CrossRef]
- Dubois, D.; Folloy, L.; Mauris, G.; Prade, H. (2004). Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities. Reliab. Comput., 10, 273–297. Available online: https://www.irit.fr/~Henri.Prade/Papers/DFoulMauP.pdf.
- Ersen, H. Y., Tas, O., & Kahraman, C. (2018). Intuitionistic fuzzy real-options theory and its application to solar energy investment projects. Engineering Economics, 29(2), 140-150. [CrossRef]
- Ersen, H. Y., Tas, O., & Ugurlu, U. (2022). Solar Energy Investment Valuation With Intuitionistic Fuzzy Trinomial Lattice Real Option Model. IEEE Transactions on Engineering Management.). [CrossRef]
- Gatzert, N., & Klotzki, U. (2016). Enhanced annuities: Drivers of and barriers to supply and demand. The Geneva Papers on Risk and Insurance-Issues and Practice, 41, 53-77. [CrossRef]
- Gatzert, N. (2010). The secondary market for life insurance in the UnitedKingdom, Germany, and the United States: Comparison and overview. Risk Management and Insurance Review, 13 (2), 279-301. [CrossRef]
- Haktanır, E., & Kahraman, C. (2023). Intuitionistic fuzzy risk adjusted discount rate and certainty equivalent methods for risky projects. International Journal of Production Economics, 257, 108757. [CrossRef]
- Heberle, J., & Thomas, A. (2014). Combining chain-ladder claims reserving with fuzzy numbers. Insurance: Mathematics and Economics, 55, 96-104. [CrossRef]
- Heberle, J., & Thomas, A. (2016). The fuzzy Bornhuetter–Ferguson method: an approach with fuzzy numbers. Annals of Actuarial Science, 10(2), 303-321. [CrossRef]
- Jiménez, M., & Rivas, J. A. (1998). Fuzzy number approximation. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 6(01), 69-78. [CrossRef]
- Kahraman, C., Çevik Onar, S., & Öztayşi, B. (2015). Engineering economic analyses using intuitionistic and hesitant fuzzy sets. Journal of Intelligent & Fuzzy Systems, 29(3), 1151-1168. [CrossRef]
- Kahraman, C., Ruan, D., & Tolga, E. (2002). Capital budgeting techniques using discounted fuzzy versus probabilistic cash flows. Information Sciences, 142(1-4), 57-76. [CrossRef]
- Kaufmann, A.: (1986) Fuzzy subsets applications in OR and management. In: Jones, A., Kaufmann, A., Zimmermann, H.J. (eds.) Fuzzy sets theory and applications, pp. 257–300. Springer, Netherlands.
- Kita, M. W. (1988). The rating of substandard lives. In Medical Selection of Life Risks (pp. 61-88). London: Palgrave Macmillan UK.
- Koissi, M. C., & Shapiro, A. F. (2006). Fuzzy formulation of the Lee–Carter model for mortality forecasting. Insurance: Mathematics and Economics, 39(3), 287-309. [CrossRef]
- Kreinovich, V., Kosheleva, O., Shahbazova, S.N. (2020). Why Triangular and Trapezoid Membership Functions: A Simple Explanation. In: Shahbazova, S., Sugeno, M., Kacprzyk, J. (eds) Recent Developments in Fuzzy Logic and Fuzzy Sets. Studies in Fuzziness and Soft Computing, vol 391. Springer, Cham. [CrossRef]
- Kumar, G., & Bajaj, R. K. (2014). Implementation of intuitionistic fuzzy approach in maximizing net present value. International Journal of Mathematical and Computational Sciences, 8(7), 1069-1073.
- Kumar, P. S., & Hussain, R. J. (2015). A method for solving unbalanced intuitionistic fuzzy transportation problems. Notes on Intuitionistic Fuzzy Sets, 21(3), 54-65.
- Kung, K. L., Hsieh, M. H., Peng, J. L., Tsai, C. J., & Wang, J. L. (2021). Explaining the risk premiums of life settlements. Pacific-Basin Finance Journal, 68, 101574. [CrossRef]
- Lee, R. D., & Carter, L. R. (1992). Modelling and forecasting US mortality. Journal of the American statistical association, 87(419), 659-671. [CrossRef]
- Lemaire, J. (1990). Fuzzy insurance. ASTIN Bulletin: The Journal of the IAA, 20(1), 33-55.
- Lim, H. B., & Shyamalkumar, N. D. (2022). Evaluating Medical Underwriters in Life Settlements: Problem of Unreported Deaths. North American Actuarial Journal, 26(2), 298-322. [CrossRef]
- Lubovich, J., Sabes, J., & Siegert, P. (2008). Introduction to Methodologies Used to Price Life Insurance Policies in Life Settlement Transactions. [CrossRef]
- Mahapatra, G. S., & Roy, T. K. (2013). Intuitionistic fuzzy number and its arithmetic operation with application on system failure. Journal of uncertain systems, 7(2), 92-107. Available online: https://www.researchgate.net/publication/286377011_Intuitionistic_fuzzy_number_and_its_arithmetic_operation_with_application_on_system_failure.
- Meyricke, R., & Sherris, M. (2013). The determinants of mortality heterogeneity and implications for pricing annuities. Insurance: Mathematics and Economics, 53(2), 379-387. [CrossRef]
- Mircea, I., & Covrig, M. (2015). A discrete time insurance model with reinvested surplus and a fuzzy number interest rate. Procedia Economics and Finance, 32, 1005-1011. [CrossRef]
- Mitchell, H. B. (2004). Ranking-intuitionistic fuzzy numbers. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 12(03), 377-386. [CrossRef]
- Muzzioli, S., & De Baets, B. (2016). Fuzzy approaches to option price modeling. IEEE Transactions on Fuzzy Systems, 25(2), 392-401. [CrossRef]
- Nguyen, H.T. (1978). A note on the extension principle for fuzzy sets, J. of Mathematical Analysis and Aplications 64 (1978) 369-380. [CrossRef]
- Nowak, P., & Romaniuk, M. (2017). Catastrophe bond pricing for the two-factor Vasicek interest rate model with automatized fuzzy decision making. Soft Computing, 21, 2575-2597. [CrossRef]
- Olivieri, A. (2006). Heterogeneity in survival models. Applications to pensions and life annuities. Belgian Actuarial Bulletin, 6(1), 23–39. [CrossRef]
- Olivieri, A., & Pitacco, E. (2016). Frailty and risk classification for life annuity portfolios. Risks, 4(4), 39. [CrossRef]
- Pitacco, E. (2017). Life Annuities. Products, Guarantees, Basic Actuarial Models. Available online: https://ssrn.com/abstract=2887359. [CrossRef]
- Pitacco, E. (2019). Heterogeneity in mortality: a survey with an actuarial focus. European Actuarial Journal, 9, 3-30. [CrossRef]
- Pitacco, E., & Tabakova, D. Y. (2022). Special-rate life annuities: analysis of portfolio risk profiles. Risks, 10(3), 65. [CrossRef]
- Promislow, S. D. (2014). Fundamentals of actuarial mathematics. John Wiley & Sons.
- Rasheed, F., Kousar, S., Shabbir, J., Kausar, N., Pamucar, D., & Gaba, Y. U. (2021). Use of intuitionistic fuzzy numbers in survey sampling analysis with application in electronic data interchange. Complexity, 2021, 1-12. [CrossRef]
- Richards, S. J. (2008). Applying survival models to pensioner mortality data. British Actuarial Journal, 14(2), 257-303. [CrossRef]
- Ryan Jr, J. A., & Harbin, R. F. (1998). Structured settlements. In Medical Selection of Life Risks (pp. 173-180). London: Palgrave Macmillan UK.
- Sfiris, D.S.; Papadopoulos, B.K. Nonasymptotic fuzzy estimators based on confidence intervals. Inf. Sci. 2014, 279, 446–459. [Google Scholar] [CrossRef]
- Shapiro, A. F. (2004). Fuzzy logic in insurance. Insurance: Mathematics and Economics, 35(2), 399-424. [CrossRef]
- Shapiro, A. F. (2005). Fuzzy regression models. Article of Penn State University, 102(2), 373-383.
- Shapiro, A. F. (2013). Modelling future lifetime as a fuzzy random variable. Insurance: Mathematics and Economics, 53(3), 864-870. [CrossRef]
- Shen, Y., & Chen, W. (2012). Multivariate extension principle and algebraic operations of intuitionistic fuzzy sets. Journal of Applied Mathematics. Article ID 845090. [CrossRef]
- Szymański, A., & Rossa, A. (2021). The modified fuzzy mortality model based on the algebra of ordered fuzzy numbers. Biometrical Journal, 63(3), 671-689. [CrossRef]
- Terceño, A., Andrés-Sánchez, J., Barberà, G., & Lorenzana, T. (2003). Using fuzzy set theory to analyse investments and select portfolios of tangible investments in uncertain environments. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 11(03), 263-281. [CrossRef]
- Tereszkiewicz, P., & Południak-Gierz, K. (2021). Liability for incorrect client personalization in the distribution of consumer insurance. Risks, 9(5), 83. [CrossRef]
- Terceno, A., Andrés-Sánchez, J., Belvis, C., & Barbera, G. (1996). Fuzzy methods incorporated to the study of personal insurances. In 1st International Symposium on Neuro-Fuzzy Systems, AT'96. Conference Report (pp. 187-202). IEEE.
- Ungureanu, D., & Vernic, R. (2015). On a fuzzy cash flow model with insurance applications. Decisions in Economics and Finance, 38, 39-54. [CrossRef]
- Villacorta, P. J., González-Vila Puchades, L., & de Andrés-Sánchez, J. (2021). Fuzzy Markovian Bonus-Malus Systems in Nonlife Insurance. Mathematics, 9(4), 347. [CrossRef]
- Woundjiagué, A.; Bidima, M.L.D.M.; Mwangi, R.W. (2019). A fuzzy least-squares estimation of a hybrid log-poisson regression and its goodness of fit for optimal loss reserves in insurance. International Journal of Fuzzy Systems, 21, 930-944. [CrossRef]
- Wu, L., Liu, J. F., Wang, J. T., & Zhuang, Y. M. (2016). Pricing for a basket of LCDS under fuzzy environments. SpringerPlus, 5(1), 1-12. [CrossRef]
- Zadeh, L. A. (1965). Fuzzy sets. Information and control, 8(3), 338-353. [CrossRef]
- Xu, J. (2020) Dating death: An empirical comparison of medical underwriters in the US life settlement market, North Am. Actuar. J. 24 (1) 36–56. [CrossRef]
- Xu, J., Hoesch, A. (2018) Predicting longevity: An analysis of potential alternatives to life expectancy reports, J. Invest. 27 (supplement) 65–79. 79. [CrossRef]
| Issue | Papers |
|---|---|
| Life insurance pricing (cash-flow discounting) | Lemaire (1990), Ostaszewski (1993), Terceño et al. (1996), Andrés-Sánchez and Terceño (2003), Shapiro (2004), Andrés-Sánchez and González-Vila (2012), Andrés-Sánchez and González-Vila (2017a), Andrés-Sánchez and González-Vila (2017b), Andrés-Sánchez et al. (2020), Aalaei (2022), Dębicka et al. (2022), Andrés-Sánchez and González-Vila (2023). |
| Life insurance pricing (final value) |
Cassú et al. (1996), Betzuen et al. (1997), |
| Insurance pricing (option pricing) |
Anzilli and Fachinetti (2017), Nowak & Romaniuk (2017), Anzilli et al. (2018). |
| Nonlife insurance (cash-flow discounting) |
Derrig and Ostazewski (1997), Cummins and Derrig (1997), Andrés-Sánchez and Terceño (2003), Andrés-Sánchez (2014), |
| Nonlife insurance (terminal value) |
Mircea and Covrig (2015), Ungureanu and Vernic (2015), |
| Claim reserving | Andrés-Sánchez and Terceño (2003), Shapiro (2004), Apaydin and Baser (2010), Andrés-Sánchez (2012), Heberle and Thomas (2014), Heberle and Thomas (2016), Woundjiagué et al. (2019). |
| 10-year life probability for x=65 | Life expectancy for x=65 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| α | β | ||||||||
| 1 | 0 | 0.4592 | 0.4592 | 0.4592 | 0.4592 | 9.10 | 9.10 | 9.10 | 9.10 |
| 0.75 | 0.25 | 0.4439 | 0.4749 | 0.4364 | 0.4830 | 8.87 | 9.34 | 8.77 | 9.47 |
| 0.5 | 0.5 | 0.4290 | 0.4912 | 0.4146 | 0.5079 | 8.66 | 9.59 | 8.45 | 9.86 |
| 0.25 | 0.75 | 0.4146 | 0.5079 | 0.3938 | 0.5340 | 8.45 | 9.86 | 8.16 | 10.29 |
| 0 | 1 | 0.4007 | 0.5252 | 0.3740 | 0.5612 | 8.26 | 10.15 | 7.89 | 10.77 |
| α | β | ||||||||
| 1 | 0 | 0.4592 | 0.4592 | 0.4592 | 0.4592 | 9.10 | 9.10 | 9.10 | 9.10 |
| 0.75 | 0.25 | 0.4445 | 0.4757 | 0.4379 | 0.4847 | 8.89 | 9.36 | 8.80 | 9.52 |
| 0.5 | 0.5 | 0.4299 | 0.4922 | 0.4166 | 0.5102 | 8.68 | 9.62 | 8.50 | 9.94 |
| 0.25 | 0.75 | 0.4153 | 0.5087 | 0.3953 | 0.5357 | 8.47 | 9.88 | 8.19 | 10.35 |
| 0 | 1 | 0.4007 | 0.5252 | 0.3740 | 0.5612 | 8.26 | 10.15 | 7.89 | 10.77 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.0015 | 0.0015 | 0.0034 | 0.0035 | 0.002 | 0.002 | 0.004 | 0.006 |
| 0.5 | 0.5 | 0.0021 | 0.0020 | 0.0047 | 0.0045 | 0.002 | 0.003 | 0.005 | 0.008 |
| 0.25 | 0.75 | 0.0016 | 0.0015 | 0.0037 | 0.0033 | 0.002 | 0.002 | 0.004 | 0.006 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
0.0017 =0.0017 0.0017 |
0.0039 =0.0038 0.0038 |
0.0020 =0.0026 =0.0023 |
0.0043 0.0062 0.0053 |
||||||
| Whole life annuity | Whole life insurance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| α | β | ||||||||
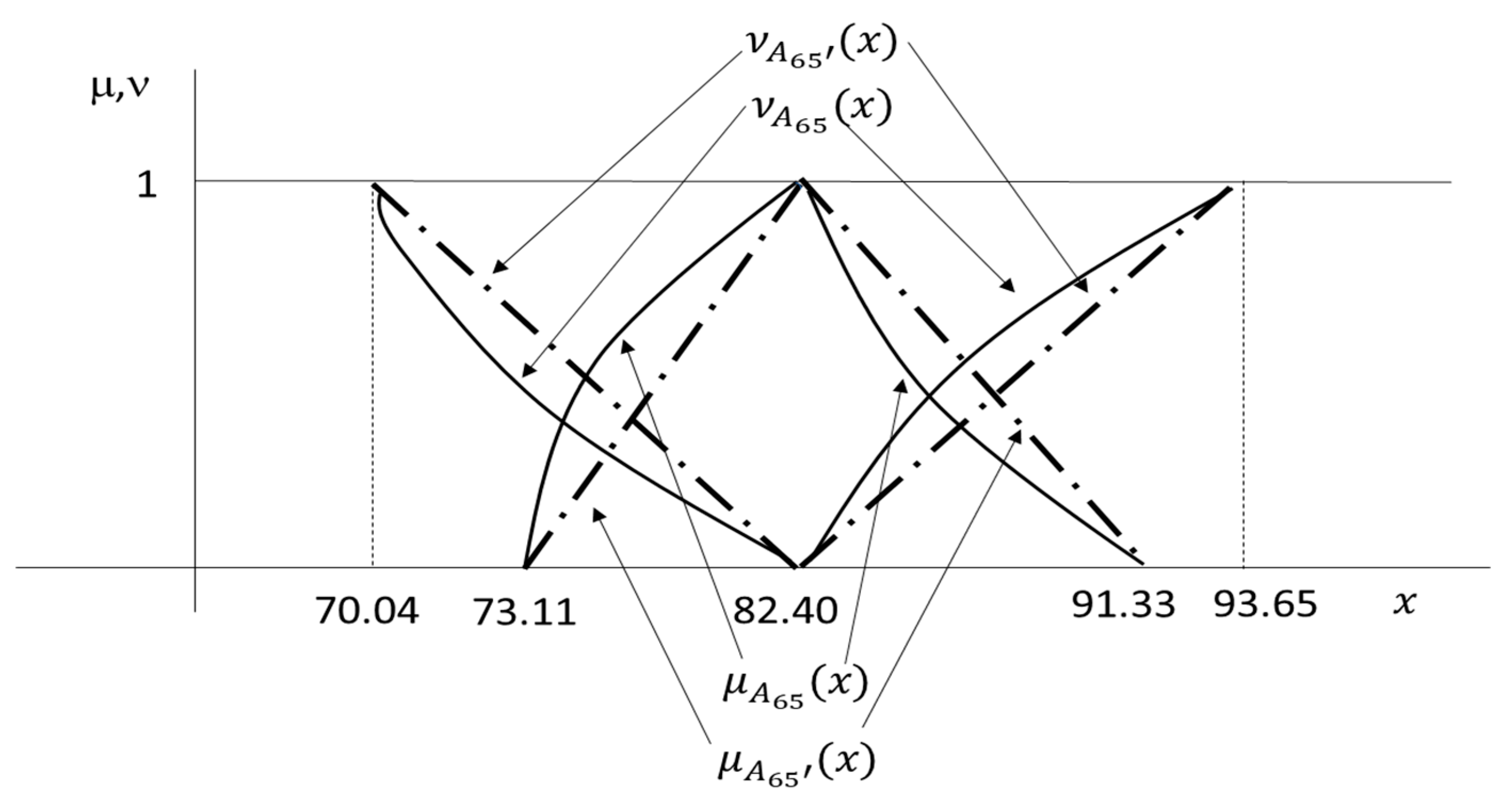
| 1 | 0 | 797.57 | 797.57 | 797.57 | 797.57 | 82.40 | 82.40 | 82.40 | 82.40 |
| 0.75 | 0.25 | 767.44 | 829.95 | 756.02 | 843.58 | 80.12 | 84.66 | 79.43 | 85.30 |
| 0.5 | 0.5 | 739.34 | 864.85 | 718.32 | 894.83 | 77.81 | 86.91 | 76.39 | 88.14 |
| 0.25 | 0.75 | 713.06 | 902.56 | 683.94 | 952.27 | 75.47 | 89.13 | 73.26 | 90.92 |
| 0 | 1 | 688.45 | 943.44 | 652.47 | 1017.14 | 73.11 | 91.33 | 70.04 | 93.65 |
| α | β | ||||||||
| 1 | 0 | 797.57 | 797.57 | 797.57 | 797.57 | 82.40 | 82.40 | 82.40 | 82.40 |
| 0.75 | 0.25 | 770.29 | 834.04 | 761.30 | 852.46 | 80.08 | 84.63 | 79.31 | 85.21 |
| 0.5 | 0.5 | 743.01 | 870.51 | 725.02 | 907.35 | 77.75 | 86.87 | 76.22 | 88.02 |
| 0.25 | 0.75 | 715.73 | 906.97 | 688.74 | 962.25 | 75.43 | 89.10 | 73.13 | 90.83 |
| 0 | 1 | 688.45 | 943.44 | 652.47 | 1017.14 | 73.11 | 91.33 | 70.04 | 93.65 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.0037 | 0.0049 | 0.0070 | 0.0105 | 0.0005 | 0.0003 | 0.0015 | 0.0010 |
| 0.5 | 0.5 | 0.0050 | 0.0065 | 0.0093 | 0.0140 | 0.0007 | 0.0004 | 0.0022 | 0.0013 |
| 0.25 | 0.75 | 0.0037 | 0.0049 | 0.0070 | 0.0105 | 0.0005 | 0.0003 | 0.0018 | 0.0009 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
= 0.00248 =0.00327 =0.00288 |
=0.00466 =0.00700 0.00583 |
=0.00082 =0.00056 =0.00069 |
=0.00271 =0.00166 =0.00218 |
||||||
| α | β | ||||||||
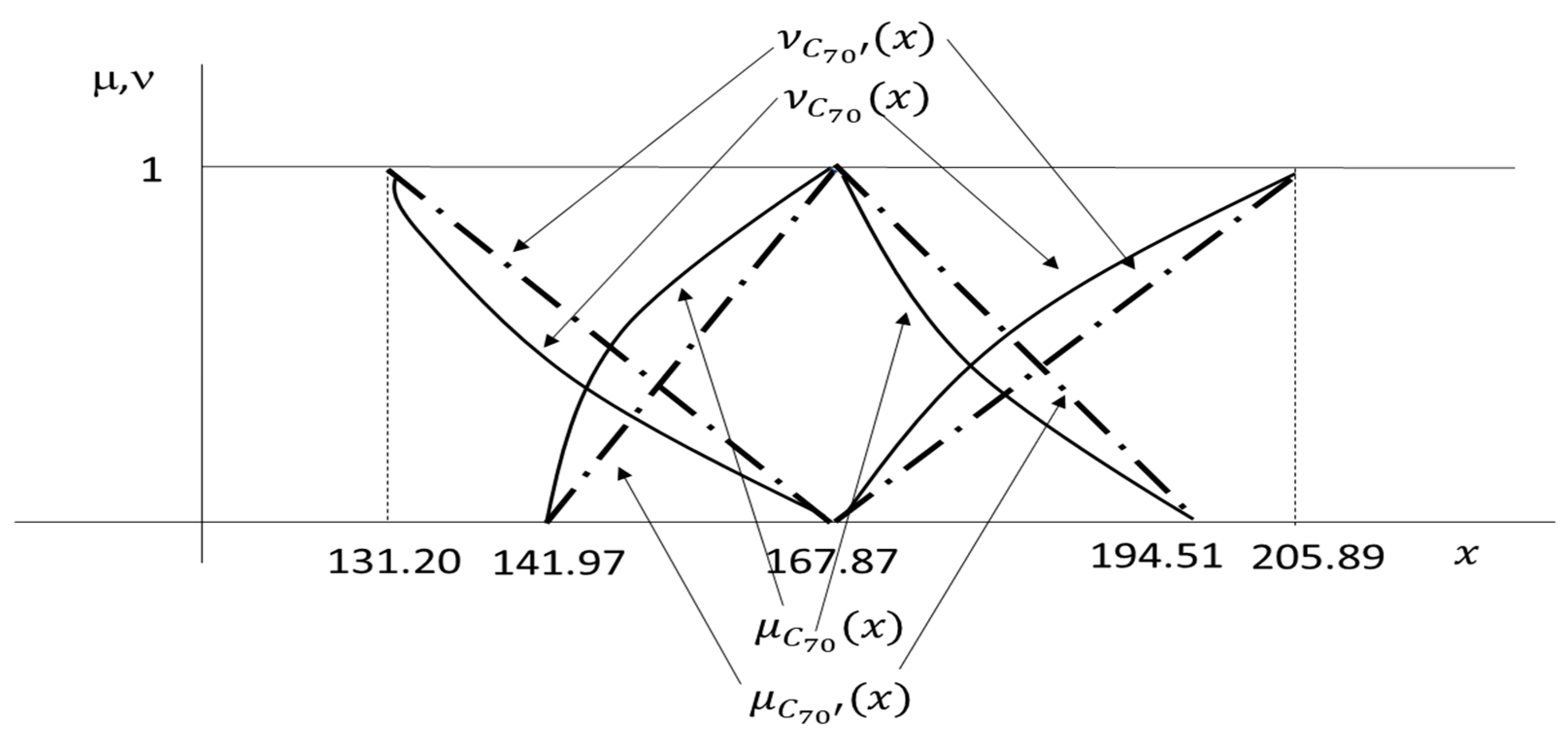
| 1 | 0 | 125.38 | 125.38 | 125.38 | 125.38 | 167.87 | 167.87 | 167.87 | 167.87 |
| 0.75 | 0.25 | 120.49 | 130.30 | 118.54 | 132.27 | 161.33 | 174.46 | 158.59 | 177.24 |
| 0.5 | 0.5 | 115.63 | 135.26 | 111.75 | 139.21 | 154.83 | 181.09 | 149.39 | 186.69 |
| 0.25 | 0,75 | 110.80 | 140.24 | 105.01 | 146.21 | 148.38 | 187.78 | 140.26 | 196.24 |
| 0 | 1 | 106.00 | 145.25 | 98.32 | 153.26 | 141.97 | 194.51 | 131.20 | 205.89 |
| α | β | ||||||||
| 1 | 0 | 125.38 | 125.38 | 125.38 | 125.38 | 167.87 | 167.87 | 167.87 | 167.87 |
| 0.75 | 0.25 | 120.53 | 130.35 | 118.61 | 132.35 | 161.39 | 174.53 | 158.70 | 177.37 |
| 0.5 | 0.5 | 115.69 | 135.32 | 111.85 | 139.32 | 154.92 | 181.19 | 149.54 | 186.88 |
| 0.25 | 0.75 | 110.84 | 140.29 | 105.08 | 146.29 | 148.44 | 187.85 | 140.37 | 196.38 |
| 0 | 1 | 106.00 | 145.25 | 98.32 | 153.26 | 141.97 | 194.51 | 131.20 | 205.89 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.00038 | 0.00035 | 0.00061 | 0.00061 | 0.00041 | 0.00041 | 0.00073 | 0.00077 |
| 0.5 | 0.5 | 0.00052 | 0.00045 | 0.00085 | 0.00078 | 0.00057 | 0.00052 | 0.00101 | 0.00099 |
| 0.25 | 0.75 | 0.00041 | 0.00033 | 0.00066 | 0.00056 | 0.00044 | 0.00038 | 0.00078 | 0.00071 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
= 0.00026 = 0.00023 = 0.00024 |
= 0.00042 = 0.00040 0.00041 |
= 0.00028 = 0.00027 = 0.00027 |
= 0.00050 = 0.00050 0.00050 |
||||||
| α | β | ||||||||
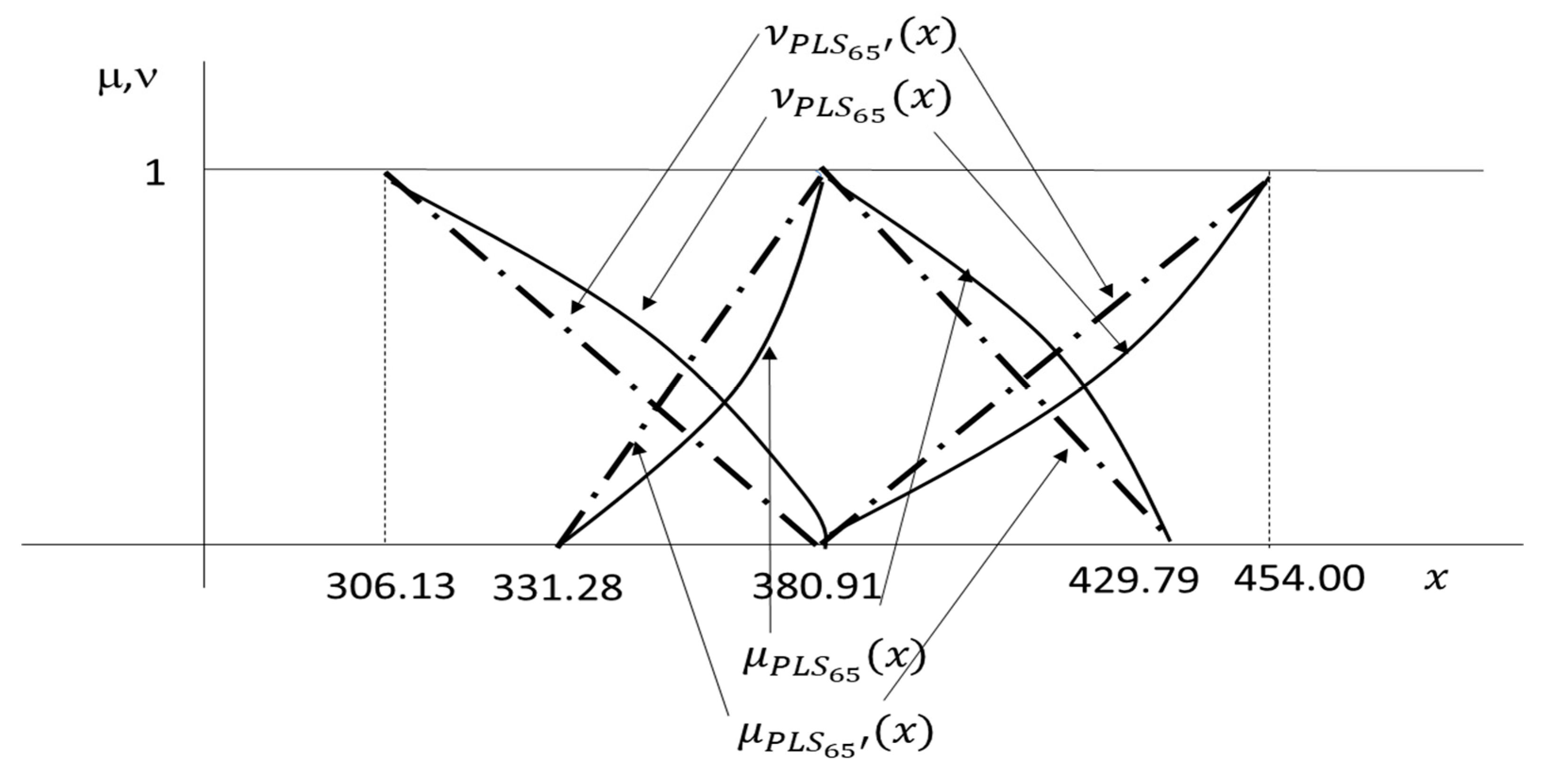
| 1 | 0 | 380.91 | 380.91 | 380.91 | 380.91 | 597.07 | 597.07 | 597.07 | 597.07 |
| 0.75 | 0.25 | 368.58 | 393.19 | 362.39 | 399.32 | 585.46 | 608.44 | 579.56 | 614.05 |
| 0.5 | 0.5 | 356.20 | 405.43 | 343.77 | 417.63 | 573.60 | 619.59 | 561.48 | 630.52 |
| 0.25 | 0.75 | 343.77 | 417.63 | 325.02 | 435.86 | 561.48 | 630.52 | 542.79 | 646.53 |
| 0 | 1 | 331.28 | 429.79 | 306.13 | 454.00 | 549.09 | 641.25 | 523.44 | 662.09 |
| α | β | ||||||||
| 1 | 0 | 380.91 | 380.91 | 380.91 | 380.91 | 597.07 | 597.07 | 597.07 | 597.07 |
| 0.75 | 0.25 | 368.50 | 393.13 | 362.21 | 399.18 | 585.07 | 608.11 | 578.66 | 613.33 |
| 0.5 | 0.5 | 356.09 | 405.35 | 343.52 | 417.45 | 573.08 | 619.16 | 560.26 | 629.58 |
| 0.25 | 0.75 | 343.69 | 417.57 | 324.82 | 435.73 | 561.08 | 630.20 | 541.85 | 645.84 |
| 0 | 1 | 331.28 | 429.79 | 306.13 | 454.00 | 549.09 | 641.25 | 523.44 | 662.09 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.00021 | 0.00016 | 0.00050 | 0.00034 | 0.0007 | 0.0005 | 0.0015 | 0.0012 |
| 0.5 | 0.5 | 0.00029 | 0.00021 | 0.00072 | 0.00043 | 0.0009 | 0.0007 | 0.0022 | 0.0015 |
| 0.25 | 0.75 | 0.00023 | 0.00015 | 0.00059 | 0.00030 | 0.0007 | 0.0005 | 0.0017 | 0.0011 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
= 0.00014 = 0.00011 = 0.00012 |
= 0.00035 = 0.00022 0.00029 |
= 0.00046 = 0.00034 = 0.00040 |
= 0.00106 = 0.00077 = 0.00092 |
||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





