Prerpints.org logo
Preprint
Article

Assessing the Delay, Cost and Quality Risks of Claims on Construction Contract Performance

Altmetrics

Downloads

127

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
Conflicts are frequent within the complex professional environment of the construction industry. If claims cannot be overcome amicably, they result in disputes that lead to litigation. Identification of the causes of these claims and their impact on the duration, cost, and quality of the final project is expected to facilitate the prevention of unsuccessful performance of construction contracts. The novelty of this study is that after codifying the most common causes of construction contract claims derived from the extant literature, they are further investigated in terms of their probability of occurrence and the perceived impact they have on the project completion time, its total cost, and quality. Based on calculated relative importance indices from expert opinion, this paper proposes probability and severity of impact values for 39 common causes of claims in the construction industry. These can be applied to calculate their risk values for stakeholders in public construction contracts to plan mitigation measures of contractual claims. The findings show that the top five riskiest causes of contractual claims in the Greek construction industry are changes in quantities, work, or scope, design quality deficiencies or errors, payment delays, delays in work progress, and the financial failure of the contractor.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The construction sector in Greece experienced a substantial decline after the fiscal crisis of 2008, following the downward trend of GDP and the subsequent fiscal and banking crisis. However, in recent years, it has managed to recover, especially after 2017, when growth rates were observed in the country [1]. Since then, the number of public works construction contracts has been increasing, and copious amounts of money have been allocated by the country's public entities operating in the construction sector. As with all construction industries, the Greek construction industry is plagued with delays and cost overruns that inevitably lead to claims and disputes that, in many cases, end up in litigation, which inevitably cost additional money to both disputing parties.
Within this complex professional environment, where different objectives and benefits compete, according to each involved stakeholder's perspective, conflicts are sure to arise [2]. If these differences cannot be overcome with common courtesy or the use of management skills, they may result in a submission of a claim, i.e., a request for compensation for damages incurred by any party to the contract [3] that if rejected by the other party result in a dispute [4], which are slow to be resolved, especially if they end up in court. Therefore, the submission and rejection of a claim define the start of dispute evolution [5] which may or may not have significant impacts on contract performance. Therefore, identification of the causes of these claims and their impact on the duration, cost, and quality of the final project is expected to facilitate successful performance of the construction project.
Initially, a non-exhaustive literature review was conducted regarding research on claims in the construction industry since 1990. The search was implemented through the Google Scholar platform and through databases such as www.scopus.com, www.researchgate.com, where hundreds of scientific articles, which included the keywords "construction claims" or "construction disputes" were identified. Following this, 50 research papers were chosen to undergo complete content analysis. As seen in Table 1, the research scope for eighteen of these was related to determining and evaluating the causes of construction claims, and eight were regarding dispute resolution methodologies, while two examined both. Also, fourteen studies were dedicated to claim management issues, and four proposed specific claims negotiation processes. Three articles discussed the dispute development process [6], investment risks associated with claims [7], and stakeholders' perceptions of organizational justice and cooperative behavior related to claims management [8], respectively. Finally, Olalekan et al. [9] conducted a bibliometric study of construction disputes. Their result showed that research in this area has focused on managing already existing disputes by litigation, arbitration, and Alternative Dispute Resolution (ADR), while a gap remains around dispute prevention methods.
Furthermore, the content analysis of the 50 examined articles revealed that four types of data sources were used. Data were obtained from the literature, questionnaire surveys, interviews, case studies, or a combination of these. Noteworthy is their geographical spread as they referred to construction claim research in 19 different countries. This is to be expected as the legal, social, and political environments of construction industries around the world are highly diverse. As a result, the findings of one country cannot necessarily be applied to other countries. As a result, research work on construction contract claims in the Greek construction industry was not found.
During the content analysis, it was discovered that regardless of the scope of the research paper, most provided a list of common causes of claims that were investigated from their point of view. Researchers like Ali et al. [10], Arditi & Pattanakitchamroon [11] and Yusuwan and Adnan [12] focused on one specific cause of the claim, i.e., extension of time (EOT) claims, while Ballesteros-Pérez et al. [13] by analyzing severe weather conditions leading to work stoppages and productivity loss leading to project delays created a model that offers advantages for predicting weather-related productivity losses at the design stage.
On the other hand, other researchers examine a significantly greater number of causes of claims (Table 1). For example, Yousefi et al. [14] included sixty risks leading to claims, which they classified into nine categories, i.e., integration, scope, time, procurement, communication, risk, human resource cost, cost, and quality management categories. Using this classification, they developed a model based on the probability impact matrix and used the Analytical Hierarchy Process (AHP) and Artificial Neural Networks (ANNs) to predict the frequency of claims in construction projects. Similarly, Chau [15] created ANN models as a prior to litigation prediction tool for estimating the resolution of a claim. Cakmak and Cakmak [16] used the Analytical Network Process and showed that contractor-related causes of contractual claims and their subcategories are the most common in the Turkish construction industry.
Both Iskandar et al. [17] and Mishmish et al. [3] examined how the ranking of the importance of claims in construction vary between different category of stakeholders. Their research differed in terms of data sources as Iskandar et al. [17] relied on questionnaires, while Mishmish et al.[3] relied on case studies as well as questionnaires.
The quest of numerous researchers was to determine the most common causes of claims for a particular type of project. For example, Nabi and El-Adaway [18] examined the associations between 40 causes of claims for a specific type of construction, that of modular construction in the USA. They found that modular construction disputes are prompted by multiple causes rather than just one cause at a time. Similarly, Bakhary et al. [19] examined the causes of contractual claims in cases of public and private projects in Malaysia's transport, oil, and gas sectors. They found that lack of awareness among on-site staff to proactively identify contractual claims, lack of access or unavailability of relevant documents, and conflicts that arise during negotiation between CA and contractor are the main problems associated with the contractual claim management process. Furthermore, Kisi et al. [20] examined transport construction projects in Nepal with data collected from a questionnaire investigation. They found that contractual claims related to variations, location, conditions, and delays were the most common.
Finally, Shen et al. [21] examined how contractual claims are managed for diverse types of projects worldwide. They considered external risks (social, political, physical, and financial), organizational behavior of clients (untimely payments, change orders, inefficient processing), and the definition of the project in the contract (unclear technical specifications, unclear scope of work) as causes of contractual claims. Their study findings suggest that external risk, client organizational behavior, and project definition in the contract can directly influence contractual claims.
One example of research work aiming to bring claim management techniques up to date with the use of digital tools is by Ibraheem & Mahjoob [22], who showed the potential of BIM in the prevention of causes of claims related to inaccurate quantity estimates, excessive change orders, errors and design changes, drawing and specification defects, and lack of communication between various design disciplines by taking advantage of specific BIM functions such as 3D visualization, clash detection, coordination, and quantity measurement take-off. Before their research, no system was being implemented in most construction projects in Iraq to manage contractual claims, indicating the benefits to be achieved in terms of claim reduction by applying innovative technologies in construction contract management.
For green building projects in Turkey, Mohammadi and Birgonul [7] evaluated the relative importance index (RII) for factors leading to (a) professional liability risks, (b) third-party certification risks, (c) financial risks, and (d) legal contractual risks based on expert opinion and found that legal risks are the ones that cause the contractual claims between the parties involved in sustainable construction projects indicating the significance of being able to identify and assess potential contractual claims in advance through appropriate risk management techniques.
Based on the existing literature described in the previous subsections, there is excellent research interest in the causes of contractual claims and the prediction of the probability of their occurrence. However, no relevant recent research examines this issue in the construction industry in Greece. Moreover, even though each study examines similar causes, comparisons of their results are obstructed due to a lack of standard coding. Therefore, after the content analysis of the selected studies, this paper defines a causes of claims breakdown structure (CCBS) that includes the 39 most common causes of claims as found in the literature that are encountered in real projects internationally.
The novelty of this study is that these common causes of claims, as defined by the literature review and content analysis, are further investigated in terms of their probability of occurrence and the perceived impact they have on the project completion time, its total cost, and quality. As a result, a risk assessment tool for claim prevention can be provided for use by practitioners to fill the gap determined by Olalekan et al. [9] in their recent bibliometric review.
Therefore, the research questions (RQ) are:
  • What is the frequency of occurrence of each cause of contractual claim?
  • What is the perceived impact of each cause of claims on the project's duration?
  • What is the perceived impact of each cause of claims on the project's final cost?
  • What is the perceived impact of each cause of claims on the quality of the project?
  • What are the top five riskiest causes of claims on the overall performance of construction contracts?
Preprints 92878 g001
Figure 1. Causes of Claims Breakdown Structure (CCBS).
Figure 1. Causes of Claims Breakdown Structure (CCBS).
Preprints 92878 g001
Table 1. Literature review content analysis.
Table 1. Literature review content analysis.
Authors Year Data Source1 Research Scope Causes Country
Abdul-Malak et al. [23] 2002 LR Claims management 0
Aibinu et al. [8] 2011 Q/CS Stakeholder perception 0 Singapore
Ali et al. [10] 2020 Q/I/CS Claims management 1 Pakistan
Al-Sabah et al. [24]. 2003 LR Causes of claims 7 Kuwait
Arditi & 2006 LR Claims management 1 N/A
Bakhary et al. [19] 2015 Q Causes of claims 8 Malaysia
Ballesteros-Pérez [13]. 2017 LR Dispute resolution 1 Spain
Barman & Charoenngam 2017 CS Claims management 6 UK
Cakmak & Cakmak [16] 2014 Q/CS Causes of claims 28 Turkey
Chan & Suen [26] 2005 Q Causes of claims and Dispute 16 China
Chan et al., [27] 2006 I Dispute resolution 2 Hong Kong
Chaphalkar et al. [4] 2015 CS Causes of claims 10 India
Chau [15] 2007 LR Dispute resolution 24 Hong Kong
Cheung & Pang [28] 2013 LR Causes of claims and Dispute 8 Hong Kong
Cheung & Suen [29] 2002 LR/I Dispute resolution 0 Hong Kong
Cheung et al. [30] 2019 Q Dispute resolution 56 Hong Kong
Diekmann & Girard [31] 1995 Q/CS Claims management 0 USA
Gardiner & Simmons [32] 1998 I/CS Causes of claims 3 UK
Gould [33] 1998 Q Dispute resolution 0 UK
Ho & Liu [34] 2004 LR Claims management 0
Ibraheem & Mahjoob [22] 2021 Q/CS Causes of claims 16 Iraq
Ilter & Bakioglu [35] 2018 CS Claims management 19 Turkey
Iskandar [17]. 2021 Q Causes of claims 43 Indonesia
Jahren & Dammeier [36] 1990 I Claims management 7 USA
Kartam [37] 1999 LR Claims management 0
Kilian et al. [38] 2005 CS Causes of claims 7 USA
Kisi et al. [20] 2020 Q Dispute resolution 7 International
Kululanga et al. [39] 2001 Q/CS Claims management 0 Malawi
Kumaraswamy [40] 1998 LR/Q/ CS Causes of claims 29 Hong Kong
Mishmish & El-Sauegh [3] 2018 Q/CS Causes of claims 16 UAE
Mitropoulos & Howell [6] 2001 LR Dispute Development Process 14 USA
Mohammadi & Birgonu 2016 Q Investment Risks 4 Turkey
Nabi & El-Adaway [18] 2022 CS Causes of claims 40 USA
Olalekan et al. [9] 2021 LR Bibliometric Review of 0 International
Ren & Anumba [41] 2002 LR Claims Negotiation 0
Ren et al. [42] 2003 CS Claims Negotiation 2
Ren et. Al. [43] 2002 LR Claims Negotiation 4
Scott &Harris, [44] 2004 Q/I Claims management 4 UK
Semple et al. [45] 1994 CS Causes of claims 4 Canada
Shen et al. [21] 2017 Q Claims management 10 International
Stamatiou et al. [46] 2019 LR Claims management 19 Greece/UK
Treacy [47] 1995 LR Dispute resolution 0 USA
Vidogah & Ndekugri [48] 1997 Q/I/CS Claims management 4 UK
Viswanathan et al. [49] 2020 LR/Q Causes of claims 14 India
Wong & Maric [50] 2016 CS Causes of claims 7 Australia
Yogeswaran et al. [51] 1998 CS Causes of claims 11 Hong Kong
Yousefi et al. [14] 2016 LR/CS Causes of claims 60 Iran
Yuan & Ma [52] 2012 LR Claims Negotiation 0
Yusuwan & Adnan [12] 2013 Q Causes of claims 1 Malaysia
Zaneldin [53] 2006 Q/CS Causes of claims 26 UAE
1LR=Literature Review, CS=Case Studies, I=Interviews, Q=Questionnaire
Table 2. Demographic data of the sample
Table 2. Demographic data of the sample
Sex Men (68,2%) Women (31,8%)
Age: 26-34 (4,5%) 35-44 (9,1%) 45-54 (45,5%) 55-64 (31,8%) 65 and over (9,1%)
Highest Academic Degree First University Degree (45,5%) Postgraduate Degree (45,5%) PhD (9,1%)
Profession: Civil Engineer (72,7%) Architect (4,5%) Electrical Engineer (4,5%) Other (18,2%)
The present study follows a mixed-methods research approach using a questionnaire addressed to 22 professionl engineers who have been active in Greece for the last few years and engage in public procurement for construction projects from different workplaces. Data from 50 articles examining the causes of contractual claims in different countries for construction projects in public and private sectors was used to create the questionnaire. Data analysis included descriptive statistical analysis, reliability testing, use of relative importance index, and risk analysis.
The rest of this paper includes section two, which presents the methods for development of the Causes of Claims Breakdown Structure (CCBS), data collection and analysis. The results are presented and discussed in section three. Finally, section four presents the conclusions and limitations of the research, plus recommendations for future research.

2. Research Methods

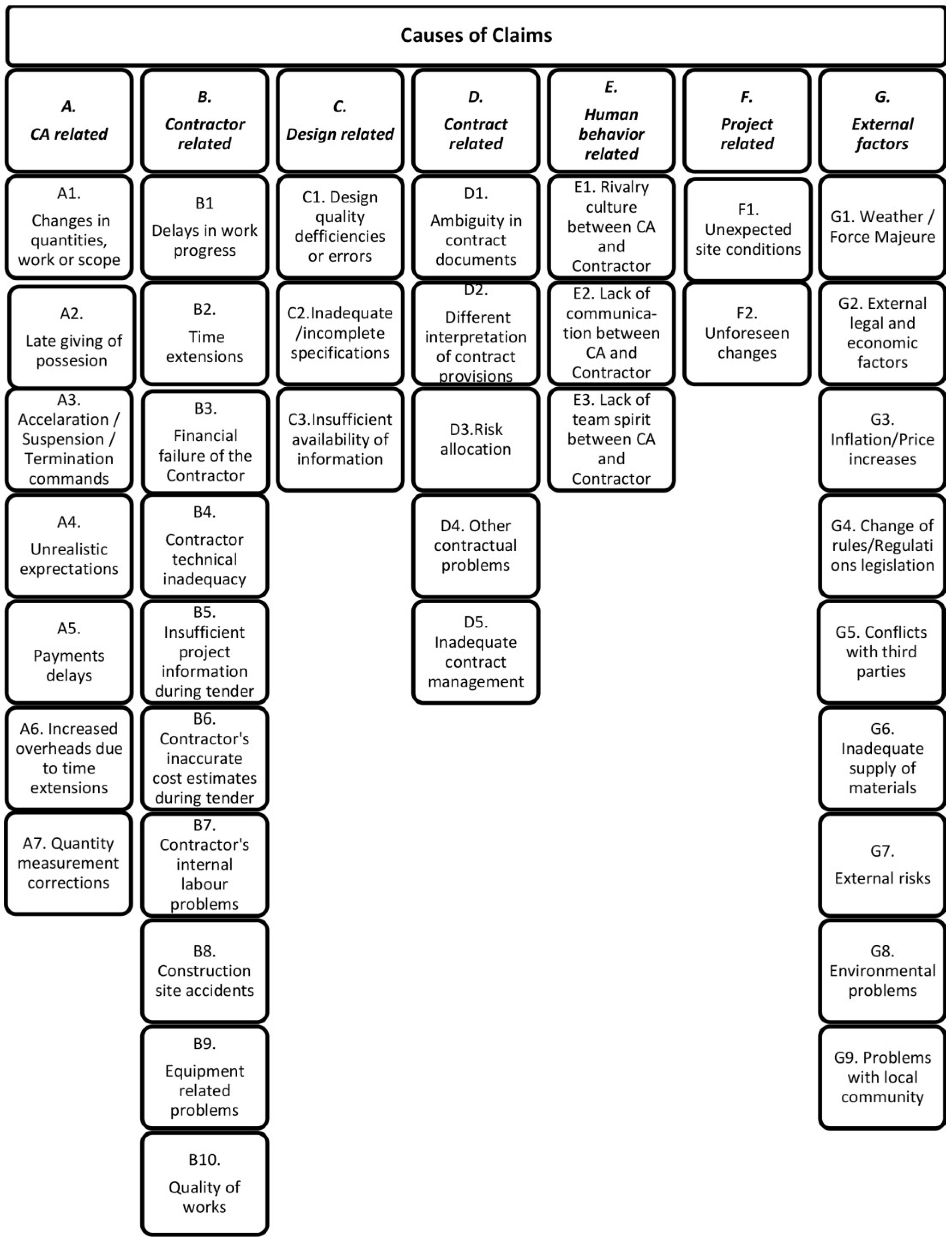
2.1. Causes of Claims Breakdown Structure (CCBS)

The studies in Table 1 defined a series of causes of claims from literature reviews, questionnaire surveys, and/or case studies and then proceeded to categorize and rank them in various ways. The number of causes each researcher utilizes and analyses also differs. Developing a unified classification of causes of claims in construction contracts and creating a common codification can provide a basis for comparing the results of international research. Eight studies examined over twenty causes, while twenty considered less than ten (Table 1).
After the initial collection and production of a study versus causes table with 539 causes (rows) and the 50 studies (columns) and following the removal of causes with the same name or grouping of others with similar meanings, they were consolidated to obtain a final list of 39 causes each appearing at least once and up to 23 times in the selected studies.
Causes of claims, like all risk sources, can be structured and codified to provide a standard representation to help understand, manage, and communicate on a project and industry level while allowing easy comparison between scientific research endeavors. A risk breakdown structure (RBS) is the categorization of risk sources in a hierarchical structure [54]. As a result, 39 factors were coded and classified in the CCBS, as shown in Figure 1. It provides a comprehensive yet detailed view of the hierarchy of the predominant causes of claims examined in the selected studies. Based on Cakmak & Cakmak’s [16] categorization, the 39 factors were classified into the following seven categories relating to the contracting authority (CA), the contractor, the design, the contract, human behavior, the project itself, and external factors.

2.2. Data Collection

The questionnaire examined the opinions of experts on 39 common causes of contractual claims in public construction contracts according to: (a) the frequency of their occurrence, (b) the perceived impact they have on the time to complete the project, (c) the perceived impact on the total cost of the project and (d) the perceived impact on the quality of the final project.
A mixed-methods research approach [55] was applied that integrated qualitative data (opinions of experts) in quantitative form (based on closed-ended responses to a relevant survey) with quantitative research analysis methods (Likert scale ratings, relative importance index, and risk value). It was designed to describe quantitatively a population's trends, attitudes, or opinions [55] based on the qualitative views of the expert participants instead of actual data from claims made in real projects. This survey research method can be called the 'knowledge mining' method that has been used in construction management research by the authors and others to determine expert opinion and practitioners' insight on delay factors [56], cost escalation [57], contract types [58], project procurement systems [59,60], project managers' attributes [61], barriers to energy upgrading of buildings [62], safety control [63] as well as for claim management problems [19].
The questions were mostly multiple-choice, closed-ended questions. The first part of the questionnaire consists of 11 questions that relate to the demographic and personal data of the survey participants, who are active engineers of different specializations. The second part includes an assessment of the causes of contractual claims in public works contracts in terms of the four variables (frequency of occurrence, impact on project completion time, total project cost, and quality of the final project). This section uses the five-point Likert scale, with the assessment being made using two ways of scoring:
  • 1- Never, 2- Rarely, 3- Often, 4- Many times and 5- Always. (RQ1)
  • 1- Not at all, 2- Very little, 3 - A little, 4 - A lot, and 5 - Very much (RQ2-4)
Participants expressed their opinions on the level of agreement for each variable using the above scales, which were later transformed into numerical scores with values from 1 to 5 in SPSS. In addition, the questionnaire included an open-ended question on ways to address or reduce the incidence of claims in the management of public construction contracts, which was not compulsory and was answered by 11 out of 22 sample participants.
From the onset, the questionnaire was chosen to be addressed to experts rather than the general population because of the nature and scope of the subject matter, which requires knowledge and experience in public works contracting. Professionals with knowledge of public construction project management have also faced contractual claims and disputes and can objectively capture the root causes of construction contractual claims. It should be noted that the corresponding author, who has decades of personal experience in claim management for highway construction contracts, retained numerous experienced contacts in the industry to whom a private direct message was sent to inform them of the purpose of the survey. Thus, this convenience sampling method [64] collected 22 responses by posting on the LinkedIn social media platform and sending 36 personal invitations through Meta Messenger and Viber. The questionnaires were distributed via Google Forms and were completed and submitted anonymously from January to February 2023.

2.3. Data Analysis Methodology

The data from the questionnaire survey were analyzed using the IBM SPSS statistical tool. For the Likert scale questions, it was found that the mean and standard deviation of the variables were not sufficient, as most of the results were near the neutral answer. Thus, it was chosen to perform the subsequent data analysis by calculating each variable's Relative Importance Index (RII) and use the results to carry out a risk analysis by calculating the resulting Risk Value (RV) to measure the risk of each cause of contractual claim on the duration, time, quality, and overall performance of the final project.
The RII has been used in construction management research to assess the severity of identified delay factors on project duration and cost escalation [65,66,67,68], to rank the significance of accident contributing factors [63], and to conduct meta-analyses of data from multiple studies [69].
In this study, the RII was calculated using Microsoft Excel according to equation 1, adapted from Holt [70], for each of the 156 variables (39 causes X 4 research questions) rated on a five-point Likert scale.
R I I = ∑ a = 1 m P i U i n N
Where,
m = number of integers on the response scale (in this case 5)
Pi= takes values 1 to 5 in increasing frequency/severity
Ui= number of respondents that selected Pi
N = Total number of respondents (N = 22)
n = maximum value of maximum rating (in this case 5)
It should be clarified that all questions were compulsory (except the open-ended question), and thus, there were no blank answers. As a result, the RII can take values from 0 to 1 and is therefore taken as a measure of the probability of occurrence of a particular cause of claims. In this case the lowest possible value is 0.2 since the worst-case scenario of all respondents choosing Never or Not at all the formula produce an RII value of 0.2.
The risk analysis complements the RII analysis, as the RII method, although effective in ranking the various causes of claims in terms of their perceived frequency of occurrence, does not take into account the magnitude of their impact or the vulnerability that a particular construction project may have for each cause of claim and thus does not provide all the knowledge required to conduct contractual claim risk analysis for a new project [68].
Risks on the successful outcome of a construction contract correspond to uncertain events or situations which, if they manifest, may have a positive or negative impact on the objectives of the construction project [54]. In this case, the causes of claims are risks that, if they occur, will have a negative impact on the objective of completing the project within the planned schedule, budgeted cost, and expected quality. In this context, the risk is considered a multidimensional quantity approximated by a point estimate as the expected value resulting from multiplying the probability of the cause of the claim occurring (P) by its consequence, impact, or severity (S) given that it has taken place. Thus, the Risk Value (RV) of the cause of a claim can be calculated by equation 2 [54].
RV =Pi *Si,

3. Results and Discussion

3.1. Demographic and Personal Characteristics

Table 2 and Table 3 present the demographic data and experience of the 22 survey participants. All participants have experience in public contract management either as engineers of the construction contractor or as engineers of the contracting authority (CA) or both. Furthermore, 17 participants responded that they have experience in construction contract management as engineers of the construction contractor, and 16 people answered that they have experience in construction contract management as supervising engineers of the CA (72.73%) and 50% both. Overall, it is judged that the sample is quite experienced in managing public construction contracts in the capacity of construction contractor engineer and the capacity of CA engineer.

3.2. Relative Importance Indices (RII)

Cronbach's alpha reliability index was calculated for each of the four research questions by including the 39 tested causes derived from the literature in each of them. A high internal consistency for the data set is observed (Table 4) as the Cronbach's alpha index takes in each case values greater than 0.7 [71].
Chen et al. [72] suggest that the comparison of RII should be made with the corresponding level of importance as measured by the following transformation scheme:
  • High for values greater than 0.8
  • High-medium for values between 0,6 and 0,8
  • Medium for values between 0,4 and 0,6
  • Medium-low for values between 0.2 and 0.4
  • Low for values less than 0.2
Table 5 presents the mean, standard deviation, and RII index of the respondents' answers to RQ1-RQ4 as well as the number of times each cause appeared in the 50 studies. First, regarding the frequency of occurrence of the examined causes of claims as they have experienced during their professional career, we observe that in the Greek construction industry, the most frequently occurring cause of claims is "Changes in quantities, work, or scope (A1)" with RII = 0.75. Next, the results related to RQ2 show that in the Greek construction sector the most significant impact on the project duration is caused by “Financial failure of the contractor (B3)” with RII=0.78. Furthermore, regarding the perceived severity of the impact of the various causes of claims on the total project cost (RQ3), we observe that the cause with the most significant impact on the total project cost (RII = 0.79) is the “Inflation/Price Rises (G3).” Finally, from the responses to RQ4, it is observed that in the Greek construction sector, the cause of contractual claims with the greatest impact on the quality of the final project is “Time extensions (B2)” (RII = 0.81).
Table 6 depicts the causes ranked in the top ten for each research question, i.e., the most frequent causes and the ten causes with the most severe perceived impact on the final duration, cost, and quality. It is interesting to note that while “Changes in quantities, work or scope (A1)” is the most probable cause, it is perceived to have a significant impact (>0.6) on cost (RIIC=0.75) and duration (RIID=0.78) and not on quality. On the other hand, the cause perceived to have the greatest impact on the quality of the project “Time extensions (B2)” is not in the top 10 frequent causes at all.

3.3. Risk Analysis

The degree of risk refers not only to the probability of something happening but also to the impact of the risk in question. The RII index calculated for the frequency of occurrence of the causes as rated by the respondents (Table 6) was used to determine the (P) probability values. The S (severity) value is subjective and varies according to the risk aversion of the decision maker and the actual conditions for each project [68]. However, in the case of this research, the RII indicators obtained by processing the respondents' answers on the extent to which they believe that each cause impacts the duration (RIIid ), cost (RIIic ), and quality of the final project (RIIiq) were calculated (Table 6)
The degree of risk in terms of time (RVt), cost (RVc), and quality (RVq) of the final project was then calculated as follows:
RVD=Pi*Sid=RIIi*RIid,
RVC=Pi*Sic=RIIi*RIic,
RVQ=Pi*Siq=RIIi*RIiq
Table 7 presents the risk values (RVD, RVC, RVQ ) and their ranking according to the their calculated risks on project duration (Rank RVD ), total project cost (Rank RVC ), and project quality (Rank RVQ). The three causes with the highest risk value in terms of project duration are “Changes in the quantities, work, or scope (A1), “Financial failure of the contractor (B3)” and “Delays in work progress (B1).” Of the three, only “Financial failure of the contractor (B3)” was perceived as having the greatest impact on duration while “Changes in quantities, work or scope (A1)” ranked 6th with a significant RIID value of 0, 75 and “Delays in work progress (B1)” ranked 3rd with RIID =0.76 but with medium to high probability of occurrence RIIi = 0.66. Obviously changes in scope take time to take effect and if design changes are required and in cases of increased quantities also require additional time to be completed. Similarly, financial problems endured by the contractor will lead them to adjust their resource planning which will inevitably take their toll on project progress. Finally, it goes without saying that any delays on the progress of work will have detrimental effects on project completion.
The riskiest causes of claims regarding the increase in project costs are, again, “Changes in quantities, work, or scope (A1).” Notably instead of “Inflation/Price Increases (G3)” emerging as the second riskiest cause on cost increase which was perceived with the highest impact on cost, this time, in second place is “Design quality deficiencies or errors (C1), and in third place is “Payment delays (A5)” in terms of risk value on cost increases. It is found that change orders and design deficiencies are risks with a greater potential to lead to project cost overruns than causes related directly to payment delays. Finally, to prevent significant impacts on the quality of projects, mitigation measures to prevent claims arising from “Design quality deficiencies or errors (C1) and “Payment delays (A5)”and “Changes in quantities, work or scope (A1)”should be implemented.
An attempt is then made to synthesize the results to determine which causes have the highest overall risk level considering all three risk values (RVD, RVC, RVQ ). Based on the results of the individual RVs for the three variables considered, weight is given to each risk level by considering two scenarios. The first probability scenario (Scenario 1) calculates a weighting factor of 70% for the project duration (wd), 15% for the impact on the total cost (wc), and another 15% for the effect on the quality of the final project (wq). That is, the decision maker, in this case, considers the impact on duration more important than the impact on cost and time. The results differ in the case of the second scenario (Scenario 2), in which the weighting factor for the impacts on duration, cost, and quality of the final project are considered equal and thus calculated at 33.3% for each variable. Table 7 presents the results of Scenario 1 and Scenario 2 with the ranking of each cause according to the resulting TRV as follows:
TRVi=wd *RViD + wc *RViC + wq *RVQ,
We observe that in both scenarios agree on the top 5 most dangerous causes of contractual claims that affect overall project performance although in a slightly different, These are once again “Changes in quantities, work, or scope (A1)”, in both scenarios followed by “Design quality deficiencies or errors (C1), “Payment delays (A5)”, “Delays in work progress (B1)” and the “Financial failure of the contractor (B3).”

3.4. Expert Proposals for Mitigation Measures

The questionnaire included an open-ended question on the participants' views on how claims can be addressed or reduced in the management of public construction contracts. Participant P3 believes that one way is "to better inform potential contractors about the project and the site conditions during the formulation of the financial offer, and another is to promote a team spirit between the contractor and the contracting authority."
According to Participant P7, one way is to "draw up detailed rules, specifications and studies." Similarly, participant P11 considers that the solution is "better designs and more elaborate contract documents." The twelfth participant, P12, suggests more “professionalism and proper training.” Participants P14 and P16 respectively mention as a way of resolution "the most comprehensive designs possible, timely giving possession of the land, ensuring financial flow throughout the project, timely response CA to problems" and "better designs with supervision by the designer during construction," respectively.
There is another view expressed by the thirteenth participant (P13) that "better preparation of the pre-contractual stage for all kinds of licensing and anything related" is needed. Participant P18 suggests "tendering with a design-build system." In contrast, participant P20, based on their experience in the execution of public works, considers that "the Amicable Settlement Committee or as it is now called Arbitration can help all stakeholders" and believes "the activation of article 176 of Law 4412/16 is necessary for a wider range of projects and not only for projects above 10.000.000€". This stipulation refers to the procedures for applying arbitration as a dispute resolution method instead of the administrative and judicial procedures that can be used in all cases of public works contracts in Greece.

4. Conclusions

Based on calculated RII values from the opinions of experts in the field, this paper proposes probability and severity of impact values for 39 common causes of claims in the construction industry in Greece. These can be applied for the calculation of their RVs to guide Greek stakeholders in public construction contracts to plan mitigation measures for the consequences of contractual claims on construction contract performance. From the ranking of the causes based on the TRV, the causes of contractual claims that most affect the performance of construction projects in Greece are highlighted. In response to RQ 5, it is shown that the top five riskiest causes of contractual claims in the Greek construction industry that affect overall project performance are “Changes in quantities, work, or scope (A1)” followed by “Design quality deficiencies or errors (C1), “Payment delays (A5)”, “Delays in work progress (B1)” and the “Financial failure of the contractor (B3)”.
This paper contributes to the international literature on the causes of contractual claims in construction projects as it pioneers by simultaneously examining the views of experts on the frequency of occurrence of causes of contractual claims and their perceived impact on the time, total cost, and quality of the final project, for which there is a research gap in the literature. In addition, this paper defines a causes of claims breakdown structure (CCBS) that includes the most common causes of claims that are encountered in real projects internationally, as found in the literature, which international researchers can use to facilitate comparison of results to provide global conclusions. Limitations of this study are that it needs to be more focused on specific construction types and is based only on expert opinion, and should, therefore, be verified based on existing project claims data.
Nevertheless, the results of this study can be used as a springboard for the development of an optimal streamlined dispute prevention method for which a gap in the literature remains [9]. The research team envisages that this can be achieved by the adoption of advanced technologies such as BIM, Blockchain, and Smart Contracts to address the above-flagged issues by improving and automating progress payments as suggested recently by Shojaei et al. [73], Di Giuda et al. [74], Hamledari and Fischer [75] and Sonmez et al. [76], better-managing delays in work progress and associated EOT claims [10] while utilizing specific BIM functions such as 3D visualization, clash detection, coordination, and quantity measurement take-off to ensure minimization of changes in quantities, work, or scope and design quality deficiencies or errors [22]. Finally, provisions in the tender procedures to prevent the selection of a contractor with indications of financial difficulties can be implemented to avoid claims caused by the financial failure of the contractor.

Author Contributions

Conceptualization, F.A.; methodology, F.A..; software, A.T.; validation, F.A. and A.T.; formal analysis, A.T.; investigation, A.T.; data curation, A.T..; writing—original draft preparation, F.A. and A.T.; writing—review and editing, F.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Monastiriotis, V.; Psycharis, Y. Between Equity, Efficiency and Redistribution: An Analysis of Revealed Allocation Criteria of Regional Public Investment in Greece. Eur Urban Reg Stud 2014, 21, 445–462, doi:10.1177/0969776412455990. [CrossRef]
  2. Cheung, S.O.; Yiu, T.W. Are Construction Disputes Inevitable? IEEE Trans Eng Manag 2006, 53, 456–470, doi:10.1109/TEM.2006.877445. [CrossRef]
  3. Mishmish, M.; El-Sayegh, S.M. Causes of Claims in Road Construction Projects in the UAE. International Journal of Construction Management 2018, 18, 26–33, doi:10.1080/15623599.2016.1230959. [CrossRef]
  4. Chaphalkar, N.B.; Iyer, K.C.; Patil, S.K. Prediction of Outcome of Construction Dispute Claims Using Multilayer Perceptron Neural Network Model. International Journal of Project Management 2015, 33, 1827–1835, doi:10.1016/j.ijproman.2015.09.002. [CrossRef]
  5. Naji, K.K.; Mansour, M.M.; Gunduz, M. Methods for Modeling and Evaluating Construction Disputes: A Critical Review. IEEE Access 2020, 8, 45641–45652, doi:10.1109/ACCESS.2020.2976109. [CrossRef]
  6. Mitropoulos, P.; Howell, G. Model for Understanding, Preventing, and Resolving Project Disputes. J Constr Eng Manag 2001, 127, 223–231. Doi: 10.1061/(asce)0733-9364(2001)127:3(223). [CrossRef]
  7. Mohammadi, S.; Birgonul, M.T. Preventing Claims in Green Construction Projects through Investigating the Components of Contractual and Legal Risks. J Clean Prod 2016, 139, 1078–1084, doi:10.1016/j.jclepro.2016.08.153. [CrossRef]
  8. Aibinu, A.A.; Ling, F.Y.Y.; Ofori, G. Structural Equation Modelling of Organizational Justice and Cooperative Behaviour in the Construction Project Claims Process: Contractors’ Perspectives. Construction Management and Economics 2011, 29, 463–481, doi:10.1080/01446193.2011.564195. [CrossRef]
  9. Olalekan, O.T.; Ariffin, H.L.B.T.; Ali, K.N.; Raslim, F.M.; Mohamad, M.B. Bibliometric Analysis of Construction Dispute. Malaysian Construction research Journal Special Issue 2021, 12.
  10. Ali, B.; Zahoor, H.; Nasir, A.R.; Maqsoom, A.; Khan, R.W.A.; Mazher, K.M. BIM-Based Claims Management System: A Centralized Information Repository for Extension of Time Claims. Autom Constr 2020, 110, doi:10.1016/j.autcon.2019.102937. [CrossRef]
  11. Arditi, D.; Pattanakitchamroon, T. Selecting a Delay Analysis Method in Resolving Construction Claims. International Journal of Project Management 2006, 24, 145–155, doi:10.1016/j.ijproman.2005.08.005. [CrossRef]
  12. Yusuwan, N.M.; Adnan, H. Issues Associated with Extension of Time (EoT) Claim in Malaysian Construction Industry. Procedia Technology 2013, 9, 740–749, doi:10.1016/j.protcy.2013.12.082. [CrossRef]
  13. Ballesteros-Pérez, P.; Rojas-Céspedes, Y.A.; Hughes, W.; Kabiri, S.; Pellicer, E.; Mora-Melià, D.; del Campo-Hitschfeld, M.L. Weather-Wise: A Weather-Aware Planning Tool for Improving Construction Productivity and Dealing with Claims. Autom Constr 2017, 84, 81–95, doi:10.1016/j.autcon.2017.08.022. [CrossRef]
  14. Yousefi, V.; Yakhchali, S.H.; Khanzadi, M.; Mehrabanfar, E.; Šaparauskas, J. Proposing a Neural Network Model to Predict Time and Cost Claims in Construction Projects. Journal of Civil Engineering and Management 2016, 22, 967–978, doi:10.3846/13923730.2016.1205510. [CrossRef]
  15. Chau, K.W. Application of a PSO-Based Neural Network in Analysis of Outcomes of Construction Claims. Autom Constr 2007, 16, 642–646, doi:10.1016/j.autcon.2006.11.008. [CrossRef]
  16. Cakmak, E.; Cakmak, P.I. An Analysis of Causes of Disputes in the Construction Industry Using Analytical Network Process. Procedia Soc Behav Sci 2014, 109, 183–187, doi:10.1016/j.sbspro.2013.12.441. [CrossRef]
  17. Iskandar; Hardjomuljadi S.; Sulistio H. The Most Influencing Factors on the Causes of Construction Claims and Disputes in the EPC Contract Model of Infrastructure Projects in Indonesia. Review of Internationa Geographical Education (RIGEO) 2021, 11, 80–91.
  18. Abdul Nabi, M.; El-adaway, I.H. Understanding Disputes in Modular Construction Projects: Key Common Causes and Their Associations. J Constr Eng Manag 2022, 148, doi:10.1061/(asce)co.1943-7862.0002208. [CrossRef]
  19. Bakhary, N.A.; Adnan, H.; Ibrahim, A. A Study of Construction Claim Management Problems in Malaysia. Procedia Economics and Finance 2015, 23, 63–70, doi:10.1016/s2212-5671(15)00327-5. [CrossRef]
  20. Kisi, K.P.; Lee, N.; Kayastha, R.; Kovel, J. Alternative Dispute Resolution Practices in International Road Construction Contracts. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2020, 12.
  21. Shen, W.; Tang, W.; Yu, W.; Duffield, C.F.; Hui, F.K.P.; Wei, Y.; Fang, J. Causes of Contractors’ Claims in International Engineering-Procurement-Construction Projects. Journal of Civil Engineering and Management 2017, 23, 727–739, doi:10.3846/13923730.2017.1281839. [CrossRef]
  22. Ibraheem, R.A.R.; Mahjoob, A.M.R. Facilitating Claims Settlement Using Building Information Modeling in the School Building Projects. Innovative Infrastructure Solutions 2022, 7, doi:10.1007/s41062-021-00646-2. [CrossRef]
  23. Abdul-Malak, M.A.U.; El-Saadi, M.M.H.; Abou-Zeid, M.G. Process Model for Administrating Construction Claims. Journal of Management in Engineering 2002, 18, 84–94.
  24. Al-Sabah, S.S.J.A.; Fereig, S.M.; Hoare, D.J. A Database Management System to Document and Analyse Construction Claims. Advances in Engineering Software 2003, 34, 477–491. Doi: 10.1016/s0965-9978(03)00044-9. [CrossRef]
  25. Barman, A.; Charoenngam, C. Decisional Uncertainties in Construction Projects as a Cause of Disputes and Their Formal Legal Interpretation by the Courts: Review of Legal Cases in the United Kingdom. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2017, 9.
  26. Chan, E.H.W.; Suen, H.C.H. Disputes and Dispute Resolution Systems in Sino-Foreign Joint Venture Construction Projects in China. Journal of Professional Issues in Engineering Education and Practice 2005, 131, 141–148, doi:10.1061/(ASCE)1052-3928(2005)131:2(141). [CrossRef]
  27. Chan, E.H.; Suen, H.C.; Chan, C.K. MAUT-Based Dispute Resolution Selection Model Prototype for International Construction Projects. J Constr Eng Manag 2006, 132, 444–451, doi:10.1061/(asce)0733-9364(2006)132:5(444). [CrossRef]
  28. Cheung, S.O.; Pang, K.H.Y. Anatomy of Construction Disputes. J Constr Eng Manag 2013, 139, 15–23, doi:10.1061/(asce)co.1943-7862.0000532. [CrossRef]
  29. Cheung, S.O.; Suen, H.C.H. A Multi-Attribute Utility Model for Dispute Resolution Strategy Selection. Construction Management and Economics 2002, 20, 557–568, doi:10.1080/01446190210157568. [CrossRef]
  30. Cheung, S.O.; Li, K.; Levina, B. Paradox of Bias and Impartiality in Facilitating Construction Dispute Resolution. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2019, 11.
  31. Diekmann, J.E.; Girard, M.J. Are Contract Disputes Predictable? J Constr Eng Manag 1995, 121, 355–363. Doi: 10.1061/(ASCE)0733-9364(1995)121:4(355). [CrossRef]
  32. Gardiner, P.D.; Simmons, J.E.L. Conflict in Small- and Medium-Sized Projects: Case of Partnering to the Rescue. Journal of Management in Engineering 1998, 14, 35–40. Doi: 10.1061/(asce)0742-597x(1998)14:1(35). [CrossRef]
  33. Gould, N. Alternative Dispute Resolution in the UK Construction Industry; 1998; Vol. 2;.
  34. Ho, S.P.; Liu, L.Y. Analytical Model for Analyzing Construction Claims and Opportunistic Bidding. J Constr Eng Manag 2004, 130, 94–104, doi:10.1061/(asce)0733-9364(2004)130:1(94). [CrossRef]
  35. Ilter, A.D.; Bakioglu, G. Modeling the Relationship between Risk and Dispute in Subcontractor Contracts. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2018, 10.
  36. Jahren, C.T.; Dammeier, B.F. Investigation into Construction Disputes. Journal of Management in Engineering 1990, 6. Doi: 10.1061/(ASCE)9742-597X(1990)6:1(39). [CrossRef]
  37. Kartam, S. Generic Methodology for Analyzing Delay Claims. J Constr Eng Manag 1999, 125, 409–419. https://doi.org/10.1061/(asce)0733-9364(1999)125:6(409). [CrossRef]
  38. Kilian, J.J.; Gibson, G.E.; Asce, M. Construction Litigation for the U.S. Naval Facilities Engineering Command, 1982-2002. J Constr Eng Manag 2005, 131, 945–952.
  39. Kululanga, G.K.; Kuotcha, W.; Mccaffer, R.; Edum-Fotwe, F. Construction Contractors’ Calaim Process Framework. J Constr Eng Manag 2001, 127, 309–314. https://doi.org/10.1061/(ASCE)0733-9364(2001)127:4(309). [CrossRef]
  40. Kumaraswamy, M.M. Consequences of Construction Conflict: A Hong Kong Perspective. Journal of Managnement in Engineering 1998, 14, 66–74. https://doi.org/10.1061/(asce)0742-597x(1998)14:3(66). [CrossRef]
  41. Ren, Z.; Anumba, C.J. Learning in Multi-Agent Systems: A Case Study of Construction Claims Negotiation. Advanced Engineering Informatics 2002, 16, 265–275, doi:10.1016/S1474-0346(03)00015-6. [CrossRef]
  42. Ren, Z.; Anumba, C.J.; Ugwu, O.O. The Development of a Multi-Agent System for Construction Claims Negotiation. In Proceedings of the Advances in Engineering Software; Elsevier Ltd, 2003; Vol. 34, pp. 683–696.
  43. Ren, Z.; Anumba, C.J.; Ugwu, O.O. Negotiation in a Multi-Agent System for Construction Claims Negotiation. Applied Artificial Intelligence 2002, 16, 359–394, doi:10.1080/08839510290030273. [CrossRef]
  44. Scott, S.; Harris, R.A. United Kingdom Construction Claims: Views of Professionals. J Constr Eng Manag 2004, 130, 734–741, doi:10.1061/(asce)0733-9364(2004)130:5(734). [CrossRef]
  45. Semple, C.; Hartman, F.T.; Jergeas, G. Construction Claims and Disputes: Causes and Cost/Time Overruns. J Constr Eng Manag 1994, 120, 785–795. https://doi.org/10.1061/(ASCE)0733-9364(1994)120:4(785). [CrossRef]
  46. Stamatiou, D.R.I.; Kirytopoulos, K.A.; Ponis, S.T.; Gayialis, S.; Tatsiopoulos, I. A Process Reference Model for Claims Management in Construction Supply Chains: The Contractors’ Perspective. International Journal of Construction Management 2019, 19, 382–400, doi:10.1080/15623599.2018.1452100. [CrossRef]
  47. Treacy, T.B. Use of Alternative Dispute Resolution in the Construction Industry. Journal of Management in Engineering 1995, 11, 58–63. https://doi.org/10.1061/(ASCE)0742-597X(1995)11:1(58). [CrossRef]
  48. Vidogah, W.; Ndekugri, I. Improving Management of Claims: Contractors’ Perspective. Journal of Management in Engineering 1997, 13, 37–44. https://doi.org/10.1061/(ASCE)0742-597X(1997)13:5(37). [CrossRef]
  49. Viswanathan, S.K.; Panwar, A.; Kar, S.; Lavingiya, R.; Jha, K.N. Causal Modeling of Disputes in Construction Projects. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2020, 12.
  50. Wong, P.S.P.; Maric, D. Causes of Disputes in Construction Planning Permit Applications. 2016.
  51. Yogeswaran, K.; Kumaraswamy, M.M.; Miller, D.R.A. Claims for Extensions of Time in Civil Engineering Projects. Construction Management and Economics 1998, 16, 283–293, doi:10.1080/014461998372312. [CrossRef]
  52. Yuan, H.; Ma, H. Game Analysis in the Construction Claim Negotiations. In Proceedings of the Procedia Engineering; 2012; Vol. 28, pp. 586–593. https://doi.org/10.1016/j.proeng.2012.01.773. [CrossRef]
  53. Zaneldin, E.K. Construction Claims in United Arab Emirates: Types, Causes, and Frequency. International Journal of Project Management 2006, 24, 453–459, doi:10.1016/j.ijproman.2006.02.006. [CrossRef]
  54. Ayyub, B.M. Risk Analysis in Engineering and Economics; 2nd ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2014;
  55. Creswell, J.W. Research Design. Qualitative, Quantitative and Mixed Methods Approaches; 4th ed.; Sage Publications, 2014;
  56. Arantes, A.; Ferreira, L.M.D.F. A Methodology for the Development of Delay Mitigation Measures in Construction Projects. Production Planning & Control 2021, 32, 228–241, doi:10.1080/09537287.2020.1725169. [CrossRef]
  57. Keng, T.C.; Mansor, N.; Ching Y. K. An Exploration of Cost Overrun in Building Construction Projects. Global Business and Management Research: An International Journal 2018, 10, 638–646.
  58. Antoniou, F.; Aretoulis, G.N.; Konstantinidis, D.K.; Kalfakakou, G.P. An Empirical Study of Researchers’ and Practitioners’ Views on Compensating Major Highway Project Contractors. International Journal of Management and Decision Making 2013, 12, 351–375, doi:10.1504/IJMDM.2013.056883. [CrossRef]
  59. Antoniou, F.; Konstantinidis, D.; Aretoulis, G.N. Application of the Multi Attribute Utility Theory for the Selection of Project Procurement System for Greek Highway Projects. International Journal of Management and Decision Making 2016, 15, 83–112, doi:10.1504/IJMDM.2016.077761. [CrossRef]
  60. Noorzai, E. Performance Analysis of Alternative Contracting Methods for Highway Construction Projects: Case Study for Iran. Journal of Infrastructure Systems 2020, 26, doi:10.1061/(ASCE)IS.1943-555X.0000528. [CrossRef]
  61. Aretoulis, G.N.; Papathanasiou, J.; Antoniou, F. PROMETHEE-Based Ranking of Project Managers Based on the Five Personality Traits. Kybernetes 2020, 49, 1083–1102, doi:10.1108/K-10-2018-0551. [CrossRef]
  62. Antoniou, F.; Demertzidou, F.; Mentzelou, P.; Konstantinidis, D. Energy Upgrading of Buildings in Greece with Eco-Materials: An Investigation of Public Awareness. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics, 2022; Vol. 1123. DOI: 10.1088/1755-1315/1123/1/012033. [CrossRef]
  63. Antoniou, F.; Merkouri, M. Accident Factors per Construction Type and Stage: A Synthesis of Scientific Research and Professional Experience. Int J Inj Contr Saf Promot 2021, 28, 439–453, doi:10.1080/17457300.2021.1930061. [CrossRef]
  64. 64. Bryman, A. Social Research Methods; New York: Oxford University Press Inc., 2012;
  65. Amoatey, C.T.; Ankrah, A.N.O. Exploring Critical Road Project Delay Factors in Ghana. Journal of Facilities Management 2017, 15, 110–127, doi:10.1108/JFM-09-2016-0036. [CrossRef]
  66. Kaliba, C.; Muya, M.; Mumba, K. Cost Escalation and Schedule Delays in Road Construction Projects in Zambia. International Journal of Project Management 2009, 27, 522–531, doi:10.1016/j.ijproman.2008.07.003. [CrossRef]
  67. Mahamid, I.; Bruland, A.; Dmaidi, N. Causes of Delay in Road Construction Projects. Journal of Management in Engineering 2012, 28, 300–310, doi:10.1061/(ASCE)ME.1943-5479.0000096. [CrossRef]
  68. Antoniou, F. Delay Risk Assessment Models for Road Projects. Systems 2021, 9, doi:10.3390/systems9030070. [CrossRef]
  69. Antoniou, F.; Agrafioti, N.F. Meta-Analysis of Studies on Accident Contributing Factors in the Greek Construction Industry. Sustainability 2023, 15, 2357, doi:10.3390/su15032357. [CrossRef]
  70. Holt, G.D. Asking Questions, Analysing Answers: Relative Importance Revisited. Construction Innovation 2014, 14, 2–16, doi:10.1108/CI-06-2012-0035. [CrossRef]
  71. Field, A. Discovering Statistics Using SPSS; London: SAGE Publications Ltd, 2009;
  72. Chen, Y.; Okudan, G.E.; Riley, D.R. Sustainable Performance Criteria for Construction Method Selection in Concrete Buildings. Autom Constr 2010, 19, 235–244, doi:10.1016/j.autcon.2009.10.004. [CrossRef]
  73. Shojaei, A.; Flood, I.; Moud, H.I.; Hatami, M.; Zhang, X. An Implementation of Smart Contracts by Integrating BIM and Blockchain. In; 2020; pp. 519–527.
  74. Di Giuda, G.M.; Giana, P.E.; Pattini, G. The Shortening and the Automation of Payments: The Potentiality of Smart Contract in the AEC Sector. Proceedings of International Structural Engineering and Construction 2020, 7, doi:10.14455/ISEC.2020.7(2).CON-12. [CrossRef]
  75. Hamledari, H.; Fischer, M. Role of Blockchain-Enabled Smart Contracts in Automating Construction Progress Payments. Journal of Legal Affairs and Dispute Resolution in Engineering and Construction 2021, 13.
  76. Sonmez, R.; Ahmadisheykhsarmast, S.; Güngör, A.A. BIM Integrated Smart Contract for Construction Project Progress Payment Administration. Autom Constr 2022, 139, 104294, doi:10.1016/j.autcon.2022.104294. [CrossRef]
Table 3. No of participants experienced in different types of construction projects.
Table 3. No of participants experienced in different types of construction projects.
Construction Type No. of Experienced Participants Construction Type No. of Experienced Participants
Buildings 15 (68,18%) Ports 5 (22,73%)
Roads 19 (86,36%) Airports 4 (18,18%)
Water networks 17 (77,27%) Railway 4 (18,18%)
Sewage networks 13 (59,09%) Metro 3 (13,64%)
Table 4. Cronbach's alpha reliability index
Table 4. Cronbach's alpha reliability index
Research Question Degree of reliability (Cronbach's alpha) Research Question Degree of reliability (Cronbach's alpha)
RQ1 Frequency of occurrence 0,949 RQ3 Severity of impact on cost 0,985
RQ2 Severity of impact on duration 0,977 RQ4 Severity of impact on quality 0,984
Table 5. Statistical Results of research questions 1 to 4
Table 5. Statistical Results of research questions 1 to 4
CCBS CODE Νο.of Occurrences in Literature RQ1
Frequency of Occurrence		 RQ2
Severity of Impact on Duration		 RQ3
Severity of Impact on Cost		 RQ 4
Severity of Impact on Quality
Mean Sd. RIIi Mean Sd. RIIid Mean Sd. RIIic Mean Sd. RIIip
A1 23 3.73 1.03 0.75 3.77 0.61 0.75 3.91 0.87 0.78 2.82 0.80 0.56
A2 9 3.05 1.13 0.61 3.82 1.10 0.76 3.23 0.97 0.65 2.45 0.67 0.49
A3 18 2.41 0.85 0.48 3.05 0.95 0.61 3.00 0.98 0.60 2.55 0.91 0.51
A4 6 2.68 0.89 0.54 2.91 1.02 0.58 3.00 1.07 0.60 2.64 0.95 0.53
A5 12 3.23 0.81 0.65 3.86 1.04 0.77 3.59 1.05 0.72 3.23 0.87 0.65
A6 7 3.23 1.02 0.65 3.36 1.05 0.67 3.50 1.01 0.70 2.91 1.07 0.58
A7 3 3.14 0.83 0.63 3.23 0.81 0.65 3.23 0.92 0.65 2.64 0.49 0.53
B1 19 3.32 0.72 0.66 3.82 0.85 0.76 3.41 0.96 0.68 2.86 0.94 0.57
B2 17 3.41 0.96 0.51 3.91 0.87 0.61 3.18 0.91 0.65 2.73 1.03 0.81
B3 6 2.82 0.73 0.68 3.82 0.91 0.78 3.27 1.03 0.64 3.45 1.14 0.55
B4 12 2.18 0.66 0.56 3.68 0.84 0.76 3.36 1.09 0.65 3.55 1.14 0.69
B5 5 2.27 0.70 0.44 3.18 1.05 0.74 3.05 1.09 0.45 3.09 1.11 0.71
B6 8 3.73 1.03 0.45 3.77 0.61 0.64 3.91 0.87 0.61 2.82 0.80 0.62
B7 8 3.05 1.13 0.51 3.82 1.10 0.64 3.23 0.97 0.69 2.45 0.67 0.61
B8 4 2.41 0.85 0.50 3.05 0.95 0.63 3.00 0.98 0.60 2.55 0.91 0.59
B9 3 2.68 0.89 0.36 2.91 1.02 0.55 3.00 1.07 0.56 2.64 0.95 0.52
B10 16 3.23 0.81 0.45 3.86 1.04 0.60 3.59 1.05 0.61 3.23 0.87 0.61
C1 13 3.23 1.02 0.65 3.36 1.05 0.75 3.50 1.01 0.76 2.91 1.07 0.74
C2 11 3.14 0.83 0.52 3.23 0.81 0.66 3.23 0.92 0.64 2.64 0.49 0.67
C3 3 3.32 0.72 0.51 3.82 0.85 0.65 3.41 0.96 0.60 2.86 0.94 0.65
D1 12 3.41 0.96 0.49 3.91 0.87 0.63 3.18 0.91 0.61 2.73 1.03 0.60
D2 8 2.82 0.73 0.53 3.82 0.91 0.67 3.27 1.03 0.63 3.45 1.14 0.60
D3 8 2.18 0.66 0.44 3.68 0.84 0.58 3.36 1.09 0.55 3.55 1.14 0.53
D4 4 2.27 0.70 0.45 3.18 1.05 0.61 3.05 1.09 0.55 3.09 1.11 0.52
D5 11 2.55 0.80 0.43 3.18 0.91 0.63 3.45 1.14 0.61 3.05 1.05 0.57
E1 6 2.50 0.86 0.45 3.14 1.04 0.61 3.00 1.16 0.63 2.95 1.13 0.56
E2 16 1.82 0.73 0.45 2.73 1.03 0.63 2.82 1.01 0.63 2.59 1.10 0.57
E3 6 2.23 0.69 0.44 3.00 1.02 0.62 3.05 1.13 0.62 3.05 1.09 0.56
F1 13 2.55 0.86 0.51 3.05 0.79 0.67 3.23 0.97 0.62 4.05 1.17 0.61
F2 5 3.23 0.75 0.56 3.77 0.97 0.70 3.82 1.01 0.69 3.68 1.25 0.60
G1 11 2.59 0.91 0.56 3.32 1.00 0.62 3.18 1.05 0.66 3.64 1.29 0.60
G2 9 2.55 0.80 0.47 3.23 1.19 0.61 3.00 1.07 0.63 3.27 1.32 0.53
G3 6 2.45 1.06 0.56 3.14 1.13 0.71 3.05 1.05 0.79 3.00 1.16 0.66
G4 6 2.64 0.90 0.48 3.36 1.22 0.62 3.14 1.08 0.66 3.00 1.31 0.57
G5 7 2.18 0.96 0.49 2.91 0.97 0.58 2.77 1.07 0.59 2.64 1.05 0.55
G6 6 2.23 0.87 0.49 3.05 0.90 0.70 2.77 0.81 0.72 2.59 0.91 0.61
G7 3 2.14 0.83 0.42 3.14 1.17 0.55 3.05 1.05 0.55 2.86 1.17 0.53
G8 2 2.23 0.87 0.45 3.05 1.21 0.62 3.14 1.17 0.62 2.82 1.01 0.54
G9 2 2.27 0.83 0.47 3.14 1.21 0.62 3.14 1.21 0.58 2.86 0.99 0.51
Table 6. Top Ten Causes of claims in terms of frequency and severity of impact on duration, cost, and quality
Table 6. Top Ten Causes of claims in terms of frequency and severity of impact on duration, cost, and quality
Freq. RIIi Rank Duration RIIid Rank Cost RIIic Rank Quality RIIiq Rank
A1 0,75 1 B3 0,78 1 G3 0,79 1 B2 0,81 1
B3 0,68 2 A5 0,77 2 A1 0,78 2 C1 0,74 2
B1 0,66 3 B1 0,76 3 C1 0,76 3 B5 0,71 3
A5 0,65 4 A2 0,76 3 A5 0,72 4 B4 0,69 4
A6 0,65 4 B4 0,76 3 G6 0,72 4 C2 0,67 5
C1 0,65 4 A1 0,75 6 A6 0,7 6 G3 0,66 6
A7 0,63 7 C1 0,75 6 F2 0,69 7 A5 0,65 7
A2 0,61 8 B5 0,74 8 B7 0,69 7 C3 0,65 7
B4 0,56 9 G3 0,71 9 B1 0,68 9 B6 0,62 9
F2 0,56 9 F2 0,7 10 G1 0,66 10 G6 0,61 10
G1 0,56 9 G6 0,7 10 G4 0,66 10 B7 0,61 10
G3 0,56 9 F1 0,61 10
B10 0,61 10
Table 7. =Ranking by RV on project time, cost, and quality
Table 7. =Ranking by RV on project time, cost, and quality
CCBS Code RVD Rank RVD RVC Rank RVC RVQ Rank RVQ TRV1 Rank TRV1 TRV2 Rank TRV2
A1 0.56 1 0.59 1 0.42 3 0.54 1 0.52 1
A2 0.46 6 0.40 9 0.30 19 0.43 7 0.39 9
A3 0.29 25 0.29 26 0.24 33 0.28 25 0.28 28
A4 0.31 21 0.32 18 0.29 23 0.31 20 0.31 20
A5 0.50 4 0.47 3 0.42 2 0.48 4 0.46 3
A6 0.44 7 0.46 4 0.38 6 0.43 6 0.42 6
A7 0.41 9 0.41 8 0.33 13 0.40 10 0.38 10
B1 0.50 3 0.45 5 0.38 7 0.47 5 0.44 5
B2 0.31 22 0.33 17 0.41 4 0.33 17 0.35 12
B3 0.53 2 0.44 7 0.37 8 0.49 2 0.45 4
B4 0.43 8 0.36 12 0.39 5 0.41 8 0.39 8
B5 0.33 19 0.20 39 0.31 16 0.30 23 0.28 26
B6 0.29 27 0.27 30 0.28 24 0.28 26 0.28 25
B7 0.33 18 0.35 14 0.31 17 0.33 18 0.33 17
B8 0.32 20 0.30 22 0.30 21 0.31 21 0.30 21
B9 0.20 39 0.20 38 0.19 39 0.20 39 0.20 39
B10 0.27 36 0.27 30 0.27 25 0.27 33 0.27 30
C1 0.49 5 0.49 2 0.48 1 0.49 3 0.49 2
C2 0.34 14 0.33 16 0.35 10 0.34 14 0.34 14
C3 0.33 17 0.31 21 0.33 14 0.33 19 0.32 18
D1 0.31 23 0.30 23 0.29 22 0.31 22 0.30 22
D2 0.36 12 0.33 15 0.32 15 0.35 13 0.34 15
D3 0.26 37 0.24 36 0.23 37 0.25 37 0.24 37
D4 0.27 32 0.25 35 0.23 36 0.26 36 0.25 36
D5 0.27 35 0.26 34 0.25 32 0.27 35 0.26 35
E1 0.27 32 0.28 27 0.25 29 0.27 32 0.27 31
E2 0.28 30 0.28 27 0.26 28 0.28 30 0.27 29
E3 0.27 34 0.27 32 0.25 31 0.27 34 0.26 34
F1 0.34 16 0.32 20 0.31 17 0.33 16 0.32 18
F2 0.39 11 0.39 10 0.34 11 0.38 11 0.37 11
G1 0.35 13 0.37 11 0.34 11 0.35 12 0.35 13
G2 0.29 28 0.30 24 0.25 30 0.28 28 0.28 27
G3 0.40 10 0.44 6 0.37 9 0.40 9 0.40 7
G4 0.30 24 0.32 19 0.27 26 0.30 24 0.30 23
G5 0.28 29 0.29 25 0.27 27 0.28 27 0.28 24
G6 0.34 15 0.35 13 0.30 19 0.34 15 0.33 16
G7 0.23 38 0.23 37 0.22 38 0.23 38 0.23 38
G8 0.28 31 0.28 29 0.24 34 0.27 31 0.27 33
G9 0.29 26 0.27 33 0.24 35 0.28 29 0.27 32
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated