Constructability and Rigor of Angles Multiples of 3 in Euclidean Geometry

1. Introduction

Euclidean geometry [1,2,3,4], a venerable cornerstone of mathematical inquiry [5], has ingrained its enduring construction principles and proofs into the annals of mathematical thought. Across centuries, its significance remains steadfast, serving as the bedrock for developing various mathematical concepts. This paper explores the multi-stage process of constructing and proving angles multiples of $3$ (Definition 2.1). Within the confines of the Euclidean geometric system, the objective here is to delve deep into this complex process, unveiling the subtleties that underscore the versatility and comprehensiveness inherent in Euclidean geometry.

This paper’s motivation rests upon Euclidean geometry’s profound ability to tackle the challenge of constructing and proving angles multiples of $3$. This enterprise is far from trivial; it ventures into the intricate interplay between angles, lines, and circles, forming the basis for intricate geometric constructions and persuasive proofs [6]. As we journey through this geometric background, we aim to illuminate not just the success of Euclidean geometry in addressing this problem but also to cast a discerning eye on its limitations and the drawbacks that emerge when alternative, non-Euclidean methods are embraced as authoritative substitutes. Central to this inquiry is the acknowledgment that Euclidean geometry extends beyond being merely a mathematical field. It represents a rich tapestry intricately woven with the elements of logical reasoning, accuracy, and inventive intuition.

This paper, therefore, navigates the path of this intricate tapestry, connecting the techniques, strategies, and insights that underpin the construction and proof of angles multiples of $3$. However, we endeavor to extend beyond mere exposition as it necessitates a critical gaze into non-Euclidean methods. These alternate avenues, while innovative, must be scrutinized for their potential to distort the genetic and geometric rigor that characterizes the Euclidean geometric system. Essentially, the unfolding narrative is not merely a chronological recounting of methods and solutions but rather a harmonious interplay between the advantages of Euclidean geometry and the possibility of misconceptions. The paper intends to not only pay homage to the longevity and robustness of Euclidean geometry but also to stimulate introspection, urging us to question the appeal of non-Euclidean methods. In doing so, we recognize the importance of refining the discerning lens of mathematical inquiry, cultivating an appreciation for Euclidean geometry’s intrinsic merits, and deciphering its methodologies’ intricacies.

2. Unveiling Euclidean Geometry’s Bounds-From Past to Present

Upon exploring alternative methodologies, a glaring realization emerges that an exclusive reliance on non-Euclidean methods, particularly analytical approaches, to resolve geometric problems inevitably engenders a range of limitations and misconstructions [3,7]. The implications of these missteps reverberate across the landscape of mathematical reasoning, distorting the fabric of geometric solutions. Foremost among these limitations is the perplexing transformation of geometric problems into algebraic statements [3,7]. What once resided within spatial relationships, lines, and angles is now expressed in the obscure terminology of algebraic equations. In this transformation, the eloquence of geometric solutions is forsaken, making room for a clinical and disconnected domain of symbolic manipulation. The geometrical beauty inherent in Euclidean methods is substituted with a mechanical process of solving equations, fundamentally reshaping the essence of the problem [3,7,8].

2.1. Structural Limitations and Misconstructions of Non-Euclidean Methods

In the quest for alternative approaches, it becomes evident that an overreliance on non-Euclidean methods, particularly analytical strategies, introduces a series of limitations and misconstructions that warrant scrutiny. These missteps cast a shadow over the landscape of mathematical reasoning, distorting the very essence of geometric solutions. Among these limitations, a notable concern arises from converting geometric quandaries into algebraic formulations. The once-visual domain of spatial relationships, lines, and angles undergoes a curious metamorphosis, adopting the esoteric language of algebraic equations [3,5,7,8]. This transformation sacrifices the eloquence inherent in geometric solutions, ushering in a system of detached symbolic manipulation. The intrinsic geometric elegance synonymous with Euclidean methods gives way to a mechanized equation-solving process, profoundly reshaping the problem’s essence. The rift deepens as non-Euclidean methods plunge into the sea of analytical abstraction [3,5]. The complex geometric pattern created using Euclidean techniques is deciphered, revealing the clear simplicity of algebraic expressions. While these approaches have their value in specific situations, the profound consequence of separating the problem from its geometric origins is significant.

The precision demanded by algebra replaces the intuitive spatial understanding fostered by Euclidean geometry, creating an intellectual vacuum where geometric insight once flourished. This transformation, which separates geometric challenges from their inherent spatial essence, initiates a troubling reinterpretation of Euclid’s original purpose. His eloquent language, crafted to communicate geometric principles and realities, is compelled to adapt to a fresh structure aligned with the algebraic framework. The result is a distortion of Euclid’s eloquent geometric prose into an algebraic dialect, eroding the very essence of his teachings and veiling the geometric subtleties his words sought to convey. Thus, it is imperative to underscore that the transformation from Euclidean to non-Euclidean methods alters the mode of mathematical inquiry and skews the solutions. In embracing alternative methodologies, we inadvertently tinker with the fundamental genetic and geometric rigor that Euclidean geometry upholds. This, in turn, reverberates in the very solutions we seek, rendering them more similar to algebraic artifacts than geometric insights.

2.2. Divergence of Euclidean and Non-Euclidean Geometry

Beyond the evident limitations of substituting Euclidean geometry with non-Euclidean methods, an intricate web of challenges emerges from the incompatibility between the two perspectives geometric essence of Euclidean geometry and the analytical framework of non-Euclidean methods [3,7]. This incongruity becomes glaringly evident when attempting to prove specific problems, particularly those involving the constructability of angles. The allure of replacing innate geometric rigor with analytical techniques shrouds these problems in a paradoxical dimension. In Euclidean geometry, proving the constructability of angles multiples of $3$ has long been an engaging pursuit. The geometric solutions, intricate in their execution, reveal the nuanced dance between lines, angles, and circles [3]. However, adopting non-Euclidean analytic methods to navigate this territory introduces a discordant note, creating an irksome tension between the geometric and the algebraic. The crux of this limitation lies in the intricate web of contradictions that surfaces as one tries to reconcile the geometric constructability with the analytical framework. Attempting to replace geometric elegance with algebraic prowess, we face perplexing contradictions - for instance, the angles trisection problem tantalizing challenges at the heart of this dichotomy. While Euclidean geometry wrestles with the challenge of trisecting an angle, analytical approaches frequently present a contrasting perspective. The impossibility of trisecting some angles emerges as an incongruence that challenges the foundations of geometric rigor [7].

Moreover, the disconnect between the geometric and analytic intensifies in the commensurability and incommensurability of geometric magnitudes like angles. Euclidean geometry uniquely navigates this intricate landscape, showcasing the nuances of relationships between angles and other geometric magnitudes. However, the delicate balance falters when viewed through the prism of non-Euclidean analytical methods. The intricate dance between ratios and geometric realities is lost in the rigid framework of equations and variables. These limitations highlight Euclidean geometry's delicate balance between geometric insight and analytical rigor. The resulting misconstructions are profound when we attempt to sever this equilibrium by replacing one with the other. The intricate and beautifully entwined fabric of geometry is torn asunder, revealing the dissonance that surfaces when the innate geometric rigor of Euclidean geometry is traded for the exacting analytical methods of non-Euclidean frameworks.

2.3. Historical to Modern Contrast

The journey from the historical origins of Euclidean geometry, dating back to the ancient Greeks and their foundational contributions, to the modern context is an enduring testament to its unparalleled strength in tackling a diverse array of geometric problems. Throughout this temporal domain, Euclidean geometry has proven to be not merely a static branch of mathematics but a dynamic and robust framework that transcends time [9,10]. At its heart, the efficacy of Euclidean geometry stems from its unique ability to provide specific, concise, and unambiguous solutions to complex geometric problems.

Euclidean geometry has consistently demonstrated its prowess in illuminating the geometric landscape, from the intricate constructions of ancient civilizations to the sophisticated proofs of contemporary mathematics. Its inherent specificity ensures that solutions are not vague approximations but precise and tangible insights into the world of shapes and relationships. Another distinguishing feature that underscores the lasting importance of Euclidean geometry is its remarkable geometric precision. Its axioms, postulates, and theorems are elegantly crafted to be self-evident, forming an intelligible foundation upon which elaborate proofs are built [1]. This clarity extends beyond formalism and permeates Euclidean geometry’s essence, enabling even the novice to grasp and appreciate its principles. This attribute has allowed Euclidean geometry to serve as an educational cornerstone for generations, fostering an understanding of mathematics and the beauty of geometric reasoning [1,9].

Further, another remarkable feature of Euclidean geometry is its inherent capacity to grasp geometric relationships. It goes beyond mere calculations, involving a profound comprehension of spatial connections and their consequences. This comprehension has enabled Euclidean geometry to address problems that demand numerical results and insights into how geometric entities interact. Euclidean geometry's true brilliance lies in its ability to turn apparent limitations into advantages. The structural and tool-related constraints intrinsic to the Euclidean system can be transformed into strengths. Instead of being obstacles, these limitations become guiding principles that steer mathematical exploration toward elegant solutions. This self-sufficient nature is evidence of Euclidean geometry’s resilience, demonstrating its ability to thrive within its own framework. The most powerful affirmation of Euclidean geometry’s strength is its capacity to establish the constructability of angles multiples of $3$. Armed with its rigorously genetic geometric methods, Euclidean geometry provides a clear and direct route to demonstrate the constructability of these angles. This accomplishment is a beacon that shines a light on Euclidean geometry’s ability to navigate complex problems without deviating from its principles. Thus, Euclidean geometry exemplifies mathematical inquiry that has stood the test of time [5,9,11,12]. From its roots in antiquity to its relevance in the modern age, its strengths-specificity, clarity, and the understanding of geometric relationships make it an invaluable tool for understanding the world of shapes and spaces. The construction and proof of angles multiples of $3$ within this framework are a testament to the enduring power of Euclidean geometry and the elegance it brings to the realm of mathematics.

2.4. The Richness of Euclidean Geometry

In the continually changing realm of mathematical exploration, developing non-Euclidean geometries has unquestionably brought forth fresh dimensions, viewpoints, and practical uses [5,9,10,11,12,13,14]. However, it is imperative to tread with caution and ensure that the allure of the new does not cast an unjust shadow over the enduring merits of Euclidean geometry timeless discipline that continues to stand tall as a beacon of rigor and clarity. Non-Euclidean geometries offer alternative viewpoints, expanding the horizons of mathematical thought [9,10,13]. They provide avenues to comprehend spaces that diverge from the familiar Euclidean realm. Yet, in this exploration, it becomes paramount to remember that Euclidean geometry’s legacy cannot be easily overshadowed. Its rigor, clarity, and elegant precision form an unmatched foundation upon which mathematical investigations have been built for centuries. The unparalleled rigor of Euclidean geometry ensures that every deduction is rooted in solid logical reasoning. The principles of axioms, postulates, and theorems have stood the test of time, offering an unwavering framework that fosters the discovery of mathematical truths and the development of critical thinking skills. In a world where complexities often cloud understanding, Euclidean geometry is a steadfast anchor realm where each step is transparent, and every conclusion is irrefutable. Clarity, another hallmark of Euclidean geometry, resonates through its elegant language. Concepts are expressed with precision, and relationships are articulated with grace. This clarity is not mere linguistic dexterity; it reflects a deep understanding of geometric relationships. The very act of formulating these principles with such transparency cultivates an environment where mathematics becomes accessible to all who engage with it. The richness of Euclidean geometry extends beyond its foundational axioms and theorems. It thrives in its ability to harness structural limitations as contextually relevant assets. These limitations, rather than hindering progress, channel mathematical inquiry in productive directions. They encourage creative problem-solving, nudging mathematicians to extract elegant solutions from a palette of restricted tools.

Euclidean geometry offers a self-sustaining ecosystem where structural limitations are not weaknesses to overcome but sources of strength that illuminate pathways to elegant solutions. It embraces its boundaries, recognizing that the seeds of deeper understanding lie within them. This embracing of limitations contextualizes Euclidean geometry as a living, breathing discipline that thrives on its terms. While non-Euclidean geometries undoubtedly bring innovation and broader perspectives, it is essential not to undermine the virtues of Euclidean geometry. Its rigor, clarity, and ability to transform limitations into assets offer a solid foundation for geometric investigations. Euclidean geometry’s timeless notes continue to resonate in the symphony of mathematical exploration, enriching our understanding and appreciation of the intricate dance of shapes, spaces, and relationships.

Definition 2.1. (Angles Multiples of 3 in Euclidean Geometric Language).

In Euclidean geometry, the term angles multiples of $3$ will refer to the geometric construction of an angle as a magnitude. Specifically, this angle is constructed in such a way that within its geometric context, a dense set of other larger angles exists. Notably, the ratio of larger angles to the made angle consistently remains at a constant value of $3$. This geometric concept serves as a foundational element in the broader exploration of constructability using compass and straightedge methods, showcasing the inherent intricacies and symmetries within the realm of geometric constructions.

Clarity (Between Euclidean geometry and the Modern perspective). Consider a circle with its center at $O$ and radius $OA$. Let angle $\theta$, subtended by an arc $AB$, be a multiple of $3$. In Euclidean terms, this implies that the arc $AB$ and the circumference of the circle are commensurable, meaning they share a common unit of measurement without leaving any remainder. This commensurability speaks to the inherent geometric connection between the angle and the arc. Geometrically, this commensurability is expressible through the ratio of the arc length $AB$ to the circle's circumference. Let this ratio be denoted as $r\left(AB\right)/C$, where $r\left(AB\right)$ represents the length of arc $AB$, and $C$ signifies the circle's circumference. Since both quantities are commensurable, the ratio $r\left(AB\right)/C$ equals a simple fraction. Furthermore, this ratio embodies the essence of Euclidean geometry by revealing the proportional relationship between the subtended angle $\theta$ and the arc length $AB$. As angle $\theta$ increases, the corresponding arc length $AB$ also increases in a commensurable manner, forming a fundamental geometric link.

This definition assumes a pivotal role within the interface that converges Euclidean geometry and the contemporary constructability perspective. It emerges as a bridging link that artfully unites the intuitive geometric realm of Euclidean geometry with the nuanced contours of modern constructability theory. The inherent commensurability binding angles multiples of $3$ to their corresponding arc lengths resonates harmoniously with the contemporary ethos of constructability, wherein angles metamorphose from mere geometric magnitudes in the Euclidean setting to numerically imbued entities. This transition is navigated through the profound lens of ratios, whereby angles embody a nuanced tapestry of proportions that transcend the boundary between geometry and number theory. This inherent geometric definition encapsulates the harmonious interplay between Euclidean geometry’s language of commensurability, ratios, and geometric relationships. It elegantly showcases the way angles multiples of $3$ interact with the geometric structures they inhabit and how this connection remains relevant in both classical and modern interpretations, seamlessly blending the ageless wisdom of Euclid’s geometry with contemporary mathematical perspectives.

3. Navigating Angle Constructability - A Comparative Exploration

This section focuses on the intricate task of angle constructability, exploring both the Euclidean and non-Euclidean perspectives. We establish Euclidean geometry’s remarkable capacity to provide robust constructions and proofs for angles multiples of $3$, utilizing the fundamental tools of a straightedge and compass. As we embark on this journey, we also extend our inquiry into non-Euclidean methods, particularly analytical approaches, which attempt to bridge the gap between algebraic and geometric viewpoints. This intermediary phase serves as a critical occasion for the exploration, highlighting the potential pitfalls and misconceptions that can arise when non-Euclidean methods are introduced into the discussion of Euclidean geometric problems. Within this context, we delve deeper into constructability within the non-Euclidean geometric scheme, seeking to unravel the limitations and complexities that emerge when geometric concepts are scrutinized through alternative perspectives.

3.1. Constructability within the Non-Euclidean Geometric Scheme

While Euclidean geometry forms the cornerstone of our understanding, non-Euclidean methods, particularly analytical techniques, have emerged as intriguing alternatives. Exploring non-Euclidean methods offers unique insights into the interplay between algebraic and geometric viewpoints, shedding light on the complexities and challenges that can arise. We closely investigate the non-trisection of the angles. This classic problem has puzzled mathematicians for centuries, focusing on showcasing the inherent limitations of depending solely on non-geometric proofs as authoritative alternatives to Euclidean geometric proofs. By considering the ${60}^{°}$ angle as a representative example of non-trisectable angles within a non-Euclidean framework, we shed light on the complexities and challenges that arise when seeking to reconcile differing geometric perspectives.

Consider a familiar scenario, a common example that provides insight into the interplay between Euclidean and non-Euclidean geometric approaches. We begin with the known trigonometric relation; $\cos {72}^{°}=\frac{\sqrt{5}-1}{4}$. Thus, we can construct ${72}^{°}$ angle using the following series of steps:

• Construct a line of length $\sqrt{5}$ (This notion is ingrained in the algebraic view of constructing square roots [15]).
• Subtract $1$.
• Divide by $4$ (Assume performing multiple bisection operations; this creates $\cos {72}^{°}$)
• Construct a right triangle with the hypotenuse $1$ and the adjacent $\cos {72}^{°}$ (Draw a perpendicular line from the line segment of length $\cos {72}^{°}$ constructed earlier and intersected with a circle of length $1$).
• The angle formed between the two lines is ${72}^{°}$.

The goal of this section is not to present an alternative proof using non-Euclidean language but to highlight the inherent limitations and vagueness that arise when adopting such an approach. While non-Euclidean methods can serve as tools for verification [5], they often lack the generality and precision that the Euclidean framework offers, especially in cases where measurements are not essential.

For instance, let us consider the generic perspective that one may make from the provided construction (an assumed construction starting diagram. The described construction here follows a common non-Euclidean geometric approach [10,13], and so it is not geometrically validated but applied carefully to complete the argument). In the absence of a standardized unit-length segment for comparison, the length of a segment becomes entirely arbitrary. Consequently, it lacks a definitive value, rendering the concept of taking its square root meaningless. Consider a given segment denoted as $AB$, with a length represented as $x$. Let point $C$ reside on ray $AB$, such that $BC$ measures $1unit$. By constructing the midpoint $M$ of segment $AC$, forming a circle with center $M$ that encompasses point $A$, and constructing a perpendicular line from $B$ to $AB$, we can locate the points $D$ and $E$ as intersections of the line with the circle. Notably, $BD$ equals the square root of $x$.

Within this arrangement, both $AC$ and $DE$ serve as chords of the circle, intersecting at point $B$. Following the principle of the power of a point theorem, the product of $AB$ and $BC$ equals the product of $DB$ and $BE$, resulting in the equation $x\times 1=x=DB\times BE$. Additionally, since $DE$ forms a perpendicular angle to $AC$ and $AC$ serves as a diameter of the circle, $DE$ is bisected by $AC$, and thus, $DB$ equals $BE$. This leads to the realization that $x$ equals $DB$ squared or equivalently, $DB$ equals the square root of $x$. The assertion that this construction represents a special instance of the broader geometric-mean construction deserves attention. When confronted with two lengths, $AB$ and $BC$, arranged as described above, the presented construction yields the length $BD$, which is the square root of the product of $AB$ and $BC$. This relationship between lengths aligns with the geometric-mean concept, where the length $BD$ represents the geometric mean of $AB$ and $BC$.

3.2. Geometric Critique of the Algebraic Construction

The presented algebraic construction (Section 3.1) seeks to establish the angle of ${72}^{°}$ through a series of algebraic operations and trigonometric relationships. However, upon closer examination, it becomes apparent that this construction ventures beyond the traditional realm of Euclidean geometric methodology, introducing measurements and quantities that deviate from the core principles of pure geometric constructions. Euclidean geometry operates within a framework that inherently avoids using measurements, relying instead on the interplay of geometric figures and relationships. The absence of numerical values and measures ensures Euclidean constructions’ contextual universality and purity, making them accessible and applicable across various contexts. The introduction of specific numerical lengths, such as a line of length $5-\sqrt{5}$ or a circle of length $1$, inherently undermines the genetic language of Euclidean geometry. These quantities are not established purely through geometric relationships but through external measurements that depend on numerical values. In the genetic Euclidean framework, lengths are not quantified but expressed in relationships, proportions, and ratios.

Further, while the point theorem is a legitimate geometric principle, its application in the construction involves specific measurements, such as $AB\times BC=DB\times BE$ . This equation is not derived solely from the geometric properties of the figure but only relies on the numerical values assigned to the lengths $AB$, $BC$, $DB$, and . This departure from the geometric language compromises the genetic rigor of Euclidean constructions. Moreover, constructing angles through algebraic operations like subtraction and division deviates from the Euclidean method, where angles are traditionally constructed based on the interplay of lines, arcs, and circles without resorting to numerical calculations [3]. The view that the construction is a special case of geometric-mean construction also raises concerns. While geometric mean has its place in Euclidean geometry, attempting to retroactively fit this algebraic construction into the framework of geometric mean ignores that the construction relies on measurements and algebraic relationships, which contradicts the pure geometric essence of Euclidean constructions. In its real sense, the presented algebraic construction, while mathematically valid, stretches the boundaries of Euclidean geometry by incorporating specific measurements and algebraic operations. This departure from the genetic language of Euclidean construction blurs the line between the traditional geometric framework and algebraic methods, undermining the intrinsic elegance and rigor of pure geometric constructions.

3.3. Constructability of Angles Multiples of 3 within the Euclidean Geometric Framework

In Euclidean geometry, the constructability of angles multiples of $3$ relies on the foundational principles of straightedge and compass constructions. This section will provide rigorous proof for the constructability of angles multiples of $3$ following Euclidean geometric principles.

Important Contextual Terminology: The subsequent sections of the proof will also rely on a set of assumptions and axioms of Euclidean geometry [1,2,3,4,6], as outlined in this section.

Axiom 1: Things that are equal to the same thing are equal to one another.

Axiom 2: If equals are added to equals, then the wholes are equal.

Axiom 3: If equals are subtracted from equals, then the remainders are equal.

Axiom 4: Things that coincide with one another are equal to one another.

Axiom 5: The whole is greater than the part.

Assumptions: In the Euclidean geometric framework, we assume the fundamental principles laid out by Euclid, such as the congruence of geometric figures and the axiomatic foundation of geometry, including the principle of superposition.

Applying the wisdom of the stated axioms and assumption, consider $Claim1$.

Claim 1. It is geometrically possible to construct every angle  $\theta$, a multiple of $3,$ using a straightedge and compass.

As mentioned earlier, the geometric construction of an angle is rather intricate, and it concerns the use of other magnitudes, such as straight-line segments (they will be referred to through the paper as chords) and curves, to prove using geometric reasoning that an angle is constructible. This section sets up an elegant construction, which begins with the construction of $36°$ and $54°$ angles as the geometric foundation for the constructability of any other angle that is a multiple of $3$.

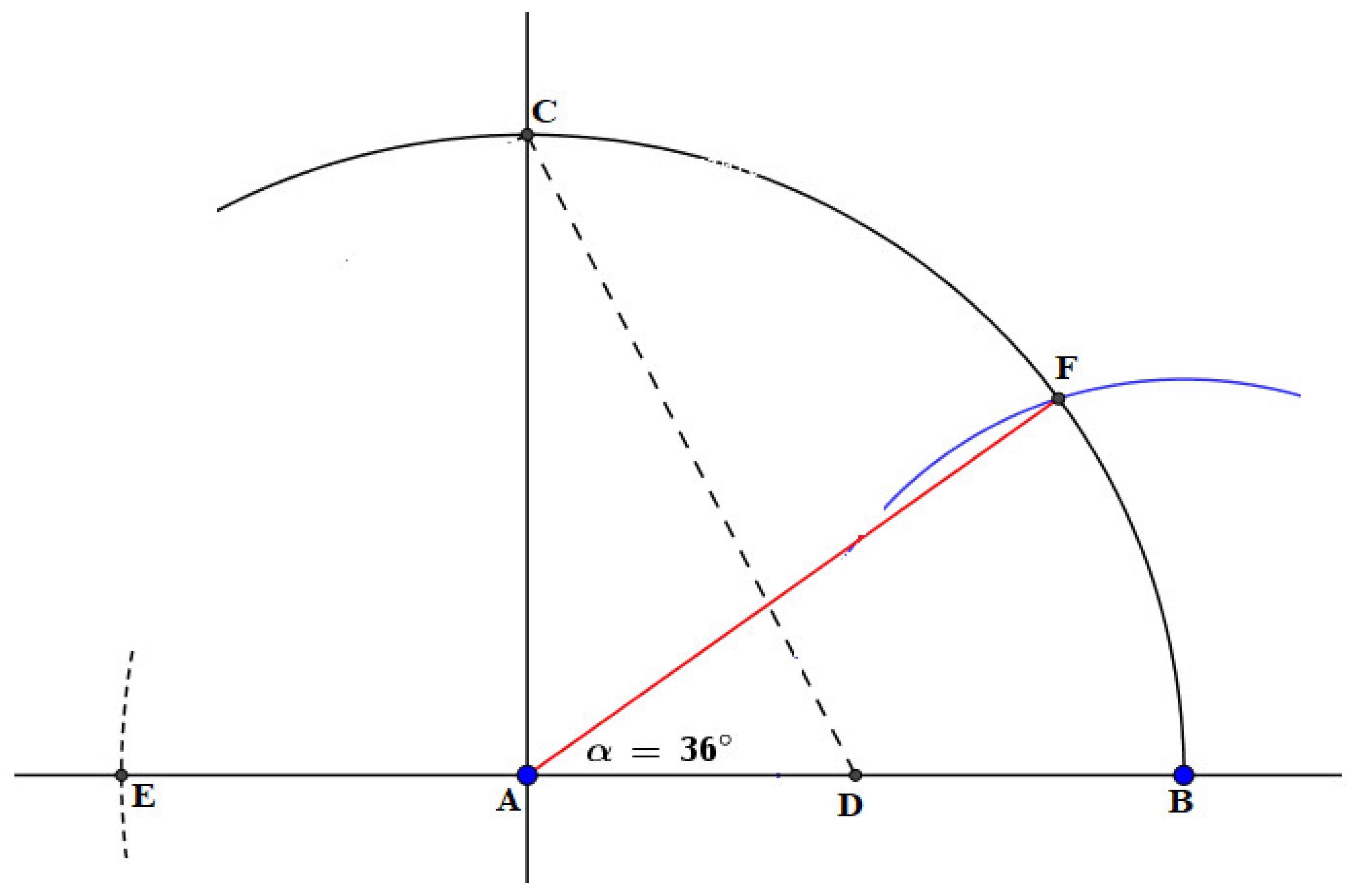
3.3.1. Geometric Construction of $36°$ and $54°$ Angles

Consider the following straightedge-compass construction steps, performed in a geometric plane for given two points $A$ and $B$.

• Construct a straight line (a baseline) through the given two points $A$ and $B$.
• Construct a perpendicular to the baseline $\overline{AB}$ through point $A$.
• Using radius $\overline{AB}$, construct an arc that intersects the perpendicular line constructed through point $A$ at point $C$. $\angle CAB=90°$ since $\overline{AB}\perp \overline{AC}$.
• Construct the midpoint of the radius $\overline{AB}$, at a point, $D$.
• Construct a straight line through points $C$ and $D$ using a straightedge.
• Using radius $\overline{CD}$ and point $D$ as the center of construction, construct an arc that intersects $\overline{BA}$ on the side of $A$ at a point,$E$.
• Using the straight-line segment $\overline{AE}$, construct an arc that intersects the curve $\widehat{BC}$ at a point, F as depicted in Figure 1. The straight-line segment $\overline{AE}$ will be referred to as the ($36°$ Angle Chord) in the subsequent workflow.

Definition 3.1. (36° Angle Chord).

The $36°$ angle chord is a line segment connecting two points on the circumference of a circle, such that the central angle subtended by the chord at the center of the circle is, geometrically, exactly $36°$

Geometric Clarity (Validation of the 36° Angle Chord Property). In the pursuit of constructing angles multiples of $3$ within the Euclidean geometric framework, a crucial step has been the establishment of the $36°$ Angle Chord. The focus here is to validate the provided geometric construction following a detailed computational analysis (using MATLAB software), specifically focusing on the chord $EF$ as a representation of the $36°$ angle. The goal of the provided MATLAB code is to computationally validate the geometric property of the “$36°$ Angle Chord”. This property involves geometric construction of a line segment between two points on the circumference of a circle, such that the central angle subtended by the chord at the center of the circle is precisely $36°$.

Clarity Case 1 (Validation through Geometric Constructions). The geometric construction involves a sequence of steps methodically designed to ensure the accuracy of the resulting angles. The construction begins with the formation of a perpendicular at point $A$ to a given baseline $\overline{AB}$. By constructing an arc intersecting this perpendicular, we establish a point $C$ such that $\angle CAB=90°$. The midpoint $D$ of the radius $\overline{AB}$ is then geometrically determined. The critical step involves drawing a straight line through points $C$ and $D$, creating a line segment $\overline{CD}$. Subsequently, an arc is constructed from point $D$ intersecting the baseline $\overline{BA}$, forming a point $E$. The final step is drawing an arc from point $B$, intersecting the curve $\widehat{BC}$ at point $F$. The straight line segment $\overline{AE}=\overline{BF}$ is then defined as the “$36°$ Angle Chord”. To validate this geometrically, we turn to Euclidean axioms and assumptions. Axioms 1 through 5 establish fundamental principles of equality, coincidence, and order. Importantly, the assumption of congruence of geometric figures and the principle of superposition in Euclidean geometry forms the basis for geometric constructions. This geometric validation is worked out through the subsequent sections of proof.

Clarity Case 2 (Validation through Geometric Analysis). For clarity, we will focus on a computational analysis, translating the described geometric algorithm to a symbolic computer code, and extracting the desired specific floating point results from the computations. Consider Appendix A. The provided code rigorously applies Euclidean axioms and assumptions, ensuring the validity of the constructed angles. Key to the validation is the use of well-established geometric principles, including the congruence of geometric figures and the axiomatic foundations of Euclidean geometry. In Euclidean geometry, the process of constructing angles involves careful considerations of chords, arcs, and their relationships within a geometric plane. The code, by demonstrating the construction of the “$36°$ Angle Chord”, essentially proves that angles multiples of $3$ are geometrically constructible within the Euclidean framework by demonstrating the equality between the line segments $\overline{AE}=\overline{BF}$, following the construction of the $36°$ Angle.

Definition 3.2. (Isosceles Angle).

An isosceles angle, as illustrated in Figure 1 with the vertex at the point $A$, is a rectilinear angle enclosed by two intersecting lines emanating from the center of a circle. Specifically, considering the central angle $\mathit{\angle }FAB$ in the construction context, these lines correspond to the radii of the circle. Notably, the equality of the two lines $\overline{AB}=\overline{AF}$ (radii of the circle), characterizes the isosceles nature of the angle. The constructed straight-line segment $\overline{EA}=\overline{FB}$ is the “$36°$ Angle Chord”, forming the base of an isosceles triangle $ABF$ such that the base angles $\mathit{\angle }ABF=\mathit{\angle }AFB$. Hence, $\mathit{\angle }FAB$ is contextually an isosceles angle.

Geometrical Context (On the Isosceles Angle). In the geometric context of an isosceles angle, the vertex $A$ serves as the center of a circle. The equality of the two line segments $\overline{AB}=\overline{AF}$ is established when these segments coincide with the radii of the circle. The formation of an isosceles triangle $ABF$ is marked by the equality of the angles $\angle ABF$ and $\angle AFB$, both sharing the base $\overline{EA}=\overline{FB}$. For clarity, this contextual validation of an Isosceles angle is extended through the following axioms, as outlined earlier.

Axiom 1. Things that are equal to the same thing are equal to one another. This axiom validates the equality of $\overline{AB}$ and $\overline{AF}$ as radii of the circle, ensuring the isosceles nature of the angle.

Axiom 4. Things that coincide with one another are equal to one another. The coincidence of $\overline{AB}$ and $\overline{AF}$ with the radii at the circumference affirms their equality and, consequently, the isosceles property.

Proposition 3.3.

The chord $\overline{EA}=\overline{FB}$ or such a segment, when constructed in a similar configuration, would subtend an angle of $36°$ at the vertex of an isosceles triangle. From Figure 1 $\overline{AB}\perp \overline{AC}$ implying that $\mathit{\angle }CAB=90°$. Therefore, $\mathit{\angle }CAF=90°-36°=54°$

Definition 3.4. (Trisection Angle).

Within the context of this paper, the term trisection angle, denoted as $\alpha$ refers to an angle that is achieved through a specific sequence of finite steps involving straightedge and compass constructions. This sequence is applied to a given angle referred to as the trisected angle $\theta$. The trisection angle $\alpha$ is characterized by the ratios $\frac{\alpha }{\theta }=\frac{1}{3}$ and $2\frac{\alpha }{\theta }=\frac{2}{3}$

Proof. 

One of the ways to show that angles multiples of $3$ are constructible is by performing the trisection of an angle that is a multiple of $3$. Reasonably, suppose both 36° and 54° angles are constructible. In that case, it must be possible to construct both $12°$ and $18°$ angles (this perspective benefits from the flawed modern notion of angles trisection interpretation that concerns reversing the problem from its desired solution [13,16,17]). This proof will be based on the constructability of the $18°$ sufficiently to serve the purpose.

Definition 3.5. (Equality of Angles as Magnitudes).

An angle $\theta$ is said to be a multiple of another angle $\alpha$ if there exists a positive ratio $n$ between $\theta$ and $\alpha$ such that, if $\alpha$ is put together $n$ times in the order $\alpha n=\beta$, then $\beta$ is an angle equal in magnitude to angle $\theta$

Remark 3.6.

This definition is applied in proving the claims about the construction of angles as magnitudes.

Definition 3.6. (Equality of Angles as Measurements).

Suppose a particular angle 𝜃 (an angle of known size) is a multiple of another specific angle 𝛼 such that there exists a whole number ratio 𝑛 between θ and 𝛼. In that case, $\alpha$ measures $\mathsf{\theta },$ and $\mathsf{\theta }$ is a multiple of $\alpha$

Remark 3.7.

This definition is used at the discretion of the revealed construction results, where the relation between the constructed results is based on measurements.

3.3.2. Proof by Geometric Construction

Consider the following construction steps aimed at developing a genetic generic proof of the claim that angles $36°$ and $54°$ are constructible following the rules of Euclidean constructions.

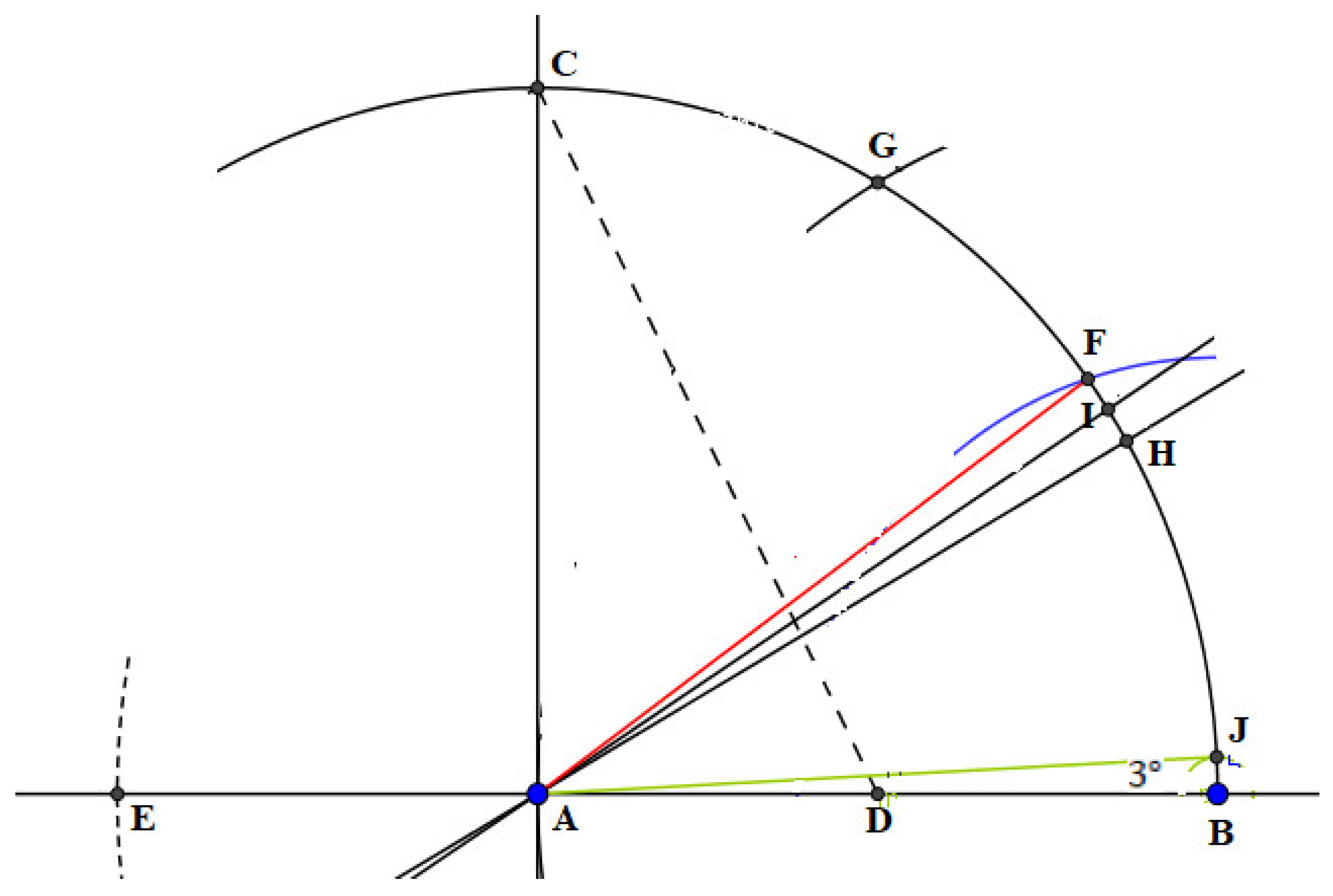
• Construct a straight line (a baseline) through the given two points $A$ and $B$.
• Construct a perpendicular to the baseline $\overline{AB}$ through point $A$.
• Using radius $\overline{AB}$, construct an arc that intersects the perpendicular line constructed through point $A$ at a point $C$ such that $\overline{AB}\perp \overline{AC}$.
• Construct the midpoint of the radius $\overline{AB}$, at a point, $D$.
• Construct a straight-line segment through points $C$ and $D$ using a straightedge.
• Using radius $\overline{CD}$ and center $D$, construct an arc that intersects $\overline{BA}$ on the side of $A$ at a point,$E$.
• Using the straight-line segment $\overline{AE}$, construct an arc that intersects the curve $\widehat{BC}$ at a point, $F$.
• Construct point $B\prime$, a geometric reflection of point $B$, to be the point of intersection between the arc $\widehat{BC}$ and the baseline $\overline{BA}$.
• Using chord $\overline{FC}$ and center $B$, construct an arc that intersects the curve $\widehat{BC}$ at a point, $G$.
• With the compass adjusted to the chord $\overline{FG}$ and using $B\prime$ as the center, construct an arc that intersects the curve $\widehat{CB\prime }$ ($C_1$) at a point, $H$.
• Construct a straight line through points $G$ and $H$, to intersect the baseline $\overline{BB\prime }$ externally, at a point, $I$.
• Using the straight-line segment $\overline{IH}$ and point $H$ as the center of construction, construct a circle that passes through points $I$ and $A$, circle ($C_2$).

The construction results are depicted in Figure 2. For this proof, circle $C_1$ is the original (the black circle), and the circle $C_2$ is the green circle. First, consider the circle $C_1$ and circle $C_2$; constructed using different radii and distinct points as centers of construction (circle $C_1$ of radius $\overline{AB}=\overline{AH}$ centered at point $A$ and circle $C_2$ of radius $\overline{IH}$ centered at point $H$), circle $C_1$ pass exactly through the point $H$, and circle $C_2$ pass exactly through point $A$. This implies that $\overline{AB}=\overline{AH}=\overline{IH}$, with $\overline{IH}$ as the radius of the constructed circle, $C_2$. Considerably, circle $C_2$ is inherently constructed as a result of the trisection process.

Let the radius of the circle $C_1$ be $r$. This implies that the circle $C_2$ equally, has radius $r$, since $\overline{AB}=\overline{AH}=\overline{IH}$. The relationship can now be reformulated as

$$\overline{AB}=\overline{AH}=\overline{IH}=r$$

(1)

Equation (1) aids in deriving the geometric properties, useful for showing that $\angle GAF=\angle FA{H}_1=\angle H_{1}AB=1/3(\angle GAB)$. Taking $\angle GAF=\angle HAB\prime =\theta$, and that point $B\prime$ is a reflection of point $B$ (by a geometric construction), then $\angle HAI=\angle HIA=\theta$. Base angles of the isosceles triangle $AHI$ since

$$\overline{IH}=\overline{AH}=\overline{AB}=r$$

(2)

This implies that. Triangle $HAB\prime \equiv GAF$, (Congruence property $Side-Angle-Side\left(SAS\right)$). Again, $\angle AHG=2\theta$ (by the property, an exterior angle of a triangle equals the sum of the opposite interior angles). Moreover,

$$\angle AGH=2\theta$$

(3)

(Base angles of isosceles triangle $HAG$). It follows that

$$\angle HAG=180°-4\theta$$

(4)

Consider; $\angle B^{\prime }AH+\angle HAG+\angle GAB=180°$ (Sum of angles on a straight line add up to $180°$). Making $\angle GAB$ the subject

$$\angle GAB=180°-(\angle B^{\prime }AH+\angle HAG)$$

(5)

From Equations (2) and (4), we have $\angle B\prime AH=\theta$ and $\angle HAG=180°-4\theta$, respectively. Substituting for angles $\angle B^{\prime }AH$ and $\angle HAG$ in Equation 5, we obtain

$$\angle GAB=180°-(\theta +(180°-4\theta \left)\right)$$

(6)

The equation reduces to $\angle GAB=-\theta +4\theta =3\theta$. Equation 6 implies that $\angle GAB=3\angle B\prime AH$, which can be rewritten as

$$1/3(\angle GAB)=\angle B\prime AH$$

(7)

Thus, $1/3\left(\angle GAB\right)=\angle GAF=\angle IAH=\angle AIH$. Since $\angle GAF=\angle B\prime AH$, hence the claim is proven. Substituting the constructed $\angle GAB$ in Equation (7), we $\angle B^{\prime }AH=18°$. Therefore, if 18° is constructible, so are $36°$ and $54°$ angles. This implies the possibility of constructing all angles multiples of $3$. Hence, the problem is solved.

This form of proof involving comparing angles as magnitudes is analogous to Euclid’s notion of testing for commensurability between magnitudes of a similar kind, using ratios of the constructed geometric magnitudes. The generated proof implies that the chords $\overline{B\prime H}$, $\overline{B{H}_1}$, $\overline{H_{1}F}$ and, $\overline{FG}$, are equal. For this reason, $\angle B^{\prime }AH=\angle B^{\prime }IH=\angle BA{H}_1=\angle H_{1}AF=\angle FAG=18°$. Further, based on Equation 4, one can deduce that triangle $IHA$ is isosceles. Therefore, this justifies the exactness of the construction from the Euclidean plane geometric perspective as constructing a perpendicular through point $H$, to intersect the baseline $\overline{IA}$ through a point, $Z$. Using radius $\overline{ZA}$ and point Z as the center of construction, construct a circle through point $A$. The constructed circle also passes evenly through point $I$, implying $C_1$ is congruent to $C_2$ and thus proving the geometric exactness of the constructed results.

3.4. Assessing Constructive Accuracy (Non-Euclidean Geometric Validation)

In Euclidean geometry, constructing various geometric objects and angles has long been a fundamental pursuit. The ancient Greeks were particularly intrigued by the challenge of constructing regular polygons, angles, and lengths using only a straightedge and compass. The field flourished with the discovery of solutions for constructing certain angles, particularly those divisible by three, which unlocked the construction of many regular polygons. This achievement marked a significant milestone in the history of geometry, showcasing the remarkable capabilities of compass and straightedge constructions. However, it is essential to acknowledge that not all constructions involving angles divisible by three (multiples of $3$) have been exhaustively demonstrated using these traditional methods. The quest to validate the constructability of angles multiples of three has led to exploring alternative approaches beyond the confines of Euclidean geometry. Despite the prevailing belief that such constructions are achievable through compass and straightedge, the intricacies and complexities of certain cases have prompted mathematicians to seek alternative paths to verification. Enter the realm of Non-Euclidean techniques that may not necessarily negate Euclidean geometry’s principles but offer a different vantage point for examining geometric challenges. While not intending to replace the established Euclidean proofs, these approaches serve as valuable verification tools. They shed light on the congruence, proportionality, and inherent properties of geometric figures and angles. However, the relationship between Euclidean geometry and algebraic methods is not always seamless.

While Euclidean constructions can be elegant and intuitive, certain proofs and constructions can become increasingly complex and intricate, often relying on concepts like commensurability and incommensurability. The most famous example of this complexity arises in the geometric proof of the Pythagorean theorem [19,20]. This reliance on commensurability, or the inability to perfectly compare the lengths of two quantities, introduces inherent limitations to the straightforwardness of Euclidean geometry. In this section, we delve into a different perspective- a perspective that does not aim to offer new proofs or replace the provided construction methods. Instead, we explore how non-Euclidean geometric techniques can be employed to validate the correctness and accuracy of Euclidean constructions. The purpose of introducing non-Euclidean methods is not to establish new proofs but to serve as tools for verifying the validity of geometric solutions. Here, we extend the previously discussed geometric proof of the constructability of angles divisible by three to the construction of a regular pentagon. The construction of a regular pentagon is a captivating challenge that showcases the power of Euclidean methods and reveals certain intricacies in their application. By utilizing non-Euclidean geometric techniques, we aim to verify the geometric exactness of the solutions and shed light on the congruence and proportionality inherent in these constructions. Furthermore, we will focus on a specific example of the construction of the $3^{°}$ angle. This case represents an application demonstrating the interplay between Euclidean and non-Euclidean techniques. It is important to emphasize that the analytic measurements and methods used throughout the paper are not meant to replace or challenge the Euclidean proofs. Rather, they provide an additional layer of scrutiny and verification, ensuring that the constructed angles and figures align with the desired outcomes.

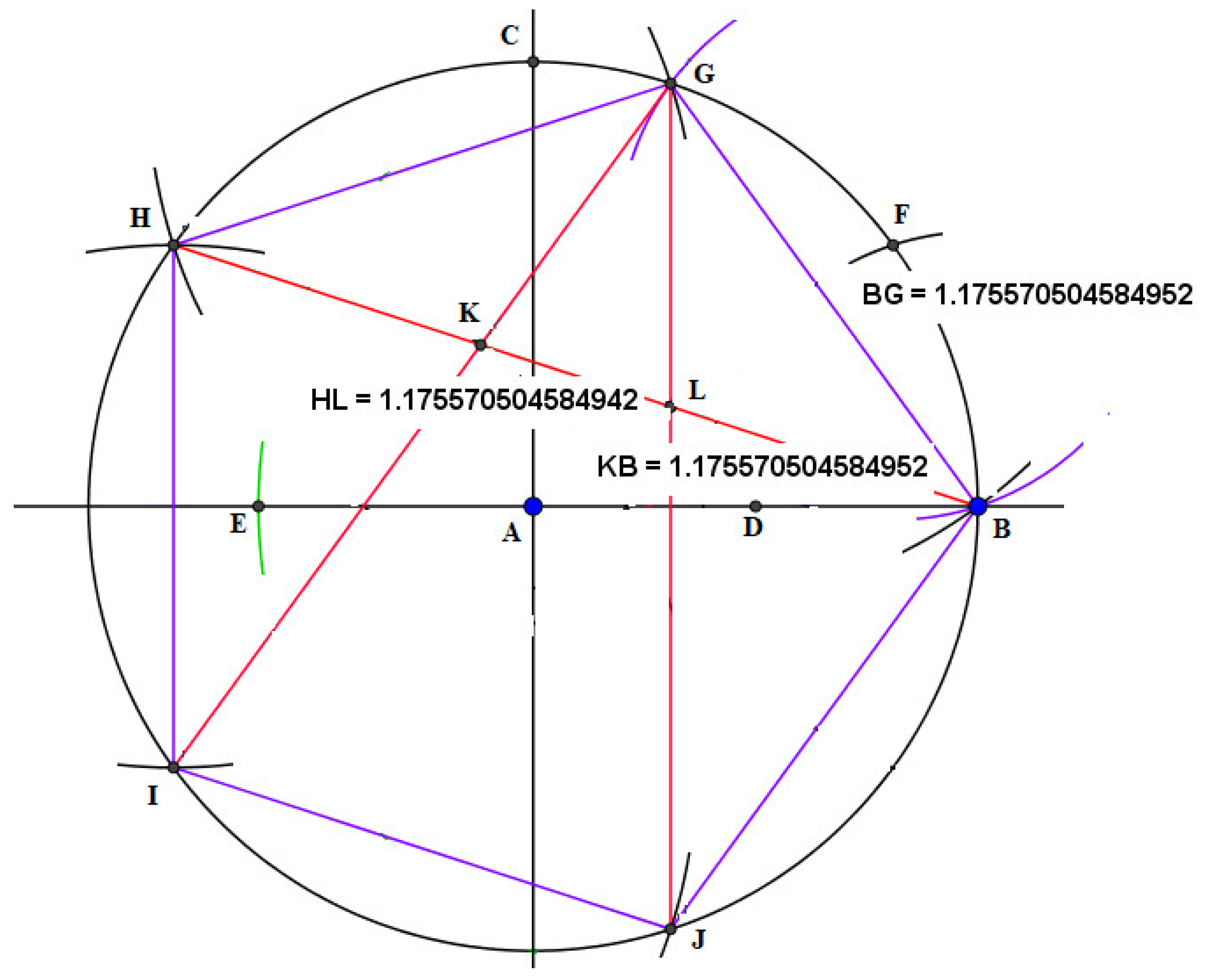
3.4.1. Construction of a Regular Pentagon

According to algebra, the constructability of geometric magnitudes is restricted to three basic algebraic conditions, which state: ($i$) A length is constructible if and only if it represents a constructible number. ($ii$) An angle is constructible if and only if its cosine is a constructible number. ($iii$) A number is constructible if and only if it can be written in the four basic arithmetic operations and the extraction of square roots but not on higher roots. One limitation of the algebraic norm of geometric understanding is that algebra treats a geometric magnitude as a number, whereas numbers in Euclidean plane geometry do not represent geometric magnitudes [3]. This algebraic approach offers a serious fallacy in translating geometry to algebra. Previously, it has been shown that all multiples of $3$ are constructible strictly following straightedge-compass operations, starting with the construction of $36°$ angle. The constructability of a $36°$ angle implies the possibility of constructing a $72°$ angle and, equally, the geometric construction of a regular pentagon using a straightedge and compass.

Consider the following steps for constructing the regular pentagon ($72°$ angle).

• Construct a straight line (a baseline) through the given two points $A$ and $B$.
• Construct a perpendicular to the baseline $\overline{AB}$ through point $A$.
• Using radius $\overline{AB}$, construct an arc that intersects the perpendicular line constructed through point $A$ at point $C$. $\angle CAB=90°$ since $\overline{AB}\perp \overline{AC}$.
• Construct the midpoint of the radius $\overline{AB}$, at a point, $D$.
• Construct a straight-line segment through points $C$ and $D$ using a straightedge.
• Using radius $\overline{CD}$ and center $D$, construct an arc that intersects $\overline{BA}$ externally at a point,$E$.
• Using the straight-line segment $\overline{AE}$, construct an arc that intersects the curve $\widehat{BC}$ at a point, $F$. $\angle FAB=36°$ as shown in Figure 1.
• With the compass adjusted radius $\overline{AE}$ and using point $F$ as the center, construct an arc that intersects the curve $\widehat{FC}$ at a point, $G$.
• Using the chord $\overline{BG}$ as radius and starting with point $G$ as the center of the construction, stroke along the curve $\widehat{BGC}$ three times to produce points $H$, $I$, and $J,$ respectively. Points $G$, $H$, $I$, $J$, and $B$ are equidistant along $\widehat{BC}$.
• Construct the chord $\overline{BG}$, $\overline{GH}$, $\overline{HI}$, $\overline{IJ}$, and $\overline{JB}$, as shown in Figure 3. These chords (the blue lines) are the sides of the regular pentagon.
• Construct the diagonals $\overline{GI}$, $\overline{GJ}$, and $\overline{HB}$.
• Label points $K$ and $L$, as the points of intersections between the diagonals $\overline{HB}$ and $\overline{GI}$, and $\overline{HB}$ and $\overline{GJ}$ respectively.

Extending Proof for Claim 1. This section is constructed in the interface between plane geometry and the algebraic means of proof based on Figure 3. A regular polygon has five sides with vertices evenly spaced from the center. We establish the geometric proof starting with triangle $BGH$. The straight-line segment; $\overline{BG}=\overline{GH}$ (sides of the regular pentagon). Moreover, $\overline{BG}=\overline{GH}=\overline{HL}=\overline{KB}$ (this can be proven, geometrically by the construction of a circle of radius $\overline{HL}$ and any of the vertices of the pentagon as the center of the construction. The constructed circle will pass exactly through two vertices of the pentagon, thus proving $\overline{BG}=\overline{GH}=\overline{HL}=\overline{KB}$). The size of an interior angle ($\theta$) of any regular polygon can be expressed as $\theta =180°-\frac{360°}{n}$, where $n$ is the number of sides of the regular polygon. Therefore, for a pentagon ($n=5$), $\theta =180°-\frac{360°}{5}=108°$. Therefore, $\angle BGH=108°$. The sum of angles in a triangle is $180°$. Thus, the base angles in triangle $BGH$ are each $36°$ (triangle $BGH$ is isosceles). This deduction produces two isosceles triangles, triangle $GHL$ and triangle $GBK$. It can also be deduced that triangle $BGH$ is geometrically sectioned into three small isosceles triangles: triangle $GKH$, triangle $KGL$, and triangle $GLB$. This implies that the segment $\overline{HK}=\overline{KG}=\overline{GL}=\overline{LB}$. Further, this deduction shows that triangle $BGH$ is similar to triangles $GKH$ and $GLB$ (by the property $Side-Angle-Side\left(SAS\right)$).

To verify this proof, we will need some of the constructed pieces. Let a side of the pentagon $\overline{BG}=x$, and a side of the smaller isosceles triangles be $\overline{LB}=y$. Therefore, the diagonal $\overline{HB}=\overline{HL}+\overline{LB}=x+y$. The similarity between triangles $BGH$ and $GKH$ can be expressed proportionally, as shown in Equation (8).

$$\frac{x}{y}=\frac{x+y}{x}$$

(8)

Rearranging Equation 8 provides the quadratic Equation 9.

$$y^2+xy-x^2=0$$

(9)

Using the quadratic formula Equation 9, it reduced to Equation 10 as follows:

$$y=\frac{-x\pm \sqrt{x^2+4\times 1\times x^2}}{2}=\frac{x(-1\pm \sqrt{5})}{2}$$

Since $y$ is a length and geometrically negative magnitudes are not allowed; therefore, there are no other geometrically necessary reasons for dropping the negative magnitudes and proceeding with Equation (10).

$$\frac{y}{x}=\frac{\sqrt{5}-1}{2}$$

(10)

It has already been established that the base of triangle $BGH$, $\overline{HB}=x+y$. Therefore,

$$x+y=x\left(1+\frac{y}{x}\right)=x\frac{\sqrt{5}+1}{2}$$

(11)

With the aid of a straightedge and compass, we can construct a perpendicular through point $G$, to bisect the base $\overline{HB}$ at a point such that we have a right triangle with hypotenuse $x$ and a side $\frac{x+y}{2}$ Considering the algebraic condition that an angle is constructible if and only if its cosine is a constructible number, Equation (12) shows that the cosine of a base angle $\angle GHZ$ is a constructible number since it is possible to take square roots for the expression $\frac{\sqrt{5}+1}{4}$ using a straightedge and compass. The trigonometric ratio cosine is extracted from a right triangle following Equation (12), which implies the geometric construction of a line segment or the geometric construction of a ratio corresponding to the measure $\cos GHZ$.

$$\cos GHZ=\frac{x-y}{2x}=\frac{\sqrt{5}+1}{4}$$

(12)

Equation (12) can be verified using GeoGebra’s angle measurement tool, which provides a numerical approximation for $\angle GHZ=36°$. It therefore follows that the $36°$ angle is constructible. Considerably, a $30°$ angle is also constructible via straightedge and compass constructions. Thus, the $6°$ angle is constructible by ($36°-30°=6°$), and so is the $3°$ angle (the constructability of the $3°$ angle is provided later). It is thus legitimate to state that any angle that is an integer multiple of $3°$ is constructible using a straightedge and compass.

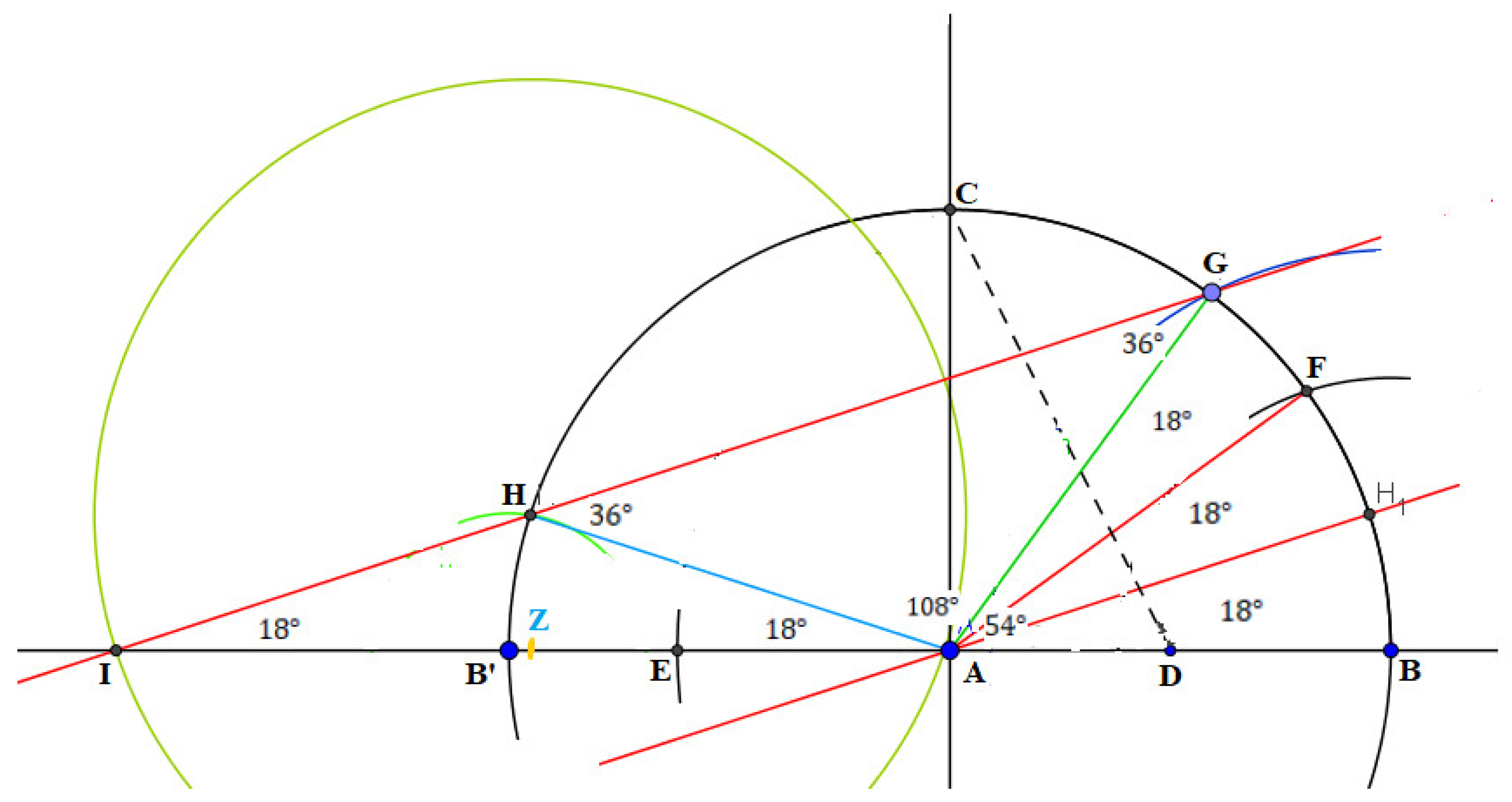
3.4.2. Geometric Construction of $3°$ Angle

The previous section has verified (Equation (7) provides the general analysis of a geometric construction) that angles multiples of $3$ are constructible following the rules of Euclidean constructions, and so equally, is the construction of the $3°$ angle. This section provides a simplified series of steps for constructing a $3°$ angle using straightedge and compass operations. To get a $3°$ angle, this section offers a construction procedure that requires to construct the bisection of the geometric angle difference $36°-30°=6°$. This construction is possible, as depicted in Figure 4. The following construction steps result in the construction of a $3°$ angle.

• Construct a straight line (a baseline) through the given two points $A$ and $B$.
• Construct a perpendicular to the baseline $\overline{AB}$ through point $A$.
• Using radius $\overline{AB}$, construct an arc that intersects the perpendicular line constructed through point $A$, at a point $C$.
• Construct the midpoint of the radius $\overline{AB}$, at a point, $D$.
• Construct a straight-line segment through points $C$ and $D$ using a straightedge.
• Using radius $\overline{CD}$ and point $D$ as the center of construction, construct an arc that intersects $\overline{BA}$ on the side of $A$ at a point,$E$.
• Using the straight-line segment $\overline{AE}$, construct an arc that intersects the curve $\widehat{BC}$ at a point, $F$. $\angle FAB=36°$ as shown in Figure 1.
• Using radius $\overline{AB}$, and center $B$, construct an arc that intersects the curve $\widehat{BC}$ at a point, $G$. $\overline{AB}=\overline{AG}=\overline{GB}$, implying triangle $GAB$ is equilateral, and $\angle GAB=60°$.
• Construct the bisection of $\angle GAB$ to intersect the curve $\widehat{BG}$ at a point, $H$. $\angle HAB=30°$, since $\angle HAB$ is a bisection of $\angle GAB$. This implies $\angle FAH=6°$.
• Construct the bisection of $\angle FAH$ to intersect $\widehat{FH}$ at a point, $I$. $\angle IAH=\angle IAH=3°$.
• Using either chord $\overline{IH}$ or chord $\overline{IF}$ and center $B$, construct an arc that intersects the curve $\widehat{BH}$ at a point, $J$. $\angle JAB=3°$, as shown in Figure 4.

3.5. Practical Limitations of Non-Geometric Proofs (The Case of Non-Trisectability Angles)

Following the outline of the structural limitations of the non-Euclidean methods in geometry (section $2$), this section focuses on a specific case aimed at extending the limitations of this system from structural to their practical essence. The adoption of non-Euclidean methods in addressing geometric problems, particularly concerning the constructability of angles multiples of 3, has inadvertently obscured the inherently geometric nature of these challenges. While non-Euclidean approaches may offer alternative perspectives [13], they fall short of upholding the rigorous standards of Euclidean geometry. In this section, we will explore the limitations of non-geometric proofs, specifically focusing on the non-trisectability of angles, and dissect the misconceptions that arise when non-Euclidean methods are employed as substitutes for the desired geometric norms.

3.5.1. Misalignment of Geometric Concepts

The concept of the Misalignment of Geometric Concepts highlights a critical issue when non-Euclidean methods are applied to geometric problems. In this context, misalignment refers to the inappropriate conflation of two distinct geometric ideas: the constructability of an angle and the trisection of an angle. Non-Euclidean methods, while attempting to provide solutions to geometric problems, often obscure the boundaries between these two geometric concepts. First, we need to clarify what each of these concepts entails.

Remark 3.8. (Constructability of an Angle). This concept focuses on whether a specific angle can be created using only a straightedge and compass. It is a standalone problem that seeks to determine if a particular angle can be geometrically formed using the tools allowed by Euclidean geometry.

Remark 3.9. (Trisection of an Angle). Trisection pertains to the division of a given angle into three equal parts. It is a separate geometric problem that explores developing a generic procedure that, when applied to a given angle, can be divided into three congruent angles, each of which measures one-third of the original angle.

The misalignment occurs when non-Euclidean methods attempt to solve the trisection problem by proving the constructability of an angle different from the trisected angle. This is fundamentally flawed because these two problems are distinct. The cornerstone of Euclid’s geometry is its rigorous adherence to defined axioms and principles. Within this framework, each problem has a unique set of conditions and criteria for its solution. Attempting to substitute the constructability of one angle for the trisection of another is similar to trying to fit a square peg into a round hole. It contradicts the foundational principles of Euclidean geometry, which demand precision and clarity in problem-solving. To draw an analogy, imagine trying to prove that it is impossible to construct a square with the same area as a given circle using only a straightedge and compass. If one mistakenly substitutes this problem with proving the constructability of a square with a different area, the result would be misleading and invalid. In essence, the misalignment of geometric concepts highlights the importance of respecting the uniqueness of each geometric problem and not assuming that solutions to one problem can automatically be applied to another. It underscores the need for precision and rigor in geometric reasoning, principles that lie at the core of Euclid’s geometry.

3.5.2. Lack of Geometric Foundation

The lack of rigorous geometric foundations within non-Euclidean methods reveals a significant issue regarding the constructability of angles multiples of $3$ and its implications on the trisection problem. In greater depth, we can explore this concept as follows:

Assumption vs. Geometric Proof. Historically, non-Euclidean methods have assumed that angles multiples of $3$ are constructible using straightedge and compass, primarily based on algebraic viewpoints rather than rigorous geometric proofs. This assumption implies that certain angles can be constructed from a purely algebraic perspective, but it doesn’t provide concrete geometric constructions to support this claim.

Introduction of a Geometric Construction. As demonstrated earlier in this paper, the introduction of a geometric construction challenges the long-standing assumption that angles multiples of $3$ are inherently constructible within the Euclidean geometric system. The paper underscores the need for concrete geometric foundations in solving problems within Euclidean geometry by providing an actual geometric construction for such angles.

The Modern Mathematical Perspective. From a modern mathematical viewpoint, it is essential to acknowledge that the claim that a dense set of angles is geometrically trisectable lacks irrefutable evidence when considered solely from the perspective of non-Euclidean methods. While algebraic insights can offer alternative viewpoints and solutions, they should not be mistaken for geometric rigor.

The Role of Geometric Proof. In Euclidean geometry, the cornerstone of any claim is a rigorous geometric proof. Without such proof, assertions about geometric constructability can lack the necessary foundation. Introducing a geometric construction for angles multiples of $3$ emphasizes that geometric proof is paramount in establishing the validity of claims within the Euclidean geometric system.

In the broad sense, this limitation underscores the need for solid geometric proofs when addressing geometric problems within the Euclidean framework. It highlights the potential pitfalls of relying solely on algebraic viewpoints or unproven assumptions and emphasizes the importance of rigor, precision, and clarity in Euclidean geometric reasoning.

3.5.3. The Inadequacy of Non-Euclidean Approaches

Here, we present an additional constraint, the inadequacy of non-Euclidean methods. When utilized as substitutes for Euclidean geometric demonstrations, they emphasize various crucial distinctions between these two geometric frameworks.

Fundamental Genetic Distinctions. Euclidean geometry and non-Euclidean geometry are fundamentally distinct in their genetic makeup. Euclidean geometry is founded on specific axioms and principles developed over centuries. These axioms provide a rigorous foundation for geometric reasoning, and any proof within this system adheres to these principles. On the other hand, non-Euclidean systems deviate from these axiomatic foundations, often exploring alternative geometries.

Lack of Depth and Rigor. When non-Euclidean methods are applied as substitutes within the Euclidean geometric system, they may lack the necessary depth and rigor to meet Euclidean standards. Euclidean proofs demand precision, clarity, and strict adherence to established axioms. Non-Euclidean approaches, while valuable in their own right, can introduce concepts and techniques that do not align with the rigorous requirements of Euclidean geometry.

Complexity of Geometric Relations. Euclidean geometry strongly emphasizes the precise relationships between geometric entities, such as angles, lines, and triangles. Non-Euclidean approaches, which often diverge from the traditional Euclidean framework, may introduce complexities or variations that make it challenging to establish these relationships with the same level of clarity and rigor.

Preservation of Euclidean Identity. The Euclidean geometric system has retained its identity and relevance over centuries due to its robustness and clarity. While non-Euclidean approaches offer alternative perspectives and insights, the claim here is that they should be applied judiciously to avoid compromising the integrity of the Euclidean system.

The Role of Geometric Proof. Euclidean geometry strongly emphasizes geometric proof as the standard for establishing claims. Non-Euclidean methods, while valuable for expanding mathematical horizons, may not always adhere to this strict standard. This discrepancy in proof methodology can lead to questions about the validity of claims made within the Euclidean framework.

This restriction is a constant reminder of the fundamental genetic differences between Euclidean and non-Euclidean geometry. While non-Euclidean methods can offer valuable insights and alternative perspectives, they should be employed with caution within the Euclidean system to ensure that the foundational principles of Euclidean geometry remain intact. The importance of precision, rigor, and adherence to Euclidean axioms cannot be understated in the pursuit of geometric knowledge and understanding.

3.5.4. Completeness of Euclidean Geometry

The notion of the Completeness of Euclidean Geometry highlights an important aspect of the Euclidean geometric system: its enduring comprehensiveness and resilience in detail.

Historical Significance. Euclidean geometry, developed by the ancient Greek mathematician Euclid, has stood the test of time and remains one of the most influential branches of mathematics. For centuries, it has been the foundational framework for geometric reasoning and has played a pivotal role in shaping mathematical thought.

Established Axioms. Euclidean geometry is built upon a well-defined set of axioms, postulates, and principles refined and validated over centuries. These axioms serve as the bedrock upon which all Euclidean proofs are constructed. The clarity and precision of these axioms are a testament to the completeness of the system.

Robust Problem Solving. Euclidean geometry has consistently demonstrated its capacity to address various geometric problems. The Euclidean framework has provided elegant and rigorous solutions from elementary constructions to complex proofs. This ability to encompass diverse problem sets underscores its completeness.

Absence of Concrete Incompleteness Proof. While various branches of mathematics have explored the concept of mathematical incompleteness (most notably Gödel’s incompleteness theorems [20–22]), there is no concrete proof that the Euclidean geometric system is incomplete or incapable of addressing its problems. In other words, no definitive mathematical evidence suggests that Euclidean geometry falls short of its scope.

Embracing Euclidean Strengths. It is crucial to recognize that while non-Euclidean methods can offer alternative perspectives and insights, they should not diminish the sophistication and comprehensiveness of Euclidean geometry. Euclidean geometry’s unique strengths lie in its clarity, precision, and logical rigor, which should be embraced and celebrated.

This limitation emphasizes the enduring significance and robustness of the Euclidean geometric system. While mathematical thought has expanded to include non-Euclidean approaches, Euclidean geometry remains a cornerstone of mathematical knowledge. Its well-established axioms, problem-solving capabilities, and absence of concrete incompleteness proof highlight its completeness and enduring relevance in mathematics.

4. Independence of Euclidean Geometry

The imperative of maintaining the independence of typical Euclidean geometric systems from the sway of non-Euclidean approaches arises from the fundamental character inherent to Euclidean geometry [7]. Rooted in a lineage of development spanning centuries, Euclidean geometry rests upon well-defined axioms and principles that collectively form an intricate framework for precise geometric reasoning. This framework has stood the test of time and provided a reliable foundation upon which many mathematical and scientific theories have been built. Non-Euclidean approaches [10,11,13], while introducing intriguing and valuable alternative viewpoints, must be approached with caution within the context of Euclidean geometry. The inherent structure of Euclidean axioms and the systematic arrangement of its principles have established a specific realm in which geometric proofs and constructions unfold with elegance and rigor. The axiomatic foundation of Euclidean geometry ensures coherence and consistency in the deductions drawn from its premises, facilitating a seamless process of reasoning and problem-solving. However, when non-Euclidean perspectives permeate the Euclidean domain, a delicate interplay emerges between the established norms and the newly introduced viewpoints. This interplay requires scrupulous consideration to ensure that the Euclidean framework’s inherent harmony and logical flow remain unmarred [3]. Non-Euclidean methods should be integrated in a manner that respects the distinct axiomatic structure of Euclidean geometry and does not disrupt the established rules and principles that have made it a cornerstone of mathematical inquiry. While non-Euclidean approaches can broaden the horizons of mathematical understanding, they must be integrated thoughtfully, keeping in mind the essence of Euclidean geometry’s foundational elements. The axiomatic integrity of Euclidean geometry and its historical significance necessitate that any infusion of non-Euclidean ideas is carefully balanced to preserve the coherence and robustness that have defined Euclidean geometry for centuries.

5. Conclusions

In this explorative expedition through the complex domain of angle construction in Euclidean geometry, we have delved into the core inquiries of this mathematical discipline. The focus has involved revealing the system’s inherent strengths and addressing the challenges that emerge when non-Euclidean approaches influence its traditional principles. We began with a clear confirmation of Euclidean geometry’s enduring ability to deliver precise constructions and rigorous proofs for angles multiples of $3$, all accomplished using only the basic tools of a straightedge and compass. We have showcased the elegance and generative power of the Euclidean framework, demonstrating its harmony with a diverse array of geometric problems. In doing so, we reaffirmed that the intrinsic essence of Euclidean geometry lies in its ability to bridge the abstract with the tangible, the algebraic with the geometric. However, we didn’t confine ourselves to the principles of Euclidean geometry; instead, we delved into the world of non-Euclidean techniques, particularly analytical methods that aim to establish links between algebraic and geometric domains. In doing so, we unearthed fascinating revelations and alternative problem-solving approaches. Yet, we also encountered the inherent vulnerability of these methods to misinterpretations and errors, especially when attempting to create specific angles, causing a blurred line between the notions of constructability and trisection. This misalignment of geometric concepts unveiled a fundamental misunderstanding of the rigorous standards governing Euclidean geometry-this paper’s pivotal lesson centers on embracing Euclidean geometry in its pristine form. The misalignment of non-Euclidean methods with the core principles of Euclidean geometry underscores the perils of misinterpretation, inaccuracies, and the potential erosion of generality that can arise from shifting toward analytical solutions. While non-Euclidean approaches offer valuable alternative perspectives, their limitations in capturing the true essence of Euclidean rigor and the intricate interplay of geometric relations become evident upon closer scrutiny. The journey reached its zenith with the presentation of the first rigorous geometric proof affirming the constructability of all angles multiples of $3$ within the Euclidean geometric system. This accomplishment not only solidified Euclidean geometry’s mastery in addressing these fundamental geometric inquiries but also underscored the need to preserve its intrinsic strengths and profundity. We recognized that the uniqueness of Euclidean geometry stems from its ability to encompass a diverse range of problems while maintaining coherence and clarity. As we conclude through the rich tapestry of geometry, we leave behind a trail of insights, discoveries, and reflections. May it inspire future generations of mathematicians and scholars to continue navigating the boundless seas of mathematical inquiry, ever guided by the unwavering light of Euclidean wisdom.