Prerpints.org logo
Preprint
Article

Atomistic Modelling of Spinel Oxide Particle Shapes and Reshaping under OER Reaction Conditions

Altmetrics

Downloads

237

Views

110

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (3.89MB )

This version is not peer-reviewed

Submitted:

02 December 2023

Posted:

05 December 2023

Read the latest preprint version here

Alerts
Abstract
The surface configurations of the low-index facets of a set of spinel oxides are investigated using DFT+U calculations to derive surface energies and predict equilibrium nanoparticle shapes via the Wulff construction. Two very different conditions are investigated, corresponding to appli-cation either in heterogeneous catalysis or in electrocatalysis. First, the bare stoichiometric sur-faces of NiFe2O4, CoFe2O4, NiCo2O4, ZnCo2O4 spinels are studied to model their use as high-temperature oxidation catalysts. Second, focusing attention on the electrochemical oxygen evolution reaction (OER), and on the CoFe2O4 inverse spinel as the most promising OER catalyst, we generate systematically surface configurations by adsorbing OER intermediates, and recal-culate surface energies taking into account adsorption and environmental conditions, i.e., ap-plied electrode potential and O2 pressure. We predict that, under OER operating conditions, (111) facets are dominant in CoFe2O4 nanoparticle shapes, in fair agreement with microscopy meas-urements. Importantly, in the OER case we predict a strong dependence of nanoparticle shape upon O2 pressure. Increasing O2 pressure increases the size of the higher-index (111) and (110) facets at the expense of the (001) catalytically active facet, whereas the opposite occurs at low O2 pressure. These predictions should be experimentally verifiable and help define the optimal OER operative conditions.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

Nanomaterials, such as metal or metal oxide nanoparticle systems, find applications in many areas of technology, such as biomedical, sensors, optics, storage and energy harvesting materials, as well as in heterogeneous catalysis, where they play a dominant role [1]. Their function is closely linked to their structure in terms of nanoparticle size and shape [2]. Therefore, controlling the shape of metal or metal oxide nanoparticles is one of the major challenges in applications, as this has a dramatic effect on material properties, e.g., determining number and type and performance of active sites in catalysis.
The shapes of nanoparticles can be determined via the Wulff construction, proposed by the mineralogist George Wulff at the beginning of the twentieth century [3]. This method was used in geology, mineralogy and crystallography, and was then rediscovered in materials science to predict the shapes of nanoparticles. The Wulff construction allows one to predict the nanoparticle shape through knowledge of their surface energies, data which can be and have been calculated for many systems via e.g. theoretical simulations based on first-principles quantum-mechanical methods [1]. Some characteristic equilibrium shapes often found in materials with cubic symmetry are shown in Figure 1.
Following the fundamental work by Gibbs [4], and introducing the principle of minimum surface free energy to determine the shape of a crystal at equilibrium, Wulff proposed [3] that the shape of a crystalline material to be constructed via the following recipe:
γ h k l n r h k l = c o n s t a n t , ∀ h k l
where γhkl is is the energy required to create a surface of unit area normal to the (hkl) vector, and rhkl is the distance from the center of the crystal to the hkl plane. This process is repeated for all sets of Miller indexes, hkl, uniquely identifying a surface. The ratio of the surface energy, γhkl, to the distance from the center of the crystal, rhkl, to any plane is constant in the Wulff construction.
In heterogeneous catalysis by metal nanoparticles, the catalytic functionality is strongly linked to their shape, especially for structure-sensitive reactions, which makes predictions of their morphology via e.g. computational methods an important goal. For example, Nørskov et al. obtained the equilibrium polyhedron shape of Ru nanoparticles, and hence estimated the catalytic rates by summing contributions of the various facets, then comparing with experimentally measurements of transmission electron microscopy (TEM) and catalytic rates, finding reasonable agreement with experiment [5]. Vilé et al. investigated supported Ag catalyst nanoparticles (2-20 nm in diameter) to determine active sites for the olefin reaction using the atomistic Wulff construction and reported that the nanoparticles have the highest density of B5 sites, which are the active centers in the reaction [6]. Larger nanoparticles may expose higher-index facets: Wulff shapes of large Au nanoparticles were predicted to include (332), (001), (111), (211), and (322) facets, whereas nanoparticles smaller than 16 nm in diameter expose only (111) and (001) facets [7]. However, the equilibrium shape rarely contains facets with indexes higher than (001), (111), (110): high-index surfaces have a higher surface tension than low-index faces, and even if a high-index surface and a low-index surface have equal surface tensions, the low-index face will have a larger area as the high-index face will be steeper and be hidden in the Wulff construction [1].
Bare metal oxide facets have also been considered. In a systematic study, the surface structure, energies and morphology of bare cubic cobalt spinel nanocrystals with the formula M[CoM′]O4 (M = Mg, Zn, Fe, Co and M′ = Ni, Al, Mn, Co) were investigated via Density-Functional Theory plus Hubbard correction (DFT+U) calculations, and compared directly with TEM and STEM experiments [8]. The authors predicted that the abundance of the (110) faces is always low (below 9%) and the surface energies typically increase in the sequence γ100 < γ111 < γ110 for cobalt spinel nanocrystals.
Computational studies of bare metal or metal oxide nanoparticles are appropriate for modeling high-temperature and low-coverage conditions, such as those occurring in oxidation processes: chemical looping, water gas shift reaction [9], methanol [10] and propanol [11] oxidation, H2 production [12], etc. For nanoparticles under lower temperature and therefore higher-coverage conditions, the influence of the chemical environment should be included in the Wulff construction by rescaling surface energies with adsorption energies [13]. For example, Au nanoparticles exposed to CO were found to be more spherical and more reactive compared to Au nanoparticles in a non-interacting environments, in agreement with experimental data [7] and also in agreement with previous studies investigating the shape and chemical ordering upon CO and H adsorption of mono- and bi-metallic explicit atomistic nanoparticle models, thus going beyond the ideal Wulff construction [14]. Similarly, the surface free energy of MgO low-index crystal facets were investigated as a function of the temperature and water pressure through density functional theory, also comparing predictions with experimental observations [15]. It was suggested that (110) is a transient and metastable facet due to its fast kinetics of formation compared to the (111) facet, and that the equilibrium Wulff shape of MgO crystals only involves (001) and (111) facets. Additionally, experiment and theory agreed on the pattern of the hydroxylated surface energies as γ111 < γ100 < γ110, supporting the partial dissociation of water on MgO(001).
At the next level of complexity, the important question is how Wulff shape changes under reaction conditions, and how to account for this phenomenon at the theoretical prediction level [16, 17]. In a pioneering study, the size- and corresponding morphology-dependent theoretical activity and selectivity of silver nanoparticles between 9 and 23 nm in diameter for the partial oxidation of propylene and the evolution of these quantities along the progress of the reaction were experimentally measured and compared with theoretical predictions based on the Wulff construction and explicit reaction mechanisms, finding an excellent agreement with experimental observations of aspect ratio evolution [16]. More recently, the concept of dynamical Wulff construction was explicitly introduced to account for particle reshaping under reaction conditions and employed to predict the shape of Si-doped iron nanoparticles during ammonia synthesis [17].
In contrast with thermal catalysis, application of Wulff-based theoretical protocols in the field of electro-catalysis is to the best of our knowledge very limited, despite the ever growing interest of the scientific and technological communities in this field [18,19]. In particular, the oxygen evolution reaction (OER) in Anion Exchange Membrane Water Electrolysis (AEMWE, or water splitting) represents a critical step in the realization of a sustainable hydrogen production whence a global hydrogen economy would arise, so that discovering and optimizing active and non-critical-material OER catalysts is one of the major challenges to XXI century chemistry.
Here, we try to fill this gap in electro-catalysis by investigating spinel-type oxides via theoretical atomistic Wulff construction in a wide range of conditions, ranging from high-temperature to OER electro-catalysis. Note that spinel-like iron-based spinels are promising OER electro-catalysts [20] due to their significant electrical conductivity, structural stability and catalytic performance, stemming from multiple valence of the cations and the ability to switch among different oxidation states [21,22]. We predict via first-principles DFT+U the surface energies of the most abundant (001), (110), and (111) facets of selected spinel oxide structures, and we derive the equilibrium atomistic Wulff shapes of the corresponding nanoparticles under two very different sets of conditions:
(i)
NiFe2O4, CoFe2O4, NiCo2O4 and ZnCo2O4 (inverse or normal) spinels as bare stoichiometric surfaces to be compared with characterization experiments and catalytic investigations under low-coverage conditions, such as those occurring in heterogeneous catalysis [20], and previous studies [8];
(ii)
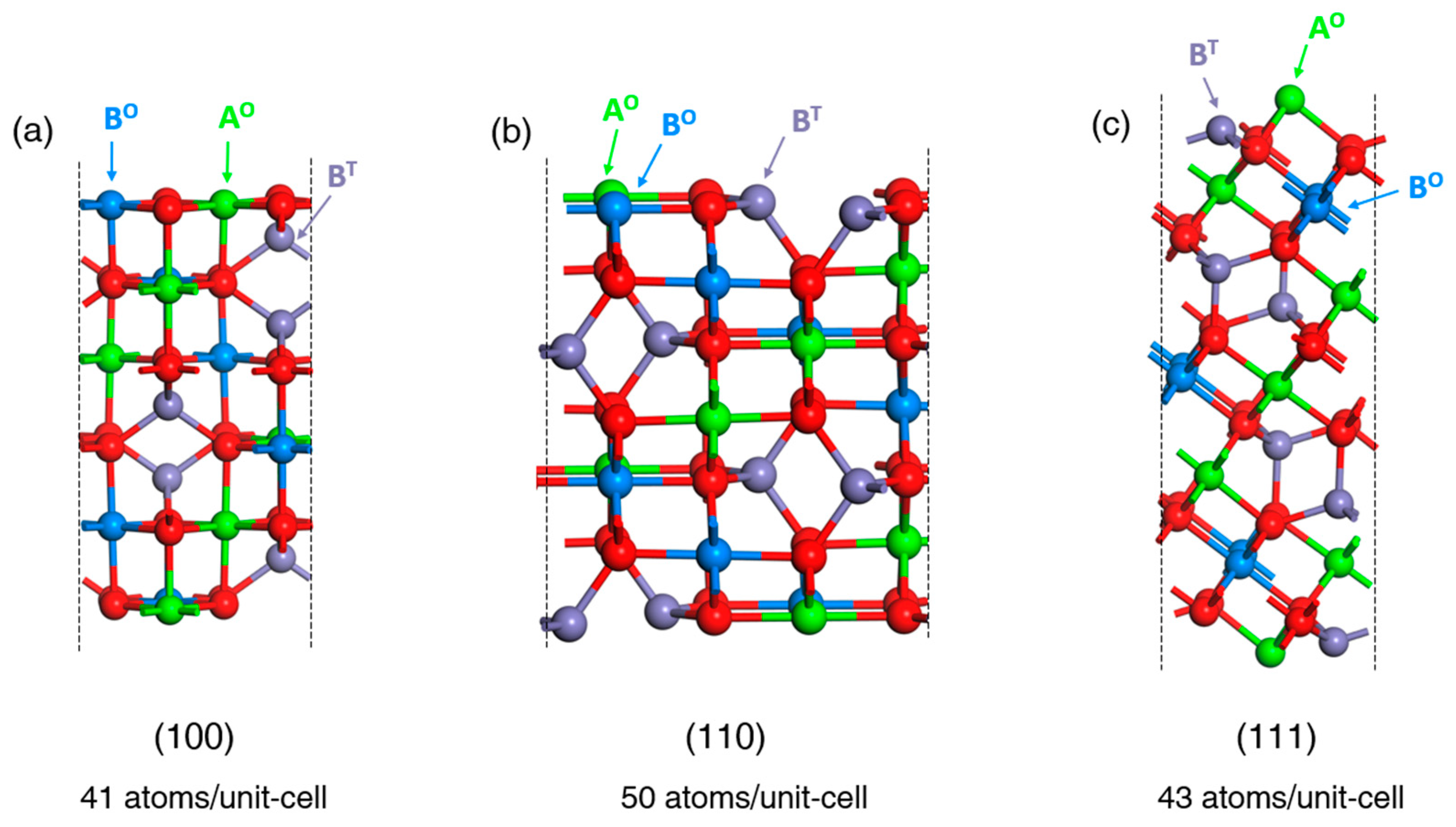
the CoFe2O4 inverse spinel, the most promising OER catalyst [23], for which we consider an extensive set of surface configurations with various coverage of adsorbate intermediates relevant during the electrochemical OER (H, OH, H2O, O, O2).
For the latter case, we also explore a wide set of environmental variables (applied electrode potential and O2 pressure), so as to determine Wulff reshaping under different OER reaction conditions, then finally comparing our predictions with experimental characterization. In agreement with experiment and a previous systematic study [8], we predict that under low-coverage conditions (100) typically dominate. Also in agreement with experiment, for CoFe2O4 we find that the most abundant facets change from (100) for bare particles to (111) under OER conditions. Moreover, importantly, in the CoFe2O4 OER case we find a strong phenomenon of nanoparticle reshaping upon O2 pressure: increasing O2 pressure reshapes the catalyst, increasing the size of the higher-index facets, i.e., (111) and (110), at the expense of the (001) facet, whereas the opposite occurs at low O2 pressure. Given that the OER catalytic activity of CoFe2O4 spinels is strongly dependent upon exposure of different facets [49-51], these predictions should be experimentally verifiable and help defining the optimal operative conditions for both oxidative and OER catalysis, with potential implications, e.g., on the design of OER electro-catalysts fulfilling societal requirement on activity, selectivity, efficiency, and cost.

2. Materials and Methods

Spin-polarized density functional theory plus Hubbard correction (DFT+U [24]) calculations were performed using a plane wave and ultrasoft pseudopotential framework [25] as implemented in the Quantum- Espresso [26] suite of codes. The Perdew-Burke-Ernzerhof (PBE) [27] exchange-correlation functional was used as DFT, augmented with Hubbard U parameters chosen as 3.3, 5.5, 3.0, 2.0 eV for Fe, Ni, Co, and Zn, respectively. It should be noted that we use an Ueff value of 3.0 eV for all type Co atoms (i.e., octahedrally or/and tetrahedrally coordinated, depending on spinel type) to be consistent with a previous systematic theoretical study by Selloni et al. [28,29,30]. In our previous study [23], we used a value for Ueff of 4.5 eV as optimal for describing iron-based inverse spinels, in which cobalt only occupies an octahedral coordination. However, we verified that there is no significant difference between those two values in terms of configuration energetics. Kinetic energy cutoffs of 40 and 200 Ry were chosen for describing the wave function and the charge density, respectively. A 3 × 3 × 1 Monkhorst−Pack k-point mesh was utilized for energy and structural calculations. The WulffPack package was used to predict theoretical equilibrium shapes [31].
Spinels have general chemical formula AB2X4 where AII is a divalent cation like Mg, Cr, Mn, Fe, Co, Ni, Cu, Zn, Cd, Sn, and BIII is a trivalent cation like Al, Ga, In, Ti, V, Cr, Mn, Fe, Fe, Co, Ni, and X as O, S, Se etc. A normal spinel can be represented as: (AII)tet(BIII)2octO4, whereas an inverse spinel can be represented as: (BIII)tet (AII )tet(BIII)octO4, where the subscript “tet” and “oct” refer to tetrahedral and octahedral sites (as discussed in Section 2). The selected catalysts with inverse spinel structure (NiFe2O4, CoFe2O4 and NiCo2O4) are ferrimagnetic [28], i.e., they exhibit a spin arrangement: ↑↓↑ for A(Oh)/B(Td)/B(Oh), using the notation: (A=Ni,Co; B=Fe,Co), spin up (↑), spin down (↓), and Oh and Td refer to octahedral and tetrahedral sites, respectively. At variance, ZnCo2O4 only exists in the normal spinel structure and is ferromagnetic [32, 33], with spin arrangement: ↑↑ for A(Td)/B(Oh), where (A=Zn; B=Co). We verified that our DFT+U predictions are consistent with these expectations.
For the surface energy calculations under vacuum, the stoichiometric/symmetric slabs utilized for the three considered facets [(001), (110), (111)], including dipole correction, for inverse and normal spinel slab models are shown in Figure 2 and Figure 3.
For the (001) orientation, our model corresponds to a total of 56 atoms per unit cell for a thickness of 9 layers. For the (110) orientation, our slab with a thickness of 9 layers contains 126 atoms per unit cell, while for the (111) orientation our unit cell 9-layer thick contains 112 atoms. Note that there are two types of possible terminations for the (110) spinel orientation, which are usually labeled A and B in the literature [8, 34]. As the 110-A termination was reported to be more stable than the 110-B one in previous work [35], the latter was excluded from our analysis. Therefore, the (110) label only refers to the most stable (110)-A termination in this study.
We use Eq.(2) to calculate surface energies from optimized energies of bare slab models:
E s u r f b a r e = E s l a b o f n f o r m u l a u n i t − n . E ( b u l k o f 1 f o r m u l a u n i t ) 2 A
The lattice parameters a,b,c of each stoichiometric slab have been derived after implementing variable-cell (vc) relaxation on the bulk phases of the investigated spinels, and are shown in Table S1 of the Supporting Information (SI).
We use the bulk optimized lattice parameters also to build non-stoichiometric/symmetric inverse spinel models to investigate surfaces with various coverage of adsorbed OER reaction intermediates on CoFe2O4. Non-stoichiometric but symmetric slab unit cells with dimensions of 5.99 Å × 5.99 Å × 25 Å for (001), 5.99 Å × 8.48 Å × 25 Å for (110), and 5.99 Å × 5.19 Å × 25 Å for (111) of inverse spinel slabs were built as shown in Figure 4.
The total number of atoms per unit cell for (001), (110), (111) slabs used in bare and adsorbed surface calculations is also summarized in Table S2 of the SI, and brief details about comparison of those slabs are also shown in Figure S1.
To calculate surface energies for surfaces with adsorbates, we re-scale them as shown in Eq.3, where adsorption energies are taken from optimization calculations of non-stoichiometric slab models [36]:
E s u r f a d s = E s u r f b a r e + E a d s A r e a
In the surfaces covered with oxygen, hydrogen and water, it is essential to include entropy terms in the chemical potentials of these species, to obtain the system free energy (G). Free energies are calculated using the same scheme utilized in previous studies [37, 38a] and explained in detail in our previous work [23]. The total energy (E) of each configuration was obtained directly via DFT. The contributions (∆H, ∆ZPE, T∆S) to the free energies (∆G) of small molecules (H2O, hydrogen and oxygen) were added empirically as: ΔGi = ΔEi + ΔHi + ΔZPEi −TΔSi [38a], where standard thermodynamic data [38b] are used to obtain the T and P contributions to the G values of aqueous H2O and gaseous H2.
The standard hydrogen electrode electrochemistry model [39] was finally used to calculate how the configuration energies depend upon the applied bias U via the proton-electron (H+ + e−) transfer steps. In this approach, the standard hydrogen electrode (SHE) is used as a reference, so the proton (G[H+]) and electron (G[e−]) free energies are replaced by ½ G[H2]-|e|U, where G[H2] is the free energy of H2 and U is the electrode potential versus SHE. To get rid of the dependence of the applied potential upon pH, a reversible hydrogen electrode (RHE) reference is employed, so that the equilibrium potential required for OER is always 1.23 V vs. RHE at all pH values [40]. In other words, in calculating the over-potential, the pH term is canceled by taking the difference between predicted onset potentials and the equilibrium OER potential [41].

3. Results & Discussion

As anticipated in the Introduction, we focus first on NiFe2O4, CoFe2O4, NiCo2O4 and ZnCo2O4 systems as bare stoichiometric surfaces corresponding to experiments at high temperature and low coverage, i.e., under the conditions of thermal heterogeneous catalysis [9-12]. This will allow us also to compare our predictions with and validate against previous studies [8] (Section 3.1). Then, in Section 3.2 we consider the CoFe2O4 system and study configurations with various coverage of (H, OH, H2O, O, O2) adsorbate species under electrochemical OER and varying environmental variables (applied electrode potential, O2 pressure), so as to be able to make predictions on the optimal experimental conditions for OER [20].

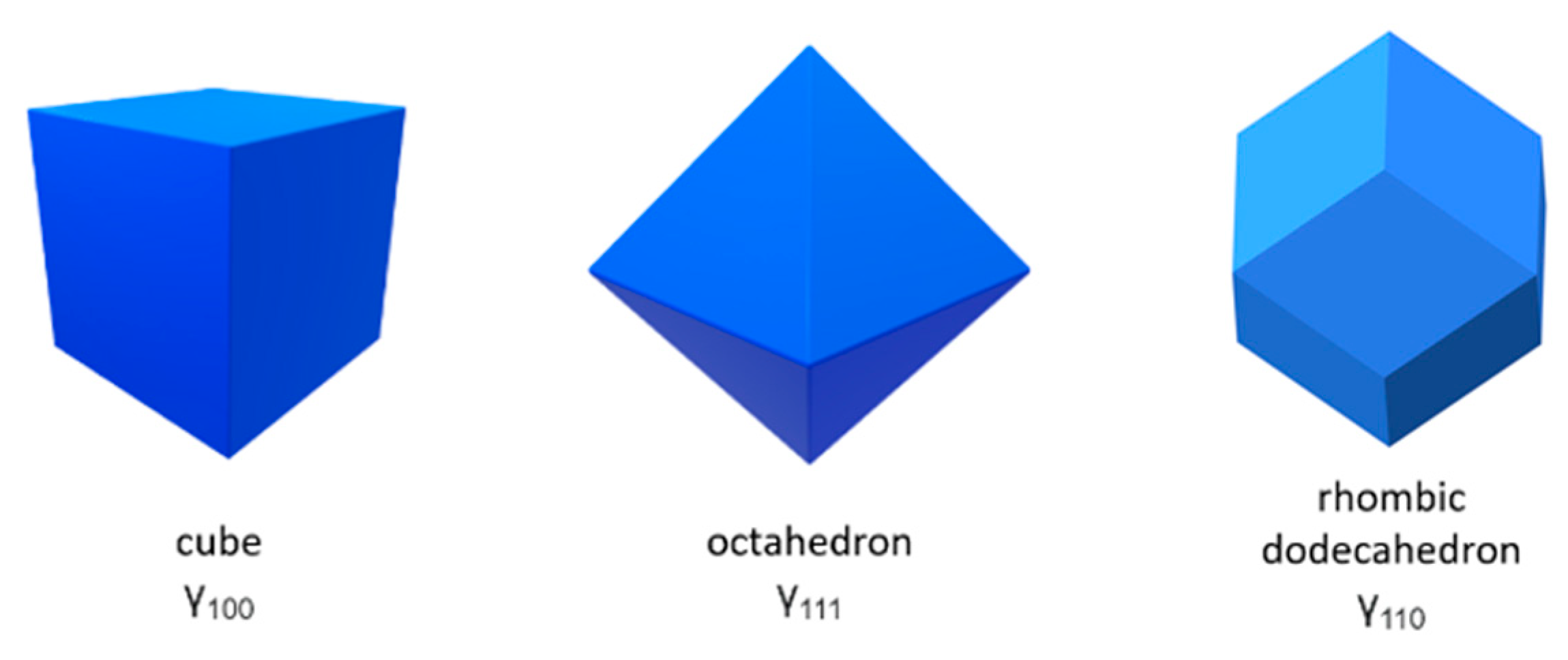
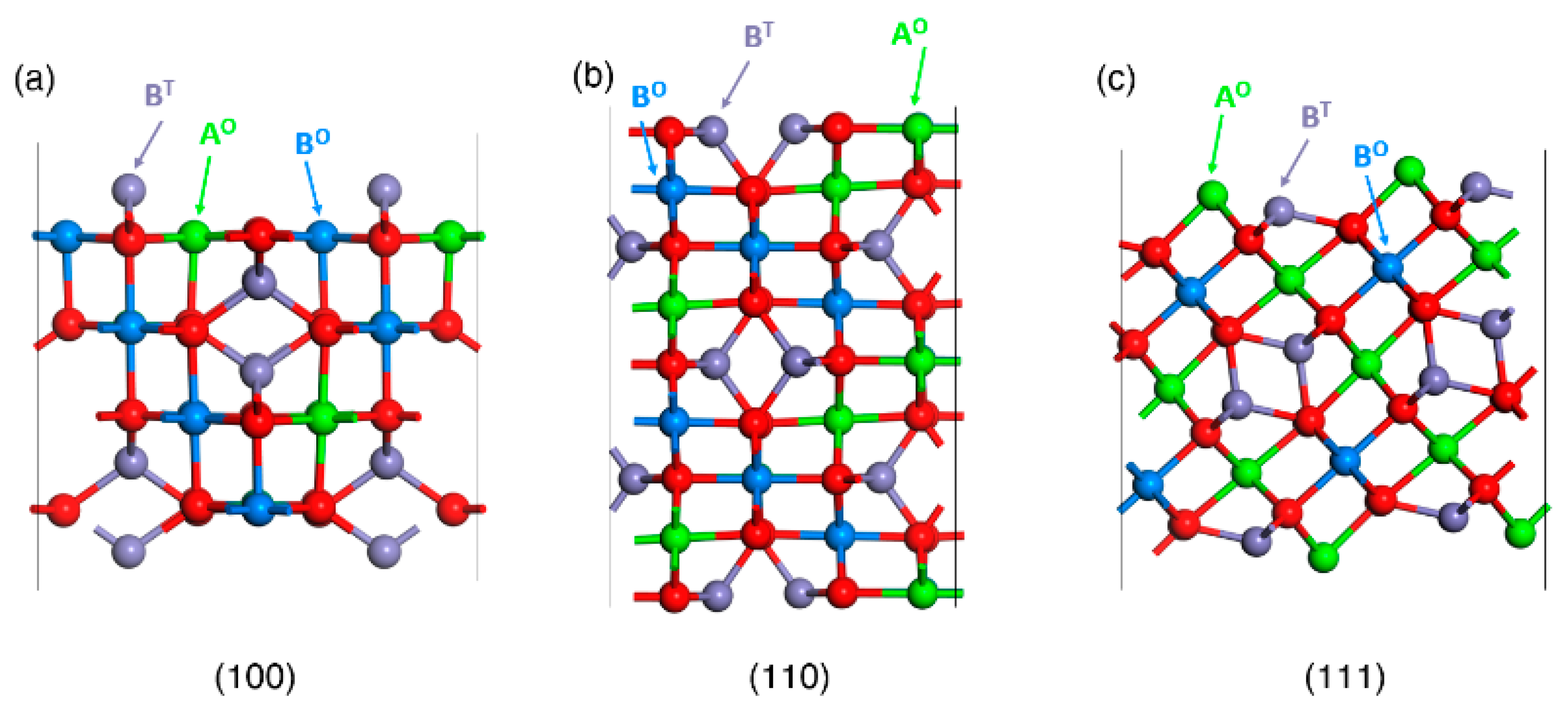
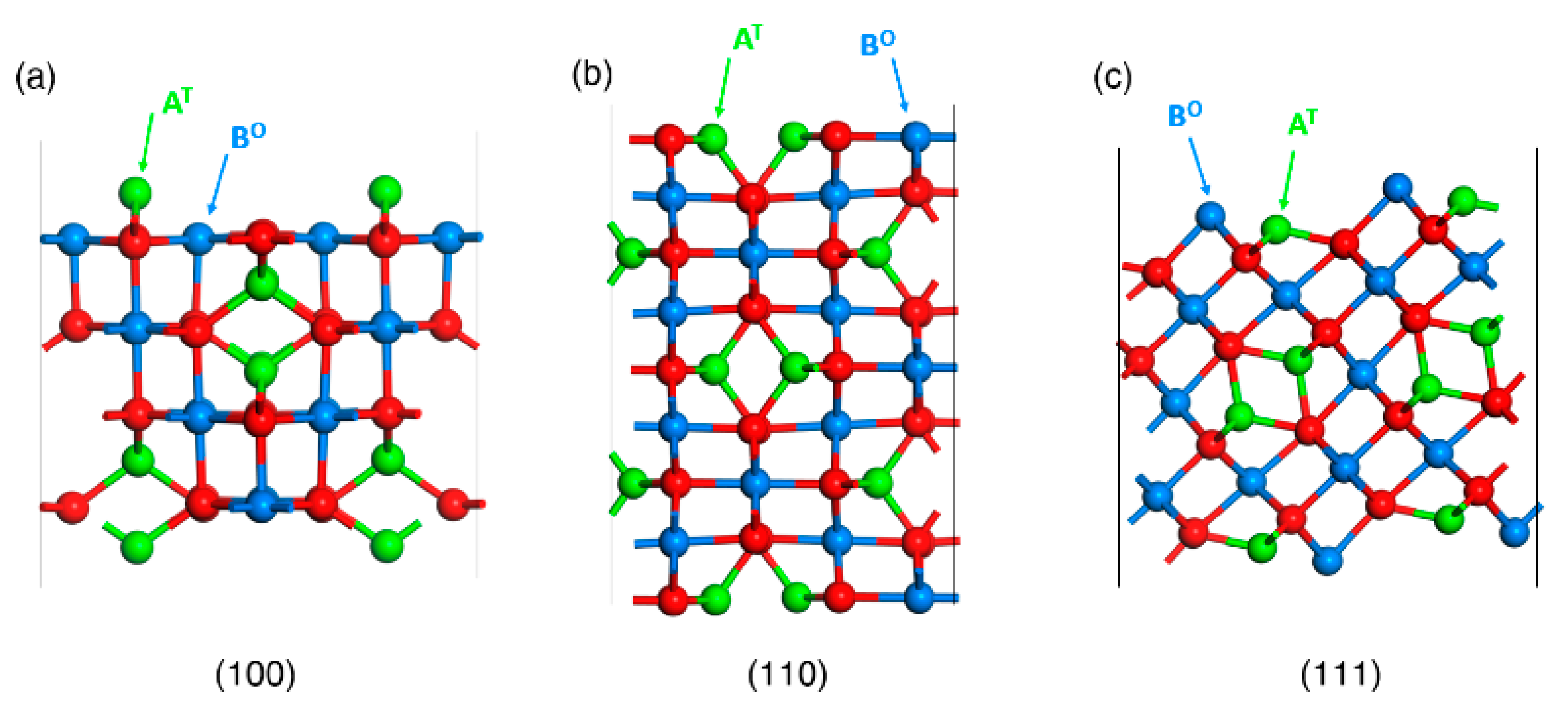
3.1. Wulff Shapes of Bare Spinel Surfaces as Heterogenous Catalysts

For each investigated spinel: the NiFe2O4, CoFe2O4, NiCo2O4 and ZnCo2O4 oxides, stoichiometric (n. AB2O4) surface slab models were constructed for all considered terminations as shown in Figure 2 and Figure 3. In the case of inverse spinels: NiFe2O4, CoFe2O4 and NiCo2O4, A++ (M= Ni, Co) cations occupy octahedral sites and B3+ (M=Fe, Co) cations occupy both octahedral and tetrahedral sites. For the normal spinel ZnCo2O4, A++ (M= Zn) cations occupy tetrahedral sites and B3+ cations (M=Co) occupy octahedral sites. Protruding cations on tetrahedral sides (BT and AT) on top and bottom surface in (001) plane were retained to maintain the stoichiometry in both inverse and normal spinels.
After imposing the lattice parameters derived from variable-cell (vc) relaxation of the bulk, slab models were constructed, Cartesian coordinates were relaxed, and surface energies (in J/m2) of each facets were calculated based on the Eq. 2 and reported in Figure 5 (top).
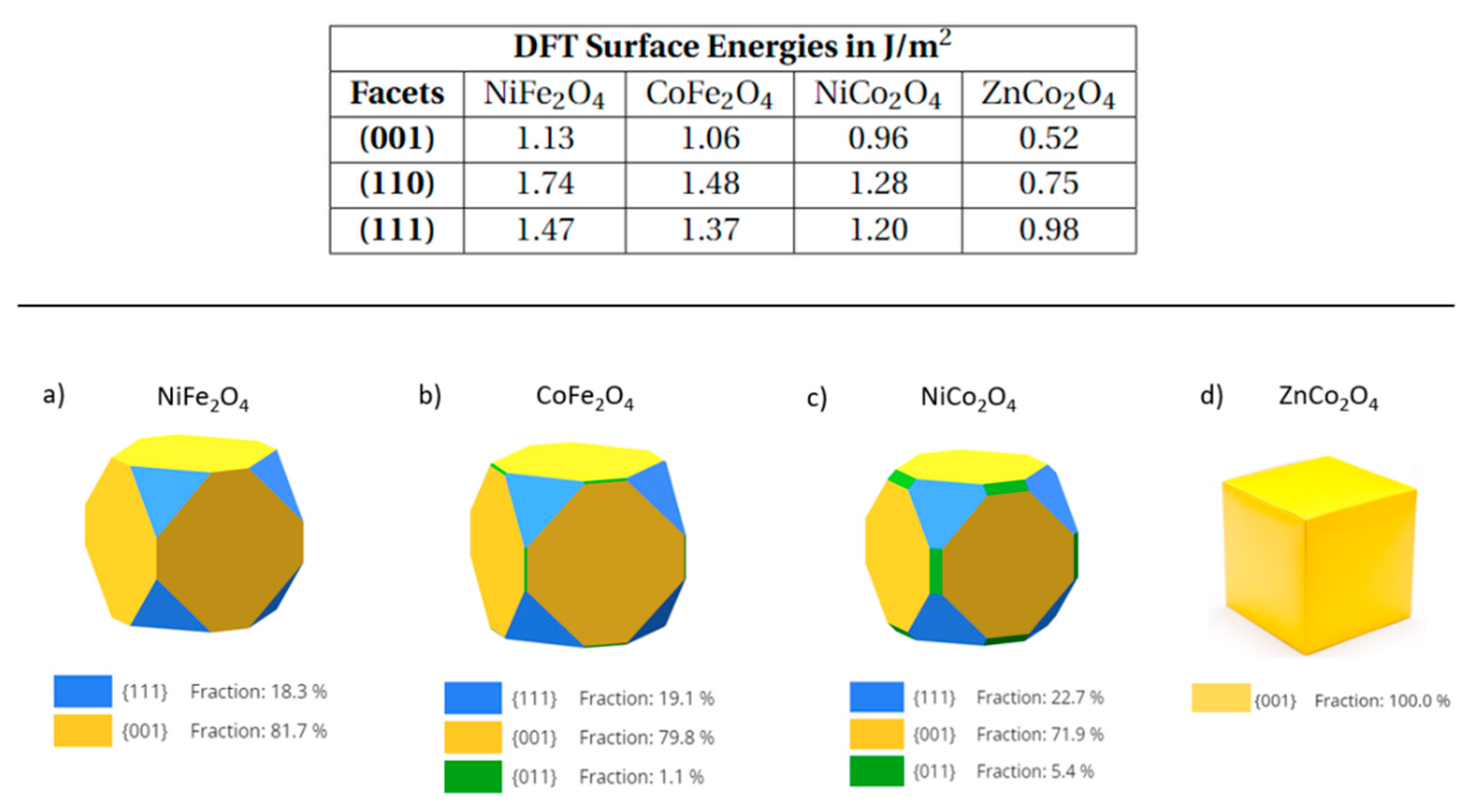
Preprints 92110 g005
Figure 5. (Top) Calculated DFT Surface Energies (J/m2) for bare surfaces of selected spinel oxide structures. (Bottom) Calculated Wulff nanoparticle shapes of: (a) NiFe2O4, (b) CoFe2O4, (c) NiCo2O4, (d) ZnCo2O4 based on optimized bare slab surfaces.
Figure 5. (Top) Calculated DFT Surface Energies (J/m2) for bare surfaces of selected spinel oxide structures. (Bottom) Calculated Wulff nanoparticle shapes of: (a) NiFe2O4, (b) CoFe2O4, (c) NiCo2O4, (d) ZnCo2O4 based on optimized bare slab surfaces.
Preprints 92110 g005
As apparent from Figure 5, the calculated surface energies increase in the sequence γ001 < γ111 < γ110 for the three inverse spinels (NiFe2O4, CoFe2O4 and NiCo2O4). We thus expect the (001) facets to have a larger extension since they exhibit the lowest surface energy in all cases. For the normal spinel ZnCo2O4, the sequence changes to: γ100 < γ110 < γ111. However, the (001) facet is still expected to be dominant, actually up to the point of being unique (see later), whence a predicted cubic equilibrium shape for ZnCo2O4.
By using surface energies as calculated above, the predicted equilibrium Wulff configurations of nanoparticle structures were modeled, and schematically depicted in Figure 5 (bottom): Fe-based spinels, NiFe2O4 and CoFe2O4, are shown in Figure 5(a) and (b), respectively, while Co-based spinels, NiCo2O4 and ZnCo2O4, are shown in Figure 5(c) and (d), respectively. For NiFe2O4, the predicted Wulff shape consist of (001) facets with a fraction of 81.7% and of (111) facets with a fraction of 18.3%, while for CoFe2O4 we find a little fraction of (110) (1.1%) as well, together with 19.1% fraction of (111) and a bigger fraction of (001) (79.8%). For Co-based spinels, the Wulff shape of NiCo2O4 exhibits all three facets with fraction of 71.9%, 22.7% and 5.4% for (001), (111) and (110) facets, respectively, whereas in contrast, the Wulff shape of the normal spinel ZnCo2O4 has a pure cube shape without any inclusion of (111) or (110) facets.
The above preliminary modelling of spinels above refers to vacuum/low-coverage/high-temperature conditions. In the study of Zasada et al. [8], a similar approach employed periodic DFT+U calculations for a different set of spinel oxide materials and the predictions were compared with TEM/STEM experiments. As in the present study, the three most stable, (001), (110), and (111), planes exposed by mixed cobalt spinel nanocrystals were reported [8]. In their finding, the abundance of the (110) faces is always low (below 9%) regardless of the nature of the secondary metal in the mixed cobalt spinels. These predictions match very well our findings predicting a very low abundance of (110) facets in the Wulff nanoparticle shapes, and the fact that the (001) facet dominates all investigated spinels with a high abundance (>70%). Our predictions should set the ground for a detailed study of the activity of these different materials and their surfaces in heterogeneous catalysis [9-12, 20].

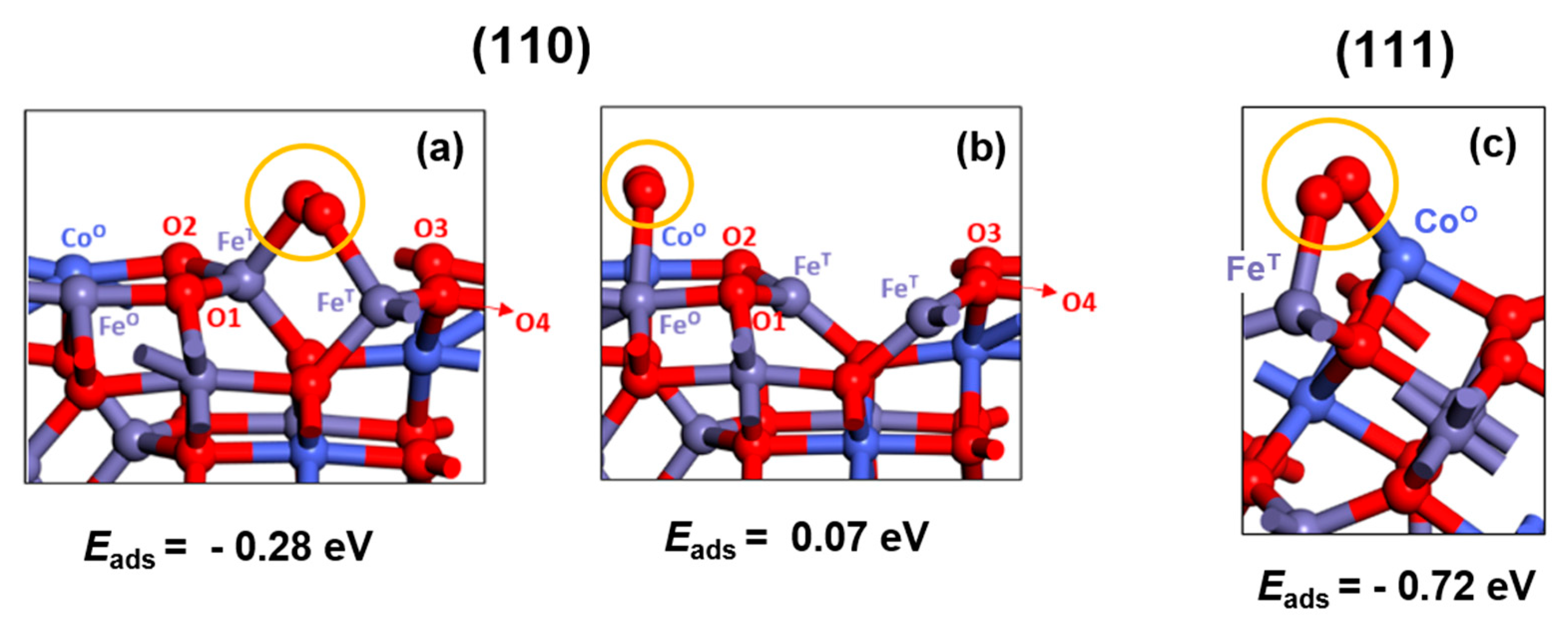
3.2. Wulff Shapes of Spinel Surfaces under Electrochemical Conditions

In Section 3.1 we have not included the effects of reaction conditions and of chemical environment on spinal oxide nanoparticle shapes. Rescaling of surface energies must be considered to get Wulff nanoparticle shapes under operative electrochemical conditions, on which we focus in this subsection. Therefore, we investigate OH, H2O, and O2 adsorption on (001), (110) and (111) facets of CoFe2O4, we predict Wulff reshaping of CoFe2O4 nanoparticles under OER electrochemical conditions, and we compare with experimental microscopy observations.
CoFe2O4 is selected to investigate the change of nanoparticle shape under OER conditions because of its higher OER performance [23]. For example, Li et al. prepared various inverse spinel MFe2O4 (M = Co, Ni, Cu, and Mn) nanofibers by the electrospinning technique [42], and found that the OER performance increases in the order: MnFe2O4 < NiFe2O4 < CuFe2O4 < CoFe2O4, with CoFe2O4 exhibiting the highest catalytic activity (overpotential, η = 408 mV at 5 mA cm−2). Moreover, CoFe2O4 is the system on which there are more experimental characterization results to compare with, as we will discuss in section 3.2.1.
According to the Wulff-Kaishev theorem [43], for particles deposited on a substrate the surface energy in the Wulff construction has to be rescaled by the adhesion energy. As adhesion stabilizes the system, the rescaled surface energy will be lower and the corresponding facet will increase in size. Analogously, in the case of particles immersed in a chemical environment the adsorption energies of ligand species the must be included in the rescaling of surface energies [36]. Clearly, it is necessary to explore a thorough set of adsorbate configurations to determine the lowest-energy state of the system (corresponding to the resting state under reaction conditions). A variety of adsorption coverages and modes of OH, H2O, O2 on CoFe2O4 slab models was therefore investigated to predict Wulff reshaping. Non-stoichiometric but symmetric slabs were built for the three planes [(001), (110), (111)] of CoFe2O4 inverse spinel, as shown in Figure 4.
One important initial observation is that for (110) and (111) the bare-surface termination ended up with a significant distortion of the tetrahedral (under-coordinated) surface Fe atoms upon DFT relaxation. O2 adsorption was found to be effective in solving this issue. An O2 molecule can indeed be put on (110) as a chelate ligand in bridge adsorption mode in two different positions: (a) on tetrahedral Fe-Fe atoms and (b) on octahedral Co-Fe atoms (see Figure 6a, b). Note that for clarity the 4 surface lattice oxygens are labeled as O1, O2, O3, O4 along with octahedrally coordinated Co (CoO) and Fe (FeO) atoms and tetrahedrally coordinated Fe (FeT) atoms as shown in Figure 6. The addition of O2 in a bridge absorption mode brought about a surface stabilization of -0.28 eV when O2 was put on (a) Fe-Fe tetrahedral atoms, whereas in the (b) case a destabilization of +0.07 eV was observed. O2 was thus kept on tetrahedral Fe sites for (110) surface adsorption calculations. On (111), O2 can be put in bridge between one tetrahedral Fe and one octahedral Co site (see Figure 6.c). Because of the surface cut, one Fe valence coordination and three Co valence coordination are missing. The addition of O2 in a bridge absorption mode has the effect of partially completing the coordination of the upper layer, and indeed we found that O2 adsorption stabilizes the surface by -0.72 eV. Note however that, while tetrahedral Fe has now completed its four-fold coordination, two coordinated species are still missing for octahedral Co.
Preprints 92110 g006
Figure 6. O2 bridged (110) CoFe2O4 surfaces sited on (a) tetrahedral Fe-Fe atoms (b) octahedral Co-Fe atoms. (c) O2 bridged (111) CoFe2O4 surface sited on octahedral Co – tetrahedral Fe atoms.
Figure 6. O2 bridged (110) CoFe2O4 surfaces sited on (a) tetrahedral Fe-Fe atoms (b) octahedral Co-Fe atoms. (c) O2 bridged (111) CoFe2O4 surface sited on octahedral Co – tetrahedral Fe atoms.
Preprints 92110 g006
Then, as in our previous investigation of the (100) facet of CoFe2O4 [23], undissociated water molecules were used to fill in the missing coordination of metal sites on each surface [(001), (110), (111)]. In a further step, the transformation of waters into hydroxyls and hydrogen adatoms via dissociation (*H2O → *OH + *H) was considered, and the affinity of *H2O, *OH, and *H on the metal sites were predicted by calculating the relative energy of the configurations associated with each coverage pattern. The sampling of several coverage patterns on the catalyst surface allowed us to determine the lowest energy state (i.e., the resting state under reaction conditions) on each of the three facets of CoFe2O4. Note that, along with stoichiometric coverage (i.e., dissociated and/or un-dissociated water coverage), off stoichiometric patterns with excess hydrogens on surface oxygens, as well as deprotonated surfaces were also considered. The complete set of studied structures is shown and discussed in Figure S2-S6 of the SI. Here, we only show the configurations which we predict as resting states under selected applied potentials, i.e., U = 1.23 V, 1, 48 V and 1.63 V vs SHE.
After adsorption of reaction intermediates, the surface energies were recalculated by adding adsorption energies ( E a d s ) as formalized in Eq. 5. Note that free-energy contributions of reaction species must be added to the DFT energetics and included into adsorption energy as shown in Eq. 4. Finally, E a d s terms including free energy contributions must be divided by the area of adsorbed surfaces for normalization.
E a d s = E s y s t e m − [ E b a r e − E a d s o r b a t e s ]
E s u r f a d s = E s u r f b a r e + E a d s A r e a
The lowest energetic structures (i.e., the resting states) resulting from these calculations under different applied potential (U= 1.23 V, 1.48 V, 1.63 V vs SHE) spanning a realistic set of reaction conditions for OER are shown in Figure 7A.B.C.
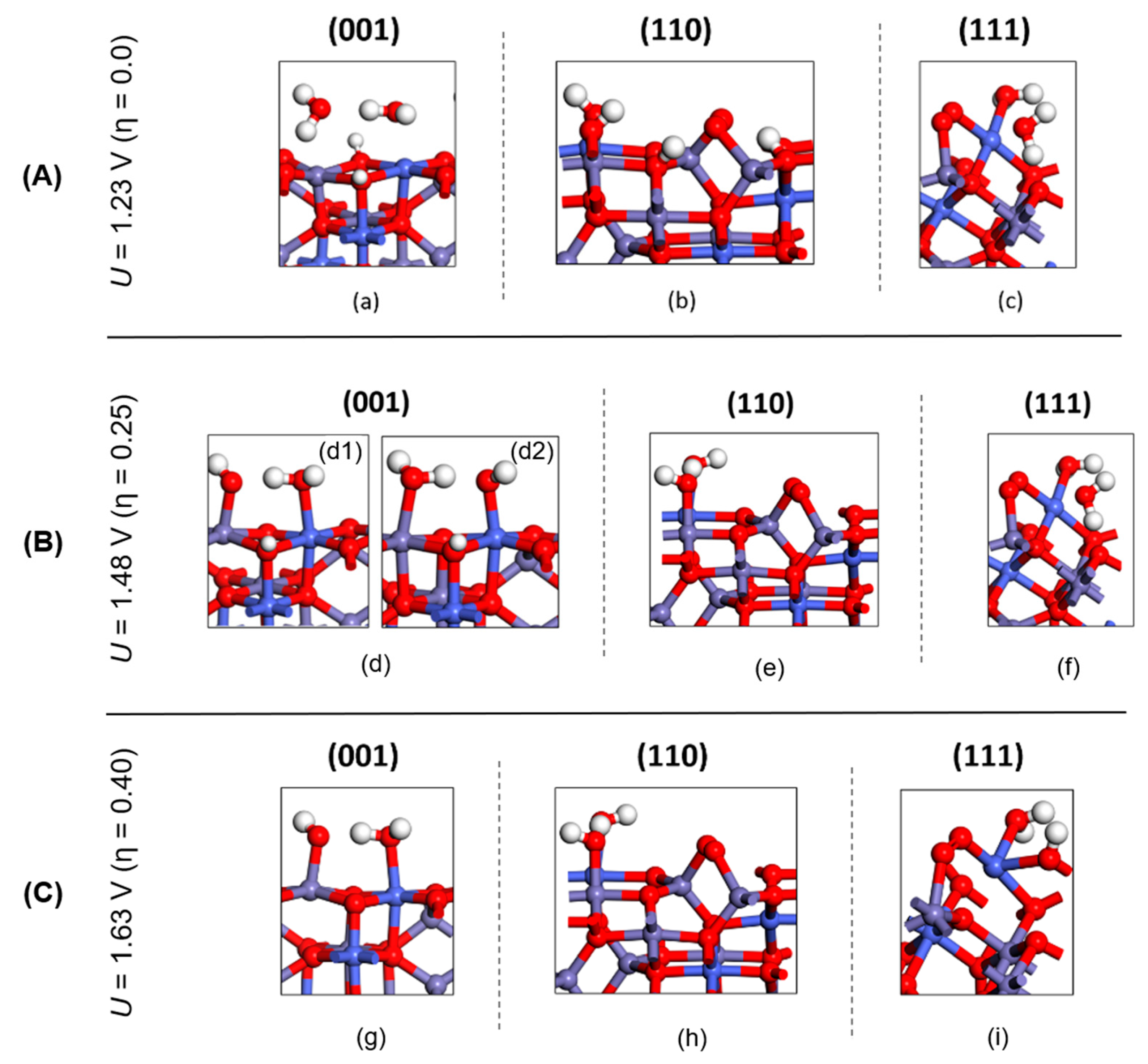
Preprints 92110 g007
Figure 7. Resting state configurations of (001), (110), (111) surfaces of CoFe2O4 at (A) U = 1.23 V, at (B) U = 1.48 V, (C) U = 1.63 V vs SHE. Oxygen, hydrogen, iron, and cobalt atoms are colored red, white, violet, and indigo-blue, respectively.
Figure 7. Resting state configurations of (001), (110), (111) surfaces of CoFe2O4 at (A) U = 1.23 V, at (B) U = 1.48 V, (C) U = 1.63 V vs SHE. Oxygen, hydrogen, iron, and cobalt atoms are colored red, white, violet, and indigo-blue, respectively.
Preprints 92110 g007
The three selected resting states for (001), (110) and (111) under bias U= 1.23 V (η = 0.0) are shown in panel Figure 7A. As for the (001) surface, water adsorption on metal sites along with excess hydrogens on lattice oxygens gave the lowest energy at U = 1.23 V. For (110), the pattern (b) which has an *OH adsorbed on a bridge region between octahedral Co and Fe atoms along with two hydrogens on lattice oxygens (O1 and O4) gave the lowest energy. For the (111) facet, the state in which two water adsorbates complete the surface Co’s missing two octahedral coordination was predicted as the resting state under U= 1.23 V, shown as (c) in Figure 7A (see also panel (a) in Figure S7 of the SI).
In Figure 7B, four selected resting states for (001), (110) and (111) under bias U= 1.48 V (η = 0.25) are shown. For the (001) surface there are two resting states corresponding to minimum energy (i.e., dissociated waters on Fe and Co site respectively as shown in Figure S2 (b),(c) of the SI), that are shown in Figure 7B (d1, d2). As for (110), the deprotonated pattern with respect to two waters gave the lowest energy at U > 1.24 V among adsorbed patterns. For (111), the same resting state as at U= 1.23 V case (two water coordinated to Co cations) was predicted.
Finally, the resting states under bias U= 1.63 V (η = 0.40) are shown in Figure 7C. For all facets [(001), (110), (111)] of CoFe2O4, fully deprotonated surfaces are preferred in this case, providing the lowest energy surfaces at U= 1.63 V.
As a next step, the energies of resting state configurations under U= 1.23 V, 1.48 V, 1.63 V vs SHE (shown in Figure 7) were used to recalculate the surface energy based on equation 5, and thus to estimate the Wulff nanoparticle shapes of CoFe2O4 under the given bias.
In the Table in Figure 8.A, a comparison of surface energies calculated from non-adsorbed (i.e., bare) surfaces with the surface energies recalculated for adsorbed surfaces under applied potentials (U= 1.23 V, 1.48 V, 1.63 V vs SHE) for CoFe2O4 inverse spinel is reported. As apparent from this Table, the adsorption process reduces the value of the surface energy for each surface, as expected. The recalculated surface energies for adsorbed facets now increase in the sequence γ111< γ001 < γ110, which is different from the sequence for bare surfaces: γ001 <γ111 < γ110, thus we predict an inversion from low-coverage to OER conditions in that we now expect to have larger extension of (111) in the Wulff nanoparticle shape under electrochemical conditions (applied potential). Note that we did not include in our estimates the reaction energy to transform the stoichiometric bare facets to non-stoichiometric covered facets: this reaction involves desorption of Fe cations from the stoichiometric facets, whose energetics is difficult to estimate as it will depend upon environmental conditions (the chemical potential of Fe cations). However, in both free and OER conditions the (110) facets have the highest surface energy (thereof the least stable plane) for spinel surfaces. This is consistent with experimental results, see the discussion below.
Using Eq. 5 and the WulffPack python package [26], the surface energy values in Figure 8A were used to obtain Wulff nanoparticle shapes of CoFe2O4 under applied potentials, and the results are shown in Figure 8B. We find that, under OER applied potentials, (111) dominates in all cases with a fraction higher than 90%, while (001) facets occupy less than 10% and (110) facets do not contribute to the Wulff shape. Note that, as the U value increases, (111) occupies a larger and larger area: at U= 1.23 V, (111) has a fraction of 90.2%, then passing to 92.8% fraction at U= 1.48 V, and ending up to 97.1% at U= 1.63 V. However, these changes as a function of the bias U are not drastic and may be difficult to be observed experimentally.
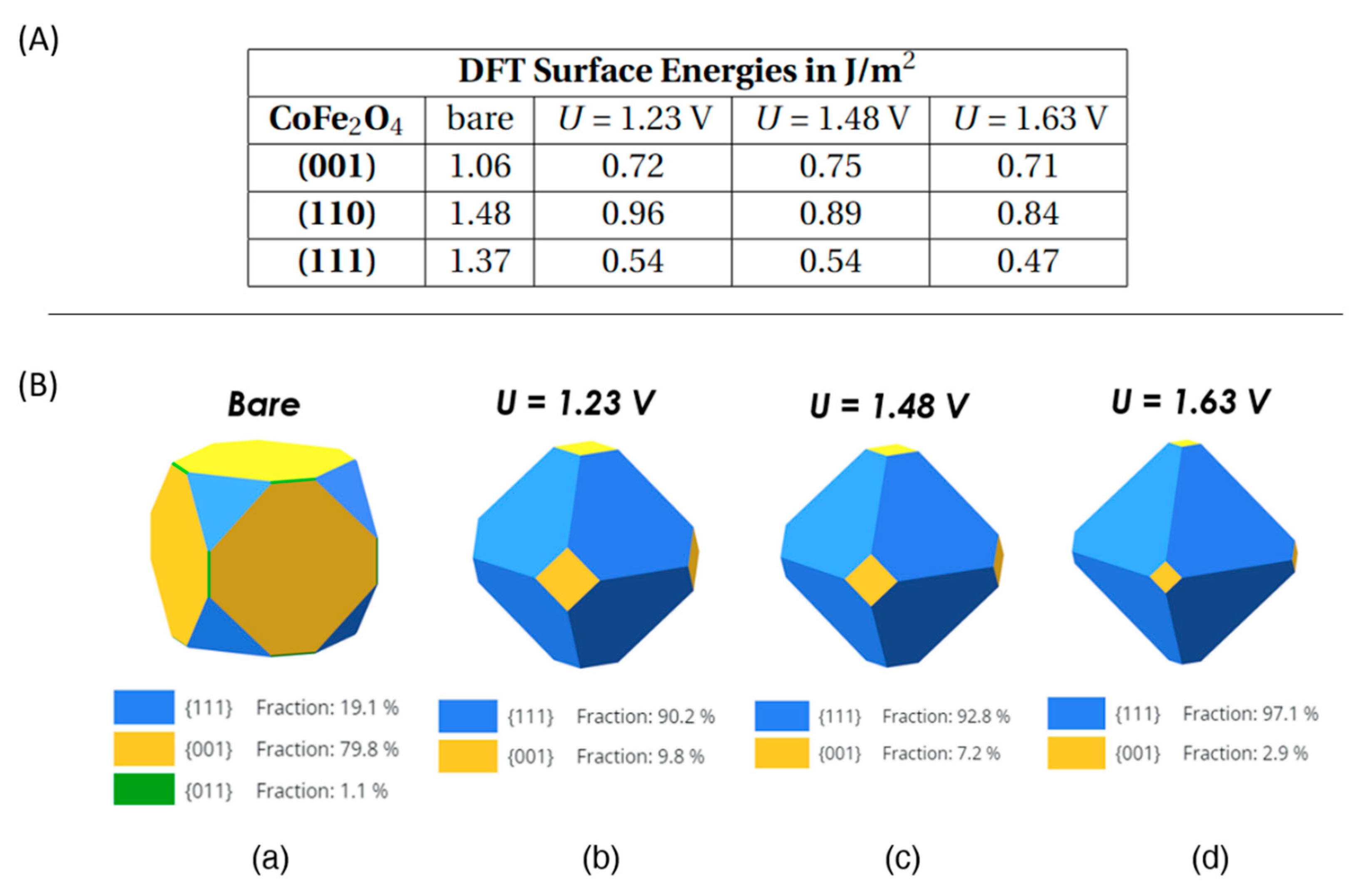
Preprints 92110 g008
Figure 8. (A) Calculated DFT Surface Energies for bare versus adsorbed surfaces of CoFe2O4 under applied potentials (U). (B) Wulff NP shapes of CoFe2O4 based on (a) bare (i.e., non-adsorbed) terminations, and (b-d) adsorbed/covered surfaces at (b) 1.23 V, (c) 1.48 V and (d) 1.63 V vs SHE, respectively.
Figure 8. (A) Calculated DFT Surface Energies for bare versus adsorbed surfaces of CoFe2O4 under applied potentials (U). (B) Wulff NP shapes of CoFe2O4 based on (a) bare (i.e., non-adsorbed) terminations, and (b-d) adsorbed/covered surfaces at (b) 1.23 V, (c) 1.48 V and (d) 1.63 V vs SHE, respectively.
Preprints 92110 g008

3.2.1. Comparison with experiment

In order to compare our predictions with experiment on CoFe2O4, it would be ideal to have microscopy measurements on CoFe2O4 nanoparticles detected under OER conditions. However, there are only few examples in the literature of such operando experiments, or even on nanoparticles after electrochemical treatment. Hence, we will also compare with TEM and HRTEM images of as-prepared CoFe2O4 nanoparticles.
Gebrelase et al. observed a transformation of the CoFe2O4 structure to CoFe alloy by controlling and optimizing the ratio of CoFe2O4 and dopamine contents in a peculiar synthesis recipe [44], reporting an over-potential of 440 mV at 10 mA/cm2 for pristine CoFe2O4. Regarding CoFe2O4 nanoparticle shape (3 to 45 nm in diameter), using HRTEM imaging Gebrelase et al. reported an octahedron-like structure for pristine CoFe2O4 before the OER. The experimental TEM and HRTEM images from their work are reported in Figure 9.a and Figure 9.b, and clearly show dominance of the (111) surface, matching the predicted Wulff shapes in Figures 8.b-d.
Xiang et al. used atom probe tomography (APT) to elucidate the 3D structure of 10nm-sized Co2FeO4 and CoFe2O4 nanoparticles during OER [45]. They observed no significant structural changes in the CoFe2O4 nanoparticle surface after 100 cycles of OER. After 1000 cycles, they discerned the formation of a (FeIII, CoIII)O3 phase, speculating that Fe2O3 forms as the potential increases according to the Fe Pourbaix diagram [46]. Also, they reported an OER activity of pristine CoFe2O4 with an over-potential of 432 mV at 10 mA/cm2 (1.66 V vs RHE), and reported TEM images of CoFe2O4 nanoparticles that are also shown for comparison in Figure 9.c. Comparing microscopy images of pristine CoFe2O4 nanoparticles in Ref. [45] with our calculated nanoparticles at U=1.63 V in Figure 8.c, one notice that the TEM images often show a more spherical shape than that predicted by the present study. However, in the experiments one can find more faceted nanoparticles as well: for example, the nanoparticle enclosed in a yellow circle in Figure 9.c seems to exhibit (111) planes due to its prismatic/sharp edges, and compares very favorably with our predictions.
Preprints 92110 g009
Figure 9. (a) TEM image of pristine CoFe2O4 nanoparticles. (b) HRTEM images with and lattice fringe analyses of pristine CoFe2O4. (a-b) Figures adapted from Ref [44]. (c) TEM image of the pristine CoFe2O4 nanoparticles in Xiang et al. work. Figure adapted from Ref [45].
Figure 9. (a) TEM image of pristine CoFe2O4 nanoparticles. (b) HRTEM images with and lattice fringe analyses of pristine CoFe2O4. (a-b) Figures adapted from Ref [44]. (c) TEM image of the pristine CoFe2O4 nanoparticles in Xiang et al. work. Figure adapted from Ref [45].
Preprints 92110 g009
Arrassi et al. analyzed 4 nm-sized CoFe2O4 spinel nanoparticles, and revealed that these particles retain their size and crystal structure after OER as observed via area electron diffraction measurements (SAED) [47]. CoFe2O4 was tested in its intrinsic catalytic response without binders or additives and OER was recorded at a potential of 1.86 V vs RHE. Arrassi et al. also detected (111) faceting in nanoparticles with SAED analysis before and after electrochemistry experiments, and observed no structural changes after OER, in agreement with theoretical calculations under a wide range of bias in the present study.
Finally, in the experimental study of Kargar et al. [48], the sample morphology and material composition of CoFe2O4 nanoparticles on carbon fiber papers (NPs-on-CFPs) were examined after long-term stability testing under OER. After more than 15 hours of long cycle testing (>1000 cycles), the sample was thoroughly examined using SEM imaging, XRD and elemental mapping analyses. Similarly to previous studies, they reported that the morphology of CoFe2O4 NPs-on-CFP did not change significantly, and the samples showed long term stability without any morphological or compositional modifications.

3.2.1. Effect of oxygen pressure on nanoparticle shape

We noted above that O2 adsorption has a role in stabilizing the (110) and (111) surfaces of CoFe2O4. The physical reason of this unusually high adsorption energy lies in the charge state of the O2 molecule. We have performed a Bader analysis of the configuration depicted in Figure 6.c, which exhibit the highest O2 desorption energy, and found that each oxygen atom bears a charge of -0.4 e, for a total of a charge of -0.8 e for the O2 molecule. For reference, the oxygen anions in the bulk, which formally correspond to doubly negatively charged species, bear a Bader charge of -1.2 e. The adsorbed O2 thus corresponds essentially to a peroxide anion, O2-. A perusal of bond distances confirms this analysis: the O-O distance in the configuration depicted in Figure 6.c is 1.36 Å, to be compared with a distance of 1.22 Å for the neutral O2 molecule, 1.35 Å in the singly negative peroxide LiO2 molecule, and 1.58 Å in the doubly negative peroxide Li2O2, respectively. In this section, we will thus explore whether it is possible to change the nanoparticle shape by controlling the O2 pressure. We use standard thermodynamics to calculate the Gibbs free energy of O2 in actual conditions (∆G), which is related to the Gibbs free energy in the standard state (∆G◦) by the relationship:
∆G = ∆G◦ + RT lnQr
Here, Qr is the reaction quotient which allows one to estimate the changes (i.e. temperature, concentration, pressure etc.) under non-standard conditions. The effect of pressure was therefore included by adding the last term in the equation 6 to the adsorption energy (Eads ) calculations (see eq.5) for (110) and (111) facets. We focused on a bias of U = 1.48 V (also considering 1.63 V in the SI) and investigated both increasing oxygen pressure up to 30 atm (1 atm, 5 atm, 15 atm and 30 atm), and also decreasing oxygen pressure down to 10-4 atm. Note that the (001) surface energy was kept as 0.75 J/m2 and 0.71 J/m2 at U = 1.48 V and 1.63 V, respectively, as this facet does not carry O2 in its resting state. Rescaled surface energies and Wulff constructions are reported in Figure 10 at U = 1.48 V, as this bias is presently the optimal target of only 0.25 V over-potential and is considered as the one realistically closest to the minimum voltage necessary for water electrolysis (1.23 V). Results at U =1.63 V are additionally shown in Figure S8 of the SI. Figure 10 clearly demonstrates that changing the oxygen pressure has a dramatic effect on the surface energies and then Wulff shape, with the (111) facet favored at high O2 pressure, and the (100) facet favored at low O2 pressure. In contrast, it can be noted that, despite these dramatic changes, the (110) surface energies are still too high to make the contribution of this facet significant compared to other surfaces of CoFe2O4. Under 15 to 30 atm of O2 pressure at U = 1.43 V - 1.63 V, the surface energies of (110) were computed lower than (001), nonetheless the (111) surface energy values get in parallel very small, so that eventually we have a full fraction 100% in a purely octahedron shape (see Figure 10.e). At the opposite, when the O2 pressure is decreased down to 0.5 atm, the surface energy of (111) approaches the value of (001), and the (001) area on the nanoparticles gradually increases. Dramatically, when the O2 pressure is reduced to very low values of 10-4 atm, the nanoparticle surfaces become a full fraction 100% of (001) with a purely cube shape, as shown in Figure 10.
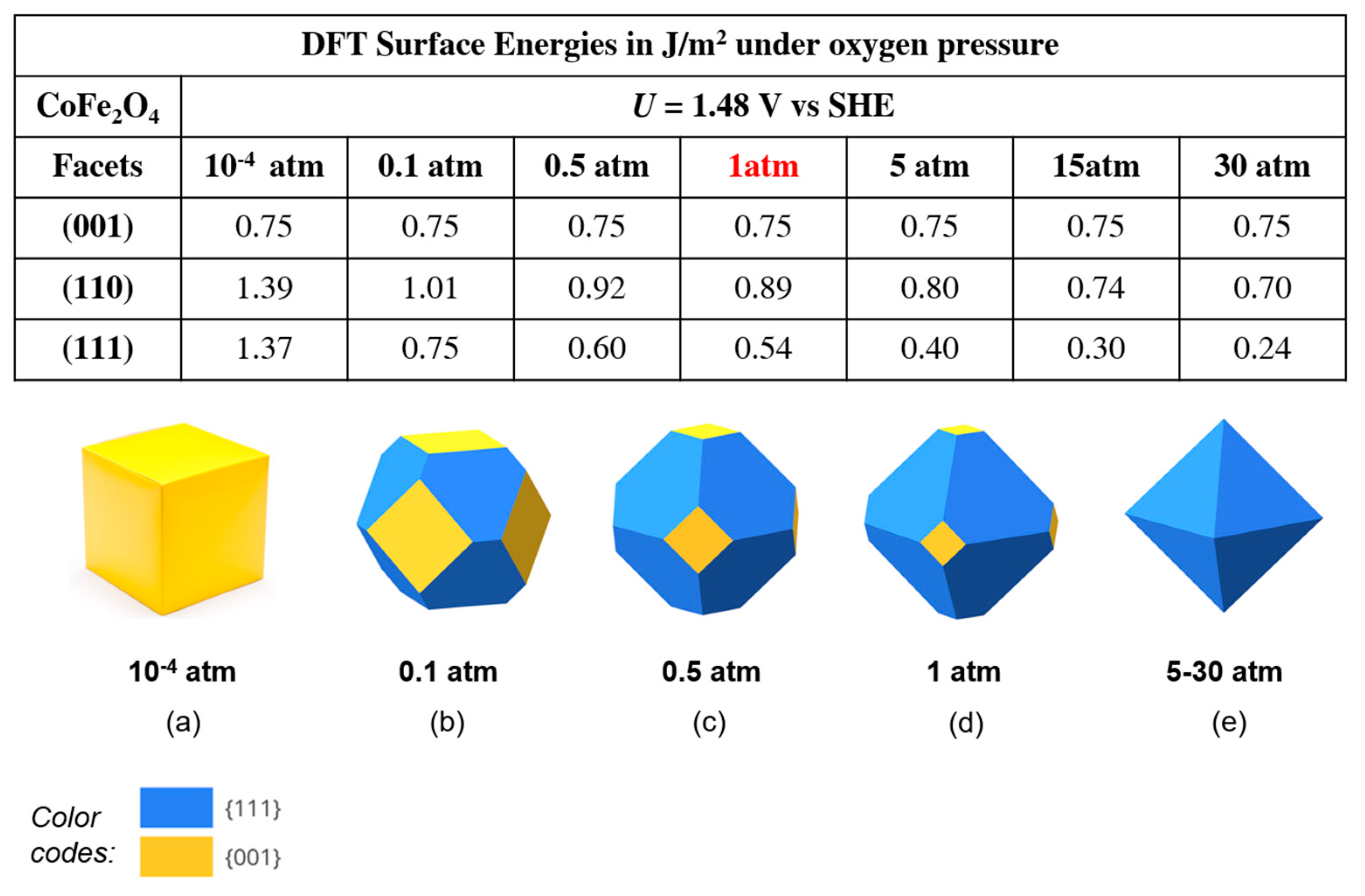
Preprints 92110 g010
Figure 10. Calculated DFT Surface Energies with oxygen pressure (10-4 to 30 atm) on (001), (110) and (111) surfaces of CoFe2O4 under applied potential U = 1.48 V vs SHE (above). Wullf NP shapes of CoFe2O4 under U= 1.48 V, ranged from 10-4 atm (a) to 30 atm (e). Color codes: blue for (111), yellow for (001) facets.
Figure 10. Calculated DFT Surface Energies with oxygen pressure (10-4 to 30 atm) on (001), (110) and (111) surfaces of CoFe2O4 under applied potential U = 1.48 V vs SHE (above). Wullf NP shapes of CoFe2O4 under U= 1.48 V, ranged from 10-4 atm (a) to 30 atm (e). Color codes: blue for (111), yellow for (001) facets.
Preprints 92110 g010
In the light of above findings, we conclude that increasing O2 pressure might poison the catalyst in the OER process, depending on the conditions. Indeed, increasing O2 pressure increases the size of the higher-index facets, i.e., (111) and (110), at the expense of the low-index (001) facet, whereas decreasing O2 pressure has the opposite effect. Now, although the (111) facets is catalytically active at low O2 pressure [49-51], its activity can be poisoned by the adsorption of the O2 adsorption reaction product, whereas the catalytic activity of the (001) facet should not be affected by O2 pressure [23]. These findings thus suggest to work experimentally at as low O2 pressure as possible in order to maximize OER catalytic activity of CoFe2O4 – in general, spinel oxide – materials. According to our DFT modeling, in fact, the (001) facet should completely dominate the nanoparticle shape at an O2 pressure of 10−4 atm.

4. Conclusions

The surface structures of the low-index facets [(001), (110) and (111)] of a set of selected spinel oxides (NiFe2O4, CoFe2O4, NiCo2O4, ZnCo2O4) were investigated using periodic DFT+U calculations under two different sets of conditions, corresponding to the two possible catalytic applications of these systems: (i) as bare surfaces under vacuum or low-coverage high-temperature conditions typical of chemical looping or oxidation reactions [9-12], and (ii) as adsorbate-covered facets under OER (limiting to the CoFe2O4 system as a paradigmatic example) [20-23]. The calculated surface energies were then used in the Wulff construction to predict the equilibrium nanoparticle shapes of spinel oxides under the different environmental conditions. Our aim is to predict and elucidate nanoparticle shape under diverse environments, for both validation and production purposes, to provide ground for operando monitoring of these promising catalysts and compare with available experimental data.
For bare surfaces under vacuum, regardless of the nature of the alien metal in the mixed iron and cobalt spinels, we found that the abundance of the (110) faces is always low (below 6%) and surface energies were calculated in the sequences: γ001 < γ111 < γ110 for inverse spinels, and γ001 < γ110 < γ111 for normal spinel ZnCo2O4. As a result, the (001) facet dominates the nanoparticles for all investigated spinels with a high abundance (higher than 70%). This is in agreement with experiment and a previous systematic study [8].
CoFe2O4 was then selected to comprehensively study the surface structures of low index surfaces [(001), (110) and (111)] under OER conditions, due to its being a promising non-critical-material candidate for OER/AEMWE catalysis and the relative abundance of experimental data on this system. From a previous extensive study [23], starting plausible adsorbate-covered surface configurations were taken as candidates for both resting and intermediate states under different conditions including those relevant to OER/AEMWE for the (100) facet, and then extended to (111) and (110) facets.
First and most importantly, we found that, after considering adsorbate-covered resting state surfaces, i.e., under OER, the ordering of surface energies changes with respect to bare systems from γ001 < γ111 < γ110 to γ111 < γ001 < γ110 under a wide range of realistic applied potentials. Indeed, building the optimal nanoparticle shape via the Wulff construction, we predict that CoFe2O4 basically retains a structure with a dominant (111) facet in simulated shapes even when increasing the bias up to 1.63 V vs SHE (η = 0.40 V). Importantly, these predictions are in fair agreement with experimental TEM and HRTEM observations.
Additionally, we investigated the effect of oxygen pressure, to the best of our knowledge here for the first time. We predict that, upon O2 adsorption, a stabilization takes place for the (110) and (111) surfaces of CoFe2O4. We rationalize this prediction in terms of the formation of a strongly adsorbed peroxide-like species on (110) and (111) facets. The (110) surface remains high-energy, and changes in O2 pressure are not sufficient to make it appear in the Wulff construction. In contrast, dramatic changes are predicted in the ratio between (100) and (111) surfaces: at high O2 pressure, the (111) facet will dominate in a purely octahedron nanoparticle shape, whereas, at low O2 pressure, the area of the (001) will increase and eventually become dominant, until the Wulff construction achieves a purely cubic nanoparticle shape. Considering that (001) is a catalytically active facet whose activity does not depend on O2 pressure [23], whereas (111) is catalytically active [49-51], but may be poisoned by the adsorption of the reaction product, this implies that O2 can poison the catalysts, and ideal OER conditions may correspond to as low O2 pressure as possible.
In conclusion, we underline the perspective importance of investigating computationally nanoparticle reshaping of spinel oxides and experimental operando characterization of these systems under operating conditions. This should open the way to a closer comparison and cross-validation between theory and experiment, that should lead to a deeper understanding and then eventually to a rational design of much-needed more efficient and sustainable optimized catalysts in both oxidation and OER catalysis.

Supplementary Materials

The following supporting information can be downloaded at: Preprints.org, Slab Models for Surface Energy Calculations, Surface Coverage for [(001), (110), (111)] planes of CoFe2O4, Wulff shapes as a function of oxygen pressure.

Author Contributions

Conceptualization, A.F.; Methodology, A.F. and L.S.; Validation, O.N.A.; Formal Analysis, X.X.; Investigation, L.S. and O.N.A.; Resources, A.F.; Data Curation, O.N.A.; Writing – Original Draft Preparation, O.N.A.; Writing – Review & Editing, A.F., L.S., and O.N.A.; Visualization, O.N.A.; Supervision, A.F. and L.S.; Funding Acquisition, A.F.

Funding

This research was funded by European Union’s Horizon 2020 Research and Innovation programme under the Marie Skłodowska-Curie Actions-Innovative Training Networks (MSCA-ITN) Grant Agreement 813748 (BIKE project).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

Financial support from the European Union’s Horizon 2020 Research and Innovation programme under the Marie Skłodowska-Curie Actions-Innovative Training Networks (MSCA-ITN) Grant Agreement 813748 (BIKE project) is gratefully acknowledged. Computational support from CINECA supercomputing centre within the ISCRA programme is also gratefully acknowledged.

Conflicts of Interest

The authors declare no competing financial interest.

References

  1. Barmparis, G.D.; Lodziana, Z.; Lopez, N.; Remediakis, I.N. Nanoparticle Shapes by Using Wulff Constructions and First-Principles Calculations. Beilstein J. Nanotech. 2015, 6, 361–368. [Google Scholar] [CrossRef] [PubMed]
  2. Sun, Y.; Xia, Y. Shape-controlled synthesis of gold and silver nanoparticles. Science. 2002, 298, 2176–2179. [Google Scholar] [CrossRef] [PubMed]
  3. Wulff, G. Zur Frage der Geschwindigkeit des Wachsthums und der Auflösung der Krystallflächen, Zeitschrift für Kristallographie. Crystalline Materials 1901, 34, 449–530. [Google Scholar]
  4. Gibbs, J.W. On the Equilibrium of Heterogeneous Substances. Am. J. Science 1878, s3-16, 441–458. [Google Scholar] [CrossRef]
  5. Honkala, K.; Hellman, A. , Remediakis, I.N., Logadottir, A., Carlsson, A.; Dahl, S.; Christensen, C.H.; Nørskov, J.K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. [Google Scholar] [CrossRef] [PubMed]
  6. Vilé, G.; Baudouin, D.; Remediakis, I.N.; Copéret, C.; López, N.; Pérez-Ramírez, J. Silver Nanoparticles for Olefin Production: New Insights into the Mechanistic Description of Propyne Hydrogenation. ChemCatChem. 2013, 5, 3750–3759. [Google Scholar] [CrossRef]
  7. Barmparis, G.D.; Remediakis, I.N. Dependence on CO Adsorption of the Shapes of Multifaceted Gold Nanoparticles: A Density Functional Theory. Phys. Rev. B. 2012, 86, 085457. [Google Scholar] [CrossRef]
  8. Zasada, F.; Gryboś, J.; Indyka, P.; Piskorz, W.; Kaczmarczyk, J.; Sojka, Z. Surface Structure and Morphology of M[CoM′]O4 (M = Mg, Zn, Fe, Co and M′ = Ni, Al, Mn, Co) Spinel Nanocrystals—DFT+U and TEM Screening Investigations. J. Phys. Chem. C 2014, 118, 19085–19097. [Google Scholar] [CrossRef]
  9. Zhu, M.; Wachs, I.E. Iron-Based Catalysts for the High-Temperature Water–Gas Shift (HT-WGS) Reaction: A Review. ACS Catalysis 2016, 6, 722–732. [Google Scholar] [CrossRef]
  10. Villa, R. Ni Based Mixed Oxide Materials for CH4 Oxidation under Redox Cycle Conditions. Journal of Molecular Catalysis A: Chemical 2003, 204-205, 637–646. [Google Scholar] [CrossRef]
  11. Anke, S.; Bendt, G.; Ilya Sinev; Hamidreza Hajiyani; Antoni, H; Ioannis Zegkinoglou; Hyo Sang Jeon; Rossitza Pentcheva; Beatriz Roldan Cuenya; Schulz, S.; Muhler, M. Selective 2-Propanol Oxidation over Unsupported Co3O4 Spinel Nanoparticles: Mechanistic Insights into Aerobic Oxidation of Alcohols. ACS Catalysis 2019, 9, 5974–5985. [CrossRef]
  12. Scheffe, J.R.; Allendorf, M.D.; Coker, E.N.; Jacobs, B.W.; McDaniel, A.H.; Weimer, A.W. Hydrogen Production via Chemical Looping Redox Cycles Using Atomic Layer Deposition-Synthesized Iron Oxide and Cobalt Ferrites. Chemistry of Materials 2011, 23, 2030–2038. [Google Scholar] [CrossRef]
  13. Chmielewski, A.; Meng, J.; Zhu, B.; Gao, Y.; Guesmi, H.; Prunier, H.; Alloyeau, D.; Wang, G.; Louis, C.; Delannoy, L.; Afanasiev, P.; Ricolleau, C.; Nelayah, J. Reshaping Dynamics of Gold Nanoparticles under H2 and O2 at Atmospheric Pressure. ACS Nano. 2019, 13, 2024–2033. [Google Scholar] [CrossRef] [PubMed]
  14. West, P.S.; Johnston, R.L.; Barcaro, G.; Fortunelli, A. The Effect of CO and H Chemisorption on the Chemical Ordering of Bimetallic Clusters. J. Phys. Chem. C 2010, 114, 19678–19686. [Google Scholar] [CrossRef]
  15. Geysermans, P.; Finocchi, F.; Goniakowski, J.; Hacquart, R.; Jupille, J. Combination of (100), (110) and (111) Facets in MgO Crystals Shapes from Dry to Wet Environment. Phys. Chem. Chem. Phys. 2009, 11, 2228–2233. [Google Scholar] [CrossRef] [PubMed]
  16. Molina, L.M.; Lee, S.; Sell, K.; Barcaro, G.; Fortunelli, A.; Lee, B.; Seifert, S.; Winans, R.E.; Elam, J.W.; Pellin, M.J. Size-Dependent Selectivity and Activity of Silver Nanoclusters in the Partial Oxidation of Propylene to Propylene Oxide and Acrolein: A Joint Experimental and Theoretical Study. Catal. Today 2011, 160, 116–130. [Google Scholar] [CrossRef]
  17. An, Q.; McDonald, M.; Fortunelli, A.; Goddard, W.A. Controlling the Shapes of Nanoparticles by Dopant-Induced Enhancement of Chemisorption and Catalytic Activity: Application to Fe-Based Ammonia Synthesis. ACS Nano 2020, 15, 1675–1684. [Google Scholar] [CrossRef] [PubMed]
  18. Akbashev, A.R. Electrocatalysis Goes Nuts. ACS Catal. 2022, 12, 4296–4301. [Google Scholar] [CrossRef]
  19. Suen, N.-T.; Hung, S.-F.; Quan, Q.; Zhang, N.; Xu, Y.-J.; Chen, H.M. Electrocatalysis for the Oxygen Evolution Reaction: Recent Development and Future Perspectives. Chem. Soc. Rev. 2017, 46, 337–365. [Google Scholar] [CrossRef] [PubMed]
  20. Zhao, Q.; Yan, Z.; Chen, C.; Chen, J. Spinels: Controlled Preparation, Oxygen Reduction/Evolution Reaction Application, and Beyond. Chemical Reviews 2017, 117, 10121–10211. [Google Scholar] [CrossRef]
  21. Pandiarajan, T.; John Berchmans, L.; Ravichandran, S. Fabrication of Spinel Ferrite Based Alkaline Anion Exchange Membrane Water Electrolysers for Hydrogen Production. RSC Adv. 2015, 5, 34100–34108. [Google Scholar] [CrossRef]
  22. Cheng, F.; Shen, J.; Peng, B.; Pan, Y.; Tao, Z.; Chen, J. Rapid Room-Temperature Synthesis of Nanocrystalline Spinels as Oxygen Reduction and Evolution Electrocatalysts. Nature Chem. 2010, 3, 79–84. [Google Scholar] [CrossRef] [PubMed]
  23. Avcı, Ö.N.; Sementa, L.; Fortunelli, A. Mechanisms of the Oxygen Evolution Reaction on NiFe2O4 and CoFe2O4 Inverse-Spinel Oxides. ACS Catal. 2022, 12, 9058–9073. [Google Scholar] [CrossRef] [PubMed]
  24. Tolba, S.A.; Gameel, K.M.; Ali, B.A.; Almossalami, H.A.; Allam, N.K. The DFT+U: Approaches, Accuracy, and Applications. Density Functional Calculations - Recent Progresses of Theory and Application, in Density Functional Calculations. Yang, G. ed. 2018, 2018. [Google Scholar] [CrossRef]
  25. Vanderbilt, D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B. 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
  26. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; Dal Corso, A.; de Gironcoli, S.; Fabris, S.; Fratesi, G.; Gebauer, R.; Gerstmann, U.; Gougoussis, C.; Kokalj, A.; Lazzeri, M.; Martin-Samos, L.; Marzari, N.; Mauri, F.; Mazzarello, R.; Paolini, S.; Pasquarello, A.; Paulatto, L.; Sbraccia, C.; Scandolo, S.; Sclauzero, G.; Seitsonen, A.P.; Smogunov, A.; Umari, P.; Wentzcovitch, R.M.J. Phys.: Condens. Matter. 2009, 21, 395502.
  27. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  28. Shi, X.; Bernasek, S.L.; Selloni, A. Formation, Electronic Structure, and Defects of Ni Substituted Spinel Cobalt Oxide: A DFT+U Study. J. Phys. Chem. C 2016, 120, 14892–14898. [Google Scholar] [CrossRef]
  29. Selcuk, S.; Selloni, A. DFT+U Study of the Surface Structure and Stability of Co3O4(110): Dependence on U. J. Phys. Chem. C 2015, 119, 9973–9979. [Google Scholar] [CrossRef]
  30. Wang, L.; Maxisch, T.; Ceder, G. Oxidation Energies of Transition Metal Oxides within TheGGA+Uframework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
  31. Rahm, J.; Erhart, P. WulffPack: A Python Package for Wulff Constructions. J. Open Source Software. 2020, 5, 1944. [Google Scholar] [CrossRef]
  32. Wen, X.L.; Chen, Z.; Liu, E.H.; Lin, X. Structural and Magnetic Characterization of ZnCo2O4 Thin Film Prepared by Pulsed Laser Deposition. Appl. Surf. Sci. 2015, 357, 1212–1216. [Google Scholar] [CrossRef]
  33. Chen, Z.; Wen, X.L.; Niu, L.W.; Duan, M.; Zhang, Y.J.; Dong, X.L.; Zhang, R.L.; Chen, C.L. Transport and Magnetic Properties of ZnCo2O4/Si Heterostructures Grown by Radio Frequency Magnetron Sputtering. Thin Solid Films. 2014, 573, 90–94. [Google Scholar] [CrossRef]
  34. Montoya, A.; Haynes, B.S. Periodic Density Functional Study of Co3O4 Surfaces. Chem. Phys. Lett. 2011, 502, 63–68. [Google Scholar] [CrossRef]
  35. Zasada, F.; Piskorz, W.; Stelmachowski, P.; Kotarba, A.; Paul, J.-F.; Płociński, T.; Kurzydłowski, K.J.; Sojka, Z. Periodic DFT and HR-STEM Studies of Surface Structure and Morphology of Cobalt Spinel Nanocrystals. Retrieving 3D Shapes from 2D Images. J. Phys. Chem. C 2011, 115, 6423–6432. [Google Scholar] [CrossRef]
  36. Chmielewski, A.; Meng, J.; Zhu, B.; Gao, Y.; Guesmi, H.; Prunier, H.; Alloyeau, D.; Wang, G.; Louis, C.; Delannoy, L.; Afanasiev, P.; Ricolleau, C.; Nelayah, J. Reshaping Dynamics of Gold Nanoparticles under H2 and O2 at Atmospheric Pressure. ACS Nano. 2019, 13, 2024–2033. [Google Scholar] [CrossRef] [PubMed]
  37. Li, Y.-F.; Selloni, A. Mechanism and Activity of Water Oxidation on Selected Surfaces of Pure and Fe-Doped NiOx. ACS Catal. 2014, 4, 1148–1153. [Google Scholar] [CrossRef]
  38. Li, Y.-F.; Liu, Z.-P.; Liu, L.; Gao, W. Mechanism and Activity of Photocatalytic Oxygen Evolution on Titania Anatase in Aqueous Surroundings. J. Am. Chem. Soc. 2010, 132, 13008–13015, (b) Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; Ed.; CRC Press: Boca Raton, FL, 2003. [Google Scholar] [CrossRef]
  39. Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
  40. Gong, M.; Dai, H. A Mini Review of NiFe-Based Materials as Highly Active Oxygen Evolution Reaction Electrocatalysts. Nano Res. 2014, 8, 23–39. [Google Scholar] [CrossRef]
  41. Xiao, H.; Shin, H.; Goddard, W.A. Synergy between Fe and Ni in the Optimal Performance of (Ni,Fe)OOH Catalysts for the Oxygen Evolution Reaction. Proc. Nat. Ac. Sci. 2018, 115, 5872–5877. [Google Scholar] [CrossRef] [PubMed]
  42. Li, M.; Xiong, Y.; Liu, X.; Bo, X.; Zhang, Y.; Han, C.; Guo, L. Facile Synthesis of Electrospun MFe2O4(M = Co, Ni, Cu, Mn) Spinel Nanofibers with Excellent Electrocatalytic Properties for Oxygen Evolution and Hydrogen Peroxide Reduction. Nanoscale. 2015, 7, 8920–8930. [Google Scholar] [CrossRef] [PubMed]
  43. Müller, P.; Kern, R. Equilibrium Nano-Shape Changes Induced by Epitaxial Stress (Generalised Wulf–Kaishew Theorem). Surf. Sci. 2000, 457, 229–253. [Google Scholar] [CrossRef]
  44. Gebreslase, G.A.; Martínez-Huerta, M.V.; Sebastián, D.; Lázaro, M.J. Transformation of CoFe2O4 Spinel Structure into Active and Robust CoFe Alloy/N-Doped Carbon Electrocatalyst for Oxygen Evolution Reaction. J. Colloid Interface Sci. 2022, 625, 70–82. [Google Scholar] [CrossRef]
  45. Xiang, W.; Yang, N.; Li, X.; Linnemann, J.; Hagemann, U.; Ruediger, O.; Heidelmann, M.; Falk, T.; Aramini, M.; DeBeer, S.; Muhler, M.; Tschulik, K.; Li, T. 3D Atomic-Scale Imaging of Mixed Co-Fe Spinel Oxide Nanoparticles during Oxygen Evolution Reaction. Nature Commun. 2022, 13, 179. [Google Scholar] [CrossRef] [PubMed]
  46. Beverskog, B.; Puigdomenech, I. Revised Pourbaix Diagrams for Iron at 25–300 °C. Corrosion Sci. 1996, 38, 2121–2135. [Google Scholar] [CrossRef]
  47. El Arrassi, A.; Liu, Z.; Evers, M.V.; Blanc, N.; Bendt, G.; Saddeler, S.; Tetzlaff, D.; Pohl, D.; Damm, C.; Schulz, S.; Tschulik, K. Correction to “Intrinsic Activity of Oxygen Evolution Catalysts Probed at Single CoFe2O4 Nanoparticles. ” J. Am. Chem. Soc.. 2019, 141, 10565–10565. [Google Scholar] [CrossRef] [PubMed]
  48. Kargar, A.; Yavuz, S.; Kim, T.K.; Liu, C.-H.; Kuru, C.; Rustomji, C.S.; Jin, S.; Bandaru, P.R. Solution-Processed CoFe2O4 Nanoparticles on 3D Carbon Fiber Papers for Durable Oxygen Evolution Reaction. ACS Appl. Mater. Interfaces 2015, 7, 17851–17856. [Google Scholar] [CrossRef] [PubMed]
  49. Zhang, Y.; Zhang, G.; Li, W.; Li, X.; Uchiyama, K.; Chen, C. Enhancing Oxygen Reduction Activity by Exposing (111) Facets of CoFe2O4 Octahedron on Graphene. Chemistry Select 2017, 2, 9878–9881. [Google Scholar] [CrossRef]
  50. Chen, Z.; Cronawitter, C.X.; Koel, B. Facet-dependent activity and stability of Co3O4 nanocrystals towards the oxygen evolution reaction. Phys. Chem. Chem. Phys. 2015, 17, 29387–29393. [Google Scholar] [CrossRef] [PubMed]
  51. Li, A.; Kong, S.; Guo, C.; Ooka, H.; Adachi, K.; Hashizume, D.; Jiang, Q.; Han, H.; Xiao, J.; Nakamura, R. Enhancing the stability of cobalt spinel oxide towards sustainable oxygen evolution in acid. Nature Catal. 2022, 5, 109–118. [Google Scholar] [CrossRef]
Preprints 92110 g001
Figure 1. Examples of Wulff constructions for shapes of high cubic symmetry.
Figure 1. Examples of Wulff constructions for shapes of high cubic symmetry.
Preprints 92110 g001
Preprints 92110 g002
Figure 2. Stoichiometric surface slab models for all considered surface terminations of inverse spinel (AB2O4) systems in the ball and stick representation: (100) (a), (110) (b), (111) (c). O and T denote octahedral and tetrahedral coordination of A and B metals, respectively.
Figure 2. Stoichiometric surface slab models for all considered surface terminations of inverse spinel (AB2O4) systems in the ball and stick representation: (100) (a), (110) (b), (111) (c). O and T denote octahedral and tetrahedral coordination of A and B metals, respectively.
Preprints 92110 g002
Preprints 92110 g003
Figure 3. Stoichiometric surface slab models for all considered surface terminations of normal spinel (AB2O4) systems in the ball and stick representation: (100) (a), (110) (b), (111) (c). T and O denote tetrahedral and octahedral coordination of A and B metals, respectively.
Figure 3. Stoichiometric surface slab models for all considered surface terminations of normal spinel (AB2O4) systems in the ball and stick representation: (100) (a), (110) (b), (111) (c). T and O denote tetrahedral and octahedral coordination of A and B metals, respectively.
Preprints 92110 g003
Preprints 92110 g004
Figure 4. Non-stoichiometric/symmetric slab models for all considered surface terminations of inverse spinel systems in the ball and stick representation: (a) (001), (b) (110), (c) (111). O and T denote octahedral and tetrahedral coordination of A(Co) and B(Fe) metals, respectively.
Figure 4. Non-stoichiometric/symmetric slab models for all considered surface terminations of inverse spinel systems in the ball and stick representation: (a) (001), (b) (110), (c) (111). O and T denote octahedral and tetrahedral coordination of A(Co) and B(Fe) metals, respectively.
Preprints 92110 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated