1. Introduction
The broad utilization of gas turbine engines is highly advantageous, and their thrust-weight ratio and thermal efficiency are significantly affected by the turbine inlet temperature, which has exceeded 2000K. For the purposes of reducing thermal loading of the gas turbine blades and extending their life time, protection of the turbine blades against extremely hot gases is typically carried out via film cooling. The extraction of coolant from compressor is undertaken in the film cooling, followed by injection of coolant into the hot gas in the blade surface, and the interaction of coolant with the hot gas is made, which may lead to formation of complicated vortex structures. Hence, the film cooling is a convective heat transfer problem dominated by the vortex structures, especially the major counter rotating vortex pair (CRVP) lifts the coolant off the wall surface and entrains the hot gas beneath the coolant, resulting in a greatly reduction of the film cooling efficiency (FCE). Therefore, improving the FCE through controlling the vortex structures of the film cooling is crucial for gas turbine engines.
Scholars have presented diverse strategies to enhance FCE, and among these, the employment of shaped cooling holes emerges as a particularly efficacious. Goldstein et al. [
1] originally found that the film cooling efficiency could be noticeably improved using fan-shaped holes, which could enhance the adherence and the lateral coverage of the coolant. Thereafter, numerous scholars have concentrated on the shaped holes and proposed various shaped holes. Later, Bunker et al. [
2] reviewed the origins of the classical shaped film cooling holes and summarized the concerning knowledge of the shaped film cooling holes, and demonstrated that the shaped film cooling hole also had some drawbacks (e.g., high aerodynamic mixing losses). Recently, it was attempted [
3] to further figure out the effects of inclination angle, expansion angle, and length of inlet cylindrical section on the FCE of the fan-shaped holes, and reported that the changes of geometrical parameters could significantly affect the FCE. Other than the shaped holes, auxiliary mechanisms devices were suggested in order weaken the destructive features of the vortex structures for enhancing the FCE. The double-jet holes were invented with compound angles to improve the FCE, and it was revealed that the CRVPs of the double-jet hole were mutually interfered and counteracted with each other, thereby enhancing the FCE, while the double-jet holes required a reasonable arrangement [
4]. In order to stop the CRVP development by forming another vortex group, a ramping vortex generator was positioned downstream from the cooling hole. As a result, the cooling fluid was positioned near the wall surface and extended downstream [
5]. Recently, the film cooling performance (FCP) of a novel furcate hole was examined, and it was found that the lateral coverage of the coolant was more comprehensive than that of the traditional cylindrical holes [
6].Generally, the previously mentioned approaches constitute passive flow control techniques, yet their effectiveness is inherently restricted. The dynamic nature of film cooling flow highlights the need for an active film cooling control methodology, which is a flow control method that can make modifications in real-time during different flow phases.
Scholars attempted to propose pulsed film cooling to optimize the film cooling efficiency. Ekkad et al. [
8] firstly used solenoid valves to directly control the cooling jet for improving the FCE, and found that the effects of pulsed jets on film cooling showed promising outcomes. Thereafter, the FCE and flow field temperature were examined at different BRs for a variety of pulsing frequencies and duty cycles, and it was revealed that pulsing at high frequencies was beneficial to reduce overall jet lift-off in some cases, thereby improving the FCE, whereas pulsing at low frequencies tended to produce the adverse effect [
9]. The influences of duty cycle and Strouhal number on the pulsed FCE, particularly at high BRs were numerically figured out [
10], and it was observed which pulsing significantly decreased the recirculation region, leading to the increment of the FCE. Multiple scholars [
11] examined how pulsed film cooling affected the heat flux in the turbine blades, and superiority of the steady film cooling was to the pulsed film cooling at low BRs was confirmed, while pulsed film cooling could be beneficial at high BRs, confirming the flat plate film cooling. The LES was employed to indicate how the square-wave pulsating film cooling jet could be interacted with recirculation vortexes, and the noticeable role of entraining recirculation vortexes in the near-wall region (NWR) was figured out [
12]. In recent years, the coolant pulsation, as one of the active control techniques, has exhibited a great efficiency that could improve the FCE, while further clear conclusive outcomes are essential [
13], and evidence is required to prove the role of coolant pulsation in enhancing the FCE. It is noteworthy that the hot gas unsteadiness would inevitably cause coolant pulsation in the real engines, as well as the large-scale pulsed film cooling vortex structures were more complicated than those of the steady film cooling. Therefore, exploring active flow control techniques to effectively improve the pulsed FCE may be advantageous for the gas turbine engines.
There are many fields where the dielectric barrier discharge (DBD) plasma actuator (DBDPA) is being effectively used [
14,
15]. Yang et al. [
16] assessed the influence of the DBDPA on the whole spatial-temporal development (STD) of flow field in quiescent air. For the purpose assessment of integrating the plasma and fluid dynamics, the phenomenological model and First-principles-based model of the DBD were proposed, facilitating the integration of multi-dimensional plasma dynamics with the fluid dynamics [
17]. Thus, the phenomenological model appeared highly advantageous. Hence, Roy and Wang [
17,
18] firstly utilized the DBD PAA to improve the film cooling efficiency, and numerical findings revealed the actively alteration of flow structures by the plasma aerodynamics near the DBDPA, thereby inducing attachment of the coolant to the wall surface. Later, He et al. [
19,
20,
21] greater understanding of the PAA mechanism for increasing the FCE by examining the impacts of the location, energy information, quantity, and shape of the DBDPA on the FCP. Lately, Dolati et al. [
23] employed neural networks to generalize the complicated communication that involved variables (e.g., flow, geometric and electrical variables), thus gaining a useful correlation with different input-output parameters. Accordingly, Audier et al. [
24] explored the ability of the PAA for the film cooling efficiency enhancement through an experimental set-up, and the experimental results confirmed the advantages of the PAA for improving the film cooling efficiency, as predicted by the abovementioned numerical findings. More recently, it was demonstrated that the PAA could actively control the large-scale coherent structures (LSCSs), as well as the coherent structure reduced in size and number, making them beneficial for the film cooling [
25,
26]. In general, the promising potentials of the PAA for the film cooling efficiency enhancement has been well demonstrated in the film cooling numerically and experimentally. However, it is essential to indicate how the PAA can control a pulsed film cooling.
In the current research, the pulsed film cooling flow coupled with the PAA was simulated via LES, and then, comparative evaluation of the time-averaged flows was made in an effort to identify the full impact of both the PAA and coolant pulsation on the efficiency from film cooling. In order to provide more insight into how coolant pulsation and PAA may affect the coolant-gas interaction, the STD of these LSCSs was then measured.
2. Domain of computation and boundary conditions (BCs)
The research of Kohli and Sinha et al. [
27,
28] served as the basis for defining the computational domain for the current investigation.
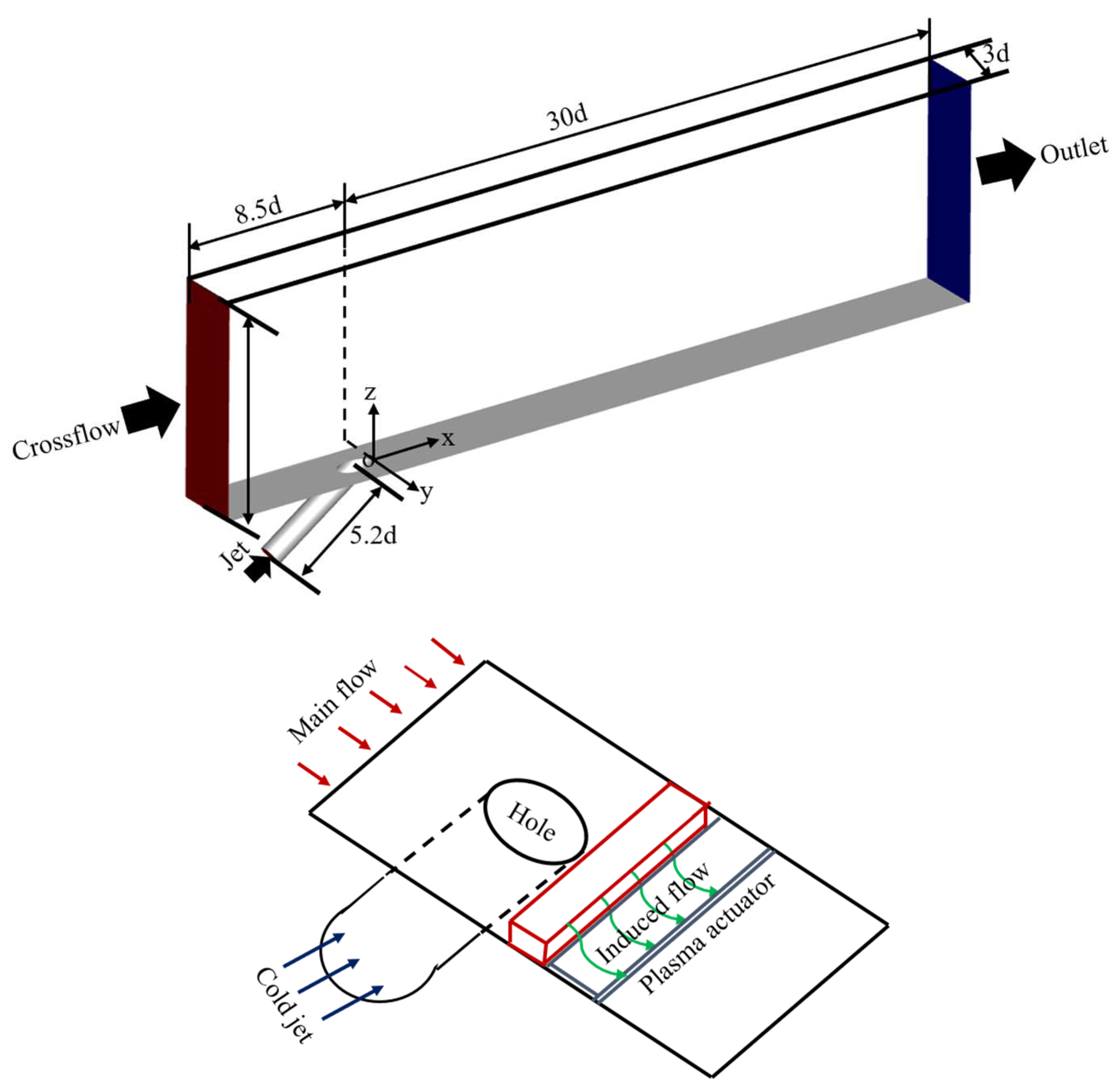
Figure 1 shows the computational domain of the film cooling and the arrangement of the DBDPA, and the computational domain consisted of a cooling hole (diameter of the cooling hole (
d = 12.5 mm), its length (5.2
d), and the streamwise angle of the cooling hole (35°)) and a crossflow channel. The height, width, and length of the crossflow channel were 10
d, 3
d, and 38.5
d, respectively. The cooling hole exit’s trailing edge was considered to place the Cartesian coordinate system’s origin, and the computational domain's streamwise, lateral, and normal directions were denoted by
x-,
y-, and
z-axis, respectively. At the end of the cooling hole is where the DBDPA is placed.
The ANSYS CFD software was utilized for generating hexahedral meshes of the computational domain (
Figure 2). Near the flat plate's walls and the cooling hole, the grid points are incredibly finely tuned, and
y+ of the first layer mesh near the walls was less than 1.0. To avoid generation of excessive meshes, the stretching factor was about 1.05 in the wall-normal direction, and about 7 million meshes could be generated.
The BCs utilized in the current research were consistent with those presented in Kohli and Sinha et al.’s research [
27,
28], in which the crossflow atmosphere was ambient and the cooling jet was the mixture of CO
2 and N
2 at the temperature of 188 K. At the crossflow channel inlet, the boundary conditions were set, taking into account variables such as the velocity of the crossflow (
u∞=20 m/s), temp 298 K, as well as border layer thicknesses 1.0
d. At the crossflow channel outlet, an effort was made to provide pressure-outlet boundary conditions that included static pressure 101325 Pa, Reynolds number 15625, and kinematic viscosity 1.6×10
-5m
2/s. Periodic conditions were imposed along the lateral direction of the crossflow channel to take into consideration how it affects from adjacent cooling jets. For every wall, adiabatic and non-slip conditions were assigned.
The density ratio (DR) was equal to 1.6 (
ρc/
ρ∞), application of the velocity-inlet boundary occurred at the cooling hole's inlet, and the adjustment od coolant inlet velocity was on the basis of BR (
M =
ρcuc/
ρ∞u∞). For the un-pulsed film cooling, the BR was 1.0, thus, 12.5 m/s was allocated to the cooling jet velocity (
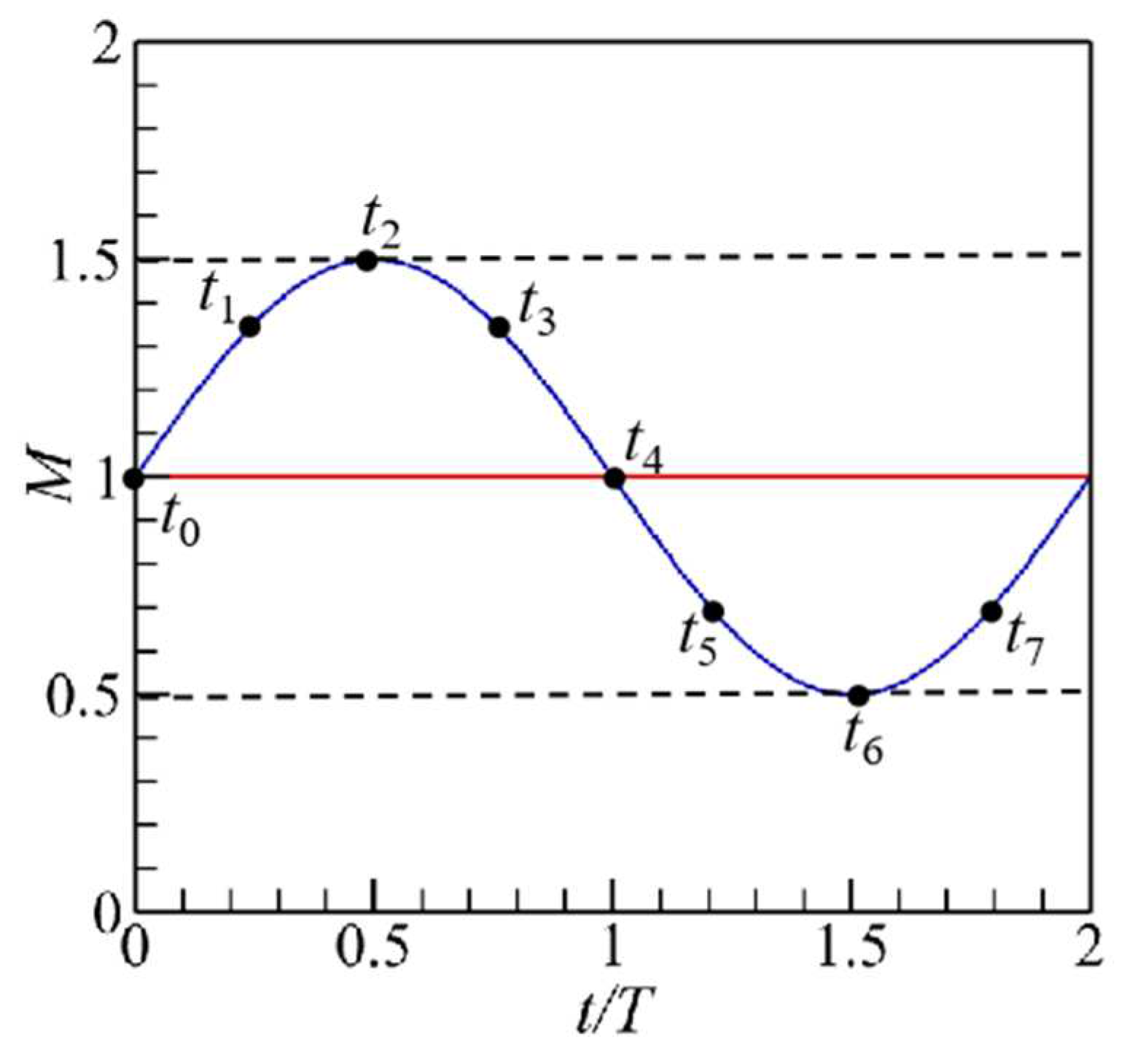
uc). For the pulsed film cooling, the total amount of the coolant was the same as the un-pulsed film cooling in an operating cycle, thus, the time-averaged BR of the pulsed film cooling was 1.0, and the BR was in the range of 0.5-1.5 in a cycle (
Figure 3). Therefore, the cooling jet velocity was specified as
uc(1.0+0.5sin(2π
ft)), where
f is the pulsation frequency of the cooling jet. The Strouhal number (
St) of the coolant pulsation was defined as
St=
df/
u∞, and
St was set to 0.25.
The asymmetric installation of the DBDPA was carried out at cooling hole exit’s downstream (
x/d=0.0). The widths of the exposed electrode and covered electrode were 5 and 10 mm, respectively,
l=0.25 mm was indicative of the gap between the two electrodes, and a noticeable number of polyimide films were involved in dielectric barrier. The length of the two electrodes was 3
d to avoid the restriction on the plasma generation along the lateral direction. The power supply of the DBDPA had a high frequency (6.0 kHz) and a high voltage (8.0 kVpp), so an estimate of the electrohydrodynamic (EHD) force of roughly 2 kN/m3 was made, that is consistent with an amount that had been previously obtained. [
27,
28] and no power consumption was taken into account. Notably, two thin copper electrodes were involved in the DBDPA (thickness, 440
μm), therefore, the geometric effects of the DBDPA were herein regarded.
3. phenomenological plasma model
The LES can directly solve the LSCSs and simulate the sub-grid scale vortex structures via sub-grid model approximately, thus, the influences of the pulsation and the PAA on the LSCSs can be perfectly figured out, dominating the coolant-hot gas interaction. The Algebraic Wall-Modeled LES (WMLES) model [
29] was herein employed to assess the subgrid scale dynamic effects, where the equation can be expressed as
In the equation (2), the subgrid-scale and viscous stress terms are defined as
and
respectively. In the equation (3), the eddy viscosity is defined as
, and more detailed parameters can be found in Ref. [
29].
Fi is the EHforce vector generated by the DBDPA.In the following sections, an attempt will be made to describe the phenomenological plasma model.
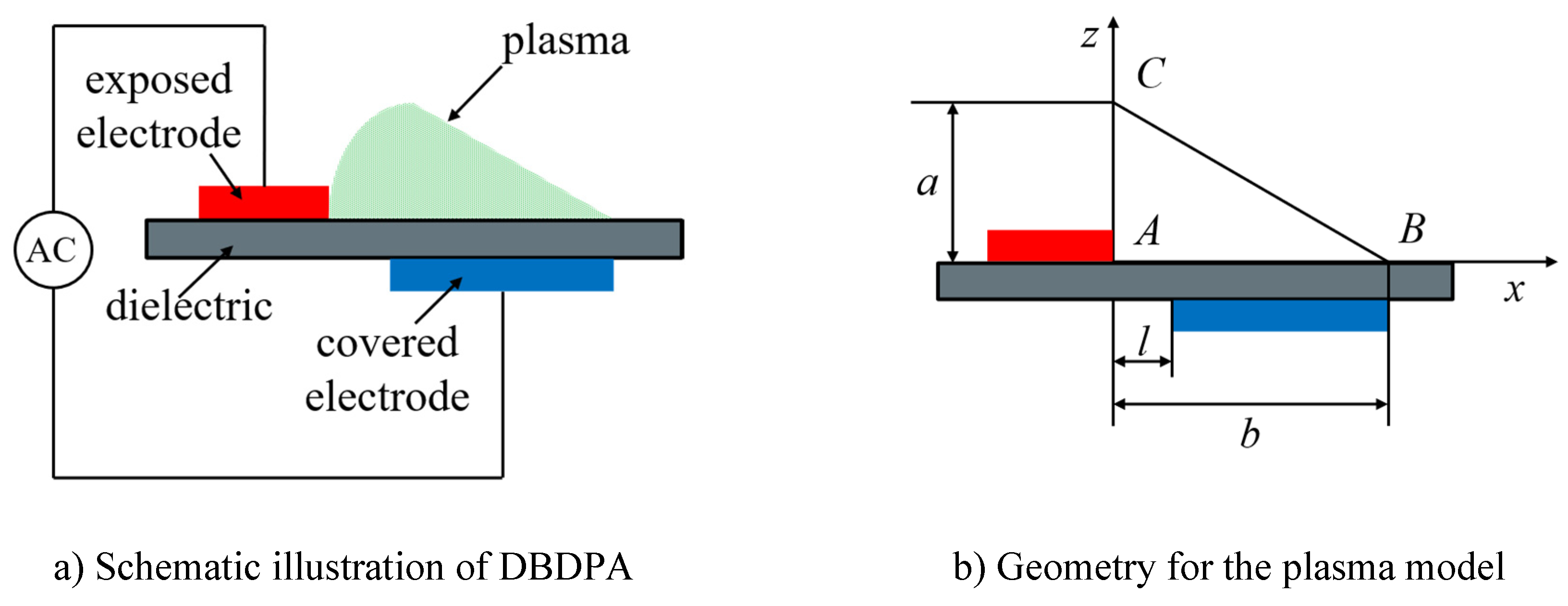
A typical DBDPA is schematically illustrated in
Figure 4, which comprises a pair of electrodes positioned on the wall surface and separated by a dielectric barrier. Following the application of a strong voltage alternation to the exposed electrode, a non-thermal plasma barrier forms upon the covered electrode and the surrounding air is weakly ionized as a result of the barrier discharge [
30]. It was previously revealed that EHD forcegenerated by the DBDPA is the main mechanism of active flow control [
31]. The Shyy et al.’s phenomenological plasma model [
32] was herein utilized to account for the EHD force, neglecting the momentum collision between the charged particles and the airflow. Hence, less computational resources are essential for this model and it was successfully exerted to diverse plasma-based flow control applications [
33]. Film cooling flows were herein simulated via LES requiring numerous demands upon computational resources, confirming the appropriateness of the phenomenological plasma model for solving the EHD force [
34]. The plasma occurs mainly in a tiny region just downstream the exposed electrode and over the covered electrode (
Figure 4a). Therefore, it was assumed that the DBDPA-generated EHD force acts on the airflow only in the triangular region ABC, whose height and length were denoted by
a and
b, respectively (
Figure 4b). The point A was the location of maximum electric field intensity (
E0 =
Vpp/
l), where
l is the space between the two electrodes in the
x-axis. The linear decrease of electric field intensity is achievable with its movement from the source A, and the electric field intensity fluctuates that can be formulated as
In equation (4), the field strength of
Eb=30 kV/cm is employed to assess
k1=(
E0-
Eb)/
b and
k2=(
E0-
Eb)/
a at the plasma boundary. Hence, the electric field intensity components in diverse directions are formulated as
The plasma discharge occurs at only one-half cycle, and the time
tp is about 67 μs during which the plasma formation, thus, the EHD force components in the
x and
z directions can be formulated as
where
ρe=10
17/m
3 is the electron number density,
ϑ=6.0kHz is the applied voltage frequency, and
ζ is the collision efficiency explanatory factor. High frequency of the plasma discharge (6.0 kHz) is correlative with the EHD force acting on the airflow as a constant, and therefore, the DBDPA-generated EHD force is assumed as a steady-state body force acting on the film cooling flow.
User-defined function (UDF) was employed to add EHD force components (i.e., body force terms) into the momentum equations, carrying the effects of the plasma discharge on the film cooling. The pressure interpolation was undertaken via the body force weighted scheme. The momentum and energy equations were solved discretely using bounded central scheme and second-order upwind scheme, respectively. The solvation of transient equations was carried out by the bounded second-order implicit scheme (time step, 1.0×10-5 s; maximum number of iterations, 40/time step). When a quasi-steady state could be reached by the film cooling flow, six cycles were allocated to the flow field to obtain time-averaged statistical information, where one cycle was shown by the time that it took the crossflow across the flow path.
The adiabatic film cooling efficiency was herein formulated as
The adiabatic FCE was tried to be averaged along the whole lateral length for a lateral-averaged FCE, which could be written as
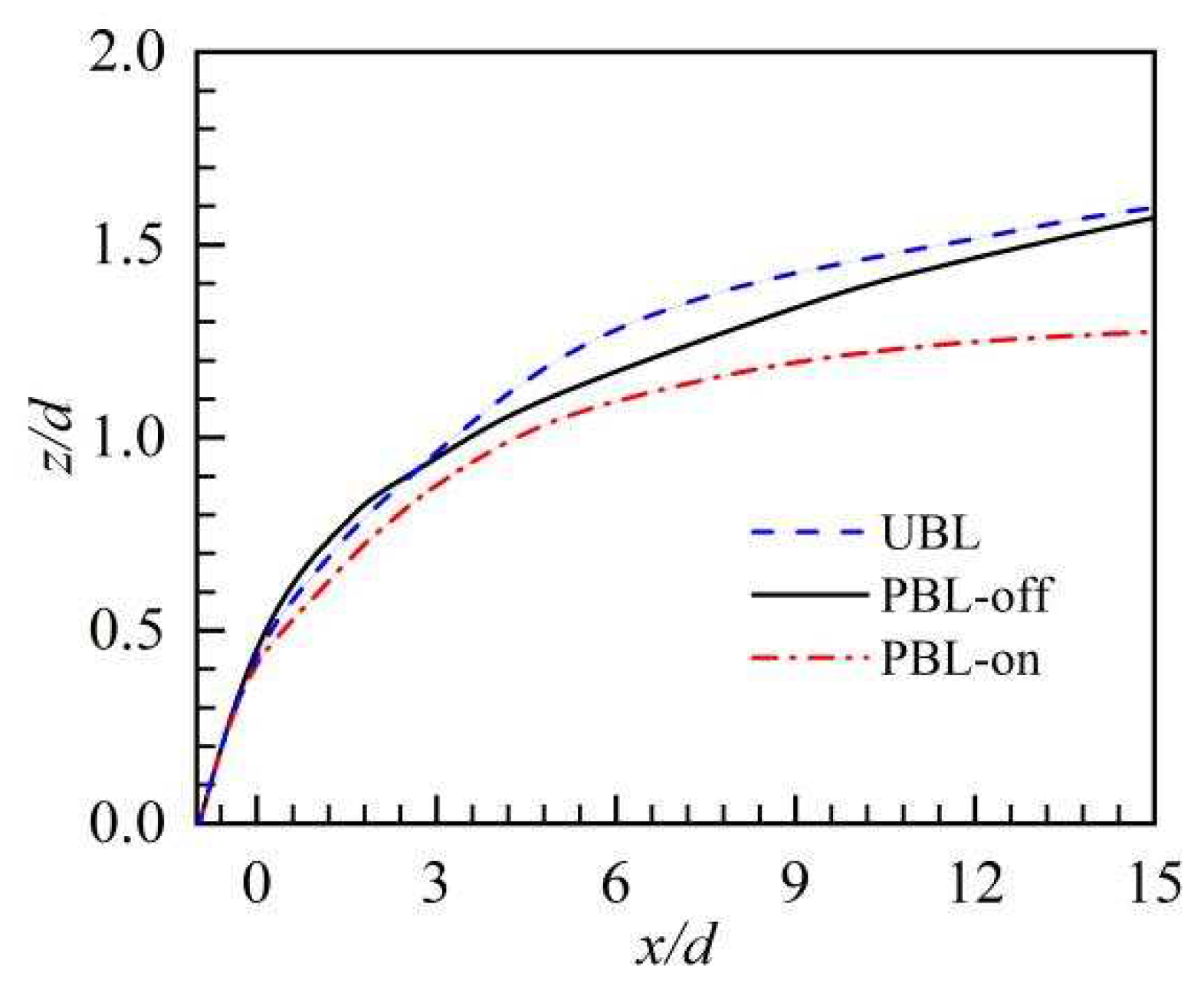
The UBL case was representative of un-pulsed film cooling flow, the PBL-off case and the PBL-on case represent the on/off switch of DBDPA, respectively, in the current research.
6. Conclusions
LESs of the pulsed film cooling without and with the PAA are conducted to uncover the underlying control mechanisms. After a qualitative and quantitative analysis of the time-averaged film cooling flow fields, a spatial-temporal evolution of the coherent structures was examined to determine the influences in greater detail. The main conclusions can be summarized as follows:
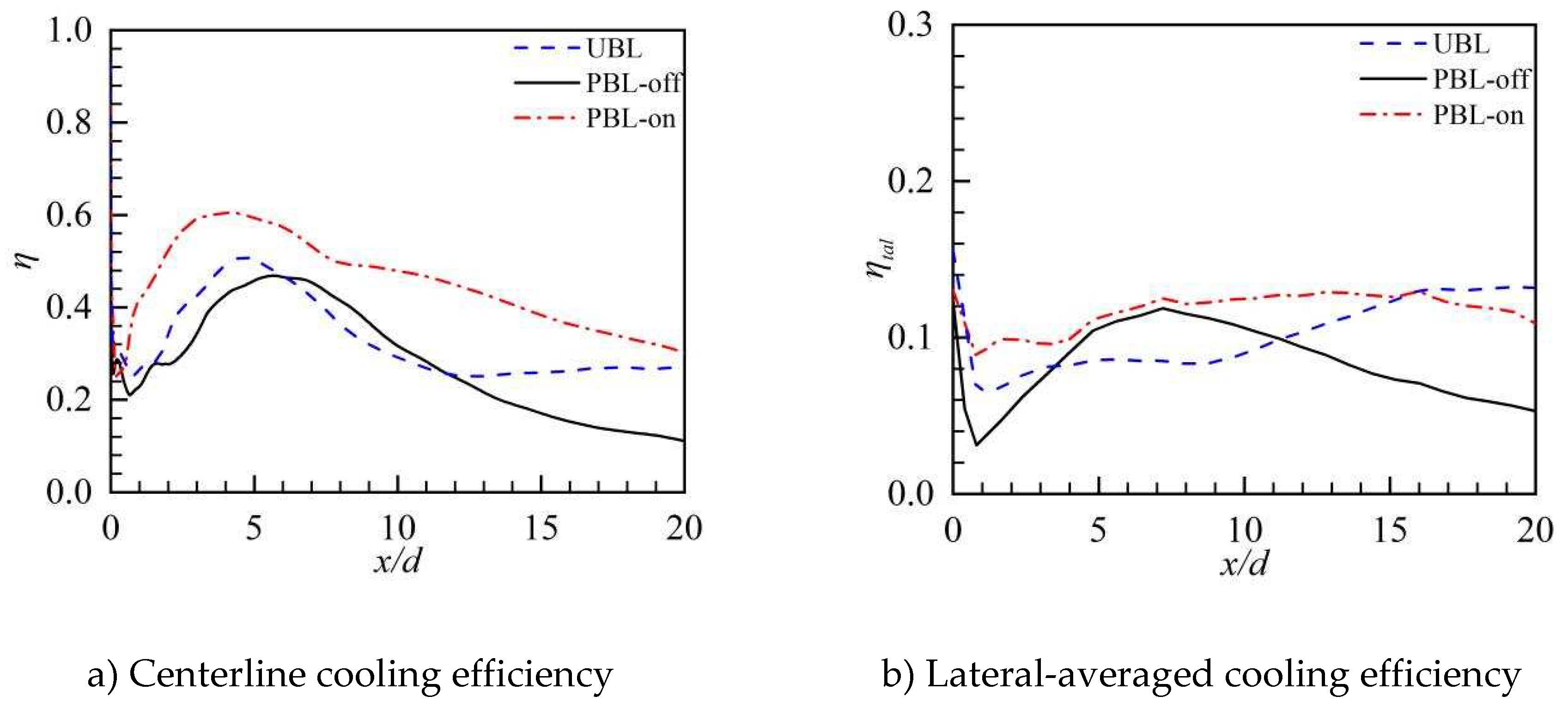
(1) The coolant pulsation might cause a slight reduction in the film cooling efficiency as the averaged pulsation BR was 1.0, while the PAA could effectively improve the pulsed film cooling efficiency and it would be superior to the steady-state film cooling.
(2) The pulsed cooling jet could penetrate deeper than the steady-state film cooling in the near hole region, thus, the jet-crossflow interactions produced large-scale CRVP, promoting the turbulent integration. Because of PAA, the penetration depth of the pulsed cooling jet was greatly reduced that could be attributable to the downward force, and the detrimental lift-off effect and entrainment of the CRVP were weakened.
(3) Rather than hairpin vortices, the intermittent coherent structure groups formed in the pulsed film cooling, along with their upcast behavior, these groups shifted off of the the wall surface and evolved downstream, thereby aggravating the turbulent integration of the coolant with the crossflow. The coherent structure groups were reduced in size and strength owing to the PAA, and their upcast behaviors were attenuated, thus, the turbulent integration was suppressed fundamentally and the film cooling efficiency was enhanced.
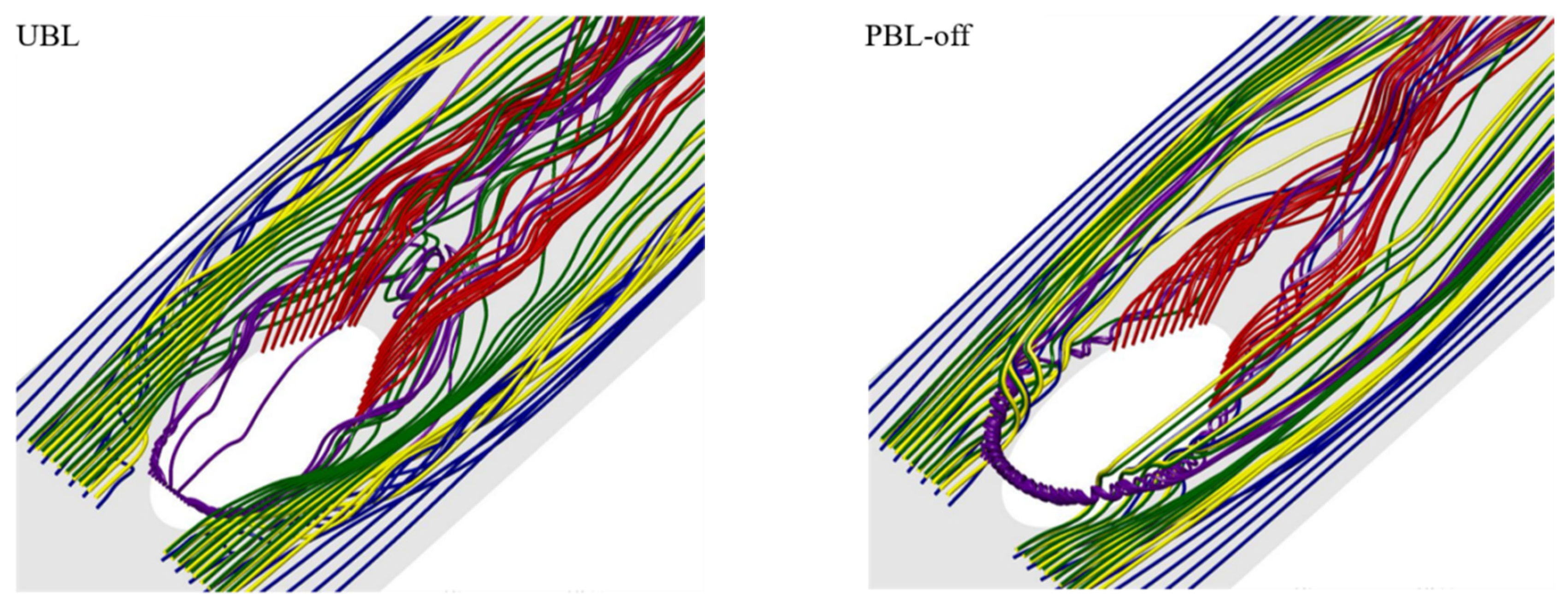
(4) The three-dimensional streamlines also confirmed that the PAA could effectively control the unsteady dynamic behaviors of the LSCSs, and the height of the three-dimensional streamlines was significantly reduced, indicating that the pulsed cooling jet flow was positioned close to the wall surface owing to the PAA.
Figure 1.
The flat plate film cooling physical model.
Figure 1.
The flat plate film cooling physical model.
Figure 2.
The meshing of computational domain.
Figure 2.
The meshing of computational domain.
Figure 3.
The BR variations of the pulsed and un-pulsed film cooling.
Figure 3.
The BR variations of the pulsed and un-pulsed film cooling.
Figure 4.
Schematically illustration of DBDPA and the phenomenological plasma model.
Figure 4.
Schematically illustration of DBDPA and the phenomenological plasma model.
Figure 5.
The flow induced by the DBDPA [
25,
32].
Figure 5.
The flow induced by the DBDPA [
25,
32].
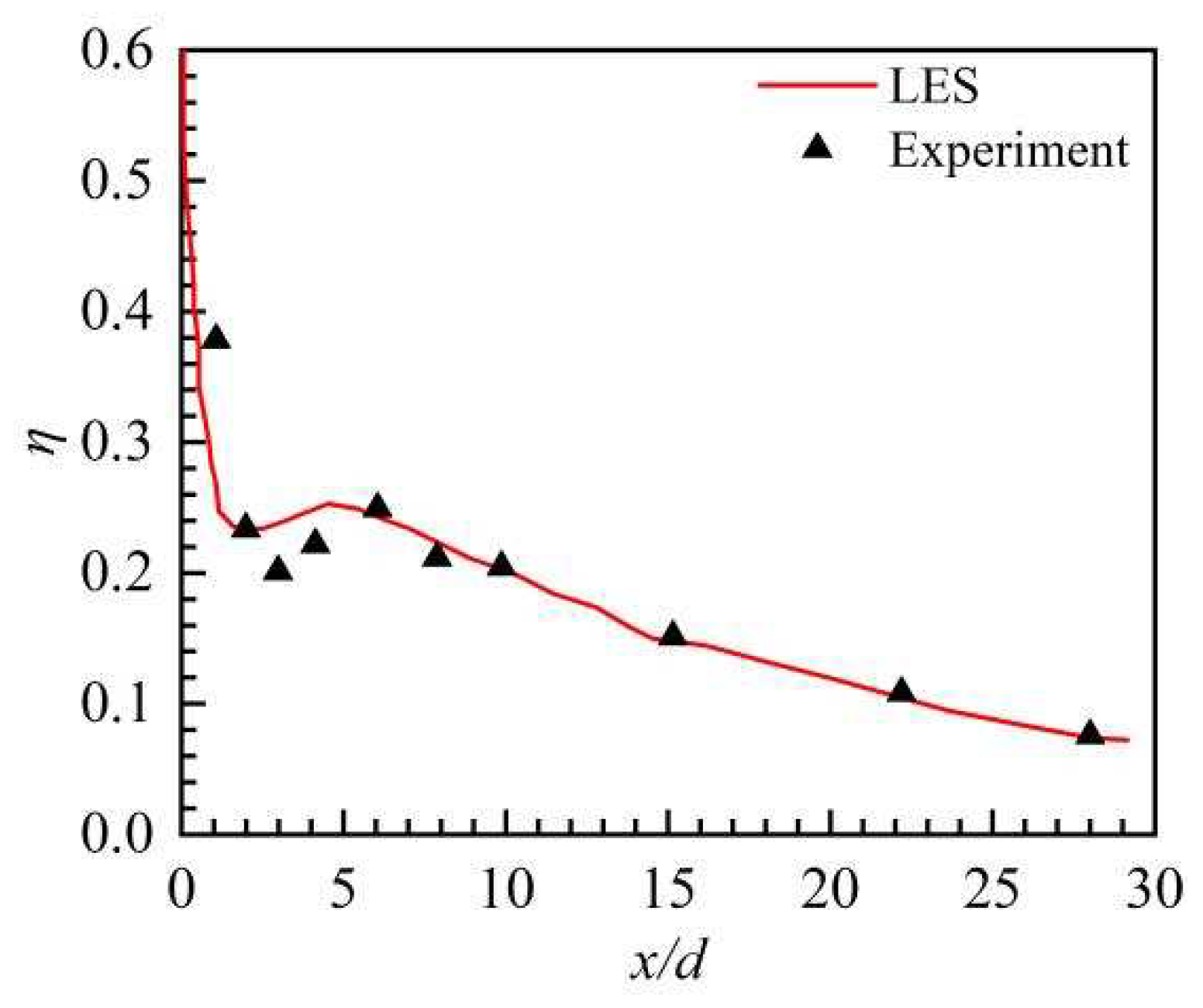
Figure 6.
Comparison of centerline film cooling efficiency [
25,
27,
28].
Figure 6.
Comparison of centerline film cooling efficiency [
25,
27,
28].
Figure 7.
Jet trajectories.
Figure 7.
Jet trajectories.
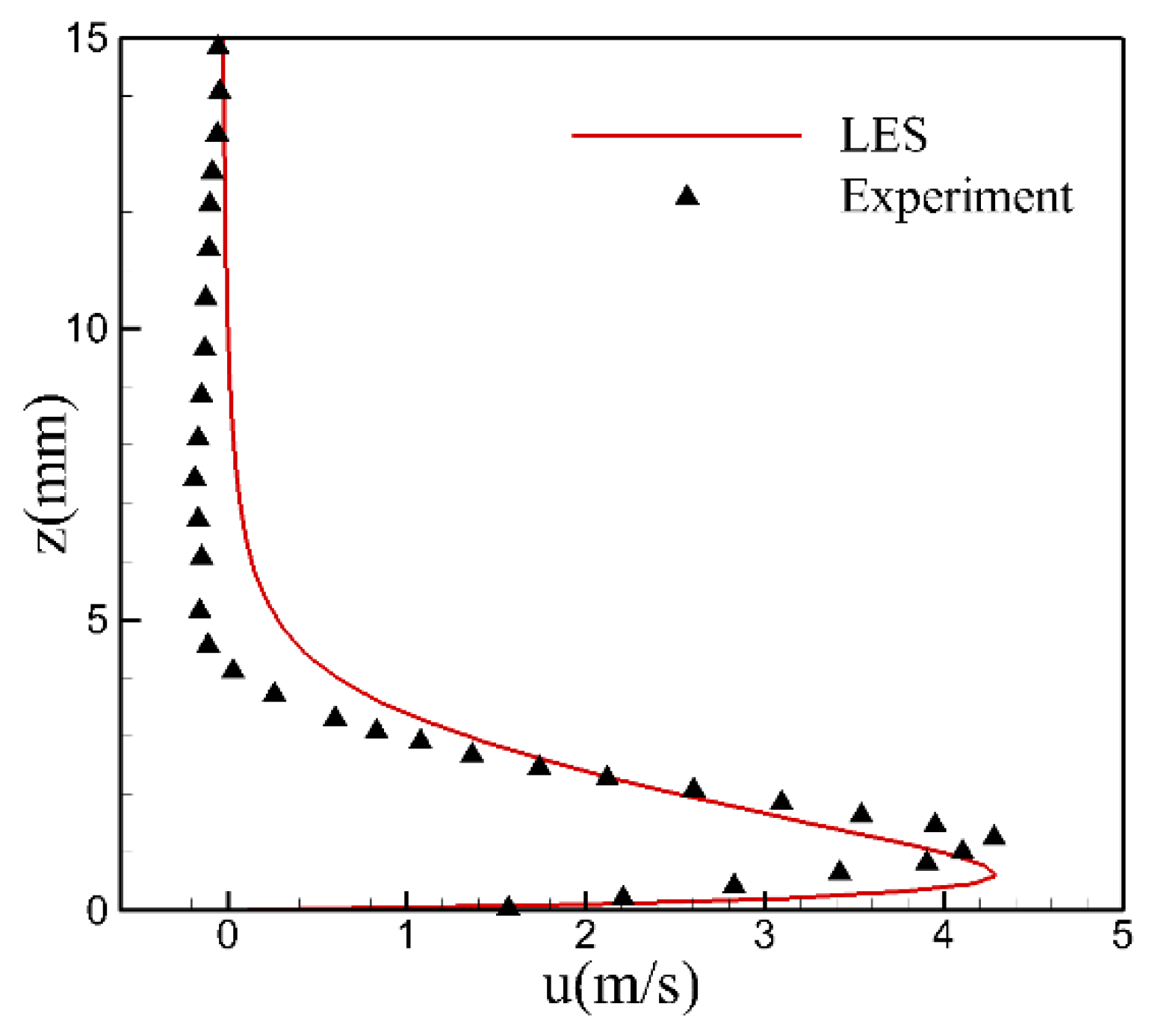
Figure 8.
Time-averaged velocity profiles at the exit of the cooling hole(y/d=0, z/d=0.015).
Figure 8.
Time-averaged velocity profiles at the exit of the cooling hole(y/d=0, z/d=0.015).
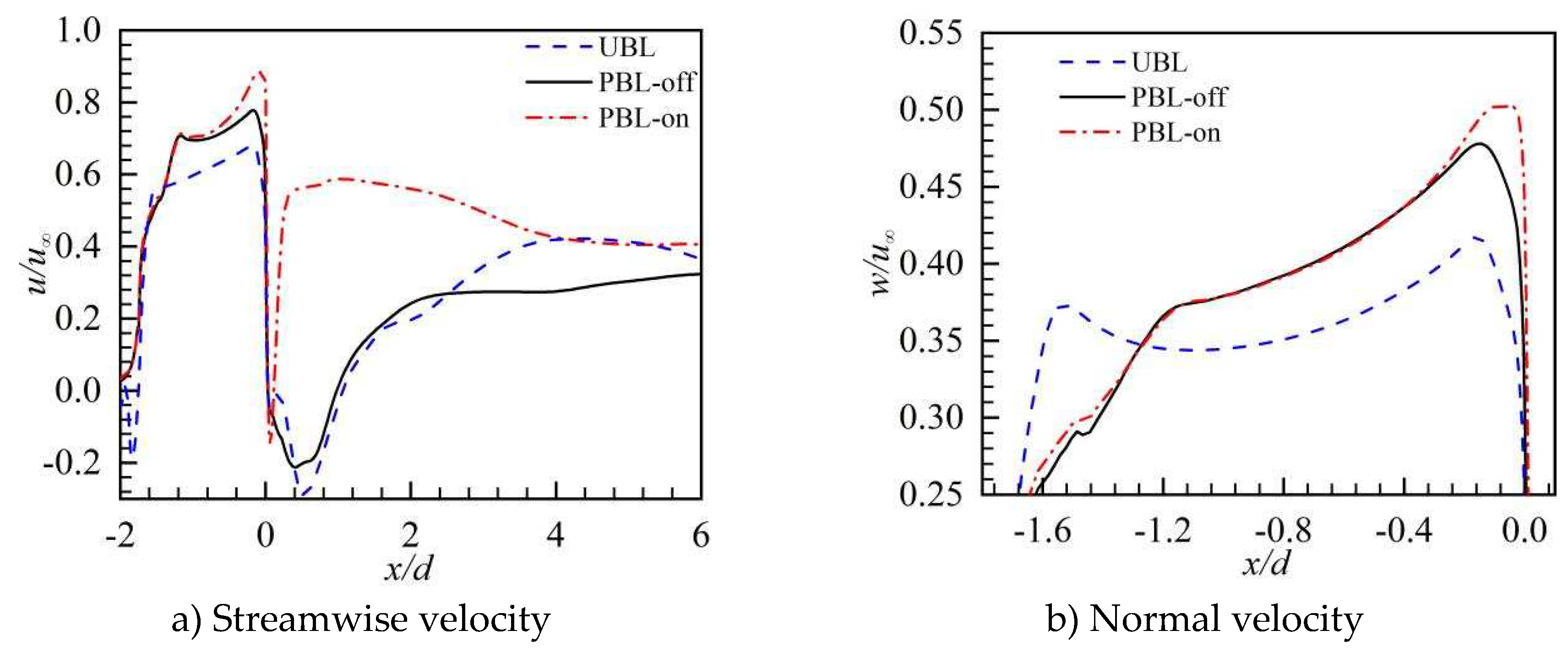
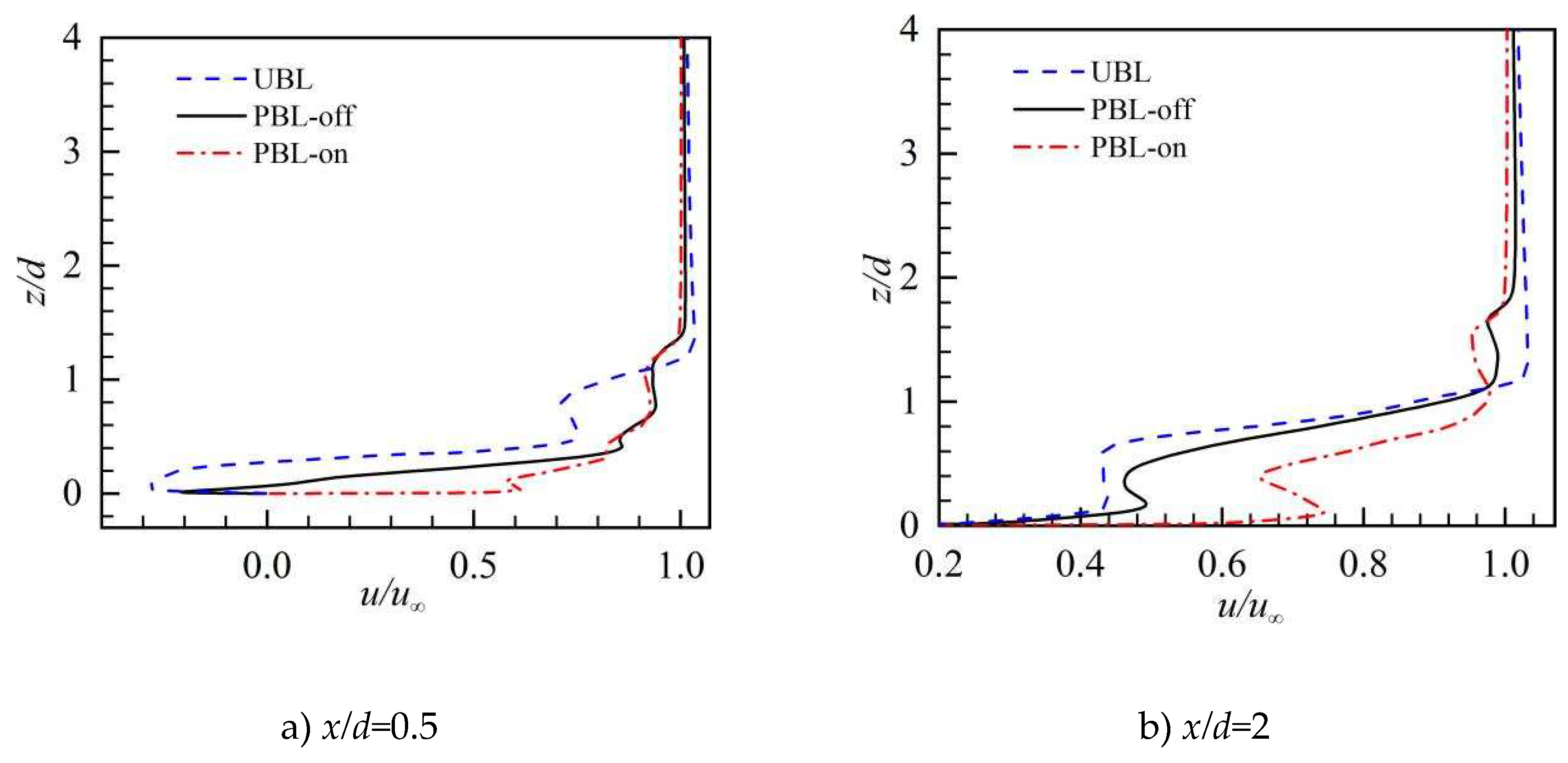
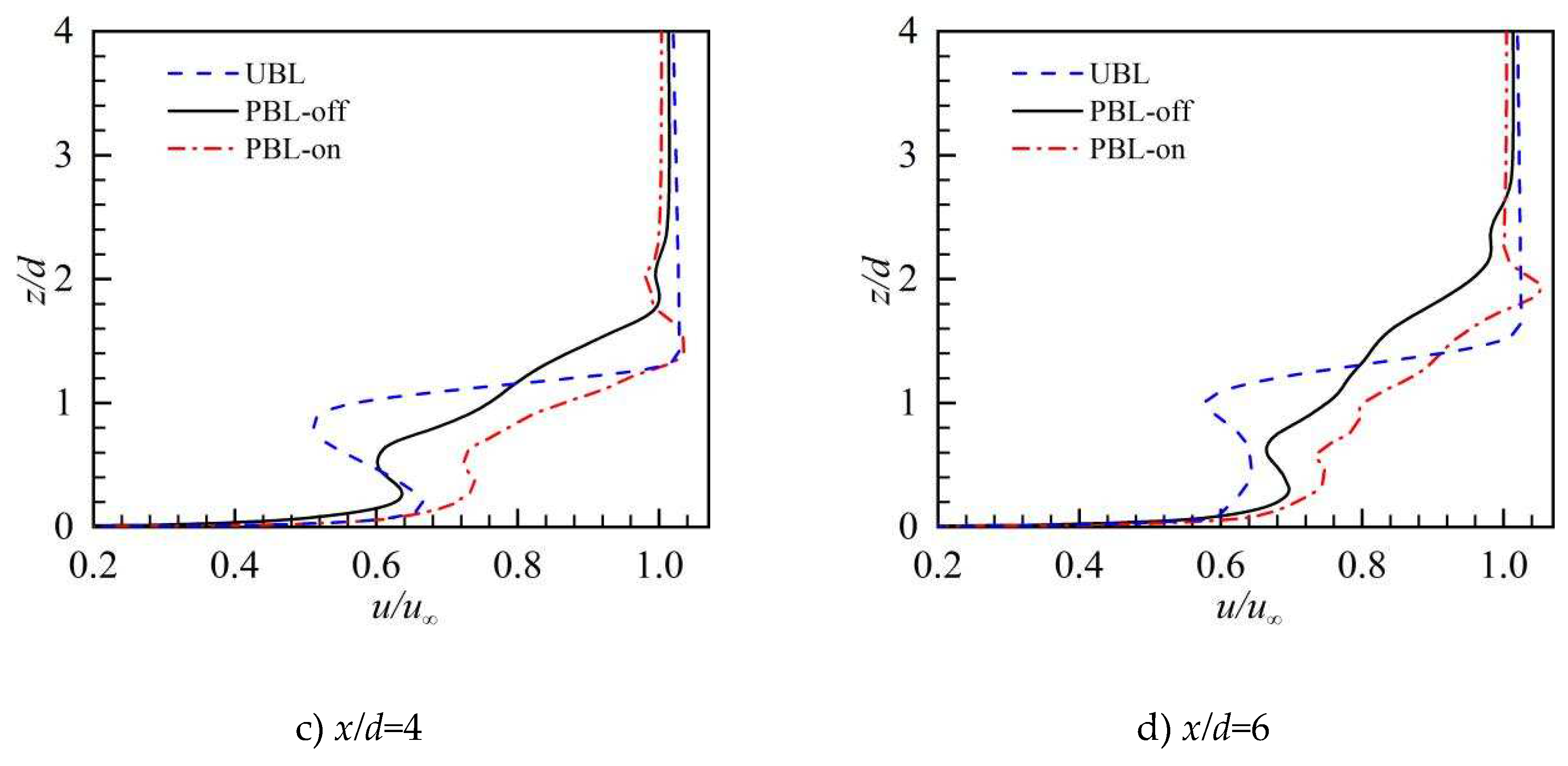
Figure 9.
The streamwise velocity profiles with time average in the y/d = 0 plane.
Figure 9.
The streamwise velocity profiles with time average in the y/d = 0 plane.
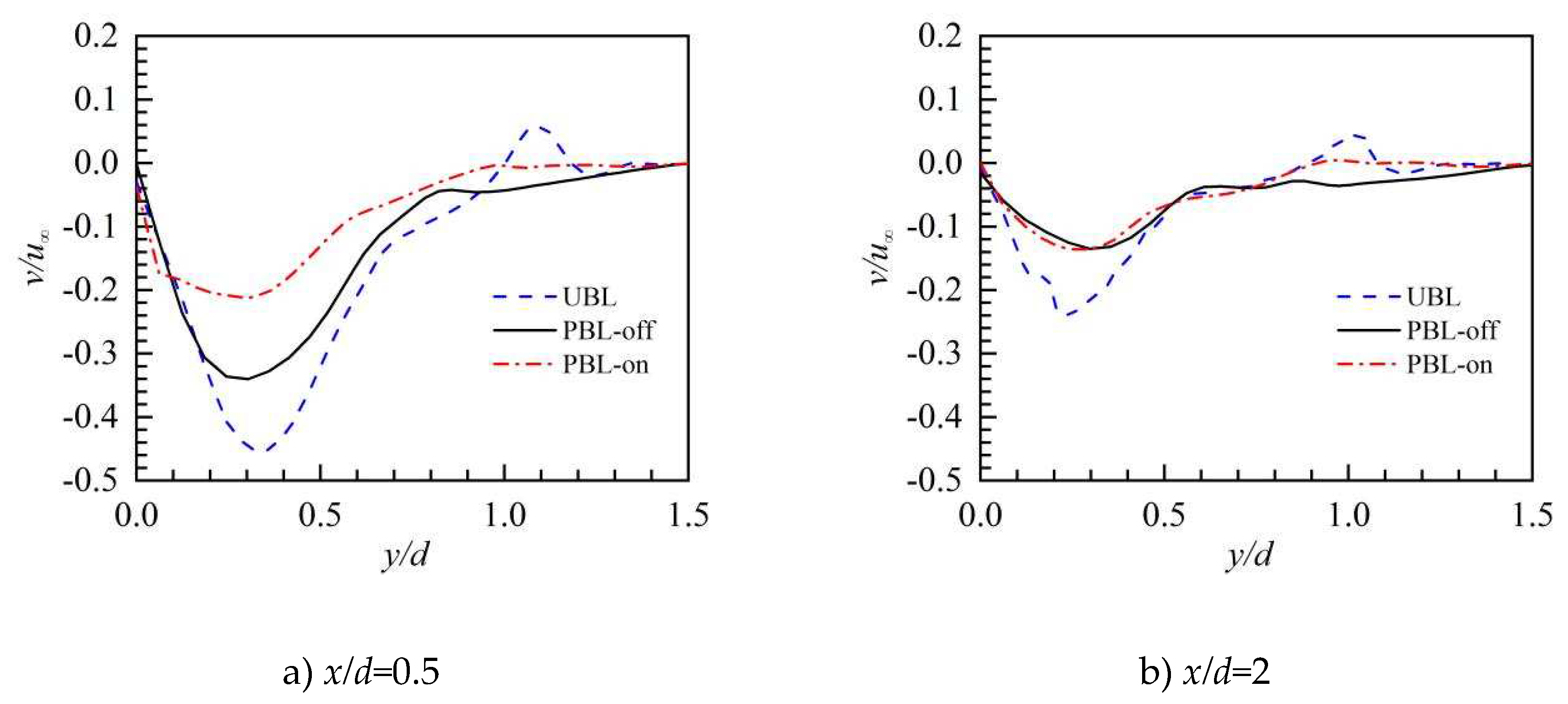
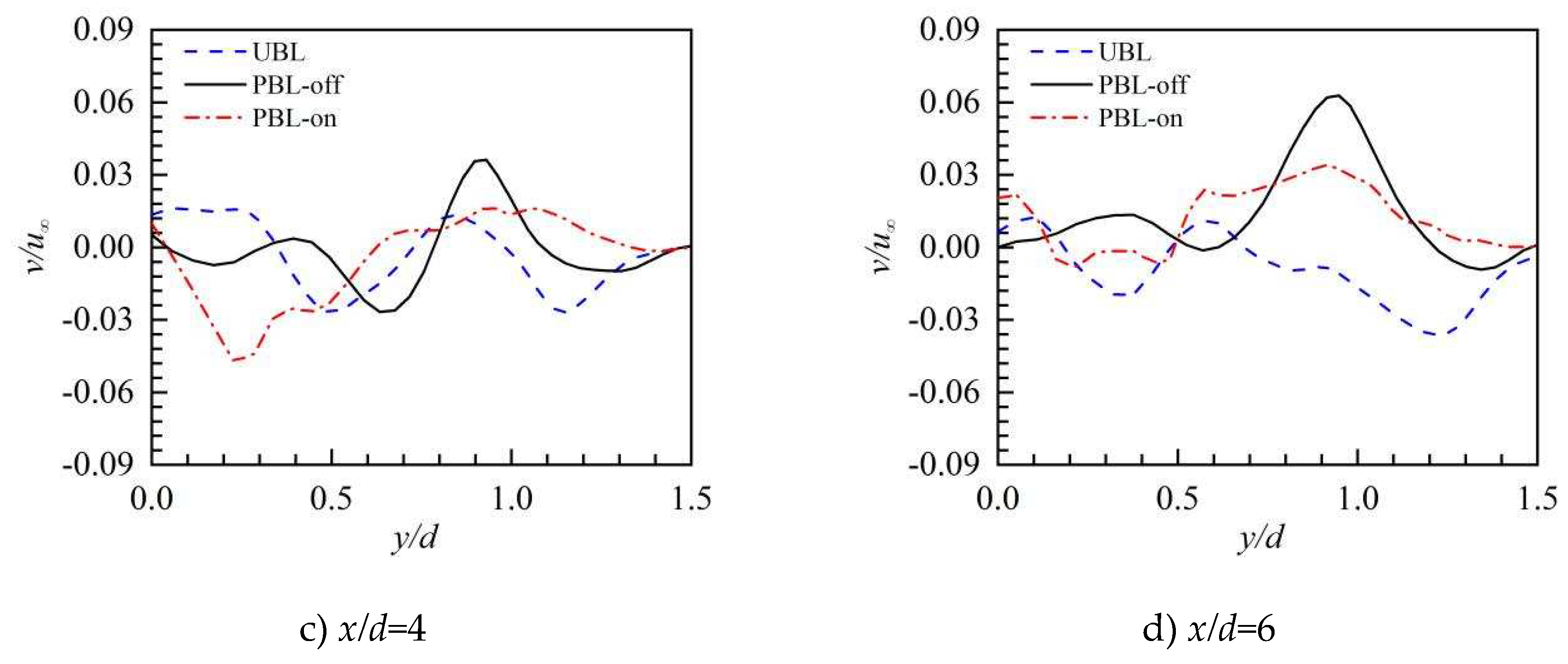
Figure 10.
The profiles of time-averaged lateral velocity along the lateral direction.
Figure 10.
The profiles of time-averaged lateral velocity along the lateral direction.
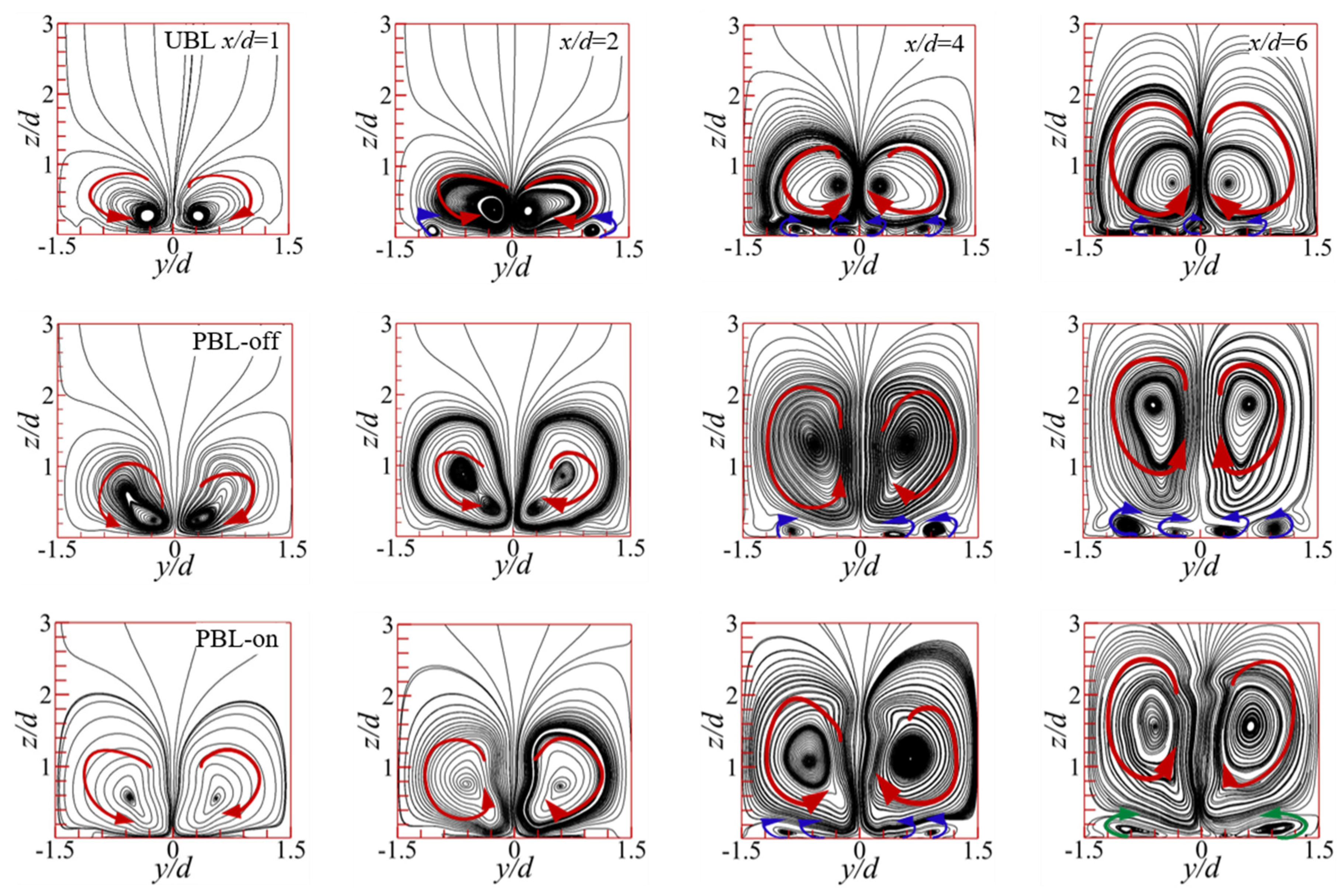
Figure 11.
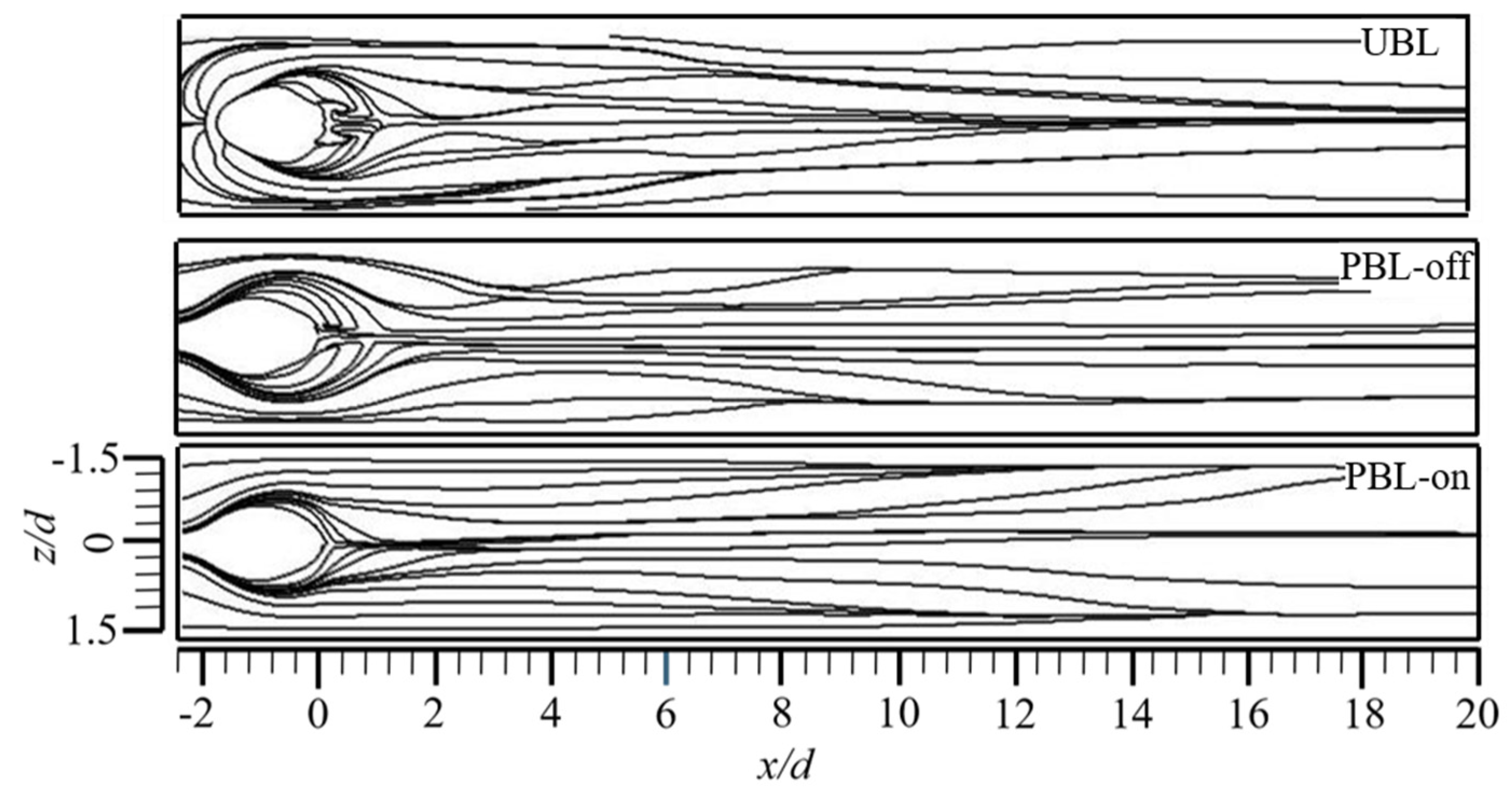
The time-averaged streamlines in the cross-sections downstream of the cooling hole.
Figure 11.
The time-averaged streamlines in the cross-sections downstream of the cooling hole.
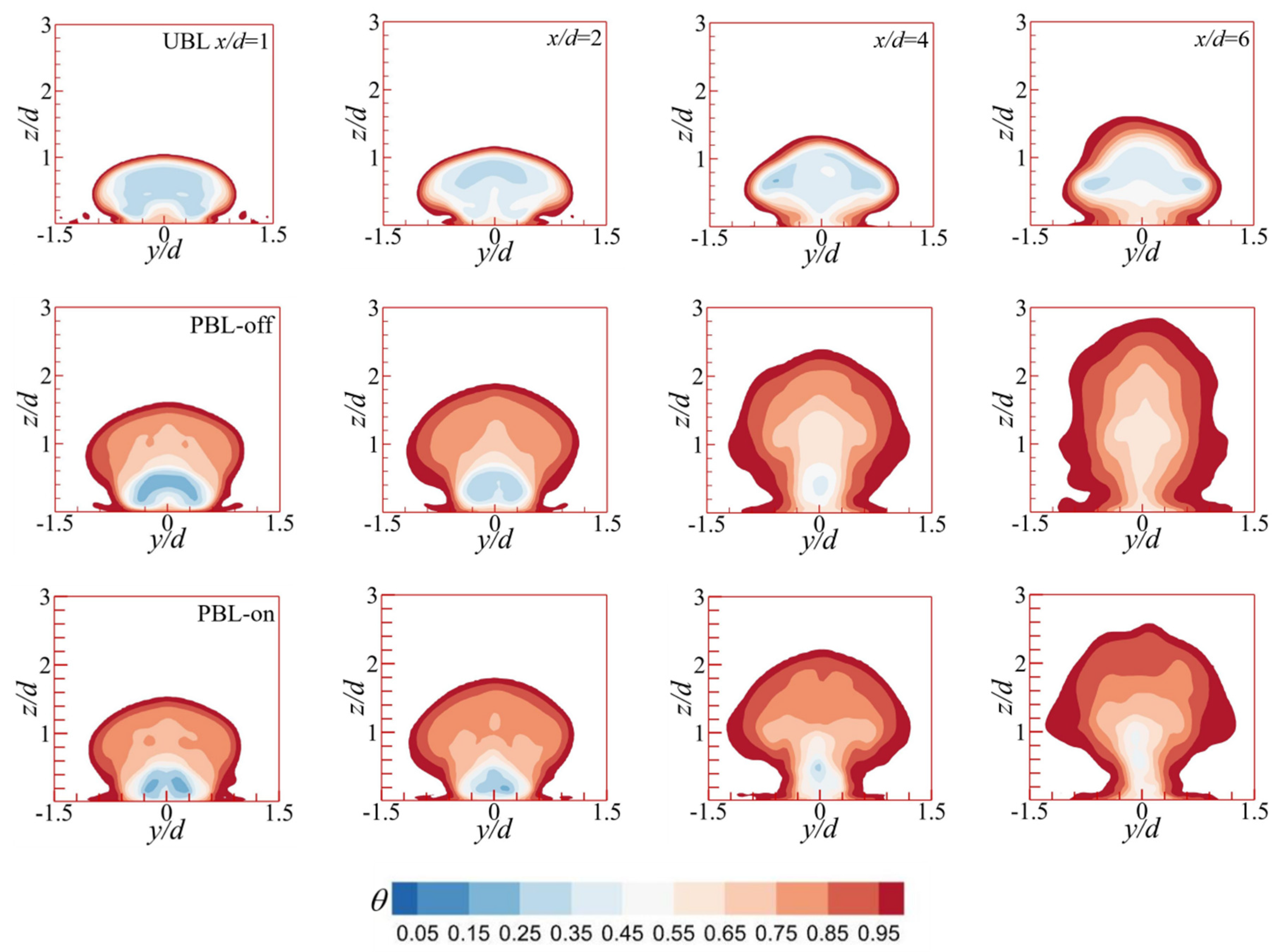
Figure 12.
The cross-sectional profiles of the time-averaged dimensionless temperature downstream of the cooling hole.
Figure 12.
The cross-sectional profiles of the time-averaged dimensionless temperature downstream of the cooling hole.
Figure 13.
The contours of the time-averaged film cooling efficiency on the wall surface.
Figure 13.
The contours of the time-averaged film cooling efficiency on the wall surface.
Figure 14.
The time-averaged streamlines on the wall surface.
Figure 14.
The time-averaged streamlines on the wall surface.
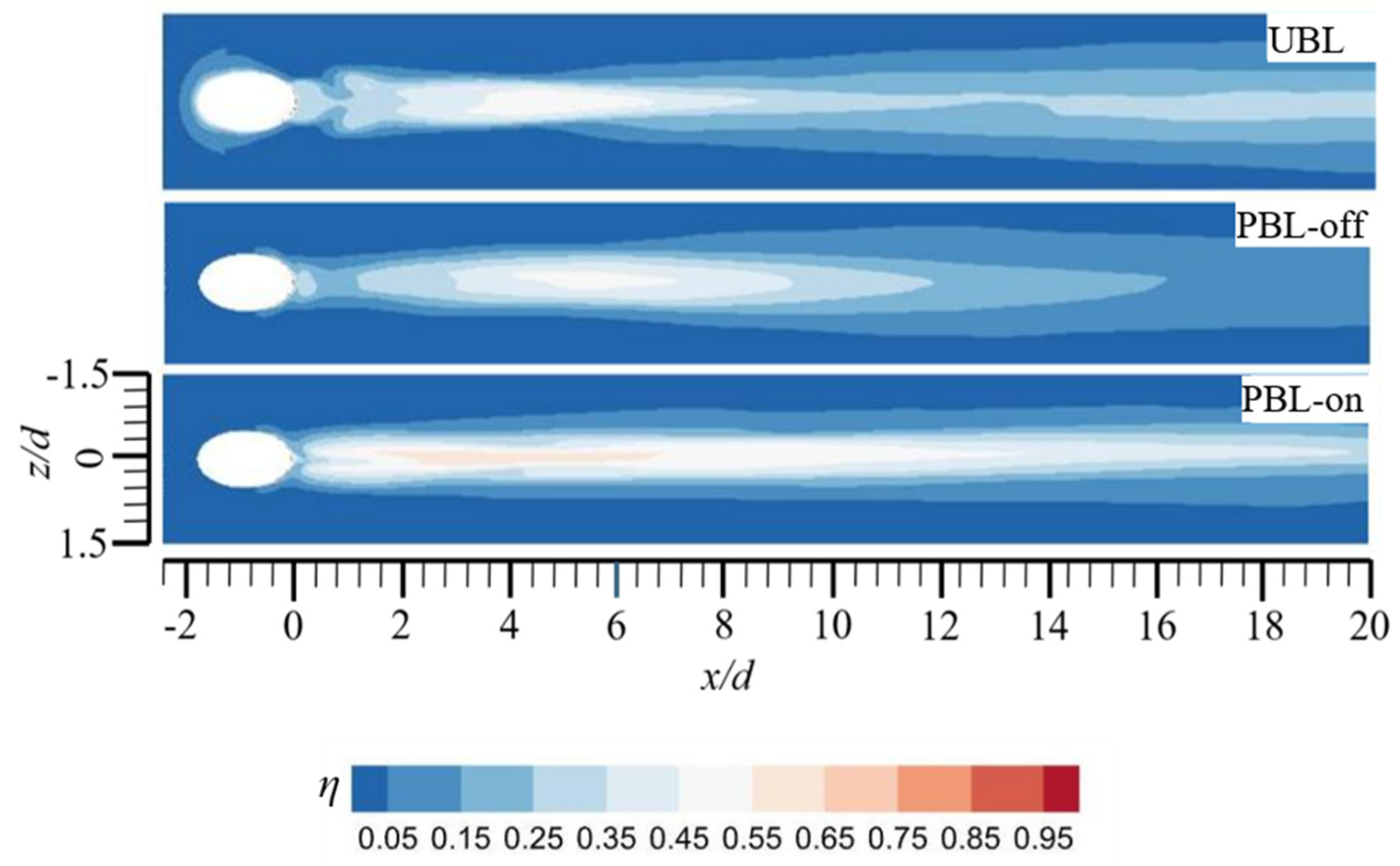
Figure 15.
The distributions of the film cooling efficiency along the streamwise direction.
Figure 15.
The distributions of the film cooling efficiency along the streamwise direction.
Figure 16.
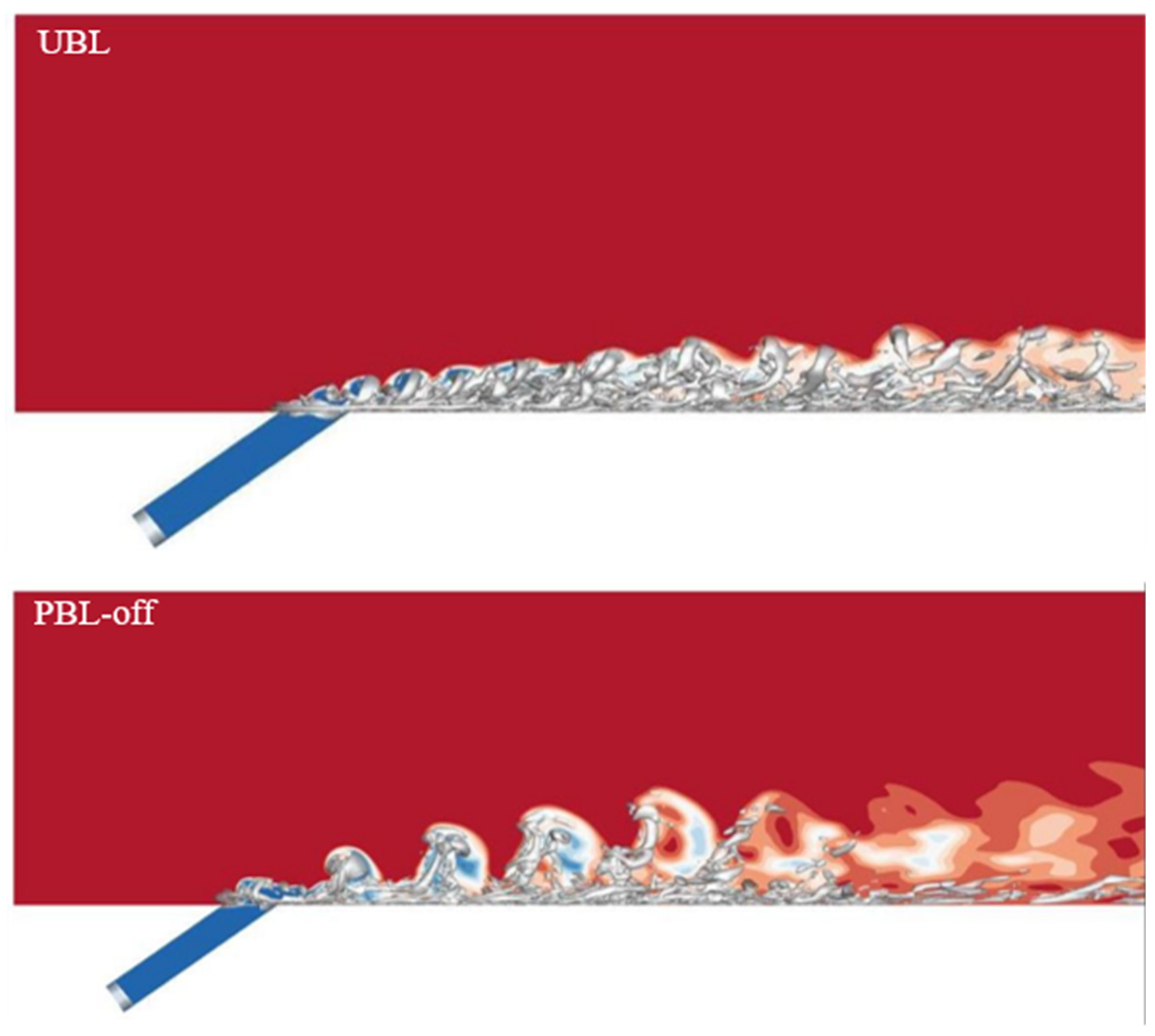
The instantaneous Q iso-surface colored by temperature in the UBL case (Q = 5.0×105).
Figure 16.
The instantaneous Q iso-surface colored by temperature in the UBL case (Q = 5.0×105).
Figure 17.
The temperature-dependent instantaneous Q iso-surface in the PBL-off case (Q = 5.0×105).
Figure 17.
The temperature-dependent instantaneous Q iso-surface in the PBL-off case (Q = 5.0×105).
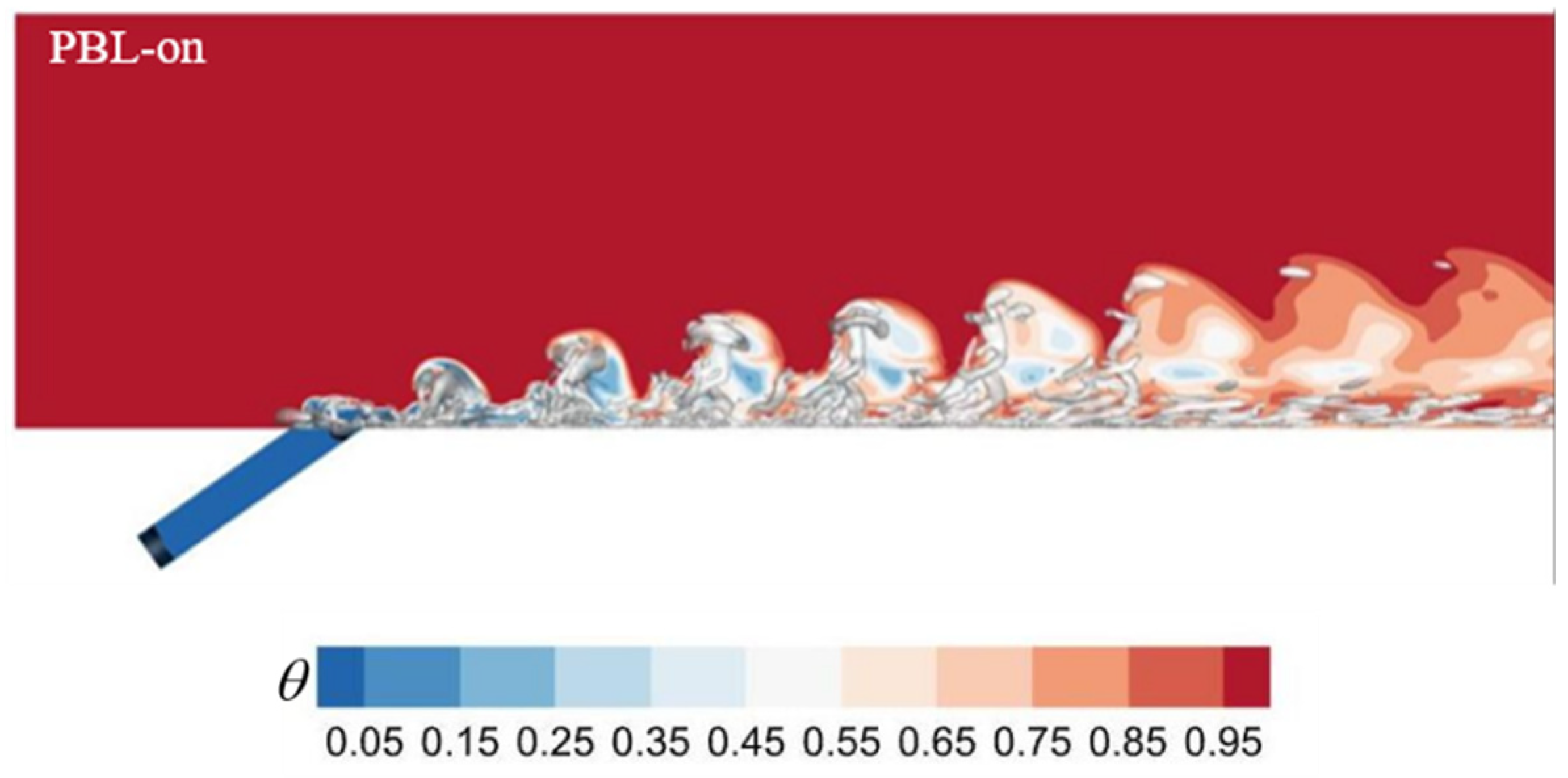
Figure 18.
The instantaneous Q iso-surface colored by temperature in the PBL-on case (Q = 5.0×105).
Figure 18.
The instantaneous Q iso-surface colored by temperature in the PBL-on case (Q = 5.0×105).
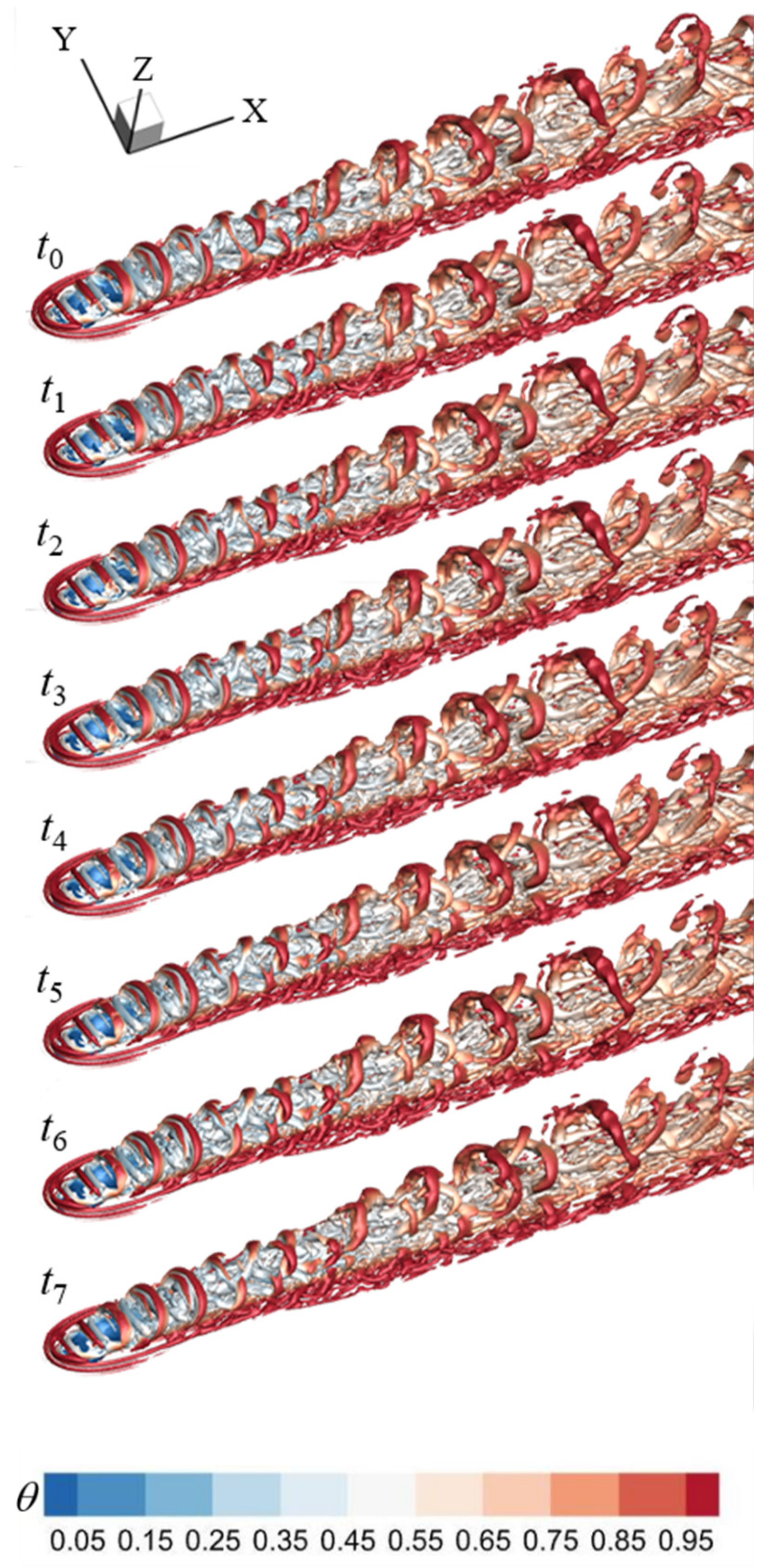
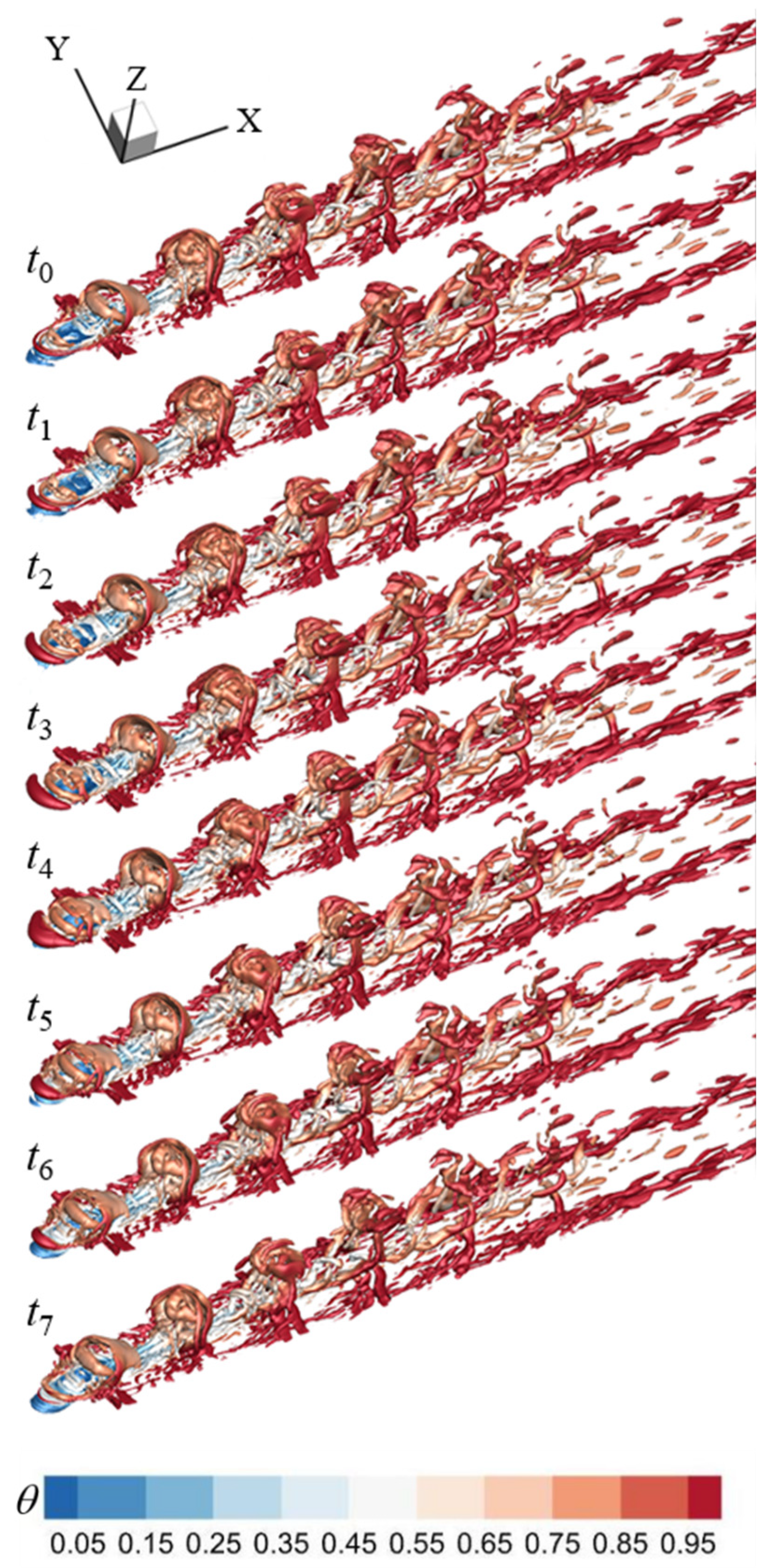
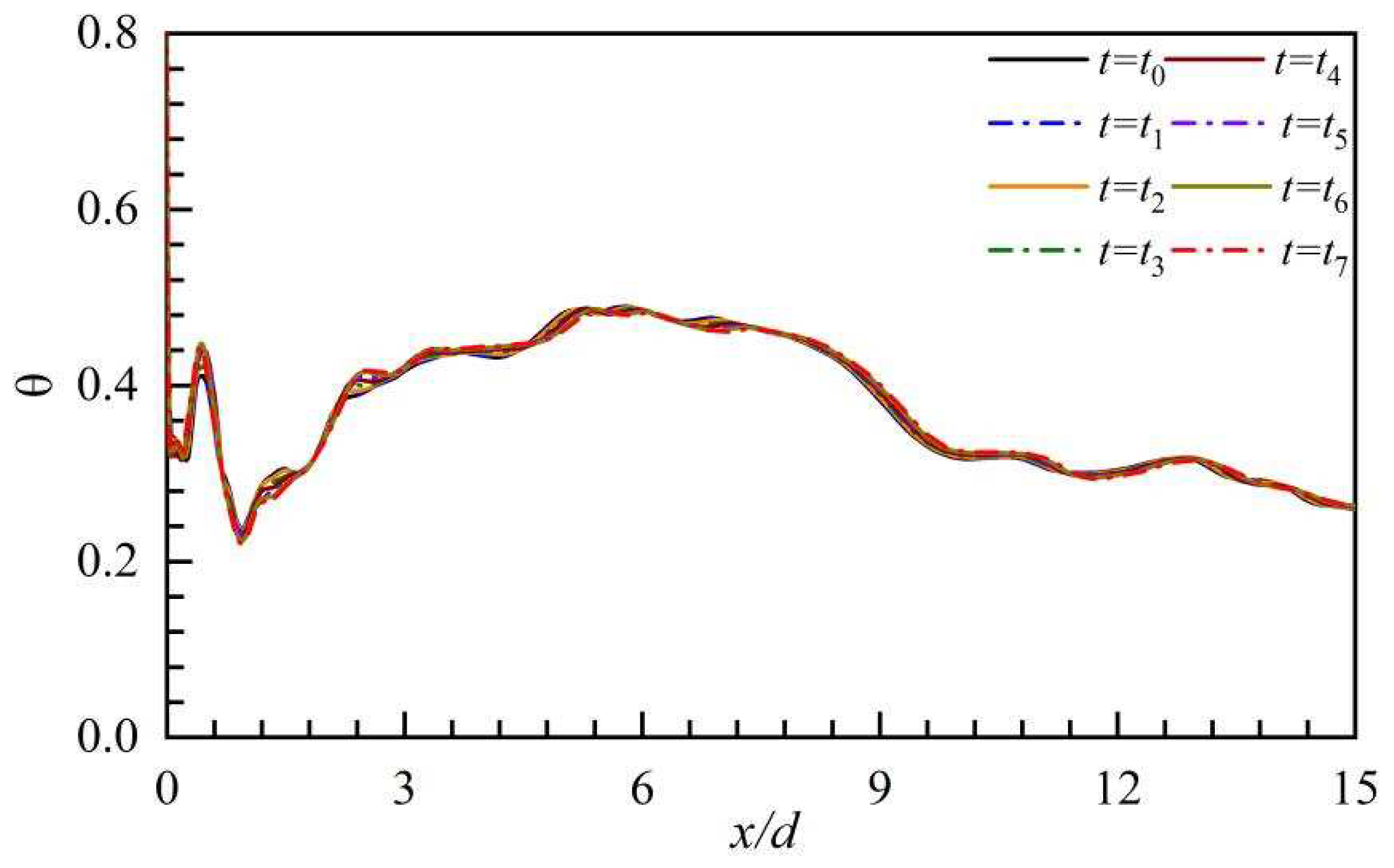
Figure 19.
The variations of the DT on the hole centerline in the UBL case.
Figure 19.
The variations of the DT on the hole centerline in the UBL case.
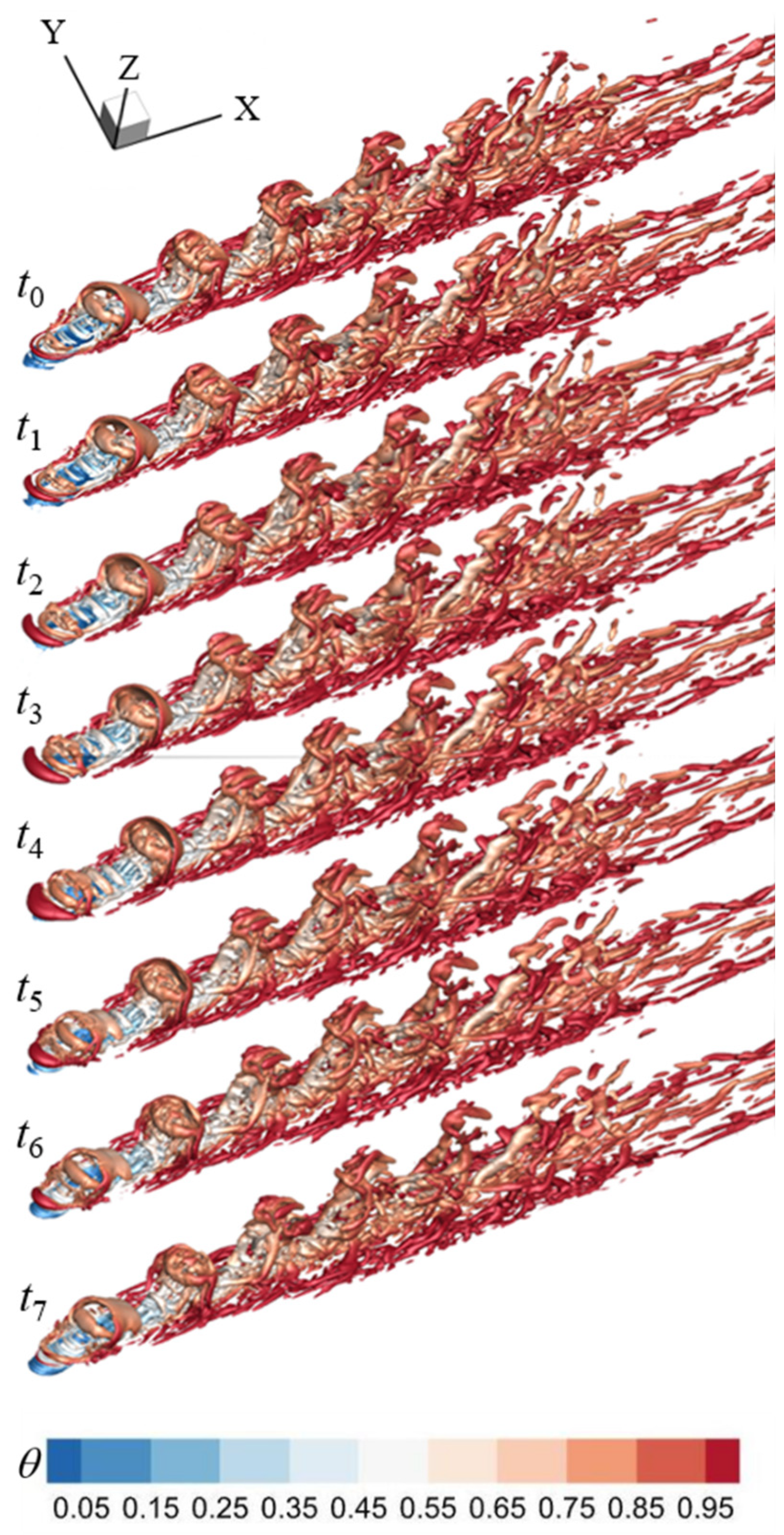
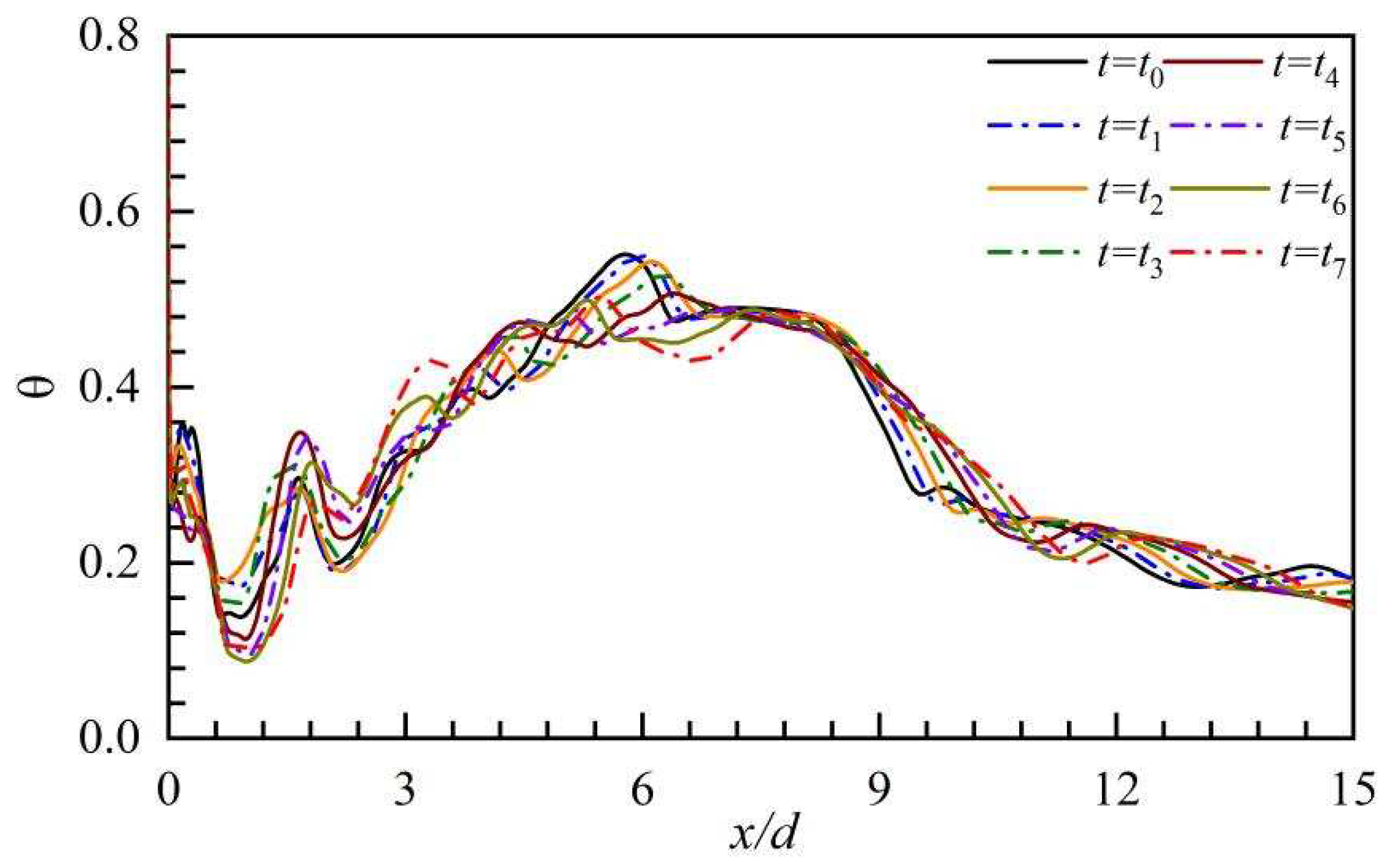
Figure 20.
The variations of the DT on the hole centerline in the PBL-off case.
Figure 20.
The variations of the DT on the hole centerline in the PBL-off case.
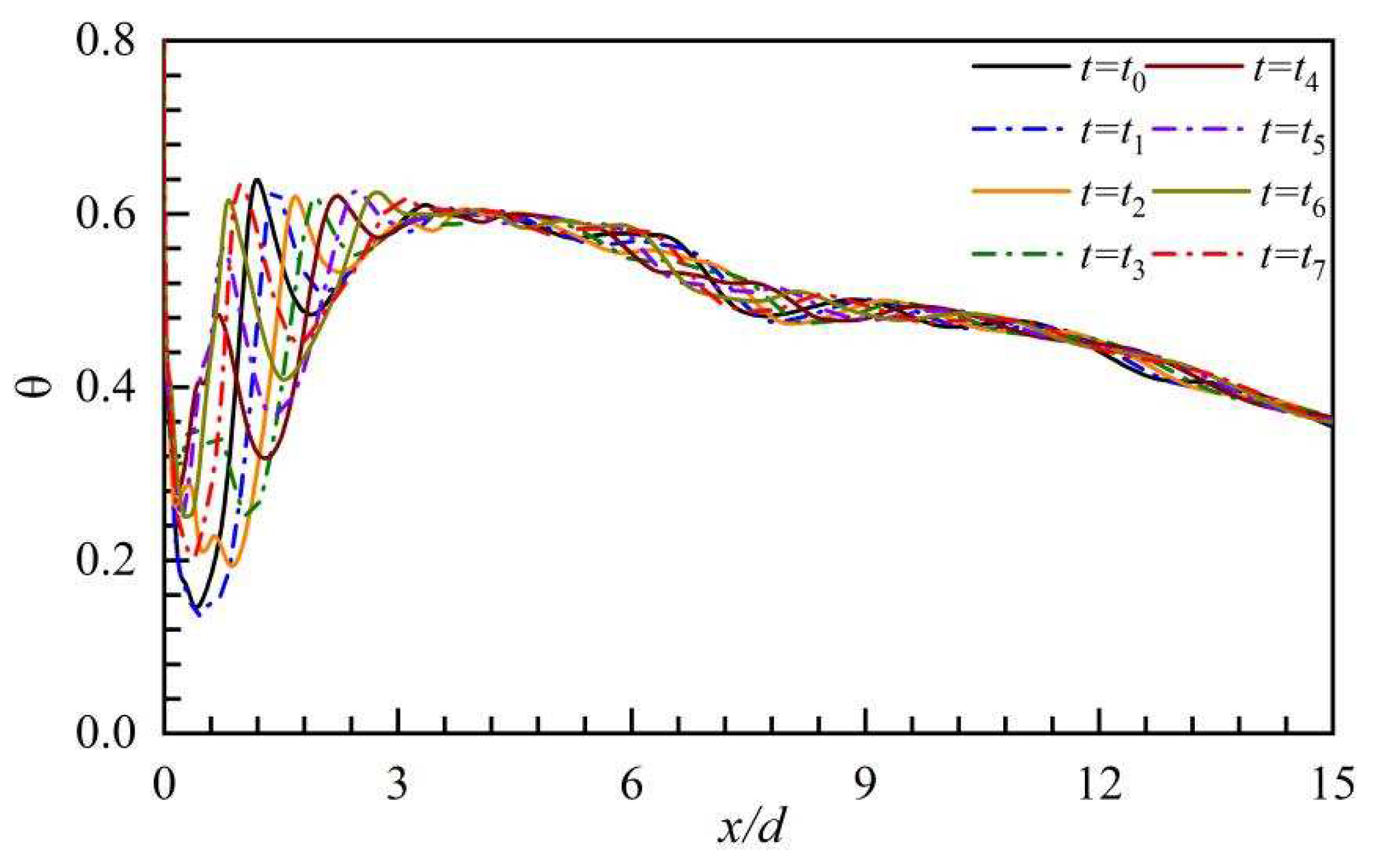
Figure 21.
The variations of the DT on the hole centerline in the PBL-on case.
Figure 21.
The variations of the DT on the hole centerline in the PBL-on case.
Figure 22.
The contours of instantaneous temperature in the z/d = 0.0 plane.
Figure 22.
The contours of instantaneous temperature in the z/d = 0.0 plane.
Figure 23.
Interaction of the upstream flow with the jet and the cross at the same moment.
Figure 23.
Interaction of the upstream flow with the jet and the cross at the same moment.