Preprint

Article

Toward Optimal Robot Machining considering the Workpiece Surface Geometry in a Task-Oriented Approach

Altmetrics

Downloads

110

Views

Comments

A peer-reviewed article of this preprint also exists.

Aleš Hace^*

This version is not peer-reviewed

Submitted:

28 November 2023

Posted:

29 November 2023

You are already at the latest version

Alerts

Abstract

Robot workpiece machining is interesting in industry since it offers some advantages, such as higher flexibility in comparison with the conventional approach based on the CNC technology. However, in recent years we have been facing a strong progressive shift to custom based manufacturing and low volume/high mix production, which require a novel approach to automation by the employment of collaborative robotics. However, collaborative robots feature only limited motion capability, to provide safety in cooperation with human workers. Thus, it is highly necessary to perform more detailed robot task planning to ensure its feasibility and optimal performance. In this paper, we deal with the problem of studying kinematic robot performance in the case of such manufacturing tasks, where the robot tool is constrained to follow the machining path embedded on the workpiece surface at a prescribed orientation. The presented approach is based on the well-known concept of manipulability, although the latter suffers from physical inconsistency due to mixing different units of linear and angular velocity in a general 6 DOF task case. Therefore, we introduce the characteristics of the workpiece surface constraint in the robot kinematic analysis, that enables evaluation of its available velocity capability in a reduced dimension space. Such constrained robot kinematics transform the robot`s task space to a two-dimensional surface tangent plane, and the manipulability analysis may be limited to the space of linear velocity only. Thus, the problem of physical inconsistency is avoided effectively. We show the theoretical derivation of the proposed method, which was verified by numerical experiments.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Nowadays, robotics is an indispensable technology in many industries, especially in manufacturing, since it represents a major building block for fully automated production lines such as in the automotive industry. Typically, standard applications of industrial robots are designed such that they perform well-defined repetitive tasks of manipulation, assembly, palletizing, welding, painting, etc [1]. However, on the other hand, a shift from high volume/low mix to low volume/high mix and custom based production impacts manufacturing seriously. It requires robots which are easier to install, program and operate, in order to increase robotization in small and medium-sized enterprises, where collaborative and more flexible automation appears to be a useful option. Thus, collaborative robots (cobots), not only provide safe physical coexistence and interaction and cooperation in a common workspace with human workers [2,3], but are also easier to use, and are gaining popularity in industries with a growing demand for highly customized products, since they increase manufacturing flexibility, filling the gap between fully automated systems and manual production [4,5]. However, in order to guarantee safe physical human-robot interaction, collaborative robots are designed with substantially reduced capabilities of speed and force/torque in comparison with standard industrial robot arms [6].

Beside the above mentioned industrial robot applications there are also others, such as more complex robot machining [7] or milling [8], deburring [9], surface finishing [10], grinding [11], polishing [12,13], hammer-peening [14,15], etc. In some processes the technology requires a significant machining force in the tool feed direction, and in some the machining force is required in the direction only toward the workpiece surface. The technological process of metal surface treatment with hammer-peening, which is applied in the tool- or mold- or die-making industry, is such a cold forging process, in which a ball made of a carbide solid is struck with a high frequency on the metal surface of the workpiece by a micro-forging hammer tool [16]. Hammer-peening improves the smoothness of the surface, hardens it, and eliminates internal stresses. In this manufacturing process, the machine hammer-peening tool (MHP tool) is moving freely along the surface of the workpiece (that may have a complex geometry) following the machining path, which connects all surface points of the patch area to be forged. The working angle of the MHP tool to the workpiece is usually determined as perpendicular to its surface along the direction of travel of the tool. However, such surface finishing process is complex and thus a very wasteful process, which has a large impact on the cost of the overall processing in the tool-making industry. It demands to combine both a collaborative, intelligence-based and a cooperative human-robot-based technological approach, as in the robotic polishing application [17]. Thus, it may involve not only robotized solutions, e.g., such as [18,19], but also the collaborative automation with a proper flexibility due to the customized high mix/low volume nature of the production type in the tooling industry. Therefore, cobots can be considered as a justified replacement for traditional industrial robots in such applications.

However, due to low power built-in cobot actuators (in comparison with standard industrial robot arms) their introduction in a machining process requires more careful trajectory planning, in order to assure the feasibility of the robot task, especially in the case of manufacturing processes with complex continuous paths where the complexity of robot path planning increases significantly [20]. Optimal relative workpiece/robot placement and robot path/trajectory planning considering this issue thus become even more important, in order to provide rapid set-up of a robotic system in flexible high mix/low volume applications. Such planning problems have been interesting research topics for many years, and their application in practice still attracts attention in the research community. The researchers optimized the location of the robot for generating maximum task-space velocity with minimum joint velocities [21], and robot-to-workpiece placement for large scale welding systems [22], generated a kinematic performance map based on a kinetostatic condition index that was used to optimize robot configurations in a polishing application [23], introduced a custom index for robot base placement optimization demonstrated in a trim application in shoe manufacturing [24], and optimized a workpiece placement for the robotic operation in challenging manufacturing tasks [25,26] and surface finishing [20,27]. An interesting new optimization approach was also introduced, to maximize the available velocities of the end-effector during a task execution of path following in robot machining called the Decomposed Twist Feasibility method [28].

There have been several attempts at trajectory optimization for an industrial robot with different objectives. However, the main well-known basic concept that enables analysis of robot motion capability is called manipulability [29]. The pioneering work was presented by Yoshikawa in 1985 [30], who introduced a qualitative method for assessment of robot motion capabilities based on the so-called manipulability ellipsoid, that was derived from a robot velocity kinematics description by the application of the singular value decomposition of the associated Jacobian matrix and Euclidean norm metrics. The introduced manipulability index was proportional to the ellipsoid volume, and it should measure how easy or difficult it is for a robot to move in its Cartesian operational workspace, and it may also represent a distance to the singular configuration of the robotic arm. Beside the volume of the ellipsoid, other indices also derived from the ellipsoid appeared later, such as minimal singular value and condition number [31]. However, the operational space twist vector involves different units of linear and angular velocity; beside this, robot joints can also be of different types. These complicate the manipulability analysis from the point of view of physical consistency [32,33]. Thus, in order to avoid the problem of the dimensional dependence when both position and orientation of the robot end-effector are included in kinematic equations, new manipulability indices were introduced, which were based on the introduction of auxiliary points on the end-effector that provided additional linear velocity information and a redundant formulation of the velocity equations, instead of the combination of linear and angular velocities [34]. However, in this point-based approach the determination of the auxiliary points is arbitrary, and the measure of the obtained dimensionally homogeneous Jacobian matrix is not invariant with respect to changes of the auxiliary points used to express the end-effector velocity. A general approach to the problem of dimensional nonhomogeneous matrices in the velocity kinematics description presents the introduction of weighted norms [35], and the selection of the corresponding weighting matrices to set translational components of the Jacobian matrix in relation with the rotational components [36] is again arbitrary, e.g., manual selection of the weights in a task dependent measure [37], or their selection can be based on the computation of the minimal principal angle between the translational and rotational subspace in a task-oriented approach [38]. However, it has been shown that all such manipulability indices suffer from the nonexistence of “natural” metrics, and therefore from non-invariance in the sense of the choice of the selected artificial metric functions, which is arbitrary, employed in their definition [39,40]. Although the translational and rotational operational velocities can be separated by exploiting and extending of the concept of manipulability in both weak and strong senses [41], the problem remains. Another possibility to overcome the problem of a non-homogeneous Jacobian matrix is based on the apparent power concept of the robot mechanism, resulting in a homogeneous formulation of the problem, regardless of having mixed units in the velocity kinematics description [42]. However, the relation of the proposed measure to the relevant robot operational quantity such as velocity is unclear. An alternative to manipulability ellipsoids is presented by manipulability polytopes [28,43,44,45,46,47,48], which can provide more accurate information about the operational space motion capability, since they consider infinity norm metrics instead of Euclidean norm metrics. However, the problem of dimensional a non-homogeneous Jacobian matrix due to the unit inconsistency in robotics still present a challenge, since most approaches demonstrated limitations in terms of their physical interpretations, though task-oriented homogeneous Jacobians and associated performance indices showed some promising results and potential for further development [28,49].

All the performance indices above and many others not mentioned are based on the Jacobian matrix of the velocity kinematics description. In this paper, we focus on the problem of path following velocity performance in robot machining of a workpiece with complex geometry, similarly as in our previous work [28] , where we considered a workpiece with a predefined path. Now, we propose a task-oriented robot kinematics description, which considers motion constraints imposed by the workpiece surface geometry explicitly; thus, a priori knowledge about the machining path is not required to evaluate the available velocity performance. We show that the associated manipulability ellipsoid is reduced in dimension, such that we can perform velocity planning solely within the translational operational space projected on the surface tangent plane, and thus the problem is avoided of the nonhomogeneous twist space due to the mixed units. The proposed constrained kinematics description can provide a basis, not only for workpiece/robot placement optimization, but also for optimal path planning based on kinematic manipulability. We demonstrate the proposed approach by a numerical simulation case study on two different workpiece examples.

The rest of the paper is organized as follows: in Section 2 we provide the necessary background information from the surface differential geometry, in Section 3 we develop the proposed approach, in Section 4 we show the numerical experiments, and section 5 concludes the paper.

2. Background

In this Section we provide some basic information about the differential geometry of surfaces and curves on surfaces which are relevant to this paper.

Let us consider surface

S

in a three-dimensional Euclidean space that is parametrized by the position vector

r

r = [x (u, v), y (u, v), z (u, v)],

(1)

as a function in the parametric form

r = r (u, v),

(2)

where

u

and

v

are independent parameters in a closed rectangle [50,51]. In this paper, we consider an explicit surface such that the z-coordinate can be expressed as a function of both the x- and y-coordinates:

z = f (x, y),

(3)

where

f

is at least twice the differentiable real-valued function, and the parametric form is derived by setting

x = u

and

y = v

, with

[x, y] \in D

, where

D

is a bounded connected domain in the real xy-plane. The surface is then given by

r = [x, y, f (x, y)] .

(4)

A curve on the surface is given by the parametrization

x = x (t)

y = y (t)

, and

z = f (x (t), y (t))

, where

t \in [0, T]

, and with

[x, y] \in D

. Then

r = r (t)

is a curve lying on and embedded in the surface (4). The tangent vector to the curve on the surface is evaluated by differentiating

r (t)

with respect to the parameter

t

using the chain rule, and is given by:

\dot{r} (t) = r_{x} \dot{x} + r_{y} \dot{y},

(5)

where the subscripts x and y denote partial differentiation with respect to x and y such that

r_{x} = \partial r / \partial x

and

r_{y} = \partial r / \partial y

, respectively, and the dot denotes differentiation with respect to the parameter

t

, such that

\dot{x} = d x / d t

and

\dot{y} = d y / d t

. Note that (5) can be written in a form independent of the choice of parameter:

d r = r_{x} d x + r_{y} d y,

(6)

where

d (.)

denotes a differential. The differential arc length of the curve

d s

is given as:

d s = |\frac{d r}{d t}| d t = |\dot{r}| d t = \sqrt{\dot{r} \circ \dot{r}} d t,

(7)

where

\circ

stands for the vector dot product operator.

Let

P = P (x, y)

be a point on the regular surface

S

. Then

r_{x}

and

r_{y}

are two independent surface tangent vectors at point

P

, which span a tangent plane. The tangent plane at point

P

on surface

S

can be considered as a union of all tangent vectors which can be formed as a linear combination of

r_{x}

and

r_{y}

. The unit normal vector

\hat{n}

on the surface at point

P

can be defined as

\hat{n} = \hat{n} (x, y) = \frac{r_{x} \times r_{y}}{‖r_{x} \times r_{y}‖} .

(8)

The unit normal vector is mapped from the tangent vectors

r_{x}

r_{y}

. It is perpendicular to the tangent plane, and, obviously, it is also orthogonal to both

r_{x}

and

r_{y}

. Thus, at any point on the surface we have a triple of vectors

r_{x}

r_{y}

, and

\hat{n}

, that are linearly independent on the regular surface

S

. Note that the differential change of the unit normal vector can be written as:

d \hat{n} = {\hat{n}}_{x} d x + {\hat{n}}_{y} d y,

(9)

where

{\hat{n}}_{x} = \partial \hat{n} / \partial x

and

{\hat{n}}_{y} = \partial \hat{n} / \partial y

denote partial differentials of the unit normal vector with respect to x and y, respectively.

The first fundamental form describes the way of measuring the distances on a surface, i.e., a surface metric. It determines the arc length of a curve on the surface, and is defined as [51]:

Ι : d s^{2} = d r \circ d r .

(10)

If we consider (6) then it can be derived as follows

Ι (d x, d y) : d s^{2} = E d x^{2} + 2 F d x d y + G d y^{2},

(11)

where the coefficients

E = r_{x} \circ r_{x}

F = r_{x} \circ r_{y}

, and

G = r_{y} \circ r_{y}

are called the coefficients of the first fundamental form. Due to its quadratic-bilinear form of the coordinates’ differentials on the surface, it is often presented by the symmetric matrix:

Ι = [\begin{matrix} E & F \\ F & G \end{matrix}],

(12)

which is a positive definite, i.e.,

E G - F^{2} > 0

at regular points on the surface.

The second fundamental form characterizes the local structure of the surface shape in a neighborhood of a point. It describes how the surface deviates from the tangent plane. It can be defined as [51]

Ι Ι : (- d r \circ d \hat{n}),

(13)

It can be derived as

Ι Ι (d x, d y) : L d x^{2} + 2 M d x d y + N d y^{2},

(14)

where the coefficients

L = - r_{x} \circ {\hat{n}}_{x} = r_{x x} \circ \hat{n}

M = - r_{x} \circ {\hat{n}}_{y} = - r_{y} \circ {\hat{n}}_{x} = r_{x y} \circ \hat{n} = r_{y x} \circ \hat{n}

, and

N = - r_{y} \circ {\hat{n}}_{y} = r_{y y} \circ \hat{n}

are called the coefficients of the second fundamental form. The matrix of the second fundamental form can be read as:

Ι ​ Ι = [\begin{matrix} L & M \\ M & N \end{matrix}] .

(15)

The differential

d \hat{n}

is called a Weingarten map, that describes the change in the normal direction as we move from one point to another. It can be expressed in terms of the first derivatives of the position vector, and the partial derivatives of the unit normal vector can then be expressed in terms of the basis

\{r_{x}, r_{y}\}

[51,52]:

[\begin{matrix} {\hat{n}}_{x} & {\hat{n}}_{y} \end{matrix}] = - [\begin{matrix} r_{x} & r_{y} \end{matrix}] W,

(16)

where

W

is the matrix, that can be calculated by (12) and (15) as:

W = Ι^{- 1} \cdot Ι ​ Ι = \frac{1}{E G - F^{2}} [\begin{matrix} G L - F M & G M - F N \\ E M - F L & E N - F M \end{matrix}],

(17)

where the operator

\cdot

stands for matrix multiplication. The result is known as Weingarten equations:

{\hat{n}}_{x} = \frac{F M - G L}{E G - F^{2}} r_{x} + \frac{F L - E M}{E G - F^{2}} r_{y},

(18)

{\hat{n}}_{y} = \frac{F N - G M}{E G - F^{2}} r_{x} + \frac{F M - E N}{E G - F^{2}} r_{y} .

(19)

which map from the tangent plane to the tangent plane, i.e., the vectors

{\hat{n}}_{x}

and

{\hat{n}}_{y}

are expressed as a linear combination of the tangent vectors

r_{x}

r_{y}

, respectively. Thus, they lie in the tangent plane, and are orthogonal to the unit normal vector

\hat{n}

An important surface characteristic is also its curvature, which shows us how much the surface bends or deviates from a flat surface. The curvature measure should involve the rate at which surface

S

leaves the tangent plane to

S

at point

P

. A crucial tool to measure the curvature on a surface is the Weingarten map, which contains complete information about a surface’s curvature. It can be used to derive scalar measures to show how ‘curved’ the surface is at some point. There are several measures for the curvature of a surface in

ℝ^{3}

. Gauss curvature

K

and Mean curvature

H

on surface

S

at point

P

can be formulated by (20) and (21), respectively.

K = \det (W) = \frac{L N - M^{2}}{E G - F^{2}}

(20)

H = \frac{1}{2} trace (W) = \frac{E N + G L - 2 F M}{2 (E G - F^{2})}

(21)

Other measures, such as normal curvature and principal curvatures, are also possible [52].

3. Methodology

3.1. Preliminaries

The serial robot arm manipulator can be described as an open chain mechanism connecting links and joints having n- degrees-of-freedom (DOF). The base link is normally considered fixed to the ground, and the final link, with mounted end-effector, may operate freely in the robot task space. To provide all possible positions and orientations within its 3D workspace, the manipulator must have proper mechanism geometry with at least 6 DOFs. The velocity mapping from the joint space to the operational space can be described as the forward velocity kinematics model [29]:

ν = J (θ) \dot{θ},

(22)

where

J \in ℝ^{6 x n}

is the geometric Jacobian matrix in the robot`s base frame,

θ \in ℝ^{n}

and

\dot{θ} \in ℝ^{n}

are the vectors of joint positions, which define the current mechanism configuration, and their velocities, respectively. Furthermore, we denote the so-called twist vector with

ν \in ℝ^{6}

ν = [\begin{matrix} v \\ ω \end{matrix}],

(23)

which represents the combination of two physically different components:

v \in ℝ^{3}

is the vector of the end-effector linear velocity, and

ω \in ℝ^{3}

is the vector of the end-effector angular velocity. The inverse velocity kinematics problem can be defined as finding a proper solution of the joint velocity

\dot{θ}

for the given twist

ν

. Note that the twist vector is not homogeneous in physical units.

In the following, we consider a nonredundant manipulator with

n = 6

in a non-singular configuration. Although in general the joints can be of different types, we assume rotational joints without a significant loss of generality, since most modern robot manipulators use only rotary joints with one DOF.

The most widely used kinematic measure that refers to manipulator manipulability and indicates how dexterous a robot is at a given configuration

θ

is derived from the condition [30]:

{\dot{θ}}^{T} \dot{θ} \leq 1,

(24)

which maps the unit sphere in the joint velocity space to the velocity manipulability ellipsoid in the operational task space:

ν^{T} {(J J^{T})}^{- 1} ν \leq 1 .

(25)

Here, we consider that the solution to the inverse velocity kinematics can be expressed by the full rank Jacobian as:

\dot{θ} = J^{- 1} ν .

(26)

We can factorize the Jacobian matrix by Singular Value Decomposition (SVD) into

J = U Σ V^{T},

(27)

where

Σ

is a diagonal matrix with positive singular values

σ_{1} \geq σ_{2} \geq ... \geq σ_{6} > 0

on the diagonal, and

U

and

V

are unitary matrices representing the orthonormal base of the Jacobian column space

C o l (J)

and the orthonormal base of the Jacobian row space

R o w (J)

, respectively [53,54]. If we insert (27) into (25), it yields:

{(U^{T} ν)}^{T} Σ^{- 2} (U^{T} ν) \leq 1,

(28)

where

Σ^{- 2}

is a diagonal matrix with

σ_{1}^{- 2}, σ_{2}^{- 2}, ..., σ_{6}^{- 2}

on the diagonal. One can introduce a new variable

w = U^{T} ν

w = {[w_{1}, w_{2}, ..., w_{6}]}^{T}

; then (28) can be rewritten as:

w^{T} Σ^{- 2} w = \sum_{i = 1}^{6} {(\frac{w_{i}}{σ_{i}})}^{2} \leq 1,

(29)

which describes an ellipsoid geometrically with the axes` directions defined by the columns of the unitary matrix

U

, whereas the singular values

σ_{i}

determine the axes` lengths. The manipulability ellipsoid shows how far away the manipulator is from a singular configuration in a certain direction in the task space: if the manipulator is near the singular configuration, then the dexterity is low, and contrarily, if the manipulator is far from the singular configuration, then the dexterity is better. Using the manipulability ellipsoid one can quantify how close a given robot posture is to a singularity. Note that the ellipsoid is described in the 6-dimensional Euclidian space, which is not suitable for visual geometrical representation, and is not intuitive.

Although the manipulability ellipsoid is quite popular among the research community since it enables the derivation of numerous manipulability indices [55], it suffers from serious limitations, that arise due to the physical non-homogeneity of the twist vector and physical inconsistency of the Jacobian matrix [32,41].

3.2. The end-effector motion constraints

During the workpiece machining the tool tip must follow a certain path embedded to the workpiece surface. The tool path is constrained by position and orientation. In our case, we assumed that the tool must maintain orthogonal orientation to the curved workpiece surface, i.e., the tool orientation must be adjusted continuously while traveling along the path. In this Section, we derive velocity synchronization, which arises due to the constraints described above.

The tool tip must follow the position of the path embedded on the workpiece surface. Let a particle refer to the tool tip. If a particle is moving in time along the path constrained on the workpiece surface, then the particle velocity can be expressed as:

v = \dot{r},

(30)

If we consider (5), then the tool tip velocity can be derived as

v = [\begin{matrix} r_{x} & r_{y} \end{matrix}] [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}] .

(31)

Note that the tool linear velocity vector

v

is a linear combination of the tangent vectors

r_{x}

and

r_{y}

. Thus, it lies in a tangent plane of the workpiece surface. On the other side, (31) it can be read in a way that

v

is to be synchronized with the velocity vector in the xy-plane

{[\begin{matrix} \dot{x} & \dot{y} \end{matrix}]}^{T}

by the matrix

S_{v}

S_{v} = [\begin{matrix} r_{x} & r_{y} \end{matrix}],

(32)

such that we can express:

v = S_{v} [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(33)

where

S_{v} \in ℝ^{3 \times 2}

is with full rank, i.e.

rank (S_{v}) = 2

The tool orientation must be aligned by the normal vector perpendicular to the curved workpiece surface. Let a particle refer to the tool tip. If a particle is traveling along the path constrained on the workpiece surface, then, in each point of the path, the normal vector associated to the particle position can have a different orientation. Not only that the particle is translating, but also that the associated surface normal vector can rotate synchronously in this case. We can observe the velocity of the unit normal vector

\hat{n} = \hat{n} (t)

that can be described as:

\dot{\hat{n}} = ω \times \hat{n},

(34)

where

\times

refers to the vector cross product operator. If we assume reasonably that the normal vector rotation about itself is zero, then the rotation axis is orthogonal to the unit normal vector, and it lies in the surface tangent plane of the observed point on the path. Then the angular velocity of the unit normal vector can be derived as:

ω = \hat{n} \times \dot{\hat{n}} .

(35)

Since the surface normal vector dependence can be expressed as

\hat{n} = \hat{n} (x, y)

and by the application of the chain rule, we can derive:

\dot{\hat{n}} = {\hat{n}}_{x} \dot{x} + {\hat{n}}_{y} \dot{y},

(36)

and furthermore

ω = [\begin{matrix} \hat{n} \times {\hat{n}}_{x} & \hat{n} \times {\hat{n}}_{y} \end{matrix}] [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(37)

where

\dot{x}

and

\dot{y}

are linear velocities in the

x

- and

y

- Cartesian coordinates, respectively. Now we can recall the Weingarten equations (16)-(19) and after some manipulation one can derive:

ω = \frac{[\begin{matrix} r_{x} & r_{y} \end{matrix}]}{\sqrt{E G - F^{2}}} [\begin{matrix} M & N \\ - L & - M \end{matrix}] [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}] = \frac{[\begin{matrix} r_{x} & r_{y} \end{matrix}]}{\sqrt{E G - F^{2}}} (A \cdot Ι ​ Ι) [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(38)

where

Ι Ι

is the second fundamental form matrix (15), and

A

is defined as:

A = [\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}] .

(39)

The angular velocity vector

ω

is expressed by (38) as a linear combination of the tangent vectors

r_{x}

and

r_{y}

. Therefore, it belongs to the tangent plane of the workpiece surface, and it will not produce tool rotation about itself. Furthermore, the tool angular velocity vector

ω

will be synchronized with the linear velocity in the xy-plane

{[\begin{matrix} \dot{x} & \dot{y} \end{matrix}]}^{T}

by the matrix

S_{ω}

S_{ω} = \frac{[\begin{matrix} r_{x} & r_{y} \end{matrix}]}{\sqrt{E G - F^{2}}} Π = \frac{S_{v} Π}{\sqrt{E G - F^{2}}},

(40)

where we denote

Π = A \cdot Ι ​ Ι

. Thus, we can express:

ω = S_{ω} [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(41)

where

S_{ω} \in ℝ^{3 \times 2}

and its rank is

rank (S_{ω}) \leq 2

In the following, we rewrite the velocity constraints described by equations (33) and (41) such that they read as:

v_{C} = S_{v} [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(42)

and

ω_{C} = S_{ω} [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}],

(43)

where

v_{C}

and

ω_{C}

represent linear velocity and angular velocity constrained to the surface, respectively. Note that

v_{C}

(

ω_{C}

) belongs to the range-space of matrix

S_{v}

(

S_{ω}

). Furthermore, from (42) we can express

[\begin{matrix} {\dot{x}}_{C} \\ {\dot{y}}_{C} \end{matrix}] = S_{v}^{†} v_{C},

(44)

where we consider

v_{C} = {[{\dot{x}}_{C}, {\dot{y}}_{C}, {\dot{z}}_{C}]}^{T}

, and the operator

{(.)}^{†}

stands for the Moore-Penrose pseudoinverse of a matrix, such that

S_{v}^{†} = {(S_{v}^{T} S_{v}^{})}^{- 1} S_{v}^{T}

is the left pseudo-inverse of

S_{v}

. If we insert the last result into (43). It yields:

ω_{C} = S_{ω} S_{v}^{†} v_{C} = S_{C} v_{C} .

(45)

Here,

S_{C}

represents the so-called surface velocity constrained matrix, that can be expressed as:

S_{C} = S_{ω} S_{v}^{†} = \frac{S_{v} Π S_{v}^{†}}{\sqrt{E G - F^{2}}} .

(46)

Note that

S_{C} \in ℝ^{3 \times 3}

and its rank is

rank (S_{C}) \leq 2

. It maps the linear velocity vector from the surface tangent plane to the angular velocity vector on the surface tangent plane.

3.3. The constrained robot kinematics model

The velocity kinematics play a central role in the robot manipulability analysis. In this Section, we formulate the problem as seeking the inverse velocity kinematics solution of (22)-(23) considering the velocity constraints given by synchronization expressions for linear and angular velocity (42)-(46), which constrain the motion of the end-effector on the path embedded on the workpiece surface, such that the end-effector maintains normal orientation. If, furthermore, we consider the joint velocity limitation given by (24) , then it will yield the constrained manipulability ellipsoid of a reduced dimension, as we will show later.

Similarly, as in [28], the Jacobian matrix is partitioned into two submatrices, i.e., the translational submatrix

J_{T} \in ℝ^{3 \times n}

and the rotational submatrix

J_{R} \in ℝ^{3 \times n}

J = [\begin{matrix} J_{T} \\ J_{R} \end{matrix}],

(47)

such that

J_{T} \dot{θ} = v

and

J_{R} \dot{θ} = ω

, where

v

and

ω

are the linear velocity vector and the angular velocity vector in the robot operational space, respectively. In the following, we derive a solution of the velocity inverse kinematics considering the partitioned matrix(47). Baksalaray [56,57] discussed the problem of the Moore-Penrose inverse of a partitioned matrix. The application of such a solution formula in the case of the Jacobian (47) can be written by the augmented Jacobian submatrices that incorporate additional restrictions [28,41,58]:

{\tilde{J}}_{T} = J_{T} P_{R}^{n} .

(48)

{\tilde{J}}_{R} = J_{R} P_{T}^{n} .

(49)

where

P_{T}^{n} = (I - J_{T}^{†} J_{T})

and

P_{R}^{n} = (I - J_{R}^{†} J_{R})

are orthogonal projection matrices into the translational and rotational null space, respectively. Here,

I

is the identity matrix of a proper dimension. Note that the definition of

{\tilde{J}}_{T}

(

{\tilde{J}}_{R}

) imposes such a constraint that the angular (linear) velocity is additionally zero, and thus it can be called a strong translational (rotational) Jacobian matrix [41]. The inverse of the partitioned squared Jacobian (n = 6,

J \in ℝ^{6 \times 6}

) can now be expressed as the block matrix:

J^{- 1} = {[\begin{matrix} J_{T} \\ J_{R} \end{matrix}]}^{- 1} = [\begin{matrix} {\tilde{J}}_{T}^{†} & {\tilde{J}}_{R}^{†} \end{matrix}],

(50)

where

{\tilde{J}}_{T}^{†} \in ℝ^{n \times 3}

and

{\tilde{J}}_{R}^{†} \in ℝ^{n \times 3}

. We can apply the inverse Jacobian in the block form (50) in the computation of the inverse velocity kinematics solution as

\dot{θ} = J^{- 1} [\begin{matrix} v \\ ω \end{matrix}] = [\begin{matrix} {\tilde{J}}_{T}^{†} & {\tilde{J}}_{R}^{†} \end{matrix}] [\begin{matrix} v \\ ω \end{matrix}] = {\tilde{J}}_{T}^{†} v + {\tilde{J}}_{R}^{†} ω .

(51)

The solution consists of two joint velocity components: the first component

{\tilde{J}}_{T}^{†} v

is responsible for the end-effector translational motion without affecting its rotation, since it belongs to the null-space of

J_{R}

, whereas the second component

{\tilde{J}}_{R}^{†} v

is responsible solely for the end-effector rotational motion with zero contribution to its translation, since it belongs to the null-space of

J_{T}

. Indeed, if we apply the solution (51) in the forward velocity kinematics mapping (22), it yields the desired result:

\begin{matrix} J \dot{θ} = [\begin{matrix} J_{T} \\ J_{R} \end{matrix}] ({\tilde{J}}_{T}^{†} v + {\tilde{J}}_{R}^{†} ω) = [\begin{matrix} J_{T} ({(J_{T} P_{R})}^{†} v + {(J_{R} P_{T})}^{†} ω) \\ J_{R} ({(J_{T} P_{R})}^{†} v + {(J_{R} P_{T})}^{†} ω) \end{matrix}] = [\begin{matrix} J_{T} (P_{R} {(J_{T} P_{R})}^{†} v + P_{T} {(J_{R} P_{T})}^{†} ω) \\ J_{R} (P_{R} {(J_{T} P_{R})}^{†} v + P_{T} {(J_{R} P_{T})}^{†} ω) \end{matrix}] = \\ = [\begin{matrix} J_{T} P_{R} {(J_{T} P_{R})}^{†} v + J_{T} P_{T} {(J_{R} P_{T})}^{†} ω \\ J_{R} P_{R} {(J_{T} P_{R})}^{†} v + J_{R} P_{T} {(J_{R} P_{T})}^{†} ω \end{matrix}] = [\begin{matrix} I v + 0 ω \\ 0 v + I ω \end{matrix}] = [\begin{matrix} v \\ ω \end{matrix}] \end{matrix} .

(52)

Here, we exploit the well-known property of the Moore-Penrose pseudo inverse with the orthogonal projector, i.e.

{(J_{T / R} P_{R / T}^{n})}^{†} = P_{R / T}^{n} {(J_{T / R} P_{R / T}^{n})}^{†}

[54,59]; consequently,

J_{T / R} {\tilde{J}}_{T / R}^{†} = I

and

J_{T / R} {\tilde{J}}_{R / T}^{†} = 0

In the following, we replace

v

and

ω

in (51) with

v_{C}

and

ω_{C}

, respectively, and consider the expressions (42) and (43). It yields:

\dot{θ} = {\tilde{J}}_{T}^{†} v_{C} + {\tilde{J}}_{R}^{†} ω_{C} = ({\tilde{J}}_{T}^{†} S_{v} + {\tilde{J}}_{R}^{†} S_{ω}) [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}] .

(53)

Furthermore, we consider (44) , and then (53) it can be rewritten as:

{\dot{θ}}_{C} = ({\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†}) v_{C} = J_{C}^{#} v_{C},

(54)

where

{\dot{θ}}_{C}

stands for such joint velocities, which provide robot tool motion constrained on the workpiece surface, and

J_{C}^{#} \in ℝ^{n \times 3}

(with

n = 6

) denotes the so-called inverse Jacobian matrix of the constrained kinematics,

J_{C}^{#} = {\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†} .

(55)

Note that

S_{v} S_{v}^{+}

represents the orthogonal projector to the range space of matrix

S_{v}

(with the following properties

{(S_{v} S_{v}^{+})}^{2} = {(S_{v} S_{v}^{+})}^{T} = S_{v} S_{v}^{+}

), such that

v_{C} = S_{v} S_{v}^{+} v

, and from (45) it follows directly that

S_{ω} S_{v}^{+}

maps any

v_{C}

to the range space of matrix

S_{ω}

. Furthermore, if we consider the orthogonal decomposition of the operational space velocity vector

v

, such that:

v = v_{C} + v_{C}^{⊥},

(56)

where

v_{C}^{⊥} = (I - S_{v} S_{v}^{+}) v

is orthogonal to

v_{C}

, i.e.

v_{C}^{⊥} ⊥ v_{C}

, then it is easy to show that (54) it can also be written as:

{\dot{θ}}_{C} = ({\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†}) v = J_{C}^{#} v

(57)

since matrix

J_{C}^{#}

maps the velocity component vector

v_{C}^{⊥}

to zero:

\begin{matrix} J_{C}^{#} v_{C}^{⊥} = ({\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†}) (I - S_{v} S_{v}^{†}) v = ({\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} (I - S_{v} S_{v}^{†}) + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†} (I - S_{v} S_{v}^{†})) v = \\ = ({\tilde{J}}_{T}^{†} (S_{v} S_{v}^{†} - (S_{v} S_{v}^{†}) 2) + {\tilde{J}}_{R}^{†} S_{ω} (S_{v}^{†} - S_{v}^{†} S_{v} S_{v}^{†})) v = ({\tilde{J}}_{T}^{†} (S_{v} S_{v}^{†} - S_{v} S_{v}^{†}) + {\tilde{J}}_{R}^{†} S_{ω} (S_{v}^{†} - S_{v}^{†})) v = 0 \end{matrix} .

(58)

Finally, we show that the derived solution above provides such velocities in the operational robot space, which are constrained to the workpiece tangent plane. It is rather straightforward to derive that the forward velocity kinematics mapping (22) on

{\dot{θ}}_{C}

results as

J {\dot{θ}}_{C} = J (J_{C}^{#} v_{C}) = [\begin{matrix} J_{T} \\ J_{R} \end{matrix}] ({\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†}) v_{C} = [\begin{matrix} J_{T} {\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + J_{T} {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†} \\ J_{R} {\tilde{J}}_{T}^{†} S_{v} S_{v}^{†} + J_{R} {\tilde{J}}_{R}^{†} S_{ω} S_{v}^{†} \end{matrix}] v_{C} = [\begin{matrix} S_{v} S_{v}^{†} \\ S_{ω} S_{v}^{†} \end{matrix}] v_{C} = [\begin{matrix} v_{C} \\ ω_{C} \end{matrix}]

(59)

which confirms the solution described by (54), (55) and (57) provides the desired constrained motion (42)-(43) in the robot operational space. Furthermore, if we consider that the inverse Jacobian of the constrained kinematics can also be represented as

J_{C}^{#} = (J^{- 1} S) S_{v}^{†}

, where

S^{T} = [\begin{matrix} S_{v}^{T} & S_{ω}^{T} \end{matrix}]

, it can also be shown easily that its rank equals

rank (J_{C}^{#}) = 2

; on the basis of the Sylvester rank inequality formula [60] it is possible to derive

rank (J^{- 1} S) = 2

and in the following also

rank ((J^{- 1} S) S_{v}^{†}) = 2

, since the matrix

S_{v}^{†}

is of full rank, i.e.

rank (S_{v}^{†}) = 2

3.4. The manipulability ellipsoid of the constrained motion

Now, we can construct the manipulability ellipsoid of the constrained motion following a procedure that is similar to the steps determined by (24)-(29). Firstly, we consider the constraint in the joint space given by the condition (24) , that is derived as:

{\dot{θ}}^{T} \dot{θ} = v^{T} (J_{C}^{#}^{T} J_{C}^{#}) v \leq 1,

(60)

where

J_{C}^{#}

is defined by (55). In the next step, we can factorize matrix

J_{C}^{#}

by SVD into

J_{C}^{#} = U Σ V^{T} .

(61)

However, due to the fact that the matrix is tall and its rank is deficient

r = rank (J_{C}^{#}) = 2

, the factorized matrices

U

Σ

and

V

have the following structure:

U = [\begin{matrix} U_{1} & U_{2} \end{matrix}], Σ = [\begin{matrix} Σ_{1} & 0 \\ 0 & 0 \end{matrix}], and V = [\begin{matrix} V_{1} & V_{2} \end{matrix}]

(62)

respectively. Here, the columns of

U_{1}

represent an orthonormal base of the column space

C o l (J_{C}^{#})

, whereas the columns of

U_{2}

represent an orthonormal base of the left null space

N u l l (J_{C}^{#}^{T})

. Furthermore, the columns of

V_{1}

represent an orthonormal base of the row space

R o w (J_{C}^{#})

, whereas the columns of

V_{2}

represent an orthonormal base of the null space

N u l l (J_{C}^{#})

. The (sub)matrices` dimensions are

\dim (U_{1}) = n \times r

\dim (U_{2}) = n \times (n - r)

\dim (V_{1}) = 3 \times r

\dim (V_{2}) = 3 \times (3 - r)

and

\dim (Σ_{1}) = r \times r

, respectively. Note that

U

and

V

are unitary matrices with orthonormal columns, and

Σ_{1}

is a diagonal square matrix with the positive singular values

σ_{1} \geq ... \geq σ_{r} > 0

on the diagonal. We can derive:

J_{C}^{#} = [\begin{matrix} U_{1} & U_{2} \end{matrix}] Σ = [\begin{matrix} Σ_{1} & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} V_{1}^{T} \\ V_{2}^{T} \end{matrix}] = U_{1} Σ_{1} V_{1}^{T},

(63)

and further

J_{C}^{#}^{T} J_{C}^{#} = {(U_{1} Σ_{1} V_{1}^{T})}^{T} (U_{1} Σ_{1} V_{1}^{T}) = (V_{1} Σ_{1} U_{1}^{T}) (U_{1} Σ_{1} V_{1}^{T}) = V_{1} Σ_{1} U_{1}^{T} U_{1} Σ_{1} V_{1}^{T} = V_{1} Σ_{1}^{2} V_{1}^{T} .

(64)

Thus, (60) it can be rewritten as

v^{T} V_{1} Σ_{1}^{2} V_{1}^{T} v \leq 1 .

(65)

If we introduce a new variable of reduced order

w = V_{1}^{T} v

, then it yields the ellipsoid,

w_{}^{T} Σ_{1}^{2} w \leq 1

(66)

that can be rewritten as

\frac{w_{1}^{2}}{σ_{1}^{- 2}} + \frac{w_{2}^{2}}{σ_{2}^{- 2}} \leq 1,

(67)

since

r = 2

, and thus

w_{}^{T} = [\begin{matrix} w_{1}^{} & w_{2}^{} \end{matrix}]

diag (Σ_{1}) = [\begin{matrix} σ_{1} & σ_{2} \end{matrix}]

. Obviously, the constrained manipulability ellipsoid is reduced to an ellipse in the tangent plane of the workpiece surface.

4. Numerical Experiments and Discussion

In this Section we show the results of some numerical experiments that we performed in order to verify the proposed approach of the robot manipulability evaluation in the case of the robot tool motion constrained by the workpiece surface. In the numerical experiments we applied a collaborative robot arm and two workpiece models with different surface characteristics. In the following, we firstly introduce the experimental setup. Then, we show the ellipsoids related to the velocity synchronization on the workpiece surface, which can be derived from (45)-(46). Next, we present the manipulability ellipsoids of the robot motion with the tool constrained to the surface geometry derived from (54)-(55), and it is described further in Section 3.4. Finally, we verify the drawn manipulability ellipsoids by the calculation of the robot tool velocity in selected directions. The numerical experiments were performed by the MATLAB computing environment [61].

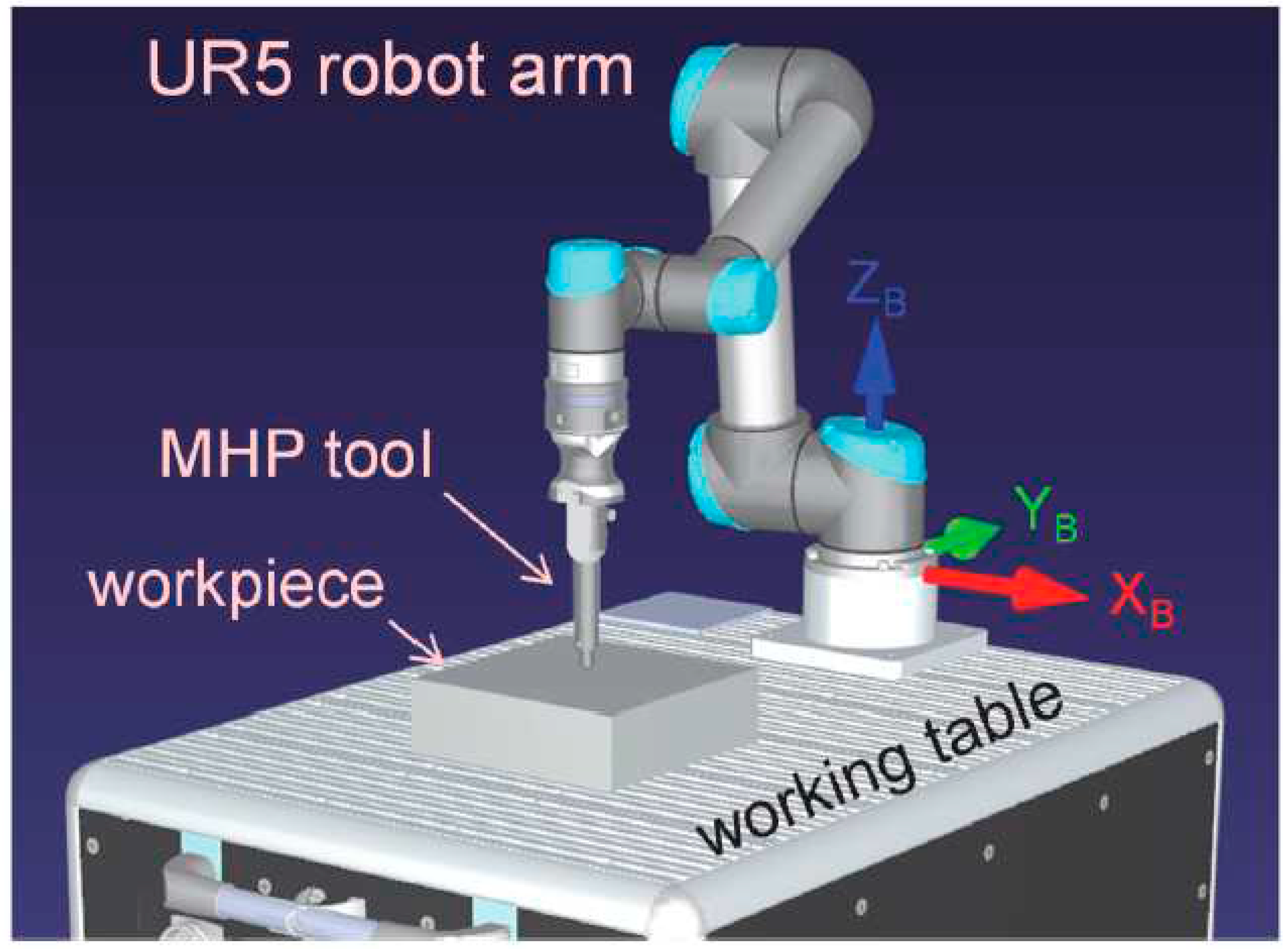
4.1. Experimental setup

The robotic setup is shown in Figure 1. We applied a collaborative robot arm UR5 with a reach radius of 850 (mm); the kinematic parameters of the robot arm are available in reference [62]. The reference robot frame is shown by the red-green-blue axes located at the robot base. The MHP tool length was modeled as 284.5 (mm). The workpiece size was 250 x 250 x 75 (mm), and was placed with its center of the bottom face at the point [0, -525, -97] (mm) of the reference robot frame. In our numerical experiments, we applied two workpiece surface models, i.e., Workpiece surface model No.1 (WP1) and Workpiece surface model No.2 (WP2), which are shown by Figure 2 and Figure 3, respectively. WP1 had a relatively monotone curvature, while WP2 had a more vivid curvature. The colormap shown on the workpiece surface is coded by its height.

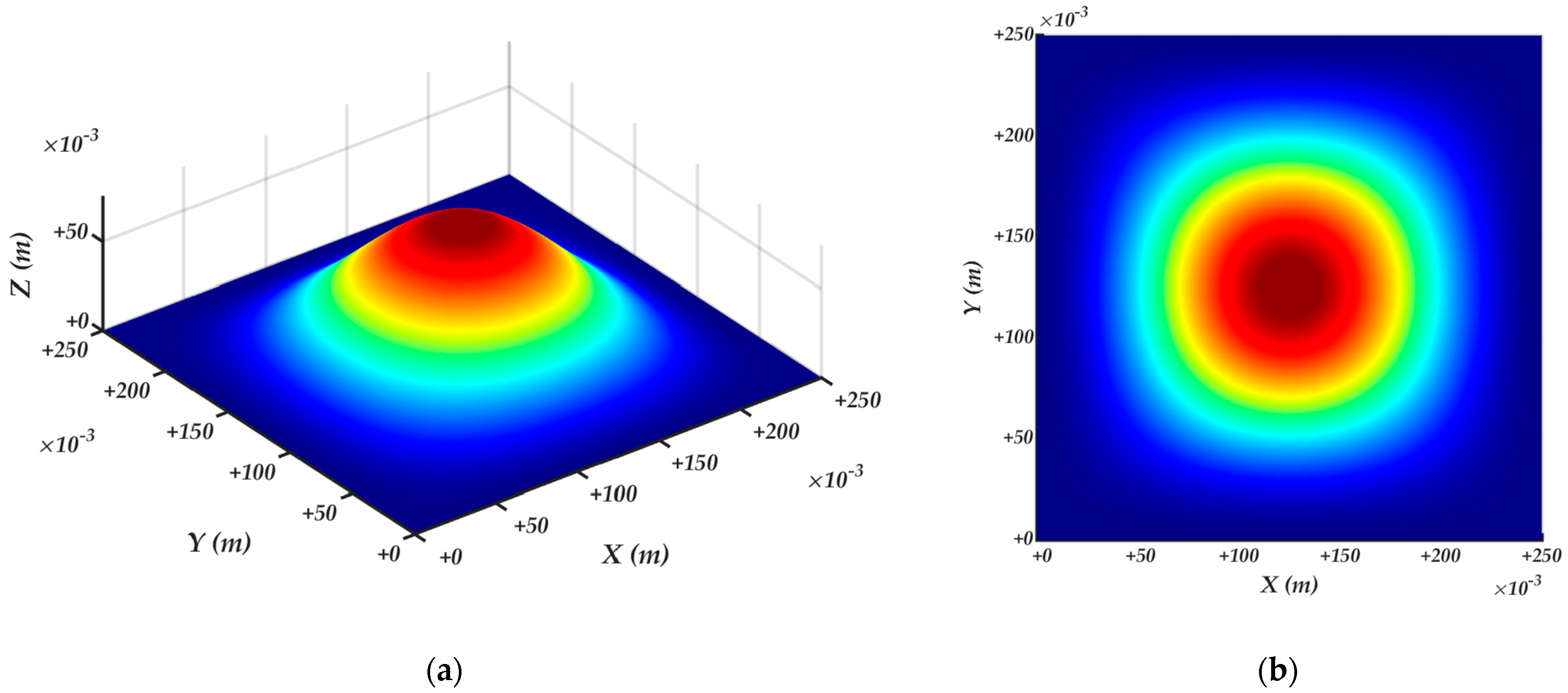
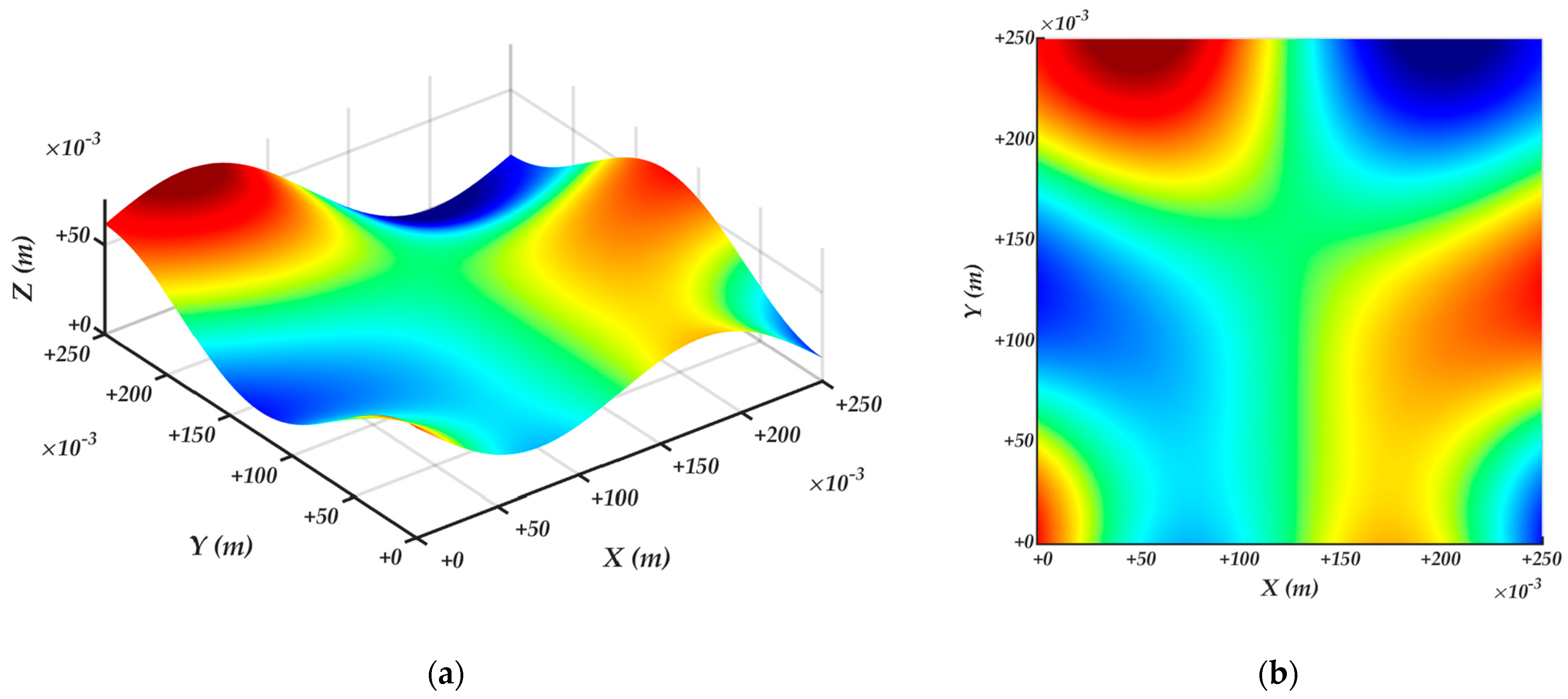
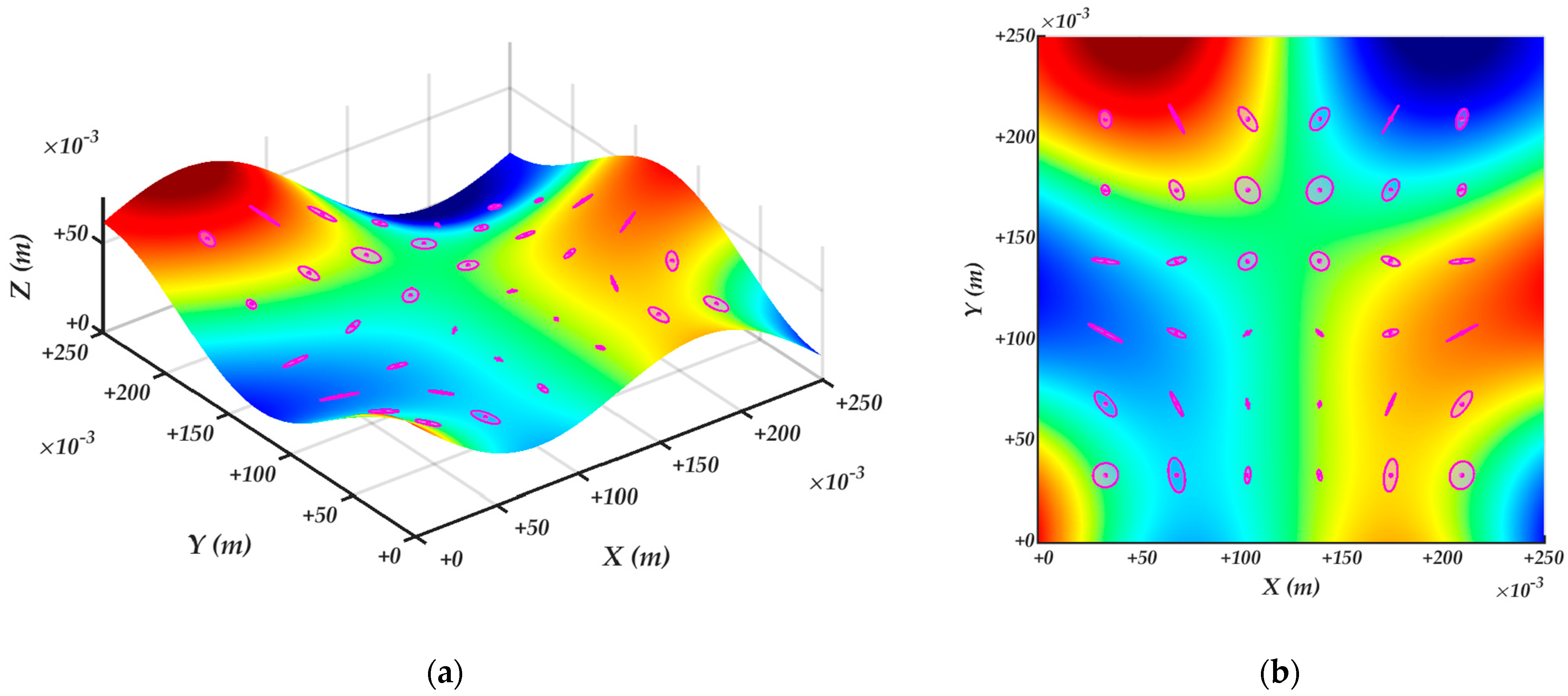
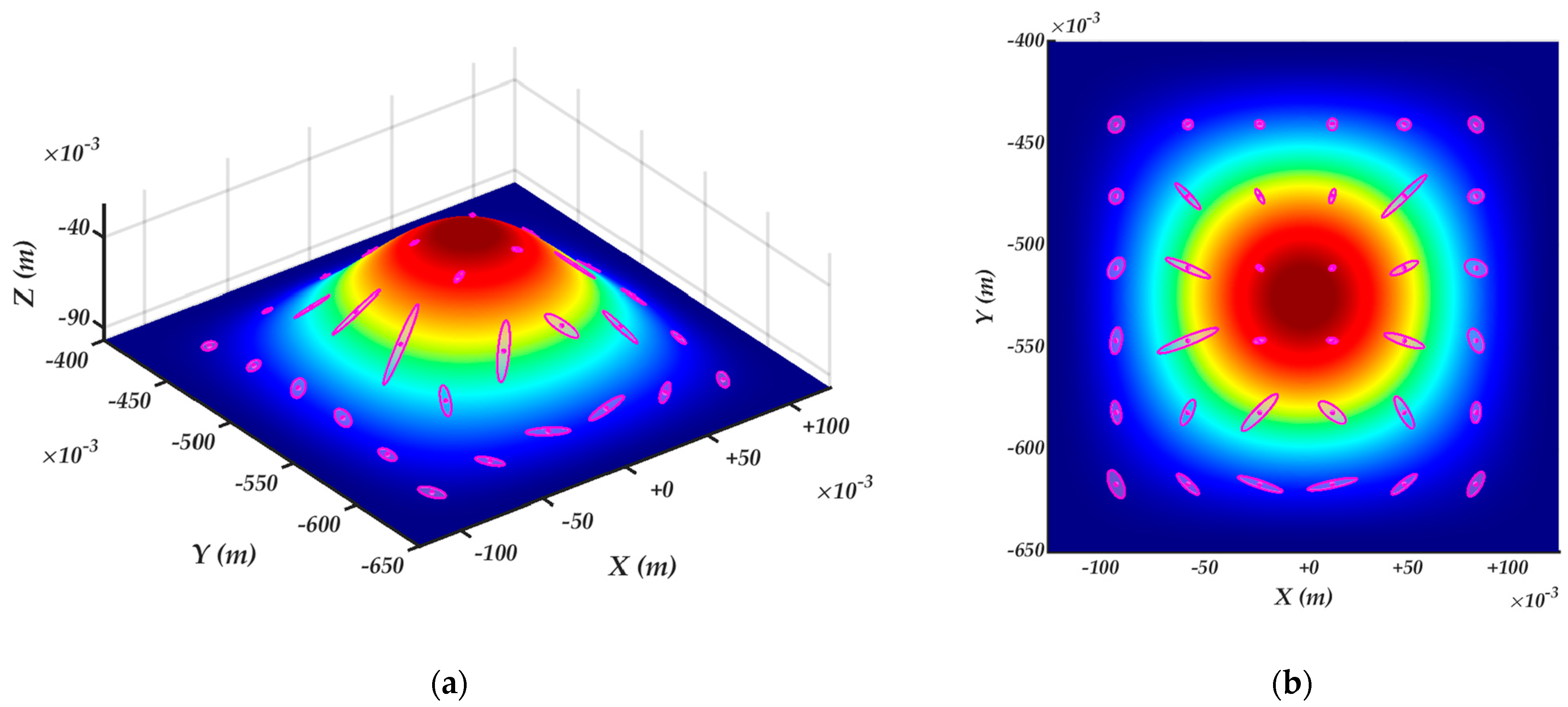
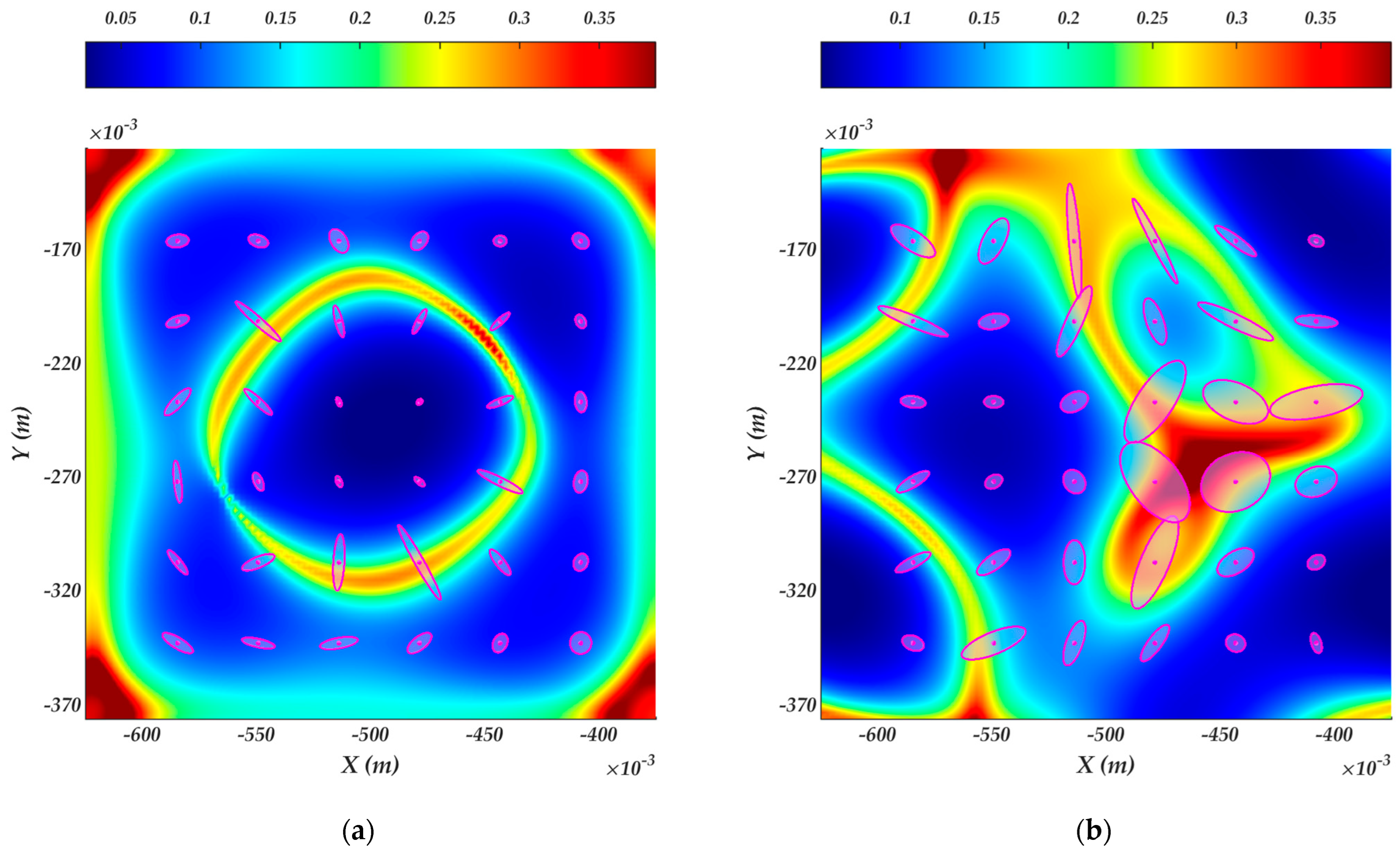
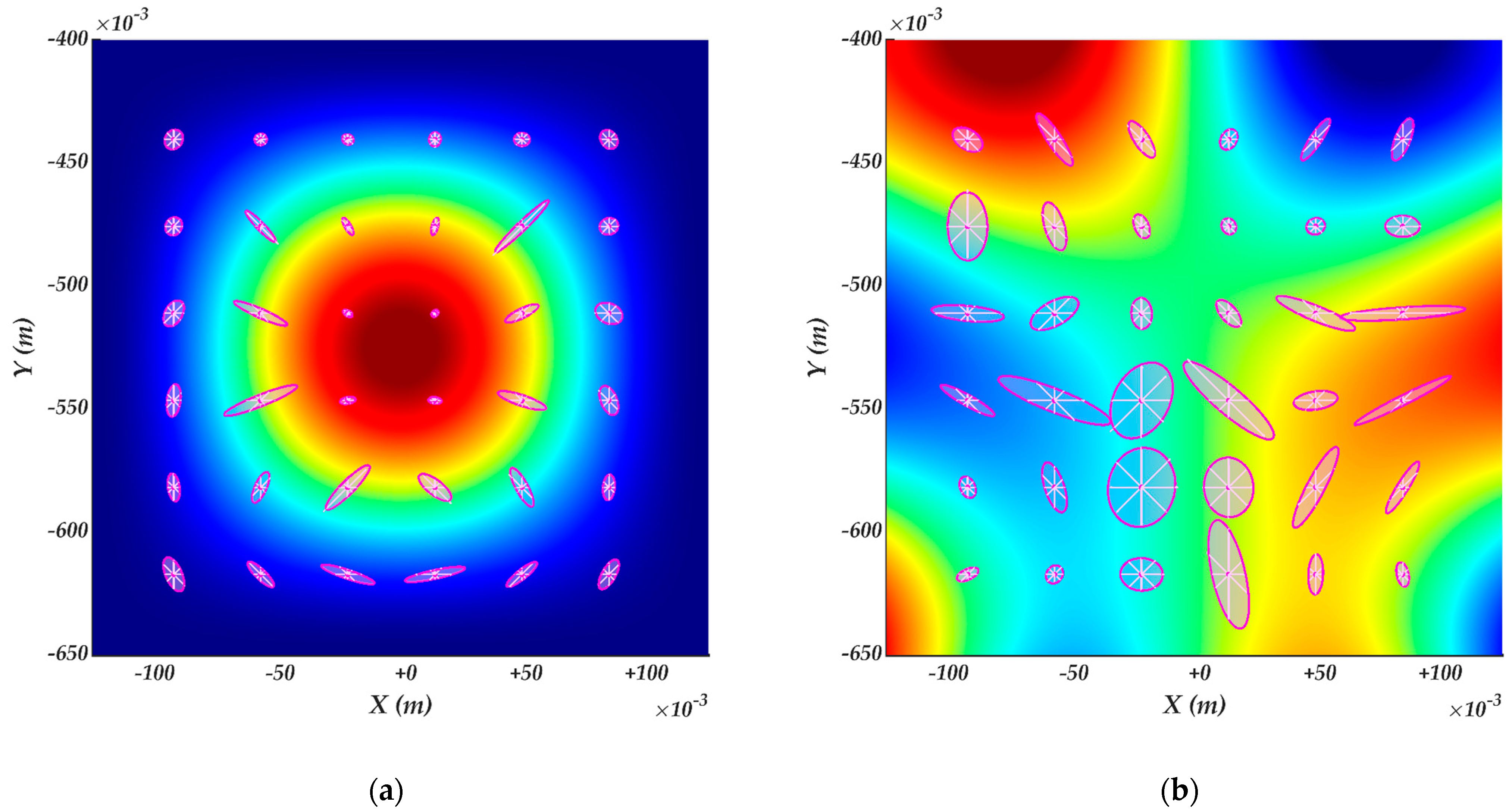
4.2. Surface velocity ellipsoids

The ellipsoids related to the velocity synchronization on the workpiece surface are presented by Figure 4, Figure 5 and Figure 6. They are developed in the selected points on the workpieces’ surface, and represent the omnidirectional angular velocity (

ω_{C}

) performance of a particle moving along the path constrained on the workpiece surface under the condition

‖v_{C}‖ \leq 1

. The surface velocity synchronization ellipsoids, which can be derived from (45)-(46), are shown firstly by Figure 4 for WP1 and Figure 5 for WP2. The ellipsoids are clearly of reduced dimension, such that they convert to ellipses and appear in the tangent planes attached to the selected points on the surface. The shown ellipses were all scaled by the factor of 0.00075. The angular velocity ellipses were of different sizes and eccentricity. Thus, the angular velocity performance depended both on the selected direction of the linear movement, and on the geometry of the close neighborhood of the selected point on the workpiece surface. If a big ellipse similar to a circle was drawn, then a relatively high angular velocity would occur in all directions of the linear movement. In the case of an eccentric ellipse, the highest angular velocity would occur in the direction of the major ellipse axis, and the lowest in the direction of the minor ellipse axis. The angular velocity performance depends highly on the surface slope (the surface gradient of the first order), its gradient (the surface gradient of the second order), and, thus, on the surface curvature.

The same angular velocity ellipses are again shown in Figure 6. However, in this case, the surface colormap is coded by its Mean curvature measure. A red/blue color means a high/low curvature measure value. It can be observed clearly that the drawn ellipses’ characteristics correspond highly to the surface curvature measure at the selected points on both WP1 and WP2: at the surface points with low value of the curvature measure, we can notice small ellipses, whereas at the surface points with high value of the surface curvature measure, we can see big ellipses; in the case of the medium value curvature points, we can observe medium size ellipses, or ellipses with a longer major axis (and a medium average axes` length), that again match with the average curvature at the surface point. We can conclude that the angular velocity ellipses shown obviously correlate with the surface curvature characteristics.

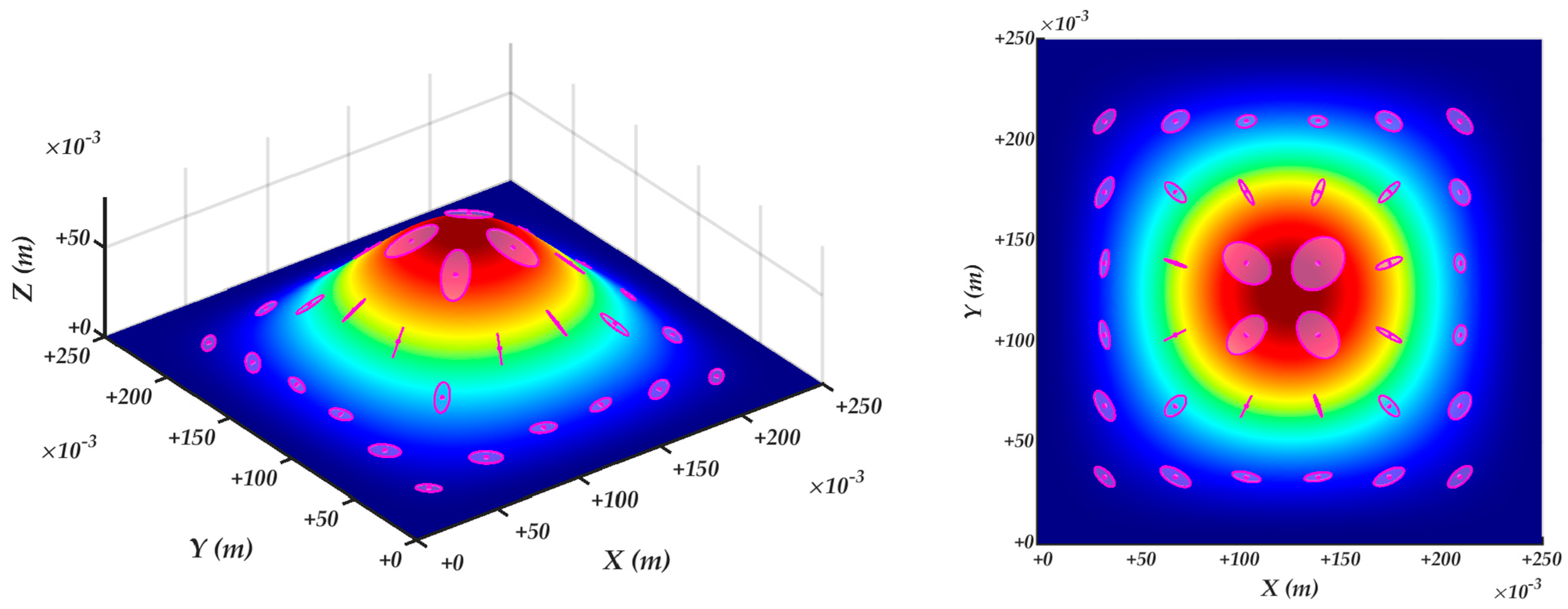
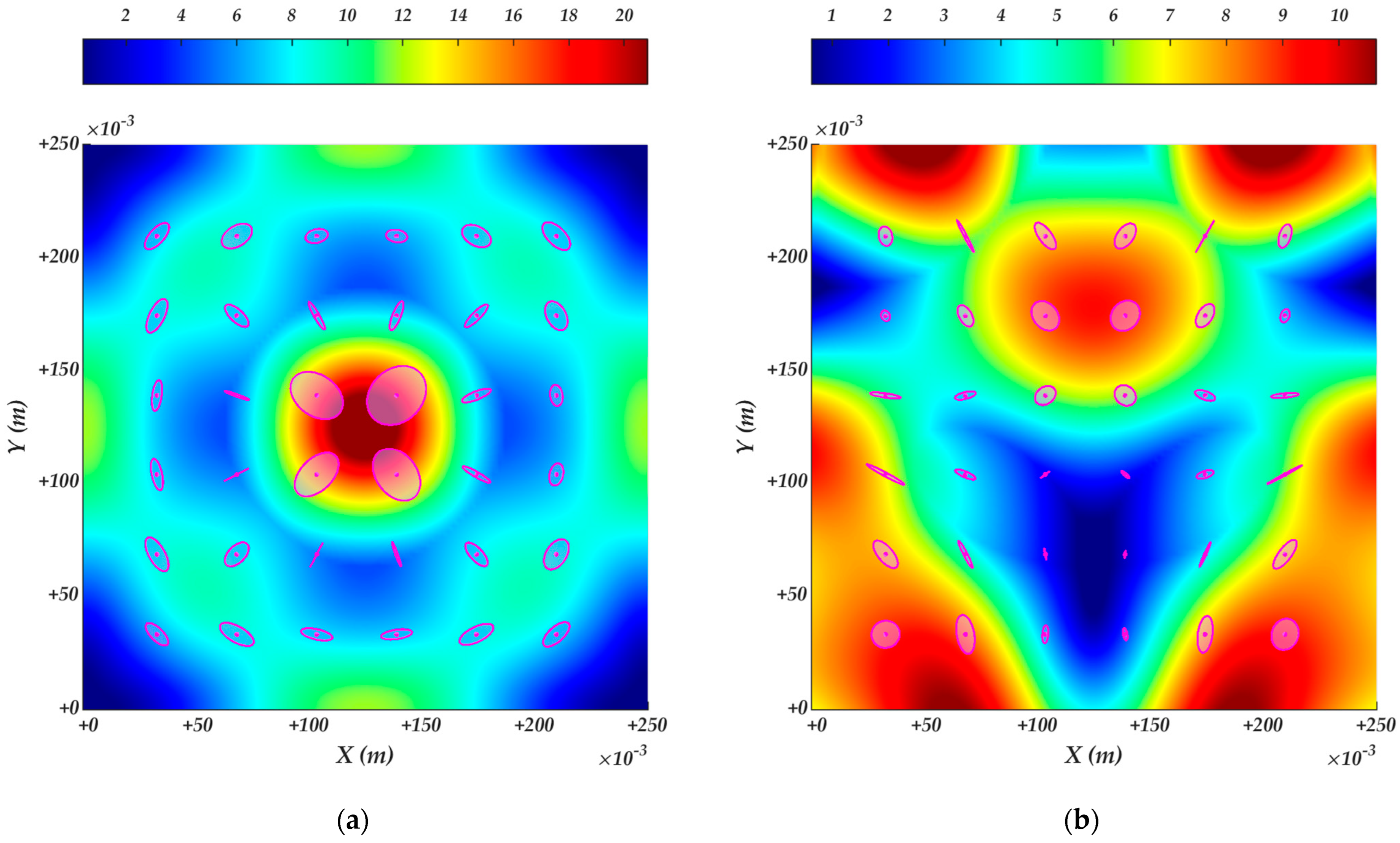
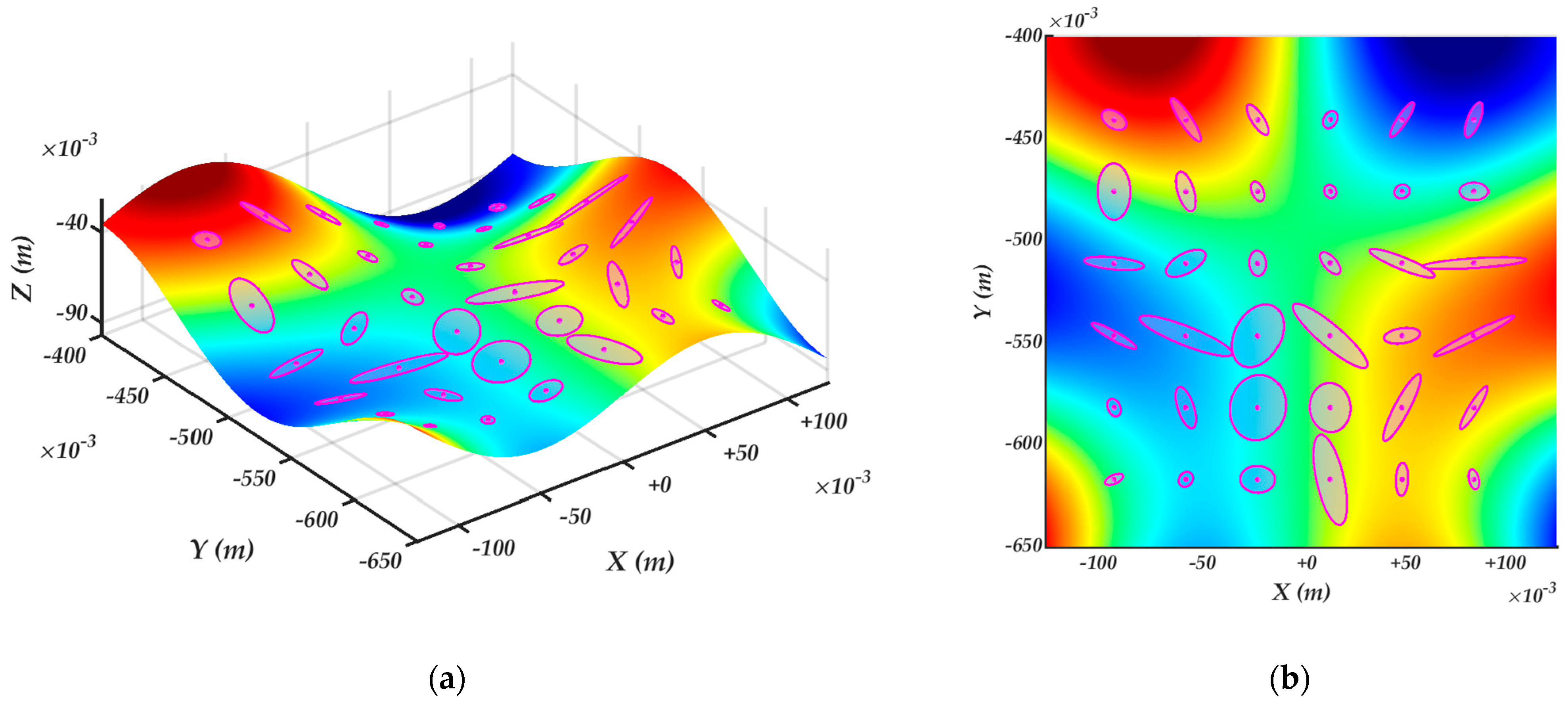
4.3. Robot manipulability ellipsoids of the constrained kinematics

The ellipsoids related to the robot translational velocity along the path constrained on the workpiece with a curved surface and with the robot tool orientation normal to the surface are presented by Figure 7, Figure 8, Figure 9 and Figure 10. They express the robot linear velocity performance at the positions in the robot operational space determined by the selected points on the workpiece surface under the condition of unity Euclidian norm of the robot joint velocities

‖\dot{q}‖ \leq 1

. The constrained manipulability ellipsoids, which can be derived from (54)-(55), are shown firstly by Figure 7 for WP1 and Figure 8 for WP2. The ellipsoids are again clearly of reduced dimensions, such that they convert to ellipses and appear in the tangent planes attached to the selected points on the surface. The shown ellipses were all scaled by a factor of 0.05.

At the bottom of WP1, all around in Figure 7 (b), we can see ellipses with different sizes and orientations. Most of them are of medium size; some ellipses at the bottom side of the picture are longer and thinner, that determines a larger linear velocity performance in the direction of the ellipses’ major axes, and poorer in the direction of the minor axes; however, on the upper side of the picture the ellipses are of small size, which is connected to poor linear velocity performance in all directions. Along the slope of WP1 we can see many rather long ellipses, with a major axis directed towards the top of the workpiece; it means that a straightway motion from the bottom to the top of the surface would be allowed at relatively high speed. Finally, on the top of the workpiece we can observe very small velocity ellipses, since the surface in this area changed rapidly.

The velocity manipulability ellipsoids on WP2, with more vivid curvature surface in Figure 8, are with different sizes, orientations, and widths. Their shape depends on the surface characteristics at the specific point and the specific robot configuration required to provide the robot tool position and orientation that comply with the imposed surface constraints. Some big/medium size and only slightly eccentric ellipses, which can be observed mostly in the bottom half of the surface presented by Figure 8 (b), allow for high/medium linear omnidirectional velocity performance along the tangent planes attached to certain surface points. Thin ellipses on highs at the right side and in lows at the left side provide better velocity performance in certain directions determined by the ellipses’ major axis. Many small size ellipses at different points all around the workpiece surface show only poor linear velocity performance.

A more detailed insight into the linear velocity performance is presented by Figure 9, where the surface colormap is coded by the mean (average) value of the ellipses’ minor and major axes` lengths at all surface definition points. The red/blue color means roughly good/bad velocity manipulability. Figures 9 (a)/(b) show the surface constrained robot velocity manipulability for WP1/WP2. These characteristics can be used as a robot tool velocity regulation map on the surface at a certain workpiece location, since they incorporate not only robot kinematics performance, but also the workpiece surface curvature feature.

Finally, we verified the presented velocity ellipses for both WP1 and WP2. In the verification procedure we simply calculated the robot tool linear velocity of maximal possible speed that can be achieved under condition

‖\dot{q}‖ \leq 1

during the motion along the path from the selected point to a certain neighboring point. In every ellipse we selected 8 neighboring points around the ellipse center point. In order to determine the maximum linear speed, we applied the following formula:

V_{\max} = \frac{1}{{‖{\tilde{J}}_{T}^{+} u_{T} + h^{- 1} {\tilde{J}}_{R}^{+} u_{R}‖}_{2}},

(68)

where

u_{T}

and

u_{R}

are linear and angular directions along the path, whereas the parameter

h

is related to the surface shape/curvature in our case, and can be calculated as

h = s / φ

where

s

and

φ

stand for linear path length and rotational path length (angle), respectively. The formula above is similar to the DTF method formula [28], however, please note that the DTF method employs the infinity norm in the denominator, whereas we used the Euclidean L2 norm. The verification results for WP1/WP2 are shown by Figures 10 (a)/(b). Here, the surface colormap is coded by the surface height. Again, we can see the before mentioned manipulability ellipses, as in Figure 7 and Figure 8. Beside these, there are the verification linear velocity vectors drawn in the bright pale pink color. They were all scaled by the factor of 0.05, which is of the same value as the manipulability ellipses` scaling factor. We can observe that the vector lines drawn from the ellipses’ center point end at the ellipses’ edge. Thus, they correspond to the velocities, which could be determined from the manipulability ellipses in the verification directions, and therefore confirm the correctness of the presented manipulability ellipses of the robot kinematics imposed by the workpiece surface constraints.

5. Conclusions

In this paper, we discussed the robot kinematics` capability and velocity performance in the case of workpiece machining. We consider such machining tasks as the hammer-peening workpiece surface polishing, in which the robot tool is required to follow a prescribed path on the workpiece with zero exerted force in the path direction that enforces certain kinematics constraints to the robot`s motion. In the presented study, we have considered a workpiece with complex surface characteristics, to derive the robot`s constrained kinematics description. Thus, we introduced a so-called surface velocity constrained matrix, which describes the synchronization of the linear velocity and the angular velocity constrained on the surface tangent plane. The surface velocity synchronization was then applied in the derivation of the constrained robot kinematics. The derived Jacobian kinematics matrix with incorporated workpiece surface constraints was, in the following, used for the ellipsoid-based manipulability analysis. We have shown that, in this case, the general non-homogeneous 6-dimensional manipulability ellipsoids, which mix different units of linear velocity and angular velocity, can be reduced to the 2-dimensional ellipses in the homogeneous space of translational motion. The results from the theoretical development have been proven by numerical experiments. In the future, the presented approach of the surface-based constrained manipulability can be employed in the kinematic optimization of the robot-workpiece position and planning of the optimal robot machining path. Furthermore, future experimental validation may include real world manufacturing examples in a real robotic cell with a collaborative robot.

Funding

This research was funded by the Slovenian Research Agency (ARRS) under a Grant for the Research Program P2–0028, and in part by a Project of the Republic of Slovenia and the European Union from the European Regional Development Fund, ROBOTOOL-1, Grant number OP20.03540.

Conflicts of Interest

The author declares no conflict of interest.

References

International Federation of Robotics: World Robotics Industrial Robots. Available online: https://ifr.org/worldrobotics (accessed on August 8th, 2023).
Magrini, E.; Ferraguti, F.; Ronga, A.J.; Pini, F.; De Luca, A.; Leali, F. Human-robot coexistence and interaction in open industrial cells. Robotics and Computer-Integrated Manufacturing 2020, 61, 101846. [Google Scholar] [CrossRef]
Taesi, C.; Aggogeri, F.; Pellegrini, N. COBOT Applications: Recent Advances and Challenges. Robotics 2023, 12. [Google Scholar] [CrossRef]
Gajšek, B.; Stradovnik, S.; Hace, A. Sustainable Move towards Flexible, Robotic, Human-Involving Workplace. Sustainability 2020, 12. [Google Scholar] [CrossRef]
Weidemann, C.; Mandischer, N.; van Kerkom, F.; Corves, B.; Hüsing, M.; Kraus, T.; Garus, C. Literature Review on Recent Trends and Perspectives of Collaborative Robotics in Work 4.0. Robotics 2023, 12. [Google Scholar] [CrossRef]
Aivaliotis, P.; Aivaliotis, S.; Gkournelos, C.; Kokkalis, K.; Michalos, G.; Makris, S. Power and force limiting on industrial robots for human-robot collaboration. Robotics and Computer-Integrated Manufacturing 2019, 59, 346–360. [Google Scholar] [CrossRef]
Ji, W.; Wang, L. Industrial robotic machining: a review. The International Journal of Advanced Manufacturing Technology 2019, 103, 1239–1255. [Google Scholar] [CrossRef]
Qu, X.; Wan, M.; Shen, C.-J.; Zhang, W.-H. Profile error-oriented optimization of the feed direction and posture of the end-effector in robotic free-form milling. Robotics and Computer-Integrated Manufacturing 2023, 83, 102580. [Google Scholar] [CrossRef]
Onstein, I.F.; Bjerkeng, M.; Martinsen, K. Automated Tool Trajectory Generation for Robotized Deburring of Cast Parts Based on 3D Scans. Procedia CIRP 2023, 118, 507–512. [Google Scholar] [CrossRef]
Bogue, R. Finishing robots: a review of technologies and applications. Industrial Robot: An International Journal 2009, 36, 6–12. [Google Scholar] [CrossRef]
Yang, J.; Chen, H.; Qi, R.; Ding, H.; Yin, Y. A novel approach to robotic grinding guaranteeing profile accuracy using rigid-flexible coupling force control for free-formed surfaces. CIRP Annals 2023, 72, 313–316. [Google Scholar] [CrossRef]
Kharidege, A.; Ting, D.T.; Yajun, Z. A practical approach for automated polishing system of free-form surface path generation based on industrial arm robot. The International Journal of Advanced Manufacturing Technology 2017, 93, 3921–3934. [Google Scholar] [CrossRef]
Ke, X.; Yu, Y.; Li, K.; Wang, T.; Zhong, B.; Wang, Z.; Kong, L.; Guo, J.; Huang, L.; Idir, M.; et al. Review on robot-assisted polishing: Status and future trends. Robotics and Computer-Integrated Manufacturing 2023, 80, 102482. [Google Scholar] [CrossRef]
Bleicher, F.; Lechner, C.; Habersohn, C.; Kozeschnik, E.; Adjassoho, B.; Kaminski, H. Mechanism of surface modification using machine hammer peening technology. CIRP Annals 2012, 61, 375–378. [Google Scholar] [CrossRef]
Hagen, L.; Baumann, J.; Heidelmann, M.; Biermann, D.; Tillmann, W. Machine Hammer Peening and Its Effect on the Surface Integrity of Arc-Sprayed WC-W2C-FeCMnSi Coatings. Coatings 2023, 13, 1563. [Google Scholar] [CrossRef]
Schulze, V.; Bleicher, F.; Groche, P.; Guo, Y.B.; Pyun, Y.S. Surface modification by machine hammer peening and burnishing. CIRP Annals 2016, 65, 809–832. [Google Scholar] [CrossRef]
Hähnel, S.; Pini, F.; Leali, F.; Dambon, O.; Bergs, T.; Bletek, T. Reconfigurable Robotic Solution for Effective Finishing of Complex Surfaces. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), 4-7 Sept. 2018; 2018; pp. 1285–1290. [Google Scholar]
KUKA. Surface processing with a KR QUANTEC and KUKA.CNC. Available online: https://www.kuka.com/en-de/industries/solutions-database/2016/07/solution-robotics-sematek (accessed on 9th August 2023).
Robotmaster. Offline Programming Software is Single Solution for Robotic Hammer Peening of Automotive Stamping Dies. Available online: https://www.roboticstomorrow.com/article/2017/12/offline-programming-software-is-single-solution-for-robotic-hammer-peening-of-automotive-stamping-dies/11173 (accessed on August 9th, 2023).
Weingartshofer, T.; Bischof, B.; Meiringer, M.; Hartl-Nesic, C.; Kugi, A. Optimization-based path planning framework for industrial manufacturing processes with complex continuous paths. Robotics and Computer-Integrated Manufacturing 2023, 82, 102516. [Google Scholar] [CrossRef]
Nektarios, A.; Aspragathos, N.A. Optimal location of a general position and orientation end-effector's path relative to manipulator's base, considering velocity performance. Robotics and Computer-Integrated Manufacturing 2010, 26, 162–173. [Google Scholar] [CrossRef]
Doan, N.C.N.; Lin, W. Optimal robot placement with consideration of redundancy problem for wrist-partitioned 6R articulated robots. Robotics and Computer-Integrated Manufacturing 2017, 48, 233–242. [Google Scholar] [CrossRef]
Xia, Y.; Zhao, L.; Liu, Z.; Zhu, K. Optimization of Machining Position for Wheel Hub Polishing Robot Based on the Kinematic Index. In Proceedings of the 2022 8th International Conference on Control, Automation and Robotics (ICCAR), 8-10 April 2022; 2022; pp. 155–160. [Google Scholar]
Weingartshofer, T.; Hartl-Nesic, C.; Kugi, A. Optimal TCP and Robot Base Placement for a Set of Complex Continuous Paths. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), 30 May-5 June 2021; 2021; pp. 9659–9665. [Google Scholar]
Malhan, R.K.; Kabir, A.M.; Shah, B.; Gupta, S.K. Identifying Feasible Workpiece Placement with Respect to Redundant Manipulator for Complex Manufacturing Tasks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), 20-24 May 2019; 2019; pp. 5585–5591. [Google Scholar]
Malhan, R.K.; Shembekar, A.V.; Kabir, A.M.; Bhatt, P.M.; Shah, B.; Zanio, S.; Nutt, S.; Gupta, S.K. Automated planning for robotic layup of composite prepreg. Robotics and Computer-Integrated Manufacturing 2021, 67, 102020. [Google Scholar] [CrossRef]
Balci, B.; Donovan, J.; Roberts, J.; Corke, P. Optimal Workpiece Placement Based on Robot Reach, Manipulability and Joint Torques. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023, 29 May-2 June 2023; 2023; pp. 12302–12308. [Google Scholar]
Stradovnik, S.; Hace, A. Task-Oriented Evaluation of the Feasible Kinematic Directional Capabilities for Robot Machining. Sensors 2022, 22. [Google Scholar] [CrossRef]
Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: 2017.
Yoshikawa, T. Manipulability of Robotic Mechanisms. International Journal of Robotics Research 1985, 4, 3–9. [Google Scholar] [CrossRef]
Klein, C.A.; Blaho, B.E. Dexterity Measures for the Design and Control of Kinematically Redundant Manipulators. The International Journal of Robotics Research 1987, 6, 72–83. [Google Scholar] [CrossRef]
Schwartz, E.; Manseur, R.; Doty, K. Noncommensurate systems in robotics. Int. J. Robot. Automat. 2002, 17, 86–92. [Google Scholar]
Melchiorri, C.; Chiaccio, P.; Chiaverini, S.; Sciavicco, L.; Siciliano, B. Comments on "Global task space manipulability ellipsoids for multiple-arm systems" and further considerations" [with reply] P. Chiacchio, et al. IEEE Transactions on Robotics and Automation 1993, 9, 232–236. [Google Scholar] [CrossRef]
Gosselin, C.M. The optimum design of robotic manipulators using dexterity indices. Robotics and Autonomous Systems 1992, 9, 213–226. [Google Scholar] [CrossRef]
Dubey, R.; Luh, J.Y.S. Redundant robot control using task based performance measures. Journal of Robotic Systems 1988, 5, 409–432. [Google Scholar] [CrossRef]
Vahrenkamp, N.; Asfour, T.; Metta, G.; Sandini, G.; Dillmann, R. Manipulability analysis. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), 29 Nov.-1 Dec. 2012; 2012; pp. 568–573. [Google Scholar]
Chiu, S.L. Task Compatibility of Manipulator Postures. International Journal of Robotics Research 1988, 7, 13–21. [Google Scholar] [CrossRef]
Wang, Y.; Wang, L. Reactive task-oriented redundancy resolution using constraint-based programming. 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 2016, 5689-5694.
Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Transactions on Robotics and Automation 1995, 11, 462–468. [Google Scholar] [CrossRef]
Staffetti, E.; Bruyninckx, H.; De Schutter, J. On the Invariance of Manipulability Indices. In Advances in Robot Kinematics: Theory and Applications, Lenarčič, J., Thomas, F., Eds.; Springer Netherlands: Dordrecht, 2002; pp. 57–66. [Google Scholar]
Yoshikawa, T. Translational and rotational manipulability of robotic manipulators. In Proceedings of the 1991 International Conference on Industrial Electronics, Control and Instrumentation (IECON '91), 28 Oct.-1 Nov. 1991; 1991; pp. 1170–1175. [Google Scholar]
Mansouri, I.; Ouali, M. The power manipulability - A new homogeneous performance index of robot manipulators. Robotics and Computer-Integrated Manufacturing 2011, 27, 434–449. [Google Scholar] [CrossRef]
Mansfeld, N.; Keppler, M.; Haddadin, S. Speed Gain in Elastic Joint Robots: An Energy Conversion-Based Approach. IEEE Robotics and Automation Letters 2021, 6, 4600–4607. [Google Scholar] [CrossRef]
Kokkinis, T.; Paden, B. Kinetostatic performance limits of cooperating robot manipulators using force-velocity polytopes. Proceedings of the ASME Winter Annual Meeting-Robotics Research 1989, 14. [Google Scholar]
Lee, J. A study on the manipulability measures for robot manipulators. In Proceedings of the 1997 IEEE/RSJ International Conference on Intelligent Robot and Systems. Innovative Robotics for Real-World Applications. IROS '97, Grenoble, France, 7-11 Sept. 1997; 1997; pp. 1458–1465. [Google Scholar]
Finotello, R.; Grasso, T.; Rossi, G.; Terribile, A. Computation of kinetostatic performances of robot manipulators with polytopes. In Proceedings of the Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), 20-20 May 1998; 1998; vol. 3244, pp. 3241–3246. [Google Scholar]
Long, P.; Padir, T. Evaluating Robot Manipulability in Constrained Environments by Velocity Polytope Reduction. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), 6-9 Nov. 2018; 2018; pp. 1–9. [Google Scholar]
Long, P.; Padir, T. Constrained Manipulability for Humanoid Robots Using Velocity Polytopes. International Journal of Humanoid Robotics 2019, 17. [Google Scholar] [CrossRef]
Kang, L.; Kim, S.H.; Kim, W.; Yi, B.J. Review of Dimension Inhomogeneity in Robotics. In Proceedings of the 2019 16th International Conference on Ubiquitous Robots (UR), 24-27 June 2019; 2019; pp. 143–148. [Google Scholar]
Patrikalakis, N.M.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer Berlin, Heidelberg: 2002.
Kobayashi, S. Differential Geometry of Curves and Surfaces; Springer Singapore: 2019.
Hertrich-Jeromin, U. Differential Geometry (Lecture Notes). 2019.
Strang, G. Introduction to Linear Algebra, Fifth ed.; Wellesley - Cambridge Press: 2016.
Nakamura, Y. Advanced Robotics: Redundancy and Optimization; Addison-Wesley: 1991.
Patel, S.; Sobh, T. Manipulator Performance Measures - A Comprehensive Literature Survey. J Intell Robot Syst 2014, 77, 1–24. [Google Scholar] [CrossRef]
Baksalary, J.K.; Baksalary, O.M. Particular formulae for the Moore–Penrose inverse of a columnwise partitioned matrix. Linear Algebra and its Applications 2007, 421, 16–23. [Google Scholar] [CrossRef]
Baksalary, O.M.; Trenkler, G. On formulae for the Moore–Penrose inverse of a columnwise partitioned matrix. Applied Mathematics and Computation 2021, 403, 125913. [Google Scholar] [CrossRef]
Moulianitis, V.; Katrantzis, E.; Stravopodis, N.; Aspragathos, N. A Comparative Study of Three Manipulator Performance Measures; 2018; pp. 19-27.
Maciejewski, A.A.; Klein, C.A. Obstacle Avoidance for Kinematically Redundant Manipulators in Dynamically Varying Environments. The International Journal of Robotics Research 1985, 4, 109–117. [Google Scholar] [CrossRef]
Piziak, R.; Odell, P.L. Matrix Theory - From Generalized Inverses to Jordan Form, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL USA, 2007. [Google Scholar]
MathWorks: MATLAB. Available online: https://ch.mathworks.com/products/matlab.html (accessed on November 15th, 2023).
Universal Robots: DH parameters for calculations of kinematics and dynamics. Available online: https://www.universal-robots.com/articles/ur/application-installation/dh-parameters-for-calculations-of-kinematics-and-dynamics/ (accessed on November 15th, 2023).

Figure 1. The flexible workstation for machine hammer-peening with the collaborative robot UR5.

Figure 2. Workpiece surface model No.1: (a) Perspective view; (b) Top view.

Figure 3. Workpiece surface model No.2: (a) Perspective view; (b) Top view.

Figure 4. The surface velocity ellipses on WP1: (a) Perspective view; (b) Top view.

Figure 5. The surface velocity ellipses on WP2: (a) Perspective view; (b) Top view.

Figure 6. The surface velocity ellipses with Mean surface curvature colormap code: (a) WP1; (b) WP2.

Figure 7. The velocity manipulability ellipses with robot kinematic constraints on WP1: (a) Perspective view; (b) Top view.

Figure 8. The velocity manipulability ellipses with robot kinematic constraints on WP2: (a) Perspective view; (b) Top view.

Figure 9. The velocity manipulability ellipses with mean velocity colormap code: (a) WP1; (b) WP2.

Figure 10. Verification of the manipulability velocity ellipses with robot kinematic constraints: (a) Workpiece surface No.1 (top view); (b) Workpiece surface No.2 (top view).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Toward Optimal Robot Machining considering the Workpiece Surface Geometry in a Task-Oriented Approach

Abstract

1. Introduction

2. Background

3. Methodology

3.1. Preliminaries

3.2. The end-effector motion constraints

3.3. The constrained robot kinematics model

3.4. The manipulability ellipsoid of the constrained motion

4. Numerical Experiments and Discussion

4.1. Experimental setup

4.2. Surface velocity ellipsoids

4.3. Robot manipulability ellipsoids of the constrained kinematics

5. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe