Population Models of Epidemics with Infection Age and Vaccination Age Structure

1. Introduction

The objective of this work is to model the effects of quarantine, vaccination, and hospital isolation on the transmission of infection in an epidemic population. The focus of the model is on the infectious and symptomatic periods of an infective, which may or may not overlap. For a viral respiratory disease with severe morbidity and mortality, the symptomatic period typically results in hospital isolation as soon as the disease is recognized as a major public health problem. If the infectious and symptomatic periods coincide, or if the infectious period follows the appearance of symptoms, then the hospitalization of symptomatic patients is effective isolation of infectious individuals. If, however, the infectious period precedes the symptomatic phase, then there is much greater potential for disease transmission to susceptibles. The efficacy of vaccination during the epidemic is incorporated into the model, to account for the acquisition of immunity over a time period of vaccinated individuals.

The model is applicable to influenza epidemics such as the SARS epidemic of 2003 and the current COVID-19 pandemic. The 2003 SARS epidemic was contained, in part, because SARS infectives were infectious after manifesting symptoms, which allowed their identification and controlled isolation in hospitals. Vaccination has played a key role in the containment of the current COVID-19 pandemic. The central point of the study here is that in a future epidemic comparable to the 2003 SARS epidemic and the current COVID-19 pandemic, quarantine, vaccination, and hospitalization (isolation) will be critical elements of containment.

There is an extensive literature of works involving epidemic dynamics and vaccination implementations. In our References, we have listed many of these works.

The organization of this paper is as follows: In Section 2 we present the compartments and parameters of the model. In Section 3 we present the equations of the model. In Section 4 we analyze the model. In Section 5 we apply the model to the 2003 SARS epidemic in Taiwan. In Section 6 we apply the model to the COVID-19 epidemic in New York State. In Section 7, we provide a discussion of our results and highlight some future work.

2. Materials and Methods

The compartments of the model are susceptibles (S), vaccinated (V), exposed infectives (E), infectious infectives (I), hospitalized infectives (H) (including mortality), quarantined infectives (Q), and recovered infectives (R) (see Figure 1). The key features of this model are (1) infected individuals are tracked by disease age $a_i$, and the incubation, infectious, and symptomatic stages of the disease are modeled by the disease age of the infected individual, and (2) vaccinated individuals are tracked by vaccination age $a_v$, and their susceptibility to infection depends on their vaccination age as they gradually acquire and lose immunity.

The infected population has infection age density $i(a_i,t)$. Infectives begin the disease course at age $a_i=0$, are infected but noninfectious (exposed) from age $a_i=0$ to age $a_i=r$, and infectious from age $a_i=r$ to age $a_i=r+s$. Infectives are no longer infectious after reaching the disease age $a_i=r+s$ and are considered recovered, with the assumption that they cannot be re-infected. Thus,

$$\begin{array}{ccc}& & E\left(t\right)={\int }_0^{r}i(a_i,t)d{a}_i,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & I\left(t\right)={\int }_r^{r+s}i(a_i,t)d{a}_i,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & R\left(t\right)={\int }_0^{t}i(r+s,\widehat{t})d\widehat{t},t\ge 0.\hfill \end{array}$$

(3)

Infectives with infection age $a_i\le r+s$ can be removed from the exposed class $E\left(t\right)$ or the infectious class $I\left(t\right)$ at time t due to hospitalization or quarantine. Mortality due to the disease is included in the hospitalized compartment. Transmission of infection to susceptibles, hospitalization, manifestation of symptoms, and quarantine all depends on disease age. It is also assumed that hospitalized, quarantined, and recovered infectives do not transmit the disease to susceptibles.

The vaccinated population has vaccination age density $v(a_v,t)$. Vaccinated individuals begin with vaccination age $a_v=0$ and then have increasing or decreasing immunity to infection as their vaccination age $a_v$ increases over time. We assume there are no vaccinated individuals at $t=0$, and the vaccination starts on or after $t=0$, thus $a_v\le t$. The number of vaccinated individuals at time t is

$$V\left(t\right)={\int }_0^{t}v(a_v,t)d{a}_v.$$

(4)

The population of vaccinated individuals has a gain from the susceptible class and a loss to the infected class, since vaccination efficacy is incomplete.

The model does not take into account demographics (births and deaths) of the population. The time scale of the model (the units of t are typically days) is comparable to a small fraction of the lifespan of individuals in the population. The asymptotic behavior of the model populations, corresponding to large time, is comparable to a small fraction of the typical lifespan of individuals. For human populations, the typical time units are days and the meaningful time scale of the model is several years.

The parameters of the model are as follows: $\alpha \left(a_i\right)$ is the disease transmission rate from an infectious individual with infection age $a_i$ to a susceptible individual, $\nu$ is the rate of vaccination of susceptibles, 1-$\sigma \left(a_v\right)$ is the effectiveness of vaccination for a vaccinated individual with vaccination age $a_v$, ${\beta }_H\left(a_i\right)$ is the transition rate of infectives with infection age $a_i$ to hospitalization and ${\beta }_Q\left(a_i\right)$ is the transition rate of infectives with infection age $a_i$ to quarantine.

2.1. Equations of the Model

The equations of the model are as follows: for $t\ge 0$,

$$\frac{d}{dt}S\left(t\right)=-\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d{a}_i+\nu \right)S\left(t\right),$$

(5)

$$\frac{\partial }{\partial t}i(a_i,t)+\frac{\partial }{\partial a_i}i(a_i,t)=-\left({\beta }_H\left(a_i\right)+{\beta }_Q\left(a_i\right)\right)i(a_i,t),0\le a_i\le r+s,$$

(6)

$$i(0,t)={\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d{a}_i\left(S\left(t\right)+{\int }_0^t\sigma \left(a_v\right)v(a_v,t)d{a}_v\right),$$

(7)

$$\frac{\partial }{\partial t}v(a_v,t)+\frac{\partial }{\partial a_v}v(a_v,t)=-\sigma \left(a_v\right)\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d{a}_i\right)v(a_v,t),0\le a_v\le t,$$

(8)

$$v(0,t)=\nu S\left(t\right),$$

(9)

with initial conditions

$$S\left(0\right)=S_0,i(a_i,0)=i_0\left(a_i\right),v(a_v,0)=v_0\left(a_v\right)\equiv 0.$$

(10)

(we assume there are no vaccinated individuals at $t=0$).

2.2. Analysis of the Model

Assume the following hypothesis: $\nu \ge 0,\alpha$ is nonnegative and piecewise continuous on $[r,r+s)$, ${\beta }_H$ and ${\beta }_Q$ are nonnegative and piecewise continuous on $[0,r+s)$, $\sigma$ is nonnegative and piecewise continuous on $[0,\infty )$, $S_0>0$, $i_0$ is nonnegative and piecewise continuous on $[0,r+s)$, and $v_0\equiv 0$ on $[0,\infty )$. The existence of unique nonnegative solutions in $[0,\infty )\times L^1[0,r+s)\times L^1[0,\infty )$ to the system of equations (3.1) - (3.5), with initial conditions (3.11), can be proven with the techniques developed in [1]. The asymptotic behavior of this system without vaccination is investigated in [2,3]. We prove the following asymptotic behavior of the solutions with vaccination:

Theorem 1. 

Assume that for $0\le a_i\le r+s$, ${\beta }_H\left(a_i\right)+{\beta }_Q\left(a_i\right)\ge \overline{\beta }>0$, $0\le \alpha \left(a_i\right)\le \overline{\alpha }>0$, and $0\le \sigma \left(a_i\right)\le \overline{\sigma }>0$. The solutions of (3.1) - (3.5) with initial conditions (3.11) have the following asymptotic behavior:

$$\underset{t\to \infty }{lim}S\left(t\right)=S_{\infty }\ge 0,\underset{t\to \infty }{lim}E\left(t\right)=0,\underset{t\to \infty }{lim}I\left(t\right)=0.$$

(11)

If $\nu >0$ (vaccination), then $S_{\infty }=0$. If $\nu =0$ (no vaccination), then $S_{\infty }$ satisfies

$$S_{\infty }=exp\left[-\left(\Gamma +(S\left(0\right)-S_{\infty })\Lambda \right)\right]S\left(0\right),$$

(12)

where

$$\Gamma ={\int }_r^{r+s}\alpha \left(a_i\right){\int }_0^{a_i}{i}_0\left(u\right)exp\left[-{\int }_u^{a_i}({\beta }_H\left(b\right)+{\beta }_Q\left(b\right))db\right]dud{a}_i,$$

(13)

$$\Lambda ={\int }_r^{r+s}\alpha \left(a_i\right)exp\left[-{\int }_0^{a_i}({\beta }_H\left(b\right)+{\beta }_Q\left(b\right))db\right]d{a}_i.$$

(14)

Proof. 

Let $\beta \left(a_i\right)={\beta }_H\left(a_i\right)+{\beta }_H\left(a_i\right)\ge \overline{\beta }>0,0\le a_i\le r+s$. We first prove (11). From (5) for $t\ge 0$

$$\begin{array}{ccc}\hfill S\left(t\right)& =& exp(-\nu t)exp\left[-{\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)d\widehat{t}\right]S\left(0\right)\hfill \end{array}$$

(15)

Then, it implies that $S\left(t\right)$ is non-increasing and $S_{\infty }={lim}_{t\to \infty }S\left(t\right)\ge 0$. It is also clear that $S_{\infty }=0$ if $\nu >0$. In addition, by evaluating the integral of (5) from 0 to t, we have

$$S\left(t\right)-S\left(0\right)=-{\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)S\left(\widehat{t}\right)d\widehat{t}-\nu {\int }_0^{t}S\left(\widehat{t}\right)d\widehat{t},$$

which is equivalent to

$$S\left(t\right)+{\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)S\left(\widehat{t}\right)d\widehat{t}=S\left(0\right)-\nu {\int }_0^{t}S\left(\widehat{t}\right)d\widehat{t}.$$

(16)

We then derive equations for $V\left(t\right)$. Combining (4), (8), and (9), we obtain, for $t\ge 0$,

$$\begin{array}{cc}\hfill V^{\prime }\left(t\right)& =\frac{d}{dt}\left({\int }_0^{t}v(a_v,t)d{a}_v\right)=v(t,t)+{\int }_0^t{v}_t(a_v,t)d{a}_v\hfill \\ \hfill & =v(t,t)+{\int }_0^t\left[-v_{a_v}(a_v,t)-\sigma \left(a_v\right)\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d_{a_i}\right)v(a_v,t)\right]d{a}_v\hfill \\ \hfill & =v(t,t)-v(t,t)+v(0,t)-{\int }_0^t\sigma \left(a_v\right)\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d_{a_i}\right)v(a_v,t)d{a}_v\hfill \\ \hfill & =\nu S\left(t\right)-{\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d_{a_i}\right)\sigma \left(a_v\right)v(a_v,t)d{a}_v,\hfill \end{array}$$

which integrates to

$$\begin{array}{cc}\hfill V\left(t\right)& +{\int }_0^t\left({\int }_0^{\widehat{t}}\left[\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)\sigma \left(a_v\right)v(a_v,\widehat{t})\right]d{a}_v\right)d\widehat{t}\hfill \\ \hfill & =V\left(0\right)+{\int }_0^t\nu S\left(\widehat{t}\right)d\widehat{t}.\hfill \end{array}$$

(17)

Then (15), (17), and the nonnegativity of solutions imply ${lim}_{t\to \infty }V\left(t\right)$ exists. Next, we consider $E\left(t\right)$ and $I\left(t\right)$. Using equations (1), (2), and (6), we have, for $t\ge 0$,

$$\begin{array}{cc}\hfill E^{\prime }\left(t\right)& =\frac{d}{dt}\left({\int }_0^{r}i(a_i,t)d{a}_i\right)={\int }_0^r{i}_t(a_i,t)d{a}_i={\int }_0^r\left(-i_{a_i}(a_i,t)-\beta \left(a_i\right)i(a_i,t)\right)d{a}_i\hfill \\ \hfill & =i(0,t)-i(r,t)-{\int }_0^r\beta \left(a_i\right)i(a_i,t)d{a}_i,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill I^{\prime }\left(t\right)& =\frac{d}{dt}\left({\int }_r^{r+s}i(a_i,t)d{a}_i\right)={\int }_r^{r+s}{i}_t(a_i,t)d{a}_i={\int }_r^{r+s}\left(-i_{a_i}(a_i,t)-\beta \left(a_i\right)i(a_i,t)\right)d{a}_i\hfill \\ \hfill & =i(r,t)-i(r+s,t)-{\int }_r^{r+s}\beta \left(a_i\right)i(a_i,t)d{a}_i,\hfill \end{array}$$

(19)

where the boundary condition $i(0,t)$ is defined in (7). Adding up these two equations gives

$$E^{\prime }\left(t\right)+I^{\prime }\left(t\right)=i(0,t)-i(r+s,t)-{\int }_0^{r+s}\beta \left(a_i\right)i(a_i,t)d{a}_i,$$

which integrates to

$$E\left(t\right)+I\left(t\right)=E\left(0\right)+I\left(0\right)+{\int }_0^t\left(i(0,\widehat{t})-i(r+s,\widehat{t})-{\int }_0^{r+s}\beta \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)d\widehat{t}.$$

(20)

In equation (20), we use (7) to derive

$$\begin{array}{cc}\hfill {\int }_0^{t}i(0,\widehat{t})& ={\int }_0^t{\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\left(S\left(\widehat{t}\right)+{\int }_0^{\widehat{t}}\sigma \left(a_v\right)v(a_v,\widehat{t})d{a}_v\right)d\widehat{t}\hfill \\ \hfill & ={\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)S\left(\widehat{t}\right)d\widehat{t}\hfill \\ \hfill & +{\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)\left({\int }_0^{\widehat{t}}\sigma \left(a_v\right)v(a_v,\widehat{t})d{a}_v\right)d\widehat{t}\hfill \\ \hfill & ={\int }_0^t\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)S\left(\widehat{t}\right)d\widehat{t}\hfill \\ \hfill & +{\int }_0^t\left({\int }_0^{\widehat{t}}\left[\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)\sigma \left(a_v\right)v(a_v,\widehat{t})\right]d{a}_v\right)d\widehat{t}.\hfill \end{array}$$

(21)

We observe that the first term in (21) is equal to the second term in the left-hand side of (16), and the second term in (21) equals the second term in the left-hand side of (17). Therefore, when summing up equations (16), (17), (20), we find that the two terms in (21) cancel out. Consequently, for $t\ge 0$, we have,

$$\begin{array}{cc}\hfill S\left(t\right)& +V\left(t\right)+E\left(t\right)+I\left(t\right)+{\int }_0^{t}i(r+s,\widehat{t)}d\widehat{t}+{\int }_0^t\left({\int }_0^{r+s}\beta \left(a_i\right)i(a_i,\widehat{t})d{a}_i\right)d\widehat{t}\hfill \\ \hfill & =S\left(0\right)+V\left(0\right)+E\left(0\right)+I\left(0\right)\hfill \end{array}$$

(22)

Since $\beta \left(a_i\right)\ge \overline{\beta }$ for $0\le a_i\le r+s$, (22) implies

$${\int }_0^{\infty }\left(E\left(t\right)+I\left(t\right)\right)dt<\infty .$$

(23)

Thus, (15), (17), (22), and (23) imply

$$\underset{t\to \infty }{lim}E\left(t\right)=\underset{t\to \infty }{lim}I\left(t\right)=0.$$

Lastly, we prove that if $\nu =0$ (no vaccination), then $S_{\infty }>0$ and satisfies (12). From (6)

$$i(a_i,t)=\left\{\begin{array}{cc}{i}_0(a_i-t)exp[-{\int }_{a_i-t}^{a_i}\beta \left(b\right)db],\hfill & a_i>t;\hfill \\ i(0,t-a_i)exp[-{\int }_0^{a_i}\beta \left(b\right)db],\hfill & a_i\le t.\hfill \end{array}\right.$$

(24)

From (5), (7), and (24) with $\nu =0$, for $t\ge 0$,

$$S^{\prime }\left(t\right)=-i(0,t)\Rightarrow S\left(0\right)-S_{\infty }={\int }_0^{\infty }i(0,t)dt.$$

(25)

For $t\ge 0$, (24) and (25) imply

$$\begin{array}{cc}\hfill & {\int }_0^{\infty }{\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d{a}_{i}dt\hfill \\ \hfill & ={\int }_r^{r+s}\alpha \left(a_i\right)\left({\int }_0^{a_i}i(a_i,t)dt+{\int }_{a_i}^{\infty }i(a_i,t)dt\right)d{a}_i\hfill \\ \hfill & ={\int }_r^{r+s}\alpha \left(a_i\right)\left({\int }_0^{a_i}{i}_0(a_i-t)e^{-{\int }_{a_i-t}^{a_i}\beta \left(b\right)db}dt+{\int }_{a_i}^{\infty }i(0,t-a_i)e^{-{\int }_0^{a_i}\beta \left(b\right)db}dt\right)d{a}_i\hfill \\ \hfill & ={\int }_r^{r+s}\alpha \left(a_i\right)\left(-{\int }_{a_i}^0{i}_0\left(u\right)e^{-{\int }_u^{a_i}\beta \left(b\right)db}du+{\int }_0^{\infty }i(0,u)e^{-{\int }_0^{a_i}\beta \left(b\right)db}du\right)d{a}_i\hfill \\ \hfill & ={\int }_r^{r+s}\alpha \left(a_i\right)\left({\int }_0^{a_i}{i}_0\left(u\right)e^{-{\int }_u^{a_i}\beta \left(b\right)db}du+\left({\int }_0^{\infty }i(0,u)du\right)\left(e^{-{\int }_0^{a_i}\beta \left(b\right)db}\right)\right)d{a}_i\hfill \\ \hfill & =\Gamma +(S\left(0\right)-S_{\infty })\Lambda .\hfill \end{array}$$

Then, (12) follows from (15). □

Remark. We claim that $|E^{\prime }\left(t\right)+I^{\prime }\left(t\right)|$ is bounded for $t\ge 0$. We shall prove this statement in two cases. For $t\ge r+s$, (7), (22), and (24) imply there exists $C_1>0$ such that

$$\begin{array}{cc}\hfill i(r+s,t)& =i(0,t-r-s)exp\left[-{\int }_0^{r+s}\beta \left(b\right)db\right]\hfill \\ \hfill & \le \left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t-r-s)d{a}_i\right)\hfill \\ \hfill & \left(S(t-r-s)+{\int }_0^{t-r-s}\sigma \left(a_i\right)v(a_v,t-r-s)d{a}_v\right)\hfill \\ \hfill & \le \left(\overline{\alpha }I(t-r-s)\right)\left(S(t-r-s)+\overline{\sigma }V(t-r-s)\right)\le C_1.\hfill \end{array}$$

For $t<r+s$, we again use (24) to derive

$$i(r+s,t)=i_0(r+s-t)exp\left[-{\int }_{r+s-t}^{r+s}\beta \left(b\right)db\right]\le i_0(r+s-t).$$

Since the initial condition $i_0$ is piecewise continuous on $[0,r+s)$, there exists $C_2>0$ such that

$$i(r+s,t)\le i_0(r+s-t)\le C_2,$$

for $t<r+s$.

Let $C^{*}=max\{C_1,C_2\}$. Combining (7), (18), and (19), we have, for $t\ge 0$,

$$\begin{array}{cc}\hfill |E^{\prime }\left(t\right)+I^{\prime }\left(t\right)|& =|i(0,t)-i(r+s,t)-{\int }_0^{r+s}\beta \left(a_i\right)i(a_i,t)d{a}_i|\hfill \\ \hfill & =|\left({\int }_r^{r+s}\alpha \left(a_i\right)i(a_i,t)d{a}_i\right)\left(S\left(t\right)+{\int }_0^t\sigma \left(a_v\right)v(a_v,t)d{a}_v\right)\hfill \\ \hfill & -i(r+s,t)-{\int }_0^{r+s}\beta \left(a_i\right)i(a_i,t)d{a}_i|\hfill \\ \hfill & \le \overline{\alpha }I\left(t\right)\left(S\left(t\right)+\overline{\sigma }V\left(t\right)\right)+C^{*}+\overline{\beta }\left(E\left(t\right)+I\left(t\right)\right).\hfill \end{array}$$

By (22), $|E^{\prime }\left(t\right)+I^{\prime }\left(t\right)|$ is bounded for $t\ge 0$.

2.3. Application of the Model to the 2003 SARS Epidemic in Taiwan

This example is based on results in [4,5,6,7], and illustrates the case that the period of infectiousness coincides with the symptomatic period. In the SARS epidemic in Taiwan in 2003, the seriousness of the disease was recognized after an initial period, and by April 24, 2003, infected individuals were quickly identified and isolated in hospitals, with stringent control measures to prevent further disease transmission. The incubation period of SARS was from two to seven days. In this epidemic in Taiwan 2003, vaccination was not available. We first consider the model without vaccination ($\nu =0$).

We assume that the incubation (exposed) period lasts from the moment of infection to day 5, and the infectious period lasts from day 5 to day 26. We overlap the symptomatic and infectious periods, and assume that after April 24, 2003, a certain percentage of symptomatic infectives were isolated in hospitals, and gave no further transmissions to susceptibles. We will then extrapolate the model to the case that the period of symptoms and infectiousness overlapped one day and the case that the period of symptoms and infectiousness overlapped two days (see Figure 2).

All parameters are based on fitting the model to data ([4]). The initial population of susceptibles is set at $S\left(0\right)=6.0\times {10}^6$. It is assumed that the exposed period lasts from day 0 until day $r=5$, and the infectious period lasts $s=21$ days, from day $r=5$ to day $r+s=26$. The asymptomatic period and the exposed period coincide, as do the symptomatic period and the infectious period (see Figure 2). The transmission rate is defined as (see Figure 3):

$$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 3.1\times {10}^{-8}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+10,\hfill \\ 3.1\times {10}^{-7}\left(1.0-\frac{a_i-r-10}{11}\right)\hfill & \mathrm{if}r+10\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$

The hospitalization rate is $54.5\%$ per day after manifestation of symptoms at day 5 and $0.0\%$ per day before day 5 (see Figure 3):

$${\beta }_H\left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<5,\hfill \\ .545\hfill & \mathrm{if}5\le a_i\le 26.\hfill \end{array}\right.$$

We assume only pre-symptomatic infected individuals are quarantined. The quarantine rate is $2.0\%$ per day from day 0 to day 5 and then $0.0\%$ per day after day 5 (see Figure 3):

$${\beta }_Q\left(a_i\right)=\left\{\begin{array}{cc}.020\hfill & \mathrm{if}0\le a_i<5,\hfill \\ 0\hfill & \mathrm{if}5\le a_i\le 26.\hfill \end{array}\right.$$

It is assumed that at time 0 the distribution of infectives $i(a_i,0)$ is given by (see Figure 3):

$$i(a_i,0)=\left\{\begin{array}{cc}12\hfill & \mathrm{if}{a}_i\le 1,\hfill \\ 5\hfill & \mathrm{if}1<a_i\le 2,\hfill \\ 19\hfill & \mathrm{if}2<a_i\le 3,\hfill \\ 9\hfill & \mathrm{if}3<a_i\le 4,\hfill \\ 15\hfill & \mathrm{if}4<a_i\le 5,\hfill \\ \frac{1}{2}(17-a)\hfill & \mathrm{if}5<a_i\le 17,\hfill \\ 0\hfill & \mathrm{if}17<a_i.\hfill \end{array}\right.$$

With this initial distribution $i(a,0)$, the total number of exposed at time $t=0$ is $E\left(0\right)=60$ and the total number of infectious at time $t=0$ is $I\left(0\right)=36$. It is assumed that $H\left(0\right)=0$, $Q\left(0\right)=0$, and $R\left(0\right)=0.$ In Figure 4 the graphs of the exposed population $E\left(t\right)$, the infectious population $I\left(t\right)$, the cumulative number of new cases ${\int }_0^{t}i(0,\widehat{t})d\widehat{t}$, and the daily number of new cases $i(0,t)$ are given and compared to the data of the epidemic from April 28 to June 25, 2003. The total number of new cases is $\approx 230$. Data for the epidemic is given in [4], with 232 cases reported for this time period.

The model can be used to evaluate the role of the susceptible size population $S\left(0\right)$ in predicting the number of cases $S\left(0\right)-S_{\infty }$ in the epidemic, with all other parameters and initial conditions held fixed. For this example, $S\left(0\right)=6,000,000$ and $S_0-S_{\infty }\approx 230$. In Figure 5, we use the formula (12) to plot $S\left(0\right)-S_{\infty }$ as a function of $S\left(0\right)$, as $S\left(0\right)$ increases from ${10}^5$ to ${10}^7$. We find that the number of cases $S\left(0\right)-S_{\infty }$ increases as the initial susceptible population size $S\left(0\right)$ increases.

Remark. The asymptotic behavior of the solutions of (5), (6), (7) without vaccination ($\nu =0$), is analogous to the asymptotic behavior of the solutions of the classic Kermack-McKendrick SEIR model [8,9]:

$$S^{\prime }\left(t\right)=-\alpha S\left(t\right)I\left(t\right),t\ge 0,$$

(26)

$$E^{\prime }\left(t\right)=\alpha S\left(t\right)I\left(t\right)-\beta E\left(t\right),t\ge 0,$$

(27)

$$I^{\prime }\left(t\right)=\beta E\left(t\right)-\gamma I\left(t\right),t\ge 0,$$

(28)

$$R^{\prime }\left(t\right)=\gamma I\left(t\right),t\ge 0.$$

(29)

The limiting behavior as $t\to \infty$ depends on the initial conditions $S\left(0\right),E\left(0\right),I\left(0\right)$:

$$\underset{t\to \infty }{lim}E\left(t\right)=0,\underset{t\to \infty }{lim}I\left(t\right)=0,\underset{t\to \infty }{lim}S\left(t\right)=S_{\infty }>0,$$

where $S_{\infty }$ satisfies

$$S_{\infty }=S\left(0\right)+E\left(0\right)+I\left(0\right)+\frac{\gamma }{\alpha }log\left(\frac{S_{\infty }}{S\left(0\right)}\right).$$

(30)

Examples are given in Figure 6. This result is of major scientific importance because it explains why epidemic diseases, which can occur hundreds of thousands of times over evolutionary time scales, do not annihilate biological species.

The role of hospitalization (isolation) and quarantine of infectives in the 2003 Taiwan SARS epidemic can be analyzed in the model. We consider two scenarios in which the infection period precedes the symptomatic period - the period of infectiousness begins on day 5 and the period of symptoms begins on day 6 or day 7 (see Figure 2). We also consider three scenarios in which the quarantine rate is 2.0 % per day, 4.0% per day, and 10.0% per day. We assume only pre-symptomatic infected individuals are quarantined. The parameters $\alpha$ and ${\beta }_H$ are as before, and $\nu =0$ (no vaccination).

In the case that exposed infectives are symptomatic at day 6 (infectious 1 day before symptoms) and the maximum quarantine rate is 2.0%, the cumulative number of cases reaches 2000 in 1 year and the cumulative number of quarantined reaches 150 in 1 year. In the case that exposed infectives are symptomatic at day 7 (infectious 2 days before symptoms) and the maximum quarantine rate is 2.0%, the cumulative number of cases is approximately 3,700,000 and the cumulative number of quarantined reaches 300,000 in 1 year. (see Figure 7)

In the case that exposed infectives are symptomatic at day 6 (infectious 1 day before symptoms) and the maximum quarantine rate is 4.0%, the cumulative number of cases reaches approximately 800 in 150 days and the cumulative number of quarantined reaches 120 in 150 days. In the case that exposed infectives are symptomatic at day 7 (infectious 2 days before symptoms) and the maximum quarantine rate is 4.0%, the cumulative number of cases is approximately 2,700,000 in 450 days and the cumulative number of quarantined reaches 400,000 in 450 days. (see Figure 8)

In the case that exposed infectives are symptomatic at day 6 (infectious 1 day before symptoms) and the maximum quarantine rate is 10.0%, the cumulative number of cases reaches approximately 350 in 50 days and the cumulative number of quarantined is approximately 100 in 50 days. In the case that exposed infectives are symptomatic at day 7 (infectious 2 days before symptoms) and the maximum quarantine rate is 10.0%, the cumulative number of cases is approximately 1,000 in 200 days and the cumulative number of quarantined reaches approximately 300 in 200 days. (see Figure 9)

For the disease age structured model (5 ), (6), (7), without vaccination ($\nu =0$), the epidemic reproduction number ([7]) $R_0$ of the epidemic is

$$R_0=S\left(0\right){\int }_r^{r+s}\alpha \left(a_i\right)exp\left(-{\int }_0^{a_i}\left({\beta }_Q\left(b\right)+{\beta }_H\left(b\right)\right)db\right)d{a}_i.$$

The reproduction number $R_0$ is the number of secondary infections generated by 1 infected individual over the disease course. For the parameters s, r, $I_0\left(a_i\right)$, $\alpha \left(a_i\right)$ and ${\beta }_H\left(a_i\right)$ as before, $R_0$ is graphed as a function of the number of days infectiousness pre-symptomatic p and the maximum quarantined rate in Figure 10. If $R_0>1$, then the epidemic is severe, although it ultimately subsides as the susceptible population is exhausted. In Figure 11 the graph of the total number of cases ${\int }_0^{\infty }i(0,t)dt$ as a function of the number of days of infectiousness pre-symptomatic p and the maximum quarantine rate is given. The number of cases rises sharply as the quarantine rate falls below 5% and the number of days infectious pre-symptomatic exceeds 1.

We modify the model of the 2003 Taiwan SARS epidemic without vaccination to include vaccination, which was not available in Taiwan in 2003. This example will illustrate the epidemic evolution with alternate elements, including vaccination. We take the vaccination parameter $\nu =0.05$. Vaccinated individuals begin with vaccinated age $a_v=0$ and then acquire increasing immunity as their vaccination age increases over a period of days or weeks. The total number of vaccinated at time t is ${\int }_0^{t}v(a_v,t)d{a}_v$. Susceptibles are vaccinated at a constant rate $\nu$ per day. The proportion of vaccinated still susceptible at vaccination age $a_v$ is $\sigma \left(a_v\right)$.

In this example $\nu =0.05$, $\sigma \left(a_v\right)=.7e^{-.25a_v}+.3$ (which means vaccination results in incomplete immunity, and as vaccination age $a_v$ advances, 30% of vaccinated individuals remain susceptible). We assume, $V\left(0\right)=0$. Infectiousness precedes symptom onset by 2 days and the maximum quarantine rate is 4.0%. All other parameters are as before. The evolution of the epidemic is graphed in Figure 12, where it is seen that the cumulative number of cases is approximately 175,000. This example can be compared to the model with the same parameters, except without vaccination in the bottom graph in Figure 8, where the cumulative number of cases is approximately 350,000.

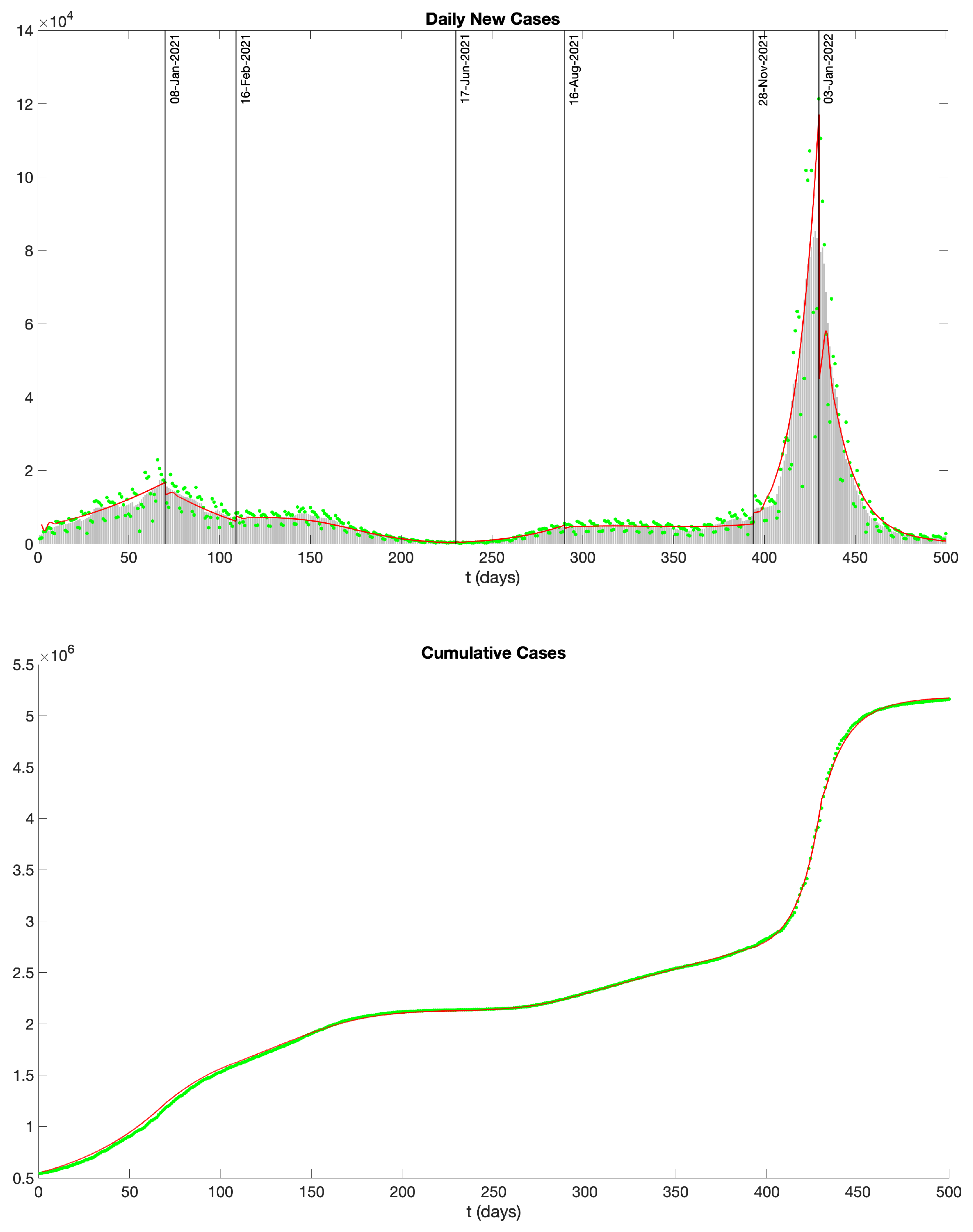
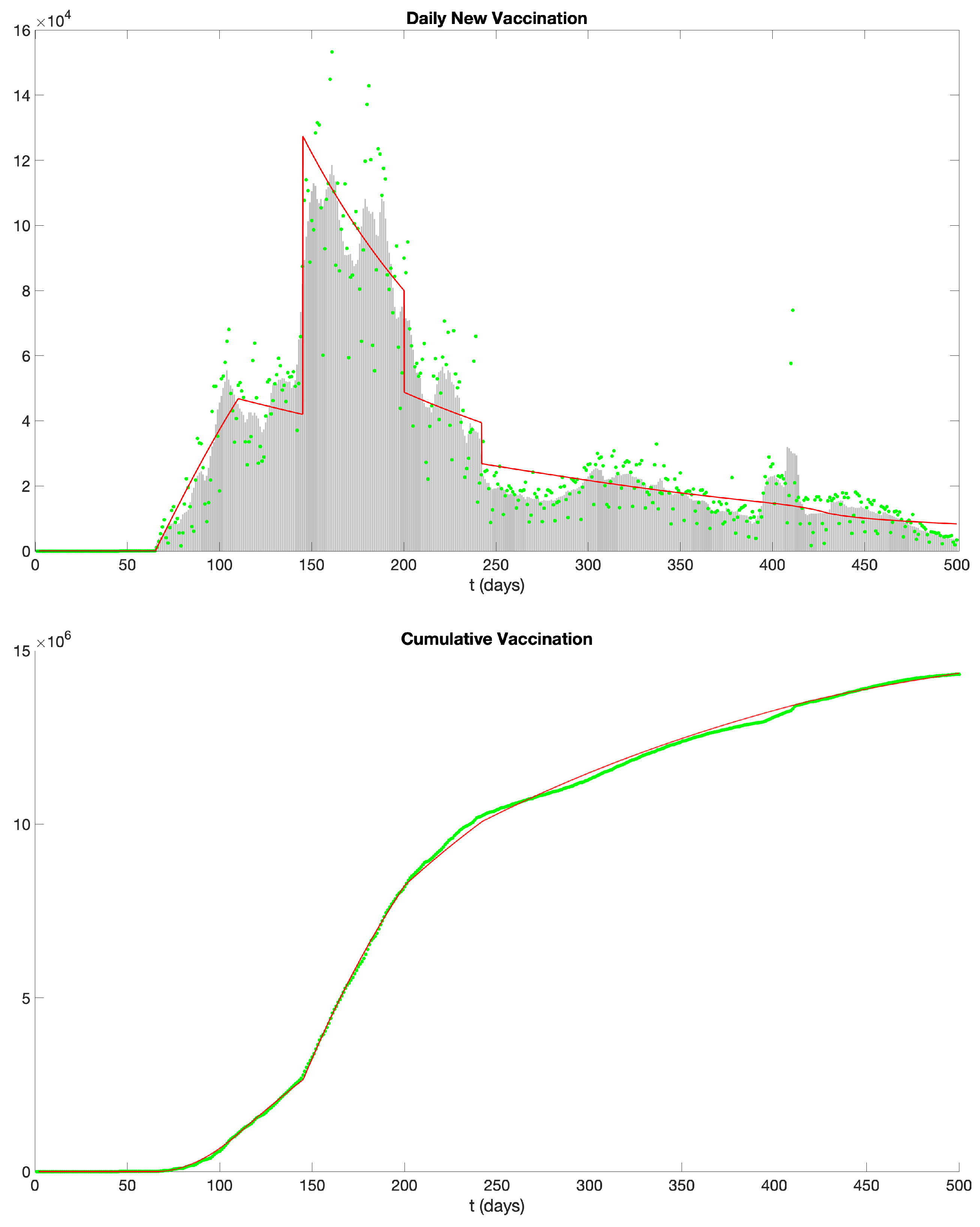
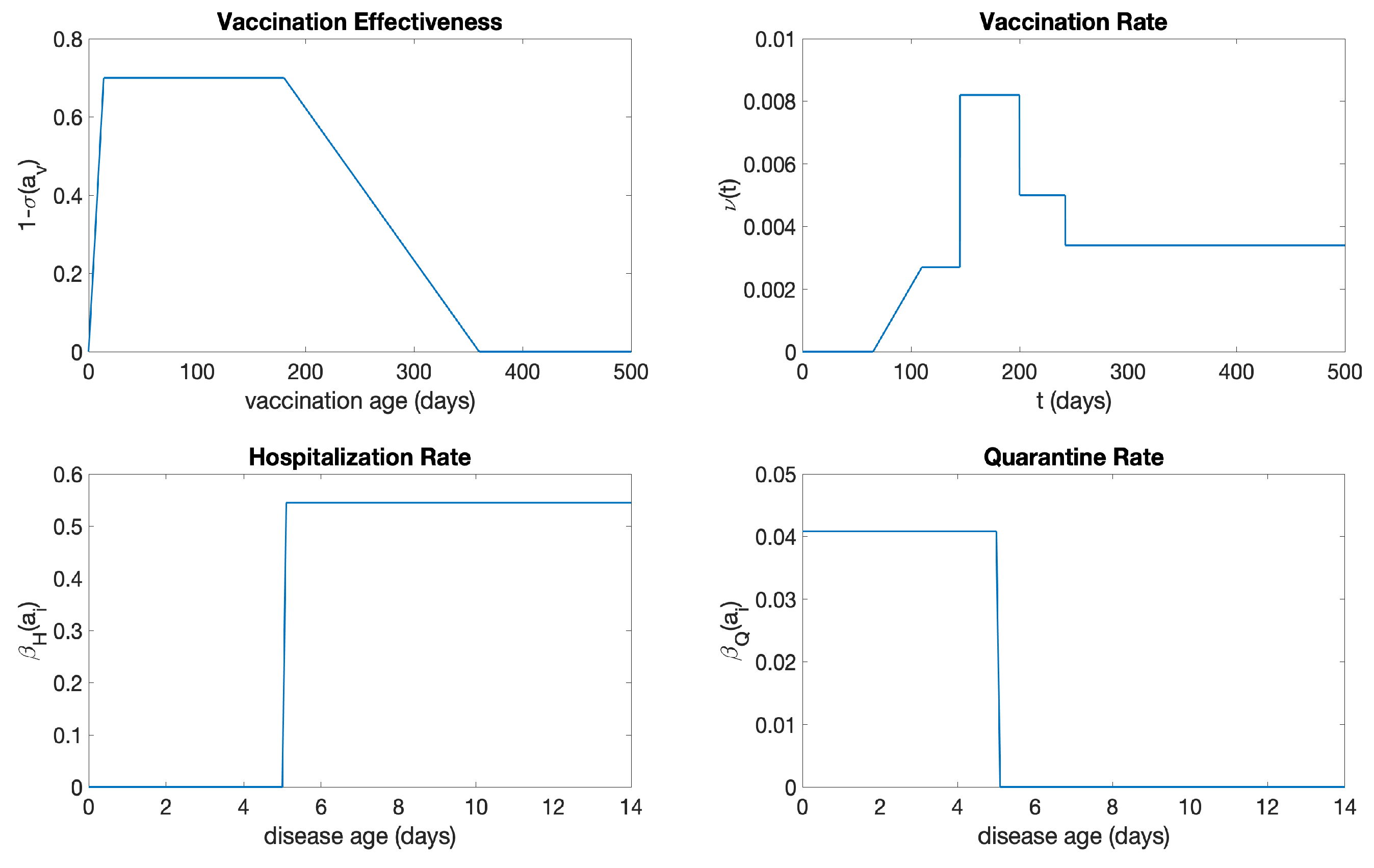
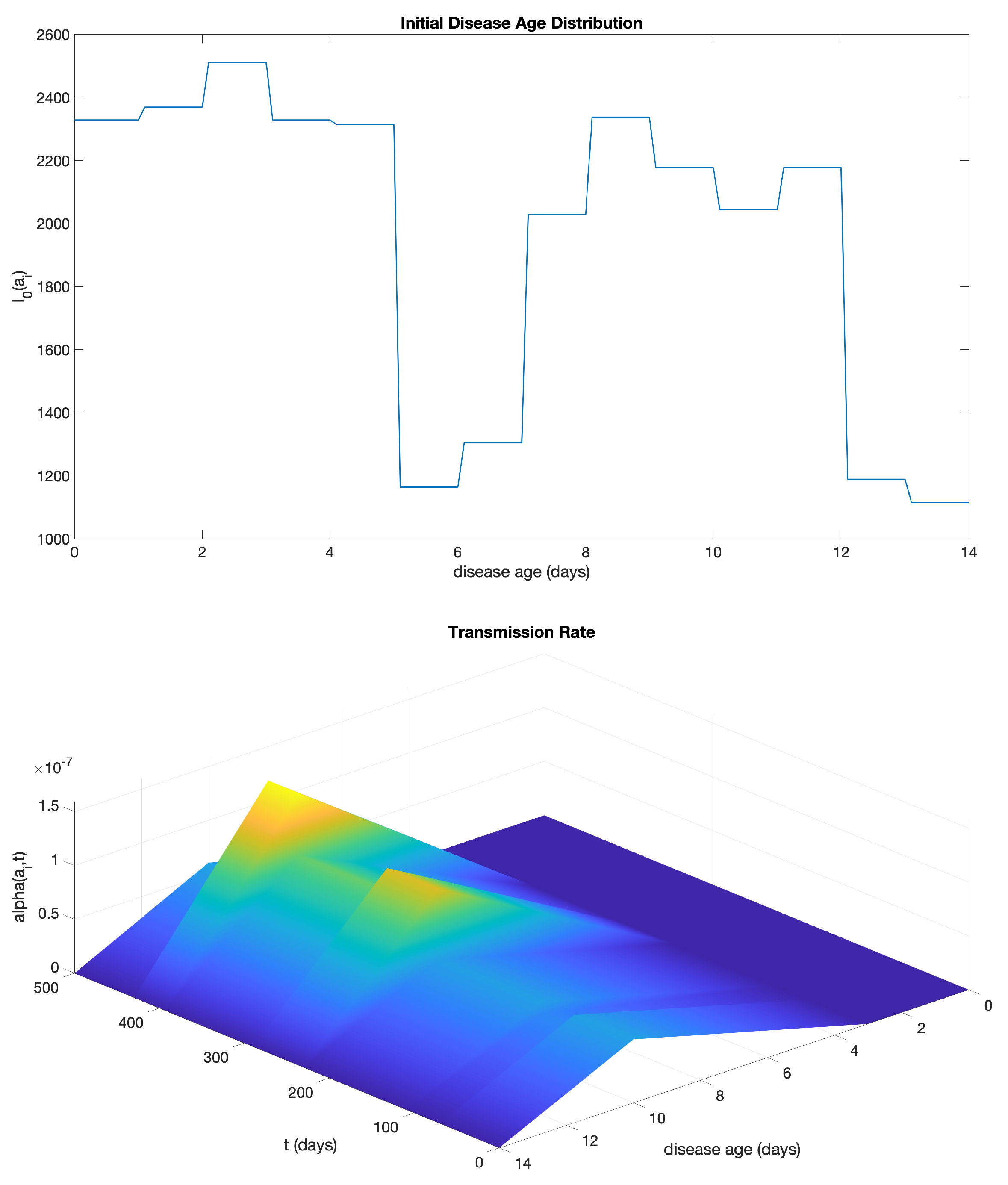
2.4. Application of the Model to the COVID-19 Epidemic in New York State

In this section, we apply our mathematical model to analyze the transmission dynamics of COVID-19 in New York State. Numerous factors influence COVID-19 transmission, including vaccination rates, the emergence of more contagious variants, the public’s reaction to and understanding of the virus, and governmental responses and policies. To provide a more detailed analysis, we segment the data into different phases, aligned with the timeline of COVID-19 transmission and the New York State government’s response [9].

Figure 13. Timeline of infectious periods relative to symptom onset for COVID-19. The top segment displays the exposed-infectious period. Segments 2 to 4 illustrate scenarios where the infectious period starts two days before, one day before, and simultaneously with symptom onset, respectively.

Figure 13. Timeline of infectious periods relative to symptom onset for COVID-19. The top segment displays the exposed-infectious period. Segments 2 to 4 illustrate scenarios where the infectious period starts two days before, one day before, and simultaneously with symptom onset, respectively.

We obtain data from the New York State Department of Health (https://health.data.ny.gov/). The state of New York confirmed its first case of COVID-19 during the pandemic on March 1, 2020, while the first complete vaccination (i.e., two-dose vaccination) began on December 15, 2020. Our analysis focuses on the timeframe from October 30, 2020, to March 13, 2022.

In Figure 14, the green dots depict daily reported cases. Since this data tends to be erratic and is subject to ongoing updates, a standard approach is to use a rolling weekly average. Accordingly, the gray bars in the figure represent this rolling weekly average. The top figure in Figure 15 follows a similar presentation: green dots for daily vaccinated individuals and gray bars for the rolling weekly averages.

On average, symptoms of COVID-19 manifest in newly infected individuals approximately 5-6 days later (WebMD,https://www.webmd.com/covid/coronavirus-incubation-period) and last for about two weeks. We set the minimum age of infectiousness $r=3$, the number of days of pre-symptomatic infectiousness $p=2$, the number of days when symptoms appear $r+p=5$, and the number of days of infectiousness $s=11$. It is assumed that the hospitalization rate ${\beta }_H\left(a_i\right)$ per day is 54.5% once symptoms appear (after day $r+p=5$), with a rate of 0.0% per day before day 5 (Figure 16).

$${\beta }_H\left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r+p,\hfill \\ .545\hfill & \mathrm{if}r+p\le a_i\le 14.\hfill \end{array}\right.$$

We assume only pre-symptomatic infected individuals are quarantined. The quarantine rate is 4.0% per day from day 0 to day 5 and then 0.0% per day after day 5 (see Figure 16)

$${\beta }_Q\left(a_i\right)=\left\{\begin{array}{cc}.020\hfill & \mathrm{if}0\le a_i<r+p,\hfill \\ 0\hfill & \mathrm{if}r+p\le a_i\le 14.\hfill \end{array}\right.$$

In the case of COVID-19, the infectious period precedes the symptomatic phase. Individuals with COVID-19 can transmit the virus up to 48 hours before they begin to show symptoms. Based on this understanding, we assume the exposed period for COVID-19 spans from the moment of infection to day 3 (i.e., $r=3$). The infectious period then continues from day 3 to day 14, resulting in a two-day overlap between the onset of symptoms and infectiousness (see Figure 13). As mentioned, many factors influence the transmission of COVID-19. Therefore, we divide the entire timeframe into different phases. Upon fitting the data, we have different values of transmission rate in different phases:

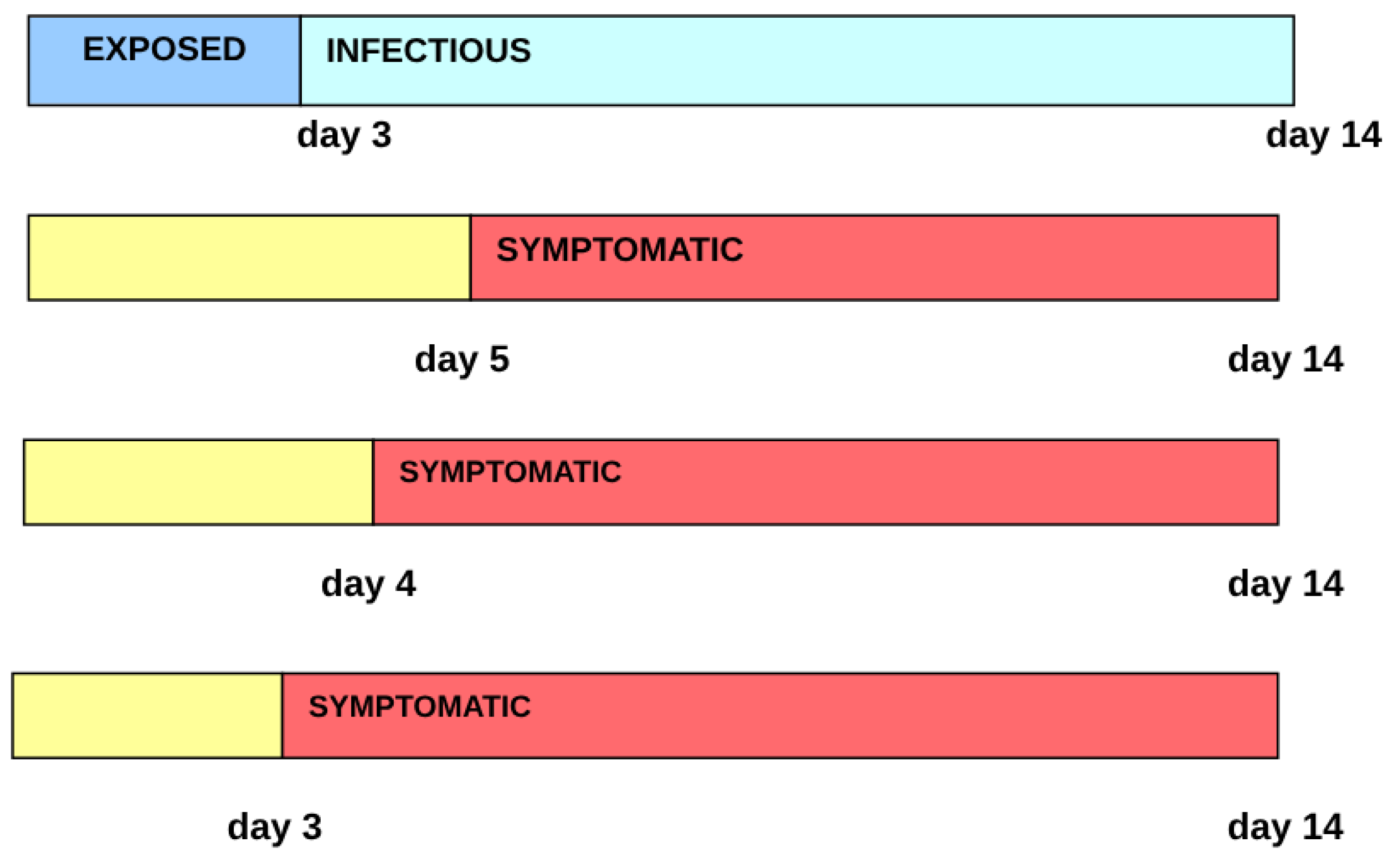
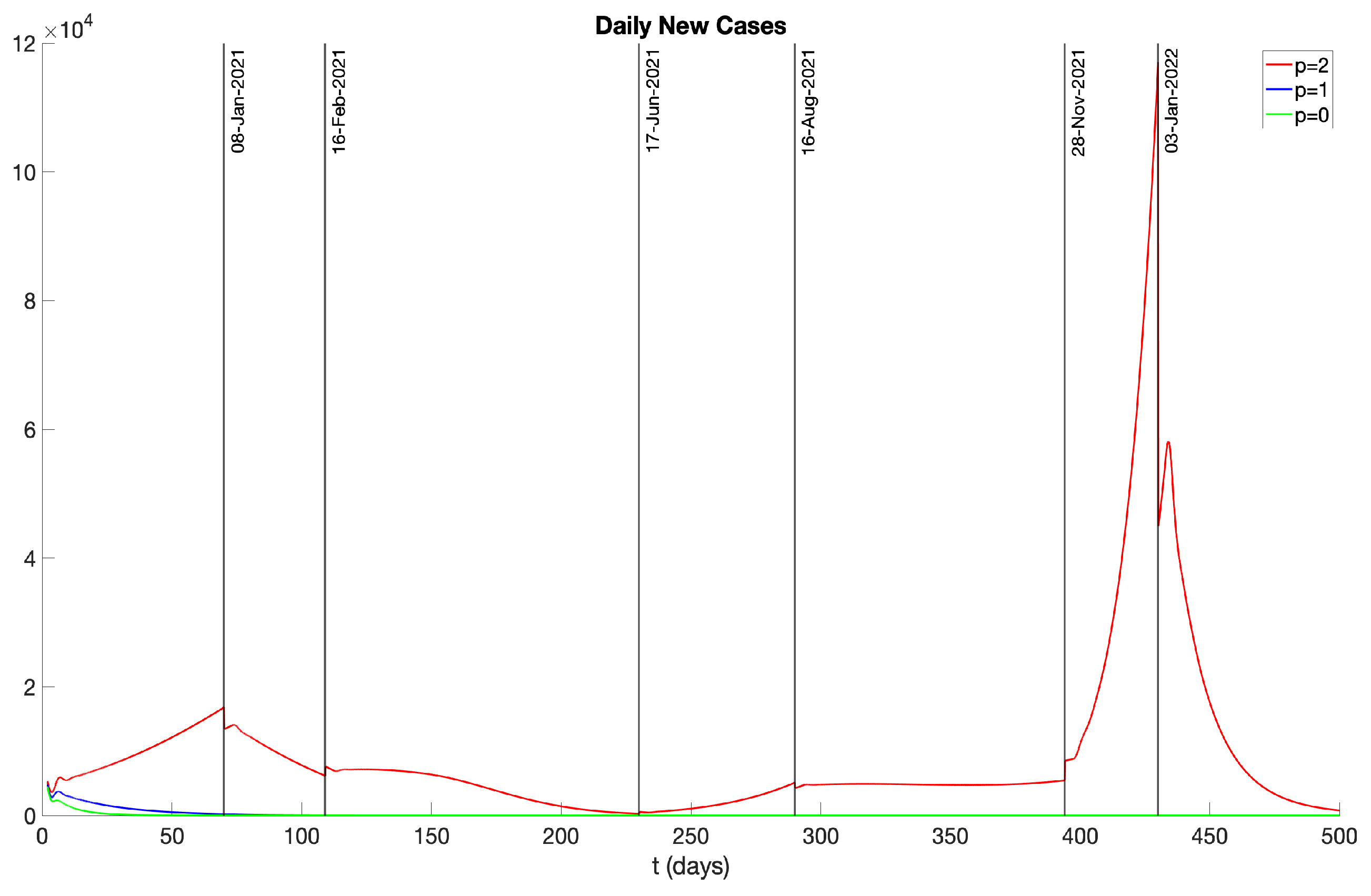
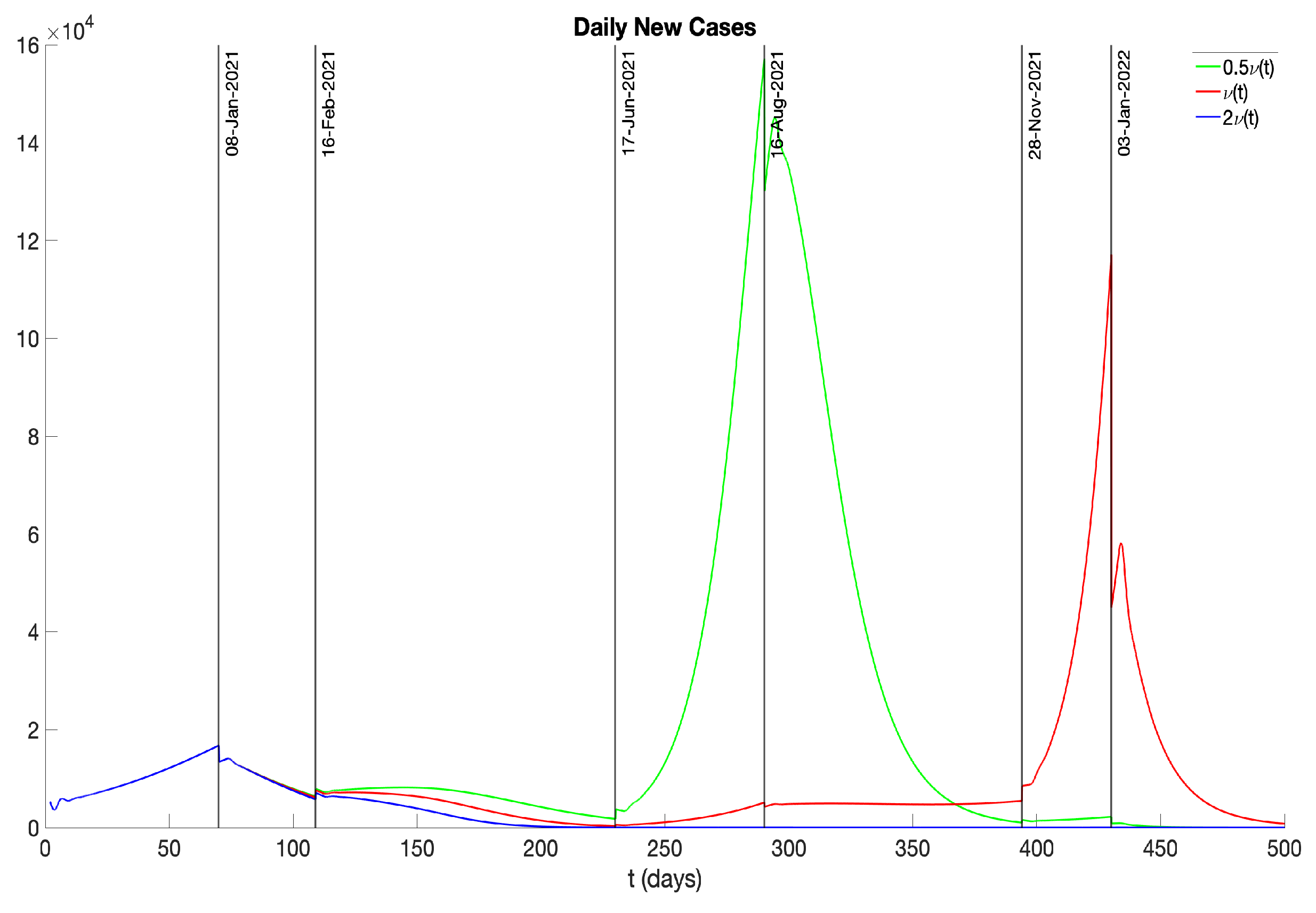
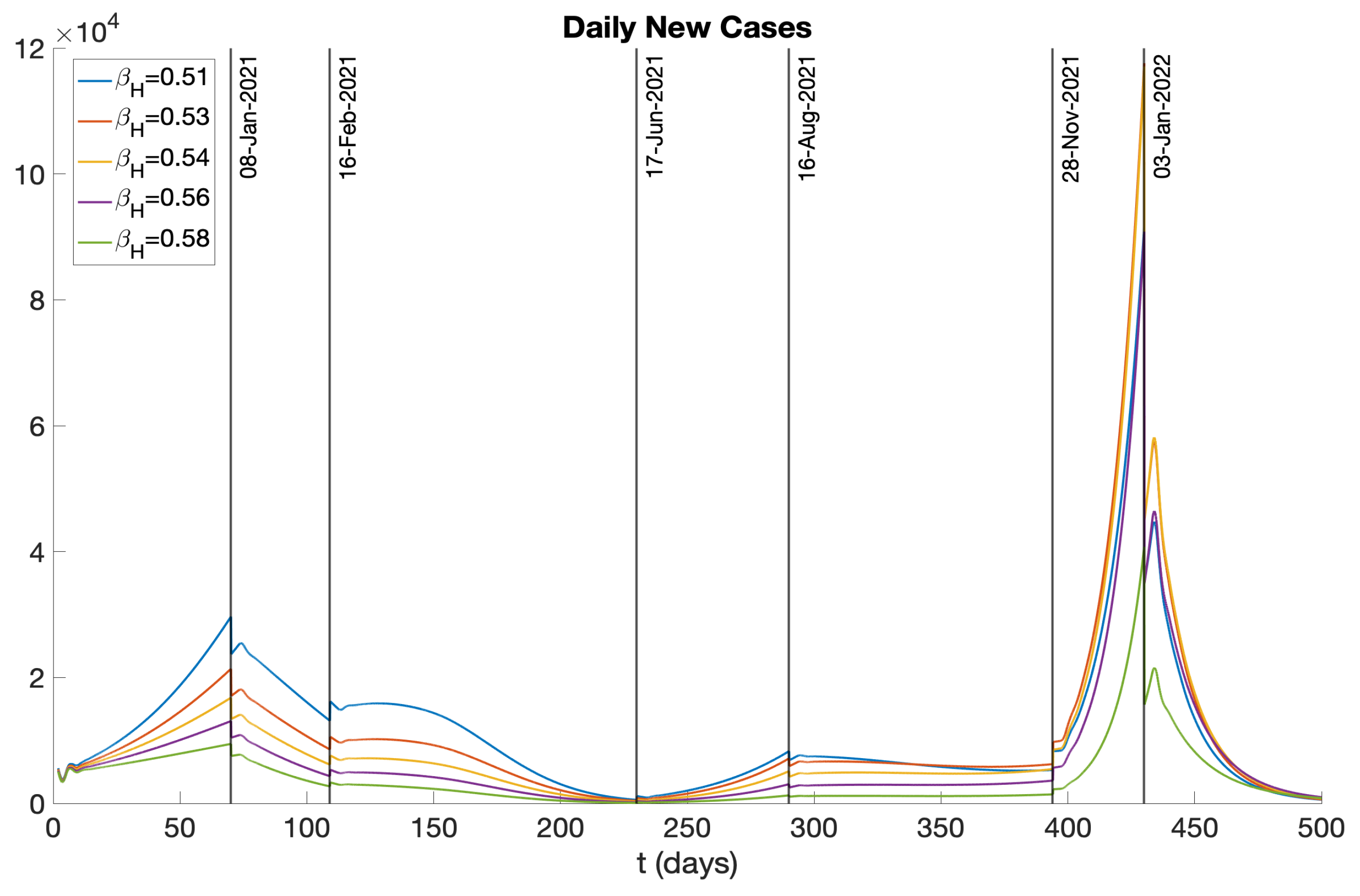
• Phase 1 (11/01/2020 – 01/08/2021) There was no vaccination in this phase.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 8.4\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 8.4\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 2 (01/08/2021 – 02/16/2021) With the commencement of vaccination campaigns and growing public caution, there was a small decrease in the COVID-19 transmission rate.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 6.7\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 6.7\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 3 (02/16/2021 – 06/17/2021) The emergence and prevalence of the Alpha variant [10] brought a small increase in the transmission rate.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 8.3\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 8.3\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 4 (06/17/2021 – 08/16/2021) In June 2021, the arrival of the Delta variant [11] led to a rapid surge in COVID-19 cases. It is estimated that the Delta variant is 60%–90% more transmissible than the Alpha variant [11,12].

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 17.7\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 17.7\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 5 (08/16/2021 – 11/28/2021) In response to the rise of the Delta variant in August 2021, policies such as a universal mask mandate for all public and private schools were implemented [9], leading to a reduced transmission rate.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 14.2\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 14.2\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 6 (11/28/2021 – 01/03/2022) The Omicron variant [13] was first discovered in Botswana and South Africa in November 2021 and quickly spread to other countries, including the United States. In December 2021, the emergence of the Omicron variant led to a significant surge in COVID-19 cases.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 23.6\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 23.6\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$
• Phase 7 (01/03/2022 – 03/13/2022) Reacting to the emergence of the Omicron variant, various preventive policies, such as mask mandates and “Comprehensive Winter Surge Plans”, were introduced [9], leading to a decrease in the transmission rate.

  $$\alpha \left(a_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le a_i<r,\hfill \\ 8.7\times {10}^{-9}(a_i-r)\hfill & \mathrm{if}r\le a_i<r+7,\hfill \\ 8.7\times {10}^{-9}\times \frac{7}{s-7}(r+s-a_i)\hfill & \mathrm{if}r+7\le a_i<r+s,\hfill \\ 0\hfill & \mathrm{if}r+s\le a_i.\hfill \end{array}\right.$$

The transmission rate $\alpha (a_i,t)$ as a function of disease age $a_i$ and time t is depicted in Figure 17.

Similar to the example of SARS, we utilize the daily reported data from October 16, 2020, to October 29, 2020 (a 14-day period before October 30, 2020) as the initial distribution of $i(a_i,0)$. Specific, at $t=0$,

$$i(a_i,0)=\left\{\begin{array}{cc}2328\hfill & \mathrm{if}{a}_i\le 1,\hfill \\ 2369\hfill & \mathrm{if}1<a_i\le 2,\hfill \\ 2511\hfill & \mathrm{if}2<a_i\le 3,\hfill \\ 2328\hfill & \mathrm{if}3<a_i\le 4,\hfill \\ 2314\hfill & \mathrm{if}4<a_i\le 5,\hfill \\ 1164\hfill & \mathrm{if}5<a_i\le 6,\hfill \\ 1304\hfill & \mathrm{if}6<a_i\le 7,\hfill \\ 2028\hfill & \mathrm{if}7<a_i\le 8,\hfill \\ 2337\hfill & \mathrm{if}8<a_i\le 9,\hfill \\ 2177\hfill & \mathrm{if}9<a_i\le 10,\hfill \\ 2044\hfill & \mathrm{if}10<a_i\le 11,\hfill \\ 2177\hfill & \mathrm{if}11<a_i\le 12,\hfill \\ 1189\hfill & \mathrm{if}12<a_i\le 13,\hfill \\ 1115\hfill & \mathrm{if}13<a_i\le 14.\hfill \end{array}\right.$$

The graph of this initial disease age distribution $i(a_i,0)$ is plotted in Figure 16. We assume $S\left(0\right)=19,500,000$ (https://usafacts.org/data/topics/people-society/population-and-demographics/).

In contrast to the SARS outbreak in Taiwan in 2003, where vaccination was not an option, the availability and administration of COVID-19 vaccines have significantly influenced the dynamics of its transmission. While COVID-19 vaccines have proven to offer substantial protection to those who are susceptible, they are not infallible—people can still get COVID-19 after vaccination. This means that the COVID-19 vaccination is not 100% effective. We assume that the vaccination age-dependent function $\sigma \left(a_v\right)$ decreases from 1 to 0.3 within two weeks, resulting in a 70% effectiveness for COVID-19 vaccines. This level of effectiveness persists for six months and then steadily wanes, reaching 0% (i.e., $1-\sigma =0$) after a year. This assumption is based on the administration of annual boosters, indicating that the COVID-19 vaccines’ protection wanes after a year. The graph of $\sigma \left(a_v\right)$ is shown in Figure 16.

The vaccination rate $\nu \left(t\right)$ (see Figure 16) is fitted using the daily vaccination data for New York State (https://health.data.ny.gov/Health/New-York-State-Statewide-COVID-19-Vaccination-Data/duk7-xrni). It takes the form

$$\nu \left(t\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}t\le 65,\hfill \\ 6\times {10}^{-5}(t-65)\hfill & \mathrm{if}65<t\le 110,\hfill \\ 0.27\%\hfill & \mathrm{if}110<t\le 145,\hfill \\ 0.82\%\hfill & \mathrm{if}145<t\le 200,\hfill \\ 0.50\%\hfill & \mathrm{if}200<t\le 242,\hfill \\ 0.33\%\hfill & \mathrm{if}t>242.\hfill \end{array}\right.$$

We assume a vaccination rate of 0 before $t=65$, aligning with the actual start of complete vaccinations (i.e., two-dose vaccination) in New York State on December 15, 2020. The rising vaccination rate from $t=65$ to $t=110$ reflects the initial scarcity of vaccine doses, which were prioritized for older adults and high-risk hospital workers. As vaccine production ramped up and more vaccination sites were established, the pace of vaccinations increased, making an increasing vaccination rate. After $t=110$ we assume a series of distinct constant vaccination rates, each applicable to specific time intervals, to best represent the varying pace of vaccination during those periods. These constant rates for each interval have been determined based on data fitting.

We employ the Forward Euler Scheme with a time step of 0.1 to discretize our model using the parameter values mentioned above. The resulting graph depicting the daily and cumulative infections is represented by the red curves in Figure 14. It agrees well with the data, and our simulated curve aptly captures the significant surge in COVID-19 cases attributed to the Omicron variant.

We analyze the effects of p on the number of infectives in the model. The parameter p represents the number of days during which the infectious and symptomatic periods overlap. We explore two scenarios: $p=1$, where the infectious period precedes symptoms by a day, and $p=0$, where the infectious period and the symptomatic period coincide (see segments 3 and 4 in Figure 13). With other parameters held constant, the results for daily new and cumulative infectious cases are illustrated in Figure 18 and Figure 19. Notably, for $p=0,1$, daily new cases near zero after 50 days, indicating effective disease control. This underscores the efficacy of hospitalizing symptomatic patients as a means to isolate infectious individuals and control the disease’s progression.

In addition, we further examine the effects of varying vaccination rates on the number of infectives. Specifically, we consider two scenarios: one with a vaccination rate of $0.5\nu \left(t\right)$ and another with $2\nu \left(t\right)$. Figure 20 and Figure 21 display the daily new and cumulative infectious cases for vaccination rates of $\nu \left(t\right)$, $0.5\nu \left(t\right)$, and $2\nu \left(t\right)$. Our findings suggest that a lower vaccination rate results in a higher number of infectious cases. Moreover, if the vaccination rate is doubled in the initial stage, the disease can be fully suppressed by approximately day 200. Another noteworthy observation is that with a vaccination rate of $0.5\nu \left(t\right)$, there is a peak in daily new infections around day 300. Yet, during the phase attributed to the Omicron variant, the number of new infections is significantly lower. This can be attributed to our assumption that infectives are not susceptible to re-infection. Consequently, the peak of infections around day 300 significantly reduces the number of susceptible individuals, and thus there are not many new infectious cases after day 400.

Building on our analysis of vaccination rates, we next turn our attention to the role of hospitalization rates in controlling the spread of COVID-19. We investigate how variations in the hospitalization rate (after symptoms appear), denoted by ${\beta }_H$, affect the number of infections. In Figure 22, we present the daily new cases, and in Figure 23, we illustrate the cumulative cases, each for a range of values from 0.51 to 0.58. The different curves in these figures demonstrate the sensitivity of the infection dynamics to hospitalization practices, revealing that higher hospitalization rates can significantly flatten the curve and reduce the total number of infections over time. These insights point to the critical impact of hospitalization rates on the management of the disease, alongside vaccination strategies.

3. Conclusions

We have developed a population model of an epidemic structured by infection age and vaccination age. The population dynamics are analyzed with respect to infection age of infected individuals before symptoms appear, the fraction of pre-symptomatici infected individuals placed in quarantine, and the vaccine efficacy of vaccinated individuals with respect to their vaccination age. the model is applied to the 2003 SARS epidemic in Taiwan and the current COVID-19 epidemic in New York State. The computer codes for our numerical simulations are available upon request in both MATHEMATICA and MatLab.

In the application of the model to the 2003 SARS epidemic in Taiwan, in which vaccination was not available, the on-set of symptoms and the beginning of the infectious period coincided. The quarantine rate of susceptibles was approximately $2\%$ per day. The epidemic was contained with the maximum cumulative number of infecteds at approximately 230 in 100 days (Figure 1).

We modified the pre-symptomatic and infectious periods to $p=1$ and $p=2$ days infectious pre-symptomatic. we also modified the quarantine rate to $4\%$ and $10\%$. The results are shown in Figure 7, Figure 8 and Figure 9, where it is seen that the value $p=2$ has much higher cumulative cases than the value $p=1$. When $p=2$, the quarantine rate must be very high to significantly reduce the cumulative number of cases.

We also modified the 2003 SARS epidemic model to illustrate the impact of vaccination. In Figure 10 it is seen that infectious 2 days pre-symptomatic ($p=2$), quarantine rate $4\%$, and the vaccine efficacy $\sigma \left(a_v\right)=.7exp(-.25a_v)+.3$, results in a reduction of the maximum cumulative number of cases to $175,000$ compared to $350,000$ without vaccination.

In the application of the model to the current COVID-19 epidemic in New York State, the infectious period is pre-symptomatic by $p=2$ days. This pre-symptomatic infectious period is a key feature of COVID-19 epidemic dynamics. From data sources, we parameterized the model into seven phases corresponding to vaccine implementation, viral variants, and social responses. The model simulations agree with the observed infection and vaccination (Figure 14 and Figure 15).

We examined the consequences of modifying the pre-symptomatic infectious period, initially set at $p=2$ days, by considering $p=1$ day and $p=0$ days. Figure 18 and Figure 19 display numerical simulations for $p=0,1,2$. It is seen that $p=0$ and $p=1$ result in a major reduction of the epidemic impact. We also investigated the impact of varying the vaccination rate parameter $\nu \left(t\right)$. Figure 20 and Figure 21 show that an increase in $\nu \left(t\right)$ significantly mitigates the epidemic, while a decrease in $\nu \left(t\right)$ exacerbates the epidemic. Furthermore, we explored the effects of changing the hospitalization parameter ${\beta }_H\left(a_i\right)$. In Figure 22 and Figure 23, we observed that higher values of ${\beta }_H\left(a_i\right)$ significantly decrease the epidemic’s severity, whereas lower values of ${\beta }_H\left(a_i\right)$ increase the epidemic’s severity.

In general, incorporating infection age and vaccination age into our analysis enables a detailed examination of key factors affecting epidemic outcomes. The continuum formulation of the infection age and vaccination age provides applicable parameter identification and numerical simulation of this age structure. Specifically, infection age and vaccination age can be connected to critical elements, such as pre-symptomatic infectiousness, vaccination efficacy, and hospitalization rate, which are integral to understanding and predicting epidemic dynamics.

While our model incorporates various factors, it remains a simplified representation of real-world disease transmission. It’s important to highlight potential areas for refinement to make the model more realistic. For instance, reinfections are notably common with COVID-19 [14]. As the Omicron variant became predominant, data indicated a significant rise in reinfection rates among all COVID-19 cases [15]. Additionally, revaccination is another factor to account for, given the CDC’s recommendation for individuals aged 12 and older to receive an updated COVID-19 vaccine annually [16]. A refined flow diagram that provides a more realistic depiction of disease transmission is presented in Figure 24. This diagram incorporates transitions such as $R\to S$, $Q\to S$, and $H\to S$ to account for reinfection, as well as the $V\to S$ transition for revaccination. We will consider models for this enhanced flow diagram in our future study. Notably, another promising direction for enhancement is the integration of chronological age. Data on COVID-19 often categorizes by age groups, and different age brackets might exhibit varied transmission rates [17,18,19]. This consideration will be a focus in our subsequent analyses.