Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

TAEF: A Task Allocation-based Ensemble Fuzzing Framework for Optimizing the Advantages of Heterogeneous Fuzzers

A peer-reviewed article of this preprint also exists.

Submitted:

14 November 2023

Posted:

14 November 2023

You are already at the latest version

Abstract
Ensemble fuzzing in parallel with heterogeneous fuzzers has been proposed to leverage the advantages of diverse fuzzers and improve testing efficiency. However, in current ensemble fuzzing methods, the collaboration among different fuzzers is achieved solely by synchronizing the seeds discovered by each fuzzer. This results in a high likelihood of different fuzzers choosing the same seeds and creating a large number of equivalent testcases, thus reducing overall fuzzing efficiency. Meanwhile, the existing task division method proposed by AFLTeam is highly coupled with the fuzzer specially designed for it, making it challenging to apply to ensemble fuzzing directly. So, in this paper, we proposed a callgraph-based task division method suitable for ensemble fuzzing. Firstly, we divided the target program’s callgraph into subgraphs (subtasks) balancing expected workloads. Then, we divided the global seed corpus into sub-corpora, each corresponding to a subtask, making fuzzers easily accept the subtasks. Finally, we designed synchronization mechanisms for coverage bitmaps and seeds to realize the collaborative fuzzing among different fuzzers, and a cyclic subtask scheduling strategy to fully leverage the benefits of ensemble fuzzing. We have implemented a prototype called TAEF. The evaluation results show that in the best-case scenario, our method has up to 24% more branch coverage than previous work.
Keywords: 
Fuzz testing
;  
Software testing
;  
Grey-box fuzzing
;  
Ensemble fuzzing
;  
Callgraph division
Subject: 
Computer Science and Mathematics  -   Security Systems

I. Introduction

Fuzzing is an efficient software testing method [1,2], which has become one of the primary technologies for detecting vulnerabilities [3]. Fuzzing can be categorized into various types, including black-box fuzzing, white-box fuzzing, and grey-box fuzzing, based on the accessibility of the target program [4]. The most widely adopted method for testing source code defects is coverage-guided grey-box fuzzing (CGF) [5,6,7,8,9,10], which uses lightweight instrumentation to obtain execution trace (coverage information) of the target program, and utilizes coverage feedback to guide testcases generation to get more branch coverage [11,12].
To speed up the fuzzing process, a method using multi-core named parallel fuzzing is proposed. This type of method parallels multiple instances of the same fuzzer, like AFL, to increase the number of test cases executed per unit of time [13], and regularly synchronize newly discovered seeds among paralleled instances to make them work together. However, the key strategies that determine the effectiveness of fuzzing, such as seed selection, seed energy allocation, and seed mutation, are identical for all instances, making parallel fuzzing hard to overcome the inherent limitations of the fuzzer used. Hence, EnFuzz [14] proposed an ensemble fuzzing framework that employs several heterogeneous fuzzers for parallel execution on the target program while periodically synchronizing new seeds to realize collaborative testing among the fuzzing instances. EnFuzz has ascertained that the ensemble fuzzing of multiple heterogeneous fuzzers can indeed achieve a higher branch coverage compared to parallel fuzzing which uses multiple instances of a single fuzzer. However, these parallel fuzzing methods synchronize newly discovered seeds between paralleled fuzzing instances or fuzzers without any task division mechanism. It could lead to a high possibility of each paralleled fuzzing instance or fuzzer similar mutations on the same seed selected, resulting in a significant amount of redundant work, and consequently decreasing the overall efficiency of parallel fuzzing.
Several task division strategies are proposed in the research on parallel fuzzing. The PAFL [15] proposed a bitmap-based task division method. It partitions the coverage bitmap into equally sized blocks. Each paralleled fuzzing instance is allocated one of these blocks as its subtask for testing. During the process of fuzzing, the fuzzer only mutates seeds whose rarest covered branch falls within its assigned bitmap block. The evaluation of this approach indicates that it can indeed enhance the efficiency of parallel fuzzing to some extent. However, the adjacent branches on the bitmap, generated through hash mapping, probably do not correspond to related branches in the control flow. Therefore, the various subtasks of PAFL are actually intertwined, which limits the efficiency improvement brought about by this task division approach.
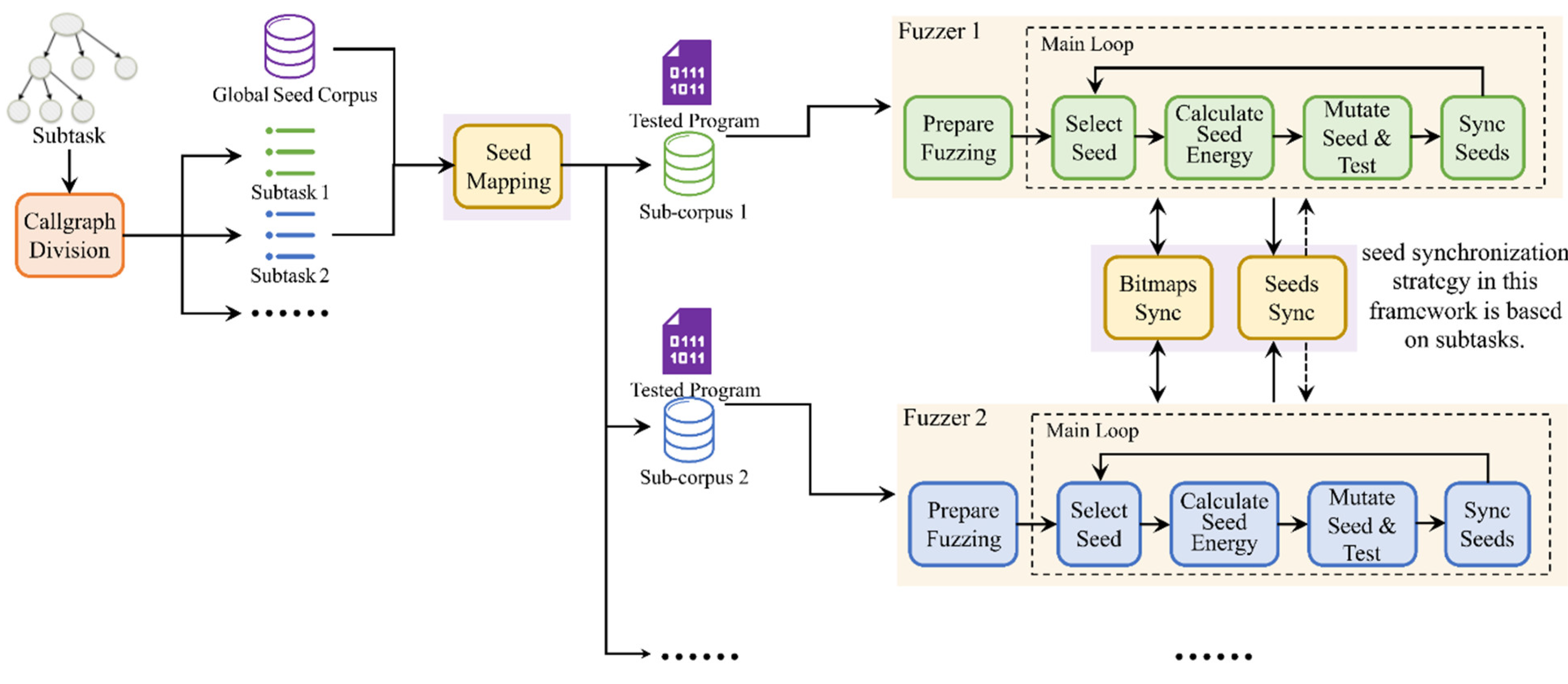
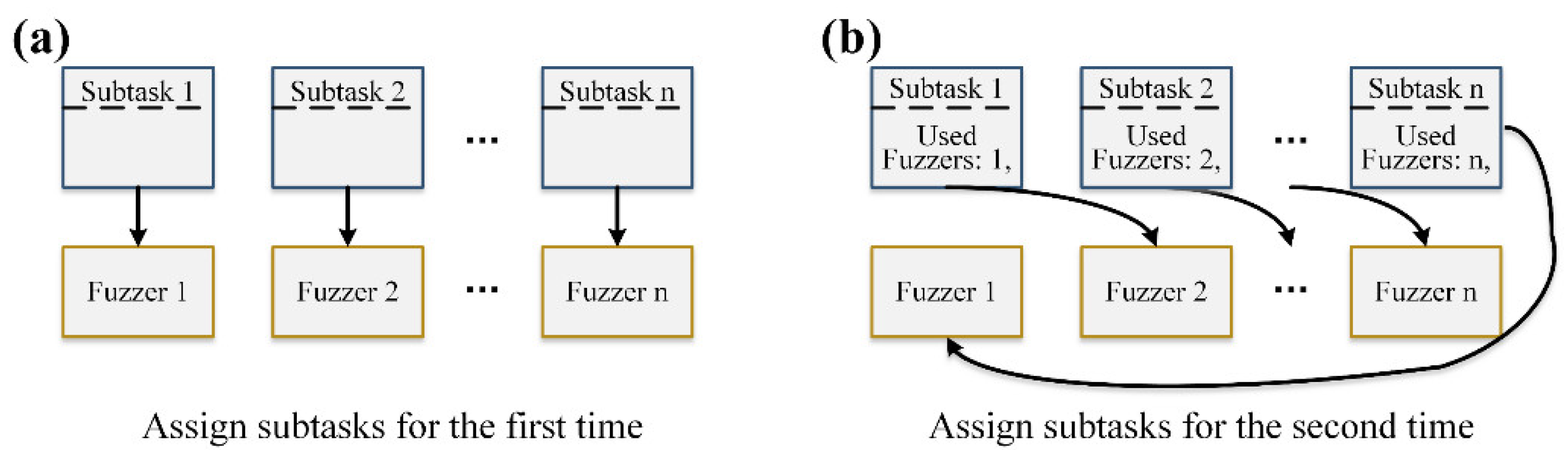
AFLTeam [16] introduced a callgraph-based task division method, dividing the function call graph of the tested program into subgraphs. Each fuzzing instance is assigned one of these subgraphs as its fuzzing task and would only mutate seeds hit its task. Thus, AFLTeam reduces duplicate work and improves the efficiency of parallel fuzzing. However, this kind of task division mechanism is highly coupled with the used fuzzer in implementation. As depicted in Figure 1a, most original coverage-based grey-box fuzzers (CGFs) can only take the tested program and the initial seed corpus as inputs. Therefore, it is obvious that extensive modifications are required for fuzzers to meet AFLTeam's requirement of parsing subtasks and leveraging them for guiding the fuzzing process. Specifically, as shown in Figure 1b, it is essential to add subtask parsing and storing functions in the step of preparing before starting the main loop of fuzzing. Meanwhile, within the main loop of fuzzing, adjustments must be made to the seed selection strategy which adds a seed filter function, to avoid mutating and testing seeds that do not cover any functions in assigned subtasks. Thus, utilizing such task division method directly in ensemble fuzzing frameworks, which use various fuzzers in parallel, to reduce duplicate work in fuzzing seems to be an exceedingly massive work and lacks scalability. Furthermore, it may impact the selection of the seed and potentially decrease the diversity of paralleled fuzzers in ensemble fuzzing, thereby undermining the effectiveness of ensemble fuzzing, which surpasses the parallel fuzzing of a single fuzzer.
To address these challenges, this paper presents a task allocation-based ensemble fuzzing method to coordinate parallel heterogeneous fuzzers. As illustrated in Figure 2, our approach implements all functions related to filtering out seeds, which are the main modifications made in the fuzzer specially designed for AFLTeam, beyond the fuzzers. Therefore, we effectively decouple the task division strategy from the fuzzers and thus enhance the scalability to a great extent. However, this would result in each paralleled fuzzer in our framework only accessing a subset of the global seed corpus, which may prevent the fuzzer from acquiring the complete coverage of the tested program. In this case, the fuzzer may save seeds already found by other paralleled fuzzers or new seeds not associated with the assigned subtask to it, into its seed queue, causing the fuzzer bias from the subtask currently assigned to it. To avoid this, we designed bitmaps & seeds synchronization methods, which are also above the fuzzers. To the best of our knowledge, there are no such solutions in ensemble fuzzing yet.
To be more specific, our method mainly includes three parts, which are as follows:
  • Callgraph division. Firstly, the program’s callgraph was partitioned into small, closely related subgraphs based on the function invocation dependencies by utilizing the existing tree division method. Then, these small subgraphs were merged into the given quantity of subgraphs (equal to the number of parallel fuzzing instances) with approximately equal estimated fuzzing workloads, and every subgraph is easy to explore.
  • Subgraph association and seed mapping. According to the total weight of functions belonging to each subgraph in the function-level trace of every seed, the global seed corpus was divided into sub-corpora dynamically. The task division problem with heterogeneous ensemble fuzzing is then resolved by assigning these sub-corpora to each fuzzer.
  • Bitmaps & seeds synchronization and task scheduling. Bitmaps and seeds synchronization strategies are designed to synchronize the progress of each fuzzer. Specifically, the bitmaps of all paralleled fuzzers will periodically synchronize to their union, enabling each fuzzer to acquire the current overall branch coverage status of the program under test. New seeds discovered by every fuzzer will be immediately allocated to the fuzzer currently performing fuzzing on the corresponding sub-task. Additionally, there is also a task scheduling strategy. The sub-corpus corresponding to each sub-task is allocated using the strategy of cyclic scheduling, ensuring the full utilization of the advantages of ensemble fuzzing in all sub-tasks.
The main contributions of this paper are as follows:
  • We designed a scalable callgraph-based task division method for ensemble fuzzing. By mapping the target program’s callgraph division to the division of the global seed corpus, the problem of dynamic task division in heterogeneous ensemble fuzzing was solved. The method is scalable and can be extended to more heterogeneous fuzzers.
  • We implement a prototype of our method and evaluate its efficiency. In the experiment, four heterogeneous fuzzers in the ensemble fuzzing system including AFLFast, MOPT, QSYM, and radamsa were incorporated. Compared to the collaborative parallel fuzzing of AFLTeam, the developed system achieved up to 24.04% more branch coverage.

II. Background and Related Work

Fuzzing is an automated software testing technique that finds program crashes and exposes software bugs by generating a substantial amount of random testcases as input to the program under test [17]. In recent years, related researchers have proposed various improvements to enhance the effectiveness of fuzzing, including coverage-guided grey-box fuzzing (CGF) [5,6,7,8,9,10], directed fuzzing [18,19,20,21], and hybrid fuzzing that combines dynamic symbolic execution [22,23,24] and taint analysis [25,26]. Coverage-guided grey-box fuzzing is the predominant method at present, which obtains the execution path coverage information of the test case through program instrumentation, to guide the generation of subsequent testcases and increase coverage of the target program [4].
The parallelization of fuzzers is a primary way to enhance the efficiency of fuzz testing, which can be classified into two major categories: parallel fuzzing with multiple instances of the same fuzzer [15,16,27,28]; and ensemble fuzzing with paralleled instances of different fuzzers [14,29].

A. ENSEMBLE FUZZING

The traditional approaches of parallel fuzzing run multiple instances of a single fuzzer in parallel to speed up the fuzzing process. However, this type of method can result in each fuzzing instance having the same characteristics, meaning they tend to cover the same branches of the tested program. As a result, traditional parallel fuzzing is limited in effectively covering those branches that are difficult to reach with a single fuzzing instance.
In reference [14], it is discovered through experimentation that different fuzzers tend to explore different parts of the target program. Based on this finding, the first ensemble fuzzing framework named EnFuzz was proposed. EnFuzz utilizes different fuzzers for every paralleled fuzzing instance rather than the same one and synchronizes their seed corpora regularly. Thus, it can fully leverage the strengths of every fuzzer it uses. The evaluation of EnFuzz shows that the ensemble fuzzing framework, which parallels multiple heterogeneous fuzzers, can indeed cover more branches of the target program than the traditional parallel fuzzing framework.
Building upon this work, CUPID [29] proposes a combined optimization method for heterogeneous fuzzers used in ensemble fuzzing, further improving testing efficiency. It provides a method for obtaining a combination of fuzzers that are universally applicable to various tested programs through pre-training with every candidate fuzzer singly. The fuzzer combination it offers is more complementary than what is manually provided by EnFuzz, meaning that they tend to explore different program spaces, thereby achieving better overall efficiency.
However, the ensemble fuzzing frameworks lack mechanisms for task division. Whether in EnFuzz or CUPID, each paralleled fuzzer adopts the seeds synchronization method similar to that of AFL, causing the seed corpora corresponding to each of them to be highly analogous. Meanwhile, the seed mutation strategies of different fuzzers are also similar. As a result, there is a significant amount of duplicate work in current ensemble fuzzing frameworks, resulting in a reduction in the overall fuzzing efficiency.

B. Task Division in Parallel Fuzzing

The problem of duplicate work also exists in parallel fuzzing using a single fuzzer and impacting the overall efficiency of the parallel fuzzing seriously. So, there is already some research aiming to overcome this limitation for parallel fuzzing by using task division. The methods have been proposed are as follows:
Global seeds scheduling: Both P-Fuzz [27] and UltraFuzz [28] are designed based on this type of approach. They implement a manager called the main node on top of the fuzzer and centralize the management and selection of seeds in the main node. Whenever a fuzzing instance needs to select the next seed for mutation, it requests a seed from the main node. Similarly, when any fuzzing instance discovers a new seed, it sends the new seed to the main node. However, this is not a method of task division in actuality. In this type of work, the fuzzer they used can no longer operate the whole fuzzing process without being combined with the main node. In other words, in the framework using this type of method, the fuzzer is no longer an individual part. So, they actually treat the tested program as a complete task. Indeed, it is precisely because the fuzzer used in this type of approach is inherently incomplete that it is theoretically unsuitable for generalization to the ensemble fuzzing.
Bitmap-based task division: Diverging from the aforementioned global seeds scheduling method, a framework named PAFL [15] introduces a novel approach for addressing the issue of significant redundancy among paralleled fuzzing instances. Specifically, PAFL evenly divides the bitmap, which is widely used in CGF to indicate the covered branched of the tested program, into multiple blocks, with the number of blocks matching the number of paralleled fuzzing instances, and assigns each block to a fuzzing instance in sequential order. The fuzzer it provided will only mutate seeds whose rarest covered branch falls within the bitmap region allocated to it. However, as adjacent branches on the bitmap have no logical relationship with each other, the corresponding subtasks of the bitmap blocks are composed of scattered branches in various functions of the program under test. So, it is difficult for each fuzzing instance in PAFL to conduct concentrated and in-depth testing on their allocated subtasks.
Callgraph-based task division: To overcome the issue of PAFL, a parallel fuzzing framework called AFLTeam [16] proposes a task division approach based on the function call graph of the target program. In AFLTeam, the callgraph of the tested program, represented as a minimum spanning tree, is partitioned into subgraphs based on workload balancing principles. Each subgraph is sequentially assigned to a fuzzing instance as its allocated subtask. The fuzzer will only mutate those seeds that can reach at least one function in its assigned subtask.

C. Challenges in Applying Task Division in Ensemble Fuzzing

The task division methods, especially the callgraph-based task division method proposed by AFLTeam, do improve the efficiency of parallel fuzzing. However, these task division methods are highly coupled with the fuzzers specifically designed for them. First of all, as shown in Figure 1a, the most widely used general-purpose fuzzers are incapable of parsing and saving the tasks assigned to them at all, regardless of whether those tasks are based on bitmap-division or callgraph-division. As depicted in Figure 1b, to apply task division methods, AFLTeam modified the fuzzer by adding a function to parse the assigned task and related data structures to save all the target functions in the task. Moreover, simply modifying the fuzzer to be capable of parsing and saving the assigned tasks is not sufficient. Within the main loop of fuzzing, when selecting the next seed to mutate, it is necessary to check the execution trace of the tested program when using the alternative seed as input, thus filtering out seeds that do not cover any functions belonging to the assigned task.
Therefore, it is evident that applying the current task division method to a new fuzzer would require extensive and non-generic modifications to the fuzzer. Consequently, directly applying such a method to ensemble fuzzing frameworks entails significant modifications to each paralleled fuzzer, resulting in a massive workload and lack of scalability.
Thus, to reduce workload and enhance scalability, there is no choice but to decouple the task division method from the fuzzer. In other words, the functionality of task parsing, seed filtering, and other related operations must be implemented on a higher level above the fuzzer, which means the task division is transparent to fuzzers. However, such an approach brings additional issues. Among them, the most significant problem is that each fuzzer would be unable to acquire the global fuzzing progress of the tested program, such as the global branch coverage, which leads to the generation of duplicate seeds or seeds that deviate from the assigned objectives of the current fuzzer. If this problem cannot be resolved, the efficiency of fuzzers will rapidly deteriorate throughout the fuzzing process, rendering the task division method ineffective.

III. Concepts and Methods

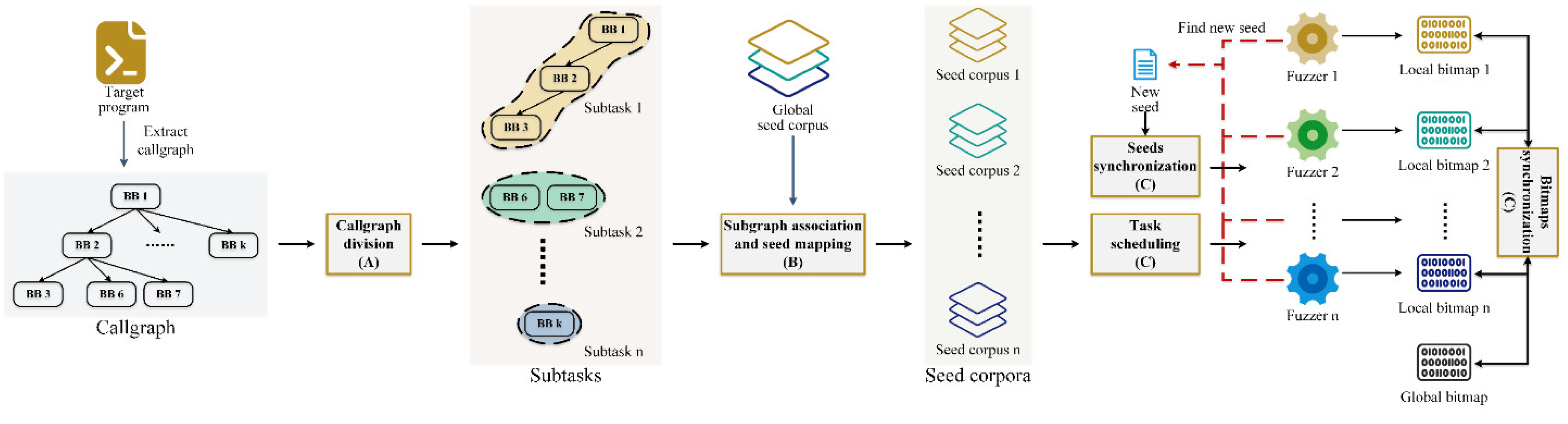
In this paper, a task allocation-based ensemble fuzzing framework for reducing repetitive work was designed. This framework first divides the callgraph of the target program into multiple subgraphs. Then, it divides the global seed corpus into sub-corpora based on the association between the subgraphs obtained above and the execution trace of each seed. These sub-corpora are allocated as fuzzing tasks to different heterogeneous fuzzers. More importantly, the framework introduces strategies for synchronizing bitmaps and seeds between the heterogeneous fuzzers, as well as a task scheduling method. As shown in Figure 3, the framework consists of three main parts:
Callgraph division (Section III-A): The callgraph of the program under test was obtained through static analysis, updated with seeds execution traces, and then transformed into a minimum spanning tree. After that, the callgraph is divided into subgraphs by using the minimum spanning tree partitioning algorithm [30]. Finally, the large number of subgraphs obtained through partitioning are merged into a given number of subtasks, aiming to achieve a balanced expected workload for each subtask and ensure that every subtask is easily accessible.
Subgraph association and seed mapping (Section III-B): The tested program is executed using each seed from the global seed corpus one by one as input. Then, based on the association between the execution paths of the tested program when using each seed as input and the subgraphs of the callgraph corresponding to each subtask, the global seed corpus is divided into sub-corpora, each corresponding to a subtask.
Bitmaps & seeds synchronization and task scheduling (Section III-C): During the process of fuzzing, the global bitmap is synchronized with the current bitmap of each paralleled fuzzer at fixed intervals. The updated global bitmap is then used to replace the bitmap of each fuzzer, allowing each paralleled fuzzer to access the progress of other subtasks. When a fuzzer discovers a new seed, instead of adding it to its local seed queue, it is sent to the global seed division program. Once receiving a new seed from any fuzzer, the global seed division program synchronizes it to the corresponding fuzzer currently fuzzing the subtask to which the execution path of the tested program using this seed as input mostly belongs. In addition, the divided subtasks are cyclically allocated to each fuzzer, enabling every subtask to be tested by all fuzzers. This ensures that the advantages of ensemble fuzzing can be utilized on each subtask.

A. Callgraph Division

Firstly, trim the initial callgraph of the tested program obtained during compilation, and convert the trimmed callgraph into a minimum spanning tree. Then, use existing tree partitioning algorithms [30] to divide the converted callgraph into numerous subgraphs. Finally, merge the obtained subgraphs into a specified number of subtasks, where each subtask corresponds to a merged subgraph. The aforementioned task can be divided into two major steps, as detailed below:
1)
Callgraph partition: The tested program is executed sequentially using each seed from the current global seed corpus as input. Based on the execution traces of the tested program, the functions (nodes) and function call relationships (edges) that are not present in the initial callgraph of the tested program obtained while compiling are added to the callgraph. Subsequently, duplicate edges, nodes without any basic blocks in their corresponding functions, and those nodes that cannot be accessed from the node corresponding to the "main" function are removed from the callgraph. Finally, the pruned callgraph is transformed into a minimum spanning tree and divided into a significant quantity of subgraphs with tight internal connectivity using the existing tree partitioning algorithm named Lukes' algorithm [30].
2)
Subgraph merging: After obtaining a considerable amount of subgraphs in the callgraph, firstly, each of those subgraphs that have no functions that can be called directly by the "main" function was merged to the subgraph that can call it to ensure that each subtask ultimately partitioned can be reached easily from the "main" function. Then, based on the total weight of all functions contained in each subgraph, they were merged as evenly as possible into a given number of subtasks and marked on the callgraph.

1). Callgraph Partition

Callgraph partition consists of four specific steps, which are as follows:
1)
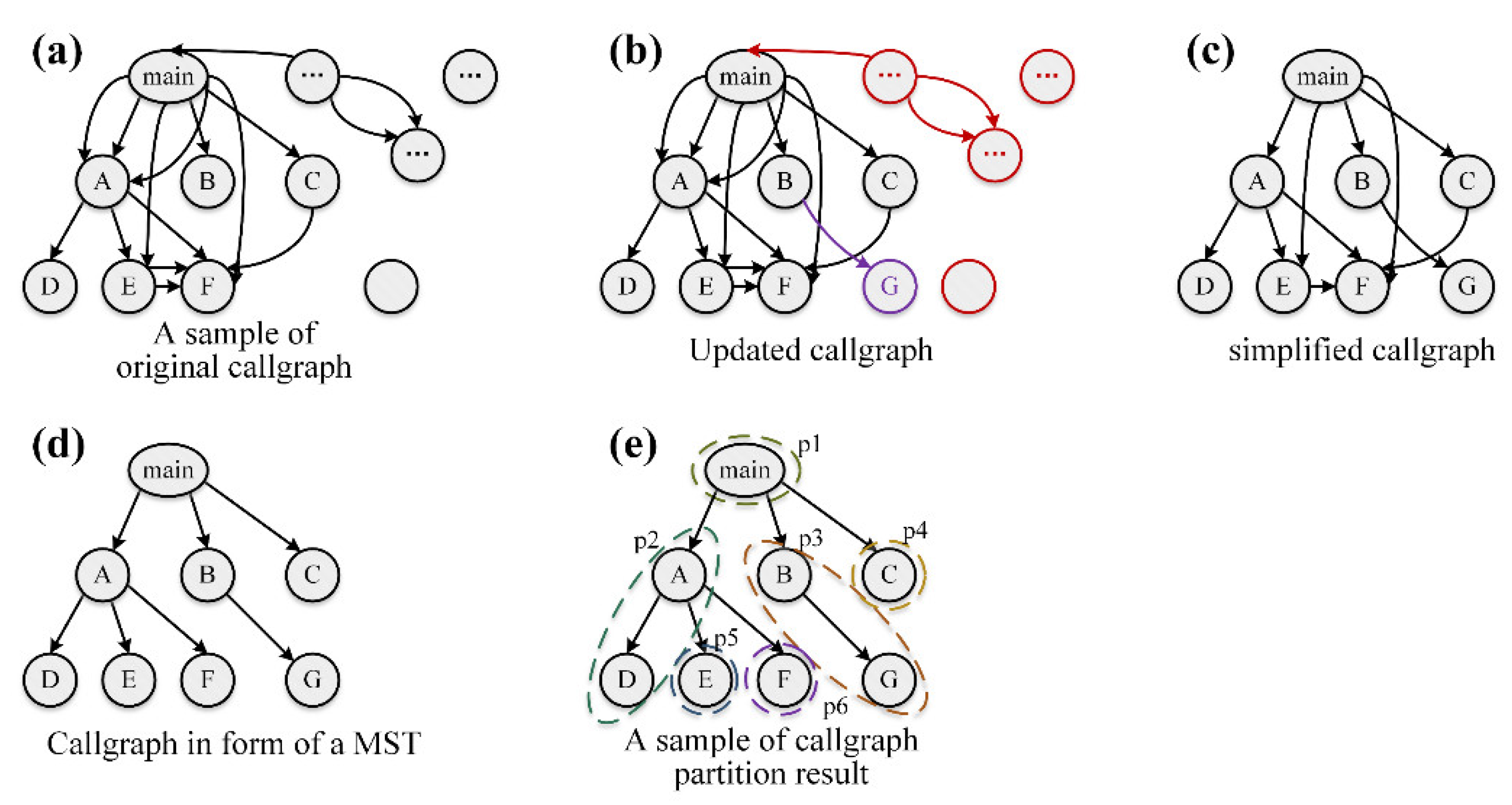
Callgraph updating. Before dividing the task, it is necessary to update the initial callgraph (as shown in Figure 4a as an example) obtained during the compilation of the tested program based on the fuzzing results up to now. Specifically, each seed in the current global seed corpus is used as input sequentially to execute the tested program and obtain the execution trace for each execution. Then, the functions (nodes) and function call relationships (edges) existing in the execution traces but not in the initial callgraph are added to the callgraph. Then, for each function (node) in the callgraph, the number of basic blocks, branches, and uncovered branches were attached to the node based on the execution results. A sample of the updated callgraph is shown in Figure 4b.
2)
Callgraph simplification. After updating the callgraph, duplicate edges and nodes containing no basic blocks or untraversable from the "main" function were deleted to trim the callgraph. The simplified callgraph is shown in Figure 4c. Then, the callgraph was transformed into the form of a minimum spanning tree, as illustrated in Figure 4d.
3)
Calculation of nodes' weights. From the perspective of balancing the workload of fuzzing, as shown in Figure 4d, the minimum spanning tree was weighted for each function node to estimate its fuzzing workload. The weight assignment principle is that the more branches a function has, the more complex it is, so the longer time it needs to take for fuzzing; at the same time, functions with more uncovered branches have more exploration potential, so they also require more fuzzing time. Specifically, the weighted sum of the total number of branches contained in the function and the number of uncovered branches was used as this function's weight, as shown in the following formula:
w e i g h t = α B t + β B u c * B u c γ * B t       i f   f u n c t i o n   = m a i n α B t + β B u c                                                                                       o t h e r w i s e
Among them, B t represents the total number of branches contained in the current function. B u c represents the number of uncovered branches in this function. α , β , and γ are all constants (in our evaluation, α = 1 , β = 3 , γ = 3 ). Since the "main" function serves as the entry point for every C/C++ program and will be explored by all fuzzing instances, its weight should be appropriately reduced. In addition, when the weight of a certain function is too large, Luke's algorithm would be unable to divide it, so the weight needs to be corrected. Specifically, the formula for correcting weights is as follows:
f i n a l W e i g h t = w e i g h t                     i f   w e i g h t ≤ W t n W t n                                                         o t h e r w i s e
Among them, W t represents the total weight of all functions the target program has; the character n represents the number of subgraphs to be ultimately partitioned.
4)
Callgraph partition. After obtaining the weight of each function (node) in the callgraph, the classic algorithm for tree partitioning named Lukes’ algorithm was used to partition the whole callgraph into a large number of divisions with close internal relationships, as shown in Figure 4e.
Further, the pseudocode for the callgraph partitioning algorithm is as follows:
Preprints 90486 i001
Remarks on the algorithm of callgraph division: Firstly, functions (nodes) and function call relationships (edges) that are unavailable from the static analysis were added to the callgraph by using the execution traces of seeds in the global seed corpus (lines 3 to 15). Secondly, the number of basic blocks, branches, and uncovered branches contained in each function was attached to each node in the callgraph (lines 17 to 20). Thirdly, duplicate edges (line 22) and function nodes without any basic blocks or cannot be reached from the "main" function (line 23) were deleted. Fourthly, the callgraph was transformed into the form of a minimum spanning tree (line 24). Then, the weight of each function node (line 26) was calculated and attached to each function node in the callgraph (line 27). Finally, Lukes' algorithm was used to partition the callgraph into a massive collection of subgraph divisions (line 29).

2). Subgraph Merging

Since the number of subgraphs divided from callgraph by Lukes' algorithm far exceeds the number of fuzzers’ instances, it is necessary to merge these subgraphs.
During actual testing, we found that AFLTeam had difficulty accessing certain subtasks of the tested program, which could potentially waste the fuzzing time of the fuzzing instances assigned to these subtasks. Therefore, unlike AFLTeam, we first merge the subgraphs that cannot be directly accessed by the "main" function in MST with the preceding subgraphs that can directly access those subgraphs. The result of this step is illustrated in Figure 5b. After that, merged subgraphs were arranged in descending order of the total weight of all functions contained in them, and the result was as shown in Figure 5c. Then, each subgraph was assigned to the subtask with the minimum total weight in turn to balance the expected workloads of each subtask, and the subtasks were as shown in Figure 5d. Finally, the merged subtasks were labeled on the callgraph, and the callgraph subgraphs representing each subtask were obtained as shown in Figure 5e.
Further, the pseudocode for the subgraph merging algorithm is as follows:
Preprints 90486 i002
Remarks on subgraph merging algorithm: Firstly, the subgraph containing the "main" function (line 2) was located, and the remaining subgraphs that cannot be called by the subgraph containing the "main" function directly were merged with the subgraph that can directly call this subgraph (lines 4 to 8). Then, merged subgraphs were arranged in descending order of the total weight of all functions included (line 10), and each subgraph was assigned to the subtask with the minimum total weight at that time in order (lines 17 to 21). Finally, the subtask number that each function node belongs to was attached to the node of the MST (lines 23 to 27).

B. Subgraph Association and Seed Mapping

The existing fuzzers are unable to directly utilize the callgraph of the target program to guide the fuzzing process, while all coverage-guided grey-box fuzzers essentially drive the fuzzing process by guiding seed selection. Generally, the execution traces of testcases generated by mutating seeds are highly likely to be the same as or adjacent to those of the original seeds. When the closely related callgraph subgraphs of the program under test are divided into the same subtask, testcases generated by mutating the seeds belonging to a certain subtask still belong to this subtask with a high probability.
Based on the key observations above, this article proposes a method to map the callgraph-based task division to the division of the seed corpus, to introduce task division into the ensemble fuzzing framework. The global seed corpus is divided into sub-corpora, each corresponding to a sub-task, by considering the portion of each seed's execution trace that belongs to the sub-callgraph of the corresponding sub-task. Subsequently, each sub-corpus is assigned to a different fuzzer to guide focused fuzzing on different spaces of the target program.
Specifically, after obtaining the callgraph with subtask division information, all seeds in the global seed corpus were used as the input to execute the tested program sequentially, and for each seed, the total weight of functions belonging to each subtask along its execution trace was tallied up. Then, the seed was assigned to the subset of the global seed corpus corresponding to the subtask with the highest weight sum.
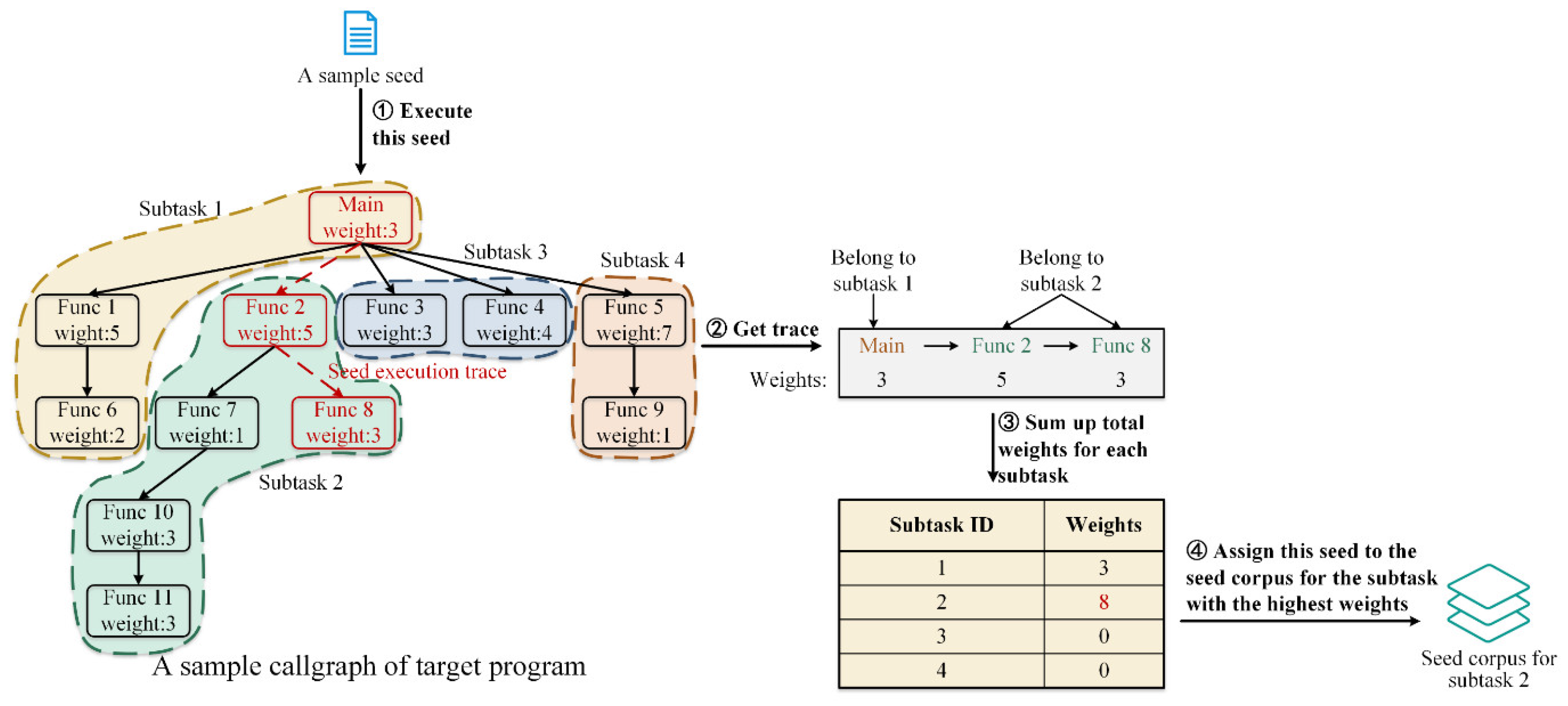
Taking one seed from the global seed corpus as an example, Figure 6 illustrates the method of determining which specific subtask a given seed belongs to. Firstly, the seed was used as the input to execute the target program, and the execution trace was marked on the callgraph. In this specific example, the execution trace corresponding to this seed is "Main" → "Func 2" → "Func 8", as shown in the red path on the callgraph. Next, the execution trace corresponding to this seed was extracted and each function in the trace was labeled with the subtask ID it belongs to and its weight. Specifically, the first function in the execution trace is "Main", which belongs to Subtask 1 with a weight of 3; the second and third functions in the trace are "Func 2" and "Func 8", which belong to Subtask 2 with weights of 5 and 3 respectively. After that, the total weight of each subtask corresponding to the execution path corresponding to this seed was counted. For this specific seed, the weight for Subtask 1 is just the weight of the "Main" function, which is 3; the weight for Subtask 2 is the sum of the weights of "Func 2" and "Func 8", which is 8; the trace does not pass through any functions belonging to Subtask 3 or Subtask 4, so its weights for these two subtasks are both 0. Finally, the seed was assigned to the subtask with the highest total weight, which in this example is Subtask 2 with a weight of 8.
When using the method mentioned above to divide the global seed corpus, there is a problem that the subsets of the global seed corpus corresponding to some of the sub-tasks can be empty. In this scenario, if a fuzzer is assigned to a sub-corpus that does not contain any seeds, the fuzzing process cannot even be initiated. Therefore, our approach must ensure that each sub-corpus has a sufficient number of seeds to fit the minimum requirement. Specifically, when dividing the seed corpus, a two-dimensional array was used to record the weights and the top k seeds for each subtask (the value of k is dynamic; when the total number of seeds is less than 100, k takes the value of the total number of seeds divided by 10 and rounded down, otherwise k takes the value of 10). After all the seeds in the global seed corpus have been assigned, these seeds will be additionally copied to the corresponding subset of the global seed corpus.
Further, the pseudocode for the seed mapping algorithm is as follows:
Preprints 90486 i003
Remarks on seed division algorithm: Firstly, each seed collected from the previous stage was used as the input to execute the target program sequentially (line 5). Then, the total weights of functions corresponding to each subtask on the execution trace corresponding to each seed were calculated respectively (lines 9-15). After that, the seed was assigned to the subtask with the highest weight (lines 17 and 18). Finally, to avoid scenarios where a subset of a specific seed corpus is empty, the top k seeds with the highest weights for each subtask will be additionally assigned to that subtask (lines 25-29), even if the weight of other subtasks corresponding to this seed is higher.

A. Bitmaps & Seeds Synchronization and Task Scheduling

1). Bitmaps Synchronization

In the ensemble fuzzing framework proposed in this paper, due to the division of the global seed corpus, each fuzzer’s instance maintains only its local bitmap, without knowledge of the current global branch coverage status during the fuzzing process. When the testcase generated by a fuzzing instance covers a new branch in its local bitmap, it would be considered that a new seed has been generated. However, other subtasks may already have seeds covering the same branch.
To this end, a strategy for bitmaps synchronization was designed: inter-process shared memory was used to store the bitmap, and the intersection of the coverage branch sets of all fuzzing instances was taken regularly to form a global bitmap, which was then directly written into the shared bitmap of each fuzzer’s instance. In this way, each fuzzer is able to obtain complete branch coverage of the tested program without knowledge of the seeds used by other fuzzers.

2). Seeds Synchronization

In the fuzzing process, testcases generated through the mutation of a particular seed may no longer belong to the original subtask. Suppose the deviations of the new seeds discovered by the fuzzer from the current task are not detected promptly. In that case, the new testcases are likely to deviate entirely from the task assigned to the fuzzer after several iterations. This renders the task allocation strategy practically ineffective. Therefore, it is necessary to introduce a seeds synchronization strategy, whereby after a fuzzer discovers a new seed, it is assessed to which subtask it belongs and then assigned to the fuzzer currently conducting fuzzing on that subtask.
To this end, a strategy for seeds synchronization was designed: when identifying a testcase as an interesting seed, it would be stored in a cache folder instead of the local queue of interesting seeds. The cache folders of all fuzzing instances would be monitored by a new seed division module, and when a new seed is detected, the subgraph association and seed mapping mechanism is used to determine the corresponding subtask of this seed and the seed would be synchronized to the seed corpus corresponding to that subtask. The fuzzers in our framework do not directly synchronize new seeds generated by other fuzzing instances anymore.

3). Task Scheduling

Unlike traditional parallel fuzzing, in ensemble fuzzing, different fuzzers are used for each fuzzing instance, so those fuzzing instances are not equivalent. Therefore, it is not suitable to randomly assign each subtask to a fuzzing instance after dividing the tasks, as done in works based on traditional parallel fuzzing such as AFLTeam. Otherwise, from the perspective of each subtask, it can only be fuzzed by one of the fuzzers, violating the basic principle of ensemble fuzzing to comprehensively utilize the advantages of different fuzzers on the same target. In other words, at each subtask, ensemble fuzzing degenerates into traditional parallel fuzzing, which leads to serious performance degradation.
To this end, we designed a rotating sub-task scheduling strategy based on the topology structure of a token ring. The periodic and sequentially rotating subtasks allocation strategy designed for n heterogeneous fuzzers and n subsets of seed corpora is as follows: As shown in Figure 7a, for the first time to allocate subtasks, subtasks were assigned to each fuzzer in order according to their respective IDs; And, as shown in Figure 7b, every test cycle, the subtasks were rotated sequentially among the fuzzers until each subtask has been fuzzed by all fuzzers.

IV. Fuzzing Processes and Framework

A. Fuzzing Processes

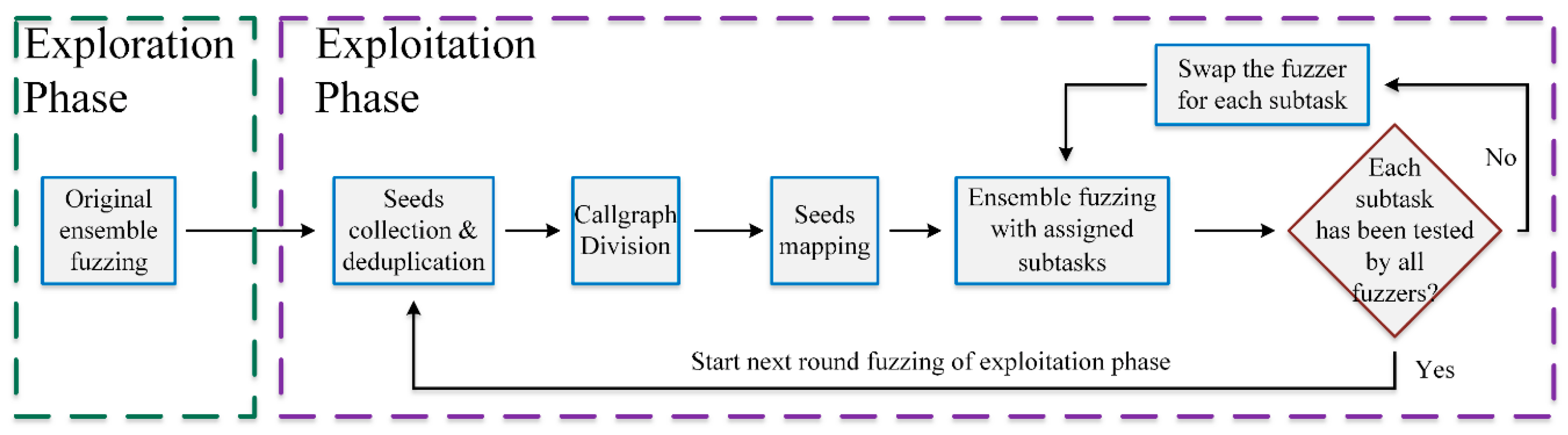
Overall, as shown in Figure 8, the actual fuzzing process of the ensemble fuzzing framework proposed in this paper, which is based on callgraph task division, can be divided into two main phases depending on whether the task division mechanism is enabled. The first phase is the Exploration Phase, during which the task division strategy is not activated. The second phase is the Exploitation Phase, where the task division strategy is used. Typically, in a complete fuzzing process, this phase will be executed multiple times. These two phases together constitute our entire fuzzing process and contribute to the final test results.

1). Exploration Phase

In general, during the initial phase of fuzzing a program, the fuzzer often discovers a large number of new seeds within a short period. However, after a certain period, the speed of finding new seeds significantly slows down. Therefore, if the task division strategy we designed above is used right from the start of fuzzing, it would result in a large number of seeds that need real-time division, and the time interval for synchronizing the bitmaps of each fuzzer would also need to be set to a very short period. All of these factors would significantly decrease the efficiency of the fuzzing itself. Therefore, in our approach, we first enter a phase called the exploration phase where no task division is applied, to quickly cover the easily covered branches in the program under test.
During this phase, the fuzzing was conducted without using the task division mechanism, but with using the original ensemble fuzzing approach. At this moment, multiple heterogeneous fuzzers specified by the user perform simultaneous fuzzing on the target program, which was the same as the original ensemble fuzzing approach, and synchronize the newly discovered seeds from each fuzzer at every fixed interval.
Besides rapidly covering those branches that are easily covered by fuzzing in the target program, this phase provides the seeds for updating the callgraph and the number of uncovered branches for each function in the target program in preparation for the subsequent subtask division making our task division method more efficient.

2). Exploitation Phase

Generally, after the initial period of quickly discovering new seeds, the fuzzing process enters a long period of slow seed discovery. During this time, the fuzzer needs to extensively mutate the seeds to find new ones, which can lead to parallel fuzzers performing redundant work. Therefore, after rapidly finding easily discoverable new seeds in the exploration phase, we use our previously designed task division method to reduce potential duplication and improve overall efficiency. This phase is referred to as the Exploitation Phase. Additionally, to adapt task division according to the current progress of the fuzzing, this phase would be executed usually more than once in a complete fuzzing process of our method.
Specifically, at the beginning of each round of the exploitation phase, all seeds created until the previous phase were gathered and deduplicated to generate the initial global seed corpus for this phase. Then, the task division method described above was employed: firstly, those collected seeds were used to update the callgraph of the target program; then a callgraph partition algorithm was used to divide the callgraph into subgraphs; finally, the subgraphs were combined into a given number of subgraphs (subtasks) with similar expected workloads. After dividing the subtasks, the initial seed corpus was divided into corresponding subsets for each subtask according to the execution trace of each seed in the initial seed corpus. After completing the above preparations, each subset of the global seed corpus corresponding to each subtask was sequentially assigned to different fuzzing instances (using different fuzzers), and the bitmap of each fuzzing instance was initialized with the global bitmap based on the global seed corpus. Then, the bitmaps of each fuzzer were synchronized with the global branch coverage bitmap at fixed intervals. After a given time of fuzzing, the fuzzing instances allocated from the subset of the global seed corpus corresponding to every subtask were rotated sequentially. If before a rotation it was found that each subtask has been tested by all parallel fuzzing instances, then this round of the exploitation phase is concluded, and the next round of the exploitation phase begins.

B. Fuzzing Framework

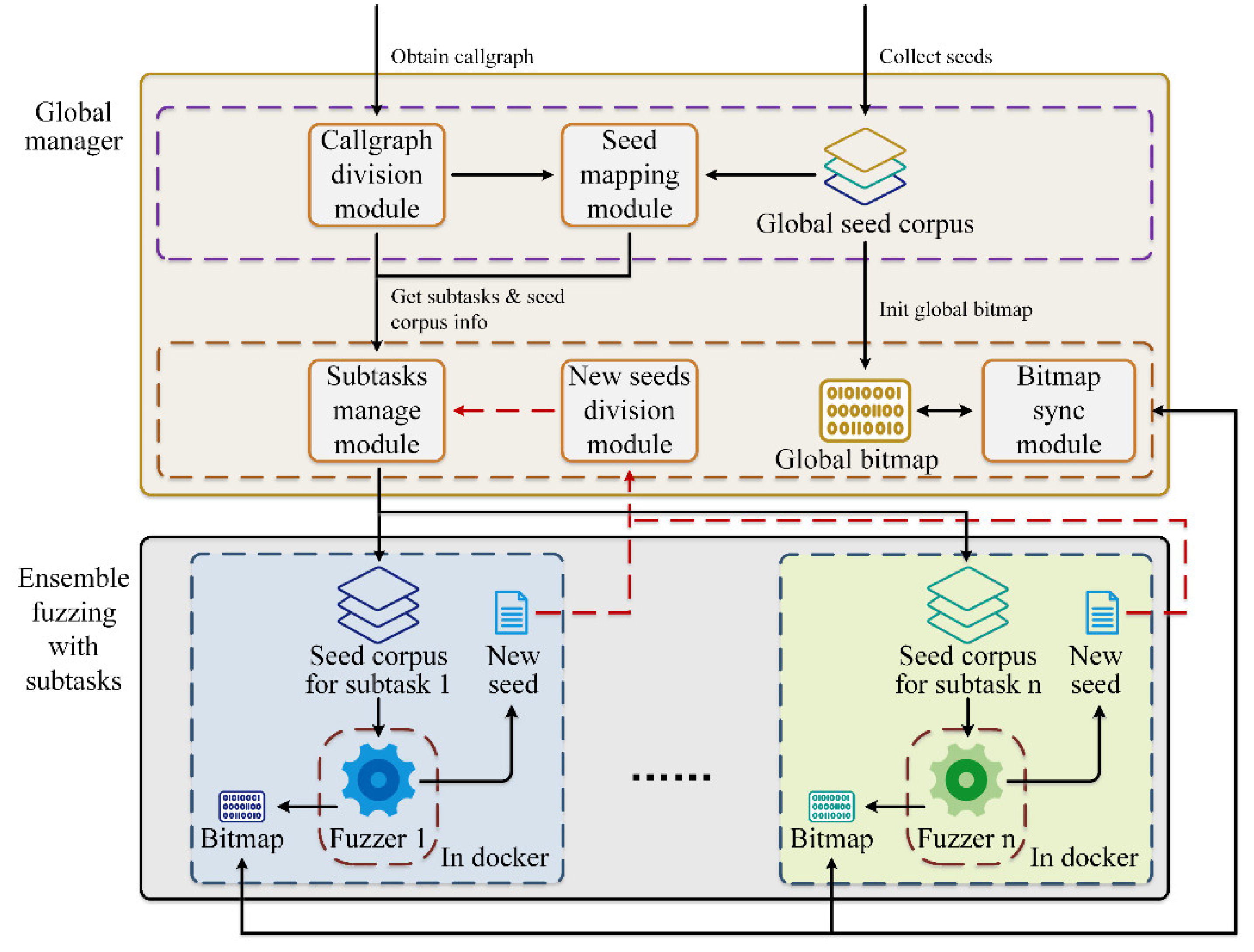
The ensemble fuzzing framework based on the function callgraph task division is shown in Figure 9. From a high-level perspective, it can be divided into two major components: the global manager and the ensemble fuzzing section with subtasks.
Specifically, the global manager can be further divided into the preprocessing section and the fuzzer managing section. The preprocessing section includes two modules: the callgraph division module, which implements the callgraph division and subgraph merging functions described in Section III-A to generate allocated subtasks in the form of subgraphs; and the seed mapping module, which maps each of the divisions of the callgraph to a subset of the global seed corpus as described in Section III-B to generate sub-corpus corresponding to each subtask. The fuzzer managing section includes three modules: the subtasks manage module, which maintains a subtasks management table that records the mapping between subtasks and sub-corpora as well as the fuzzers that have been used for each subtask, and regularly assigns subtasks to the fuzzers according to the subtask allocation strategy described above; the new seeds division module, which monitors the cache folders of all fuzzers throughout the entire fuzzing process, and once a new seed is discovered, arranges it to a certain subtask using the seed mapping method described in Section III-B and sends it to the corresponding fuzzer through the subtask managing module; and the bitmap synchronization module, which initializes a global bitmap using the global seed corpus, and then regularly collects new covered branches by each fuzzer and synchronizes the current global bitmap to all fuzzers through shared memory during the fuzzing process.
The ensemble fuzzing section with subtasks primarily modifies all the fuzzers to run one fuzzer per docker and maintains an output cache folder for newly discovered seeds and an input cache folder for allocated new seeds.

V. Evaluation

To evaluate the effectiveness of our framework, we designed a prototype of the ensemble fuzzing system based on task division, which consists of over 4000 lines of code (LoCs) in Python and over 1000 LoCs in C. The experiments are conducted on a server with 24 Intel Xeon E5-2620 v3 cores and 256GB of RAM running Ubuntu 18.04.

A. EXPERIMENTAL SETUP

Fuzzers for evaluation. The main contribution of this paper is utilizing task allocation based on callgraph in ensemble fuzzing to improve its efficiency by reducing duplicate work. Therefore, to demonstrate the effectiveness of our approach, we compare our Task Allocation-based Ensemble Fuzzing framework (TAEF) with AFLTeam, which uses task allocation in parallel fuzzing of homomorphic fuzzer, and Original Ensemble Fuzzing framework (OEF) without task allocation. Specifically, as shown in Table 1, considering the diversity of fuzzers, in our ensemble fuzzing framework (TAEF), we use four different fuzzers including AFLFast [5], MOPT [9], QSYM [23], and radamsa [31] to conduct fuzzing using the approach described in this paper. In the Original Ensemble Fuzzing framework (OEF), we select the same four fuzzers as in our framework, while they run the tests independently, only with periodical synchronization among the seeds to coordinate the work of fuzzers. As for AFLTeam, we use four instances of the provided fuzzer, which is highly coupled to its task division strategy, in parallel.
Programs under test. Due to the requirements of the fuzzing frameworks that need to be evaluated, the tested programs have to meet the following stringent conditions. Firstly, AFLTeam requires the tested programs to have fixed input formats, and aflsmart needs to support these input formats. This greatly limits the number of programs that can be chosen for evaluation. After searching for commonly used benchmarks for fuzzing, we found over forty programs in addition to the four programs used by AFLTeam. However, we also need to evaluate the ensemble fuzzing frameworks, and qsym used in the ensemble fuzzing framework requires the Ubuntu 16.04 version, while other fuzzers require the Ubuntu 18.04 version. This means that the selected programs need to be able to run on both versions of the system simultaneously. Furthermore, the selected programs must have identical execution paths on both versions of the Ubuntu system, otherwise, the comparison of branch coverage loses its meaning.
Finally, after testing over a hundred different versions of the pre-selected programs, we found six programs that fully meet the aforementioned challenging conditions, including three out of the four programs used by AFLTeam. Details of these programs and the additional parameters used are shown in Table 2.
Parameters configuration. For AFLTeam, we configured it to use 4 cores and set the exploration phase to 2 hours, and the exploitation phase to 4 hours with 2 repetitions. Both the evaluation of the Original Ensemble Fuzzing framework (OEF) and our prototype (TAEF) were executed in Docker containers due to the different environments required by the fuzzers they contain. Each fuzzer is assigned to a Docker container with a single core bound to it. For the original ensemble fuzzing, we set the time limit to 10 hours, while for our prototype, which was consistent with AFLTeam, the exploration phase was set to 2 hours, and the exploitation phase was set to 4 hours with 2 repetitions. Afterward, we reported the number of covered branches as the integer average of the five testing results.
It is worth noting that the chosen program for testing has a longer execution time, which may exceed the default settings of these fuzzers. So, we have to set a longer timeout for each testcase. In our experimental environment, a timeout of 2000ms can ensure that the majority of testcases do not exceed the time limit. However, the timeout duration for each testcase is dependent on the execution speed of the tested program in the current environment. Therefore, the required timeout duration varies in different environments. However, in situations where the exact duration of timeout is uncertain, it will be appropriate to set a longer timeout period. In fact, unless the timeout is set too short and causes a large number of normal testcases to timeout, setting a longer timeout will have little impact on the final results.

B. Experimental Results and Analysis

After 3600 CPU hours of testing, we obtained the results shown in Table 3. The unpaired t-test was selected by us for evaluating significance. We hypothesized that the results of each fuzzing framework on each tested program followed a Gaussian distribution. Additionally, we assumed that for each tested program, the results were sampled from a population with the same standard deviation. The significance level is represented by "*", where "ns" indicates a P-value >= 0.05, "*" represents a P-value < 0.05, "**" represents a P-value < 0.01, "***" represents a P-value < 0.001, and "****" represents a P-value < 0.0001.
OEF compares with AFLTeam: The AFLTeam and the Original Ensemble Fuzzing framework (OEF) are the two fundamental works of our Task Allocation-based Ensemble Fuzzing framework (TAEF). From the experimental results, it is evident that these two fuzzing frameworks excel in different areas. However, overall, the performance of OEF is better than AFLTeam. Indeed, OEF outperformed AFLTeam on 4 out of 6 tested programs with a maximum improvement exceeding 10%; and the decrease ratios on the other two lagging tested programs did not exceed 5%. This suggests that ensemble fuzzing indeed can leverage the strengths of all the paralleled fuzzers to achieve better coverage than the multiple-instance parallelism of a single fuzzer. Thus, in theory, applying the task division method to ensemble fuzzing should yield better results than applying it to parallel fuzzing with a single fuzzer (such as AFLTeam).
TAEF compares with AFLTeam: The obtained results align with the theory discussed earlier. Our Task Allocation-based Ensemble Fuzzing framework (TAEF) achieved higher branch coverage than AFLTeam in all six tested programs. Overall, TAEF covered an average of 8.9% more branches than AFLTeam. Particularly, there was a significant improvement of over 24% in the tested program named nm-new. Moreover, the improvements of our framework compared to AFLTeam in five out of the six tested programs show significance. This indicates that applying the task division strategy to the ensemble fuzzing is more advantageous than applying it to parallel fuzzing with a single fuzzer, and should be a future direction of development.
TAEF compares with OEF: It can be seen that our Task Allocation-based Ensemble Fuzzing framework (TAEF) achieves a higher branch coverage than the Original Ensemble Fuzzing framework (OEF) in five out of the six tested programs. Overall, TAEF covers 4.1% more branches than OEF. Notably, the most significant improvement is observed in the program called nm-new, with an increase of over 13%. Although the average coverage improvement of our framework compared to OEF is not substantial, all the improvements in these five tested programs are statistically significant. This indicates that our framework outperforming OEF in terms of branch coverage is not by coincidence. The limited increase in coverage may be attributed to the fact that OEF already achieved near-saturation coverage in these programs, making further improvement challenging. In the only program where TAEF has a lower branch coverage than OEF, the decrease of less than 1% is not statistically significant. In conclusion, our framework indeed enhances the efficiency of ensemble fuzzing, aligning with our initial objectives.

VI. Discussing

It can be observed that our task allocation-based ensemble fuzzing method does improve the overall testing effectiveness on most of the tested programs. This indicates that our proposed method is genuinely effective in enhancing the efficiency of fuzzy testing. However, during the experiment, we did observe some limitations in the division method based on the callgraph of the tested program. Our task division method may be ineffective or even have negative effects for certain specially tested programs. Specifically, our method may encounter the following challenges:
Firstly, before dividing the callgraph, we transform it into a minimum spanning tree, which eliminates any possible cyclic calls in the callgraph. It means that, in programs that commonly use cyclic calls, the results of task division deviate from the original structure of the program being tested, and therefore may not effectively guide fuzzing. In such cases, our task division method may be considered invalid.
Furthermore, we assume that the callgraph of the program being tested, when converted into a minimum spanning tree, is a fairly balanced tree (which is indeed the case in most situations). However, if a tested program has a single and deep function call relationship, where most nodes in the resulting minimum spanning tree only have one child node, it becomes necessary to cover previous functions to test the generated functions of that program. In this scenario, the task division itself loses its purpose. This not only renders our method potentially ineffective but also runs the risk of wasting some of the fuzzing instances that are meant for testing deep-level functions, thereby achieving the opposite effect.
Finally, we calculate the expected effort for each function based on the number of branches it contains and the number of branches that have not been covered yet to balance the workload among sub-tasks. In theory, the more uncovered branches in a function, the more exploration time should be allocated to exploring this function hoping to cover these remaining branches. Therefore, the expected workload for exploring this function should be greater. However, in reality, some entry conditions for certain branches in the tested program are too difficult for fuzzers and are almost impossible to reach. Spending significant amounts of time attempting to cover these branches is unlikely to yield any benefits and will only hinder the overall efficiency of fuzzing. In exceptional circumstances, if a function contains a large number of branches that are virtually impossible to enter, the calculated expected effort (i.e., weight) for that function will be high. If a subtask consists entirely of such functions, no effective new seeds will likely be found for that subtask, resulting in wasting precious fuzzing time.

VII. Conclusions and Prospect

The existing fuzzing task division methods can only apply to the case of multiple instances of a single fuzzer in parallel. To overcome this limitation, we proposed a Task Allocation-based Ensemble Fuzzing framework. Specifically, we divided the callgraph of the target program into subgraphs and mapped each of these subgraphs to a subset of the global seed corpus, to divide the fuzzing tasks of heterogeneous fuzzers in ensemble fuzzing. Upon these, we also designed a task scheduling strategy to address the issue of non-equivalence of each fuzzing instance in ensemble fuzzing. In addition, we proposed a bitmaps synchronization strategy and a seeds synchronization strategy to tackle the problem of fuzzing progress synchronization among different fuzzing instances in ensemble fuzzing. These strategies overcome the challenges posed by using different fuzzers in parallel, ensuring the effectiveness of task allocation in ensemble fuzzing. The evaluation of our framework demonstrates that it outperforms both the parallel fuzzing using a single fuzzer with the task division strategy and the original ensemble fuzzing without any task division method. However, as mentioned in the previous section, our approach still has some limitations at present. We believe that by addressing these issues in future work, there can be a more efficient method of adding task allocation to the ensemble fuzzing framework.

Funding

This work was supported by “Pioneer” and “Leading Goose” R&D Program of Zhejiang, China under Grant 2022C03132, 2017C01065.

References

  1. Manes, V.J.; et al. The Art, Science, and Engineering of Fuzzing: A Survey. IEEE Trans. Softw. Eng. 2019, 47, 2312–2331. [CrossRef]
  2. Boehme, M.; Cadar, C.; Roychoudhury, A. Fuzzing: Challenges and Reflections. IEEE Softw. 2021, 38, 79–86. [CrossRef]
  3. Li, J.; Zhao, B.; Zhang, C. Fuzzing: a survey. Cybersecurity 2018, 1, 1–13, . [CrossRef]
  4. Liang, H.; Pei, X.; Jia, X.; Shen, W.; Zhang, J. Fuzzing: State of the Art. IEEE Trans. Reliab. 2018, 67, 1199–1218.
  5. M. BohmeV. Pham and A. Roychoudhury, Coverage-based greybox fuzzing as markov chain, Proc. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 2016, pp. 1032-1043.
  6. C. Lemieux and K. Sen, Fairfuzz: a targeted mutation strategy for increasing greybox fuzz testing coverage, Proc. Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, ACM, 2018, pp. 475-485.
  7. Fioraldi, D. Maier, H. Eißfeldt and M. Heuse, Afl++: combining incremental steps of fuzzing research, Proc. 14th USENIX Workshop on Offensive Technologies (WOOT 20), 2020.
  8. Pham, V.-T.; Boehme, M.; Santosa, A.E.; Caciulescu, A.R.; Roychoudhury, A. Smart Greybox Fuzzing. IEEE Trans. Softw. Eng. 2019, 47, 1980-1997.
  9. Lyu, et al., Mopt: optimized mutation scheduling for fuzzers, Proc. 28th USENIX Security Symposium (USENIX Security 19), 2019, pp. 1949-1966.
  10. American fuzzy lop. [online]. Available: https://lcamtuf.coredump.cx/afl/. Accessed on: 2023-3-9.
  11. M. BöhmeV.J. Manès and S.K. Cha, Boosting fuzzer efficiency: an information theoretic perspective, Proc. Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, 2020, pp. 678-689.
  12. Aschermann, S. Schumilo, T. Blazytko, R. Gawlik and T. Holz, Redqueen: fuzzing with input-to-state correspondence., Proc. Network and Distributed System Security Symposium(NDSS), 2019, pp. 1-15.
  13. K. Serebryany, Oss-fuzz-google’s continuous fuzzing service for open source software, Proc. USENIX Security symposium, USENIX Association, 2017.
  14. Y.L. Chen, et al., Enfuzz: ensemble fuzzing with seed synchronization among diverse fuzzers, Proc. PROCEEDINGS OF THE 28TH USENIX SECURITY SYMPOSIUM, USENIX Association, 2019, pp. 1967-1983.
  15. J. Liang, Y. Jiang, Y. Chen, M. Wang, C. Zhou and J. Sun, Pafl: extend fuzzing optimizations of single mode to industrial parallel mode, Proc. Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, ACM, 2018, pp. 809-814.
  16. V. Pham, M. Nguyen, Q. Ta, T. Murray and B.I.P. Rubinstein, Towards systematic and dynamic task allocation for collaborative parallel fuzzing, Proc. 2021 36th IEEE/ACM International Conference on Automated Software Engineering (ASE), IEEE, 2021, pp. 1337-1341.
  17. M. SuttonA. Greene and P. Amini, "Fuzzing: brute force vulnerability discovery,", San Antonio, USA: Pearson Education, 2007, pp. 1-576.
  18. M. Böhme, V. Pham, M. Nguyen and A. Roychoudhury, Directed greybox fuzzing, Proc. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017, pp. 2329-2344.
  19. Z. Du, Y. Li, Y. Liu and B. Mao, Windranger: a directed greybox fuzzer driven by deviation basic blocks, Proc. Proceedings of the 44th International Conference on Software Engineering, 2022, pp. 2440-2451.
  20. M. Nguyen, S. Bardin, R. Bonichon, R. Groz and M. Lemerre, Binary-level directed fuzzing for use-after-free vulnerabilities, Proc. RAID, 2020, pp. 47-62.
  21. V.J. ManèsS. Kim and S.K. Cha, Ankou: guiding grey-box fuzzing towards combinatorial difference, Proc. Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering(ICSE), 2020, pp. 1024-1036.
  22. Stephens, N.; et al. Driller: Augmenting Fuzzing Through Selective Symbolic Execution. NDSS 2016, 1–16.
  23. Yun, S. Lee, M. Xu, Y. Jang and T. Kim, Qsym: a practical concolic execution engine tailored for hybrid fuzzing, Proc. 27th USENIX Security Symposium (USENIX Security 18), 2018, pp. 745-761.
  24. H. Liang, L. Jiang, L. Ai and J. Wei, Sequence directed hybrid fuzzing, Proc. 2020 IEEE 27th International Conference on Software Analysis, Evolution and Reengineering (SANER), IEEE, 2020, pp. 127-137.
  25. P. Chen and H. Chen, Angora: efficient fuzzing by principled search, Proc. 2018 IEEE Symposium on Security and Privacy (S&P), pp. 711-725.
  26. S. Rawat, V. Jain, A. Kumar, L. Cojocar, C. Giuffrida and H. Bos, Vuzzer: application-aware evolutionary fuzzing, Proc. Symposium on Network and Distributed System Security (NDSS), 2017, pp. 1-14.
  27. Song, C.; Zhou, X.; Yin, Q.; He, X.; Zhang, H.; Lu, K. P-Fuzz: A Parallel Grey-Box Fuzzing Framework. Appl. Sci. 2019, 9, 5100. [CrossRef]
  28. Zhou, X.; et al. UltraFuzz: Towards Resource-Saving in Distributed Fuzzing. IEEE Trans. Softw. Eng. 2022.
  29. Guler, et al., Cupid: automatic fuzzer selection for collaborative fuzzing, Proc. 36TH ANNUAL COMPUTER SECURITY APPLICATIONS CONFERENCE (ACSAC 2020), Association for Computing Machinery, 2020, pp. 360-372.
  30. Lukes, J.A. Efficient Algorithm for the Partitioning of Trees. IBM J. Res. Dev. 1974, 18, 217–224.
  31. Aki helin/radamsa · gitlab. Available online: https://gitlab.com/akihe/radamsa (accessed on 13 May 2023).
Preprints 90486 g001
Figure 1. Modifications of the fuzzer provided by AFLTeam: (a) Workflow of common CGFs; (b) Modified workflow of CGF in AFLTeam to suit task division method.
Figure 1. Modifications of the fuzzer provided by AFLTeam: (a) Workflow of common CGFs; (b) Modified workflow of CGF in AFLTeam to suit task division method.
Preprints 90486 g001
Preprints 90486 g002
Figure 2. Workflow of our Task Allocation-based Ensemble Fuzzing framework, which decouples related functions with fuzzers.
Figure 2. Workflow of our Task Allocation-based Ensemble Fuzzing framework, which decouples related functions with fuzzers.
Preprints 90486 g002
Preprints 90486 g003
Figure 3. Three main parts of our ensemble fuzzing method: (a) Callgraph division. (b) Subgraph association and seed mapping. (c) Task scheduling and synchronization.
Figure 3. Three main parts of our ensemble fuzzing method: (a) Callgraph division. (b) Subgraph association and seed mapping. (c) Task scheduling and synchronization.
Preprints 90486 g003
Preprints 90486 g004
Figure 4. A sample of callgraph partition. (a) Initial callgraph. (b) Updated callgraph. (c) Simplified callgraph. (d) Callgraph in form of a minimum spanning tree. (e) A sample of partition result.
Figure 4. A sample of callgraph partition. (a) Initial callgraph. (b) Updated callgraph. (c) Simplified callgraph. (d) Callgraph in form of a minimum spanning tree. (e) A sample of partition result.
Preprints 90486 g004
Preprints 90486 g005
Figure 5. A sample of subgraph merging. (a) A sample of the result of callgraph partition. (b) The result of merging the subgraphs that cannot be directly called by the main function with the one that can directly call it. (c) The result of arranging subgraphs in descending order of weight. (d) The result of subgraph merging (in chart). (e) The result of subgraph merging marked in the callgraph.
Figure 5. A sample of subgraph merging. (a) A sample of the result of callgraph partition. (b) The result of merging the subgraphs that cannot be directly called by the main function with the one that can directly call it. (c) The result of arranging subgraphs in descending order of weight. (d) The result of subgraph merging (in chart). (e) The result of subgraph merging marked in the callgraph.
Preprints 90486 g005
Preprints 90486 g006
Figure 6. An example of seed mapping.
Figure 6. An example of seed mapping.
Preprints 90486 g006
Preprints 90486 g007
Figure 7. Illustration of the allocation strategy for subtask cyclic rotation. (a) Allocation method for the first round of subtask assignment. (b) Cyclic rotation method for subsequent subtask assignments, taking the second round as an example.
Figure 7. Illustration of the allocation strategy for subtask cyclic rotation. (a) Allocation method for the first round of subtask assignment. (b) Cyclic rotation method for subsequent subtask assignments, taking the second round as an example.
Preprints 90486 g007
Preprints 90486 g008
Figure 8. The workflow of our task allocation-based ensemble fuzzing framework.
Figure 8. The workflow of our task allocation-based ensemble fuzzing framework.
Preprints 90486 g008
Preprints 90486 g009
Figure 9. The framework of our task allocation-based ensemble fuzzing.
Figure 9. The framework of our task allocation-based ensemble fuzzing.
Preprints 90486 g009
Table 1. Fuzzers’ settings of AFLTeam, OEF, and our prototype named TAEF.
Table 1. Fuzzers’ settings of AFLTeam, OEF, and our prototype named TAEF.
Frameworks Number of instances Used fuzzers Time and memory limit
AFLTeam 4 horsefuzz -t 2000+ -m none
OEF 4 AFLFast, MOPT, QSYM, and radamsa -t 2000+ -m none
TAEF 4 AFLFast, MOPT, QSYM, and radamsa -t 2000+ -m none
Table 2. Programs used for testing, their requisite input formats, and the parameters employed during fuzzing.
Table 2. Programs used for testing, their requisite input formats, and the parameters employed during fuzzing.
Program Test driver Input format Option
libpng pngimage PNG @@
libjpeg-turbo djpeg JPEG @@
jasper jasper JP2 --input @@ --output-format jp2
guetzli guetzli JPEG @@ /dev/null
Binutils readelf ELF -agteSdcWw --dyn-syms -D @@
Binutils nm-new ELF -a -C -l --synthetic @@
Table 3. The number of branches covered by AFLTeam, OEF, and TAEF respectively.
Table 3. The number of branches covered by AFLTeam, OEF, and TAEF respectively.
Target AFLTeam OEF TAEF TAEF vs. AFLTeam TAEF vs. OEF
Improvement Significance Improvement Significance
pngimage 4624 4604 4636 0.26%↑ ns 0.70%↑ *
djpeg 2563 2905 3015 17.64%↑ **** 3.79%↑ **
jasper 7566 7413 7901 4.43%↑ * 6.58%↑ **
guetzli 7468 7488 7570 1.37%↑ ** 1.10%↑ **
readelf 14095 15003 14895 5.68%↑ *** -0.72%↓ ns
nm-new 8115 8889 10066 24.04%↑ **** 13.24%↑ ***
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated