An Efficient Computational Analysis and Modelling of Transferred Aerodynamic Loading on Direct-Drive System of 5MW Wind Turbine and Results Driven Optimisation for a Sustainable Generator Structure

Preprint

Article

An Efficient Computational Analysis and Modelling of Transferred Aerodynamic Loading on Direct-Drive System of 5MW Wind Turbine and Results Driven Optimisation for a Sustainable Generator Structure

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts

Abstract

The study presents an efficient computational investigation on the behaviour of the direct-drive system integrated into the offshore 5MW NREL wind turbine model under demanding aerodynamic loading conditions with the aim of optimising and developing more sustainable key structural components. The research was based on computational simulation packages to verify the use of real-world wind data, the loading conditions on the blade structures through aero-elastic simulation studies, as well as analyse the behaviour of the drive system. Through the application of validated aerodynamic loading conditions, resulting normal forces on the blades structure were obtained and applied to a dedicated simplified model that was also previously validated, to estimate the transferred loads into the powertrain. The adopted methodology allowed for the identification of shaft misalignment induced air-gap eccentricity. The impact of shaft deflections on resulting magnetomotive force was considered by making use of the Maxwell stress distribution expression. By taking into account the resulting loading cases on the generator structure, as well as the inherent typical loads generated by the electrical machine, a procedure including structural parametric and topology optimisation was developed and performed, achieving a rotor mass reduction between 8.5 and 9.6% if compared with the original model.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Renewable energy sources have grasped the attention of the media and public in recent years. This is mainly due to the prospect of decarbonising the economy, tackling the ever growing climate change issue and supporting the idea of a sustainable future. With increased popularity, the electricity generation from wind power in the UK has increased by 715% from 2009 to 2020, resulting in a turnover of nearly £6 billion in 2019 [1]. With planned investments regarding the installation of offshore wind turbines and Europe’s predictions reaching 85GW in the Baltic Sea alone, the need for well designed and optimised turbines is significant [2].

The following investigation presents a study on the 5MW reference direct-driven wind turbine designed by National Renewable Energy Laboratory (NREL). This model is a benchmark structure for the majority of the conducted academic investigations towards improvement of the structure. Large horizontal axis wind turbines can be divided into gearbox driven and direct-driven. Typically, gearbox driven wind turbines are designed to transfer the mechanical energy from a low rotational speed rotor to the double fed induction generator with high rotational speed. Direct-driven wind turbines (Figure 1) have a rotor directly coupled to permanent magnet synchronous generator, omitting additional components required for the change of rotational speed via gear ratio [3]. Ultimately the elimination of additional components simplifies the structure and limits the probability of standard gearbox failures, as well as the costs associated with these occurrences. However, the heavier rotor system in direct-drive turbines results in higher loads on supporting structures such as bearings.

Mass optimisation of direct drive electrical generator wind turbines’ structures became a crucial study area. It results in lower maintenance, handling costs and more sustainable systems. It has been stated that the total inactive mass (supporting structures) of rotor and stator structures share up to 82% of total mass for a 5MW turbine [5].

The main components of the generator structure are presented in Figure 2. The blades of the wind turbine generate mechanical rotation by capturing the kinetic energy of the wind. This motion energy is then transferred by the shaft to the rotor. This results in a spinning motion of the rotor inside the stator structure. Rotor and stator are separated from each other by a fixed distance called an air-gap. Moreover, stator is fitted with strong magnets, whereas the rotor accommodates coils of wire. Ultimately, changing magnetic field is introduced to the system by the spinning magnets, thus inducing an electrical current through electromagnetic induction. Further instrumentation within the nacelle, convert the current into more stable form of electricity.

An in-depth investigation of the loads and structural integrity of the machinery is essential in order to enable any optimisation attempts, without compromising model reliability. Typically, the loading conditions consist of the magnetic attraction of the moving parts and previously mentioned stationary components of the generator, shear loading, gravitational loading due to the weight of the structure, thermal expansion of the generator structure and centrifugal loading. The representation of these loads can be seen in Figure 3.

Furthermore, when looking at the behaviour of the rotor, it is essential to understand how the structure can deflect under loading conditions. Four modes of deflection were presented in Figure 4. In mode 0 the rotor will deflect in a uniform manner in radial direction. In case of a local deformation, frequently caused by the shaft misalignment in the system, the structure will experience mode 1 deflection. For mode 2, the structure tends to ovalise, whereas in mode 3, the structure will deflect following the pattern of ripples.

Shaft misalignment can be one of the main contributors to nonuniformity of the air-gap in the stator and rotor system. This can result in an unbalanced magnetic pull, ultimately disturbing the equilibrium of the magnetic attraction forces that result in a dynamic radial load on the bearings, undesirable noise and vibration due to the increase in space harmonics [7]. Therefore, it is essential to carry out the numerical simulations of the drivetrain to correctly predict the behavioural response of the analysed system. An air gap in wind turbines refers to the distance between the rotor and stator of the generator. The rotor is the part of the wind turbine that rotates and contains the magnets, while the stator is stationary and contains the teeth and wire coils that transfer the electricity to the grid going through the converter first.

Due to the rotational movement, depicted in Figure 5, magnetic and gravitational pull present at the rotor. Therefore, the structure will experience deformation. In consequence the air-gap will be reduced. This phenomenon will be further magnified by the recognised shaft misalignment caused by aerodynamic loading. Additional forces in five degrees of freedom, as well as forces caused by thermal expansion and shear can be identified. However, they were deemed negligible for the purpose of this study. The allowable resultant air-gap deflection is stated to be 10-20% for direct-drive structures. This limit ensures that the air-gap flux density will not increase to dangerous levels that can produce the collapse of the machine [7,8].

In order to conduct viable simulations on the wind turbine structure and obtain the loads present, wind data has to be collected. According to IEC 61400-50:2022 “Wind measurement- Overview” all data will be typically reduced to 10-minute statistics (mean, minimum, maximum, standard deviation) for use as input to an analysis. Wind measurements are more detailed and accurate by the use of remote sensing devices (RSDs) such as lidars and sodars. They are more reliable than cup anemometers since they provide full three-dimensional wind measurements and are not influenced by mechanical limitations due to environmental conditions (humidity, temperature, icing). IEC 61400-50 series of standards specify requirements and methods for the use, calibration and classification of conventional cup anemometers, whereas standardized ultrasonic anemometers must be compliant with the rules [9].

The proposed approach in this study indicates that the loading conditions, stresses and behavioural shaft response can be obtained through the application of real-world data sets after appropriate site selection and analysis. Moreover, by referencing technical reports on 5MW NREL reference wind turbine [10], a simplified assembly CAD model can be produced, which can significantly reduce the computing time and is valid to conduct structural optimisations leading to more sustainable systems.

2. Methodology

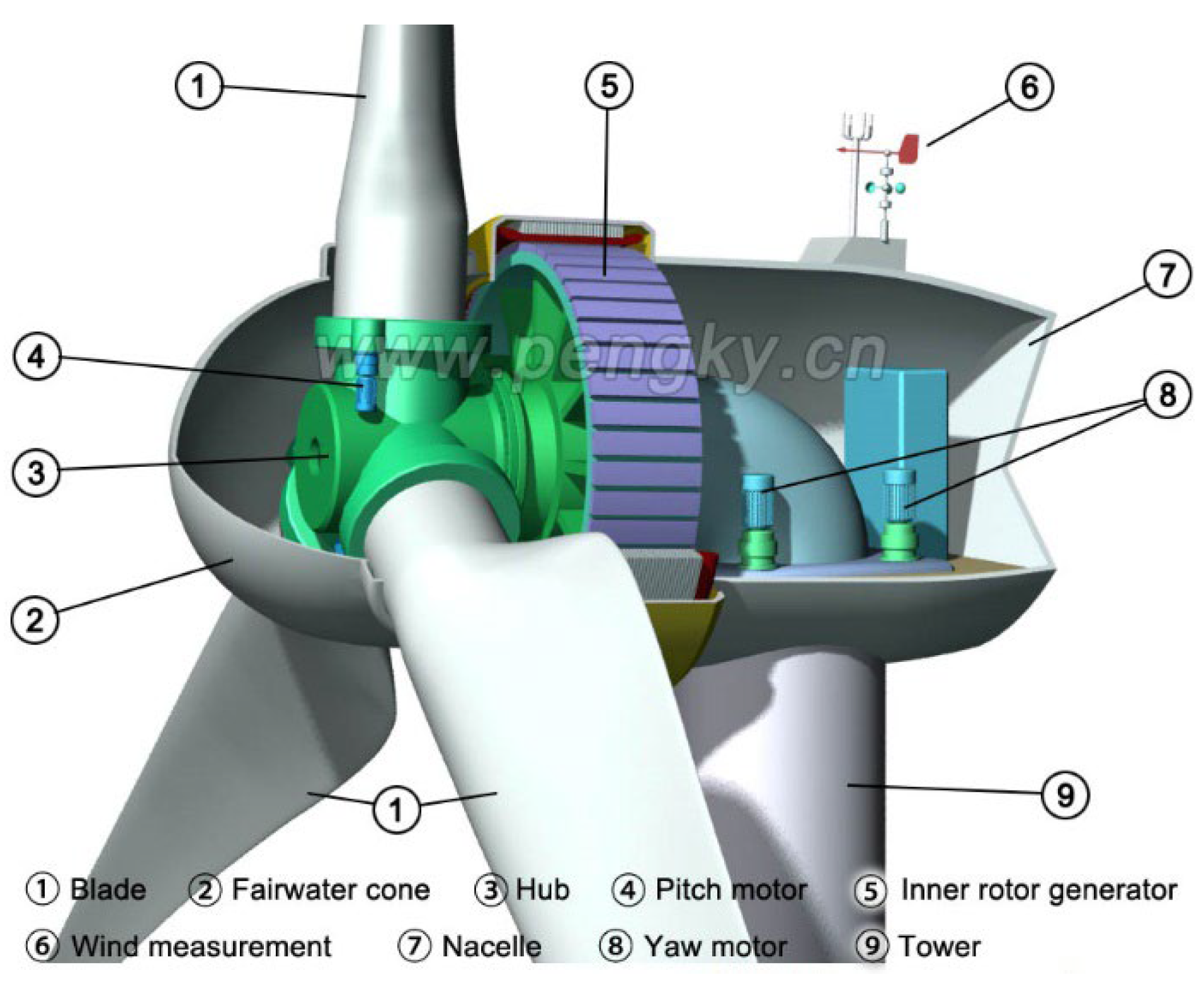
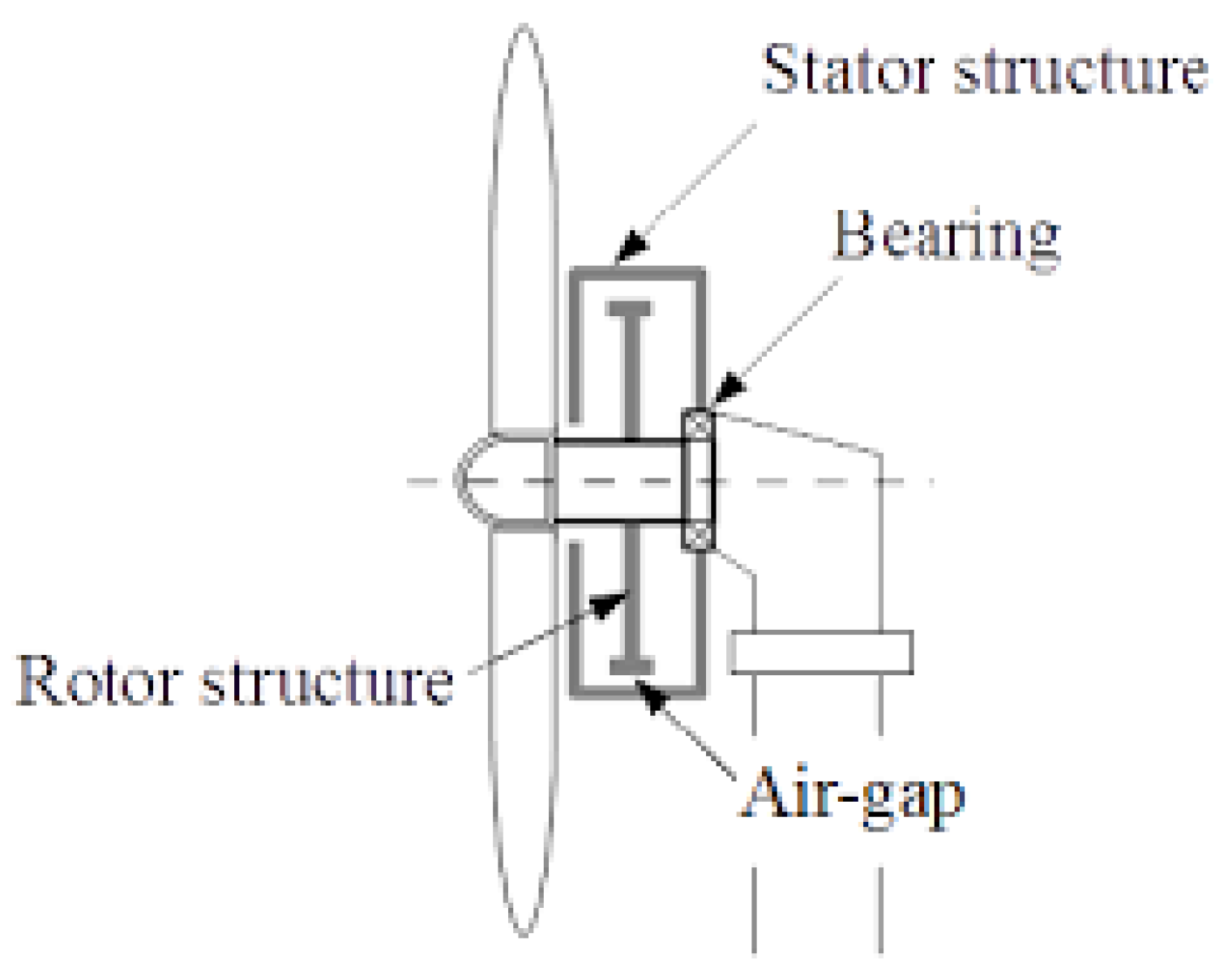
In this study, the authors present a novel procedure to develop and validate an efficient computational model that can be analysed and employed to optimise multi-MW electrical generator rotor supporting structures using only the variables affecting the most. With the use of this model and following the proposed methodology, one can reduce the amount of material needed to withstand the demanding loading conditions, which include not only the typically considered inherent generator operation loads but also the external conditions. The manufacturing, labour, installation and transportation time as well as the associated resources can be diminished with the consequent reduction in CO₂ and methane emissions, water usage and costs. The effect of those modifications can be quantified by looking at the changes in the structure’s natural frequencies and the impact in the generator operating range and turbine energy harvesting capability.

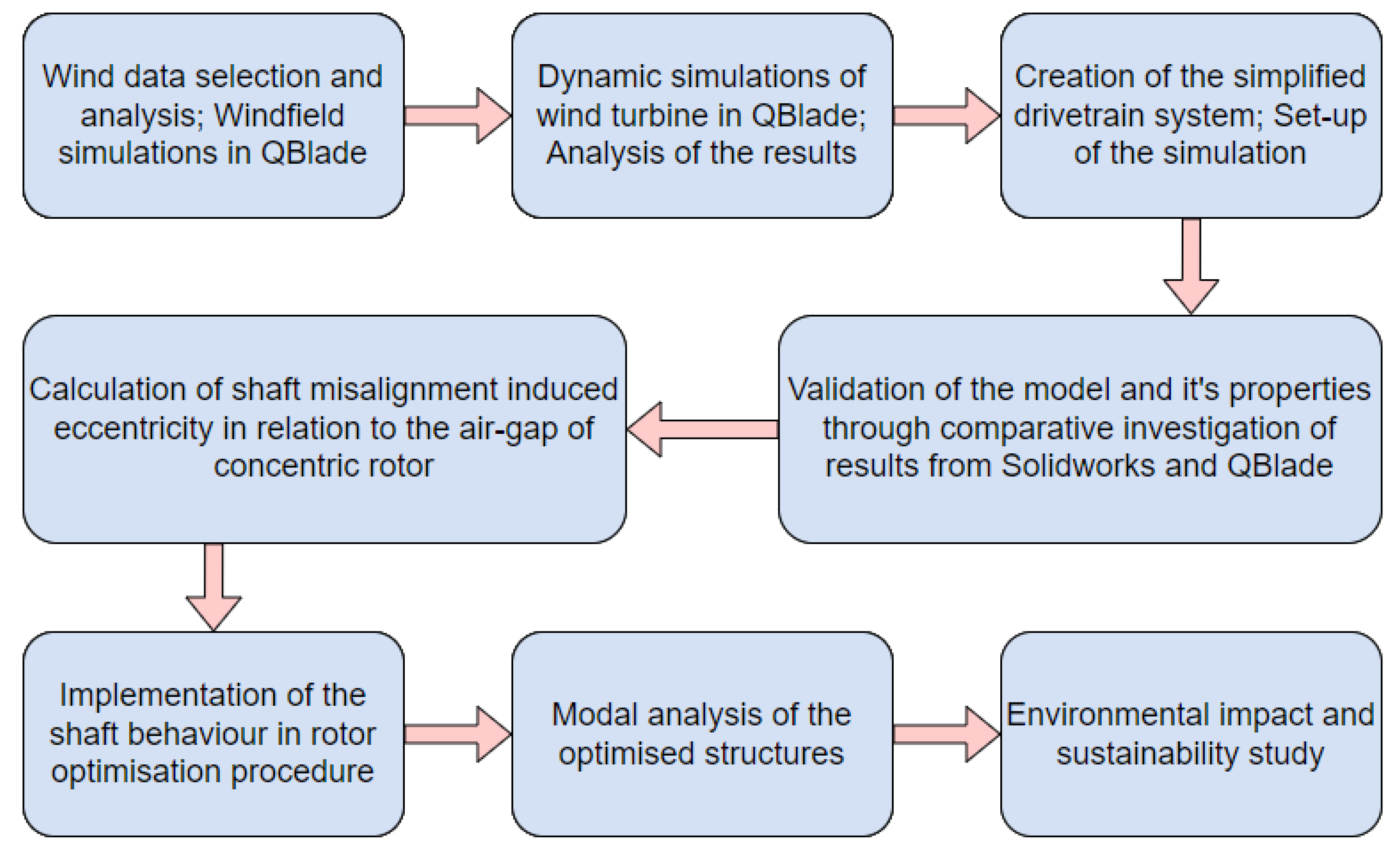
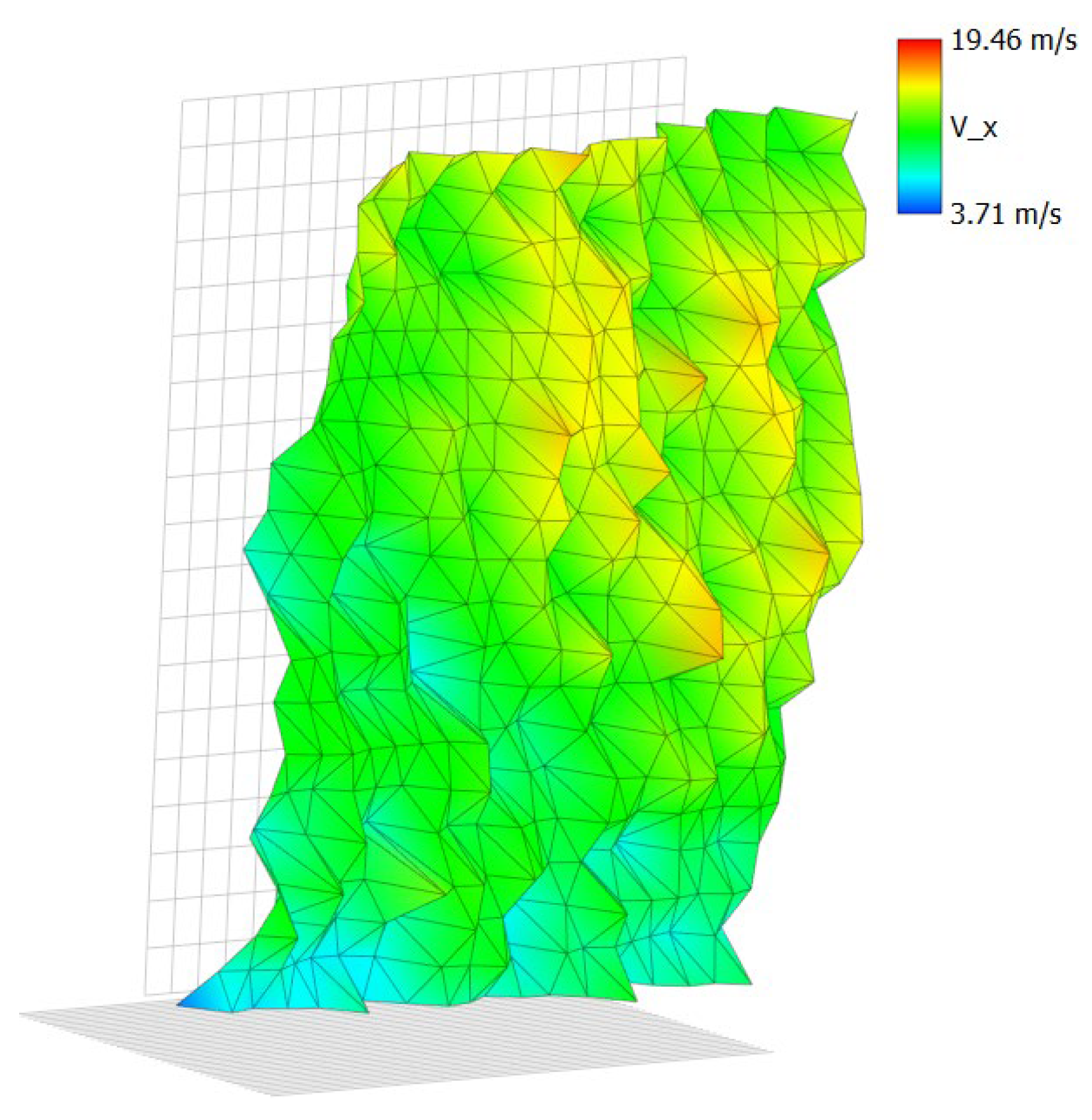
The methodology of the conducted research can be found in Figure 6. Firstly, real-world wind data sets were obtained and selected after careful investigation and appraisal of the corresponding wind farms. The chosen data package was then further analysed and edited. This resulted in the creation of 3 aerodynamic settings corresponding to the considered wind speeds: Low, Rated and High. Moreover, the wind patterns at the chosen site were specified. The obtained data was validated through a correlation study of wind speeds and corresponding altitudes. To translate the real-world wind behaviour to software aided analysis, windfield simulations in QBlade were conducted. The obtained results were compared against the real-world data. Subsequently, the validated windfield data was used in dynamic, structural simulations on a 5 MW wind turbine in QBlade, thus output values for normal stresses on the blades were acquired. Following the analysis of the wind turbine in QBlade, a simplified drivetrain system was created. Finite element analysis of the system was conducted after the simulation set-up procedure in Solidworks, which consisted of material properties specification, application of fixtures and mesh independence study. The results were then validated through comparative investigation between the gathered data from QBlade and Solidworks. Furthermore, the shaft misalignment induced eccentricity in relation to the air-gap of concentric rotor was calculated for the Rated and High aerodynamic settings. The resultant shaft deflections were included in the rotor optimisation procedure, which consisted of rotor structural configuration selection, static FE analysis, topology optimisation, parametric table optimisation and modal analysis of the optimised structures. Lastly, the environmental impact and sustainability of the proposed designs and procedures were studied.

2.1. Wind Data Analysis

The total of 3 different wind data sets from wind farm sites: Penmanshiel, Anholt, and Westermost Rough were found and taken into account. Penmanshiel wind farm data set was obtained from online repository Zenodo [11] and released by Cubico Sustainable Investments Ltd. [12], whereas Anholt and Westermost Rough wind farm data sets were supplied by Ørsted [13]. The chosen data sets for this study came from Anholt wind farm located in eastern Denmark. They were found suitable, as they cover the measurement height requirement for further studies and come with already transposed values e.g., wind direction, thus reducing the workload during the analysis. The technical data and location for Anholt site is provided in Table 1.

The overall wind turbine power is smaller than the investigated structure in this study. However, the data provided from this site covers a range of altitudes for even the biggest commercially used structures at the time (up to 315.6 m above lowest astronomical tide). Therefore, the wind data is only dependent on the environmental conditions present at the site. The data sets from the Anholt wind farm were found to be suitable for further analysis and validation. The obtained data package consists of various signals produced by continuous measurements in 10-minute intervals taken at the site for over 726 days, which sums up to approximately 2 years and ultimately produces over 100,000 data rows and 150 columns. The columns specify the type of measurement taken over the period and consist of wind speed values, wind directions and 12 different corresponding altitudes. The first 10 altitudes (65.6 m – 315.6 m) were taken into consideration, as those heights would cover the operational area of the studied wind turbine.

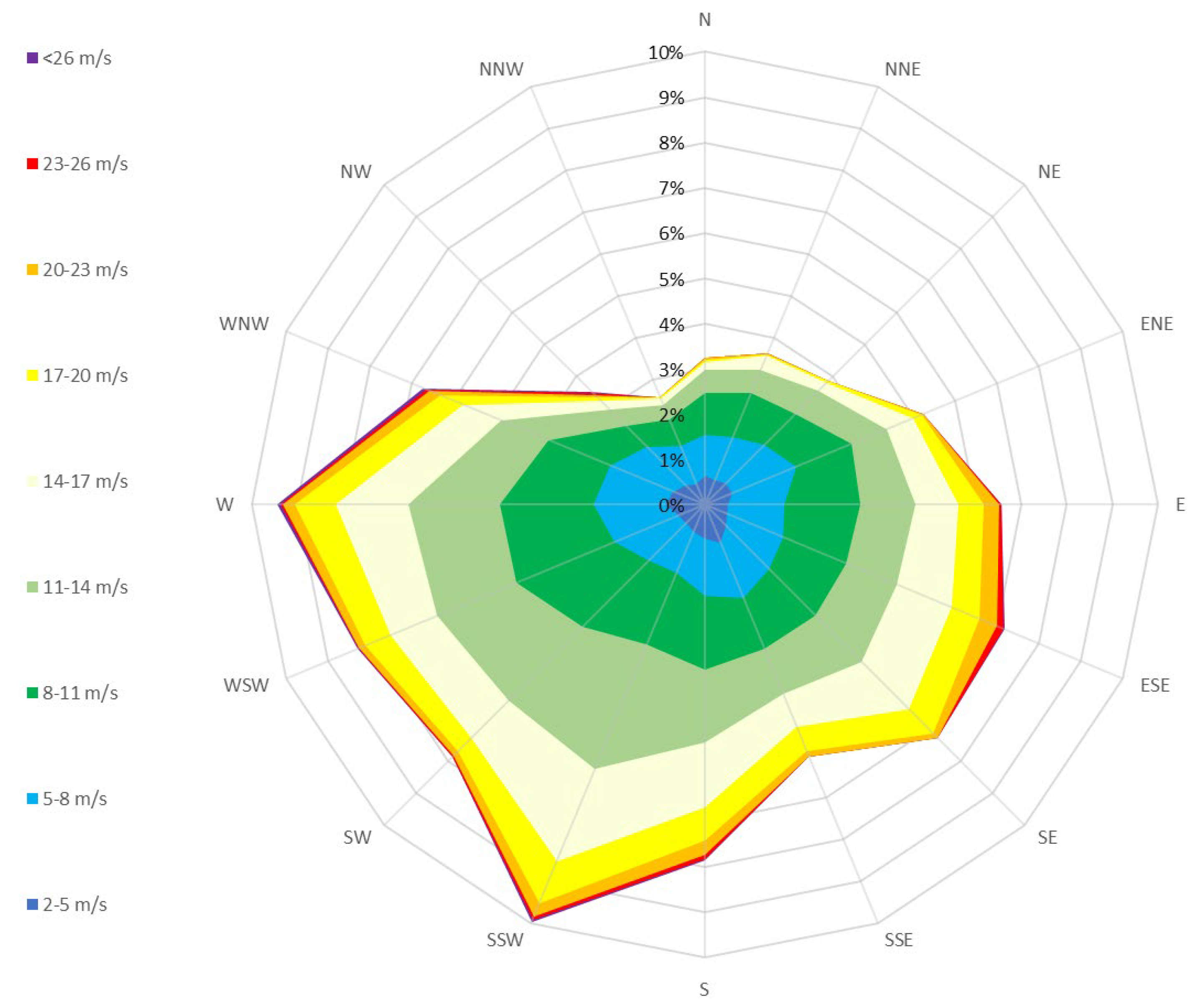
Having a significant amount of data measured over 2 years period, wind direction probability can be identified in order to analyse the working environment of wind turbine while operating. Firstly, the wind data for wind directions and wind speeds was limited to only one column set corresponding to closest hub-height altitude of 5MW wind turbine – altitude 2. The chosen data was then sorted by the wind directions with 22.5° increments, ultimately resulting in a specified data set with identified 16 cardinal directions. The wind speeds were then divided into 9 categories corresponding to the chosen values, sorted and then counted in excel in order to produce a clear probability table that refers to the wind speed and wind direction values over the measurement period – 2 years. The data can be presented as a wind rose (Figure 7) for better presentation of the results.

The chosen wind speeds were colour coded. The graphed areas correspond to the wind direction, as well as probability of occurrence at Anholt wind farm. The highest probability of 10% occurs at SSW direction for 4 wind speed categories with values over 17

\frac{m}{s}

. The overall probability of the wind speed being over 5

\frac{m}{s}

is 89.55% and 69% for speeds over 8

\frac{m}{s}

. Moreover, a recommended annual wind speed average for utility-scale wind turbines is at least 5.8

\frac{m}{s}

. The average wind speed at Anholt wind farm is 10.83

\frac{m}{s}

, which validates the site’s operational requirements.

In order to conduct further analysis, 3 wind speed scenarios were created: low, rated and high which respectively correspond to: lowest possible operational wind speed of

3 \frac{m}{s}

(cut-in speed), rated wind speed of

11.4 \frac{m}{s}

and highest possible operational wind speed

25 \frac{m}{s}

(cut-off speed) for 5MW wind turbine. For the purpose of data filtering, the 3 settings were given a range of wind speed values of

1 \frac{m}{s}

. For low and high settings lowest and highest possible operational wind speeds (cut-in/cut-off) was one of the boundaries. Whereas, for rated wind speed of

11.4 \frac{m}{s}

the boundaries were set to

\pm 0.5 \frac{m}{s}

. This results in higher data count that is centralised about the specified value for each of the settings. As previously mentioned, the data was filtered against the closest altitude to the hub height (90m) of the 5 MW WT.

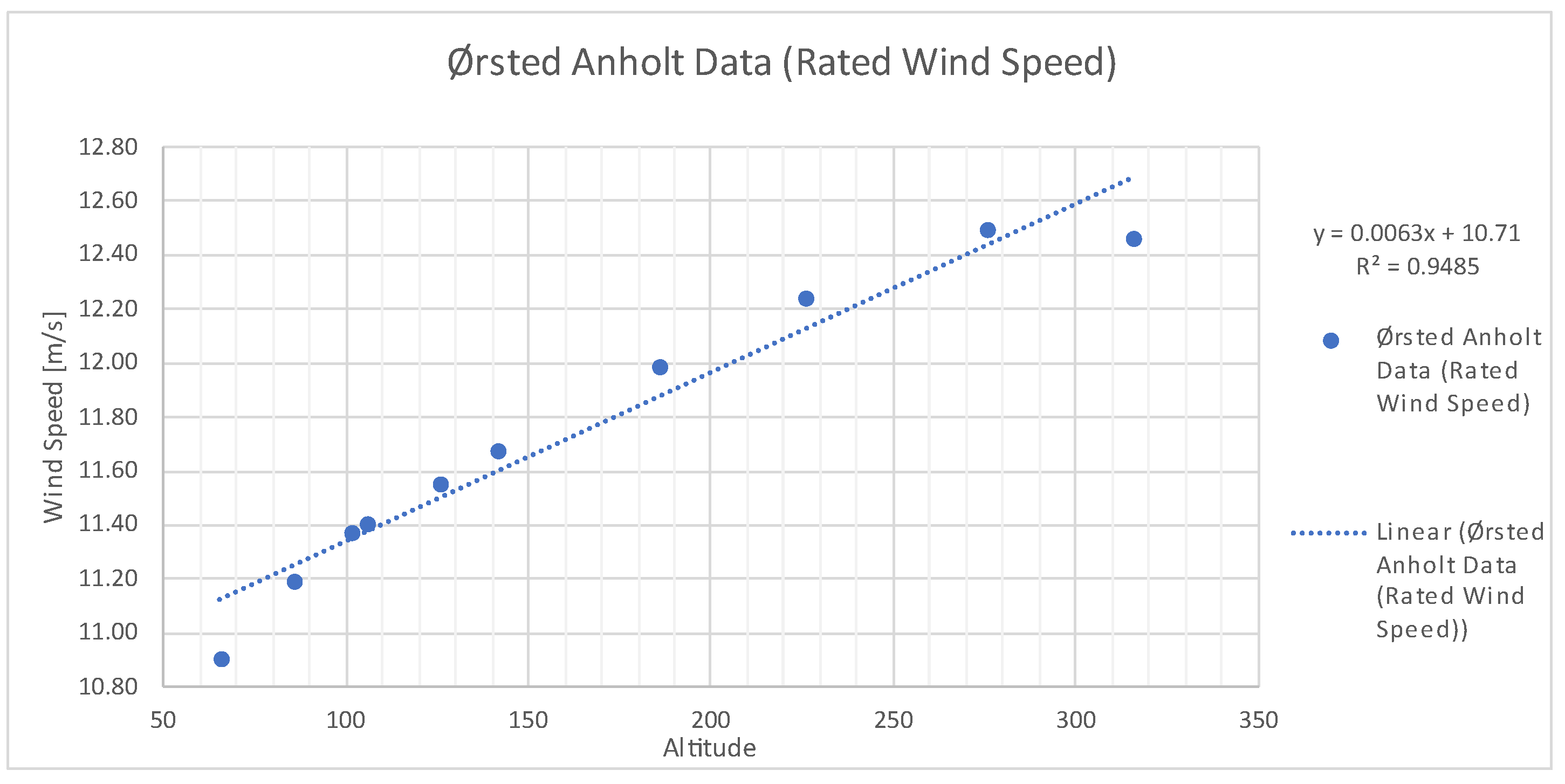
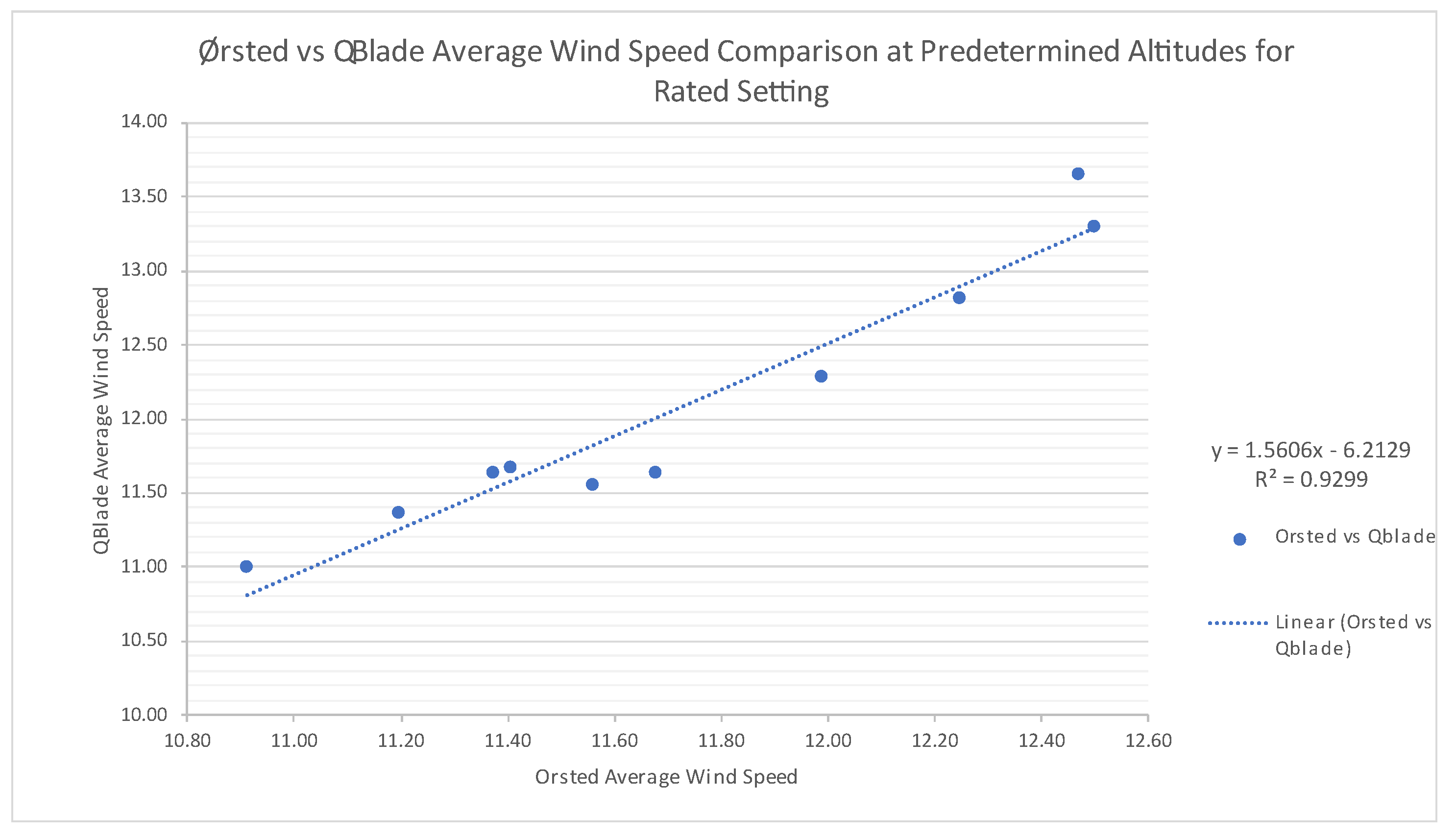
The average wind speeds were then calculated for each of the 3 settings for 10 predetermined altitudes. The obtained results followed a normalised pattern with coefficient of determination R² of over 0.94, which shows a good correlation of the data and minimum impact of the irregularities. The exemplary correlation graph for Rated Wind Speed can be seen in Figure 8.

2.2. Windfield Simulations and Validation

With the average wind speeds found at specified altitudes, further validation study can be conducted. By using the QBlade simulation software, it is possible to create a windfield – a three-dimensional spatial pattern of winds, which will be used in the following structural simulations as an aerodynamic load on blades. However, firstly the already verified Anholt wind farm data needed to be compared to the software’s output data, in order to correlate and validate the 2 sources of data against each other. For this purpose, the wind speeds for Low, Rated and High settings were recreated in the software and compared to the real-world data. The simulated windfields can be shown as three-dimensional graphs and an example of an output graph can be seen in Figure 9. The windfield changes over time of the simulation, acting like a turbulent model and mimicking the natural flow.

Using the export function of the software, it is possible to obtain exact values at particular points of the windfield. Therefore, after setting up the control points (wind probes) at heights corresponding to the measurement altitudes at Anholt wind farm, new data sets have been obtained. The results for Low, Rated and High setting windfields (simulated data) were obtained through a set up of 10 wind probes, data export and conversion to Excel. Subsequently, the average wind speed at a specific altitude for 3 different settings were calculated from the data sets. The final values of the windfield simulations can be seen in Appendix A. Previous average wind speed values from Anholt wind farm analysis were included in the same tables for better result presentation along with the percentage difference in value.

To correctly validate the QBlade data against Anholt data, another correlation study was performed. Instead of comparing the wind speed average values against the altitude, the windspeed values from 2 sources were compared against each other. With the high correlation of the data sources (R² > 0.929) it can be demonstrated that the translation of real-world data at Anholt wind farm to QBlade’s software was validated. The exemplary correlation graph for Average Wind Speed can be seen in Figure 10.

2.3. Structural Analysis of the Wind Turbine Structure

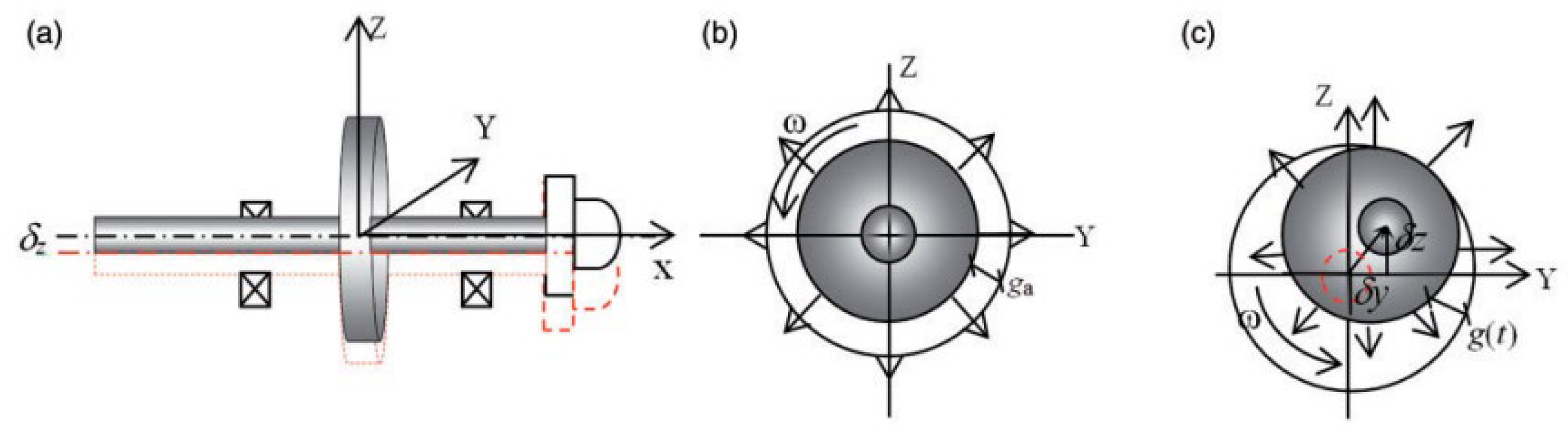
The main goal of this investigation was to produce a simplified and validated process for direct drive system analysis of 5MW wind turbine. For that, the structural analysis of the wind turbine structure was conducted in 2 software programmes: QBlade and Solidworks through built-in features, as well as finite element analysis. The process started by using the validated windfield data as an input towards development of aerodynamic loading on blade’s structure in QBlade and resulted in calculation of the shaft eccentricity in relation to the air-gap of concentric rotor. The displacement of the shaft was found through finite element analysis in Solidworks after conducting necessary validation techniques, since QBlade does not offer drivetrain component-based results.

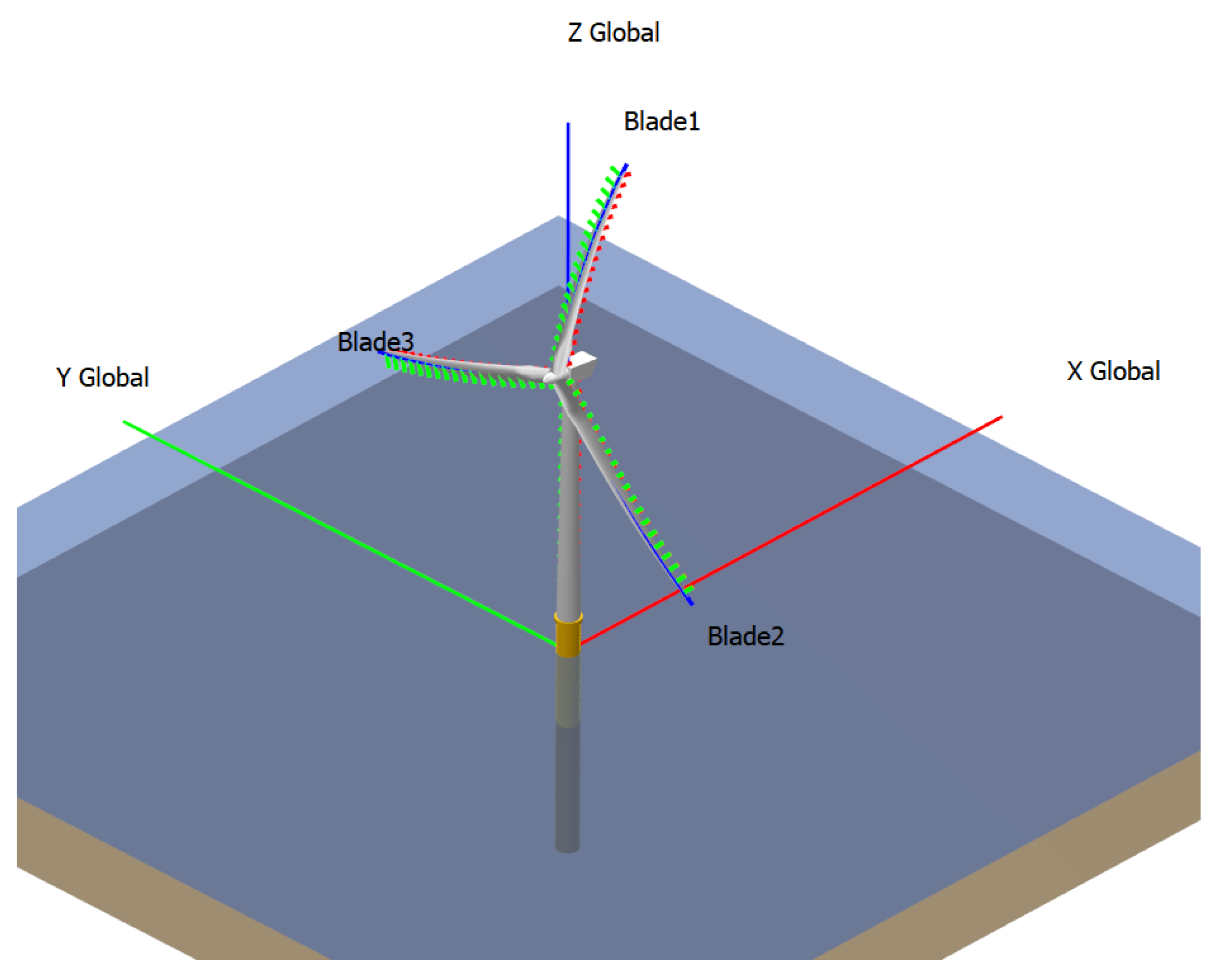
For the purpose of conducting the study, a computationally designed 5MW monopile wind turbine structure was needed. QBlade offers advanced capabilities of modelling and designing such equipment without necessary CAD models. The structure investigated in this study was taken from an official online repository website owned by QBlade [15], which shares the same technical parameters as described in the technical reports from NREL. In order to find the loads on the blades exerted by the wind conditions, the verified windfields were introduced to the system along with the 5MW NREL monopile wind turbine model. The schematic model of the system is shown in Figure 11.

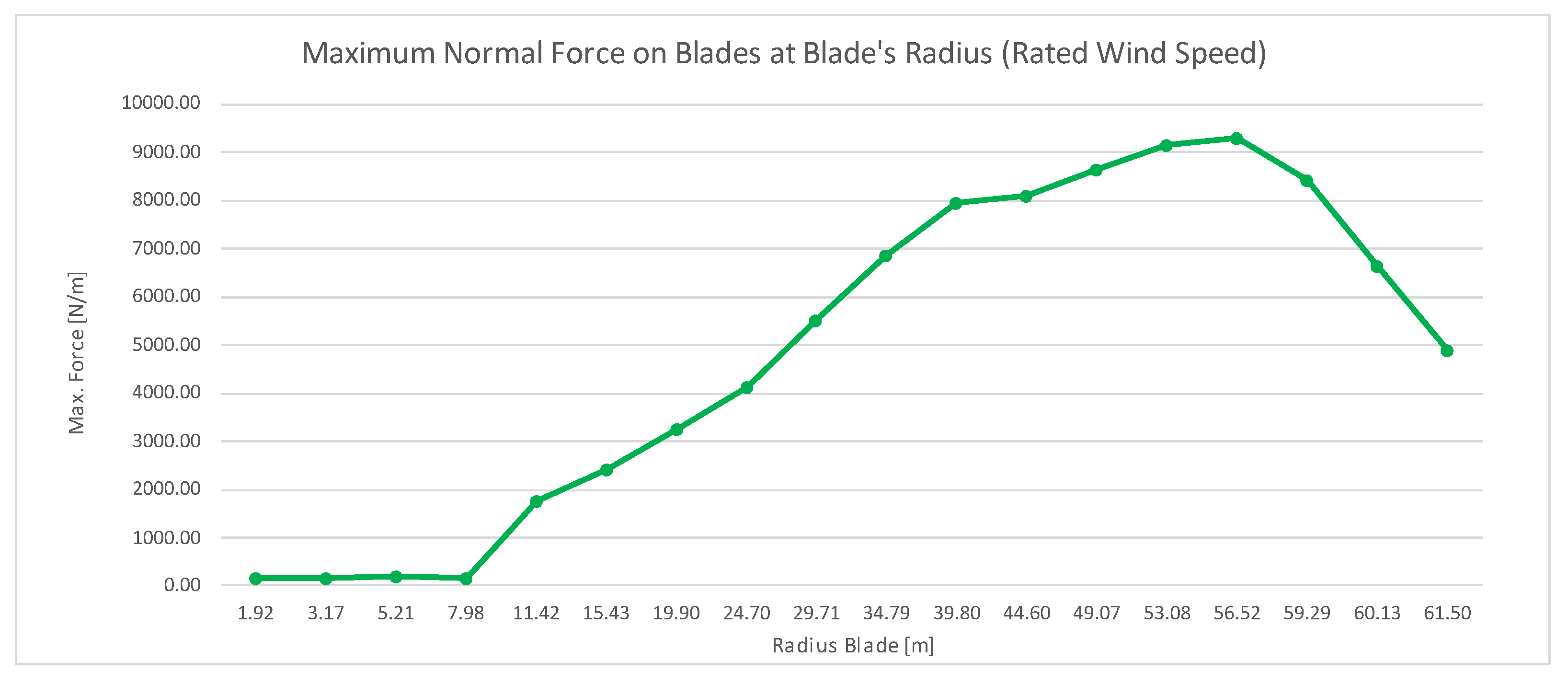
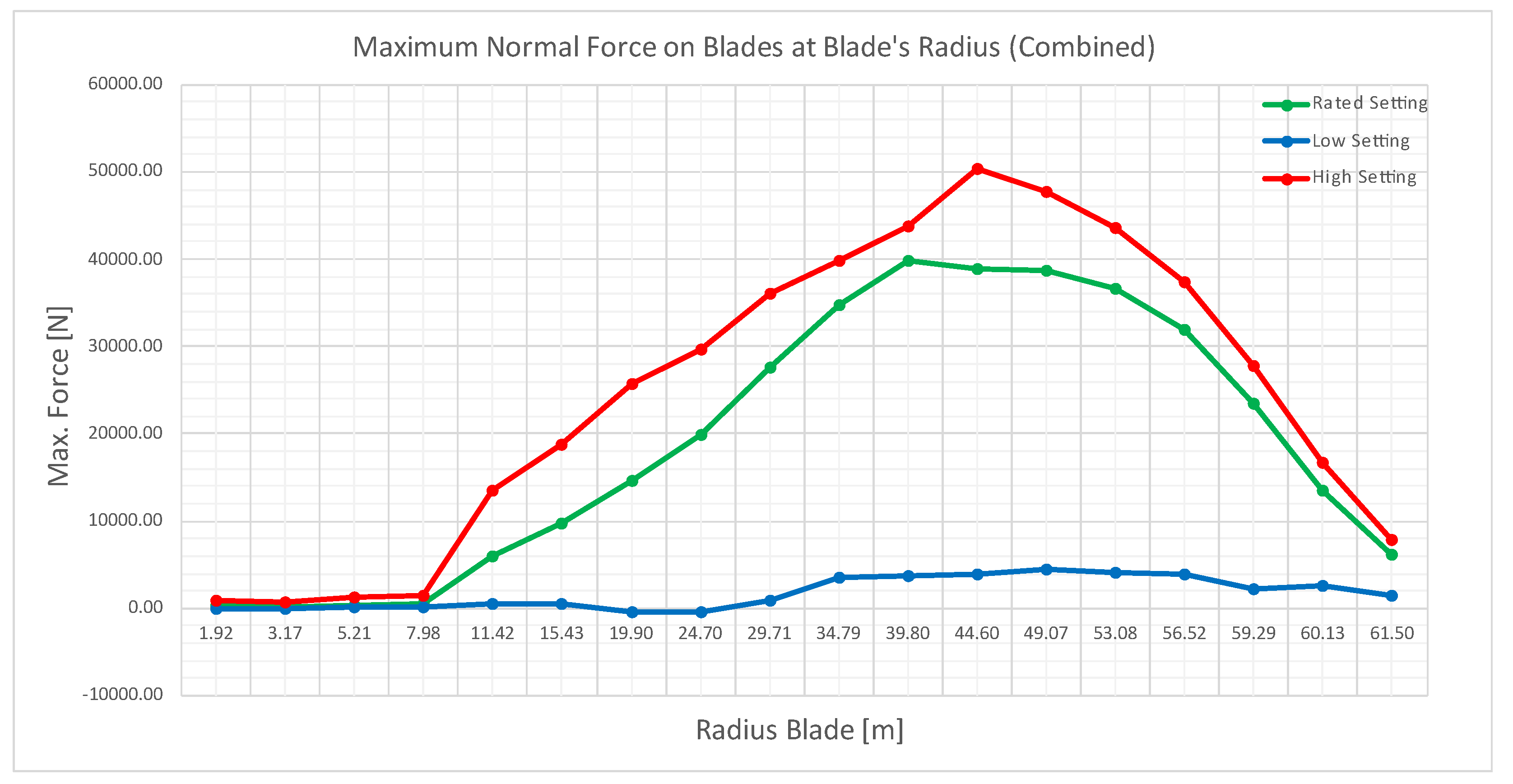
The dynamic simulation of the wind turbine model comprised of 1,000 timesteps, during which the data was gathered. Moreover, at the beginning of the simulation study the wind turbine was given an independent ramp-up time of 20 seconds (ramp-up of rotational speed up to predetermined rated rpm of 12.126). The main outputs for these simulations are normal forces on blades for 3 different settings. The results are presented as numerical values per section of the blade. This means that the blade was divided into 18 sections and corresponding forces specified in

\frac{N}{m}

. The exemplary results for Rated setting and its maximum normal forces are presented in Figure 12.

Results for High and Rated settings followed a pattern, which can be seen by the shape of the sketched curve. Low setting results are mainly inconclusive due to the obtained values. The shown pattern of normal forces acting on the blade does not follow a normal distribution due to extremely low wind speed with a set of negative values for the blade section between 11.42 m and 34.79 m and maximum stress at the tip of the blades. Therefore, this setting will not be analysed in further simulations, due to the indeterminate results.

Rated and High settings have the highest normal forces at sections between 49.07m to 56.52 m. Moreover, they show low values at roots of the blades and decreasing values at the tips.

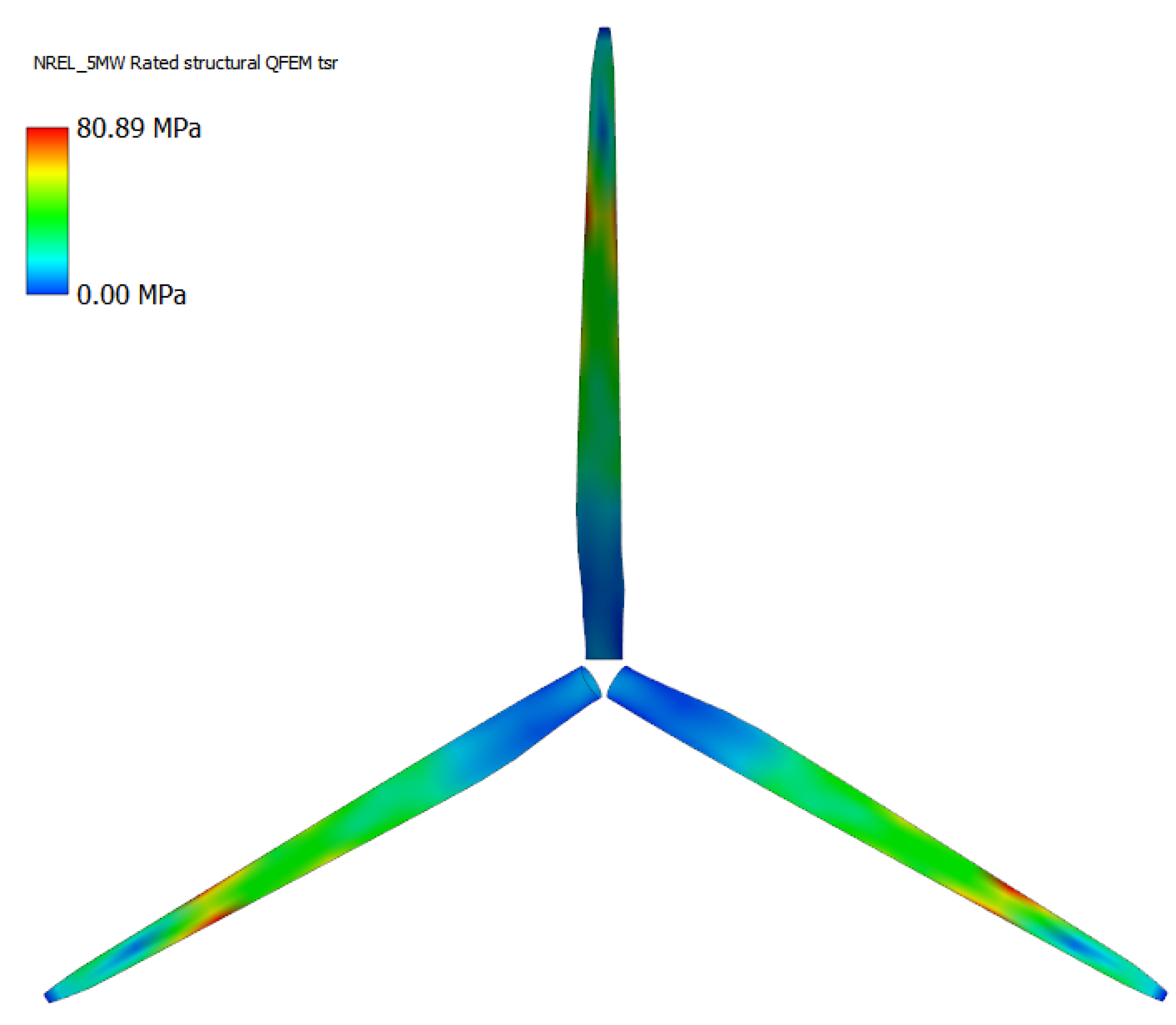
To validate the next simulations in Solidworks in relation with QBlade results, steady boundary element method (BEM) analysis was conducted. This feature is used to run simulations on rotor performance (rotor simulation) with accurate preliminary results. It was used in this investigation to produce a simulated set of data for evaluation of the blade stresses and maximum loads present at the blades in quadratic finite element method (QFEM) – structural blade design and analysis feature. For this purpose, wind speed, tip speed ratio range from 1 to 12 and wind variables were specified. Subsequently, the loading conditions were imported to QFEM – static blade design and analysis feature through the carried-out BEM simulation, along with the specified tip speed ratio value taken from previous wind turbine simulation study properties.

After specifying the rotor blade file, structural model developed in blade design and blade static loading conditions, the maximum blade stress of 80.89 MPa for Rated setting was obtained. This value will be used to compare the output values on the rotor structure from Solidworks and validate the simulation. The graphical and numerical solution for this simulation can be seen in Figure 13.

With the aim of performing structural analysis through finite element analysis in Solidworks, CAD models of the assembly containing blades, bearings and shaft had to be developed. Considering the computational expense and solution time of the structural study a more efficient and validated model was generated.

Since the blades would act as a load bearing structure for transferring the stresses to the drive system, it was decided to simplify the model to a rectangular beam. The length of the developed beam would correspond to the blade length. Thickness and breadth of the beam would be taken as an average value from the blade CAD file and 5MW NREL wind turbine technical report [10]. The blade has also been divided into 18 sections of the identical length to the ones proposed by QBlade software as referenced in Figure 12. Structural dimensions of the blades are given in Table 2.

Shaft dimensions and properties are referenced from [8]. The dimensions of the shaft, as well as locations of 2 concentric bearing supports are presented in Table 3.

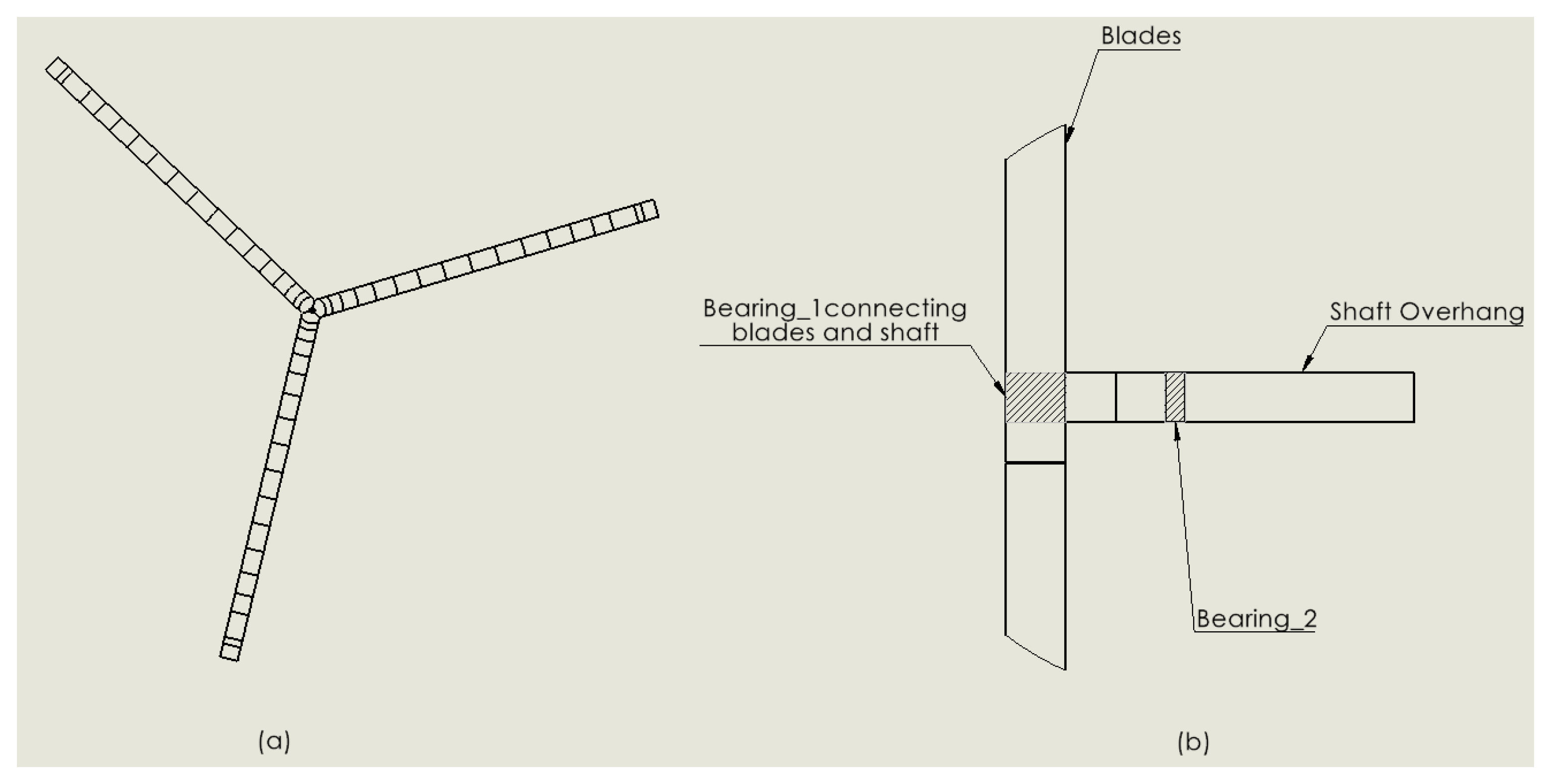
The bearings were located at:

The connection area between the blades and shaft. Therefore, the breadth of the Bearing_1 was set to 1,200 mm (equal to simplified blade thickness), in order to cover the whole connection area.
3,200 mm from the front face of the shaft. This results in creation of 2,000 mm long section of unsupported shaft, which corresponds to identified and investigated generator area.

Bearings were not modelled in Solidworks. Instead, the bearing fixture feature was used, which would resulted in ideal connections between blades and shaft. Moreover, it fixed the shaft about X and Y axis and allowed for rotational movement. The shaft structure was given an overhang section of 4,600 mm after bearing_2. This resulted in a transposed end face of the shaft, which was fixed along the Z axis, and limited the impact of the fixture on the studied shaft section – generator area. This was done in accordance with the St. Venant’s principle, which states that the strain produced by forces applied at one end of a long cylinder are much larger near the loaded end than at points at a larger distance [15] [16]. As a result, the deformation at the corresponding generator area was not affected by introducing the additional constraint. When applying the bearing fixtures, the shaft has been divided into 4 sections using the split line feature in Solidworks. Lengths of the sections were dependent on the structural properties of: Bearing_1 breadth, Bearing_2 breadth, Shaft overhang and Shaft length between Bearing_1 and Bearing_2 (generator area), as it can be seen in Figure 14. Two types of bearing fixtures were considered: rigid and flexible, where flexible fixtures had a combined radial stiffness of 3.81E+10

\frac{N}{m}

[7]. Rigid fixtures were taken into consideration and later compared to the flexible fixtures, although it was assumed that flexible bearing fixtures will better portray the behaviour of the system under loading conditions. For the purpose of constraining the model and calculating the radial stiffness for individual bearings, the parallel spring theory was used by using Equation (1),

K_{T o t a l} = k_{1} + k_{2}

(1)

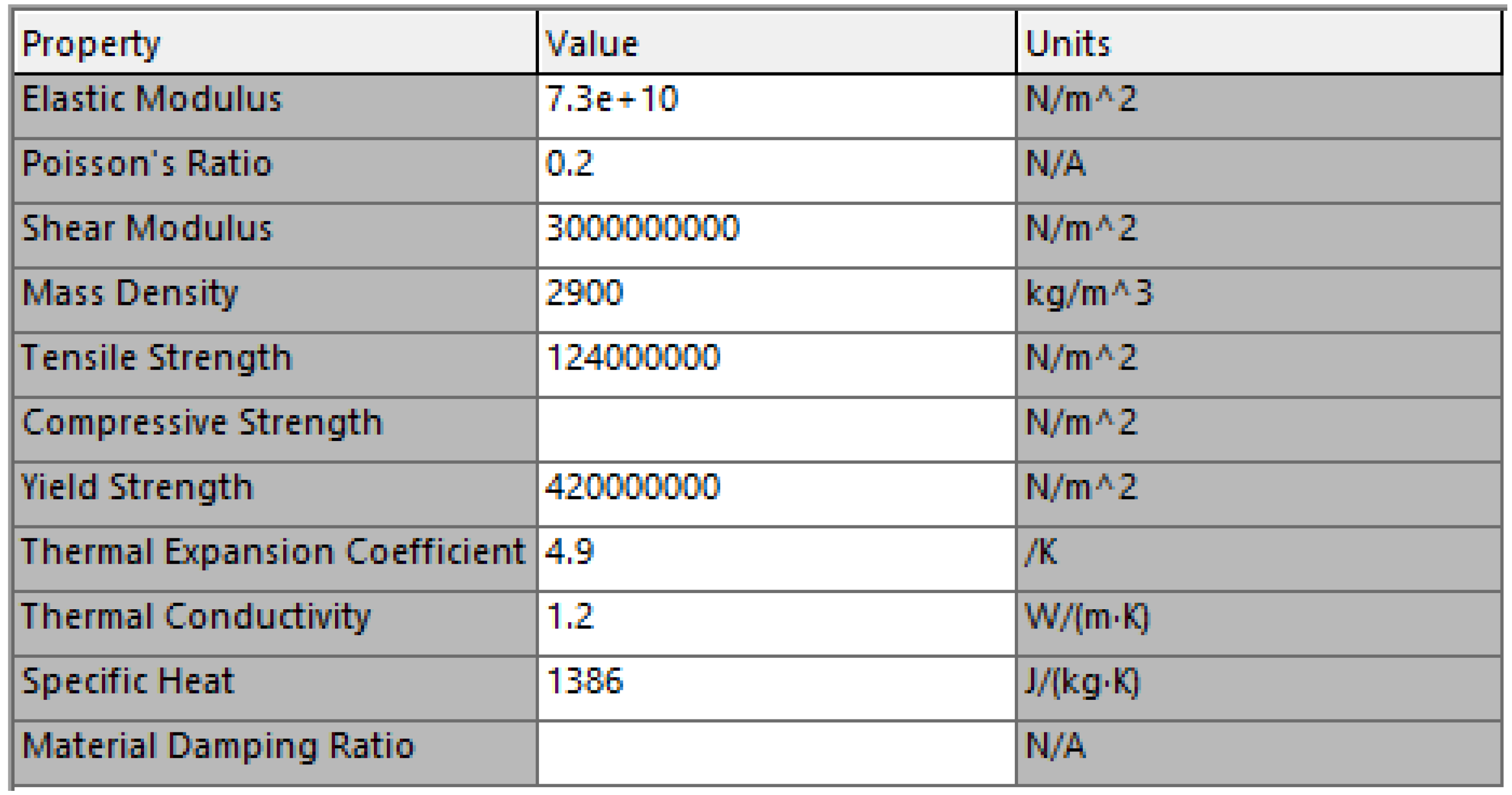
It was necessary to specify the material properties of the created CAD models to produce accurate simulations. Since the analysis of the system in Solidworks was preceded by QBlade simulations, elastic modulus and density, as well as isotropic characteristic of the blade material were taken from the QFEM - static blade design and analysis feature. Any values not specified in QBlade simulations were researched and obtained from MatWeb [17] and referenced paper [18]. The blade material was assumed to be made out of E-Glass composite. QBlade finite element package does not consider orthotropic materials. Therefore, the authors used the same approach. 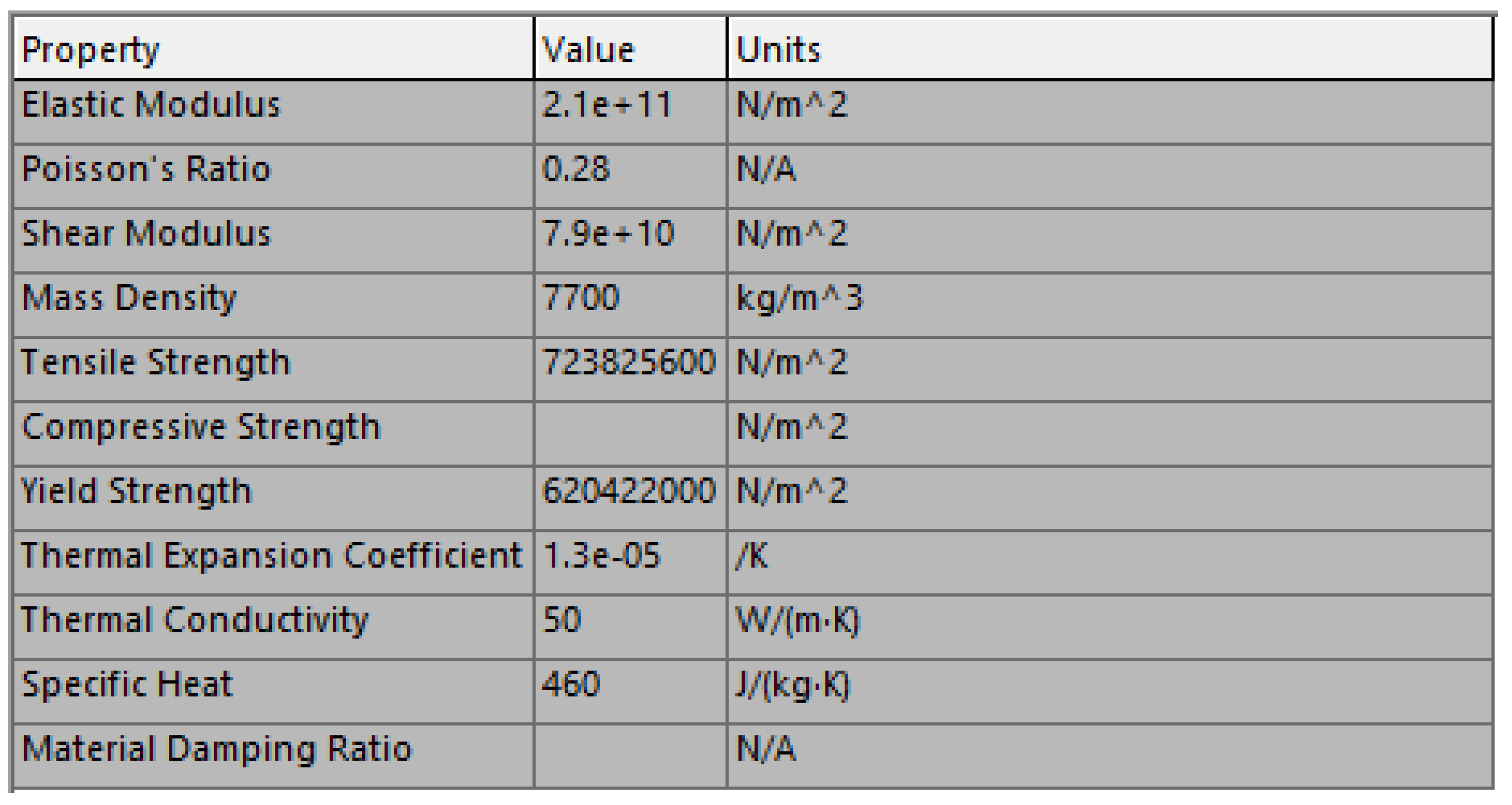The corresponding material properties of the blade are shown in Figure 15. The assumed shaft material properties, shown in Figure 16, are similar to those of an alloy steel.

The loading conditions have been applied on the blade structure after calculating the corresponding normal forces for Rated and High settings taken from QBlade for all 18 blade sections for each blade condition according to the wind field previously generated. Since the forces from QBlade were specified in

\frac{N}{m}

, the obtained values were multiplied by the section length on which the normal forces were acting upon. In total 54 different forces (per setting) were applied on the 3 blades in assembly. The comparison between the calculated normal forces for 3 different settings for one blade were presented in Figure 17. The results for Low setting were included in the figure, in order to present the minimal influence of the wind speed on the normal forces present.

Due to the significant size of the assembly, blended curvature-based meshing feature was used. Ultimately, two different mesh sizes were used for the model. A coarser mesh was chosen for the blades, whereas by using local mesh control on the shaft, smaller sized mesh was introduced. Once the general characteristics of the meshing technique were examined, a mesh independence study was conducted. Mesh for the blades had a maximum element size of 100 mm and a minimum element size of 10 mm, whereas the shaft had maximum and minimum element sizes of 62 mm and 55.8 mm, respectively. This resulted in 7,816,261 total number of nodes and 5,543,022 total number of tetrahedral elements.

3. Structural Analysis Results

The results for maximum displacement present at the shaft generator area were obtained through the usage of probe plot tool in Solidworks. The results for Rated and High settings are shown in Table 4 and Table 5.

The resultant eccentricity of the shaft was obtained from Equation (2):

s h a f t e c c e n t r i c i t y = \frac{m a x . s h a f t d e f l e c t i o n}{n o m i n a l a i r g a p} \times 100,

(2)

where nominal air-gap is 6.36 mm [7].

By using the values obtained for the shaft displacement in radial direction in Solidworks simulation, the non-uniformity (eccentricity) of the rotor for Rated and High settings can be calculated.

Shaft displacements in radial direction ranged from 0.191 mm to 0.379 mm for Rated and High settings respectively and were dependent on the flexibility of the bearing fixtures. The calculated resultant eccentricity, ranged from 3.00% for rated wind speed of 11.4

\frac{m}{s}

with flexible bearings to 5.96% for maximum operable wind speed of 25

\frac{m}{s}

with fixed bearings. The implementation of flexible bearings reduced the overall deformation of the shaft in the generator area. Therefore, by adding this additional factor to the simulation proved to reduce the shaft eccentricity in respect to the air-gap.

4. Rotor Optimisation

The initial structure was assumed to be positioned at the midspan of the shaft generator area and made of mild steel (Figure 18). The resultant mass of the model was 50,721.06 kg. The dimensions of the rotor were presented in Table 7 [7,10].

The presented structure was statically analysed. The typical three main loads present during the electrical machine operation were applied to the structure: radial expansion load (400 kPa) due to magnetic attraction, gravitational load (9.81 m/s²), corresponding to the weight of the structure and tangential load (40 kPa), also known as shear stress, caused by the generated torque (Figure 19).

The gravitational load represents the worst-case conditions due to the operation angle of 0°. Moreover, the tangential force has been calculated as a moment and applied to the outer rotor surface. Gravitational load was applied in the vertical direction pointing downwards. The rotor structure was fix constrained at the shaft. The resultant displacement was obtained from the simulation study, after applying the validated mesh containing 138,680 nodes and 77,501 elements consisting of tetrahedral solid elements. The mesh was validated through manual mesh independence study. The final displacement of the structure was 0.2625 mm.

This displacement was recognized as a mean deflection of the structure. In addition to the mean deflection, a variable deflection (shaft misalignment) has to be taken into account. As a result, it will not only increase the total deflection of the rotor structure, but also change the magnetic attraction. For this purpose, a derived model for the Maxwell stress calculation from [6] was used.

σ_{P M} (θ, \bar{δ}, δ_{Δ}) = \frac{{\hat{F_{P M}}}^{2} {c o s}^{2} (ρ θ) μ_{0}}{2 {(g + \frac{h_{m}}{μ_{r}} - \bar{δ})}^{2}} [1 + \frac{2 δ_{Δ} \sin (n θ)}{g + \frac{h_{m}}{μ_{r}} - \bar{δ}} + \frac{{δ_{Δ}}^{2} {s i n}^{2} (n θ)}{{(g + \frac{h_{m}}{μ_{r}} - \bar{δ})}^{2}}] \approx \frac{{\hat{F_{P M}}}^{2}}{4 {(g + \frac{h_{m}}{μ_{r}} - \bar{δ})}^{2}} [1 + \frac{2 δ_{Δ} s i n (n θ)}{g + \frac{h_{m}}{μ_{r}} - \bar{δ}} + \frac{{δ_{Δ}}^{2} {s i n}^{2} (n θ)}{{(g + \frac{h_{m}}{μ_{r}} - \bar{δ})}^{2}}]

(3)

where,

σ_{P M}

is the normal component of the Maxwell stress, θ is the circumferential angle,

\bar{δ}

is the radial mean deflection,

δ_{Δ}

is the variable deflection,

\hat{F}

is the magnetomotive force,

ρ

is the number of pole pairs,

μ_{0}

is the permeability of free space,

n

is the mode of deflection,

g

is the nominal air-gap,

h_{m}

is the magnet height, and

μ_{r}

is the relative permeability.

The obtained mean deflection and variable deflection are used to calculate the total deflection of the structure as described in [6]. Subsequently, the total deflection values are used in Equation (3) to determine the stress at a corresponding segment. The studied structure was divided into 36 segments in respect to the circumferential angle. This allowed for the application of the stresses calculated with Equation (3) on the outer faces of the cylinder.

The main objective of the structural optimisation is to reduce the amount of material in the rotor, while considering the conformity of the designs with the possible manufacturing operations. During the process, the material that does not carry the load will be removed from the initial structure design. This can be done by using topology optimisation feature in Inventor. This software package was a preferred choice due to the capabilities and simplicity of shape generation function powered by NASTRAN [20]. By applying shape generation study along with the validated mesh settings, 3 different mass reduction results have been obtained. As can be seen in Table 8, the proposed mass reduction of 35% might not be structurally applicable due to extensive material being removed. However, it is still desirable to conduct topology optimisation for higher mass reduction percentages, as it shows the general trend of the resultant shapes.

The generated shapes propose the removal of the material based on the specified loading conditions. By observing the results across different mass reduction settings, it is possible to determine the optimal design for the structure. Two geometries for possible cut-outs were proposed and introduced – circular and elliptical. To perform an optimisation study, a parametric table optimisation was conducted as described in [6]. Firstly, a set of design constraints was imposed. Then, the structure’s dimensions that could lead to potential mass reduction and overall optimisation were introduced as independent parameters with variable values. This included the shape and position of the cut-outs, as well as the wall thickness.

Determined design constraints:

Deflection limit of 10% of the air-gap. This resulted in deflection limit of 0.636 mm, which was further decreased to 0.341 mm by the shaft displacement.
Maximum Von Mises Stress – in range 0-200 MPa.
Mass – minimized.

For the purpose of this study, a maximum shaft displacement for High aerodynamic setting and flexible bearings was considered. This choice was expected to represent the working conditions in a best way, by also investigating the performance of the structure for more demanding operational wind speed. The proposed cut-outs were generated and simulated. Figure 20a,b, as well as Figure 21a,b show the obtained rotor structures and mass reducing geometries.

Table 9 and Table 10 present characteristics of the optimised structures.

Conducted simulations validated the possibility of the mass reduction with the proposed constraints and operational conditions. The final models showed a mass reduction of 8.45% for circular cut-outs and 9.62% for elliptical cut-outs in comparison to the initial structure. Moreover, by referencing [21] the environmental impacts of the production processes were extrapolated. The production of original rotor design at a mass of 50.721 tonnes, would emit 37.08 tonnes of CO₂ and CO₂ equivalents according to the Solidworks data extrapolation and require 1.53 million litres of water. By further analysing the environmental impacts and the overall reduction of emissions and water usage due to the optimisation procedure, Table 11 was created.

The costs associated with the rotor structure can be also defined (Table 12). They were broken down into manufacturing costs and financial impact. The financial impact includes manufacturing energy costs, supply costs for manufacturing, transportation, as well as the end-of-lifecycle costs. Similarly, as in the environmental impact study, the 3 existing revisions of the design were included in this investigation. The production of the original rotor design was estimated to cost approximately $78,167.

Careful consideration of vibration characteristics is important in many fields of engineering. It contributes to structural safety, performance, as well as longevity of components. Authors in [6] point out the importance of modal analysis and avoidance of frequency ranges, which promote excitation. The studied structure can experience fatigue damage and noise at any mode shape if excited. Therefore, any structural natural frequencies should be avoided or quickly passed. The structure can be activated through excitation frequencies such as: wind turbine rotational speed frequency, fundamental electrical frequencies and the frequencies of the rotor blades passing in front of the tower. Further studies proved that the optimised structures experienced a change in natural frequencies, with the biggest change in value for modal frequency 4 of 10.61% (circular vs original). The graphical comparison of modal analysis results can be seen in Figure 22. This demonstrates that there is room for further optimisation in this area if modal analyses are linked to the static optimisation study.

4.1. Computational Sustainability

During the project a large number of simulations had to be conducted. Therefore, it was assumed that computational times and overall performance of the simulations should be optimised and studied in order to explore the concept of sustainable modelling and analysis. The solution times for the simulations should always be minimised, regardless of the available resources and hardware without putting the accuracy of the study in question at risk. Shorter solution times can result in more cost-effective, productive and comfortable workflow. Hence, during the development of the project the software packages were interchanged depending on the preference and performance. By simplifying the model of the wind turbine drive system and creating less complex geometries, the resultant solution times were decreased. This was done by the use of parallel spring theory, St Venant’s theory and introduction of rectangular beam representation for the wind turbine’s blades. Moreover, by the use of additional tools, such as mesh independence study during FEA and smart set of configurations generated during the optimisation process, the computational times were further reduced.

The results of the performed study were presented in Table 13. For the example of the Rotor FEA simulation in Inventor, it was concluded that the impact of mesh size can significantly increase the solution times. The verified mesh size used in the study was reduced by 50%, which as a result increased the solution time to 2.15 minutes from 1 minute. This relatively small increase can prove substantial if the studied model was of larger size or greater complexity e.g., drive system assembly. This issue was resolved by applying local mesh control on shaft structure in drive system assembly FEA, thus, enabling more accurate results at a point of interest.

Furthermore, after conducting the drive system FEA in Solidworks, a change of software was applied. This was enforced by the substantially longer solution times of rotor shape generation studies of up to 40 minutes, which in comparison to Inventor were reduced to 3 minutes. Subsequently, a smart set of configurations was applied to the rotor parametric table optimisation in Inventor, which resulted in shorter solution times by reducing the number of predetermined configurations that have to be solved. On the example of elliptical cut-outs, this number was reduced from 2,304 to 29. Instead of generating all of the proposed configurations, a smart set of configurations changes one parameter value, while keeping remaining parameters at their base configuration. The values for all of the remaining configurations are then interpolated based on the smart set of configurations [22]. All of the simulations were conducted on the computer with system specifications listed in Table 14.

5. Discussion

By comparing the maximum stress values on rotor structure obtained in QFEM analysis in QBlade and FEA analysis in Solidworks for Rated setting, the overall simulation process can be validated. QBlade output value was 80.89 MPa, whereas Solidworks output value was 80.1 MPa. This results in a value difference of 0.98%. Therefore, the proposed investigation technique was assessed to be justified.

Moreover, by referencing the research conducted in [23] and comparing the obtained value to the findings in the study for Blade FEA in vertical position for rated rotational speed of 12.1 rpm, the total value difference of 6.01MPa or 6.98% can be seen (80.1 MPa to 86.11 MPa). The difference can be attributed to the approximation of the blade geometry and no consideration of the in-plane loading conditions. However, this would not be applicable in the case where the Solidworks simulation is validated through QBlade simulation with a value difference of below 1%. Furthermore, the main focus of the study was the creation of efficient full powertrain model, which considers the loads on the rotor. Therefore, some divergence in obtained values was expected in comparison to referenced, detailed analysis of the blade structure.

In spite of using the same model of reference wind turbine, the compared results were slightly divergent. Marginal errors are acceptable in FEA. Different sources present varying margins of errors ranging from 5% up to 13% of difference between results, dependent on the considered approach of the study [24]. Therefore, it was determined that the value difference of less than 10% verifies the results of the conducted study.

In [7], the air-gap eccentricity induced by the radial shaft displacements ranged from 2.99% to 10.38% and radial shaft displacements of 0.19 mm to 0.66 mm for wind speeds between 4

\frac{m}{s}

and 25

\frac{m}{s}

. This can be compared to the findings of this paper, which resulted in air-gap eccentricity ranging from 3.00% to 4.64% caused by the radial shaft displacements of 0.191 mm and 0.295 mm for Rated and High settings, respectively. The recognized value difference in the radial shaft displacements could be caused by a more precise definition of the direct drive system and the loads present. The addition of forces caused by unbalanced magnetic pull, their eccentricity induced nature due to shaft displacements and vibratory response of the system were identified as the main variables responsible for the value differences in this paper.

By introducing the environmental and cost investigations, the significance of the optimisation process was further magnified. On the example of the elliptical cut-outs optimisation, it can be observed that the total mass reduction of 9.62%, in comparison to the original design, would result in reduction in CO₂ emissions, water usage and costs of 3.57 tonnes, 146,816.8 litres and $7,523. If the studied Anholt wind farm was using 5MW NREL wind turbines, then the proposed optimisation strategy would result in total cost reduction of $835,053 split between 111 machines. It is worth noting at this point that a similar procedure can be used for the stator supporting structure.

6. Conclusions

The carried-out investigation on the direct-drive system of a 5MW NREL reference wind turbine, resulted in identifying the process of obtaining maximum von-mises stress and deflection on blade and shaft structures under aerodynamic loads, as well as resultant air-gap eccentricity due to radial displacements of the shaft. The applied loading conditions, resulted in air-gap eccentricity ranging from 3.00% to 4.64% caused by the radial shaft displacements of 0.191 mm and 0.295 mm, respectively.

The process consisted of the calculation and validation of wind characteristics acting on the structure based on real-world data taken from the selected Anholt wind farm site for 3 chosen wind settings: Low, Rated and High. A high level of convergence between the simulated settings and the wind farm data package was obtained. Subsequently, the results for aerodynamic conditions were used as an input in the wind turbine simulations in QBlade software, in order to determine the aerodynamic loads present at the blades of the wind turbine and validate further analysis in Solidworks simulations. The obtained loading conditions were then used to conduct finite element analysis in Solidworks and show the behaviour response of the system, which were later used in further studies for optimisation of the direct-driven wind turbine structure. The implementation of these findings resulted in the overall mass reduction of 8.45% and 9.62% for the proposed geometries, which accounts for the overall reduction in CO₂ emissions of 3.13 and 3.57 tonnes, 128,853.1 and 146,816.8 litres of water usage, as well as $6,603 and $7,523 of rotor associated costs, for circular and elliptical cut-outs respectively.

The final results were critically compared against existing studies. The differences in obtained values and problem approaches were identified and discussed. Overall, the current study shows in detail the steps taken to conduct the study on 5MW NREL reference direct-driven wind turbine and presents the importance of external loading consideration, when conducting the optimisation process of the studied structure.

Further research could incorporate a wider range of aerodynamic settings. This could help to identify in detail the pattern of the structural behaviour under changing environmental conditions. By expanding the scope of the project, the influence of floating wind turbine structures and sea conditions can be implemented and compared against the existing results for monopile structure. Moreover, the conducted modal analysis identified the possible development of the optimisation process, by linking the modal analyses to the static optimisation studies.

7. Acknowledgments

We would like to thank Ørsted for their valuable contribution to the paper in the form of data sharing and granting access to operational offshore wind farm data as well as offshore meteorological data.

Appendix A

Table A1. Anholt Wind Farm vs QBlade Simulated Average Wind Speeds at Predetermined Altitudes for Low Setting.

Altitude [m]	Corrected Altitude [m]	$Anholt Windspeed (Low) (\frac{m}{s})$	$QBlade Windspeed (Low) (\frac{m}{s})$	Percentage Difference
40	65.6	3.56	3.43	-3.83%
60	85.6	3.56	3.53	-0.79%
76	101.6	3.55	3.59	1.12%
80	105.6	3.54	3.59	1.50%
100	125.6	3.58	3.58	-0.10%
116	141.6	3.63	3.60	-0.71%
160	185.6	3.92	3.78	-3.48%
200	225.6	4.21	3.97	-6.20%
250	275.6	4.57	4.11	-11.27%
290	315.6	4.85	4.21	-15.26%

Table A2. Anholt Wind Farm vs QBlade Simulated Average Wind Speeds at Predetermined Altitudes for Rated Setting.

Altitude [m]	Corrected Altitude [m]	$Anholt Windspeed (Rated) (\frac{m}{s})$	$QBlade Windspeed (Rated) (\frac{m}{s})$	Percentage Difference
40	65.6	10.91	11.01	0.87%
60	85.6	11.19	11.37	1.52%
76	101.6	11.37	11.64	2.27%
80	105.6	11.40	11.68	2.36%
100	125.6	11.56	11.55	-0.03%
116	141.6	11.68	11.64	-0.29%
160	185.6	11.99	12.29	2.46%
200	225.6	12.24	12.82	4.47%
250	275.6	12.50	13.30	6.03%
290	315.6	12.47	13.65	8.70%

Table A3. Anholt Wind Farm vs QBlade Simulated Average Wind Speeds at Predetermined Altitudes for High Setting.

Altitude [m]	Corrected Altitude [m]	$Anholt Windspeed (High) (\frac{m}{s})$	$QBlade Windspeed (High) (\frac{m}{s})$	Percentage Difference
40	65.6	23.34	23.60	1.10%
60	85.6	23.96	24.42	1.92%
76	101.6	24.37	24.95	2.31%
80	105.6	24.46	25.04	2.31%
100	125.6	24.79	24.81	0.08%
116	141.6	25.02	25.00	-0.10%
160	185.6	25.73	26.38	2.46%
200	225.6	26.17	27.47	4.73%
250	275.6	26.68	28.55	6.56%
290	315.6	26.92	29.32	8.17%

References

1. Wind Energy in the UK: June 2021; Office for National Statistics; 14 June 2021; https://www.ons.gov.uk/economy/environmentalaccounts/articles/windenergyintheuk/june2021.
WindEurope Taskforce Baltic, Mattia Cecchinato, WindEurope; Boosting offshore wind energy in the Baltic Sea; Wind Europe; Nov. 2019; https://windeurope.org/wp-content/uploads/files/about-wind/reports/WindEurope-Boosting-offshore-wind.pdf.
Teng, Wei & Jiang, Rui & Ding, Xian & Liu, Yibing & Ma, Zhiyong; Detection and Quantization of Bearing Fault in Direct Drive Wind Turbine via Comparative Analysis; Shock and Vibration; 2016; 1-12 . [CrossRef]
Ding Liao, Shun- Peng Zhu, José A.F.O. Correia, Abílio M.P. De Jesus, Milan Veljkovic, Filippo Berto; Fatigue reliability of wind turbines: historical perspectives, recent developments and future prospects; Renewable Energy; Vol. 200; 2022; Pages 724-742; ISSN 0960-1481.
Tartt, K & Kazemi Amiri, Abbas (Mehrad) & McDonald, Alasdair & Jaen Sola, Pablo; Structural Optimisation of Offshore Direct-Drive Wind Turbine Generators Including Static and Dynamic Analyses; Journal of Physics: Conference Series; 2018; 012040. [CrossRef]
P. Jaen-Sola, E. Oterkus, A.S. McDonald; Parametric lightweight design of a direct-drive wind turbine electrical generator supporting structure for minimizing dynamic response; Taylor & Francis; Ships and Offshore Structures; 2021; Vol. 16; No.51; 5266-5274. [CrossRef]
Sethuraman L, Xing Y, Venugopal V, Gao Z, Mueller M, Moan T. A 5 MW direct-drive generator for floating spar-buoy wind turbine: Drive-train dynamics. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2017;231(4):744-763. [CrossRef]
Baseer, R. Schelenz, M. Cardaun, T. Duda, G. Jacobs; Study of Direct Drive Turbine Concept with respect to Air Gap Sensitivity by means of Multibody Simulation; Center for Wind Power Drives; Campus-Boulevard 61, 52074 Aachen, Deutschland.
International Electrotechnical Commission; IEC 61400-50:2022, Wind energy generation systems – Part 50: Wind measurement – Overview; Edition 1.0; 2022-08; ISBN 978-2-8322-5600-8.
J. Jonkman, S. Butterfield, W. Musial, and G. Scott; Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory, Technical Report, February 2009.
Plumley, Charlie; Penmanshiel Wind Farm Data; Zenodo; February 2022; https://zenodo.org/record/5946808.
Cubico Sustainable Investments; https://www.cubicoinvest.com/.
Ørsted; https://orsted.com/en/our-business/offshore-wind/wind-data.
QBlade; https://qblade.org/.
Toupin, R.A.; On, St. Venant’s principle; Görtler, H.; Applied Mechanics; Springer, Berlin, Heidelberg; 1966. [CrossRef]
Henrik Sönnerlind; Applying and Interpreting Saint-Venant’s Principle; COMSOL; January 2018; https://www.comsol.com/blogs/applying-and-interpreting-saint-venants-principle/.
MatWeb; Material Property Data; https://www.matweb.com/index.aspx.
National Research Council; Assessment of Research Needs for Wind Turbine Rotor Materials Technology; Washington, DC: The National Academies Press. [CrossRef]
Aristeidis Zavvos; Structural Optimisation of Permanent Magnet Direct Drive Generators for 5MW Wind Turbines; The University of Edinburgh; 2013.
Matthew W. Perenich; Finite Element and Computational Capabilities of Commercial Software for Composites; Clemson University; Clemson, SC; 2020.
Bichan, M. , Jack, A. , Jaen-Sola, P; Establishing the Importance of Operating Temperature in the Structural Integrity of Large-Scale Direct-Drive Wind Turbine Generators; Machines 2023, 11, 780; [Google Scholar] [CrossRef]
Ravi Burla; Autodesk; 2014; https://forums.autodesk.com/t5/inventor-forum/parametric-stress-analysis-meaning-of-quot-smart-set-of/td-p/5326799.
Meng-Kao Yeh and Chen-Hsu Wang; Stress analysis of composite wind turbine blade by finite element analysis; 2017; IOP Conf. Ser.: Mater. Sci. Eng. 241 012015.
H. A. Rahman; Finite Element Model Updating of Dissimilar Plate with Rivet Joint; 2019; J. Phys.: Conf. Ser. 1262 012035.

Figure 1. Wind Turbine Structure Diagram [4].

Figure 2. Generator Structure [6].

Figure 3. (a) shear loading, (b) magnetic attraction of the moving and stationary components, (c) Gravitational loading, (d) Thermal expansion of the generator structure, (e) Centrifugal loading [6].

Figure 4. (a) Mode 0 – uniform deflection, (b) Mode 1 – eccentricity, (c) Mode 2 – ovalisation, (d) Mode 3 – pattern of ripples [6].

Figure 5. (a) Shaft Displacement, (b) Concentric Rotor, (c) Eccentric Rotor [7].

Figure 6. Schematic of the Workflow and Methodology.

Figure 7. Anholt Wind Farm Data Wind Rose.

Figure 8. Rated Wind Speed Anholt Data Correlation.

Figure 9. Graphical Representation of Windfield for Rated Setting.

Figure 10. Average Wind Speed Correlation Study for Rated Setting (Anholt Site vs QBlade).

Figure 11. Schematic Model of the Developed System for Dynamic Simulations.

Figure 12. Maximum Normal Force vs Blade’s Radius Graph for Rated Setting.

Figure 13. QFEM – Static Blade Design and Analysis Result for Rated Setting.

Figure 14. (a) Divided Blades Sections, (b) Schematic of the Simplified Model (Cropped Blades).

Figure 15. Material Properties for E-Glass Composite Blade.

Figure 16. Material Properties for Alloy Steel Shaft.

Figure 17. Maximum Normal Forces at Blades vs Blade’s Radius Graph for Combined Settings.

Figure 18. Developed CAD Model of the Rotor Structure.

Figure 19. (a) Normal Component of Maxwell Stress, (b) Gravity Acting on the Structure in Vertical Direction, (c) Shear Stress [19].

Figure 20. (a,b) Front and Isometric View of Optimised Structure with Circular Cut-outs.

Figure 21. (a,b) Front and Isometric Views of Optimised Structure with Elliptical Cut-outs.

Figure 22. Modal Analysis Comparison Between Original and Optimised Geometries.

Table 1. Anholt Wind Farm Technical Data.

Title 1	Title 2
Latitude	56°35'44.4"N
Longitude	11°09'09.8"E
No. of Turbines	111
Total Nominal Power	400 MW
Turbine Nominal Power	3.6 MW
Turbine Rotor Diameter	120 m
Location	Offshore
Status *	Operational

* as of 10.09.2023.

Table 2. Structural Dimensions of Simplified 5 MW WT Blades.

Structural Property	Value [m]
Blade Thickness	1.2
Blade Breadth	3.3
Blade Length	61.5

Table 3. Structural Properties of 5 MW WT Shaft.

Structural Property	Value [mm]
Shaft Length	8,200
Shaft Internal Diameter	500
Shaft Outside Diameter	1,000
Bearing_1 Breadth	1,200
Bearing_1 distance from shaft origin point	0
Bearing_2 Breadth	400
Bearing_2 distance from shaft origin point	3,200
Shaft Overhang	4,600
Shaft Length between Bearing_1 and Bearing_2	2,000

Table 4. Maximum Stress and Deflection for Blade and Shaft Structures, Rated Setting.

Structural Property	Value
Max. stress at blades [MPa]	80.1
Max. displacement at blades [mm]	484.5
Max. displacement at shaft in generator area for rigid bearings [mm]	0.265
Max. displacement at shaft in generator area for flexible bearings [mm]	0.191

Table 5. Maximum Stress and Deflection for Blade and Shaft Structures, High Setting.

Structural Property	Value
Max. stress at blades [MPa]	99.7
Max. displacement at blades [mm]	591.5
Max. displacement at shaft in generator area for rigid bearings [mm]	0.379
Max. displacement at shaft in generator area for flexible bearings [mm]	0.295

Table 6. Shaft Eccentricity Due to Aerodynamic Load for Rated and High Settings.

Setting	Shaft Displacement in Radial Direction [mm]	Air-Gap Eccentricity
Rated Setting (Flexible Bearings)	0.265	4.17%
High Setting (Flexible Bearings)	0.379	5.96%
Rated Setting (Rigid Bearings)	0.191	3.00%
High Setting (Rigid Bearings)	0.295	4.64%

Table 7. Structural Properties of the Rotor Structure Geometry.

Structural Property	Value [mm]
Outer Diameter	6,360
Inner Diameter	1,000
Cylinder Length	1,720
Cylinder Thickness	87
Wall Thickness	123

Table 13. Details of Performed Simulations Regarding Computational Performance.

Software	Type of Simulation	No. of Simulations	Solution Time (Average)
Solidworks	Drive System Assembly FEA	4	20 min
Inventor	Rotor FEA	2	1 min
Inventor	Rotor Shape Generator	6	3 min
Inventor	Rotor Parametric Table Optimisation	2	4 min
Inventor	Modal Analysis	3	1 min

Table 8. Schematic Representation of Generated Shapes During Optimisation Process.

Table 9. Details and Results of Parametric Table Optimisation for Circular Cut-outs..

Property	Value
Total Number of Generated Set-ups	3,240
Maximum Displacement [mm]	0.3401
Maximum Von Mises Stress [MPa]	21.56
Resultant Mass [kg]	46,436

Table 10. Details and Results of Parametric Table Optimisation for Elliptical Cut-outs.

Property	Value
Total Number of Generated Set-ups	2,304
Maximum Displacement [mm]	0.3403
Maximum Von Mises Stress [MPa]	1,720
Resultant Mass [kg]	45,839

Table 11. Environmental Impact of Rotor Structure Production.

Revision	Mass [tonnes]	CO₂ Emissions [tonnes]	Water Usage [Litres]
Original	50.721	37.083	1,525,378.204
Circular Cut-outs	46.436	33.951	1,396,525.062
Elliptical Cut-outs	45.839	33.514	1,378,561.413

Table 12. Rotor Associated Costs.

Table 14. Computer Specifications.

Property	Specification
GPU	NVIDIA GeForce GTX 1650
CPU	Intel(R) Core(TM) i5-9300H CPU @ 2.40GHz
RAM	16 GB
Disk	SSD

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Efficient Computational Analysis and Modelling of Transferred Aerodynamic Loading on Direct-Drive System of 5MW Wind Turbine and Results Driven Optimisation for a Sustainable Generator Structure

Abstract

1. Introduction

2. Methodology

2.1. Wind Data Analysis

2.2. Windfield Simulations and Validation

2.3. Structural Analysis of the Wind Turbine Structure

3. Structural Analysis Results

4. Rotor Optimisation

4.1. Computational Sustainability

5. Discussion

6. Conclusions

7. Acknowledgments

Appendix A

References

MDPI Initiatives

Important Links

Subscribe