Prerpints.org logo
Preprint
Communication

Beyond Deep Learning—Space, Time, and Emergence

Altmetrics

Downloads

322

Views

322

Comments

0

This version is not peer-reviewed

Advances in Artificial Neural Networks

Submitted:

02 November 2023

Posted:

03 November 2023

You are already at the latest version

Alerts
Abstract
In this perspective article, we ponder topographical enhancements of artificial neural networks. In our recent paper in JMLR, we proved a quasi-equivalence between the network width and depth and also discussed the power of intra-links, which can be viewed as network height. In 1982, Hopfield published a network to model human associative memory, which contains many loops for dynamic evolution toward fixed points. Based on noising-denoising loops, diffusion models are recently developed to enable Bayesian modeling and inference with big data. Furthermore, we envision development of multi-AI-agent systems through “netware” engineering as a quantum leap of software engineering for emergent behaviors and autonomous AI at individual and population levels. We believe that the novel use of links and loops in space and time via multi-scale coupling would catalyze the next-generation neural networks.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Over the past decade, the success of deep learning models such as ResNet [1] and Transformer [2] reinforced the notion that "the deeper the better" [3,4]. More recently, the emergence of large models like ChatGPT [5,6,7] sparked competition to design and train increasingly massive models using vast amounts of data on high-performance computing platforms, giving an impression of “the larger the better”. Given the high system cost and low energy efficiency of the current large models, the trend is unsustainable for creating deeper/larger AI models [8]. Indeed, it is estimated that training a large model like ChatGPT would cost millions of dollars [9]. Also, the dominance of large companies and labs distorts the eco-system of AI [10]. Hardware-wise, in the foreseeable future the most advanced GPUs will be based on 3nm or 1nm fabrication, approaching the atomic scale and meeting a physical ceiling to accommodate larger models. Therefore, it is high time to consider how to sustain the momentum of AI development toward artificial general intelligence [11], the holy grail of AI research.
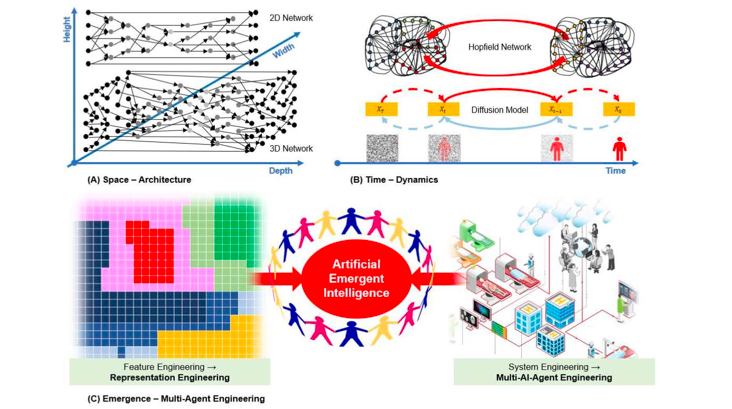
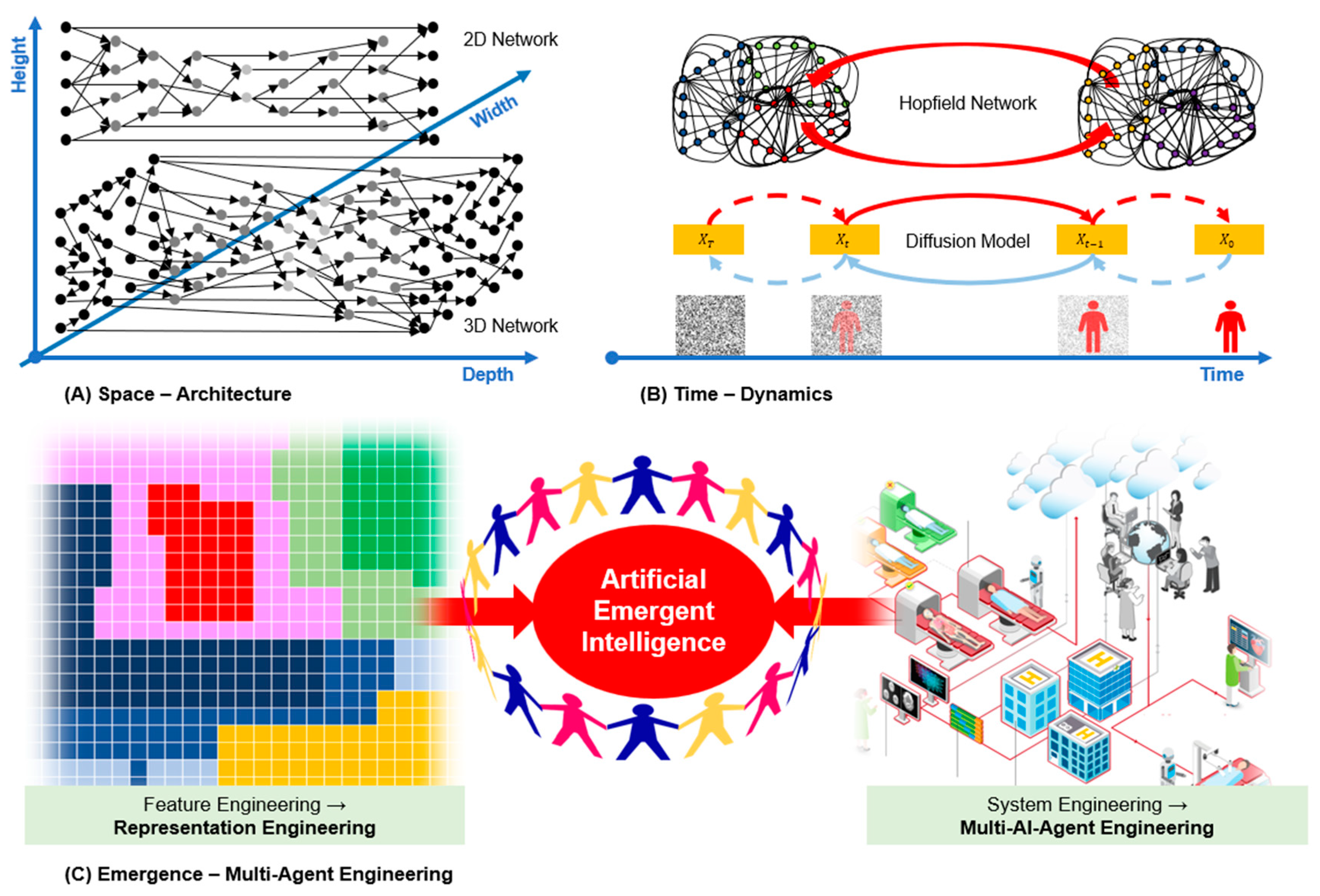
As illustrated in Figure 1, here we ponder the novel use of links and loops in space and time via multi-scale coupling to catalyze the next-generation neural networks. In our recent paper [12], we proved a quasi-equivalence between the network width and depth, and discussed the power of intra-links, which can be viewed as network height. In 1982, Hopfield published a network to model human associative memory, which contains many loops and allows dynamic evolution toward fixed points. Based on noising-denoising loops, diffusion models are recently developed to enable Bayesian modeling and inference with big data. Furthermore, we envision development of multi-AI-agent systems through “netware” engineering as a quantum leap of software engineering for emergent behaviors and autonomous AI at both individual and population levels.

2. Methods and Results

2.1. Interaction between Depth, Width, and Height

Naively deepening models may not be beneficial [6]. In terms of expressivity, the width and depth of an artificial neural network are theoretically equivalent, meaning that a wide network can be transformed into a deep network at an arbitrarily small error, and vice versa [12]. Practically, deepening a network often yields better performance than widening it but a decent performance of a deep network assumes a specific requirement of the width. It has been proven that, to approximate a function from Rm to Rn, the minimum width required is m+n [13,14]. The interplay between width and depth is intricate; for example, in transformers, widening becomes necessary when deepening. If the width and depth are not balanced well, increasing depth becomes inefficient [15]. While a deeper network implies more sequential computations and higher latency, a wider network allows for easier parallelization. It was demonstrated in [16] that a wider network with only 12 layers can achieve performance comparable to that of deep networks with 30 layers.
In addition to the width and depth, the height of the network is an overlooked dimension. The concept of network height is rare in the literature. The height can be introduced with intra-layer links within a layer, as pointed out in our recent paper [12] and in relevant prior studies [21,22]. Shortcuts, which bypass layers, have worked well [17,18,19,20]. Different from the commonly used shortcuts that connect layers, intra-layer links incorporate shortcuts within a layer, as shown in Figure 1(a). The concept of height is a natural extension beyond the width and depth of neural networks. Simply wrapping a linear array of neurons within a 2D array does not change the fact that these neurons can still be straightened out. On the other hand, intra-layer links implement neural interconnections within a layer so that neurons in the layer cannot be linearly unrolled, thus making the height direction meaningful and necessary.
Introducing height is different from increasing depth in the following three senses. First, it increases neither the number of affine transformations nor the number of nonlinear activations, while increasing depth does. Second, the use of intra-layer links (height) is a parallel mechanism to enhance representation power, while the use of layers (depth) is a compositional mechanism [12]. Third, the mechanism behind intra-layer links involves breaking symmetry and reinforcing the mutual information among neurons within the same layer [23], thus reducing the hypothesis space of interest. A network with the rectified linear unit (ReLU) for activation defines a piecewise linear function. Intra-linked neurons can produce exponentially more linear pieces [12]. Consequently, a narrower network with intra-layer links can possess the same potential as an exponentially wider network. Coupling the width, depth, and height of a network empowers its performance without increasing the number of network parameters significantly.
Introducing the network height can significantly enhance deep learning capabilities. We should consider "height separation". This emphasizes the importance of height for network design, suggesting that a tall network can only be expressed by a short network with very large width and depth. It is important to note that width, depth, and height of a network could be flexibly converted for universal approximation, meaning that tall, wide, and deep networks can be transformed from one type to another. Therefore, instead of blindly increasing depth, we advocate for optimal balance among width, depth, and height of a network to maximize its representation power and computational efficiency.

2.2. Integration of Feedforward and Feedback Mechanisms

With the intra-/inter-links, loops can be naturally formed to induce dynamics of a data-processing workflow. In the physical world, many systems are composed of numerous basic elements, and generate emergent properties driven by the least action principle [60,61]. In the human brain, intelligent behaviors arise from collective activities of interacting neurons. The Hopfield network is a pioneering example [23]. Unlike deep networks, which use primarily feedforward links without feedback loops, the Hopfield network and its variants [23,24,25,26,27] rely on a feedback mechanism that fundamentally differs from a feedforward network and produce intriguing outcomes such as associative memory. To harness the full potential of connectionism, as shown in Figure 1(b) we should extend the Hopfield network to combine the feedforward and feedback mechanisms in innovative ways. Such a combination of links and loops would bring significant advantages. Substantial evidence indicates that our brain works at critical points [28,29], such as “the aha moment”, which means abrupt changes between order and disorder or between distinct states. While a one-dimensional Ising model lacks phase transition, a two-dimensional Ising model exhibits phase transition, since clustered interactions form loops on a two-dimensional grid [30]. Therefore, a network that incorporates loops and links in multiple dimensions would behave more like our brain, giving rise to critical behaviors that have not yet been a focus of today’s AI research. Furthermore, we should use a state-based method that can describe the behaviors of networks with feedback loops more effectively and efficiently. Fang et al. utilized a state-oriented representation to demonstrate that gradient descent search can discover a global minimum in the mean-field regime [31]. Zhang et al. leveraged the state representation to illustrate that the network depth can induce a Gaussian process [32].
While the Hopfield network is featured by recurrent feedback loops (circular loops embedded in the architecture), the recently emerging diffusion models / score-matching networks [33] allow that an original data distribution is gradually noised into a featureless random field, and then incremental noise components can be gradually removed from the random field to sample the original data distribution (linear feedback in forward and reverse directions sequentially), also shown in Figure 1(b). The whole noising-denoising loop can be done in hundreds or even thousands of steps, leading to powerful dynamics with the solution existence, uniqueness, and stability established by the stochastic differential equation theory [34]. Increasingly more independent studies report that the diffusion models set the state-of-the-art performance of generative AI, outperforming famous GAN and VAE networks [35]. The conventional wisdom of deep learning is that given a dataset one can learn the data distribution in the supervised learning mode. However, when data are highly diverse, and labels are rather scarce, supervised learning is handicapped. In this and other important scenarios, the diffusion model and its variants represent a great research direction. Although the sample efficiency using the diffusion model is relatively low, further research will hopefully address this weakness [36].

2.3. Synergizing Multiple AI Agents through “Netware” Engineering

Currently, either small artificial neural networks or large multimodal models are typically treated as single entities. At a higher level, as shown in Figure 1(c), we consider the relationship among AI models in a “super-network” perspective to engender the emergent properties and behaviors of AI systems at both individual and population levels.
Development of multi-AI-agent systems needs to start with an initial relationship between components. To this end, we can draw parallels to software engineering concepts [37] and define the “netware” engineering principles. Naturally, all key relations between objects in software engineering can be parallel-transported to capture relations between networks. For example, dependency, as a one-directional relationship, signifies that one object is constructed with another object, as demonstrated in hypernets [38,39,40]. Netware engineering focuses on relationships, thus instantiating category theory [41]. By Yoneda’s lemma [42] in category theory that X and Y are isomorphic if and only if their represented functors are isomorphic. Thus, the network performance is determined and comprehended by the relationships among components, while the traditional understanding of a network is based on its input-output responses.
What sets netware engineering apart from software engineering is the autonomous potential of networks, which is evidenced by emergent capabilities. This can be better understood and controlled using the top-down approach through representation engineering (RepE) [43] and potentially other ways. RepE draws inspiration from the Hopfieldian view of cognitive science [44], which considers cognition as a result of activity patterns in a population of neurons. In [43], a technique called “low-rank representation adaptation” (LoRRA) was proposed to capture emergent cognitive functions at a semantic level. In the context of honesty, two contrasting prompts such as "pretend you are a dishonest or an honest person, tell me about ABC” are prepared to elicit different activity patterns among the population of neurons in a network. This process metaphorically resembles performing an fMRI scan on the model. Subsequently, the contrastive activity vector serves as the representation target, allowing the model to be fine-tuned towards being honest. RepE can be generalized to address other important AI-specific issues such as uncertainty and stability.

3. Discussion and Conclusion

A subsequent goal of synergizing multiple AI agents is to generate the emergence phenomina at the population level. A multi-AI-agent system would have emergent behaviors that cannot be explained by specific behaviors of individual neurons or neural circuits. In social science, emergent phenomena are widely observed at the population level, known as “large is different” [7]. A famous Chinese proverb says, “three cobblers with their wits combined equal a master mind”. In biophysics, the collective and coherent motions, also known as flocking, can emerge in a large number of self-propelled organisms such as birds, fish, and bees [45]. Flocking behaviors are equilibrium states characterized by the Toner-Tu equation, with the velocity violates the conservation of momentum [45]. To some extent, this characterization also applies to multi-AI-agent systems, which feature communication between agents, action coordination, and coalition formation. The “flocking” signifies that consensus emerges among agents [46]. By designing control-theoretic and game-theoretic rules that prescribe the information exchange among agents, one can modulate the cooperation and competition of agents to stimulate the emergence properties. Other types of rules should be also feasible for emergence of intelligent behaviors.
Given the current challenges encountered in the development of deep/large networks, our above analyses suggest transcending the territory of deep learning from spatial, temporal, and relational angles. This perspective represents a convergence of classic science and contemporary technology with the central focus on the development of the next-generation artificial neural networks. There are also other interesting perspectives, such as the fusion of rule-based [47] and data-driven approaches, embodied artificial intelligence [48], and quantum deep learning [49]. We welcome further brainstorming for empowerment of artificial neural networks.

Acknowledgment

This work was supported in part by NIH grants R01CA237267, R01HL151561, R01CA227289, R37CA214639, R01CA237269, R01CA233888, R01EB026646, and R01EB032716.

References

  1. He, K., Zhang, X., Ren, S., & Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770-778.
  2. Vaswani, A., et al. Attention is all you need. Advances in Neural Information Processing Systems, 2017, 30.
  3. Poggio, T. , Banburski, A., & Liao, Q. Theoretical issues in deep networks. Proceedings of the National Academy of Sciences, 2020, 117(48), pp. 30039-30045. [CrossRef]
  4. Belkin, M., Hsu, D., Ma, S., & Mandal, S. Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences, 2019, 116(32), pp. 15849-15854. [CrossRef]
  5. Thirunavukarasu, A. J., et al. Large language models in medicine. Nature Medicine, 2023, pp.1-11. [CrossRef]
  6. Wei, J., et al. Emergent abilities of large language models, 2022, arXiv preprint. arXiv:2206.07682.
  7. Anderson, P. W., More Is Different: Broken symmetry and the nature of the hierarchical structure of science. Science, 1972, 177(4047), pp. 393-396. [CrossRef]
  8. Van Dis, E. A., Bollen, J., Zuidema, W., van Rooij, R., & Bockting, C. L. ChatGPT: five priorities for research. Nature, 614(7947), 224-226, 2023. [CrossRef]
  9. How Much Does ChatGPT Cost to Run? $700K/day. 2023: https://www.businessinsider.com/how-much-chatgpt-costs-openai-to-run-estimate-report-2023-4.
  10. Kidd, C., & Birhane, A. How AI can distort human beliefs. Science, 380(6651), 1222-1223, 2023. [CrossRef]
  11. French, R. M. Moving beyond the Turing test. Communications of the ACM, 55(12), pp. 74-77, 2012. [CrossRef]
  12. Fan, F., Lai, R., & Wang, G. Quasi-Equivalence between Width and Depth of Neural Networks. Journal of Machine Learning Research, 24(183), pp.1-22, 2023.
  13. Park, S., Yun, C., Lee, J., & Shin, J. Minimum Width for Universal Approximation. In International Conference on Learning Representations, 2020.
  14. Lu, Z., Pu, H., Wang, F., Hu, Z., & Wang, L. The expressive power of neural networks: A view from the width. Advances in Neural Information Processing Systems, 30, 2020.
  15. Levine, Y., Wies, N., Sharir, O., Bata, H., & Shashua, A. Limits to depth efficiencies of self-attention. Advances in Neural Information Processing Systems, 33, pp. 22640-22651, 2020.
  16. Goyal, A., Bochkovskiy, A., Deng, J., & Koltun, V. Non-deep networks. Advances in Neural Information Processing Systems, 35, pp. 6789-6801, 2022.
  17. Huang, G., Liu, Z., Van Der Maaten, L., & Weinberger, K. Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4700-4708, 2017.
  18. Xie, S., Kirillov, A., Girshick, R., & He, K. Exploring randomly wired neural networks for image recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 1284-1293, 2019.
  19. Geirhos, R., Jacobsen, J. H., Michaelis, C., Zemel, R., Brendel, W., Bethge, M., & Wichmann, F. A. Shortcut learning in deep neural networks. Nature Machine Intelligence, 2(11), pp. 665-673, 2020. [CrossRef]
  20. Fan, F. L., et al. On a sparse shortcut topology of artificial neural networks. IEEE Transactions on Artificial Intelligence, 3(4), pp. 595-608, 2021. [CrossRef]
  21. Shahir, R. S., Humayun, Z., Tamim, M. A., Saha, S., & Alam, M. G. R. Connected Hidden Neurons (CHNNet): An Artificial Neural Network for Rapid Convergence. arXiv preprint 2023. arXiv:2305.10468.
  22. Fan, F. L., Li, Z. Y., Xiong, H., & Zeng, T. Rethink Depth Separation with Intra-layer Links. arXiv preprint 2023. arXiv:2305.07037.
  23. Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, 79(8), pp. 2554-2558, 1982. [CrossRef]
  24. Krotov, D., & Hopfield, J. J. Dense associative memory for pattern recognition. Advances in Neural Information Processing Systems, 29, 2016.
  25. Folli, V., Leonetti, M., & Ruocco, G. On the maximum storage capacity of the Hopfield model. Frontiers in computational neuroscience, 10, 144, 2017. [CrossRef]
  26. Demircigil, M., Heusel, J., Löwe, M., Upgang, S., & Vermet, F. On a model of associative memory with huge storage capacity. Journal of Statistical Physics, 168, pp. 288-299, 2017. [CrossRef]
  27. Ramsauer, H., et al. Hopfield networks is all you need. International Conference on Learning Representations, 2020.
  28. de Arcangelis, L., & Herrmann, H. J. Learning as a phenomenon occurring in a critical state. Proceedings of the National Academy of Sciences, 107(9), 3977-3981, 2010. [CrossRef]
  29. Levina, A., Herrmann, J. M. & Geisel, T. Dynamical synapses causing self-organized criticality in neural networks. Nature Phys. 3, 857–860, 2007. [CrossRef]
  30. Kager, W., Lis, M., & Meester, R. The signed loop approach to the Ising model: foundations and critical point. Journal of Statistical Physics, 152(2), 353-387, 2013. [CrossRef]
  31. Fang, C., Lee, J., Yang, P., & Zhang, T. Modeling from features: a mean-field framework for over-parameterized deep neural networks. In Conference on learning theory, pp. 1887-1936, 2021.
  32. Zhang, S. Q., Wang, F., & Fan, F. L. Neural network gaussian processes by increasing depth. IEEE Transactions on Neural Networks and Learning Systems, 2022. [CrossRef]
  33. Ho, J., Jain, A., & Abbeel, P. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33, 6840-6851, 2020.
  34. Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. Score-Based Generative Modeling through Stochastic Differential Equations. In International Conference on Learning Representations, 2020.
  35. Kazerouni, A., et al., “Diffusion Models in Medical Imaging: A comprehensive Survey,” Medical Image Analysis, vol. 88, p. 102846, 2023. [CrossRef]
  36. Song, Y., Dhariwal, P., Chen, M., & Sutskever, I. Consistency models, In International Conference on Learning Representations, 2023.
  37. Coplien, J. O. Advanced C++ programming styles and idioms. Addison-Wesley Longman Publishing Co., Inc., 1991.
  38. Stanley, K. O., D'Ambrosio, D. B., & Gauci, J. A hypercube-based encoding for evolving large-scale neural networks. Artificial life, 15(2), pp. 185-212, 2009. [CrossRef]
  39. Ha, D., Dai, A, & Le, Q. V. Hyper networks. International Conference on Learning Representations, 2017.
  40. Chauhan, V. K., Zhou, J., Lu, P., Molaei, S., & Clifton, D. A. A Brief Review of Hypernetworks in Deep Learning. arXiv preprint 2023. arXiv:2306.06955.
  41. Leinster, T. Basic category theory. Cambridge University Press, 2014.
  42. https://en.wikipedia.org/wiki/Yoneda_lemma.
  43. Zou, A., et al. Representation Engineering: A Top-Down Approach to AI Transparency. arXiv preprint 2023. arXiv:2310.01405.
  44. Barack, D. L., & Krakauer, J. W. Two views on the cognitive brain. Nature Reviews Neuroscience, 22(6), 359-371, 2021. [CrossRef]
  45. Toner, J., & Tu, Y. Flocks, herds, and schools: A quantitative theory of flocking. Physical review E, 58(4), 4828, 1998. [CrossRef]
  46. Olfati-Saber, R., Fax, J. A., & Murray, R. M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 95(1), 215-233, 2007. [CrossRef]
  47. Mendel, J. M. Fuzzy logic systems for engineering: a tutorial. Proceedings of the IEEE, 83(3), pp. 345-377, 1995. [CrossRef]
  48. Chrisley, R. Embodied artificial intelligence. Artificial intelligence, 149(1), 131-150, 2003. [CrossRef]
  49. Cerezo, M., Verdon, G., Huang, H. Y., Cincio, L., & Coles, P. J. Challenges and opportunities in quantum machine learning. Nature Computational Science, 2(9), 567-576, 2022. [CrossRef]
Preprints 89547 g001
Figure 1. Future of artificial neural networks. (a) A 3D neural network with width, depth, and height dimensions, (b) dynamics through feedforward and feedback mechanisms, and (c) a multi-AI-agent system with emergent behaviors at both individual and population levels.
Figure 1. Future of artificial neural networks. (a) A 3D neural network with width, depth, and height dimensions, (b) dynamics through feedforward and feedback mechanisms, and (c) a multi-AI-agent system with emergent behaviors at both individual and population levels.
Preprints 89547 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated