Theory of Relationships Between Spaces to Obtain Numerical Knowledge

1. Introduction

The theory helps to obtain information about whether the result is even or odd, as well as to obtain information about whether the origins are even or odd. Therefore, based on the meaning of mathematics that accurately describes the real world and through representations of an element or fact that are linked to space, thus, using the relationships between spaces it is possible to understand even and odd numbers. In this sense, the study presents itself as a new possibility to reduce all the complexity of laborious information about parity of numbers, making the information simpler and easier to obtain knowledge of parity, that is, the study deals with a new applicable computational thinking. In addition, this study presents a possible model for understanding formations.

Note: The study uses a rescue diagram developed by John Venn.

2. Math Sense

The knowledge of mathematics today is not the same as it was at the beginning of the history of mathematics, because in the trajectory of thousands of years ago there was an evolution in the knowledge of mathematics, just as in the future of mathematics thousands of years ago will continue to evolve its knowledge , with the aim of describing the world with rigor and precision.

The first signs of knowledge of mathematics occurred due to the need to represent elements, giving rise to mathematics that emerged in Ancient Egypt and the Babylonian Empire, around 3500 BC. However, in prehistoric times, human beings already used the concepts to count and measure. An example of the first elements to represent were stones and sheep, where each stone represented a sheep. An example if there were 15 stones and because there were also 15 sheep, in this case two stones are missing during the count and because there are also two sheep missing. This need to represent the elements in the case of sheep arose with the aim of avoiding losses of sheep, that is, avoiding losses.

The emergence of the representation of elements aims to describe the world with rigor and precision. Many people benefit from mathematics because mathematics makes life easier for everyone, as is the case with the sheep counter who, because of mathematics, did not suffer any harm.

Therefore, based on the meaning of mathematics, it is possible to state that mathematics is related to physical spaces.

3. The Use of Mathematics in Everything

Furthermore, mathematics is used in many things, such as probability, which analyzes the possibility of an event occurring. Percentage is used to compare quantities, profits, discounts and losses. Geometry is present in traffic signs, houses and buildings. The quadratic or 2-degree function is used to calculate projectile launches and motions. Set theory helps determine the number of respondents and their groups. The exponential function explains radioactive decay and ecological and sociological growth.

4. Detailed Examples of Mathematical Usage

Example 01: A group of friends made up of 8 people goes to eat at a pizzeria, where they buy 2 pizzas of 8 slices each, that is, 16 slices in total. When the two pizzas arrive, one of the friends tries to get everyone to eat the same number of slices, so the division calculation was made: if the total is 16 slices and there are 8 people to eat, each person can eat 2 slices equally each one.

In this case, the division is calculated so that none of the 8 friends eats more or less than any member of the group, the division arises to maintain equality.

Example 02: In research there is an intense presence of mathematics in their work. A survey, for example, aims to understand the profile of crime in Brazil, that is, characteristics of crime. The numbers indicate the reality of crime in Brazil: poorer regions have more violence, richer regions have less violence.

In this case, it is up to public policies to act in the poorest regions, through the implementation of opportunities for people to escape poverty. All this because numbers present information and from that it is possible to deduce solutions.

Example 03: Mathematics is strongly linked to health, as numbers indicate information that may be contained in food products or medical tests. The information, through numbers, can tell you the ideal amount of consumption or not of this food. Additionally, medical exams can diagnose illnesses. If so, numbers can help humanity stay healthy.

Example 04: Numbers can help with people's safety, showing limits for people in elevators, boats, planes and cars. The limits are known through a study with numbers. Furthermore, the numbers indicate the speed limit of a means of transport.

Example 05: The existence of commerce depends on mathematics, as the product that commerce sells has a value, but the value can be changed as you seek the ideal profit from the product.

In this case, knowledge of the number is essential to know the value of a product, to obtain the desired profit.

In general, mathematics is present in everything, that is, in any physical space, because it arose from the need to describe the world with rigor and precision.

5. Even and Odd Numbers

An even number is a whole number that is divisible by 2 without a remainder (ex: 2, 4 and 6), and an odd number is a number that is not divisible by 2 without a remainder (ex: 1, 3 and 5).

6. Examples of Forming Even Numbers

Source: prepared by the author. Table 1 Legend: imagination of space

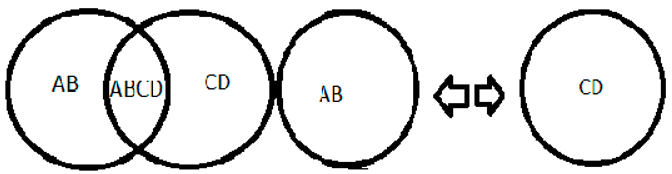
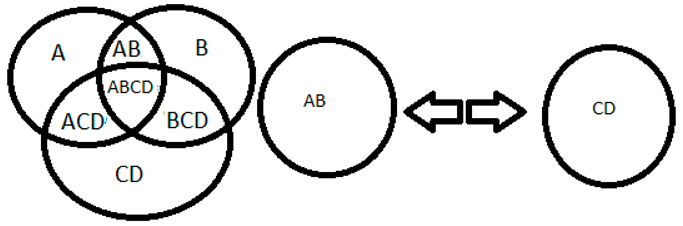
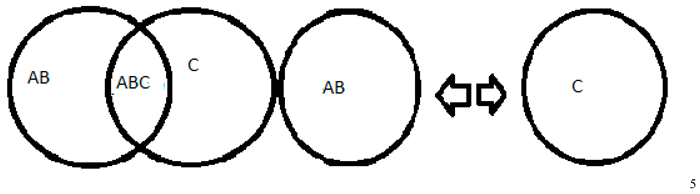
2+8=10, the number 2 is represented by AB, as both 2 and AB are divisible by two, characterizing a pair, the same is represented by CD and 10 is represented by ABCD, making it possible to divide ABCD into two parts, making up AB and CD.

Source: prepared by the author. Table 2 Caption: imagination of space

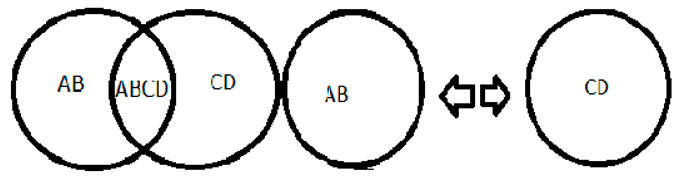
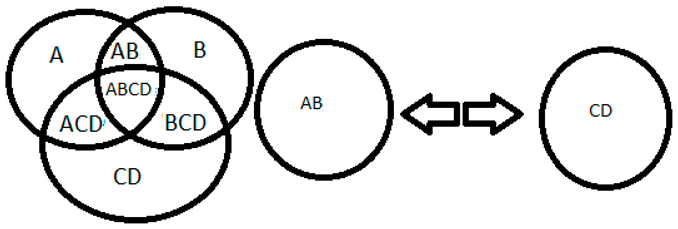
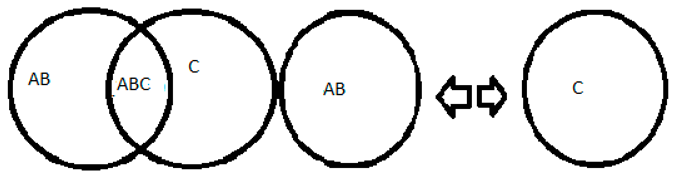
10+4=14, the number 10 is represented by AB, as both 10 and AB are divisible by two, characterizing a pair, the same is 4 represented by CD and 14 is represented by ABCD, making it possible to divide ABCD into two parts, becoming AB and CD.

Source: prepared by the author. Table 3 Caption: imagination of space

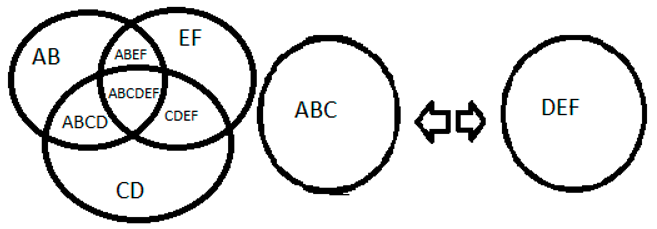
2+10+8=20, the number 2 is an even number represented by AB, the number 10 is an even number represented by CD, the number 8 is an even number represented by EF, forming an even number 20 represented by ABCDEF and can be divided into two parts ABC and DEF. To obtain the origins you need to know the result and know how many terms there were, so I divided it by the number of terms ABCDEF= AB+CD+EF

Source: prepared by the author. Table 4 Caption: imagination of space

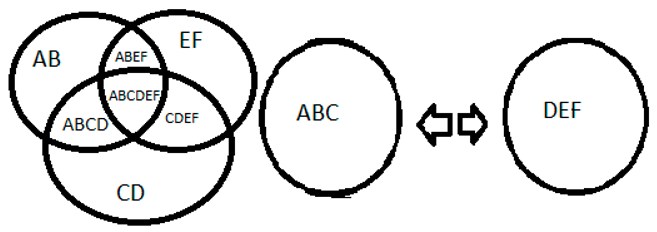
4+12+8=24, the number 4 is an even number represented by AB, the number 12 is an even number represented by CD, the number 8 is an even number represented by EF, forming an even number 24 represented by ABCDEF and can be divided into two parts ABC and DEF. To obtain the origins you need to know the result and know how many terms there were, so I divided it by the number of terms ABCDEF= AB+CD+EF

Source: prepared by the author. Table 5 Caption: imagination of space

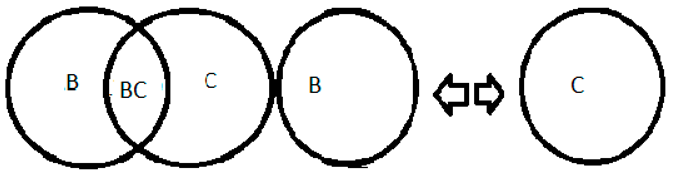
9+1=10, 9 is odd represented by B as both 9 and B are not divisible into parts, the same is the number 1 which is odd represented by C, forming the number 10 which is even represented by BC and can be divided into B and C.

Source: prepared by the author. Table 6 Caption: imagination of space

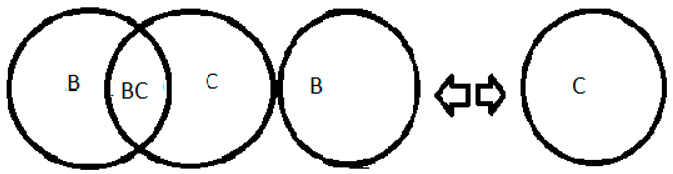
13+5=18, 13 is odd represented by B, both 13 and B are not divisible into parts, the same is the number 5 which is odd represented by C, forming the number 18 which is even represented by BC and can be divided in B and C.

Source: prepared by the author. Table 7 Caption: imagination of space

9+5+4=18, the number 9 is odd represented by A, the number 5 is odd represented by B, the number 4 is even represented by CD, forming number 18 represented by ABCD and can be divided into AB and CD. To obtain the origins you need to know the result and know how many terms there were, so divide by the number of terms ABCD= A+B+CD.

Source: prepared by the author. Table 8 Caption: imagination of space

3+7+10=20, the number 3 is odd represented by A, the number 7 is odd represented by B, the number 10 is even represented by CD, forming the number 20 represented by ABCD and can be divided into AB and CD . there was, then divide by the number of terms ABCD= A+B+CD.

7. Examples of Forming Odd Numbers

Source: prepared by the author. Table 9 Caption: imagination of space

10+3=13, the number 10 is even represented by AB, number 3 is odd represented by C, forming 13 odd represented by ABC not divisible into equal parts.

Source: prepared by the author. Table 10 Caption: imagination of space

18+5=23, the number 18 is even represented by AB, number 5 is odd represented by C, forming 23 odd represented by ABC not divisible into equal parts.

Source: prepared by the author. Table 11 Caption: imagination of space

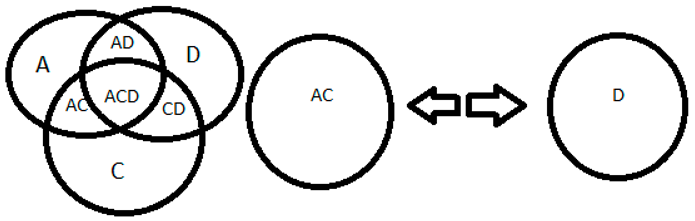
3+7+5=15, the number 3 is odd represented by A, 7 is odd represented by C, 5 is odd represented by D, forming an odd number 25 not divisible into two parts. It is possible to obtain the origins just by knowing what the result is and then dividing by the number of terms ACD= A+C+D.

Source: prepared by the author. Table 12 Caption: imagination of space

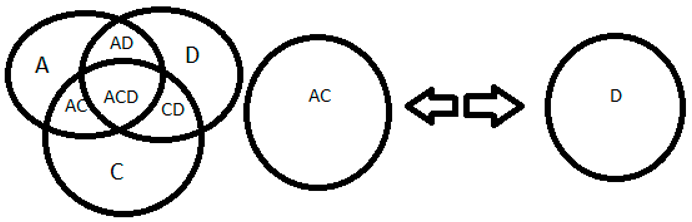
9+13+15=37, the number 9 is odd represented by A, 13 is odd represented by C, 15 is odd represented by D, forming the number 37 which is odd represented by ACD. It is possible to obtain the origins just by knowing what the result is and then dividing by the number of terms ACD= A+C+D.

Source: prepared by the author. Table 13 Caption: imagination of space

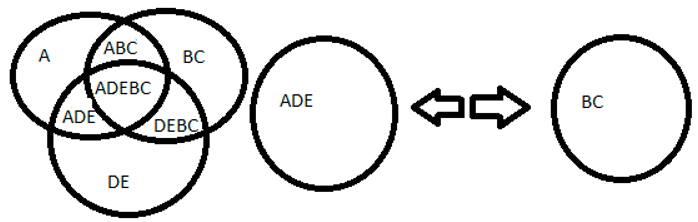
3+10+4=17, the number 3 is odd represented by A, 10 is even represented by BC, 4 is even represented by DE, forming 17 which is odd represented by ADEBC. It is possible to obtain the origins just by knowing the result and dividing by the number of terms ADEBC= A+DE+BC.

Source: prepared by the author. Table 14 Caption: imagination of space

3+8+2=13, the number 3 is odd represented by A, 8 is even represented by BC, 2 is even represented by DE, forming 13 which is odd represented by ADEBC. It is possible to obtain the origins just by knowing the result and dividing by the number of terms ABCDE= A+BC+DE.

8. Logic in Larger Numbers

Example 01: 3+3+3+3+8+4=24

assuming that the values of the origins are unknown and knowing only that the result is 24 even, it is possible to know the origins just by keeping the even number and then finding a correct amount of division for each existing term. Note that the origins have four odd numbers and two even numbers.

ABCDEFGH must be kept in pairs, that is, in two equal parts: ABCD and EFGH (correct).

ABCDEFGH= A+B+C+D+EF+GH, that is, in addition to keeping the even result, it was possible to divide six (6) terms of the origins. Note that the number formed by 24 could have other origins, such as four even numbers and two odd numbers, such as ABCDEFGHIJ, and can be divided into equal parts ABCDE and FGHIJ, that is, it is even and can have another origin, AB+CD+EF+GH+I+ J.

Example 02: 4+6+9+3+1 = 23

assuming that the values ​​of the origins are unknown and knowing only that the result is odd 23, it is possible to know the origins simply by keeping the odd number and then finding the right amount of division for each existing term. Note that the origins have three odd numbers and two even numbers.

ABCDEFG it is necessary to keep the odd parts, that is, unequal parts: ABCD and EfG

ABCDEFG= AB+CD+E+F+G, that is, in addition to keeping the odd result, it was possible to divide the origins into 5 (five) terms. Note that the odd number formed by 23 can have other origins such as four even and one odd ABCDEFGHI and can be divided into unequal parts ABCD and EFGHI, that is, it is odd and can originate AB+CD+EF+GH+I.

9. Conclusion

Therefore, the theory that states that interrelated spaces provide numerical knowledge is observable and coherent based on the meaning of mathematics that interacts with spaces. In addition, a characterization of a new computational thinking is observable, given that there is a reduction in the complexity of information, making information simpler and easier to obtain parity knowledge. The study aims to present a model for understanding numerical formations.