1. Introduction
General theory (GR) and quantum mechanics (QM) are fundamentally distinct theories that independently shape our perception of reality and predict how Nature works. Despite the many attempts to reconcile the principles of GR and QM over the last century [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10], a reliable grand unified theory is still challenging brilliant minds. The yet-unveiled nature of gravitation and the classical representation of spacetime coordinates, metric tensor, etc. are reasons why GR is still fundamentally different from QM. In this report we introduce a novel approach to extend the sensical predictions of GR to cover the quantum domain as well. To this end, we first impose the possible consequences of finite gravitational fields and/or relativistic energies on the fundamental theory of QM, the Heisenberg uncertainty principle (HUP), for instance. The most recent progress in this direction is the relativistic generalization of HUP (RGUP), which suggests modifications to the momentum operator. On the other hand, we put forward another generalization, this time, to the Riemann geometry. For this purpose we consider the Finsler geometry. The combination of both attempts results in discretized quantum geometry, additional curvature, and importantly generalized fundamental tensor. The resulting generalized fundamental tensor, which becomes quantum [
11,
12] and dynamical [
13], represents the profound ingredient imposed on the generalized GR. For this basic change GR gains novel quantum-mechanical aspects. On top of such aspects are the additional geometric structures and curvatures. As the name says, these are apparently new sources of gravitation, whose nature is likely orthogonal to that of the conventional curvature. With conventional curvature we mean the spacetime curvature whose entire information is encoded in the conventional metric tensor,
. The generalized fundamental tensor,
, which is linearly related to
, on the other hand, encodes information about both conventional and emerged curvatures. This report aims at presenting some of the properties of the additional curvatures, analytically. Numerically, we consider both types of curvatures on the surface of a three-sphere. Second, we compare the curvatures obtained for
with that for
. Finally, we analyze the emerged curvatures, especially whether they are intrinsic essential, e.g., not artifact prompted in some coordinate systems.
As discussed, it seems that the Born reciprocity principle (BRP) suits well the direct implication of the relativistic four-dimensional GUP, known as RGUP. On the other hand, the generalization of Riemannian to Finslerian geometry allows to generalize the Finsler structure
F, whose homogeneity property plays an essential role in this study. With a postive mass of a test particle,
F could be reexpressed in coordinates and momenta instead of coordinates and velocities. This allows for a direct implication for RGUP on
F and thereby the derivation of the generalized metric tensor, on which quantum-mechanical ingredients are imposed [
14,
15,
16,
17].
The proposed construction introduces an extension to the classical GR. With this modification the classical GR is preserved but its sensical predictions are enlarged to cover the quantum scale. With ”quantized GR”, we apparently refer to the emerged extension.
The present report introduces analytical and numerical analyses for the additional geometric structures and curvatures that emerged from the proposed quantum geometric approach. For a simple visualization, the numerical analyses are designed for the surface of three-sphere. While the analytical analyses introduce dynamics with possible nonlinear connection, i.e., mean-field approximation is utilized in the numerical analyses.
Despite the approximations that should be introduced to the numerical analyses, the key conclusions are convincingly affirmed, namely that the proposed quantization i) preserves the classical theory of GR, especially at large scales, ii) extends the sensical predictions of GR to cover low (quantum) scales as well, and iii) reveals additional geometric structures and curvatures, at low (quantum) scales, whose nature shall be studied elsewhere. The present report introduces some properties of the additional geometric structures and curvatures.
We find that the additional curvature, whose Kretschann invariant scalar [
18,
19] assures its intrinsicality, essentiality, and reality, is associated with a maximal proper force which apparently emerges quantum-mechanical properties, such as discretizations, noncommutations, and jumps, especially in the relativistic quantum regimes [
11,
12]. The predicted maximal proper force is introduced as a new physical constant, a new fundamental invariant quantity observed in nature and appears in the fundamental equations of the additional curvatures [
16,
17]. The maximal proper force is related the maximal proper acceleration which was predicted by Caianellio, about four decades ago [
20,
21].
This report is structured as follows.
Section 2 introduces the formalism. The formulation of spacetime with distance-momentum duality-symmetry is given in
Section 2.1. A short review of the relativistic generalized uncertainty principle (RGUP) is outlined in
Section 2.2. The characteristics of the Finsler-Hamilton spacetime with velocity-momentum duality-homogeneity are discussed in
Section 2.3. In this regard, the quantized fundamental tensor on Riemann manifold is derived in
Section 2.4. The roles that the parameter
, which introduces RGUP and discretized Finsler structure, plays on determining the properties of the additional geometric structures curvatures and its relation to the Randers metric are summarized in
Section 2.5. The results shall be presented in
Section 3. The results obtained from the quantized Riemann curvature tensor and Einstein spacetime curvature on three-Sphere are elaborated in
Section 3.1 and
Section 3.2, respectively. Last but not least, the assessment of the resulting additional curvatures, especially, whether they are depending on the coordinate system and their smoothness or roughness is reported in
Section 3.3 (Kretschmann invariant scalar) and
Section 3.4 (parallel transport), respectively.
Section 4 is devoted to the final conclusions.
2. Formalism
We begin with the distance-momentum duality-symmetry and Born reciprocity principle. Then we give a short review on the relativistic generalized uncertainty principle (RGUP), which plays a central role in deriving our quantum geometric approach for the generalization of the spacetime curvature.
2.1. Spacetime with Distance-Momentum Duality-Symmetry
For a free particle in curved spacetime, Born introduced invariant wavefunctions [
22] and duality-symmetry configurations of distances and momenta [
4,
23,
24],
and
, where
and
are constants. Accordingly, the angular momentum
and the canonical equations
and
are invariant under the proposed transformation, where
H represents the Hamiltonian specifying the total energy, for example, the sum of the kinetic and potential energy [
24]. Born concluded that the invariance is valid in classical and quantum mechanics, and therefore, the following noncommutative relation was suggested,
In this regard, it is noteworthy emphasizing that the duality-symmetry configuration, known as the Born reciprocity principle (BRP), suggests that the laws of Nature - either classical or quantum - are symmetric. By exchanging distance and momentum or spacetime and momentum-energy, the laws of Nature are invariant [
23,
24,
25]. The combination of distance the momentum operators, known as the quantum metric operator, is also invariant
[
26]. Another essential feature to be highlighted here is that BRP is not only introducing invariant transformations but also dynamics to GR. Furthermore, BRP reveals the phase-space structure of the GR’s metric structure [
24,
25].
The derivation of a relativistic version of the generalized HUP, know as RGUP, would be venerated as one pillar upon which the potential success of the present approach is built. RGUP represents the key progress that crowned the pioneering last-century attempts towards reconciling principles of GR and QM.
Section 2.2 is devoted to a short review of RGUP.
2.2. Relativistic Generalized Uncertainty Principle
At relativistic energies and finite gravitational fields, the noncommutative relations of the distance and momentum operators, the Heisenberg uncertainty principle (HUP), must be replaced by generalized uncertainty principle (GUP) [
27,
28]. Various theories including doubly-special relativity [
10], black hole physics [
29], string theory [
30], and quantum-gravity induced quantum mechanics [
31] support the GUP approach and also predict the existence of a minimal measurable length uncertainty [
32]. In 1966, Karolyhazy concluded that the minimal measurable length uncertainty could be understood as quantum fluctuations emerged at the relativistic scales [
33,
34]. The minimum length uncertainty, the low-energy effect of quantum gravity, could be integrated in quantum mechanics via the generalization of HUP [
35]. Whether the RGUP-inspired revisited QM is indeed gravitized should be conservatively expressed.
On the other hand, ”gravitizing the quantum” would be possible by turning the Hilbert-space scalar product into dynamical similar to the GR’s dynamical metric [
13] or applying Penrose’s spontaneous collapse model [
36]. The present script introduces and alternative approach and even reports on the consequences of making the metric quantum and dynamical, the additional geometric structures and curvatures. For gravitizing the quantum one would need to prove that the particles motion in spacetime and the spacetime itself are turned out into quantum. This should be worked out elsewhere.
A few remarks on GUP are now in order. While the position and momentum operators are not canonically conjugates [
37], the physical operators are. The physical operators can be expressed as auxiliary four-vectors,
and
. Then,
, where
is the fundamental tensor in curved spacetime. Then, the distance and momentum operators can respectively be expressed as
and
[
37,
38,
39,
40]. Therefore, the distance and momentum generalized noncommutation relations, which produce Lorentz invariant minimum measurable length and simultaneously preserve the Poincare algebra, could be expressed as
The corresponding noncommutativity of the coordinates reads
At vanishing
, the RGUP parameter, the conventional Heisenberg uncertainty principle (HUP) could be retrieved, straightforwardly,
. That the resulting RGUP, Eq. (
2), seems to depend on the fundamental tensor,
, is a remarkable finding to be reported here. First, this allows a direct implication of the RGUP approach on the curved spacetime. Second, it awards the spacetime coordinates with the physical interpretations. Then, the distance and momentum operators in discretized isotropic curved spacetime could be expressed in their auxiliary canonically conjugate four-vectors
and
[
37]
where
and
is a dummy index. We notice that the ”deformation” is not exclusively dictated by the RGUP parameter. It is rather conducted by
, which depends on the auxiliary momentum, i.e., the deformation would not just amount to a constant scaling, although
is constant.
has the units of inverse squared momentum. Then, the distance operator can simply be replaced by its auxiliary four-vector, while that of the momentum should be first RGUP-modified by
and then replaced by its auxiliary four-momentum operator.
A few remarks on the proposed RGUP is now in order. Equations (
4), on one hand, inherently produces a commutative geometry [
31]. On the other hand, the deformed commutator immediately implies that the coordinates are noncommutative, Eq. (
3). It should be emphasized that such noncommutativity appears at the level of higher-order
. Thus, the deformed Heisenberg algebra must be understood at a small
expansion. An upper bound on
was suggested by one of the authors [
41]. Equations (
4) is the key expression of our construction, which defines which deformation should be performed.
From Robertson and Schrödinger uncertainty relations [
42,
43], the distance and momentum noncommutation relations, Eq. (
2) determine the corresponding uncertainties in their measurements,
with
. At small
, the uncertainties in the distance and momentum measurements in curved spacetime, Eq. (
5), could be approximated to
All quantities in Eq. (
7) including the metric
are represented in their expectation values. We emphasize that neither the minimal length nor any of these expectation values enters the present calculations. We derive them for the sake of completeness and to present which approaches impact our construction.
From Eq. (
7), the minimum measurable length uncertainty, which sets an upper bound on the possible real solutions of this quadratic equation, could be derived. Also, the uncertainties in distance and momentum measurements could be well determined [
11,
12]. The procedure to derive the minimal length is just mentioned for the sake of completeness. Obviously, this result is the quantum-mechanical description of the physical reality that emerged from the curved spacetime at relativistic scales.
To summarize this section, we emphasize that all quantities in Eq. (
7) including the metric are represented in their expectation values. Second, with this expression, it is merely intended to get a precise estimation of the minimal length and uncertainties of length and momentum, etc. Third, this is not the main goal of the present report. The key expression of our construction is Eqs. (
4), which define the deformation that shall be performed. In other words, the expectation values of the minimal length and uncertainties are not considered in the present calculations. Fourth, the present script aim at characterizing the additional curvatures which i) are emerged from the proposed quantization and ii) extend the GR’s sensical predictions to the quantum regime. At the quantum regime, the conventional geometric structures and curvatures are no longer predictable, while the additional one dominate..
The section that follows summarizes a few remarks about the Finsler-Hamilton spacetime either with velocity-momentum duality or based on the homogeneity property of the Finsler structure. In the present study, we assure that the resulting Finsler structure is solely based on homogeneity of the Finsler structure. Its astonishing similarity with the Hamilton structure shall be discussed in
Section 2.6.
2.3. Finsler-Hamilton Spacetime with Velocity-Momentum Duality-Homogeneity
Caianiello suggested that the additional curvatures that emerged in the relativistic eight-dimensional spacetime tangent bundle
mimic the quantization of the metric tensor in the four-dimensional Riemannian spacetime
[
5,
44,
45,
46]. With Finsler manifold, we mean a smooth
n-dimensional differentiable manifold
equipped with a continuous positive Finsler norm of the structure
defined on the tangent bundle. At each point
x on the manifold
, whose coordinates are composed as
, so that
, where
are tangent vectors and
, with the tangent bundle
at the point
x and
is the tangent bundle on
M, it is conjectured that the Finsler norm (structure)
satisfies the following properties:
Positive definiteness, i.e., F is smooth on the complement of the zero section on ,
Positive homogeneity, i.e., F is positively 1-homogeneous in , the relativistic four-velocity, i.e., , and
Subadditivity, i.e., for the two vectors and tangent to at the point x, F fulfills pointwise the triangle inequality .
For a free particle with mass
m normalized to the Planck mass
, the homogeneous Finsler structure could be reexpressed as
The resulting Finsler structure preserves all properties of
including the homogeneity.
With the RGUP approach, the relativistic four-dimensional distance and momentum operators can be expressed in their auxiliary four-vectors, and , respectively. In this regard, we must assure the 1-homogeneity of the resulting Finsler structure in . This requires that must be 0-homogeneous. Indeed, is -homogeneous and both and are not dependent on x. Therefore, the resulting is 1-homogeneous in . .
With a parameterization of coordinates and momenta on Finsler space
,
, the metric tensor at the point
x can be deduced from the Hessian of
,
where the resulting
is positive. In this regard, we refer to the properties that the structure
F possesses,
Section 2.3. The coordinates on tangent bundle
are of phase-space type and could be expressed as
, where index
. At the point
x on Finsler space, the corresponding metric is related to the Finsler structure
By Euler’s theorem on homogeneous
, Eq. (
10) can be derived from Eq. (
9). With Eq. (
10), we realize that the Finsler geometry is the same as the Riemann geometry but without the restriction that the line element must be quadratic. In Finsler space, the line element is given as
. The resulting
is the fundamental tensor which is apparently distinct from the Riemann metric tensor
. In this regard, we emphasize that the
-operator in the Finsler geometry is not simply linearly replaced by the
-operator as the case in the Hamilton geometry [
47]. The rigorous mathematical procedure applied to
is solely based on the homogeneity of the Finsler structure. The Finsler geometry whose structure is characterized by the coordinates and the directions of the velocities is dual to the Hamilton geometry whose structure is characterized by the coordinates and directions of the momenta of the free particle. Both geometries are mappings connecting spaces of velocities and momenta, respectively [
48]. In this regard, we recall that by conventional Legendre transformation, the velocity in the Finsler geometry could be replaced by momentum in the Hamilton geometry.
The discretized metric tensor derived from the discretized Finsler structure, Eq. (
9), must be now related to the Riemann manifold. In this way, we preserve the postulates of the conventional GR as well as its geometric formulation. The section that follows gives details on how to derive the generalized fundamental tensor.
2.4. Riemann Spacetime with Quantized Fundamental Tensor
Per definition, the line elements on
and
are identical, so that
where the eight-dimensional metric tensor,
, can be substituted from Eq. (
9),
and the index
. For the sake of simplicity, we limit the discussion to the simplest Finsler metrics, for example Klein metric [
49],
where
and
are the standard Euclidean norm and inner product in
, respectively. The Klein metric describes a hyperbolic or concretely speaking a projective geometry where the geodesics are given by Euclidean line segments [
3].
For discretized Finsler structure
to remain 1-homogeneous in
, it is necessary that
must be 0-homogeneous. Because the auxiliary four-momentum
and
, where
G is the gravitational constant,
c is the speed of light,
ℏ is the Planck constant, and
is the Planck length [
27,
28,
41,
50], are not depending on
, then,
is
-homogeneous and
is 0-homogeneous in
. Not only this positive homogeneity, but also the other properties of
are preserved in
.
Smoothness, i.e., F is smooth on , on the complement of the zero section,
Subadditivity, i.e., for the two vectors and tangent to at the point x, F fulfills pointwise the triangle inequality so that .
Positive definitions, i.e., the resulting metric tensor can be positive definite on
,
51]
Strong convexity, the resulting metric tensor can be non-degenerate.
From Eqs. (
9) and (
11), the quantized fundamental tensor on Riemann space is then deduced as
where
is the inverse of the maximal proper force related to
the maximal proper acceleration [
8,
20,
21,
52].
plays the role of normalization absorbing the dimensions of
, on one hand. The resulting maximal proper force could be interpreted as the maximum physically measured force that drives the quantum-mechanical jumps taking place in the curved spacetime at the relativistic scales. These jumps happen along the additional curvatures which are emerged from the proposed quantization.
Section 2.7 elaborates details about i) the construction of the metric tensor in the discretized Finsler geometry, ii) foundation of the quantum geometry, and iii) formulation of the quantized fundamental tensor in Riemann geometry, Eqs. (
20), (
21), and (
22).
As introduced, the parameter plays a crucial role in the present study. The following section summarizes the various contributions that comes up with.
2.5. Parameter and Curvature Properties of Randers Metric
Let us start with a summary of the roles that the parameter
played so far. First, the generalization of the quantum mechanical HUP to the relativistic regime requires to generalize the corresponding momentum operator, which is achieved by
,
Section 2.2. Second, because of its 0-homogeneity
is well capable of generalizing the Finsler structure and thereby preserving its 1-homogeneity,
Section 2.3. Accordingly, the Finsler manifold is at least discretized if not entirely quantized.
Now we introduce how
is also capable of retaining the special curvature properties of Randers metric, where
is the RGUP parameter and
is auxiliary four-momentum with either covariant or contravariant dummy index
. From Eq. (
10), we find that the 0-homogeneous
can be reexpressed as
For the sake of simplicity, let us abbreviate
as
F. When multiplying both sides of Eq. (
15) by
F and expressing
as
, we find that
Now, we can rewrite this expression by assuming that
Equation (
17) looks very similar to the Randers metric. We remark that such a conclusion is conditioned to the two terms on right-hand side. The first term,
F, could be straightforwardly related to the Riemann metric
, where
. For Eq. (
17) to form Randers metric, the second term,
, should be a closed 1-form on manifold
M at the point
p. Concretely,
must be expressed as
with
.
Fortunately, we find that i) the first term is straightforwardly related to the Riemann metric
, and ii) the second term
is 1-homogeneous in
. The importance of this finding is coupled to the fact that Randers metric was developed as an attempt to unifying gravitation and electromagnetism [
53].
The proposal to determine how the resulting version of Randers metric could be associated with the calculated curvatures would not fit well with the scope of the present script. This might be studied elsewhere.
The results shall be discussed in the section that follows. First, we derive the Christoffel symbols (affine connections) and Riemann curvature tensor for the generalized fundamental tensor, . Then, we introduce a three-sphere and rederive the Riemann curvature tensor on its surface. This allows to determine Ricci curvature tensor and Ricci scalar by successive contractions and then construct the Einstein spacetime curvature. To assure that the resulting curvatures are not artifact prompted in some coordinate systems, we calculate the Kretschmann invariant scalar and conclude that that additional curvatures are intrinsic essential. Furthermore, to assure that the resulting curvatures are no longer smooth, we calculate the parallel transport of a vector and conclude that the additional curvatures are rather rough and discretized.
2.6. Finsler–Hamilton Duality
In obtaining Eq. (
8), we merely utilized the homogeneity property of the Finsler structure
. Also, when applying RGUP on the momentum operator of
, we assured that
is 0-homogeneous. As mentioned, the duality of
on Finsler manifold and
on Hamilton manifold dose not allow to directly map
into
p. The connection between Finsler-type tangent bundle
and Hamilton-type cotangent bundle
is nonlinear, because the geometric structures of
and
are different from
and
. From the similarity of the resulting
and the Hamilton structure
, we recall that the Legendre transformation is the recommended procedure to obtain
from Finsler structure
[
48,
54].
To assure that the resulting
is equivalent to
, we perform Legendre transformation on
. The Hamilton space is characterized by manifold
M and Hamilton structure
and defined by contangent
, where
is differentiable on
and continuous on the null section
. Now, we define a Langrange space by a function
. This new Langrange space is apparently characterized by
M and
. Then, the Legendre transform leads to [
55]
where
are solutions of
.
If we identify
with
, Eq. (
12), the solution of
fulfills Eq. (
18), where the indices are lowered or raised by using the corresponding metric tensor obtained from the Hessian of
, Eq. (
9).
The question which arises now is why we guess that and would be identical. First, is obtained from a rigorous consideration of the homogeneity properties, i.e., the present study applies homogeneity to reexpress as but not necessarily the duality. Second, either velocity or constructed momentum is there to borrow its direction to the tangent bundle, i.e., both entities come up with orientations but not their physical quantities. Last but not least, the interplay between Finsler and Hamilton goes beyond the scope of this work.
2.7. Remarks on GR and QM Generalization
As introduced, the main idea is reconciling principles of GM and GR. The recipe which we invented dictates the follow steps. First, introducing gravitational impacts to the fundamental theory of QM. Second, introducing quantum geometry, i.e., additional curvatures, to mimic the proposed quantization of Riemann spacetime. To this end, we generalized the four-dimensional Riemann manifold to the eight-dimensional Finsler manifold. To express the resulting quantized metric tensor back on Riemann manifold, We utilized the property that the ratio of the lengths of any two collinear vectors does not depend on the underlying metric tensor. The deep characteristics of our approach all are stemming from this core assumption. Apart from any other superficial argumentation pro or contra this quantization proposal, we intentionally openly highlight that our approach still assumes that the measures of both line elements are precise with deterministic outcomes. Accordingly, ultimate full quantization is conditioned to quantum line element and uncertain measure, Eq. (
11).
To express the line element measure in the quantum context, one must opt to integrating probability distribution to the metric tensor and to the 1-form
. Alternative, one would need to suggest noncommutation relations. In this regard, we recall that neither
nor
(neither its generalized version) has an obvious noncommutation translation [
56]. On the other hand, defining a noncommutative differential calculus [
57,
58] and a noncommutative metric tensor [
59], could be conducted. This is conjectured to allow for integrating both procedures in defining a noncommutative measure of the line element [
60]. Furthermore, the modified relativistic kinematics, which is geometrically described by Finsler geometry, describes conceivable vacuum state of quantum gravity, at low energies [
61]. Allowing the length element to be RGUP-discretized-Finslerian seems to amount to a quantization of spacetime. A detailed study should be performed elsewhere.
Apart from the nonconservative manifestation of the shortcut connected with the line element measure, we managed to derive a quantized metric tensor, Eq. (14). In this regard, we also nonconservatively highlight that the
-term of Eq. (14) is largely approximated. Accordingly, some quantum-mechanical ingredients would be missing. This kind to approximation is unavoidable although their physically and mathematically not-fully-justified restrictions. The eight-dimensional second-order Finsler metric reads
where
is much more structured than
and thus must be approximated.
where
F is the Klein metric, Eq. (
12) and
The generalized first-order fundamental tensor on Riemann manifold requires to introduce one common metric representing both
and
. No doubt that this task represents a huge mathematical challenge. To move forward, we found no other alternative but the mathematically physically not-fully-justified approximation that the entire
would be satisfied with just one term, only, i.e., the second term,
, vanishes. The only justification is the huge mathematical difficulties to derive the generalized first-order fundamental tensor on Riemann manifold from equation (
20). On the other hand, the massive price demanded by this approximation is nothing less than vanishing
, whose roles in the proposed construction are crucial.
The present work claims to quantize GR in quantum geometry. This is much more than just replacing Riemannian by Finslerian length element. This is coupled to additional curvature, which per definition differs from the general relativity curvature, that shall be characterized in the present report. For example, the prediction of maximal proper acceleration along the additional curvature [
20,
62]. The maximal proper force was predicted by one of the authors (AT) to drive the motion and acceleration along the additional curvature [
11,
12].
The proposed quantization does not introduce an alternative to GR. The classical GR continues being a classical one, especially at large scale. At low (quantum) scale, the quantum-mechanically inspired revision becomes dominant. In this regard, we emphasize that the present script focuses on the properties of the additional curvatures, which as the name says emerges, at low (quantum) scale. Other characteristics shall be elaborated elsewhere. In this regard, we would like to comment on the sole generalization of Riemannian spacetime to Finslerian spacetime [
63]. It is natural that the resulting theory is as before classical. The proposed recipe to generalize Riemann to Finsler geometry does not include either quantum geometry or quantum-mechanically imposed revision of GR.
With the terminology quantum spacetime curvatures, we concretely mean the additional curvatures, which only emerge, at quantum scale. The present report does not claim to quantize the classical spacetime curvatures. These are kept classical as conjectured by the classical GR, which is dominant at large scale. The GR’s predictions, at low (quantum) scale, are non-sensical, on one hand. Our approach, on the other hand, introduces a new domain, a quantum scale, in which GR’s predictions become again sensical. In this quantum scale, we claim to at least discretize if not fully quantize the quantum spacetime curvatures.
An effective description of particle kinematics is possible with the integration of quantum gravitational degrees of freedom [
64]. A modification in relativistic kinematics could be geometrically described in Finsler and Hamilton geometry, in which the vacuum states of quantum gravity could be characterized, at low energies. On the other hand, the Finslerian length element would not amount to a quantization of spacetime. The Finslerian length element in our approach which is more genetic shall be studied elsewhere.
3. Results
The main goal of this study is analyzing some properties of the additional geometric structures and curvatures especially whether they are intrinsic essential or artifact in some coordinate systems. Even if we briefly discuss singularities on 3-sphere, the present study is not designed to cover this topic. Both space and initial singularities are studied elsewhere. For a simple visualization, we present an exemplary illustration and limit this to the Riemann curvature tensor and Einstein spacetime curvature. In other words, the spacetime curvature on the surface of 3-sphere represents an illustrative example.
The 3-sphere is defined as a higher-dimensional analogue of a sphere. It describes a surface of a 4-dimensional sphere or a 3-dimensional compact connected manifold without boundary and represents an example of a 3-manifold and an n-sphere.
Let us first assume that Eq. (14), which encodes all information about the local geometry of the corresponding curved spacetime, could be summarized as
where
C differs from unity. At
, the conventional fundamental tensor on Riemann manifold
, the key quantity in Einstein’s GR, is straightforwardly retained. The quantity
combines the proposed quantum-mechanical revision of
. Despite the quantum-mechanical nature of
C, the precise expectation values of all its operators, metrics, and quantities would not influence the present calculations in the sense that we still away from an accurate estimation of the curvatures and singularities, etc. The accurate estimation of the additional curvatures, for instance, becomes sensical, if Eq. (14) turns to be exact,
Section 2.7.
For the sake of simplicity, we assume that the value of the squared bracket could be approximated to unity. With this proposal the resulting
becomes mainly affected by i) coordinate- and momentum-discretization, ii)
and all its influences, and iii) new sources of gravitation (curvature). As this bracket factorizes
, the precision of
might be reduced, on one hand. On the other hand, the proposed approximation does not overthrow the main physical meanings but drastically reduces the computational costs. When applied to Eq. (
20), the proposed approximation is then interpreted as
so that
. To summarize this proposal, Eq. (14) can be reduced to
where
and
combines
.
For the conventional metric tensor
, the affine connections (Christoffel symbols) are defined as
Due to the properties of the quantized metric tensor
, the corresponding affine connections (Christoffel symbols) read
The quantized Riemann curvature tensor is then given as
By substituting the affine connections, Eq. (
28), into Eq. (
29), we get
The successive contractions of result in Ricci curvature tensor and scalar , respectively, from which the Einstein curvature tensor could be combined. While the Riemann curvature tensor confirms whether a vector is twisted when it is parallel transported around a small loop in curved space, the Ricci curvature tensor tracks the volume change along the geodesics and therefore represents how quickly a volume changes along the geodesics. Hence, the Ricci curvature tensor obviously represents the gravity in GR. The Ricci scalar gives how the volume in curved space deviates from its equivalent flat-space size. The Einstein curvature tensor is a rank-2 tensor describing the spacetime curvature. Obviously, it is a nonlinear function of the metric tensor . But, it is linear in the second partial derivatives of the metric tensor and also linear with respect to the Riemann curvature tensor. should have a null divergence and also nullify in flat spacetime. Furthermore, in the Newtonian limit, is apparently reduced to with representing the mass density.
We notice that the affine Connections, Eq. (
28) and Riemann curvature tensor, Eq. (
30) still depend on velocities or accelerations or momenta which are introduced by the proposed quantum geometric approach. As mentioned, the present report does not target these generic quantities. Only if Eq. (14) turns to be accurate, the estimations of all these quantities could be performed elsewhere.
In order for
to be applied to 3-sphere, we recall that the 3-sphere could be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. With the Cartesian coordinate transformations
the line element on the surface of 3-sphere can be expressed as
With the assumptions
,
,
, and
, the nonvanishing affine connections can be summarized as follow.
3.1. Quantized Riemann Curvature Tensor on Three-Sphere
From the nonvanishing affine connections, Eq. (
32), the Riemann curvature tensor on 3-sphere, Eq. (
30), can be constructed as
By substituting with Eq. (
32),
where
is the nonquantized
classical Riemann curvature tensor on 3-sphere,
From Eq. (
34) and (
35), the contributions added by the proposed quantization can be determined, straightforwardly, by subtracting
from
. It is apparent that the structure of the metric, Eq. (
34), depends on velocities or accelerations or momenta. Given this dependence, it would not be trivial to obtain a connection since this depends on a nonlinear form involving velocities or accelerations or momenta with partial derivatives of the metric. To avoid this situation we assigned constant expectation values to the various quantities, i.e., a mean-field approximation. In the analytical analyses, we have to take this nonlinear dependence into consideration.
Before we present the graphical analyses, some details about the calculations are now in order. First, the calculations are limited to the surface of 3-sphere. Second, the analytical analyses on generic spacetime introduce dynamics and quantization to GR. Third, the numerical analyses apply rough estimations for the various quantities, mean-field approximation. Concretely, the present calculations assume , , , , and .
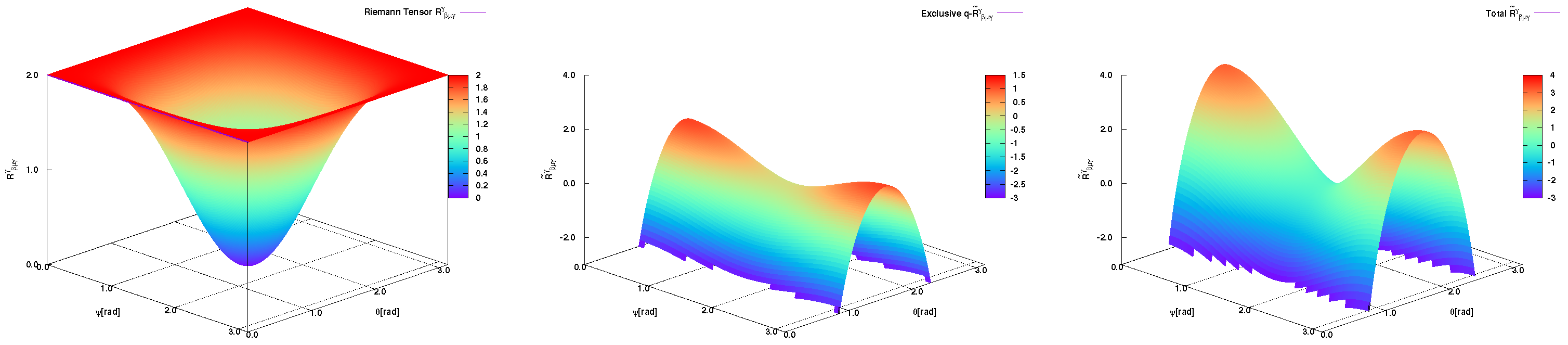
The Riemann curvatures on 3-sphere depicted in
Figure 1 illustrate i) the nonquantized
classical curvatures (left-hand panel), ii) the quantized curvatures (middle panel), and iii) the sum of both sets of curvatures (right-hand panel). There are remarkable differences to be highlighted. First, without quantization, the curvatures are relatively small and point upwards. Second, the quantizations seem to contribute with large curvatures pointing downwards. Third, the quantized curvatures in the
-direction are tiny, while they are huge in the
-direction. Fourth, the quantized contributions are dominated by the sum of both sets of curvatures. Fifth, the curvature seems neither smooth nor continuous nor finite.
As discussed earlier, no change at all in the main postulates of GR is introduced. Therefore, the Einstein curvature tensor on 3-sphere could be now constructed.
Section 3.2 is devoted to the quantized Einstein spacetime curvature on the surface of a 3-sphere.
3.2. Quantized Einstein Spacetime Curvature on Three-Sphere
The Einstein spacetime curvature is constructed as
The first line gives the nonquantized
classical spacetime curvature, whose coefficient has a quantum-mechanical nature. The second and third lines express additional geometric structures and curvatures that emerged from the proposal quantization. Similar to the Riemann curvature tensor, Eq. (
34), the Einstein spacetime curvature, Eq. (
36), refers to a key conclusion that the present approach for quantization obviously preserves the conventional GR, especially in the non-relativistic scales so that at
,
. In the relativistic scales, i.e., at finite
, the proposed quantization becomes dominant. Throughout the second and third lines are no longer vanishing so that the region, where GR gives sensical predictions, is obviously extended to the quantum scales.
Also here, we notice that the Einstein spacetime curvatures, Eq. (
38) still depend on velocities or accelerations or momenta. As Eq. (14) is still approximated, the calculations of Eq. (
38) shall be performed elsewhere.
On 3-sphere, the Einstein spacetime curvature is the sum of
,
Without quantization, the Einstein tensor is given as
In Eq. (
38), we find that the structure of the metric depends on velocities or accelerations or momenta. Thus, the resulting metric structure nonlinearly depends on its partial derivatives. With the mean-field approximation, i.e., constant expectation values, the nonlinearity dependence would be avoided.
Also on 3-sphere, the quantized spacetime curvature, Eq. (
37), conserves the original curvature suggested in the conventional GR. At large scales, the dominance of
as
is obvious, while at low scales, i.e., at nonvanishing
, the quantum contributions come into place.
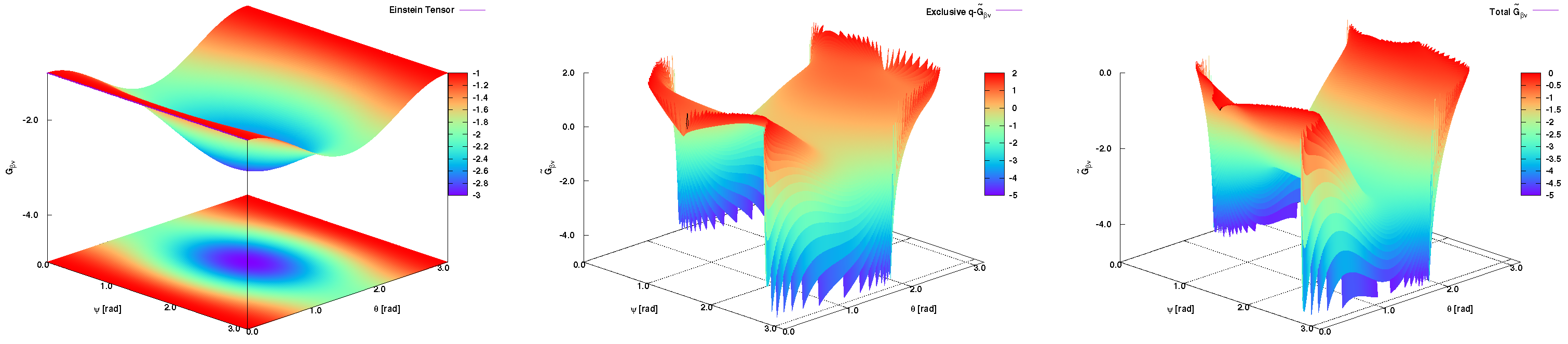
The results presented in
Figure 2 compare the spacetime curvatures with and without quantization. The left-hand panel depicts the spacetime curvatures as defined by the conventional Einstein tensor, Eq. (
38). Here, in the nonrelativistic regime, the curvatures are continuous, smooth, and finite everywhere. On the other hand, the proposed quantization remarkably changes the nature of the spacetime curvatures. The middle panel shows the pure quantum spacetime curvatures, in the relativistic regime. It is apparent that the spacetime curvature becomes neither continuous nor smooth nor finite, especially at certain values of
and
. When summing up both types of spacetime curvatures, Eq. (
37), as the present theory suggests, we find that the resulting curvatures are dominated by the quantum nature. Contrary to conventional GR, Eq. (
38), the proposed theory, Eq. (
37) is simultaneously valid at low and large scales. The sencial predictions are likely feasible, everywhere.
From the spacetime curvatures on 3-sphere presented in
Figure 2, although the approximations and rough estimations, one is now able to draw the conclusion that the quantum spacetime curvatures seem to be discretized, lumpy, and infinite. This phenomenological prediction stimulates a quantitative estimation of the spacetime curvature and singularity on 3-sphere.
The section that follows introduces a quantitative coordinate-independent estimation of the curvature and singularity. Finite Kretschmann scalar assures that the additional curvatures are intrinsic essential.
3.3. Kretschmann Invariant as Measure of Spacetime Curvature and Singularity on Three-Sphere
For an algebraic description for the spacetime curvature, we suggest to utilize the Kretschmann scalar (one of the basic polynomial curvature invariants in GR) to determine the amount of curvature of spacetime [
65,
66,
67]
where
are Riemann curvature tensors, Eq, (
34) or Eq. (
35). Eq. (
39) is a quadratic polynomial invariant composed of sums of the squares of the Riemann tensor components.
The Kretschmann invariant helps to tell the nature of curvature and thereby singularity, whether intrinsic essential or artifact removable. The latter happens with the choice of coordinates and therefore could be eliminated by a specific coordinate transformation. As the coordinate transformations are not a closed set, distinguishing real from artifact singularities should not be limited to the existing coordinate transformation alone. The Ricci and Kretschmann scalars are examples of the spacetime curvature and singularity measures that not depending on the choice of coordinates. Unlike Ricci, the Kretschmann scalar, Eq. (
39), is not vanishing everywhere. For Kretschmann scalar
K to assess whether the curvatures are intrinsic essential not artifact removable, it is enough to show that
K is finite. The accuracy of
K plays a minor role. The singularities themselves are not targeted in the present script. The space and initial singularities shall be analyzed elsewhere.
For the conventional spacetime curvature, Eq. (
35), we find that
For the quantized spacetime curvature, Eq, (
34), the resulting
K reads
It is obvious that the Kretschmann invariant tells that the quantized spacetime approaches singularity as
. This is similar to the unique space singularity of the unquantized spacetime curvature, Eq. (
40). Another conclusion to be drawn is that the spacetime curvature also becomes singular, as
. Such a result might be qualitatively affected by the approximations including the one imposed on Eq. (
26). Furthermore, there are additional two singularities emerged in relativistic regimes, Eq. (
41). Both trigonometric
and
also approach infinite, at certain
- and
-coordinates,
Figure 3.
So far, we conclude that in non-relativistic regimes, the Kretschmann invariant is exclusively related to the radial distance
r, Eq. (
40), a single singularity, while in the relativistic regimes, the Kretschmann invariant assures the existence of quadruple singularities (
r,
,
, and the quantization).
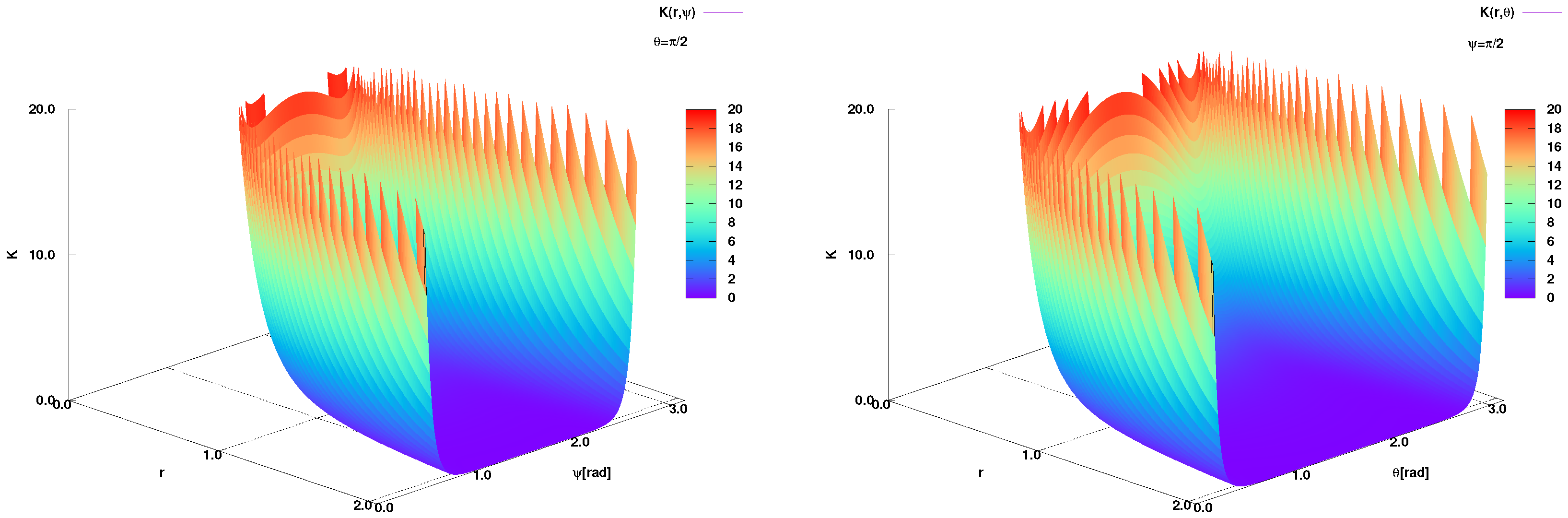
The left-hand panel of
Figure 3 draws the values of the Kretschmann invariant
K in dependence on the radial distance
r and angle
, while the other angle
is kept constant,
. The right-hand panel depicts the same as the left-hand panel but here
K is given as a function of
r and
, at
. Both panels share common features. First,
K rapidly increases with decreasing
r. Second, at small as well as large angles, there is a rapid increase in
K, even if
r remains finite. At small and large angles as well as small radial distance,
K approaches infinity. This means that the singularities of the quantized spacetime curvature on 3-sphere likely takes place in each of
r,
, and
coordinates, independently.
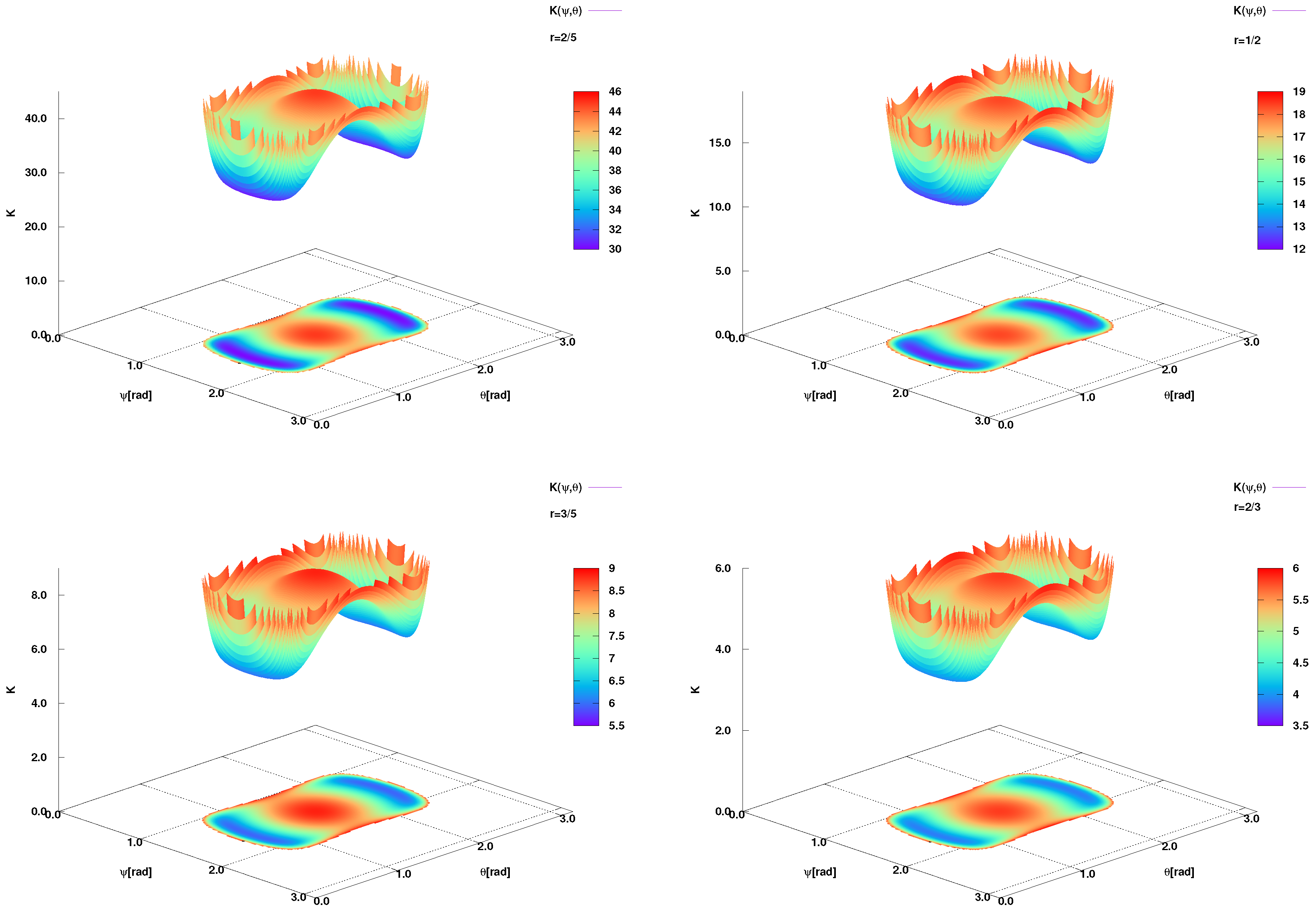
To illustrate this finding, we draw in
Figure 4 how
K varies with
and
, at constant values of the radial distance,
(top left-hand panel),
(top right-hand panel),
(bottom left-hand panel), and
(bottom right-hand panel). Here, we find that the finite curvatures are only positioned in a small region in the
domain. The remaining domain is obviously singular. In other words, the singularity is not rare over the entire
domain, even at finite
r. Moving from larger to lower
r, although the values of
K rapidly increase both curvatures and singularities are likely preserved. In Eq. (
41),
appears once in the common factor, so that it equally factorizes the other terms. We find that i) the nature of the spacetime curvature remains almost unchanged with the change in
r. ii) the values of
K are strongly dependent on
r. Both findings are also apparent in Eq. (
41), so that at constant
,
, and quantization
, we find that
. The proportionality factor varies from unquantized, Eq. (
40) to quantized spacetime curvature, Eq. (
41). At vanishing
, Eq. (
41) reduces to Eq. (
40).
The color palette on the right of all figures encodes the resulting values. We notice, at least phenomenologically, that the spacetime curvature seems not being smooth everywhere. Specially where the curvature is large, the roughness of the quantized spacetime is rather apparent.
The section that follows introduces a systematic analysis of the tangency of a parallel-transported vector, from which we would be able to tell whether the curved spacetime is smooth, continuous, and finite.
3.4. Parallel Transport as Measure of Smoothness or Roughness on Quantized Spacetime
As done with the quantitative measure of the quantized spacetime curvature and singularity, we would like now to quantitatively determine the degree of spacetime smoothness and roughness. In flat space, which is apparently smooth, the vector components and basis vectors are differentiable. Thus, the covariant derivatives are just the ordinary derivatives. In curved space, on the other hand, the differentiation of the basis vectors could be expressed by the affine connections. Among the common features of flat and curved spaces are the covariant derivatives, which are defined as the rates of change of the tangent vector fields with the normal component subtracted. This is the parallel transport of a vector [
68]. Vanishing covariant derivatives of a vector
defines that
is parallel-transported, i.e., move while keeping its tangency as constant as possible
This is the definition of the geodesic equation; the world-line that preserves tangency under parallel transport.
Therefore, we proposed to utilize the parallel transport, Eq. (
42), for a quantitative estimation of the spacetime smootheness or roughness.
This is the affine connection between
parameterized in
and its parallel-transported counterpart, at
;
. With the partial derivative replaced by the limit
, we have
Then, the change in both vectors
and
is given as
Thus, we conclude that finite
is accompanied with non-vanishing
. Also, we find that although
could be differentiable everywhere, its parallel transport is not always guaranteed. Only vanishing quantization assures smoothness, i.e., parallel transport, Eq. (
45). Otherwise, the quantized spacetime is derived into roughness. Therefore, the tangency under parallel transport seems not assuring "staying on curve" or "inertial moving". With finite quantization, we mean i) the RGUP discretization ii) the quantum geometry, and iii) the additional curvatures. Even if the RGUP discretization is disregarded, i.e.
, the quantization term
is still determined by finite
.
The next section draws the main conclusions and suggests a future outlook.
4. Conclusions and outlook
Quantizing general relativity is a challenging problem in theoretical physics. One approach to tackle this problem is loop quantum gravity, which attempts to quantize spacetime itself. Another approach is string theory, which attempts to unify general relativity with quantum mechanics by describing particles as one-dimensional strings. The alternative approach introduced in the present report builds on the differential and quantum geometry, reciprocity principle, recent progress on the relativistic noncommutation relations, and quantization through additional curvatures.
While Born reciprocity principle assures symmetric classical and quantum law of Nature if the distance is replaced by momentum operators, the proposed velocity-momentum duality-symmetry in Finster geometry allows a direct implication of RGUP, the fundamental theory of modified quantum mechanics. From definiteness, subadditivity, and homogeneity of the discretized Finsler structure, the quantized fundamental tensor in the four-dimensional Riemann geometry could be deduced, Eq. (14).
We conclude that the four-vectors are essential for the quantization of the fundamental tensor and hence the unification of general relativity and quantum mechanics. In Eq. (14), at vanishing RGUP, such as , we get a non-vanishing conformal transformation, , where is a normalization factor. represents the maximal proper force that emerged from the additional curvature. Thus, we conclude that the proposed quantization is not fully due to RGUP. We also emphasize that the relativistic regime, in which RGUP and hence the spacetime quantization are possible, additional sources of spacetime curvature apparently emerge. The curvature associated with the mass , whose motion is caused by the force is an example, which paves the path to define the maximum gravitational force as a new universal physical constant.
We conclude that the parameter seems to represent a fundamental ingredient in unifying GR and QM. It plays dual roles in a) imposing gravitational consequences on QM and b) simultaneously introducing quantum-mechanical aspects to GR. On the other hand, is likely capable of retaining the special curvature properties of the Randers metrics. The resulting Randers metric, if the proposed axioms are proved, likely suggests a unification of gravitation and electromagnetism. The homogeneity properties of seem to support all these findings.
The proposed quantization seems to create additional geometric structures and curvatures whose intrinsicality, essentiality, and reality are doubtlessly confirmed. They are not not artifact or removable in any coordinate transformation. Obviously, they are sources of gravitation, whose nature, not necessary as classical as that of Einstein’s GR, should be discovered elsewhere. These sources of gravitation i) arise at relativistic quantum scales, and ii) are overcast at nonrelativistic classical scales, i.e., they are literately entirely overlooked in Einstein’s GR. From the Kretschmann invariant on 3-sphere, we draw the conclusion that the unquantized curvature is indeed real but monotonic. Also, the resulting singularity is likely spacial, at vanishing radial distance. On the other hand, for the quantized spacetime, the curvature is also real but nonmonotonic. There is a spacial singularity, at vanishing radial distance. Furthermore, both angles and and the proposal quantization independently create additional singularities. At large scale, i.e., the GR’s conventional scale, a unique singularity emerges on 3-sphere. This is the one at vanishing spacial distance. At low scales, i.e., in the quantum limit, additional singularities emerge, as well. To illustrate this finding, a magnifying lens could be proposed. At large scale, the lens’ resolution of the spacetime texture is merely capable of depicting the r-singularity. By reducing the scales, i.e., by increasing the lens’ magnifications, additional spacetime structures become resolvable including the other three types of singularities.
Last but not least, we have introduced an analytic qualitative measure for the spacetime smoothness. This is the tangency of a parallel-transposed vector over the resulting curved spacetime. Its constancy likely defines the geodesic. We found that the quantization seems to emerge slight chunky structures. A quantitative analysis should be presented elsewhere.
As for potential outlooks, we emphasize two aspects. The first one is a crucial one, a precise estimation of the quantized fundamental tensor, which so-far is conditioned to immense mathematical challenges. In the present calculations, we are utilizing an approximated version of the Finsler metric, whose limitations are known to the authors. The second aspect is a detailed analysis of the numerical calculations. To achieve a deeper interpretation of the quantum contributions, a good control of , either analytical or numerical, should be introduced. The effect of on the level of the singularity, for instance, should be suggested for a reliable interpretation.
The proposal to use mean-field approximation would prevent an adequate construction of the non-linear connection in the tensors and scalars. It might hide some ”quantum” effects. Therefore, other methods such as minimum perturbation theory, shall be utilized elsewhere.
Author Contributions
AT proposed the conception of the present study, designed and managed the research, interpreted the results, derived the expressions, drawn the figures, and prepared the manuscript. TFD prepared the calculations of the Kretschmann scalar and the curvatures on the three-sphere. All authors contributed to the analysis, reviewed the results, and approved the final version of the manuscript.
Funding
The authors declare that this research received no specific grants from any funding agency in the public, commercial, or not-for-profit sectors.
Data Availability Statement
All data generated or analyzed during this study are included in this published article. The data used to support the findings of this study are included within the published article and properly cited! The row data and the thermal model calculations that support the findings of this study are also available from the corresponding author upon reasonable request. All of the material is owned by the authors.
Acknowledgments
AT acknowledges the generous support by the Egyptian Center for Theoretical Physics (ECTP) at the Future University in Egypt (FUE)!
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this published article! As defined by Nature Research, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
References
- H. Weyl. Gravitation and electricity. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys. ), 1918:465, 1918.
- Th. Kaluza. Zum Unitätsproblem der Physik. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys. ), 1921:966–972, 1921. doi. [CrossRef]
- Oskar Klein. Quantum Theory and Five-Dimensional Theory of Relativity. (In German and English). Z. Phys., 37:895–906, 1926. doi. [CrossRef]
- Max Born. A suggestion for unifying quantum theory and relativity. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 165(921):291–303, 1938.
- Eduardo R. Caianiello. Some Remarks on Quantum Mechanics and Relativity. Lett. Nuovo Cim., 27:89, 1980. doi. [CrossRef]
- E. R. Caianiello, G. Marmo, and G. Scarpetta. (Pre)quantum Geometry. Nuovo Cim. A, 86:337–355, 1985. doi. [CrossRef]
- G. Scarpetta. Relativistic Kinematics with Caianiello’s Maximal Proper Acceleration. Lett. Nuovo Cim., 41:51–58, 1984. doi. [CrossRef]
- Howard E. Brandt. Maximal Proper Acceleration and the Structure of Space-time. Found. Phys. Lett., 2:39, 1989. doi. [CrossRef]
- Dharam Vir Ahluwalia. Wave particle duality at the Planck scale: Freezing of neutrino oscillations. Phys. Lett. A, 275:31–35, 2000. doi. [CrossRef]
- Giovanni Amelino-Camelia. Relativity in space-times with short distance structure governed by an observer independent (Planckian) length scale. Int. J. Mod. Phys. D, 11:35–60, 2002. doi. [CrossRef]
- Abdel Nasser Tawfik and Tahia F. Dabash. Born reciprocity and discretized Finsler structure: An approach to quantize GR curvature tensors on three-sphere. Int. J. Mod. Phys. D, 32(10):2350068, 2023a. doi. [CrossRef]
- Abdel Nasser Tawfik and Tahia F. Dabash. Born reciprocity and relativistic generalized uncertainty principle in Finsler structure: Fundamental tensor in discretized curved spacetime. Int. J. Mod. Phys. D, 32(09):2350060, 2023b. doi. [CrossRef]
- Per Berglund, Tristan Hübsch, David Mattingly, and Djordje Minic. Gravitizing the quantum. Int. J. Mod. Phys. D, 31(14):2242024, 2022. doi. [CrossRef]
- Abdel Nasser Tawfik, Abdel Magied Diab, Sameh Shenawy, and Eiman Abou El Dahab. Consequences of minimal length discretization on line element, metric tensor and geodesic equation. Astron. Nachr., 342(1-2):54–57, 2021. doi. [CrossRef]
- Abdel Nasser Tawfik. On quantum-induced revisiting Einstein tensor in the relativistic regime. Astron. Nachr., 344(1-2):e220071, 2023a. doi. [CrossRef]
- Abdel Nasser Tawfik. On possible quantization of the fundamental tensor in the relativistic regime. Astron. Nachr., 344(1-2):e220072, 2023b. doi. [CrossRef]
- Abdel Nasser Tawfik. Discretized Finsler Structure: An Approach to Quantizing the First Fundamental Form. Phys. Sci. Forum, 7(1):36, 2023c. doi. [CrossRef]
- R. D. Sorkin. An example relevant to the Kretschmann-Einstein debate. Mod. Phys. Lett. A, 17:695–700, 2002. doi. [CrossRef]
- Ioannis Gkigkitzis, Ioannis Haranas, and Omiros Ragos. Kretschmann Invariant and Relations Between Spacetime Singularities, Entropy and Information. Physics International, 5(1):103–111, 2014. doi. [CrossRef]
- E. R. Caianiello. There a Maximal Acceleration? Lett. Nuovo Cim., 32:65, 1981. doi. [CrossRef]
- C. S. Sharma and S. Srirankanathan. On caianiello’s maximal acceleration. Lett. Nuovo Cimento, 44:275–276, 1985.
- Max Born. Quantised field theory and the mass of the proton. Nature, 136(2992):952–953, 1935.
- Max Born. Elementary Particles and the Principle of Reciprocity. Nature, 163(4136):207–208, 1949a. doi. [CrossRef]
- Max Born. Reciprocity Theory of Elementary Particles. Rev. Mod. Phys., 21(3):463–473, 1949b. doi. [CrossRef]
- Laurent Freidel, Robert G. Leigh, and Djordje Minic. Born Reciprocity in String Theory and the Nature of Spacetime. Phys. Lett. B, 730:302–306, 2014. doi. [CrossRef]
- Jan Govaerts, Peter D Jarvis, Stuart O Morgan, and Stephen G Low. World-line quantization of a reciprocally invariant system. Journal of Physics A: Mathematical and Theoretical, 40(40):12095–12111, sep 2007. doi. [CrossRef]
- Abdel Nasser Tawfik and Abdel Magied Diab. Generalized Uncertainty Principle: Approaches and Applications. Int. J. Mod. Phys. D, 23(12):1430025, 2014. doi. [CrossRef]
- Abdel Nasser Tawfik and Abdel Magied Diab. Review on Generalized Uncertainty Principle. Rept. Prog. Phys., 78:126001, 2015. doi. [CrossRef]
- Roberto Casadio, Octavian Micu, and Piero Nicolini. Minimum length effects in black hole physics. Fundam. Theor. Phys., 178:293–322, 2015. doi. [CrossRef]
- D. Amati, M. Ciafaloni, and G. Veneziano. Can spacetime be probed below the string size? Physics Letters B, 216(1):41–47, 1989. ISSN 0370-2693. doi. [CrossRef]
- Pasquale Bosso, Luciano Petruzziello, Fabian Wagner, and Fabrizio Illuminati. Spin operator, Bell nonlocality and Tsirelson bound in quantum-gravity induced minimal-length quantum mechanics. Commun. Phys., 6(1):114, 2023. doi. [CrossRef]
- Abdel Nasser Tawfik and Eiman Abou El Dahab. Review on Dark Energy Models. Grav. Cosmol., 25(2):103–115, 2019. doi. [CrossRef]
- F. Karolyhazy. Gravitation and quantum mechanics of macroscopic objects. Nuovo Cim. A, 42:390–402, 1966. doi. [CrossRef]
- Surajit Chattopadhyay, Antonio Pasqua, Abdel Nasser Tawfik, and Ratbay Myrzakulov. Cosmology of a generalized version of holographic dark energy and reconstruction of different scalar field models. Phys. Scripta, 95(8):085005, 2020. doi. [CrossRef]
- Fabian Wagner. Generalized uncertainty principle or curved momentum space? Phys. Rev. D, 104(12):126010, 2021. doi. [CrossRef]
- Roger Penrose. On gravity’s role in quantum state reduction. Gen. Rel. Grav., 28:581–600, 1996. doi. [CrossRef]
- Vasil Todorinov. Relativistic Generalized Uncertainty Principle and Its Implications. PhD thesis, Lethbridge U., 2020.
- Howard E. Brandt. Riemann curvature scalar of space-time tangent bundle. Found. Phys. Lett., 5:43, 1992. doi. [CrossRef]
- Sandor Benczik, Lay Nam Chang, Djordje Minic, Naotoshi Okamura, Saifuddin Rayyan, and Tatsu Takeuchi. Short distance versus long distance physics: The Classical limit of the minimal length uncertainty relation. Phys. Rev. D, 66:026003, 2002. doi. [CrossRef]
- Yeo Cheng Xun. Generalized Uncertainty Principle and its Applications. PhD thesis, National University of Singapore, Singapore, 2014.
- Abdel Magied Diab and Abdel Nasser Tawfik. A Possible Solution of the Cosmological Constant Problem Based on GW170817 and Planck Observations with Minimal Length Uncertainty. Adv. High Energy Phys., 2022:9351511, 2022. doi. [CrossRef]
- H. P. Robertson. The uncertainty principle. Phys. Rev., 34(1):163–64, 1929. doi. [CrossRef]
- E. Schroedinger. Zum heisenbergschen unschaerfeprinzip. Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl., 1930:296–303, 1930.
- E. R. Caianiello, A. Feoli, M. Gasperini, and G. Scarpetta. Quantum Corrections to the Space-time Metric From Geometric Phase Space Quantization. Int. J. Theor. Phys., 29:131, 1990a. doi. [CrossRef]
- E. R. Caianiello, M. Gasperini, and G. Scarpetta. Phenomenological Consequences of a Geometric Model With Limited Proper Acceleration. Nuovo Cim. B, 105:259, 1990b. doi. [CrossRef]
- E. R. Caianiello, M. Gasperini, and G. Scarpetta. Inflation and singularity prevention in a model for extended-object-dominated cosmology. Class. Quant. Grav., 8(4):659–666, 1991. doi. [CrossRef]
- R. Miron, D. Hrimiuc, H. Shimada, and S.V. Sabau. The Geometry of Hamilton and Lagrange Spaces. Fundamental Theories of Physics. Springer Verlag, Netherlands, 2006.
- Saulo Albuquerque, Valdir B. Bezerra, Iarley P. Lobo, Gabriel Macedo, Pedro H. Morais, Ernesto Rodrigues, Luis C. N. Santos, and Gislaine Varão. Quantum Configuration and Phase Spaces: Finsler and Hamilton Geometries. Physics, 5:90–115, 2023. doi. [CrossRef]
- Xiaohuan Mo. An Introduction to Finsler Geometry. World Scientific Publishing, Singapore, 2006.
- Abdel Tawfik and Abdel Diab. Emergence of cosmic space and minimal length in quantum gravity: a large class of spacetimes, equations of state, and minimal length approaches. Indian J. Phys., 90(10):1095–1103, 2016. doi. [CrossRef]
- G.S. Asanov. Finsleroid-finsler spaces of positive-definite and relativistic types. Reports on Mathematical Physics, 58(2):275–300, 2006. doi. [CrossRef]
- EE Caianiello. Maximal acceleration as a consequence of heisenberg’s uncertainty relations. Lettere al Nuovo Cimento (1971-1985), 41(11):370–372, 1984.
- Gunnar Randers. On an Asymmetrical Metric in the Four-Space of General Relativity. Phys. Rev., 59(2):195, 1941. doi. [CrossRef]
- Richard S. Hamilton. Three-manifolds with positive ricci curvature. Journal of Differential Geometry, 17:255–306, 1982.
- Radu Miron and Mihai Anastasiei. The Geometry of Lagrange Spaces: Theory and Applications. Fundam.Theor.Phys. Springer Netherlands, Dordrecht, 1994. doi. [CrossRef]
- Pierre Martinetti. Line element in quantum gravity: The Examples of DSR and noncommutative geometry. Int. J. Mod. Phys. A, 24:2792–2801, 2009. doi. [CrossRef]
- Michel Dubois-Violette. Lectures on graded differential algebras and noncommutative geometry. Math. Phys. Stud., 23:245–306, 2001. doi. [CrossRef]
- J. Madore. An introduction to noncommutative differential geometry and its physical applications, volume 257. 2000.
- S. C. Ulhoa, A. F. Santos, and R. G. G. Amorim. On Non-Commutative Correction of the Gödel-type Metric. Gen. Rel. Grav., 47(9):99, 2015. doi. [CrossRef]
- P. L. FitzGerald. The Superfield quantisation of a superparticle action with an extended line element. Int. J. Mod. Phys. A, 20:2639–2655, 2005. doi. [CrossRef]
- Christian Pfeifer and José Javier Relancio. Deformed relativistic kinematics on curved spacetime: a geometric approach. Eur. Phys. J. C, 82(2):150, 2022. doi. [CrossRef]
- Howard E Brandt. Maximal-acceleration invariant phase space. In The Physics of Phase Space Nonlinear Dynamics and Chaos Geometric Quantization, and Wigner Function, pages 413–416. Springer, 1987.
- Christian Pfeifer and Mattias N. R. Wohlfarth. Finsler geometric extension of Einstein gravity. Phys. Rev. D, 85:064009, 2012. doi. [CrossRef]
- Laurent Freidel and Etera R. Livine. 3D Quantum Gravity and Effective Noncommutative Quantum Field Theory. Phys. Rev. Lett., 96:221301, 2006. doi. [CrossRef]
- Erich Kretschmann. Über die prinzipielle bestimmbarkeit der berechtigten bezugssysteme beliebiger relativitätstheorien (i), (ii). Annalen der Physik, 48:907–982, 1915.
- Erich Kretschmann. Über den physikalischen sinn der relativitätspostulate: A. einsteins neue und seine urprüngliche relativitätstheorie. Annalen der Physik, 53:577–614, 1917.
- Richard C. Henry. Kretschmann scalar for a kerr-newman black hole. Astrophys. J., 535:350, 2000. doi. [CrossRef]
- M. S. Knebelman. Spaces of Relative Parallelism. Annals of Mathematics, 53(3):387–399, 1951.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).