Quantum-Cosmos Nexus Theory

Abdulrahman Sheikh Nemeh

doi:10.20944/preprints202310.1554.v1

Submitted:

23 October 2023

Posted:

25 October 2023

Read the latest preprint version here

Abstract

The Quantum-Cosmos Nexus Theory delves into the intricate web of relationships that tie together fundamental constants, cosmological properties, and the boundaries of our comprehension in the realm of physics. It unveils a profound interconnection between the gravitational constant (G), the speed of light (c), and the parameters of the observable universe. It introduces a unification equation that hints at a connection between the fundamental constants. It also introduces a new constant, , which is similar to the Planck constant but, on a large scale, signifies the ultimate unit of action or energy on a cosmic scale. With this new constant, new units similar to Planck units have been introduced. They are the equivalence of Planck units in the sense that they represent the limits of our current understanding of physics on the largest scale. The theory also shows that most of the fundamental constants of nature, including the gravitational constant (G), the speed of light (c), vacuum permittivity (ε₀) vacuum permeability (u₀), the Boltzmann constant (K_B), and the fine-structure constant (α), can be derived from these new units and Planck units. The first derived equation suggests a potential weakening of the gravitational constant over time, assuming the density remains relatively constant. Although this is a matter of speculation, it has the potential to explain observations related to dark matter. The theory also makes use of the Planck force, defining it as the maximum force on the quantum and cosmic scales. It also emphasizes that the Planck scale is not the ultimate limit and reveals our observational constraints, offering a unique perspective on the universe's fundamental workings. The Quantum-Cosmos Nexus Theory reveals how fundamental constants, cosmic dynamics, and the limits of our understanding converge, opening the door to fresh perspectives on the underlying principles of the universe.

Keywords:

cosmic scale

;

Planck scale

;

gravity

;

fundamental constants

Subject:

Physical Sciences - Theoretical Physics

Introduction

The Quantum-Cosmos Nexus Theory presents a compelling exploration of the intricate relationship between the fundamental constants of the universe, encompassing both the quantum and cosmic scales. This theory delves into the profound interconnections that exist among key constants, such as the gravitational constant, the speed of light, and various Planck and cosmic units, shedding new light on their intrinsic ties.

As we delve into the depths of this theory, it is crucial to first confront the enigma of the gravitational constant, symbolized as G, which has persisted since Sir Isaac Newton first laid the foundations of gravitational theory in 1665 [1]. Over centuries of scientific progress, our understanding of why G assumes its specific numerical value remains incomplete. We have gleaned knowledge of G exclusively through meticulous measurements and experiments, emphasizing the depth of our cosmic ignorance and our enduring quest to decipher the fundamental laws governing our universe.

In the mid-20th century, the illustrious physicist Paul Dirac introduced the Large Number Hypothesis [2], sparking intrigue within the scientific community. This hypothesis hinted at a potential connection between two seemingly unrelated cosmic constants: G and the age of the universe. Dirac's insight derived from the observation that certain significant numerical ratios in physics, such as the age of the universe and the strength of gravitational forces, shared a comparable order of magnitude. While the Large Number Hypothesis did not lead to a universally accepted theory, it underscored Dirac's innovative thinking and the ongoing pursuit of uncovering hidden connections within the universe.

Building on this historical perspective, we venture further into the realm of gravitational theory with Gunnar Nordström, an early 20th-century Finnish theoretical physicist. Nordström's unconventional proposal suggested that the gravitational constant, a cornerstone of physics determining the strength of gravitational forces, might depend on the distribution of matter throughout the universe [3]. This concept challenged the established principles of gravity, particularly Einstein's theory of general relativity. While it did not supplant Einstein's theory, Nordström's work provided valuable insights into alternative approaches to understanding gravity, reflecting the spirit of exploration and innovation that propels scientific progress.

In the 1960s, Robert H. Dicke and Carl H. Brans introduced the Brans-Dicke theory of gravitation [4]. Departing from traditional views, this theory introduced a scalar field, 'phi,' capable of varying with time, resulting in fluctuations in gravity's strength. This notion defied the notion of gravity as a fixed and unchanging force, opening the door to the idea that gravity's fundamental nature might evolve over time. While not supplanting general relativity, the Brans-Dicke theory enriched our exploration of gravitational physics, exemplifying scientific inquiry's boldness in questioning established paradigms.

Some theoretical physicists, working within frameworks such as string theory and theories involving extra dimensions [5], have suggested that fundamental constants, including gravity's strength, might not be as constant as traditionally believed. These speculations challenge our conventional understanding, hinting at a dynamic universe where gravity could vary under different cosmic conditions, reflecting the adventurous spirit of theoretical physics and its ongoing exploration of the universe's fundamental forces.

In the realm of cosmological models, the concept of time-varying gravitational coupling has garnered attention. Various scientists have contributed insights to our evolving understanding of how gravity, a fundamental cosmic force, may not be immutable but subject to change over time [6,7]. Their collective efforts illuminate the dynamic nature of cosmological research, as scientists continue their quest to unravel the mysteries of our ever-changing cosmos.

The speed of light, denoted as 'c,' stands as a fundamental constant precisely measured in the late 19th century [8]. While its value is known, the specific reason for 'c' holding that exact numerical value remains an intriguing enigma. Despite meticulous measurements, the origins of this constant continue to captivate our scientific curiosity.

In summary, the Quantum-Cosmos Nexus Theory emerges as a response to a series of fundamental questions. Delving deep into the heart of our universe, this theory sets out to uncover the origins of key constants like the gravitational constant and the speed of light, shedding light on their mysterious values that underpin the very laws of nature.

Intriguingly, it asks whether, just as there are limits to our understanding at the subatomic scale, there might exist an upper threshold to our cosmic knowledge. Does the universe conceal its deepest secrets, beyond which our comprehension may never extend?

The theory also ventures into the realms of the quantum and cosmic scales, probing the existence of a constant that represents the largest unit of action, akin to the reduced Planck constant's role on the smallest scale proposed by the physicist Max Karl Ernst Ludwig Planck [9]. In doing so, it seeks to establish a profound connection between these two seemingly disparate worlds, unravelling the threads that unite them.

Furthermore, the Quantum-Cosmos Nexus Theory endeavours to derive the critical constants of nature, spanning the expanse from cosmic to quantum scales, fostering a comprehensive understanding of how these constants interrelate.

The intriguing question of whether the gravitational constant weakens over time introduces a provocative notion, offering a potential explanation for enigmatic cosmic phenomena like the early universe's structural formations and the elusive nature of dark matter.

Exploring the meaning and purpose of the Planck force, this theory ponders whether it signifies the maximum force achievable on a cosmic scale, unravelling its significance in the grand tapestry of universal laws.

In the pursuit of knowledge, it questions whether the Planck length is truly the ultimate limit in our quest to fathom the fabric of space and time.

Lastly, it seeks to unravel the ultimate structure of the Planck and cosmic scales, providing an illuminating insight into their foundational nature. The Quantum-Cosmos Nexus Theory stands as a beacon of inquiry, beckoning us to explore the boundaries of our cosmic understanding, and its quest to uncover answers to these profound questions holds the promise of a new era of enlightenment and discovery in the realms of physics and cosmology.

Method

We will start with Newton's gravitational constant (G), which has the unit

\frac{N m^{2}}{k g^{2}} = \frac{m^{3}}{k g . s^{2}}

by deriving an equation from these units.

m^{3}

is the unit of volume

V

,

k g

is unit of mass

M

and

s

is the unit of time

t

.

We get The Gravitational Clock Equation:

G = \frac{V}{M \cdot t^{2}} = \frac{R^{3}}{M \cdot t^{2}}

(1)

Upon substituting the established value of the age of the universe [11] and

G \approx 6.6743 \cdot 10^{- 11} m^{3} . k g^{- 1} . s^{- 2}

[12], resolving for both mass and volume, and then striving to achieve equilibrium within the equation, our objective is to attain the precise value of the gravitational constant.

We find that the radius is equal to the Hubble radius (all the upcoming units and parameters have been named in honor of the esteemed astronomer Edwin Hubble):

R_{H} = 1.30435091 \cdot 10^{26} m e t e r s = 13.787 b i l l i o n l i g h t y e a r s

With a cubic volume equal to the Hubble radius cubed:

V_{H} = R_{H}^{3} = 2.21913302 \cdot 10^{78} m^{3}

The mass of the Hubble cube is:

M_{H} = 1.75642709 \cdot 10^{53} k g

The age of the universe (Hubble time) [11]:

1 y e a r \approx 31557600 s e c o n d s s

Age (in seconds)

t_{H} = 13.787 b i l l i o n y e a r s \cdot 1,000,000,000 \frac{y e a r s}{b i l l i o n y e a r s} \cdot 31557600 \frac{s e c o n d s}{y e a r s}

t_{H} \approx 4.35084631 \cdot 10^{17} s e c o n d s G = \frac{V_{H}}{M_{H} \cdot t_{H}^{2}} = \frac{2.21913302 \cdot 10^{78}}{1.75642709 \cdot 10^{53} \cdot {(4.35084631 \cdot 10^{17})}^{2}} = 6.6743 \cdot 10^{- 11} m^{3} \cdot k g^{- 1} \cdot s^{- 2}

Density of the Hubble Cube $ρ_{H}$

ρ_{H} = \frac{M_{H}}{V_{H}} = \frac{M a s s o f t h e H u b b l e s p h e r e}{V o l u m e o f t h e H u b b l e s p h e r e} = \frac{1.75642709 \cdot 10^{53}}{2.21913302 \cdot 10^{78}} = 7.91492477 \cdot 10^{- 26} \frac{k g}{m^{3}} ρ_{H}^{- 1} = \frac{V_{H}}{M_{H}} = 1.26343589 \cdot 10^{25} \frac{m^{3}}{k g} G = \frac{1}{ρ_{H} . t_{H}^{2}}

(2)

Figure 1.

Figure 1. illustrates the difference in size between the Hubble cube and the cosmological horizon (light from the CMB), which has a radius of approximately 46.508 billion light years [10].

After solving the gravitational clock equation for

t_{H}

, substituting

t_{H}

for

\frac{d}{v}

, and then solve for v, the speed of light is calculated. (

v = c

), (

d = R_{H}

).

t_{H}^{2} = \frac{1}{ρ_{H} \cdot G} \to \frac{R_{H}^{2}}{c^{2}} = \frac{1}{ρ_{H} \cdot G}

c = \pm \sqrt{ρ_{H} \cdot G \cdot R_{H}^{2}}

(3)

c = \pm 299792458.1 \frac{m}{s}

By applying the speed of light equation [8], which relates speed of light c, vacuum permittivity

ε_{0}

, and vacuum permeability

μ_{0}

. We get unification between the fundamental constants.

c = \frac{1}{\sqrt{μ_{0} \cdot ε_{0}}}

\frac{1}{\sqrt{μ_{0} \cdot ε_{0}}} = \sqrt{ρ_{H} \cdot G \cdot R_{H}^{2}}

(4)

‘Unification Equation’

1 = G \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0} \cdot ε_{0}

(5)

Applying the speed of light equation

\frac{1}{c^{2}} = μ_{0} \cdot ε_{0}

and the gravitational clock equation

∆ G = \frac{1}{ρ_{H} \cdot {∆ t}_{H}^{2}}

to the unification equation reveals the relationship between the speed of light, the Hubble radius, and the age of the universe.

1 = \frac{1}{ρ_{H} \cdot ∆ t_{H}^{2}} \cdot ρ_{H} \cdot R_{H}^{2} \cdot \frac{1}{c^{2}}

∆ c^{2} = \frac{{∆ R}_{H}^{2}}{{∆ t}_{H}^{2}}

c = H_{0} \cdot R_{H} = \frac{R_{H}}{t_{H}} = \frac{1.30435091 \cdot 10^{26} m}{4.35084631 \cdot 10^{17} s}

(6)

c = 299792458.1 m \cdot s^{- 1}

According to the formula, the length of the Hubble radius is always the same as the radius of the universe's 4-sphere, and both are rising at the speed of light; thus, both are increasing in length by one light-year every year. However, the two are not equivalent. (The radius of the 4-sphere is in 4D space, whereas the Hubble radius is in 3D space.)

Planck units' relationship with the Hubble parameters

By integrating the gravitational clock equation (1) and equation (6) with Planck units [13], we attain the connection between Planck units and the Hubble parameters.

l_{P l a n c k} = \sqrt{\frac{ℏ \cdot G}{c^{3}}} = \sqrt{\frac{ℏ}{c^{3} \cdot ρ_{H} \cdot t_{H}^{2}}}

= \sqrt{\frac{ℏ \cdot t_{H}}{R_{H}^{3} \cdot ρ_{H}}}

(7)

∆ l_{P l a n c k} = 1.61625502 \cdot 10^{- 35} m

t_{P l a n c k} = \sqrt{\frac{ℏ \cdot G}{c^{5}}} = \sqrt{\frac{ℏ}{c^{5} \cdot ρ_{H} \cdot t_{H}^{2}}} = \sqrt{\frac{ℏ \cdot t_{H}^{3}}{R_{H}^{5} \cdot ρ_{H}}} = 5.39124644 \cdot 10^{- 44} s

(8)

T_{p l a n c k} = \sqrt{\frac{ℏ \cdot c^{5}}{G \cdot K_{B}^{2}}} = \sqrt{\frac{ℏ \cdot c^{5} \cdot ρ_{H} \cdot t_{H}^{2}}{K_{B}^{2}}} = \sqrt{\frac{ℏ \cdot R_{H}^{5} \cdot ρ_{H}}{t_{H}^{3} \cdot K_{B}^{2}}} = 1.41678416 \cdot 10^{32} K

(9)

m_{P l a n c k} = \sqrt{\frac{ℏ \cdot c}{G}} = \sqrt{ℏ \cdot c \cdot ρ_{H} \cdot t_{H}^{2}} = \sqrt{ℏ \cdot R_{H} \cdot ρ_{H} \cdot ∆ t_{H}} = 2.17643434 \cdot 10^{- 8} k g

(10)

Reduced Planck constant integration

ℏ = \frac{m_{P} \cdot l_{P}^{2}}{t_{P}} k g \cdot m^{2} \cdot s^{- 1}

(11)

l_{P} = \sqrt{\frac{ℏ \cdot ∆ t_{H}}{R_{H}^{3} \cdot ρ_{H}}} = \sqrt{\frac{m_{P} \cdot l_{P}^{2} \cdot t_{H}}{t_{P} \cdot R_{H}^{3} \cdot ρ_{H}}}

1. t_{P} \cdot R_{H}^{3} \cdot ρ_{H} = m_{P} \cdot t_{H}

(12)

t_{P} = \frac{m_{P} \cdot t_{u}}{R_{H}^{3} \cdot ρ_{H}} = \sqrt{\frac{ℏ \cdot {∆ t}_{H}^{3}}{R_{H}^{5} \cdot ρ_{H}}} = \sqrt{\frac{m_{P} \cdot l_{p}^{2} \cdot t_{H}^{3}}{t_{P} \cdot R_{H}^{5} \cdot ρ_{H}}}

\frac{m_{P}^{2} \cdot t_{H}^{2}}{R_{H}^{6} \cdot ρ_{H}^{2}} = \frac{m_{P} \cdot l_{P}^{2} \cdot t_{H}^{3}}{t_{P} \cdot R_{H}^{5} \cdot ρ_{H}}

2. m_{P} \cdot t_{P} = l_{P}^{2} \cdot R_{H} \cdot ρ_{H} \cdot t_{H}

(13)

By solving equation one and two for

m_{P}

:

m_{P} = \frac{l_{P}^{2} \cdot R_{H} \cdot ρ_{H} \cdot t_{H}}{t_{P}} = \frac{t_{P} \cdot R_{H}^{3} \cdot ρ_{H}}{t_{H}}

l_{P}^{2} \cdot t_{H}^{2} = t_{P}^{2} \cdot R_{H}^{2}

\frac{l_{P}}{t_{P}} = \frac{R_{H}}{t_{H}}

(14)

R_{H} = \frac{t_{H} \cdot l_{P}}{t_{P}} = 1.30435091 \cdot 10^{26} m

Largest Quanta $ℏ_{M a x}$

The Planck constant [9] (denoted as "

h

") is often regarded as the fundamental constant that sets the scale for the smallest possible quanta in quantum mechanics. It plays a crucial role in quantum physics and defines the smallest unit of action in the universe. The Planck constant, along with other fundamental constants like the speed of light (c) and the gravitational constant (G), defines the Planck units, which are natural units for various physical quantities.

We can derive the largest quanta possible by simply looking at the units of the reduced Planck constant that have been proposed by Max Karl Ernst Ludwig Planck and replacing the units with the calculated Hubble parameters

M_{H}, R_{H}, t_{H}

.

ℏ h a s t h e u n i t s k g \cdot m^{2} \cdot s^{- 1}

ℏ_{M a x} = \frac{M_{H} \cdot R_{H}^{2}}{t_{H}} = 6.86823704 \cdot 10^{87} k g \cdot m^{2} / s

(15)

Hubble Units

Hubble Length:

R_{H} = \sqrt{\frac{ℏ_{M a x} \cdot G}{c^{3}}} = 1.30435091 \cdot 10^{26} m

(16)

Hubble Time:

t_{H} = \sqrt{\frac{ℏ_{M a x} \cdot G}{c^{5}}} = 4.35084631 \cdot 10^{17} s

(17)

Hubble Temperature:

T_{H} = \sqrt{\frac{ℏ_{M a x} \cdot c^{5}}{G \cdot K_{B}^{2}}} = 1.14337384 \cdot 10^{93} K

(18)

Hubble Mass:

M_{H} = \sqrt{\frac{ℏ_{M a x} \cdot c}{G}} = 1.75642709 \cdot 10^{53} k g

(19)

Hubble Charge:

q_{H} = \sqrt{ε_{0} \cdot ℏ_{M a x} \cdot c} = 4.26979824 \cdot 10^{42} C

(20)

Hubble Area:

A_{H} = R_{H}^{2} = \frac{ℏ_{M a x} \cdot G}{c^{3}} = 1.70133129 \cdot 10^{52} m^{2}

(21)

Hubble Volume:

V_{H} = \sqrt{\frac{{{(ℏ}_{M a x} \cdot G)}^{3}}{c^{9}}} = 2.21913302 \cdot 10^{78} m^{3}

(22)

Hubble Momentum:

ϑ_{H} = \sqrt{\frac{ℏ_{M a x} \cdot c^{3}}{G}} = 5.26563595 \cdot 10^{61} k g \cdot m \cdot s^{- 1}

(23)

Hubble Energy:

E_{H} = \frac{ℏ_{M a x}}{t_{H}} = \sqrt{\frac{ℏ_{M a x} \cdot c^{5}}{G}} = 1.57859795 \cdot 10^{70} J

(24)

Hubble Force

F_{H} = \frac{E_{H}}{R_{H}} = \frac{ℏ_{M a x}}{R_{H} \cdot t_{H}} = 1.21025556 \cdot 10^{44} N

(25)

Hubble Density:

ρ_{H} = \frac{c^{5}}{ℏ_{M a x} \cdot G^{2}} = 7.91492478 \cdot 10^{- 26} k g \cdot m^{- 3}

(26)

Hubble Acceleration

a_{H} = \frac{c}{t_{H}} = \sqrt{\frac{c^{7}}{ℏ_{M a x} \cdot G}} = 6.89044008 \cdot 10^{- 10} m / s^{2}

(27)

Gravitational constant derivation from Planck's units and Hubble units

G = \frac{R_{H}^{3}}{M_{H} \cdot t_{H}^{2}} = \frac{l_{P}^{3}}{m_{P} \cdot t_{P}^{2}}

(28)

G = {6.6743 \cdot 10}^{- 11} m^{3} \cdot k g^{- 1} \cdot s^{- 2}

Derivation of vacuum permittivity $ε_{0}$ [14], vacuum permeability $μ_{0}$ [15], and speed of light from Planck units [13] and Hubble Units

q_{P} = \sqrt{ε_{0} \cdot ℏ \cdot c} = 5.29081769 \cdot 10^{- 19} C q_{H} = \sqrt{ε_{0} \cdot ℏ_{M a x} \cdot c} = 4.26979824 \cdot 10^{42} C ε_{0} = \frac{F}{m} = \frac{s^{4} \cdot A^{2}}{k g \cdot m^{2}} = \frac{s^{2} \cdot C^{2}}{k g \cdot m^{3}}

ε_{0} = \frac{q_{P}^{2} \cdot t_{P}^{2}}{m_{P} \cdot l_{P}^{3}} = \frac{q_{H}^{2} \cdot t_{H}^{2}}{M_{H} \cdot R_{H}^{3}} = 8.85418891 \cdot 10^{- 12} F \cdot m^{- 1}

(29)

μ_{0} = \frac{N}{A^{2}} = \frac{k g \cdot m}{s^{2} \cdot A^{2}} = \frac{k g \cdot m}{C^{2}}

μ_{0} = \frac{m_{P} \cdot l_{P}}{q_{P}^{2}} = \frac{M_{H} \cdot R_{H}}{q_{H}^{2}} = 1.25663691 \cdot 10^{- 6} N \cdot A^{- 2}

(30)

c^{2} = \frac{1}{μ_{0} \cdot ε_{0}} c^{2} = \frac{q_{P}^{2}}{m_{P} \cdot l_{P}} \cdot \frac{m_{P} \cdot l_{P}^{3}}{q_{P}^{2} \cdot t_{P}^{2}} c = \frac{l_{P}}{t_{P}} = \frac{1.61625502 \cdot 10^{- 35}}{5.39124644 \cdot 10^{- 44}} = 299792457.6 \frac{m}{s}

c = \frac{l_{P l a n c k}}{t_{P l a n c k}} = \frac{R_{H u b b l e}}{t_{H u b b l e}}

(31)

Boltzmann constant derivation from Planck units and Hubble units

K_{B} = \frac{J}{K} = \frac{k g \cdot m^{2}}{K \cdot s^{2}}

K_{B} = \frac{m_{P} \cdot l_{p}^{2}}{T_{P} \cdot t_{P}^{2}} = \frac{M_{H} \cdot R_{H}^{2}}{T_{H} \cdot t_{H}^{2}} = \frac{m_{P} \cdot c^{2}}{T_{P}} = \frac{M_{H} \cdot c^{2}}{T_{H}}

(32)

K_{B} = 1.380649 \cdot 10^{- 23} J \cdot K^{- 1}

Unification Equation Application

By applying the unification equation to solve for 'G,' followed by a similar approach with Newton's Law of Universal Gravitation [1]. Subsequently, we merge these two equations to provide a fresh perspective on the Law of Universal Gravitation.

G = \frac{F_{g} \cdot d^{2}}{M_{1} \cdot m_{2}} = \frac{1}{ρ_{H} \cdot R_{H}^{2} \cdot μ_{0} \cdot ε_{0}}

F_{g} = \frac{M_{1} \cdot m_{2}}{d^{2} \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0} \cdot ε_{0}} = \frac{M_{1} \cdot m_{2}}{d^{2} \cdot ρ_{H} \cdot t_{H}^{2}}

(33)

We do the same thing again for Coulomb's law for electrostatic force [16] by solving for

ε_{0}

.

ε_{0} = \frac{q_{1} \cdot q_{2}}{4 \cdot π \cdot d^{2} \cdot F_{c}} = \frac{1}{G \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0}}

F_{c} = \frac{q_{1} \cdot q_{2} \cdot G \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0}}{4 \cdot π \cdot d^{2}} = \frac{q_{1} \cdot q_{2} \cdot R_{H}^{2} \cdot μ_{0}}{{4 \cdot π \cdot d}^{2} \cdot t_{H}^{2}} = \frac{q_{1} \cdot q_{2} \cdot c^{2} \cdot μ_{0}}{4 \cdot π \cdot d^{2}}

(34)

Now for Coulomb’s Laws of Magnetic Force [21] by solving for

μ_{0}

.

μ_{0} = \frac{4 \cdot π \cdot d^{2} \cdot F_{m a}}{m_{a 1} \cdot m_{a 2}} = \frac{1}{G \cdot ρ_{H} \cdot R_{H}^{2} \cdot ε_{0}}

F_{m a} = \frac{m_{a 1} \cdot m_{a 2}}{4 \cdot π \cdot d^{2} \cdot G \cdot ρ_{H} \cdot R_{H}^{2} \cdot ε_{0}} = \frac{m_{a 1} \cdot m_{a 2}}{4 \cdot π \cdot d^{2} \cdot c^{2} \cdot ε_{0}}

(35)

We can merge the three equations into the unification equation.

1 = \frac{F_{g} \cdot d^{2}}{M_{1} \cdot m_{2}} \cdot \frac{q_{1} \cdot q_{2}}{4 \cdot π \cdot d^{2} \cdot F_{c}} \cdot \frac{4 \cdot π \cdot d^{2} \cdot F_{m a}}{m_{a 1} \cdot m_{a 2}} \cdot ρ_{H} \cdot R_{H}^{2}

\frac{F_{c}}{F_{g} \cdot F_{m a}} = d^{2} \cdot \frac{q_{1} \cdot q_{2}}{(M_{1} \cdot m_{2}) \cdot (m_{a 1} \cdot m_{a 2})} {\cdot ρ}_{H} \cdot R_{H}^{2}

(36)

The integration of Newton's Law of Universal Gravitation and Coulomb's Law into the unification equation provides the strength ratio between the gravitational force and the Coulomb's force.

1 = G \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0} \cdot ε_{0}

(37)

1 = \frac{F_{g} \cdot d^{2}}{M_{1} \cdot m_{2}} \cdot \frac{q_{1} \cdot q_{2}}{4 \cdot π \cdot d^{2} \cdot F_{c}} \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0}

\frac{F_{c}}{F_{g}} = \frac{q_{1} \cdot q_{2}}{{4 π \cdot M}_{1} \cdot m_{2}} \cdot ρ_{H} \cdot R_{H}^{2} \cdot μ_{0}

(38)

We can calculate the strength ratio by plugging in the charge and mass of the electron and proton.

Mass of the electron is

m_{e} = 9.1093837 \cdot 10^{- 31} k g

Mass of the proton is

m_{p r o .} = 1.67262192 \cdot 10^{- 27} k g

Proton/Electron charge

q = \pm 1.60217663 \cdot 10^{- 19} C

\frac{F_{c}}{F_{g}} = 2.26866143 \cdot 10^{39}

Fine-Structure Constant

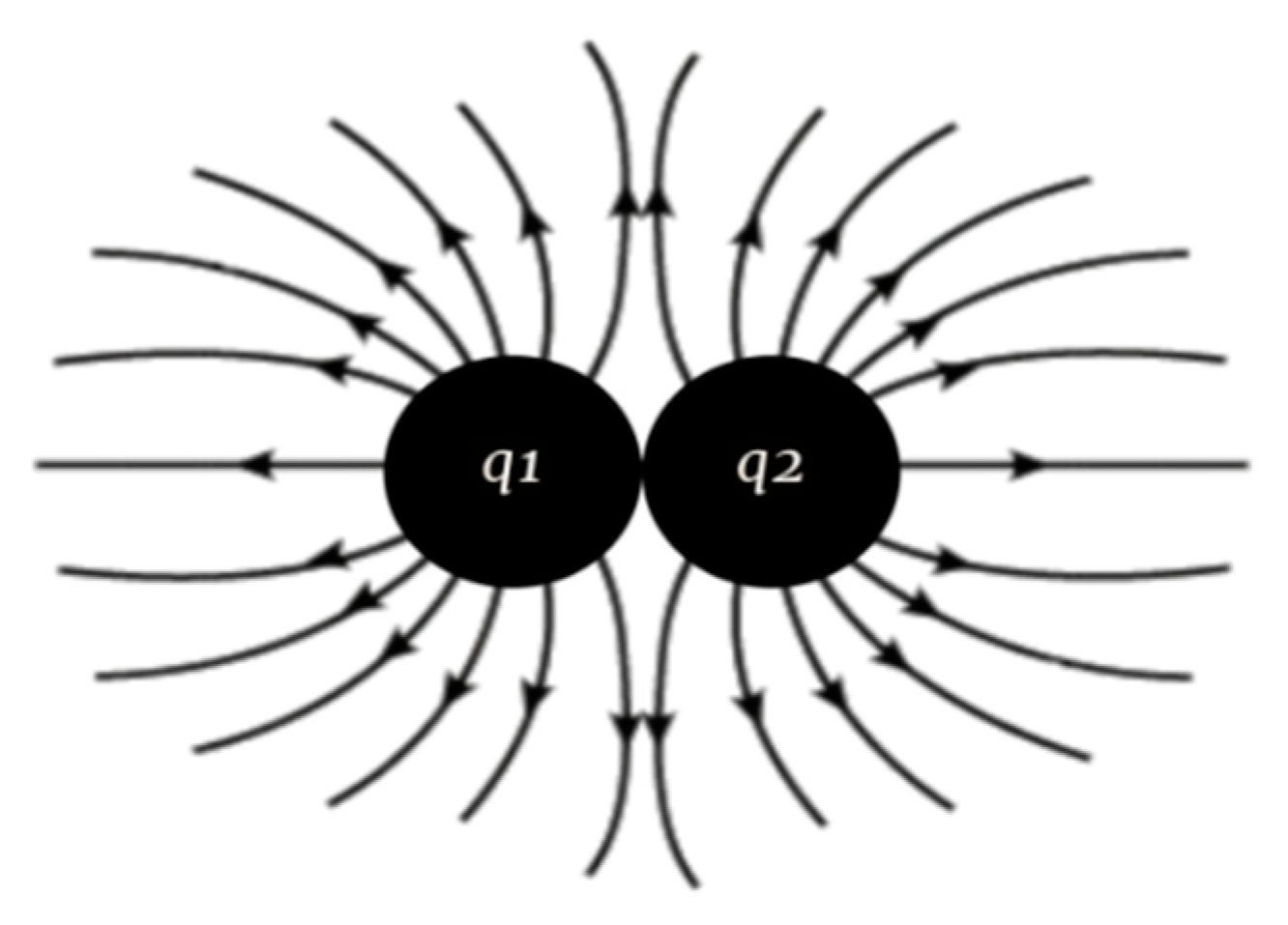
We will start by calculating the classical radius of the electron and proton.

Figure 2.

let's picture Two electrons touch each other, meaning they are separated by one electron diameter. If we assume, for simplicity, that the electron q1 is stationary, the force felt by the second electron

q_{2}

is

F = \frac{m \cdot c^{2}}{r}

(39)

and the force is also equal to the Coulomb force

F_{c} = \frac{q^{2}}{4 \cdot π \cdot ε_{0} \cdot r^{2}}

(40)

We can set the two forces equal and then solve for the electron radius

r_{e}

.

r_{e} = \frac{q_{1,2}^{2}}{4 \cdot π \cdot ε_{0} \cdot m_{e} \cdot c^{2}}

(41)

r_{e} = 2.81794031 \cdot 10^{- 15} m

Now we do the same for the proton radius

r_{p r o .}

(

m_{p r o .}

Not be confused with Planck mass

m_{P}

)

r_{p r o .} = \frac{q_{1,2}^{2}}{4 π \cdot ε_{0} \cdot m_{p r o .} \cdot c^{2}} r_{p r o .} = 1.53469826 \cdot 10^{- 18} m

Now

r_{e} \cdot m_{e} = 2.56696996 \cdot 10^{- 45} k g \cdot m

and

r_{p r o .} \cdot m_{p r o .} = 2.56696996 \cdot 10^{- 45} k g \cdot m

Therefore

r_{e} \cdot m_{e} = r_{p r o .} \cdot m_{p r o .}

(42)

Relation with Planck units

m_{P} \cdot l_{P} = 3.51767293 \cdot 10^{- 43} k g \cdot m

α = \frac{r_{e} \cdot m_{e}}{m_{P} \cdot l_{P}} = \frac{r_{p r o .} \cdot m_{p r o .}}{m_{P} \cdot l_{P}} = \frac{1}{137}

(43)

\frac{r_{e} \cdot m_{e}}{m_{P} \cdot l_{P}} = \frac{r_{p r o .} \cdot m_{p r o .}}{m_{P} \cdot l_{P}} = \frac{e^{2}}{4 π \cdot ε_{0} \cdot ℏ \cdot c}

(44)

after substituting equations (11) and (29)

α = \frac{e^{2} \cdot l_{P}^{2}}{4 π \cdot q_{P}^{2} \cdot t_{P}^{2} \cdot c^{2}}

\frac{l_{P}^{2}}{t_{P}^{2}} = c^{2}

α = \frac{e^{2}}{4 π \cdot q_{P}^{2}}

(45)

Relation with Hubble units

e_{H} = q_{H} \cdot \sqrt{4 π \cdot α}

(46)

α = \frac{e_{H}^{2}}{4 π \cdot ε_{0} \cdot ℏ_{M a x} \cdot c}

after substituting equations (15) and (29)

α = \frac{e_{H}^{2}}{4 π \cdot q_{H}^{2}}

(47)

\frac{e^{2}}{q_{P}^{2}} = \frac{e_{H}^{2}}{q_{H}^{2}}

(48)

\frac{r_{e} \cdot m_{e}}{m_{P} \cdot l_{P}} = \frac{r_{p r o .} \cdot m_{p r o .}}{m_{P} \cdot l_{P}} = \frac{e_{H}^{2}}{4 π \cdot ε_{0} \cdot ℏ_{M a x} \cdot c}

(49)

(50)

Potential Change in the Gravitational Constant

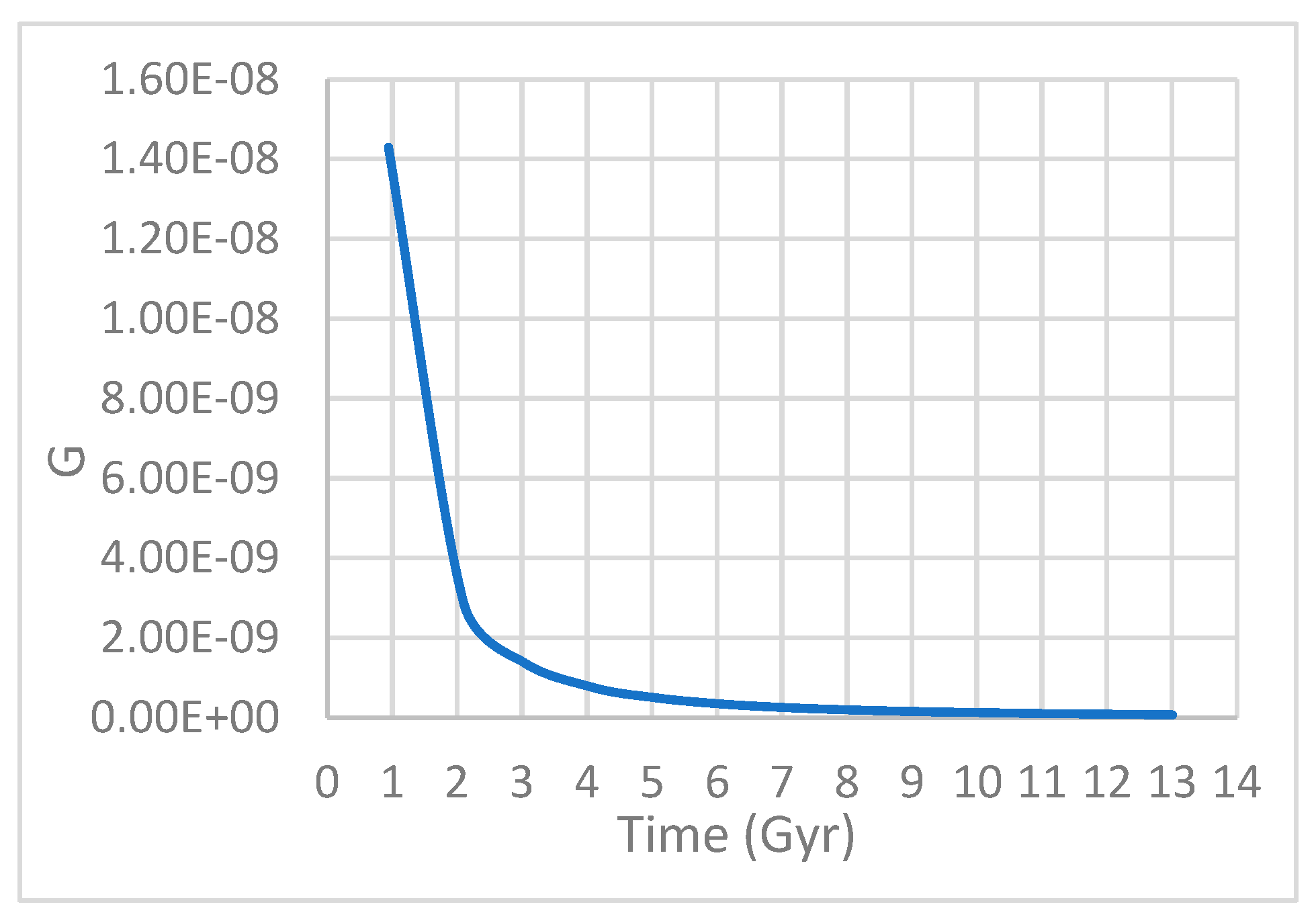
The gravitational clock equation suggests a potential variation in the gravitational constant over time. Assuming the density of the Hubble cube remains relatively constant, we can calculate this change in the gravitational constant.

A change in the gravitational constant, G, has the potential to offer an alternative explanation for dark matter by reevaluating our understanding of this fundamental constant. although this remains a matter of speculation. It is worth investigating further. Unfortunately, I have been unable to locate the necessary data to support this hypothesis through calculations. I hope that experts will test this equation by incorporating a calculated value for G at each specific time when conducting calculations for galaxy rotation curves.

∆ G = \frac{1}{ρ_{H} . {∆ t}_{H}^{2}}

(2)

Figure 3.

Figure 3. shows the decrease of the gravitational constant G from 1 to 13 billion years after the Big Bang (Most of the galaxies in the universe, as we know them today, began to take shape approximately 1 to 2 billion years after the Big Bang [18]).

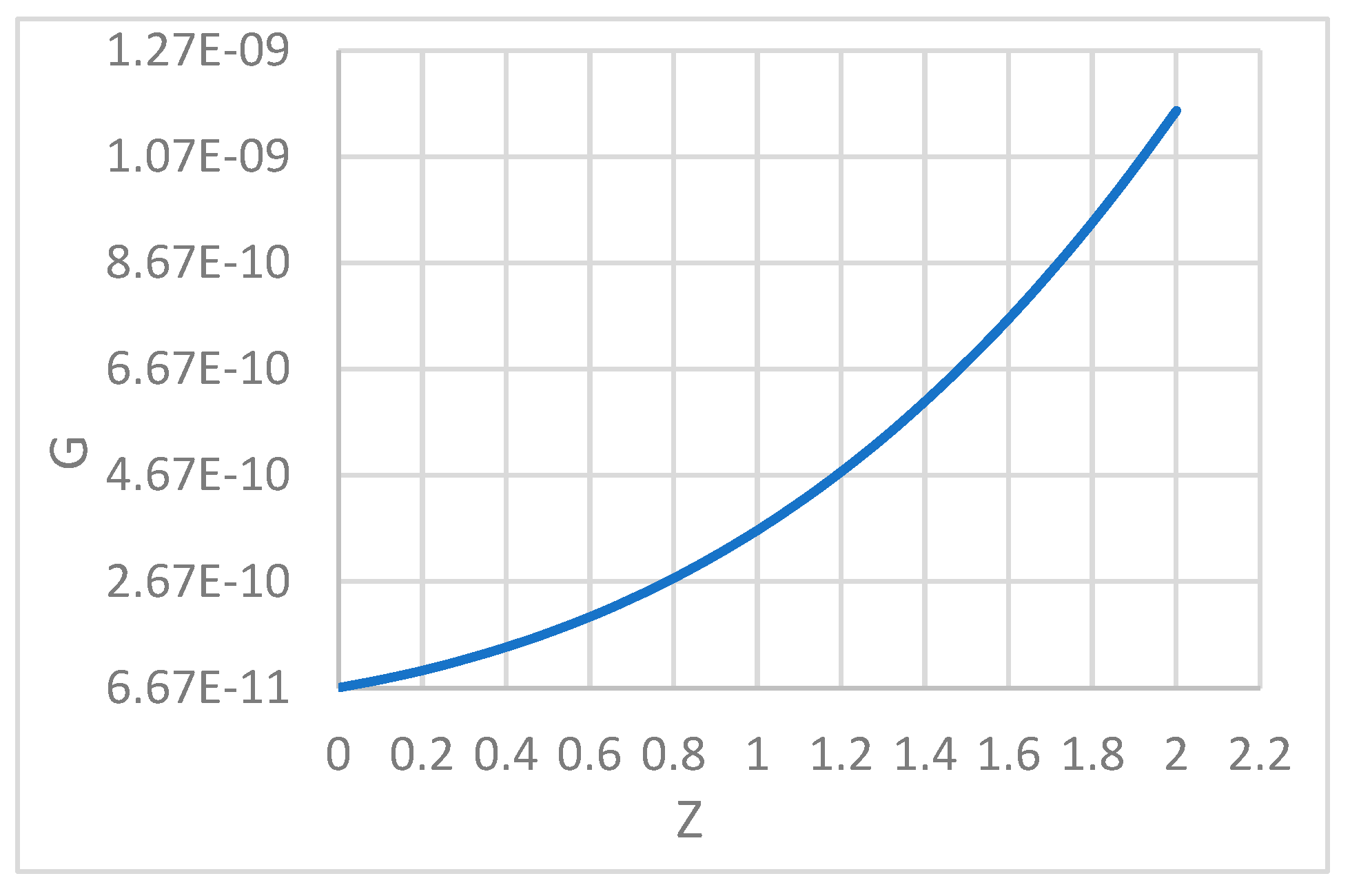
Figure 4.

Figure 4. illustrates the increase in the gravitational constant (G) as Redshift z increases. (Calculated with

Ω_{M} = 0.286, Ω_{V a c} = 0.714 a n d H_{0} = 69.6

).

Figure 4. illustrates the increase in the gravitational constant (G) as Redshift z increases. (Calculated with

Ω_{M} = 0.286, Ω_{V a c} = 0.714 a n d H_{0} = 69.6

).

Calculation of the Hubble Cube Pressure (Energy Density)

Figure 5.

As photons lack both mass and volume, yet carry momentum and can’t directly interact with each other, we can think of them as representations of pure kinetic energy. With this idea, picture a single photon held within the Hubble cube. It has an x-direction in its velocity. (We can refer to it as the velocity of light, considering that we are discussing the phase velocity with which wavefronts propagate. This interpretation is essential to account for the ± sign that arises from the calculations of the speed of light. However, it's important to note that when we shift our focus to the group velocity, we are essentially determining the speed at which intensity propagates.). Keeping in mind that a photon can have a velocity in any direction, that velocity will have X, Y, and Z components. Since they don’t interact, all of them have X, Y, and Z components in their velocity:

c_{x}^{2} = c_{y}^{2} = c_{z}^{2}

Momentum:

ϑ = m \cdot c_{x}

, change in Momentum:

∆ ϑ = 2 \cdot m \cdot c_{x}

Impulse:

I = ∆ ϑ = F \cdot ∆ t

Since the photon is traveling from one end of the interior surface of the Hubble cube to the other end and back, we know that it only happens once every time it travels twice across the length of the cube interior.

F = \frac{∆ ϑ}{∆ t} = \frac{2 \cdot m \cdot c_{x}}{∆ t} \to t = \frac{d}{c_{x}} = \frac{2 L}{c_{x}} \to F = \frac{m \cdot c_{x}^{2}}{L}

this is for only one photon in the

x

direction, but if we take all the photons into account and they all go in different directions, we can say:

c_{x} = c_{y} = c_{z} \to c_{x}^{2} = c_{t o t a l}^{2}

Now we replace

c_{x}^{2}

by

c_{t o t a l}^{2}

\to F = \frac{m \cdot c_{t o t a l}^{2}}{L}

now the pressure (energy density):

Ρ_{H} = \frac{F}{A} = \frac{m \cdot c^{2}}{L \cdot L^{2}} = \frac{M_{H} \cdot c_{t o t a l}^{2}}{V_{H}}

(21)

we plug in the mass

M_{H}

and the volume

V_{H}

of the Hubble cube:

Ρ_{H} = \frac{1.75642709 \cdot 10^{53}}{2.21913302 \cdot 10^{78}} \cdot {(299792458)}^{2} = 7.11357963 \cdot 10^{- 9} P a E_{H} = Ρ_{H} \cdot V_{H} = M_{H} \cdot c^{2}

United Force $F_{M a x}$

If skepticism arises regarding the accuracy of this pressure value, let me introduce a new method for discerning the accuracy and authenticity of most cosmological parameters inside the Hubble cube. using Planck units and the known parameters of the Hubble cube.

F_{M a x} = F_{H} = \frac{M_{H} \cdot R_{H}}{t_{H}^{2}} = \frac{m_{P} \cdot l_{P}}{t_{P}^{2}} = \frac{E_{P}}{l_{P}} = \frac{E_{H}}{R_{H}}

(51)

F_{M a x} = 1.21025556 \cdot 10^{44} N

Now, by simply analyzing the pressure unit (energy density), we can derive an equation to apply the maximum force.

1 P a = \frac{N}{m^{2}} = \frac{F_{M a x}}{R_{H}^{2}} \frac{F_{M a x}}{R_{H}^{2}} = \frac{1.21025556 \cdot 10^{44}}{{(1.30435091 \cdot 10^{26})}^{2}} Ρ_{H} = 7.11357963 \cdot 10^{- 9} P a

Waves Equation

The Newton-Laplace equation [17] is a fundamental concept in physics that originally emerged in the context of acoustics, describing how waves propagate through a medium such as air or water. However, its applicability is not limited to sound; it can also be extended to describe the behavior of light. Given that we have calculated the density and pressure of the Hubble cube, we can apply the wave equation to calculate the speed of light.

c = \sqrt{\frac{P_{H}}{ρ_{H}}} = \frac{7.11357963 \cdot 10^{- 9}}{7.91492477 \cdot 10^{- 26}} = 299792458.1 m \cdot s^{- 1}

(52)

c^{2} = \frac{1}{μ_{0} \cdot ε_{0}} = \frac{P_{H}}{ρ_{H}}

(53)

P_{H} = G \cdot ρ_{H}^{2} \cdot R_{H}^{2}

(54)

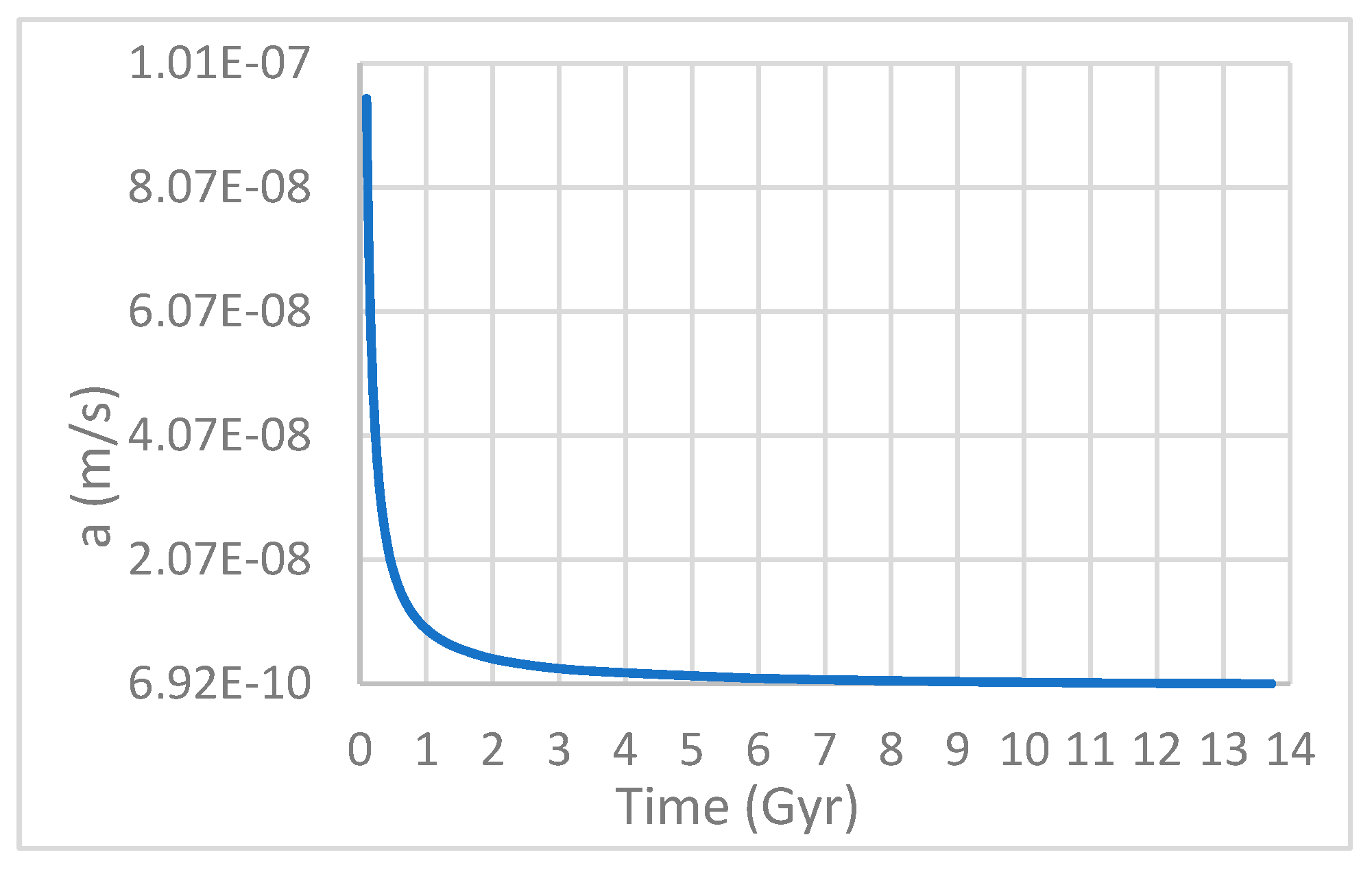
Hubble Acceleration $a_{H}$

a_{H} = \frac{R_{H}}{t_{H}^{2}} = \frac{c}{t_{H}} = \frac{299792458}{4.35084631 \cdot 10^{17}} = 6.89044008 \cdot 10^{- 10} m \cdot s^{- 2}

(27)

Since Planck acceleration is defined as the acceleration from absolute rest to the speed of light in one Planck time [19], Hubble acceleration can be defined as the acceleration from absolute rest to the speed of light in Hubble time. This does not imply that the speed of light is changing, but rather that the direction of the velocity vector changes over time.

And since the Hubble acceleration is decelerating as the universe ages, this might indicate that space was once curved in the early universe, and it's becoming flatter as the universe ages and expands. As a result, light from very distant galaxies might not travel in a perfectly straight line.

Figure 6.

Figure 6. illustrates the decrease (deacceleration) of the Hubble acceleration between 0.1 and 13.7 billion years.

Since the Hubble acceleration is calculated, a new formula can be introduced.

P_{H} = ρ_{H} \cdot R_{H} \cdot a_{H} = ρ_{H} \cdot c^{2} = 7.11357963 \cdot 10^{- 9} P a

(26)

Maximum Force, Energy, and power

Maximum Force

(For both Hubble and Planck scale)

F_{M a x} = m_{P} \cdot a_{P} = M_{H} \cdot a_{H}

F_{M a x} = \frac{ℏ}{l_{P} \cdot t_{P}} = \frac{ℏ_{M a x}}{R_{H} \cdot t_{H}}

F_{M a x} = \frac{E_{P}}{l_{P}} = \frac{E_{H}}{R_{H}}

F_{M a x} = m_{P} \cdot \frac{l_{p}}{t_{P}^{2}} = M_{H} \cdot \frac{R_{H}}{t_{H}^{2}} = 1.21025556 \cdot 10^{44} N

(55)

Maximum Energy

(For the Hubble scale)

E_{M a x} = P_{H} \cdot V_{H} = M_{H} \cdot c^{2}

E_{M a x} = M_{H} \cdot a_{H} \cdot R_{H}

E_{M a x} = ℏ_{M a x} \cdot f = ℏ_{M a x} \cdot \frac{1}{t_{H}} = 1.57859794 {\cdot 10}^{70} J

(56)

Maximum Power

(For both Hubble and Planck scale)

P = F_{M a x} \cdot c = \frac{E_{M a x}}{t_{H}}

P = \frac{F_{M a x} \cdot R_{H}}{t_{H}} = \frac{F_{M a x} \cdot l_{P}}{t_{P}} = \frac{E_{P}}{t_{P}} = 3.62830244 {\cdot 10}^{53} W a t t

(57)

Hubble and Planck Cubes Properties and Similarities

Both the Hubble and Planck cubes are hypothetical concepts. The Planck cube is based on the Planck length

l_{P}

and has a volume of

V_{P} = l_{P}^{3} = 4.2217 \cdot 10^{- 105} m^{3}

.

The Planck length is not the smallest length possible, and there is no reason or evidence to suggest such a claim, just like the Hubble length (radius) is not the longest possible. In 1973, Jacob Bekenstein [20] published a paper in which he showed that the surface area of a black hole increases by

1 A_{P}

for every bit of information which crosses the event horizon.

(1 A_{P} = l_{P}^{2})

The surface area of a sphere is given by

4 π R^{2}

. Therefore, the new surface area is given by

4 π R_{n e w}^{2} = 4 π R_{o l d}^{2} + l_{P}^{2}

Then:

R_{n e w} = \sqrt{R_{o l d}^{2} + \frac{l_{P}^{2}}{4 π}}

Therefore, the change in radius is given by:

δ R = R_{n e w} - R_{o l d} δ R = R_{o l d} \cdot \sqrt{1 + \frac{l_{P}^{2}}{4 π \cdot R_{o l d}^{2}}} - R_{o l d}

We then expand the brackets (since

R_{o l d} ⋙ l_{P}

for any Black hole), such that:

δ R \approx R_{o l d} (1 + \frac{l_{P}^{2}}{8 π \cdot R_{o l d}^{2}}) - R_{o l d}

Therefore:

δ R \approx \frac{l_{P}^{2}}{8 π \cdot R_{o l d}} ≪ l_{P}

Therefore, via Bekenstein’s result, the change in radius of a black hole when 1 bit of information is added is much smaller than 1 Planck length.

The Hubble cube is based on the Hubble length (

R_{H}

) has a volume of

V_{H} = 2.21913302 \cdot 10^{78} m^{3}

. When we look up at the sky, we see light that's, at most, 13.787 billion years old, originating from stars and galaxies now positioned around 46.5 billion light years away. Anything beyond this point is beyond our observational horizon. However, each passing second brings us new, even older light from slightly more distant sources. Consequently, our perspective on the cosmos is continually expanding. All we need to do is be patient and observe as the universe ages, allowing light from more distant places the time it needs to reach us. The Hubble distance sets our observational boundary, and this limit is consistent for all observers, regardless of their location within the universe. From each observer's viewpoint, the observable universe extends to a radius of roughly 13.787 billion light-years.

The Planck length and the Hubble length are both critical in defining observation limits. While the Hubble length sets an upper boundary for what we can observe in the vastness of the cosmos, the Planck length does the same for the subatomic world. Importantly, these limits are consistent for all observers throughout the universe, regardless of their location. And just as the Hubble length doesn't represent the maximum possible distance, the Planck length doesn't signify the smallest conceivable scale. Both of these lengths establish the boundaries of our observations, from the largest cosmic structures to the tiniest quantum realms.

Properties

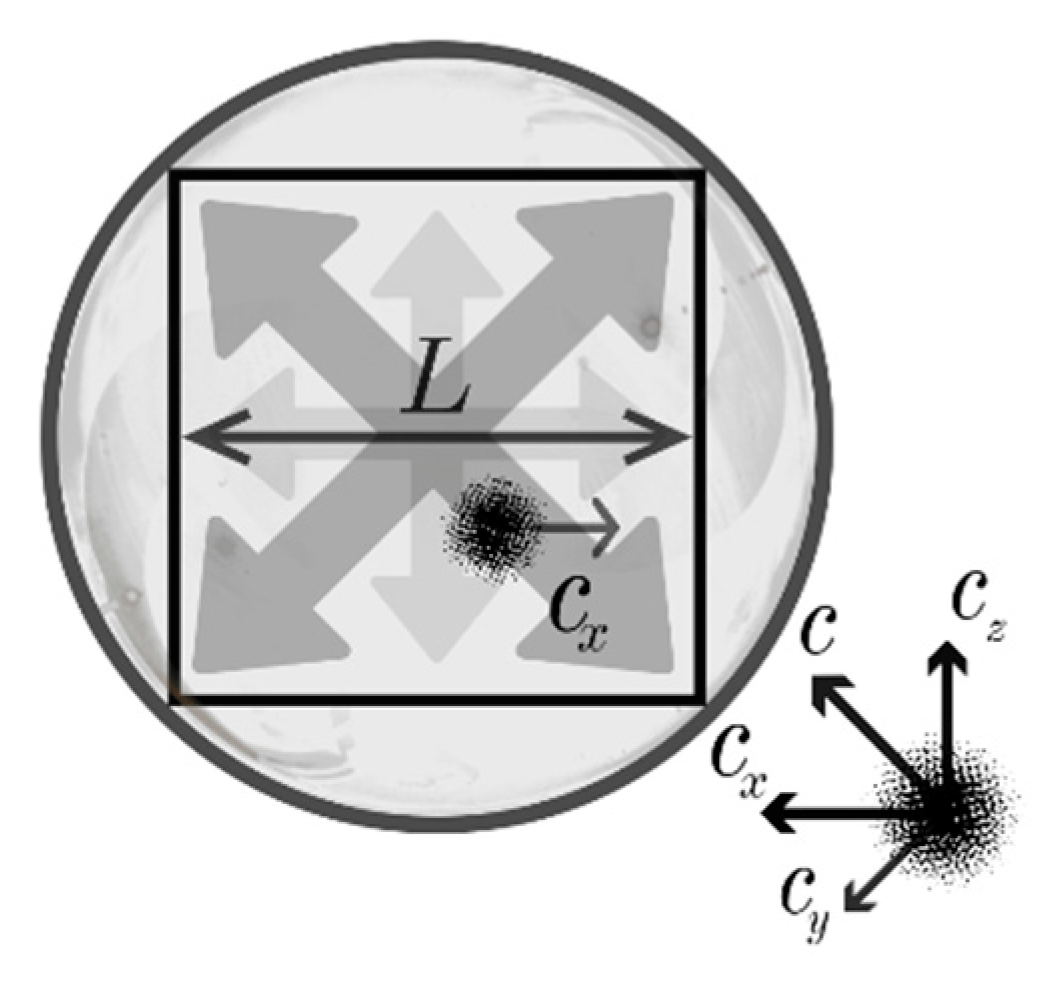
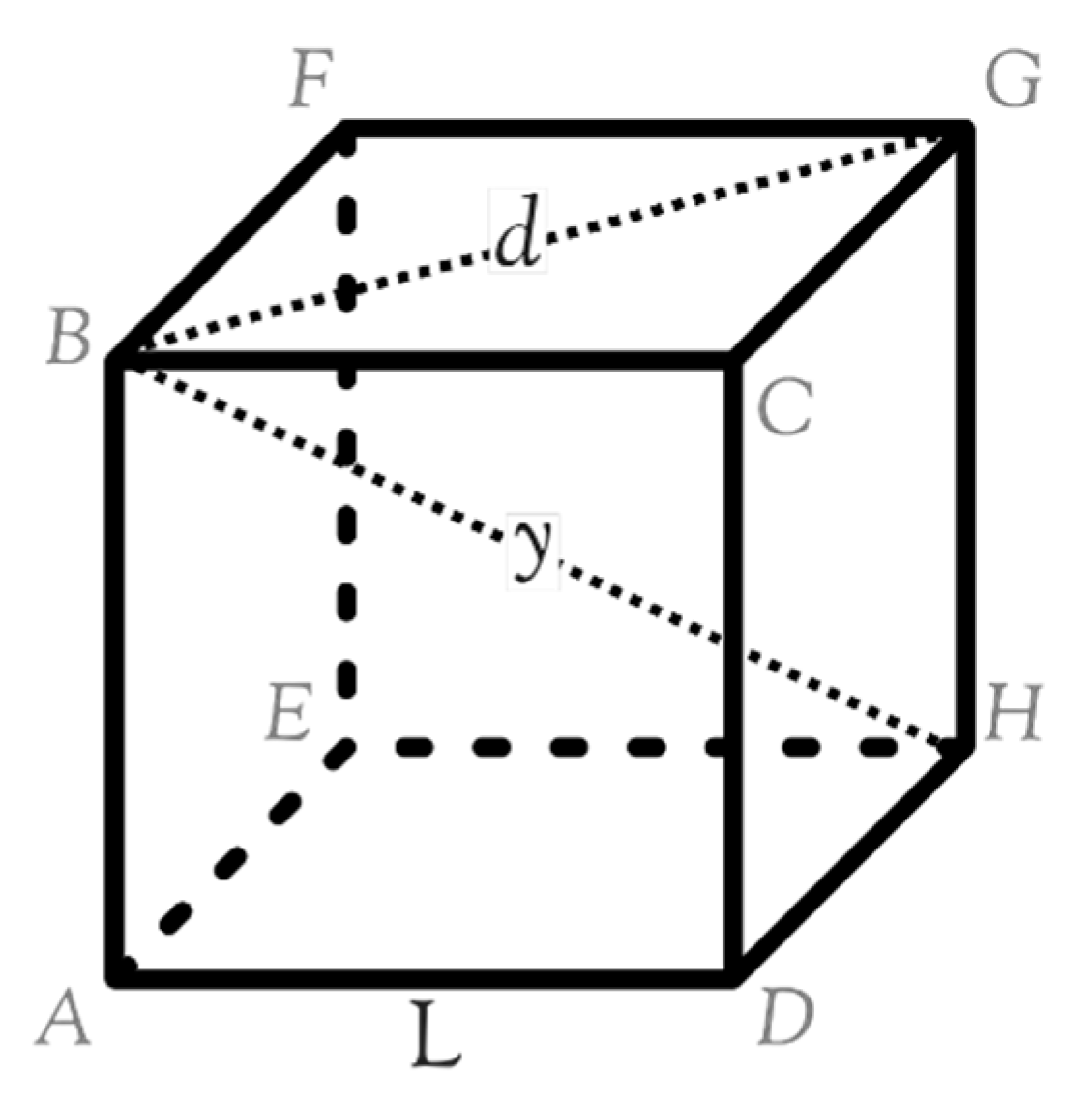
Figure 7.

First, let's calculate the distance between B and G for the Hubble cube (d).

L = L_{H} = R_{H} d_{H}^{2} = L_{H}^{2} + L_{H}^{2} = 2 \cdot L_{H}^{2} d_{H} = \sqrt{2 \cdot L_{H}^{2}} = 1.84463075 \cdot 10^{26} m

Now the diagonal between H and B (y)

y_{H}^{2} = L_{H}^{2} + d_{H}^{2} = L_{H}^{2} + 2 \cdot L_{H}^{2} = 3 L_{H}^{2} y_{H} = \sqrt{3 \cdot L_{H}^{2}} = 2.25920205 \cdot 10^{26} m

Planck Cube

L = l_{P} d_{P} = \sqrt{2 \cdot l_{p}^{2}} = 2.28572977 \cdot 10^{- 35} m y_{P} = \sqrt{3 {\cdot l}_{P}^{2}} = 2.79943581 \cdot 10^{- 35} m

Both the Hubble and Planck Schwarzschild radii (

r_{s_H}

,

r_{s_P}

), are two times bigger than the Hubble and Planck lengths. (This is just to show similarities and does not necessarily mean anything.)

r_{s_H} = \frac{2 \cdot G \cdot M_{H}}{c^{2}} = 2 \cdot R_{H} = \frac{d_{H}^{2}}{R_{H}} r_{s_P} = \frac{2 \cdot G \cdot m_{P}}{c^{2}} = 2 \cdot l_{P} = \frac{d_{P}^{2}}{l_{P}} \frac{r_{s_P}}{l_{P}} = \frac{r_{s_H}}{R_{H}}

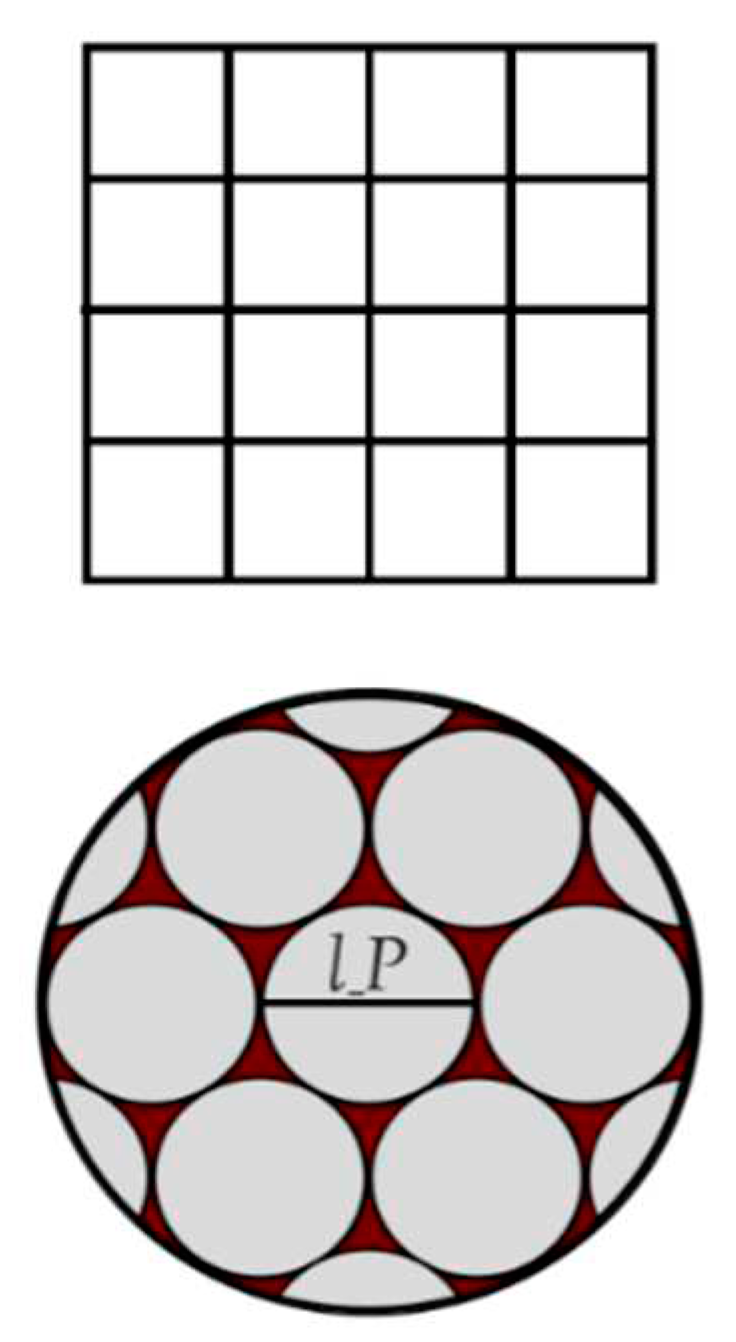
Why the Ultimate Structure of Planck and Hubble Scales Resembles a Cube

The Perpetual Reducibility Dilemma: The universe's capacity for perpetual reducibility presents a fundamental challenge. If the universe were perpetually reducible, every event's occurrence would necessitate an infinitely extended waiting period. This is because even the smallest constituent entity, be it a particle, string, or wave, would need an indeterminately long time to influence larger physical scales, thereby instigating any event.

Non-Existence of a Smallest Particle: The assertion that the universe is perpetually reducible inevitably leads to the conclusion that there is no smallest, indivisible particle, or unit.

Existence of a Fundamental Level: Therefore, it logically follows that the universe must possess a fundamental level of existence, a point beyond which reduction is unattainable, imposing an inherent limit on the divisibility of the cosmos.

The Fundamental Level's Shape: This fundamental level of existence must also possess a specific shape or geometry.

Void less Fundamental Structure: The shape of this fundamental level must exhibit the property of gap-lessness. In other words, it cannot leave voids or gaps between itself and other fundamental points of existence, whether they are larger or smaller than the shape itself. If it were larger, the principle of perpetual reducibility would be violated, and if it were smaller, it would indicate that the chosen shape is not truly fundamental.

Irregular Shapes Contradict Fundamental Nature: Irregular shapes are incompatible with the concept of a fundamental level of existence. Irregular shapes inherently comprise both larger and smaller facets, which undermines the notion of a fundamental, non-reducible structure, as explained in the previous point.

The Necessity of Regularity: Hence, the shape at the fundamental level must be regular. Regular shapes are uniform and do not contain larger or smaller facets, aligning with the concept of a fundamental existence.

The Cube as the Ideal Shape: Considering the requirement for a regular, gapless structure, the cube emerges as the most suitable candidate. The cube is the only solid shape that possesses these characteristics, as it can be stacked infinitely without leaving voids, regardless of the number of cubes stacked.

The Problem with Spherical Fundamental Structures: If the universe's smallest structure is a sphere, a critical issue arises - the presence of gaps. Despite these gaps being smaller than the spheres themselves, they still have volume. This lack of true gaplessness leads to an infinite reduction process, creating a hierarchy of sizes within the universe. This challenges the idea of an indivisible unit. Hence, alternatives like the cube, with its uniformity and gapless arrangement, offer a more fitting solution to the problem of perpetual reducibility.

Relations Between the Planck Scale and the Hubble Scale

r_{H}^{2} \cdot M_{H} \cdot t_{P}^{2} \cdot c^{2} = m_{P} \cdot l_{P} \cdot V_{H} . . V_{H} \cdot m_{P} \cdot t_{P}^{2} = M_{H} \cdot t_{H}^{2} \cdot l_{P}^{3} . . ℏ_{M a x} \cdot l_{P} \cdot t_{P} = ℏ \cdot R_{H} \cdot t_{H} . . m_{P} \cdot t_{P} = l_{P}^{2} \cdot R_{H} \cdot ρ_{H} \cdot t_{H} . . t_{H}^{3} \cdot m_{P} \cdot l_{P}^{2} = r_{H}^{5} \cdot ρ_{H} \cdot t_{P}^{3} . . l_{P} = G \cdot ρ_{H} \cdot r_{H} \cdot t_{H} \cdot t_{P} . . m_{P}^{2} \cdot l_{P}^{2} \cdot G = t_{P}^{2} \cdot ℏ \cdot c^{3} . . l_{P}^{2} = G \cdot c^{2} \cdot t_{H}^{2} \cdot ρ_{H} \cdot t_{P}^{2} . . t_{P}^{2} \cdot r_{H}^{2} \cdot c^{3} = ℏ \cdot G \cdot t_{H}^{2} . . t_{P} \cdot r_{H}^{3} \cdot ρ_{H} = m_{P} \cdot t_{H} . . G \cdot m_{P} \cdot l_{P} = c^{4} \cdot t_{P}^{2} . . M_{H} \cdot l_{P} = m_{P} \cdot R_{H} . . M_{H} \cdot t_{P} = m_{P} \cdot t_{H} . . l_{P} \cdot t_{H} = t_{P} \cdot r_{H}

Conclusion

There exists a profound interrelationship between the gravitational constant (G), the age of the universe (Hubble time), and density (Hubble density).
Likewise, the speed of light (c) is intricately tied to the gravitational constant, density, and the area of the observable universe. The speed of light remains invariably constant, specifically within the Planck and Hubble scales.
The unification equation postulates a profound connection among fundamental constants, including the gravitational constant, vacuum permittivity, and vacuum permeability. It is crucial to note that this equation does not propose a merger of the four fundamental forces of nature but underscores a profound connection among fundamental constants. Beyond offering a fresh perspective on the Law of Universal Gravitation, Coulomb's law for electrostatic force, Coulomb's law of magnetism, and the ratio between these forces, its practical applicability is limited.
The variable constant of the largest quanta, denoted as $ℏ_{M a x}$ , can be conceptualized as the maximum conceivable quantum unit, which escalates with the universe's expansion and aging. $ℏ_{M a x}$ signifies the ultimate unit of action or energy on a cosmic scale, imposing a fundamental boundary on our capacity to acquire knowledge beyond a particular distance.
The Hubble units are the equivalence of Planck units in the sense that they represent the limits of our current understanding of physics, and they are a set of units of measurement defined exclusively in terms of four universal physical constants, in such a manner that these physical constants take on the numerical value of 1 when expressed in terms of these units.
The majority of fundamental constants in nature, such as the speed of light $(c)$ , the gravitational constant $(G)$ , the Boltzmann constant $(K_{B})$ , vacuum permittivity $(ε_{0})$ , and vacuum permeability $(μ_{0})$ , can be derived from Planck and Hubble units.
The fine structure constant $(α)$ can be calculated by multiplying the mass and classical radius of an electron or proton and dividing them by the Planck mass and length, and it can also be determined using $ℏ_{M a x}$ and the Hubble units.
The gravitational clock equation postulates potential weakening of the gravitational constant $(G)$ as the universe ages, under the presumption of constant density. While this remains speculative, it could offer an explanation for phenomena like the early universe's large-scale structure and other observations associated with dark matter Figure 3 and Figure 4.
If the gravitational constant is indeed getting weaker with time, then that would indicate that Planck length and time are both increasing as the universe expands and ages. Planck temperature would decrease, and Planck mass would increase as the universe ages and expands.
The calculation of pressure (energy density) is solely applicable to the Hubble scale (cube) and does not encompass the entire universe's energy density. The calculated pressure can be envisaged as the force exerted by photons on the Hubble cube in all directions.
The Planck force was first proposed by the physicist Max Planck; although it wasn't clear what the meaning or purpose of this force value was, I would propose that this is the maximum force possible for both the Hubble and Planck scales. The new method utilizing the maximum force for verifying the precision and authenticity of values can be a valuable tool for understanding values within and between these two scales.
The wave equation, known as the Newton-Laplace equation, can be employed to compute the speed of light when considering the Hubble cube as a closed system. As the Hubble cube expands, both pressure and density increase proportionally, ensuring the constancy of the speed of light during this expansion.
The Hubble acceleration may indicate that the universe was initially curved in its early stages, subsequently evolving towards a flatter configuration as it expands.
There is profound correlation exists between small and large scales, specifically the Planck and Hubble scales, and their mutual connection is evident.
The Hubble scale does not represent the universe's ultimate scale, just as the Planck scale does not signify the smallest possible scale. Rather, they serve as markers of our observational limitations in this universe, with nature delineating the boundaries of our ability to perceive and understand phenomena beyond these scales.

To test variation in the gravitational constant, I suggest the following simple experiments:

The Torsion Balance Experiment:

The Torsion Balance Experiment could be designed to investigate small changes in the gravitational force. This experiment is formulated with the intent of providing methodology that can be implemented to validate this hypothesis.

Experimental Setup: The experiment employs a Torsion Balance apparatus, which consists of a horizontal bar suspended from a very thin and delicate torsion wire or fiber. Thinner wires are more sensitive to small forces and can detect subtle changes in gravitational force. At each end of the bar, large masses are affixed. Larger masses will result in more significant twists for the same gravitational force, making variations easier to detect. This balance is placed within a controlled environment to minimize external disturbances, such as air currents and vibrations.

Experimental Procedure:

Calibration: Before commencing data collection, the Torsion Balance apparatus is carefully calibrated to establish a baseline measurement of the twist angle corresponding to the known, current value of G.

Environmental Control: The experimental setup is placed in a controlled environment to mitigate external influences. Temperature, humidity, and air currents are carefully regulated.

Data Collection: Over the course of the experiment, continuous measurements of the twist angle are recorded with high precision. These measurements are taken at regular intervals and span an extended period.

Data Analysis: The collected data is subjected to rigorous analysis. Statistical methods are applied to assess the significance of any observed variations in the twist angle. Special attention should be given to identifying trends and patterns in the data.

Key Considerations:

Control Experiments: Control experiments are conducted to account for potential sources of experimental error and external influences. These controls may involve altering environmental conditions or introducing known masses to validate the apparatus's sensitivity.
Data Validation: To ensure data integrity, data validation procedures are implemented, including the identification and elimination of outliers or data artifacts.
Long-Term Monitoring: The experiment extends over an extended duration to increase the statistical significance of any observed variations. Long-term monitoring is essential for detecting gradual changes in G.
Remote Monitoring: To minimize human interference and enable continuous data collection, remote monitoring and data transmission capabilities have to be incorporated. This feature facilitates uninterrupted data acquisition over extended durations.

Simple Pendulum Experiment:

f = \frac{1}{2 \cdot π} \cdot \sqrt{\frac{g}{L}}, g = \frac{G \cdot M_{E a r t h}}{R_{E a r t h}^{2}}, f = \frac{1}{2 \cdot π} \cdot \sqrt{\frac{M_{E a r t h}}{L (R_{E a r t h}^{2} \cdot ρ_{H} \cdot t_{H}^{2})}}

Measurement Principle: The experiment leverages the principles of pendulum motion and gravity. Variations in G could potentially influence the frequency of the oscillation over time.

Pendulum Setup: One end of the string is attached to the heavy weight, and the other end is secured to a stable support structure, such as a hook or a ceiling anchor. The length of the string remains consistent throughout the experiment.

Initial Measurement: The length of the pendulum is measured accurately, and this initial length is recorded.

Vacuum Chamber Setup: The entire pendulum apparatus, including the weight and string, is placed inside the vacuum chamber.

Evacuation of Air: The vacuum chamber is used to remove air from the environment, creating a near-perfect vacuum inside the chamber. This step eliminates air resistance, allowing the pendulum to swing without interference.

Pendulum Swing: The weight is slightly displaced to one side and released to initiate the pendulum's motion. It swings freely back and forth within the vacuum chamber.

Time Measurement: A stopwatch or timer is used to measure the time it takes for the pendulum to complete one full oscillation.

Data Recording: The time taken for the pendulum to complete each oscillation is recorded. The experiment is repeated multiple times to ensure accuracy.

Extended Observations: Over an extended period, the experiment is periodically repeated within the vacuum chamber, and the time taken for the pendulum to complete one oscillation is recorded.

Analysis: The inclusion of a vacuum chamber in the Simple Pendulum Experiment serves to eliminate air resistance, enhancing the accuracy of the experiment. This improved setup still provides a basic exploration of gravity's changes over time. Since gravity is weakening over time, the period of the pendulum will gradually increase.

If a consistent and gradual increase in the pendulum's period is observed over an extended period within the vacuum chamber, it suggests a weakening of gravity. However, this experiment, even with the vacuum chamber, offers a simplified and indirect way to assess this phenomenon.

Key Considerations:

While the vacuum chamber eliminates air resistance, other factors such as temperature fluctuations, vibrations, and equipment stability could still affect the pendulum's period. This experiment provides a basic introduction to weakening gravity. For more precise assessments of variations in G, sophisticated experiments and instruments are required.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

References

Wikipedia contributors. (2023, September 6). Newton's law of universal gravitation. In Wikipedia, The Free Encyclopedia. Retrieved 08:01, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Newton%27s_law_of_universal_gravitation&oldid=1174047566.
Wikipedia contributors. (2023, September 6). Dirac large numbers hypothesis. In Wikipedia, The Free Encyclopedia. Retrieved 14:30, September 17, 2023, from https://en.wikipedia.org/w/index.php?title=Dirac_large_numbers_hypothesis&oldid=1174190426].
Wikipedia contributors. (2022, September 15). Nordström's theory of gravitation. In Wikipedia, The Free Encyclopedia. Retrieved 14:43, September 17, 2023, from https://en.wikipedia.org/w/index.php?title=Nordstr%C3%B6m%27s_theory_of_gravitation&oldid=1110420553.
Wikipedia contributors. (2023, January 9). Brans–Dicke theory. In Wikipedia, The Free Encyclopedia. Retrieved 14:42, September 17, 2023, from https://en.wikipedia.org/w/index.php?title=Brans%E2%80%93Dicke_theory&oldid=1132599971.
Wikipedia contributors. (2023, September 1). String theory. In Wikipedia, The Free Encyclopedia. Retrieved 14:42, September 17, 2023, from https://en.wikipedia.org/w/index.php?title=String_theory&oldid=1173220557.
Date: Submitted on 23 Oct 2005 , Author: Forough Nasseri https://arxiv.org/abs/hep-th/0510197.
Date: Submitted on 12 Jan 2022, author: Ekim Taylan Hanımeli, Isaac Tutusaus, Brahim Lamine, Alain Blanchard https://arxiv.org/abs/2201.04629.
Wikipedia contributors. (2023, September 17). Speed of light. In Wikipedia, The Free Encyclopedia. Retrieved 15:04, September 17, 2023, from https://en.wikipedia.org/w/index.php?title=Speed_of_light&oldid=1175742254.
Wikipedia contributors. (2023, September 22). Planck constant. In Wikipedia, The Free Encyclopedia. Retrieved 10:59, October 18, 2023, from https://en.wikipedia.org/w/index.php?title=Planck_constant&oldid=1176562206.
Wikipedia contributors. (2023, August 17). Observable universe. In Wikipedia, The Free Encyclopedia. Retrieved 08:22, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Observable_universe&oldid=1170823348.
Wikipedia contributors. (2023, August 17). Age of the universe. In Wikipedia, The Free Encyclopedia. Retrieved 10:56, August 29, 2023, from https://en.wikipedia.org/w/index.php?title=Age_of_the_universe&oldid=1170877571.
Wikipedia contributors. (2023, September 17). Gravitational constant. In Wikipedia, The Free Encyclopedia. Retrieved 08:39, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Gravitational_constant&oldid=1175794859.
Wikipedia contributors. (2023, August 30). Planck units. In Wikipedia, The Free Encyclopedia. Retrieved 08:43, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Planck_units&oldid=1172970096.
Wikipedia contributors. (2023, August 10). Permittivity. In Wikipedia, The Free Encyclopedia. Retrieved 08:45, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Permittivity&oldid=1169723635.
Wikipedia contributors. (2023, August 22). Vacuum permeability. In Wikipedia, The Free Encyclopedia. Retrieved 08:46, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Vacuum_permeability&oldid=1171639696.
Wikipedia contributors. (2023, September 16). Coulomb's law. In Wikipedia, The Free Encyclopedia. Retrieved 08:49, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Coulomb%27s_law&oldid=1175631940.
Wikipedia contributors. (2023, September 7). Acoustic wave equation. In Wikipedia, The Free Encyclopedia. Retrieved 08:53, September 18, 2023, from https://en.wikipedia.org/w/index.php?title=Acoustic_wave_equation&oldid=1174343619.
https://www.nasa.gov/universe/back-to-the-beginning-probing-the-first-galaxies-with-webb/#:~:text=%E2%80%9CGalaxies%2C%20we%20think%2C%20begin,1%20to%202%20billion%20years.
https://en.wiktionary.org/wiki/Planck_acceleration.
Author: Jacob D. Bekenstein, Date: 15 April 1973 https://journals.aps.org/prd/abstract/10.1103/PhysRevD.7.2333.
Wikipedia contributors. (2023, September 22). Force between magnets. In Wikipedia, The Free Encyclopedia. Retrieved 11:00, October 22, 2023, from https://en.wikipedia.org/w/index.php?title=Force_between_magnets&oldid=1176567492.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Quantum-Cosmos Nexus Theory

Abstract

Keywords:

Subject:

Introduction

Method

Density of the Hubble Cube $ρ_{H}$

Planck units' relationship with the Hubble parameters

Reduced Planck constant integration

Largest Quanta $ℏ_{M a x}$

Gravitational constant derivation from Planck's units and Hubble units

Derivation of vacuum permittivity $ε_{0}$ [14], vacuum permeability $μ_{0}$ [15], and speed of light from Planck units [13] and Hubble Units

Boltzmann constant derivation from Planck units and Hubble units

Unification Equation Application

Potential Change in the Gravitational Constant

Calculation of the Hubble Cube Pressure (Energy Density)

United Force $F_{M a x}$

Waves Equation

Hubble Acceleration $a_{H}$

Maximum Force, Energy, and power

Hubble and Planck Cubes Properties and Similarities

Conclusion

Key Considerations:

Key Considerations:

Supplementary Materials

References

MDPI Initiatives

Important Links

Subscribe

Quantum-Cosmos Nexus Theory

Abstract

Keywords:

Subject:

Introduction

Method

Density of the Hubble Cube ρ H

Planck units' relationship with the Hubble parameters

Reduced Planck constant integration

Largest Quanta ℏ M a x

Gravitational constant derivation from Planck's units and Hubble units

Derivation of vacuum permittivity ε 0 [14], vacuum permeability μ 0 [15], and speed of light from Planck units [13] and Hubble Units

Boltzmann constant derivation from Planck units and Hubble units

Unification Equation Application

Potential Change in the Gravitational Constant

Calculation of the Hubble Cube Pressure (Energy Density)

United Force F M a x

Waves Equation

Hubble Acceleration a H

Maximum Force, Energy, and power

Hubble and Planck Cubes Properties and Similarities

Conclusion

Key Considerations:

Key Considerations:

Supplementary Materials

References

MDPI Initiatives

Important Links

Subscribe

Density of the Hubble Cube $ρ_{H}$

Largest Quanta $ℏ_{M a x}$

Derivation of vacuum permittivity $ε_{0}$ [14], vacuum permeability $μ_{0}$ [15], and speed of light from Planck units [13] and Hubble Units

United Force $F_{M a x}$

Hubble Acceleration $a_{H}$