A Feasible Proposal for Energy-Efficient Roof Retrofitting in Southern European Obsolete Residential Neighborhoods

1960s Europe saw a large number of residential neighborhoods built to house those migrating from the countryside. Today, more than 50 years later, these neighborhoods suffer high levels of functional, social, and technical obsolescence. In response to this, University of Seville developed the Aura Strategy as an intervention methodology to find global solutions to issues in outdated neighborhoods. To provide visibility to this aspect of the Aura strategy, the retrofit proposal presented in this article provides a solution to improve the roofing of buildings in a case study neighborhood (Polígono de San Pablo, Seville) and an analysis of the results in terms of energy and financial savings for local residents. The results show that for a population of roughly 18,000 (in 2018), net savings, including energy and retrofitting costs, ranging from nearly 6.5 to over 8.6 million can be made over the 20-year life cycle span. Likewise, the results obtained on the reduction of thermal loads indicate a 72% decrease in energy consumption, equivalent to a saving of close to 4,500 tons of greenhouse gas emissions for the district and the entire life cycle time period, with the consequent benefits on the impact on air quality and and the fight against climate change. climate change.

Keywords:

Subject: Engineering - Architecture, Building and Construction

1. Introduction

The neighborhoods built in Europe during the 1950s and 1960s in response to the mass migration of workers from the countryside to cities need rehabilitation. To do so, architectural retrofitting should be considered rather than demolition or new construction. To reduce the carbon footprint of the process, the intervention strategy in these outdated neighborhoods should be based on methodologies that enable the refurbishment and transformation of buildings through the conservation and reuse of the existing urban fabric instead of demolition and the generation of new buildings. This is the intervention methodology proposed by the Aura strategy. This strategy has been developed by a group of researchers from the University of Seville and has been tested in various editions of the Solar Decathlon competition [1,2]. It is currently being applied in the Polígono San Pablo neighborhood within the framework of the “Direct application of the SOLAR DECATHLON-U.S Team Aura Strategy in the rehabilitation of obsolete Andalusian neighborhoods” research project financed by the regional government of Andalusia, Spain. The Aura strategy is an “urban acupuncture strategy” that proposes a gradual requalification of social identity, material, and energy, ensuring an effective improvement in the health and comfort of residents, leading to an increase in quality of life. The Aura Strategy proposes actions centered on four lines of intervention. These are:

Comfort and Health
Materiality
Cultural Identity and Accessibility
Retrofitting and energy

This article examines the line of MATERIALITY and centers on one of the most evident weaknesses present in the buildings of this case study neighborhood: ROOFS. The aim of this research is to use a dynamic time dependent analysis of the energy and economic variables of the life cycle time span and to propose and assess a retrofit solution for the roofing of the buildings in the neighborhood of Polígono de San Pablo. This refurbishment solution is implemented with the purpose of reducing the energy consumption required to provide thermal comfort conditions in homes on the top floor, with the consequent benefits in the reduction of energy poverty, which has such a strong impact on the social context under study, while at the same time, through the consequent reduction of greenhouse gases, it implies important benefits for air quality and the fight against climate change.

1.1. Passive Roofs Strategies

On a typical hot sunny day in the summer, as usually are under mediterranean climate conditions, building rooftop surfaces can be

27 - 50^{\circ}

C hotter than the surrounding air temperature [3], which means that the heat transmitted by convection to the surrounding air and by thermal radiation to taller buildings can be very significant and contributes to urban heating and the so-called Urban Heat Island effect. Therefore, reducing the temperature of the rooftop influences the improvement of the quality of the urban environment [4] at the same time that it reduces the cooling loads necessary to obtain internal thermal comfort conditions [5], which in turn reduces the rejection of heat from heating systems, further strengthening the urban heat island while producing a decrease in greenhouse gas emissions through the reduction of energy consumption.

A large body of research has been conducted for generating strategies for roof heat mitigation with multiple approaches among which passive strategies are especially interesting in the context of this work.

The role of the inclination and orientation of the rooftop was analyzed in [6] for lightweight and heavyweight roofs, equipped or devoid of an insulation material during the cooling period in Italy and Greece.

Different insulation materials in arid zones were studied in [7] where four different structures to cool the roof in Jordania were analyzed and it was found that clay thermal insulation over the roof provided the best results for cooling of building for better comfort conditioning in arid areas

Authors in [8] concluded using thermal models developed using Energy Plus that the application of cool roofs results to

17 %

reduction in the annual cooling demand for the case study building at the urban region of Acharnes municipality in Greece.

In [9] it was explored the potential energy savings of using dynamic cool roofs (DCRs) with seasonally variable reflective surface for various building prototypes when compared to static cool roofs; they found that when a variable reflective costing is applied to low insulation buildings, source energy savings can be achieved and range from 4.33 to 19.44 MJ/m² (i.e.,

1.6 - 4.9 %

) for residential units and from 1.17 to 18.00 MJ/m² (i.e.,

0.3 - 3.9 %

) for offices.

In [10] it was used building energy simulation to isolate how improvements in rooftop radiative properties impacts surface temperatures and heat fluxes and concluded that increasing rooftop solar reflectance from 0.2 to 0.96, while fixing emissivity at 0.9, results in a mean reduction in the rooftop temperature of about

10^{\circ}

In [11] it was analyzed the effect of the installation of an innovative cool clay tile on the rooftop of historic residential buildings in central Italy and found maximum primary energy saving for cooling about

51 %

,while heating energy penalty was slower than

2 %

Ventilated roof is proposed and implemented in [12] as a passive cooling technique that allows environmental heat sinks such as night ventilation and evaporative cooling. Energy impact analysis showed that implementing the ventilated roof solution can reduce cooling needs by

65 %

without a resulting heating penalty.

In [13] different urban surface parameters were evaluated from several perspectives to assess their comparative effectiveness as heat mitigation strategies and concluded that roofs with high albedos are found to be the best heat mitigation for reducing daytime temperatures (0.85 albedo,

1 . 29^{\circ}

C) while green roofs show the best nighttime efficacy

(100 %, 1 . 15^{\circ}

C).

Diurnal Selective Radiative Cooling based in roof panels RC roofs were studied in [14] where it was found that in terms of surface temperature, RC panels outperformed high performance cool roofs, but in terms of anthropogenic heat reduction and microclimate air temperature reduction, they both had a similar impact.

On the other hand, in the framework of the Mediterranean climate one of the proven effective measures to save cooling energy is through the use of a suitable combination of thermal insulation and a rooftop coatings highly reflective of solar radiation; this combination, when well designed, has proven to provide significant savings energy to get thermal indoor comfort and to be cost-efficient [15,16]. This combination of thermal insulation and cool coating is the constructive solution used here to retrofit the roof of the case study buildings considered in this work.

1.2. The Case Study Approach

Construction of the Polígono de San Pablo began in year 1961. Around 57,000 people were expected to live there, divided into five districts (A,B,C,D,and E), each with 2000 homes Figure 1. This research aims to quantify the relevance of planning a comprehensive intervention that covers all five districts of the neighborhood.

The neighborhood includes different types of 4, 8 and 12 story residential buildings. Among these, there are 707 free-standing buildings and an estimated 112,000 m² of roof area, Figure 2. Considering that most building types are two homes per floor, 1414 homes will benefit directly from this intervention. In other words, all of the top-story homes in each retrofitted building.

2. Materials and Methods

2.1. Methodology for Energy Computation

This section outlines the methodology followed to evaluate the thermal energy crossing the roof. First, the physical assumptions are presented, then the associated mathematical equations are shown, and finally, the aging effect for the retrofitted roof and its practical implementation are described.

2.1.1. Physical Framework

In this section, the physical framework involving the heat flux through the roof is described. Specifically, thermal flux through the roofs is determined by the following:

Thermal gains due to solar radiation impacting the roof’s outer surface.
Infrared radiative heat transfer between the roof’s outer surface and the open sky and taller buildings.
Convective heat transfer between the roof’s exterior surface and the surrounding air.
Conduction-based thermal transfer within the roof’s multiple layers.
Convective heat transfer between the roof’s interior surface and the indoor air.
Infrared radiative heat transfer between the roof’s inner surface and the room indoor surfaces.

Section 2.2.2 provides details on how to compute the solar radiation absorbed by the roof’s outer surface. This result is based on the solar radiation values obtained from climatic data, such as the Energy Plus Weather (EPW) files, or from monitoring data that are entered into the model. When computing the solar radiation gain, it is important to consider the absorptivity of the outer surface. As it is subject to the so-called ageing effect, it is non-constant in time. The pattern of change in the solar absorptivity of the outer surface of the roof is described in Section 2.3.

The radiative heat exchange between the outer surface of the roof and the sky is computed by calculating the downward horizontal infrared radiation intensity through the use of the sky emissivity as described in Section 2.2.3.

The convective heat transfer between the outer surface of the roof and the surrounding air is calculated by a two-fold approach: on the one hand, using convective heat transfer correlations to calculate the energy balance on the outer surface of the roof, and, on the other hand, by calculating the thermal boundary layer of the air on the roof. Both procedures are described in Section 2.2.4.

To estimate the heat transfer by conduction through the different layers of the roof, the physical model is based on the models of thermal conduction through a multilayer wall considering the different thermophysical values of each layer that makes up the roof as described in Section 2.2.5.

Finally, the infrared radiative and convective heat transfer between the roof’s inner surface and the building indoor is carried out using a combined convective-radiative transfer coefficient applied to the energy balance on the inner roof surface as described in Section 2.2.5.

2.2. Mathematical Formulation

In this section, drawing on the physical principles established in the earlier section, we bring forth the mathematical equations relevant to heat transfer across the roof.

2.2.1. Energy Balance on the Outer Roof Surface

As a result of the energy processes taking place on the outer surface of the roof listed in Section 2.1.1, an energy balance is produced on that surface. This balance can be represented by the equation:

κ \frac{\partial T_{S_{e x t}}}{\partial \vec{n}} + {\dot{q}}_{c o n v, e x t} + {\dot{q}}^{S W} + {\dot{q}}^{L W} = 0

where

\vec{n}

is the outward normal vector to the roof external surface

S_{e x t}

;

κ

is the conductivity of the material composing

S_{e x t}

, and

T_{S_{e x t}}

is the temperature on surface

S_{e x t}

;

{\dot{q}}_{c o n v, e x t}

is the intensity of convective heat flux between

S_{e x t}

and the ambiance air;

{\dot{q}}^{S W}

is the intensity of the solar radiation flux reaching

S_{e x t}

and

{\dot{q}}^{L W}

represents the balance of thermal radiation between

S_{e x t}

and the sky and surroundings.

2.2.2. Absorbed Solar Radiation Calculation

Regarding solar radiation, a relevant quantity for the computation of the thermal flux through the roof is the quantity of solar energy absorbed by the roof surface facing outward, that is computed here as:

\begin{matrix} {\dot{q}}^{S W} = α^{S W} \cdot (I_{b} \cdot c o s (θ) \cdot \frac{S_{s}}{S_{r o o f}} + I_{s d} \cdot F_{r s} + I_{g d} \cdot F_{r g} + I_{r n} \cdot F_{r n}), [W / m^{2}] \end{matrix}

(1)

where

α^{S W}

represents the solar absorptance coefficient of the roof’s outermost layer,

θ

denotes the solar beam’s angle of incidence on the roof,

I_{b}

is the intensity of the normal direct solar radiation,

S_{s}

is the sunlit area of the external roof surface,

S_{r o o f}

is the entire roof area,

I_{s d}

and

I_{g d}

are the reflected diffuse solar radiation intensity from the sky and the ground,

F_{r s}

is the view factor roof-sky,

F_{r g}

is the view factor roof-ground,

I_{r n}

represents the intensity of radiation reflected by the nearby buildings or any other vertical object such as trees, and

F_{r n}

represents the view factor between the roof and the neighboring objects.

When there are no structures or shading elements surpassing the specified roof in height,

F_{r s}

and

F_{r g}

are given by

F_{r s} = \frac{1 + c o s (φ)}{2}, F_{r g} = \frac{1 - c o s (φ)}{2}

where

φ

is the angle that defines the tilt of the roof plane relative to the horizontal plane. In the case of an unshaded horizontal flat roof,

φ

is equal to 0 and Equation (1) becomes

{\dot{q}}^{S W} = α^{S W} \cdot I_{H}, [W / m^{2}],

(2)

where

I_{H}

is the intensity of the global horizontal solar radiation reaching the roof that is given by

I_{H} = I_{b} \cdot c o s (θ) + I_{s d} .

(3)

2.2.3. Long-Wave Radiative Exchange with the Sky

The long-wave radiative exchange between the external roof surface and the sky is calculated using the expression

{\dot{q}}^{L W} = {\dot{Q}}_{s k y}^{L W} - \dot{Q} {L W}_{w}

where

{\dot{Q}}_{w}^{L W}

is the intensity of the thermal long-wave radiation emitted by the external roof surface and

{\dot{Q}}_{s k y}^{L W}

is the sky downwelling long-wave radiation.

{\dot{Q}}_{w}^{L W}

is calculated using the Stefan-Boltzmann law:

{\dot{Q}}_{w}^{L W} = ϵ_{w} σ T^{4}

(4)

where

ϵ_{w}

and T are the emissivity and the temperature in Kelvin degrees of the external surface of the roof, and

σ

is the Stefan-Boltzmann constant given by

σ = 5.67 \cdot 10^{- 8} [W / m^{2} K^{4}]

To compute the sky downwelling long-wave radiation

{\dot{Q}}_{s k y}^{L W}

, following [17,18] the correlation used is:

{\dot{Q}}_{s k y}^{L W} = ϵ_{s k y} σ T_{e x t}^{4},

(5)

where

ϵ_{s k y}

is the sky emissivity and

T_{e x t}

is the ambiance dry-bulb temperature in Kelvin degrees. From the same references [17,18],

ϵ_{s k y}

is computed by

\begin{matrix} ϵ_{s k y} = (. 787 + . 764 ln (\frac{T_{d p}}{273})) (1 + \frac{224}{10^{4}} n - \frac{35}{10^{4}} n^{2} + \frac{28}{10^{5}} n^{3}) \end{matrix}

where n is the opaque sky cover in tenths and

T_{d p}

is the dew point temperature in kelvin degrees. This approach is the same used by some well known software of Building Energy Simulation as Energy Plus [19].

2.2.4. Heat Exchange between the Roof and the Ambiance Air

The heat exchange between the roof and the ambiance air,

{\dot{q}}_{c o n v, e x t}

in Equation (2.2.1), is one of the processes that most affect the thermal behavior of the roof, hence the need to explore ways to ensure the accuracy of the calculation of this process.

In this work two ways of estimate

{\dot{q}}_{c o n v, e x t}

have been analyzed. The first is a typical approach based in the use of convective heat transfer coefficients

h_{c o n v, e x t}

. The coefficient

h_{c o n v, e x t}

used here is based in the work of Hagishima and Tanimoto [20] and was obtained from experimental measurements on building roofs. The obtained correlation was;

h_{c, e x t} = 8.18 + 2.28 V_{R} [W / m^{2} K],

(6)

where

V_{R}

expresses the wind velocity above the roof, measured in meters per second. Then, the convective heat flux is given by

{\dot{q}}_{e x t} = h_{c, e x t} (T_{e x t} - T_{S_{e x t}}), {[W / m}^{2}] .

(7)

In the second approach used to estimate the heat exchange between the roof and the ambiance air no external convective heat transfer coefficient has been used. Instead, the air flow over the roof has been modeled using the Navier–Stokes thermodynamic equations together with a turbulence modeling using the well known

κ - ε

model. From these equations the velocity and temperature of the air in the boundary layer adjacent to the outer surface have been determined. Then, the value thus calculated for the air temperature in the zone of the thermal boundary layer closest to the roof surface is the one used to determine the heat exchange

{\dot{q}}_{e x t}

To carry out this modeling of the air flow over the roof, a parabolic air profile, used in energy performance of buildings [21], has been considered in the input of the calculation domain:

V (h) = V_{r} {(\frac{h}{h_{r}})}^{γ} (m / s)

(8)

In this equation,

V (h)

represents the wind velocity at height h,

V_{r}

denotes the wind speed measured at the reference altitude

h_{r}

, and

γ

is a coefficient that varies depending on the local orographic and roughness characteristics.

The remaining border conditions for air velocity are non-slip velocity on the outer roof surface, slip condition on the top of the domain and finally free outflow in the outlet boundary surface.

2.2.5. Heat Conduction through the Roof

The conduction of heat through the roof can be modeled as a specific case of diffusion through a multilayer wall [22] and employing boundary conditions as defined by the energy balance equations for both the exterior and interior surfaces of the roof.

The boundary conditions for the roof outer surface are described in Section 2.2.1 and Section 2.2.4.

Regarding the roof’s interior surface, when conducting the energy balance analysis for this surface, a mixed convective-radiative transfer coefficient

h_{c o n v, r a d}

was used. Here, following the values recommended by [23], the values considered for this coefficient were

h_{c o n v, r a d} = 9.26 [W / m^{2} K]

for upward heat flux and

h_{c o n v, r a d} = 6.13 [W / m^{2} K]

for downward heat flux.

Finally, the model approximation for the simulation of the heat through the roof is the model for heat conduction through a multilayer wall introduced in [24] which is based on an approximation that takes into account specific continuity conditions between layers for temperature and heat flux.

2.3. Changes in Cool Roof Reflectivity due to Aging

It has been established in previous literature [25,26,27,28,29] that cool coatings, based on paints or elastomeric materials, are affected by an aging effect that alters their solar reflectivity. The thermal performance of roofs is significantly impacted by this aging effect, as indicated in [5]. In this last work, the comparison between the heat flux through a roof considering the aging effect and the same roof without taking this effect into account showed a significant difference that can lead to erroneous estimates of energy consumption and the results of the economic cost effectiveness analysis of energy retrofit measures on roofs. Therefore, when calculating heat flux through roofs, this aging effect must be taken into account and included in its energy calculation to draw reliable conclusions. In conclusion, to simulate realistic conditions, the aging effect must be considered to draw accurate conclusions with respect to the energy and economic outcomes of the retrofitted roofs.

In conclusion, to simulate realistic conditions, the aging effect must be considered to draw accurate conclusions with respect to the energy and economic outcomes of the retrofitted roofs.

To account in the energy calculations this aging effect, the first stage is to establish the pattern of aging. In [28] it was shown that for all types of reflective roof coatings tested, in the early two years after installation, roughly 95% of aging happened, with 98% occurring within the first three years after installation; similarly, research has demonstrated that when considering unwashed cool roof coatings on various substrates, there is typically a decrease in initial solar reflectivity of approximately 20-25% within the first few months to one year, with minimal alterations thereafter, and substrate type typically has limited impact. On the other hand, Bretz and Akbary [29], found that the majority of the decline in solar reflectivity takes place within the initial year, potentially even within the first few months, and then the value of solar reflectivity tends to remain stable. Eilert [30] also illustrated that the decline in solar reflectivity of white roofs is in the order of 10-30%, and the greatest decrease typically occurs during the first year. Based on the field survey [28], the recommendation is to perform energy calculations using reflectivity values aged for a minimum of one year, which usually range from 75% to 80% of the initial values.

Similar conclusion was reached in [25]. The study’s field measurements yielded results indicating a decrease in solar reflectance ranging from 19% to 25% for various cool paints In this study, it was also noted that the aging of the cool coating layer has a minimal impact on its thermal reflectivity.

On the other hand, field measurements [28,29] suggest that periodic washing can reinstate the original reflectivity values to 90-100%. Nonetheless, as indicated by the author of this field research, the use of roof washing as a maintenance strategy for cool-coated roof surfaces is not a cost-effective approach for retaining or renewing solar-reflectance values, especially given the expectation that most solar reflectance loss will reoccur within three to six months. While washing can typically renew most of the solar reflectivity, especially during the early aging years, the effects are temporary (typically for three to six months) and deliver limited economic benefits.

According to the consensus in most of the studies we’ve examined, the aging trend considered for the cool roof coating is as follows: during the first year, there is a reduction in solar reflectivity amounting to 20% of its initial value, with the majority occurring in the initial months of the year, and a further loss of 8.5% in the second year. A reduction of 0.9% is expected for the third year. Afterwards, the drop in reflectance tends to become steady [29], resulting in a total loss of 30% over the complete life cycle. Therefore, as indicated in [28], nearly 95% of the aging takes place within the initial two years, and approximately 98% occurs during the first three years after installation.

On the other hand, when a wash is done some years after installation, the relating literature supports that solar reflectivity is restored to 90% of the initial value. Subsequently, we consider the same pattern observed after the initial application of the cool coating.

The solar reflectivity loss considered in this work as a result of the aging effect is estimated following the aforementioned aging patterns. In Figure 3, the estimated percentage of reflectivity loss for each year is shown.

2.4. Roof Energy Calculation

2.4.1. Case Buildings

In this study, we considered a typical building from the social housing edified in Seville before 1979. The analyzed building belongs to a social housing development named Polígono de San Pablo, built in the city of Seville, Spain, in the decade of the 1960s. This development showcases the typical construction style seen in social housing throughout this era, where the absence of energy insulation measures is a prominent feature.

The roofs, as shown in Figure 2, are of the flat type. The development is made up of equal height buildings, and there are no adjacent structures of superior elevation that could cause shading over the roofs analyzed. Thus, the solar radiation flux reaching the roofs can be described by Equation (2).

Figure 4a shows the layout of the roofs, while in Table 1 the thermophysical values and dimensions of the roofs layer are described. These types of roofs will be considered as the reference roofs to quantify the energy reduction obtained from implementing the retrofit measure. The data presented in this table corresponds to the nominal values and were based on [31].

The reference roof is coated with a layer of bituminous paint on its outer surface. Consequently, a solar radiation absorptivity coefficient equal to 0.8 has been considered in line with typical absorptivity values for this coating type [32].

The energy retrofit measure proposed for the obsolete energy reference roof is a combined measure consisting of the installation of 0.08 m thick EPS insulation with the addition of an external coating of cool, white elastomeric paint, featuring an absorptivity value of 0.1. These values were taken based on a previous study [16] on the thermal performance of this type of combined energy retrofitting measures, which showed that the referred values give very good energy and economic results as demonstrated by a cost-effectiveness analysis conducted for the whole life cycle of the retrofitting measure.

Figure 4b illustrates the proposed retrofitted roof layout, while Table 2 includes the dimensions and thermophysical values. The analysis of the energy and economic performance of the roof involves optimizing the combination of insulation thickness and the absorptivity value of the cool paint, while considering the previously discussed time-varying reflectivity of the cool coating.

Figure 5 shows the climatic chart for Seville, whose values are collected from information sourced from the Spanish Gouvernamental Meteorological Agency (AEMET) [33]. According to the referred data, throughout the year, the temperature averages 19.2 degrees Celsius, with July and August experiencing maximum averages of 40 degrees Celsius, and January registering a minimum average of 5.7 degrees Celsius.

Thus, winter can be defined as mild, with summers being hot, dry, and experiencing high levels of solar radiation. Lastly, autumns and springs see rainfall along with moderate temperatures. The normal solar radiation reaches its peak at 8.3 kWh/m² in July and it decreases to a minimum of 2.3 kWh/m² in December. Considering the described meteorological values, the K

\ddot{o}

ppen-Geiger climate classification system identifies the region’s climate as Mediterranean Csa.

2.5. Numerical Resolution

The spatial approximation to the equation governing the heat transfer across the roof was based in the 1D finite difference scheme introduced and validated in [24]. To perform the entire computation process a code was developed using the FreeFem++ software [34].

In the approach that uses Navier–Stokes thermodynamic equations to determine the heat exchange between the roof and the ambiance air, the numerical resolution of the governing equations for the external air and the equations for the heat conduction through the roof were performed in a coupled way.

Since, as can be seen in Figure 2, buildings can have different orientations, a sensitivity analysis of the influence of building orientation on heat transfer through the roof was first performed. This preliminary analysis was performed using a 3D approximation of the thermodynamic airflow equations and showed that the changes in heat transfer through the roof due to building orientation were negligible, being the difference between all the orientations considered less than

0.6 %

. This made it possible to solve the Navier-Stokes equations using a 2D approximation where the relevant variable for the dynamic of the air was the wind velocity.

As for the approach using the convective heat transfer coefficient, the heat exchange between the roof and the outside air is calculated using Equation (7) and using the value obtained from the energy balance 2.2.1 on

S_{e x t}

, which is the boundary condition on the outside surface of the roof for the numerical method that calculates the heat transfer through the roof.

With respect to the impact on the heat flux through the roof, a difference less than

1 %

, was observed between the two approaches used for the calculation of the convective flux with the ambiance air, a difference this may make it advisable to use the convective correlation methodology for the present case, due to its greater simplicity of use and lower computational cost.

To evaluate the accuracy of the proposed numerical scheme, an inter-model validation was first performed by comparing the model results with the results obtained from the Energy Plus software [19]. This was executed by adopting short time spans for the calculation, typically in the order of months due to time-dependent solar reflectivity is not supported by Energy Plus, as it is built to accommodate only constant values of solar reflectivity. It should be noted that in the developed numerical model, the change in time of the solar reflectivity was implemented in order to enable the simulation of the impact of aging on cool roof absorption over extended time frames, often spanning decades, as applied in our Life Cycle Cost Assessment (LCCA) calculations.

In addition, from a numerical perspective, we validated the method through analytical calculations of temperature evolution at the nodes employed in the finite difference method. These calculations utilized a limited number of nodes for roof discretization [35].

Within the interior zone beneath the roof, our approach involves a test zone that draws inspiration from [15,36,37], with the underlying assumption that the building envelope is adiabatic, except for the roof.

The roof’s thermal response is determined by the conditioning system’s operational mode. Several operational modes are documented in the literature, encompassing continuous air conditioning [15,38,39,40,41], intermittent air conditioning with a consistent indoor set-point temperature [42], and no air conditioning with indoor temperature variations [43]. When examining the energy behavior of the roof and its implications for energy consumption, we make the assumption that the ambient indoor temperature remains uniform for each season.

We consider a continuous mode of operation for the conditioning system, with the indoor set point temperature set at

25 ° C

during the cooling season,

20 °

C during the heating season, and

22.5 ° C

during the seasons in between. These values have been chosen while keeping in mind the comfort temperature intervals defined in the Spanish regulation for thermal installations in buildings (RITE) [44].

Finally, two maintenance scenarios were considered: the first assumed that a powerful washing of the cool coat is not performed, and the second assumed a powerful washing of the roof with a periodicity of five years. This periodicity, according to [17], achieves very positive outcomes from both energy and economic viewpoints. On the other hand, as is supported in the relating literature cited in Section 2.3, if a wash is done some years after the installation, the solar reflectivity is restored to

90 %

of its original value. In the aftermath, we follow the same pattern as seen following the initial application of the cool coating.

2.6. Methodology for the Life Cycle Cost Analysis

To perform an economic analysis of the energy and retrofit costs and draw conclusions about its financial suitability, the usual approach is to carry out a cost-effectiveness analysis through a life cycle cost analysis (LCCA) that considers future costs [45]. Therefore, the objective of the LCCA performed in this section is to evaluate the economic benefits of the proposed roof retrofit measure compared to the reference case.

Using the method introduced in [45], it is possible to establish a comparison of future costs with current costs and, in addition, to obtain the savings obtained by using the retrofitted roof over the life cycle time span. To perform the LCCA, anticipated costs are estimated and then discounted to reflect their present value. For this, we account for the future values of the elements that drive the costs; then, each annual variable cost is discounted to reflect its current value. Finally, the LC cost is the sum of the present values for all variables involved in the study. Once the LC cost for the retrofitted roof has been determined, its cost effectiveness is assessed by comparing this cost with the LC cost obtained for the reference case. If the LC cost produced by the retrofitted roof is lower than that caused by the reference case, the retrofitted roof is considered cost-effective and yields positive monetary savings.

To perform the LCCA, a lifetime equal to 20 years is considered; this is the average service life of the retrofit measures considered [46]. Then the LC cost, the LC monetary savings or net cost savings (NCS), and the return-on-investment period or payback period (PB) are estimated for the retrofitted roof. The variables involved in this analysis are the initial investment cost of installing the reflective coating and the thermal insulation layer, the annual costs of energy, and the maintenance costs of the periodic washing of the cold roof coating, along with the economic parameters that influence the economic process: the monetary discount rate

d r

and the increase in energy costs index i. In order to calculate the current value of one monetary unit of a future period m (typically measured in years) at a market discount rate

d r

(expressed as a fraction per time period), the applicable formula is as follows

P W_{m} = 1 / {(1 + d r)}^{m} .

Assuming that

P_{e, C}

and

P_{e, H}

denote the current energy prices for cooling and heating, and that i is the energy cost inflation rate index, the present value of the future energy cost

C_{e} (m)

in the period m is given [45] by

P W_{m} (C_{e} (m)) = C_{e} (m) / {(1 + d r)}^{m}

being

C_{e} (m) = (\frac{Q_{c} (m) \times P_{e, c}}{S E E R \times (3.6 \times 10^{6})} + \frac{Q_{h} (m) \times P_{e, h}}{S C O P \times (3.6 \times 10^{6})}) {(1 + i)}^{m - 1}

(9)

with SEER representing the seasonal energy efficiency ratio for cooling and SCOP denoting the seasonal performance coefficient for heating of the conditioning equipment in use. In Equation (9), it is considered that the loads

Q_{c} (m)

and

Q_{h} (m)

for the cool roofs fluctuate annually as a result of both aging and the maintenance applied to the cool coating.

C_{e} (m)

calculations always assume the use of electricity for cooling and heating.

Similarly, if the inflation rate index for maintenance costs is noted as

i_{M}

, the current worth of any forthcoming maintenance payment

C_{M} (m)

in time period m is

P W_{m} (C_{M} (m)) = C_{M} (m) / {(1 + d r)}^{m} = δ (m) C_{M} {(1 + i_{M})}^{m - 1} / {(1 + d r)}^{m}

where

δ (m)

is equal to 1 if maintenance is done in year m or equal to 0 if not,

C_{M}

is the current price of maintenance per unit area of roof surface and A is the area of the roof surface.

Next, the current life-cycle total cost per unit of roof surface area is provided as follows:

C_{t} = C_{e} + C_{M} + C_{I}

where

C_{e}

and

C_{M}

refer to the present worth of the overall life cycle costs for energy and maintenance, respectively, as determined by

C_{e} = \sum_{k = 1}^{n} P W_{k} (C_{e} (k)) a n d C_{M} = \sum_{k = 1}^{n} P W_{k} (C_{M} (k)),

Lastly,

C_{I}

represents the expense associated with the initial investment of cool roof coating installation.

In contrast to the initial reference roof, the retrofit will bring about annual changes in energy usage and the corresponding economic adjustments, primarily linked to energy costs. To determine the cost differential between employing cool roofs and the reference case, we calculate the net cost savings (NCS) for the entire life cycle period using the following expression

N C S = \sum_{m = 1}^{n} [P W_{m} (C_{e}^{(r e f)} (m)) - P W_{m} (C_{e} (m)] - C_{M} - C_{I} .

(10)

where now

P W_{m} (C_{e}^{(r e f)} (m))

represents the current value of energy costs for the roof reference case at period m, determined as:

P W_{m} (C_{e}^{(r e f)} (m)) = C_{e}^{(r e f)} (m) / {(1 + d r)}^{m},

where

C_{e}^{(r e f)} (m)

is computed as

C_{e}^{(r e f)} (m) = (\frac{Q_{c}^{(r e f)} (m) \times P_{e, c}}{S E E R \times (3.6 \times 10^{6})} + \frac{Q_{h}^{(r e f)} (m) \times P_{e, h}}{S C O P \times (3.6 \times 10^{6})}) {(1 + i)}^{m - 1}

(11)

being

Q_{c}^{(r e f)} (m)

and

Q_{h}^{(r e f)} (m)

the cooling and heating loads respectively for the reference roofs in the time period m.

Then

P W_{m} (C_{e}^{(r e f)} (m)) - P W_{m} (C_{e} (m))

is the energy cost differential for period m between the reference and the retrofitted roofs.

When the NCS is positive, it means that the use of the retrofit measure on the roof generates cost savings compared to the reference case.

It’s worth noting that energy consumption varies from year to year due to the aging phenomenon. Consequently, the expression (10) cannot be reduced to a singular analytical representation as ussually found in the literature [15].

In [47] the payback period (PB) is defined as the time t, at which the NCS becomes zero. Since the coefficients in the series presented in (10) change with each time step m, the payback period t, is determined by computing the cumulative net savings over each time horizon,

m_{0}

, as follows:

N C S (m_{0}) = \sum_{m = 1}^{m_{0}} [P W_{m} (C_{e}^{(r e f)} (m)) - P W_{m} (C_{e} (m)] - C_{M} - C_{I} .

(12)

Then, if

N C S (m_{0}) < 0

and

N C S (m_{0} + 1) > 0

the payback time t is estimated using the formula

t = m_{0} - \frac{N C S (m_{0})}{N C S (m_{0} + 1) - N C S (m_{0})} .

(13)

This value of t obtained from (13) is in agreement with the predominant value usually found in the literature [15,45], which usually assume that energy consumption is constant for all years.

2.7. Economics Indicators

The variables used for the economic computations in the LCCA are detailed in Table 3.

The cost of installing the combined retrofit measure on the roof and its maintaining it is sourced from [46]. The electricity price is determined as the price in Spain, which includes taxes, for household consumers, as defined in reference [48]. Following the approach detailed in [49], three different sets of values for energy inflation and discount rates have been explored, as indicated in Table 3. Lastly, the maintenance discount rate

i_{M}

is assumed to be equal to

d r

, based on the assumption that the evolution of both indices is closely aligned.

As for the conditioning equipment, our working assumption is that conditioning is invariably performed by an air-conditioning pump exclusively powered by electricity. Considering the relatively low buying capacity of the home occupants, we have chosen air conditioning units of mid-range quality with an A++ energy rating in line with European regulations. This selection is based on the common understanding that these devices are often priced lower than those carrying an A+++ energy certification. The efficiency parameters for the conditioning equipment are established at SEER = 3.4 for cooling and SCOP = 3 for heating. These pump efficiency values represent the averages of the values outlined in EU Regulation 626/2011 [50] for air conditioning equipment classified as A++.

3. Results and Discussion

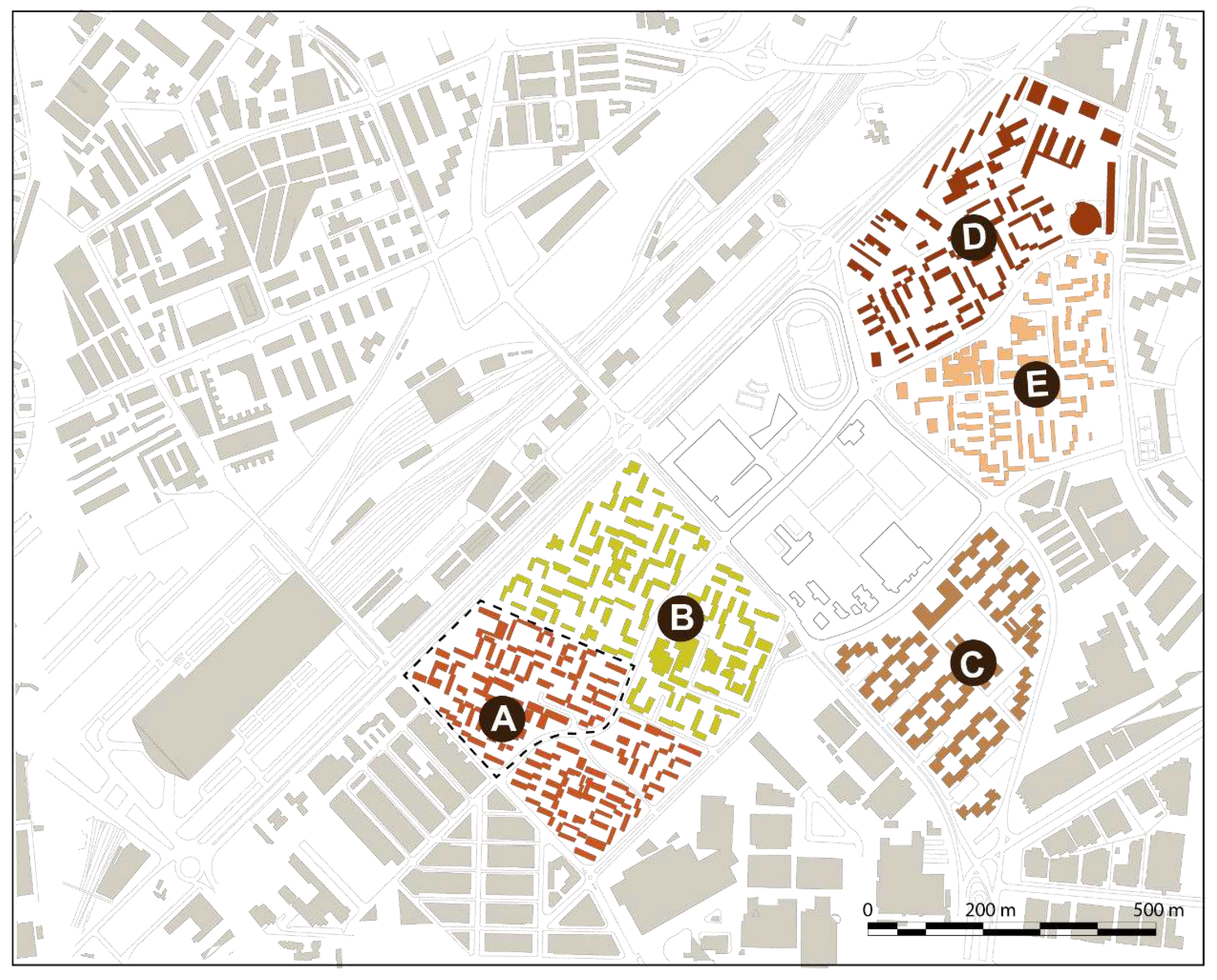
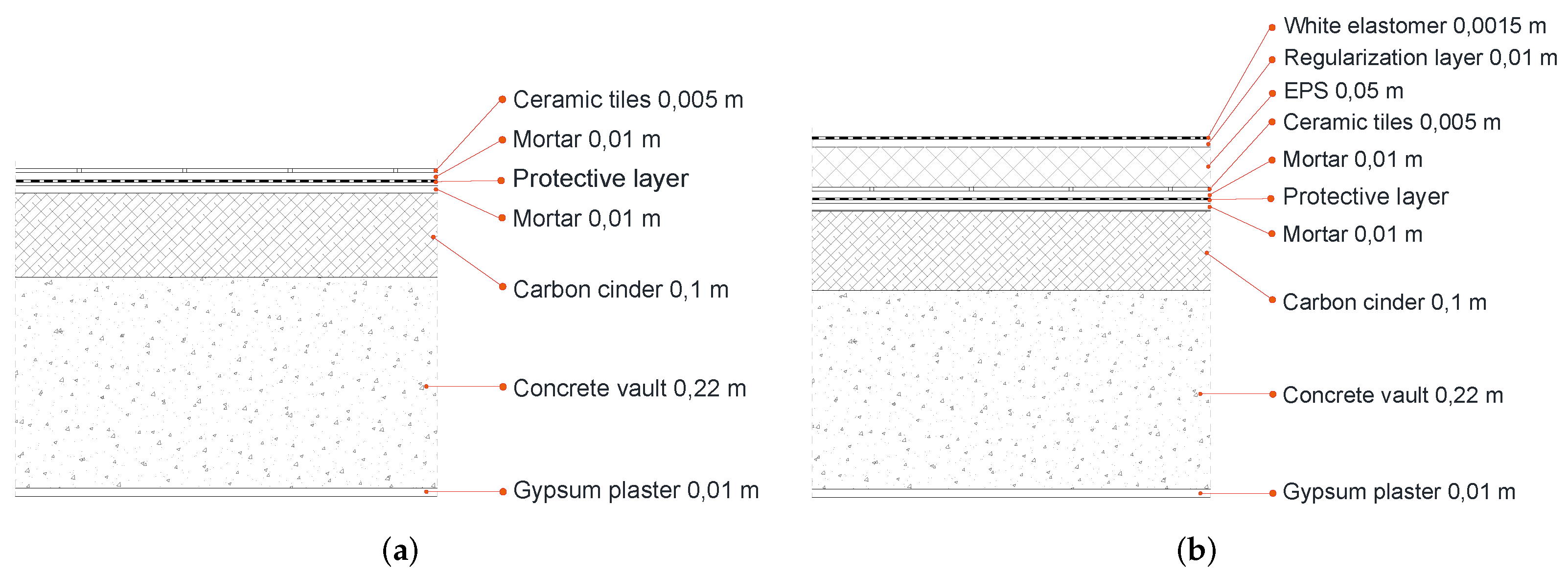
3.1. Energy Results

Within this current section, the findings regarding the energy effectiveness of the roof retrofit proposal are presented for the case study mentioned above. The heating, cooling, and total loads generated by the heat flux through the reference and the retrofitted roofs are computed for each year of the LCCA whole time period. Then the loads are compared, and energy savings estimates are obtained for each year and for the entire LCCA span time.

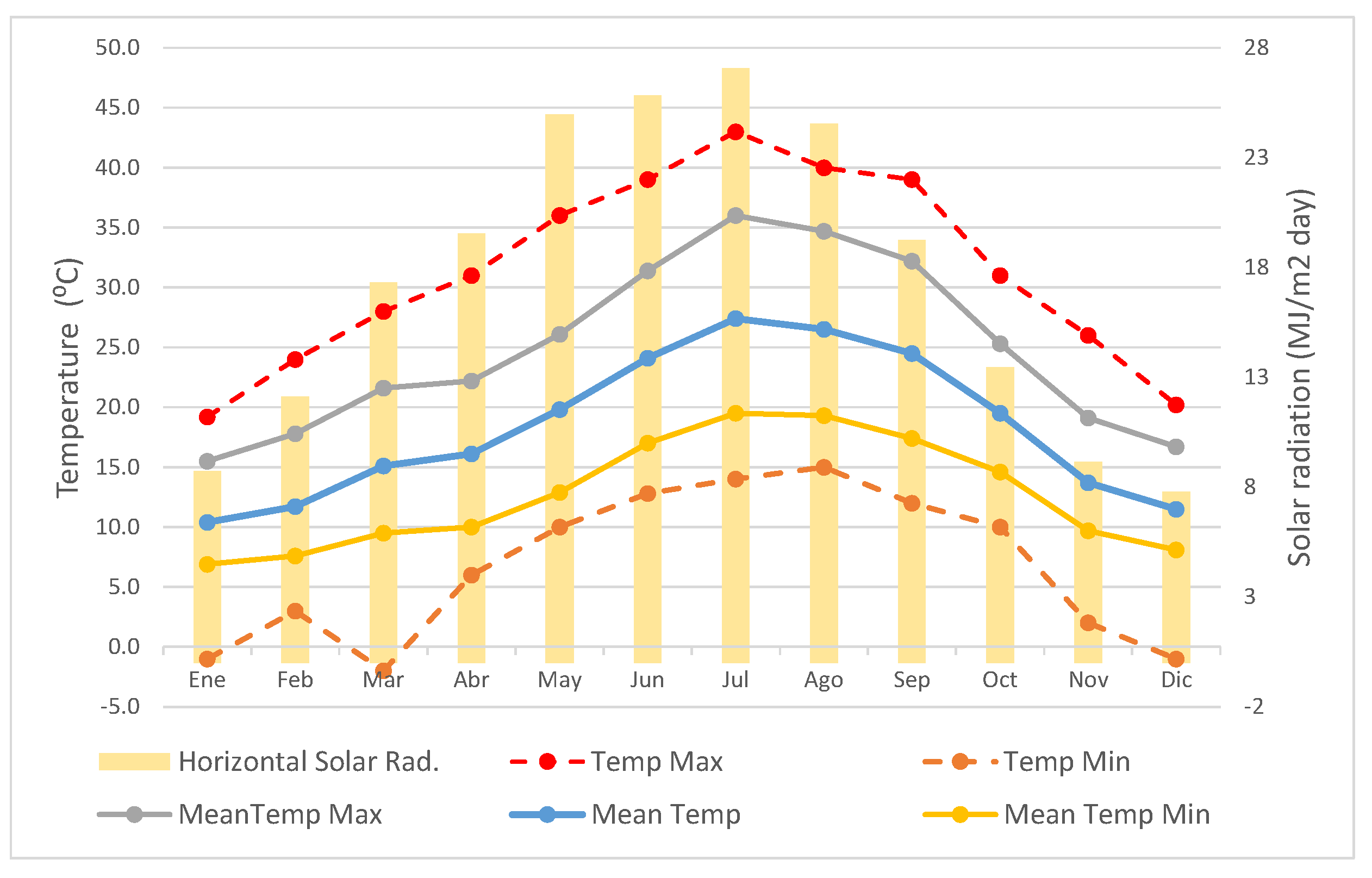
To perform analysis, the heat flux per unit area of the roof surface for the complete year is calculated, taking into consideration the hourly climatic data available in the weather files specific to Seville, as previously described. Then, when this flux is incoming, as happens in the cooling season, the flux is computed as cooling load, and when the heat flux goes out, as happens in the heating season, the flux is computed as heating load. The addition of the cooling and heating loads provides the total flux.

In these computations, as mentioned above, two protocols for cool roof maintenance have been considered: no washing and quinquennial power washing of the outer elastomeric paint.

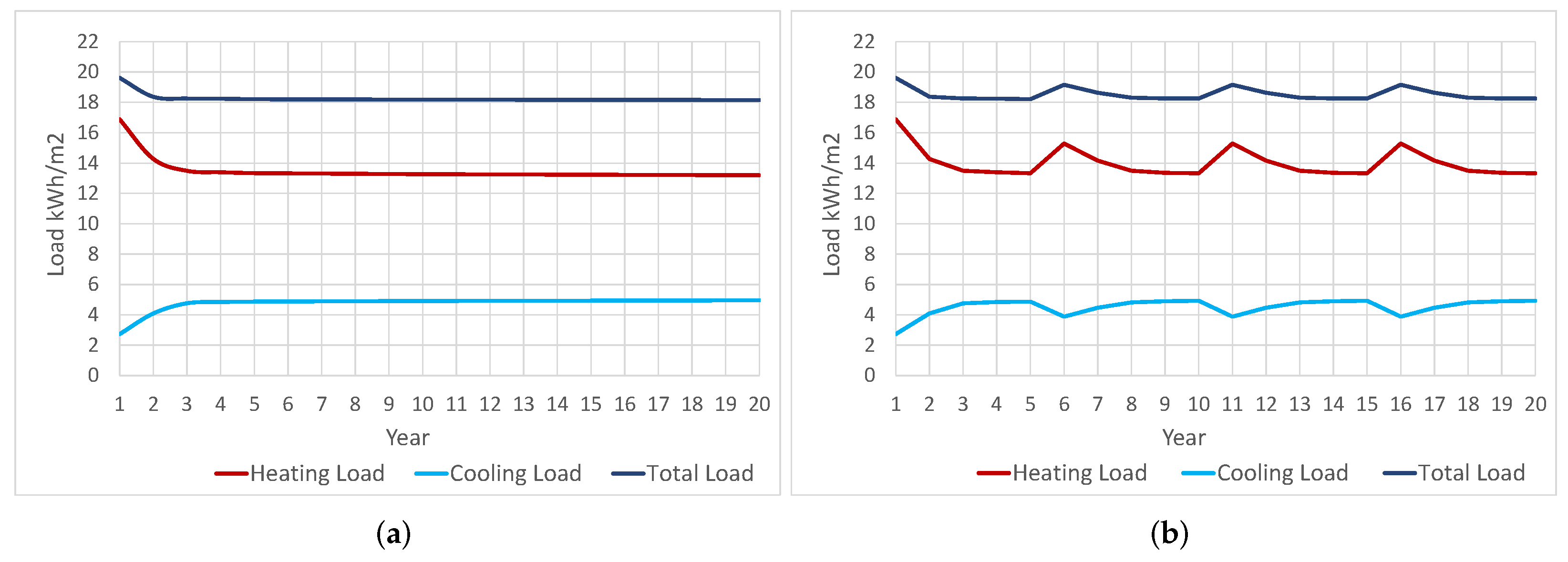
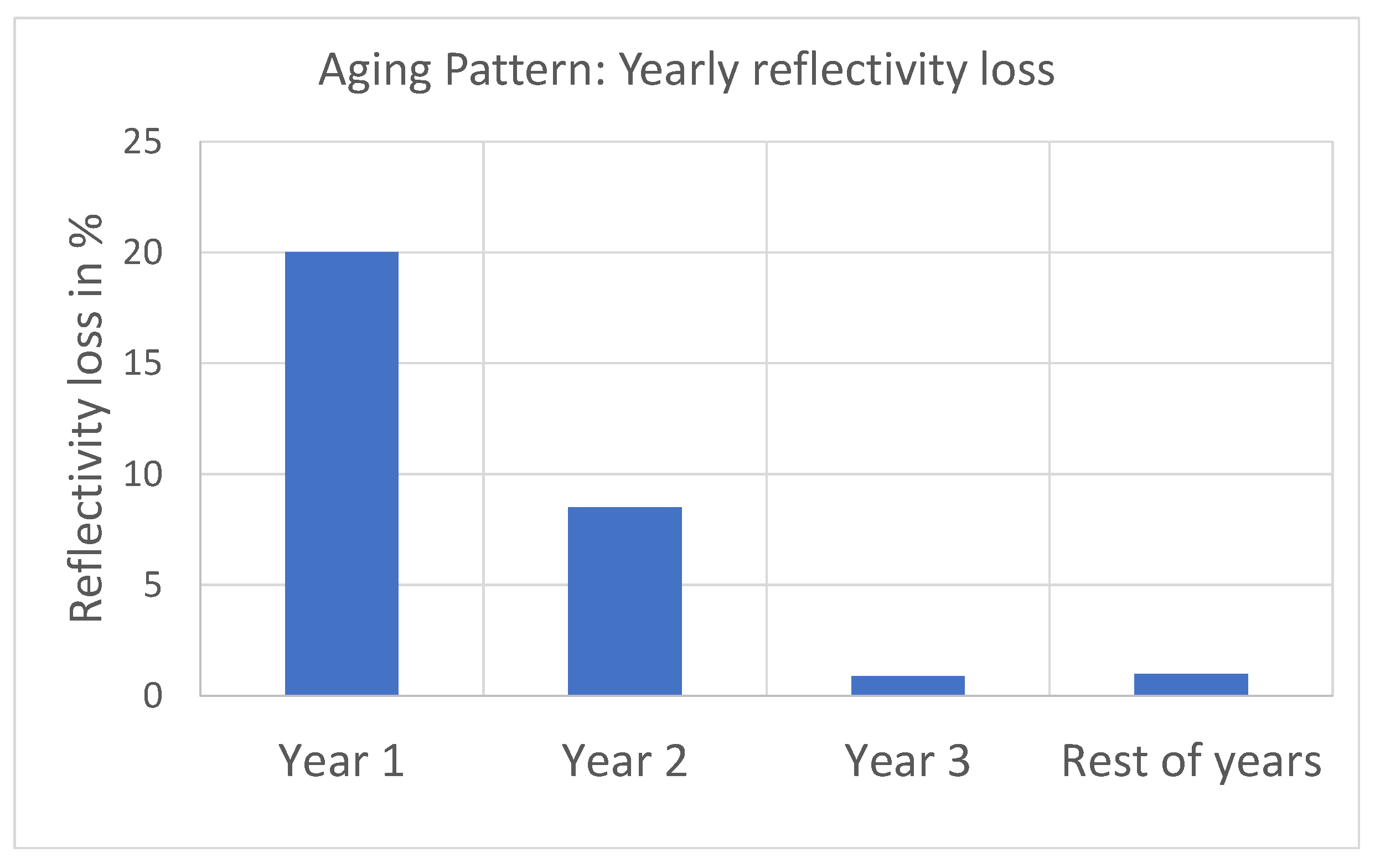
In Figure 6a the yearly heating, cooling and total loads by m² of retrofitted roof are shown for the case of no washing of the cool coating. It can be observed that as a result of the high initial values of the cool-coating solar reflectivity, the values of the heating loads are higher in the first two years than for the remaining years due to the solar gain penalty; on the contrary, for the first two years, the cooling loads are lower than for the remaining years for the same reason. Regarding the total loads, this opposing behavior of the cooling and heating loads produces a final result that must be estimated considering the effect on the loads of the aging pattern. For the case study considered, the results depict a trend where total loads are notably higher in the first two years and then maintain a stable course in the remaining years.

It should be noted that the heating loads in the present case study are higher than the cooling loads for the whole LCCA time span, in line with the effect that the high solar reflectivity produces in the thermal flux through the roof. In Figure 6b, the yearly heating, cooling and total loads by m² of retrofitted roof are shown for the case of a periodic quinquennial wash of the cool coating. The first observation that can be made from this figure is how the quinquennial washing of the roof produces a cyclic behavior of the loads, which is very similar for each 5-year period between two consecutive washes. As can be seen, the effect of the cool paint on decreasing solar gain produces lower values for the cooling loads than for the heating loads throughout the 20 years of the considered life cycle time span.

It is worth noting that when the solar reflectivity of the cool paint reaches its highest values, that is, in the initial year, and then, after the quinquennial washing, years 6, 11 and 16, the cooling load reaches its minimum values; after each of these years, cooling loads are gradually increasing in each time interval between two consecutive washings, in line with the increasing loss of solar reflectivity produced by the aging effect of the cool paint. For the heating load, the pattern is just the opposite: when the solar reflectivity is maximum in years 1, 6, 11 and 16, the heating loads are maximum in accordance with the lowest values of solar gain; then in the following years the heating load follows a decreasing pattern produced by the aging effect that causes a loss of reflectivity and an increase of solar gain.

This opposing behavior in the cooling and heating loads produces a certain balance in all the years except for the initial year of each inter-washing time period. In these initial years, the predominant effect is the reduction of solar gain, so that the rise in heating load is not balanced by the reduction in cooling load, resulting in an increase in the total load for those years. For the remaining years of each period between washings, it is observed that the variations in cooling and heating loads caused by the effect of the aging of the cold layer are approximately compensated for by each other, producing a very small variation of the loads over the different years of each period.

On the other hand, the calculation of the heat flux for the reference roof gives a heating load equal to 28.72 kWh/m² and a cooling load equal to 38.32 kWh/m² that implies a total load equal to 67.04 kWh/m² for every year of the LCCA span time. By comparing these values with the loads for the retrofitted roof shown in Figure 6, it can be stated that the heating, cooling, and total loads for the retrofitted roof have lower values than the same loads for the reference roof and this for all the years of the LCCA time span and for the two washing protocols considered; consequently, it can be stated that the retrofitted roof yields positive energy savings for all the years of the considered LCCA time span, as can be seen in Figure 7.

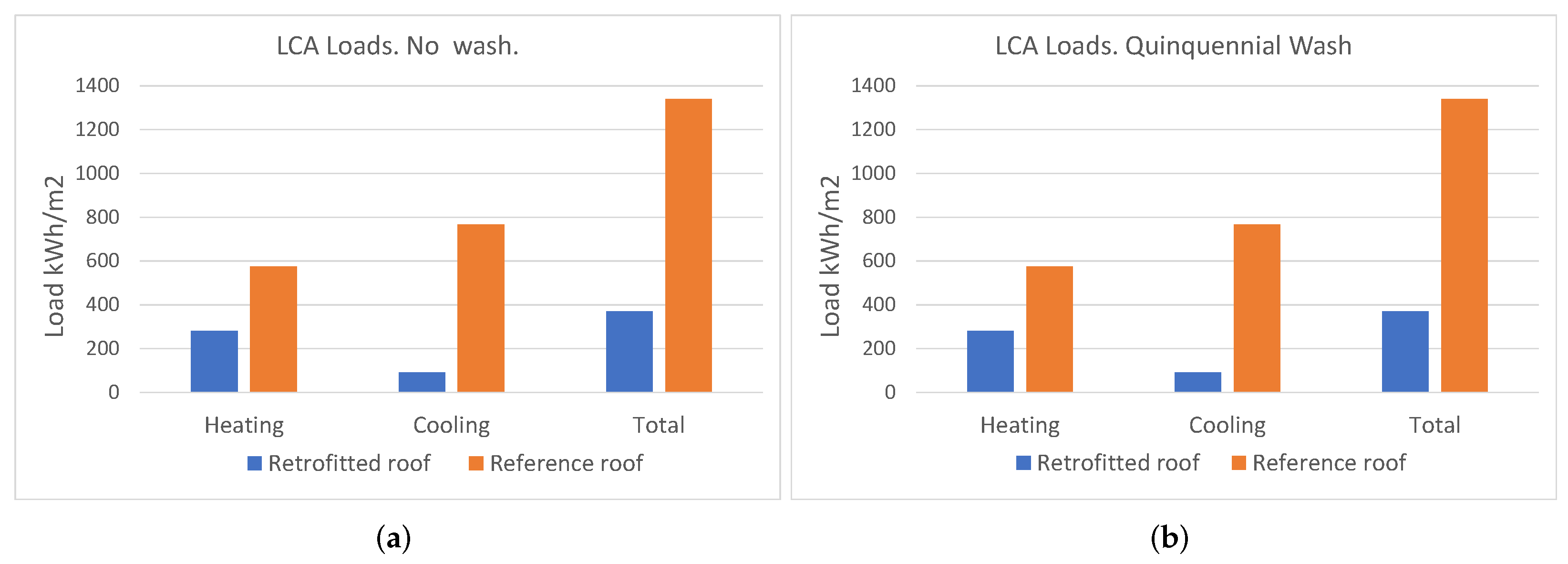
In Figure 8, the loads for the entire LCCA time span are shown for the reference and retrofitted roofs. According to Figure 6 and the subsequent discussion for heating and cooling loads and thus for the total load, the retrofitted roof exhibits lower values than the reference roof and, as can be appreciated in the figure, the highest reduction is achieved for the cooling loads. In Table 4, the values of the different loads for the LCCA span are shown for the retrofitted and reference roofs.

The energy savings for each specific load are defined as the difference between the load for the reference roof and the load for the retrofitted roof. Thus, positive energy savings mean that the load on the reference roof is higher than the same load on the retrofitted roof. As can be observed in Table 4, the retrofitted roof has positive or true total energy savings when compared to the reference case. 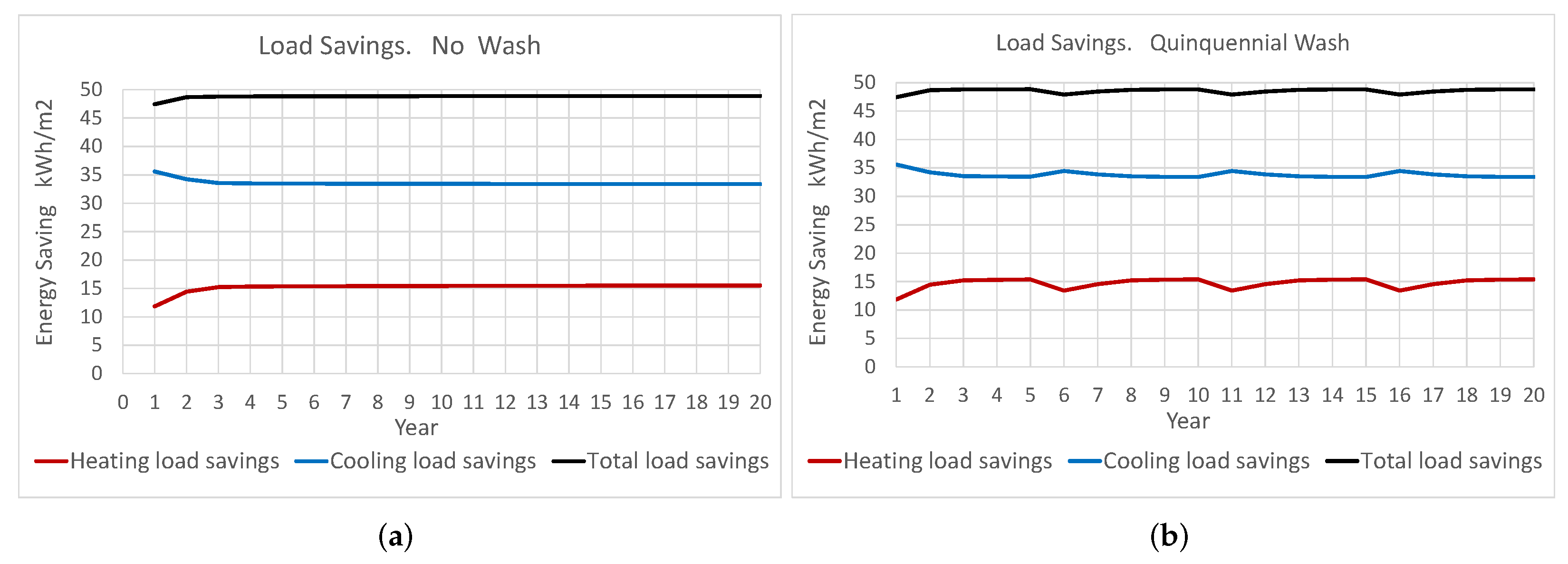In Figure 7 the heating, cooling, and total savings are displayed for each year of the LCCA span time.

It can be noted that the case of periodic quinquennial wash of the cool coating provides slightly better results with respect to the total load and energy savings compared to the case of no wash.

According to the above discussion, for the case of no wash of the cool coating, Figure 7a, the lowest values for the energy savings are obtained in the two initial years and then tend to stabilize for the remaining years. It should be noted that the savings for cooling load are much higher than the savings for heating load.

In Figure 7b, the load savings for the case of a quinquennial wash of the cool coating are shown. It can be observed that the lowest values for the energy savings are obtained in the two initial years and then in the years in which the washing is carried out due to the penalty in the solar gain produced by the high values of solar reflectivity. For the remaining years of each period, the decrease in the solar reflectivity produced by the aging lowers the solar reflectivity and, as can be seen in the figure, this makes the total load go down.

Likewise, in Figure 7 the greatest effect in producing savings is observed for the cooling load when compared to the heating load, as a result of the decision to install a cool paint with very reduced solar reflectivity.

Finally, in Table 5, the LCCA energy savings are shown for all housing in every district of the neighborhood and the neighborhood as a whole.

Taking into account the assumed SEER and SCOP coefficients, the savings in thermal loads shown in Table 5 are equivalent to a total reduction in energy consumption of 32,500 mWh for the entire neighborhood and the entire life cycle, which is equivalent to a 72% of reduction in energy consumption to achieve indoor thermal comfort. This value of energy consumption decrease implies a total reduction in CO2 emissions of 4,488.31 tons.

3.2. LCCA Results

In this section, the net savings and payback periods are used as performance indicators to perform the LCCA. Due to the investment in refurbishment made compared to the reference case, the NCS and PB are assessed under the economic framework described previously and considering the impact on energy loads of the effect of aging as described previously.

In Table 6 the monetary net savings per unit of roof surface area, NCS, and the payback period, PB, are shown for the two maintenance protocols considered: no powerful wash during the entire LCCA time period and a periodic quinquennial wash. Additionally, net savings are presented for the roof with three standard surface areas in the framework of social housing, that is, roof areas equal to 60, 70 and 80 m²: the usual range of roof surfaces for this kind of dwelling.

As can be seen in Table 6 the proposed retrofitting measures are cost-efficient for all the cases analyzed. However, it can be stated that the results obtained for the no-wash maintenance protocols are better than those obtained for the quinquennial washing, with higher values of monetary savings and thus shorter PB periods for the no wash case. It should be highlighted that the payback periods for all the cases are not long and range between 6.84 and 8.12 years. These can be considered reasonable time intervals to recover the investment made in the retrofitting.

Regarding the economic indicators, it can be observed that the proposed combined retrofit measure yields the highest monetary savings for high values of the energy inflation index and the monetary discount rate represented here by i = 6 % and dr = 3%. Taking into consideration the present economic situation characterized by very high energy price growth and very high inflation rates, it can be concluded that, financially speaking, the proposed retrofitting measure is highly effective.

In the same table, net monetary savings are presented for three typical roof areas of social dwellings. As can be observed, the value of these savings is relevant, and their impact on the household economy of regular residents of social housing, usually characterized by low incomes, can be described as of great significance and with a high potential to achieve indoor comfort and health conditions and reduce the high rates of energy poverty found among the inhabitants of this type of housing.

Finally, in the Table 7 the monetary savings for the whole LCCA time span for all the retrofitted dwellings in each district and for the entire neighborhood are shown for all the different economic scenarios of energy inflation and discount rate considered.

As can be observed, the quantities saved during the analysis period, the life cycle time span, are significant for all the analyzed scenarios in terms of both economy and maintenance protocols. It is observed that for the entire neighborhood quantities saved range from

€ 6.4

million to over

€ 8.6

million in the No Wash case, depending on the economic scenario.

4. Conclusions

This architectural solution impacts 3 out of the 4 lines of intervention: Health and Comfort, Materiality, Cultural Identity, and Energy and Conditioning that the AURA strategy proposes as the focus of all urban regeneration interventions.

From an energy perspective, the effectiveness of the proposed retrofit measure, which combines a cool coating with insulation to reduce energy loads and achieve interior comfort in affected dwellings, is confirmed. For the LCCA time period, the load reduction reaches 975.62 kWh/m² for the no-wash maintenance protocol and 970.40 kWh/m² for the Quinquennial Wash maintenance protocol. When these savings are quantified for all roofed dwellings in the neighborhood, the results are 109,109.44 and 108,525.54 mWh, respectively. These results of the thermal load reduction indicate a 72% reduction in energy consumption to achieve indoor thermal comfort. This load reduction is equivalent to a saving of almost 4,488 tons of greenhouse gas emissions for the entire district and the entire lifetime of the roof retrofit measure implemented. Therefore, it can be concluded that the implementation of the proposed retrofitting measure to reduce energy consumption leads to a significant capacity for energy savings and the resulting reduction in spending to achieve interior comfort, reduction in levels of energy poverty, improvement in interior living conditions and its repercussions on health and well-being, as well as involves a very positive effect on the reduction of greenhouse gas emissions and consequent impact in the fight against climate change.

From a financial perspective, the Life Cycle Cost Analysis provides net economic cost savings for the entire analysis period. In the case of the No-wash maintenance protocol, these range between 57.26 and 77.18

€ m^{2}

per dwelling, depending on the economic scenario, with return-on-investment periods between 7.69 and 6.84 years. In the case of the Quinquennial Wash maintenance protocol, net savings are between 52.45 and 72.03

€ / m^{2}

and return-on-investment periods are between 8.12 and 6.93 years. This allows us to establish the cost effectiveness of the proposed retrofit measure for family dwellings and homeowners. If all affected homes in the neighborhood are considered, financial savings for the LCCA time span range from

€ 5, 865, 798.20

€ 8, 055, 547.08

in the case of the quinquennial Wash maintenance protocol, and from

€ 6, 403, 729.36

€ 8, 631, 502.48

in the case of the no-wash maintenance protocol. Therefore, financially speaking, the economic viability of the proposed retrofitting is confirmed, as well as the significant savings that its implementation implies for individual households and for the neighborhood as a whole.

To put these figures in context, it should be highlighted that in 2018, the annual income per capita in the Polígono de San Pablo was

€ 8, 128.86

while the household income was

€ 19, 973.84

(Source: National Institute of Statistics, Spain). Thus, savings would constitute a significant percentage of the economic capacity of residents of the neighborhood.

In the end, this retrofitting proposal fulfills the premises set out by the AURA strategy: the regeneration of obsolete neighborhoods through specific interventions that offer global benefits to the population in the case study, as described in this article. In turn, this has a direct effect on people’s health, especially among elderly residents of the neighborhood and in the fight against climatic change.

Author Contributions

Conceptualization, methodology, software, formal analysis, investigation, writing—original draft preparation, writing—review and editing, all the authors. All authors have read and agreed to the published version of the manuscript.

Funding

This article is included in the project “Aplicación directa de la Estrategia Aura del Equipo Solar Decathlon–U.S., en rehabilitación de barriadas obsoletas andaluzas” granted by the Ministry of Development, Infrastructure and Territorial Planning of the Local Andalusian Government (Spain), with ref. US.20–11, but for its production no economic financing has been received

Data Availability Statement

Data are available under request to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Herrera-Limones, R.; León-Rodríguez, Á.; López-Escamilla, Á. Solar Decathlon Latin America and Caribbean: Comfort and the Balance between Passive and Active Design. Sustainability 2019, 11, 3498. [Google Scholar] [CrossRef]
Herrera-Limones, R.; HernÁndez Valencia, M.; Roa FernÁndez, J.; Vargas Palomo, A. C.; Guadix Martín, J.; Torres García, M. (2021). La Universidad de Sevilla En “Solar Decathlon Europe 19”: Innovación Docente a Través de Un Proceso de Transferencia Del Conocimiento; McGraw-Hill Interamericana de España: Editorial Aula Magna.
Berdahl, P.; Bretz, S. E. (1997). Preliminary survey of the solar reflectance of cool roofing materials. Energy Build. 1997, 25, 149–158. [Google Scholar] [CrossRef]
Kim, H.; Gu, D.; Kim, H. Y. Effects of Urban Heat Island mitigation in various climate zones in the United States. Sustain. Cities Soc. 2018, 41, 841–852. [Google Scholar] [CrossRef]
Domínguez-Delgado, A.; Domínguez-Torres, H.; Domínguez-Torres, C.A. Energy and Economic Life Cycle Assessment of Cool Roofs Applied to the Refurbishment of Social Housing in Southern Spain. Sustainability 2020, 12, 5602. [Google Scholar] [CrossRef]
Mazzeo, D.; Kontoleon, K.J. The role of inclination and orientation of different building roof typologies on indoor and outdoor environment thermal comfort in Italy and Greece. Sustain. Cities Soc. 2020, 60, 102111. [Google Scholar] [CrossRef]
Hamdan,M.A.; Yamin,J.; Hafez, E.M.A. Passive cooling roof design under Jordanian climate. Sustain. Cities Soc. 2012, 5, 26–29. [CrossRef]
Kolokotsa,D.;Giannariakis,G.; Gobakis, K.;Giannarakis,G.;Synnefa, A.; Santamouris, M. Cool roofs and cool pavements application in Acharnes, Greece. Sustain. Cities Soc. 2018, 37, 466–474. [CrossRef]
Testa,J.; Krarti, M. Evaluation of energy savings potential of variable reflective roofingsystems for US buildings. Sustain. Cities Soc. 2017, 31, 62–73. [CrossRef]
Anand, J.; Sailor, D.; Baniassadi, A. The relative role of solar reflectance and thermal emittance for passive daytime radiative cooling technologies applied to rooftops. Sustain. Cities Soci. 2021, 65, 102612. [Google Scholar] [CrossRef]
Pisello,A.L. Thermal-energy analysis of roof cool clay tiles for application in historic buildings and cities. Sustain. Cities Soci. 2015, 19, 271–280. [Google Scholar] [CrossRef]
Guerrero Delgado,M.C.; SÁnchez Ramos,J.; Palomo Amores, T.R.; Castro Medina,D.; Álvarez Domínguez,S. Improving habitability in social housing through passive cooling: A case study in Mengíbar (Jaén, Spain). Sustain. Cities Soci. 2022, 78, 103642. [CrossRef]
Herath, P.; Thatcher, M.; Jin, H.; Bai, X. Effectiveness of urban surface characteristics as mitigation strategies for the excessive summer heat in cities. Sustain. Cities Soci. 2021, 72, 103072. [Google Scholar] [CrossRef]
Younes,J; Ghali,K.; Ghaddar,N. Diurnal Selective Radiative Cooling Impact in Mitigating Urban Heat Island Effect. Sustain. Cities Soci. 2022, 83, 103932. [CrossRef]
Saafi, K. and Daouas, N. A life-cycle cost analysis for an optimum combination of cool coating and thermal insulation of residential building roofs in Tunisia. Energy 2018, 152. [Google Scholar] [CrossRef]
Domínguez-Torres, C.A.; Domínguez-Torres, H.; Domínguez-Delgado, A. (2021). Optimization of a Combination of Thermal Insulation and Cool Roof for the Refurbishment of Social Housing in Southern Spain. Sustainability 2022, 13, 10738. [Google Scholar] [CrossRef]
Walton,G.N., 1983. Thermal Analysis Research Program Reference Manual. NBSSIR 83-2655. National Bureau of Standards, p. 21.
Clark, G., Allen, C., (1978). The Estimation of Atmospheric Radiation for Clear and Cloudy Skies. Proc. of 2nd National Passive Solar Conference (AS/ISES), pp. 675–678.
Energy Plus Software. U.S. Department of Energy (DOE). Building Technologies Office (BTO). https://energyplus.net/downloads.
Hagishima, A., Tanimoto, J. Field measurements for estimating the convective heat transfer coefficient at building surfaces. Build. Environ., 2003, 38, 873–881. [CrossRef]
Gagliano, A.; Nocera, F.; Aneli, S. Thermodynamic analysis of ventilated façades under different wind conditions in summer period. Energy Build. 2016, 122, 131–139. [Google Scholar] [CrossRef]
Hickson,R.I., Barry,S.I., Mercer, G.N.and Sidhu H.S. Finite difference schemes for multilayer diffusion. Math. Comput. Model. 2011, 54, 210–220. [CrossRef]
ASHRAE Fundamentals Handbook (S.I.), American Society of Heating, Refrigerating and Air Conditioning Engineers Inc., 1997.
C.A. Domínguez-Torres, R. Suárez, A.L. León-Rodríguez and A. Domínguez-Delgado. Experimental validation of a dynamic numeric model to simulate the thermal behavior of a facade. Appl. Therm. Eng. 2022, 204, 1359–4311. [CrossRef]
De Masi, R. F., Ruggiero, S., and Vanoli, G. P. Acrylic white paint of industrial sector for cool roofing application: Experimental investigation of summer behavior and aging problem under Mediterranean climate. Solar Energy 2018, 169, 468–487. [CrossRef]
Mastrapostoli, E., Santamouris, M., Kolokotsa, D., Vassilis, P., Venieri, D. and Gompakis, K. On the ageing of cool roofs: Measure of the optical degradation, chemical and biological analysis and assessment of the energy impact. Energy Build. 2016, 114, 191–199. [CrossRef]
Xue, X., Yang, J., Zhang, W., Jiang, L., Qua, J., Xu, L., Zhang, H., Song, J., Zhang, R., Li, Y., Qin, J., Zhang, Z. The study of an energy efficient cool white roof coating based on styrene acrylate copolymer and cement for waterproofing purpose. Part I: Optical properties, estimated cooling effect and relevant properties after dirt and accelerated exposures. Constr. Build. Mat. 2015, 98, 176–184. [CrossRef]
Allen Zielnik, A.; (2008) Durability, pausing for reflection on aging of the cool roof. Journal of Architect Coatings. June/July 2008:63-65. Available online: https://www.paintsquare.com/library/articles/Durability Pausing for reflection on aging of the cool roof.pdf (accessed on).
Bretz, S. E. and Akbari, H. Long-term performance of high-albedo roof coatings. Energy and Buildings 1997, 25, 159–167. [Google Scholar] [CrossRef]
Eilert, P. (2000). High albedo (cool) roofs: Codes and standards enhancement (CASE) study. San Francisco, USA: Pacific Gas and Electric Company. https://www.everglow.us/pdf (accessed on).
Prontuario de soluciones constructivas del CTE. Instituto de Ciencias de la Construcción Eduardo Torroja. Available online: http://cte-web.iccl.es/materiales.php (accessed on 12 March 2020).
Pedro Fernández Díaz. Centrales Térmicas. Biblioteca sobre Ingeniería Energética. Universidad de Cantabria. Available online: https://pfernandezdiez.es/es/libro?id=15 (accessed on 15 March 2020).
Agencia Estatal de Meteorología de España, 2010. Guía resumida del clima en España (1981-2010).
Auliac S, Le Hyaric A, Morice J, Hecht F, Ohtsuka K, Pironneau O, (2017). FreeFem++. Third Edition, Version 3.31-2. http:www.freefem.orgr.
Çengel, Y. (2007). Heat and Mass Transfer. A Practical Approach. McGraw Hill. Third Edition. [CrossRef]
Gentle, A. R., Aguilar, J. L. C.,Smith, G. B. Optimized cool roofs: Integrating albedo and thermal emittance with R-value. Sol. Energy Mater. Sol. Cells 2011, 95, 3207–3215. [CrossRef]
Rossi, M., Rocco, V. M. External walls design: The role of periodic thermal transmittance and internal areal heat capacity. Energy Build. 2014, 68, 732–740. [CrossRef]
Al-Sanea, S. A., Zedan, M. F., Al-Ajlan, S. A. Effect of electricity tariff on the optimum insulation-thickness in building walls as determined by a dynamic heat-transfer model. Appl. Energy 2005, 82, 313–330. [CrossRef]
Ozel, M. (2011). Effect of wall orientation on the optimum insulation thickness by using a dynamic method. Appl. Energy 2011, 88, 2429–2435. [Google Scholar] [CrossRef]
Daouas, N. Impact of external longwave radiation on optimum insulation thickness in Tunisian building roofs based on a dynamic analytical model. Appl. Energy 2016, 177, 136–148. [Google Scholar] [CrossRef]
Yuan, J., Farnham, C., Emura, K., Alam, M. A. Proposal for optimum combination of reflectivity and insulation thickness of building exterior walls for annual thermal load in Japan. Build. Environ. 2016, 103, 228–237. [CrossRef]
Arumugam, R. S., Garg, V., Ram, V. V., Bhatia, A. Optimizing roof insulation for roofs with high albedo coating and radiant barriers in India. Journal of Building Engineering 2015, 2, 52–58. [CrossRef]
Synnefa, A., Saliari, M.,Santamouris, M. Experimental and numerical assessment of the impact of increased roof reflectance on a school building in Athens. Energy Build. 2012, 55, 7–15. [CrossRef]
Reglamento de Instalaciones Térmicas en los Edificios. Ministerio para la Transición Ecológica y el Reto Demográfico. Available online: https://energia.gob.es/desarrollo/EficienciaEnergetica/RITE/Paginas/InstalacionesTermicas.aspx (accessed on).
Duffie, J.A., Beckman, W.(2006). Solar engineering of thermal processes. John Wiley and Sons Inc.
CYPE Engineers. (2017).CYPE Ingenieros Construction Price Generator. Last accessed: 28 March 2020.
Vincelas, FFC., Ghislain, T., Robert,T. Influence of the types of fuel and building material on energy savings into building in tropical region of Cameroon. Appl. Therm. Eng. 2017, 122, 806–819. [CrossRef]
Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Natural-gas-price-statistics (accessed on 22 March 2022).
Nydahl, H., Andersson, S., Astrand, A. P. and Olofsson, T. Including future climate induced cost when assessing building refurbishment performance. Energy Build. 2019, 203, 5. [CrossRef]
Commission Delegated Regulation (EU) No 626/2011 of 4 May 2011 supplementing Directive 2010/30/EU of the European Parliament and of the Council with regard to energy labelling of air conditioners.

Figure 1. Floor plan of the test cells.

Figure 2. Aerial photo taken using UAV technology.

Figure 3. Pattern of solar yearly reflectivity loss in %.

Figure 4. Layout of: (a) the reference roof; (b) the retrofitted roof.

Figure 5. Climatic chart of Seville.

Figure 6. Yearly heating, cooling, and total loads for the retrofitted roof with: (a) no wash of the cool coating; (b) quinquennial wash of the cool coating.

Figure 7. Yearly heating, cooling and total energy savings for the retrofitted and the reference roofs for: (a) no wash of the cool coating; (b) quinquennial wash of the cool coating.

Figure 8. LC heating, cooling, and total loads for the reference and retrofitted roofs with: (a) no wash of the cool coating; (b) quinquennial wash of the cool coating.

Table 1. Thermophysical characteristics of the reference roof.

Layer	Description	Thickness	Density	Specific Heat	Conductivity
		$(m)$	( $k g / m^{3}$ )	( $J / k g K$ )	( $W / m K$ )
1( Ext.)	Bituminous paint	0.0015	1150	1000	0.23
2	Ceramic tiles	0.005	2000	800	1.00
3	Mortar	0.01	2000	1000	1.40
4	Protective Layer	0.015	1150	1000	0.23
5	Mortar	0.01	2000	1000	1.40
6	Carbon cinders	0.1	640	657	1.40
7	Concrete vault	0.22	1330	1000	1.32
8 (Int.)	Gypsum plaster	0.01	1000	1000	0.32

Table 2. Thermophysical properties of the retrofitted roof.

Layer	Description	Thickness	Density	Specific Heat	Conductivity
		$(m)$	( $k g / m^{3}$ )	( $J / k g K$ )	( $W / m K$ )
1( Out.)	White elastomer	0.0015	1150	1000	0.23
2	Regularization layer	0.01	2000	1000	1.40
3	EPS	0.08	30	1210	0.04
4-10 (Int.)	Same as layers 1 to 7 of the reference roof (Table 1)

Table 3. Economic variables for the LCCA.

Variable	Value
EPS cost	116	$€ / m^{3}$
Insulation installation cost	13.15	$€ / m^{2}$
Cool paint cost	9.45	$€ / m^{2}$
Washing cost	1.63	$€ / m^{2}$
Bituminous paint cost	8.01	$€ / m^{2}$
Bituminous paint maintenance	0.4	$€ / m^{2}$ yearly
Electricity cost	0.2403	kWh
Energy inflation rate	$1.5 - 3.0 - 6.0$	%
Discount rate	$1.0 - 1.5 - 3.0$	%
Lifetime	20	years

Table 4. Life Cycle loads and energy savings kWh/m².

	Heating Load	Cooling Load	Total Load	Total Energy Saving
Reference roof	574.35	766.56	1340.91	-
Retrofitted roof (No Wash)	269.23	103.03	365.29	975.62
Retrofitted roof (Quinq. Wash)	280.23	90.27	370.51	970.40

Table 5. Life Cycle Energy Savings for the districts and neighborhood as a whole.

District	No Wash	Quinquennial Wash
A	21796326.4 kWh	21679684.1 kWh
B	22781702.6 kWh	22659787.1 kWh
C	24696844.7 kWh	24564680.3 kWh
D	22923167.5 kWh	22800494.9 kWh
E	16911397.1 kWh	16820896.3 kWh
All	109109.44 mWh	108525.54 [] mWh

Table 6. Life Cycle monetary savings and associated payback periods.

No Wash
				NCS [ $€]$ for roof surface
i	dr	NCS [ $€ / m^{2}$ ]	PB [years]	60 m²	70 m²	80 m²
0.015	0.01	57.26	7.69	3435.6	4008.2	4580.8
0.03	0.015	64.96	7.15	3897.6	4547.2	5196.8
0.06	0.03	77.18	6.84	4630.8	5402.6	6174.4
Quinquennial Wash
				NCS [ $€]$ for roof surface
i	dr	NCS [ $€ / m^{2}$ ]	PB [years]	60 m²	70 m²	80 m²
0.015	0.01	52.45	8.12	3147	3671.5	4196
0.03	0.015	60.03	7.42	3601.8	4202.1	4802.4
0.06	0.03	72.026	6.93	4321.56	5041.82	5762.08

Table 7. Net Savings [€] for the districts and the entire neighborhood. The values of i and dr are given in %.

	No Wash			Quinquennial Wash
District	i=1.5 ,d=1	i=1,d=1.5	i=6,d=3	i=1.5,d=1	i=1,d=1.5	i=6, d=3
A	1279245.66	1451271.36	1724278.38	1171785.45	1341130.23	1609222.23
B	1337078.26	1516880.96	1802230.18	1224759.95	1401760.53	1681972.53
C	1449479.64	1644397.44	1953734.52	1327719.30	1519599.42	1823367.42
D	1345380.96	1526300.16	1813421.28	1232365.20	1410464.88	1692416.88
E	992544.84	1126016.64	1337838.12	909168.30	1040560.02	1248568.02
All	6403729.36	7264866.56	8631502.48	5865798.20	6713515.08	8055547.08

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Feasible Proposal for Energy-Efficient Roof Retrofitting in Southern European Obsolete Residential Neighborhoods

Abstract

1. Introduction

1.1. Passive Roofs Strategies

1.2. The Case Study Approach

2. Materials and Methods

2.1. Methodology for Energy Computation

2.1.1. Physical Framework

2.2. Mathematical Formulation

2.2.1. Energy Balance on the Outer Roof Surface

2.2.2. Absorbed Solar Radiation Calculation

2.2.3. Long-Wave Radiative Exchange with the Sky

2.2.4. Heat Exchange between the Roof and the Ambiance Air

2.2.5. Heat Conduction through the Roof

2.3. Changes in Cool Roof Reflectivity due to Aging

2.4. Roof Energy Calculation

2.4.1. Case Buildings

2.5. Numerical Resolution

2.6. Methodology for the Life Cycle Cost Analysis

2.7. Economics Indicators

3. Results and Discussion

3.1. Energy Results

3.2. LCCA Results

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe