Prerpints.org logo
Preprint
Article

The Fatigue Response's Fingerprint of Composite Materials Subjected to Constant and Variable Amplitude Loadings

Altmetrics

Downloads

63

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 October 2023

Posted:

20 October 2023

You are already at the latest version

Alerts
Abstract
This paper discusses the theoretical and experimental correlations between fatigue and static strength statistical distributions. We use a two-parameter residual strength model that obeys the qualitative Strenght-Life Equal-Rank (SLERA) assumption for guidance. The modeling approach consists of recovering the model's parameters by best fitting the constant amplitude (CA) fatigue data at a given stress ratio, R, and the experimental Weibull parameters of the static strength distribution function. Once the model's parameters are fixed, its capabilities, potential, and limits are discussed by comparing its predictions with residual strength and fatigue data obtained at different stress ratios, R. Moreover, from a preliminary analysis, the theoretical extension of the model's capabilities to variable amplitude loadings is conceptualized. The application of Miner's rule is also discussed and compared with a new damage rule to analyze the fatigue responses under variable amplitude loadings.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

The mechanical properties of polymer composites are broadly scattered and require statistical treatments based on large data sets under static or cyclic loading conditions. The scatter is attributed to the accumulation of diffuse damage mechanisms that synergistically develop at different lengths and time scales and are eventually triggered by existing defects, including voids, fiber misalignments, and residual stress from the production process. Matrix cracking, fiber-matrix detachment, fibers and ply rupture, fibers buckling, and delamination progressively degrade the composites’ mechanical properties.
For these reasons, designing a composite structure requires more extensive mechanical tests than metal structures quantified in Ref. [1]. Thus, the mechanical characterization of composites still represents one of the more expensive activities in structural applications, a requirement for which some industrial compartments do not have the resources or the time. Depending on the unicity of each composite structure, the different origins and locations of the damage mechanisms, rather than the propagation of a single crack, prevent any possibility of establishing sound inspection and maintenance criteria, as in metals. To this end, reliable simulation techniques may significantly reduce testing procedures. Two substantial approaches have been followed over the years. Mechanistic/hierarchical models are based on specific failure criteria depending on the length scales and the sequence/interaction of the damage mechanisms [2,3,4,5,6]. However, the intricacy of damage accumulation mechanisms forces researchers to develop phenomenological models [7,8,9,10,11,12,13,14] without providing any information about the damage mechanisms, the events being predicted based on empirical criteria involving macro-stress components. The mechanistic and phenomenological approaches are not in contrast, the latter being addressed to supply analytical tools to perform reliability and scatter analysis on large databases of specific categories of composites subjected to particular loading conditions of fully developed structures. The Reifsnider’s "Critical Element Model" [2], based on micromechanical representations of strength at increasing length scales, and the "Generalized Material Property Degradation Model" implemented by Shokrieh and Lessard [4] belong to the same model’s category, representing an intermediate level of modeling the fatigue process between phenomenological and mechanistic approaches. In both cases, the phenomenological models from the macro level are combined with failure criteria and property degradation rules. However, neither Reifsnider’s nor Shokrieh and Lessard’s models account for the highly stochastic behavior observed in the fatigue life of composites, a prerogative of some phenomenological modeling approaches. The argument was discussed comprehensively by Vassilopoulos and Keller [7] and y Philippidis and Passipoularidis [8], where several models tested on the same set of fatigue life and residual strength data revealed that the statistical predictions at various stress levels and life fractions were largely unreliable. As a guide, this paper considers the fatigue’s stochastic nature in composites using a two-parameter formulation, inherently obeying the Strength-Life Equal-Rank Assumption (SLERA), and explicitly accounting for the stress ratio, R, [9,10,11].
The SLERA states that if a sample of components could be tested for static strength and fatigue life expectancy, each member would occupy the same rank in the strength and life data sets. However, despite its potential powerfulness, the SLERA cannot be proved from one side, and its application to notched specimens is debated.
Based on the literature data, the reliability of the modeling procedure in predicting the fatigue life and the residual strength kinetics of open-hole (OH) laminates will be verified. Then, its robustness is further explored for variable amplitude loadings.

2. Experimental data

In this paper, we analyze a large set of fatigue life and residual strength data for AS4 carbon/epoxy 3k/E7K8 Plain Weave Fabric with [45/-45/90/45/-45/45/-45/0/45/-45]S layup. The experimental data belong to a series of extensive campaigns under the Federal Aviation Administration (FAA) aegis, where 384 specimens of the same material with different geometries were subjected to various loading conditions [1].
Here, we analyze the fatigue data sets obtained on specimens subjected to tension-tension (OHT) at R=0, prevailing tension (OHT) at R=-0.2, pure compression (OHC) at R=5, and tension/compression (OHTC) at R=-1.
As a common practice in the aerospace industry, the experimental characterization included approximately twenty-one fatigue tests performed at three stress levels, six static and three residual strength tests, and given the stress ratio, R [15].
The OH test methods were designed to produce tensile or compressive strength data for structural design allowable. Deeper details on materials and specimen geometry (including hole diameter, diameter-to-thickness ratio, and width-to-diameter ratio) can be found in Ref [1].
The model presented in [15] will be recalled in what follows. Then, the procedure for determining residual strength and fatigue life of carbon fiber-reinforced composites is illustrated.

3. Model description

Our approach is based on a formulation that fulfills the following commonly accepted assumption:
i)
A two-parameter Weibull distribution function represents the composites’ static strength.
ii)
The fatigue limits seem unlikely in composite materials or irrelevant in the cycles encountered in practical applications. Thus, every load cycle potentially damages a composite structure and should be considered in life prediction calculations.
iii)
The residual strength, that is, the strength measured on a sample subjected to cyclic loading under a given loading condition, slowly degrades in the first cycle’s decades and suddenly drops towards the maximum applied stress within a narrow cycle interval.
Moreover, the model obeys the Strength-Life Equal-Rank assumption (SLERA) formulated by Hahn and Kim [16] and then by Chou and Croman [17] : "A specimen of a certain rank in the fatigue life distribution is assumed to be equivalent in strength to the specimens of the same rank in the static strength distribution".
In addition, the fatigue formulation described below simultaneously analyzes fatigue and static strength data, provided the loading rates used to measure the static strength are comparable with those in fatigue. This aspect will be discussed in what follows.
Our fatigue life formulation first developed was:
σ 0 = σ m a x 1 − R ( N β − 1 ) + 1
where N is the number of cycles to failure, σ m a x the maximum applied cyclic stress, R = σ m i n σ m a x , σ 0 the static strength, and α and β the model’s parameters obtained by best fitting the fatigue data through Equation (1a) rearranged as follows:
σ m a x = σ 0 α N ∗ β − 1 1 − R + 1
We recall that the monotonic material strength, σ0, is well represented by a two-parameter Weibull distribution. Therefore, the probability of finding a σ0 value≤x is given by:
F σ 0 x = P σ 0 ≤ x = 1 − e x p − ( x / γ ) δ
where γ is the scale parameter or the characteristic strength, and δ is the shape parameter.
Indeed, from Equation (1a) and (2), the original strength of the virgin samples, σ0N, fatigued until failure at cycle N*, can be recovered, and it should coincide with the statistical distribution of static strength, σ0.
Furthermore, coupling Equations (1a) and (2) one obtains:
F N ( N ∗ ) = P N ∗ ≤ N = 1 − e x p − σ m a x   1 + α N ∗ β − 1 1 − R γ δ
From equation (3), given σmax and R, the scatter in fatigue life exhibited by different samples conforms to the variability in monotonic strength. Thus, in principle, Equation (3) obeys the Strength-Life Equal Rank Assumption (SLERA) [16, 17] and accounts for the stochastic nature of strength and fatigue life. Solving Equation (3) for N*, one obtains
N ∗ = 1 + 1 α ( 1 − R ) γ σ m a x l n 1 − F N N ∗ 1 δ − 1 β
from which the classical S-N curve for a fixed probability of failure F N N ∗ can be calculated, given the stress ratio, R.
Concerning the residual strength, once the parameters α, β, γ and δ are known, according to the developments already shown in [18], the following distribution function can represent the strength evolution with cycles:
F σ n ≥ σ N ∗ = σ n i − σ m a x σ O N i − σ m a x = e x p − σ m a x   1 + α n β − 1 1 − R γ i δ
In Equation (4) σ n i is the strength of a sample fatigued n≤N cycles under given σ m a x ad R; σ O N i is the virgin strength of the sample with a given rank in the nominal static strength distribution function. Thus, Equation (5) describes the residual strength of a generic sample, σ n i    as it degrades progressively from its virgin value, σ O N i , to the maximum cyclic stress, σ m a x , where failure occurs. Equation (5) can also be used to describe the statistics of the residual strength experimentally obtained at a given number of cycles, n, given σ m a x and R.
Incidentally, rearranging Equation (5), when σ n ≅ σ m a x , namely in the vicinity of failure, when n ≅ N, Equation (1) is recovered as follows:
− l n σ n i − σ m a x σ O N i − σ m a x 1 δ = σ m a x   1 + α N β − 1 1 − R γ ≅ 1
Equation (6) confirms that the fatigue life predictions, namely Equations (1a,b), can be regarded as an extreme case of the residual strength model, n according to Chou and Croman [6].

4. Results and Discussion

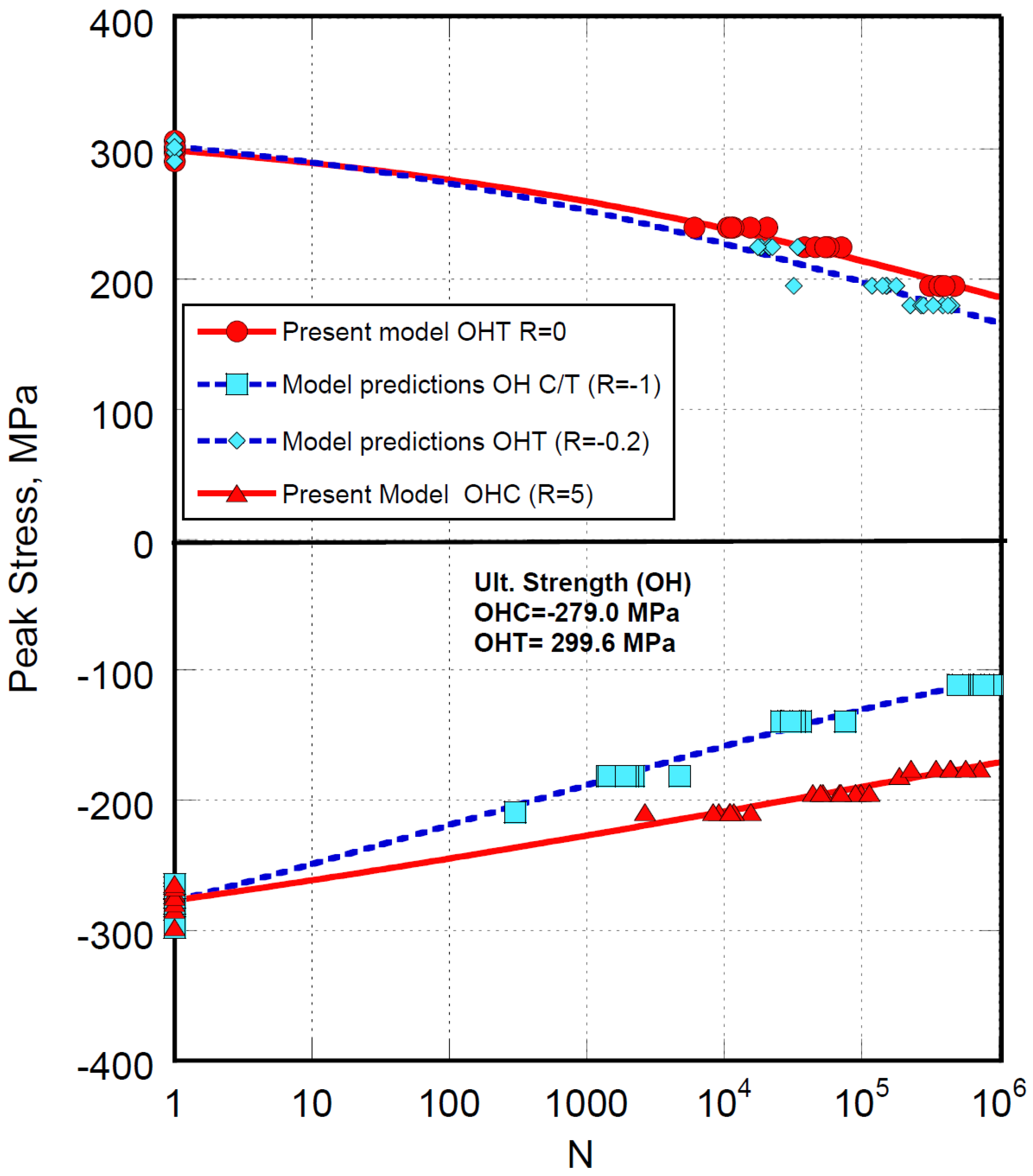
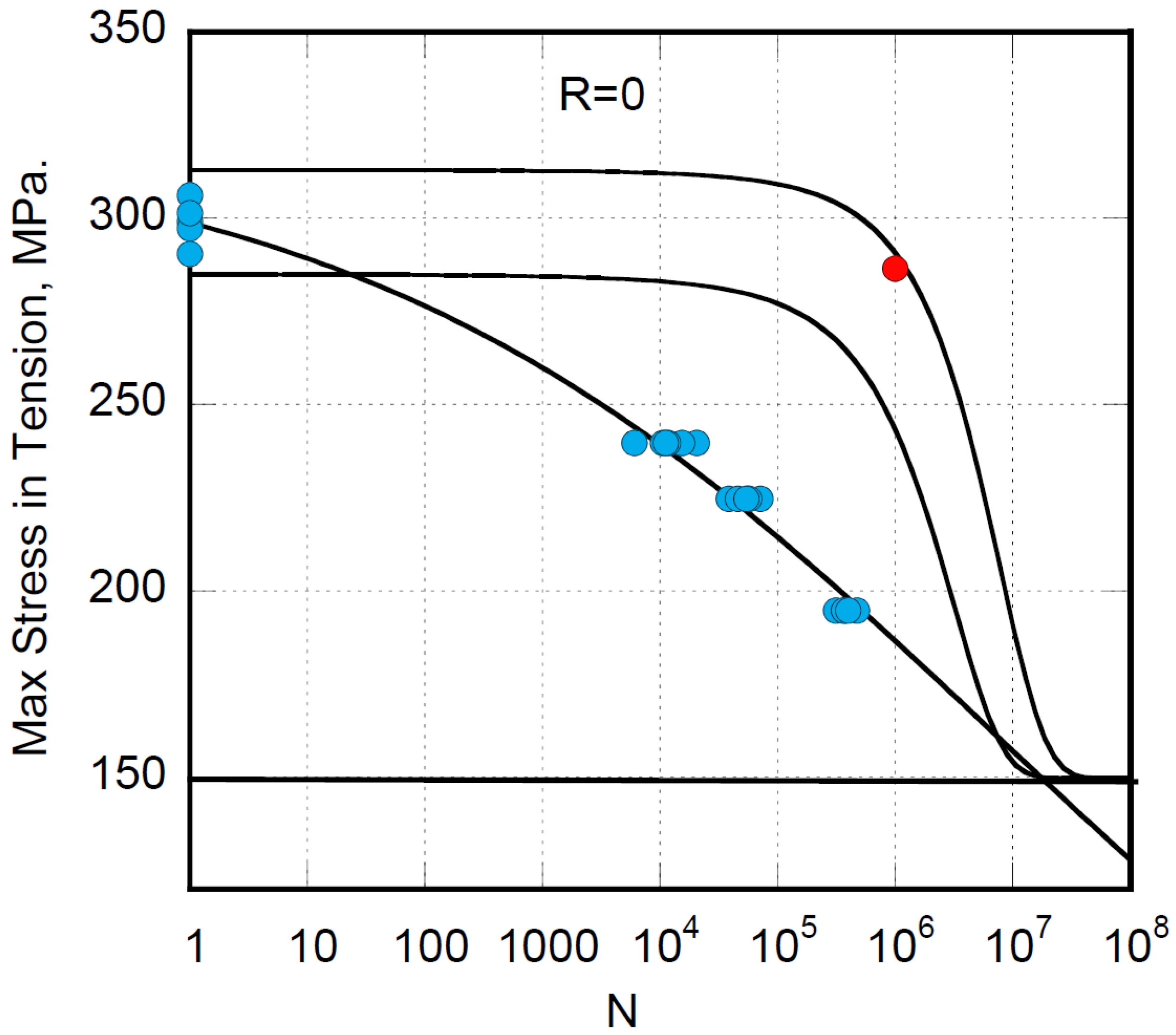
The fatigue life data of open-hole tension (OHT) and compression (OHC) samples at different stress ratios, R, are reported in Figure 1. The data at R=0 and R=5 have been analyzed using Equation (1), allowing, by least square methods, the calculation of the two model’s parameters under pure tension and compression, namely αt=0.074 and βt=0.160 and . αc=0.127 and βc=0.174, respectively.
Preprints 88310 g001
Figure 1. Model predictions of fatigue life at different loading ratios, R, as indicated in the inset. The experimental data are taken from Ref.[1].
Figure 1. Model predictions of fatigue life at different loading ratios, R, as indicated in the inset. The experimental data are taken from Ref.[1].
Preprints 88310 g001
The deterministic nature of Equation (1) was converted to its statistical counterpart by applying the Strength-Life Equal Rank assumption (SLERA), namely, a longer fatigue life belongs to specimens exhibiting a higher static strength. To substantiate this statement Equation (1) was solved for σ 0 in Ref. [11]:
σ 0 = σ 0 N = σ m a x 1 − R ( N β − 1 ) + 1
According to the proposed procedure, the fatigue data under prevailing tension, namely R=-0.2 are predicted with the model’s parameter αt and βt. Moreover, despite the arithmetic symmetry of the stress ratio, the compression damage mechanisms developing at R=-1 prevail, with higher loading severity in compression, given that the distance from the static strength in compression is lesser than the counterpart in tension. Consequently, the data at R=-1 will be predicted with the parameters already obtained under pure compression, namely αc and βc.
From Figure 1, the model predictions at R=-0.2 and R=-1 show that the fatigue data fall reasonably on the predicted curves.
As shown above, Weibull’s and model parameters are easy to obtain and remain fixed in predicting fatigue beyond the experiments. Thus, no adjustments will be allowed in what follows. We only mention that the stress ratio, ROHC, is normalized in modeling compression-dominated fatigue data. For instance, at ROHC=5, R = 1 R O H C = 0.2 in Equation (1)
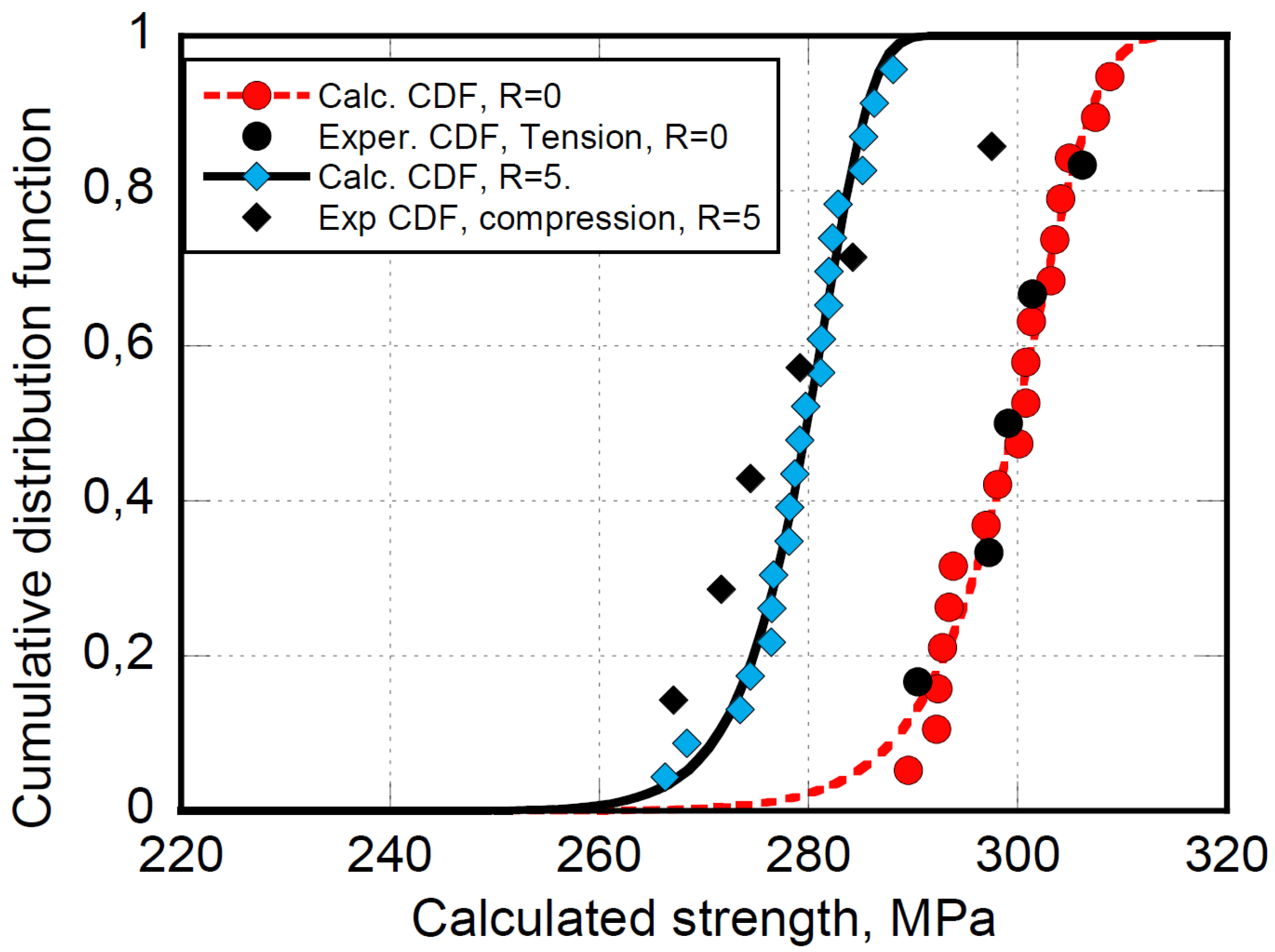
Equation (7) states that the static material strength, labeled by the symbol σ 0 N to identify the calculated virgin strength, can be evaluated from the fatigue data, and the calculated statistical distribution coincides with the Weibull distribution of the measured strength, namely σ 0 = σ 0 N . Thus, from Equation (7), the nominal static strength distribution, σ0N, of samples subjected to fatigue until failure can be recovered and reported in Figure 2 for OHT at R=0 and OHC at R=5. The corresponding experimental static strength data set, also reported in Figure 2, appears well described in both cases. According to a two-parameter Weibull statistical distribution, the nominal strength’s scale and shape factors are γt= 302 MPa and δt=53, and γc=281 MPa and δc=61, respectively.
Preprints 88310 g002
Figure 2. Experimental and calculates static strength distributions.
Figure 2. Experimental and calculates static strength distributions.
Preprints 88310 g002
It is worth mentioning that the application of Equation (7), namely the superposition of the experimental and calculated static strength, as shown in Figure 2, is subjected to well-defined conditions. The literature frequently reports that static strength is measured at loading rates much lower than fatigue, or no information is given on the loading rates adopted to measure it. In those cases, the fatigue life model’s parameters, Equation (1), are obtained by excluding the static data. This argument has been largely debated so far [NIJISSEN]. The discussion is of primary importance in polymer-based composites where the matrix’ viscoelastic nature plays a dominant role at low content of fibers. The loading rate also influences the kinetics of damage accumulation since higher loading rates give rise to higher strength and longer life expectancy. Therefore, scaling procedures are needed when high frequencies are used to minimize the experimental characterization time to predict the responses of composite structures eventually subjected to lower in-service loading frequencies. This aspect is strictly connected with the random loading that composite structures may suffer during their service life. From above, it comes out that the complexity of fatigue response under CA loadings, including the SLERA assumption, can only be managed with coherent data sets and that models predicting the VA response are far to come. For instance, the loading rate, LR, in fatigue can be approximated by the following Equation:
L R = 2 ∗ ∆ σ ∗ f = 2 ∗ σ m a x 1 − R ∗ f
where f is the loading frequency. To roughly illustrate, with σ m a x = 250   M P a , R=0 and f=10Hz, it results LR=5,000 MPa/s.Therefore, the static tests under load control for samples with a cross-section of 12 mm2 require the application of 60,000 N/s. If the elastic modulus along the direction of the applied load is 25,000 MPa, then, under displacement control, the strain rate is ε ˙ =0.2 s-1, and the static strength of samples of length L=100 mm should be measured at a cross-head speed of 120 mm/s. However, when dealing with high-performance carbon fiber composites, the stacking sequence consists of layers oriented along the load direction. In those cases, the strength sensitivity to the loading rate is very low []. For instance, unidirectional carbon fiber composites’ strength shows negligible loading rate dependence. In all the other cases, measuring the strength as a function of the strain rate is mandatory.
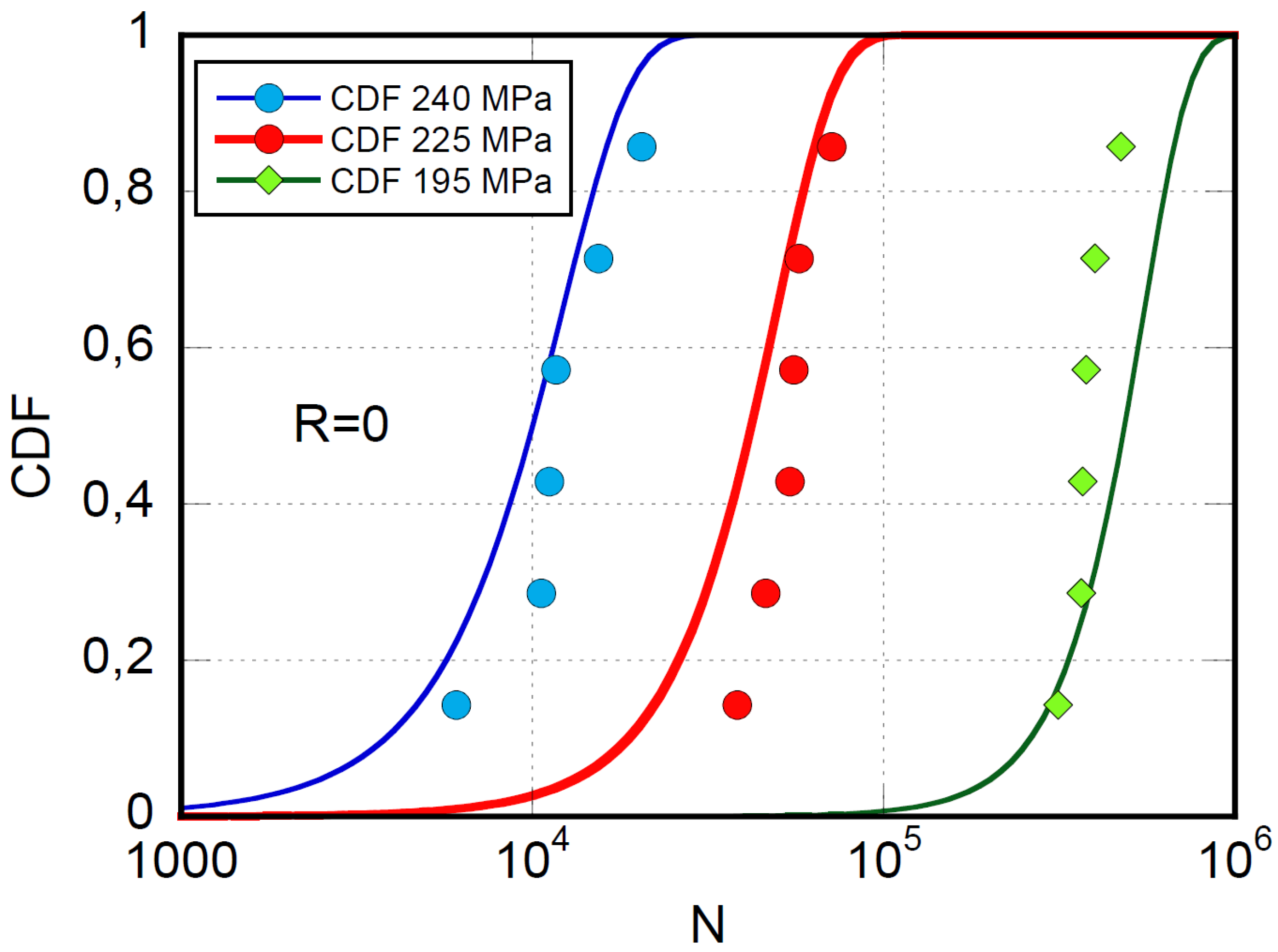
A further implication of the modeling procedure is described by Equation (3), describing the statistics of failure cycles, given σ m a x   and R. With the model’s parameters already found, the experimental data at R=0 and σ m a x = 240 ,   225   a n d   195   M P a , and the model’s predictions are reported in Figure 3.
Preprints 88310 g003
Figure 3. The fatigue life distribution function at different maximum stresses and R=0.
Figure 3. The fatigue life distribution function at different maximum stresses and R=0.
Preprints 88310 g003
With the relatively narrow data set available, we consider satisfying the predictions. Not reported here, the model’s capability to replicate the experimental distribution of fatigue data was verified at different stress ratios, R, with the same quality. Thus, Equation (3) establishes a robust analytical correlation between the static strength and the fatigue distribution functions.
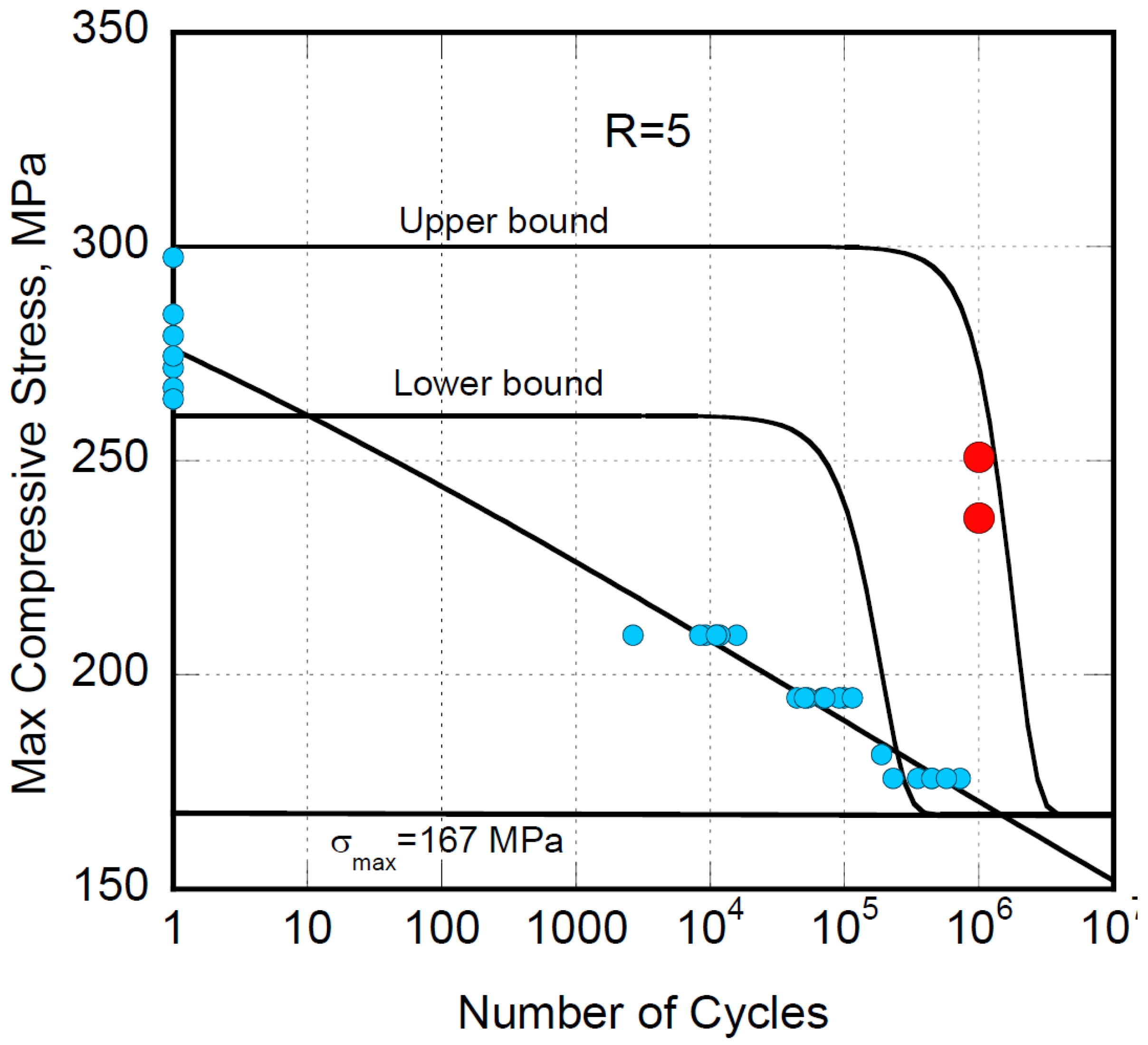
Moreover, based on Equation (5), the statistical distribution of residual strength can be predicted under different loading conditions. To illustrate, let us first recall that, given the loading conditions, namely, σ m a x   and R, stronger samples will fail at a higher number of cycles, according to the strength-life-equal rank assumption (SLERA). Accordingly, the residual strength data should remain confined between the strongest and weakest samples’ strength degradation curves routinely taken from the extreme tails of the static strength’s cumulative distribution function, namely when F=0.95 and 0.05, respectively. 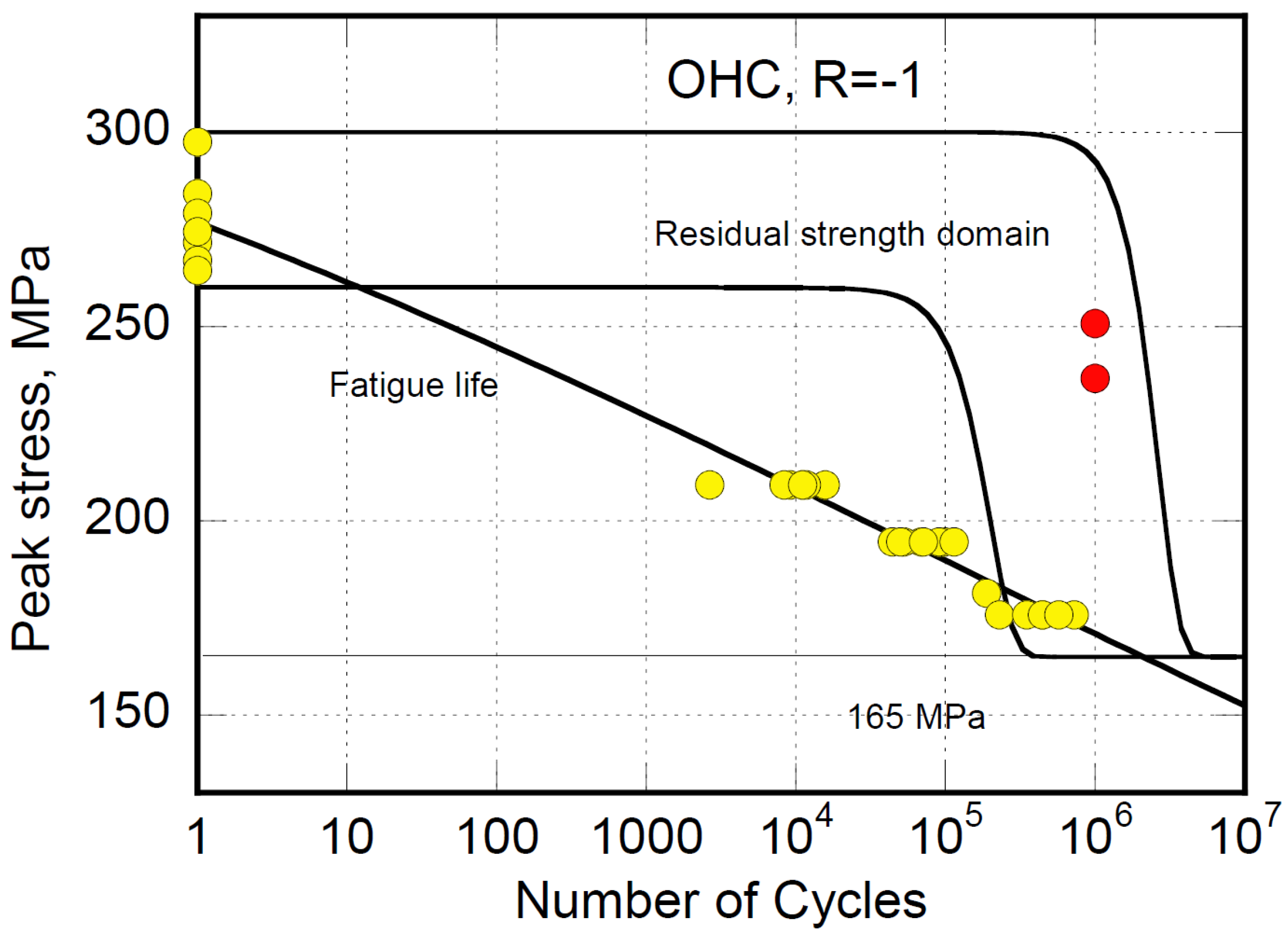To this end, Figure 4, Figure 5 and Figure 6 report the model predictions for (OHT) at R=5, R=0, and R=-1 respectively. As expected, the residual strength data taken after a million cycles are well within the domain confined between the boundaries referred to as upper and lower bounds, describing the strength degradation kinetics of the weaker and stronger samples. Furthermore, at R=-1, the substantial degradation mechanisms are debited to macro stresses acting in compression and tension. However, it should be mentioned that even if the nominal cyclic loading severity in tension and compression is the same ( σ m a x = σ m i n ) the damage accumulation and strength degradation kinetics result in compression failure. In the framework of our approach modeling it is evident that, given σmax and R, the strength degradation kinetics depend on the "distance" from the virgin strength, which is lower in compression than in tension for the laminate under study. Thus, the predictions at R=-1 use scale and shape factors, γ and δ, of the cumulative distribution function coming from the calculations based on Equation (1) applied to the pure compression data, namely , R=5. Such deliberate approximation is strong proof of the approach’s robustness, even if deeper insight can be obtained by recovering the shape and scale factors from the data at R=-1 using Equation (7). Herein, we are just proposing a general procedure that, at first glance, appears promising. Furthermore, it is worth mentioning that in Equation (5), describing the continuous upper and lower bound curves of Figure 4, Figure 5 and Figure 6 delimiting the pertinent residual strength domain, the parameters αc, βc, γc, and δc are already fixed and come from a different data set while n is the running variable. Thus, the procedure so far illustrated is entirely predictive.
In summary, the fatigue life, the statistical distribution of cycles to failure, and the residual strength can be managed simultaneously through a single set of parameters, namely, α, β, γ and δ, provided the sign of the prevailing macro stress is recognized. For instance, in composites, the dominant fracture occurs in compression when R=5 and R=-1, where both tension and compression stresses are in play.
Preprints 88310 g004
Figure 4. Residual strength (red circles) prediction at R=5.
Figure 4. Residual strength (red circles) prediction at R=5.
Preprints 88310 g004
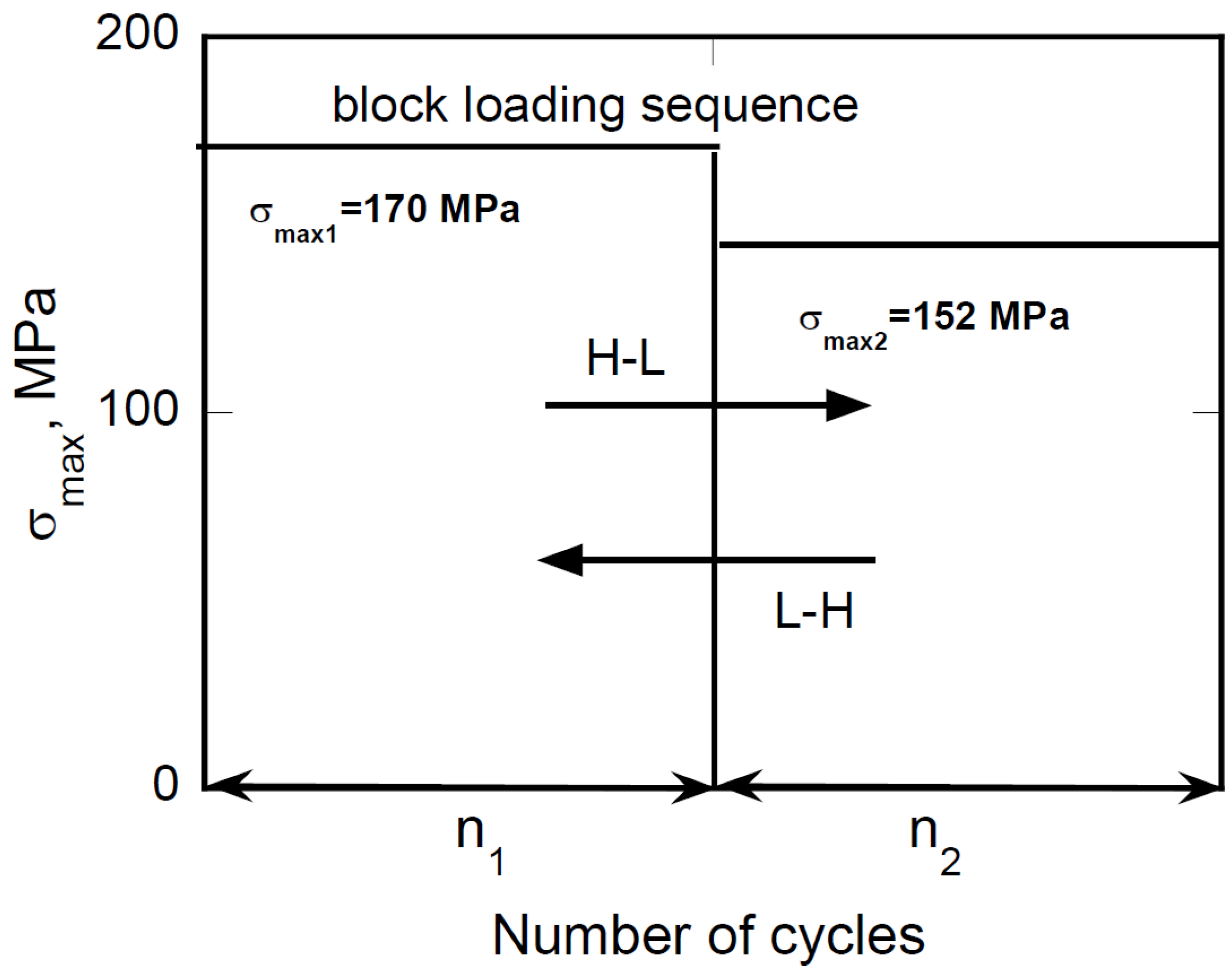
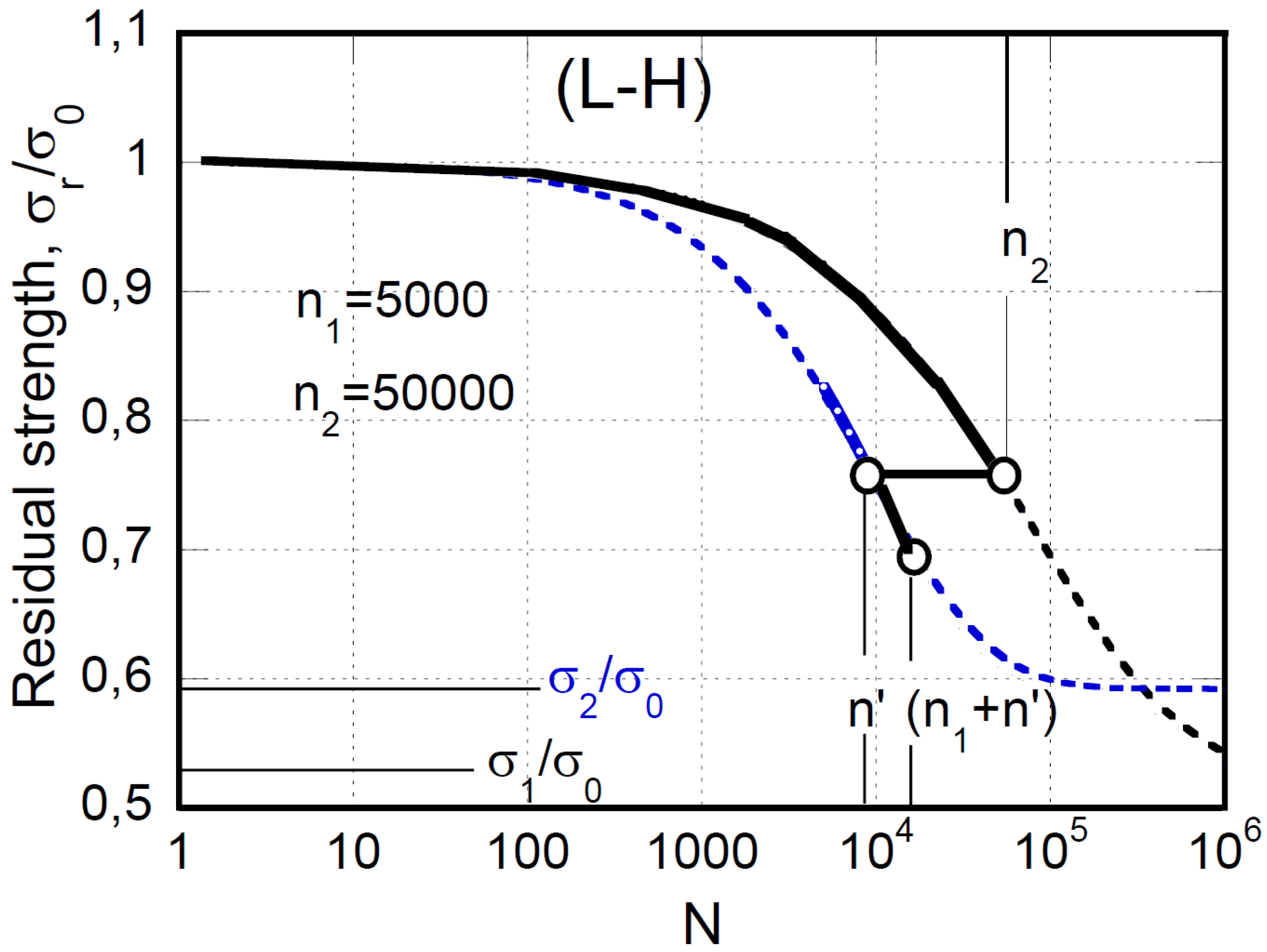
It should be underlined that only two of the four parameters come from the fitting procedure, namely α and β, while γ and δ come from the experimental statistical distribution of strength data. In the framework of our approach, the four parameters represent the material’s fingerprint, even limiting our discussion to the experimental data obtained under constant amplitude loading. A different story and complexity emerge when random loadings are in play. To this end, in what follows a preliminary approach to circumvent the complexity of fatigue response under variable amplitude loadings. The discussion is confined to the simplest case of two-block loading. The blocks have different durations, namely 50,000 and 5,000 cycles, and loading is performed at constant amplitude at a given stress ratio, R, and different maximum applied stress, σ m a x = 170   M P a   a n d   σ m a x = 152   M P a , respectively, as depicted in Figure 7, where the schematic of high-to-low (H-L) and low-to-high (L-H) loading sequences is reported.
Preprints 88310 g005
Figure 5. Residual strength (red circles) prediction at R=0.
Figure 5. Residual strength (red circles) prediction at R=0.
Preprints 88310 g005
Preprints 88310 g006
Figure 6. Residual strength (red circles) prediction at R=-1.
Figure 6. Residual strength (red circles) prediction at R=-1.
Preprints 88310 g006
The sequence is arbitrary, yet it allows discussing Miner’s rule for damage accumulation in detail when variable amplitude loadings are in play. Symbolically, the Miner’s rule can be expressed as:
D = ∑ i n i N i
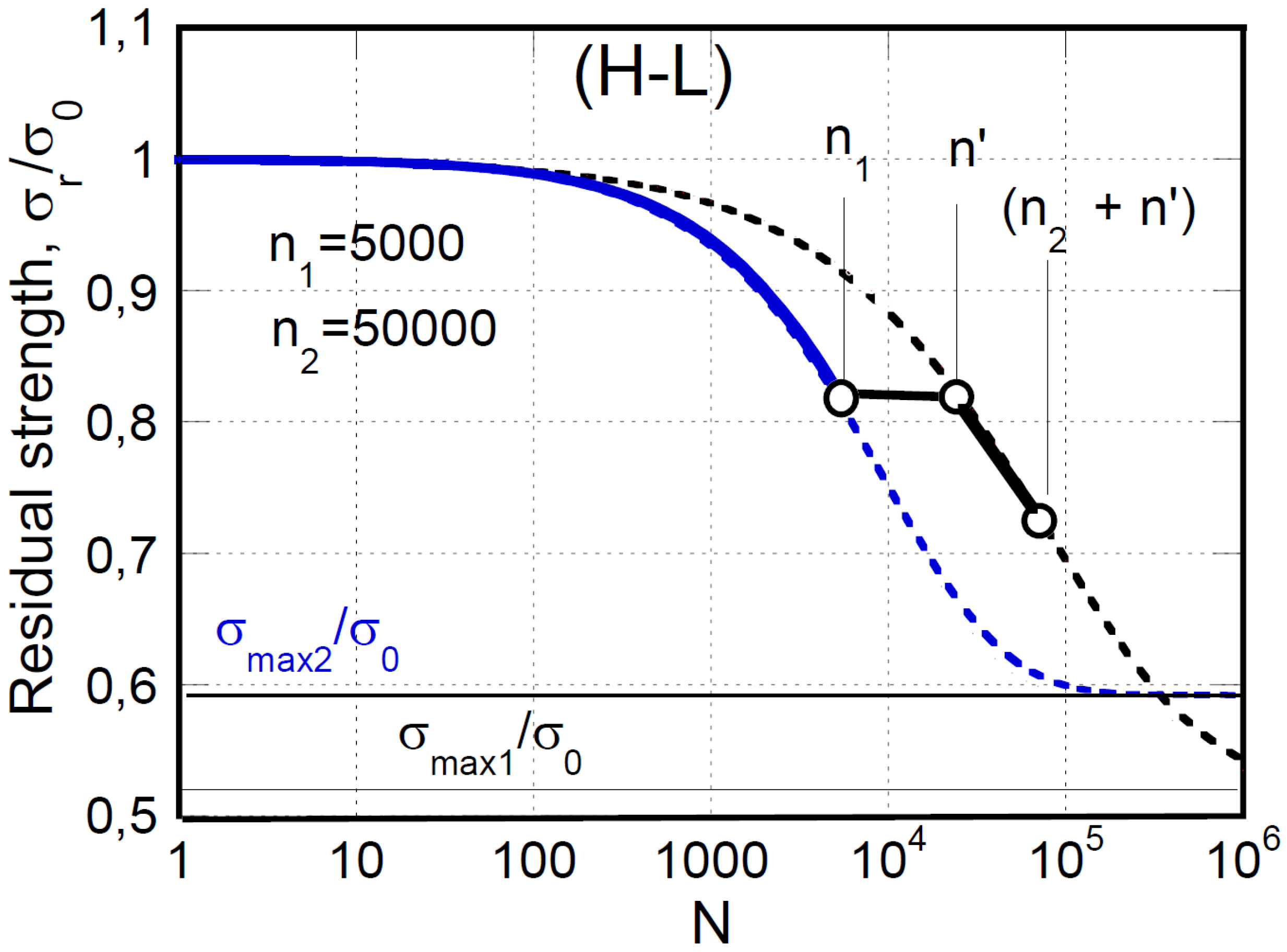
where ni is the number of cycles elapsed under given CA loading condition, and Ni is the number of cycles to failure under the same loading condition. For the case under study, the number of cycles to failure were N( σ m a x 1 )≈ 1x105 and N( σ m a x 2 ) ≈ 1106, respectively, and the damage calculated through the Miner’s rule is D≈0.1, regardless of the loading sequence, as expected. In Figure 8, the strength degradation path for H-L sequence is schematically described. Starting from the normalized mean static strength, i.e., σr/σ0=1, the strength degrades following the baseline degradation curve at higher applied maximum stress, σ m a x 1 , until the end of the first loading block when n=5000. The second bloc starts with the strength reached at the end of the first block and from the adjourned number of cycles, n’. The strength degradation proceeds for n2 cycles following the degradation curve at a lower stress, σ m a x 2 . Similarly, the response to the ascending L-H sequence is illustrated in Figure 9.
Preprints 88310 g007
Figure 7. Schematic of the H-L and L-H block cycle sequence.
Figure 7. Schematic of the H-L and L-H block cycle sequence.
Preprints 88310 g007
The effect of the loading sequence can be quantified employing the damage, D, accumulated within the materials [18,19] , defined here as follows:
D = ∑ i = 1 k σ i r − σ ( i + 1 ) r σ 0 − σ m a x i
Where σ i r − σ ( i + 1 ) r is the residual strength variation under the ith loading block characterized by ,    σ m a x i and Ri, and σ 0 − σ m a x i is the total degradation extent under the same loading condition. The damage so far defined is compared with the one calculated through Miner’s rule, and the data are reported in Table 2.
Preprints 88310 g008
Figure 8. Schematic of two-block H-L strength degradation path.
Figure 8. Schematic of two-block H-L strength degradation path.
Preprints 88310 g008
Preprints 88310 g009
Figure 9. Schematic of two-block L-H strength degradation path.
Figure 9. Schematic of two-block L-H strength degradation path.
Preprints 88310 g009
Table 2. The damage accumulation predictions based on Miner’s rule and Equation (10).
Table 2. The damage accumulation predictions based on Miner’s rule and Equation (10).
Miner’s rule Equation (10)
H-L sequence 0.1 0.63
L-H sequence 0.1 0.65
Our results evidence the fault of the Miner’s rule. First, it cannot discriminate the loading sequence; secondly, the accumulated damage appears highly unconservative. Nonetheless, the Miner’s rule is still used in a series of commercial software and as a reference in predicting the damage accumulation with different formulations [20]. Our approach discriminates the loading sequence, and the predicted damage is at least more conservative regarding Miner’s rule.
Finally, the utterly arbitrary loading sequence adopted herein allows the use of our approach cycle-by-cycle for random loadings.

5. Conclusions

A statistical model is needed to predict the stochastic responses of composite materials subjected to fatigue loadings. Based on strength degradation, a phenomenological two-parameter model has been used to predict the residual strength and fatigue life of open-hole (OH) carbon/epoxy laminates subjected to different loading conditions from pure tension to compression and mixed tension/compression.
The residual strength and the fatigue life data on samples subjected to tension and compression loadings were used to fix the model’s parameters. Then, the procedure was applied to predict the fatigue data under prevailing compression or tension loadings with the pertinent set of model parameters.Based on two-blochs loadings, it was highlighted that the damage accumulation mechanisms show different kinetics depending on the loading sequence. This aspect is reflected (even if not strictly correlated) to the strength degradation kinetics and implies the possibility of considering our model parameters as the material fingerprint. The approach seems quite promising, since under uniaxial loadings, a single set of parameters is required in tension or compression and used at different loading ratios, R provided the dominant strength in tension or compression are accounted for. The Miner’s damage rule is critically discussed, highlighting our approach’s conservative characteristics and reliability.

References

  1. DOT/FAA/AR-10/6 (2011) "Determining the Fatigue Life of Composites Aircraft Structures Using Life and Load-Enhancement Factors" http://www.tc.faa.gov/its/worldpac/techrpt/ar10-6.pdf.
  2. Reifsnider K.L. , The Critical Element Model: A modeling philosophy, Eng. Fract. Mech. 25(1986), pp 739-749. [CrossRef]
  3. K.L. Reifsneider Ed., Fatigue of Composite Materials, Elsevier Publ., New York, 1990, pp. 231-237. [CrossRef]
  4. Shokrieh M.M., Lessard L.B., Progressive fatigue damage modelling of composite materials, Part I: Modeling, J. Compos. Mater.34(2000), pp.1056-1080.
  5. R. D. B. Sevenois, W. Van Paepegem , Fatigue Damage Modeling Techniques for Textile Composites: Review and Comparison, Applied mechanics reviews (2015), 67 (2), .020802-(1-12). [CrossRef]
  6. M. Quaresimin, P. A. Carraro, L. Pilgaard Mikkelsen, N. Lucato, L. Vivian, P. Brøndsted, B. F. Sørensen., J. Varna, R. Talreja. Damage evolution under internal and external multiaxial cyclic stress state: a comparative analysis, Composites: Part B, 61(2014): 282–290.
  7. Vassilopuolos A.P., Keller T., Fatigue of Fiber-Reinforced Composites, (2011) Springer, ISBN 978-1-84996-180-6.
  8. T.P. Philippidis, V.V. Passipoularidis Residual strength after fatigue in composites:Theory vs. experiment Int. J. Fatigue 29 (2007) 2104-2116.
  9. D’Amore A., Caprino G., Stupak P., Zhou J., Nicolais L., "Effect of stress ratio on the flexural fatigue behaviour of continuous strand mat reinforced plastics", Science and Engineering of Composite Materials 5, 1-8 (1996). [CrossRef]
  10. D’Amore A., Giorgio M., Grassia L., Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading, International Journal of Fatigue 78 (2015) 31–37. [CrossRef]
  11. D’Amore A, Caprino, G., Nicolais, L., Marino, G. (1999). Long-term behaviour of PEI and PEI-based composites subjected to physical aging. Composites Science and Technology, vol. 59, p. 1993-2003, ISSN: 0266-353. [CrossRef]
  12. Sendeckyj, G.P., "Fitting Models to Composite Materials Fatigue Data," Test Methods and Design Allowables for Fibrous Composites, ASTM STP 734, Chamis, C.C., ed., American Society for Testing and Materials (1981) pp. 245-260.
  13. Sendeckyj G.P., 1991, ’Life Prediction for Resin-Matrix Composite Materials’, in Composite Material Series, Vol. 4, 10. Amsterdam: Elsevier, pp. 431-483.
  14. Kassapoglou, C., "Fatigue Life Prediction of Composite Structures Under Constant Amplitude Loading" Journal of Composite Materials, 2007, Vol. 41, No. 22.
  15. Nixon-Pearson O.J. , Hallett S.R., Withers P.J., Rouse J. Damage development in open-hole composite specimens in fatigue.Part 1: Experimental investigation Composite Structures 106 (2013) 882–889.
  16. Hahn H.T., Kim R.Y., ’Proof Testing of Composite Materials’, J Compos Mat (1975), 9, pp. 297-311.
  17. Chou P.C., Croman R., ’Residual strength in fatigue based on the strength-life equal rank assumption’, Journal of. Composite Materials (1978), 12, pp. 177-194.
  18. D’Amore, A., & Grassia, L. (2019). A method to predict the fatigue life and the residual strength of composite materials subjected to variable amplitude (va) loadings. Composite Structures, 111338. [CrossRef]
  19. D’Amore, A., Califano, A., & Grassia, L. (2021). Modelling the loading rate effects on the fatigue response of composite materials under constant and variable frequency loadings. International Journal of Fatigue, 150, 106338. [CrossRef]
  20. Post, N.L., Case, S.W., and Lesko, J.J., 2008, "Modeling the Variable Amplitude Fatigue of Composite Materials: A Review and Evaluation of the State of the Art for Spectrum Loading. "Int. J. Fatigue, 30 (12) , pp 2064-2086. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated