Prerpints.org logo
Preprint
Article

Comparative Analysis of Integrated Filtering Method Using UWB Localization in Indoor Environments

Altmetrics

Downloads

97

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 October 2023

Posted:

23 October 2023

You are already at the latest version

Alerts
Abstract
This research paper investigates ultra-wideband (UWB) localization systems by focusing on the use of average filter (AVG), Kalman filter (KF), and extended Kalman filter (EKF) algorithms, as well as a novel integrated filtering method that incorporates low-pass filter (LPF) into AVG, KF, and EKF. The study aims to improve localization loss in indoor environments using a TurtleBot robot equipped with a camera to observe ground truth positions. To evaluate the effectiveness of the proposed algorithms, a comprehensive comparison of the raw and filtered data with the camera-based ground truth observations is performed. Quantitative analyses of the results, including max, min, max-min, and mean error, are performed to evaluate the localization performance of the algorithms and the integrated filtering method. The results reveal that the integrated filtering method has performed better accuracy in comparison with existing methods.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

In recent years, localization and positioning systems for wireless sensor networks (WSNs) have gained popularity, being successfully utilized in various applications, such as product tracking in warehouses and equipment localization in hospitals [1]. Indoor positioning systems require accurate and low-cost estimation schemes due to the unique characteristics of indoor channels. Unlike outdoor positioning systems, such as the Global Positioning System (GPS), no general scheme for indoor positioning exists. Thus, a well-designed solution considering the limited capacity, low infrastructure cost, and energy constraints of a wireless sensor network (WSN) is required [2]. Various techniques have been utilized for indoor positioning systems, including measuring the distance or range between the target and the anchor sensor using methods such as the angle of arrival (AOA), received signal strength (RSS), time of arrival (TOA), time difference of arrival (TDOA), and time of flight (TOF) [3]. TOF, which measures the round-trip time of packets and averages the results, is a promising low-cost solution to real-time applications. Location algorithms such as trilateration, location fingerprinting, and proximity algorithms are designed to calculate the position based on distance measurements. Trilateration is preferred for its simplicity and high processing speed [4].
However, the accuracy of position estimation is compromised by measurement noise. Modeling radio propagation and time delay for WSNs in indoor environments, while considering factors such as low signal-to-noise ratio (SNR), severe multipath effects, reflections, and link failures, presents challenges that lead to measurement errors and data loss. To overcome these challenges, the KF has been introduced in WSN systems. KF, a recurve linear filtering model, is widely used for estimating tracks through noisy measurements. It has been successful in smoothing random deviations from the true target path [5]. Despite its advantages, KF is still liable to errors when the measurement noise is excessive. The distributed Kalman filter has been proposed to reduce noise, but it requires global information, which is not feasible in real-world positioning systems, where sensors can only provide partial range values. RADAR systems utilize KFs but do not strongly consider environmental changes, making them unsuitable for real-world applications [6]. Additionally, KF assumes that noise conforms to additive white Gaussian distribution and linear systems, which is challenging to model in indoor environments where wireless channels frequently change with object movement and surface reflections. This paper seeks to address the above issues through the following contributions:
  • To implement a real-time tracking system, the method provides robot localization to perform ground truth observations captured by a camera using a visual tracking system.
  • The data processing component applies by localization methods to obtain two-dimensional positions, but some noise remains. To filter out this noise, the AVG, KF, and EKF are implemented.
  • An integrated filtering method has been proposed combining LPF as (LPF+AVG), (LPF+KF), and (LPF+EKF) to reduce the loss and improve the trajectory accuracy.
Experiments are conducted to compare the performance of each method, and the results reveal that the integrated method exhibit different performance in different trajectories, suggesting the superiority of LPF+EKF for indoor positioning.
Section 2 begins with a comprehensive review of previous research in the field of indoor localization and filtering algorithms. We analyze the strengths and weaknesses of existing approaches and highlight how the proposed method addresses some of these challenges. Section 3 delves into the methodology used, in particular the system architecture involving the integration of ultra-wideband (UWB) technology with a visual tracking system. Section 4 then explains the ROS ecosystem and flowchart. Section 5, presents the core of the research, introducing the proposed method for accurate localization. The method comprises AVG, KF, and EKF, as well as a novel integrated model that incorporates UWB sensors. The integrated model is designed to improve localization accuracy and reliability [7]. To provide practical insights, Section 6 presents detailed information on the experimental setup and the various components used during the evaluations. Finally, Section 7, concludes the paper by discussing the obtained data results and potential directions for future research. We highlight the importance of improving the accuracy and loss of robotic localization using UWB sensors, paving the way for further advancements in this field.

2. Related Works

Ultra-wideband (UWB) localization systems utilize UWB signals to estimate the position of an object or person in an environment. UWB signals have some advantages for localization, such as high accuracy, resolution, and data rate, as well as robustness to multipath effects [8]. However, UWB localization systems also face some challenges, such as noise, interference, non-line-of-sight (NLOS) propagation, and high time resolution [9].
Various algorithms have been proposed to address these challenges and improve the localization accuracy and robustness of UWB systems. Some common methods are based on time-of-arrival (TOA), angle-of-arrival (AOA), or phase-difference-of-arrival (PDoA) measurements. These methods can be further classified as deterministic or probabilistic, depending on whether they use geometric or statistical models to estimate position [10]. Among the deterministic approaches AVG, KF, and EKF are widely used to reduce the noise and interference effects on UWB measurements. However, these algorithms may not perform well in NLOS scenarios where the UWB signals are obstructed by obstacles and reflect from multiple paths [11,12,13].
Among the probabilistic approaches, the particle filter (PF), Bayesian filter (BF), and support vector machine (SVM) are popular algorithms for dealing with the NLOS problem by incorporating prior knowledge or learning from data [14,15]. However, these algorithms may suffer from high computational complexity or low generalization ability. The integrated model involves applying LPF to the raw UWB data before feeding it to the AVG, KF, or EKF algorithms [16]. The LPF is used to smooth the UWB data and reduce the high-frequency noise and interference effects. The AVG, KF, and EKF algorithms are used to further reduce the noise and interference effects and estimate the position based on the filtered UWB data [17].
To overcome the limitations of single algorithms, some integrated methods have been proposed, which involve combining different algorithms or models to achieve better localization performance. For example, an integrated method based on CNN-SVM and a integrated localization algorithm were proposed to classify and mitigate NLOS errors using convolutional neural networks (CNNs) and SVMs and then estimate the position using a weighted least squares (WLS) method [18]. Another integrated method based on particle swarm optimization (PSO) and a integrated localization algorithm has been proposed to optimize the PSO and a combination of TOA and AOA measurements.
Thus far, we have explored different types of indoor localization systems. While these systems have reduced localization errors and solved localization challenges, further positioning accuracy improvements are needed to improve indoor localization and accuracy. In this paper, we propose UWB localization approaches using an integrated filtering methods for indoor localization, tracking, and navigation.

3. Working Methodology

This section explains the ultra-wideband (UWB) system architecture, the vision tracking system, and the ROS ecosystem. The UWB system architecture is designed to enable robot positioning and localization. The vision tracking system utilizes camera vision techniques to track and monitor the movement of the robot to find the ground truth [19]. ROS is a software framework that allows communication between software and hardware, thus providing tools for building, testing, and deploying in localization.

3.1. System Architecture

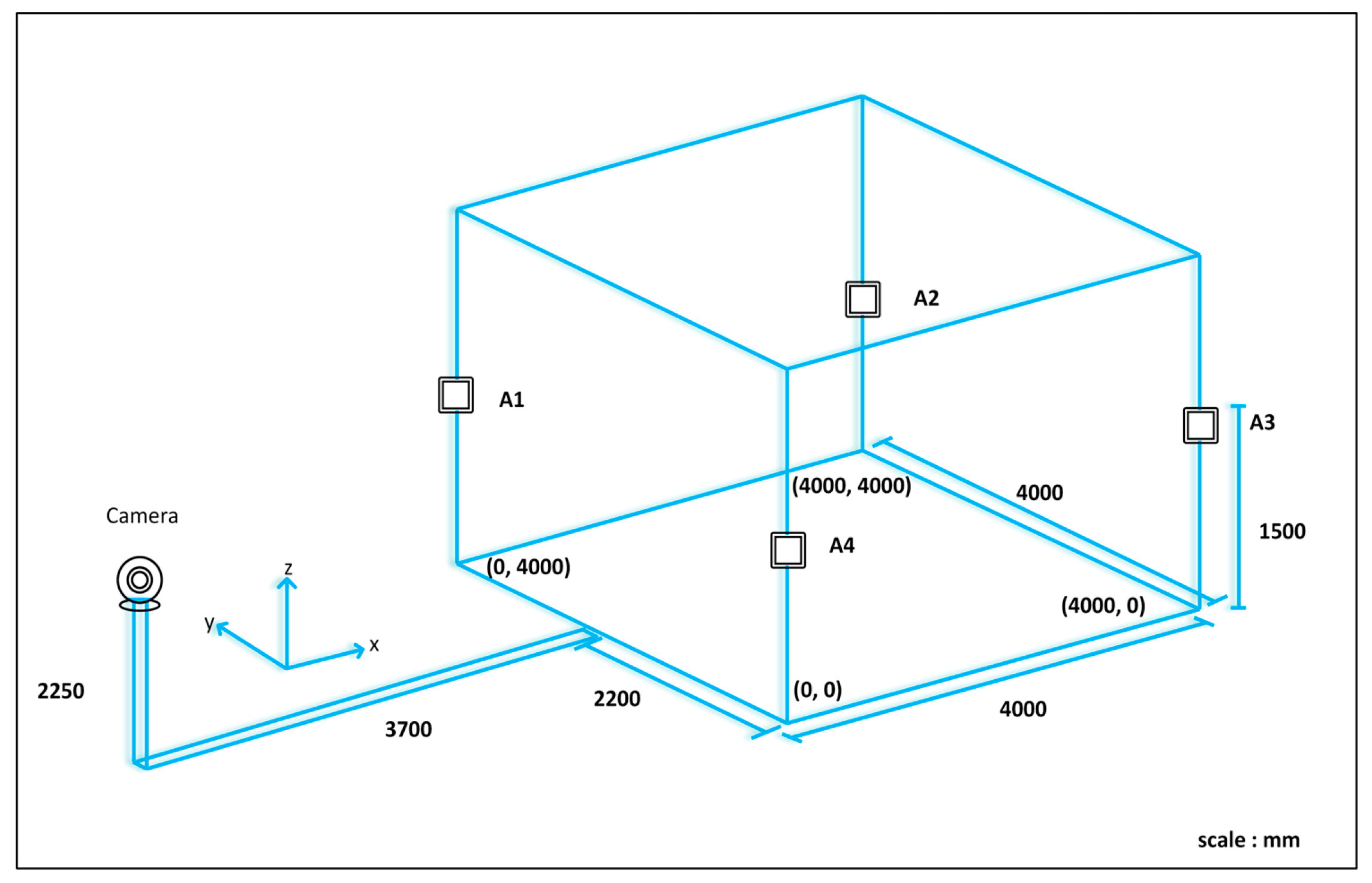
As shown in Figure 1, the robot positioning system consists of a UWB positioning subsystem, a remote computer, and a mobile robot. The UWB positioning subsystem consists of UWB anchors fixed in the environment and a UWB robot tag [20]. By measuring the distance between the UWB tag and the anchors, the computer executes positioning algorithms to determine the robot's position and coordinates. The remote computer communicates wirelessly with the robot, processes positioning data, calculates the robot's coordinates, and controls its motion. The system performs various functions such as interactive communication, robot control, position estimation, and robot position display [21]. A single sensor cannot achieve high accuracy due to errors or instability. The combined use of UWB tags and anchor sensors can improve positioning accuracy and stability. In this study, a position estimation and error correction method based on the EKF algorithm was proposed. The robot positioning system can simultaneously acquire and integrate the data from UWB tags and anchors, as shown in Figure 1.
The UWB positioning, mobile robot, and computer control systems are the three main blocks of the proposed system architecture. The first block consists of multiple UWB tags and anchors. The next block consists of the robot development system, which is a mobile robot system. TurtleBot 3 was used as the mobile robot for the initial position experiment. The system consists of a motor for locomotion, a driver unit for controlling the motor, and a LiDAR sensor for scanning and detecting obstacles. A Raspberry Pi processor was used to control all these systems, which are connected to a power supply. Finally, a computer control system with the ROS environment installed and the POZYX library was used, which communicates through Raspberry Pi as a read-and-write device. Different algorithms can be tested and simulated to improve localization and positioning [22]. TurtleBot3 is equipped with UWB tag nodes that can be integrated into the ROS ecosystem. These sensor measurements are used in the EKF along with wheel odometry and LPF algorithm output for localization, and the LiDAR-based navigation stack is initialized with UWB ranging and LiDAR scanning. In addition, the TurtleBot3 ROS library facilitates the implementation of a simulation environment.

3.2. UWB System

UWB technology has traditionally been used for wireless communications but has recently gained popularity in positioning applications. Its wide bandwidth makes it resistant to interference from other radio frequency signals and allows the signal to penetrate obstacles and walls, making it a reliable positioning technology in non-line-of-sight and multipath environments [23]. In addition, the unique identification of tags in a UWB system automatically solves data association problems. To determine distances, the technology transmits radio signals from a mobile transceiver (tag) to a group of known anchors, measures the time of flight (TOF), and calculates distances. This study used the POZYX system, a UWB-based hardware solution for precise position and motion sensing. The UWB configuration settings can be customized based on four different parameters that can affect the overall performance of the system. However, the presence of noise and uncertainty in the measurement data collected by UWB sensors requires advanced filtering techniques for accurate position estimation, including KF and EKF, which can improve the accuracy of indoor localization systems based on UWB technology.

3.3. Visual Tracking System

Visual tracking is a computer vision technique that involves tracking and estimating the motion of objects in a sequence of images or video frames captured by a webcam. It is a fundamental task in various applications, including surveillance, robotics, augmented reality, and human computer interaction [24]. Visual tracking methods aim to accurately and robustly locate and track objects of interest despite changes in appearance, scale, orientation, and occlusion, as shown in Figure 2.
The following steps present a basic process for visual tracking using a webcam installed and tested at the IRRI laboratory of Sun Moon University, South Korea, as shown in Figure 2. We installed a webcam in a suitable location while ensuring that all corners of the tracking area on the webcam were visible. We captured and saved four positions in a 2D projected coordinate system based on the webcam capture. Using the saved positions, we created a perspective transformation matrix that maps the view of the webcam to the desired tracking area. We then computed the image matrix and the perspective transformation matrix using a 512 × 512 resolution for optimal tracking performance.
The visual tracking process began after applying the perspective transformation. We selected a high-contrast area of the robot for tracking. An appropriate tracking algorithm, such as the discriminative correlation filter with a channel and spatial reliability (CSRT) algorithm was implemented to track the robot within the 512 × 512 image [25]. The tracking data provide the position within the 512 × 512 image and are is converted to the corresponding position in the real environment, which may have different dimensions. By scaling the tracked position using Equation (1), the tracked position is mapped to the 4000   m m × 4000   m m environment in X and Y, where   x ¯   and y ¯ represent the positions within the 512 × 512 image.
x = x ¯ 512 . × 4000 ,         y = y ¯ 512 × 4000
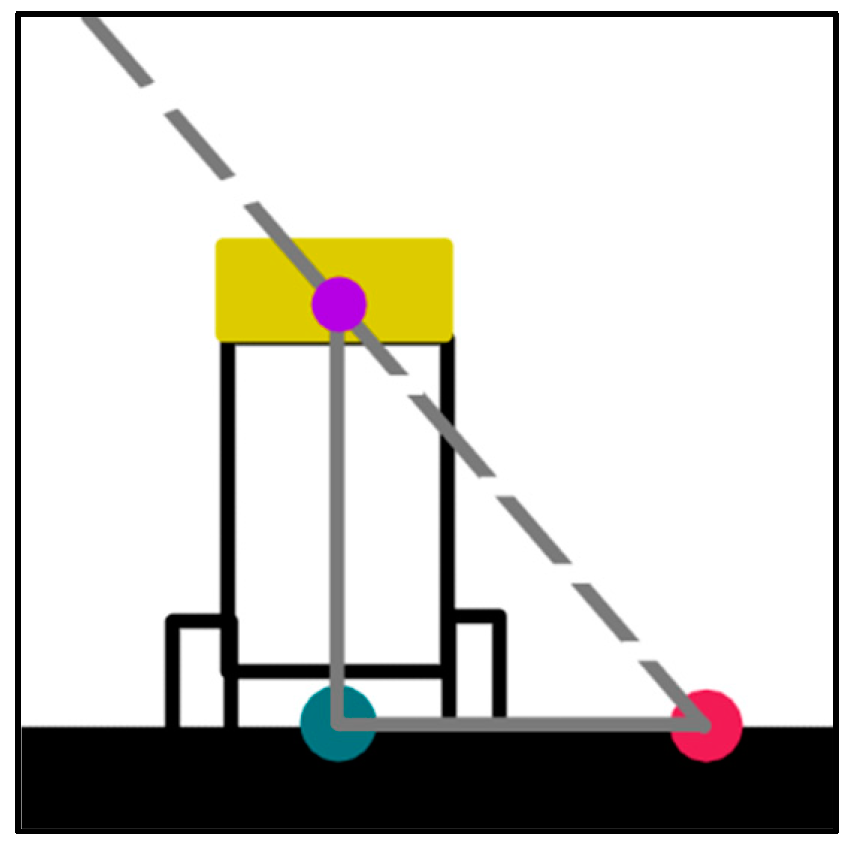
To ensure accuracy, it is important to eliminate any bias in the tracking system. The robot was moved to known positions, such as [1000, 2000], [2000, 2000], [3000, 2000], [2000, 1000], and [2000, 3000], and the tracking data were observed. Figure 3 shows the line of sight of the webcam, which is represented by a dotted line, and the real position, webcam position, and tracking point are represented by green, pink, and purple dots, respectively. The bias length is the distance between the green and pink dots.
If the bias is consistently the same along the axis, an average is used to correct the bias. Alternatively, if the bias has a linear pattern, a one-dimensional polynomial fit is performed to estimate the bias and adjust the tracked positions accordingly [26]. The visual tracking method was implemented in this study using a webcam to provide accurate and reliable tracking information over the following steps.

3.4. ROS Ecosystem

In this section, we focus on the ROS ecosystem and its components, including nodes, topics, and messages, and how the UWB sensors can be integrated with ROS. We also discuss how UWB sensors are used to measure the distance between a robot and its environment and how this information can be used to improve the robot's localization and mapping capabilities.
Position information is the most important information for navigation systems. UWB sensors are an excellent choice for robot localization because they provide low-noise-range information that is resistant to multipath interference [27]. Fusing their information with odometry data provides a robust solution for challenging environmental conditions. The POZYX system utilizes UWB technology to achieve centimeter-level accuracy, which is far superior to that of traditional positioning systems based on Wi-Fi and Bluetooth. The algorithm calculates the position of the robot; applies the KF, which utilizes odometry data to set the motion model; and updates the pose using UWB range measurement pose information. The GUI displays the map and the current robot position, and the navigation stack can be fed with KF-based pose information on demand. Several ROS packages are available for collecting and processing IMU sensor data in mobile robots, such as the ROS IMU package, which provides an implementation of an IMU sensor driver and a filter for estimating the orientation of the robot using sensor data [28]. Other packages include robot localization, which provides an implementation of EKF for fusing data from multiple sensors, including IMU data, to estimate the position and orientation of the robot [29].
In addition, the UWB node-based source localization algorithm determines the location of a robot but cannot determine its orientation with respect to a map. To solve this problem, a map and LiDAR scan matching technique are introduced. Once the initial heading is estimated, the robot's pose can be published to the initial pose topic. Figure 4 illustrates the difference in the robot's pose before and after the initialization process. Before autonomous initialization, the robot's pose is incorrect and the scan data do not match the real map, as shown in Figure 4a, but after initialization, the scan data and map are aligned, as shown in Figure 4b.
Once the robot's starting position has been determined, the robot starts moving to point A using the move-base algorithm available in the ROS navigation stack. The final position of the robot is then determined, both on the map and in the real world, after starting with a precise initialization. The accuracy of the robot's arrival at its destination is confirmed by analyzing the LiDAR scans on the map.

3.5. System Flow chart

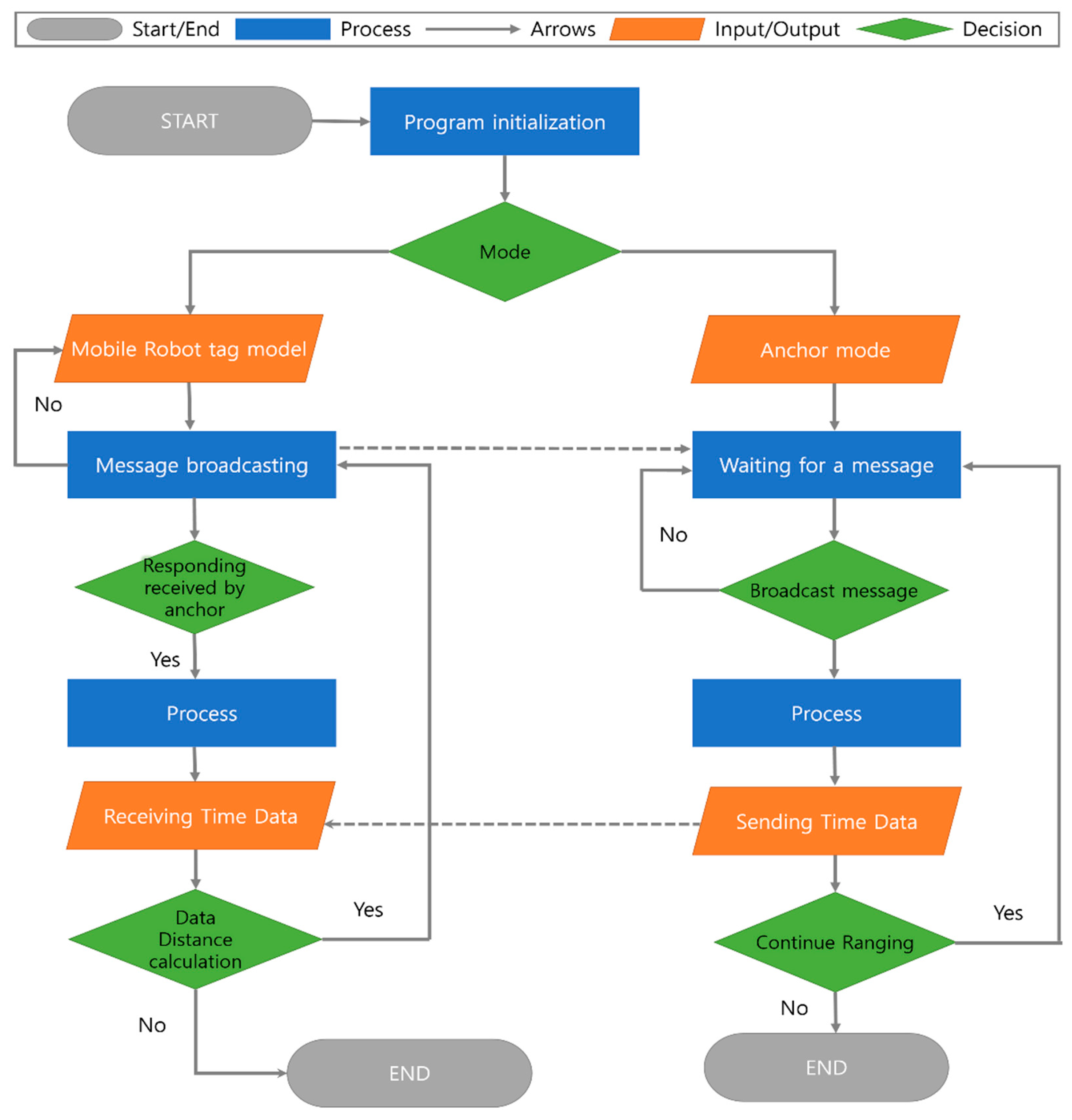
The flow chart of an indoor UWB localization system is a visual representation of the steps and processes involved in the operation of the system. It outlines the sequence of events that occur from start to finish, providing a comprehensive view of how the system works. A flow chart outlines the entire process in this system. The system provides both simulation and real-world test environments for different tasks [30]. The user chooses whether to run the application in a simulation or the real world. If the application is run in a simulation, the Gazebo and POZYX simulations are started, and synthetic sensor data and map data are obtained. If the application is running in the real world, real sensor data are obtained [31]. The initialization package then utilizes the UWB range and LiDAR scan data to complete the autonomous initialization process, regardless of whether the data are synthetic or real. Figure 5 shows a system flowchart of the UWB localization system, which outlines the various components involved in the system and how they interact with each other.
The flowchart first initializes the program. Either the mobile tag mode or the anchor mode is selected. If the mobile tag mode is chosen, the program will start sending messages and wait for a response from the anchor. Once a response is received, the program processes the data and sends time data to the tag mode as the receiving data mode. The data distance is then calculated, which involves calculating the distance between the mobile tag and the anchor.
When the anchor mode is selected, the program waits for a message from the mobile tag. Once the message is received, the program processes the data and responds to the mobile tag. The flowchart in Figure 5 shows a high-level overview of the UWB indoor localization system. It clarifies the steps involved in the operation of the system and how the different components interact to achieve the desired result.

4. Filtering Algorithm

In this section, we discuss the filtering algorithm and provide an example code for implementing the filtering process [32,33,34]. The filtering algorithm aims to extract relevant information from noisy or incomplete data by applying mathematical techniques.

4.1. Average Filtering

The average filter is a simple method used to smooth data by calculating the sampled average and eliminating noise [35]. The average equation is as follows
X k ¯ = ∑ n = 1 k x n k
The equation represents the conventional method of calculating the average of a given set of values. In this equation, variable k denotes the size of the acquired data, whereas X ¯ k represents the resulting average value [33]. Equation (2) can be expressed differently as follows:
X ¯ k = α X ¯ k − 1 + 1 − α X k
Where, α = 1 − 1 / k   and   X ¯ k − 1 = ∑ n = 1 k − 1   x n k − 1 . Equation (3) represents the main function of a recursive average filter.

4.2. Kalman Filtering

The KF is a mathematical framework that includes estimation and correction steps and consists of a set of equations divided into two main steps: prediction (estimation equations) and correction (measurement equations), as described in the references. In the prediction step, the estimated value is determined and can be represented by equations.
x k + 1 = A x k + q k
Here, the state vectors x k = X k , X ˆ k , Y k , Y ˆ k T are the positions X k and Y k and the velocities X ˆ k and Y ˆ k at sample k . The state transition matrix A in Equation (1) is time-invariant and given by
A = 1 Δ t 0 0 0 1 0 0 0 0 1 Δ t 0 0 0 1
The transition matrix is responsible for predicting the next state based on the previous state using a constant movement model, element Δ t is the sample period of each step, and x k = X k , X k ^ , Y k , Y k ^ T is a probabilistic vector of processing errors and noise due to estimation uncertainty. Elements x error   and y error   are transition position errors, and x ˙ error   and y ˙ error   are the velocity errors. The correction step (measurement equations) can be expressed as
z k = H   x k + r k
Matrix H is a projection to transform x k into a position, as shown in Equation (7)
H = 1 0 0 0 0 0 1 0
r k = x error   1 , y error   1 T is the measurement noise vector, and the final filtered result x ˆ k can be expressed as
x ˆ k = x k + K k z k − H x k .

4.3. Extended Kalman Filtering

EKF is a popular localization algorithm used in robotics, navigation, and autonomic systems. It is an extension of traditional KF and provides a recursive solution to the problem of estimating the state of a system over time. EKF works by incorporating nonlinear functions of the system state into a linear approximation, which can then be updated using a recursive Bayesian filter [36]. The algorithm utilizes a set of linearized system models and measurements to estimate the system state over time, considering both model uncertainty and measurement noise. The operation of the algorithm involves two steps, typically prediction and correction. In the prediction step, the EKF predicts the system state at the next time step based on the current state and control inputs. In the correction step, the algorithm updates the prediction using the latest measurement. EKF is widely used in various fields (e.g., robotic navigation and autonomous systems) because of its ability to handle nonlinear systems and provide accurate estimates even in the presence of measurement noise. It is also computationally efficient, making it suitable for real-time applications [36,37].
EKF was proposed to solve the localization problem in robotic applications. In these applications, the motion and observation models are defined as follows
x t = g x t − 1 ,   u t ,   v t − 1 ,
z t = h x t , w t .
The motion and observation noise are represented by v t − 1 and w t , respectively. If the motion and observation models are linear and the noise is independent and identically distributed (i.i.d.) Gaussian distributions, then KF is the optimal filter. Thus, if the initial belief, b e l x o , has a Gaussian distribution, with variance σ 0 and μ 0 being the peak position distribution, then,
x o ~ Ɲ μ o , σ o
b e l x o = p x o = det ⁡ 2 π σ o − 1 2 E x p − 1 2 x o − μ o T σ o − 1 x o − μ o
If the motion model is linear and the resulting noise is an additive, independent, and identically distributed Gaussian distribution then,
x t = A t     x t - 1 + B t u t + v t - 1 , v t ~ Ɲ 0 , R t ,
P x t x t - 1 ,   u t = det ⁡ 2 π R t − 1 2 E x p − 1 2 x t − A t x t - 1 − B t u t T R t − 1 x t − A t x t - 1 − B t u t ,
where R t is a positive definite matrix.
If the observation model is linear and the resulting noise is an additive, independent, and identically distributed Gaussian distribution, then,
z t = C t x t + W t , W t ~ Ɲ 0 , Q t ,
P z t x t = det ⁡ 2 π Q t − 1 2 E x p ⁡ − 1 2 z t − C t x t T Q t − 1 z t − C t x t .
The motion model used in this study utilizes odometry information to estimate the motion of the robot. Odometry information refers to the data obtained from the robot's sensors, such as wheel encoders, which provide estimates of the robot's distance traveled and orientation changes. The motion model incorporates this information to estimate the robot's position and velocity at each time step shown in proposed Algorithm 3.

5. Proposed Algorithm

5.1. Low-Pass Filter in Average Filter (LPF+AVG)

The “LPF+AVG” algorithm is specifically designed for indoor localization systems. It starts by collecting measurements, such as TOF data, from the UWB or a similar technology. AVG is applied to these measurements to reduce noise and improve accuracy. Trilateration is then performed to estimate the position of the target based on processed TOF data and reference point locations.
The Algorithm 1 introduces an LPF+AVG to further refine the position estimates by removing noise and improving the results. By combining these filtering techniques, the LPF+AVG algorithm achieves a balance between noise reduction and responsiveness, ensuring accurate and reliable position estimates even in complex indoor environments. Based on this algorithm, the robot's input position is mapped to the ground truth position according to the LPF+AVG from the robot's data point for smoothing the trajectories.
Algorithm 1 LPF+AVG
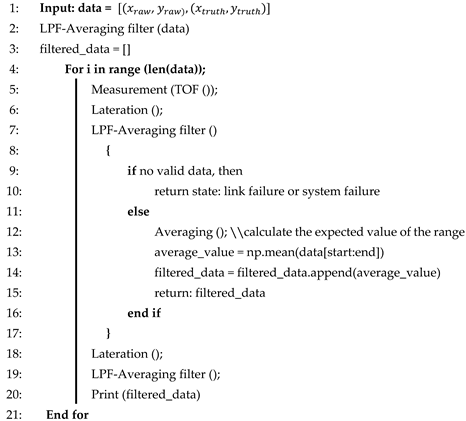Preprints 88277 i001

5.2. Low-Pass Filter in Kalman Filter (LPF+KF)

LPF+KF is a localization algorithm that uses indoor region information, such as room size, to correct measurements. It acts as a integrated filter that behaves like a KF when the data are within the boundaries of the indoor region. In this case, it calculates positions using prediction and correction steps. However, when data fall outside the bounds or the system encounters disturbance information, it behaves like a low-pass filter, relying on the predicted value from the previous state. Algorithm 2 outlines the operation of the LPF+KF to provide accurate and reliable indoor position estimates. In the presence of significant measurement noise, LPF+KF tends to rely on its predicted value. The algorithm is particularly suited for tracking motion within a confined area because such motion typically involves low speeds and generally follows simple, straight paths. This makes LPF+KF well suited for scenarios where the motion is slow and does not involve complex and tortuous paths. LPF+KF is processed by providing the estimated state of the position of the robot, and also it will calculate the effect of noise. Next step, the LPF+KF is to correct the step for the next state.
Algorithm 2 LPF+KF
Preprints 88277 i002

5.3. Low-Pass Filter in Extended Kalman Filter (LPF+EKF)

LPF+EKF is similar to LPF+KF, except for the trilateration in Algorithm 2. In Algorithm 3, LPF+EKF exhibits similar principles as those of the EKF and utilizes range values as observation inputs instead of calculating measurement positions [38]. This eliminates the need for position calculations, and the algorithm directly utilizes the range values in its filtering process. LPF+EKF can provide a more dynamic filtering method, as we can input the velocity of the robot linearly and its velocity in angle, which can provide more accuracy than other methods. The process of LPF+EKF is just more promising than LPF+KF by adding the robot's velocity to predict the next trajectory. It works well with environments that have high noise.
Algorithm 3 LPF+EKF
Preprints 88277 i003
The proposed method is suitable for specific indoor localization scenarios. LPF+KF excels in high-noise environments and simple motions; LPF+AVG provides adaptability and robustness in various indoor environments; and LPF+EKF utilizes direct range values for accurate position estimates, as shown in the proposed algorithm [39].

6. Experimental Setup

6.1. Hardware setup

In our test, we used the TurtleBot 3 robot, a Raspberry Pi onboard processor, a UWB tag module, and four POZYX anchors attached to the sensor stand in the experimental area. Ethernet cables and PoE switches connect the anchors to the computer. A UWB localization software package is installed on the computer [40]. The details of the components used in the experiment are listed in Table 1.

6.2. Environment

A relatively large indoor area with a clear line of sight between the anchors and the tag on the robot has been set up for operation. There are no large metal obstacles or reflective surfaces to interfere with the UWB signals. The environment is well lit to allow the robot to move safely, as shown in Figure 6.

6.2.1. Calibration

Before starting the experiment, the UWB localization was calibrated to obtain accurate distance measurements between the anchors and the tag. The ROS software package is used for the calibration. The calibration process typically involves collecting measurements between the anchors and the tag at various distances and angles [41].

6.2.2 Localization

After UWB, the system was calibrated, and the localization algorithm was run on the computer to estimate the position of the robot in real time. The estimated position was then displayed on a 2D map of the environment and used for navigation tasks.

7. Experiment and Results

To evaluate the accuracy and efficiency of the UWB indoor localization technology proposed in this study, an experimental scenario was considered. By leveraging the time difference and angle of arrival of the UWB pulses transmitted by the tags, the sensors were able to measure the position of the tag. The experiments were conducted under line-of-sight conditions between the tag and the wired sensors, and the system was used to measure of the position of the tag, which was then used by the developed algorithms to determine the distance between the measured position and the position of the wireless sensors based on the range measurements.

7.1. Experiment

We conducted three different trajectory path experiments (T1, T2, and T3), as shown in Figure 16. Trajectories T1, T2, and T3 are square, circular, and free paths, respectively, with UWB tags placed at fixed positions. Filtering techniques, such as AVG, KF, and EKF, were used to filter the data. We then applied our proposed integrated techniques (AVG+LPF, KF+LPF, EKF+LPF). The comparative analysis evaluated the accuracy and precision by comparing the filtered data with the ground-truth positions. The results provide valuable insights for optimizing UWB localization algorithms in real-world applications, considering accuracy, noise reduction, and handling of nonlinear motion.

7.2. Results

7.2.1. Target 1- Square Path with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) Filtering

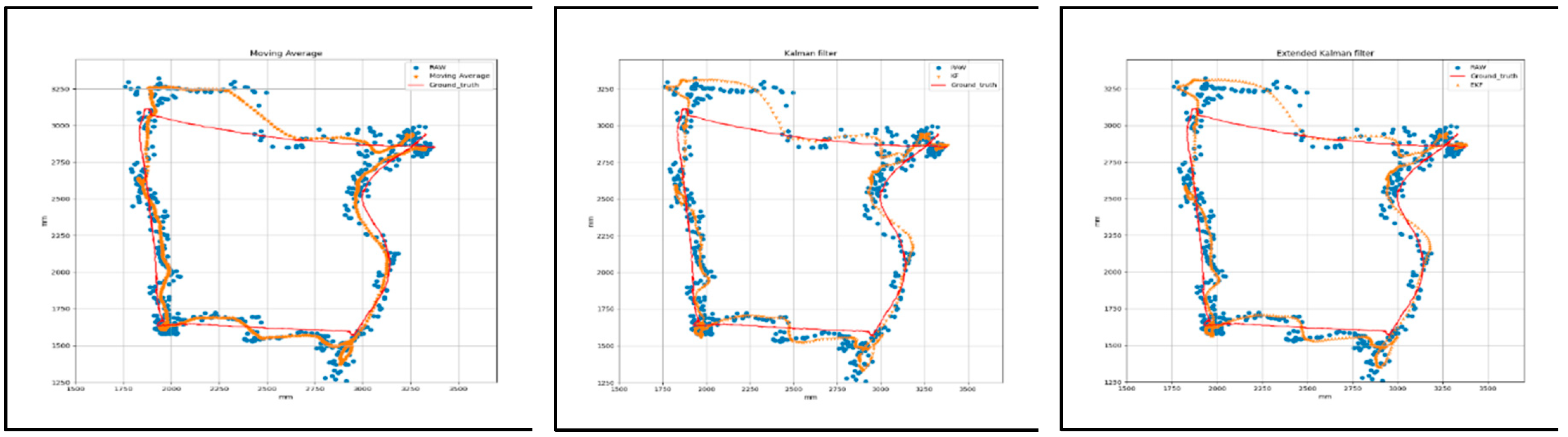
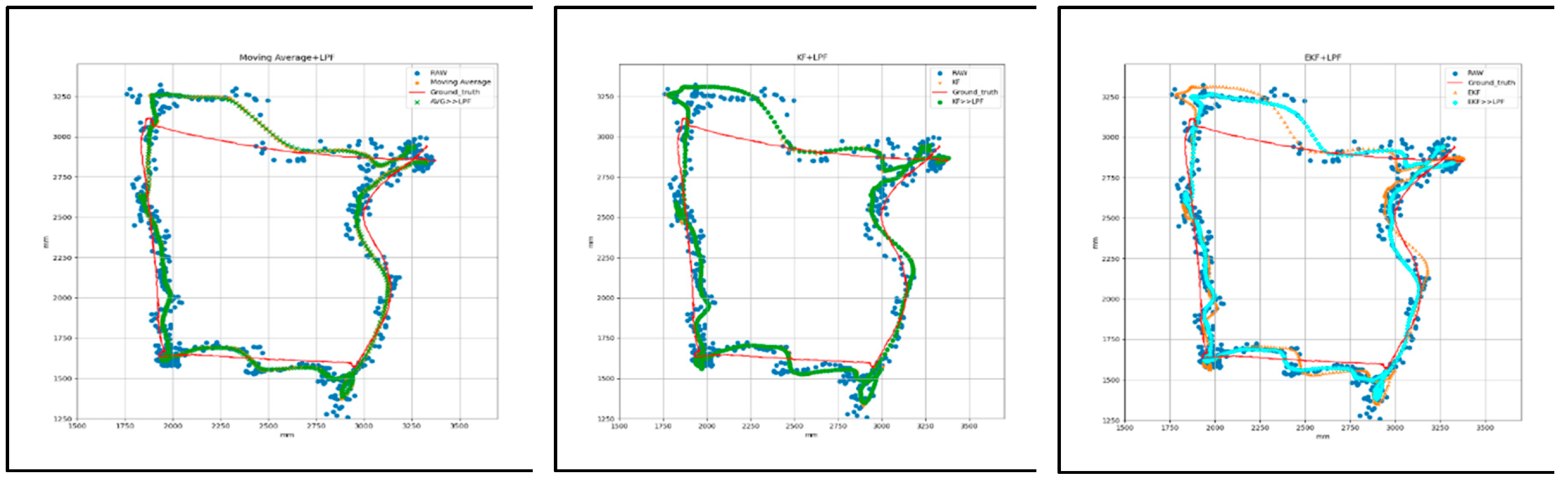
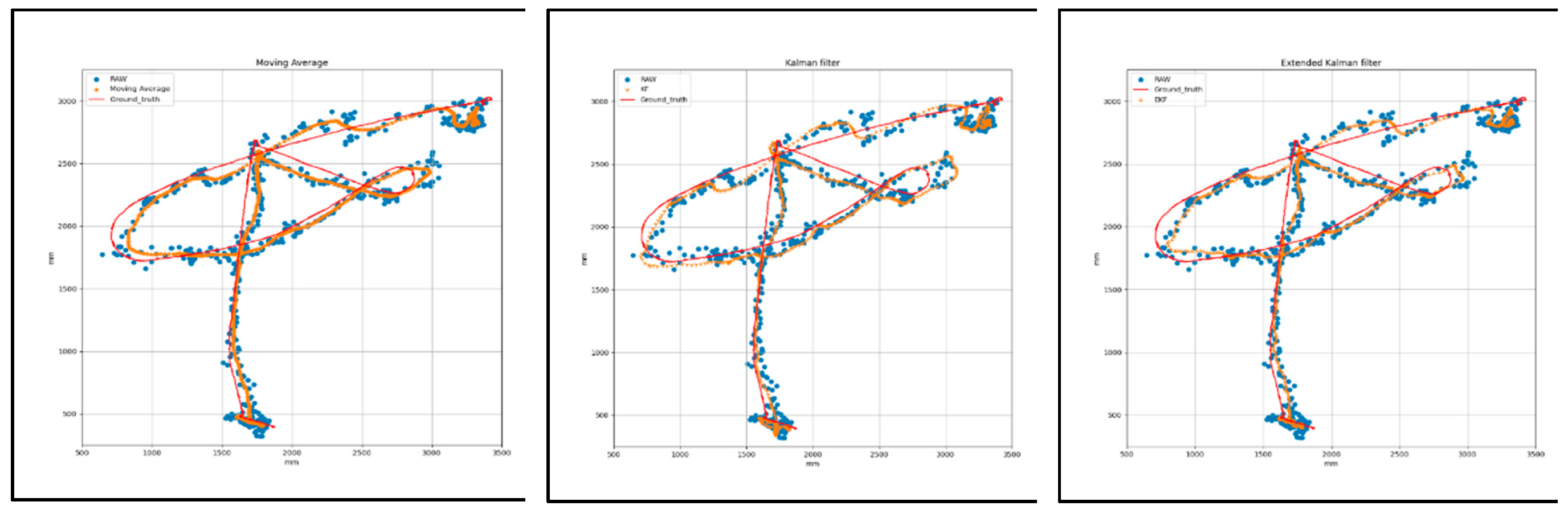
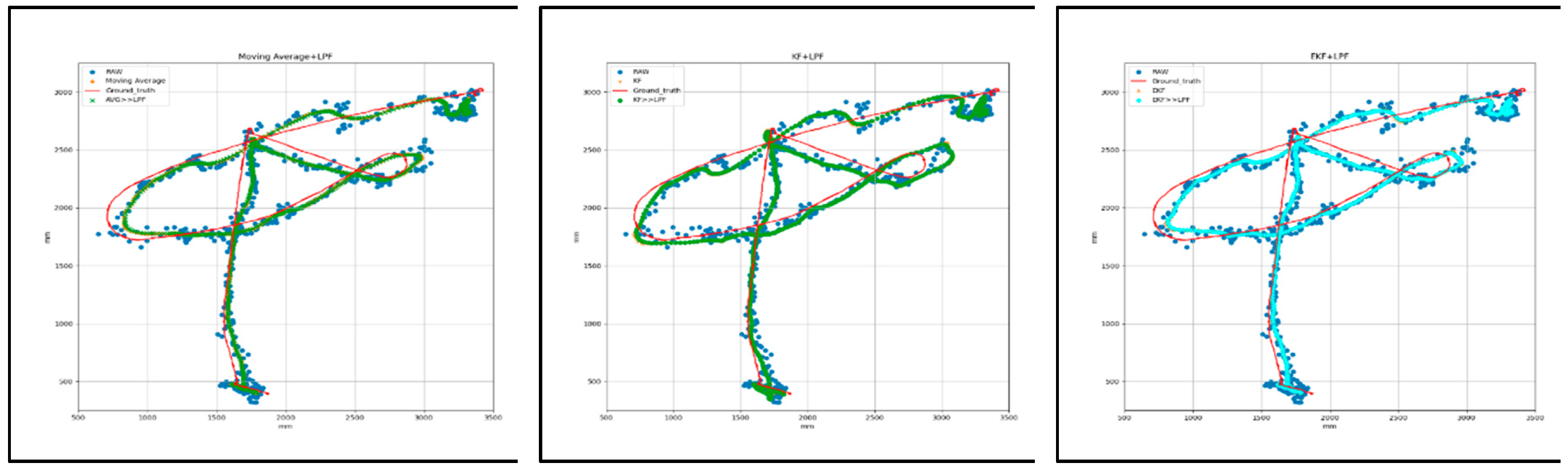
Figure 7 shows a graphical representation of the T1 square trajectory path with (AVG, KF, EKF) filtering and (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering, which measures the raw data and the filtered data collected during the experiment with respect to the ground truth. The trajectory covers 2 m at a speed of 0.5 m/s. The collected data correspond to the positions along the X and Y axes, measured in millimeters (mm).
Preprints 88277 g007
Figure 7. (a) Target 1- Square path with (AVG, KF, EKF) filtering.
Figure 7. (a) Target 1- Square path with (AVG, KF, EKF) filtering.
Preprints 88277 g007
Preprints 88277 g008
Figure 7. (b)Target 1- Square path with (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering.
Figure 7. (b)Target 1- Square path with (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering.
Preprints 88277 g008
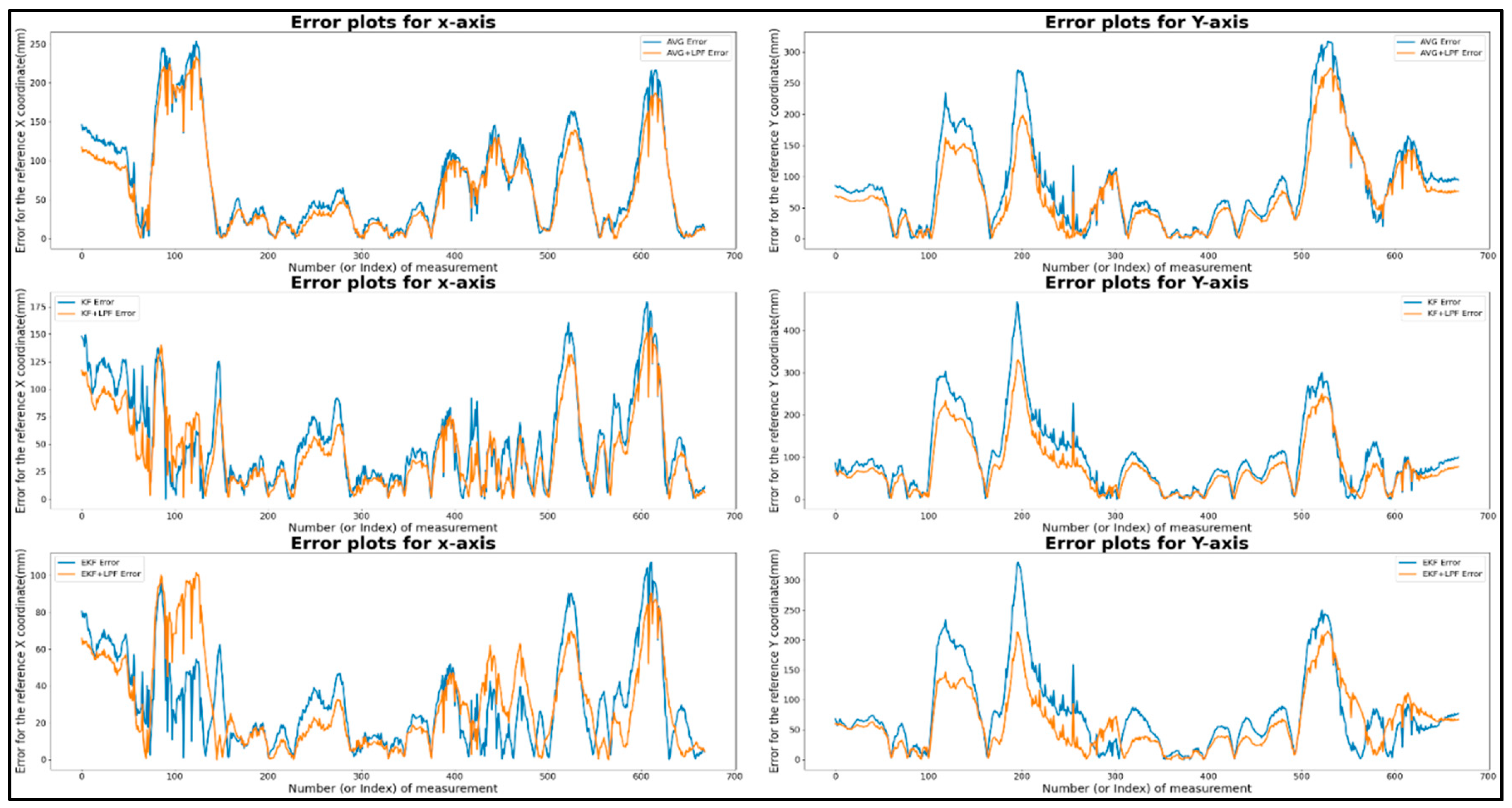
The data in Table 2, obtained from the graph in Figure 8, represent the square trajectory with (AVG, KF, EKF) filtering and (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering. Both trajectories cover 2 m and have a speed of 0.5 m/s. The table presents various measurements for these trajectories in terms of positions along the X and Y axes. For the “trajectory with (AVG, KF, EKF)” the maximum error position reached along X axis was 180.82 mm and the maximum error position Y axis was 371.07 mm. On the other hand, the minimum error along X axis was 0.12 mm, and the minimum error along Y was also 0.12 mm. The absolute error difference between the maximum and minimum error values, denoted as |Max.-Min.|, was 179.9 mm for the X axis and 371.85 mm for the Y axis. In addition, the mean error position for the X axis was 52.19, and for the Y axis, it was 89.09 mm.
"Integrated filtering method data with (AVG+LPF, KF+LPF, EKF+LPF) filtering" of the square error trajectory was collected from Figure 8; the maximum error along X position was 163.81 mm, and on Y position was 273.09 mm. The minimum error along X position was 0.13 mm, and the minimum error along Y position was 0.09 mm. The absolute error difference between the maximum and minimum values was 163.68 mm for the X axis and 273 mm for the Y axis. The average error position was 46.6 mm for the X-axis and 70.36 mm for the Y-axis. These measurements provide valuable insight into the characteristics of the two trajectories, revealing the range of positions, the average position, and the effect of the LPF on the data.

7.2.2. Target 2- Circular path with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering

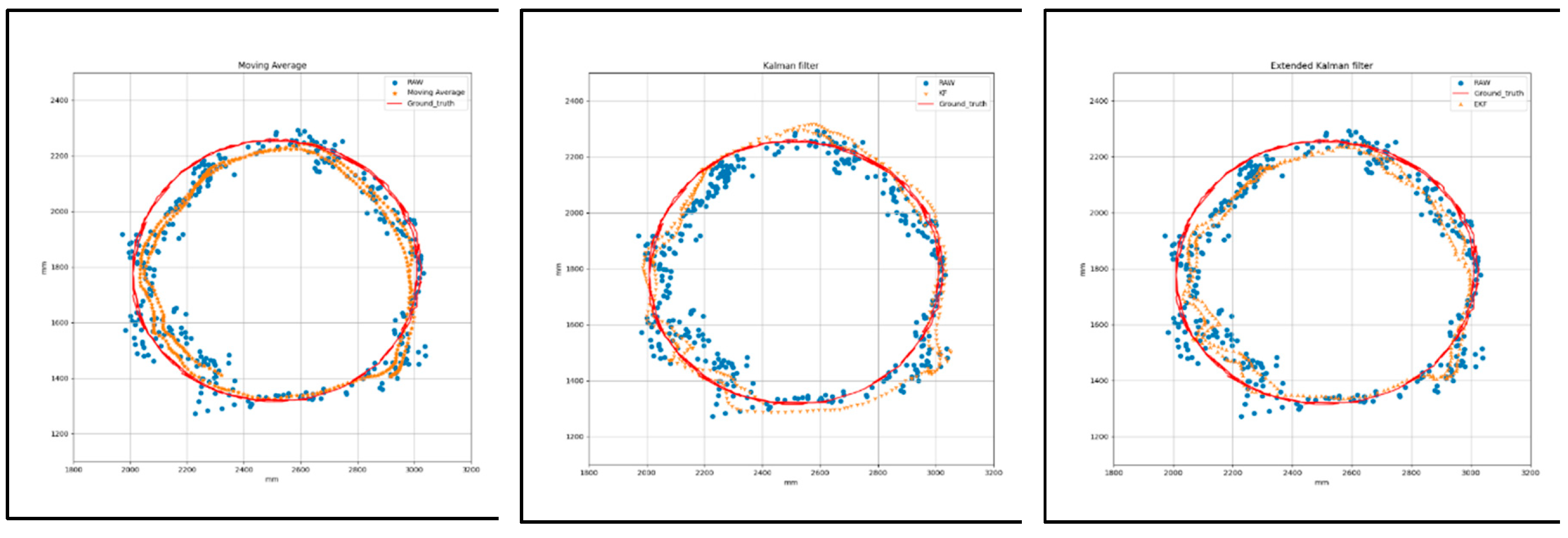
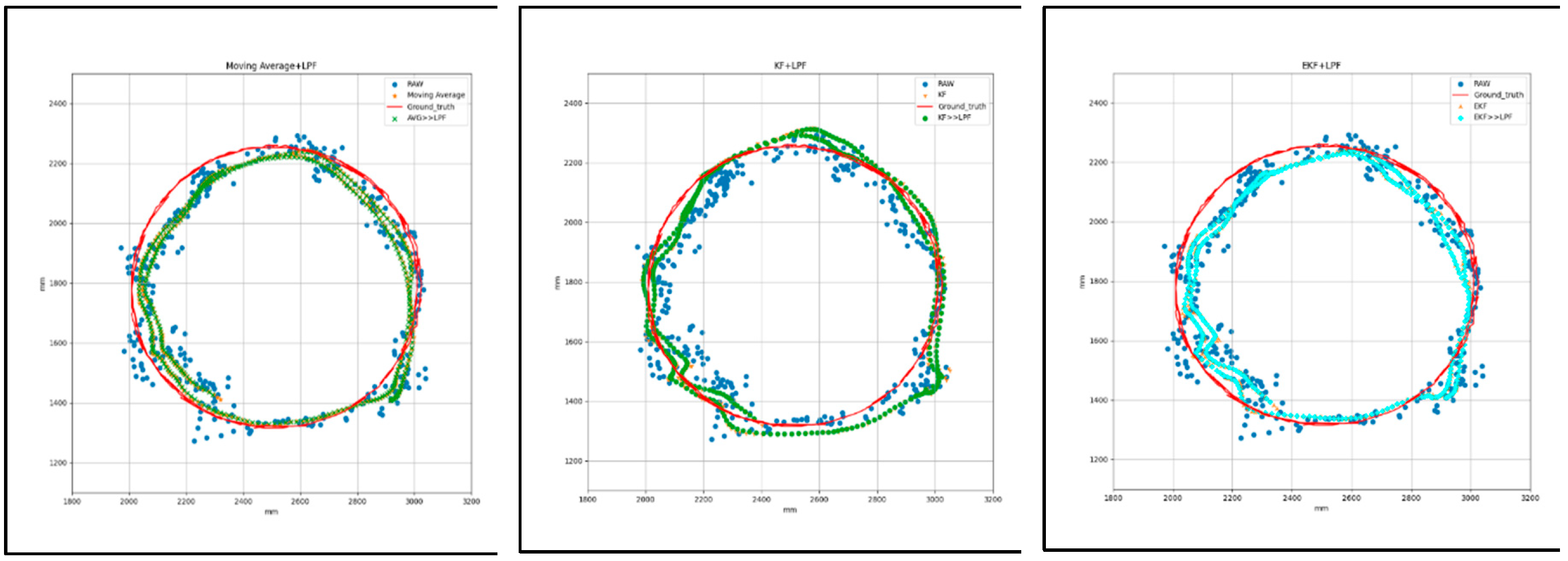
Figure 9 shows the graphical measurement of raw and filtered data collected during the circular trajectory with respect to the ground truth with (AVG, KF, EKF) filtering and (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering. The trajectory covers a distance of 2.2 m at a speed of 0.5 m/s. The data collected correspond to the positions along the X and Y axes, measured in millimeters (mm), as listed in Table 3.
Preprints 88277 g010
Figure 9. (a) Target 2- circular path with (AVG, KF, EKF) filtering.
Figure 9. (a) Target 2- circular path with (AVG, KF, EKF) filtering.
Preprints 88277 g010
Preprints 88277 g011
Figure 9. (b)Target 2- circular path with (AVG+LPF, KF+LPF, EKF+LPF) filtering.
Figure 9. (b)Target 2- circular path with (AVG+LPF, KF+LPF, EKF+LPF) filtering.
Preprints 88277 g011
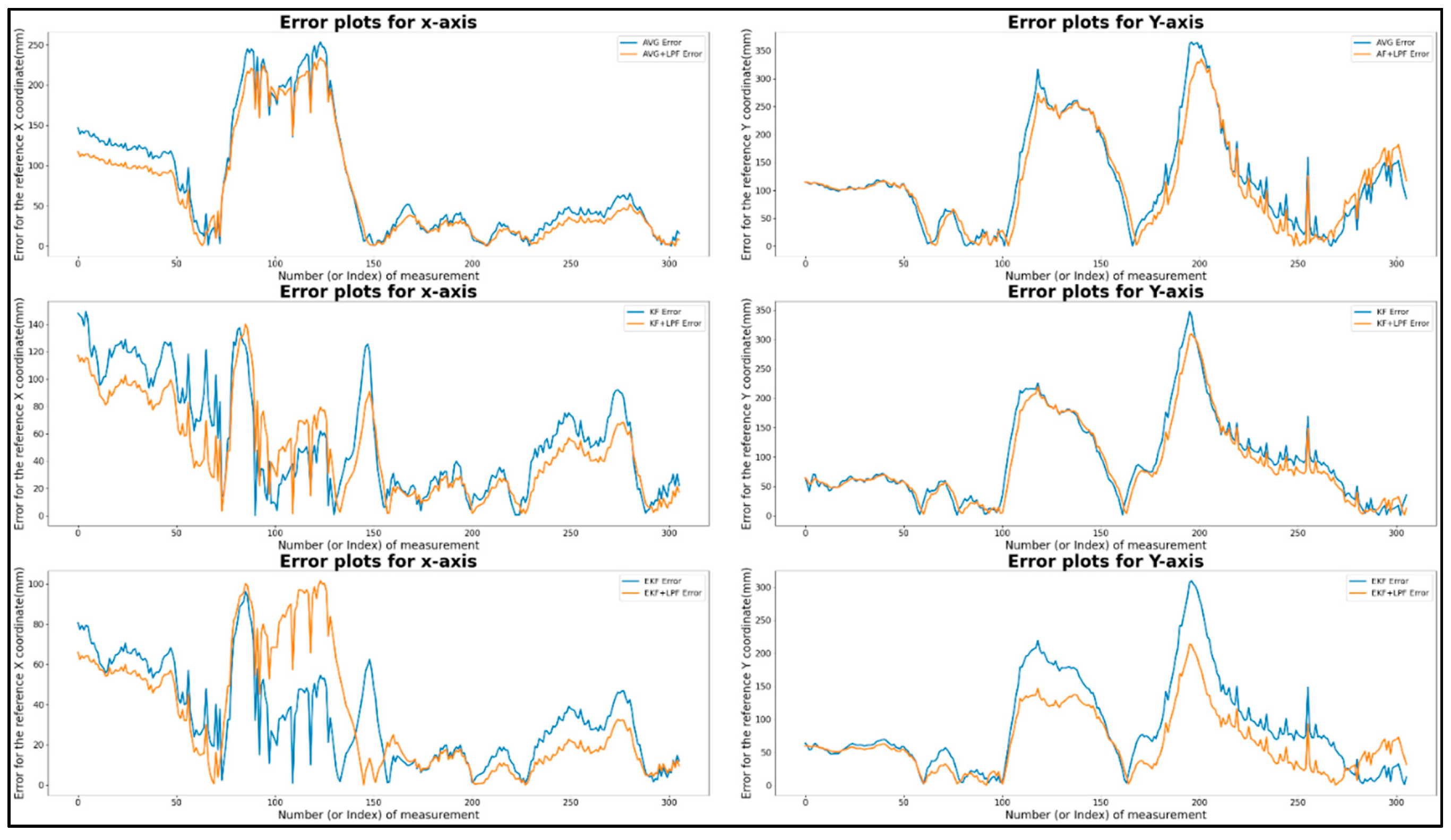
Table 3 presents the data for the filtering technique from the graph in Figure 9 "circular with (AVG, KF, EKF) filtering and (AVG+LPF, KF+LPF, EKF+LPF) with ground truth.” Both trajectories cover 2.2 m at a speed of 0.5 m/s. In the “circular trajectory without integrated filter technique,” we observed that the maximum error along X position reached was 166.38 mm, and the maximum error along Y position was 341.05 mm. However, the minimum error along X position was 0.46 mm, and the minimum error along Y position was 0.58 mm. The absolute difference error between the maximum and minimum values, called |Max.-Min.|, was 165.91 mm for the X axis and 340.47 mm for the Y axis. In addition, the mean error position was 56.34 mm for the X-axis and 100.5 mm for the Y-axis.
For the “circular trajectory with integrated filter technique” method, the maximum error along X position was 158.51 mm, and the maximum error along Y position was 286.22 mm. The minimum error along X position was 0.52 mm, and the minimum error along Y position was 0.81 mm. The absolute error difference between the maximum and minimum values was 157.99 mm along the X axis and 285.4 mm along the Y axis. The average error position along the X axis was 50.63 mm and for the Y axis, it was 88.44 mm.
This calculated value hints at the valuable data characteristics of the two filtering algorithms, with the range of positions, the average position, and the effect of the LPF (low-pass filter) on the data. The raw data improved significantly after adding the low-pass integrated filtering technique to the filtered data. The error graph reveals how the LPF as integrated with existing filters (AVG, KF, EKF) improves the accuracy of the trajectory data, effectively reducing error and noise, as shown in Figure 10.

7.2.3. Target 3- free path with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering

Figure 11 is T-3 for the free path trajectory with respect to the ground truth using an integrated filtering technique and a non-integrated technique with a distance of 5 m and a constant velocity of 0.5 m/s.
Preprints 88277 g013
Figure 11. (a)Target 3- free path with (AVG, KF, and EKF) filtering.
Figure 11. (a)Target 3- free path with (AVG, KF, and EKF) filtering.
Preprints 88277 g013
Preprints 88277 g014
Figure 11. (b) Target 3- free path with (AVG+LPF, KF+LPF, EKF+LPF) filtering.
Figure 11. (b) Target 3- free path with (AVG+LPF, KF+LPF, EKF+LPF) filtering.
Preprints 88277 g014
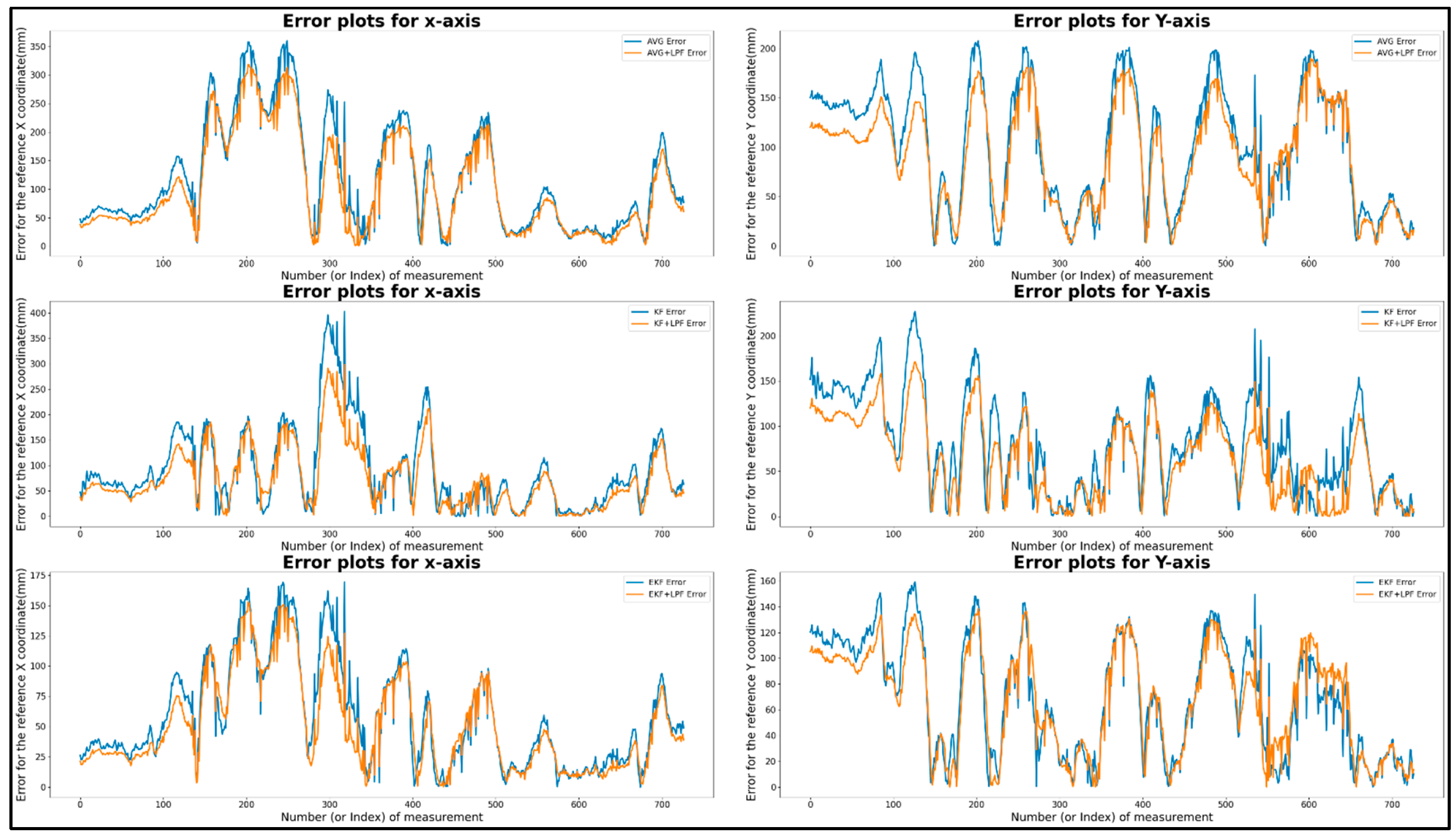
Table 4 presents the error comparison data of the free path trajectory with (AVG, KF, EKF) filtering and (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering with a ground truth of a distance of 5 m at a constant velocity of 0.5 m/s. The table provides measurements for the maximum and minimum error positions along the X and Y axes, as well as the absolute difference (|Max.-Min.|) and mean positions.
The graphical representation of (AVG, KF, EKF) filtering in Figure 12 reveals that the maximum error along X position was 310.84 mm, and the maximum error along Y position was 197.99 mm. The minimum error along X position was 0.3 mm, and the minimum error along Y position was 0.20 mm. The absolute difference error between the maximum and minimum was 310.55 mm along X axis and 197.78 mm along the Y axis. The average error position along the X-axis was 88.84 mm, along the Y-axis, it was 84.36 mm, as presented in the table. Similarly, in the (AVG+LPF, KF+LPF, EKF+LPF) integrated filtering graph, the maximum error along X position was 256.74 mm, and the maximum error along Y position was 166.50 mm. The minimum error along X position was 0.74 mm, and the minimum error along Y position was 0.36 mm. The absolute error difference between the maximum and minimum values was 255.99 along X axis and 166.13 mm along the Y axis. The mean position for the X axis was -41.72 mm, and for the Y axis, it was 22.81 mm. The average error position along the X-axis was 76.25 mm, along the Y-axis, it was 74.07 mm.
The data presented in all the Table 1, Table 2 and Table 3 reveal how these filtering techniques affect the trajectory data, and the integrated filtering (AVG+LPF, KF+LPF, EKF+LPF) adding a LPF to the raw filtered data.

8. Conclusions

In this research, we conducted an experiment to evaluate the performance of different filtering techniques for position estimation in different trajectory scenarios. Our goal was to evaluate the effectiveness of AVG, KF, and EKF techniques in improving the accuracy and reliability of measurement data. The experiment comprised three trajectory scenarios: square path, circular path, and free path, corresponding to distances of 2 m, 2.2 m, and 5 m, respectively, at a speed of 0.5 m/s. We collected measurement data along the X and Y coordinates and compared the results before and after applying the filtering techniques. Our results revealed that all three filtering methods improved the measurement data by reducing noise and fluctuations, resulting in smoother and more consistent position estimates. However, the integrated filtering method (LPF+EKF) consistently outperformed the others, demonstrating better accuracy making it a reliable solution for localization and tracking applications.
Our experiment provides valuable insights into the effectiveness of different filtering techniques for position estimation. The results contribute to advancing localization and tracking systems and provide guidance for selecting the most appropriate technique based on specific application requirements. Future work can explore additional filtering techniques, perform robustness tests, optimize parameters, and integrate multiple sensors to further improve the performance of position estimation systems. By addressing these areas, the accuracy and robustness of position estimation can be improved, and the development of advanced localization and tracking technologies furthered.

Author Contribution

Rahul Ranjan: Paper writing and experimental hardware development data, algorithm deveploment. Shin Donggyu: Development of robot position control tools and position estimation software. Younsik Jung: Data collection and analysis software development. Sanghyun Kim: Conceptualization and presentation of position correction algorithms. Jong-Hwan Yun: Enhancement of data accuracy in analysis. Chang-Hyun Kim: Analysis of experimental results and feedback. Seungjae Lee: Proposal of research methodology and paper review. Joongeup Kye: Overall project coordination. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Data used in this paper can be made available by contacting the corresponding author, subject to availability.

Acknowledgments

This research was supported by the Major Institutional Project of the Korea Institute of Machinery and Materials funded by the Ministry of Science and ICT (MSIT) (Development of Core Machinery Technologies for Autonomous Operation and Manufacturing) under Grant NK242H. This research was supported by "LINC3.0" through the National Research Foundation of Korea (NRF) established by the Ministry of Education (MOE). This research was supported by the "Regional Innovation Strategy (RIS)" through the National Research Foundation of Korea (NRF) established by the Ministry of Education (MOE).

Conflicts of Interest

The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless Sensor Networks: A Survey on Recent Developments and Potential Synergies. Journal of Supercomputing 2014, 68, 1–48. [Google Scholar] [CrossRef]
  2. Huang, B.; Zhao, J.; Liu, J. A Survey of Simultaneous Localization and Mapping with an Envision in 6G Wireless Networks. 2019. [Google Scholar]
  3. Annual IEEE Computer Conference; IEEE International Conference on Acoustics, S. and S.P. 39 2014. 05. 04-09 F.; ICASSP 39 2014.05.04-09 Florence IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2014 4-9 May 2014, Florence, Italy. ISBN 9781479928934.
  4. Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
  5. Crețu-Sîrcu, A.L.; Schiøler, H.; Cederholm, J.P.; Sîrcu, I.; Schjørring, A.; Larrad, I.R.; Berardinelli, G.; Madsen, O. Evaluation and Comparison of Ultrasonic and UWB Technology for Indoor Localization in an Industrial Environment. Sensors 2022, 22. [Google Scholar] [CrossRef]
  6. Bahl, P.; Padmanabhan, V.N. RADAR: An In-Building RF-Based User Location and Tracking System.
  7. McLoughlin, B.J.; Pointon, H.A.G.; McLoughlin, J.P.; Shaw, A.; Bezombes, F.A. Uncertainty Characterisation of Mobile Robot Localisation Techniques Using Optical Surveying Grade Instruments. Sensors (Switzerland) 2018, 18. [Google Scholar] [CrossRef] [PubMed]
  8. Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
  9. Jan, B.; Farman, H.; Javed, H.; Montrucchio, B.; Khan, M.; Ali, S. Energy Efficient Hierarchical Clustering Approaches in Wireless Sensor Networks: A Survey. Wireless Communications and Mobile Computing 2017, 1–14. [Google Scholar] [CrossRef]
  10. Geng, C.; Abrudan, T.E.; Kolmonen, V.-M.; Huang, H. Experimental Study on Probabilistic ToA and AoA Joint Localization in Real Indoor Environments. 2021. [Google Scholar]
  11. Xiong, W.; Bordoy, J.; Gabbrielli, A.; Fischer, G.; Jan Schott, D.; Höflinger, F.; Wendeberg, J.; Schindelhauer, C.; Johann Rupitsch, S. Two Efficient and Easy-to-Use NLOS Mitigation Solutions to Indoor 3-D AOA-Based Localization.
  12. Horiba, M.; Okamoto, E.; Shinohara, T.; Matsumura, K. An Improved NLOS Detection Scheme for Hy-brid-TOA/AOA-Based Localization in Indoor Environments. In Proceedings of the 2013 IEEE International Conference on Ultra-Wideband (ICUWB), September 2013; IEEE; pp. 37–42. [Google Scholar]
  13. O’Lone, C.E.; Dhillon, H.S.; Buehrer, R.M. Characterizing the First-Arriving Multipath Component in 5G Millimeter Wave Networks: TOA, AOA, and Non-Line-of-Sight Bias. IEEE Trans Wireless Communication 2022, 21, 1602–1620. [Google Scholar] [CrossRef]
  14. Abbas, H.A.; Boskany, N.W.; Ghafoor, K.Z.; Rawat, D.B. Wi-Fi Based Accurate Indoor Localization System Using SVM and LSTM Algorithms. In Proceedings of the 2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI), August 2021; IEEE; pp. 416–422. [Google Scholar]
  15. Chriki, A.; Touati, H.; Snoussi, H. SVM-Based Indoor Localization in Wireless Sensor Networks. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), June 2017; IEEE; pp. 1144–1149. [Google Scholar]
  16. Zhou, G.; Luo, J.; Xu, S.; Zhang, S.; Meng, S.; Xiang, K. An EKF-Based Multiple Data Fusion for Mobile Robot Indoor Localization. Assembly Automation 2021, 41, 274–282. [Google Scholar] [CrossRef]
  17. Yang, T.; Cabani, A.; Chafouk, H. A Survey of Recent Indoor Localization Scenarios and Methodologies. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
  18. Geng, M.; Wang, Y.; Tian, Y.; Huang, T. CNUSVM: Hybrid CNN-Uneven SVM Model for Imbalanced Visual Learning. In Proceedings of the 2016 IEEE Second International Conference on Multimedia Big Data (BigMM), April 2016; IEEE; pp. 186–193. [Google Scholar]
  19. Oajsalee, S.; Tantrairatn, S.; Khaengkarn, S. Study of ROS Based Localization and Mapping for Closed Area Survey. In Proceedings of the 2019 IEEE 5th International Conference on Mechatronics System and Robots (ICMSR), May 2019; IEEE; pp. 24–28. [Google Scholar]
  20. Yang, T.; Cabani, A.; Chafouk, H. A Survey of Recent Indoor Localization Scenarios and Methodologies. Sensors 2021, 21, 8086. [Google Scholar] [CrossRef] [PubMed]
  21. Wang, T.; Zhao, H.; Shen, Y. An Efficient Single-Anchor Localization Method Using Ultra-Wide Bandwidth Systems. Applied Sciences (Switzerland) 2020, 10. [Google Scholar] [CrossRef]
  22. Gezici, S.; Tian, Z.; Giannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, H.V.; Sahinoglu, Z. Localization via Ultra-Wideband Radios: A Look at Positioning Aspects for Future Sensor Networks. IEEE Signal Processing Magazine 2005, 22, 70–84. [Google Scholar] [CrossRef]
  23. Krishnan, S.; Sharma, P.; Guoping, Z.; Hwee Woon, O. A UWB Based Localization System for Indoor Robot Navigation.
  24. Wang, Y.; Jie, H.; Cheng, L. A Fusion Localization Method Based on a Robust Extended Kalman Filter and Track-Quality for Wireless Sensor Networks. Sensors (Switzerland) 2019, 19. [Google Scholar] [CrossRef]
  25. A Mahdi, A.A.; Chalechale, A.; Abdelraouf, A. A Hybrid Indoor Positioning Model for Critical Situations Based on Localization Technologies. Mobile Information Systems 2022, 2022. [Google Scholar] [CrossRef]
  26. Nage11, H.-H.; Haag’, M. Bias-Corrected Optical Flow Estimation for Road Vehicle Tracking.
  27. OĞUZ EKİM, P. ROS Ekosistemi Ile Robotik Uygulamalar Için UWB, LiDAR ve Odometriye Dayalı Ko-numlandırma ve İlklendirme Algoritmaları. European Journal of Science and Technology 2020. [CrossRef]
  28. Li, J.; Gao, T.; Wang, X.; Bai, D.; Guo, W. The IMU/UWB/Odometer Fusion Positioning Algorithm Based on EKF. In Proceedings of the Journal of Physics: Conference Series; Institute of Physics, 2022; Vol. 2369. [Google Scholar]
  29. Crețu-Sîrcu, A.L.; Schiøler, H.; Cederholm, J.P.; Sîrcu, I.; Schjørring, A.; Larrad, I.R.; Berardinelli, G.; Madsen, O. Evaluation and Comparison of Ultrasonic and UWB Technology for Indoor Localization in an Industrial Environment. Sensors 2022, 22. [Google Scholar] [CrossRef]
  30. Queralta, J.P.; Martínez Almansa, C.; Schiano, F.; Floreano, D.; Westerlund, T. UWB-Based System for UAV Localization in GNSS-Denied Environments: Characterization and Dataset. Available online: https://ieeexplore.ieee.org/abstract/document/9341042/ (accessed on 22 November 2022).
  31. Long, Z.; Xiang, Y.; Lei, X.; Li, Y.; Hu, Z.; Dai, X. Integrated Indoor Positioning System of Greenhouse Robot Based on UWB/IMU/ODOM/LIDAR. Sensors 2022, 22. [Google Scholar] [CrossRef]
  32. Mahdi, A.A.; Chalechale, A.; Abdelraouf, A. A Hybrid Indoor Positioning Model for Critical Situations Based on Localization Technologies. Mobile Information Systems 2022, 2022. [Google Scholar] [CrossRef]
  33. Alatise, M.; Hancke, G. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef]
  34. A Xing, B.; Zhu, Q.; Pan, F.; Feng, X. Marker-Based Multi-Sensor Fusion Indoor Localization System for Micro Air Vehicles. Sensors 2018, 18, 1706. [Google Scholar] [CrossRef]
  35. Yi, D.H.; Lee, T.J.; Dan Cho, D. Il A New Localization System for Indoor Service Robots in Low Luminance and Slippery Indoor Environment Using A Focal Optical Flow Sensor Based Sensor Fusion. Sensors (Switzerland) 2018, 18. [Google Scholar] [CrossRef]
  36. Chen, L.; Hu, H.; McDonald-Maier, K. EKF Based Mobile Robot Localization. In Proceedings of the Proceedings - 3rd International Conference on Emerging Security Technologies, EST 2012; 2012; pp. 149–154. [Google Scholar]
  37. 2011 International Conference on Indoor Positioning and Indoor Navigation, Institute of Electrical and Electronics Engineering, 2011; ISBN 9781457718045.
  38. McLoughlin, B.J.; Pointon, H.A.G.; McLoughlin, J.P.; Shaw, A.; Bezombes, F.A. Uncertainty Characterisation of Mobile Robot Localisation Techniques Using Optical Surveying Grade Instruments. Sensors (Switzerland) 2018, 18. [Google Scholar] [CrossRef]
  39. Sesyuk, A.; Ioannou, S.; Raspopoulos, M. A Survey of 3D Indoor Localization Systems and Technologies. Sensors 2022, 22, 9380. [Google Scholar] [CrossRef] [PubMed]
  40. Dai, Y. Research on Robot Positioning and Navigation Algorithm Based on SLAM. Wireless Communications and Mobile Computing 2022, 2022, 1–10. [Google Scholar] [CrossRef]
  41. Wang, Y. Linear Least Squares Localization in Sensor Networks. EURASIP Journal on Wireless Communications and Networking 2015, 2015. [Google Scholar] [CrossRef]
Preprints 88277 g001
Figure 1. Working architecture.
Figure 1. Working architecture.
Preprints 88277 g001
Preprints 88277 g002
Figure 2. Testing environment structure.
Figure 2. Testing environment structure.
Preprints 88277 g002
Preprints 88277 g003
Figure 3. Webcam line of sight.
Figure 3. Webcam line of sight.
Preprints 88277 g003
Preprints 88277 g004
Figure 4. (a) Robot poses and LiDAR scans before the automatic initialization; (b) Robot poses and LiDAR scans after the automatic initialization.
Figure 4. (a) Robot poses and LiDAR scans before the automatic initialization; (b) Robot poses and LiDAR scans after the automatic initialization.
Preprints 88277 g004
Preprints 88277 g005
Figure 5. System flow-chart.
Figure 5. System flow-chart.
Preprints 88277 g005
Preprints 88277 g006
Figure 6. Indoor environment.
Figure 6. Indoor environment.
Preprints 88277 g006
Preprints 88277 g009
Figure 8. Error comparison graph of square trajectory path-T1 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Figure 8. Error comparison graph of square trajectory path-T1 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Preprints 88277 g009
Preprints 88277 g012
Figure 10. Error comparison graph of circular trajectory path-T2 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Figure 10. Error comparison graph of circular trajectory path-T2 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Preprints 88277 g012
Preprints 88277 g015
Figure 12. Error comparison graph of free trajectory path -T3 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Figure 12. Error comparison graph of free trajectory path -T3 with (AVG, KF, EKF and AVG+LPF, KF+LPF, EKF+LPF) filtering.
Preprints 88277 g015
Table 1. Hardware Specification.
Table 1. Hardware Specification.
Hardware Components Description
UWB Localization System
  • POZYX UWB localization system
  • Consists of UWB anchors and tags
  • Operates in the frequency range of 3.5 GHz to 6.5 GHz
  • Supports precise indoor positioning
  • Range of up to 100 meters
Camera
  • High-resolution RGB camera
  • Minimum resolution of 1080p
  • Wide field of view (FOV) of at least 90°
  • Interfaces with the computer/processing unit via USB 3.0
TurtleBot
  • TurtleBot 3 Burger model
  • Equipped with a Raspberry Pi 4 single-board
  • Features a differential drive system with two DC motors
  • Includes encoders for odometry calculations
  • Equipped with a 360-degree LiDAR sensor
Computer/Processing Unit
  • Intel Core i7 processor-based computer
  • 8GB RAM
  • 256GB SSD storage
  • Runs on Ubuntu or ROS (Robot Operating System
UWB Anchors and Tags
  • Four UWB anchor nodes
  • One UWB tag
Power Supply
  • Input voltage: 100-240V AC
  • Output voltage: 12V DC
Communication Interface
  • Gigabit Ethernet interface for high-speed data transfer
  • Communication between the computer and processing unit, UWB system, and Turtle Bot
Mounting Hardware
  • In-house 3D printed mounting brackets and fixtures for the camera, UWB anchors, and tags
Table 2. Measurement error data for the square trajectory for both algorithms.
Table 2. Measurement error data for the square trajectory for both algorithms.
Trajectory Distance Speed Max. (mm) Min. (mm) |Max.-Min.|
(mm)		 Mean (mm)
X Y X Y X Y X Y
Square 2m 0.5m/s 180.82 371.07 0.12 0.12 179.9 371.85 52.19 89.09
Square (LPF) 2m 0.5m/s 163.81 273.09 0.13 0.09 163.68 273 46.4 70.36
Table 3. Measurement error data for the circular trajectory for both algorithms.
Table 3. Measurement error data for the circular trajectory for both algorithms.
Trajectory Distance Speed Max. (mm) Min. (mm) |Max.-Min.| (mm) Mean (mm)
X Y X Y X Y X X
Circular 2.2m 0.5m/s 166.38 341.05 0.46 0.58 165.91 340.47 56.34 100.5
Circular (LPF) 2.2m 0.5m/s 158.51 286.22 0.52 0.81 157.99 285.4 157.99 285.4
Table 4. Measurement error data of free trajectory path for both algorithms.
Table 4. Measurement error data of free trajectory path for both algorithms.
Trajectory Distance Speed Max. (mm) Min. (mm) |Max.-Min.| (mm) Mean (mm)
X Y X Y X Y X X
Free 5m 0.5m/s 310.84 197.99 0.3 0.2 310.55 197.78 88.84 84.36
Free (LPF) 5m 0.5m/s 256.74 166.50 0.74 0.36 255.99 166.13 76.25 74.07
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated