1. Introduction
Since its initial discovery by the Belle Collaboration in 2003 [
1], the
state has garnered significant attention on
structure. There’s a lot of work on
structure, such as
[
2],
[
3],
[
4], and so on. Now, researchers have extensively investigated various structures involving heavy quarks and antiquarks, denoted by
, within exotic tetraquark states. Examples include the possibility of
as a
structure,
as a
configuration, and
as a
state, which can be found in Refs. [
5,
6,
7]. These studies have significantly contributed to a deeper understanding of QCD. Recent observations by the LHCb Collaboration have added to the rich landscape of exotic states with the discovery of the
resonance in the di-
invariant mass spectrum [
8]. Subsequent reports from CMS and ATLAS Collaborations have highlighted additional resonances, such as
,
, and
, sparking renewed theoretical interest in exotic states with the
configuration [
9,
10]. However, investigations into resonance states within the
configuration, particularly focusing on the tetraquark state with positive parity, are currently limited in the literature.
Studies of the
configuration may be traced back to discovery of
in 2006 [
11], which is now known as
, in the initial state-radiation (ISR) process of
. The mass of this state is measured to be
MeV with a width of
MeV. More recently, the BESIII Collaboration reported the observation of a new structure,
, in the
mass spectrum [
12]. The quantum numbers of
are still under investigation. If
, the mass is determined to be
MeV with a width of
MeV. Alternatively, if
, the mass is estimated to be
MeV with a width of
MeV. Furthermore, recent reports from the BESIII Collaboration have shed light on two distinct resonances:
observed in the context of
[
13], and the recently discovered
resonance within the
process [
14]. These discoveries have significantly expanded the
family. However, as of yet, the existence of clear positive parity
states remains elusive.
Current theoretical research is prominently focused on the
tetraquark state, particularly exploring its negative parity aspects. In Ref. [
15], the author presented standard criteria within the QCD sum rules approach and conducted a comprehensive phenomenological analysis. The author suggests that
potentially may consist of color octet constituents rather than diquark pairs. Similarly, in Ref. [
16], Chen et al. employed the QCD sum rule framework, constructing both diquark-antidiquark currents
and meson-meson currents
. They extensively studied the decay properties of
. Based on this work, Chen et al. recently utilized two independent
interpolating currents with
, calculating both their diagonal and off-diagonal correlation functions. This calculation yielded two distinct physical states, one being
and the other at an energy level near 2.41 GeV, consistent with recent experimental observations [
17]. Additionally, researchers investigated the mass spectrum of the
tetraquark states within the relativized quark model, incorporating screening effects. Notably, the observed resonance at 2239 MeV could potentially correspond to a wave
tetraquark state [
18]. On the other hand, studies pertaining to the
tetraquark state with positive parity have also made significant progress. Deng et al. utilized a chiral quark model to calculate the properties of the efficient
tetraquark state. Their results indicated that the
state had an energy of approximately 1925 MeV, suggesting a candidate for
[
19]. In the QCD sum rule framework (Chen et al., Refs. [
20,
21]), calculations for quantum numbers
,
,
of the
four-quark state were conducted, yielding energies around 2.0 GeV. Additionally, quantum numbers
and
were associated with energies approximately
GeV and
GeV, respectively. The energy of the
tetraquark state aligned with results available in the literature [
22,
23].
In this study, we employ the Gaussian Expansion Method (GEM) to investigate the tetraquark system of with quantum numbers of within the framework of a chiral quark model. Two distinct structures are considered in our calculations: the - molecular structure and the - diquark structure. In theory, all energy levels within the diquark structure and color-octet structure are expected to be bound states. However, in practice, only a limited number of structures are observed experimentally. Hence, it is imperative to couple the diquark structure with the molecular structure to investigate whether the structures produced by these diquarks decay into the molecular structures. Additionally, our calculations are conducted within a finite space, potentially resulting in energy levels that may not accurately represent the true resonance states. To address this concern, we introduce the real-scaling method in this paper. This work applies the real-scaling method to test and find resonant states below 3 GeV based on the experimental and theoretical evidence that the energies of the discovered resonant states with configuration are all lower than 3 GeV.
The structure of this paper is organized as follows: In Section I, we provide an introduction to the study. In Section II, we elaborate on the details of the Chiral Quark Model (ChQM) and Gaussian Expansion Method (GEM) employed in our investigation. Subsequently, in Section III, we describe a method for identifying and calculating the decay width of the genuine resonance state. In Section IV, we present the numerical results. Finally, in Section IV, we summarize our findings and conclude this work.
2. Chiral Quark Model, Wave Function of System
2.1. Chiral Quark Model
The chiral quark model, a well-established theoretical framework renowned for its success in describing hadron spectra and hadron-hadron interactions, has been instrumental in shaping our approach in this study. Interested readers are encouraged to refer to the comprehensive details of the model available in Refs. [
24,
25,
26]. Here only the Hamiltonian of the chiral quark model for four-quark system is shown,
where
is the constituent masse of
i-th quark (antiquark), and
is the reduced masse of two interacting quarks or quark-clusters.
is the confining potential, mimics the “confinement" property of QCD,
The second potential
is one-gluon exchange interaction reflecting the “asymptotic freedom" property of QCD.
are the
Pauli matrices;
are
color Gell-Mann matrices,
and
is an effective scale-dependent running coupling,
The third potential
is Goldstone boson exchange, coming from “chiral symmetry spontaneous breaking" of QCD in the low-energy region,
are flavor Gell-Mann matrices, are the masses of Goldstone bosons, are the cut-offs, is the Goldstone-quark coupling constant.
All the parameters are determined by fitting the meson spectrum, from light to heavy, taking into account only a quark-antiquark component. They are shown in
Table 1.
2.2. The Wave Function of System
There are two physically important structures, meson-meson and diquark-antidiquark, are considered in the present calculation. The wave functions of every structure all consists of four parts: orbital, spin, flavor and color. The wave function of each part is constructed in two steps, first write down the two-body wave functions, then coupling two sub-clusters wave functions to form the four-body one. Because there are two identical quark pairs in the system, the total wave function for the
system will be the tensor product of orbital (
), spin (
), color (
) and flavor (
) components with necessary coupling,
Where is the antisymmetrization operator. For the system, .
2.2.1. Orbital Wave Function
The orbital wave function of the four-quark system consists of two sub-cluster orbital wave function and the relative motion wave function between two subclusters (1,3 denote quarks and 2,4 denote antiquarks),
where the bracket "[ ]" indicates orbital angular momentum coupling, and
L is the total orbital angular momentum which comes from the coupling of
, orbital angular momentum of relative motion, and
, which coupled by
and
, sub-cluster orbital angular momenta. Given our focus on investigating the tetraquark state of
with positive parity, we set both
and
to zero.
donate the orbital wave functions of meson-meson structure, and
donate the wave functions of diquark-antidiquark structure. In GEM, the radial part of the orbital wave function is expanded by a set of Gaussians:
where
are normalization constants,
are the variational parameters, which are determined dynamically. The Gaussian size parameters are chosen according to the following geometric progression
This procedure enables optimization of the using of Gaussians, as small as possible Gaussians are used.
2.2.2. Spin Wave Function
Because of no difference between spin of quark and antiquark, the meson-meson structure has the same spin wave function as the diquark-antidiquark structure. The spin wave functions of the sub-cluster are shown below.
Coupling the spin wave functions of two sub-clusters by Clebsch-Gordan coefficients, total spin wave function can be written below,
The total spin wave function is denoted by , i is the index of the functions, the S is the total spin of the system.
2.2.3. Flavor Wave Function
We have two flavor wave functions of the system,
is for meson-meson structure, and
is for diquark-antidiquark structure.
2.2.4. Color Wave Function
The colorless tetraquark system has four color wave functions, two for meson-meson structure,
(
),
(
), and two for diquark-antidiquark structure,
(
) and
(
).
2.2.5. Total Wave Function
The total wave functions are obtained by the direct product of wave functions of orbital, spin, color and flavor wave functions. Because we are interested in the states with positive parity, there are three quantum number:
,
, and
. Finally, the total wave function of the system is written as:
At last, we solve the following Schrödinger equation to obtain eigen-energies of the system, with the help of the Rayleigh-Ritz variational principle.
where
is the wave function of the four-quark states, which is the linear combinations of the above channel wave functions.
3. Real-Scaling Method
The real-scaling method, originally introduced by Taylor [
27] to estimate the energies of long-lived metastable states of electron-atom, electron-molecule, and atom-diatom complexes, has since found applications in resonance state studies. Jack Simons [
28] extended this method to investigate resonance states. Emiko Hiyama
et al. [
29] were among the first to apply the real-scaling method within a quark model context to search for
states in the
system.
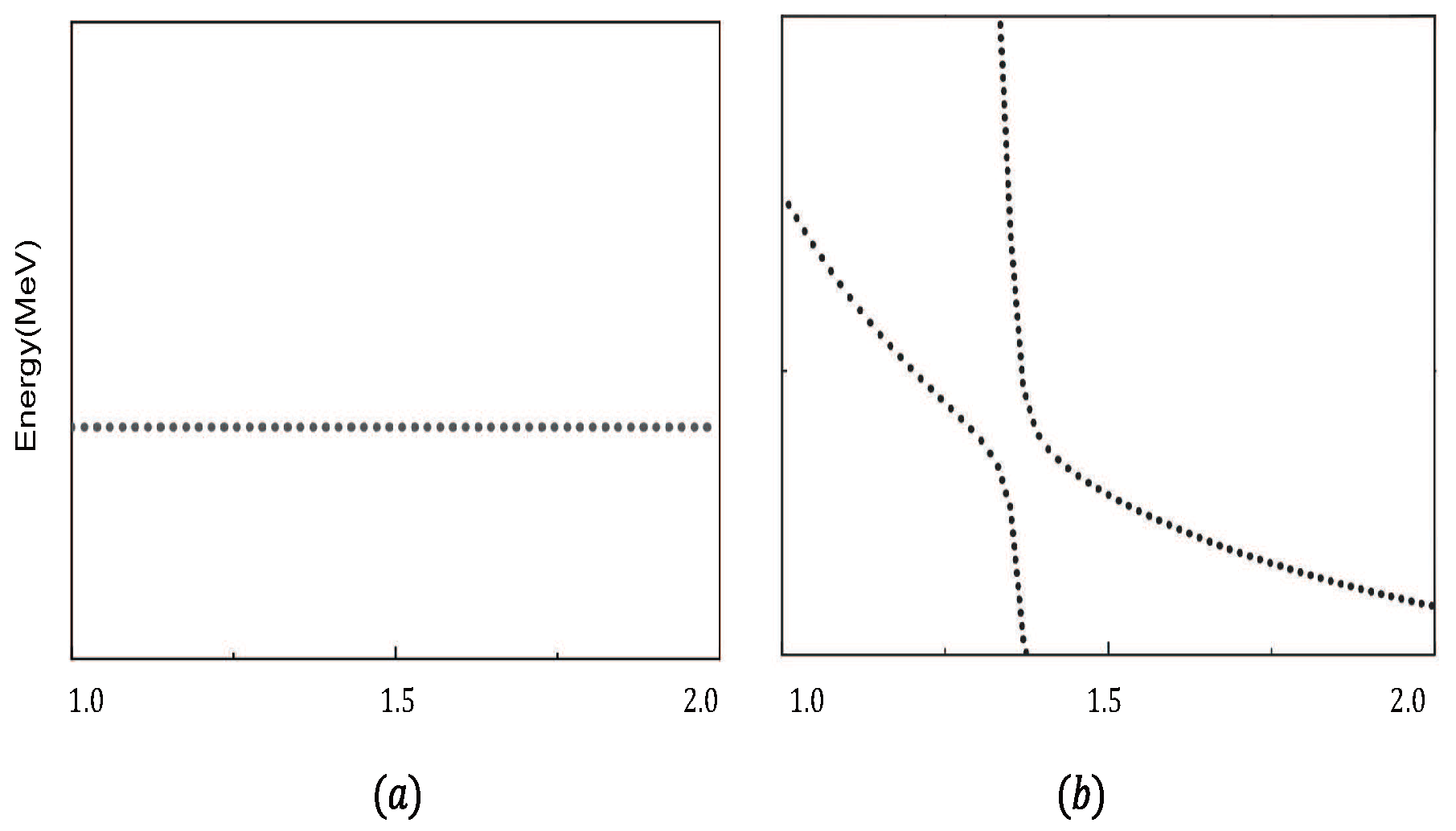
Figure 1.
Two forms of resonant states (a) the resonance has weak coupling (or no coupling) with the scattering states; (b) the resonances has strong coupling with the scattering states;
Figure 1.
Two forms of resonant states (a) the resonance has weak coupling (or no coupling) with the scattering states; (b) the resonances has strong coupling with the scattering states;
Distinguished from other resonance computation methods based on stabilized eigenvectors, the real-scaling method allows for the direct estimation of decay widths from the stabilization graph. In this approach, a scaling factor is employed to adjust the finite volume. False resonant states, reproduced by superabundant colorful subclusters (molecular hidden-color state or diquark structure), fall down to the corresponding threshold. Genuine resonances, on the other hand, persist after coupling to the scattering states and remain stable as increases. Genuine resonances manifest in two distinct forms:
(1) Weak Coupling: If the energy of a scattering state significantly differs from that of the resonance, indicating weak or no coupling between the resonances and scattering states, the resonance appears as a stable straight line.
(2) Strong Coupling: When the energy of a scattering state approaches that of the resonance, indicating strong coupling, an avoid crossing structure manifests between two declining lines.
The decay width can be estimated from the slopes of the resonance and scattering states using Eq. (
15), where
denotes the slope of the resonance,
denotes the slope of the scattering state, and
represents the energy level difference between the resonance and the scattering state. Furthermore, as
increases continually, the avoid crossing structure repeats, providing valuable insights into the resonance behavior.
4. Results and Discussions
In this section, we present the numerical results obtained from our calculations, with a primary focus on the quest for potential resonance states within the system possessing positive parity. As an initial step in our investigation, we conduct a dynamic calculation utilizing the Gaussian Expansion Method (GEM) to ascertain the presence of any bound states. By analyzing the energy levels of the diquark and color-octet structure, we aim to determine the potential for resonance states within the system. Subsequently, after extracting the energies through the generalized eigen-equation, we apply the real-scaling method to verify the stability of the computed energy levels. This methodology enables us to confirm whether the obtained energy levels indeed correspond to stable states.
4.1. Tetraquark States Analysis and Resonance Identification
In this subsection, we present a comprehensive analysis of all conceivable
tetraquark states with positive parity. The details of these states are summarized in
Table 2, which includes the indices of orbit, flavor, spin, and color wave functions for each channel. Additionally, the Table provides information on the energy, threshold, and binding energy for each physical channel. Our analysis focuses on rigorously assessing the binding energy (
) of each color-singlet state by comparing its theoretical calculated value with its corresponding threshold value (
). If
is less than 0, we will manually set it to 0. It is noteworthy that color-excited states (color-octet and diquark structure) inherently possess internal attraction due to color interactions, so we omit the
values for the color-excited structures. Subsequently, we employ the real-scaling method to investigate whether states displaying attractive interactions, encompassing both color-excited and color-singlet states with
values less than zero, can indeed form resonance states. Since we are only interested in the resonant states below 3 GeV, resonance states with energies higher than 3 GeV are not considered.
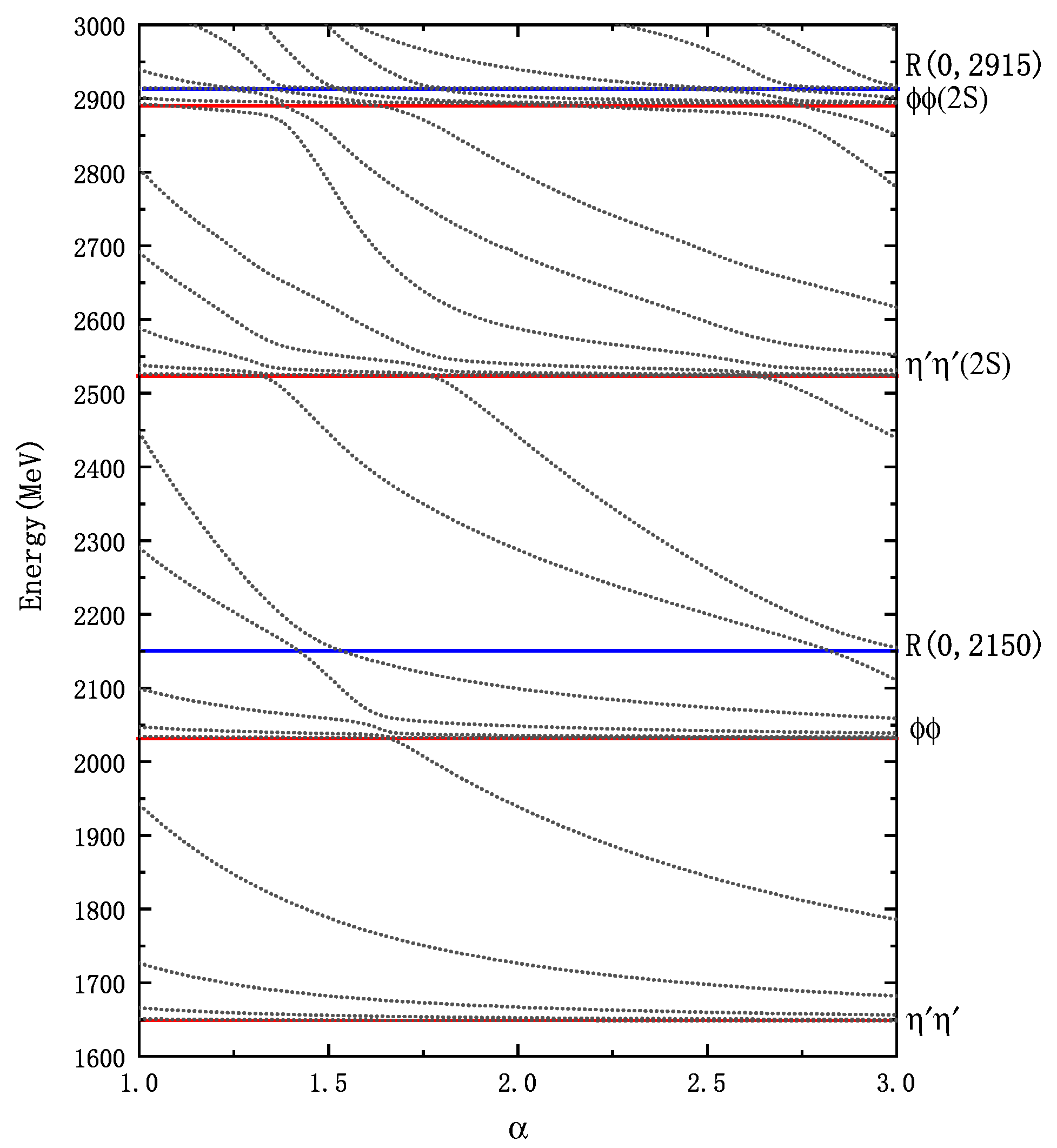
Figure 2.
Energy spectrum of states. The blue line depicts the resonant state, while the red line represents the physical threshold.
Figure 2.
Energy spectrum of states. The blue line depicts the resonant state, while the red line represents the physical threshold.
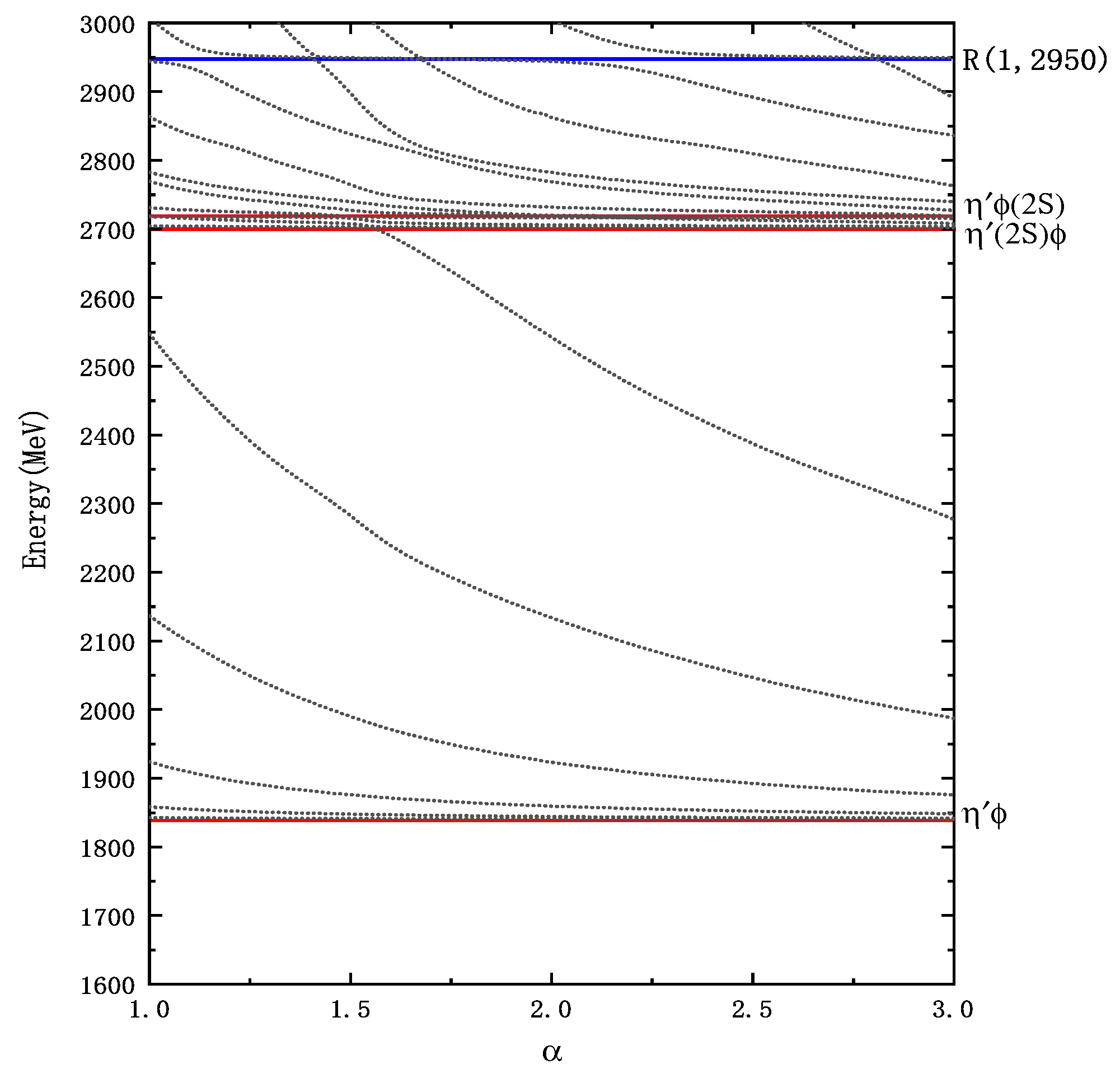
Figure 3.
Energy spectrum of states. The blue line depicts the resonant state, while the red line represents the physical threshold.
Figure 3.
Energy spectrum of states. The blue line depicts the resonant state, while the red line represents the physical threshold.
: Upon detailed analysis presented in
Table 2, we observe a total of two color-singlet states,
and
, existing in the
system. Additionally, their corresponding color-octet states and two diquark states are identified within an energy range of approximately 2.25-2.32 GeV. Remarkably, the result reveals that the color-singlet states (
and
) do not form bound states, even if the channel coupling effect is taken into consideration. To further investigate and identify resonant states, we perform structure-coupling calculations, coupling the color excitation structure with the color-singlet structure using the real-scaling method. The results demonstrate a continuous decrease in energy as the factor
increases from its initial value of 1. At approximately
, a distinct avoid-crossing structure emerges, repeating at
, which represents the resonant state in our study. We denote it as
(we label the resulting resonant state with
). Analogously, we identify another resonance state,
, positioned above the
energy level.
:In principle, a tetraquark system with a total spin of 1 should exhibit three possible combinations: , , and . These combinations, when combined with two types of spatial wave functions (, ) and four types of color wave functions (, , , ), result in a total of 12 channels for the wave function. However, due to symmetry constraints, the tetraquark system with spin is limited to only five channels: two color-singlet states (, ), two corresponding color-octet states, and one diquark state. Our calculation results indicate that the tetraquark system with does not have any bound states. The energies of the color-excited structure are predominantly centered around 2.25 GeV. The evident coupling effect among these states is noteworthy, leading to a notable reduction in the minimum energy from 2.25 GeV to 2.20 GeV due to the influence of coupling channels. This state may be a potential candidate for in experimental observations. However, within the real-scaling framework, this state undergoes decay to the corresponding threshold, implying its non-existence in our study. Intriguingly, we have identified a stable structure at approximately 2.95 GeV, denoted as .
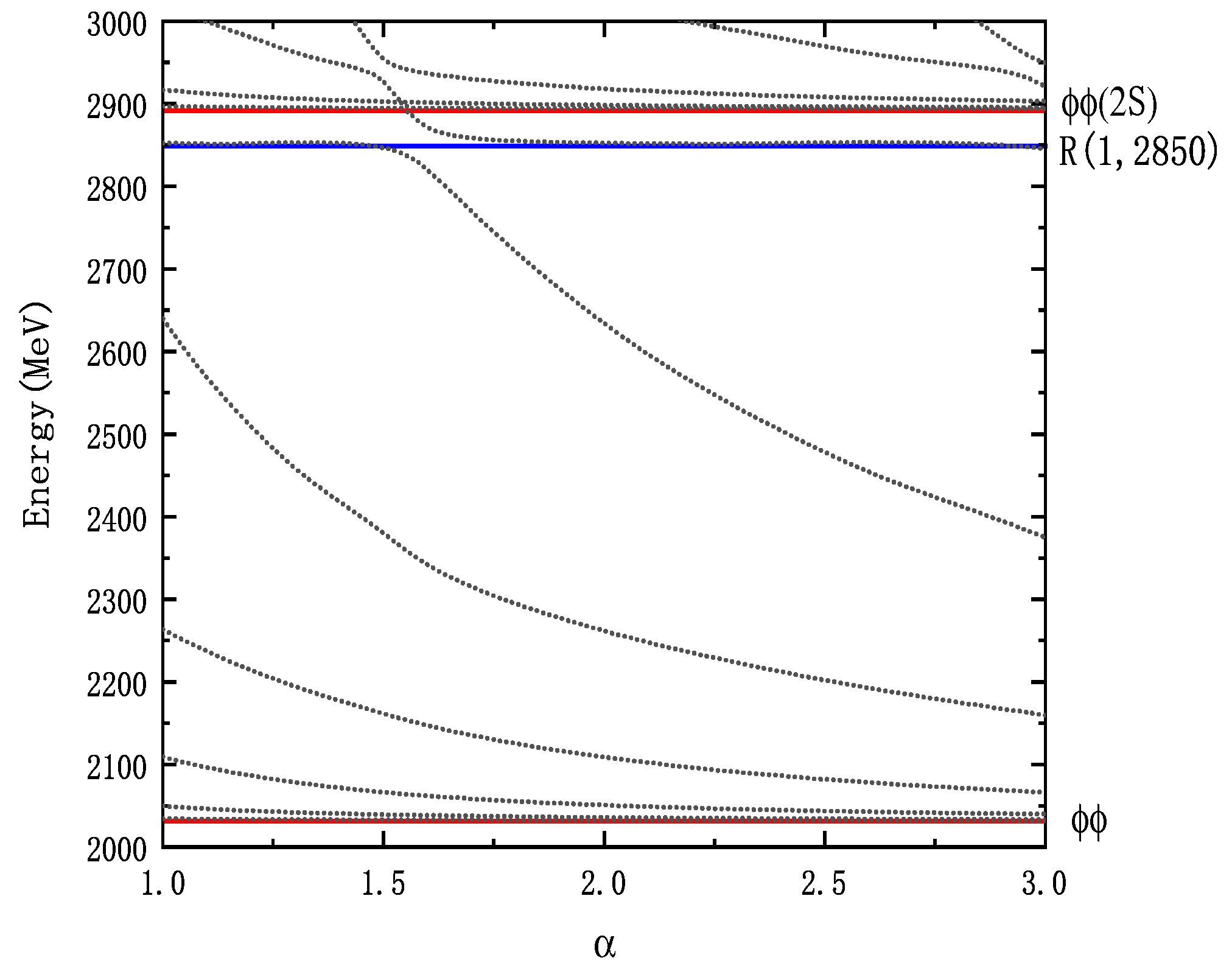
:For a tetraquark system with a total spin of 2, the available states are considerably reduced. In this scenario, there exists only one color-singlet state,
. Additionally, a color-octet molecular state
and a diquark state
are present, yielding a total of three wave functions. The energies of these states are primarily concentrated in the range of 2 GeV to 2.3 GeV. Intriguingly, resonance state calculations reveal a prominent resonance state,
, as depicted in
Figure 4.
From the comprehensive analysis discussed above, a total of four resonance states are identified: , , , and . These resonance states exhibit a root-mean-square distance concentrated around 1 fm and widths in the range of 40-90 MeV. This can be attributed to their predominant composition of diquark and color-octet states. Of particular interest is that and have energies slightly above the threshold, resembling the characteristics of , which resides just above the threshold. This similarity suggests a possible kinship, positioning and as potential counterparts to . Similarly, the energy of falls above and below , resembling the energy characteristics of . This observation leads to the hypothesis that could be a kin to . On the other hand, also can be the candidate of .
4.2. Compared with the Other Work
As highlighted in our introduction, there has been some prior research on the
tetraquark system. This diverse body of work, encompassing various models and methods, not only check the model dependence of results but also contributes to a more profound comprehension of the
tetraquark system’s nature. These research endeavors broadly fall into two categories: QCD sum rule and quark potential energy models. Our findings, as presented in
Table 4, demonstrate qualitative consistency with previous calculations. For a quantum number of
, our calculations yield two resonant states, namely
and
. Remarkably, the energy of
closely resembles the energy values reported in other studies. In Ref. [
23], up to six energy levels are presented, one of which closely matches our
energy value. Notably, the remaining potential energy levels between
and
in our calculations are found to decay into their corresponding threshold states, resulting in the identification of two resonance states. At a quantum number of
, both QCD sum rule methods yield energies approximately around 2060 MeV [
21,
22], which is notably lower than the energy associated with
in our findings. In fact, in our model’s calculations, the energies of diquark structure also falls in the vicinity of 2200 MeV. However, it’s important to note that strong channel coupling effects in our calculations lead to the decay of some energy levels into their respective threshold channels. On the other hand, the energy level of 2954 MeV in Ref. [
23] closely corresponds to our result,
. In the case of a quantum number of
, our energy level calculations exhibit significant similarities to the
quantum number scenario. The energy value associated with
is in strong agreement with results reported in Refs. [
20,
23].
5. Summary
Within the framework of the quark model, we conducted a comprehensive study on the system, exploring three different quantum number combinations, namely, , , and . Our investigations include not only the diquark structure but also molecular structures while accounting for all permissible color, flavor, and spin configurations.
The dynamic calculations yielded no bound states under any of the three quantum numbers. Nevertheless, the presence of color attraction mechanisms within the color-excited structures, encompassing both color-octet structures and diquark structures, introduced the possibility of several potential resonances. To ascertain the stability of these potential resonant states, we employed the real-scaling method. The results reveal that the majority of false resonances decayed into their corresponding threshold channels, leaving behind only four confirmed resonance states: two resonances , , one resonances , and one resonances . These four resonant states share similar compositions, primarily dominated by diquark structures and color-octet structures. Consequently, they exhibit root-mean-square distances of around 1 fm and widths within the range of 40-90 MeV.
In conjunction with experimental insights from systems, we draw parallels between our findings and the observed , which has an energy slightly above that of and a width several tens of MeV larger. Similarly, the energies of and in our results are slightly higher than that of and possess widths exceeding 45 MeV, suggesting their potential kinship to . Additionally, we propose that the which is the candidate of could be a cousin of . Given the consistency between our calculations and the work of others, we recommend that experimental efforts explore the existence of these resonant states in the future.
Acknowledgments
This work is supported partly by the National Natural Science Foundation of China under Grant Nos. 12205249, 11675080, 11775118 and 11535005, and the Funding for School-Level Research Projects of Yancheng Institute of Technology (No. xjr2022039).
References
- S. K. Choi et al. [Belle Collaboration], Phys. Rev. Lett. (2003) 91, 262001.
- B. Aubert et al. [BaBar], Phys. Rev. Lett (2005) 95, 142001. arXiv:arXiv:hep-ex/0506081. [CrossRef]
- M. Ablikim et al. [BESIII], Phys. Rev. Lett (2013) 110, 252001. arXiv:arXiv:1303.5949. [CrossRef]
- X. L. Wang et al. [Belle], Phys. Rev. Lett (2007) 99, 142002. arXiv:arXiv:0707.3699. [CrossRef]
- J. He and P. L. Lü, Nucl. Phys A (2013) 919, 1-14. arXiv:arXiv:1309.6718. [CrossRef]
- Y. Tan, X. Liu, X. Chen, H. Huang and J. Ping, Phys. Rev. (2023) 108, no.1, 014017. arXiv:arXiv:2210.16250. [CrossRef]
- H. Huang, C. Deng, X. Liu, Y. Tan and J. Ping, Symmetry (2023) 15, no.7, 1298. [CrossRef]
- R. Aaij et al. [LHCb], Sci. Bull. (2020) 65, no.23, 1983-1993. arXiv:arXiv:2006.16957. [CrossRef]
- L. Lunerti, PoS ICHEP 2022 941. [CrossRef]
- G. Aad et al. [ATLAS], Phys. Rev. Lett. (2023) 131, no.15, 151902. arXiv:arXiv:2304.08962. [CrossRef]
- B. Aubert et al. [BaBar], Phys. Rev (2006) 74, 091103. arXiv:arXiv:hep-ex/0610018. [CrossRef]
- M. Ablikim et al. [BESIII], Phys. Rev. D (2019) 99, no.11, 112008. arXiv:arXiv:1901.00085. [CrossRef]
- M. Ablikim et al. [BESIII], Phys. Rev. D (2016) 93, no.11, 112011. arXiv:arXiv:1602.01523. [CrossRef]
- M. Ablikim et al. [BESIII], Phys. Rev. D (2019) 99, no.3, 032001. arXiv:arXiv:1811.08742. [CrossRef]
- Z. G. Wang, Nucl. Phys (2007) 791, 106-116. arXiv:arXiv:hep-ph/0610171. [CrossRef]
- H. X. Chen, X. Liu, A. Hosaka and S. L. Zhu, Phys. Rev (2008) 78, 034012. arXiv:arXiv:hep-ph/0610171. [CrossRef]
- H. X. Chen, C. P. Shen and S. L. Zhu, Phys. Rev. D (2018), 98, no.1, 014011. arXiv:arXiv:1805.06100. [CrossRef]
- Q. F. Lü, K. L. Wang and Y. B. Dong, Chin. Phys. C (2020) 44, no.2, 024101. arXiv:arXiv:1903.05007. [CrossRef]
- C. Deng, J. Ping, F. Wang and T. Goldman, Phys. Rev (2010) 82, 074001. [CrossRef]
- E. L. Cui, H. M. Yang, H. X. Chen, W. Chen and C. P. Shen, Eur. Phys. J. C (2019) 79, no.3, 232. arXiv:arXiv:1901.01724. [CrossRef]
- N. Su and H. X. Chen, Phys. Rev. D (2022) 106, no.1, 014023. arXiv:arXiv:2204.13959. [CrossRef]
- Z. G. Wang, Adv. High Energy Phys 2020, 6438730. arXiv:arXiv:1901.04815. [CrossRef]
- F. X. Liu, M. S. Liu, X. H. Zhong and Q. Zhao, Phys. Rev. D (2021) 103, no.1, 016016. arXiv:arXiv:2008.01372. [CrossRef]
- J. Vijande, F. Fernandez and A. Valcarce, J. Phys G (2005) 31, 481. arXiv:arXiv:hep-ph/0411299. [CrossRef]
- Y. Yang, C. Deng, H. Huang and J. Ping, Mod. Phys. Lett A (2008) 23, 1819-1828. [CrossRef]
- Y. Tan, W. Lu and J. Ping, Eur. Phys. J. Plus (2020) 135, no.9, 716. arXiv:arXiv:2004.02106. [CrossRef]
- Howard S. Taylor, Advan. Chem. Phys. (1970) 18, 91-147. [CrossRef]
- J. Simons, J. Chem. Phys. (1981) 75, 2465. [CrossRef]
- E. Hiyama, A. Hosaka, M. Oka and J. M. Richard, Phys. Rev. C (2018) 98, no.4, 045208. arXiv:arXiv:1803.11369. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).