Prerpints.org logo
Preprint
Article

Robust Epileptic Seizure Detection using LSTM and Feature Fusion from Compressed Time-Frequency EEG Images

Altmetrics

Downloads

185

Views

76

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts
Abstract
Epilepsy is a prevalent neurological disorder with considerable risks, including physical impairment and irreversible brain damage from seizures. Given these challenges, the urgency for prompt and accurate seizure detection cannot be overstated. Traditionally, experts have relied on manual EEG signal analyses for seizure detection, which is labor-intensive and prone to hu-man error. Recognizing this limitation, the rise of deep learning methods has been heralded as a promising avenue, offering more refined diagnostic precision. On the other hand, the prevailing challenge in many models is their constrained emphasis on specific domains, potentially diminishing their robustness and precision in complex real-world environments. This paper presents a novel model that seamlessly integrates the salient features from the time-frequency domain alongside pivotal statistical attributes derived from EEG signals. This fusion process involves the integration of essential statistics, including the mean, median, and variance, combined with the rich data from compressed time-frequency (CWT) images processed using auto-encoders. This multidimensional feature set provides a robust foundation for subsequent analytic steps. A long short-term memory (LSTM) network, meticulously optimized for the renowned Bonn Epilepsy dataset, was used to enhance the capability of the proposed model. Preliminary evaluations underscore the prowess of the proposed model: remarkable 100% accuracy in most of the binary classifications, impressive performance exceeding 95% for three-class and four-class challenges, and a commendable rate exceeding 93.5% for the five-class classification.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Approximately 1% of the global population is affected by epilepsy [1]. This condition poses significant challenges that can even be life-threatening for those affected. Among these patients, one-third do not respond to medications and need physical interventions [2]. Epileptic seizures are characterized by swift and abnormal fluctuations in the electrical patterns of the brain. In severe cases, they can cause the entire body to become unresponsive [3]. Electroencephalogram (EEG) signals have been the fundamental reference for detecting epileptic seizures, helping identify the seizure origin, and facilitating treatment of the affected brain tissues through medication and surgical procedures. EEG signals contain significant features that detail both regular and irregular brain activities, particularly epileptic seizures. In addition, high-temporal-resolution EEG data from the scalp, spanning multiple input channels, can be acquired through distributed continuous sensing techniques [4]. Traditionally, diagnosing epilepsy through visual analysis of EEG recordings, both clinically and conventionally, is labor-intensive and prone to error with varying consistency among experts because of its heavy reliance on human expertise and skill [5,6].
Many EEG automatic seizure detection systems struggle with real-time specificity and sensitivity, making them less suitable for clinical applications. There is a pressing need for an advanced computer-aided system that can efficiently assist neurologists in detecting epileptic seizures, ultimately reducing the time spent analyzing extensive EEG recordings [7]. In areas with a scarcity of neurologists, the excessive dependence on human expertise can increase the costs and cause delays in treating epilepsy. Tackling these issues is essential to guarantee affordable epilepsy care in low to middle-income regions, particularly in isolated locations with restricted access to skilled professionals and advanced facilities. Improving access to automated seizure detection from EEG signals has been studied extensively to mitigate this issue [8].
Machine learning is used widely to detect diseases automatically from biomedical signals, such as ECG and EEG. For example, a previous study [9] used two distinct features to detect epileptic seizures: fractal-based nonlinear features and entropy-based features. These features were input into two machine learning classifiers: Support Vector Machine (SVM) and K-Nearest Neighbor (KNN). The classifiers were trained and tested for the binary detection tasks (e.g., Z–S, O–S, and N–S) and the three-class detection problem (ZO–NF–S). In addition, another study [10] introduced a framework that integrates fuzzy-based methods and conventional machine-learning techniques to identify epileptic EEG samples in binary classification problems. A limited set of features and linear (using the Naïve Bayes classifier) and nonlinear (using the K-Nearest Neighbor classifier) approaches were applied to classify the EEG samples [11]. Binary classification tasks involved classifying various classes, i.e., Z–S, O–S, N–S, F–S, ZO–S, and ZN–E.
Beyond traditional machine learning techniques, various deep learning architectures have been introduced to detect epileptic seizures in EEG data. A previous study [12] utilized deep learning approaches to extract the important features from EEG data. In particular, a Convolutional Neural Network (CNN) was implemented for the differentiation tasks among normal, preictal, and seizure classes. In addition, the Discrete Wavelet Transform (DWT) was used for feature extraction from the EEG data [13]. A combination of a genetic algorithm and artificial neural network (ANN) and the Support Vector Machine (SVM) classifiers were used to address binary and three-class classification challenges in the Bonn Epilepsy Database.
Many seizure detection methods concentrate on specific domains, such as utilizing time-frequency domain methods, such as Continuous Wavelet Transform (CWT), time domain, frequency domain, and statistical attributes. Unlike the other methods, the proposed epileptic detection model innovatively combines the best of these attributes. A comprehensive set of important features is obtained by leveraging the complex insights from the statistical domain that is characterized by rich features, such as the mean, median, variance, skewness, and kurtosis, with the compressed time-frequency domain images (CWT Images) processed through an auto-encoder. This hybrid integration of Convolutional Autoencoder (CAE) latent space and statistical features ensures model robustness, making it adept at capturing the most vital information for classification. A long short-term memory network was used to optimize the approach, allowing precise classifications ranging from binary to five-class classification challenges, particularly fine-tuned for the Bonn Epilepsy dataset.

1.1. Contribution

The main contributions of this work are as follows.
• This study introduces a significant advancement in epileptic seizure detection. The proposed novel deep learning method seamlessly merges the compressed latent space features from the time-frequency domain with statistical attributes of the EEG signal. This integrated feature pool captures time-frequency and statistical information, making this approach different in robustness and accuracy.
• The proposed hybrid model uses an optimal window size for EEG segmentation, ensuring minimal data loss and a set overlap ratio. After rigorous evaluation, this method selects the best window size for maximal data coverage, which is crucial for precise EEG classification. This strategy upholds data integrity, boosting the classification reliability of the model.
• A CAE was used for feature extraction from CWT images. CAEs excel at handling image data like EEG-based CWT by preserving spatial structures. The CAE retained the most important features and eliminated noise by compressing and reconstructing the image. This method reduced data dimensionality and identified the most vital EEG patterns, enhancing precision and accuracy in subsequent analysis.
• The CAE latent space features still contained some less important features. Principal Component Analysis (PCA) was applied to extract the most relevant features from the latent space, enhancing the classification accuracy.
• LSTM networks were used for classification, capitalizing on their proficiency with time-series data. Given the sequential nature of the EEG signals, LSTMs, with their ability to capture long-term dependencies, provided enhanced accuracy in detecting intricate seizure patterns.
• While many studies evaluate the Bonn dataset for binary classification, some extend to three or four classes, with few tackling a five-class problem. This study encompassed classifications from binary to five-class, achieving unprecedented accuracy: 100% for binary, > 95% for three and four classes, and above 93% for the five-class categorization, marking the highest recorded performance in terms of accuracy.
The remainder of this article is organized as follows. Section 2 provides a detailed literature survey of the epileptic-seizure detection models. An in-depth explanation of the model design and components is presented in Section 3. Section 4 reports the dataset description and the model performance on the benchmark dataset. Finally, Section 5 gives the concluding remarks on the article.

2. Related Work

Epilepsy, characterized by recurrent seizures, is a complex neurological disorder requiring precise and prompt detection for effective management. This detection process has relied heavily on manual interpretation of EEG data by clinical experts. Despite the high degree of expertise, this process can be labor-intensive, time-consuming, and subject to variability. These challenges have intensified the pursuit of more efficient, automated systems for seizure detection. On the other hand, rapid technological improvements, particularly in areas like signal processing, have made a big difference in this field. Techniques, such as Empirical Mode Decomposition and Wavelet Transformation, along with advances in artificial intelligence, have revolutionized the approach to seizure detection. Many researchers have employed these cutting-edge signal processing techniques, including machine learning and deep learning strategies, to detect epilepsy seizures in adults accurately. These techniques have improved the early detection of epilepsy and other neurological disorders to a significant degree. For example, a previous study [14] proposed a concatenated model that combines Discrete Wavelet Transform (DWT) coefficients and Empirical Mode Decomposition (EMD) intrinsic mode features for the detection of epileptic seizures. They obtained an accuracy of 99% for the binary class. Similarly, another study [15] used the statistical features and classified with SVM (AdaBoost Least-Square SVM). The resulting accuracy for the binary FNOZ-S Classification problem in the Bonn dataset was 99%. In particular, none of these authors extended the evaluation of their proposed methods to include multi-class classifications.
In addition to the time domain analysis, frequency domain analysis, such as Discrete Fourier Transform (DFT) and Fast Fourier Transform (FFT), has also been used to detect epileptic seizures in adults. Gupta et al. [16] developed a method using a Fourier series and Bessel functions for EEG signal analysis, extracting five crucial brain wave patterns and five key brain rhythms. Based on these, they calculated the Weighted Multiscale Renyi Permutation Entropy and evaluated three machine learning algorithms across seven classification problems (Z–S, O–S, F–S, N–S, NF–S, ZONF–S, and Z–N–S). The Support Vector Machine (SVM) yielded the best performance, achieving more than 97% accuracy in all tasks with 10-fold cross-validation. Similarly, Na et al. [17] introduced an approach for categorizing EEG signals converted using DFT and processed using a KNN classifier. They achieved 99.4% accuracy for the ZONF-S problem. Polat et al. [18] used the FFT to extract the spectral energy features and used the SVM Classifier. This author achieved an accuracy of 82.5% in the Z–O–N–F–S Problem.
Numerous time-frequency analysis techniques have also been developed for epilepsy detection, including methods, such as Short-Time Fourier Transform (STFT), Wavelet Analysis, Wavelet Analysis, and Empirical Mode Decomposition (EMD). These methods are designed specifically to dissect the frequency composition of EEG signals and calculate the linear and nonlinear characteristics. These methods offer enhanced insights into the dynamic behaviors of the brain by presenting the signal in a time-frequency framework, allowing for the detection of subtle fluctuations in EEG waveforms [19]. The power of time-frequency analysis stems from its capacity to provide a unified view of a signal across both the time (temporal) and frequency (spectral) domains. This dual perspective enhances the understanding of the EEG signal behavior, leading to a thorough interpretation of the underlying neurological processes [20]. Time-frequency analysis has garnered substantial interest among researchers in EEG signal processing. It facilitates a precise examination of the time–frequency spectrum and the EEG spectrogram, reducing the likelihood of detection errors. Appreciating the superior performance of time-frequency analysis in deciphering EEG signals, numerous scientists have developed various techniques that utilize this multifaceted method to gain more sophisticated and informative insights. Li et al. [21] and Mandhouj et al. [22], who used STFT to represent EEG signals in phase and amplitude images, proposed different approaches to time-frequency analysis. Li et al. [21] divided the phase and amplitude images into blocks, from which binary numbers were extracted for each segment. This method, coupled with SVM, was applied to eight classification problems (Z–S, O–S, N–S, F–S, NF–S, ZONF–S, ZO–NFS, Z–F–S, and ZO–NF–S). The outcomes indicated high levels of accuracy (ACC), sensitivity (SENS), and specificity in binary (Z–S, O–S, N–S, F–S, NF–S, ZONF–S, and ZO–NFS) and three class (Z–F–S and ZO–NF–S) classification problems. In recent years, many wavelet transformation techniques have also been adopted by researchers to analyze the time–frequency information of EEG signals and have shown significant advantages in the frequency and time–domain analysis [23]. Unlike the Fourier transform, which provides only frequency information, the Wavelet transform offers time and frequency information, making it highly suitable for non-stationary signals, such as EEG. Using wavelets, which are mathematical functions constructed to have a wave-like oscillation, the EEG signal is decomposed into different frequency bands at multiple resolutions. This allows for a more detailed understanding of how the frequency components change over time in the signal, identifying specific brain activities or states. The adaptability and precision of the Wavelet transform make it a valuable tool in the field of neuroscience and clinical diagnosis. A previous study [24] used a five-level DWT to analyze EEG signals, extracting specific statistical features. The most informative characteristics were then identified based on information gain, measuring how well a feature discriminates between classes. Subsequently, a Petri network was trained, and the classification performance was assessed for two binary scenarios using 10-fold cross-validation. The results revealed an accuracy (ACC) of 93.80% and 98.60% for the ZO-NFS and ZONF-S problem, respectively. Zubair et al. [25] utilized the DWT to extract features, such as the band energies, spike rhythmicity, relative spike amplitude, and spectral entropy from EEG signals. By applying the CatBoost classifier to these features, they achieved 97% accuracy in the ZONF-S classification problem.
This study aimed to develop an automated diagnosis system capable of detecting epileptic seizure activity, differentiating between epileptic patients and healthy individuals, distinguishing epileptic seizures and pre-seizure states, identifying the seizure status of epilepsy patients, pinpointing the region of epilepsy (focal or non-focal), and classifying EEG signals using deep learning algorithms. This research presents notable improvement in detecting epileptic seizures. This paper suggests a new deep-learning technique that effortlessly combines compressed features from the time-frequency domain with the statistical attributes of the EEG signal. The robustness and precision of this method are highlighted by combining both time-frequency and statistical data. The overall proposed model for epileptic seizure detection will be explained in the next section.

3. Proposed Method

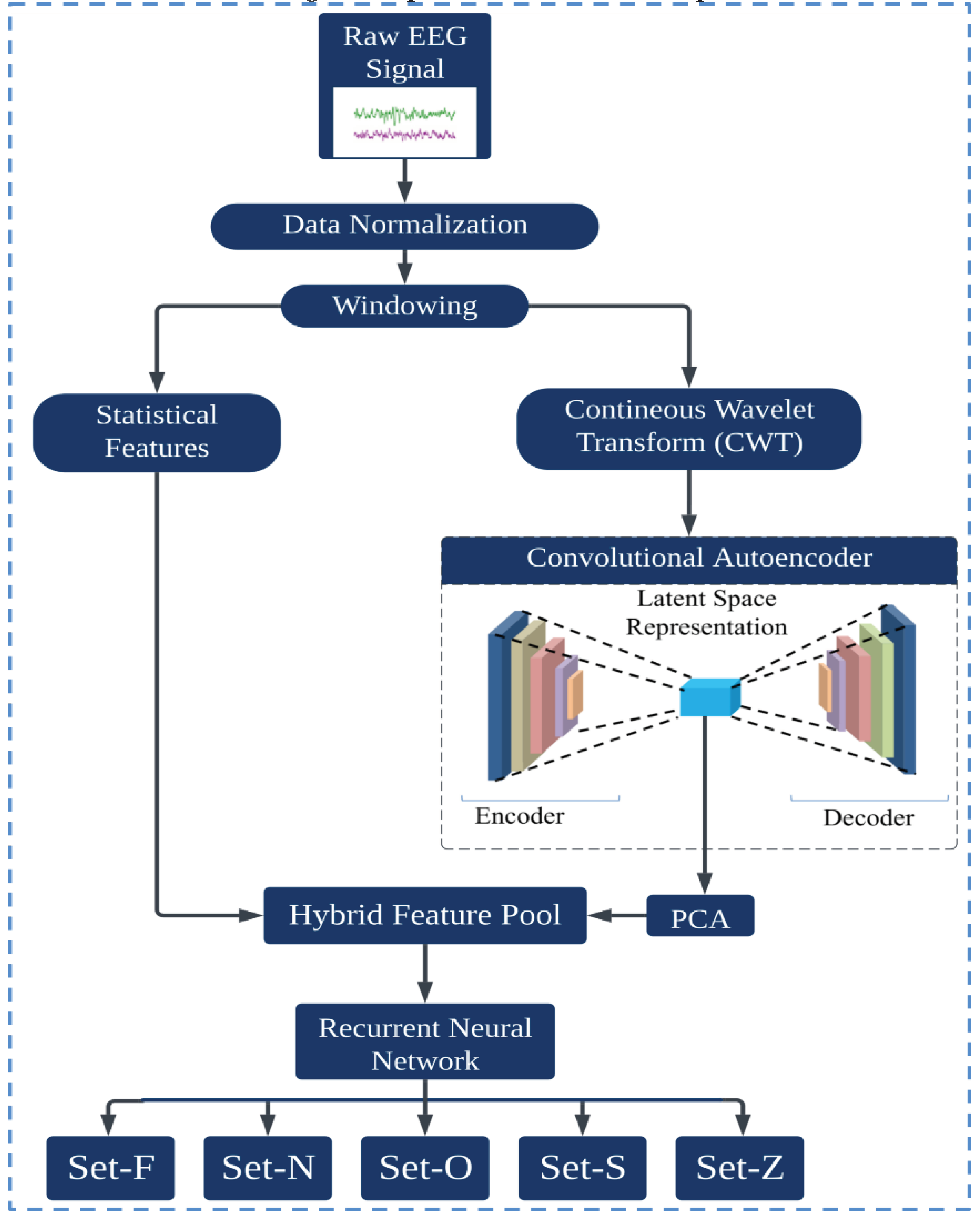
This section provides an overview of the proposed methodology for epilepsy detection, leveraging a hybrid model that combines an Autoencoder and a Recurrent Neural Network (RNN), specifically the Long Short-Term Memory (LSTM) variant. The procedure starts by preprocessing the EEG data, mitigating all artifacts and noise. A windowing technique, segmenting the continuous signal into smaller, manageable packets, is then used. This approach ensures that every datum is captured accurately. Once segmented, critical statistical features for each windowed segment are calculated, capturing the primary characteristics of the data. Subsequently, the continuous wavelet transform is applied to the segmented data. This transformation extracts time-frequency information from each segment, providing a more detailed representation of the signal dynamics. The resulting time-frequency images serve as input to the Convolutional Autoencoder, which distills the data into a latent feature space. Owing to the potential high dimensionality of this latent space, PCA was implemented to streamline the feature set, retaining only those components that contribute significantly to the variance and, by extension, the classifiability of the data. These condensed features are merged with the previously computed statistical features, producing a hybrid feature pool. This comprehensive feature set captures both the inherent characteristics of the signal and its nuanced, transformed representations. Finally, this paper introduces the LSTM model, which takes this hybrid feature set as input and determines the epilepsy state of the signal. The inherent capacity of the LSTM to process sequential data makes it particularly suited for this task, ensuring accurate classifications across various detection scenarios. Figure 1 presents a visual representation of the entire process.

3.1. Windowing

The Bonn University Epilepsy dataset consists of five subsets: Set Z, Set O, Set N, Set F, and Set S. Each subset contains 100 samples, resulting in 500 samples across the entire dataset. In the present study, all 100 samples were chained, and a windowing technique was applied to make small segments of the EEG signal. In signal processing analysis, windowing plays a pivotal role, primarily combating the challenges of spectral leakage. Spectral leakage occurs when examining signals that are not perfectly repetitive using tools, such as Fourier analysis. Moreover, windowing enhances temporal localization, ensuring that specific spectral events are precisely mapped within distinct time frames. The technique also fine-tunes the frequency resolution, delineating closely packed frequency components with clarity [26]. Given the advantage, the sliding window technique was employed to partition each sample into multiple smaller signal segments. An overlapping sliding window method, implementing a 1458 data-point window with a 486 data-point overlap, was used to ensure no data points were omitted. This window, shown in Figure 2, successively slide across the data, producing smaller signal segments, the combination of which represented the complete signal of the subject. The mathematical formulation of the sliding window technique with overlap, for a given signal S of length L , the starting and ending points of the i t h windowed segment S i is expressed below. Equation (1) indicates the starting point of each window, and Equation (2) expresses the ending point of the window.
For the i t h window:
S t a r t : S i = 1 + ( i − 1 ) × ( ω − ϑ )
E n d : S i = ω + ( i − 1 ) × ( ω − ϑ )
Where;
• ω is the window length, and in this case ω = 1458 .
• ϑ is the overlap length, and here ϑ = 486 .
• i is the window number (e.g., i = 1 for the first window, i = 2 for the second, and so on).
• Always ensure that ω > 0 for the above formulation to be valid.

3.2. Continuous Wavelet Transformation (CWT)

Electroencephalography (EEG) records the electrical activity of the brain, producing inherently non-stationary signals. This means that the frequency content of these signals can vary over time. Traditional Fourier methods, which analyze the signals in terms of sinusoids with infinite duration, may not effectively capture the transient or time-varying phenomena in EEG data [27]. On the other hand, wavelet transform is a computational method designed to analyze non-stationary signals by decomposing them into various frequency components while maintaining temporal resolution. The wavelet transform employs basis functions called "wavelets," allowing simultaneous frequency and time domain analysis [28], [29]. This dual-domain decomposition provides more important information on transient and stationary components in complex signals. Equation (3) is a mathematical expression for the wavelet transform.
W T ( s , t ) = 1 | s | ∫ − ∞ ∞ ‍ f ( τ ) ψ * τ − t s d τ
where f ( τ ) is the input signal; ψ * ( ⋅ ) represents the complex conjugate of the wavelet function; s is the scale factor (which is inversely related to frequency); t is the translation factor (related to time).
Extending this concept, the CWT is a specialized form of Wavelet Transform wherein the wavelet undergoes continuous scaling and translation, allowing temporal and spectral analysis [30]. In particular, the CWT is invaluable in EEG signal analysis because it offers a time-frequency representation, adeptly capturing transient EEG data behaviors, such as spikes and other irregularities. Commonly used in EEG signal processing, CWT plays a pivotal role in feature extraction for applications, such as seizure detection and sleep stage classification. Its multi-resolution characteristic is particularly advantageous for interpreting EEG signals, given that different physiological phenomena might present themselves at diverse scales. Furthermore, wavelets can also aid in noise reduction for EEG signals. The expression for CWT of a function f ( t ) relative to a wavelet ψ ( t ) is
C W T f ( s , t ) = ∫ − ∞ ∞ ‍ f ( τ ) ψ s , t * ( τ ) d τ
with the modified wavelet given by
ψ s , t ( τ ) = 1 | s | ψ τ − t s
• ψ is called the mother wavelet, which is a short wave-like oscillation.
• s is the scaling factor. The function is stretched if s > 1 or compressed if 0 < s < 1 .
• t is the translation factor, which shifts the function in time.
• τ is the variable of integration, typically representing time.
• The factor 1 | s | is a normalization term that ensures that the wavelet has the same energy at every scale.
Equations (3) and (4) describe how the original mother wavelet, ψ , is scaled and translated to analyze a signal at various frequencies and time positions. By adjusting the the s and t values, one can analyze different frequency components of the signal at different time points, making it particularly useful for analyzing non-stationary signals, such as EEG.
The CWT was used to convert EEG signal segments into images, employing the Morlet wavelet. The Morlet wavelet, a complex sinusoid modulated by a Gaussian envelope, is crucial in signal processing for its ability to highlight oscillatory patterns, particularly in EEG/ECG data [31]. The CWT on the individual signal windows was implemented using the Morlet wavelet as the mother wavelet. The CWT extracted both the spectral and temporal resolutions of the signal, which were subsequently represented as images. Figure 3 shows the graphical representation of CWT images of each class of the Bonn epilepsy dataset.

3.3. Convolutional Autoencoder

After being proposed by Theis et al. [32] and Balle et al. [33], the Convolutional Autoencoder (CAE) has attracted the interest of many researchers in recent years, particularly for leaned image compression. Convolution auto-encoder is a specialized neural network that encodes and decodes data with spatial hierarchies, such as images. 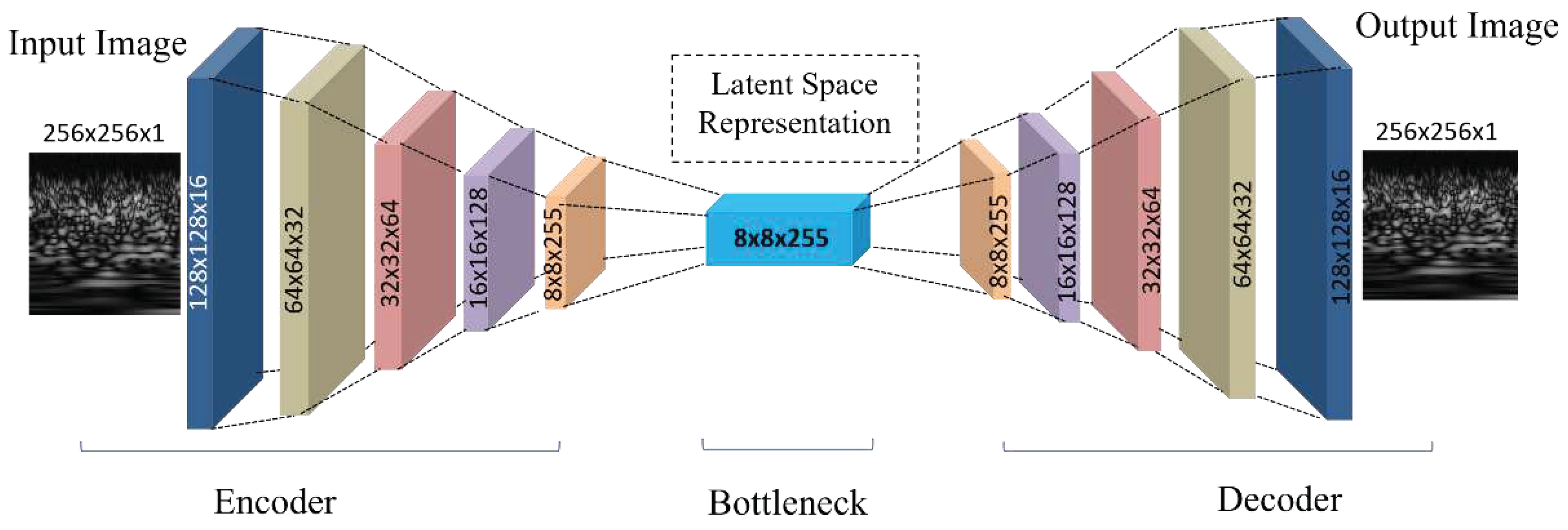Unlike traditional autoencoders, CAEs utilize convolutional layers to exploit spatial localities in data, making them particularly adept at handling images [30]. The strength of CAEs in processing EEG-transformed images stems from their ability to retain essential spatial features inherent in EEG data, allowing effective compression and reconstruction with minimal loss of information. A CAE aims to approximate an identity function while adhering to specific constraints, such as limited neurons in hidden layers. A CAE is structured into two main components:

3.3.1. Encoder

The encoder portion of a CAE serves as a funnel, responsible for mapping the input x ∈ R n to a latent (or compressed) space. This is achieved using a series of convolution operations designed to capture the spatial hierarchies in the data. Considering a feedforward neural network as the architecture, the output h e ( l + 1 ) of the l t h layer in the encoder is defined as follows:
h e ( l + 1 ) = σ ( W e ( l ) * h e ( l ) )
Where W e ( l ) denotes the convolutional filters (or kernels), which can be considered tiny feature detectors. The nonlinear activation function, σ introduces non-linearity into the system, allowing the network to learn complex patterns. As the EEG image progresses through the L e convolutional layers of the encoder, the final encoded representation, h e ( L e ) = h , serves as a compressed, but rich, encapsulation of the most salient features of the images.

3.3.2. Decoder

The decoder acts as the inverse of the encoder. The decoder takes the compressed representation h and attempts to reconstruct it back to the original space. This involves transposed convolutional operations, which can be visualized as deconvolutions or reverse convolutions. If a feedforward neural network is considered, the output h d ( l + 1 ) of the l t h layer in the decoder is:
h d ( l + 1 ) = σ ( W d ( l ) ⊙ h d ( l ) )
Where W d ( l ) are the transposed convolutional filters, which operate in a manner opposite to the encoder filters. The final output from the decoder, h d ( L d ) = x ' , aims to be a faithful reconstruction of the original image x , bringing full circle the encoding–decoding process of the CAE.
The primary objective of a CAE is to minimize the reconstruction error between the original input and its reconstruction. This error, typically termed the loss function, can be defined as follows:
L ( x ' , x ) = ∥ x ' − x ∥
Optimization algorithms, such as backpropagation, minimize this loss when training a CAE. In the architecture presented in Table 1 a CAE was used with a five-layer encoder and decoder. The input CWT image of shape (None, 256, 256, 1) is first passed to the encoder, which employs successive Conv2D layers with increasing filter counts. This encoder sequence reduces the spatial dimensions and enriches the feature representation, resulting in a latent space vector of dimensions (None, 8, 8, 255). This latent vector serves as the input to the decoder, which employs transposed convolutional layers (Conv2DTranspose) to upsample and expand the spatial dimensions, aiming to reconstruct the original CWT image from its compact representation. The final output of the CAE matches the original input dimensions, and the model efficacy is underscored by a high PSNR value of 66 dB, highlighting its precision in CWT image reconstruction. Figure 4 shows the graphical layer-wise architecture of the CAE.

3.4. Principal Component Analysis

PCA is a well-established dimensionality reduction technique that projects data into a lower-dimensional space while preserving as much of the original variance as possible [35]. This method is particularly useful for reducing the dimensionality of datasets with many correlated variables, transforming them into a new set of orthogonal variables known as the principal components [36], [37].
Mathematically, PCA involves the following steps:
1) Calculate the covariance matrix of the original data.
2) Compute the eigenvalues and eigenvectors of the covariance matrix.
3) Sort eigenvalues in decreasing order and select the top k eigenvectors, where k is the
number of principal components required.
4) Use these top k eigenvectors to transform the original data into the new lower-dimensional space.
Given a data matrix, X, of size, n × d (where n is the number of data samples and d is the number of features), the covariance matrix, C, is given by the following:
C = 1 n − 1 X T X
Its eigenvalues and eigenvectors were determined after obtaining the covariance matrix. These eigenvectors determine the directions of the new feature space, while the eigenvalues represent the magnitude or explained variance in that direction. Once these are sorted, the top k eigenvectors were selected, forming a matrix, W , of size d × k .
The original matrix was multiplied by W to transform the original data into the reduced space:
Y = X W
In the context of this study, PCA was used to reduce the dimensionality of the latent space extracted from the autoencoder. A compact representation of the data that retained most of the original variance was ensured by reducing the features to 128 dimensions using PCA. This processed latent space was combined with statistical features in a hybrid feature pool, paving the way for enhanced EEG signal classification.

3.5. Statistical Features

Electroencephalogram (EEG) signals, which represent the electrical activities of the brain, are inherently dynamic and complex. Therefore, it is imperative to extract the representative features that capture the underlying characteristics of the EEG data to discern information from these signals, particularly for applications, such as epilepsy detection. In addition, statistical features offer a compact representation of EEG signals, distilling them into metrics that reflect the distribution and behavior of the signal over time [38]. These include the mean, standard deviation, kurtosis, skewness, and various factors, such as crest, shape, and impulse. Although each of these metrics carries its significance in capturing different signal characteristics when they provide a comprehensive overview of the signal when combined. For example, the mean offers a central tendency, suggesting the average amplitude of the signal. Standard deviation and variance capture the dispersion and variability within the signal. Metrics, such as kurtosis and skewness, provide insights into the shape of the distribution of the signal, indicating the presence of any irregular peaks or asymmetries. Factors, such as crest and shape, elucidate the transient behaviors of the signal and its oscillatory nature. Combining these statistical features with the latent features of an autoencoder derived from the CWT images can significantly enhance the classification performance of EEG signals, particularly in epilepsy detection. Because statistical features capture the basic characteristics of EEG signals, the latent space of the autoencoder, derived from the CWT images, encapsulates more complex, nonlinear patterns in the data. They offer a more comprehensive representation of the EEG signal. The fusion of these two feature sets can increase the robustness of the model. This process benefits from the generalization capabilities of autoencoders and the straightforward interpretability of statistical metrics. Furthermore, epileptic seizures lead to characteristic changes in the EEG patterns. Statistical features can highlight sudden spikes, deviations, and anomalies in the signal, which are common indicators of the epileptic activities. Combined with the high-level patterns learned by the autoencoder from CWT images, the classification system can better differentiate between epileptic and non-epileptic signals. Table 2 lists the list of calculated statistical features.

3.6. Hybrid Features Pool

EEG signals are complex yet rich in information. It is very important to extract the right features to analyze them. With simple statistical features, a broader and more useful set of attributes can be obtained by combining the power of deep learning methods, such as CWT images. This approach combines detailed patterns (from CWT images) and basic signal traits (from statistical features) to provide a well-rounded view of the EEG data.
Ensuring the alignment of features accurately within this hybrid framework is essential to preserve data consistency and optimize subsequent analytical outcomes. Let, F A E represent the set of features derived from the bottleneck of the Autoencoder for a specific EEG window and F s t a t denotes the statistical features for the same window. The harmonization of these features can be represented as
F h y b r i d i = { f A E i ∪ f s t a t i | f A E i ∈ F A E ∧ f s t a t i ∈ F s t a t }
The index i in f A E i and f s t a t i ensures that the Autoencoder latent space features and statistical features are obtained from the same EEG window packet. This hybrid features pool offers a multidimensional view of EEG signals, amplifying the richness of information available in each class. This feature integration promises robustness against potential intra-class variations and maximizes the inter-class disparities, emphasizing its importance for complex data, such as EEG and EMG signal classification applications. These hybrid features are then input into an LSTM network for final classification.

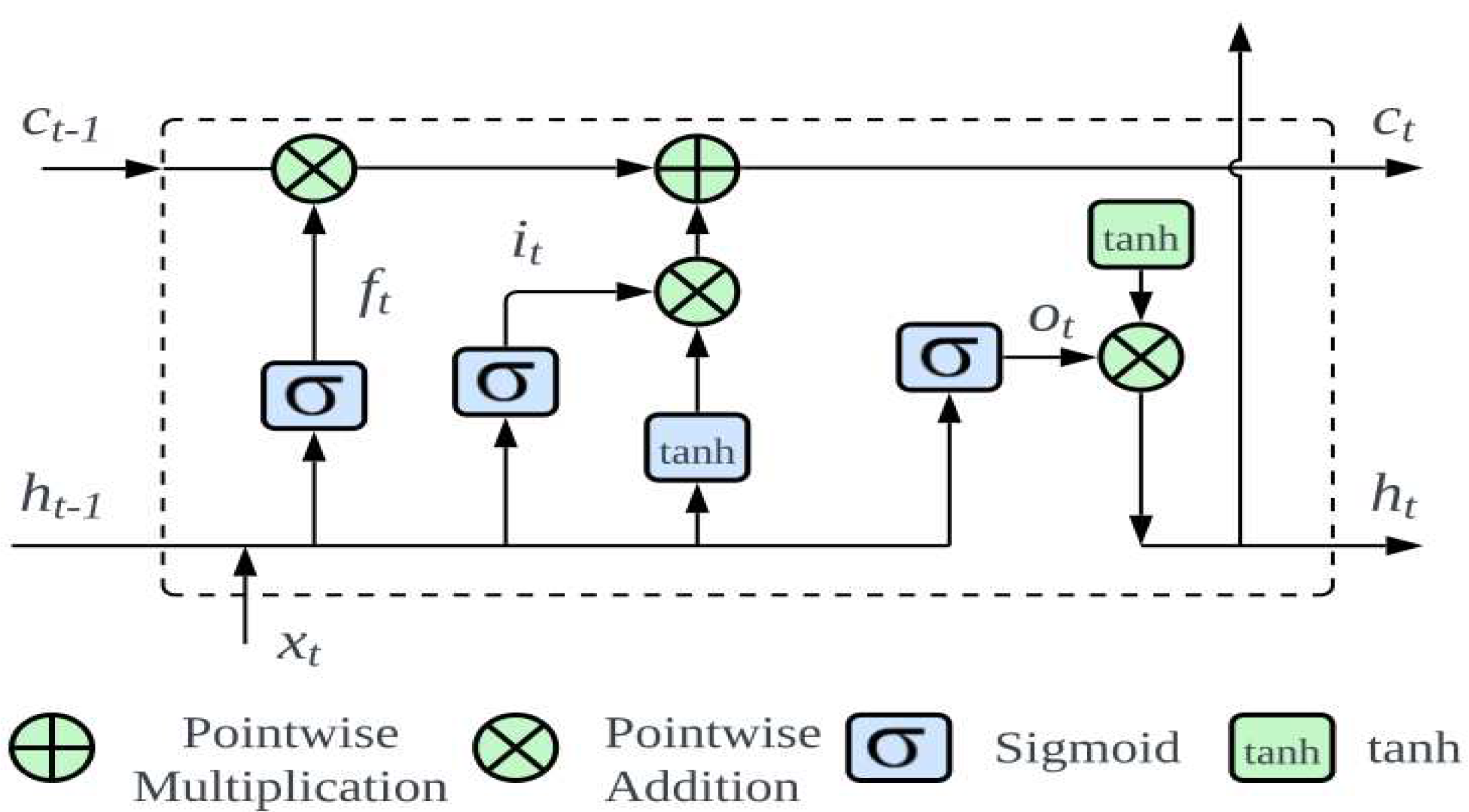
3.7. Long-Short Term Memory

LSTM networks, a specific architecture of RNNs, have attracted significant attraction for predicting time series data because of their unique cellular design. This design is essential for the LSTM to transmit information selectively, addressing issues, such as vanishing and exploding gradients during backpropagation [39]. Figure 5 presents an in-depth visualization of this architecture. At the core of an LSTM are three main gates: forget, input, and output gates.
Initially, the forget gate decides the segments of information that the cell state should discard:
f t = σ ( W f × [ h t − 1 , x t ] + b f )
Where h t − 1 denotes the prior hidden layer output; x t symbolizes the current input, with σ being the sigmoid activation; W and b representing the weight matrix and bias, respectively.
Subsequently, the input gate governs the preservation of information in the cell state, splits into identifying the data for updates and setting up an updated state. This can be expressed mathematically as follows:
i t = σ ( W i × [ h t − 1 , x t ] + b i )
C ~ t = t a n h ( W C × [ h t − 1 , x t ] + b C )
The present state of the neuron can be derived by combining Eqs. (2) and (3):
C t = f t − 1 C t − 1 + i t − 1 C ~ t
The role of the output gate is pivotal to determining the final output. The sigmoid function evaluates which segment of the cell state to output, subsequently undergoing processing by the tanh function and pointwise multiplication:
o t = σ ( W o × [ h t − 1 , x t ] + b o )
h t = o t × t a n h ( C t )
In biomedical contexts, the strength of the LSTM lies in its ability to recognize the patterns over time, making it particularly effective for detecting epileptic seizures. EEG data, characterized by detailed time-based patterns, benefits from accuracy and timely analysis by the LSTM, ultimately improving patient care and treatment outcomes.
This model uses an LSTM layer, consisting of 128 units, designed specifically to process the time-dependent patterns in EEG data. The data are passed to a dense layer using softmax activation, sorting the LSTM outputs into specific categories. The model is fine-tuned for optimal performance with the ’adam’ optimizer and the categorical_crossentropy loss function, which is suited for classifying into multiple categories. Combining the strengths of autoencoder latent space features and statistical attributes, the LSTM provides a thorough and accurate representation of the complex patterns of the EEG data. This integration enhances the model robustness and its ability to identify subtle EEG patterns accurately, which is crucial for advanced seizure detection. The effectiveness of the proposed model will be further discussed in the next section.

4. Performance Evaluation

4.1. Meta Data

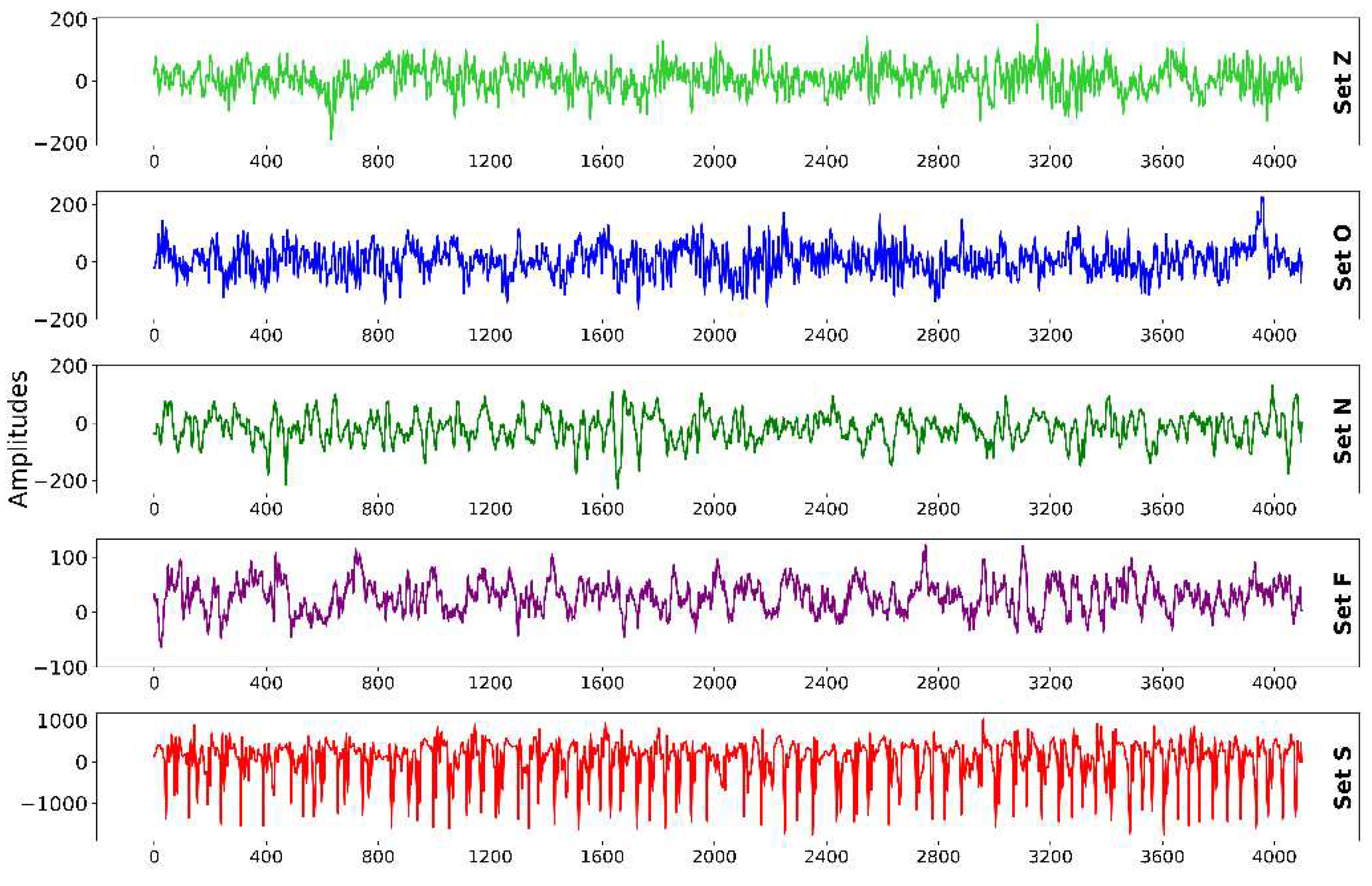
In this study, the EEG database from the University of Bonn, Germany, curated by Andrzezak et al. [40], was chosen for data incorporation. This database was selected because of its authority in the field and its frequent utilization in numerous epilepsy diagnostic studies. The dataset comprises five sets (Z, O, N, F, and S) of 100 EEG image segments each, captured via a single channel from the scalp surface. Each EEG signal spans a duration of 23.6s and includes 4097 sample points. The signals were digitized using a 12-bit A/D converter at a sampling frequency of 173.61Hz.
Sets Z and O originate from the EEG records of five healthy individuals with eyes open and closed, respectively. Sets N, F, and S derive from the preoperative EEG records of five diagnosed epileptic patients. In particular, Set N segments were from the hippocampus located in the opposite hemisphere of the brain. Set F was obtained from within the epileptogenic zone, with both sets containing measurements during seizure-free intervals. Set S solely encompassed the seizure activity. Table 3 provides detailed information regarding this data. For this study, all five sets were utilized, with representative EEG signal samples from each group presented in Figure 6.
In this study, the classification performance of epilepsy seizure detection models is evaluated using multiple metrics: Accuracy, F1 Score, Precision, Recall, and Sensitivity. The choice of these metrics provides a comprehensive understanding of the model proficiency in accurately identifying the seizures and distinguishing between the various classes.
In a binary classification framework, the terminologies employed are as follows:
  • True Positive (TP): Instances confirmed to be positive.
  • True Negative (TN): Instances confirmed to be negative.
  • False Positive (FP): Instances incorrectly identified as positive.
  • False Negative (FN): Positive instances mistakenly identified as negative.
The metrics for binary classification are given by:
A c c u r a c y = T P + T N T P + T N + F P + F N ,
P r e c i s i o n = T P T P + F P ,
R e c a l l ( o r S e n s i t i v i t y ) = T P T P + F N ,
F 1 S c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l
The scenario becomes slightly intricate when the focus is shifted to multi-class classification. Each class is treated as a positive class, with all other classes combined as a negative class. The above metrics were calculated for each class separately and averaged. This averaging can either give each class equal weight (macro-averaging) or give each instance equal weight (micro-averaging).
The following are used to interpret these metrics:
• Accuracy (18) offers a general overview of the model performance, highlighting the proportion of correctly identified instances.
• Precision (19) sheds light on the correctness of positive identifications. It becomes particularly important when the implications of false positives are significant.
• Recall or Sensitivity (20) focuses on how many of the actual positives the model captures, being crucial when missing a positive instance (false negative) has high costs.
• F1 Score (21) harmonizes precision and recall, providing a balanced perspective, which is particularly beneficial in imbalanced datasets.
In this study, the performance of the model, built upon a hybrid features pool, was examined across different classification scenarios. The aim was to assess its proficiency in distinguishing between various numbers of classes, ranging from binary classification to a more complex five-class scenario.
The dataset was restructured for each classification task, ensuring the samples were combined appropriately to reflect the intended problem. In the binary classification, the focus was on distinguishing epileptic samples from each of the other sample types. The specific scenarios for each classification problem are detailed as follows:
  • • Binary Classification: N–S, Z–S, O–S, F–S, FN–S, FNZ–S, FNO–S, NOZ–S.
  • • Three-Class Classification: F–O–S, N–Z–S, O–Z–S, FN–OZ–S.
  • • Four-Class Classification: F–O–Z–S, N–O–Z–S.
  • • Five-Class Classification: F–N–O–Z–S.
These scenarios provided a comprehensive evaluation landscape, allowing the versatility and adaptability of the hybrid features model to be determined in varying classification environments.

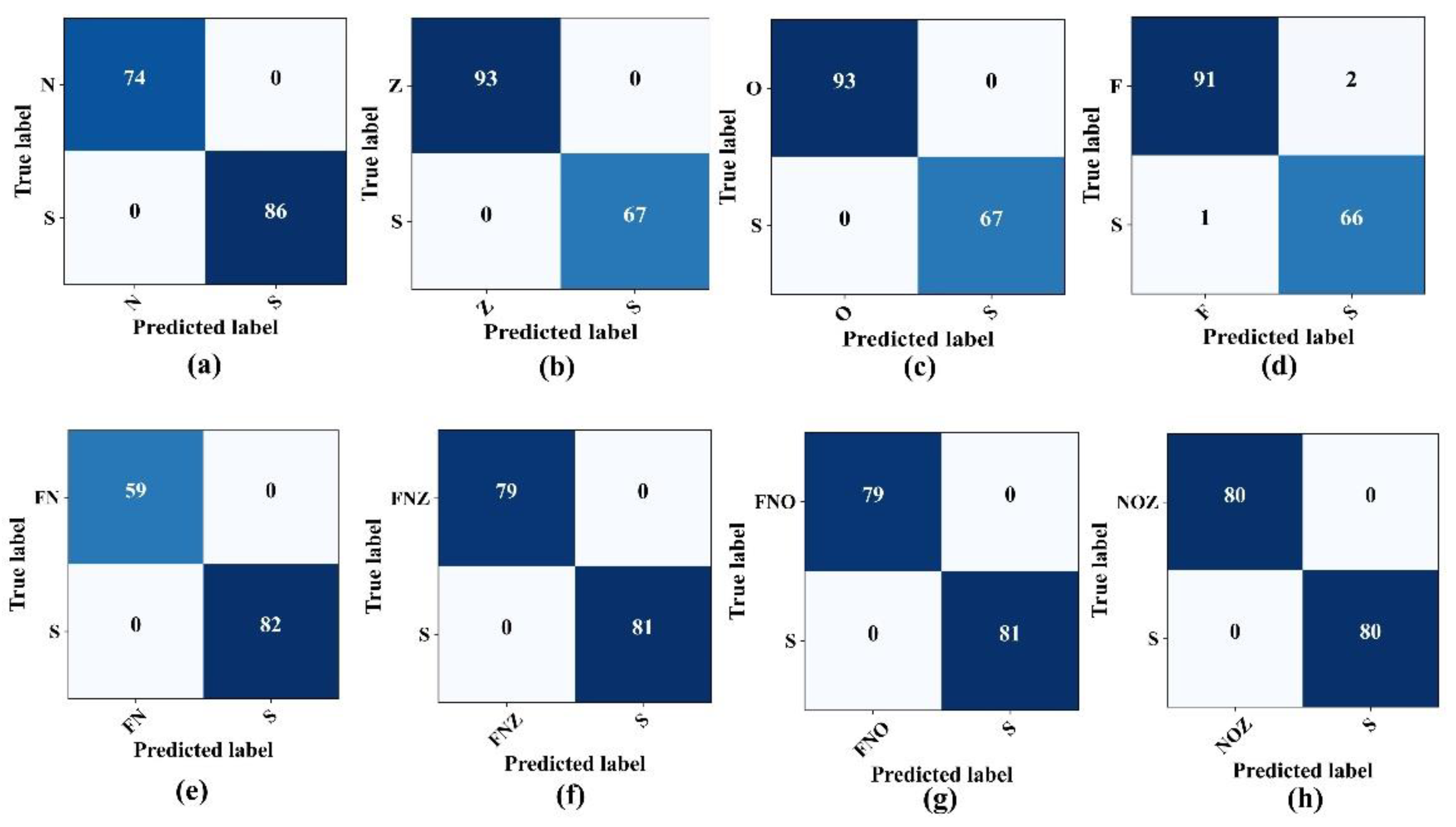
4.2. Binary Classification

The proposed classification system exhibited exceptional precision in classifying critical EEG states when assessing the model performance on the previously mentioned binary cases. As highlighted in Table 4, the model differentiates between the seizure activity (Set S) and various non-seizure states, including the eye-closed (Set O), eye-open (Set Z), and seizure-free states (Sets F and N), with remarkable accuracy, often achieving accuracy and F1-scores of 100%. Nevertheless, when classifying the F–S binary combination, the model accuracy decreased slightly, settling at 98.12%. The confusion matrices, which show the true versus predicted labels across these binary combinations, are illustrated in Figure 7.

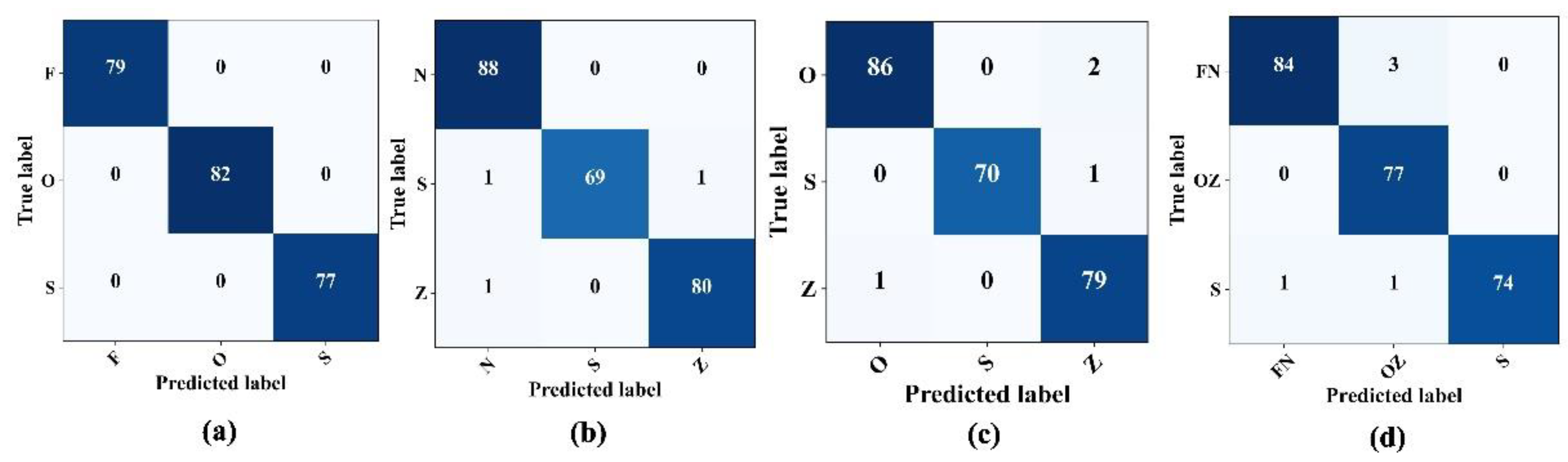
4.3. Three-Class Classification

After observing the promising results from the model performance for binary class problems, the tests were extended to multi-class problems, specifically F–O–S, N–Z–S, O–Z–S, and FN–OZ–S. The initial approach involved classifying three distinct categories: the normal state, characterized by patients with closed eyes (Class "O"); the interictal state, representing patients diagnosed with epilepsy but currently in a seizure-free state (Class F); the ictal state, indicative of active seizures. The proposed epilepsy seizure detection architecture classified these three states, achieving 100% accuracy with no misclassifications, as shown in Figure 8a. Furthermore, another set for three class classification problems, the N–Z–S classification problem, evaluated the model performance. The confusion matrix in Figure 8b shows that the model precision remained high, achieving an overall accuracy and sensitivity of 98.75% and 97.2%, respectively, for detecting seizures. This performance was consistent, with an F1-score and a precision rate of 98.76%. In the subsequent O–S–Z and FN–OZ–S classifications, the model sustained its robust performance, surpassing the accuracy and sensitivity of 96% and 98%, respectively, for seizure detection (Figure 8c,d). Table 5, lists the comprehensive performance of the proposed model for different three-class problems.

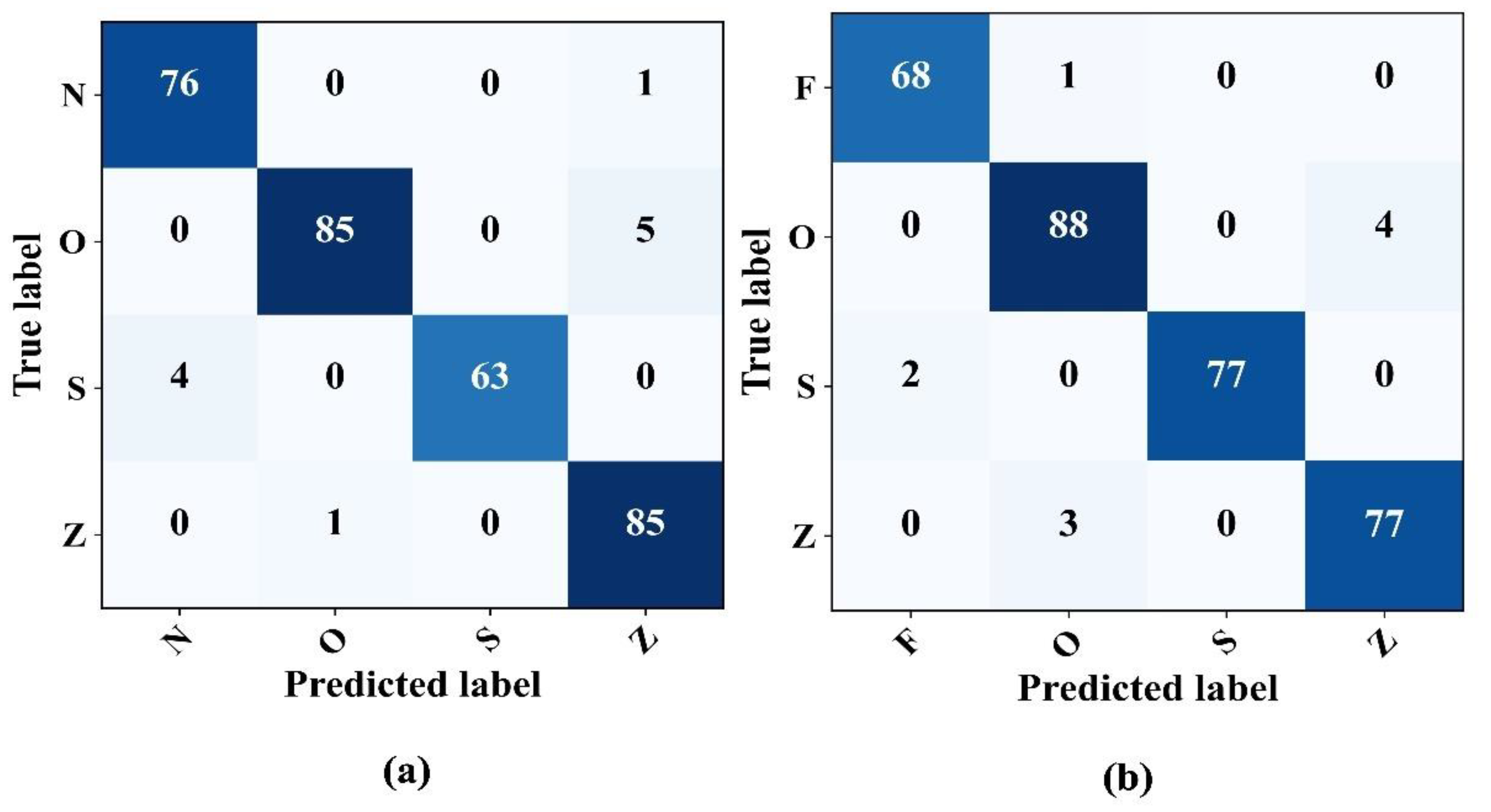
4.4. Four-Class Cassification

The model capabilities in detecting epileptic EEG signals in four class problems were assessed thoroughly. In particular, two different scenarios were examined: the N–O–Z–S and F–O–S–Z classifications. In both cases, the model showed impressive performance even in four-class problems, as illustrated in the confusion matrices in Figure 9. The classification consistently achieved an approximate accuracy and precision of 97%. Table 6 provides a detailed overview of the model metrics for these four-class classification problems.

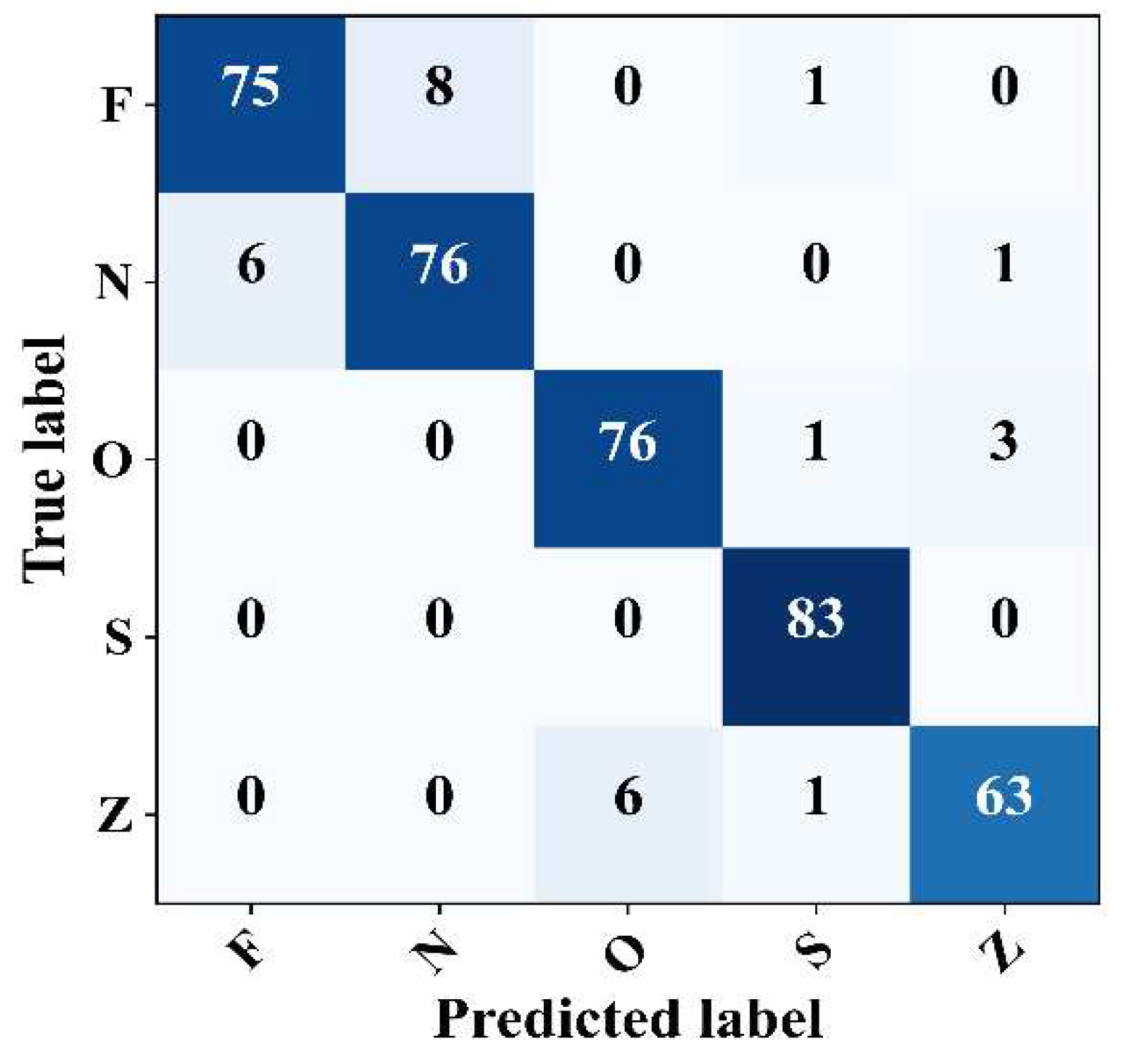
4.5. Five-Class Cassification

Finally, the proposed model was evaluated for its ability to detect epileptic EEG samples within complex signals. The model performance was evaluated using the Z–N–O–Z–S five-class problem. The confusion matrix shows that the model achieved promising results with an overall accuracy, F1-Score, precision, and general sensitivity of 93.25%, 93.21%, 93.23%, and 93.25%, respectively, as shown in Figure 10. In particular, the model revealed a sensitivity of 100% in detecting the epileptic seizure signals with no false detection. The model also recorded a sensitivity of 95.00%, 91.56%, and 90% for class O, class N, and classes Z and F, respectively. In summary, these results confirm the reliable detection performance of the model across various scenarios, be they binary, three-class, four-class, or even five-class problems.

4.6. Comparison

After evaluating the model across various classification problems, ranging from binary to three-class, four-class, and even five-class scenarios, and observing its promising results in all these tasks, the performance of the deep CAE model integrated with statistical features was compared with existing approaches. The deep CAE-statistical feature-based model consistently outperformed other methods in all classification tasks. Table 7 Comparison with some existing approaches compares the results of existing studies with the proposed model.

5. Conclusions

This paper introduced an advanced intelligent EEG recognition framework for epileptic seizure detection. This framework integrates deep autoencoders, statistical features, and LSTM networks. An optimal overlapping windowing method was used to mitigate the inherent spectral leakage. Subsequently, the CWT was used to produce time–frequency images from each window. Simultaneously, the statistical attributes, such as mean, mode, and standard deviation, were extracted during this wavelet transformation. A deep convolutional autoencoder (CAE) was trained to extract the essential features from the CWT images. The latent space of this CAE, rich with features, was then refined using PCA and concatenated with the statistical features, forming a comprehensive hybrid feature pool. This enhanced pool was processed through LSTM-based classification, addressing multiple class problems.
The model demonstrated exceptional F-1 Score precision and accuracy. In most cases, it exhibited error-free classification in binary class problems, while in three and four-class problems, it exceeded 95% and 93% accuracy, respectively. The model sensitivity metrics are equally impressive, scoring 100% for binary and some three-class situations, maintaining over 97% for all three-class and > 94% for four-class problems. Averaging across all classifications, this model achieved an accuracy exceeding 97%, highlighting its stability and validating its ability to detect epileptic events accurately within complex signal scenarios.

Author Contributions

Conceptualization, S.U.K. and S.U.J.; methodology, S.U.K.; software, S.U.K.; validation, S.U.K., S.U.J. and I.S.K.; formal analysis, S.U.K.; investigation, S.U.K.; resources, S.U.K.; data curation, S.U.K.; writing—original draft preparation, S.U.K.; writing—review and editing, S.U.J. and I.S.K.; visualization, S.U.K.; supervision, S.U.J and I.S.K.; project administration, I.S.K.; funding acquisition, I.S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the 2022 research fund of the industrial cluster program by Korea industrial complex corporation, and in part by the Regional Innovation Strategy (RIS) through the NRF funded by the Ministry of Education (MOE) under Grant 2021RIS-003.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets that support the findings of this study are openly available as below. Ralph G. Andrzejak1,Klaus Lehnertz1,Florian Mormann, Christoph Rieke1, Peter David, and Christian E. Elger1 , Bonn Epilepsy Dataset.” [Online]. Available: https://www.ukbonn.de/epileptologie/arbeitsgruppen/ag-lehnertz-neurophysik/downloads/.

Acknowledgments

The authors extend their appreciation to the industrial cluster program by Korea industrial complex corporation, and the Regional Innovation Strategy (RIS) for funding this paper through the NRF funded by the Ministry of Education (MOE) under Grant 2021RIS-003.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kuhlmann, L.; Lehnertz, K.; Richardson, M.P.; Schelter, B.; Zaveri, H.P. Seizure prediction—ready for a new era. Nat. Rev. Neurol. 2018, 14, 618–630. [Google Scholar] [CrossRef]
  2. Liu, T.; Shah, M.Z.H.; Yan, X.; Yang, D. Unsupervised feature representation based on deep boltzmann machine for seizure detection. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1624–1634. [Google Scholar] [CrossRef]
  3. Ahmad, I.; Wang, X.; Javeed, D.; Kumar, P.; Samuel, O.W.; Chen, S. A hybrid deep learning approach for epileptic seizure detection in eeg signals. IEEE J. Biomed. Health Inform. 2023. [Google Scholar] [CrossRef]
  4. Zhu, G.; Li, Y.; Wen, P.; Wang, S. Classifying epileptic eeg signals with delay permutation entropy and multi-scale k-means. Signal Image Anal. Biomed. Life Sci. 2015, 823, 143–157. [Google Scholar]
  5. Raeisi, K.; Khazaei, M.; Croce, P.; Tamburro, G.; Comani, S.; Zappa- sodi, F. A graph convolutional neural network for the automated detection of seizures in the neonatal eeg. Comput. Methods Programs Biomed. 2022, 222, 106950. [Google Scholar] [CrossRef] [PubMed]
  6. Akyol, K. Stacking ensemble based deep neural networks modeling for effective epileptic seizure detection. Expert Syst. Appl. 2020, 148, 113239. [Google Scholar] [CrossRef]
  7. da Silva Lourenc, C.; Tjepkema-Cloostermans, M.C.; van Putten, M.J. Machine learning for detection of interictal epileptiform dis- charges. Clin. Neurophysiol. 2021, 132, 1433–1443. [Google Scholar] [CrossRef] [PubMed]
  8. Yazid, M.; Fahmi, F.; Sutanto, E.; Shalannanda, W.; Shoalihin, R.; Horng, G.-J.; et al. Simple detection of epilepsy from eeg signal using local binary pattern transition histogram. IEEE Access 2021, 9, 252–267. [Google Scholar] [CrossRef]
  9. AMalekzadeh; Zare, A. ; Yaghoobi, M.; Kobravi, H.-R.; Al- izadehsani, R. Epileptic seizures detection in eeg signals using fusion handcrafted and deep learning features. Sensors 2021, 21, 7710. [Google Scholar] [CrossRef] [PubMed]
  10. Qureshi, M.B.; Afzaal, M.; Qureshi, M.S.; Fayaz, M. Machine learning-based eeg signals classification model for epileptic seizure detection. Multimed. Tools Appl. 2021, 80, 849–877. [Google Scholar]
  11. Sharmila, A.; Geethanjali, P. Dwt based detection of epileptic seizure from eeg signals using naive bayes and k-nn classifiers. IEEE Access 2016, 4, 7716–7727. [Google Scholar] [CrossRef]
  12. Beeraka, S.M.; Kumar, A.; Sameer, M.; Ghosh, S.; Gupta, B. Accuracy enhancement of epileptic seizure detection: a deep learning approach with hardware realization of stft. Circuits Syst. Signal Process. 2022, 41, 461–484. [Google Scholar] [CrossRef]
  13. Omidvar, M.; Zahedi, A.; Bakhshi, H. Eeg signal processing for epilepsy seizure detection using 5-level db4 discrete wavelet transform, ga-based feature selection and ann/svm classifiers. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1–9. [Google Scholar] [CrossRef]
  14. Jana, G.C.; Agrawal, A.; Pattnaik, P.K.; Sain, M. Dwt-emd feature level fusion based approach over multi and single channel eeg signals for seizure detection. Diagnostics 2022, 12, 324. [Google Scholar] [CrossRef] [PubMed]
  15. Adaptive boost ls-svm classification approach for time-series signal classification in epileptic seizure diagnosis applications. Expert Syst. Appl. 2020, 161, 113676. [CrossRef]
  16. Epileptic seizure identification using entropy of fbse based eeg rhythms. Biomedical Signal Processing and Control 2019, 53, 101569.
  17. Na, J.; Wang, Z.; Lv, S.; Xu, Z. An extended k nearest neighbors- based classifier for epilepsy diagnosis. IEEE Access 2021, 9, 910–923. [Google Scholar] [CrossRef]
  18. Epileptic seizure detection based on new hybrid models with electroen- cephalogram signals. IRBM 2020, 41, 331–353. [CrossRef]
  19. Miltiadous, A.; Tzimourta, K.D.; Giannakeas, N.; Tsipouras, M.G.; Glavas, E.; Kalafatakis, K.; Tzallas, A.T. Machine learning al- gorithms for epilepsy detection based on published eeg databases: A systematic review. IEEE Access 2023, 11, 564–594. [Google Scholar] [CrossRef]
  20. Time-frequency analysis methods and their application in developmen- tal eeg data. Dev. Cogn. Neurosci. 2022, 54, 101067. [CrossRef]
  21. Li, M.; Sun, X.; Chen, W.; Jiang, Y.; Zhang, T. Classification epileptic seizures in eeg using time-frequency image and block texture features. IEEE Access 2020, 8, 9770–9781. [Google Scholar] [CrossRef]
  22. Mandhouj, B.; Cherni, M.A.; Sayadi, M. An automated classification of eeg signals based on spectrogram and cnn for epilepsy diagnosis. Analog. Integr. Circuits Signal Process. 2021, 108, 101–110. [Google Scholar] [CrossRef]
  23. Akin, M. Comparison of wavelet transform and fft methods in the analysis of eeg signals. J. Med. Syst. 2002, 26, 241–247. [Google Scholar] [CrossRef] [PubMed]
  24. Chiang, H.-S.; Chen, M.-Y.; Huang, Y.-J. Wavelet-based eeg pro- cessing for epilepsy detection using fuzzy entropy and associative petri net. IEEE Access 2019, 7, 255–262. [Google Scholar] [CrossRef]
  25. Zubair, M.; Belykh, M.V.; Naik, M.U.K.; Gouher, M.F.M.; Vish- wakarma, S.; Ahamed, S.R.; Kongara, R. Detection of epileptic seizures from eeg signals by combining dimensionality reduction algo- rithms with machine learning models. IEEE Sens. J. 2021, 21, 861–869. [Google Scholar] [CrossRef]
  26. Piho, L.; Tjahjadi, T. A mutual information based adaptive window- ing of informative eeg for emotion recognition. IEEE Trans. Affect. Comput. 2020, 11, 722–735. [Google Scholar] [CrossRef]
  27. Yang, X.; Zhao, J.; Sun, Q.; Lu, J.; Ma, X. An effective dual self- attention residual network for seizure prediction. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1604–1613. [Google Scholar] [CrossRef]
  28. Shankar, A.; Dandapat, S.; Barma, S. Seizure types classification by generating input images with in-depth features from decomposed eeg signals for deep learning pipeline. IEEE J. Biomed. Health Inform. 2022, 26, 4903–4912. [Google Scholar] [CrossRef]
  29. Humairani, A.; Rizal, A.; Wijayanto, I.; Hadiyoso, S.; Fuadah, Y.N. Wavelet-based entropy analysis on eeg signal for detecting seizures. In 2022 10th International Conference on Information and Communication Technology (ICoICT), 2022; pp. 93–98.
  30. Shuvo, S.B.; Ali, S.N.; Swapnil, S.I.; Hasan, T.; Bhuiyan, M.I.H. A lightweight cnn model for detecting respiratory diseases from lung auscultation sounds using emd-cwt-based hybrid scalogram. IEEE J. Biomed. Health Inform. 2021, 25, 2595–2603. [Google Scholar] [CrossRef]
  31. Bu, R. An algorithm for the continuous morlet wavelet transform. Mechanical Systems and Signal Processing 2007, 21, 2970–2979. [Google Scholar]
  32. Theis, L.; Shi, W.; Cunningham, A.; Husza, F. Lossy image compres- sion with compressive autoencoders. arXiv 2017, arXiv:1703.00395. [Google Scholar]
  33. Balle, J.; Laparra, V.; Simoncelli, E.P. End-to-end optimized image compression. arXiv 2016, arXiv:1611.01704. [Google Scholar]
  34. Lu, J.; Verma, N.; Jha, N.K. Convolutional autoencoder-based transfer learning for multi-task image inferences. IEEE Trans. Emerg. Top. Comput. 2021, 10, 1045–1057. [Google Scholar] [CrossRef]
  35. Metzner, C.; Schilling, A.; Traxdorf, M.; Schulze, H.; Tziridis, K.; Krauss, P. Extracting continuous sleep depth from eeg data without machine learning. Neurobiol. Sleep Circadian Rhythm. 2023, 14, 100097. [Google Scholar] [CrossRef]
  36. Ashraf, M.; Anowar, F.; Setu, J.H.; Chowdhury, A.I.; Ahmed, E.; Islam, A.; Al-Mamun, A. A survey on dimensionality reduction techniques for time-series data. IEEE Access 2023, 11, 909–923. [Google Scholar] [CrossRef]
  37. Ataee, P.; Yazdani, A.; Setarehdan, S.K.; Noubari, H.A. Manifold learning applied on eeg signal of the epileptic patients for detection of normal and pre-seizure states. In 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; IEEE: 2007; pp. 5489–5492.
  38. Bird, J.J.; Manso, L.J.; Ribeiro, E.P.; Ekart, A.; Faria, D.R. A study on mental state classification using eeg-based brain-machine interface. In 2018 international conference on intelligent systems (IS); IEEE: 2018; pp. 795–800.
  39. Rabby, M.K.M.; Eshun, R.B.; Belkasim, S.; Islam, A.K. Epileptic seizure detection using eeg signal based lstm models. In 2021 IEEE Fourth International Conference on Artificial Intelligence and Knowl- edge Engineering (AIKE); 2021; pp. 131–132.
  40. Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef]
  41. Kabir, E.; Siuly; Cao, J. ; Wang, H. A computer aided analysis scheme for detecting epileptic seizure from eeg data. Int. J. Comput. Intell. Syst. 2018, 11, 663–671. [Google Scholar] [CrossRef]
  42. Zarei, A.; Asl, B.M. Automatic seizure detection using orthogonal matching pursuit, discrete wavelet transform, and entropy based features of eeg signals. Comput. Biol. Med. 2021, 131, 104250. [Google Scholar] [CrossRef] [PubMed]
  43. Wang, X.; Gong, G.; Li, N. Automated recognition of epileptic eeg states using a combination of symlet wavelet processing, gradient boosting machine, and grid search optimizer. Sensors 2019, 19, 219. [Google Scholar] [CrossRef] [PubMed]
  44. Yazid, M.; Fahmi, F.; Sutanto, E.; Shalannanda, W.; Shoalihin, R.; Horng, G.-J. Simple detection of epilepsy from eeg signal using local binary pattern transition histogram. IEEE Access 2021, 9, 252–267. [Google Scholar] [CrossRef]
  45. Gray-level co-occurrence matrix of fourier synchro-squeezed transform for epileptic seizure detection. Biocybern. Biomed. Eng. 2019, 39, 87–99. [CrossRef]
  46. Diykh, M.; Li, Y.; Wen, P. Classify epileptic eeg signals using weighted complex networks based community structure detection. Expert Syst. Appl. 2017, 90, 87–100. [Google Scholar] [CrossRef]
  47. Bari, M.F.; Fattah, S.A. Epileptic seizure detection in eeg signals using normalized imfs in ceemdan domain and quadratic discrimi- nant classifier. Biomed. Signal Process. 2020, 58, 101833. [Google Scholar] [CrossRef]
  48. Bhardwaj, A.; Tiwari, A.; Krishna, R.; Varma, V. A novel genetic pro- gramming approach for epileptic seizure detection. Comput. Methods Programs Biomed. 2016, 124, 2–18. [Google Scholar] [CrossRef]
  49. Kaur, T.; Gandhi, T.K. Automated diagnosis of epileptic seizures using eeg image representations and deep learning. Neuroscience In- formatics 2023, 3, 100139. [Google Scholar] [CrossRef]
  50. Gandhi, T.; Panigrahi, B.K.; Anand, S. A comparative study of wavelet families for eeg signal classification. Neurocomputing 2011, 74, 3051–3057. [Google Scholar] [CrossRef]
  51. Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adeli, H. Deep convolutional neural network for the automated detection and diagnosis of seizure using eeg signals. Comput. Biol. Med. 2018, 100, 270–278. [Google Scholar] [CrossRef] [PubMed]
  52. Alzami, F.; Tang, J.; Yu, Z.; Wu, S.; Chen, C.P.; You, J.; Zhang, J. Adaptive hybrid feature selection-based classifier ensemble for epileptic seizure classification. IEEE Access 2018, 6, 132–145. [Google Scholar] [CrossRef]
  53. Jaiswal, A.K.; Banka, H. Epileptic seizure detection in eeg signal using machine learning techniques. Australas. Phys. Eng. Sci. Med. 2018, 41, 81–94. [Google Scholar] [CrossRef]
  54. Zhao, X.; Zhang, R.; Mei, Z.; Chen, C.; Chen, W. Identification of epileptic seizures by characterizing instantaneous energy behavior of eeg. IEEE Access 2019, 7, 059–076. [Google Scholar] [CrossRef]
  55. Baykara, M.; Abdulrahman, A. Seizure detection based on adaptive feature extraction by applying extreme learning machines. Trait. Du Signal 2021, 38, 331–340. [Google Scholar] [CrossRef]
  56. Turk, O.; Zerdem, M.S.O. Epilepsy detection by using scalogram based convolutional neural network from eeg signals. Brain Sci. 2019, 9, 115. [Google Scholar] [CrossRef] [PubMed]
  57. Amorim, P.; Moraes, T.; Fazanaro, D.; Silva, J.; Pedrini, H. Elec- troencephalogram signal classification based on shearlet and contourlet transforms. Expert Syst. Appl. 2017, 67, 140–147. [Google Scholar] [CrossRef]
  58. Zhang, T.; Han, Z.; Chen, X.; Chen, W. Subbands and cumulative sum of subbands based nonlinear features enhance the performance of epileptic seizure detection. Biomed. Signal Process. Control. 2021, 69, 102827. [Google Scholar] [CrossRef]
  59. Zhou, D.; Li, X. Epilepsy eeg signal classification algorithm based on improved rbf. Front. Neurosci. 2020, 14, 606. [Google Scholar] [CrossRef]
Preprints 87596 g001
Figure 1. Overview of the proposed epileptic seizures detection model.
Figure 1. Overview of the proposed epileptic seizures detection model.
Preprints 87596 g001
Preprints 87596 g002
Figure 2. Windowing process.
Figure 2. Windowing process.
Preprints 87596 g002
Preprints 87596 g003
Figure 3. CWT Images of each class.
Figure 3. CWT Images of each class.
Preprints 87596 g003
Preprints 87596 g004
Figure 4. Autoencoder model architecture.
Figure 4. Autoencoder model architecture.
Preprints 87596 g004
Preprints 87596 g005
Figure 5. Basic architecture of the LSTM.
Figure 5. Basic architecture of the LSTM.
Preprints 87596 g005
Preprints 87596 g006
Figure 6. EEG Signals from different classes.
Figure 6. EEG Signals from different classes.
Preprints 87596 g006
Preprints 87596 g007
Figure 7. Confusion matrices for binary class classification. (a) N–S. (b) Z–S. (c) O–S. (d) F–S. (e) FN–S. (f) FNZ–S. (g) FNO–S. (h) NOZ–S.
Figure 7. Confusion matrices for binary class classification. (a) N–S. (b) Z–S. (c) O–S. (d) F–S. (e) FN–S. (f) FNZ–S. (g) FNO–S. (h) NOZ–S.
Preprints 87596 g007
Preprints 87596 g008
Figure 8. Confusion matrices for three-class classifications. (a) F–O–S. (b) N–S–Z. (c) O–S–Z. (d) FN–OZ–S.
Figure 8. Confusion matrices for three-class classifications. (a) F–O–S. (b) N–S–Z. (c) O–S–Z. (d) FN–OZ–S.
Preprints 87596 g008
Preprints 87596 g009
Figure 9. Confusion matrices for four-class classification. (a) N–O–S–Z. (b) F–O–S–Z.
Figure 9. Confusion matrices for four-class classification. (a) N–O–S–Z. (b) F–O–S–Z.
Preprints 87596 g009
Preprints 87596 g010
Figure 10. Confusion matrices for five-class classification.
Figure 10. Confusion matrices for five-class classification.
Preprints 87596 g010
Table 1. Summary of the auto-encoder architecture.
Table 1. Summary of the auto-encoder architecture.
Encoder
Layer (type) Output Shape Param#
Conv2D (None, 128, 128, 16) 160
Conv2D
Conv2D
Conv2D
Conv2D		 (None, 64, 64, 32)
(None, 32, 32, 64)
(None, 16, 16, 128)
(None, 8, 8, 255)		 4640
18496
73856
294015
Total params 391,167
Trainable params 391,167
Non-trainable params 0
Decoder
Layer (type) Output Shape Param#
Conv2D Transpose (None, 16, 16, 128) 293888
Conv2D Transpose
Conv2D Transpose
Conv2D Transpose
Conv2D Transpose		 (None, 32, 32, 64)
(None, 64, 64, 32)
(None, 128, 128, 16)
(None, 256, 256, 1)		 73792
18464
4624
145
Total params
Trainable params
Non- trainable params		 390,913
390,913
0
Table 2. Statistical features and their mathematical expressions.
Table 2. Statistical features and their mathematical expressions.
Feature Mathematical Expression Feature Mathematical Expression
Minimum m i n ( s ) Range m a x ( s ) − m i n ( s )
Maximum m a x ( s ) Energy ∑ ‍ s 2
Mean 1 N ∑ ‍ s Clearance Factor m a x ( | s | ) 1 N ∑ ‍ | s | 2
Standard Deviation 1 N − 1 ∑ ‍ ( s − μ ) 2 Variance 1 N − 1 ∑ ‍ ( s − μ ) 2
Kurtosis 1 N ∑ ‍ ( s − μ ) 4 σ 4 Impulse Factor m a x ( | s | ) 1 N ∑ ‍ | s |
Skewness 1 N ∑ ‍ ( s − μ ) 3 σ 3 Power ∑ ‍ s 2 N
RMS 1 N ∑ ‍ s 2 Peak to RMS m a x ( | s | ) 1 N ∑ ‍ s 2
Crest Factor m a x ( s ) 1 N ∑ ‍ s 2 Shape Factor 1 N ∑ ‍ s 2 1 N ∑ ‍ | s |
Table 3. Overview of EEG Bonn EEG Dataset, University of Bonn Germany.
Table 3. Overview of EEG Bonn EEG Dataset, University of Bonn Germany.
Patient Stage Subject Activities Number
of Samples 		Length of
Segments		 Sampling
Frequency (Hz)		 Duration (Sec)
Epileptic Ictal Set S (Seizure Activity) 100 4097 173.61 23.60
Interictal Set F (Seizure Free) 100 4097 173.61 23.60
Set N (Seizure Free) 100 4097 173.61 23.60
Healthy Normal Set O (Eyes Closed) 100 4097 173.61 23.60
Set Z (Eyes Open) 100 4097 173.61 23.60
Table 4. Performance metrics for binary classification.
Table 4. Performance metrics for binary classification.
Problem Accuracy (%) F1-Score (%) Precision (%) Sensitivity (%)
N‒S 100 100 100 Class N : 100
Class S : 100
Z‒S 100 100 100 Class Z : 100
Class S : 100
O‒S 100 100 100 Class O : 100
Class S : 100
FN‒S 100 100 100 Class FN :100
Class S: 100
FNZ‒S 100 100 100 Class FNZ : 100
Class S : 100
FNO‒S 100 100 100 Class FNO : 100
Class S : 100
NOZ‒S 100 100 100 Class NOZ : 100
Class S : 100
F‒S 98.12 98.12 98.13 Class FNZ : 97.85
Class S : 98.5
Table 5. Performance metrics for the three-class classification.
Table 5. Performance metrics for the three-class classification.
Problem Accuracy (%) F1-Score (%) Precision (%) Sensitivity (%)
F‒O‒S 100 100 100 Class F : 100
Class O : 100
Class S : 100
N‒Z‒S 98.75 98.75 98.76 Class Z : 98.76
Class N : 100
Class S : 97.2
O‒Z‒S 96.25 96.26 96.37 Class O : 93.18
Class Z : 98.60
Class S : 97.53
FN‒OZ‒S 98 97.93 97.98 Class FN : 96.56
Class OZ : 100
Class S : 97.40
Table 6. Performance metrics for four-class classification.
Table 6. Performance metrics for four-class classification.
Problem Accuracy (%) F1-Score (%) Precision (%) Sensitivity (%)
N‒O‒Z‒S 96.60 96.57 96.70 Class N : 98.72
Class O : 94.51
Class S : 94.03
Class Z : 98.84
F‒O‒Z‒S 98.75 98.75 98.76 Class F : 98.56
Class O : 95.65
Class S : 97.50
Class Z : 96.25
Table 7. Comparison with some existing approaches.
Table 7. Comparison with some existing approaches.
Author Year Method Used Classifier Classification
Problem		 Results
Kabir et al.[41] 2018 K-means clustering,
statistical features,		 SVM Z-S
O-S		 98.13
97.75
Zarei et al.[42] 2021 DWT SVM Z-S, O-S
N-S, F-S		 99.50, 99.75
99.00, 99.50
Wang et al.[43] 2019 Symlets wavelets, PCA SVM Z-S, O-S
N-S, F-S		 100
98.4, 98.1
Yazid et al.[44] 2023 DWT, Local binary pattern transition histogram, Local binary pattern mean absolute deviation KNN Z-S
O-S
N-S
F-S		 99.94
99.86
99.88
99.70
Gupta et al.[16] 2019 Fourier Bassel series expansion, and weighted multi scale Renyi permutation entropy LS-SVM Z-S
O-S
N-S
F-S		 99.50
99.50
99.50
97.50
Mamli et al.[45] 2019 Fourier Synchro-Squeezed Transform and gray level co-occurrence matrix KNN, SVM ZO-S
FN-S		 99.73
99.59
Diykh et al.[46] 2017 Statistical Features LS-SVM ZO-S
FN-S		 98.00
97.80
Mandhouj et al.[22] 2021 STFT spectograms CNN ZO-S 98.33
Bari et al.[47] 2020 EMD with Normalized Intrinsic Mode Function Quadratic Discriminant Analysis (QDA) NF-S 99.00
Diykh et al.[46] 2017 Statistical Features LS-SVM ZNF-S 96.50
Bhardwaj et al.[48] 2016 EMD Genetic Programming ZNF-S 98.61
Kaur et al.[49] 2023 Activations from conv5 SVM ZNF-S
Z-N-S		 99.75
98.00
Gandhi et al.[50] 2011 Matrix determinant MLP Z-N-S 94.75
Acharya et al.[51] 2018 Z-Score Normalization CNN O-F-S 88.00
Alzami et al.[52] 2018 DWT Adaptive hybrid feature sel.-based classifier. ZO-NF-S 96.00
Jaiswal et al.[53] 2018 SubXPCA SVM ZO-NF-S 97.40
Zhao et al.[54] 2019 Stationary WT, Entropy features Back-Propagation NN ZO-NF-S 93.30
Baykara et al.[55] 2021 Stockwell Transform, Entropies and Perservals energy ELM ZO-NF-S 90.00
Turk et al.[56] 2019 FFT, STFT, WT Transform CNN Z-N-F-S
O-N-F-S
Z-O-N-F		 90.50
91.50
93.60
Amorim et al.[57] 2017 DWT, Shearlet and Contourlet Transform Random Forest Z-O-N-F-S 88.67
Zhang et al.[58] 2021 Frequency Slice WT (FSWT), Fuzzy entropy, Higuchi FD -distributed stochastic neighbor embedding (t-SNE) Z-O-N-F-S 93.62
Zhou et al.[59] 2020 DWT Entropy Features RBF NN Z-O-N-F-S 78.40
This Proposed Study CWT, Statistical Features LSTM N-S, Z-S, O-S
FN-S, FNZ-S,
FNO-S, NOZ-S
F-S
F-O-S
N-Z-S
O-Z-S
FN-OZ-S
N-O-Z-S
F-O-Z-S
F-N-O-Z-S		 100
100
98.12
100
98.75
96.25
98.00
96.60
97.00
93.25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated