Prerpints.org logo
Preprint
Article

Measurement Modeling and Performance Analysis of a Bionic Polarization Imaging Navigation Sensor Using Rayleigh Scattering to Generate Scattered Sunlight

Altmetrics

Downloads

93

Views

41

Comments

0

This version is not peer-reviewed

Submitted:

03 October 2023

Posted:

04 October 2023

You are already at the latest version

Alerts
Abstract
The bionic polarization imaging navigation sensor (BPINS) is a navigation sensor that provides absolute heading, and it is of practical engineering significance to model the measurement error of BPINS. The existing BPINSs are still modeled using photodiode-based measurements rather than imaging measurements and are not modeled systematically enough. This paper proposes a measurement model of BPINS that takes into account the geometric and polarization errors of the optical system. Firstly, the key error factors affecting the measurement accuracy of BPINS are systematically investigated and the Stokes vector-based measurement error model of BPINS is established. Secondly, based on its measurement error model, the effect of the error source on the measurement performance of BPINS is quantitatively analyzed by using Rayleigh scattering to generate scattered sunlight as a known incident light source. The experimental results show that the coordinate deviation of the principal point has a greater impact, followed by grayscale response inconsistency of CMOS and integration angle error of micro-polarization array, and finally lens attenuation. This finding can guide the subsequent calibration of BPINS, and the quantitative results provide an important reference for its optimal design.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Polarization is another dimension of light, just like spectrum and intensity, which can provide distinct and useful information about a visual scene [1] and is applied in many scenarios, such as microscopy imaging [2], optical precision measurement [3,4], and biological navigation [5,6]. Many animals, particularly insects, are sensitive to the polarization of light and use this information for navigation, detection and communication [7]. A great deal of research has been done on the behavioral neurobiology of polarization navigation in insects [8,9,10,11,12,13]. The desert ant has to rely heavily on polarized skylight and path integration in its featureless desert habitat during foraging [14]. Biologists have recently demonstrated that greater mouse-eared bats use skylight polarization cues to calibrate a magnetic compass at sunset [15] and mantis shrimp use celestial polarization and path integration to navigate home [16]. This celestial polarization orientation method is used as a bio-inspired polarization navigation method which has attracted much attention due to its advantages, namely autonomy and no error accumulation [17]. This method is reported to have potential applications in assisting inertial navigation in the event of satellite denial [18]. However, the factors that affect the measurement performance of bio-inspired polarization navigation sensor (BPNS) remain unclear. The study of the measurement error model of BPNS is of great significance to promote the practical application of polarization navigation.
Due to the difference measurement principles of polarized skylight, the current measurement error models for BPNS are divided into photodiode-based and polarization imaging-based. In terms of photodiode-based principle, Lambrinos et al. [19] designed a photodiode-based six-channel polarization compass for ground robot navigation and proved the feasibility of using polarized skylight for navigation. Later, Chu et al. [20] built an improved version of photodiode-based BPNS and investigated the dark noise and static sensitivity of this BPNS. Ma et al. [21] studied the inconsistent amplification of six photodiodes and the misalignment angle error of polarizers and used the NSGA-II algorithm to calibrate a BPNS similar to Chu's. Wang et al. [22] presented an improved photodiode-based BPNS with a planoconvex lens, and used central-symmetry and non-continuous calibration method. Chahl et al. [23] imitated the optical stabilization organ of dragonflies, known as the ocelli, and also developed a photodiode-based six-channel BPNS. Dupeyroux et al. [24,25,26] designed a photodiode-based BPNS, which can measure ultraviolet (UV) light, conducted outdoor performance tests under various weather conditions and achieved an accuracy of 0.3° in clear sky. However, due to the fact that these photodiode-based BPNS can only measure the polarization information at a certain point in the sky, they are susceptible to external factors such as weather interference and surrounding occlusion, resulting in poor robustness. To improve the robustness of the polarization navigation method, researchers have developed several bionic polarimetric imaging navigation sensors (BPINS). Sturzl et al [27] performed a geometric calibration of BPINS based on four fisheye cameras and proposed an efficient method for reconstructing the full-sky polarization pattern. Liu et al. [28] used nanoimprint lithography to integrate a multi-directional nanowire grid polarizer on a complementary metal oxide semiconductor (CMOS) sensor to eliminate the installation angle error of the polarizer and conducted laboratory calibration. Fan et al. [29] analyzed the inconsistent response error of the CMOS and the installation angle error of the four polarizers and proposed a calibration method for a four-camera polarization imaging navigation device. Ren et al. [30] has reported a measurement model of BPINS based on the photodiode principle which takes into account the extinction ratio errors. Although the imaging prototypes are used for perception, the modeling and calibration methods of the photodiode-based principle are still used and the Mueller matrix error of an optical system is not considered [28,29,30,31]. For models based on the principle of polarization imaging, the geometric errors of BPINS, such as principal point and lens distortion, are not considered [32,33,34,35], especially for the measurement of skylight.
Motivated by this situation, this article proposes an error model for the measurement process of BPINS considering the geometrical and polarization errors of the optical system. Using Rayleigh scattering to generate the skylight with known polarization state, an analysis method is proposed for the effect of error sources on the measurement performance of BPINS. The proposed analysis method can validate the measurement performance of all bionic polarization imaging navigation sensors. The contributions of this paper can be concluded as follows:
1)
The key error factors affecting the measurement accuracy of BPINS are quantitatively investigated and the measurement error model of BPINS considering the geometrical and polarization errors of the optical system is established.
2)
A skylight with a known polarization state is generated as an incident light source (not fully linearly polarized light) using Rayleigh scattering, which is consistent with the outdoor Rayleigh sky polarization pattern.
3)
An analysis method of the influence of key error sources on the measurement performance of BPINS is proposed.
The remainder of this paper is organized as follows. Measurement principle and error model of BPINS are presented in section 2. A detailed description of the proposed performance analysis method of BPINS is presented in section 3. The conclusions are presented in section 4.

2. Measurement Principle and Error Model of BPINS

2.1. Principle of skylight polarization imaging

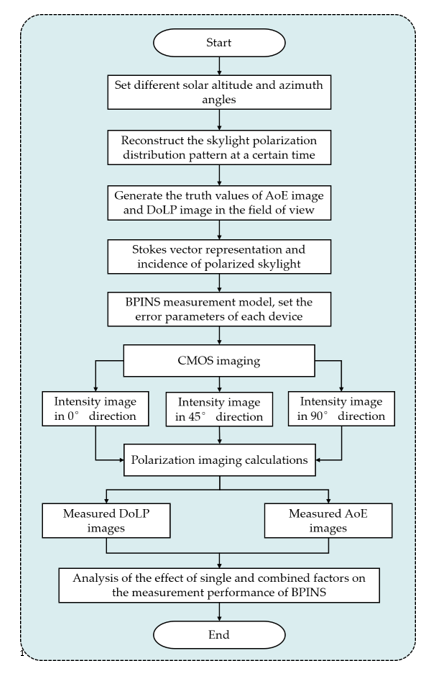
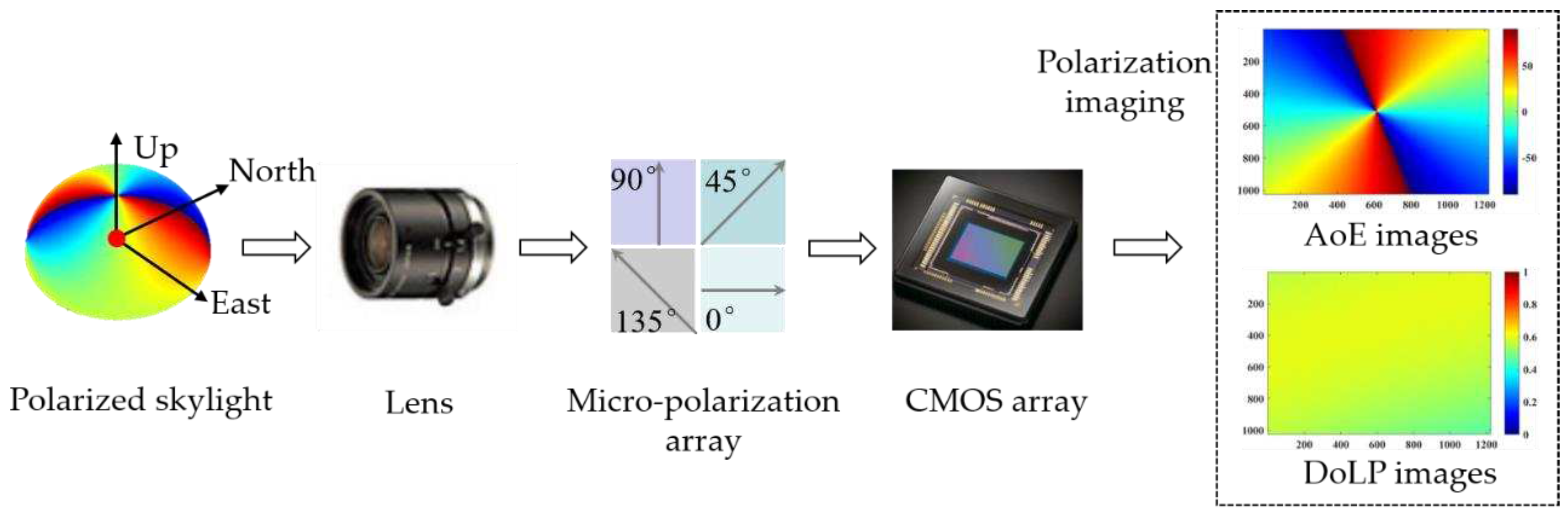
Sunlight is scattered through the atmosphere and forms polarized light in the sky. To clearly understand the factors that affect the measurement accuracy of BPINS, we need to model the measurement errors of BPINS. We analyze the whole measurement process of imaging skylight into the CMOS plane. Firstly, the polarized skylight under the local geographical system passes through multiple lenses inside the lens and is focused at the exit pupil, then it passes through the micro-polarization array and is finally imaged into the CMOS plane. The measurement process of BPINS is shown in Figure 1.
The E vector of polarized skylight is a three-dimensional representation in the East-North-up coordinate system. Skylight polarimetric imaging is the projection of each beam of polarized skylight in the field of view onto the CMOS imaging plane through the Muller matrix of the optical system of BPINS. Figure 2 shows the projection process of two-dimensional polarized skylight from a local coordinate system in the BPINS coordinate system. The Stokes vector can represent both fully and partially polarized light. Since polarized skylight is partially polarized light, and the Stokes vector for polarized skylight can be expressed as follows:
S s k y l i g h t = [ I Q U V ] = I [ 1 d cos 2 χ cos 2 ψ d cos 2 χ sin 2 ψ d sin 2 χ ]
where the I parameter is the total intensity of the skylight; the Q parameter describes the amount of linear horizontal or vertical polarization; the parameter U is the amount of linear +45° or -45° polarization. The parameter V is the amount of right or left circular polarization contained within the beam, and the content of this component in the skylight is extremely small [1], so it can be ignored in the skylight imaging. The parameter d is the degree of polarization of skylight, φ represents the angle of polarization of skylight, χ is the ellipticity angle of skylight.
According to the principle of polarized skylight imaging, polarized skylight imaging is the process of projecting each beam of polarized skylight in the field of view onto the imaging plane through the Mueller matrix of the optical system, the Stokes vector of the outgoing light as follows:
S o u t = M θ ⋅ M l e n s ⋅ S s k y l i g h t
where the incident polarized skylight is S s k y l i g h t , the Mueller matrix of the lens is M l e n s (if the error is not taken into account, M l e n s is the unit matrix), the Mueller matrix of the micro-polarizer with azimuth θ is M θ . The Stokes vector of the outgoing light is S o u t after passing through the Mueller matrix of an optical system.
Since the CMOS of BPINS can only perceive the total intensity of the Stokes vector of skylight, the general equation for the total intensity received by the CMOS imaging plane is as follows:
I θ = 1 2 ( I + Q cos 2 θ + U sin 2 θ )
Taking θ = 0 ∘ , 45 ∘ , 90 ∘ into equation (3), a linear system of equations can be obtained as follows:
[ I 0 I 45 I 90 ] = 1 2 [ 1 1 0 1 0 1 1 − 1 0 ] [ I Q U ]
According to the definition of the angle of polarization and degree of polarization, the formulae for calculating the angle of polarization and degree of polarization can be obtained as follows:
{ tan 2 α = U Q d = U 2 + Q 2 I
Based on the definition of the angle of E-vector (AoE) for polarized skylight which is the angle between the direction of E vector vibration and the local meridian, the angle of E-vector in the CMOS imaging plane can be solved as follows:
{ φ = α − β , ( − 90 ∘ ≤ φ ≤ 90 ∘ ) α = 1 2 arctan ( 2 I 45 − I 0 − I 90 ) ( I 0 − I 90 ) β = arctan ( j − v y ) ( i − u x )
where φ represents the angle of E-vector, α is the angular distances of E-vector from the reference axis X c of BPINS and β represents the azimuth angle of the local meridian from the reference axis X c of BPINS. ( i , j ) are the coordinates of the incident skylight, ( u x , u y ) is the principal point of the AoE image.

2.2. Measurement error model of BPINS

From the above equation (6), it can be seen that the factors affecting the polarimetric measurement accuracy of the BPINS mainly include the coordinate offset of principal point, the integration angle error of the micro-polarization array, the lens attenuation, and the grayscale response inconsistency of CMOS. The continuous form of the measurement error model for BPINSs is noted as:
φ ( δ I θ , δ β , δ θ , δ ρ ) = ∂ f ∂ I θ δ I θ + ∂ f ∂ β δ β + ∂ f ∂ θ δ θ + ∂ f ∂ ρ δ ρ
where δ I θ , δ β , δ θ , δ ρ respectively represent the inconsistent grayscale response of CMOS, the coordinate deviation of principal point, the installation angle error of micro-polarization array, and the lens attenuation.
(1)
Coordinate deviation of principal point
When the incident skylight is coplanar with the direction of the maximum offset of the principal point coordinates, the influence form of the coordinates deviation of the principal point is shown in Figure 3, assuming that e 1 is along the direction of the maximum offset of the principal point coordinates, e 3 is the direction of the ideal principal optical axis, and e 3 ' is the direction of the actual principal optical axis. Since the image principal point of BPINS is not calibrated, the actual principal point coordinate position is offset from the ideal principal point coordinate position, i.e., there is an error in ( u x , v y ) in β . In the case that other error variables are zero, the effect of the coordinate deviation of the principal point on the AoE image can be obtained from equation (6) and (7) as follows:
{ φ = α − β ^ β ^ = arctan ( j − v y i − u x + δ β ) , δ β = δ u x ( j − v y ) − δ v y ( i − u x ) ( j − v y − δ v y ) ( j − v y )
where ( δ u x , δ v y ) is the coordinate deviation of the principal point.
(2)
Installation angle error of micro-polarization array
The incident polarized beam interacts with the micro-polarization array after passing through the lens. The installation angle error of the micro-polarization array has an effect on the Mueller matrix of the micro-polarization array, as shown in Figure 4, the Mueller matrix of the micro-polarization array with an azimuth of θ including the installation angle error δ θ can be written as:
M θ = 1 2 [ 1 cos 2 ( θ + δ θ ) sin 2 ( θ + δ θ ) cos 2 ( θ + δ θ ) cos 2 2 ( θ + δ θ ) sin 2 ( θ + δ θ ) cos 2 ( θ + δ θ ) sin 2 ( θ + δ θ ) sin 2 ( θ + δ θ ) cos 2 ( θ + δ θ ) sin 2 2 ( θ + δ θ ) ]
(3)
Lens attenuation
When the polarized skylight through the lens, the incident skylight beam corresponding to a certain pixel can be decomposed into mutually orthogonal p light and s light. Let τ 1 and τ 2 indicate the amplitude transmittance of the lens to p light and s light, respectively, which only varies with the angle of incidence.
Each beam of incident sky light has a different angle of incidence with each optical surface and its azimuthal angle of the incident surface, which has a certain symmetry. A pixel corresponds to a beam of incident skylight, then the Mueller matrix of the lens micro-unit corresponding to a single pixel in the local coordinate system can be expressed as:
M l e n s = τ 1 2 + τ 2 2 2 [ 1 ρ 0 ρ 1 0 0 0 1 - ρ 2 ] , ρ = τ 1 2 − τ 2 2 τ 1 2 + τ 2 2
where ρ denotes the linear bidirectional attenuation of the lens.
Inconsistency of CMOS grayscale response
In visual measurement, there is an approximate linear relationship between input light intensity and image grayscale. The nonuniformity of CMOS grayscale response mainly consists of the nonuniformity of dark current response and photoelectric response. The photoelectric sensitive array outputs the light intensity I θ as image grayscale. Based on the linear model in EMVA 1288 [34], the grayscale of the CMOS output can be expressed as:
I ˜ θ = a I θ + b θ + n θ , ( θ = 0 ° , 45 ° , 90 ° )
According to the principle of polarized skylight imaging, the CMOS of BPINS can only perceive the total intensity of the Stokes vector of skylight. From equation (2), the general equation for the total intensity received by the CMOS imaging plane can be written as follows:
I ˜ θ = τ 1 2 + τ 2 2 4 ( I ˜ ( 1 + ρ cos 2 ( θ + δ θ − β ) ) + Q ˜ ( ρ + cos 2 ( θ + δ θ − β ) ) + U ˜ sin 2 ( θ + δ θ − β ) ⋅ 1 − ρ 2 )
Taking θ = 0 ∘ , 45 ∘ , 90 ∘ into equation (12), I, Q, U can be solved as follows:
{ I ˜ = − 2 ( ρ 2 − 1 ) ( τ 1 2 + τ 2 2 ) ( I ˜ 0 ( 1 − ρ ( cos 2 ( δ θ + β ) + sin 2 ( δ θ + β ) ) ) + I ˜ 90 ( 1 + ρ ( cos 2 ( δ θ + β ) + sin 2 ( δ θ + β ) ) ) − 2 I ˜ 45 ρ sin 2 ( δ θ + β ) ) Q ˜ = 2 ( ρ 2 − 1 ) ( τ 1 2 + τ 2 2 ) ( I ˜ 0 ( sin 2 ( δ θ + β ) − cos 2 ( δ θ + β ) + ρ ) + I ˜ 90 ( cos 2 ( δ θ + β ) + sin 2 ( δ θ + β ) + ρ ) − 2 I ˜ 45 sin 2 ( δ θ + β ) ) U ˜ = − 2 1 − ρ 2 ( τ 1 2 + τ 2 2 ) ( I ˜ 0 ( cos 2 ( δ θ + β ) + sin 2 ( δ θ + β ) ) + I ˜ 90 ( cos 2 ( δ θ + β ) − sin 2 ( δ θ + β ) ) − 2 I ˜ 45 cos 2 ( δ θ + β ) )
Based on the definition of the angle of E-vector and the degree of linear polarization of skylight, the polarimetric parameters of BPINS can be obtained as:
{ tan 2 φ ˜ = U ˜ Q ˜ d ˜ = U ˜ 2 + Q ˜ 2 I ˜
The measurement model of BPINS with measurement error can be written as a function expressed as:
{ φ ˜ = f ( I θ , β , θ , ρ ) d ˜ = g ( I θ , β , θ , ρ )

3. Performance Analysis Method for Generating Sunlight Using Rayleigh scattering

As seen in section 2, outdoor polarized skylight is produced by the scattering of direct sunlight through the atmosphere. It is not possible to fully generate polarized skylight indoors, but we can obtain outdoor polarized skylight by using the sky Rayleigh scattering model and the polarization imaging principle. In this section, the outdoor polarized skylights were numerically simulated for known incident light, and then we analyzed the extent to which each error source affects the measurement performance of BPINS.
Once the solar position is known in the local geographical coordinate system, the skylight polarization distribution pattern can be established. To truly simulate the polarized skylight field at a certain time on a certain day, numerical simulations are performed at a solar altitude angle of 5° and a solar azimuth angle between 10° and 80° to obtain the skylight polarization pattern formed at different positions of the sun. The true values of the angle of E-vector (AoE) image and the degree of linear polarization (DoLP) image can be obtained by the Rayleigh scattering model. The two parameters of the AoE and DoLP can be used to characterize the polarization state of each beam of polarized skylight by Poincare sphere. Any point on the equator of the Poincare sphere represents completely linearly polarized light in different directions. Since the polarized skylight is partially linearly polarized light, its maximum DoLP should be less than 1. According to the conversion relation between the Poincare sphere and the Stokes vector, we can get the Stokes vector of each beam of polarized skylight, and thus obtain the known polarization state of the skylight.
The skylight in a known polarization state is incident on the BPINS, which interacts with the micro-polarization array through the lens and is finally imaged on the CMOS plane of the BPINS. Based on the measurement error model described above, the skylight polarization imaging calculation is performed by sequentially varying each error source to form 0°, 45°, and 90° intensity images, which are then calculated to obtain the AoE images and DoLP images. Figure 5 shows the impact analysis flowchart of the measurement error model of BPINS.
Due to the need to conduct multiple numerical simulation experiments, it is necessary to simulate the distribution of each error source. Here, the distribution of each error source is set as Gaussian distribution, and the specific simulation parameters of each error source are set as shown in Table 1. To reduce the computational time, the image resolution of BPINS is set to (1024, 1224) pixel, and the maximum DoLP is set to 0.6, which corresponds to a maximum greyscale response of 153 (DN), due to cloud cover and light intensity attenuation during the transmission of polarized skylight. Based on the position of the origin of the image coordinate system in the pixel coordinate system, the ideal principal point is (512.5, 612.5) pixel, and the specific parameters of BPINS are set as shown in Table 2. We then used Monte Carlo [35] methods to analyze the effects of single and combined factors on the measurement performance of BPINS, respectively.
μ m

4. Experiments and Results

4.1. Effect of a single factor on the measurement performance of BPINS

According to the error parameter setting in Table 1 and the measurement model of BPINS, 160 numerical simulation experiments were conducted randomly for each error source, and the solar azimuth angle was changed every 20 times. The simulated skylight with known polarization state is incident into the measurement model of BPINS, and the azimuth angle is extracted from the AoE image with measurement error, and the measured azimuth is compared with the ideal azimuth. 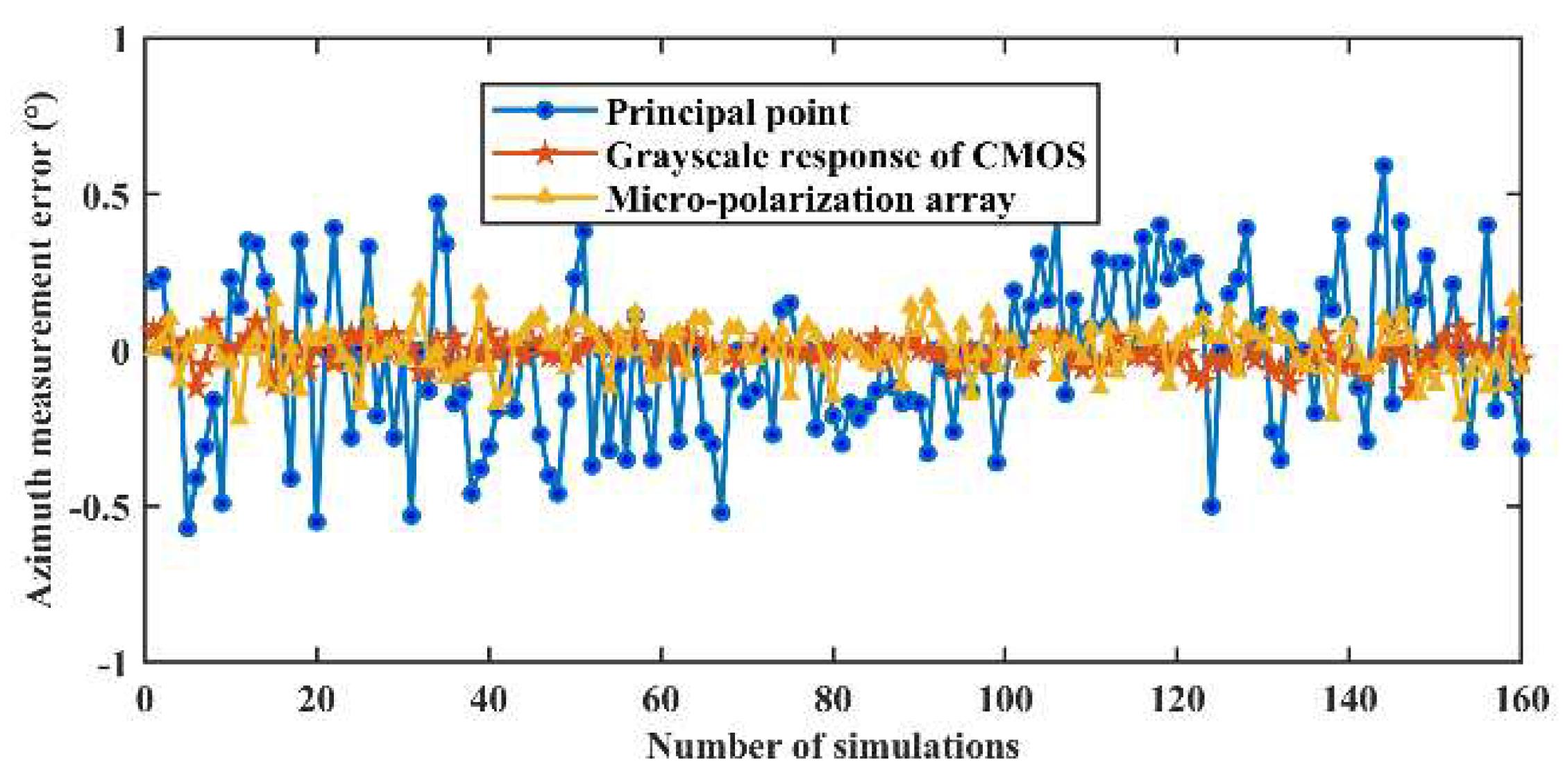Figure 6 shows azimuth measurement results for the effect of a single factor. Figure 7 shows the azimuth measurement errors corresponding to a single factor.
Table 3 shows the results of the quantitative azimuth measurement errors for each error source. As can be seen from Table 3, the azimuth measurement error is 0.2476° for the condition that the coordinate offset of a principal point satisfies the δ β ∼ N ( 0 , 2 2 ) distribution.
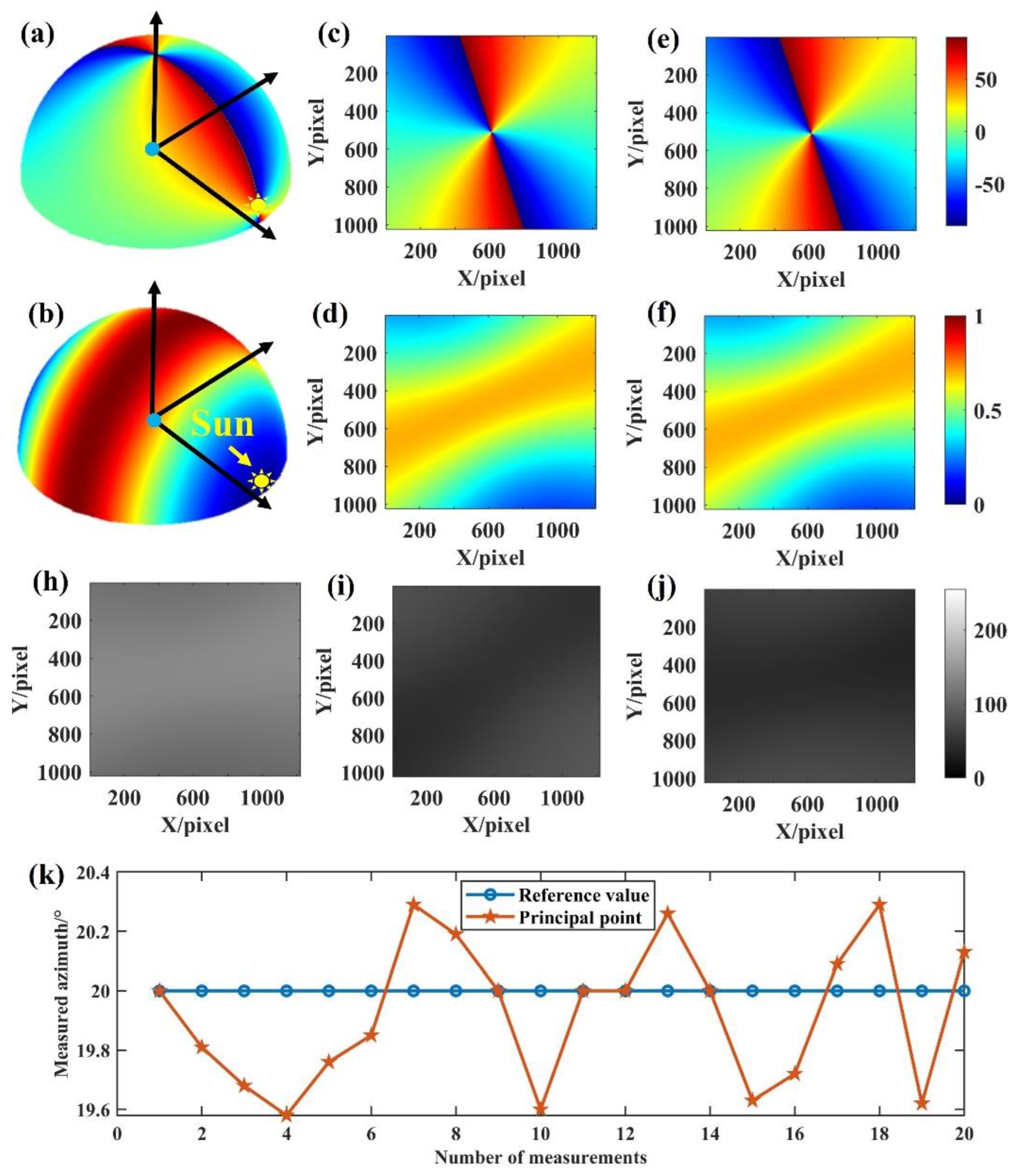
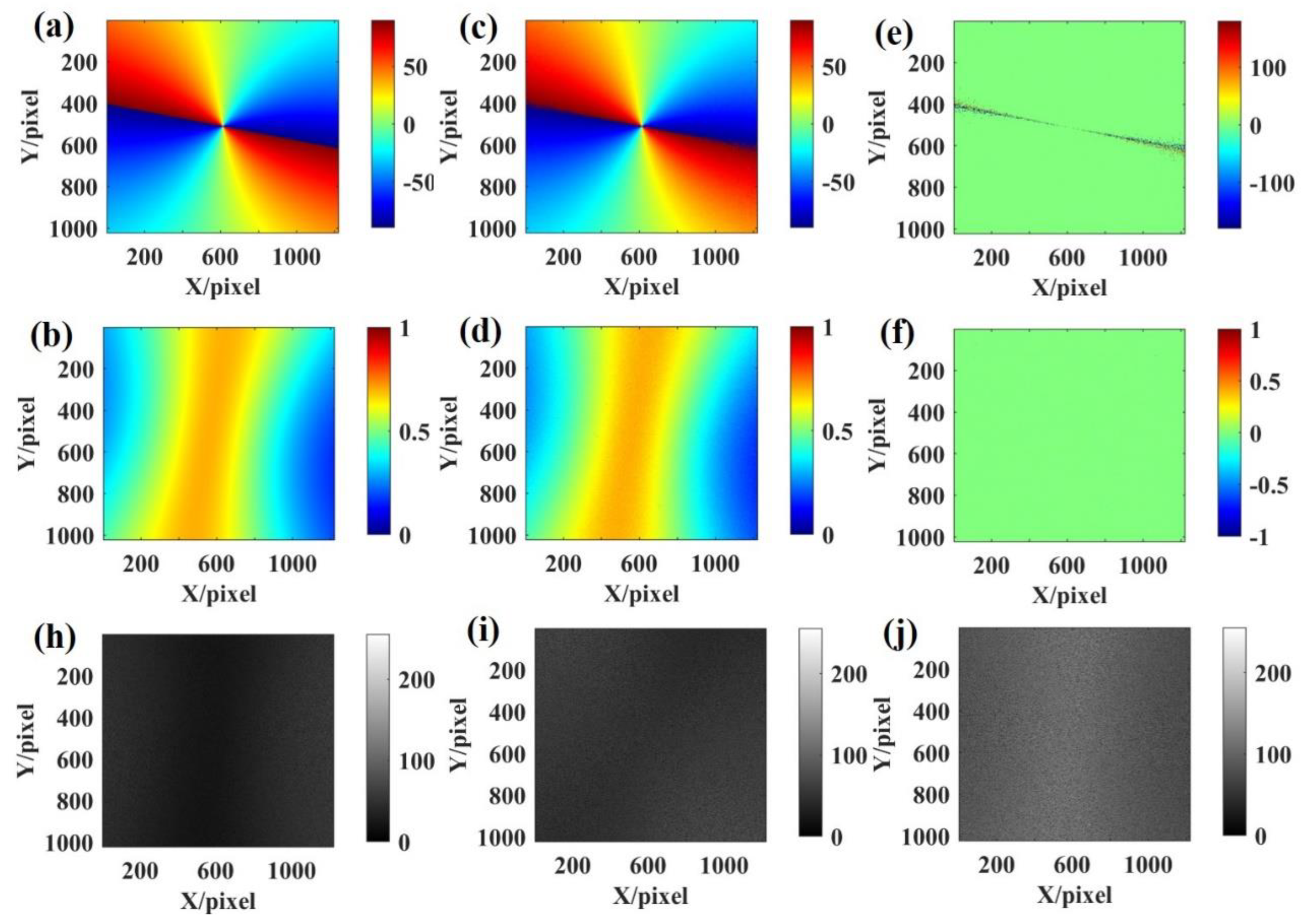
Figure 8 shows an example of the imaging results obtained by simulating the coordinate offset of a principal point. Figure 8 (a) and (b) show the three-dimensional skylight polarization pattern for a solar altitude angle of 5° and an azimuth angle of 80° in the local geographical system. Figure 8 (c) and (d) show the true value of the AoE image and the true value of the DoLP image in the field of view respectively. The Stokes vectors of scattered sunlight under the Rayleigh scattering sky can be obtained from Figure 8 (c) and (d). These scattered skylights are incident on the sensor to form the 0°, 45°, and 90° directional intensity images, as shown in Figure 8 (h)-(j). Figure 8 (e) and (f) can be solved from the 0°, 45°, and 90° intensity images. Figure 8 (k) shows the azimuth extraction results from 20 simulation experiments.
Figure 9 shows an example of the simulated experimental imaging results for the integration angle error of the micro-polarization array. Figure 9 (a) and (b) show the three-dimensional skylight polarization pattern for a solar altitude angle of 5° and an azimuth angle of 50°. Figure 9 (c) and (d) show the true value of the AoE image and the true value of the DoLP image in the field of view respectively. The Stokes vectors of scattered sunlight under the Rayleigh scattering sky are obtained from Figure 9 (c) and (d). These scattered skylights are incident on the sensor to form the 0°, 45°, and 90° directional intensity images, as shown in Figure 9 (h)-(j). It can be seen that the measured AoE image, i.e., Figure 9 (e), is as smooth as the true value of the AoE image. The same is true for the measured DoLP image. As can be seen from Table 3, the azimuthal measurement error is 0.0812° under the condition that the integration angle error of the micro-polarization array satisfies the (0, 0.1 2 ) distribution. This indicates that an integration angle error of 0.1° for the micro-polarization array has a relatively small effect on the polarization measurements of BPINS.
Figure 10 shows an example of the simulated experimental imaging results for the grayscale response inconsistency of CMOS. Figure 10 (a) and (b) show the three-dimensional skylight polarization pattern for a solar altitude angle of 5° and an azimuth angle of 30°. Figure 10 (c) and (d) show the true value of the AoE image and the true value of the DoLP image in the field of view respectively. The Stokes vectors of scattered sunlight under the Rayleigh scattering sky are obtained from Figure 10 (c) and (d). These scattered skylights are incident on the sensor to form the 0°, 45°, and 90° directional intensity images, as shown in Figure 10 (h)-(j). Figure 10 (e) shows that the measured AoE image is not as smooth as the true value, especially at the edges, and the same is true for the measured DoLP image. As can be seen from Table 3, the azimuth measurement error is 0.0405° with a mean error close to 0.0059° under the condition that the grayscale response inconsistency of CMOS satisfies the (0, 1 2 ) distribution.
As can be seen from Table 3, when the bilinear attenuation of the lens is controlled to within (0.2, 0.2), the azimuthal measurement error is zero. This indicates that the bilinear attenuation of the lens has no effect on the AoE image, but has an effect on the DoLP image, as the DoLP is determined by the light intensity.
From the above numerical simulation results, the following conclusions can be drawn: the coordinate deviation of the principal point, the installation error of the micro-polarization array and the grayscale response inconsistency of CMOS are the important error sources that affect the azimuth measurement. These simulation results can guide the later calibration of BPINS.

4.2. Effect of combined factors on the measurement performance of BPINS

The simulation results in section 4.1 provide a quantitative indication of the extent to which a single factor affects the measurement performance of BPINS. However, it is also necessary to analyze the combined effect of these four error sources on the measurement performance of BPINS. After all, the measurement accuracy of an uncalibrated BPINS is largely determined by the combination of these error sources.
The same number of combined simulation experiments as for the single factor were conducted, also changing the solar azimuth every 20 times. Figure 11 shows an example of the imaging results from one of the comprehensive simulation experiments for a solar altitude angle of 5° and an azimuth angle of 20°. Figure 11 (a) and (b) show the true AoE image and the true DoLP image, respectively, used to generate the Rayleigh scattered skylight incident into the uncalibrated BPINS. Figure 11 (h) and (i) are the AoE and DoLP measured by the BPINS, and Figure 11 (c) is the difference between the true AoE and the measured AoE. As can be seen from Figure 11 (h), the measured AoE image is not very smooth, especially at the edges, in the same way as the measured DoLP. Figure 12 shows the azimuth measurements affected by the combined effect of these four error sources. 160 combined simulation experiments show that for uncalibrated BPINS, the combined effect of these error sources has a relatively large impact on the BPINS measurements. Under the combined influence of these error sources, the azimuth measurement accuracy of BPINS is 0.8839°.
Using the above Monte Carlo simulation, for the BPINS to be calibrated, the coordinate deviation of principal point is controlled to within (2, 2) pixels, with an azimuthal measurement error of 0.2476°. the integration angle error of micro-polarization array and grayscale response inconsistency of CMOS are controlled to within 0.1° and 1.0 (DN) respectively, with azimuthal measurement errors of 0.080° and 0.0456°, within the same order of magnitude. The lens attenuation is controlled to within (0.2, 0.2) and the azimuthal measurement error is zero, indicating that the light intensity attenuation has no effect on the AoE image. From the above numerical simulation results, the following conclusions can be drawn: the combined effects of the error sources have a relatively large impact on the polarization measurements of BPINS. The coordinate deviation of the principal point, the integration angle error of the micro-polarization array and the grayscale response inconsistency of CMOS are the key error sources to be considered for subsequent calibration of BPINS.

5. Conclusions

This paper systematically analyses the measurement errors of skylight passing through the lens to the micro-polarization array and finally incident on the CMOS imaging plane. A Stokes vector-based measurement model of BPINS is developed, taking into account multiple source factors, such as the principal point, the grayscale response of CMOS, the integration angle of the micro-polarization array, and the lens. We simulated the Rayleigh scattered skylight as a known incident light source, performed outdoor measurement model simulations, and quantitatively analyzed the extent to which the error sources affect the measurement performance of BPINS. The results show that the coordinate deviation of the principal point has a more significant impact in AoE measurement, followed by the grayscale response inconsistency of CMOS and integration angle error of micro-polarization array, and finally lens attenuation; in DoLP measurement, the grayscale response inconsistency of CMOS has a more significant impact. This finding can guide the subsequent calibration of BPINS, and the quantitative results provide an important reference basis for its optimization design and calibration experiments. The proposed error model and impact analysis method for BPINS can verify the measurement performance of all BPINS.

Author Contributions

Conceptualization, Z.W. and K.Z.; methodology, Z.W.; software, H.C.; validation, Z.W. and P.F.; writing—original draft preparation, Z.W.; writing—review and editing, K.Z.; visualization, H.C.; supervision, K.Z.; project administration, K. Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Shandong Postdoctoral Science Foundation, grant number SDBX2023012.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. D. Goldstein. Polarized light, third edition, (Crc Press), 2010.
  2. R. Kuriyama et al. Two-dimensional fluid viscosity measurement in microchannel flow using fluorescence polarization imaging. Meas. Sci. Technol. 2021, 32, 095402. [Google Scholar] [CrossRef]
  3. H. Wang et al. Thermal radiation elimination method for high temperature digital image correlation using polarization camera. Meas. Sci. Technol. 2021, 32, 065203. [Google Scholar] [CrossRef]
  4. Z. Zhu et al. Calibration of line-structured light vision sensors based on simultaneous polarization imaging. Meas. Sci. Technol. 2022, 33, 115202. [Google Scholar] [CrossRef]
  5. L. Xia et al. Polarized light-aided visual-inertial navigation system: global heading measurements and graph optimization-based multi-sensor fusion. Meas. Sci. Technol. 2022, 33, 055111. [Google Scholar] [CrossRef]
  6. Li, S.; Kong, F.; Xu, H.; Guo, X.; Li, H.; Ruan, Y.; Cao, S.; Guo, Y. Biomimetic Polarized Light Navigation Sensor: A Review. Sensors. 2023, 23, 5848. [Google Scholar] [CrossRef]
  7. G. Horvath. Polarized light and polarization vision in animal sciences (Springer, Berlin, Heidelberg), 2014.
  8. J. K. Jeffery, The neurobiology of spatial behaviour | | path integration in insects, (Oxford University Press, 2003), pp. 9-30.
  9. K. Cheng. K.j. jeffery (ed) the neurobiology of spatial behaviour. Animal Cogn. 2004, 7, 1. [Google Scholar]
  10. H. Uwe. Sky compass orientation in desert locusts–evidence from field and laboratory studies. Front. Behav. Neurosci. 2015, 9, 346. [Google Scholar]
  11. G. Robin, P. N. Fleischmann, G. Kornelia, et al. The role of celestial compass information in cataglyphis ants during learning walks and for neuroplasticity in the central complex and mushroom bodies. Front. Behav. Neurosci., 2017, 11, 1–14. [Google Scholar]
  12. T. L. Warren, Y. M. Giraldo, M. H. Dickinson, et al. Celestial navigation in Drosophila. J. Exp. Biol. 2019, 222, Jeb186148.
  13. B. Ronacher. Path integration in a three-dimensional world: the case of desert ants. J. Comp. Physiol., 2020, 206, 379–387. [Google Scholar] [CrossRef]
  14. G. Horváth and D. Varjú, Polarized Light in Animal Vision (Springer, Berlin, Heidelberg), 2004.
  15. S. Greif, I. Borissov, et al. A functional role of the sky’s polarization pattern for orientation in the greater mouse-eared bat. Nat. Commun. 2014, 5, 4488. [Google Scholar] [CrossRef] [PubMed]
  16. R. N. Patel and T. W. Cronin Mantis shrimp navigate home using celestial and idiothetic path integration. Curr. Biol. 2020, 30, 1981–1987. [Google Scholar] [CrossRef] [PubMed]
  17. S. B. Powell, R. Garnett, J. Marshall, et al. Bioinspired polarization vision enables underwater geolocalization. Sci. Adv. 2018, 4, eaao6841.
  18. K. D. Pham, G. Chen, T. Aycock, A. Lompado, et al. Passive optical sensing of atmospheric polarization for gps denied operations. Proc. SPIE 9838, 2016, 98380Y. [Google Scholar]
  19. D. Lambrinos, R. Moller, T. Labhart, et al. A mobile robot employing insect strategies for navigation. Robotics Auton. Syst. 2000, 30, 39–64. [Google Scholar] [CrossRef]
  20. J. Chu, K. Zhao, Z. Qiang, and T. Wang Construction and performance test of a novel polarization sensor for navigation. Sens. Actuators, A, 2008, 148, 75–82. [Google Scholar] [CrossRef]
  21. T. Ma, X. Hu, L. Zhang, et al Calibration of a polarization navigation sensor using the nsga-ii algorithm. Opt. Commun., 2016, 376, 107–114. [Google Scholar] [CrossRef]
  22. Y.Wang, J. Chu, R. Zhang, et al. A bio-inspired polarization sensor with high outdoor accuracy and central-symmetry calibration method with integrating sphere. Sensors (Basel, Switzerland), 2019, 19.
  23. J. Chahl and A. Mizutani Biomimetic attitude and orientation sensors. IEEE Sensors J. 2011, 12, 289–297. [Google Scholar]
  24. J. Dupeyroux, S. Viollet, and J. R. Serres. An ant-inspired celestial compass applied to autonomous outdoor robot navigation. Robotics Auton. Syst., 2019.
  25. J. Dupeyroux, J. Diperi, M. Boyron, S. Viollet, and J. Serres. A bio-inspired celestial compass applied to an ant-inspired robot for autonomous navigation. European Conference on Mobile Robots (ECMR), 2017.
  26. J. Dupeyroux, J. Diperi, M. Boyron, S. Viollet, and J. Serres. A novel insect-inspired optical compass sensor for a hexapod walking robot. in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017.
  27. W. Sturzl. A lightweight single-camera polarization compass with covariance estimation. in IEEE International Conference on Computer Vision (ICCV), 2017.
  28. Z. Liu, R. Zhang, Z. Wang et al Integrated polarization-dependent sensor for autonomous navigation. J. micro/nanolithography, MEMS, MOEMS. 2015, 14, 015001. [Google Scholar] [CrossRef]
  29. C. Fan, X. Hu, J. Lian et al Design and calibration of a novel camera-based bio-inspired polarization navigation sensor. IEEE Sensors J. 2016, 16, 3640–3648. [Google Scholar] [CrossRef]
  30. H. Ren, J. Yang, X. Liu et al 2020 Sensor modeling and calibration method based on extinction ratio error for camera-based polarization navigation sensor. Sensors. 2020, 20, 3779. [Google Scholar]
  31. G. Han, X. Hu, J. Lian, X. He, L. Zhang et al. Design and calibration of a novel bio-inspired pixelated polarized light compass. Sensors. 2017, 17, 2623. [Google Scholar] [CrossRef]
  32. H. Lu, K. Zhao, Z. You et al. Angle algorithm based on hough transform for imaging polarization navigation sensor. Opt. Express. 2015, 23, 7248–62. [Google Scholar] [CrossRef]
  33. J. Tang, Z. Nan, D. Li et al, Novel robust skylight compass method based on full-sky polarization imaging under harsh conditions. Opt. Express. 2016, 24, 15834. [Google Scholar] [CrossRef]
  34. Liang, H.; Bai, H.; Liu, N.; Sui, X. Polarized Skylight Compass Based on a Soft-Margin Support Vector Machine Working in Cloudy Conditions. Appl. Opt. 2020, 59, 1271. [Google Scholar] [CrossRef]
  35. H. Zhao, W. Xu et al. Polarization patterns under different sky conditions and a navigation method based on the symmetry of the aop map of skylight. Opt. Express. 2018, 26, 28589. [Google Scholar] [CrossRef]
  36. B. Jahne. Emva 1288 standard for machine vision – objective specification of vital camera data. Optik Photonik. 2010, 5, 53–54. [Google Scholar] [CrossRef]
  37. Y. Jiang et al. Monte carlo simulation of mueller matrix of randomly rough surfaces. Opt. Commun. 2020, 474, 126113. [Google Scholar] [CrossRef]
Preprints 86870 g001
Figure 1. Measurement process of the bio-inspired polarization imaging navigation sensor
Figure 1. Measurement process of the bio-inspired polarization imaging navigation sensor
Preprints 86870 g001
Preprints 86870 g002
Figure 2. Projection of polarized light from the sky (in the local coordinate system) on the imaging plane; (a) the projection of any incident light beam; (b) the projection of the incident light beam on the solar meridian.
Figure 2. Projection of polarized light from the sky (in the local coordinate system) on the imaging plane; (a) the projection of any incident light beam; (b) the projection of the incident light beam on the solar meridian.
Preprints 86870 g002
Preprints 86870 g003
Figure 3. The influence of the coordinates offset of the principal point
Figure 3. The influence of the coordinates offset of the principal point
Preprints 86870 g003
Preprints 86870 g004
Figure 4. Installation angle error of micro-polarizer array
Figure 4. Installation angle error of micro-polarizer array
Preprints 86870 g004
Preprints 86870 g005
Figure 5. Figure 5. Flow chart of the impact analysis of the measurement error model of BPINS
Figure 5. Figure 5. Flow chart of the impact analysis of the measurement error model of BPINS
Preprints 86870 g005
Preprints 86870 g006
Figure 6. Azimuth measurement results for the effect of a single factor
Figure 6. Azimuth measurement results for the effect of a single factor
Preprints 86870 g006
Preprints 86870 g007
Figure 7. Azimuth measurement errors corresponding to a single factor
Figure 7. Azimuth measurement errors corresponding to a single factor
Preprints 86870 g007
Preprints 86870 g008
Figure 8. Imaging results of coordinate offset of a principal point
Figure 8. Imaging results of coordinate offset of a principal point
Preprints 86870 g008
Preprints 86870 g009
Figure 9. Imaging results of installation angle error of a micro-polarization array
Figure 9. Imaging results of installation angle error of a micro-polarization array
Preprints 86870 g009
Preprints 86870 g010
Figure 10. Imaging results of grayscale response inconsistent of CMOS
Figure 10. Imaging results of grayscale response inconsistent of CMOS
Preprints 86870 g010
Preprints 86870 g011
Figure 11. Imaging results of a comprehensive experiment for a solar altitude angle of 5° and an azimuth angle of 20°
Figure 11. Imaging results of a comprehensive experiment for a solar altitude angle of 5° and an azimuth angle of 20°
Preprints 86870 g011
Preprints 86870 g012
Figure 12. Azimuth measurement results affected by combined factors.
Figure 12. Azimuth measurement results affected by combined factors.
Preprints 86870 g012
Table 1. Simulation parameter settings for error sources
Table 1. Simulation parameter settings for error sources
Error sources Distribution (μ, σ)
μ σ
Coordinate deviation of principal point 0 (2, 2) pixel
Installation angle error of micro-polarization array 0 0.1°
Lens attenuation 0 (0.2, 0.2)
Grayscale response inconsistency of CMOS 0 1 (DN)
Table 2. Parameter settings of BPINS
Table 2. Parameter settings of BPINS
Parameter Specific value Unit
Pixel size 3.45 x 3.45 μ m
Image resolution (1024, 1224) pixel
Focus length 8 mm
Principal point (512.5, 612.5) pixel
Table 3. Experiments results of azimuth measurements
Table 3. Experiments results of azimuth measurements
Error sources Azimuth measurement error (μ, σ)
μ σ
Coordinate deviation of principal point -0.0237 0.2476
Installation angle error of micro-polarization array 0.0018 0.0812
Grayscale response inconsistency of CMOS 0.0059 0.0405
Lens attenuation 0.0 0.0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated