Prerpints.org logo
Preprint
Article

Uncovering the Impact of Working from Home on Employees’ Collaboration, Happiness, and Promotion Chances Using Machine Learning

Altmetrics

Downloads

199

Views

234

Comments

0

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

30 September 2023

Posted:

01 October 2023

You are already at the latest version

Alerts
Abstract
This research explores the impact of working from home on employees' happiness, collaboration, and promotion prospects using machine learning techniques. The study is guided by three research questions aiming to investigate the correlation between working from home and employees' collaboration and promotion prospects. Moreover, the research aims to find a relationship between the number of households and employees' happiness levels while working from home. The data is collected from ICT engineers working at a technology company in Sweden through a questionnaire-based survey. Probability sampling was selected for data collection to reduce bias and enhance the generalizability of the findings. The data is pre-processed and then analysed in Jupyter Notebook using the Python programming language. Various libraries and models, including Pandas, NumPy, Matplotlib, Seaborn, and Scikit-learn, were employed for data analysis. Both Pearson correlation and p-values in Pearson correlation were used in this study to analyse the relationships between different variables.However, based on the results, this study did not find any significant relationship between working from home and employees' promotion prospects or collaboration issues. Additionally, the results did not provide evidence of a significant relationship between the number of households of employees and their happiness levels while working from home.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The pandemic of COVID-19 has caused a significant rise in the number of people working from home (WFH), with WFH participation levels increasing substantially since March 2020 (Raišiene et al., 2020; Vyas & Butakhieo, 2020; Oakman et al., 2020). Businesses and policymakers have actively supported telecommuting as a way to prevent the spread of COVID-19 (International Labour Organization, 2020; Hashim et al., 2020; Jamal et al., 2021).

1.1. Background

While working remotely has been popular in organizations with advancements in information and communication technology, prior to the pandemic, there was already a significant increase in remote work (Hering, 2020). Although working from home has its benefits, such as increased temporal flexibility, autonomy, and productivity, scholars have also noted potential threats to employee well-being, such as physical and temporal separation, social isolation, and blurred work-home boundaries (Dimitrova, 2003; Golden et al., 2008; Grant et al., 2013).
Despite this, research has shown that both local worksites and teleworkers can experience increased performance and decreased absenteeism when offered alternatives to the current work environment, and key factors such as comfortable workplaces, trust in superiors, and positive work relationships with colleagues can contribute to this (Timsal & Awais, 2016; Anderson & Kelliher, 2020). In Sweden, the pandemic lockdown required all employees to work remotely, and this study aims to investigate the viability of continuing remote work initiatives by assessing work satisfaction, performance, and productivity levels in the ICT industry (Baker, Avery, & Crawford, 2007).

1.2. Research Problem

Due to the COVID-19 pandemic, many employees have been required to work from their homes, which has raised concerns about maintaining their job performance and job satisfaction in this uncertain situation. Therefore, there is an urgent need for research that identifies effective approaches and interventions to support remote workers during the COVID-19 era. This will assist both practitioners and scholars in better understanding how to assist remote workers. Workers can feel that WFH makes a positive impact on their work-life balance and consequently helps to minimise workplace costs.
When WFH, employees can feel that they have to prolong the working day or put in extra time to do their personal jobs, which could decrease job satisfaction. This is an example of when a considerable portion of WFH employees are likely to suffer from negative outcomes such as work-family conflicts and health issues (Sahni, 2020; Bernarto et al., 2020). Recent research shows that many factors can influence both performance and motivation. Identifying the correlations between these factors is the main goal of this research.
As a result of the lockdown, the internet has become the primary mode of communication for most people. Consequently, there is a question about whether employees should be allowed to work from home after the lockdown. Online transactions have increased substantially due to employees’ teleworking or remote work situations, as demonstrated in some developed countries, where public sector or government employees have been teleworking for years due to the perceived benefits (Kwon & Jeon, 2020). However, it is unknown whether the perceived benefits extend to developing countries’ employees during the lockdown. Regardless, job satisfaction is critical for both employees and administrators of the organization. Thus, this study’s goal is to provide empirical evidence on the feasibility of remote work for an ICT company in Sweden.
Several research investigated the relationship between working from home, job performance, and happiness. For example, the relationship between the number of households and employees’ job satisfaction while working remotely was investigated by Sridhar and Bhattacharya (Sridhar & Bhattacharya, 2021), but the authors did not investigate the impacts of the number of households on employees’ happiness. For another example, authors (Van Der Lippe & Lippényi, 2020) investigated the impact of working from home on a team’s performance, and authors (Song & Gao, 2020) investigated the impact of working from home on employees’ salary. However, no prior research investigated the impact of working from home on employees’ collaboration and chance of promotion.

1.3. Aim and Research Question

This study aims to investigate the correlation between working from home and employees’ collaboration and promotion chances. Moreover, the study aims to find a relation between the number of households and the level of employees’ happiness while they work from home for ICT engineers employed at a technology company based in Sweden. To achieve these objectives, the study was guided by the following research questions:
  • Is there any correlation between working from home and employees’ collaboration?
  • Is there any correlation between the number of households of employees and employees’ happiness while working from home?
  • Is there any correlation between working from home and employees’ promotion chances while working from home?

1.4. Delimitations of the Study

This study is limited to examining the impact of WFH on employee satisfaction and happiness. Due to time and resource constraints, a comprehensive and in-depth investigation is not feasible. To narrow the scope of the study population, only engineers from the ICT department of the company are included in this study. The study aims to identify the factors that contribute to collaboration between WFH and employee satisfaction, using a quantitative approach.
Moreover, the study will only investigate the impact of WFH on employee performance and happiness in Sweden. The decision to limit the study to Sweden was based on the accessibility of the company engineers in Sweden and the availability of a reasonable empirical base to analyse and draw conclusions. Additionally, the ability to reach the company engineers in Sweden via email and Slack further justifies this geographical delimitation.

1.5. Hypothesis

The pandemic of COVID-19 has led to a significant increase in remote work, and there is a need to understand the impact of WFH on employee productivity and job satisfaction. This study presents two hypotheses that aim to examine the relationship between WFH and employee outcomes. The hypotheses are as follows:
Hypothesis 1:
Working from home has an impact on collaboration.
    H0: There is no significant correlation between working from home and collaboration.
    H1: There is a significant correlation between working from home and collaboration.
Hypothesis 2:
The number of households of employees has an impact on employees’ happiness while WFH.
    H0: There is no significant correlation between the number of households of employees and Employees’ happiness.
    H1: There is a significant correlation between the number of households of employees and Employees’ happiness.
Hypothesis 3:
Working from home has an impact on employees’ promotion chances while WFH.
    H0: There is no significant correlation between working from home and employees’ promotion chances.
    H1: There is a significant correlation between working from home and employees’ promotion chances.
Understanding these relationships will help organizations develop effective WFH policies and practices that balance productivity and employee well-being.

2. Method

2.1. Research Strategy

Denscombe (2014) outlines several research strategies that can be employed to conduct successful research, including case studies, grounded theory, surveys, and action research. The selection of an appropriate research strategy depends on various factors, such as the research aim, ethical considerations, and feasibility in light of constraints (Denscombe, 2014).
Although the case study approach is suitable for small-scale, in-depth studies that aim to explain why specific outcomes might occur (Denscombe, 2014), it was not considered for the present study as the research aim is to describe how certain factors influence the population on a broader scale quantitatively.
Similarly, grounded theory, which involves generating theories from participants’ experiences and is reliant on qualitative data, was also rejected due to the uncertainty in planning the project’s duration and the aim of the present study to capture quantitative data (Denscombe, 2014).
Action research, which is typically employed in real-world settings to investigate practical problems and generate possibilities for change, was not deemed suitable for answering the research question or fulfilling the purpose of the study (Denscombe, 2014).
Ethnography, which investigates individual cultures or social relations (Denscombe, 2014), and phenomenology, which is concerned with interpretation rather than measurement (Denscombe, 2014), were also ruled out as they do not align with the research aim. After considering the various options, a survey was deemed the best fitting strategy for this study.

2.2. Data Collection Method

The present study collected individual data from engineers in a Swedish ICT company to investigate the research questions. A web-based questionnaire designed on Google Form was used as the instrument to collect primary data. This method was deemed the most suitable for the study due to its cost-effective distribution and the ability to reach respondents regardless of their location.
According to Denscombe (2014), web-based questionnaires are ideal for research projects with limited resources and enable the collection of standardized data from participants electronically, thereby facilitating quantitative analysis and hypothesis testing, which is necessary to investigate the research question. The questionnaire allowed for the calculation of descriptive and correlational analyses for all variables used in the study.
Alternative data collection approaches, such as interviews and face-to-face surveys, were considered but ultimately deemed unsuitable for the research question. Interviews were rejected due to their resource-intensive nature, and Denscombe (2014) notes that they are better suited for studies requiring in-depth insights about specific topics or phenomena. Face-to-face surveys were also deemed impractical due to the time and scheduling required to conduct them successfully. The use of web-based questionnaires was preferred due to their ease of distribution and the ability to reach respondents regardless of location or time constraints, allowing for a higher response rate and more successful data collection.
Several questions are used in the questionnaire and some of them are inspired by the research, which is done by Sridhar and Bhattacharya (Sridhar & Bhattacharya, 2021). Due to the fact that a significant number of engineers in the company operate in a hybrid capacity and often work remotely, as well as being located in various offices, including Stockholm, Gothenburg, and Lund, it was determined that conducting a web-based survey would be the most efficient method of communication. The engineers were contacted via the company’s Slack channel and provided with a link to an online questionnaire. The resulting dataset includes responses from 67 employees, of which 59.7% were male and 40.3% were female, and the average range of participants is 47.9 (SD = 9.32), from 28 to 64 years old.

2.3. Sampling

Probability sampling and convenience sampling are two widely used methods of selecting participants for research studies. Probability sampling refers to the selection of some samples from a population in which every one of the members has the same probability of being chosen (Babbie, 2016). This method of sampling helps to reduce bias and increase the generalizability of the findings. According to Bryman (2016), there are different methods for achieving probability sampling, including systematic sampling, simple random sampling, stratified sampling, and cluster sampling.
In contrast, the convenience sampling technique is a non-probability sampling technique that involves choosing members based on accessibility and availability (Creswell, 2013). Researchers often use this method when time and resources are limited or when the population under study is difficult to access. Convenience sampling is often prone to selection bias and may lead to results that are not generalizable to the larger population (Suresh, 2011). This method is often used in research studies due to its practicality and low cost.
However, there are some potential drawbacks to using convenience sampling. One of the main issues is selection bias, which means that the sample of participants may not be representative of the larger population being studied. This can occur because the participants in the sample may not be a random selection and may have certain characteristics that differ from those in the larger population.
As a result, the conclusions drawn from a convenience sample may not be generalizable to the larger population, and the findings may not accurately reflect what would be observed if the entire population were studied. Therefore, researchers should be cautious when using convenience sampling and consider other sampling methods that are more likely to produce representative samples.
The difference between probability sampling and convenience sampling is that probability sampling involves the use of random selection techniques to ensure that every population member has an equal probability of being chosen. In contrast, convenience sampling relies on the ease of access to potential participants, and researchers have little control over who is selected (Neuman 2013; Bryman, 2016). As a result, probability sampling is often preferred when a representative sample is necessary, while convenience sampling may be more practical when the study is exploratory or when the population under study is difficult to access (Suresh, 2011).
Both probability sampling and convenience sampling are useful methods of selecting participants for research studies. Probability sampling provides a more rigorous and representative sample, while convenience sampling may be more practical when time and resources are limited. However, researchers need to be aware of the potential biases associated with convenience sampling and adjust their study design accordingly.
For this study, based on all the above explanations, probability sampling was chosen for collecting data to reduce bias and increase the generalizability of the findings. In addition, based on the research questions, the target audience for the survey was engineers who work in the IT section. The reason for selecting IT engineers is that the study aims to find out the correlation between working from home and collaboration and promotion chances and working from home is much more popular in the section of IT, compared to other sections such as factory workers.
Moreover, the study aims to investigate the relationship between the number of households and employees’ happiness while working from home. To have better and more precise insights, the target audience for the survey was people in different age groups, ranging from 28 to 64 years old.

2.4. Data Analysis Method

Several different variables in this study using a five-point Likert scale ranging from 1 (strongly negative/disagree) to 5 (strongly positive/agree), including collaboration problems, reduced promotion chance, the impact of WFH on the employer, feeling left out, Feeling better with WFH, Feeling more active with WFH. In this study, all analyses were conducted with Python programming language in the Jupyter Notebook environment using NumPy, Pandas, Matplotlib, Seaborn, and Scikit-learn. Both Pearson correlation and p-values in Pearson correlation were used in this study to analyse the correlation between different variables. The type of data collected in this study was either integer or string. In this study, the categorical string variables are converted to numeric variables using Pandas get_dummies() method in Python (Cerda, Varoquaux and Kégl, 2018; Sahoo et al., 2019). Pearson’s coefficients and P-values are used to investigate the research questions in this study. Similarly, Al Jassmi et al. (2019) examined the correlation between the level of happiness exhibited by construction workers and their productivity. This investigation involved the utilization of statistical measures such as p-values and Pearson’s coefficients.

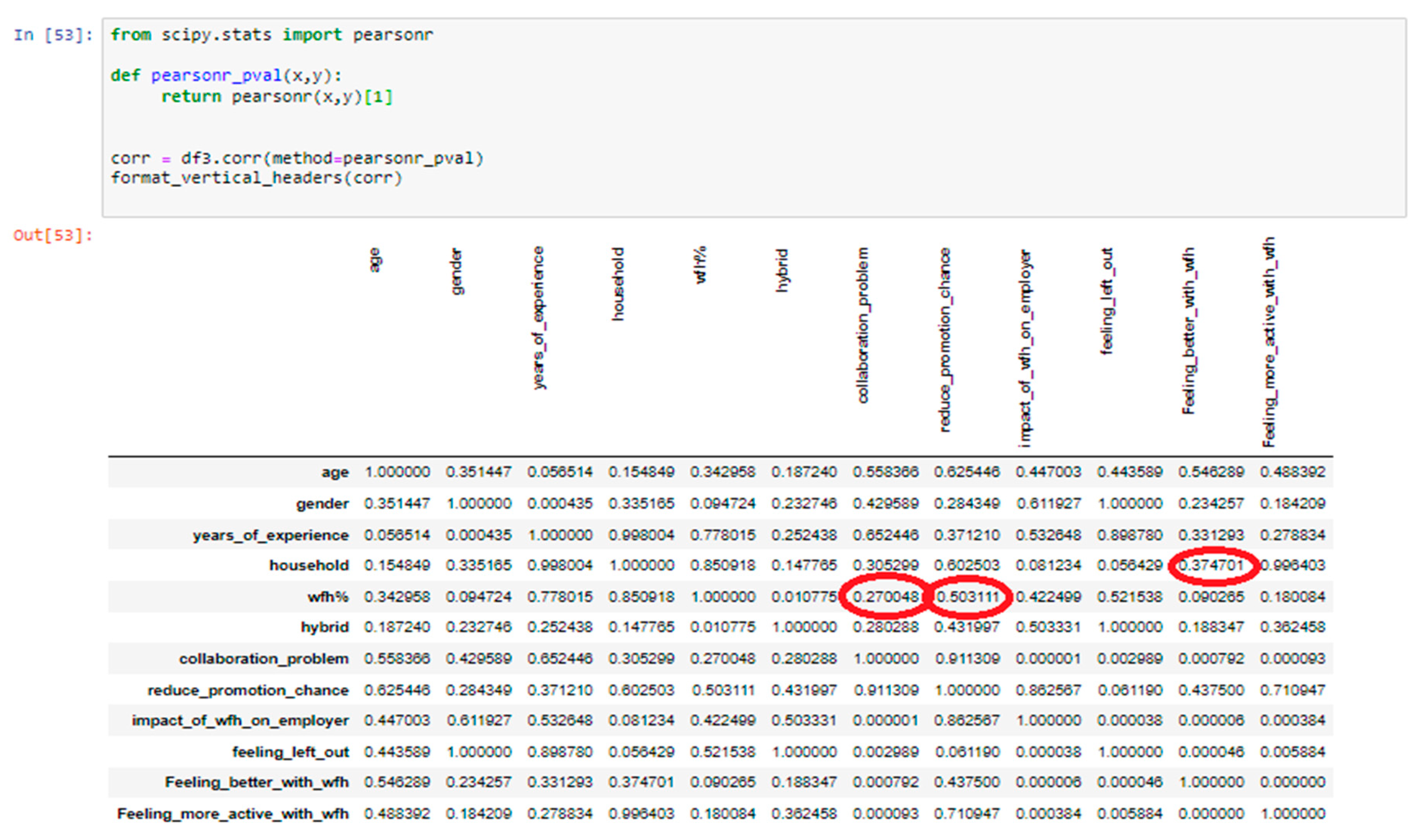
2.4.1. Pearson Correlation

Pearson correlation is one of the statistical tools that we use to evaluate both the magnitude and the direction of the linear relationship between two quantitative variables. It computes a correlation coefficient (r) that varies between -1 and +1, where values closer to -1 indicate a robust negative correlation, values closer to +1 indicate a strong positive correlation, and values near zero signify negligible correlation. This technique is widely used in research fields such as medicine, psychology, and business, among others.
According to Field (2013), Pearson correlation is “one of the most frequently used statistical techniques in data analysis” (p. 33). Pearson correlation is useful for exploring relationships between variables and can help researchers identify patterns and trends that might not be immediately obvious. In addition, Pearson correlation can be used to make predictions about the value of one variable based on the value of another variable. However, it is worth mentioning that correlation does not imply causation and additional research is often necessary to establish causal relationships between variables. Overall, Pearson correlation is a valuable tool for researchers who seek to better understand the relationships between different variables in their data.

2.4.2. P-values

The p-value in Pearson correlation is an important measure of statistical significance that helps researchers determine the probability of observing a correlation coefficient between two variables due to chance. According to Sullivan and Artino (2013), “a p-value less than .05 is generally considered statistically significant” (p. 53). For example, in a study examining the relationship between performance and WFH, a Pearson correlation coefficient equal to 0.65 with a p-value equal to 0.025 would indicate a significant positive correlation between the two variables. This would suggest that participants who work from home are more likely to achieve better performance. On the other hand, a Pearson correlation coefficient equal to 0.35 with a p-value equal to 0.35 would suggest that the observed correlation is not statistically significant, and any relationship between the two variables is probably accidental. Therefore, understanding the p-value in Pearson correlation is crucial for making informed decisions about the relationship between different variables.

2.5. Research Ethics

Research ethics are principles and guidelines that govern the conduct of research to ensure that it is conducted in a responsible and ethical manner. Ethics in research involves ensuring the protection of human subjects, animal welfare, and the integrity of the research process (Denscombe, 2014). Researchers are expected to adhere to ethical standards and regulations to ensure that their research is conducted with integrity, transparency, and accountability.
The use of human subjects in research, in particular, requires researchers to obtain informed consent from participants, protect their confidentiality and privacy, and ensure that their rights and welfare are respected (American Psychological Association, 2017). Ethical considerations in research also extend to the dissemination of research findings, which should be accurate and transparent, and avoid misleading or biased reporting (Fisher et al., 2017).
Research ethics play a critical role in ensuring that research is conducted in a responsible and ethical manner. Adherence to ethical principles and guidelines is essential for protecting the rights and welfare of human subjects, maintaining the integrity of the research process, and promoting transparency and accountability in research. In this study, all the participants were informed about the purpose, the procedure, and the confidentiality of the survey. The informed consent form can be found in Appendix A.

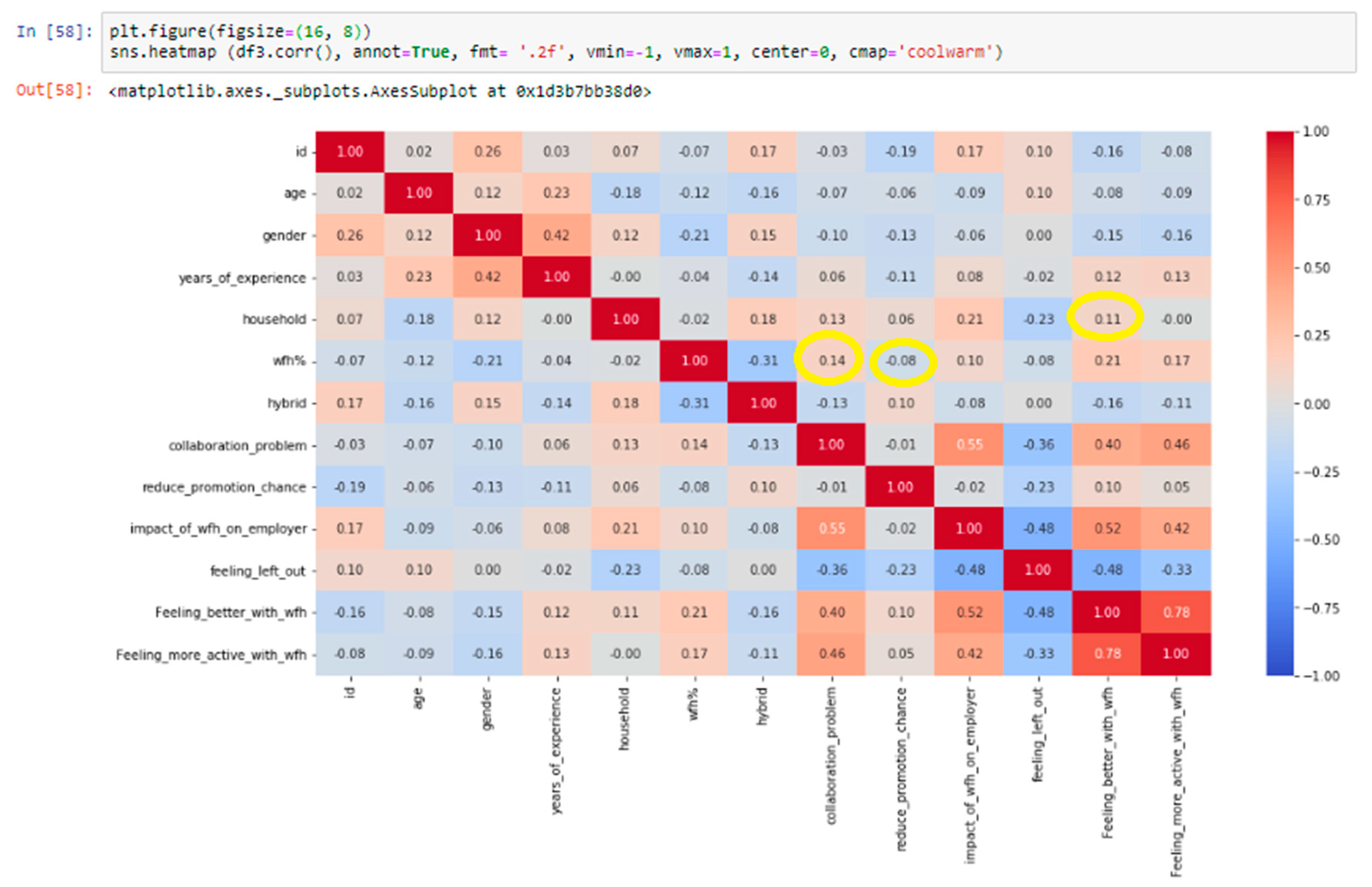
3. Results

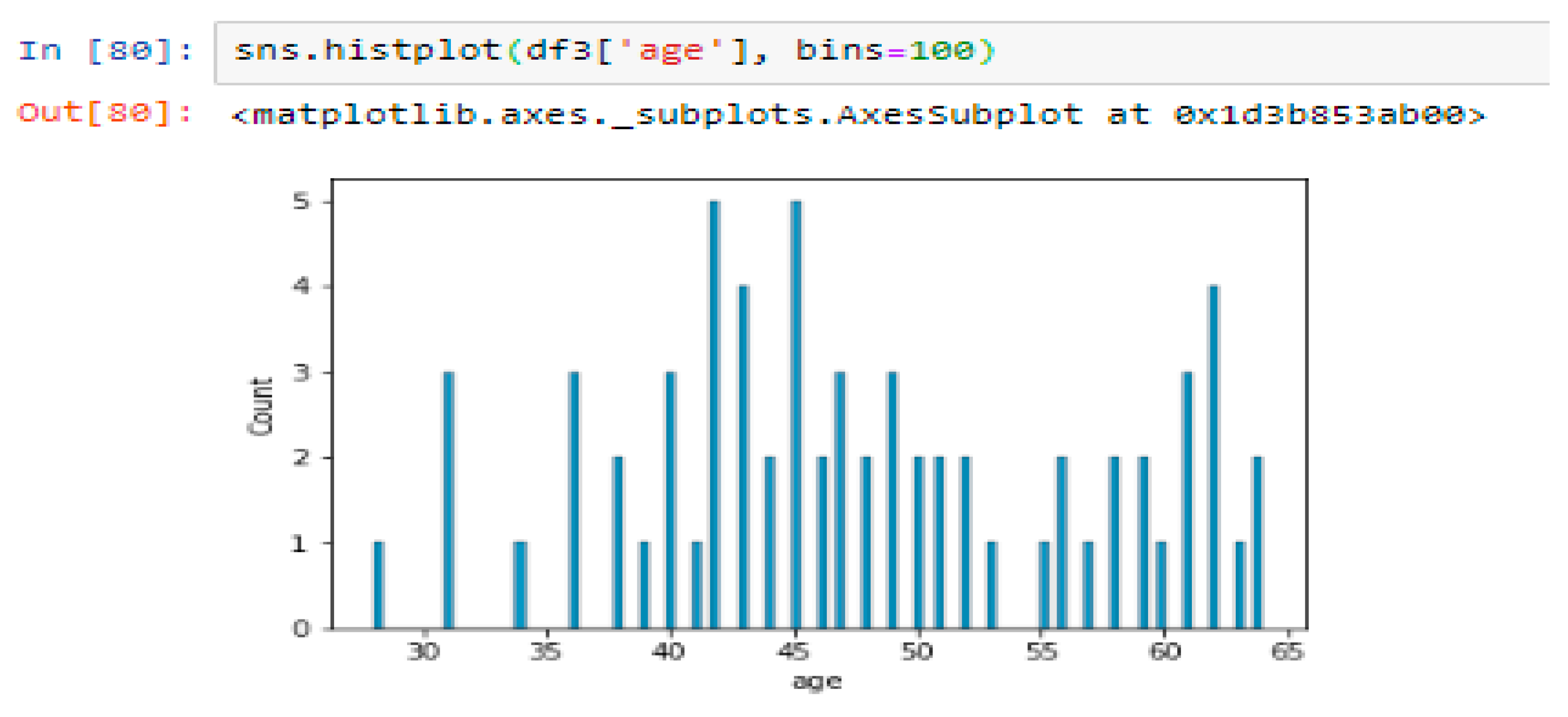
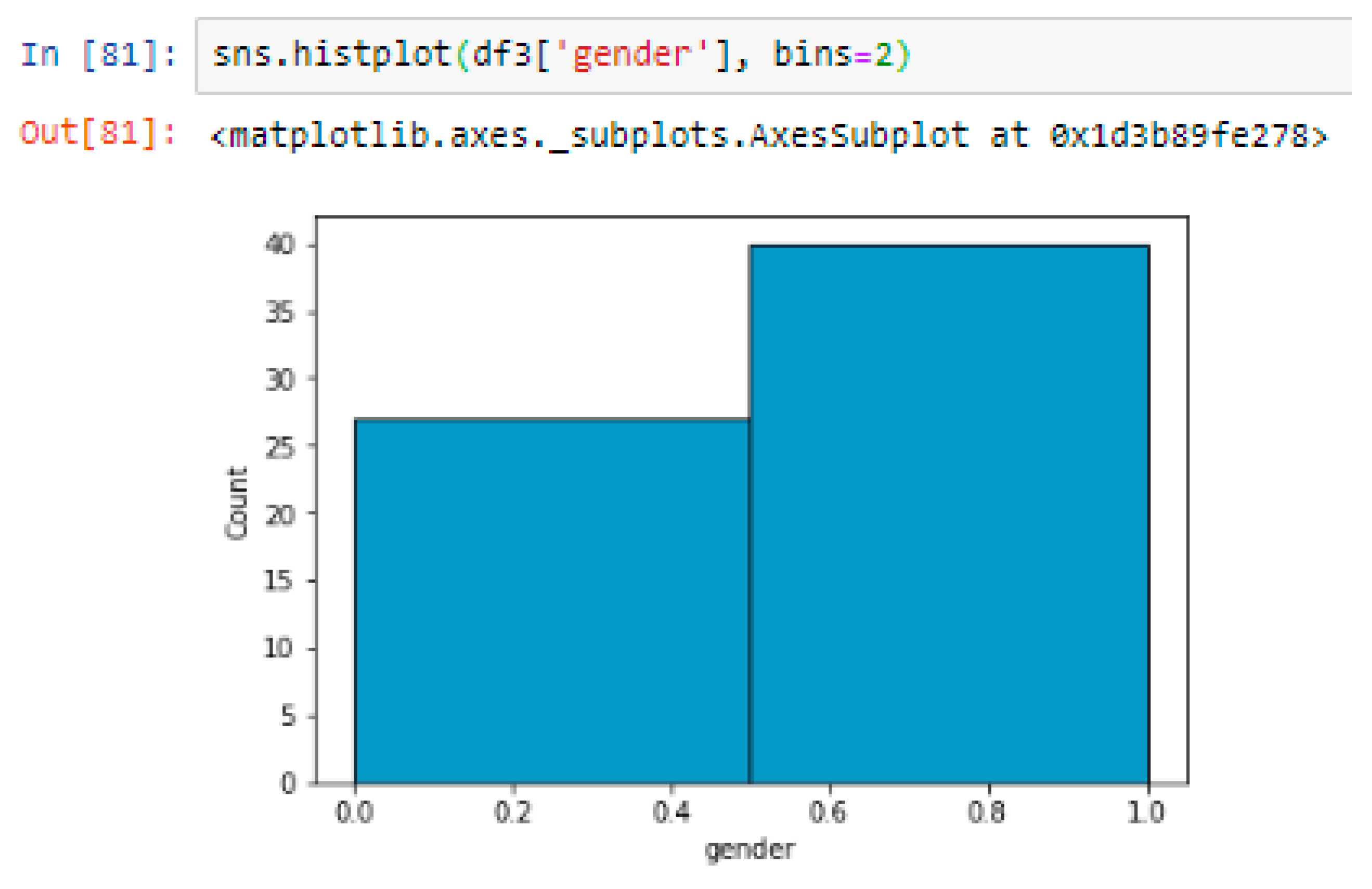
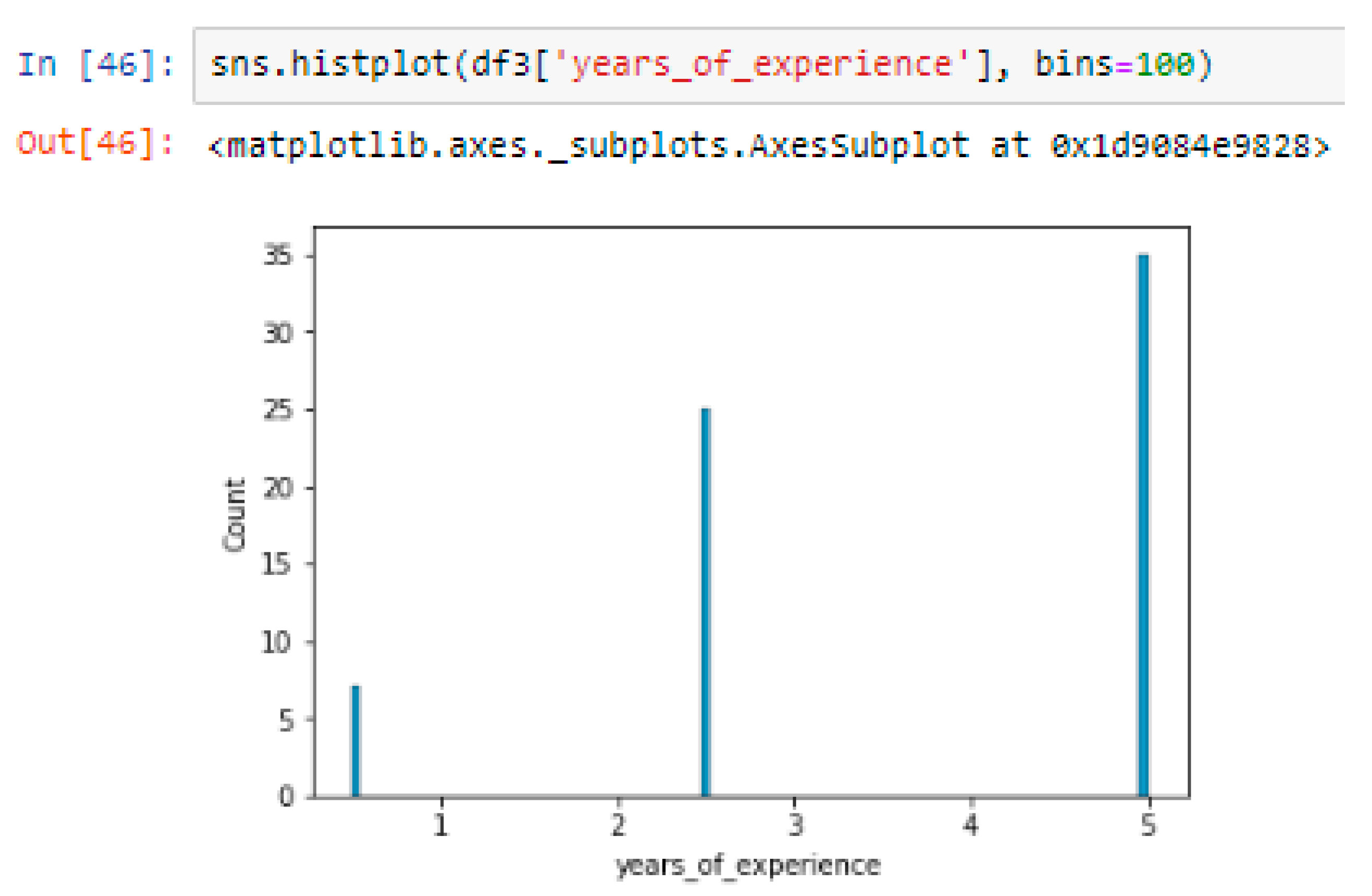
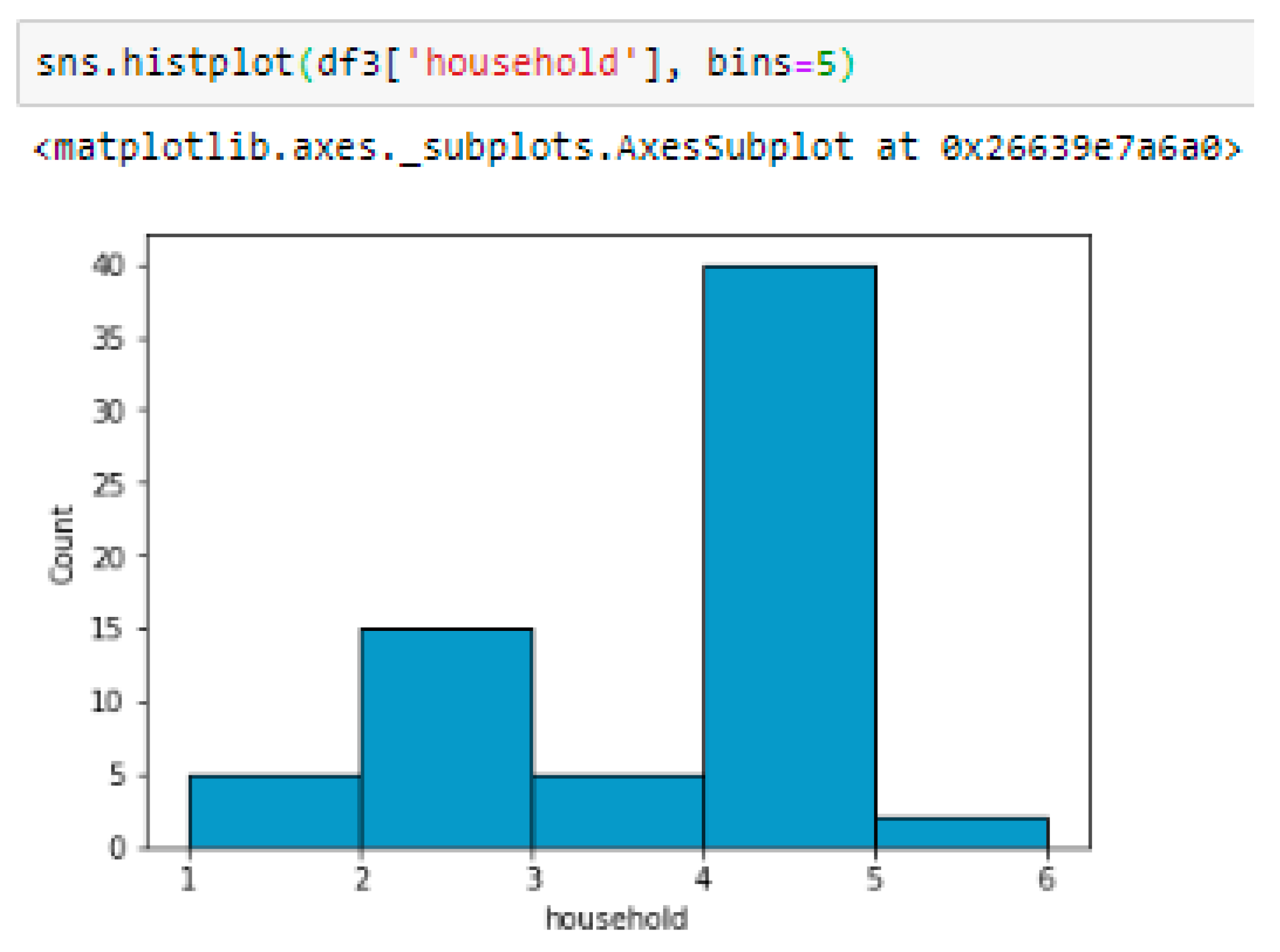
3.1. Data Collection and Analysis

The questionnaire was designed to include 12 factor-related questions, with all questions and associated references provided in Appendix B. The survey was available for participants to complete for one month in February 2023, with the survey link distributed via email and a Slack channel. Participants’ responses were automatically collected and stored in a spreadsheet for later analysis. Prior to analysis, data pre-processing steps were performed in Jupyter Notebook to ensure that all data were complete and free of errors. The questionnaire was structured in a closed-answer format, requiring participants to provide numerical (integer) or text (string) responses for each question. In this study, a pre-processing phase is used to prepare the data for analysis. The pre-processing phase includes the following steps:
Data Cleaning: This step includes several tasks such as handling missing values, handling duplicates, and finding and correcting typos. For handling missing values, there are several methods that can be used depending on the concepts and variables including 1- Dropping missing values which remove all the rows and columns that contain missing values using dropna() method from Pandas library. 2- Replacing missing values which replace the missing values with the mean, median, or mode of the values of the variables using fillna() method from Pandas library. 3- Interpolation which estimates the missing values based on other variables’ values using interpolate() method from Pandas library. 4- Imputation which predicts the missing values using some machine learning techniques such as Random Forest, Support Vector Machines (SVM), and K-Nearest Neighbors (KNN). All these algorithms are available in scikit-learn library for Python. In this study, based on the concept and needs, replacing missing values using fillna() method in Pandas library is used to handle the missing values. In this study, we employed the identical methodology as in our prior research (Imani & Arabnia, 2023).
Handling outliers: For handling outliers, we wrote the below function that uses the Interquartile Range (IQR) method to remove outliers from a dataset. The IQR is a measure of the spread of the data, defined as the difference between the third quartile (Q3) and the first quartile (Q1).
#function for removing outliers
def remove_outliers(train,labels):
     for label in labels:
          q1 = train[label].quantile(0.25)
          q3 = train[label].quantile(0.75)
          iqr = q3 - q1
          upper_bound = q3 + 1.5 * iqr
          lower_bound = q1 - 1.5 * iqr
          train[label] = train[label].mask(train[label]< lower_bound, train[label].median(),axis=0)
          train[label] = train[label].mask(train[label]> upper_bound, train[label].median(),axis=0)
 
     return train
The function first calculates the IQR for each label (i.e., column) in the dataset by using the quantile() method to find the 25th and 75th percentiles. Next, the function identifies outliers by finding values that are more than 1.5 times the IQR away from the upper or lower quartiles. These are considered extreme values that are unlikely to be representative of the underlying population and are typically removed. To remove the outliers, the function replaces values that are less than the lower bound with the median value of the column and values that are greater than the upper bound with the median value of the column. This is done using the mask() method, which replaces values in the specified range with the median value of the column. By using the IQR method to identify and remove outliers, this function provides a quick and simple way to clean datasets and improve the accuracy of statistical analyses.
Data Integration: This step aims to form a unified dataset from different sources using several tasks such as handling inconsistent data structures, handling data format differences, and handling naming conflicts. This study did not use this step as all the data were collected in a single source using a web-based survey.
Data Transformation: This step aims to convert the type of data into a suitable format for analysis. As mentioned earlier, in this study, the categorical string variables are converted to numeric variables using Pandas get_dummies() method in Python (Cerda, Varoquaux and Kégl, 2018; Sahoo et al., 2019) which is more suitable for quantitative analysis.
Data Reduction: This step includes several tasks to reduce the amount of data by removing noisy data, irrelevant data, and redundant data. To achieve this goal several dimensionality reduction techniques such as feature selection and principal component analysis (PCA) can be used. As all the questions in the survey were designed based on the specific purpose, there were no noisy and irrelevant data and therefore this study did not need to use this step for reducing the data.
Data Discretization: This step includes converting continuous data into discrete categories using some techniques such as binning, equal-width binning, and equal-frequency binning. This study used binning technique to form discrete categories for three variables such as year of experience, age, and the number of households.
Linearity check: This step refers to the relationship between two variables being analysed. Specifically, it refers to whether the relationship between the variables is a straight line or whether it exhibits a curved pattern. When conducting a Pearson correlation analysis, it is important to check for linearity to ensure that the relationship between the variables is accurately captured. A scatterplot can be used to visualize the relationship between two variables. If the points on the scatterplot form a straight line, then the relationship between the variables is linear. Figure 1, Figure 2 and Figure 3 show the scatter plot between the variables.
Normality check: This step refers to whether the data being analysed follows a normal distribution or bell curve. In the context of a Pearson correlation analysis, it is important to check for normality to ensure that the data being analysed is appropriate for the analysis. A histogram can be used to check for normality. In a histogram, the frequency distribution of the data is displayed as bars. If the bars form a bell-shaped curve, then the data follows a normal distribution.
Homoscedasticity check: This step refers to whether the variability of the data is consistent across all levels of the variables being analysed. When conducting a Pearson correlation analysis, it is important to check for homoscedasticity to ensure that the results accurately reflect the relationship between the variables being analysed. A scatterplot can be used to check for homoscedasticity. If the variability of the data is consistent across all levels of the variables being analysed, then the scatterplot will show the points evenly scattered around the line of best fit. Alternatively, a residual plot can be used to check for homoscedasticity. In a residual plot, the residuals are plotted against the predicted values. If the points on the residual plot are evenly scattered around the horizontal line at zero, then the data is homoscedastic. As we do not aim to predict a variable based on other variables in the dataset, then calculating the residuals using the best-fit line is not the case in our study.
In summary, to conduct a Pearson correlation analysis, it is important to check for linearity, normality, and homoscedasticity to ensure that the relationship between the variables is accurately captured and the results are reliable.

3.2. Findings

Figure 4, describes the statistics of the variables used in this study. This table contains statistics for a sample of 67 individuals who participated in the survey and answered several questions focusing on various aspects of working from home (WFH) and their experience with it. The variables included in the table are id (identification number), age, gender (0=Female, 1=Male), years of experience, household (number of people living in their household), WFH% (percentage of time spent working from home), hybrid (whether they work in a hybrid model or not), collaboration problem (how often they face problems collaborating with colleagues while WFH), reduce promotion chance (how much WFH reduces their chances of promotion), impact of WFH on employer (how much WFH impacts their employer), feeling left out (how often they feel left out while WFH), feeling better with WFH (how much they feel better while WFH), and feeling more active with WFH (how much they feel more active while WFH).
The “count” row shows that there were 67 individuals surveyed for each variable. The “mean” row shows the average value for each variable across the sample. The “std” row shows the standard deviation of the values for each variable, indicating how much variation there is within the sample. The “min” and “max” rows show the minimum and maximum values for each variable in the sample. Finally, the “25%”, “50%”, and “75%” rows show the quartiles for each variable, which can be used to determine the range and distribution of values for each variable.
Based on the below figure, the average age of participants is 47.9, ranging from 28 to 64 with a standard deviation of 9.32.
There are several useful and insightful diagrams that can be created based on the above table. Here are some examples:
Histogram of Age Distribution:
Figure 5 shows the distribution of ages of the participants. The x-axis represents age, and the y-axis represents the frequency of individuals at each age. This can help us understand the age range of the participants and identify any patterns or trends.
Histogram of Gender Distribution:
Figure 6 shows the distribution of genders of the participants. The x-axis represents gender, and the y-axis represents the number of participants of each gender. This can help us understand the gender range of the participants and identify any patterns or trends.
Histogram of years of experience distribution:
Figure 7 shows the distribution of years of experience of the participants. The x-axis represents the number of years of experience, and the y-axis represents the number of participants. This can help us understand the experience range of the participants and identify any patterns or trends. Figure 8 shows the distribution of the number of households of the participants. The x-axis represents the number of households, and the y-axis represents the number of participants. This can help us understand the number of households of the participants.
Figure 9 shows that the correlations between the variables in the study are generally weak. As the figure shows, a correlation coefficient of 0.14 suggests a weak positive correlation between working from home and collaboration problems, meaning that as the frequency of working from home increases, the collaboration problem also slightly increases. Similarly, a correlation coefficient of -0.08 suggests a weak negative correlation between working from home and reducing the chance of promotion, meaning that as the frequency of working from home increases, the chance of promotion slightly decreases. Finally, a correlation coefficient of 0.11 suggests a weak positive correlation between the number of households and the happiness of the employees while working from home, meaning that as the number of households increases, the happiness of the employees while working from home also slightly increases. It is important to note that while these correlations are statistically significant; the strength of the correlations is weak, indicating that the relationship between the variables is not very strong.

3.3. Hypotheses Analysis:

Figure 10 shows the p-values of the different variables.
Hypothesis 1:
The null hypothesis (H0) states that there is no correlation between working from home and collaboration, while the alternative hypothesis (H1) states that there is a correlation. The p-value for this hypothesis is 0.27.
If the significance level (α) is set to 0.05, this means that we would reject the null hypothesis if the p-value is less than 0.05, and fail to reject it if the p-value is greater than or equal to 0.05.
Since the p-value for this hypothesis is greater than α (0.27 > 0.05), we fail to reject the null hypothesis. Therefore, we cannot conclude that there is a significant correlation between working from home and collaboration.
Hypothesis 2:
The null hypothesis (H0) states that there is no correlation between the number of households of employees and employees’ happiness while WFH, while the alternative hypothesis (H1) states that there is a correlation. The p-value for this hypothesis is 0.374.
Again, if we set α to 0.05, we would reject the null hypothesis if the p-value is less than 0.05, and fail to reject it if the p-value is greater than or equal to 0.05.
Since the p-value for this hypothesis is greater than α (0.374 > 0.05), we fail to reject the null hypothesis. Therefore, we cannot conclude that there is a significant correlation between the number of households of employees and employees’ happiness while WFH.
Hypothesis 3:
The null hypothesis (H0) states that there is no correlation between working from home and employees’ promotion chance, while the alternative hypothesis (H1) states that there is a correlation. The p-value for this hypothesis is 0.503.
Once again, if we set α to 0.05, we would reject the null hypothesis if the p-value is less than 0.05, and fail to reject it if the p-value is greater than or equal to 0.05.
Since the p-value for this hypothesis is greater than α (0.503 > 0.05), we fail to reject the null hypothesis. Therefore, we cannot conclude that there is a significant correlation between working from home and employees’ promotion chances while WFH.
In conclusion, all three hypotheses failed to provide evidence to reject their respective null hypotheses. Therefore, we cannot conclude that there is a significant correlation between working from home and collaboration, employees’ happiness while WFH, and employees’ promotion chances while WFH, respectively.

4. Discussion

4.1. Analysis of the Results

The aim of this study was to find out 1- Is there any correlation between working from home and employees’ collaboration?, 2- Is there any correlation between the number of households of employees and employees’ happiness while working from home?, and 3- Is there any correlation between working from home and employees’ promotion chances while working from home?.
After analysing the data as explained above, the results and findings of this study to answer the above-mentioned questions are summarized as follows:
To answer question 1 “Is there any correlation between working from home and employees’ collaboration?” the study analysed the Pearson correlation coefficient and P-Values between the variable “working from home” and the variable “collaboration problem”. The correlation coefficient of 0.14 suggests a weak positive correlation between “working from home” and “collaboration problem”, meaning that as the frequency of working from home increases, the collaboration problem also slightly increases. In addition, the p-value between “working from home” and “collaboration problem” is 0.27 and the p-value is greater than α (0.27 > 0.05). Therefore, we cannot conclude that there is a significant correlation between working from home and collaboration.
To answer question 2 “Is there any correlation between the number of households of employees and employees’ happiness while working from home?” the study analysed the Pearson correlation coefficient and P-Values between the variable “the number of households of employees” and the variable “employees’ happiness while working from home”. The correlation coefficient of 0.11 suggests a weak positive correlation between “the number of households of employees” and “employees’ happiness while working from home”, meaning that as the number of households of employees increases, the employees’ happiness while working from home also slightly increases. In addition, the p-value between “the number of households of employees” and “employees’ happiness while working from home” is 0.374 and the p-value is greater than α (0.374 > 0.05). Therefore, we cannot conclude that there is a significant correlation between the number of households of employees and employees’ happiness while working from home.
To answer question 3 “Is there any correlation between working from home and employees’ promotion chances while working from home?” the study analysed the Pearson correlation coefficient and P-Values between the variable “working from home” and the variable “reducing the chance of promotion’. The correlation coefficient of -0.08 suggests a weak negative correlation between “working from home” and “reducing the chance of promotion”, meaning that as the frequency of working from home increases, the reducing the chance of promotion slightly decreases. In addition, the p-value between “working from home” and “reducing the chance of promotion” is 0.503 and the p-value is greater than α (0.503 > 0.05). Therefore, we cannot conclude that there is a significant correlation between working from home and reducing the chance of promotion.

4.2. Future Research

The study encountered a number of limitations, such as a small participant pool and a homogeneous group of engineers from the same company and field, which could potentially introduce bias into the results.
Future research in this area could focus on addressing the limitations identified in this study. One approach could be to conduct a larger-scale study that includes a more diverse sample of participants from different industries and domains to investigate whether the results are consistent across different populations. Additionally, future studies could also explore whether the findings of this study generalize to other types of professionals or individuals who have different levels of expertise in the same domain.
Another direction for future research could be to investigate the potential sources of bias in this study and to explore methods to mitigate these biases. For example, researchers could use different sampling methods to recruit participants from different companies or industries, or use a multi-method approach to data collection, such as combining self-report measures with behavioural or physiological measures, to provide a more comprehensive assessment of the participants’ attitudes or behaviours.

4.3. Conclusion

This study examines the viability of continuing remote work initiatives by assessing work satisfaction, performance, and productivity levels in the ICT industry in Sweden. The COVID-19 pandemic has led to a significant increase in remote work, which has raised concerns about maintaining employees’ job satisfaction and performance. The study aims to identify effective approaches and interventions to support remote workers determine the level of job satisfaction among the engineers and identify the pertinent performance indicators for their work.
In this study, three questions were developed to examine 1- the relationship between working from home and collaboration problems, 2- the relationship between the number of households of employees and employees’ happiness while working from home, and 3- the relation between working from home and employees’ promotion chance, which will help organizations develop effective remote work policies and practices that balance productivity and employee well-being.
Regarding question 1, the study finds a weak positive correlation (correlation coefficient of 0.14) between working from home and collaboration problems. However, the p-value is greater than α (0.27 > 0.05), indicating that there is no significant correlation between these variables. Therefore, the study cannot conclude that there is a significant correlation between working from home and collaboration problems.
Regarding question 2, the study finds a weak positive correlation (correlation coefficient of 0.11) between the number of households of employees and employees’ happiness while working from home. However, the p-value is greater than α (0.374 > 0.05), indicating that there is no significant correlation between these variables. Therefore, the study cannot conclude that there is a significant correlation between the number of households of employees and employees’ happiness while working from home.
Regarding question 3, the study finds a weak negative correlation (correlation coefficient of -0.08) between them, meaning that as the frequency of working from home increases, the reducing the chance of promotion slightly decreases. However, the p-value is greater than α (0.503 > 0.05), which means there is no significant correlation between them. Therefore, no conclusive evidence suggests a relationship between working from home and reducing the chance of promotion.
In overall, based on the correlation coefficients and p-values between variables in the study, we can conclude there is no strong relationship between variables in this study.

Appendix. Informed Consent Form

Informed Consent Form
Title of Study: The impacts of working from home on employees’ collaboration, happiness, and promotion chances.
Investigator: Mehdi Imani
Introduction:
You are invited to participate in a survey that is being conducted by Mehdi Imani to investigate the correlation between working from home and employee’s collaboration, happiness, and promotion chances.
Purpose:
The purpose of this study is to investigate the correlation between working from home and employee’s collaboration, happiness, and promotion chances. Participation in this study is voluntary. You may choose to participate or not. If you choose to participate, you may withdraw at any time during the survey.
Procedure:
If you agree to participate, you will be asked to complete an online survey. The survey will take approximately five minutes to complete. The survey consists of 12. Your responses will be confidential and anonymous. No identifying information will be collected during the survey.
Confidentiality:
Your survey responses will be kept confidential and anonymous. Your identity will not be revealed in any reports or publications resulting from this study. All data will be kept secure and only accessible to the research team.
Voluntary Participation:
Your participation in this study is voluntary. If you choose to participate, you may withdraw at any time during the survey. You are free to refuse to answer any questions that you do not wish to answer without penalty or negative consequences.
Contact Information:
If you have any questions or concerns about this survey, please contact the Principal Investigator, Mehdi Imani, m.imani@gmail.com.
Statement of Consent:
By clicking the “I agree” button below, you acknowledge that you have read and understood this Informed Consent Form and agree to participate in the survey.

Appendix B. Questionnaire

1- What year were you born? (Please enter year of birth)
2- What is your gender?
  • Male
  • Female
  • Other
3- How long have you been working in your current job?
  • Less than 1 year
  • 1-3 years
  • 4-6 years
  • 7-10 years
  • More than 10 years
4- Which of the following descriptions best fits your household?
  • Single
  • Single parent with 1 children
  • Single parent with 2 children
  • Single parent with 3+ children
  • Married/Partnered with no children
  • Married/Partnered with 1 children
  • Married/Partnered with 2 children
  • Married/Partnered with 3+ children
5- How many days have you worked remotely this year? Please provide a number between 1 and 5.
6- Have you ever worked remotely and on-site on the same day at your employer’s workplace?
  • Yes
  • No
7- To what extent do you agree or disagree with the statement: “It is effortless for me to work together with my colleagues while working remotely.”
  • Strongly agree (1)
  • Agree (2)
  • Neither agree nor disagree (3)
  • Disagree (4)
  • Strongly disagree (5)
8- To what extent do you agree or disagree with the statement: “Remote work decreases my prospects of getting promoted.”
  • Strongly agree (1)
  • Agree (2)
  • Neither agree nor disagree (3)
  • Disagree (4)
  • Strongly disagree (5)
9- Do you believe remote working is a positive or negative aspect for your employer?
  • Strongly Positive (1)
  • Positive (2)
  • Neither Positive nor Negative (3)
  • Negative (4)
  • Strongly Negative (5)
10- Have the following barriers to remote work improved or worsened for you: feeling left out and/or isolated?
  • Improved
  • Stayed the same
  • Worsened
11- To what extent do you agree or disagree with the statement: “I feel better on the days I work remotely.”
  • Strongly agree (1)
  • Agree (2)
  • Neither agree nor disagree (3)
  • Disagree (4)
  • Strongly disagree (5)
12- To what extent do you agree or disagree with the statement: “I am more active on the days I work remotely.”
  • Strongly agree (1)
  • Agree (2)
  • Neither agree nor disagree (3)
  • Disagree (4)
  • Strongly disagree (5)

References

  1. Al Jassmi, H.; Ahmed, S.; Philip, B.; Al Mughairbi, F.; Al Ahmad, M. E-happiness physiological indicators of construction workers’ productivity: A machine learning approach. J. Asian Archit. Build. Eng. 2019, 18, 517–526. [Google Scholar] [CrossRef]
  2. American Psychological Association. Ethical Principles of Psychologists and Code of Conduct. 2017. https://www.apa.org/ethics/code/.
  3. Anderson, D.; Kelliher, C. Enforced remote working and the work-life interface during lockdown. Gend. Manag. 2020, 35, 677–683. [Google Scholar] [CrossRef]
  4. Babbie, E. (2016). The Practice of Social Research. Cengage Learning.
  5. Baker, E.; Avery, G.C.; Crawford, J. Satisfaction and perceived productivity when professionals work from home. Res. Pract. Hum. Resour. Manag. 2007. [Google Scholar]
  6. Bernarto, I.; Bachtiar, D.; Sudibjo, N.; Suryawan, I.N.; Purwanto, A.; Asbari, M. Effect of transformational leadership, perceived organizational support, job satisfaction toward life satisfaction: Evidences from indonesian teachers. Int. J. Adv. Sci. Technol. 2020, 29, 5495–5503. [Google Scholar]
  7. Brenan, M. (2020, October 13). COVID-19 and remote work: An update. Gallup. https://news.gallup.com/poll/321800/covid-remote-work-update.aspx.
  8. Bryman, A. (2016). Social research methods. Oxford University Press.
  9. Campbell, N.; Eley, D.S.; McAllister, L. How do allied health professionals construe the role of the remote workforce? New insight into their recruitment and retention. PLoS ONE 2016, 11, e0167256. [Google Scholar] [CrossRef] [PubMed]
  10. Cerda, P.; Varoquaux, G.; Kégl, B. Similarity encoding for learning with dirty categorical variables. Mach. Learn. 2018, 107, 1477–1494. [Google Scholar] [CrossRef]
  11. Creswell, J.W. (2013). Research design: Qualitative, quantitative, and mixed methods approaches. Sage publications.
  12. Dimitrova, D. Controlling teleworkers: Supervision and flexibility revisited. New Technol. Work. Employ. 2003, 18, 181–195. [Google Scholar] [CrossRef]
  13. Duff, A.J.; Rankin, S.B. Exploring flexible home arrangements – an interview study of workers who live in vans. Career Dev. Int. 2020, 25, 747–761. [Google Scholar] [CrossRef]
  14. Evans, J.A.; Kunda, G.; Barley, S.R. Beach time, bridge time, and billable hours: The temporal structure of technical contracting. Adm. Sci. Q. 2004, 49, 1–38. [Google Scholar] [CrossRef]
  15. Field, A. (2013). Discovering statistics using IBM SPSS Statistics (4th ed.). Sage Publications.
  16. Fisher, C. B., Fried, A. L., & Goodman, S. J. (2017). Ethical issues in dissemination and implementation research. In R. C. Brownson, G. A. Colditz, & E. K. Proctor (Eds.), Dissemination and implementation research in health: Translating science to practice (2nd ed., pp. 571–588). Oxford University Press.
  17. Golden, T.D.; Veiga, J.F.; Dino, R. N. The impact of professional isolation on teleworker job performance and turnover intentions: Does time spent teleworking, interacting face-to-face, or having access to communication-enhancing technology matter? J. Appl. Psychol. 2008, 93, 1412–1421. [Google Scholar] [CrossRef]
  18. Grant, C.A.; Wallace, L.M.; Spurgeon, P.C. An exploration of the psychological factors affecting remote e-worker’s job effectiveness, well-being and work-life balance. Empl. Relat. 2013, 35, 527–546. [Google Scholar] [CrossRef]
  19. Hashim, R.; Bakar, A.; Noh, I.; Mahyudin, H.A. Employees’ Job Satisfaction and Performance through working from Home during the Pandemic Lockdown. Environ. -Behav. Proc. J. 2020, 5, 461–467. [Google Scholar] [CrossRef]
  20. Hering, B. Remote Work Statistics: Shifting Norms and Expectations. 2020. https://www.flexjobs.com/blog/post/remote-work-statistics/.
  21. International Labour Organization. (2020). An employers’ Guide on Working from Home in Response to the Outbreak of COVID-19. In International Labour Organization. https://www.ilo.org/actemp/publications/WCMS_745024/lang--en/index.htm.
  22. Imani, M., & Arabnia, H.R. (2023). Hyperparameter Optimization and Combined Data Sampling Techniques in Machine Learning for Customer Churn Prediction: A Comparative Analysis. Preprints. [CrossRef]
  23. Jamal, M.T.; Anwar, I.; Khan, N.A.; Saleem, I. Work during COVID-19: assessing the influence of job demands and resources on practical and psychological outcomes for employees. Asia-Pac. J. Bus. Adm. 2021. [Google Scholar] [CrossRef]
  24. Kelliher, C.; Anderson, D. Doing more with less? Flexible working practices and the intensification of work. Hum. Relat. 2010, 63, 83–106. [Google Scholar] [CrossRef]
  25. Kwon, M.; Jeon, S.H. Do Leadership Commitment and Performance-Oriented Culture Matter for Federal Teleworker Satisfaction With Telework Programs? Rev. Public Pers. Adm. 2020, 40, 36–55. [Google Scholar] [CrossRef]
  26. Lautsch, B.A.; Kossek, E.E.; Eaton, S.C. Supervisory approaches and paradoxes in managing telecommuting implementation. Hum. Relat. 2009, 62, 795–827. [Google Scholar] [CrossRef]
  27. Neuman, W. L. (2013). Social research methods: Qualitative and quantitative approaches. Pearson Education.
  28. Oakman, J.; Kinsman, N.; Stuckey, R.; Graham, M.; Weale, V. A rapid review of mental and physical health effects of working at home: how do we optimise health? BMC Public Health 2020, 20, 1–13. [Google Scholar] [CrossRef]
  29. Raišiene, A.G.; Rapuano, V.; Varkulevičiute, K.; Stachová, K. Working from homeWho is happy? A survey of Lithuania’s employees during the COVID-19 quarantine period. Sustainability 2020, 12. [Google Scholar] [CrossRef]
  30. Sahni, D.J. Impact of COVID-19 on Employee Behavior: Stress and Coping Mechanism During WFH (Work From Home) Among Service Industry Employees. Int. J. Oper. Manag. 2020, 1, 35–48. [Google Scholar] [CrossRef]
  31. Sahoo, K.; Samal, A.K.; Pramanik, J.; Pani, S.K. Exploratory data analysis using Python. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8, 2019. [Google Scholar] [CrossRef]
  32. Schooreel, T.; Shockley, K.M.; Verbruggen, M. What if people’s private life constrained their career decisions? Examining the relationship between home-tocareer interference and career satisfaction. Career Dev. Int. 2017, 22, 124–141. [Google Scholar] [CrossRef]
  33. Song, Y.; Gao, J. Does telework stress employees out? A study on working at home and subjective well-being for wage/salary workers. J. Happiness Stud. 2019, 21, 2649–2668. [Google Scholar] [CrossRef]
  34. Song, Y.; Gao, J. Does telework stress employees out? A study on working at home and subjective well-being for wage/salary workers. J. Happiness Stud. 2020, 21, 2649–2668. [Google Scholar] [CrossRef]
  35. Sridhar, V.; Bhattacharya, S. Significant household factors that influence an IT employees’ job effectiveness while on work from home. Int. J. Innov. Sci. 2021, 13, 105–117. [Google Scholar] [CrossRef]
  36. Steward, B. Changing Times: The Meaning, Measurement and use of Time in Teleworking. Time Soc. 2000, 9, 57–74. [Google Scholar] [CrossRef]
  37. Sullivan, G.M.; Artino, A.R. Analyzing and interpreting data from Likert-type scales. J. Grad. Med. Educ. 2013, 5, 541–542. [Google Scholar] [CrossRef]
  38. Suresh, K. An overview of randomization techniques: An unbiased assessment of outcome in clinical research. J. Hum. Reprod. Sci. 2011, 4, 8–11. [Google Scholar] [CrossRef]
  39. Timsal, A.; Awais, M. Flexibility or ethical dilemma: an overview of the work from home policies in modern organizations around the world. Human Resour. Manag. Int. Dig. 2016, 24, 12–15. [Google Scholar] [CrossRef]
  40. Van Der Lippe, T.; Lippényi, Z. Co-workers working from home and individual and team performance. New Technol. Work. Employ. 2020, 35, 60–79. [Google Scholar] [CrossRef]
  41. Vyas, L.; Butakhieo, N. The impact of working from home during COVID-19 on work and life domains: an exploratory study on Hong Kong. Policy Des. Pract. 2020, 4, 1–18. [Google Scholar] [CrossRef]
Preprints 86611 g001
Figure 1. he scatterplot between the two variables: “working from home percentage” and “number of employees’ households”.
Figure 1. he scatterplot between the two variables: “working from home percentage” and “number of employees’ households”.
Preprints 86611 g001
Preprints 86611 g002
Figure 2. he scatterplot between the two variables: “working from home percentage” and “employees’ collaboration problem”.
Figure 2. he scatterplot between the two variables: “working from home percentage” and “employees’ collaboration problem”.
Preprints 86611 g002
Preprints 86611 g003
Figure 3. he scatterplot between the two variables: “working from home percentage” and “employees’ promotion chance”.
Figure 3. he scatterplot between the two variables: “working from home percentage” and “employees’ promotion chance”.
Preprints 86611 g003
Preprints 86611 g004
Figure 4. Description of the statistics of different variables.
Figure 4. Description of the statistics of different variables.
Preprints 86611 g004
Preprints 86611 g005
Figure 5. Histogram of Age Distribution.
Figure 5. Histogram of Age Distribution.
Preprints 86611 g005
Preprints 86611 g006
Figure 6. Histogram of Gender Distribution.
Figure 6. Histogram of Gender Distribution.
Preprints 86611 g006
Preprints 86611 g007
Figure 7. Histogram of years of experience distribution.
Figure 7. Histogram of years of experience distribution.
Preprints 86611 g007
Preprints 86611 g008
Figure 8. The histogram of the number of employees’ households.
Figure 8. The histogram of the number of employees’ households.
Preprints 86611 g008
Preprints 86611 g009
Figure 9. the correlations of the different variables.
Figure 9. the correlations of the different variables.
Preprints 86611 g009
Preprints 86611 g010
Figure 10. the p-values of the different variables.
Figure 10. the p-values of the different variables.
Preprints 86611 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated