New Soliton Solutions of M-fractional Westervelt Model in Ultrasound Imaging via Two Analytical Techniques

1. Introduction

Soliton theory based on water waves, plasmas, optical fibers etc., was developed in 1960-1970. This is significant branch of applied mathematics as well as mathematical physics. It has significant uses in nonlinear optics, fluid mechanics, plasmas etc. This theory is widely applied in various natural sciences, including communication, biology, chemistry, mathematics and almost all branches of physics including fluid dynamics, condensed matter physics, plasma physics and in others.

Various naturally occurring phenomenon are shown as a nonlinear partial differential equations (NLPDEs). A variety of techniques are made to attain results for NLPDEs. For examples, modified direct algebraic technique [1], modified Khater scheme [2], generalized Kudryashov scheme [3], novel $(G^{\prime }/G)$-expansion method [4], extended mapping scheme [5].

There are two another straight forward, fruitful and reliable techniques; ${exp}_a$ function technique and modified simplest equation technique. There are various uses of these techniques. Instantly; optical wave solutions of perturbed Gerdjikov-Ivanov model by utilizing the ${exp}_a$ function scheme [6], some new optical solitons of Sasa-Satsuma higher order equation in [7], the dark soliton, bright soliton and combo optical solitons of three coupled Maccari’s model are attained [8], dark, bright and many other exact wave solutions of modified Camassa-Holm model are obtained in [9]. Similarly, some solitary wave solutions of BBM and Chan-Hilliard equations by utilizing modified simplest equation method [10], exact wave solutions of Boussinesq and coupled Boussinesq equations are obtained by using this method [11].

Our study model is the Westervelt equation along truncated M-fractional derivative. Different kinds of analytical wave solitons of concerned model are achieved by distinct techniques. For example, exact solitary wave solitons have been achieved by utilizing modified Kudryashov and generalized Kudryashov schemes [12], the periodic, exponential, hyperbolic and plane wave functions solutions are gained with the use of modified exponential rational function and modified $(G^{\prime }/G^2)$-Expansion techniques [13].

Basic aim of our research is to attain the new soliton solutions to M-fractional Westervelt model via ${exp}_a$ function and modified simplest equation techniques.

Our paper contains 5 sections; 2nd-section is about the aforementioned model and it’s mathematical analysis, 3rd-section is concerned about ${exp}_a$ function technique and it’s application to get the soliton solutions, 4th-section explain the modified simplest equation technique and apply it to get soliton solutions, 5th-section is about the explanation of some gained results by 2-dimensional, 3-dimensional and contour plots and 6th-section is the conclusion.

2. Governing model and It’s mathematical analysis

Let’s assume the space-time fractional Westervelt model given as [13]:

$$2\tau (u{D}_{M,t}^{\alpha ,{\rm Y}}u+{\left(D_{M,t}^{\alpha ,{\rm Y}}u\right)}^2)+{\rho }^2{D}_{M,2x}^{2\alpha ,{\rm Y}}u+\theta D_{M,t}^{\alpha ,{\rm Y}}\left(D_{M,2x}^{2\alpha ,{\rm Y}}u\right)-D_{M,t}^{\alpha ,{\rm Y}}u=0.$$

(1)

here

$$D_{M,t}^{\alpha ,{\rm Y}}u\left(t\right)=\underset{\tau \to 0}{lim}\frac{u\left(t{E}_{{\rm Y}}\left(\tau t^{1-\alpha }\right)\right)-u\left(t\right)}{\tau },\alpha \in (0,1],{\rm Y}>0,$$

(2)

where $E_{{\rm Y}}(.)$ denotes truncated Mittag-Leffler (TML) function shown in [14,15]. here u=u(x,t) indicates the real wave function. Parameters $\theta$ denotes the diffusivity of sound and $\rho$ represents the speed of sound. The non-linearity parameter $\tau =\frac{1+\frac{B}{2A}}{f}$ where f is the bulk modulus which is taken as $f=\eta {\rho }^2$ and $\eta$ is working as the mass density.

Applying the given wave transformations:

$$u(x,t)=U\left(\xi \right),\xi =\frac{\Gamma ({\rm Y}+1)}{\alpha }(\lambda x^{\alpha }+\delta t^{\alpha })$$

(3)

here parameters $\lambda$ and $\delta$ are the spatio and temporal coefficients. By applying Eq.(3) into Eq.(1), we get a NLODE shown as:

$$\delta \theta {\lambda }^2{U}^{{}^{‴}}+{\lambda }^2{\rho }^2{U}^{″}+{\delta }^2\left(2\tau U{U}^{″}-U^{″}+{\left(U^{\prime }\right)}^2\right)=0$$

(4)

where U denotes the polynomial and prime ${}^{\prime }$ represents the $\frac{d}{d\xi }$. By applying Homogenous Balance method, we get m=1. We will find new soliton solutions of Eq.(4) by applying two different techniques in the following.

3. The ${exp}_{\mathbf{a}}$ function technique

Here we mention the basic steps of this technique.

Assuming a NLPDE;

$$F(f,f^2{f}_y,f_t,f_{xy},f_{tt},f_{yt},...)=0.$$

(5)

Eq .(5) changed into NLODE:

$$Y(F,F^{{}^{\prime }},F^{{}^{″}},...,)=0.$$

(6)

By using the given wave transformations:

$$f(x,y,t)=F\left(\xi \right),\xi =\delta x+\mu y+\lambda t.$$

(7)

Assuming the results of Eq. (6) are shown in [16,17,18,19]:

$$F\left(\xi \right)=\frac{{\alpha }_0+{\alpha }_1{d}^{\xi }+...+{\alpha }_m{d}^{m\xi }}{{\beta }_0+{\beta }_1{d}^{\xi }+...+{\beta }_m{d}^{m\xi }},d\ne 0,1.$$

(8)

here ${\alpha }_j$ and ${\beta }_j(0\le j\le m)$ are the undetermined. Natural number m is found with the use of homogenous balance technique into Eq. (8). Inserting Eq.(8) into Eq.(6), results

$$\wp \left(d^{\xi }\right)={\ell }_0+{\ell }_1{d}^{\xi }+...+{\ell }_t{d}^{t\xi }=0,.$$

(9)

Inserting ${\ell }_j(0\le j\le t)$ into Eq. (9) taking zeo, a system of equations is attained:

$${\ell }_j=0,herej=0,...,t.$$

(10)

Applying obtain solutions, one can get exact solitons for Eq. (5).

3.1. New wave solutions by the ${exp}_a$ function technique

Eq.(8) reduces into below form for m=1:

$$U\left(\xi \right)=\frac{{\alpha }_0+{\alpha }_1{d}^{\xi }}{{\beta }_0+{\beta }_1{d}^{\xi }}$$

(11)

Substituting Eq.(11) into Eq.(4), a set of equations is gained. Evaluating these, we get distinct sets:

Set 1:

$$\left\{{\alpha }_0=\frac{{\beta }_0\left({\delta }^2-\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\delta }^2},{\alpha }_1=\frac{{\beta }_1\left({\delta }^2+\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\delta }^2},\tau =\frac{1}{2}\right\}$$

(12)

$$u(x,t)=\frac{{\beta }_1{d}^{\xi }\left({\delta }^2+\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)+{\beta }_0\left({\delta }^2-\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\delta }^2\left({\beta }_0+{\beta }_1{d}^{\xi }\right)}$$

(13)

Set 2:

$$\left\{{\alpha }_1=-\frac{{\beta }_1\left({\delta }^2+\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\delta }^2},{\beta }_0=0,\tau =-\frac{1}{2}\right\}$$

(14)

$$u(x,t)=\frac{{\alpha }_0{\delta }^2-{\beta }_1{d}^{\xi }\left({\delta }^2+\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\beta }_1{\delta }^2{d}^{\xi }}$$

(15)

Set 3:

$$\left\{{\alpha }_0=-\frac{{\beta }_0\left({\delta }^2-\delta \theta {\lambda }^{2}log\left(d\right)-{\lambda }^2{\rho }^2\right)}{{\delta }^2},{\beta }_1=0,\tau =-\frac{1}{2}\right\}$$

(16)

$$u(x,t)=\frac{{\alpha }_1{\delta }^2{d}^{\xi }+{\beta }_0\left(-{\delta }^2+\delta \theta {\lambda }^{2}log\left(d\right)+{\lambda }^2{\rho }^2\right)}{{\beta }_0{\delta }^2}$$

(17)

4. Modified simplest equation technique

Here we point out the some main steps of this technique.

Step 1:

Supposing a NLPDE:

$$G(f,f^2{f}_y,f_t,f_{xy},f_{tt},f_{yt},...)=0,$$

(18)

where $f=f(x,y,t)$ represents a wave profile.

Consider the wave transformation:

$$f(x,y,t)=F\left(\xi \right),\xi =x-\mu y+\lambda t.$$

(19)

Substituting Eq. (19) into Eq. (18), we gain the NLODE:

$$Z(F,F^2{F}^{{}^{\prime }},F^{{}^{″}},...)=0.$$

(20)

Step 2: Let Eq.(20) has the solution form:

$$F\left(\xi \right)=\sum _{j=1}^m{b}_j{\psi }^j\left(\xi \right)$$

(21)

here $b_j(j=1,2,...,m)$ are unknowns and $b_m\ne 0$.

A new function $\psi \left(\xi \right)$ fulfil below ODE:

$${\psi }^{\prime }\left(\xi \right)={\psi }^2\left(\xi \right)+\eta$$

(22)

here $\eta$ is a .

Eq.(22) have solutions for different cases of $\eta$:

Case 1: if $\eta <0$,

$$\psi \left(\xi \right)=-\sqrt{-\eta }tanh\left(\sqrt{-\eta }\xi \right)$$

(23)

$$\psi \left(\xi \right)=-\sqrt{-\eta }coth\left(\sqrt{-\eta }\xi \right)$$

(24)

$$\psi \left(\xi \right)=\sqrt{-\eta }\left(-tanh\left(2\sqrt{-\eta }\xi \right)\pm isech\left(2\sqrt{-\eta }\xi \right)\right),$$

(25)

$$\psi \left(\xi \right)=\sqrt{-\eta }\left(-coth\left(2\sqrt{-\eta }\xi \right)\pm csch\left(2\sqrt{-\eta }\xi \right)\right),$$

(26)

$$\psi \left(\xi \right)=-\frac{\sqrt{-\eta }}{2}\left(tanh\left(\frac{\sqrt{-\eta }}{2}\xi \right)+coth\left(\frac{\sqrt{-\eta }}{2}\xi \right)\right).$$

(27)

Case 2: if $\eta >0$,

$$\psi \left(\xi \right)=\sqrt{\eta }tan\left(\sqrt{\eta }\xi \right)$$

(28)

$$\psi \left(\xi \right)=-\sqrt{\eta }cot\left(\sqrt{\eta }\xi \right)$$

(29)

$$\psi \left(\xi \right)=\sqrt{\eta }\left(tan\left(2\sqrt{\eta }\xi \right)\pm sec\left(2\sqrt{\eta }\xi \right)\right),$$

(30)

$$\psi \left(\xi \right)=\sqrt{\eta }\left(-cot\left(2\sqrt{\eta }\xi \right)\pm csc\left(2\sqrt{\eta }\xi \right)\right),$$

(31)

$$\psi \left(\xi \right)=\frac{\sqrt{\eta }}{2}\left(tan\left(\frac{\sqrt{\eta }}{2}\xi \right)-cot\left(\frac{\sqrt{\eta }}{2}\xi \right)\right).$$

(32)

Case 3: if $\eta =0$,

$$\psi \left(\xi \right)=-\frac{1}{\xi }$$

(33)

Step 3: Applying Eq.(21) and Eq.(22) into Eq.(20) and sum up the co-efficients of every power of ${\psi }^j$. Substituting co-efficients of each power equal to zero, we obtain a set of equations involving $b_i$, $\lambda$, $\mu$. Evaluating the gained set of equations, we gain results.

Step 4: Inserting Eq.(21) of which $b_j$, $\lambda$, $\mu$ has been obtained into Eq.(20), we gain analytical wave solutions of Eq.(18).

4.1. New soliton solutions of Eq.(4) by MSET

Eq.(21) reduces for m=1:

$$U\left(\xi \right)=b_0+b_1\psi \left(\xi \right)$$

(34)

Using Eq.(34) into Eq.(4) with Eq.(20), we obtain solution.

Set:

$$\left\{b_0=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2},b_1=-\frac{2\theta {\lambda }^2}{\delta },\tau =\frac{1}{2}\right\}$$

(35)

Case 1: If $\eta <0$,

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }(-\sqrt{-\eta }tanh\left(\sqrt{-\eta }\xi \right))$$

(36)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }(-\sqrt{-\eta }coth\left(\sqrt{-\eta }\xi \right))$$

(37)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }\left(\sqrt{-\eta }\left(-tanh\left(2\sqrt{-\eta }\xi \right)\pm isech\left(2\sqrt{-\eta }\xi \right)\right)\right)$$

(38)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }\left(\sqrt{-\eta }\left(-coth\left(2\sqrt{-\eta }\xi \right)\pm csch\left(2\sqrt{-\eta }\xi \right)\right)\right)$$

(39)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }(-\frac{\sqrt{-\eta }}{2}\left(tanh\left(\frac{\sqrt{-\eta }}{2}\xi \right)+coth\left(\frac{\sqrt{-\eta }}{2}\xi \right)\right))$$

(40)

Case 2:

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }(\sqrt{\eta }tan\left(\sqrt{\eta }\xi \right))$$

(41)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }(-\sqrt{\eta }cot\left(\sqrt{\eta }\xi \right))$$

(42)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }\left(\sqrt{\eta }\left(tan\left(2\sqrt{\eta }\xi \right)\pm sec\left(2\sqrt{\eta }\xi \right)\right)\right)$$

(43)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }\left(\sqrt{\eta }\left(-cot\left(2\sqrt{\eta }\xi \right)\pm csc\left(2\sqrt{\eta }\xi \right)\right)\right)$$

(44)

$$u(x,t)=\frac{{\delta }^2-{\lambda }^2{\rho }^2}{{\delta }^2}-\frac{2\theta {\lambda }^2}{\delta }\left(\frac{\sqrt{\eta }}{2}\left(tan\left(\frac{\sqrt{\eta }}{2}\xi \right)-cot\left(\frac{\sqrt{\eta }}{2}\xi \right)\right)\right)$$

(45)

Case 3:

$$u(x,t)=-\frac{1}{\xi }$$

(46)

where $\xi =\frac{\Gamma (1+{\rm Y})}{\alpha }(\lambda x^{\alpha }+\delta t^{\alpha })$ for all above solutions.

5. Graphically description of solutions

Here we represent the graphically explanation of some of the attained solutions in the form of 2-dimensional, 3-dimensional and contour plots.

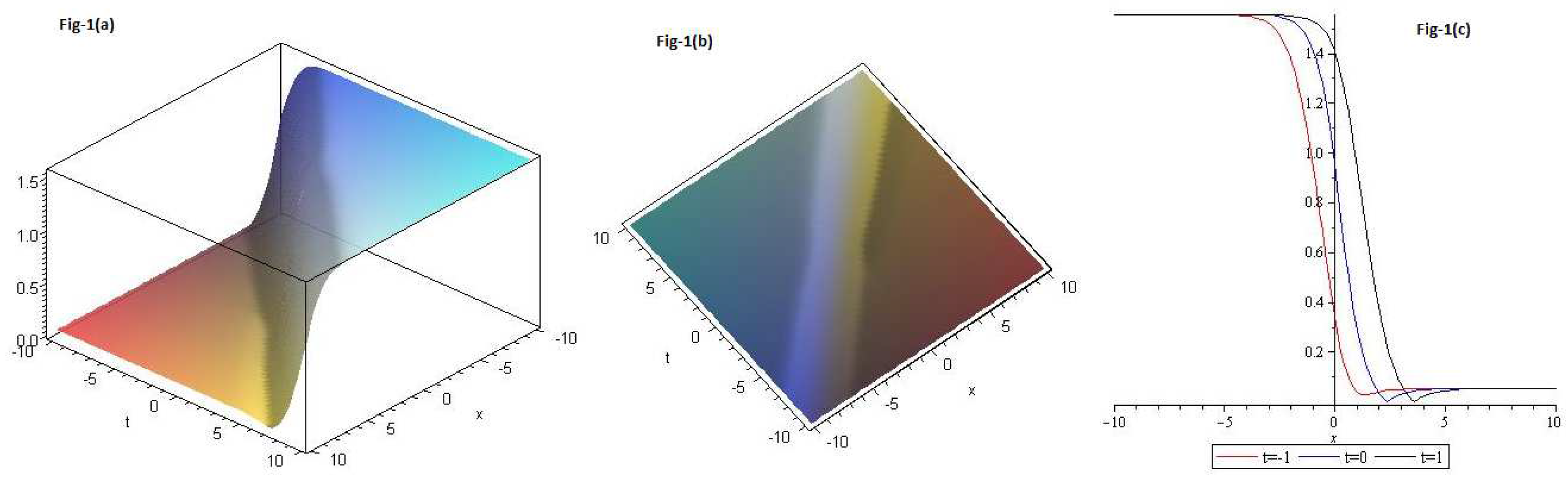
We draw plots for Eq.(13); in Figure 1. 1(a) 3D, 1(b) contour and 1(c) 2D for $-10\le t\le 10$ and $-10\le x\le 10$. Red curve is for $t=-1$, blue curve is for $t=0$ and black curve is for $t=1$ with $d=5,{\beta }_1=0.5,{\beta }_0=0.3,{\rm Y}=1,\delta =1,\lambda =-1,\rho =0.5,\theta =0.5,\alpha =0.8,$.

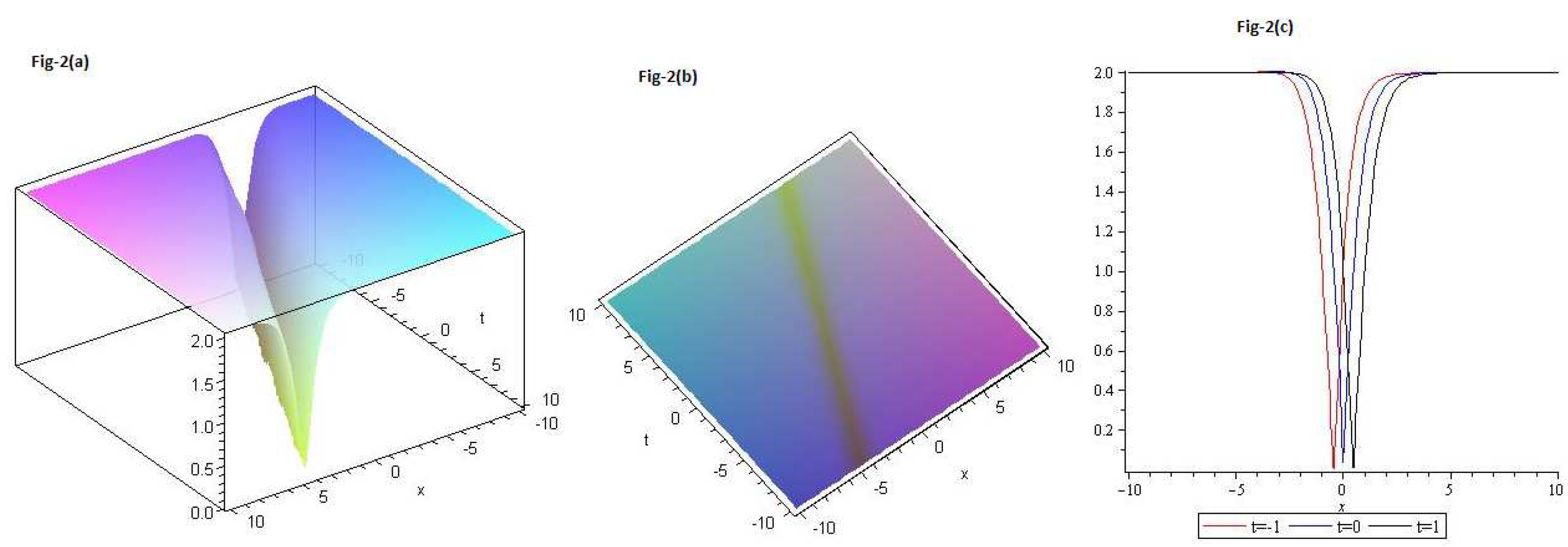
We draw plots for Eq.(36); in Figure 2. 2(a) 3D, 1(b) contour and 2(c) 2D for $-10\le t\le 10$ and $-10\le x\le 10$. Red curve is for $t=-1$, blue curve is for $t=0$ and black curve is for $t=1$ with ${\rm Y}=1,\delta =0.5,\eta =-1,\lambda =-1,\rho =0.5,\theta =0.5,\alpha =0.8,$.

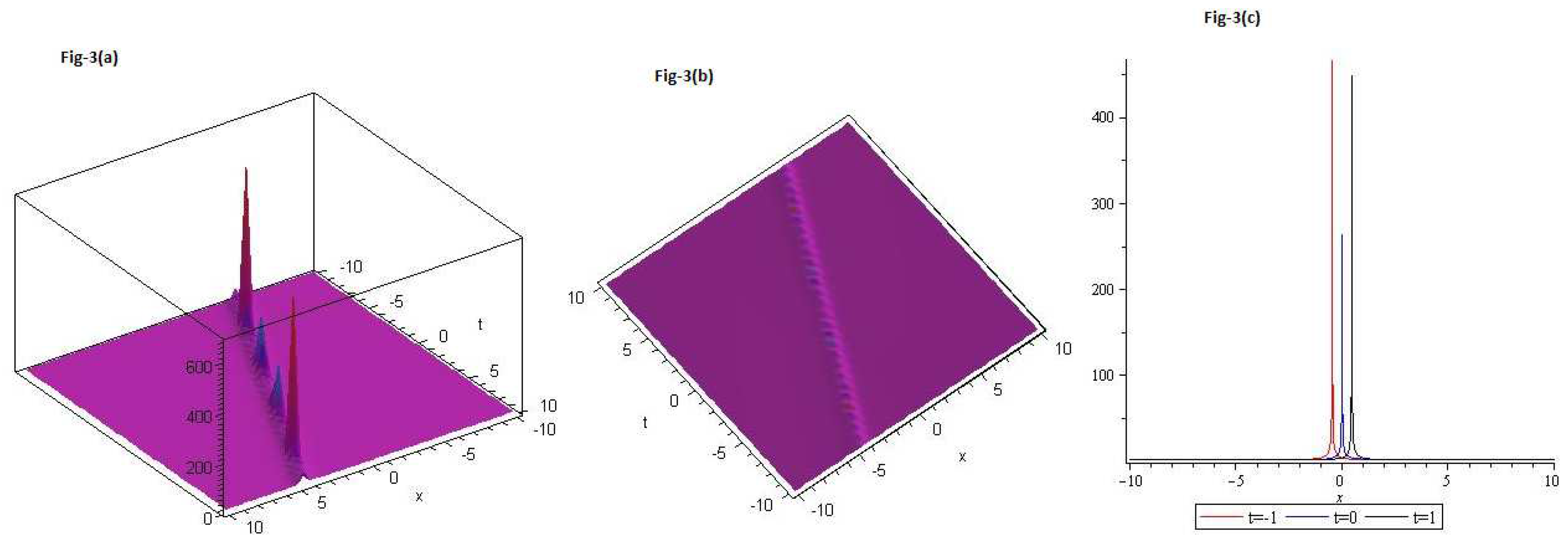
We draw plots for Eq.(37); in Figure 3. 3(a) 3D, 3(b) contour and 3(c) 2D for $-10\le t\le 10$ and $-10\le x\le 10$. Red curve is for $t=-1$, blue curve is for $t=0$ and black curve is for $t=1$ with ${\rm Y}=1,\delta =0.5,\eta =-1,\lambda =-1,\rho =0.5,\theta =0.5,\alpha =0.8,$.

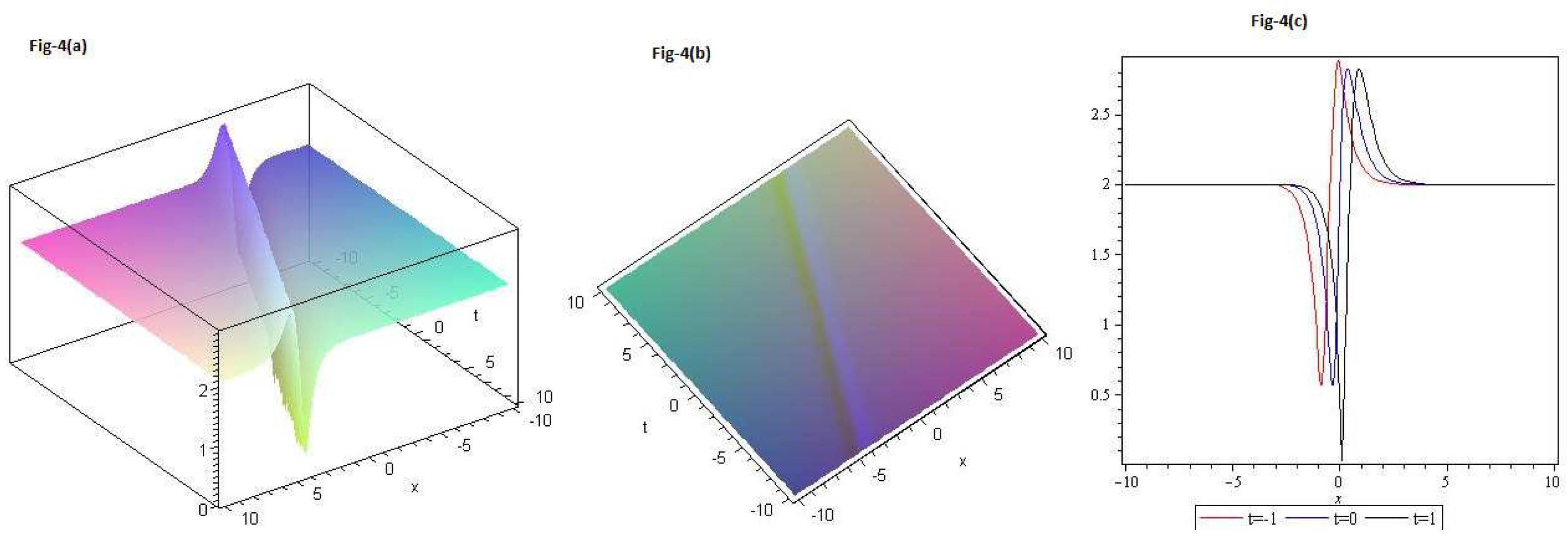
We draw plots for Eq.(38); in Figure 4. 4(a) 3D, 4(b) contour and 4(c) 2D for $-10\le t\le 10$ and $-10\le x\le 10$. Red curve is for $t=-1$, blue curve is for $t=0$ and black curve is for $t=1$ with ${\rm Y}=1,\delta =0.5,\eta =-1,\lambda =-1,\rho =0.5,\theta =0.5,\alpha =0.8,$.

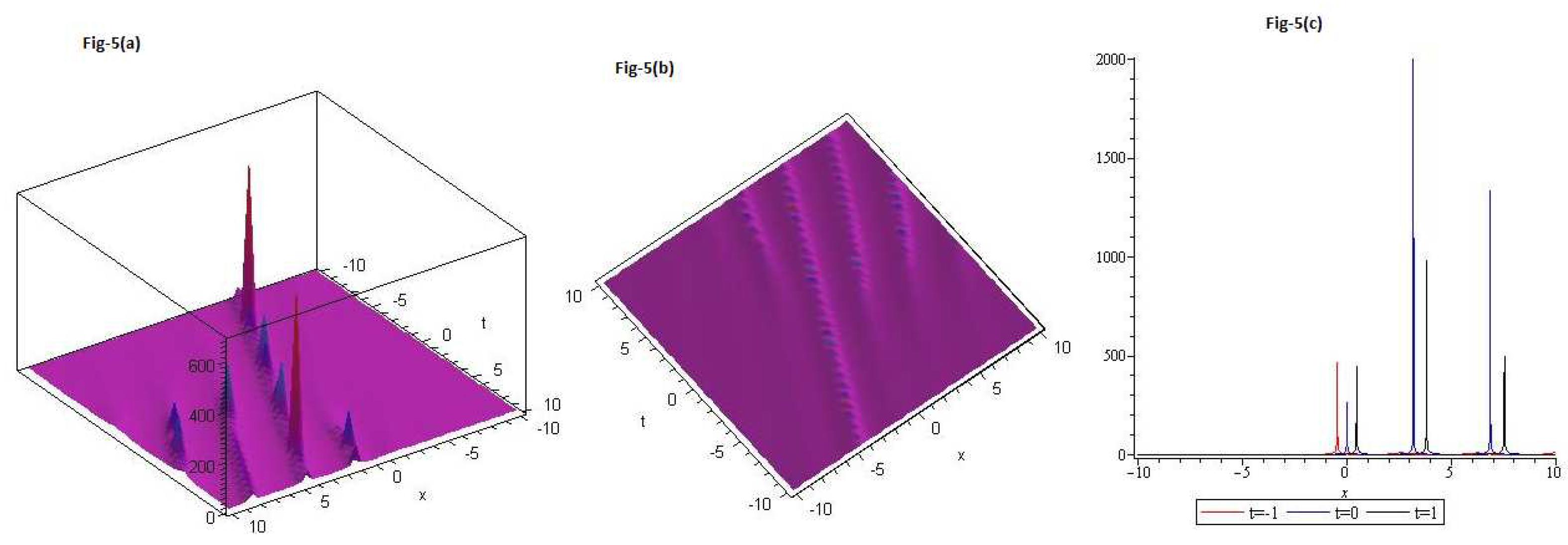
We draw plots for Eq.(42) in Figure 5. 5(a) 3D, 5(b) contour and 5(c) 2D for $-10\le t\le 10$ and $-10\le x\le 10$. Red curve is for $t=-1$, blue curve is for $t=0$ and black curve is for $t=1$ with ${\rm Y}=1,\delta =0.5,\eta =1,\lambda =-1,\rho =0.5,\theta =0.5,\alpha =0.8,$.

6. Conclusions

We are succeed to attain new soliton solutions to the M-fractional (1+1)-dimensional non-linear Westervelt model with the help of ${exp}_a$ function technique and modified simplest equation technique. Some of the gained results are represented graphically through Maple tool. The solutions achieved are helpful for the future study of this model. At the end, the techniques applied in our work are straight forward, reliable and fruitful to handle the other FPDEs.