Prerpints.org logo
Preprint
Article

The Short Time Prediction of the Dst Index Based on the LSTM and the EMD-LSTM Models

Altmetrics

Downloads

165

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
The Dst index is the geomagnetic storm index used to measure the energy level of geomagnetic storms, and the prediction of this index is of great significance for the geomagnetic storm study and the solar activity. In contrast to traditional numerical modelling techniques, machine learning, which has emerged in decades ago based on rapidly developing computer hardware and software and artificial intelligence methods, has been unprecedentedly developed in geophysics, especially solar-terrestrial space physics. This study chooses two machine learning models, the LSTM (Long-Short Time Memory, LSTM) and EMD-LSTM model (Empirical Mode Decomposition, EMD), to model and predict the Dst index. By building the Dst index data series from 2018-2023, two models were built to fit and predict the data. Firstly, we evaluated the influences of the learning rate and the amount of training data on the prediction accuracy of the LSTM model, and finally, 10-3 was thought as the optimal learning rate; secondly, the two models were used to predict the Dst index in the solar active and quiet periods, respectively, and the RMSE (Root Mean Square Error) of the LSTM model in the active period is 7.34 nT, the CC (correlation coefficient) is 0.96, those of the quiet period are 2.64nT and 0.97; the RMSE and r of EMD-LSTM model are 8.87nT and 0.93 in active time and 3.29nT and 0.95 in the quiet time. Finally, the prediction accuracy of the LSTM model in short time period is slightly better than the EMD-LSTM model. However, there will be a problem of prediction lag, which the EMD-LSTM model can then solve, and can better predict the geomagnetic storm.
Keywords: 
Subject: Environmental and Earth Sciences  -   Space and Planetary Science

1. Introduction

As an essential physical field of the Earth, the geomagnetic field is an integral part of space weather, which has a complex spatial structure and temporal evolution characteristics. A deep understanding of the spatial and temporal characteristics, origin, and relationship between the geomagnetic field and other geophysical phenomena provides excellent help for studying the magnetic field of the Earth and other planets. The Dst index, as an important index reflecting the perturbation of the geomagnetic field, was first proposed by Sugiura in 1964. It is also known as the geomagnetic hourly geomagnetic index to describe the process of magnetic storms and to reflect the change of equatorial westerly ring current [1]. This index is calculated using the horizontal component H of the geomagnetic field at four middle and low latitudes observatories after removing the secular variation and the ring current latitudinal correction [2]. The Dst index is one of the most widely used indices in geomagnetism and space physics because it can monitor the occurrence and change of magnetic storms succinctly and continuously. The modelling and prediction of the Dst index have significant scientific and applicated meanings for studying the changes in geomagnetic external fields, magnetic storms, and even solar activity.
Numerical methods, such as least squares estimation and spline interpolation [3], are generally used to predict geomagnetic indices. These traditional methods mainly carry out numerical processes like iterative from the data itself, error approximation, seeking extremum, and so on, to obtain the best-approximated value that satisfies the accuracy requirement. However, they can not highlight the characteristics of the data based on the in-depth learning and mining of the existing and constantly emerging new data. In recent years, with the continuous improvement of computing power and the rapid development of artificial intelligence (AI), deep learning, as one kind of multi-layer neural network learning algorithm, has become an essential part of the machine learning field. Deep learning is usually used to process images, sounds, text signals, etc. It is mainly applied to multi-modal classification problems, data processing, and simulation, as well as artificial intelligence [4]. The Long-Short Time Memory (LSTM) network method [5] is the most widely used simulation and forecasting algorithm model. This method has a complex hidden unit, which can selectively increase or decrease information. It, therefore, can accurately model data with short-term or long-term dependencies. of data for accurate modelling [6]. So far, the LSTM model has shown an excellent forecasting ability in long-term time series data processing [7] and has been considered very suitable for forecasting the Dst index.
Dst index prediction is usually achieved through different mathematical modelling approaches. Kim et al. [8] developed an empirical model for predicting the occurrence of geomagnetic storms based on the Dst index of the Coronal Mass Ejection (CME) parameter; results showed that this parameter predicts both the occurrence of geomagnetic storms and the Dst index. Kremenetskiy et al. [9] proposed a solution for the Dst index forecasting using an autoregressive model and solar wind parameter measurements, called the minimax approach to identification of the parameters of forecast models. Tobiska et al. [10] proposed a data-driven deterministic algorithm, the Anemomilos algorithm, which can predict the Dst up to 6 days based on the arrival time of large, medium, or small magnetic storms to the Earth. Banerjee et al. [11] used the direction and magnitude of the BZ component of the real-time solar wind and real-time Interplanetary Magnetic Field (IMF) as input parameters to model the magnetosphere based on a metric automaton, where the simulation of the Dst meets expectations. Chandorkar et al. [12] developed Gaussian Process Autoregressive (GP-AR) and Gaussian Process Autoregressive with external inputs (GP-ARX) models, whose Root Mean Square Error (RMSE) are only 14.04 nT and 11.88 nT, and CCs (correlation coefficient) are 0.963 and 0.972, respectively. Bej et al. [13] introduced a new probabilistic model based on adaptive incremental modulation and the concept of optimal state space, with CC exceeding 0.90 and very small CCs between the mean absolute error and RMSE (3.54 and 5.15 nT). Nilam et al. [14] used a new Ensemble Kalman Filter (EnKF) method based on the dynamics of the circulating flow to forecast the Dst index in real-time; the resulting RMSE and CC values are 4.3 nT and 0.99. Compared with the traditional mathematical methods, Machine learning based on deep learning models can train different models based on different training data with better pertinence, scalability, and trainability.
Some progress has been made in researching the Dst index prediction using deep learning techniques. Chen et al. [15] used a BP (Back-propagation) neural network to establish a method to forecast the Dst index one-hour in advance. Results show that it is feasible to forecast the Dst parameter in the short term, but there is still some bias. Revallo et al. [16] proposed a method based on an Artificial Neural Network (ANN) combined with an analytical model of solar wind-magnetosphere interaction, and the predicted values are more accurate than others. Lu et al. [17] combined the Support Vector Machine (SVM) with Distance Correlation (DC) coefficients to build a model, results show more minor errors than the Neural Network (NN) and Linear Machine (LM). Andriyas et al. [18] used Multivariate Relevance Vector Machines (MVRVM) to predict various indices, among which the Dst index was predicted with an accuracy of 82.62%. Lethy et al. [19] proposed an ANN technique to forecast the Dst index using 24 past hourly solar wind parameter values, results showed that for forecasting 2-hour in advance, CC can reach 0.876. Xu et al. [20] used the Bagging integrated learning algorithm, which combines three algorithms, ANN, SVM, and LSTM, to forecast the Dst index 1-6 hours in advance. They put solar wind parameters (including total interplanetary magnetic field, total IMFB field and IMFZ component, total electric field, solar wind speed, plasma temperature, and proton pressure) as inputs, the RMSE of the forecast was always lower than 8.09 nT, the CC was always higher than 0.86, and the accuracy of the interval forecast was always higher than 90%. Park et al. [21] combined an empirical model and an ANN model to build a Dst index prediction model, which showed an excellent performance compared to the model using only ANN, predicting the Dst index 6-hour ahead, the CC is 0.8 and RMSE no great than 24 nT. Hu et al. [22] built a forecasting model using a Convolutional Neural Network (CNN) that utilized SoHO images to predict the Dst index with a True Skill Statistic (TSS) of 0.62 and a Matthews Correlation Coefficient (MCC) of 0.37. Although these neural-network-based models demonstrated a good Dst forecasting ability, neural networks such as ANN, CNN, etc. mainly deal with independent and identically distributed data. At the same time, the Dst index belongs to time-series data, which exists a specific periodical change in time. It thus does not satisfy the independent and identically distributed condition, which will finally lead to long-term change errors when using these neural networks to train the model.
In order to solve these problems and consider the advantages of the LSTM method, this study will choose the LSTM model and the EMD-LSTM model (the LSTM model with the addition of the EMD algorithm), which is trained to simulate the characteristics of the Dst index itself, to obtain better forecasting of the Dst index. The EMD-LSTM method has been applied to the prediction of some other space weather indices; Zhang et al. [23] conducted a prediction of high-energy electron fluxes using this method, and it was found that the most minor prediction error can be obtained using the EMD-LSTM method compare with other models.
The second part of this paper gives the data sources and selection conditions; the third part describes the principles of the methods used; the fourth part explains the results by different methods and finally gives the results and conclusion.

2. Data

2.1. Data Sources

The Dst index used in this study was obtained from the website of the World Data Center for Geomagnetism, Kyoto. The data from 1957 to 2016 is the Final Dst index, the data from 2017 to 2021 is the Provisional Dst index, and after 2022 is the Real-time Dst index. Both 2015 and 2023 are solar active years. Dst records show three large geomagnetic storms in 2023, so this study mainly focuses on the period from 2015.01.01 to 2023.05.21, from which the appropriate data (see 2.2 for details) are selected under different prediction conditions.

2.2. Data Preprocessing

Study shows that the Dst index in 2019 is relatively flat. Most of the indices are between 20 nT and -40 nT. The data in the quiet period are more appropriate as the base modelling data set, so the data 2019 are selected as the test data set. In contrast, three major geomagnetic storms occurred until May 21, 2023, of which the Dst index most drastically varied during the April 24 storm, with an amplitude of about 200 nT, so the data between January 1, 2023, to May 21, 2023, are selected to test the prediction of the active period, more attention will be paid on the April 24’s test.

3. Method

3.1. The LSTM Model

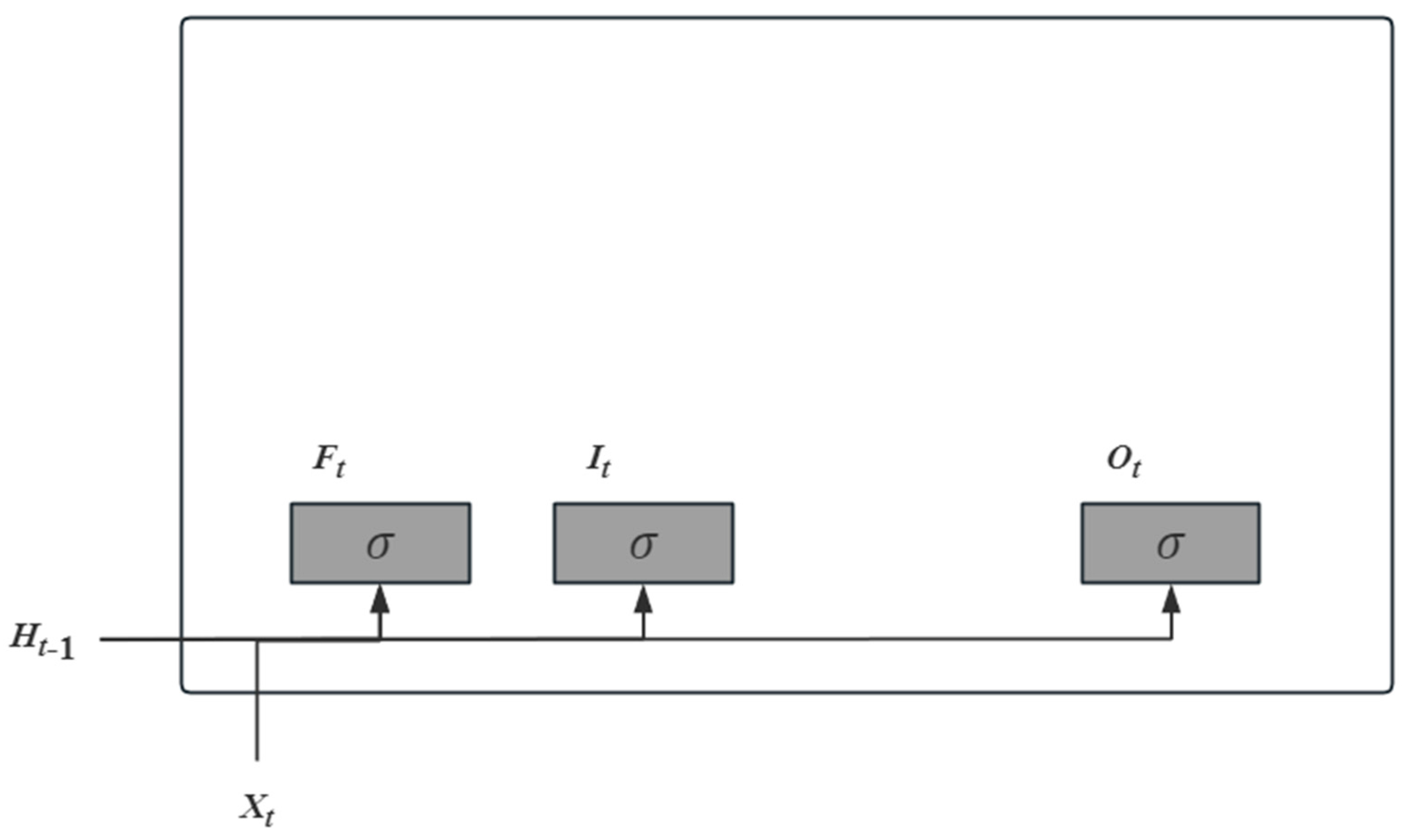
This study selects the LSTM network model for forecasting, a gated recurrent neural network model. The basic principle is that the model has a recurrent unit in which the output of the previous moment is the input of this moment, the output of this moment is the input of the next moment, and a recurrent unit contains multiple components [24]. The specific process is divided into four parts. The first part is shown in Figure 1.
According to the above figure, we have
I t = σ ( X t W x i + H t − 1 W h i + b i ) F t = σ ( X t W x f + H t − 1 W h f + b f ) O t = σ ( X t W x o + H t − 1 W h o + b o )
σ ( x ) = 1 1 + e − x
where the input Xt of the current step and the hidden state Ht-1 of the previous step will be sent into the input gate (It), forget gate (Ft), and output gate (Ot). Xt denotes the input data of the current step; the hidden state Ht-1 is the transformed result of the previous step, the later Ht can be obtained after the same way; Wx and Wh are the weights corresponding to the inputs and the hidden state, respectively, and b is the bias, all of them are parameters. The outputs of the three gates are obtained by the activation function, sigmod function (𝜎), which is used to transform the outputs nonlinearly. 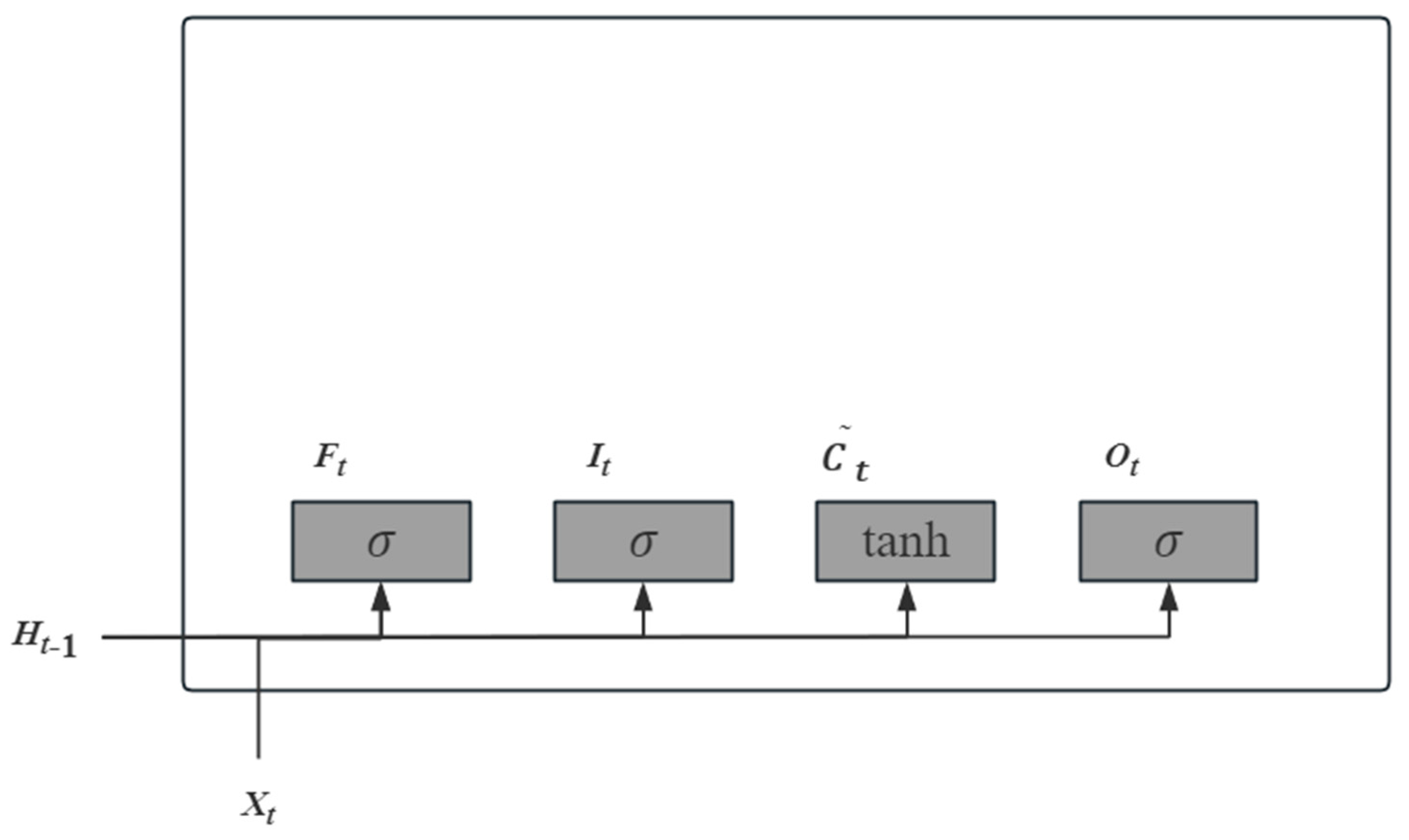The second part is shown in Figure 2,
According to the above figure, we have
C ˜ t = tanh ( X t W x c + H t − 1 W h c + b c )
tanh ( x ) = 1 − e − 2 x 1 + e − 2 x
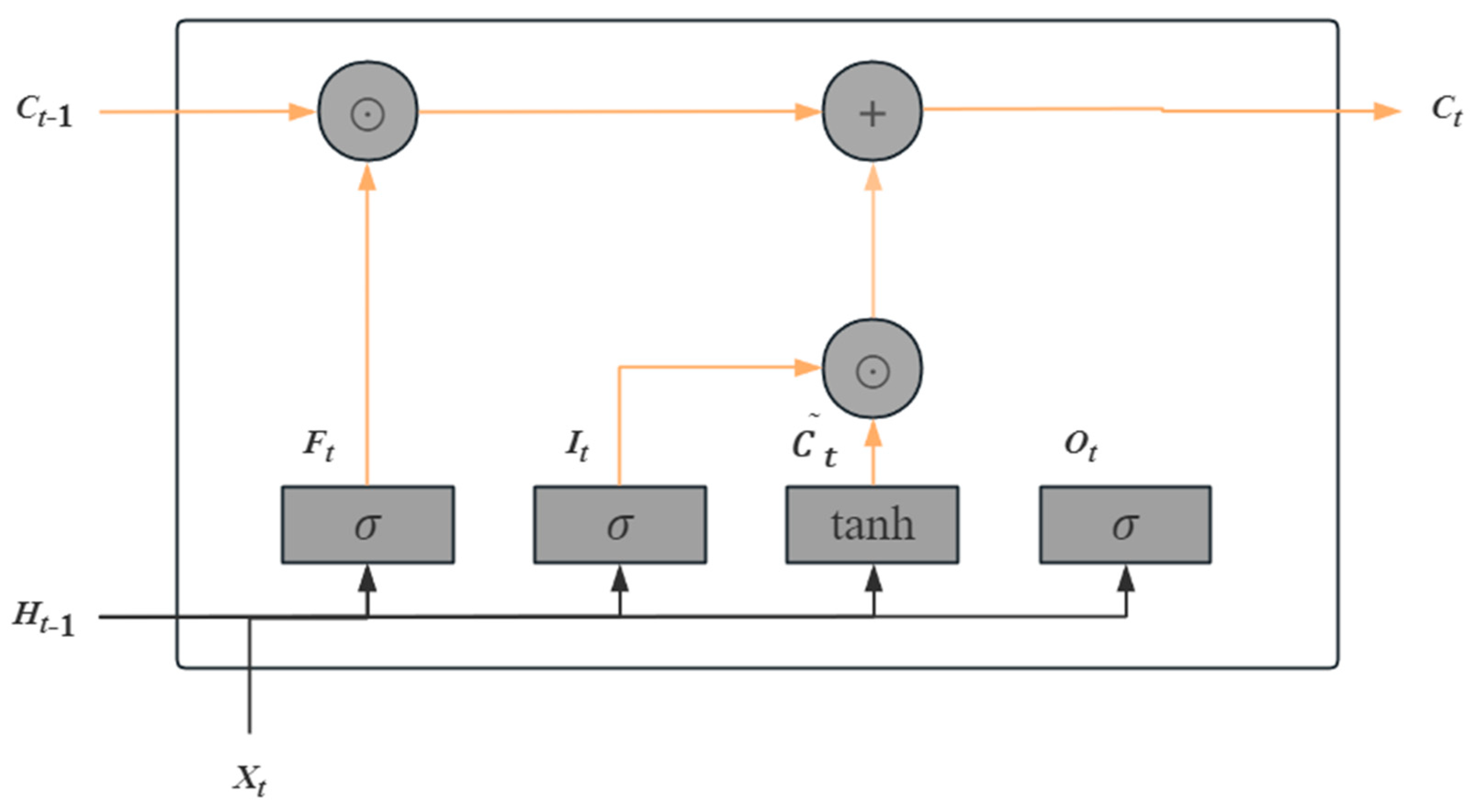
The LSTM requires calculating the candidate memory cell C ˜ t , which similar to the previous three gates, but uses the tanh function as the activation function. After that, the third part is shown in Figure 3.
According to the above figure, we have
C t = F t ⊙ C t − 1 + I t ⊙ C ˜ t
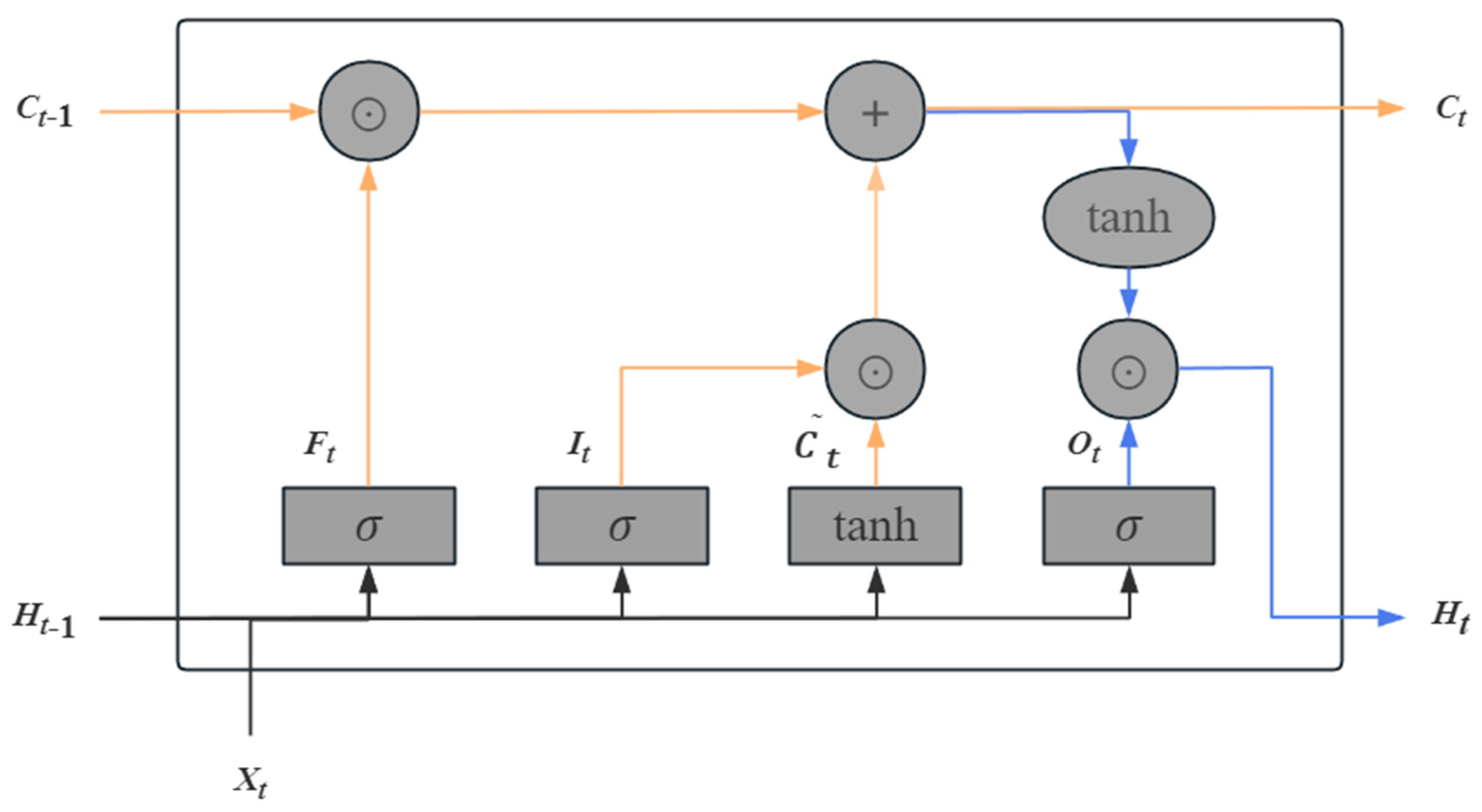
The information flow in the hidden state is controlled by input gates, forget gates, and output gates with element domains in [0,1]. The computation of the current step memory cell Ct combines the information of cell Ct-1 and the current step candidate memory cell and then controls the information flow through the forget gate and the input gate. The fourth part is shown in Figure 4.
According to the above figure, we have
H t = O t ⊙ tanh ( C t )
With the memory cells, the information flow from the memory cells to the hidden state Ht is controlled by an output gate.
After the end of a cycle unit, the hidden state Ht updates parameters and weights through the loss function and optimization algorithm, which means one training is completed. The loss function with Adam's optimization algorithm represents the mean square error.
The error(gt) between the predicted value and the measurement:
g t = ( y ^ ( i ) − y ( i ) ) 2
The optimization algorithm is used to iterate the parameters. The degree of parameter change in each training can be controlled by changing the learning rate. pt (Wx, Wh, b) can be obtained through Adam algorithm as follows,
v t = γ 1 v t − 1 + ( 1 − γ 1 ) g t s t = γ 2 s t − 1 + ( 1 − γ 2 ) g t ⊙ g t
v ^ t = v t 1 − γ 1 t , s ^ t = s t 1 − γ 2 t
g ^ t = η v ^ t s ^ t + τ p t = p t − 1 − g ^ t
where η is the learning rate and is also a hyperparameter that needs to be set by people, 𝛾 is a hyperparameter with domain [0,1]. When the model is put into the training set, and to complete the training, it is then put into the test set for forecasting, and the results are shown graphically against the exact values. The modelling error is expressed using the RMSE and the CC as follows,
RMSE ( X , h ) = 1 m ∑ i = 1 m ( h ( x i ) − y i ) 2
CC = ∑ ( x − x ¯ ) ( y − y ¯ ) ∑ ( x − x ¯ ) 2 ⋅ ∑ ( y − y ¯ ) 2

3.2. The EMD-LSTM Model

Another forecasting model used in this study is the EMD-LSTM model, which is a model that combines the Empirical Mode Decomposition (EMD) method with LSTM. The EMD was proposed by Huang et al. [25] to decompose signals into eigenmodes. The basic principle of the EMD algorithm is firstly find the maximum and minimum points of the original signal X(t) and then fit these extreme points by curve interpolation to obtain the upper envelope Xmax(t) and lower envelope Xmin(t), finally determine the average of upper and lower values:
m 1 ( t ) = X max ( t ) + X min ( t ) 2
The first intrinsic mode function (IMF) can be obtained by subtracting the original signal X(t) from the m1(t), the other IMFs will be obtained in the same way. Finally, the residual component (res) with only one extreme point that cannot be further decomposed will be acquired, which means the algorithm is finished. The core of the EMD algorithm is to decompose the original signal into several IMF components and one res component, which allows the user to extract the interested parts and analyze them in depth.
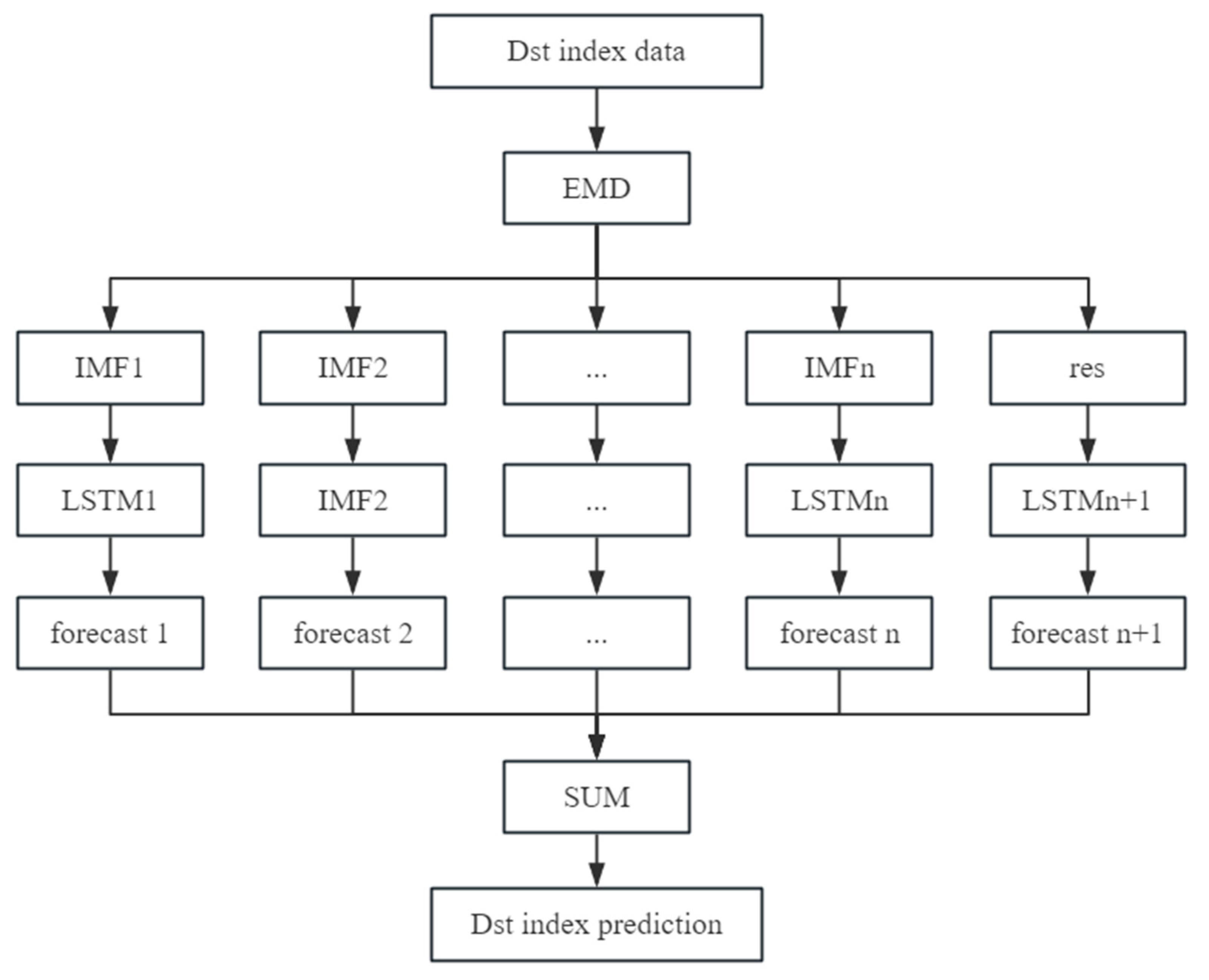
Compared with the LSTM algorithm, the EMD-LSTM is based on the idea that the EMD algorithm decomposes the training data and then put into the LSTM model for training, which effectively reduces the fitting error and improves the prediction accuracy. The working flow chart is as follows,
In Figure 5, the training data is first decomposed by EMD algorithm, then each component is trained by the LSTM model, merge all predictions to get the final prediction.

4. Results

After determining the modelling Dst data, the exact influences of different parameters on the prediction accuracy of the LSTM model will be tested, and the parameters will also be fixed for subsequent training. In order to test the validity and accuracy of the model, the Dst index will be modelled and predicted for the solar quiet and active periods, respectively, and the predictions will be analyzed.

4.1. The Results of the Short-Period Prediction by the LSTM Model

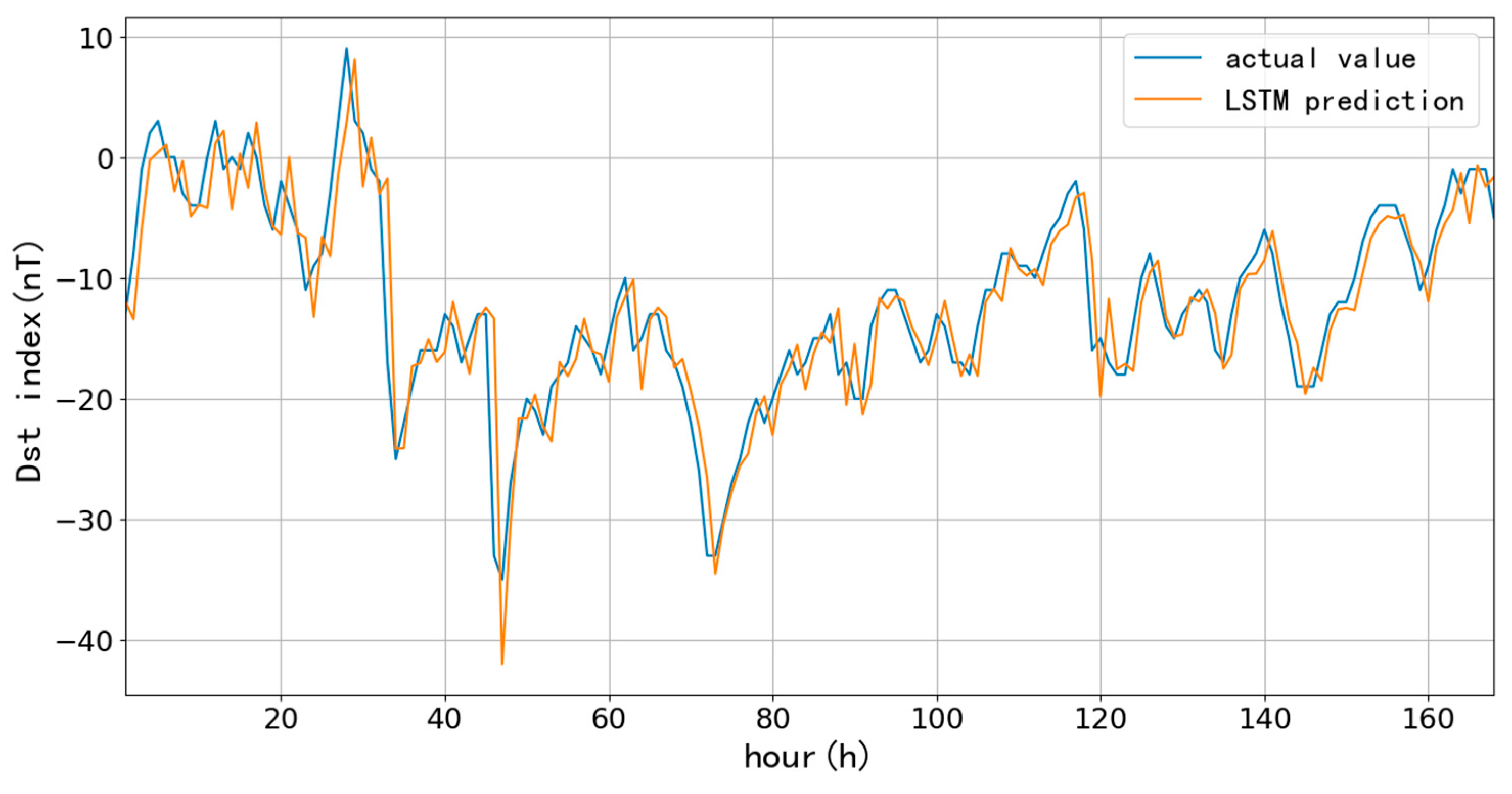
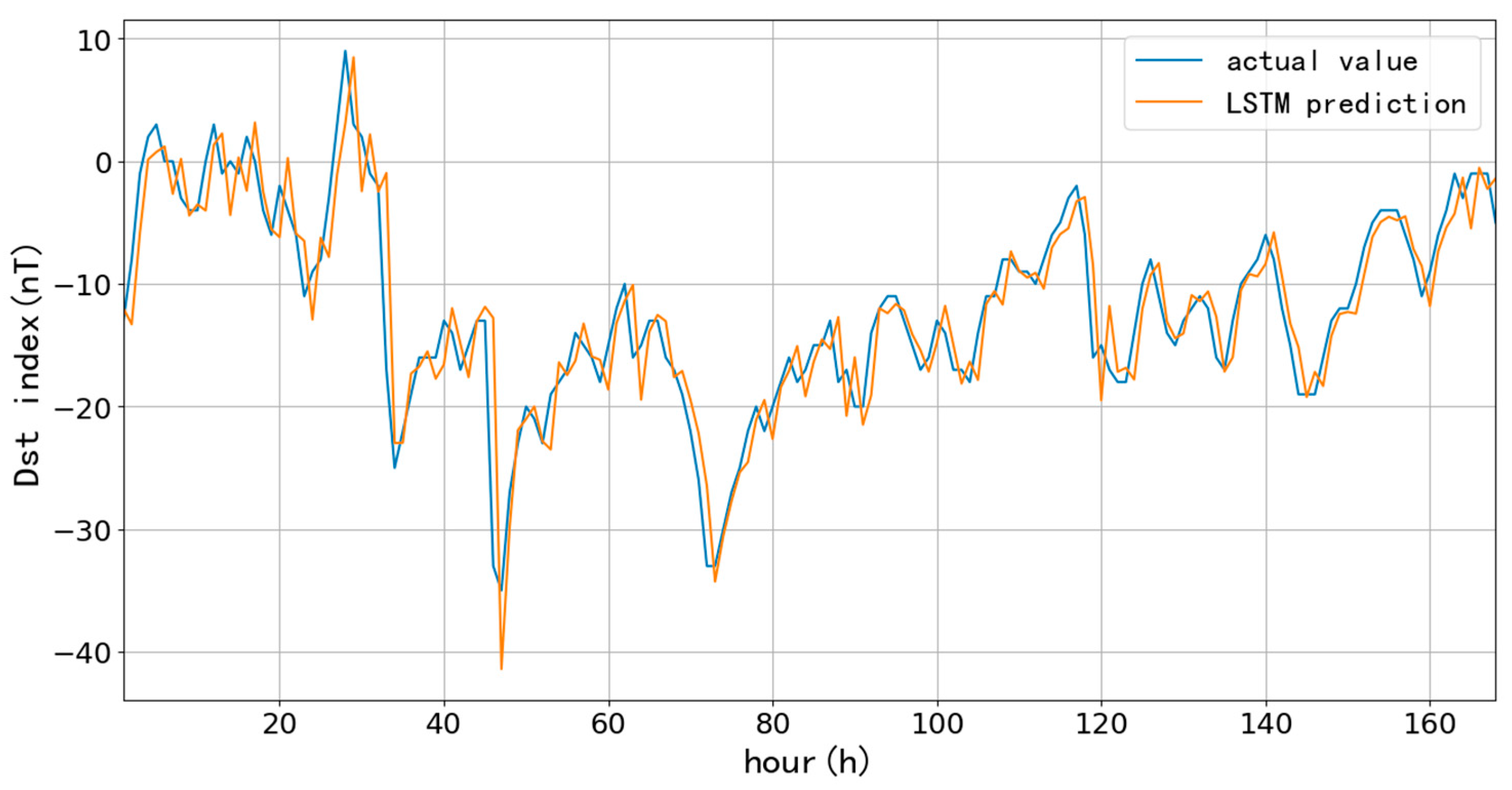
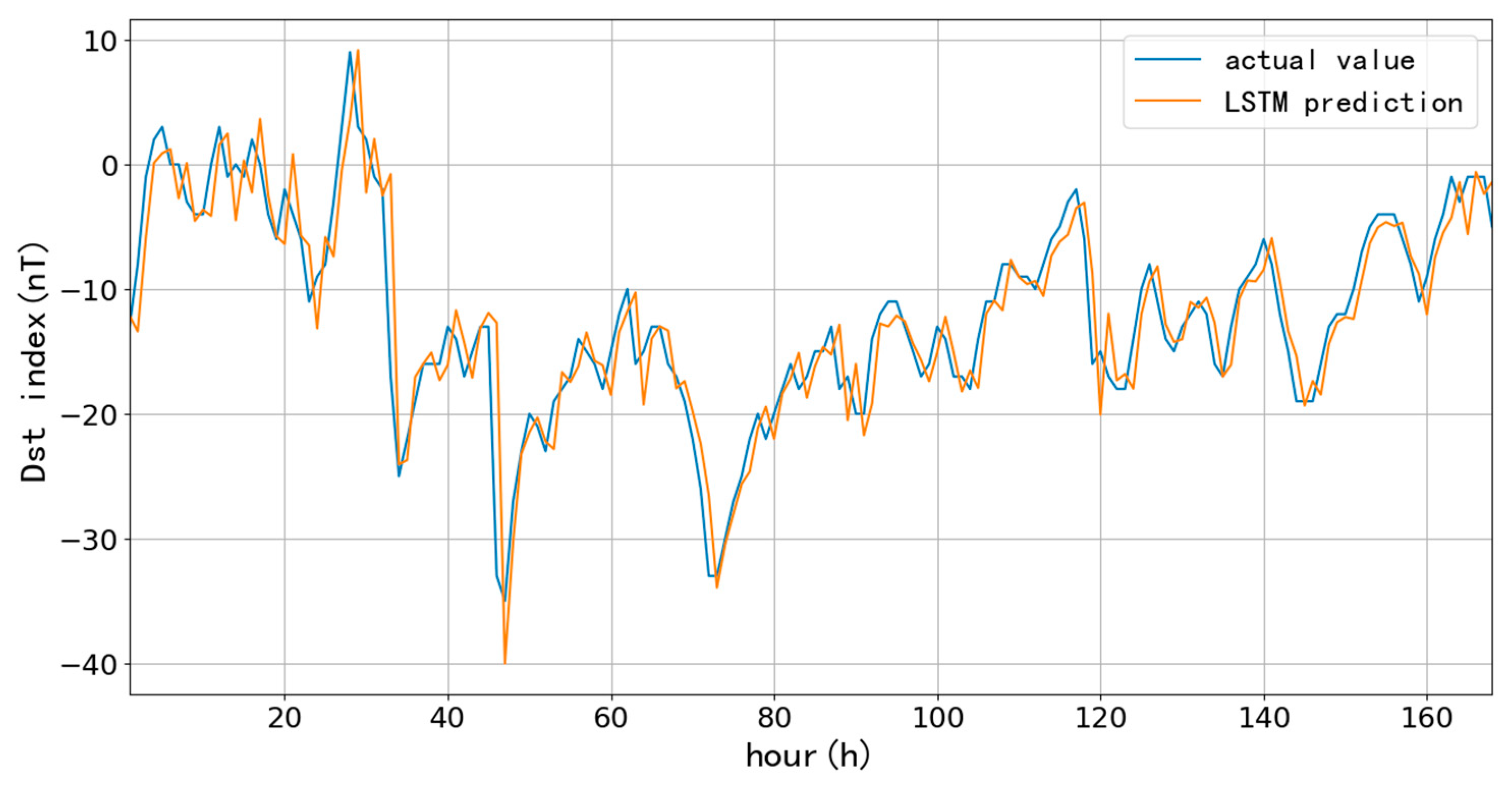
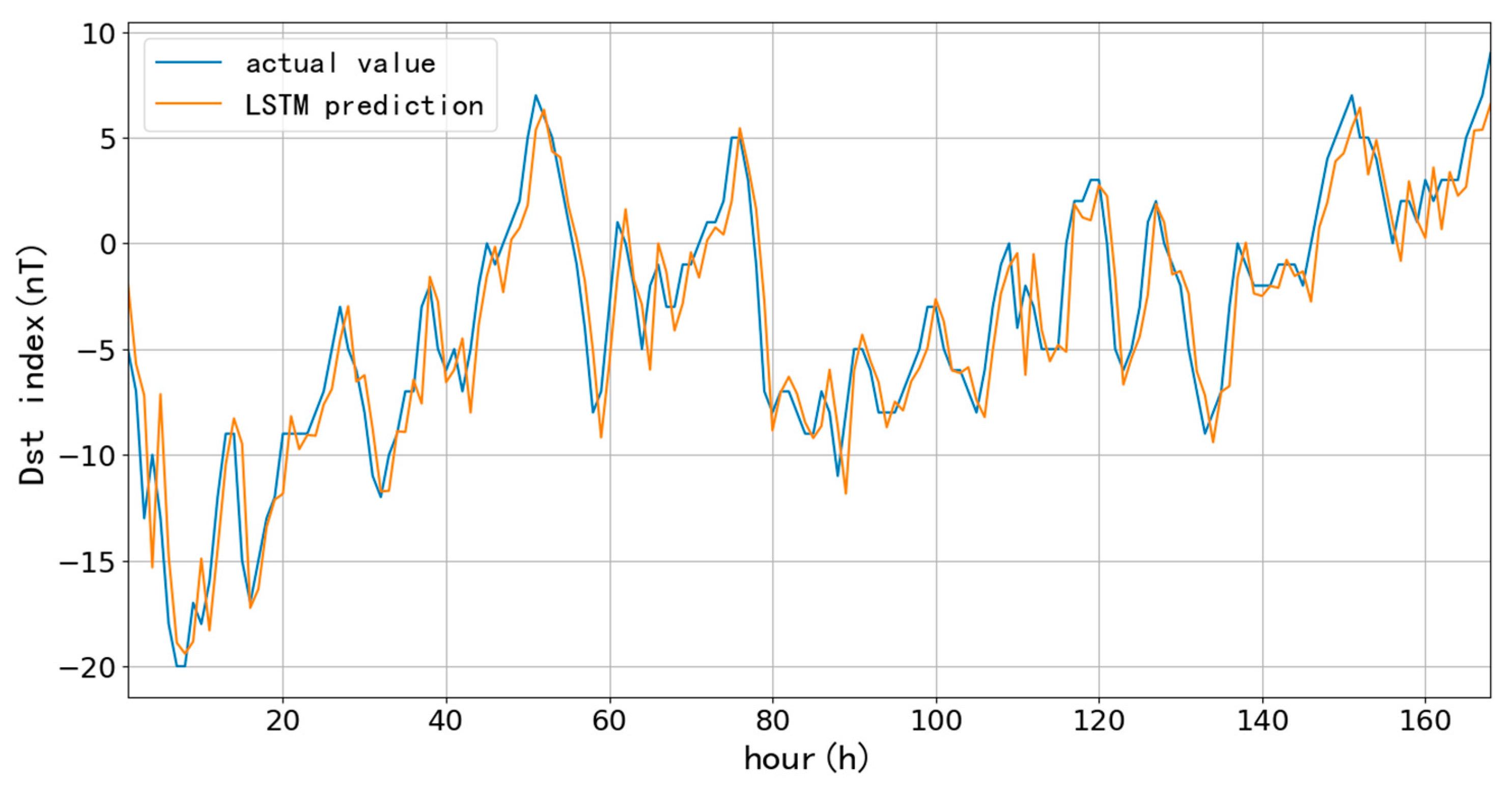
First, we selected 90-day (90 days since January 1, 2015) and 1096-day (three years since January 1, 2015) as training data to test the performance of the LSTM model for short-term (one-hour ahead) prediction, which aims to compare the influences on the prediction accuracy at different learning rates and lengths of training data. The learning rate directly affects the degree of parameter changes after each training; the more minor the parameter, the lower the amplitude of change during each training, and more training times are needed to achieve the ideal fitting effect. Usually, the learning rate is chosen to be 10-3, 10-4, 10-5, and even smaller. Since the number of training times directly affects the training time, 10-3, 10-4, and 10-5 are the learning rates to compare the prediction results. Here, we list the predictions based on 90-day with different learning rates and trainings.
Figure 6, Figure 7 and Figure 8 and Table 1 show the one-hour ahead prediction of 7-day (168 hours) using the 90-day data. As the learning rate decreases, the training number increases by around 400% to keep the close prediction error; the RMSE only decreases by 0.07 nT, and CC increases by 0.01 while the learning rate decreases from 10-3 to 10-5.
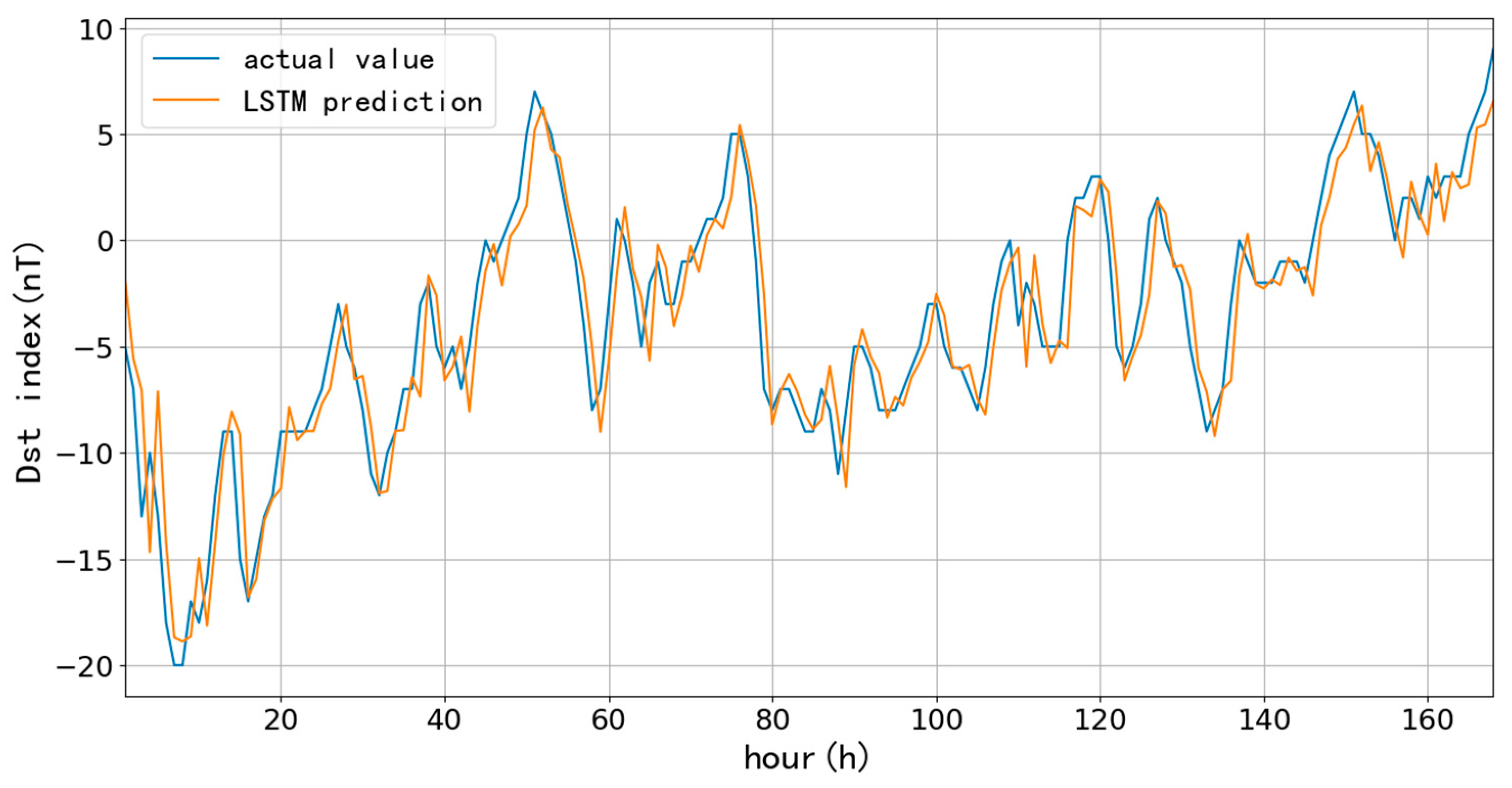
The predictions based on 1096-day are as follows,
Figure 9, Figure 10 and Figure 11 and Table 2 show the results of one-hour ahead predicting the length of 7-day using three years data since 2015. The situation is similar to 90-day’s results; the RMSE only decreases by 0.03 nT while the learning rate changes from 10-3 to 10-5. In addition, the prediction error decreases by about 1.3 nT on average relative to the RMSE of the 90-day data, and the CC improves by 0.03, which suggests that increasing the prediction data can effectively improve the accuracy.
However, the above figures show that the model-predicted values have a noticeable lag using different training data lengths. This lag phenomenon has also been observed in other studies using LSTM for prediction, such as Cai et al. [26], Yin et al. [27]. This stems from the fact that when using the LSTM model for time-series prediction, since the model algorithm is calculated using the values in the fixed time window as samples, in order to minimize the error, using the value at moment t as the prediction value of moment t+1 not only requires no any additional operations, but the error is very tiny, the algorithm will tend to use the value at moment t or t-1 as the prediction value, thus generating a lag in the final prediction. Commonly used solutions include increasing the training data length and indirect prediction. 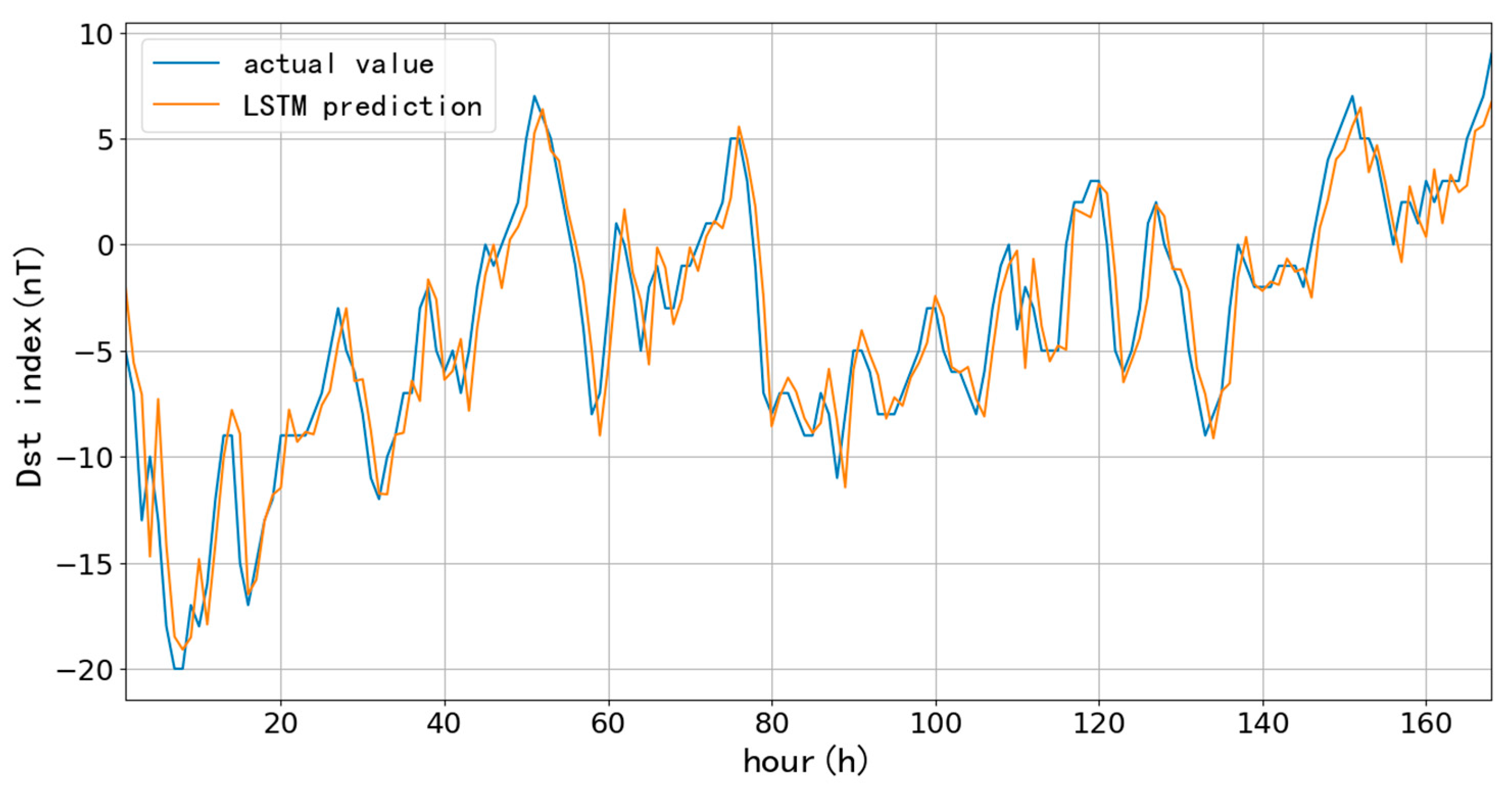To take advantage of the feature of the EMD-LSTM method to obtain segmented average values and then perform LSTM prediction, we take Figure 9 as an example to test as follows,
In Figure 12, Under the same conditions as in Figure 9, using the EMD-LSTM model, the original data is decomposed into 14 components by the EMD algorithm, which are individually predicted by LSTM fitting, and finally merged to obtain the prediction results. The EMD-LSTM model fits better than the LSTM model because the EMD algorithm can split the data series by detecting the peak and valley values of the two curves, which directly and effectively improve the lag in the prediction.
According to the above tests, a lower learning rate has few accuracy improvements. At the same time, the training times and training time increased significantly, so we chose the learning rate of 10-3 for the subsequent model training.
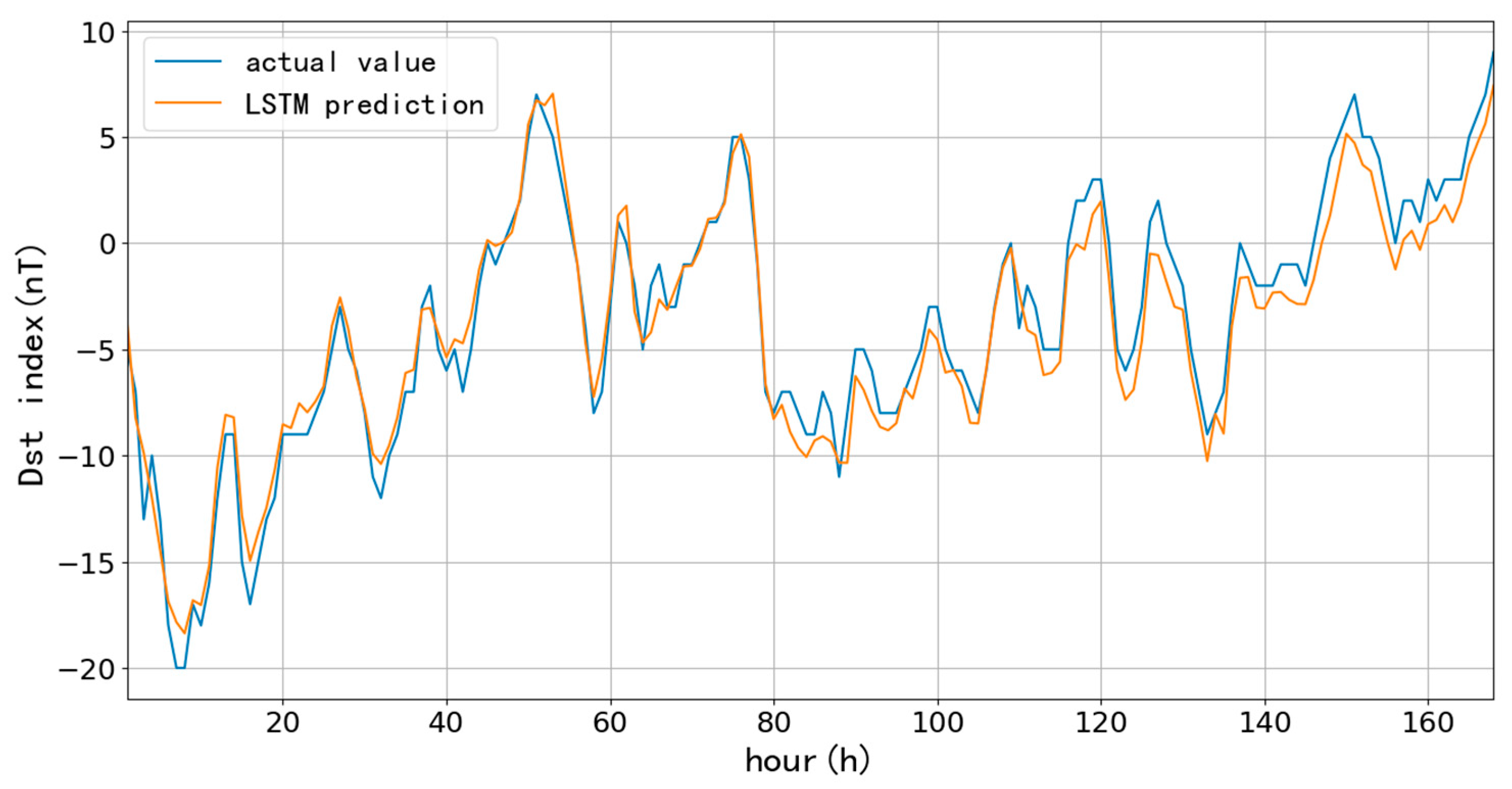
By observing the actual Dst data, the data of 2019 is selected as the test set to predict the quiet period, and the data from January 1, 2023, to May 21 is selected as the test set for active period prediction. The results are as follows.
Figure 13 shows the results of using the 2018 Dst data, with one-hour ahead forecasting for 2019. It finds that the fitted values agree well with the actual values, the RMSE is 2.64 nT, and CC is 0.97, and the precision of results is between the results of 90-day and 1096-day data by LSTM.
In order to further test the model, the dramatic changes of Dst indices in 2023 are now predicted based on the 2022 data, and we expect to model and predict the corresponding geomagnetic storms. The following are the results based on the LSTM model.
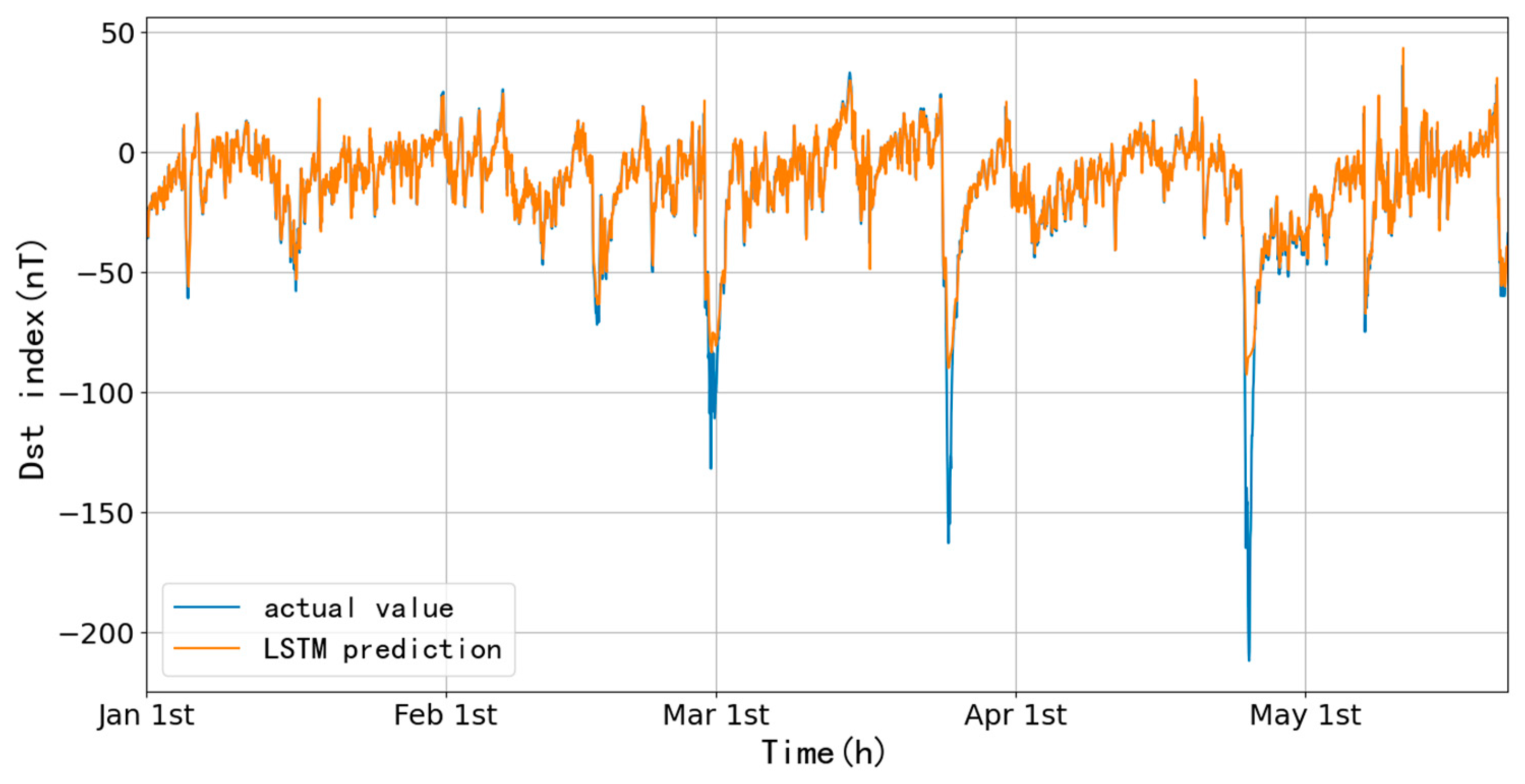
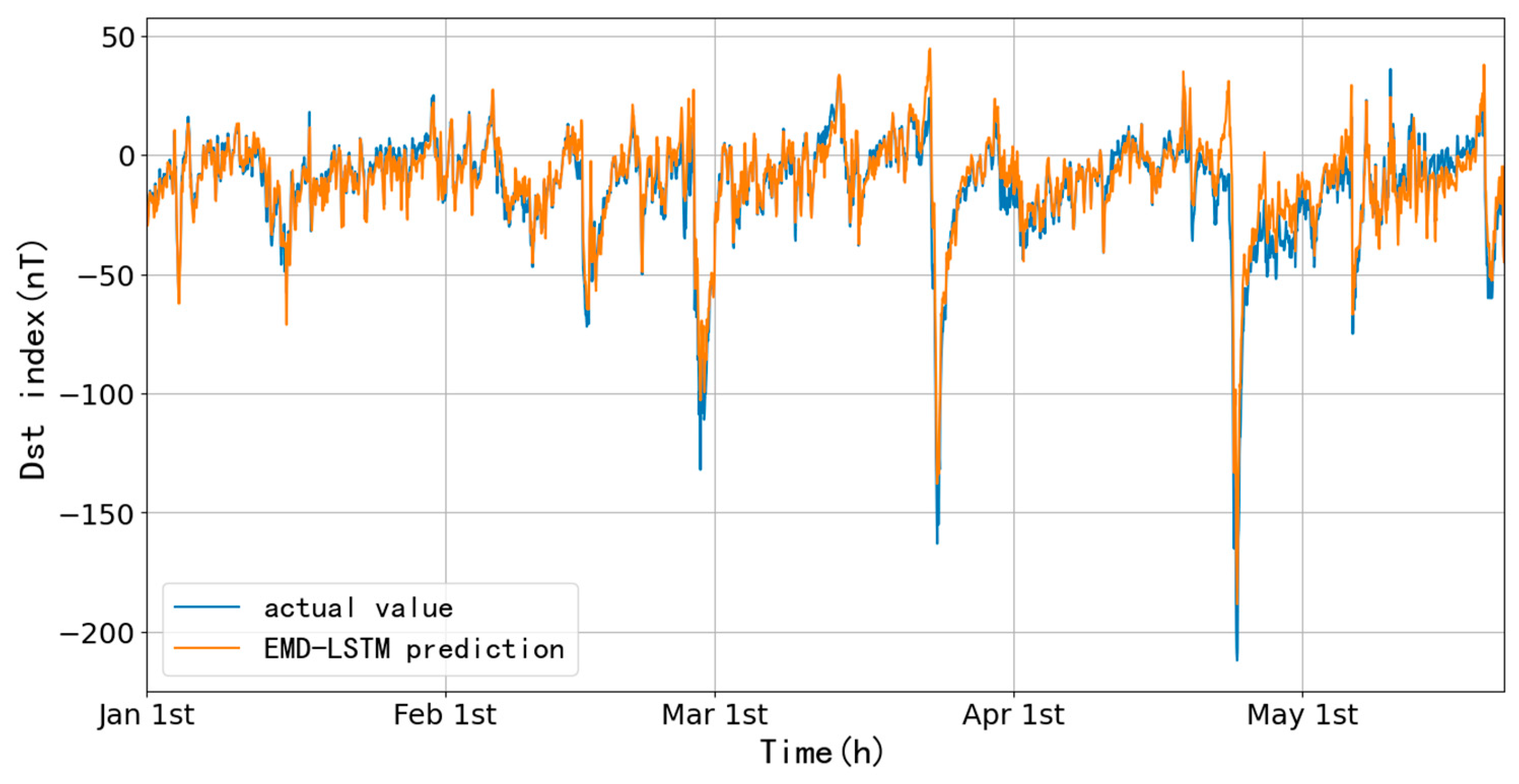
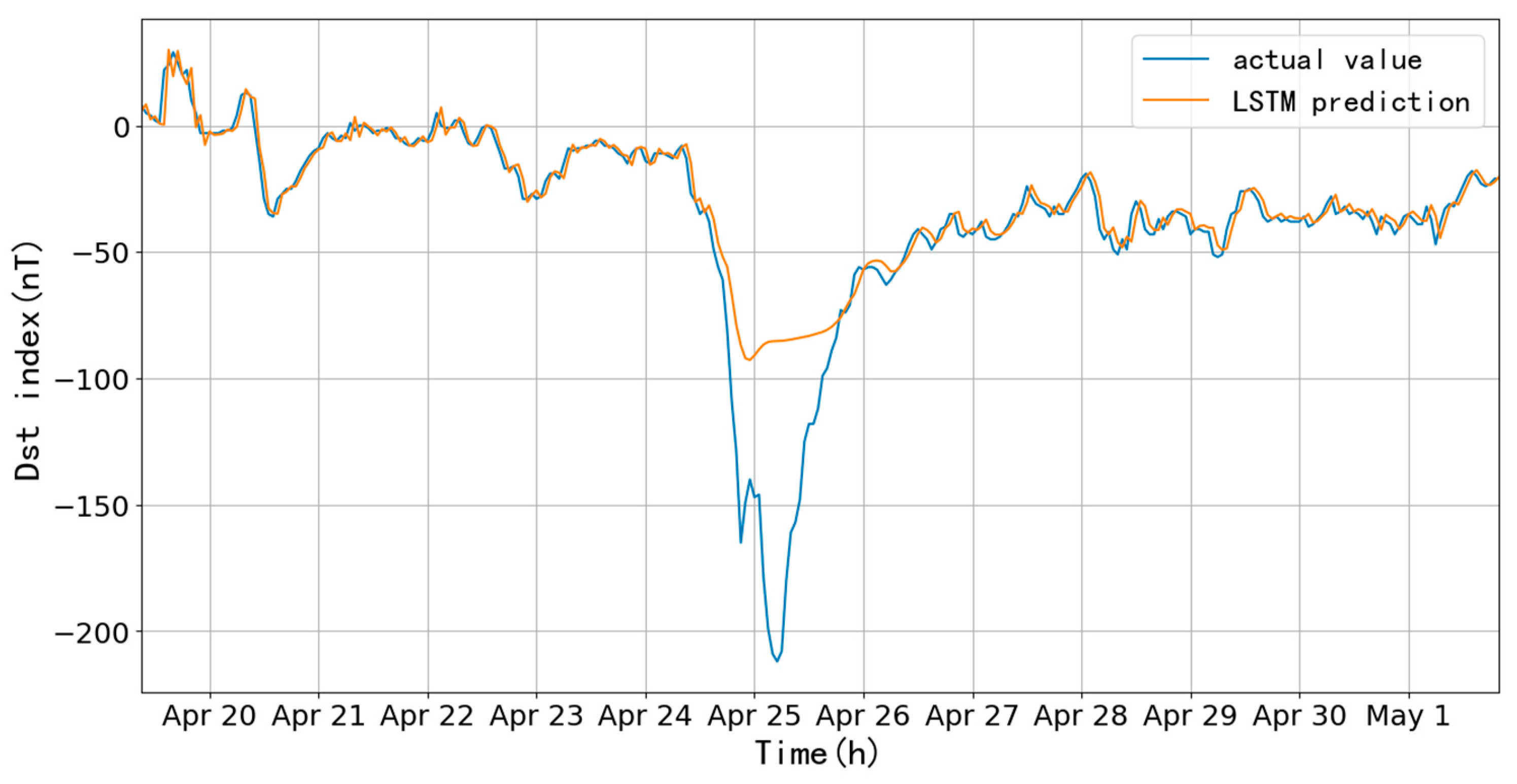
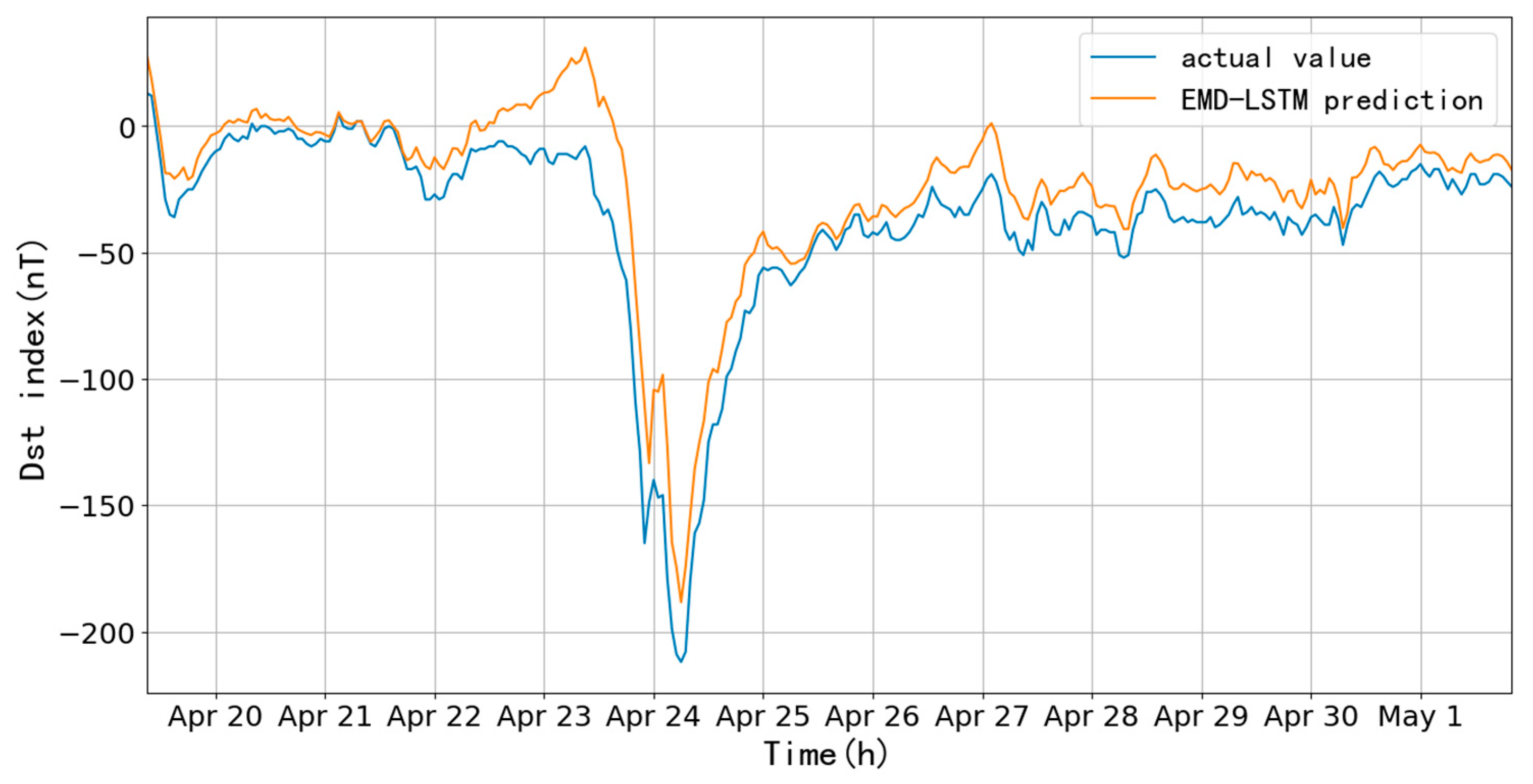
Figure 14 shows the one-hour ahead prediction of the data from January 1 to May 21, 2023, with an RMSE of 7.34 nT and CC of 0.96, using the Dst data of 2022. The storm with the largest amplitude occurred on April 24, and its prediction results are shown in Figure 15, with an RMSE of 20.47 nT and CC of 0.91 before and after the storm (300 h). It is found that the fitting before and after the storm valley is good, while the prediction of the main phase is not good, the difference is more than 100 nT.

4.2. The Results of the Short-Period Prediction by the EMD-LSTM Model

In order to effectively solve the time lag problem and to improve the accuracy of the prediction, the EMD-LSTM method is used to predict the Dst index in 2019 and 2023. Following is a part of the forecast results for the quiet period.
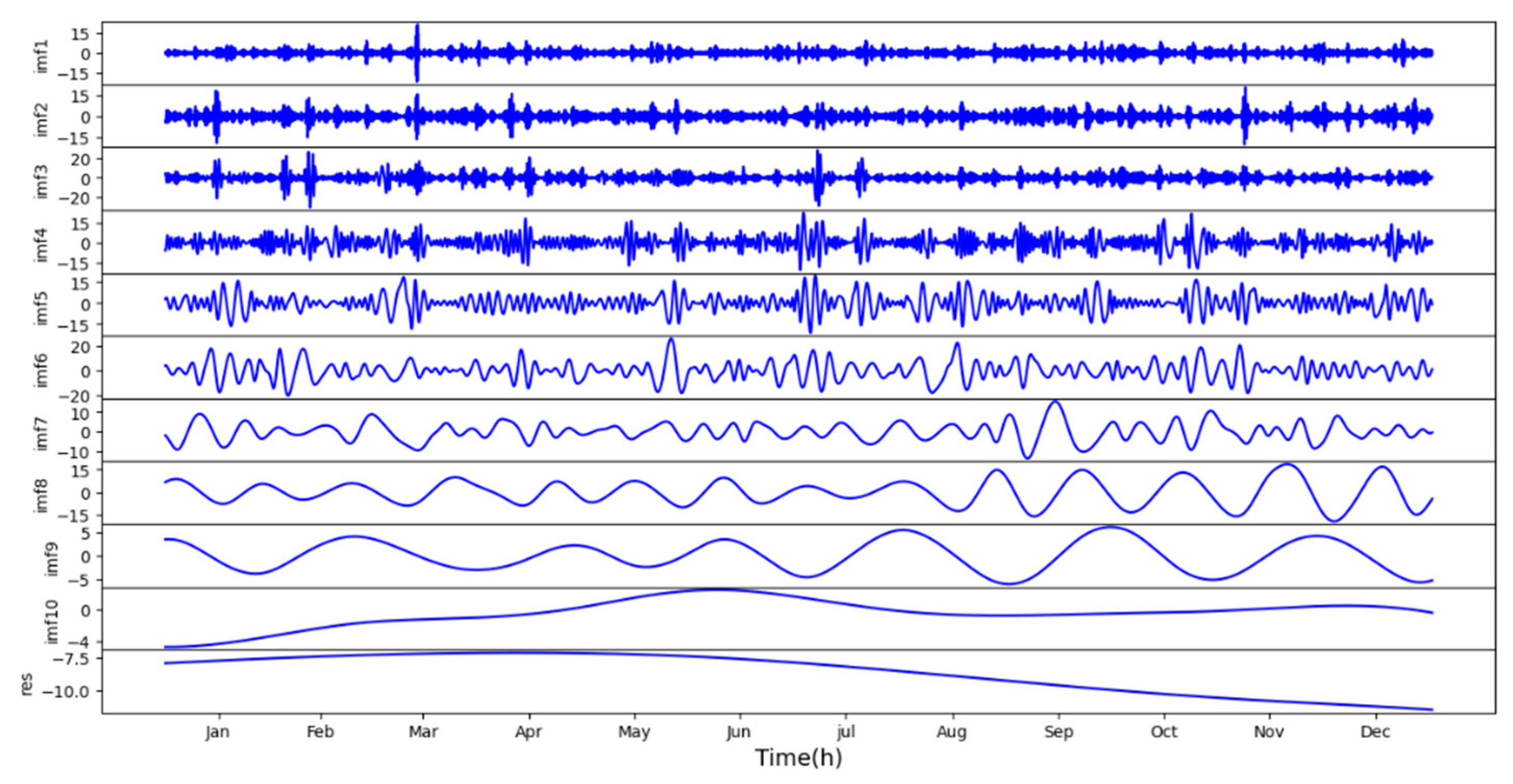
Figure 16 shows that the EMD algorithm mathematically decomposites the original Dst index data into several wavelength components. Each part possesses different characteristics (determined by the original data), and the complexity of these components decreases in order. The error during model training is mainly concentrated in the first few components rather than the entire Dst indices, so using EMD-LSTM can make the prediction closer to the actual value.
We first predict the data for 2019,
Figure 17 shows the result of using the Dst data 2018, making a one-hour ahead prediction, and predicting the data of 2019. The RMSE is 3.29 nT, and the r is 0.95, which makes the prediction effect more satisfactory. Relative to the LSTM method, RMSE increased by 0.65 nT, and CC decreased by 0.02.
Then, we test the prediction for 2023.
Figure 18 shows the different parts of the 2022 Dst index decomposed by the EMD.
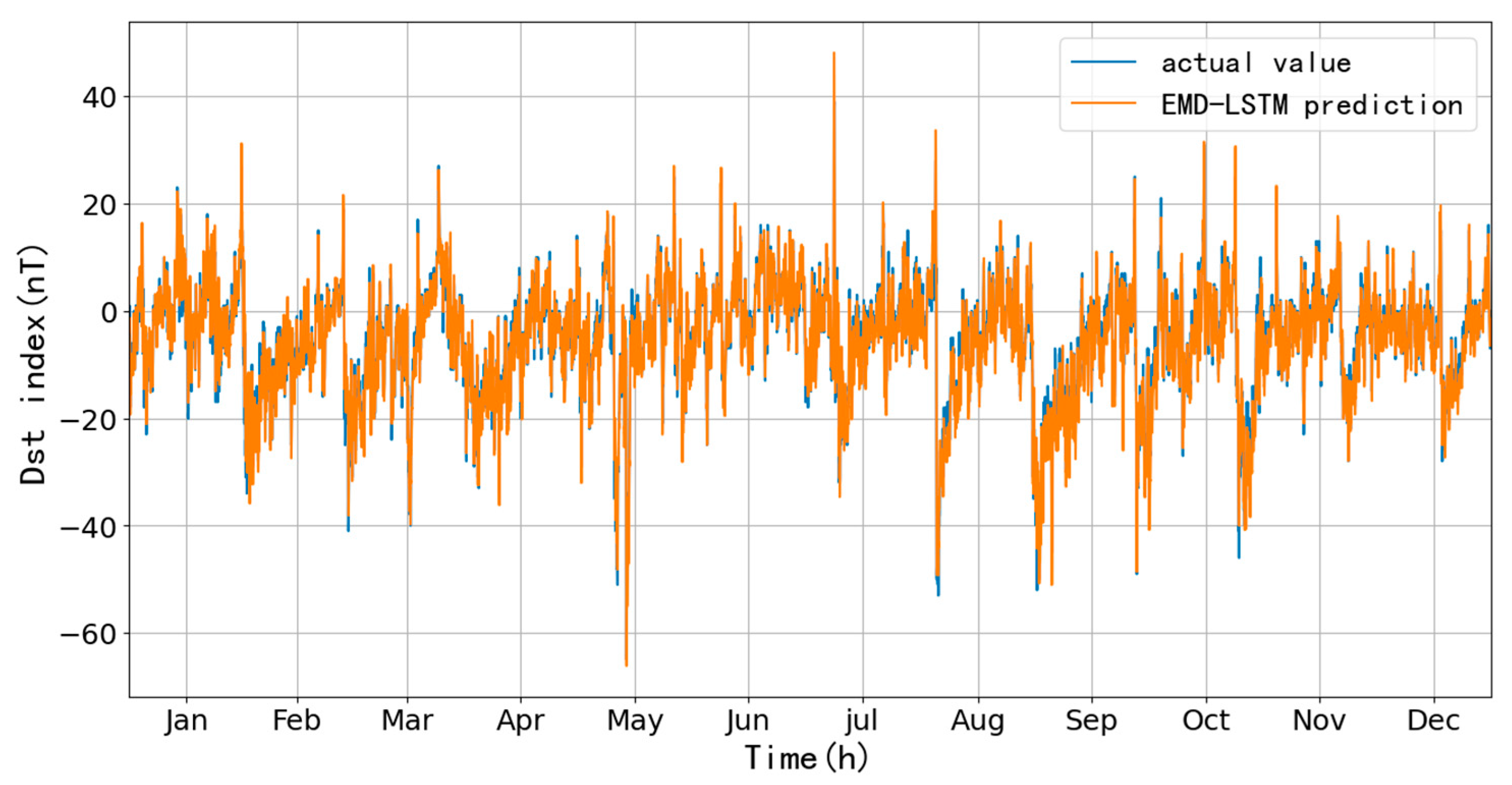
Figure 19 shows a one-hour ahead prediction from January 1-May 21, 2023, using the 2022 Dst data; results show the RMSE is 8.87 nT, and CC is 0.93, an increase of 1.53 nT in RMSE and a decrease of 0.03 in CC concerning the LSTM method, the fitting of the main phase is obviously better than the LSTM.
For further inspection, here we list the modelling of the geomagnetic storm on April 24, 2023.
Figure 20 shows that the modelling is highly consistent in the start timing, amplitude, and recovery value of the magnetic storm. In the period before and after the storm (300 hours), the RMSE is 16.91 nT, and CC is 0.96; they reduced by 3.56 nT and improved by 0.05 compared to the LSTM model. The fitted values are slightly higher during the initial and main phases, while they are more consistent during the recovery phase. The Dst index during the main phase can be effectively and precisely predicted. In addition, the lag of the predicted values is greatly improved by the indirect prediction through the decomposition of the original data by the EMD algorithm.
Comparing the two methods, from the viewpoint of RMSE and CC, LSTM is slightly better than EMD-LSTM, but EMD-LSTM is better during the magnetic storm.

5. Conclusion and Discussions

In this study, the LSTM and the EMD-LSTM models were trained and predicted by observing and comparing the exact Dst index, and selecting appropriate data segments. The factors affecting the prediction accuracy of the LSTM model were first tested, and the parameters used in the LSTM model were determined. Then, the two models were used to predict the Dst index for the quiet and active periods. After analyzing the prediction results, the related conclusions are given as follows:
1. In predicting the Dst index by the LSTM model, the decrease in the learning rate and the increase in the number of training times have no significant influences on improving the prediction accuracy. When using 90-day length data for 7-day prediction, the change of the RMSE is within 0.1 nT, and the CC varies around 0.01 under different learning rates. The change of the RMSE is within 0.05 nT, and r does not change when using 1,096-day data, whereas increasing the training data length can improve the prediction accuracy. The prediction accuracy can be improved by increasing the length of the training data; the RMSE decreases from an average of 3.25 nT to 1.95 nT, and the r improves from 0.91 to 0.94 when using 1096 days of data, which suggests that the base dataset is a critical factor in controlling the prediction;
2. The LSTM and the EMD-LSTM model have a better Dst prediction for the quiet period than the active period. The reason is that the fluctuation of the Dst index during the quiet period is slight (±50 nT), so the resulting model based on higher temporal resolution (time-averaged) is robust. The interferences from other factors, especially the solar activity, are less in the quiet period; combining the appropriate training rate and training times can predict the Dst changes better. During geomagnetic storms, the fluctuation amplitude of Dst caused by the solar wind can reach several hundred nT or more; compared to the use of the LSTM model, the error is significantly reduced while training data decomposed by the EMD algorithm and then put into the LSTM training, particular during the big magnetic storm, but the overall prediction accuracy is lower the LSTM;
3. Although the overall prediction accuracy of the LSTM model is slightly higher than the EMD-LSTM model (the RMSE is reduced by about 1.5 nT, and the CC is improved by about 0.03), however, there is a noticeable lag in the prediction results of the former, which is generated with a small error because the Dst index is a time series data, and the difference between its neighboring units is usually tiny. In practical applications, it is appropriate to select a suitable model by referencing the intensity of solar activity, such as sunspot number, and if its value is high, the EMD-LSTM model can be chosen, or the LSTM model while the situation is opposite. If the error requirement is not strict, using the LSTM method with a higher learning rate is economical to reduce the computation amount and satisfy the accuracy requirement.
There are also some shortcomings in this study; the models only use one kind of data for training and prediction and lack the necessary physical constraints, so the next step will be to screen other space weather indices, try to select indices with higher correlation with the Dst index such as the magnetospheric ring current index (RC index), geomagnetic perturbation index (Ap index) for constraints and co-estimating, using multiple input parameters to training and predicting, and obtained the realistic prediction results by adding physical constraints.
In this study, the LSTM and the EMD-LSTM models are tested for their ability of Dst index prediction, which proves the effectiveness of deep learning methods and can be used to improve the prediction accuracy of the model by changing some factors like the model parameters, length of training data, processing of training data, replacing the training data. Thus, it is worthy of a deeper study in the future. The newly launched MSS-1 satellite [28], which provides high accuracy and nearly east-west oriented (inclination angle of 41°) magnetic field data, can lay the solid foundation for studying the removal of the external field interference and even for the study of short-term changes in the ionospheric field and the magnetospheric ring current.

Author Contributions

Conceptualization, Y.F; methodology, JY.Z. and Y.F.; software, Y.L. and JX.Z.; validation, Y.F; writing—original draft preparation, Y.F; writing—review and editing, Y.F; supervision, Y.F.; funding acquisition, Y.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (42250103, 41974073, 41404053), the Macau Foundation and the pre-research project of Civil Aerospace Technologies (Nos. D020308), the Specialized Research Fund for State Key Laboratories.

Data Availability Statement

All measuring data will be available upon request.

Acknowledgments

We acknowledge the High Performance Computing Center of Nanjing University of Information Science & Technology for their support of this work, we also thank the reviewers for their constructive comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sugiura, M. Hourly values of equatorial Dst for the IGY. Annals of the International Geophysical Year. 1964, 35, 9–45. [Google Scholar]
  2. Wu, Y.Y. Problems and thoughts on the Dst index of geomagnetic activity. Advances in Geophysics. 2022, 37, 1512–1519. [Google Scholar]
  3. Tran, Q.A.; Sołowski, W.; Berzins, M.; Guilkey, J. A convected particle least square interpolation material point method. Int J Numer Methods Eng. 2020, 121, 1068–1100. [Google Scholar] [CrossRef]
  4. Sun, Z.J.; Xue, L.; Xu, Y.M.; et al. A review of deep learning research. Computer Applications Research. 2012, 29, 2806–2810. [Google Scholar]
  5. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural computation. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  6. Yang, L.; Wu, Y.X.; Wang, J.L.; Liu, Y.L. A review of recurrent neural network research. Computer Applications. 2018, 38, 1–6. [Google Scholar]
  7. Liu, J.Y.; Shen, C.L. Forecasting Dst index using artificial intelligence method. China Earth Science Joint Academic Conference. Proceedings of the 2021 China Joint Academic Conference on Earth Sciences (I)-Topic I Solar Activity and Its Space Weather Effects, Topic II Plasma Physical Processes in the Magnetosphere, Topic III Planetary Physics (pp. 12). Beijing Berton Electronic Publishing House 2021. [CrossRef]
  8. Kim, R.S.; Cho, K.S.; Moon, Y.J.; et al. An empirical model for prediction of geomagnetic storms using initially observed CME parameters at the Sun. Journal of Geophysics. 2010, 115, A12108. [Google Scholar] [CrossRef]
  9. Kremenetskiy, I.A.; Salnikov, N.N. Minimax Approach to Magnetic Storms Forecasting (Dst-index Forecasting). Journal of Automation and Information Sciences. 2011, 3, 67–82. [Google Scholar] [CrossRef]
  10. Tobiska, W.K.; Knipp, D.; Burke, W.J.; et al. The Anemomilos prediction methodology for Dst. Space Weather. 2013, 11, 490–508. [Google Scholar] [CrossRef]
  11. Banerjee, A.; Bej, A.; Chatterjee, T.N. A cellular automata-based model of Earth's magnetosphere in relation with Dst index. Space Weather 2015, 13, 259–270. [Google Scholar] [CrossRef]
  12. Chandorkar, M.; Camporeale, E.; Wing, S. Probabilistic forecasting of the disturbance storm time index: An autoregressive Gaussian process approach. Space Weather. 2017, 15, 1004–1019. [Google Scholar] [CrossRef]
  13. Bej, A.; Banerjee, A.; Chatterjee, T.N.; et al. One-hour ahead prediction of the Dst index based on the optimum state space reconstruction and pattern recognition. Eur. Phys. J. Plus. 2022, 137, 479. [Google Scholar] [CrossRef]
  14. Nilam, B.; Tulasi Ram, S. Forecasting Geomagnetic activity (Dst Index) using the ensemble kalman filter. Monthly Notices of the Royal Astronomical Society. 2022, 511, 723–731. [Google Scholar] [CrossRef]
  15. Chen, C.; Sun, S.J.; Xu, Z.W.; Zhao, Z.W.; Wu, Z.S. Forecasting Dst index one hour in advance using neural network technique. Journal of Space Science 2011, 31, 182–186. [Google Scholar]
  16. Revallo, M.; Valach, F.; Hejda, P.; et al. A neural network Dst index model driven by input time histories of the solar wind–magnetosphere interaction. Journal of Atmospheric and Solar-Terrestrial Physics. 2014, 110–111, 9–14. [Google Scholar] [CrossRef]
  17. Lu, J.Y.; Peng, Y.X.; Wang, M.; et al. Support Vector Machine combined with Distance Correlation learning for Dst forecasting during intense geomagnetic storms. Planetary and Space Science. 2016, 120, 48–55. [Google Scholar] [CrossRef]
  18. Andriyas, T.; Andriyas, S. Use of Multivariate Relevance Vector Machines in forecasting multiple geomagnetic indices. Journal of Atmospheric and Solar-Terrestrial Physics. 2017, 154, 21–32. [Google Scholar] [CrossRef]
  19. Lethy, A.; El-Eraki, M.A.; Samy, A.; et al. Prediction of the Dst index and analysis of its dependence on solar wind parameters using neural network. Space Weather. 2018, 16, 1277–1290. [Google Scholar] [CrossRef]
  20. Xu, S.; Huang, S.; Yuan, Z.; et al. Prediction of the Dst index with bagging ensemble-learning algorithm. The Astrophysical Journal: Supplement Series. 2020, 248, 14. [Google Scholar] [CrossRef]
  21. Park, W.; Lee, J.; Kim, K.C.; Lee, J.; Park, K.; et al. Operational Dst index prediction model based on combination of artificial neural network and empirical model. Journal of Space Weather and Space Climate. 2021, 11, 38. [Google Scholar] [CrossRef]
  22. Hu, A.; Shneider, C.; Tiwari, A.; et al. Probabilistic prediction of Dst storms one-day-ahead using full-disk SoHO images. Space Weather. 2022, 20, e2022SW003064. [Google Scholar] [CrossRef]
  23. Zhang, H.; Xu, H.R.; Peng, G.S.; Qian, Y.D.; Zhang, X.X.; Yang, G.L.; et al. A prediction model of relativistic electrons at geostationary orbit using the EMD-LSTM network and geomagnetic indices. Space Weather. 2022, 20, e2022SW003126. [Google Scholar] [CrossRef]
  24. Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks. 2005, 18, 5–6. [Google Scholar] [CrossRef]
  25. Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. P Roy Soc Lond A Mat Proceedings Mathematical Physical & Engineering Sciences. 1998, 454, 903–995. [Google Scholar] [CrossRef]
  26. Cai, J.; Dai, X.; Hong, L.; Gao, Z.; Qiu, Z. An air quality prediction model based on a noise reduction self-coding deep network. Mathematical Problems in Engineering. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
  27. Yin, H.; Jin, D.; Gu, Y.H.; Park, C.J.; Han, S.K.; Yoo, S.J. STL-ATTLSTM: Vegetable Price Forecasting Using STL and Attention Mechanism-Based LSTM. Agriculture 2020, 10, 612. [Google Scholar] [CrossRef]
  28. Zhang, K. A novel geomagnetic satellite constellation: Science and applications. Earth and Planetary Physics. 2023, 7, 4–21. [Google Scholar] [CrossRef]
Preprints 86076 g001
Figure 1. The first part of a single recurrent unit of the LSTM model.
Figure 1. The first part of a single recurrent unit of the LSTM model.
Preprints 86076 g001
Preprints 86076 g002
Figure 2. The second part of a single recurrent unit of the LSTM model.
Figure 2. The second part of a single recurrent unit of the LSTM model.
Preprints 86076 g002
Preprints 86076 g003
Figure 3. The third part of a single recurrent unit of the LSTM model.
Figure 3. The third part of a single recurrent unit of the LSTM model.
Preprints 86076 g003
Preprints 86076 g004
Figure 4. The fourth part of a single recurrent unit of the LSTM model.
Figure 4. The fourth part of a single recurrent unit of the LSTM model.
Preprints 86076 g004
Preprints 86076 g005
Figure 5. The overall structure of EMD-LSTM model.
Figure 5. The overall structure of EMD-LSTM model.
Preprints 86076 g005
Preprints 86076 g006
Figure 6. The model prediction through 650 trainings with a learning rate of 10-3.
Figure 6. The model prediction through 650 trainings with a learning rate of 10-3.
Preprints 86076 g006
Preprints 86076 g007
Figure 7. The model prediction through 3400 trainings with a learning rate of 10-4.
Figure 7. The model prediction through 3400 trainings with a learning rate of 10-4.
Preprints 86076 g007
Preprints 86076 g008
Figure 8. The model prediction through 20000 trainings with a learning rate of 10-5.
Figure 8. The model prediction through 20000 trainings with a learning rate of 10-5.
Preprints 86076 g008
Preprints 86076 g009
Figure 9. The model prediction through 650 trainings with a learning rate of 10-3.
Figure 9. The model prediction through 650 trainings with a learning rate of 10-3.
Preprints 86076 g009
Preprints 86076 g010
Figure 10. The model prediction through 3300 trainings with a learning rate of 10-4.
Figure 10. The model prediction through 3300 trainings with a learning rate of 10-4.
Preprints 86076 g010
Preprints 86076 g011
Figure 11. The model prediction through 18000 trainings with a learning rate of 10-5.
Figure 11. The model prediction through 18000 trainings with a learning rate of 10-5.
Preprints 86076 g011
Preprints 86076 g012
Figure 12. Results of the EMD-LSTM model when using the same parameters as in Figure 9.
Figure 12. Results of the EMD-LSTM model when using the same parameters as in Figure 9.
Preprints 86076 g012
Preprints 86076 g013
Figure 13. Results of model prediction through 750 training sessions at a learning rate of 10-3.
Figure 13. Results of model prediction through 750 training sessions at a learning rate of 10-3.
Preprints 86076 g013
Preprints 86076 g014
Figure 14. The model prediction through 750 trainings with a learning rate of 10-3.
Figure 14. The model prediction through 750 trainings with a learning rate of 10-3.
Preprints 86076 g014
Preprints 86076 g015
Figure 15. Predictions before and after the April 24, 2023 geomagnetic storm.
Figure 15. Predictions before and after the April 24, 2023 geomagnetic storm.
Preprints 86076 g015
Preprints 86076 g016
Figure 16. Data decomposition via EMD based on 2018 Dst index.
Figure 16. Data decomposition via EMD based on 2018 Dst index.
Preprints 86076 g016
Preprints 86076 g017
Figure 17. Results of model prediction through 600 training sessions at a learning rate of 10-3.
Figure 17. Results of model prediction through 600 training sessions at a learning rate of 10-3.
Preprints 86076 g017
Preprints 86076 g018
Figure 18. Results of Dst index data decomposition by the EMD method in 2022.
Figure 18. Results of Dst index data decomposition by the EMD method in 2022.
Preprints 86076 g018
Preprints 86076 g019
Figure 19. The model prediction through 650 trainings with a learning rate of 10-3.
Figure 19. The model prediction through 650 trainings with a learning rate of 10-3.
Preprints 86076 g019
Preprints 86076 g020
Figure 20. Predictions of geomagnetic storm on April 24, 2023.
Figure 20. Predictions of geomagnetic storm on April 24, 2023.
Preprints 86076 g020
Table 1. The 7-day length prediction using 90-day data.
Table 1. The 7-day length prediction using 90-day data.
Learning Rate Trainings RMSE (nT) CC
10-3 650 3.27 0.91
10-4 3400 3.29 0.91
10-5 20000 3.20 0.92
Table 2. The 7-day length prediction using 1096-day of data.
Table 2. The 7-day length prediction using 1096-day of data.
Learning Rate Trainings RMSE (nT) CC
10-3 650 1.97 0.94
10-4 3300 1.95 0.94
10-5 18000 1.94 0.94
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated