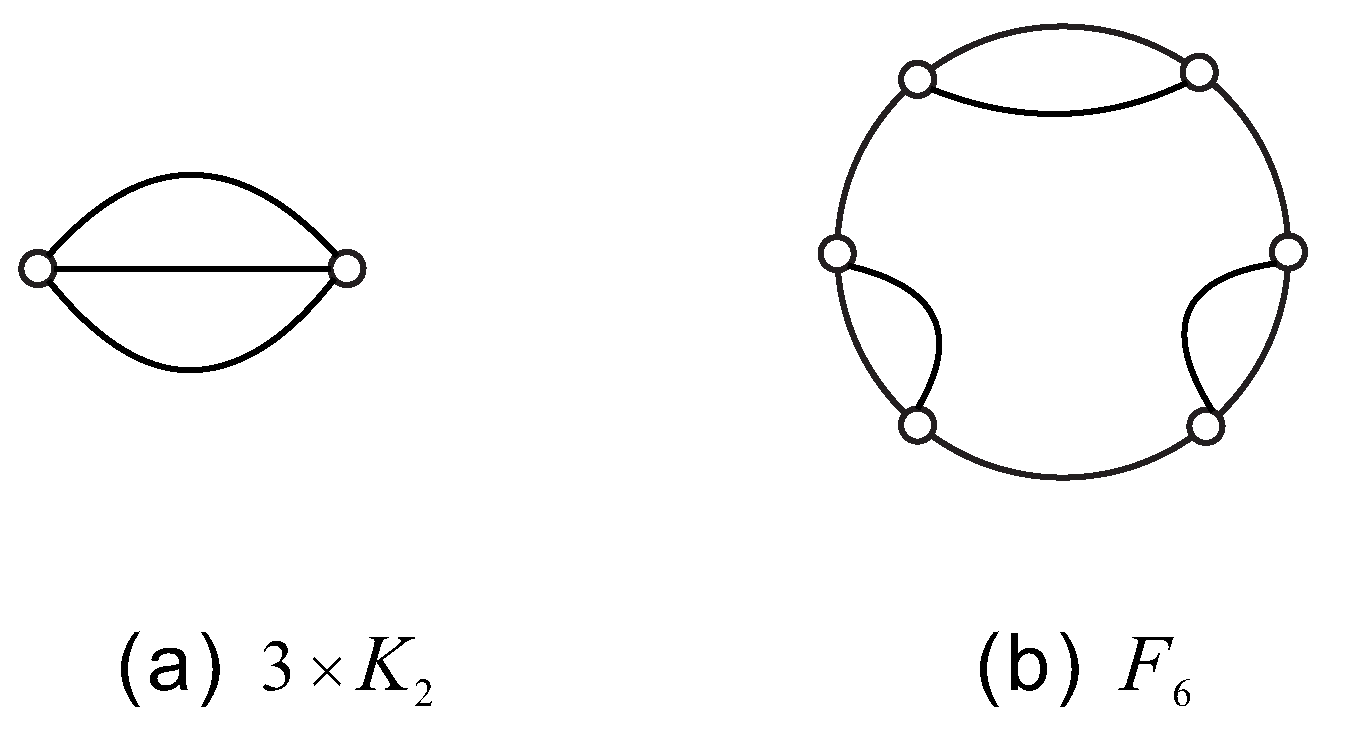The Structural Properties of (2,6)-Fullerenes

1. Introduction

A $(k,6)\text{-}$fullerene is a 2-connected cubic planar graph whose faces are only $k\text{-}$length and 6-length. Došlić showed that all $(k,6)\text{-}$fullerenes only exist for $k=2$, 3, 4 or 5 and are 1-extendable [1]. A $(5,6)\text{-}$fullerene is the usual fullerene as the molecular graph of a sphere carbon fullerene. A $(4,6)\text{-}$fullerene is the molecular graph of a boron-nitrogen fullerene. The structural properties, such as connectivity, extendability, resonance, anti-Kekulé number, are very useful for studying the number of perfect matchings in a graph[2,3]. And the number of perfect matchings is closely related to the stability of molecular graphs[4,5,6,7,8]. Therefore, many articles have studied the structural properties of graphs in both mathematics and chemistry [9,10,11]. Fullerene graphs are bicritical, cyclically 5-edge-connected, 2-extendable and 1-resonant [12,13,14,15]; Boron-nitrogen fullerene graphs are bipartite, 3-connected, 1-extendable, 2-resonant, and have the forcing number at least two [16,17]; A $(3,6)\text{-}$fullerene is 1-extendable, 1-resonant and has the connectivity 2 or 3 [18,19]. This paper is mainly concerned with the structural properties of $(2,6)\text{-}$fullerenes.

A $(2,6)\text{-}$fullerene F is a cubic planar graph such that every face is either $2\text{-}$length or $6\text{-}$length. A graph with two vertices and n parallel edges joining them is denoted by $n\times K_2$. The smallest $(2,6)\text{-}$fullerene is $3\times K_2$. A $plane$ $graph$ is a graph that can be embedded in the plane such that its edges intersect only at their ends. Any such embedding divides the plane into connected regions called $faces$. Two different faces $f_1, f_2$ are $adjacent$ if their boundaries have an edge in common. A face is said to be $incident$ $with$ the vertices and edges in its boundary, and vice versa. An edge is said to be $incident$ $with$ the ends of the edge, and vice versa. Two vertices which are incident with a common edge are $adjacent$, and two distinct adjacent vertices are $neighbours$. If S is a set of vertices in a graph F, the set of all neighbours of the vertices in S is denoted by $N\left(S\right)$, and $\left|N\right(S\left)\right|$ denotes the number of neighbours of S.

Let F be a $(2,6)\text{-}$fullerene graph with vertex-set $V\left(F\right)$ and edge-set $E\left(F\right)$. We denote the number of vertices and edges in F by $\left|V\right(F\left)\right|$ and $\left|E\right(F\left)\right|$. For $H\subseteq H$, we let $F-H$ be the subgraph of F obtained from F by removing the elements in H. A $matching$ of F is a set of disjoint edges M of F. A perfect matching of F is a matching M that covers all vertices of F. A perfect matching of a graph coincides with a Kekulé structure of some molecular graph in organic chemistry. A set $\mathcal{H}$ of disjoint even faces of a graph F is a $resonant$ $pattern$ if F has a perfect matching M such that the boundary of each face in $\mathcal{H}$ is an $M\text{-}$alternating cycle. F is said to be k-resonant ($k\ge 1$) if any i ($0\le i\le k$) disjoint even faces of F form a resonant pattern. Moreover, F is called $n\text{-}$$extendable$ ($\left|V\right(F\left)\right|\ge 2n+2$) if any matching of n edges is contained in a perfect matching of F. F is $bicritical$ if F contains an edge and $F-u-v$ contains a perfect matching, for every pair of distinct vertices $u,v\in V\left(F\right)$. In this paper, we show that every $(2,6)\text{-}$fullerene is 1-extendable, 1-resonant but not 2-extendable, bicritical.

The anti-Kekulé set of a $(2,6)\text{-}$fullerene F with perfect matchings is an edge set $S\subseteq E\left(F\right)$ such that $F-S$ is connected and has no perfect matchings. The anti-Kekulé number of F, denoted by $ak\left(F\right)$, is the cardinality of a smallest anti-Kekulé set of F. It is NP-complete to find the smallest anti-Kekulé set of a graph. Moreover, it has been shown that the anti-Kekulé set of a graph significantly affects the whole molecule structure by the valence bond theory. We have known the $(5,6)$, $(4,6)$, and $(3,6)\text{-}$fullerenes have the anti-Kekulé numbers 4, 4 and 3 respectively. In this paper, We show that every $(2,6)\text{-}$fullerene F has the anti-Kekulé number 4 with $\left|V\right(F\left)\right|>6$ .

2. Main results

An edge-cut of F is a subset of edges $E^{{}^{\prime }}\subseteq E\left(F\right)$ such that $F-E^{{}^{\prime }}$ is disconnected. An $k\text{-}$$edge\text{-}cut$ is an edge-cut with k edges. The $edge\text{-}connectivity$ of F, denoted by ${\kappa }^{\prime }\left(F\right)$, is equal to the minimum cardinality of edge-cuts. F is $k\text{-}$$edge\text{-}connected$ if F cannot be separated into at least two components by removing less than k edges.

Lemma 1.

The $(2,6)\text{-}$fullerene F has edge-connectivity 2, where $\left|V\right(F\left)\right|>2$.

Proof. 

Since every edge of F is incident with a 2-length face or a 6-length face, there is no cut edge in F. Therefore, F is 2-edge-connected. For one 2-length face C in F, denoted by $C=xyx$. Then either $F\cong 3\times K_2$ or the two edges incident with x and y respectively other than $xy$ form an 2-edge-cut of F. Therefore, ${\kappa }^{\prime }\left(F\right)=2$, where $\left|V\right(F\left)\right|>2$. □

We call an edge e is $incident$$to$ a subgraph H if $\left|V\right(e)\bigcap V(H\left)\right|=1$.

Lemma 2.

Every 2-edge-cut of a $(2,6)\text{-}$fullerene isolates a 2-length face.

Proof. 

Let F be a $(2,6)\text{-}$fullerene. If $\left|V\right(F\left)\right|=2$, then $F\cong 3\times K_2$, and the conclusion holds as F has no 2-edge-cut. So next we suppose $\left|V\right(F\left)\right|>2$. By Lemma 1, F has an 2-edge-cut. Let $E=\{e_1,e_2\}$ be an 2-edge-cut whose deletion separates F into two components, $F^{\prime }$, $F^{″}$. Then E is a matching of F as F is 3-regular and has edge-connectivity 2. Let every edge $e_i$ has one endpoint, say $x_i$, on $F^{\prime }$, the other endpoint, say $y_i$, on $F^{″}$, $i=1,2$. Suppose the outer face of $F^{″}$ is exactly the outer face of F, thus $F^{\prime }$ lies in some inner face of $F^{″}$. Then there are two hexagons, denoted by $f_1$, $f_2$, such that both $f_1$ and $f_2$ are incident with $x_1$, $x_2$, $y_1$, $y_2$. If one of $F^{\prime }$ and $F^{″}$ contains a cut edge, without losing generality, assume that $F^{\prime }$ contains a cut edge $e=uv$, then $F^{\prime }-e$ has two connected components, say $F_1$, $F_2$. Then both $e_1$ and $e_2$ cannot be incident to the same component $F_i$ ($i=1,2$), otherwise, there exists a cut edge e in F, a contradiction. Then $V\left(f_1\right)=\{u,v,x_1,y_1,x_2,y_2\}$, $V\left(f_2\right)=\{u,v,x_1,y_1,x_2,y_2\}$. That is, all of $F_1$, $F_2$ and $F^{″}$ are 2-length faces and we get a $(2,6)\text{-}$fullerene with six vertices, thus the conclusion holds. If both $F^{\prime }$ and $F^{″}$ contain cut edges, then there is a face with length more than 6, a contradiction. If neither $F^{\prime }$ nor $F^{″}$ has a cut edge, then $F^{\prime }$ and $F^{″}$ are 2-edge-connected, and in each of them there is only one face that is not 2-length or 6-length, and we denote these two boundaries of the exceptional faces by $C^{\prime }$ and $C^{″}$, respectively. Let $v^{\prime }$, $e^{\prime }$, and $f^{\prime }$ be the number of vertices, edges and faces in $F^{\prime }$, respectively. Let $l^{\prime }$ be the length of $C^{\prime }$, and $f_2^{\prime }$, $f_6^{\prime }$ be the number of 2-length faces, 6-length faces in $F^{\prime }$, respectively. By Euler’s formula and the structure of $F^{\prime }$, it follows that

$$\left\{\begin{array}{c}3v^{\prime }=2e^{\prime }+2\hfill \\ v^{\prime }-e^{\prime }+f_2^{\prime }+f_6^{\prime }=1\hfill \\ 2f_2^{\prime }+6f_6^{\prime }+l^{\prime }=2e^{\prime }.\hfill \end{array}\right.$$

(1)

By (1), we obtain that

$$l^{\prime }=4f_2^{\prime }-2.$$

(2)

Since F has no face with length more than 6, the two faces $f_1,f_2$ each has at most two additional vertices on $C^{\prime }$. Hence $2\le l^{\prime }\le 6$. By (2), we can get $1\le f_2^{\prime }\le 2$. If $f_2^{\prime }=1$, we have $l^{\prime }=2$, which means that $F^{\prime }$ is a 2-length face, thus the conclusion holds. If $f_2^{\prime }=2$, then $l^{\prime }=6$ and there are no additional vertices on $C^{″}$, which implies that $F^{″}$ is a 2-length face, thus the conclusion holds. Therefore, every 2-edge-cut of a $(2,6)\text{-}$fullerene isolates a 2-length face.

□

In [1], Došlić proved that the $(k,6)\text{-}$fullerene is 1-extendable for $k=3,4,5$. In fact, we may observe that the conclusions remain valid for $k=2$.

Lemma 3

([1]). Let F be a $(2,6)\text{-}$fullerene graph. Then F is 1-extendable.

The resonance of faces of a plane bipartite graph is closely related to 1-extendable property. It was revealed that every face (including the infinite one) of a plane bipartite graph G is resonant if and only if G is 1-extendable [20]. Combing with Lemma 3, we can know every $(2,6)\text{-}$fullerene is 1-resonant.

Corollary 1.

Every $(2,6)\text{-}$fullerene is 1-resonant.

Moreover, we can know no $(2,6)\text{-}$fullerene is 2-extendable.

Theorem 1.

No $(2,6)\text{-}$fullerene is 2-extendable.

Proof. 

Let F be a $(2,6)\text{-}$fullerene graph. Let f be a 2-length face of F with the boundary $v_1{v}_2{v}_1$. By the definition of extendability, we know that $\left|V\right(F\left)\right|\ge 4$. Then there exist two vertices $u_1,u_2$ of F which are different from $v_1,v_2$ such that $u_1{v}_1\in E\left(F\right)$ and $u_2{v}_2\in E\left(F\right)$. Since the four vertices $u_1,u_2,v_1,v_2$ must be contained in the same hexagon of F, there is a vertex $u_3\ne u_1$, $u_3\ne v_2$ of F such that $u_2{u}_3\in E\left(F\right)$. Obviously, $u_1{v}_1,u_2{u}_3$ is a matching and cannot be contained in a perfect matching of F. Thus no $(2,6)\text{-}$fullerene is 2-extendable.

□

Similarly, we can show no $(2,6)\text{-}$fullerene is bicritical.

Theorem 2.

No $(2,6)\text{-}$fullerene is bicritical.

Proof. 

Let F be a $(2,6)\text{-}$fullerene graph. Let f be a 2-length face of F with the boundary $v_1{v}_2{v}_1$. When $F\cong 3\times K_2$, then $F-v_1-v_2$ has no perfect matchings. When $F\ncong 3\times K_2$, then there exists a vertex u of F which is different from $v_2$ such that $u{v}_1\in E\left(F\right)$. Then $F-u-v_2$ has a single vertex $v_1$ as a component. So $F-u-v_2$ has no perfect matchings. That is, F is not bicritical.

□

Theorem 3

(Tutte’s Theorem [21]). A graph G has a perfect matching if and only if $c_o(G-U)\le \left|U\right|$ for any $U\subseteq V\left(G\right)$, where $c_o(G-U)$ is the number of odd components of $G-U$.

Theorem 4

(Hall’s Theorem [21]). Let F be a bipartite graph with bipartition W and B. Then F has a perfect matching if and only if $\left|W\right|=\left|B\right|$ and for any $U\subseteq W$, $\left|N\right(U\left)\right|\ge \left|U\right|$ holds.

For the connected cubic simple bipartite graph, we can know its anti-Kekulé number is 4 [22].

Theorem 5

([22]). If G is a connected cubic simple bipartite graph, then $ak\left(F\right)=4$.

The above result can be used to determine the anti-Kekulé numbers of some interesting graphs, such as, $(4,6)\text{-}$fullerenes [22], toroidal fullerenes [22] etc. Theorem 5 is also valid for $(2,6)\text{-}$fullerene when $\left|V\right(F\left)\right|>6$.

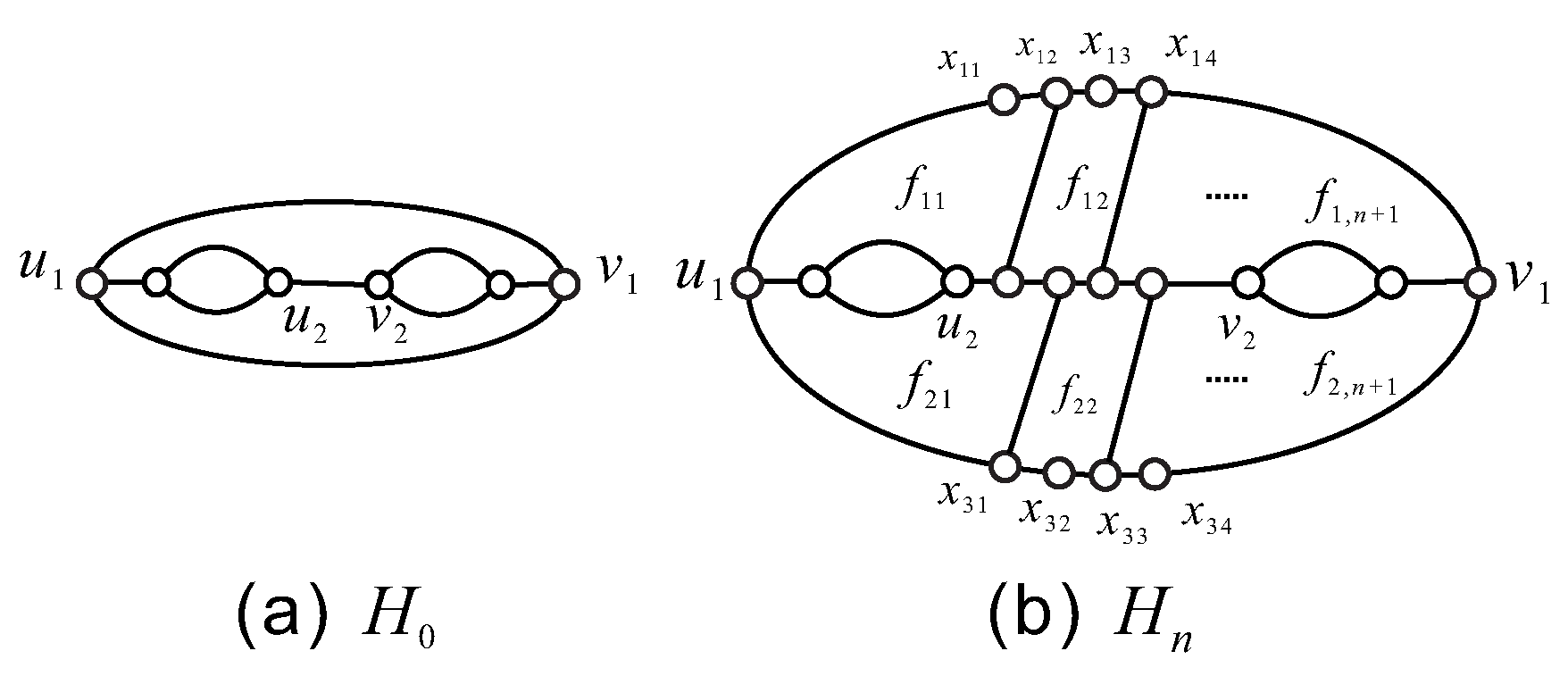
Theorem 6.

Let F be a $(2,6)\text{-}$fullerene graph with $\left|V\right(F\left)\right|>6$. Then $ak\left(F\right)=4$.

Proof. 

Let F be a $(2,6)\text{-}$fullerene. For any vertex u in F, if $\left|N\right(u\left)\right|=1$, then $F\cong 3\times K_2$ (see Figure 1(a) the graph $3\times K_2$). For any vertex u in F, if $\left|N\right(u\left)\right|=2$, then $F\cong F_6$ (see Figure 1(b) the graph $F_6$). We can easily know that both $3\times K_2$ and $F_6$ cannot exist anti-Kekulé set. On the other hand, if we let n and $f_6$ be the number of vertices and the hexagons of F, respectively, then by the Euler’s formula and the formula of degree sum, we can get $n=2f_6+2$. Thus if $f_6=0$, then $n=2$ and $F\cong 3\times K_2$. If $f_6=1$, then $n=4$, which is impossible as every hexagonal face must contain six vertices. If $f_6=2$, then $n=6$ and $F\cong F_6$ (see Figure 1(b) the graph $F_6$). Therefore, when $\left|V\right(F\left)\right|\le 6$, there is no anti-Kekulé set in F.

Next, we discuss the anti-Kekulé number of F with $\left|V\right(F\left)\right|>6$. Then there is a vertex u in F and $\left|N\right(u\left)\right|=3$. Let x, y, z be the three neighbors of u. Let $e_1$ and $e_2$ be two edges incident with x other than $ux$, and let $e_3$ and $e_4$ be two edges incident with y other than $uy$. Since every face of F is 2-length or 6-length and F is 2-edge-connected, the four edges $e_1,e_2,e_3,e_4$ are pairwise different. We claim that $\{e_1,e_2,e_3,e_4\}$ is an anti-Kekulé set. It is obvious that $F-\{e_1,e_2,e_3,e_4\}$ has no perfect matchings as the two vertices x, y cannot be contained in the same perfect matching. If $F-\{e_1,e_2,e_3,e_4\}$ is no connected, then we obtain a cut edge $uz$ in F, contradicting Lemma 1. Then we find an anti-Kekulé set of size 4 and so $ak\left(F\right)\le 4$.

In the following, we show $ak\left(F\right)\ge 3$. Let A be an anti-Kekulé set of size $ak\left(F\right)$. Then $F^{\prime }=F-A$ is connected and has no perfect matchings. According to Theorem 3, there exists $S\subseteq V\left(F^{\prime }\right)$ such that $c_0(F^{\prime }-S)>\left|S\right|$. If we choose such an S with the maximum size, then $F^{\prime }-S$ has no even components. On the contrary, suppose that $F^{\prime }-S$ has an even component H. For any vertex $v\in V\left(H\right)$, $c_0(H-v)\ge 1$. Let $S^{\prime }=S\cup \left\{v\right\}$, then $c_0(F^{\prime }-S^{\prime })\ge c_0(F^{\prime }-S)+1>\left|S\right|+1=|S^{\prime }|$, which is a contradiction to the choice of S.

Since $\left|V\right(F^{\prime }\left)\right|$ is even, then $c_0(F^{\prime }-S)\ge \left|S\right|+2$ by parity. For any edge $e\in A$, adding e to $F^{\prime }-S$ will connect at most two odd components, then $c_o(F^{\prime }+e-S)\ge c_0(F^{\prime }-S)-2$. Since A is the smallest anti-Kekulé set of F, then $F^{\prime }+e$ has a perfect matching for any edge $e\in A$. Hence, by Theorem 3, for the above subset S, $c_o(F^{\prime }+e-S)\le \left|S\right|$. Therefore, $\left|S\right|\ge c_o(F^{\prime }+e-S)\ge c_0(F^{\prime }-S)-2\ge \left|S\right|$. We obtain $c_0(F^{\prime }-S)=\left|S\right|+2$, and the edge e connects exactly two components of $F^{\prime }-S$.

Let $F_i$ be the odd components of $F^{\prime }-S$, where $1\le i\le \left|S\right|+2$. For $F_i\subseteq F$, let $d\left(F_i\right)$ denote the number of the set of edges with one end in $F_i$ and the other end in $F-F_i$. Denote the number of edges between S and the odd components by N. Since F is cubic, S sends out at most $3\left|S\right|$ to N. In addition, ${\bigcup }_{i=1}^{\left|S\right|+2}{F}_i$ sends out exactly ${\sum }_{i=1}^{\left|S\right|+2}d\left(F_i\right)-2ak\left(F\right)$ edges to N. Hence

$$N=\sum _{i=1}^{\left|S\right|+2}d\left(F_i\right)-2ak\left(F\right)\le 3\left|S\right|.$$

(3)

Because F is 2-edge-connected, $d\left(F_i\right)\ge 2$ for every i. On the other hand, since $d\left(F_i\right)=3|V\left(F_i\right)|-2|E\left(F_i\right)|$, which implies that $d\left(F_i\right)$ and $\left|V\right(F_i\left)\right|$ are of the same parity. Every $F_i$ sends odd number edges, hence $d\left(F_i\right)\ge 3$. Substituting it into (3), we have

$$3\left(\right|S|+2)-2ak\left(F\right)\le \sum _{i=1}^{\left|S\right|+2}d\left(F_i\right)-2ak\left(F\right)\le 3\left|S\right|,$$

the above inequality gives $ak\left(F\right)\ge 3$.

We find that the anti-Kekulé number of F is either 3 or 4. Suppose by the contrary that $ak\left(F\right)=3$. Then there exists an anti-Kekulé set $A=\{e_1,e_2,e_3\}$ of cardinality three in F, such that $F-A$ is connected and has no perfect matchings. Assume W and B are the bipartition of F. By Hall’s theorem, there exists $U\subseteq W$ such that

$$|N_{F-A}\left(U\right)|\le |U|-1$$

(4)

where $N_{F-A}\left(U\right)$ means $N\left(U\right)$ in $F-A$. Moreover, for $e_i\in A$, since A is the smallest anti-Kekulé set, $F-A+e_i$ has a perfect matching. Immediately by Theorem 4, for the above subset U,

$$\left|U\right|\le |N_{F-A+e_i}\left(U\right)|$$

(5)

for $i=1,2$ and 3, where $N_{F-A+e_i}\left(U\right)$ means $N\left(U\right)$ in $F-A+e_i$. In addition, the neighbors of U will be increased by at most one if we add an edge $e_i$ to $F-A$. Hence

$$|N_{F-A+e_i}\left(U\right)|\le |N_{F-A}\left(U\right)|+1.$$

(6)

Combining inequalities (4), (5) and (6), we have $\left|U\right|=|N_{F-A}\left(U\right)|+1$, and $e_i$ is incident with the vertices of U and $B-N_{F-A+e_i}\left(U\right)$ in $F-A+e_i$. Thus the edges going out from $U\subseteq V\left(F\right)$ either goes into A or goes into the edges going out from $N_{F-A}\left(U\right)$. Then the number of edges between U and $N_{F-A}\left(U\right)$ is $3\left|U\right|-3$. Since $|N_{F-A}\left(U\right)|=|U|-1$, $3|N_{F-A}\left(U\right)|=3(|N_{F-A}\left(U\right)|+1)-3=3\left|U\right|-3$, that is, there is no edge between $N_{F-A}\left(U\right)$ and $W-U$ in $F-A$. As a result, A is an edge-cut, which is a contradiction to the definition of anti-Kekulé set.

□

In [23], Grünbaum and Motzkin showed that (5,6)-fullerene and (4,6)-fullerene having n hexagonal faces exist for every non-negative integer n satisfying $n\ne 1$, and gave a similar result for (3,6)-fullerene. Therefore, we consider whether (2,6)-fullerene having n hexagonal faces also exists for any n. We tried to give a positive answer to this question, but we found that the conclusion seems quite elusive. Therefore, in this part, we mainly prove that there exists a $(2,6)\text{-}$fullerene F having $f_F$ hexagonal faces where $f_F$ is related to the two parameters n, m.

Let F be a $(2,6)\text{-}$fullerene. A $fragment$ H of F is a subgraph of F consisting of a cycle together with its interior and every inner face of H is also a face of F. We define $\partial \left(H\right)$ as the $boundary$ of the exterior face of H. A face f of F is a $neighboring$ $face$ of H if f is not a face of H and f has at least one edge in common with H. A path of length k (the number of edges) is called a k-$path$. Denote by $f_H$ the number of hexagons of H.

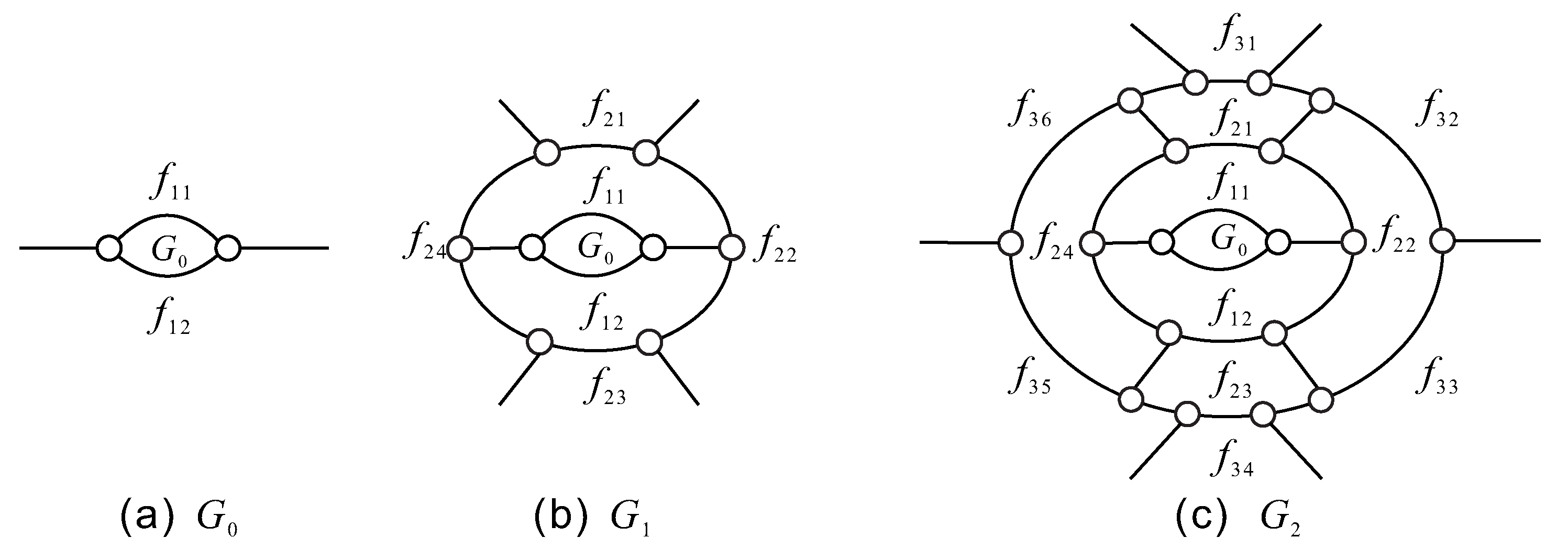
Proposition 1.

In all the (2,6)-fullerenes, there exists a fragment, say $G_n$, such that $f_{G_n}=n^2+n$, $n\in \mathbb{Z}$.

Proof. 

Let $G_0$ be a 2-length face and $f_{11},f_{12}$ be two neighboring faces of $G_0$ (see Figure 2(a)). Then $f_{G_0}=0$. Suppose that $f_{11}$, $f_{12}$ are hexagons. Set $G_1=G_0\bigcup \{f_{11},f_{12}\}$, suppose both $f_{11}$ and $f_{12}$ are inner faces of $G_1$ and let $f_{21},f_{22},f_{23},f_{24}$ be four neighboring faces of $G_1$ along the clockwise direction such that $f_{21}$ is incident with the two consecutive 2-degree vertices on $\partial \left(G_1\right)$ (see Figure 2(b)). Then $f_{G_1}=2$. Suppose that $f_{21},f_{22},f_{23},f_{24}$ are hexagons, pairwise different, and intersecting if and only if $f_{2i}$, $f_{2,i+1}$ are intersecting at only one edge for $i=1,2,3,4$, $f_{25}=f_{21}$. Set $G_2=G_1\bigcup \{f_{21},f_{22},f_{23},f_{24}\}$. Suppose $f_{21},f_{22},f_{23},f_{24}$ are the inner faces of $G_2$ and let $f_{31},f_{32},f_{33},f_{34},f_{35},f_{36}$ be six neighboring faces of $G_2$ along the clockwise direction such that $f_{31}$ is incident with the two consecutive 2-degree vertices on $\partial \left(G_2\right)$ (see Figure 2(c)). Then $f_{G_2}=2+4=6$.

Suppose that the proposition holds for any integer less than n, where $n>2$. According to the induction hypothesis, $f_{G_{n-1}}=n^2-n$ and $f_{n1},f_{n2},\dots ,f_{n,2n}$ be $2n$ neighboring faces of $G_{n-1}$ along the clockwise direction such that $f_{n1}$ is incident with the two consecutive 2-degree vertices on $\partial \left(G_{n-1}\right)$. Suppose that $f_{n1},\dots ,f_{n,2n}$ are hexagons, pairwise different, and intersecting if and only if $f_{ni}$, $f_{n,i+1}$ are intersecting at only one edge for $i=1,2,\dots ,2n$, $f_{n,2n+1}=f_{n1}$. Set $G_n=G_{n-1}\bigcup \{f_{n1},\dots ,f_{n,2n}\}$. Suppose $f_{n1},\dots ,f_{n,2n}$ are all inner faces of $G_n$ (see Figure 3). Then $f_{G_n}=n^2-n+2n=n^2+n$, $n\in \mathbb{Z}$.

□

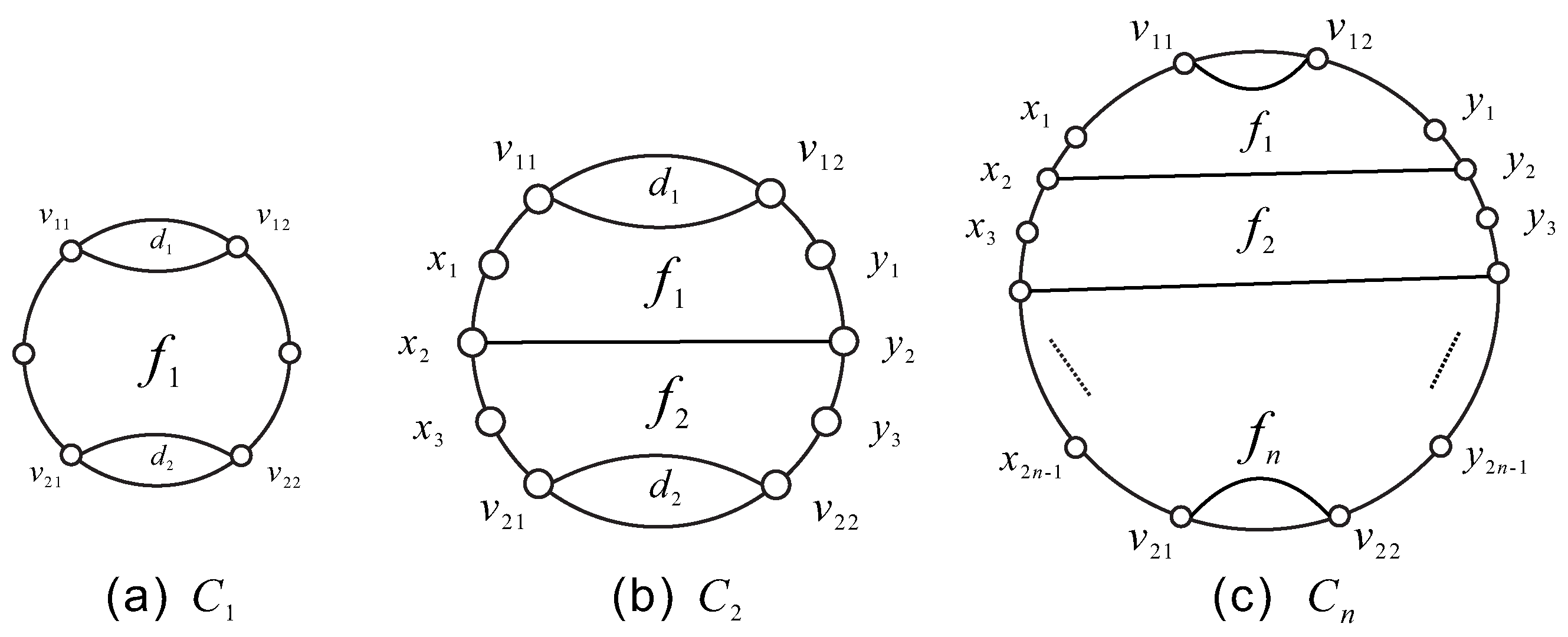
Proposition 2.

In all the (2,6)-fullerenes, there exists a fragment, say $C_n$, such that $f_{C_n}=n$, $n\in \mathbb{Z}$.

Proof. 

Let $C_0$ be a $3\times K_2$, then $f_{C_0}=0$. Let $d_1$ and $d_2$ be two 2-length faces. Its boundary $\partial \left(d_i\right)$ is labelled $v_{i1}$, $v_{i2}$ ($i=1,2$). Let $P_i$ be a path that connects two vertices $v_{1i}$, $v_{2i}$ ($i=1,2$) and $V\left(P_1\right)\bigcap V\left(P_2\right)=\varnothing$. If both $P_1$, $P_2$ are 2-paths, then as F is 2-connected, there is a hexagon, say $f_1$, such that $f_1$ contains the paths $P_1$, $P_2$ and the edges $v_{11}{v}_{12}$, $v_{21}{v}_{22}$. Set $C_1=d_1\bigcup d_2\bigcup f_1$, without lose of generality, suppose $f_1$ is the inner face of $C_1$ (see Figure 4(a)). Thus $f_{C_1}=1$. If both $P_1$, $P_2$ are 4-paths, then all of whose internal vertices are denoted by $x_1,x_2,x_3$ and $y_1,y_2,y_3$, respectively, such that $P_1=v_{11}{x}_1{x}_2{x}_3{v}_{21}$, $P_2=v_{12}{y}_1{y}_2{y}_3{v}_{22}$. Let $x_2{y}_2\in E\left(F\right)$, then there are 2 hexagons, denoted by $f_1,f_2$, such that $\partial \left(f_1\right)=v_{11}{v}_{12}{y}_1{y}_2{x}_2{x}_1{v}_{11}$, $\partial \left(f_2\right)=v_{21}{x}_3{x}_2{y}_2{y}_3{v}_{22}{v}_{21}$. Set $C_2=d_1\bigcup d_2\bigcup f_1\bigcup f_2$, also suppose $f_1,f_2$ are two inner faces of $C_2$ (see Figure 4(b)), then $f_{C_2}=2$. Suppose $P_1$, $P_2$ are $2n$-paths, $n\in {\mathbb{N}}^{+}$. Let $P_1=v_{11}{x}_1\dots x_{2n-1}{v}_{21}$ and $P_2=v_{12}{y}_1\dots y_{2n-1}{v}_{22}$. Suppose that $x_i{y}_i\in E\left(F\right)$ ($i=2,4,\dots ,2n-2$), then there are n hexagons between $P_1$ and $P_2$, denoted by $f_1,f_2\dots f_n$. Set $C_n=d_1\bigcup d_2{\bigcup }_{i=1}^n{f}_i$ such that $f_1,f_2\dots f_n$ are the inner faces of $C_n$ (see Figure 4(c)). Therefore, $C_n$ is a fragment and $f_{C_n}=n$, $n\in {\mathbb{N}}^{+}$. Thus there exists a fragment $C_n$ such that $f_{C_n}=n$, $n\in \mathbb{Z}$.

□

Proposition 3.

In all the (2,6)-fullerenes, there exists a fragment, say $L_n^m$, such that $f_{L_n^m}=2n^2+(m+3)n$, $n\in {\mathbb{N}}^{+}$, $m\in \mathbb{Z}$.

Proof. 

Let $G_n^{{}^{\prime }}$, $G_n^{{}^{″}}$ be two fragments as indicated in Figure 3. By Proposition 1, we know that $G_n^{{}^{\prime }}$ and $G_n^{{}^{″}}$ both have $n^2+n$ hexagons. Suppose n is a positive integer. Since there are $2n+2$ 2-degree vertices on $\partial \left(G_n^{{}^{\prime }}\right)$, we can record them clockwise as $u_1,u_2,\dots ,u_{2n+2}$ such that $u_1$ and $u_{2n+2}$ are adjacent. Similarly, $2n+2$ 2-degree vertices on $\partial \left(G_n^{{}^{″}}\right)$ are denoted by $v_1,v_2,\dots ,v_{2n+2}$ along the anticlockwise direction of $G_n^{{}^{″}}$ such that $v_1$ and $v_{2n+2}$ are adjacent. For $G_1^{{}^{\prime }}$ and $G_1^{{}^{″}}$. Let $e_1=u_1{v}_1,e_2=u_2{v}_2$, then $e_1$ and $e_2$ are contained in the hexagon, say $f_1$. Set $K_1=G_1^{{}^{\prime }}\bigcup G_1^{{}^{″}}\bigcup f_1$ (see Figure 5(a)), then $f_{K_1}=5$. For $G_n^{{}^{\prime }}$ and $G_n^{{}^{″}}$. Let $e_i=u_i{v}_i$, $i=1,2\dots n+1$, then $e_i$ and $e_{i+1}$ are contained in the hexagon, say $f_i$, $i=1,2\dots n$. Set $K_n=G_n^{{}^{\prime }}\bigcup G_n^{{}^{″}}{\bigcup }_{i=1}^n{f}_i$, suppose all of $f_1\dots f_n$ are the inner faces of $K_n$ (see Figure 5(b), the embedding of $K_n$), then $f_{K_n}=2(n^2+n)+n=2n^2+3n$.

Next, we construct the fragment $L_n^m$ from $K_n$ as follows. We replace each edge $e_i=u_i{v}_i$ by a path $P_i$ such that $P_i=u_i{x}_{i1}{x}_{i2}\dots x_{i,2m}{v}_i$, $i=1,2\dots n+1$, $m\in \mathbb{Z}$. Suppose that $x_{i2}{x}_{i+1,1},x_{i4}{x}_{i+1,3}\dots x_{i,2m}{x}_{i+1,2m-1}$ be the edges of F, $i=1,2\dots n$. Therefore, there are $m+1$ hexagons between $P_i$ and $P_{i+1}$, denoted by $f_{i1},f_{i2}\dots f_{i,m+1}$, $i=1,2\dots n$. Set $L_n^m=G_n^{{}^{\prime }}\bigcup G_n^{{}^{″}}{\bigcup }_{i=1}^n\{f_{i1},f_{i2}\dots f_{i,m+1}\}$, $m\in \mathbb{Z}$ (see Figure 5(c), the embedding of $L_n^m$). Therefore, $L_n^m$ is a fragment and $f_{L_n^m}=2(n^2+n)+(m+1)n=2n^2+(m+3)n$, $n\in {\mathbb{N}}^{+}$, $m\in \mathbb{Z}$.

□

Proposition 4.

In all the (2,6)-fullerenes, there exists a fragment, say $H_n$, such that $f_{H_n}=2n+2$, $n\in \mathbb{Z}$.

Proof. 

Let $H_0\cong F_6$ be the $(2,6)$-fullerene with six vertices. Without lose of generality, suppose the exterior face of $H_0$ is a 2-length face with the boundary $u_1{v}_1{u}_1$, and the remaining two 2-length faces are connected by an edge $u_2{v}_2$ (see Figure 6(a) the embedding of $H_0$ and the labelling of $u_1,v_1,u_2,v_2$). Next, we construct the fragment $H_n$ from $H_0$ as follows: we replace the two parallel edges $u_1{v}_1$ and one edge $u_2{v}_2$ by two paths $P_1$, $P_3$ and one path $P_2$ such that $P_i=u_i{x}_{i1}{x}_{i2}\dots x_{i,2n}{v}_i$, $i=1,2$, and $P_3=u_1{x}_{31}{x}_{32}\dots x_{3,2n}{v}_1$, $n\in {\mathbb{N}}^{+}$. Suppose that $x_{i2}{x}_{i+1,1},x_{i4}{x}_{i+1,3}\dots x_{i,2n}{x}_{i+1,2n-1}$ be the edges of F, $i=1,2$. We construct $n+1$ hexagons between $P_i$ and $P_{i+1}$, denoted by $f_{i1},f_{i2}\dots f_{i,n+1}$, $i=1,2$. Set $H_n=H_0-\{u_1{v}_1,u_2{v}_2\}{\bigcup }_{i=1}^2\{f_{i1},f_{i2}\dots f_{i,n+1}\}$ such that $f_{i1},f_{i2}\dots f_{i,n+1}$ are the inner faces of $H_n$, $n\in {\mathbb{N}}^{+}$ (see Figure 6(b)). Therefore, $H_n$ is a fragment and $f_{H_n}=2(n+1)=2n+2$, $n\in {\mathbb{N}}^{+}$. Thus there exists a fragment $H_n$ such that $f_{H_n}=2n+2$, $n\in \mathbb{Z}$.

□

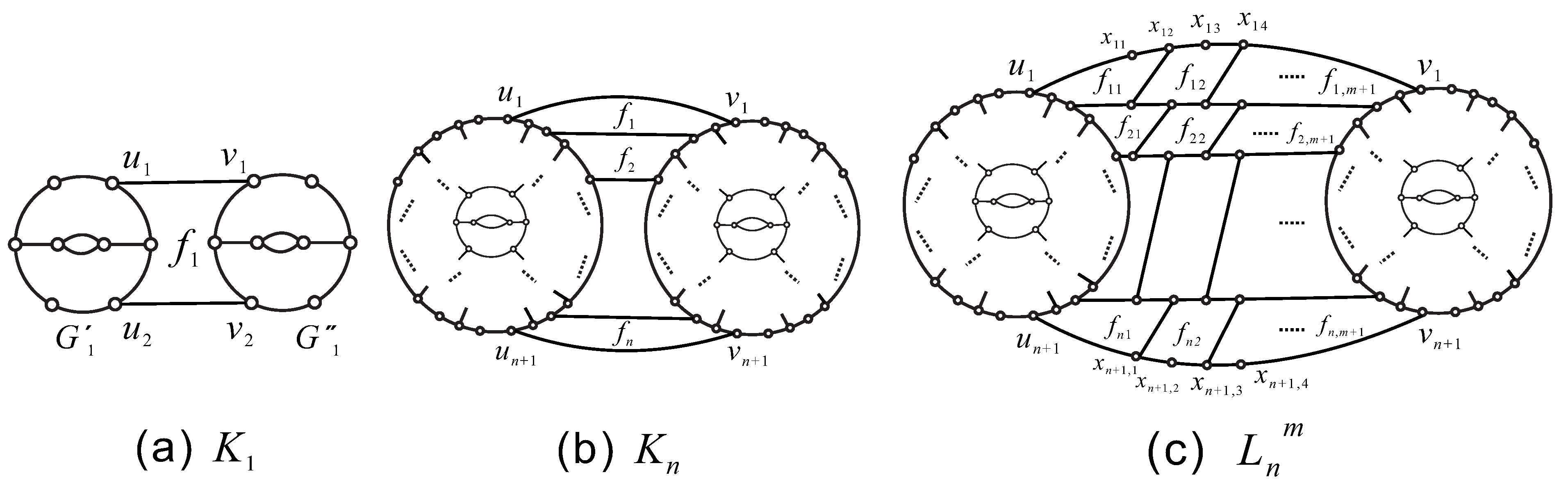
By Propositions 1–4, we can find a $(2,6)\text{-}$fullerene F having $f_F$ hexagonal faces which related to the parameters n, m.

Theorem 7.

There exists a $(2,6)\text{-}$fullerene F such that $f_F=n^2+2n$, $n\in \mathbb{Z}$.

Proof. 

Let $G_n$ be a fragment of F as shown in Figure 3. Its boundary $\partial \left(G_n\right)$ is labelled $u_1,u_2,\dots ,u_{4n+2}$ along the clockwise direction, where $u_1$ and $u_2$ are two consecutive 2-degree vertices. Let $C_n$ be a fragment of F as shown in Figure 4(c). Its boundary $\partial \left(C_n\right)$ is labelled $v_1,v_2,\dots ,v_{4n+2}$ along the clockwise direction, where $v_1$ and $v_2$ are two consecutive 3-degree vertices. Next assume the graphs $G_n$ and $C_n$ each drawn on a hemisphere, with the boundary as equator. If $\partial \left(G_n\right)=\partial \left(C_n\right)$, then set $F=G_n\bigcup C_n$. By Propositions 1 and 2, then $f_F=f_{G_n}+f_{C_n}=n^2+2n$, $n\in \mathbb{Z}$.

□

Theorem 8.

There exists a $(2,6)\text{-}$fullerene F such that $f_F=3n^2+m^2+3mn+6n+3m+2$, $n\in {\mathbb{N}}^{+}$, $m\in \mathbb{Z}$.

Proof. 

Let $G_{m+n+1}$ be a fragment of F as shown in Figure 3. Its boundary $\partial \left(G_{m+n+1}\right)$ is labelled $u_1,u_2,\dots ,u_{4m+4n+6}$ along the clockwise direction, where $u_1$ and $u_2$ are two consecutive 2-degree vertices. Let $L_n^m$ be a fragment of F as shown in Figure 5(c). Its boundary $\partial \left(L_n^m\right)$ is labelled $v_1,v_2,\dots ,v_{4m+4n+6}$ along the clockwise direction, where $v_1$ and $v_2$ are two consecutive 3-degree vertices. Next assume the graphs $G_{m+n+1}$ and $L_n^m$ each drawn on a hemisphere, with the boundary as equator. If $\partial \left(G_{m+n+1}\right)=\partial \left(L_n^m\right)$, then set $F=G_{m+n+1}\bigcup L_n^m$. By Propositions 1 and 3, then $f_F=f_{G_{m+n+1}}+f_{L_n^m}=3n^2+m^2+3mn+6n+3m+2$, $n\in {\mathbb{N}}^{+}$, $m\in \mathbb{Z}$.

□

Theorem 9.

There exists a $(2,6)\text{-}$fullerene F such that $f_F=n^2+3n+2$, $n\in \mathbb{Z}$.

Proof. 

Let $G_n$ be a fragment of F as shown in Figure 3. Its boundary $\partial \left(G_n\right)$ is labelled $u_1,u_2,\dots ,u_{4n+2}$ along the clockwise direction, where $u_1$ and $u_2$ are two consecutive 2-degree vertices. Let $H_n$ be a fragment of F as shown in Figure 6(b). Its boundary $\partial \left(H_n\right)$ is labelled $v_1,v_2,\dots ,v_{4n+2}$ along the clockwise direction, where $v_1$ and $v_2$ are two consecutive 3-degree vertices. Next assume the graphs $G_n$ and $H_n$ each drawn on a hemisphere, with the boundary as equator. If $\partial \left(G_n\right)=\partial \left(H_n\right)$, then set $F=G_n\bigcup H_n$. By Propositions 1 and 4, then $f_F=f_{G_n}+f_{H_n}=n^2+3n+2$, $n\in \mathbb{Z}$.

□

3. Conclusion

In this paper, we have obtained that every $(2,6)\text{-}$fullerene F is 1-extendable but not 2-extendable, 1-resonant and has the anti-Kekulé number 4 with $\left|V\right(F\left)\right|>6$. Moreover, every $(2,6)\text{-}$fullerene isn’t bicritical. At last, we prove that there exists a $(2,6)\text{-}$fullerene F having $f_F$ hexagonal faces, where $f_F$ is related to the two parameters n, m. There are, however, still several important open questions.

Problem 1.

Whether every $(2,6)\text{-}$fullerene is k-resonant $(k\ge 2)$?

Problem 2.

Whether for every $n\ne 1$ there exists a $(2,6)\text{-}$fullerene F such that $f_F=n$?