Prerpints.org logo
Preprint
Article

FEM Investigation of the Air Resonance in a Cretan Lyra

Altmetrics

Downloads

110

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 September 2023

Posted:

15 September 2023

You are already at the latest version

Alerts
Abstract
Cretan lyra is a stringed instrument very popular on the island of Crete, Greece and an important part of its musical tradition. For stringed musical instruments, the air mode resonance plays a vital part in their sound, especially in the low frequency range. For this study, the air mode resonance of a Cretan lyra is investigated with the use of finite element method (FEM). Two different FEM acoustic models were utilized: first, a pressure acoustics model with the Cretan lyra body treated as rigid was used to provide an approximate result; secondly, an acoustic-structure interaction model was applied for a more accurate representation. In addition, acoustic measurements were performed to identify the air mode resonance frequency. Results of this study reveal that the acoustic-structure interaction model has a 3.7% difference regarding the actual measurements of the resonance frequency. In contrast, the pressure acoustics solution is approximately 13.8% too high compared with the actual measurements. Taken together, findings of this study support the idea that utilizing FEM acoustic-structure interaction models could possibly predict more accurately the vibroacoustic behavior of musical instruments, which in turn can enable the determination of key aspects that can be used to control the instrument’s tone and sound quality.
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

Cretan lyra is considered the most representative musical instrument of the island of Crete, Greece. It is a symbol of the island’s music tradition [1] and is acknowledged among the emblems of Cretan identity [2]. The instrument was chosen as the heir and symbol of uncodaminated music folklore and reconnects present reality to a remote past [3]. The lyra occupies a central place in the Cretan music landscape and also in other Aegean and Dodecanese islands [4]. Cretan music is generally performed by a duo that consists of the lyra player (lyrist, lyraris) accompanied by the lute player (lutis, la(g)oytieris). Commonly, the lyra player also acts as the vocalist who sings the traditional 15-syllable rhyming couplets of mantinades, a wide-spread musical and poetical dialogical practice in Crete [5]. More on the subject of ethnomusicology and the Cretan lyra can be found in [6].
Cretan lyra is a pear-form, bowed chordophone (typically with three strings) which is played on the knee, held upright, with a violin-like bow. The cover of the lyra’s soundboard contains the soundholes which affect the particular timbre of the instrument. Due to the high tension exerted by the strings, usually a semi-circular bar is carved along the soundboard, on the side inside of the body of the Cretan lyra. Another essential part of the lyra is the ‘soul’, that is the soundpost, a small dowel that which functions as a sound transmitter and critically affects the instrument’s volume and its quality of sound [5]. One of the interesting aspects of the lyra has to do with the fingering technique of the left hand. In contrast to the violin and other instruments, the strings are not pressed by the fingertips of the left hand; rather they are merely touched from the side by the back of the nails [1]. The strings of a lyra are tuned in fifths (G3-D4-A4). The instrument’s fingerboard has no frets at all.
In the field of musical acoustics, physical modeling techniques are increasingly important and essential for understanding the complex behavior of musical instruments. Physical modeling has become one of the major fields when research concentrates on properties important for instrument building and musical performance [7]. Some of the most prominent methods are Boundary Element Method (BEM) [8], Finite Difference Method (FDM) [9] and Finite Element Method (FEM) [10] with the latter two being the most used [11]. Collectively, more information about physical modeling of musical instruments can be found in [11].
FEM is probably the most widespread method in numerous fields of acoustics [12,13]. For musical acoustics, FEM is commonly used for eigenproblems, in fluid dynamics, and with contact and moving mesh applications, while FDM is more used in time-dependent problems [11]. The finite element formulation has the advantage that the definition of elements is very sophisticated; elements can be defined to be very small or cover small sections for the geometry which is more difficult in the finite difference formulation [11]. The strength of finite element models lies in their ability to treat inhomogeneous media and difficult boundary conditions that may arise in real life problems. In FDM instead of describing the surface with a mesh (as with the FEM, BEM), a grid is used and the algebraic equations [14] are solved at the points of the grid. In addition, the general purpose applicability, robustness, mathematical structure and overall flexibility of FEM highlight its attractiveness and justify its applicability. From all the methods mentioned above the FEM has become sufficiently inexpensive and simplified in commercial software, for practical application. FEM has also been used to model the acoustic behavior of the soundboard of the Cretan lyra [15].
An important aspect of modeling musical instruments is the modeling of the air cavity resonance. The resonance is commonly called A0 resonance and the mode, A0 mode. It is sometimes called the "Helmholtz air resonance”, however with a debate, since the A0 resonance has been found to not follow the typical formula of Helmholtz resonators [16]. The reader can find more in [17-19]. In the majority of stringed instruments of the violin and the guitar family, the air resonance is a vital part of the instruments sound. Air cavity resonance is also very important in many other instruments, such as the concert harp [20], the ocarina [21] and instruments such as jaw harp [22] which exploit the air cavity of the human mouth. The body of these instruments usually includes an opening or openings in connection with the air cavity. The air inside the enclosed volume of the shell vibrates in and out through these openings. This resonance of the instruments is used to boost the sound of their lowest notes, which are often well below the frequencies of the lowest strongly excited, acoustically efficient, structural resonances.
The shape of the opening of the air cavity varies by instrument. For instruments of the guitar family, usually, a relatively large circular hole is cut into the front plate, while for instruments of the violin family two symmetrically facing f-holes are cut into the front plate. However, the sound holes in violins evolved from a circular shape to an elongated f-shape and it is suggested that this has an effect of increase in airflow, making the bass notes louder [23]. There is extensive research for the air resonance of violins [24-26]. In the case of the Cretan lyra, the cover of the soundboard has two similar hemispherical soundholes that define the particular timbre of the instrument.
Our study will focus on the fundamental air mode resonance of the Cretan lyra. For this reason, the air resonance will be modeled with the use of FEM. An acoustic-structure interaction model and a model with rigid walls will be utilized. Results will be verified with acoustic measurements.
This paper has been structured as follows: The methodology used in this study is described in Section 2. The results of this study are presented in Section 3. In Section 4, the data are analyzed and areas for future research are noted. Conclusion provides a concise overview and places the work in context.

2. Materials and Methods

2.1. Materials

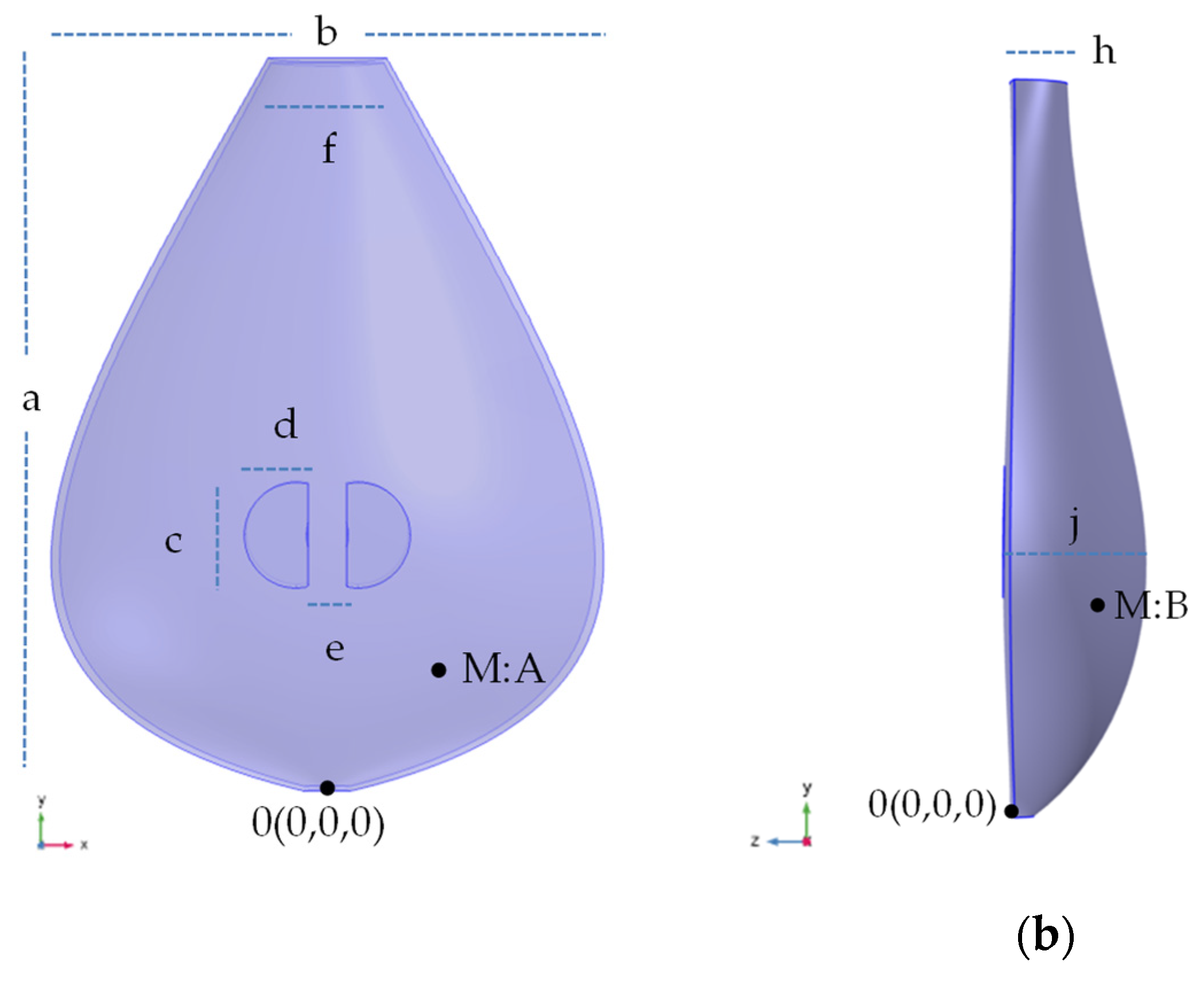
The Cretan lyra modeled and used for measurements in this study, is constructively intact and it is being used in musical activities by its owners. Therefore, the techniques of analyzing the constructive parts were chosen such that they did not harm or alter the instrument in any manner. The soundboard of the Cretan lyra is made out of cedarwood. Also, the body, neck and headstock are all one solid piece of mulberry. The above choices of woods are typical for the construction of the Cretan lyra [5]. In Figure 1(a), a picture of the Cretan lyra used in this study is included. In Figure 1(b) it can be seen that the main body of the lyra is not in contact with the fingerboard, just like a violin, allowing it to vibrate freely. This element is very important for the modeling of the lyra, which will be presented in section 2.2.2.

2.2. Methods

2.2.1. Acoustic Measurements

For the measurements of the air resonance frequency of the Cretan lyra, a methodology similar with [27] was followed. In this study a way to explore the effect of the soundholes was applied by comparing the frequency response differences with the holes closed and the holes open. Results showed a good agreement for the prediction of the air resonance. Similar approach is followed in other studies were a removable plug is tightly fitted in the sound hole [28], or holes were plugged with corks and foam for the same reason [29]. For this study, similar to the aforementioned research [27], corrugated cardboard was used to seal the soundholes due to its light weight and stiffness. The edges were sealed with heavy paper tape. Acoustic measurements were performed with the soundholes open and the soundholes closed. Acoustic measurements were performed with the lyra not including the bridge, soundpost and strings. The reason for this was for the simplification of the FEM model as will be discussed in section 2.2.2. Collectively, different methods for acoustic measurement in the similar case of violin cavity modes can be found in [17].
For the acoustic measurements, Exponential Sound Sweep (ESS) was used as an excitation signal, again similar to [27]. ESS was used for the initial measurement of the impulse response and consequently the frequency response of the Cretan lyra applying Fourier analysis. Also, a Maximum Length Sequence (MLS) signal is used [30,31] or white noise [23] for the same reason. A comparison of ESS and MLS signals can be found in [32]. All measurements were made at a controlled constant ambient. For the measurements, the Cretan lyra was suspended vertically on rubber bands. The measurements of the impulse response had a sampling frequency of 44.1 kHz. Three iterations were performed for each of the measurement points. Measurements were performed at various positions on the body of the lyra. 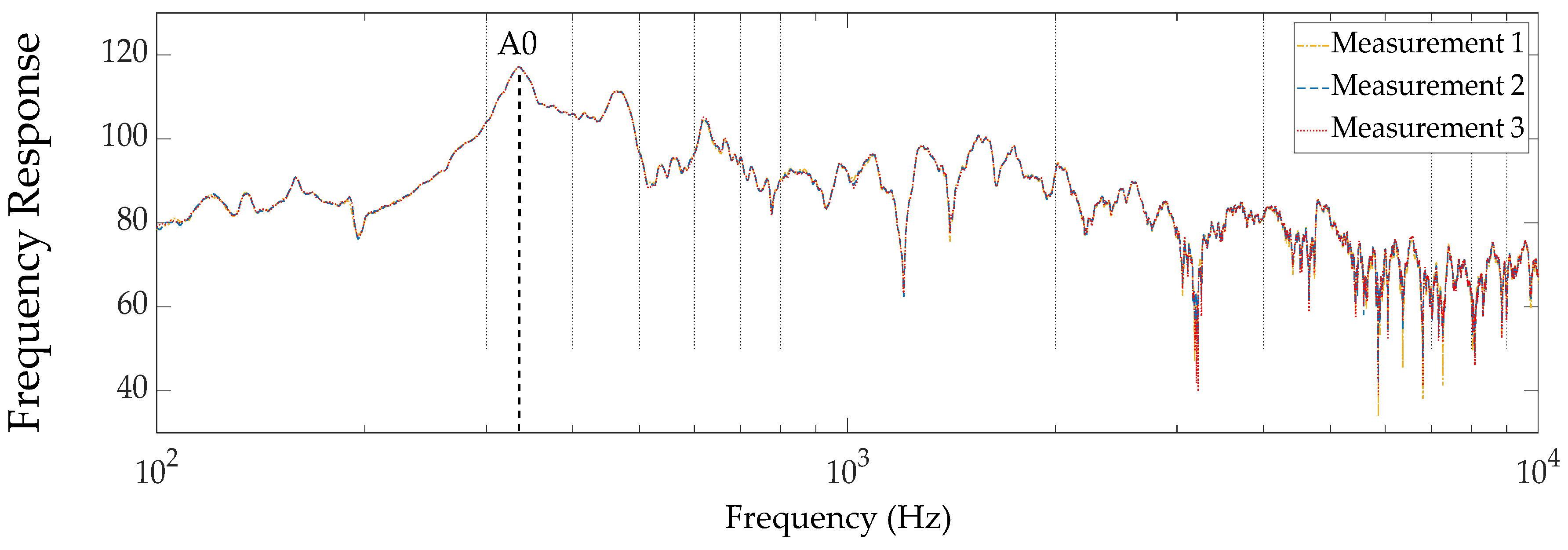Measurements positions that are used in this study are presented in Figure 2. The frequency response results of the measurements had excellent repeatability. In Appendix B the results for different measurements for the same source and receiver location are presented. A high performance, ultra-light, miniature condenser vibration pickup, C411 PP (AKG Acoustics, Vienna, Austria), was used for the measurements. As an excitation source, the transducer TB2S AII (PMC, Biggleswade, United Kingdom) was used. Alternative sources are also available [33] and applied for a variety of reasons [34-36]. The software Matlab R2021a (Mathworks, Massachusetts, USA) was used for the measurements and also for analysis of the results.

2.2.2. FEM Acoustic Modeling

For the FEM modeling, a 3D model was created, which will be also used in future studies and modeling of the Cretan lyra. For this stage, the geometry and the model has been simplified while still including the relevant parts for the modeling of the acoustic behavior of the body of the Cretan lyra. As also mentioned in section 2.2.1 (acoustic measurements), the bridge, soundpost and acoustic strings will not be modeled. The soundpost, bridge and acoustic strings were also removed from the actual Cretan lyra for the acoustic measurements. Figure 2 presents the modeling of the body of the lyre, the dimensions as well as the points where the acoustic measurements were taken. For the application of the FEM, the software Comsol v.6 (Comsol, Burlington, USA) was used. The number of degrees of freedom solved for the model was 221687.

2.2.2.1. FEM Acoustic Modeling - Acoustic-Structure Interaction

The acoustic-structure interaction approach connects the acoustics pressure variations in the fluid domain with the structural deformation in the solid domain. It can be used to solve the coupled vibroacoustics phenomena present in musical instruments such as the structure-cavity interaction [37]. In general, acoustic-structure interaction approach can provide accurate results, as it has been found in a study about the estimation of the air resonance in a violin [23].
A brief mathematical formulation of the acoustic-structure interaction is presented, based on [38]. For a more complete approach to the subject, one can refer to [39]. For an elastic solid, the dynamic behavior can be expressed as:
σ i j , j + f i = ρ s u ¨ i
where σ i j is the stress tensor, f i   is the body forces vector, ρ s is the solid density, u i   is the displacement, and i and j = x, y, z. The effect of the acoustic pressure over the solid in the intersection of the domains can be expressed as:
σ i j n i = n i p
where n i is the intersection normal vector and p is the acoustic pressure. The acoustic wave equation is expressed as follows:
∇ 2 p + 1 c O 2 p ¨ = − g
where   c O is the sound speed and g is the source field. The influence of the solid over the acoustic domain is also taken into account in the domainσ intersections. The kinematic compatibility of the solid in contact with the acoustic domain can be expressed as:
∂ p ∂ n = ρ O u ¨ n
where ρ O is the fluid density and u n   is the displacement component normal to the interface. Using the above equations, the weighted residual method [40] can be applied. The mass matrix, stiffness matrix, volumetric stiffness matrix, compressibility matrix and interface matrix can be obtained:
M e = ∫ Ω ρ s N s T N s d Ω ,   K e = ∫ Ω B s T D B s d Ω ,   E e = 1 c O 2 ∫ Ψ ρ O N f T N f d Ψ                               H e = ∫ Ψ B f T B f d Ψ ,     L e T = ∫ Γ i N f T N s d Γ i
In the above, N is the element shape function matrix, B is the nodal strain-displacement matrix, D is the constitutive law matrix. The indexes S and f refer to solid and fluid domain, respectively. The Greek letters Ω , Ψ and Γ refers to the geometry of the structural, fluid and interface domain, respectively. Combining the above into a global matrix, we have:
K − L 0 H − Λ α M 0 ρ O L T E d p = 0 0
where Λ α is a diagonal matrix of the square of the natural frequency of coupled domain and d p T   is the displacement-acoustic pressure nodal vectors of the corresponding vibration mode shapes.

2.2.2.2. FEM acoustic modeling - Rigid body

In addition to the more complex acoustic-structure interaction model, a simple rigid body model was also utilized. Unlike the previous model, all boundary conditions in the body of the Cretan lyra were defined as a hard surface. This model was used for comparison reasons of the results for the air mode resonance with that of the acoustic-structure interaction model. The simulation is based on the resolution of Helmholtz equations in air, considered as a linear elastic fluid. The corresponding speed of sound and density are supposed to be constant, taking, respectively, the values of c = 340 m/s and ρ= 1.225 kg/m3. A perfectly matched layer (PML) is applied spherically all around the model to mimic an open infinite medium.

3. Results

3.1. Acoustic Measurements

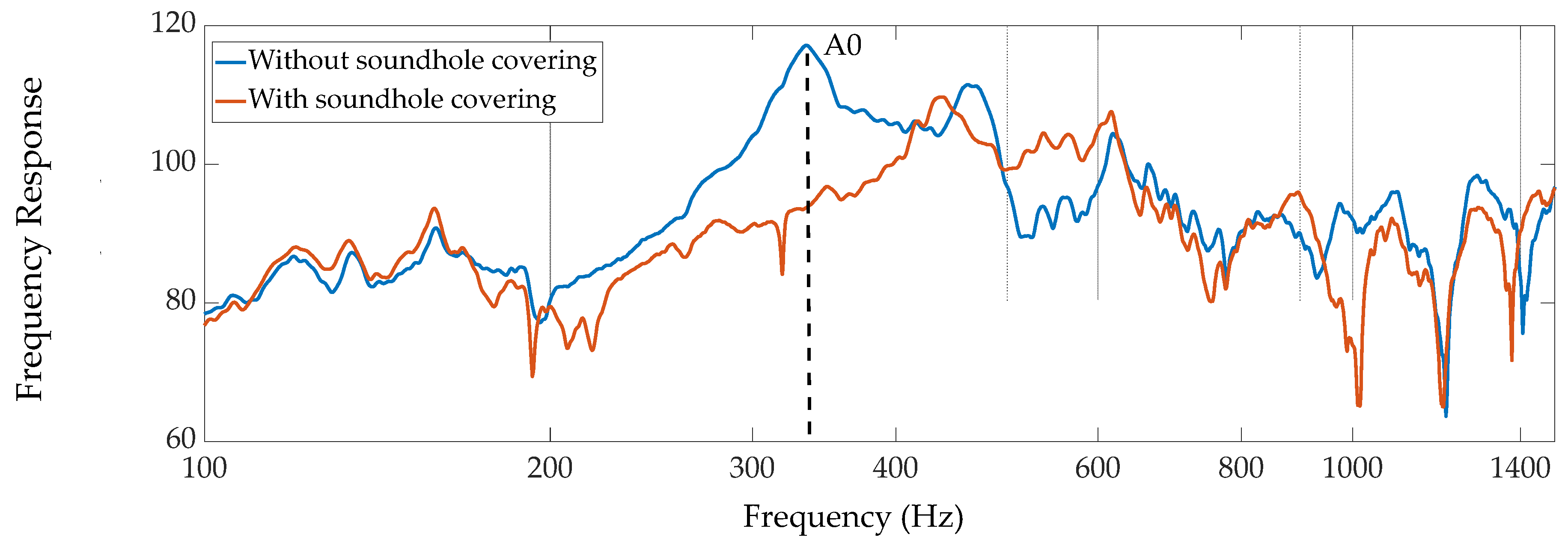
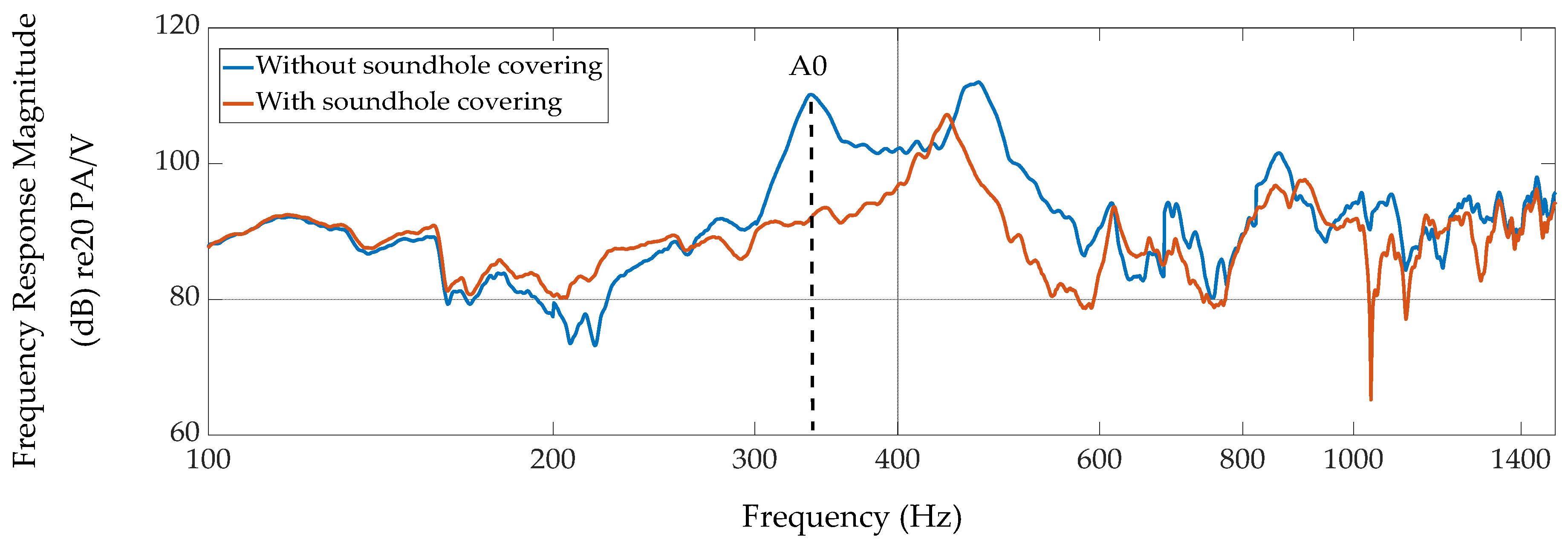
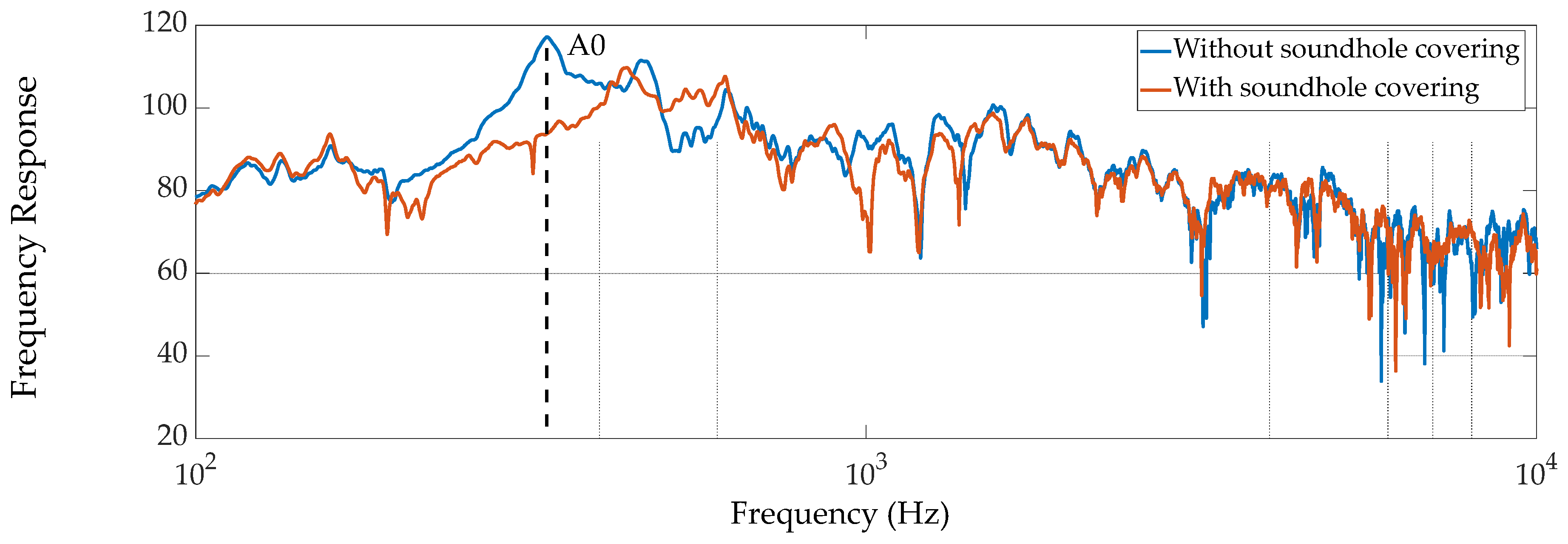
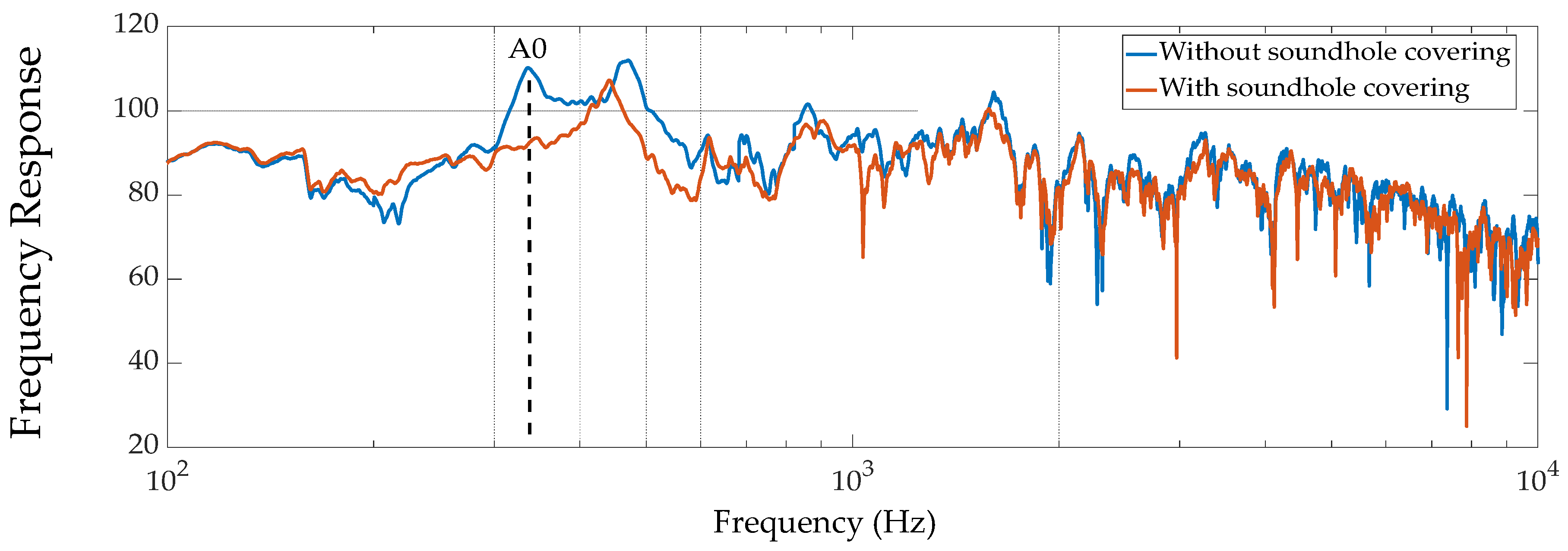
The frequency response results of the acoustic measurements with the soundholes open and the soundholes closed are presented in Figure 3, Figure 4, Figure 5 and Figure 6. Figure 3 and Figure 4 show the frequency responses for measurement locations A and B in a limited frequency range (100-1400 Hz) to better present the difference in air resonance frequency with holes closed and holes open. The air resonance frequency measured in both locations is the same, at 336.2 Hz.
Figure 5 and Figure 6 show the frequency responses for measurement locations A and B in a wider frequency range (100-10000 Hz) to better present the general differences with soundholes open and soundholes closed. It is apparent that the largest difference in frequency response magnitude is for the A0 air frequency.

3.2. Acoustic Modeling

3.2.1. Acoustic-Structure Interaction

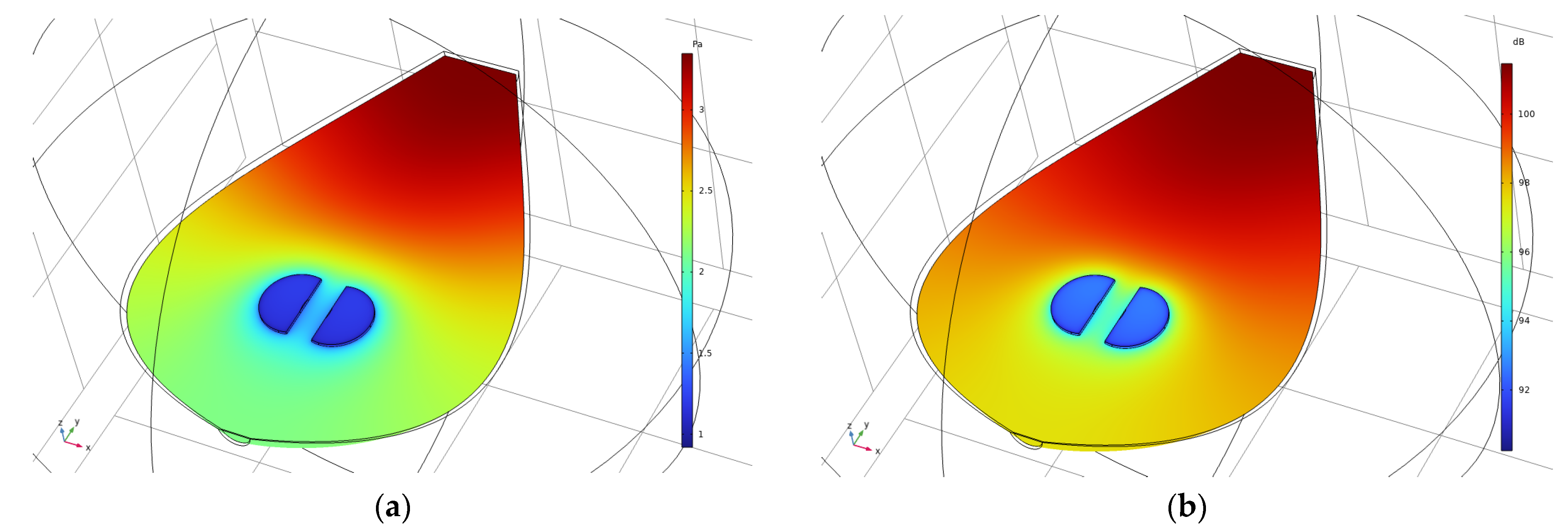
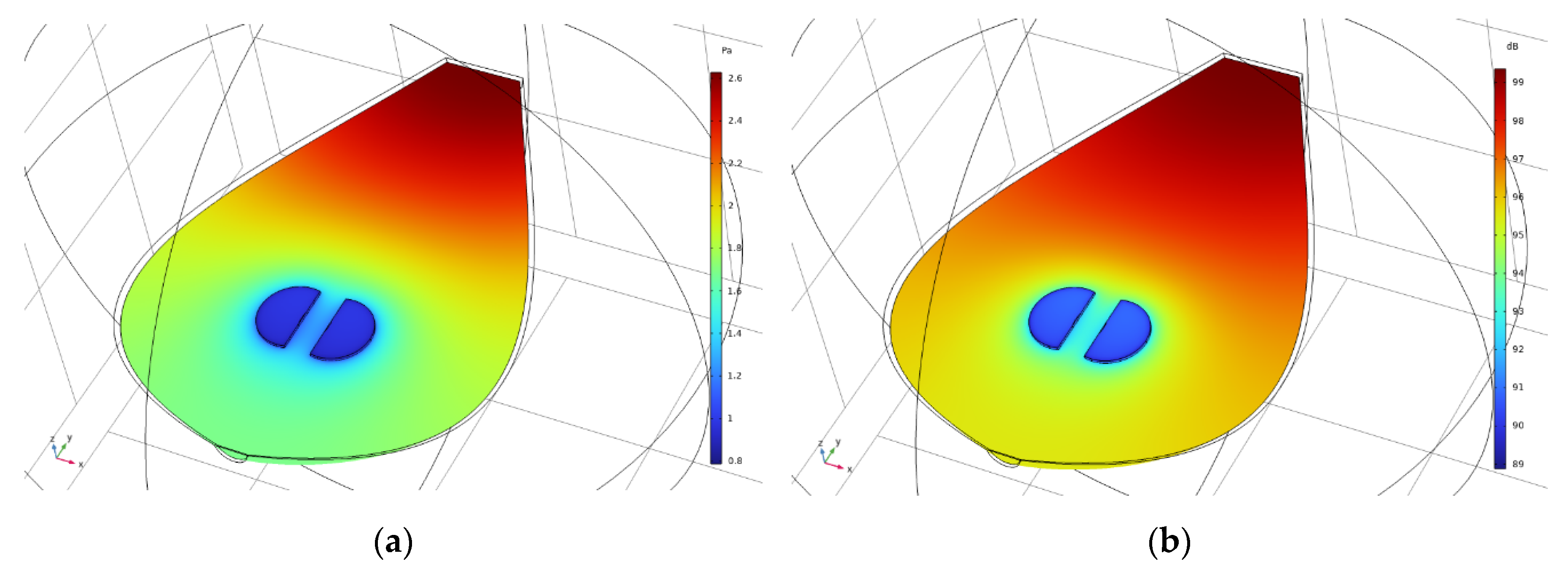
In the initial FEM modeling, an acoustic-structure interaction was utilized as presented in the methodology section. Results of the first eigenmode and the first eigenfrequency of 348.8 Hz are presented in the following figures. In Figure 7, the acoustic pressure distribution (a) and the sound pressure level distribution (b) are presented found at 348.8 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and sound pressure level is computed everywhere, but not shown in the outside air. 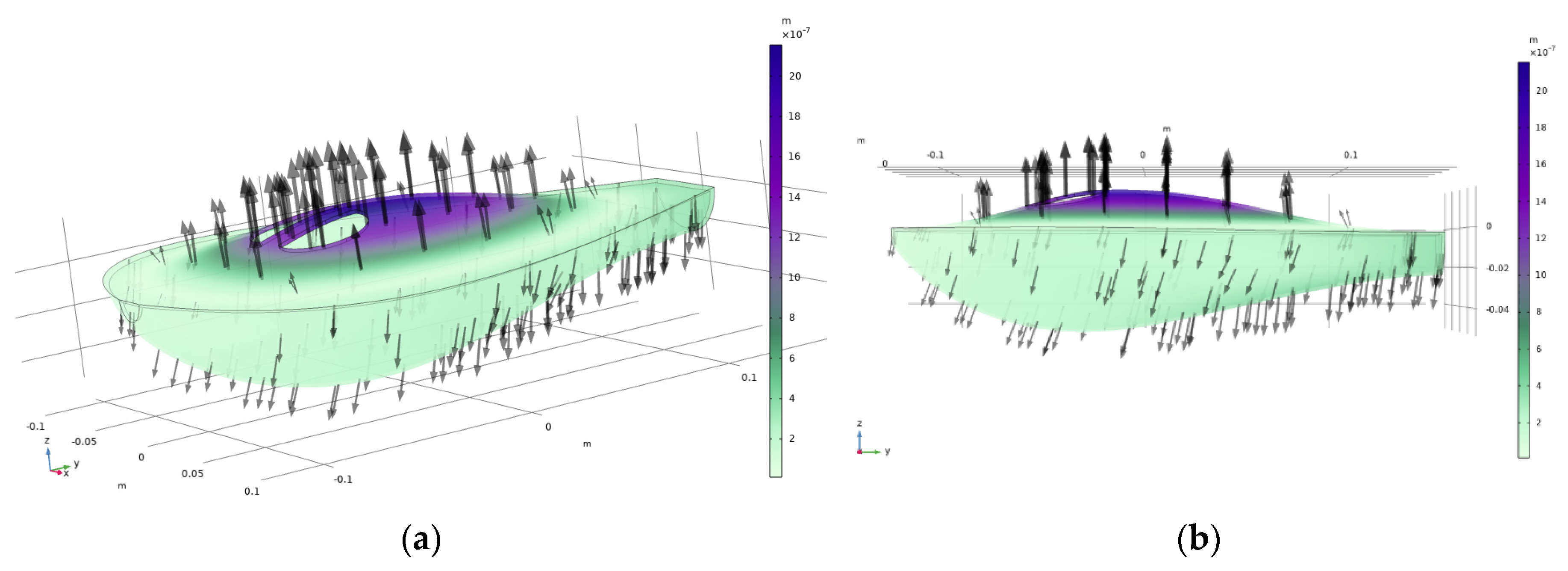Figure 8, presents three-quarter and side views of the Cretan lyra body displacements at the phase of maximum pressure in the cavity. It can be seen that the top and bottom of the Cretan lyra join in and act as springs increasing the compliance of the system. They both bend outwards to accommodate for the pressure inside the cavity.

3.2.2. Rigid Body

In addition to the more complex acoustic-structure interaction model, a simple FEM rigid body model was also utilized. Unlike the previous model, all boundary conditions in the body of the Cretan lyra were defined as a hard surface. Therefore no structural deformation of the lyra body was modeled. This model was used for comparison reasons of the results for the air mode resonance with that of the acoustic-structure interaction model. Results of the first eigenmode and the first eigenfrequency of 382.6 Hz are presented in Figure 9. More specifically, the acoustic pressure distribution and the sound pressure level distribution in the acoustic modeling (rigid walls) solution of the air mode resonance are presented, found at 382.6 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and the sound pressure level is computed everywhere, but not shown in the outside air. While the basic shape of the acoustic pressure level and sound pressure level distribution remains almost identical with the acoustic-structure interaction model (Figure 7), the top and bottom plates now don’t join in and act as springs. This is going to affect the acoustic pressure levels and sound pressure levels outside the body of the Cretan lyra that is going to be presented in the next section (section 3.2.3.).

3.2.3. Comparison of SPL Distribution Around the Cretan Lyra (Acoustic-Structure Interaction and Rigid Body)

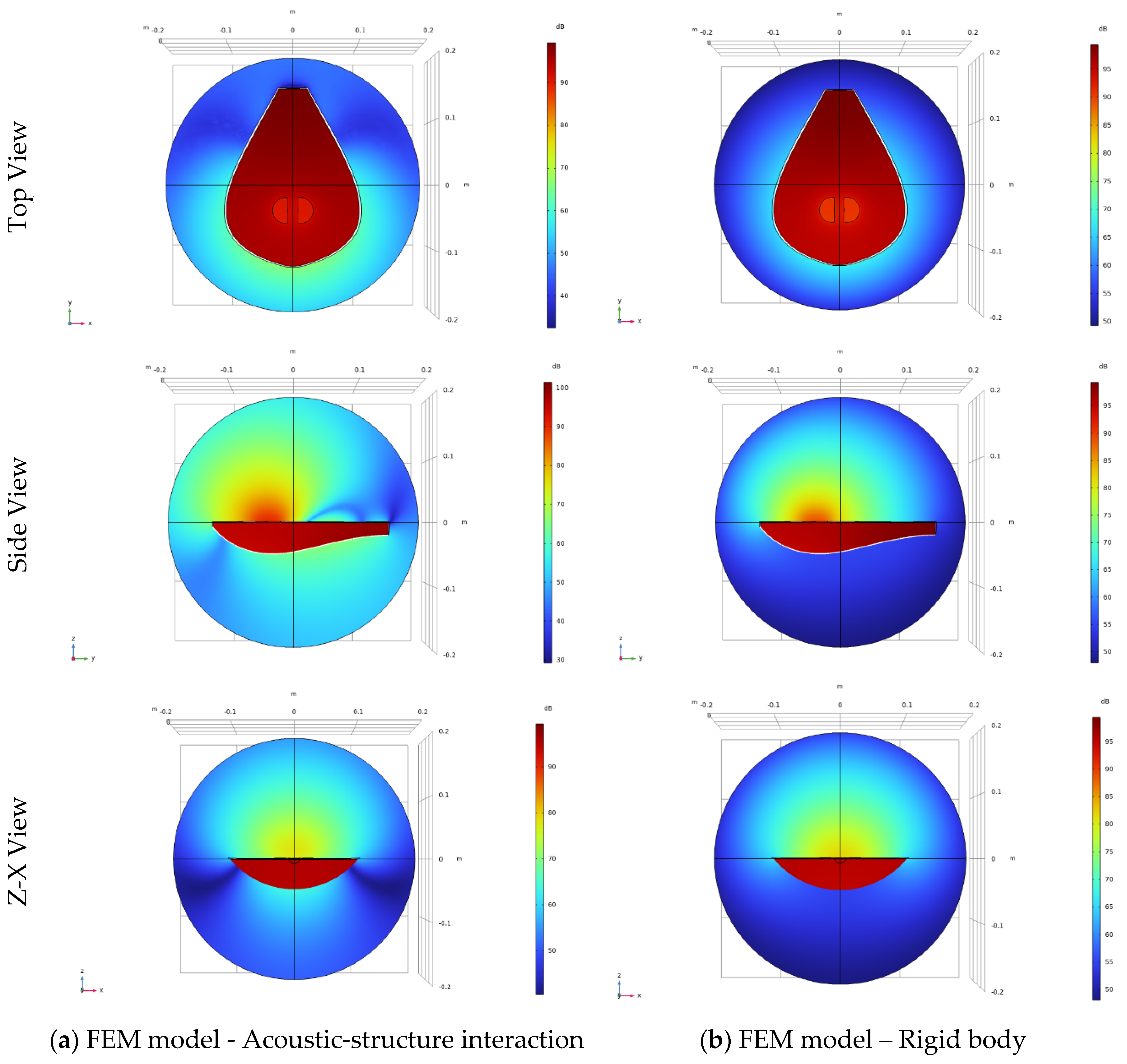
As presented in Section 3.2.1 and also in Figure 8, the top and bottom of the body of the Cretan lyra act as springs increasing the compliance of the system. They both bend outwards (and inwards in phase) to accommodate for the pressure inside the cavity. For the rigid model, the top and bottom plates don’t join in and act as springs. This is going to affect the acoustic pressure levels and sound pressure levels outside the body of the Cretan lyra. In Figure 10, the outlined air half-sphere outside of the Cretan lyra is included in order to let the mode freely decay rather than be artificially cut off just above the holes. A comparison of sound pressure level distribution for acoustic structure interaction (a) and rigid body (b) for the FEM modeling around the Cretan lyra is presented in a slice from a top-view, side-view, z-x view.

4. Discussion

The measurements results of the Cretan lyra with and without covered soundholes, as presented in Figure 3, Figure 4, Figure 5 and Figure 6, show that the air resonance frequency is at 336.2 Hz. It can be seen, especially in Figure 5 and Figure 6, that the effect of covered soundholes is more profound on the air resonance frequency than any other frequency in the whole frequency range. By changing the position of the transducer, the frequency response change, as expected, since different position of the transducer may correspond to positions with different nodes and antinodes on the body of the Cretan lyra. However, the resonance frequency remains constant regardless of the position of the transducer, as shown in Figure 3, Figure 4, Figure 5 and Figure 6.
The results for FEM modeling, in the cases of acoustic-structure interaction and rigid body, are presented in section 3.2 and in Figure 7, Figure 8, Figure 9 and Figure 10. The air resonance frequency for the acoustic-structure interaction FEM model was found to be 348.8 Hz and for the FEM model with rigid walls 382.6 Hz. Collectively, the results of the air frequency for measurements and modeling are presented in Table 1. Comparison of the results between the measurements of the air resonance frequency and the FEM modeling in the case of acoustic-structure interaction shows a difference of 3.7%, while comparison between the measurements and the FEM model with rigid walls has a larger difference of 13.8%. These results are similar to a study regarding the air frequency resonance in the case of the violin [23]. In this research, differences between measurements and modeling of the air resonance frequency applying acoustic-structure interaction were of the order of 1%, while differences between measurements and rigid wall modeling were 6%. Similar results have been observed in a study [41] (violins), where in the case of measurements with the walls fixed (rigid) the air frequency is higher than the air frequency when the walls are free to vibrate. An earlier study for acoustic guitar has also shown the necessity of acoustic-structure interaction analysis for the prediction of air resonance frequency [42]. The accuracy of results (e.g. compared to the aforementioned study [23]) is likely to be caused by several reasons. The precise knowledge of the characteristics of wood, essential for acoustic modeling, is not always possible, as these are likely to be affected by various factors (e.g. moisture content [43]). However, improving the quality of the acoustic modeling and by extension its results is very important and research into solving this problem is already underway. Conclusively, the acoustic-structure interaction approach seems to provide more accurate results for the representation of the air resonance frequency, modes and the acoustic behavior of musical instruments in general, while modeling with a rigid structure appears to be inadequate for complex problems.
Regarding some of the modeling results, it can be seen in Figure 7 (acoustic-structure interaction modeling) that the acoustic pressure distribution inside the Cretan lyra is not uniform. This is an indication that the resonance for this frequency is not a pure Helmholtz resonance, as these usually have a constant distribution. The same has been observer in similar studies that investigated the A0 resonance of the acoustic guitar [44,45]. In these studies it can be seen that the acoustic pressure distribution of the A0 resonance in the body of the acoustic guitar is non-uniform and very similar to the one found in this study regarding the A0 air resonance of the Cretan lyra (Figure 7).
In Figure 10, the outlined air half-sphere outside of the Cretan lyra has been included, in order to let the mode freely decay rather than be artificially cut off just above the holes. With this approach, with the structure included, flexibility was added to the model in order to accurately represent the acoustic behavior of the instrument. While the basic shape of the acoustic mode remains almost identical in comparison to the rigid model (Figure 7 and Figure 9 respectively), the top and bottom of the Cretan lyra now join in and act as springs, increasing the compliance of the system. As can be seen in Figure 8, they both bend, to accommodate the pressure inside the cavity. The form of the displacement of the boy of the Cretan lyra for the A0 frequency is similar to the one observed for a violin [18] and a guitar body [17]. From this kind of analysis, sound propagation can be observed in different layouts of the Cretan lyra (and any instrument). Therefore, using this approach, possible changes can be predicted that will result from variations in the shape and dimensions of the soundholes.
This study and approach has important applications, as the acoustic modeling of musical instruments is very important for optimizing their musical performance. Predicting the acoustic timbre of an instrument using acoustic modeling is vital as it provides the possibility of achieving specific goals as well as reducing costs (e.g. by using alternative materials). While perception of the sound of a musical instrument can be affected by various reasons [46-48], the results of this study show that the FEM and the acoustic-structure interaction modeling approach are very important for accurate prediction of the acoustic behavior of the instrument. We hope the results and this approach will be used in future research and practical applications.

5. Conclusions

For this study, the air resonance in a Cretan lyra is investigated with the use of finite element method (FEM) and acoustic measurements. Two different FEM acoustic models were applied in this investigation. First, a pressure acoustics model with the Cretan lyra body treated as rigid was used to provide an approximate result. Secondly, an acoustic-structure interaction model with the Cretan lyra was applied for a more accurate representation. In addition, measurements with Exponential Sine Sweep (ESS) signal were performed to identify the air resonance frequency of the Cretan lyra. Results of this study showed that the acoustic-structure interaction model had a 3.7% difference compared to the actual measurements of the resonance frequency. In contrast, the pressure acoustics solution with rigid walls is approximately 13.8% too high compared with the actual measurements.
The evidence from this study supports the idea that the acoustic-structure interaction modeling provides superior results, verified by acoustic measurements. Rigid analysis is inadequate for an accurate modeling in the case of a Cretan lyra. Our research has highlighted the importance of proper acoustic modeling for the accurate results for acoustic instruments. Improved application of numerical methods can predict accurately the vibroacoustic behavior of musical instruments which in turn will enable the determination of key parameters that can be used to control instrument tone and sound quality.

Author Contributions

Conceptualization, N.P.; methodology, N.P.; software, N.P., N.N; formal analysis, N.P., G.S.; investigation, N.P.; resources, N.P.; data curation, N.P., G.S.; writing—original draft preparation, N.P.; writing—review and editing, N.P., G.S.; visualization, N.P.; supervision, N.P. and G.S.; project administration, N.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

We gratefully acknowledge the contribution of Emmanuel Nikakis in the construction stage of the 3D model of the Cretan lyra. We would like to thank the following people for their support, without whose help this work would never have been possible: Konstantinos Papadakis, Konstantinos Plevrakis, Antonis Plevrakis and Nikolaos Perakis.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Dimensions of the modeled Cretan lyra body (Figure 2).
Table A1. Dimensions of the modeled Cretan lyra body (Figure 2).
Dimensions a b c d e f h j
mm 279 208 46 23 19 46 19 56
Table A2. Acoustic measurement positions (Figure 2).
Table A2. Acoustic measurement positions (Figure 2).
Measurement Positions A B
(x,y,z) (mm,mm,mm) (50,57,6) (41,51,-46)

Appendix B

In Figure A1, three consecutive measurements made at position A using an Exponential Sine Sweep are presented. It appears that the repeatability of the measurements in terms of frequency response is high, as there are very small differences between the measurements.
Preprints 85095 g0a1
Figure A1. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: A) The line thickness of the frequency responses of the measurements was chosen to be small so that the differences could be distinguished.
Figure A1. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: A) The line thickness of the frequency responses of the measurements was chosen to be small so that the differences could be distinguished.
Preprints 85095 g0a1

References

  1. Pavlopoulou, A. Musical tradition and change on the island of Crete. Goldsmiths, University of London, 2012.
  2. Dawe, K. Symbolic and social transformation in the lute cultures of Crete: Music, technology and the body in a Mediterranean society. Yearbook for Traditional Music 2005, 37, 58-68. [CrossRef]
  3. Hnaraki, M. Cretan Music: Unraveling Ariadne's Thread; Kerkyra publications: 2007.
  4. Dawe, K. Lyres and the body politic: studying musical instruments in the Cretan musical landscape. Popular Music and Society 2003, 26, 263-283. [CrossRef]
  5. Martin, A.R.; Mihalka, M. Music around the World: A Global Encyclopedia [3 volumes]: A Global Encyclopedia; ABC-CLIO: 2020.
  6. Fay, R. Ways of Understanding: Ethnomusicology and the Cretan Lyra. The University of Manchester, 2011.
  7. Bader, R.; Hansen, U. Acoustical analysis and modeling of musical instruments using modern signal processing methods. Handbook of signal processing in acoustics 2008, 219-247.
  8. Sakai, S.; Samejima, T. Vibro-acoustic analysis of cellos using the finite and boundary element methods and its application to studies on the effects of endpin properties. Acoustical Science and Technology 2023, 44, 259-268. [CrossRef]
  9. Bilbao, S.; Hamilton, B.; Harrison, R.; Torin, A. Finite-difference schemes in musical acoustics: A tutorial. Springer Handbook of Systematic Musicology 2018, 349-384. [CrossRef]
  10. Beaton, D.; Scavone, G. Three-dimensional tuning of idiophone bar modes via finite element analysis. The Journal of the Acoustical Society of America 2021, 149, 3758-3768. [CrossRef]
  11. Bader, R. Nonlinearities and synchronization in musical acoustics and music psychology; Springer Science & Business Media: 2013; Volume 2.
  12. Papadakis, N.M.; Stavroulakis, G.E. Time domain finite element method for the calculation of impulse response of enclosed spaces. Room acoustics application. Mechanics of Hearing: Protein to Perception: 12th International Workshop on the Mechanics of Hearing 2015, 1703, 100002. [CrossRef]
  13. Papadakis, N.M.; Stavroulakis, G.E. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Science 2020, 4, 77. [CrossRef]
  14. Ballou, G. Handbook for sound engineers. 2013, 228. [CrossRef]
  15. Bakarezos, M.; Gymnopoulos, S.; Brezas, S.; Orfanos, Y.; Maravelakis, E.; Papadopoulos, C.; Tatarakis, M.; Antoniadis, A.; Papadogiannis, N. Vibration analysis of the top plates of traditional greek string musical instruments. In Proceedings of the Proceedings of the 13th International Congress on Sound and Vibration, 2006; pp. 4939-4946.
  16. Bissinger, G. A0 and A1 coupling, arching, rib height, and f-hole geometry dependence in the 2 degree-of-freedom network model of violin cavity modes. The Journal of the Acoustical Society of America 1998, 104, 3608-3615. [CrossRef]
  17. Fletcher, N.H.; Rossing, T.D. The physics of musical instruments; Springer Science & Business Media: 2012.
  18. Rossing, T.D.; Rossing, T.D. Springer handbook of acoustics; Springer: 2014. [CrossRef]
  19. Wolfe, J. Helmholtz Resonance. Available online: https://newt.phys.unsw.edu.au/jw/Helmholtz.html (accessed on 22.7.2023).
  20. Le Carrou, J.-L.; Gautier, F.; Foltête, E. Experimental study of A0 and T1 modes of the concert harp. The Journal of the Acoustical Society of America 2007, 121, 559-567. [CrossRef]
  21. Kobayashi, T.; Takami, T.; Miyamoto, M.; Takahashi, K.y.; Nishida, A.; Aoyagi, M. 3D calculation with compressible LES for sound vibration of Ocarina. arXiv preprint arXiv:0911.3567 2009.
  22. Nikolsky, A. “Talking Jew’s Harp” and Its Relation to Vowel Harmony as a Paradigm of Formative Influence of Music on Language. The Origins of Language Revisited: Differentiation from Music and the Emergence of Neurodiversity and Autism 2020, 217-322. [CrossRef]
  23. Nia, H.T.; Jain, A.D.; Liu, Y.; Alam, M.-R.; Barnas, R.; Makris, N.C. The evolution of air resonance power efficiency in the violin and its ancestors. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2015, 471, 20140905. [CrossRef]
  24. Ting, J. The Science and Art of Violins; Scholar Books Publishing: 2023.
  25. Wali, K.C. Cremona violins: A physicist's quest for the secrets of Stradivari; World Scientific: 2010.
  26. Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A data-driven approach to violin making. Scientific reports 2021, 11, 9455. [CrossRef]
  27. French, R.M. Acoustic Guitar Design; Springer: 2022.
  28. Jansson, E.V. Acoustical properties of complex cavities. Prediction and measurements of resonance properties of violin-shaped and guitar-shaped cavities. Acta Acustica united with Acustica 1977, 37, 211-221.
  29. Hutchins, C.M. A study of the cavity resonances of a violin and their effects on its tone and playing qualities. The Journal of the Acoustical Society of America 1990, 87, 392-397. [CrossRef]
  30. Farina, A.; Langhoff, A.; Tronchin, L. Acoustic characterisation of “virtual” musical instruments: Using MLS technique on ancient violins. Journal of New Music Research 1998, 27, 359-379. [CrossRef]
  31. Morset, L.H. A low-cost PC-based tool for violin acoustics measurements. Catgut Acoustical Society (CAS) Journal 2001, 4, 45.
  32. Papadakis, N.M.; Antoniadou, S.; Stavroulakis, G.E. Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics 2023, 5, 563-574. [CrossRef]
  33. Papadakis, N.M.; Stavroulakis, G.E. Review of Acoustic Sources Alternatives to a Dodecahedron Speaker. Applied Sciences 2019, 9, 3705. [CrossRef]
  34. Papadakis, N.M.; Stavroulakis, G.E. Low Cost Omnidirectional Sound Source Utilizing a Common Directional Loudspeaker for Impulse Response Measurements. Applied Sciences 2018, 8, 1703. [CrossRef]
  35. Papadakis, N.M.; Stavroulakis, G.E. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics 2020, 2, 224-245. [CrossRef]
  36. de Vos, R.; Papadakis, N.M.; Stavroulakis, G.E. Improved Source Characteristics of a Handclap for Acoustic Measurements: Utilization of a Leather Glove. Acoustics 2020, 2, 803-811. [CrossRef]
  37. Chaigne, A.; Kergomard, J. Acoustics of musical instruments; Springer: 2016. [CrossRef]
  38. Zienkiewicz, O. Coupled vibrations of a structure submerged in a compressible fluid. In Proceedings of the Proc. of Symposium on Finite Element Techniques Held at the University of Stuttgart, 1969.
  39. Sigrist, J.-F. Fluid-structure interaction: an introduction to finite element coupling; John Wiley & Sons: 2015.
  40. Hatami, M. Weighted residual methods: principles, modifications and applications; Academic Press: 2017.
  41. Rossing, T.D. The science of string instruments; Springer: 2010. [CrossRef]
  42. Christensen, O.; Vistisen, B.B. Simple model for low-frequency guitar function. The Journal of the Acoustical Society of America 1980, 68, 758-766. [CrossRef]
  43. Güntekin, E.; Niemz, P. Prediction of Young's Modulus in Three Orthotropic Directions for Some Important Turkish Wood Species Using Ultrasound.
  44. Elejabarrieta, M.; Santamaria, C.; Ezcurra, A. Air cavity modes in the resonance box of the guitar: the effect of the sound hole. Journal of Sound and vibration 2002, 252, 584. [CrossRef]
  45. Ezcurra, A.; Elejabarrieta, M.; Santamaria, C. Fluid–structure coupling in the guitar box: numerical and experimental comparative study. Applied Acoustics 2005, 66, 411-425. [CrossRef]
  46. Bishop, L.; Goebl, W. Music and movement: Musical instruments and performers. The Routledge companion to music cognition. New York, NY: Routledge 2017.
  47. Papadakis, N.M.; Zantzas, A.; Lafazanis, K.; Stavroulakis, G.E. Influence of Color on Loudness Perception of Household Appliances: Case of a coffee maker. Designs 2022, 6, 101. [CrossRef]
  48. Thoret, E.; Caramiaux, B.; Depalle, P.; Mcadams, S. Learning metrics on spectrotemporal modulations reveals the perception of musical instrument timbre. Nature Human Behaviour 2021, 5, 369-377. [CrossRef]
Preprints 85095 g001
Figure 1. (a) Top view of a Cretan lyra (b) Side view of a Cretan lyra. It can be seen that the fingerboard is not in contact with the main body of the lyra, allowing it to vibrate freely.
Figure 1. (a) Top view of a Cretan lyra (b) Side view of a Cretan lyra. It can be seen that the fingerboard is not in contact with the main body of the lyra, allowing it to vibrate freely.
Preprints 85095 g001
Preprints 85095 g002
Figure 2. Top (a) and side (b) view of the modeled Cretan lyra body. Dimensions and measurement positions (M:A, M:B) are presented. Full dimensions and measurement positions are included in Appendix A (Table A1 and A2).
Figure 2. Top (a) and side (b) view of the modeled Cretan lyra body. Dimensions and measurement positions (M:A, M:B) are presented. Full dimensions and measurement positions are included in Appendix A (Table A1 and A2).
Preprints 85095 g002
Preprints 85095 g003
Figure 3. Measured frequency response of a Cretan lyra with and without soundhole covering (Microphone position: A).
Figure 3. Measured frequency response of a Cretan lyra with and without soundhole covering (Microphone position: A).
Preprints 85095 g003
Preprints 85095 g004
Figure 4. Measured frequency response of a Cretan lyra with and without soundhole covering (Microphone position: B).
Figure 4. Measured frequency response of a Cretan lyra with and without soundhole covering (Microphone position: B).
Preprints 85095 g004
Preprints 85095 g005
Figure 5. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: A).
Figure 5. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: A).
Preprints 85095 g005
Preprints 85095 g006
Figure 6. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: B).
Figure 6. Measured frequency response of a Cretan lyra with and without soundhole covering for frequency range 100 Hz -10000 Hz (Microphone position: B).
Preprints 85095 g006
Preprints 85095 g007
Figure 7. The acoustic pressure distribution (a) and the sound pressure level distribution (b) in the acoustic-structure interaction solution of the air mode resonance, found at 348.8 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and the sound pressure level is computed everywhere, but not shown in the outside air.
Figure 7. The acoustic pressure distribution (a) and the sound pressure level distribution (b) in the acoustic-structure interaction solution of the air mode resonance, found at 348.8 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and the sound pressure level is computed everywhere, but not shown in the outside air.
Preprints 85095 g007
Preprints 85095 g008
Figure 8. Three-quarter and side views of the Cretan lyra body displacements at the phase of maximum pressure in the cavity. The eigenfrequency is now lowered to 348.8 Hz.
Figure 8. Three-quarter and side views of the Cretan lyra body displacements at the phase of maximum pressure in the cavity. The eigenfrequency is now lowered to 348.8 Hz.
Preprints 85095 g008
Preprints 85095 g009
Figure 9. The acoustic pressure distribution (a) and the sound pressure level distribution in the acoustic modeling (rigid walls) solution of the air mode resonance, found at 382.6 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and the sound pressure level is computed everywhere, but not shown in the outside air.
Figure 9. The acoustic pressure distribution (a) and the sound pressure level distribution in the acoustic modeling (rigid walls) solution of the air mode resonance, found at 382.6 Hz. The scale ranges from blue (low) to red (high). The acoustic pressure level and the sound pressure level is computed everywhere, but not shown in the outside air.
Preprints 85095 g009
Preprints 85095 g010
Figure 10. Comparison of sound pressure level distribution for acoustic structure interaction (a) and rigid body (b). FEM modeling around the Cretan Lyra in a slice from a top-view, side-view, z-x view.
Figure 10. Comparison of sound pressure level distribution for acoustic structure interaction (a) and rigid body (b). FEM modeling around the Cretan Lyra in a slice from a top-view, side-view, z-x view.
Preprints 85095 g010
Table 1. Measured and modeled air resonance frequency of the Cretan lyra.
Table 1. Measured and modeled air resonance frequency of the Cretan lyra.
FEM Modeling
Acoustic Measurements Acoustic-Structure
Interaction		 Rigid Body
A0 (Hz) 336.2 348.8 382.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated