Prerpints.org logo
Preprint
Article

Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and SSA-LSTM

Altmetrics

Downloads

76

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts
Abstract
The performance of bearings plays a pivotal role in determining the dependability and security of rotating machinery. In intricate systems demanding exceptional reliability and safety, the ability to accurately forecast fault occurrences during operation holds profound significance. Such predictions serve as invaluable guides for crafting well-considered reliability strategies and executing maintenance practices aimed at enhancing reliability. In order to ensure the reliability of bearing operation, this article investigates the application of three advanced techniques—Maximum Correlation Kurtosis Deconvolution (MCKD), Multi-Scale Permutation Entropy (MPE), and Long Short-Term Memory (LSTM) recurrent neural networks—for the prediction of the remaining useful life (RUL) of rolling bearings. Each technique's principles, methodologies, and applications are comprehensively reviewed, offering insights into their respective strengths and limitations. Case studies and experimental evaluations are presented to assess their performance in RUL prediction. Findings reveal that MCKD enhances fault signatures, MPE captures complexity, and LSTM excels in modeling temporal patterns. The root mean square error of the prediction results is 0.007. The fusion of these techniques offers a comprehensive approach to RUL prediction, leveraging their unique attributes for more accurate and reliable predictions.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Rolling bearings are crucial components in various industrial systems, including machinery, automotive, aerospace, and wind turbines[1]. The reliable and efficient functioning of these systems heavily depends on the health and performance of rolling bearings. However, the degradation and failure of rolling bearings can lead to costly downtime, productivity losses, and safety risks. To mitigate these issues, the concept of remaining useful life (RUL) prediction has gained significant attention in recent years. RUL prediction aims to estimate the remaining operational lifespan of rolling bearings, enabling proactive maintenance strategies and optimizing asset management.
Traditional maintenance strategies, such as time-based or reactive maintenance, often result in inefficient resource allocation and unnecessary maintenance activities[2]. By accurately predicting the RUL of rolling bearings, maintenance activities can be planned in advance, leading to reduced downtime, optimized maintenance schedules, and cost savings. RUL prediction also enables condition-based maintenance, where maintenance actions are triggered based on the actual health condition of rolling bearings rather than arbitrary time intervals. This approach enhances reliability, minimizes the risk of catastrophic failures, and improves overall system performance.
Rolling bearings’ RUL prediction has traditionally relied on statistical and data-driven methods[3]. However, recent advancements in signal processing, data analytics, and machine learning techniques have provided new opportunities to enhance the accuracy and reliability of RUL prediction. In this article, we investigate the application of three innovative techniques: maximum correlation kurtosis deconvolution (MCKD)[4], multi-scale permutation entropy (MPE)[5], and long short-term memory (LSTM) recurrent neural network[6].
The objective of this article is to explore the potential of these techniques for rolling bearings’ RUL prediction, discuss their advantages and limitations, and highlight their contributions to proactive maintenance strategies and asset management. Through a comprehensive review and analysis of existing literature and research studies, we aim to provide insights into the capabilities and practical implications of MCKD, MPE, and LSTM in the context of rolling bearings’ RUL prediction.
By leveraging these advanced techniques, it is expected that rolling bearings’ RUL prediction can be improved in terms of accuracy, reliability, and timeliness. This will facilitate the implementation of condition-based maintenance practices, where maintenance activities are performed based on the actual health condition of rolling bearings, optimizing resource allocation and enhancing overall system performance.
The subsequent chapters of this article will delve into the principles, methodologies, applications, and performance evaluation of MCKD, MPE, and LSTM techniques for rolling bearings' RUL prediction. Comparative analysis and discussion of the advantages and limitations of each technique will be presented, along with potential synergies and future directions for enhanced maintenance practices in rolling element systems.

2. Correlation Methods

2.1. Maximum Correlation Kurtosis Deconvolution

(MCKD) is a signal processing technique that aims to enhance the quality and resolution of signals by effectively removing noise and distortion[7]. It is particularly useful in scenarios where the signal of interest is corrupted by additive noise and is convolved with an unknown system impulse response. The mathematical formula can be expressed as follows:
x=h * y
(1)
where: x is the signal convoluted from various signals on the transmission path, y denotes the impulse signal, h represents the response of the y signal after passing the transmission path[8].
The core principle of MCKD is to maximize the correlation kurtosis of the deconvolved signal, which is a statistical measure of the signal's non-Gaussianity. The maximum correlation kurtosis is considered as[9] :
O C K M ( T ) = ∑ n = 1 N   ∏ m = 0 M   y ( n − m T ) 2 ∑ n = 1 N   y n 2 M + 1
By maximizing correlation kurtosis, MCKD aims to enhance the signal's sparsity and separate it from the noise and distortions.
m a x f '   C K M ( T ) = m a x f '   ∑ i = 1 N   ∏ m = 0 M   y i − m T 2 ∑ i = 1 N   y i 2 M + 1
To obtain the maximum value of the relevant kurtosis, it is equivalent to solving the following equation, where the derivative function is 0.
d d f l ' C K M ( T ) = 0 ( l = 1,2 , ⋯ , L )
The final coefficients of the filter can be obtained from equations (1) to (4) and expressed in matrix form:
f ' = ∥ y ∥ 2 2 β 2 X 0 X 0 T − 1 ∑ r = T m T   X r ψ m
where:
β = y 1 y 1 − T ⋯ y 1 − M T y 2 y 2 − T ⋯ y 2 − M T ⋮ y N y N − T ⋯ y N − m T
X r = x 1 − r x 2 − r x 3 − r ⋯ x N − r 0 x 1 − r x 2 − r ⋯ x N − 1 − r 0 0 x 1 − r ⋯ x N − 2 − r ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ x N − L − r + 1 ( r = [ T , ⋯ , m T ] )
ψ m = y 1 − m T − 1 y 1 2 y 1 − T 2 ⋯ y 1 − M T 2 y 2 − m T − 1 y 2 2 y 2 − T 2 ⋯ y 1 − M T 2 ⋮ y N − m T − 1 y N 2 y N − T 2 ⋯ y N − M T 2
In conclusion, the implementation process of the MCKD algorithm can be formulated as follows:
(1) Initialize parameters such as the deconvolution period T, the number of shifts M, and the length of the filter L.
(2) Calculate the X0T and (X0X0T)^-1 of the input signal x.
(3) Compute the filtered output signal y.
(4) Calculate ψ m and β based on y.
(5) Update the coefficients of the filter f'.
If the kurtosis difference value ΔCKM(T) between the signals before and after filtering is smaller than the threshold, end the iteration. Otherwise, repeat steps 3 to 5.

2.2. Multi-Scale Permutation Entropy

Multi-Scale Permutation Entropy (MPE) is a powerful tool used for analyzing the complexity and irregularity of time series data[10]. It is particularly useful in the field of signal processing and analysis, where it can provide valuable insights into the underlying dynamics and patterns present in the data.
The core concept of MPE lies in the analysis of the ordinal patterns or permutations that occur within a time series at different scales or resolutions. Ordinal patterns capture the relative order of the data points within a sliding window of fixed length. By examining the frequency and distribution of these ordinal patterns, MPE quantifies the complexity and information content of the time series.
The MPE methodology involves the following steps:
Signal Segmentation: The time series data is divided into non-overlapping segments or windows of fixed length. The length of the window determines the scale or resolution at which the analysis is performed.
y j ( s ) = 1 s ∑ i = ( j − 1 ) s + 1 j s   x i , j = 1,2 , ⋯ , [ N / s ]
where: s denotes the scale factor; [ N / s ] represents the length of new time series.
Ordinal Pattern Generation: Within each segment, the ordinal patterns are generated by assigning a rank to each data point based on its relative position compared to other data points within the window. For example, the smallest data point is assigned rank 1, the second smallest rank 2, and so on[11].
Permutation Encoding: Each ordinal pattern is encoded into a permutation symbol, representing the order of ranks. For instance, if the ranks within a window are 3, 1, 2, the corresponding permutation symbol would be 312.
Permutation Frequency Analysis: The frequency of occurrence of each permutation symbol is calculated across all the segments at the given scale. This information reflects the distribution of ordinal patterns and provides insights into the complexity and regularity of the time series.
Entropy Calculation: The entropy is computed based on the probabilities of the permutation symbols. Entropy measures the amount of uncertainty or information content in the time series. Higher entropy values indicate higher complexity and irregularity, while lower entropy values suggest more regular and predictable patterns.
H p ( m ) = − ∑ r = 1 R   P r l n ⁡ P r
The value of Hp reaches the highest when P r = 1 / m ! .For convenience, normalization is generally accomplished[12].
H p = H p ( m ) / l n ⁡ ( m ! )
In the context of rolling bearings’ RUL prediction, MPE can be utilized to analyze the vibration signals obtained from bearings. Vibration signals contain valuable information about the health condition and fault characteristics of the bearings. By applying MPE, the complexity and irregularity of these signals can be quantified, providing useful features for fault diagnosis and RUL prediction.
MPE offers several advantages in RUL prediction analysis. First, it is a non-parametric technique, meaning it does not assume any specific underlying distribution of the data. This flexibility makes it suitable for analyzing complex and non-linear dynamics commonly observed in rolling element systems.
Second, MPE is capable of capturing both short-term and long-term temporal dependencies in the data[13]. By analyzing the ordinal patterns at different scales, MPE can reveal the presence of localized or global patterns, offering a comprehensive understanding of the bearing's health condition.
Furthermore, MPE can capture subtle changes in the complexity of the vibration signals, allowing for early detection of fault initiation and progression. This early detection can lead to timely maintenance actions and improved RUL prediction accuracy.
By quantifying the complexity and irregularity of vibration signals, MPE-based features can effectively discriminate between different fault conditions and provide valuable information for estimating the remaining operational lifespan of the bearings.

2.3. Long Short-Term Memory Recurrent Neural Network

Long Short-Term Memory (LSTM) is a type of recurrent neural network (RNN) architecture specifically designed to handle the challenges of learning and remembering long-term dependencies in sequential data. Unlike traditional RNNs[14], which suffer from the "vanishing gradient" problem and struggle to capture long-term dependencies, LSTMs are equipped with memory cells and gating mechanisms that enable them to selectively retain and update information over time[15].
The key components of an LSTM network include:
Memory Cell c t   ˆ : The memory cell serves as the main building block of an LSTM. It maintains an internal state that can be updated or preserved using gating mechanisms. The memory cell enables the LSTM to learn and store information over long sequences[16].
c ˆ t = t a n h W x c x t + W h c h t − 1 + b c
where: W x c represents the connection weight between the input layer and the hidden layer at time t. W h c denotes the connection weight between the hidden layers at time t-1 and t[17]. b c and h t − 1 respectively represent the biases of the input nodes and the previous time step's output.
Input Gate i t : The input gate determines the amount of new information to be stored in the memory cell at each time step. It takes input from the current time step and the previous hidden state and applies a sigmoid activation function to generate an input gate activation value[18].
i t = σ W x i x t + W h i h t − 1 + b i
where: W x i represents the connection weight between the input layer and the hidden layer at time t. W h i denotes the connection weight between the hidden layers at time t-1 and t. b i and h t − 1 respectively represent the biases of the input gate and the previous time step's output. σ denotes the sigmoid activation function.
Forget Gate f t : The forget gate determines the extent to which previous information should be forgotten or preserved in the memory cell. It takes input from the current time step and the previous hidden state and applies a sigmoid activation function to generate a forget gate activation value[19].
f t = σ W x f x t + W h f h t − 1 + b f
Output Gate: The output gate regulates the amount of information to be output from the memory cell to the next time step. It takes input from the current time step and the previous hidden state and applies a sigmoid activation function to generate an output gate activation value.
o t = σ W x o x t + W h o h t − 1 + b o
Hidden State: The hidden state carries information from the memory cell and previous hidden state to the next time step. It is computed by applying a tanh activation function to the current input and the memory cell state, and then scaling it by the output gate activation value.
The structure of LSTM is shown in Figure 1. The use of these gates and memory cells in LSTMs allows the network to selectively update, forget, and output information at each time step, facilitating the learning and retention of long-term dependencies in sequential data.
LSTM has gained significant attention in the field of rolling bearings’ RUL prediction due to its ability to model complex temporal dependencies and effectively handle time-series data. By processing the vibration signals obtained from rolling bearings, LSTM networks can learn the underlying patterns and characteristics indicative of bearing health conditions.
In the context of rolling bearings’ RUL prediction, LSTM networks can be utilized after data preprocessing and feature extraction:
LSTM Network Architecture: The LSTM network is constructed with input, hidden, and output layers. The input layer receives the sequence of MPE, which is fed into the LSTM layer. The hidden layer contains the LSTM units, responsible for processing and capturing the temporal dependencies in the data. The output layer generates predictions based on the learned patterns and features extracted by the LSTM layer.
Training and Optimization: The LSTM network is trained using a labeled dataset of vibration signals and corresponding RUL values[20]. The network learns to minimize the difference between its predicted RUL values and the actual RUL values. Training involves forward propagation, backpropagation through time, and optimization algorithms such as gradient descent to update the network’s weights and biases.
RUL Prediction: Once the LSTM network is trained, it can be used to predict the remaining useful life of rolling bearings[21]. Given a new sequence of vibration data, the LSTM network processes the sequence through the trained network and generates a predicted RUL value based on the learned temporal patterns and dependencies.
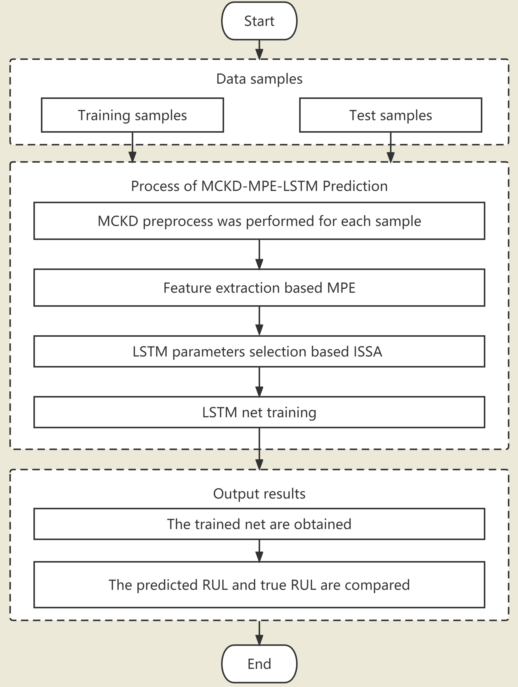
The flowchart of RUL prediction is shown as Figure 2.

3. Experiments and Results

3.1. Experimeantal Platform

To facilitate a comprehensive analysis of the acquired findings, the experimental dataset featuring LDK UER204 rolling element bearings from the XJTU–SY bearing was employed.
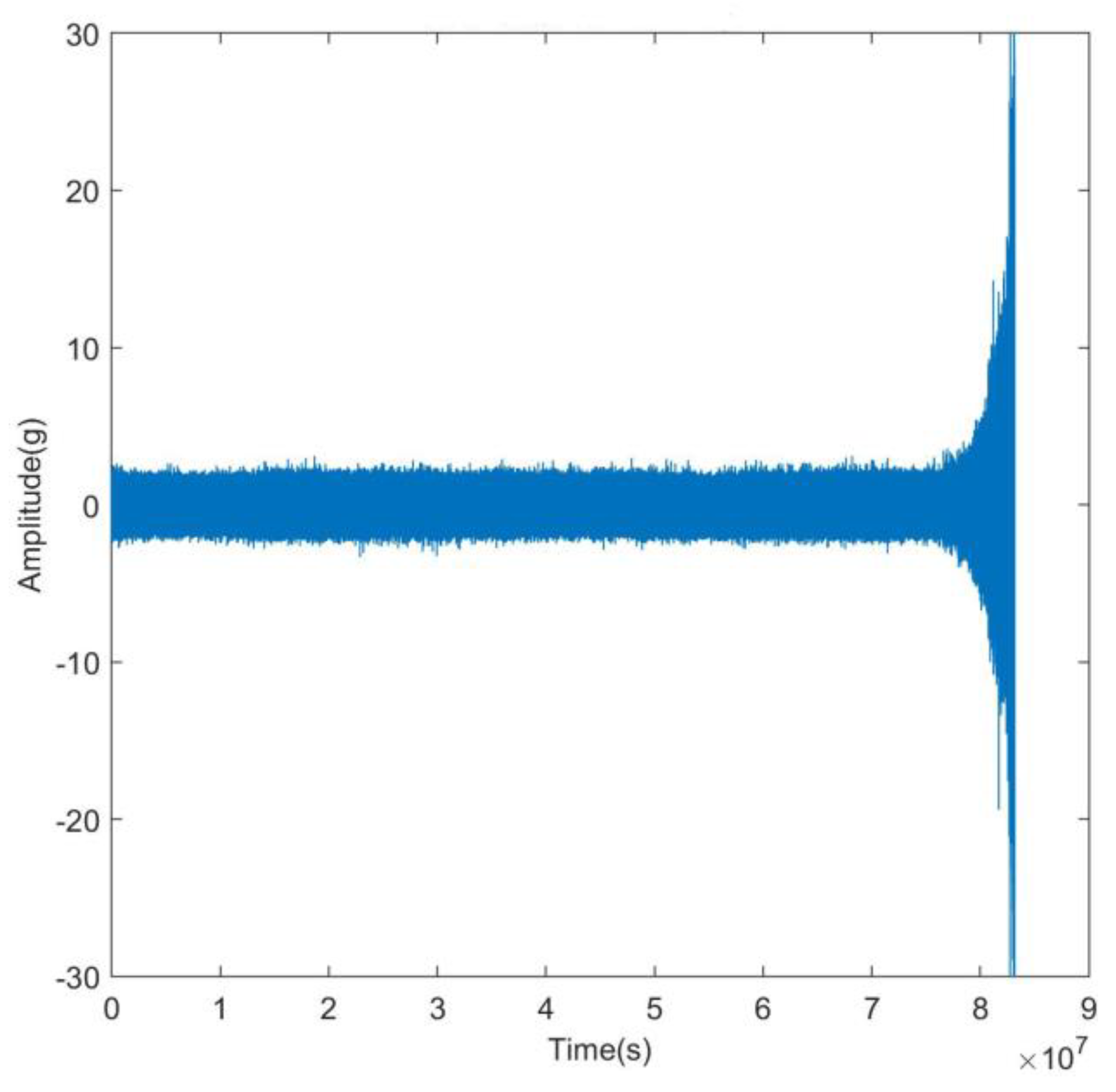
Figure 3 provides a visual depiction of the rolling bearings testbed, a sophisticated assembly comprising essential components such as an alternating current (AC) motor, motor speed controller, support shaft, heavy-duty rolling bearings serving as support bearings, and a hydraulic loading system, among others[22]. This experimental platform stands equipped to execute accelerated degradation tests on bearings across varied operational scenarios, simultaneously capturing comprehensive run-to-failure data. The parameters for data acquisition were configured with a sampling frequency of 25.6 kHz and a sampling interval of 1 minute, respectively. This arrangement culminated in a total of 32,768 individual samples being recorded. Subsequently, the analysis focused on the horizontal vibration signals originating from the dataset designated as “bearing 3_1.” The entire life cycle bearing vibration signal is shown in Figure 4.

3.2. Results and Discussion

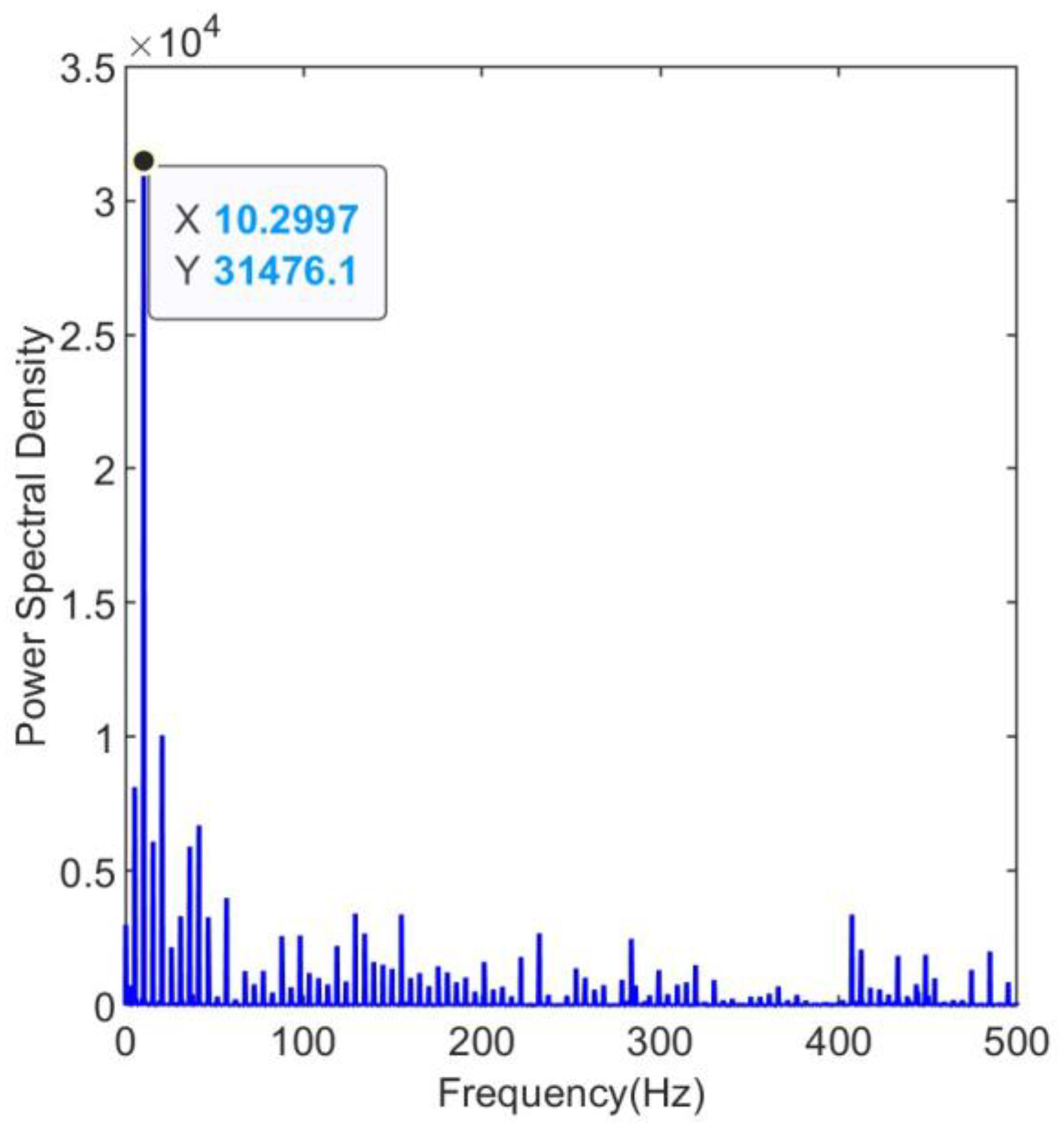
Due to the inevitable presence of noise in the collected raw vibration signals, the fault frequencies of the bearings are embedded within other spectral components.The envelope spectrum of the raw signal is shown in Figure 5. The envelope spectrum reaches its peak around 10Hz, which is not the characteristic fault frequency of a rolling bearing.
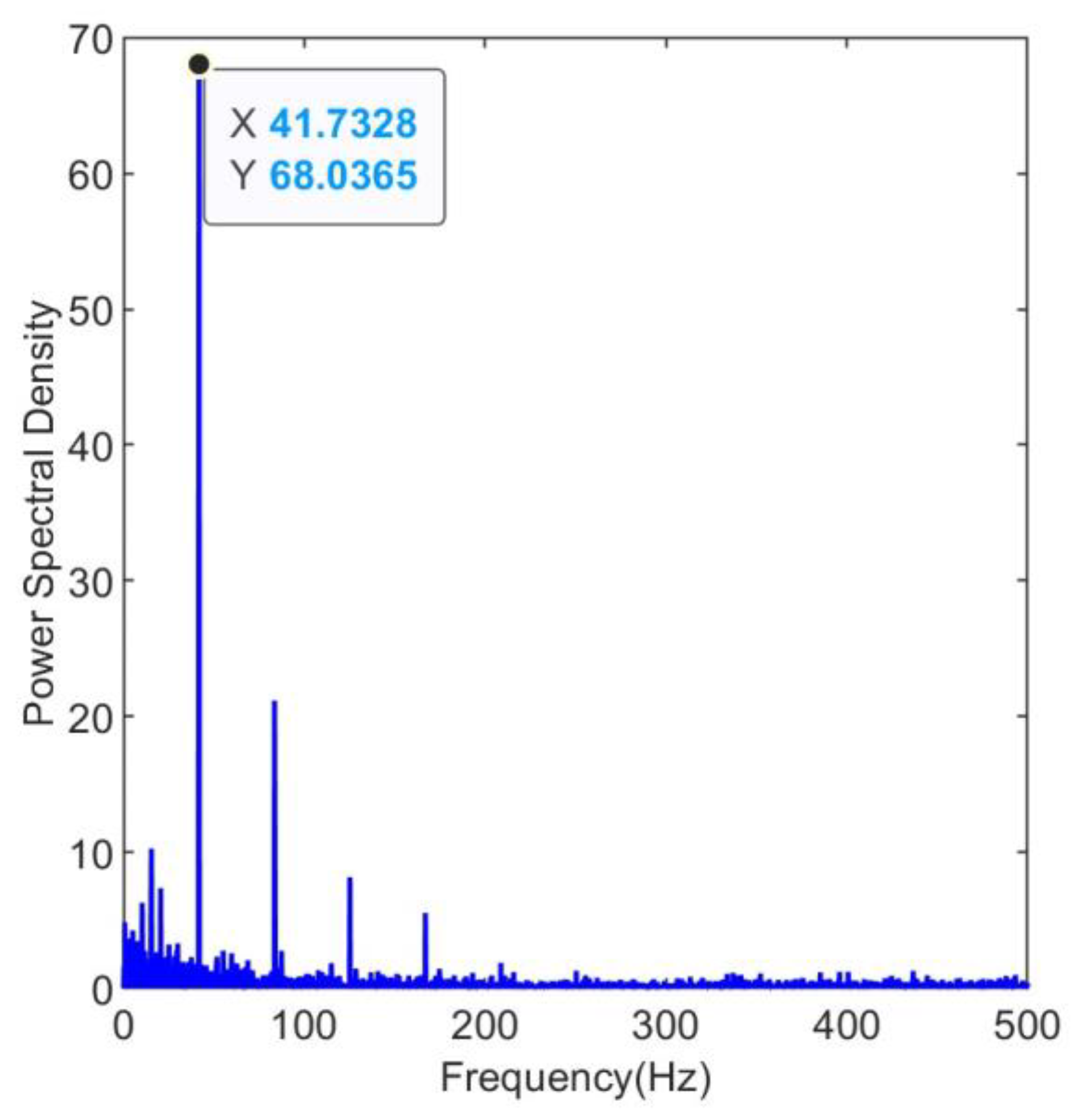
Perform maximum kurtosis deconvolution on the raw vibration signal. Set the filter length to 19. The maximum number of iterations is 30. The deconvolution period is set to 609, which is the ratio between the sampling frequency of 25.6kHz and the fault frequency of 42Hz. The shift number M is set to 3, indicating that three consecutive impacts are considered as a single valid impact.
The filtered envelope spectrum is shown in Figure 6. The envelope spectrum reaches its peak at 41.73Hz, which is very close to the fault frequency of 42Hz. The harmonics are still clearly visible, demonstrating the effectiveness of the maximum kurtosis deconvolution process.
After applying the maximum kurtosis deconvolution for data preprocessing, the multiscale permutation entropy is utilized for feature extraction. The purpose of this is to quantify the degradation information during the operational life of bearings.
Four parameters must be established before MPE can be used[23]: encapsulation dimension m, time series length N, scale factor s, and time delay τ . According to the reference literature, we set the encapsulation dimension m to 5. The time series length N is 3000, which can meet the criterion of N ≥ 5m!. The time delay τ = 1 here since the time delay τ has no significant impact on the outcome[24]. The scale factor s will influence the subsequent feature dimension. When the feature dimension is too small, it may not meet the requirements for RUL prediction. On the other hand, too many features can lead to the curse of dimensionality. Through multiple experiments, we have found that setting the scale factor s to 6 yields satisfactory results. Therefore, the scale factor s is set to 6 to obtain permutation entropy at each scales.
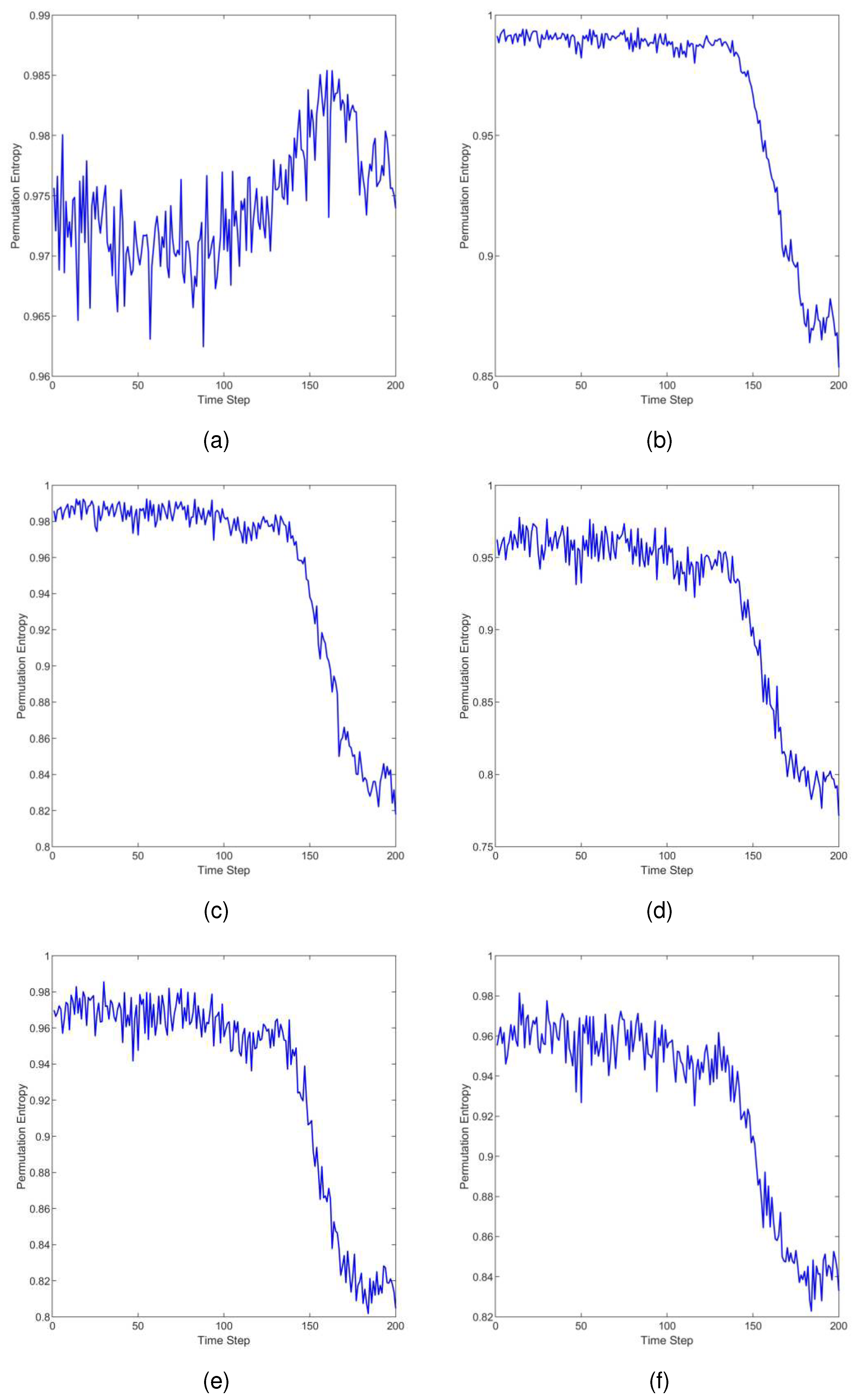
The time evolution curve of permutation entropy for six scales with bearing degradation is shown in Figure 7. It can be observed that, except for the scale factor s=1, the permutation entropy values of the other five scales remained relatively stable in the early stages, close to a value of 1. As the early stages of bearing faults emerge, the permutation entropy values gradually decrease. As the bearing faults become more severe, the permutation entropy values decrease to a new steady state.
The reason why the permutation entropy values decrease as the bearing degrades is that the magnitude of permutation entropy represents the level of disorder in the information. When the bearing is in a healthy state, the vibration signal tends to be more random. As the bearing gradually develops faults, periodic impacts occur due to cyclic collisions at the faulty region. These periodic impacts introduce a more regular pattern in the vibration signal compared to random vibrations. As a result, the permutation entropy values decrease with the bearing degrades.
Furthermore, the permutation entropy with a scale factor s=1 cannot effectively capture the degradation process of the bearing[25], while the permutation entropy with other scale factors can better accomplish this representation.This is because vibration signals can exhibit rapid variations within continuous time scales, while showing more stable trends over longer time scales. Single-scale permutation entropy might not capture these multi-scale characteristic changes, as it focuses solely on patterns within continuous time scales. Permutation entropy at other scales achieves a coarser representation of the signal across different time scales, mitigating the impact of short-term fluctuations in the signal. This aids in extracting the overall trends present in the signal, resulting in a more comprehensive and accurate feature extraction.
The other permutation entropy values apart from whose scale factor s=1 are used as feature vectors to input into the subsequent Long Short-Term Memory (LSTM) neural network model[26]. To make more efficient use of computational resources while improving the accuracy of the prediction model, we have truncated the samples to exclude the initial stable operating period. This allows the model to focus more on the later degradation phase, where the critical information for prediction lies.
To employ LSTM for remaining useful life prediction, several hyperparameters need to be set in advance, which include the number of neurons in the hidden layer, the maximum number of epochs, the initial learning rate[27]. Different parameter settings can indeed have a significant impact on the final results obtained. It’s crucial to carefully tune these parameters to ensure the best performance and meaningful predictions in specific use case. Experimenting with various parameter combinations and evaluating their effects on the model’s performance is an essential step in optimizing the prediction accuracy.
Applying the improved sparrow search algorithm mentioned in the reference literature[28] for parameter optimization is a valuable approach. This algorithm can assist in finding optimal or near-optimal parameter settings by simulating the search behavior of sparrows and their interactions within an optimization space. It’s essential to define the objective function and then use the algorithm to iteratively search for parameter combinations that yield the best results. Selecting the root mean square error (RMSE) as the objective function is a common and appropriate choice. RMSE is a widely used metric in machine learning and prediction tasks to quantify the difference between predicted and actual values, making it suitable for evaluating the performance of remaining useful life prediction model[29]. The goal of parameter optimization process would be to minimize the RMSE to achieve accurate and reliable predictions.
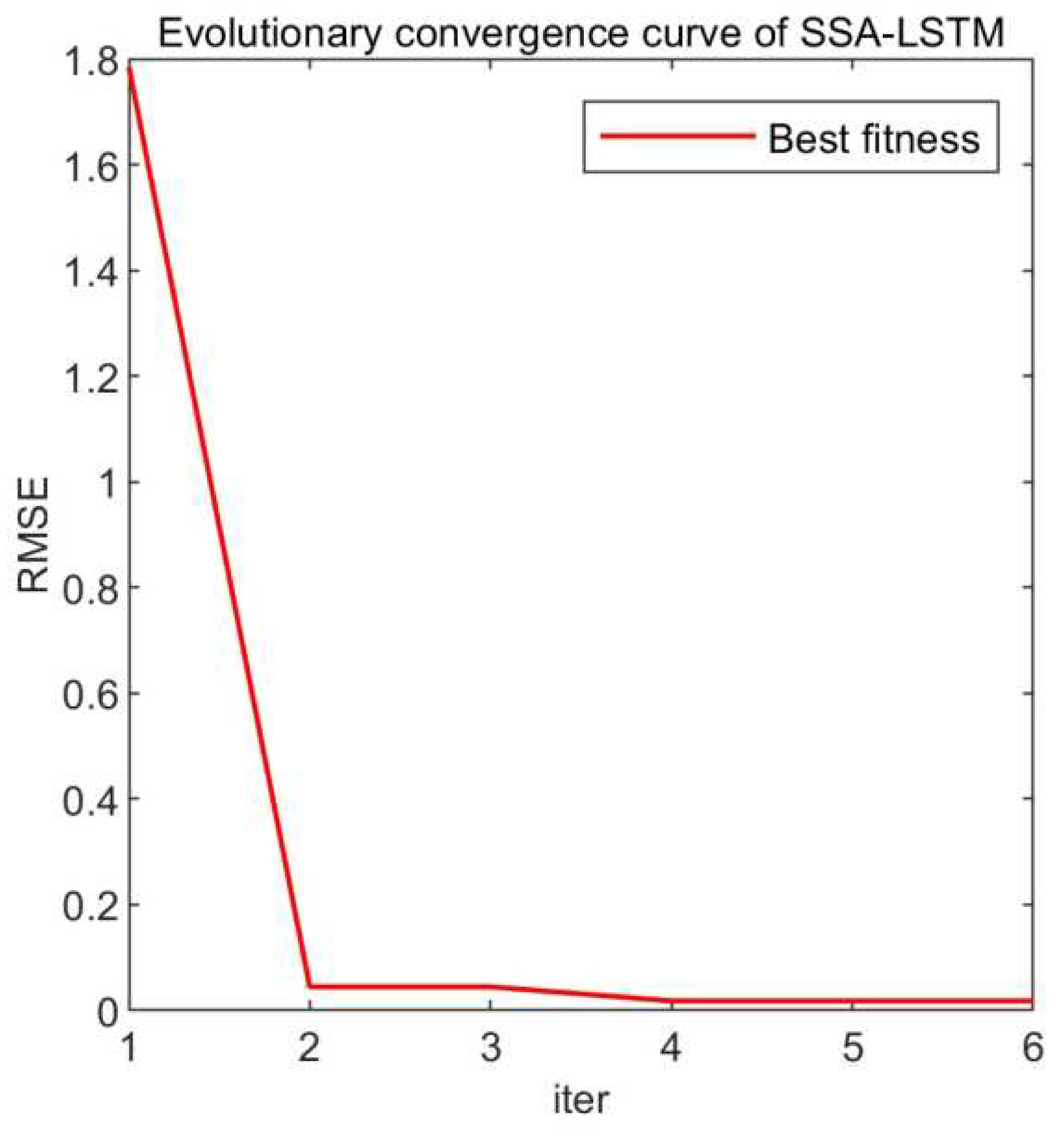
From Figure 8, it can be seen that the objective function value rapidly decreases during the first to the second iteration and converges by the fourth iteration.The parameter combination obtained through the Sparrow Search Optimization algorithm is as follows: 218, 203, 0.01, which correspond to the number of hidden units, maximum training epochs, and initial learning rate, respectively.
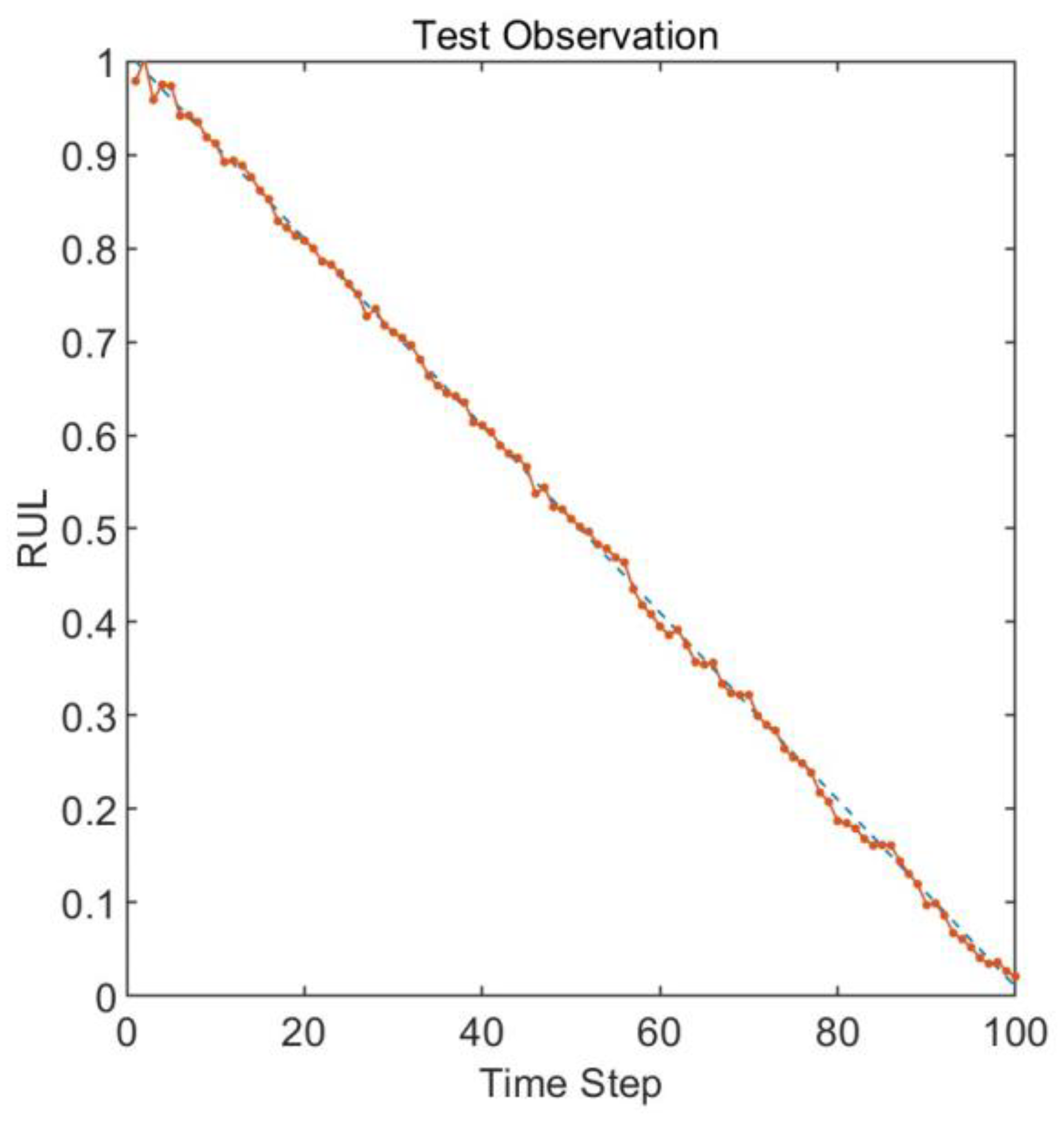
The remaining useful life prediction results obtained by inputting the feature matrix composed of multiscale permutation entropy into the Long Short-Term Memory neural network are shown in Figure 9. The root mean square error of the prediction results is 0.007. The results indicate that there is a slight drift between the predicted remaining useful life and the actual remaining useful life at the beginning and end, showing a minor endpoint effect. Around time steps 60 and 80, the predicted remaining useful life values are lower than the actual remaining useful life values. The rest of the prediction results are very close to the true values, which validates the effectiveness of the proposed model.
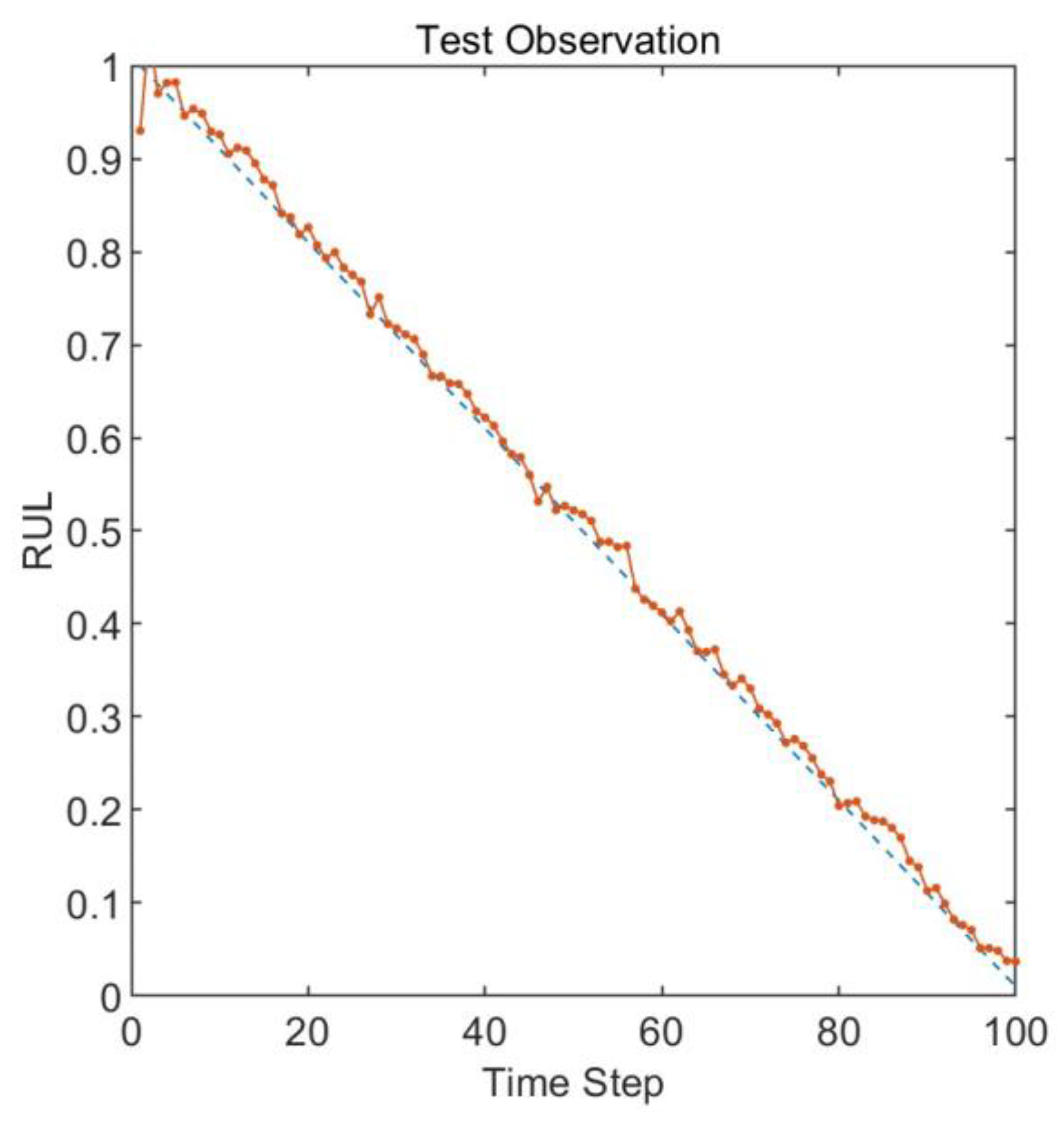
The prediction results obtained using the default initial values of 50, 50, and 0.1 for the Long Short-Term Memory neural network are shown in Figure 10. The root mean square error of the prediction results is 0.017. The root mean square error decreased by 58.8% after parameter optimization compared to the default settings. Compared to the optimized model, the results obtained with the default settings show a more pronounced endpoint effect, with a higher degree of deviation from the actual values at time steps 40, 60, and 80.

4. Conclusions

In this research, we explored the application of three different techniques for the prediction of remaining useful life of rolling bearings: Maximum Correlation Kurtosis Deconvolution (MCKD), Multi-Scale Permutation Entropy (MPE), and Long Short-Term Memory (LSTM) recurrent neural network. We presented a comprehensive review of each technique, including their underlying principles, methodologies, and applications. The main conclusions can be summarized as follows:
The MCKD technique utilizes kurtosis-based deconvolution to enhance fault signatures and improve fault detection and severity estimation. MPE quantifies the complexity and irregularity of vibration signals at multiple scales, providing valuable insights into fault conditions. LSTM networks excel at capturing long-term dependencies and modeling complex temporal dynamics in sequential data, making them suitable for RUL prediction. The integration of MCKD, MPE, and LSTM techniques offers a comprehensive approach to RUL prediction, harnessing the strengths of each technique to provide more accurate and reliable predictions.
The findings from this research pave the way for future advancements in rolling element maintenance and asset management. Further research can focus on exploring advanced fusion techniques, incorporating additional sensor modalities, and investigating novel feature selection methods. Additionally, the development of user-friendly software tools and frameworks can facilitate the practical implementation of these techniques in industrial settings.
In conclusion, the integration of MCKD, MPE, and LSTM techniques for rolling bearings’ RUL prediction holds great promise in improving maintenance practices and asset management strategies. The comprehensive analysis and accurate prediction of RUL enable timely maintenance interventions, optimizing the performance, reliability, and longevity of rolling bearings. By embracing these techniques, industries can achieve significant cost savings, minimize downtime, and enhance overall operational efficiency.

Author Contributions

X.Z. designed the main idea and revised the manuscript. H.W. designed the main methods and experiments, and wrote the paper. M.R., T.X., and C.L. participated in the design of the algorithm and carried out the relevant simulations. C.L. and Z.Z. participated in the data acquisition and field inspection. M.R. also helped to revise the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 52121003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

http://biaowang.tech/xjtu-sy-bearing-datasets, accessed on 6 September 2023.

Acknowledgments

The study was approved by the China University of Mining and Technology (Beijing). The authors would like to thank the editor and the anonymous reviewers for their constructive comments and suggestions. The authors also would like to thank Essentialslink (www.essentialslink.cn) for the help in academic language standardization.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shi, R.; Wang, B.; Wang, Z.; Liu, J.; Feng, X.; Dong, L. Research on Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition Improved by the Niche Genetic Algorithm. Entropy 2022, 24, 825. [Google Scholar] [CrossRef] [PubMed]
  2. Zhang, X.; Kang, J.; Hao, L.; Cai, L.; Zhao, J. Bearing fault diagnosis and degradation analysis based on improved empirical mode decomposition and maximum correlated kurtosis deconvolution. Journal of Vibroengineering 2015, 17, 243–260. [Google Scholar]
  3. Heng, W.; Guangxian, N.; Jinhai, C.; Jiangming, Q. Research on Rolling Bearing State Health Monitoring and Life Prediction Based on PCA and Internet of Things with Multi-sensor. Measurement 2020, 157, 107657. [Google Scholar]
  4. Kang, J.; Zhang, X.; Teng, H.; Zhao, J. Application of maximum correlated Kurtosis deconvolution on bearing fault detection and degradation analysis. 2014.
  5. Morabito; Carlo, F. ; Labate; Domenico; Foresta, L.; Fabio; Bramanti; Alessia; Morabito; Giuseppe. Entropy, Vol. 14, Pages 1186-1202: Multivariate Multi-Scale Permutation Entropy for Complexity Analysis of Alzheimer's Disease EEG. 2012, 7, 2418–2435.
  6. Akandeh, A.; Salem, F.M. Simplified Long Short-term Memory Recurrent Neural Networks: part III. 2017.
  7. Zhang, Y.; Lv, Y.; Ge, M. Time–frequency analysis via complementary ensemble adaptive local iterative filtering and enhanced maximum correlation kurtosis deconvolution for wind turbine fault diagnosis. Energy Reports 2021. [Google Scholar]
  8. Li, Z.; Bao-Wan, L.I. Roller Bearing Fault Diagnosis Method Based on Iterative Filtering and Maximum Correlation Kurtosis Deconvolution. Modular Machine Tool & Automatic Manufacturing Technique 2019. [Google Scholar]
  9. Sun, W. , YuqingCao, XinchengChen, BinqiangFeng, WeiChen, Leiqing. A two-stage method for bearing fault detection using graph similarity evaluation. Measurement 2020, 165. [Google Scholar]
  10. A, C.H.; B, T.W.; C, R.G.; B, Z.J.; B, R.M.; D, H.Q. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm – Extreme learning machine - ScienceDirect. Measurement 2020. [Google Scholar]
  11. Tang, G.; Wang, X.; He, Y. A Novel Method of Fault Diagnosis for Rolling Bearing Based on Dual Tree Complex Wavelet Packet Transform and Improved Multiscale Permutation Entropy. Mathematical Problems in Engineering,2016,(2016-5-9) 2016, 2016, 1–13. [Google Scholar] [CrossRef]
  12. Zheng, J.; Cheng, J.; Yang, Y. Multiscale Permutation Entropy Based Rolling Bearing Fault Diagnosis. Shock and Vibration,2014,(2014-3-2) 2014, 2014, 154291. [Google Scholar]
  13. Shenghan, Z.; Silin, Q.; Wenbing, C.; Yiyong, X.; Yang, C. A Novel Bearing Multi-Fault Diagnosis Approach Based on Weighted Permutation Entropy and an Improved SVM Ensemble Classifier. Sensors 2018, 18, 1934. [Google Scholar]
  14. Zaytar, M.A.; Amrani, C.E. Sequence to Sequence Weather Forecasting with Long Short-Term Memory Recurrent Neural Networks. International Journal of Computer Applications 2016, 143, 7–11. [Google Scholar]
  15. Zhou, X.G., Jing. Tool remaining useful life prediction method based on LSTM under variable working conditions. The International Journal of Advanced Manufacturing Technology 2019, 104. [Google Scholar]
  16. Song, T.; Liu, C.; Wu, R.; Jin, Y.; Jiang, D. A hierarchical scheme for remaining useful life prediction with long short-term memory networks. Neurocomputing 2022, 487, 22–33. [Google Scholar]
  17. Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Advances in Mechanical Engineering 2018, 10. [Google Scholar]
  18. Elsheikh, A.; Yacout, S.; Ouali, M.S. Bidirectional handshaking LSTM for remaining useful life prediction. Neurocomputing 2019, 323, 148–156. [Google Scholar]
  19. Chen, C.; Shi, J.; Lu, N.; Zhu, Z.H.; Jiang, B. Data-driven predictive maintenance strategy considering the uncertainty in remaining useful life prediction. Neurocomputing 2022, 494, 79–88. [Google Scholar]
  20. Xu, T.; Wei-Xiao, X.U.; Ji-Wen, T.; Yan-Song, W. Prediction for remaining useful life of rolling bearings based on Long Short-Term Memory. Journal of Machine Design 2019. [Google Scholar]
  21. Morgenroth, J.; Kalenchuk, K.; Moreau-Verlaan, L.; Perras, M.A.; Khan, U.T. A novel long-short term memory network approach for stress model updating for excavations in high stress environments Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards. 2023, 17, 196–216. [Google Scholar]
  22. Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mechanical Systems and Signal Processing 2019, 134, 106330. [Google Scholar] [CrossRef]
  23. Wu; ShuenDe; Wu; PoHung; Wu; ChiuWen; Ding; JianJiun; Wang; ChunChieh. Entropy, Vol. 14, Pages 1343-1356: Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. 2012.
  24. Zhang, Y.; Lv, Y.; Ge, M. A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy (Basel, Switzerland) 2021, 23, 191. [Google Scholar] [CrossRef] [PubMed]
  25. Zhang, W.; Zhou, J. Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef] [PubMed]
  26. Zhu, P.X., Min. A Joint Long Short-Term Memory and AdaBoost regression approach with application to remaining useful life estimation. Measurement 2021, 170. [Google Scholar] [CrossRef]
  27. Xiang, S.; Qin, Y.; Zhu, C.; Wang, Y.; Chen, H. Long short-term memory neural network with weight amplification and its application into gear remaining useful life prediction. Engineering Applications of Artificial Intelligence 2020, 91, 103587. [Google Scholar] [CrossRef]
  28. Zhang, X.; Wang, H.; Li, X.; Gao, S.; Guo, K.; Wei, Y. Fault Diagnosis of Mine Ventilator Bearing Based on Improved Variational Mode Decomposition and Density Peak Clustering. Machines 2022, 11, 27. [Google Scholar] [CrossRef]
  29. Abdelli, K.; Griesser, H.; Pachnicke, S. A Hybrid CNN-LSTM Approach for Laser Remaining Useful Life Prediction. 2022.
Preprints 84618 g001
Figure 1. The structure of LSTM.
Figure 1. The structure of LSTM.
Preprints 84618 g001
Preprints 84618 g002
Figure 2. Flowchart of the prediction process.
Figure 2. Flowchart of the prediction process.
Preprints 84618 g002
Preprints 84618 g003
Figure 3. Bearing accelerated life test bed.
Figure 3. Bearing accelerated life test bed.
Preprints 84618 g003
Preprints 84618 g004
Figure 4. Horizonal vibration signal.
Figure 4. Horizonal vibration signal.
Preprints 84618 g004
Preprints 84618 g005
Figure 5. Envelope spectrum of the raw signal.
Figure 5. Envelope spectrum of the raw signal.
Preprints 84618 g005
Preprints 84618 g006
Figure 6. Envelope spectrum of the filtered signal.
Figure 6. Envelope spectrum of the filtered signal.
Preprints 84618 g006
Preprints 84618 g007
Figure 7. Time evolution curve of permutation entropy. (a) s=1 (b) s=2 (c) s=3 (d) s=4 (e) s=5 (f) s=6.
Figure 7. Time evolution curve of permutation entropy. (a) s=1 (b) s=2 (c) s=3 (d) s=4 (e) s=5 (f) s=6.
Preprints 84618 g007
Preprints 84618 g008
Figure 8. Evolutionary convergence curve of SSA-LSTM.
Figure 8. Evolutionary convergence curve of SSA-LSTM.
Preprints 84618 g008
Preprints 84618 g009
Figure 9. RUL prediction results with optimized parameters.
Figure 9. RUL prediction results with optimized parameters.
Preprints 84618 g009
Preprints 84618 g010
Figure 10. RUL prediction results with default parameters.
Figure 10. RUL prediction results with default parameters.
Preprints 84618 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated