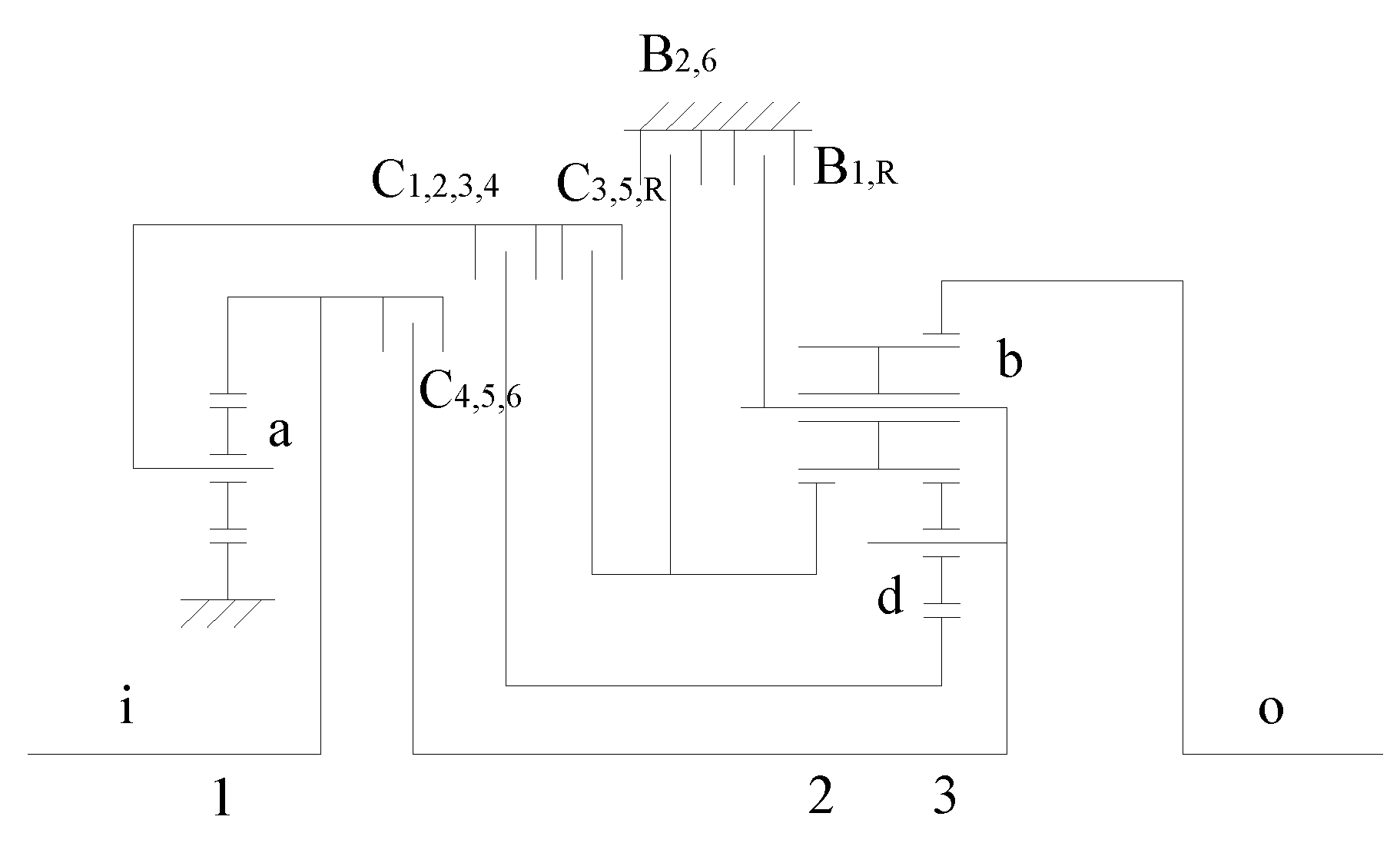Motion, Static Force and Efficiency Analysis of Planetary Gear Transmission Based on Graph Theory

Preprint

Article

Motion, Static Force and Efficiency Analysis of Planetary Gear Transmission Based on Graph Theory

Altmetrics

Downloads

100

Views

Comments

A peer-reviewed article of this preprint also exists.

Huiling Xue^*,

Lijian Li

Huiling Xue^*,

Lijian Li

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

Using graph theory, computer aided motion, static force and power flow analysis of planetary gear mechanism is realized. The motion, static force and efficiency calculations of 6HP26 automatic transmission are carried out. Based on kinematic and static force analysis model, related matrices are acquired. Hence, kinematic and static force analysis of planetary gear mechanism is achieved. The link power can be determined by the link speed and torque. Power flow diagrams of each gear are acquired. The efficiency is calculated by transmission ratio method.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Automatic transmissions (ATs) with planetary gear trains (PGTs) have long been applied in the automotive industry. The literature on the design of planetary gear trains includes conceptual designs, kinematic analysis, power flow and efficiency analysis, and configuration designs. With an increasing demand for fuel economy and dynamic performance, many companies, such as ZF and Aisin, are developing the planetary gear trains (PGTs) with more gears for vehicles. This is because it allows the engine to work in a high-efficient area to reduce fuel consumption, and the use of suitable transmission ratios can also guarantee abundant torque capacity for strong dynamic performance, thereby, helping to obtain a balance of dynamic and economic performance [1,2,3,4,5].

Knowledge of the different types of PGT is of interest both scientifically and technologically. In particular, it could lead to the design and construction of more efficient implementations of such trains. In this regard, PGT efficiency must be understood as a generic and global concept. This is because, given a certain transmission ratio, the designer would like to be able to select from all matching PGTs those that have the right combination of efficiency and simplicity of construction.

One important question is to find an efficient way to select planetary gear trains that allow a high transmission ratio without excessively sacrificing efficiency and without having recourse to great structural complexity. Some study presents a procedure to assess the sensitivity of certain characteristics of a planetary gear train – the efficiency and the transmission ratio – with respect to small variations in the design parameters. The method is only applied to a particular train by way of example rather than by performing an exhaustive analysis of numerous gear trains [6,7,8,9,10].

One key point that needs to be taken into account in analyzing and estimating the efficiency of a PGT is its structure. This is determined by the number and type of links, and by the kinematic pairs between them. In particular, the links of PGTs are of three types which in the present work we shall call suns, arms, and planets. The planets are links that undergo a planetary motion. Each planet is linked to its respective arm by a turning pair and to other members by gear pairs. The arms have a rotational movement around the PGT's principal axis, and are characterized by having at least one turning pair with a planet; they may also have gear pairs with other members. Finally, the suns are links that only have gear pairs with other links and also have a rotational movement around the PGT's principal axis. Suns and arms are central links since they rotate around the central axis of the PGT, whereas the planets are non-central links since they have a planetary motion [11,12,13,14,15].

For parallel-connected PGTs, Ross and Route introduced an AT design tool based on a lever analogy, which included the calculation of gear ratios, gear trains selection, and the construction of clutch layouts. Nadel et al. formulated the design of ATs as a constraint satisfaction problem which included kinematic, topological, stick diagram, and geometric levels. This methodology was suitable for PGTs in which two simple PGTs were combined. Dong et al. analyzed the relationship between the stationary gear ratios and transmission ratios, and achieved 9, 11 and 13 gears through the same configuration by just changing the stationary gear ratios. Jiang et al. combined different matrices representing different sub-configurations and used kinematic equations to calculate the shaft speeds. Yang et al. proposed a judgement method based on the ranks of structure matrices for three-node compound lever models [16,17,18,19,20].

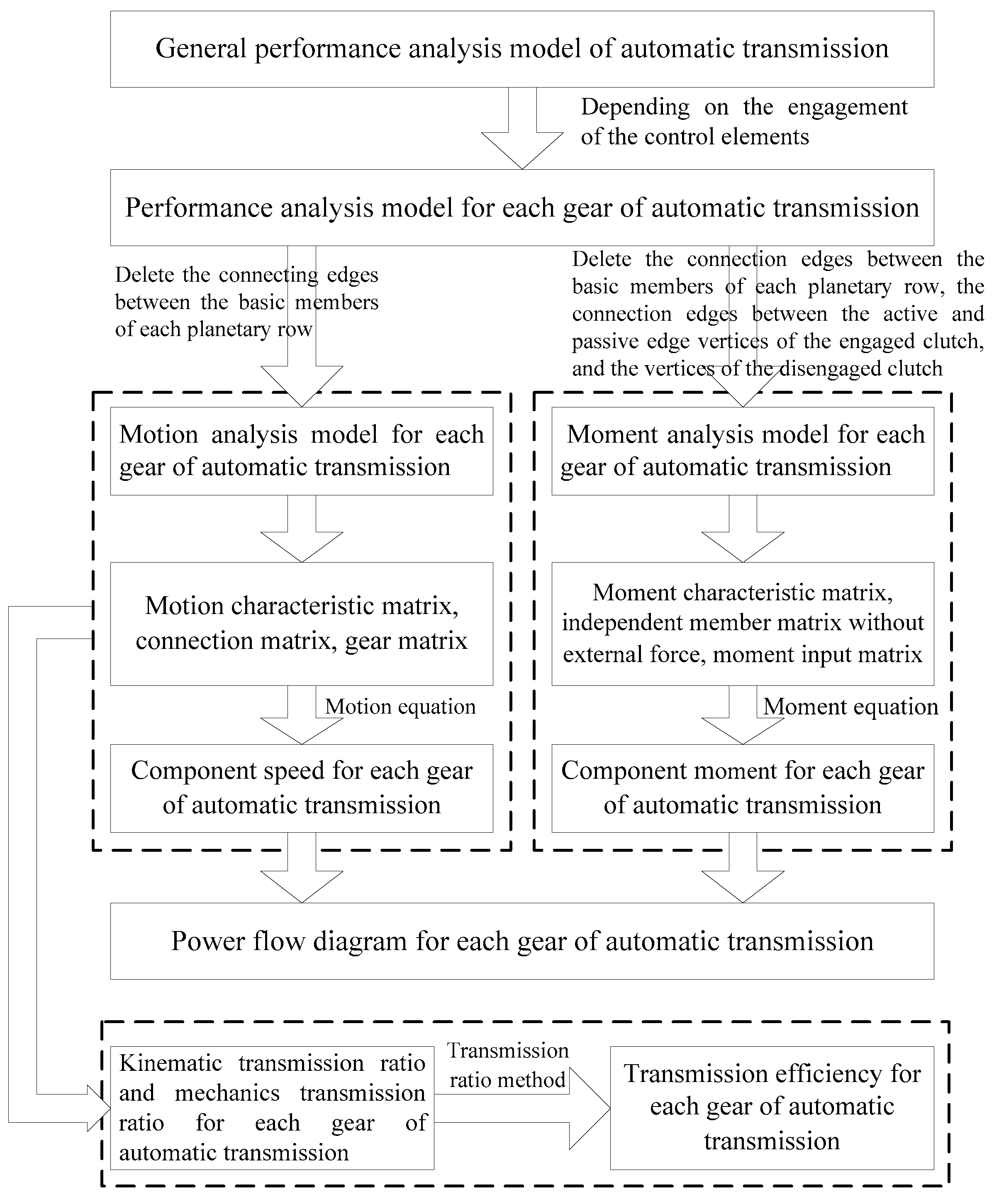
Graph theory provides a new way of thinking for the analysis of systems containing binary relations. Based on the idea of graph theory, the analysis model of planetary gear transmission is established, which provides the possibility of automatic analysis of its transmission performance. This paper will use graph theory to analyze the motion, moment, power flow and efficiency of planetary gear mechanism for automatic transmission, and it is convenient for computer programming. The flow chart of performance analysis for automatic transmission is shown in Figure 1.

2. Performance Analysis Model of Automatic Transmission

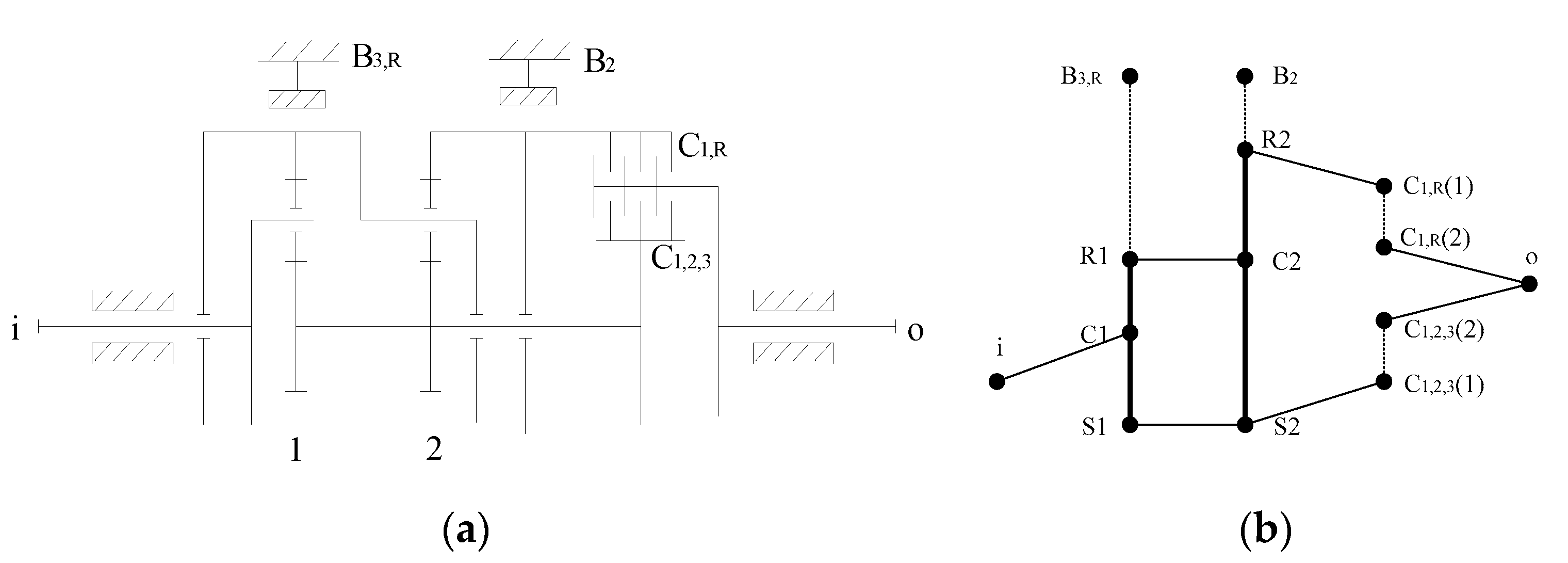
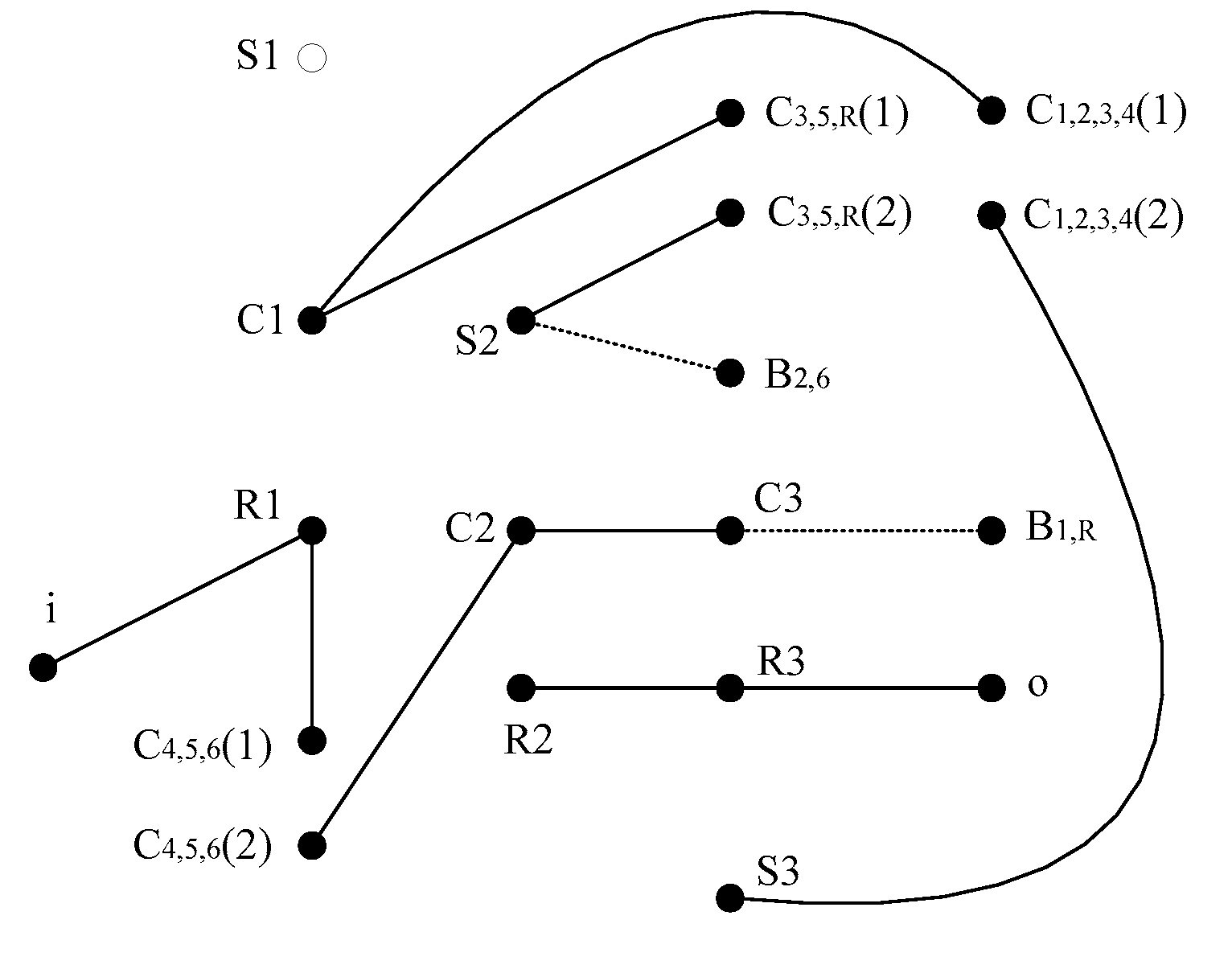
Based on graph theory, dots are used to represent various components of the planetary gear mechanism (including control elements), and lines are used to represent connection relationship between the components [21,22,23,24,25,26,27,28,29,30]. Figure 2(a) is a three-speed planetary gear transmission, and the overall performance analysis model is shown in Figure 2(b). The dotted edge in Figure 2(b) indicates that the connection relationship between components is manipulated by control elements.

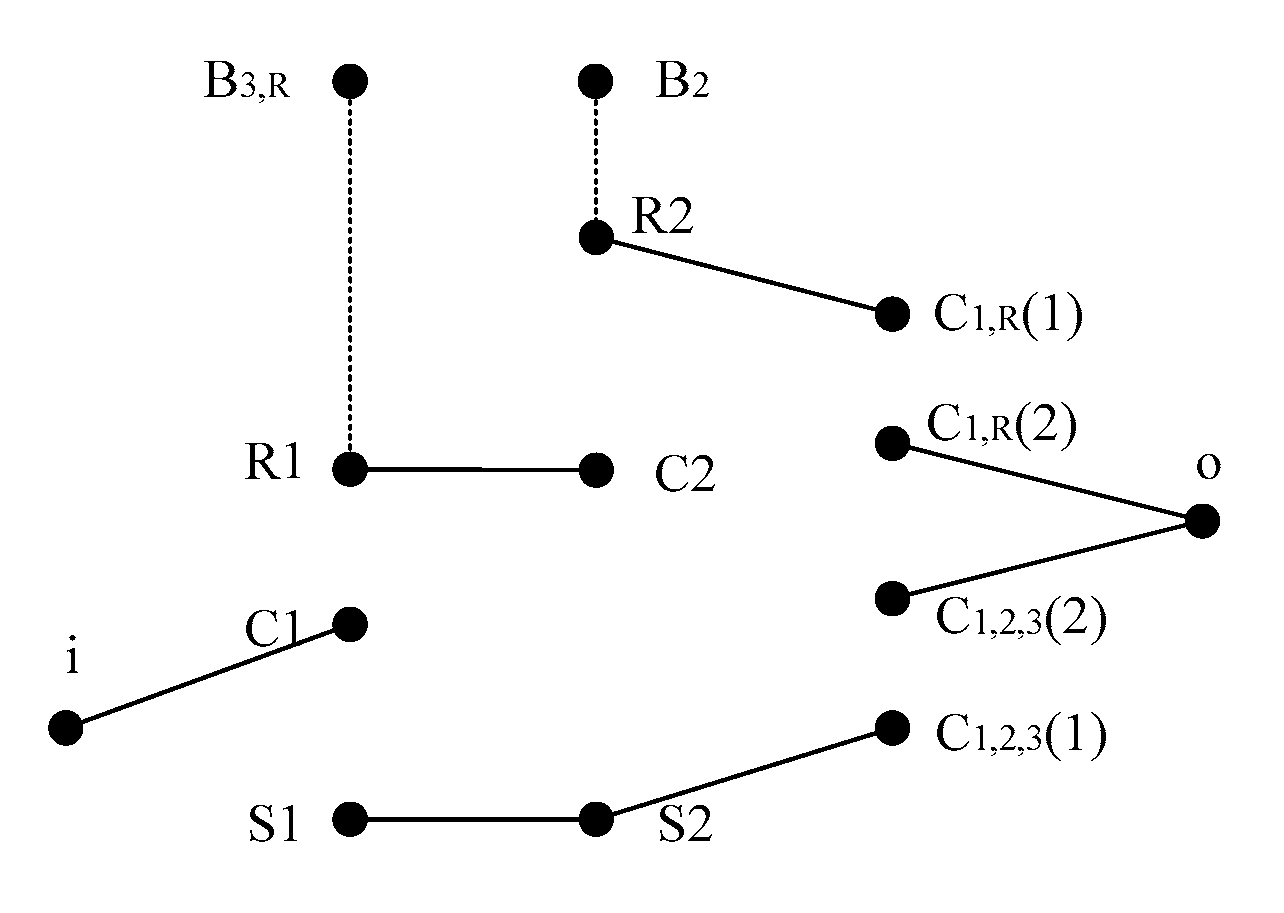
In the overall performance analysis model of planetary gear mechanism, Q connected branches can be obtained by deleting the connecting edges between basic components of each planetary row and the connecting edges between vertices of the active and passive edges of the clutch. The degree of freedom of planetary gear mechanism W=Q-k, where k is the number of planetary rows. From Figure 2(b), five connected branches can be obtained, as shown in Figure 3. Therefore, in Figure 2(a), the degree of freedom of planetary gear transmission W=5-2=3.

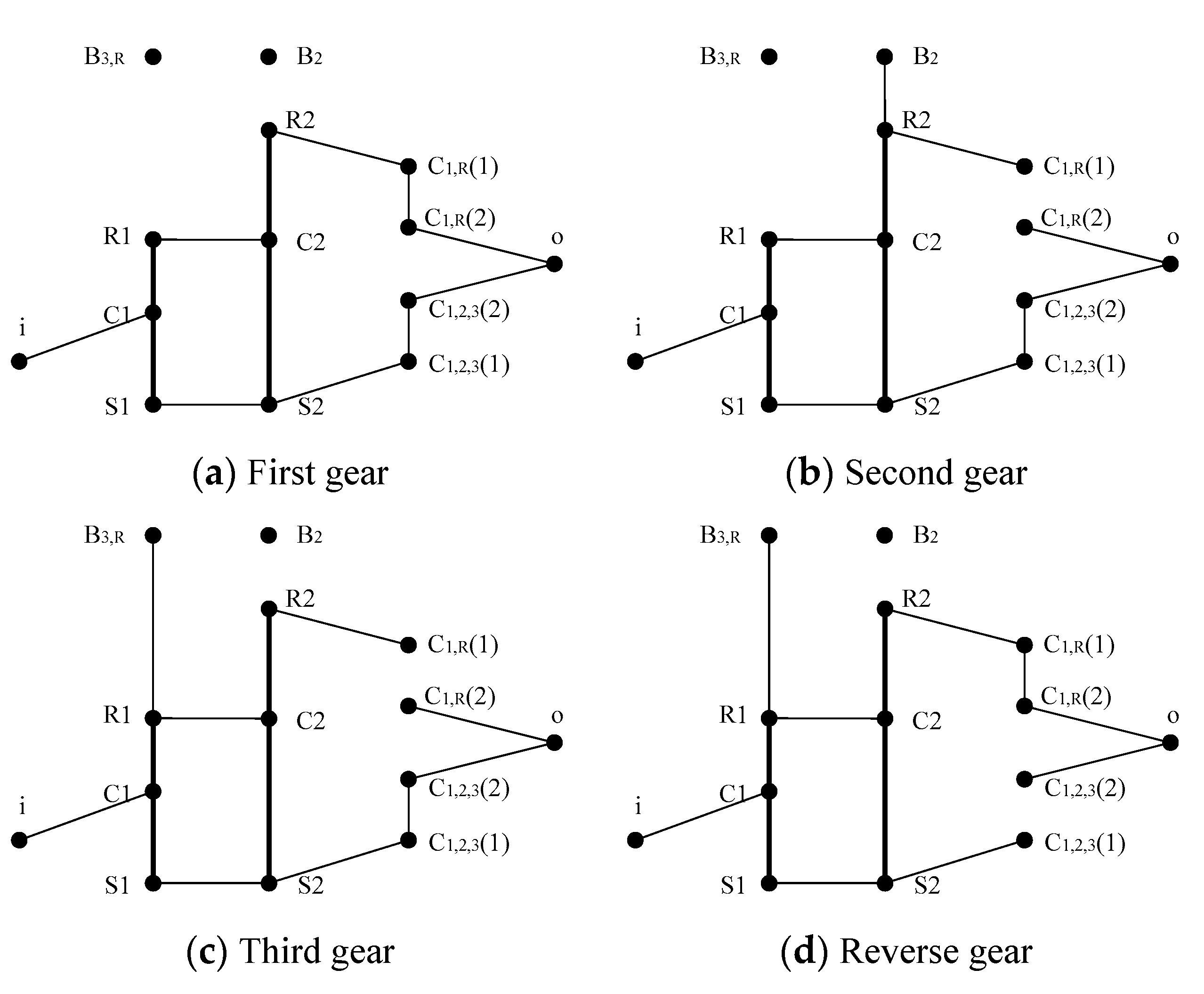
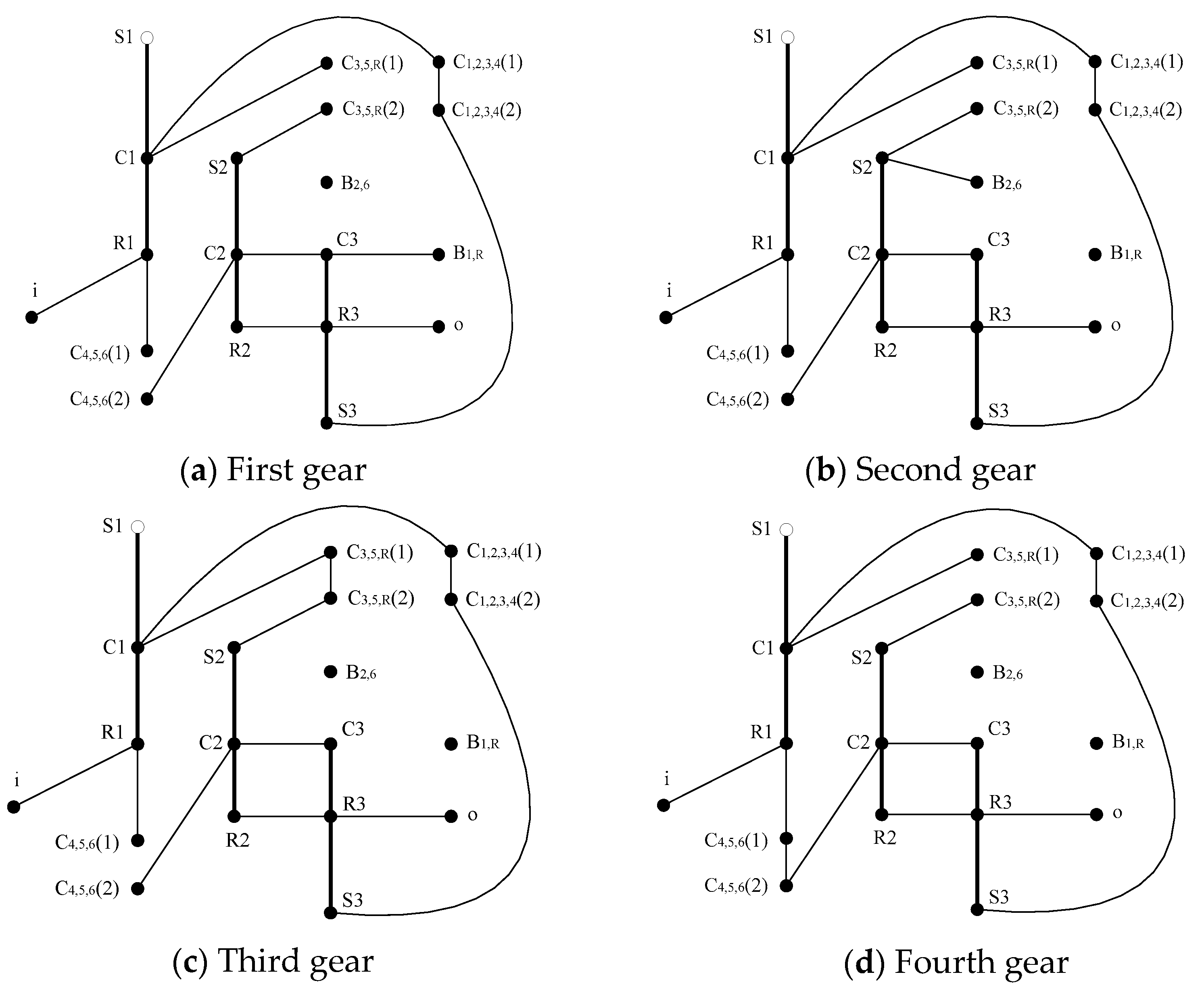
According to the engagement of control elements, on the basis of overall performance analysis model, the analysis model of each gear can be obtained. The state table of control elements for the planetary gear transmission in Figure 2(a) is shown in Table 1, and the analysis model of each gear is shown in Figure 4.

2.1. Motion Analysis of Automatic Transmission

The motion analysis model of each gear of automatic transmission can be obtained by deleting the connection edges between basic components of each planetary row in Figure 4.

(1) Motion characteristic matrix

The motion characteristic matrix

A_{1}

describes the component motion relationship of each planetary row. The single-star planetary row satisfies motion relationship:

n_{s} + α n_{r} - (1 + α) n_{c} = 0

(1)

The double-star planetary row satisfies motion relationship:

n_{s} - α n_{r} - (1 - α) n_{c} = 0

(2)

For a transmission consisting of k single-star planetary rows, its motion characteristic matrix

\begin{array}{l} \begin{matrix} S 1 & R 1 & C 1 & S 2 & R 2 & C 2 & \dots & S k & R k & C k \end{matrix} \\ A_{1} = [\begin{matrix} 1 & α_{1} & - (1 + α_{1}) & 0 & 0 & 0 & \dots & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & α_{2} & - (1 + α_{2}) & \dots & 0 & 0 & 0 \\ ⋮ \\ 0 & 0 & 0 & 0 & 0 & 0 & \dots & 1 & α_{k} & - (1 + α_{k}) \end{matrix}] \begin{matrix} 1 \\ 2 \\ ⋮ \\ k \end{matrix} \end{array}

(3)

In the formula,

α_{1}

α_{2}

,...,

α_{k}

are the characteristic parameters of each planetary row, respectively.

(2) Connection matrix

Connection matrix

A_{2}

is the matrix describing component connection relationship of each planetary row. If one of the two connected components is marked as 1, the other is marked as -1, and other components are marked as 0, then each two connected components will form a row vector containing only 1, -1, and 0, and the resulting matrix is called connection matrix.

(3) Gear matrix

Gear matrix

C_{i}

(i=1,2,3,…) is a matrix representing the brake and clutch engagement state of automatic transmission in each gear. When the brake is engaged, the brake component is marked as 1; when the clutch is engaged, one of the two constant velocity components is marked as 1, the other is marked as -1, and other components are marked as 0. The last line of gear matrix is input vector, and the input component is marked as 1, the others are 0.

For the transmission composed of k planetary rows, it satisfies the following motion equation:

[\begin{matrix} A_{1} \\ A_{2} \\ C_{i} \end{matrix}] [\begin{matrix} n_{s 1} \\ n_{r 1} \\ ⋮ \\ n_{c k} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix}] (i = 1, 2, 3, \dots)

(4)

The speed of each component of automatic transmission and the transmission ratio of each gear can be obtained by solving equation (4).

2.2. Moment Analysis of Automatic Transmission

In Figure 4, delete the connection edges between basic components of each planetary row，the connection edges between vertices of active and passive edges of the engaged clutches, and the vertices of disengaged clutches, the moment analysis model of each gear of automatic transmission can be obtained.

(1) Moment characteristic matrix

The moment characteristic matrix

U

describes the component moment relationship of each planetary row. The single-star planetary row satisfies moment relationship:

\frac{T_{s}}{1} = \frac{T_{r}}{α} = \frac{T_{c}}{- (1 + α)}

(5)

The double-star planetary row satisfies moment relationship:

\frac{T_{s}}{1} = \frac{T_{r}}{- α} = \frac{T_{c}}{α - 1}

(6)

For a transmission consisting of k single-star planetary rows, its moment characteristic matrix

\begin{array}{l} \begin{matrix} S 1 & R 1 & C 1 & S 2 & R 2 & C 2 & \dots & S k & R k & C k \end{matrix} \\ U = [\begin{matrix} 1 & 0 & 1 / (1 + α_{1}) & 0 & 0 & 0 & \dots & 0 & 0 & 0 \\ 0 & 1 & α_{1} / (1 + α_{1}) & 0 & 0 & 0 & \dots & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 / (1 + α_{2}) & \dots & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & α_{2} / (1 + α_{2}) & \dots & 0 & 0 & 0 \\ ⋮ \\ 0 & 0 & 0 & 0 & 0 & 0 & \dots & 1 & 0 & 1 / (1 + α_{k}) \\ 0 & 0 & 0 & 0 & 0 & 0 & \dots & 0 & 1 & α_{k} / (1 + α_{k}) \end{matrix}] \begin{matrix} 1 \\ 2 \\ 3 \\ 4 \\ ⋮ \\ 2 k - 1 \\ 2 k \end{matrix} \end{array}

(7)

In the formula,

α_{1}

α_{2}

,...,

α_{k}

are the characteristic parameters of each planetary row, respectively.

(2) Independent member matrix without external force

The independent member matrix without external force

D_{i}

(i=1,2,3,…) is a matrix representing the stress state of each independent member without external force. The independent member without external force is not an input and output member, and it is not a braking member. The independent member without external force is recorded as 1, the others are recorded as 0, and the final matrix is called the independent member matrix without external force.

(3) Moment input matrix

Record all input members as 1, and others as 0 to obtain the moment input matrix

I_{i}

(i=1,2,3,…).

For a transmission composed of k planetary rows, it satisfies the following torque equation:

[\begin{matrix} U \\ D_{i} \\ I_{i} \end{matrix}] [\begin{matrix} T_{s 1} \\ T_{r 1} \\ ⋮ \\ T_{c k} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix}] (i = 1, 2, 3, \dots)

(8)

Solving formula (8) can get the component moment of automatic transmission under each gear.

2.3. Power Flow and Efficiency Analysis of Automatic Transmission

(1) Power flow analysis

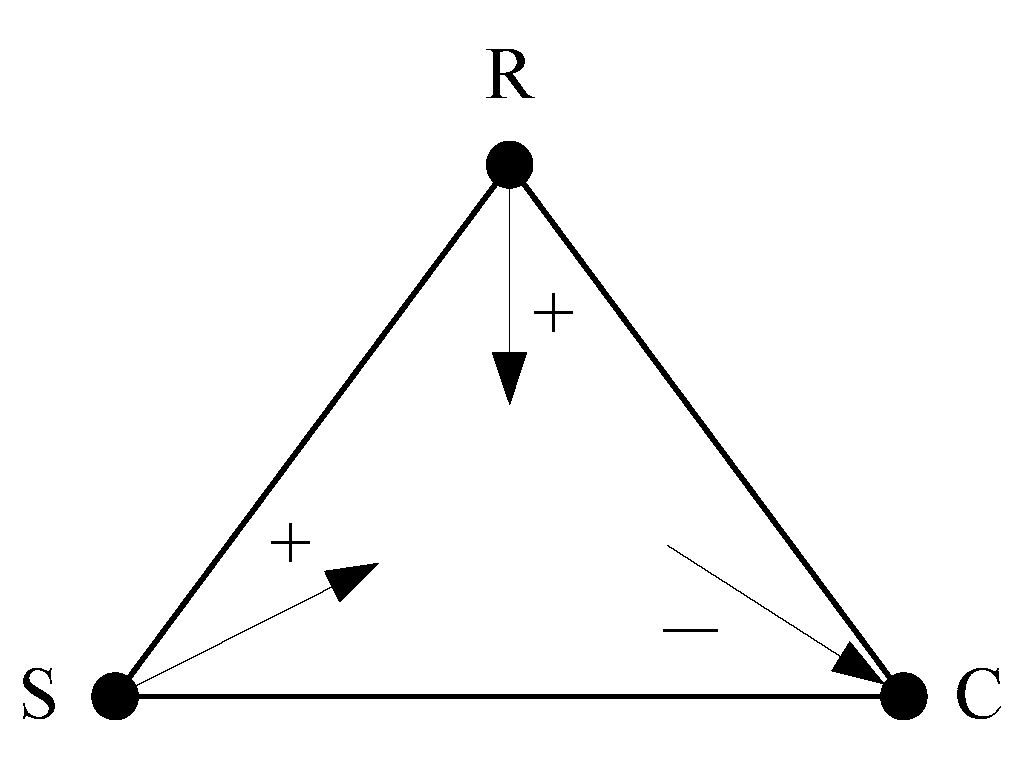
From the motion and moment analysis of automatic transmission, the rotational speed and torque of each component can be obtained respectively, thus the power flow of automatic transmission can be determined. If the component power is positive, it is input power; if the component power is negative, it is output power. The power flow diagram of a planetary row is shown in Figure 5. The arrow inward represents the input power and the arrow outward represents the output power.

(2) Efficiency analysis

At present, there are many methods to determine planetary gear transmission efficiency. In this paper, the transmission ratio method is used to calculate transmission efficiency.

For a transmission composed of k planetary rows, the efficiency of each gear

η = \frac{{\tilde{i}}_{α}}{i_{α}}

(9)

In formula (9),

i_{α} = f (α_{1}, α_{2}, \dots, α_{k})

(10)

{\tilde{i}}_{α} = f [α_{1} {(η_{d})}^{y_{1}}, α_{2} {(η_{d})}^{y_{2}}, \dots, α_{k} {(η_{d})}^{y_{k}}]

(11)

In formula (11),

η_{d}

is the transmission efficiency of a planetary row. Denote the transmission efficiency of an external meshing gear pair as

η_{w}

and the transmission efficiency of an internal meshing gear pair as

η_{n}

, then, for a single-star planetary row

η_{d} = η_{w} η_{n}

, for a double-star planetary row

η_{d} = η_{w}^{2} η_{n}

. Usually,

η_{w} = 0.97

η_{n} = 0.99

In addition, in formula (11),

y_{j} = sgn (\frac{α_{j}}{i_{α}} \times \frac{\partial i_{α}}{\partial α_{j}}) (j = 1, 2, \dots, k)

(12)

3. Performance Analysis Example of Automatic Transmission

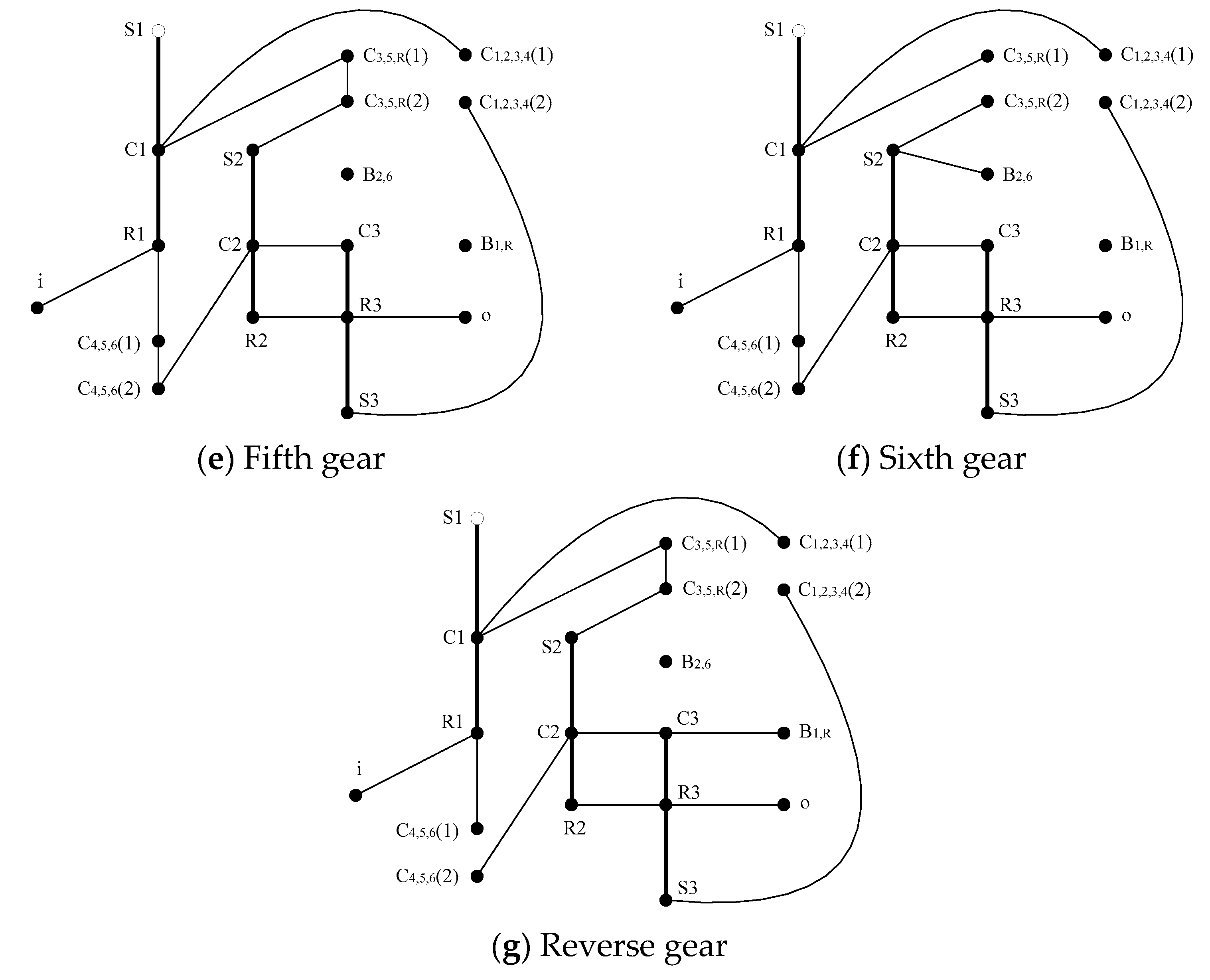
Figure 6 is a schematic diagram of 6HP26 automatic transmission developed by German ZF company. Planetary wheel of the first planetary row is represented by a. Long planetary wheel and short planetary wheel of the third planetary row are represented by b and d, respectively. 6HP26 automatic transmission will be taken as an example to analyze its motion, moment, power flow and efficiency.

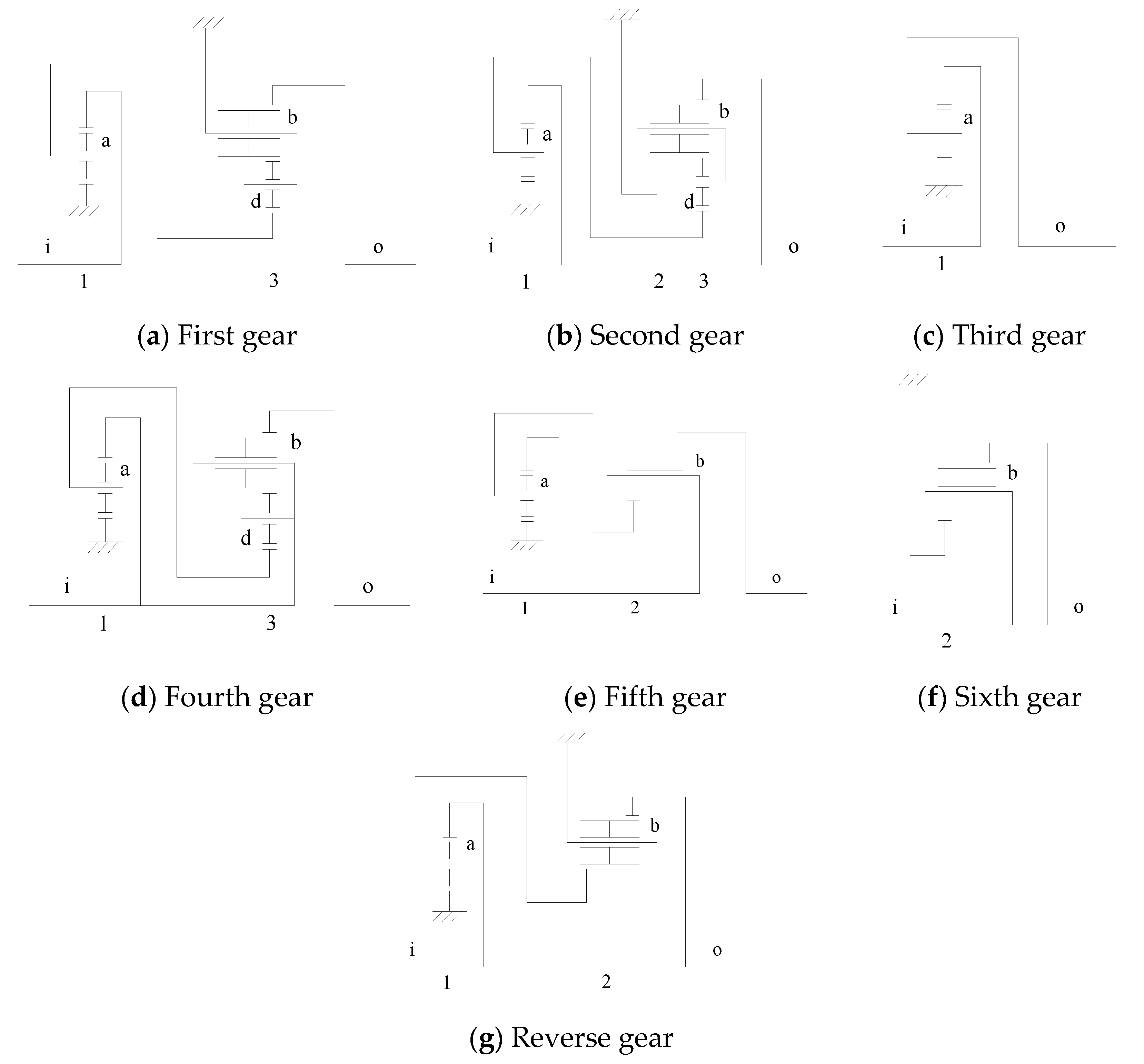
6HP26 automatic transmission can realize four reduction gears, two overdrive gears and one reverse gear. The status table of control elements is shown in Table 2. The transmission diagram of 6HP26 automatic transmission in each gear is shown in Figure 7, and gear ratio of each gear is shown in Table 3.

The number of teeth of sun gear, ring gear and planetary gear for the first planetary row of 6HP26 automatic transmission is

z_{s 1} = 37

z_{r 1} = 71

and

z_{p 1} = 17

respectively； the number of teeth of sun gear, ring gear and planetary gear for the second planetary row is

z_{s 2} = 38

z_{r 2} = 85

and

z_{p 2} = 23

respectively; and the number of teeth of sun gear, ring gear, long planetary gear and short planetary gear for the third planetary row is

z_{s 3} = 31

z_{r 3} = 85

z_{p 3_b} = 23

and

z_{p 3_d} = 28

respectively. Input speed

n_{i} = 4500 r / \min

, input moment

T_{i} = 400 N \cdot m

The performance analysis model of 6HP26 automatic transmission is shown in Figure 8. The dotted line edge in Figure 8 indicates that the connection between components is controlled by control elements.

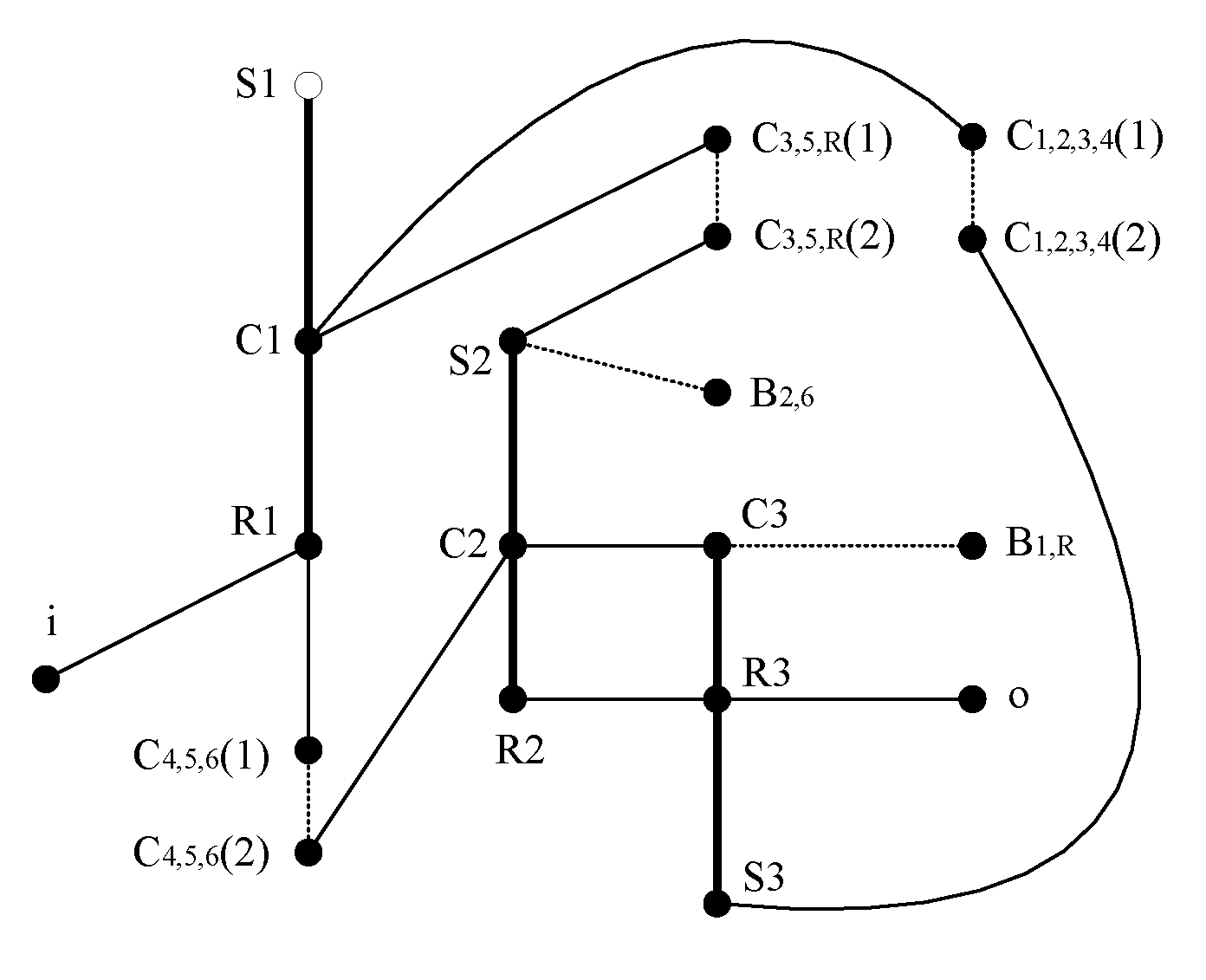
In Figure 8, 6 connected branches can be obtained by deleting the connecting edges between basic components of each planetary row and the connecting edges between vertices of the active and passive edges of the clutch，as shown in Figure 9. The degree of freedom of 6HP26 automatic transmission W=6－3=3.

According to the engagement of control elements, the analysis model of each gear can be obtained, as shown in Figure 10.

3.1. Motion Analysis

The motion analysis model of each gear of 6HP26 automatic transmission can be obtained by deleting the connection edges between basic components of each planetary row in Figure 10.

Components of the first, second and third planetary row are numbered 1, 2, ..., 9 in the order of sun gear, ring and planet carrier, and rotational speed of the components is

n_{1}

n_{2}

, ...,

n_{9}

, respectively. Characteristic parameter of the first, second and third planetary row

α_{1} = z_{r 1} / z_{s 1} = 1.92

α_{2} = z_{r 2} / z_{s 2} = 2.24

α_{3} = z_{r 3} / z_{s 3} = 2.74

Motion characteristic matrix of 6HP26 automatic transmission

A_{1} = [\begin{matrix} 1 & α_{1} & - (1 + α_{1}) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & α_{2} & - (1 + α_{2}) & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & - α_{3} & α_{3} - 1 \end{matrix}]

Connection matrix

A_{2} = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & - 1 \end{matrix}]

Gear matrix

C_{1} = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{2} = [\begin{matrix} 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{3} = [\begin{matrix} 0 & 0 & 1 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{4} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{5} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{6} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

C_{R} = [\begin{matrix} 0 & 0 & 1 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

The transmission ratio and component speed of 6HP26 automatic transmission at each gear can be obtained from the following equation, as shown in Table 4 and Table 5 respectively.

[\begin{matrix} A_{1} \\ A_{2} \\ C_{i} \end{matrix}] [\begin{matrix} n_{1} \\ n_{2} \\ ⋮ \\ n_{9} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix}] (i = 1, 2, 3, \dots)

3.2. Moment Analysis

In Figure 10, delete the connection edges between basic components of each planetary row，the connection edges between vertices of active and passive edges of the engaged clutches, and the vertices of disengaged clutches, the moment analysis model of each gear of 6HP26 automatic transmission can be obtained.

Components of the first, second and third planetary row are numbered 1, 2, ..., 9 in the order of sun gear, ring and planet carrier, and moment of the components is

T_{1}

T_{2}

, ...,

T_{9}

, respectively.

Moment characteristic matrix of 6HP26 automatic transmission

U = [\begin{matrix} 1 & 0 & 1 / (1 + α_{1}) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & α_{1} / (1 + α_{1}) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 / (1 + α_{2}) & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & α_{2} / (1 + α_{2}) & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 / (1 - α_{3}) \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & α_{3} / (α_{3} - 1) \end{matrix}]

Independent member matrix without external force

D_{1} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

D_{2} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \end{matrix}]

D_{3} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

D_{4} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

D_{5} = [\begin{matrix} 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]

D_{6} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]

D_{R} = [\begin{matrix} 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]

Moment input matrix

I_{1} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

I_{2} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

I_{3} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

I_{4} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \end{matrix}]

I_{5} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \end{matrix}]

I_{6} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \end{matrix}]

I_{R} = [\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

The component moment of 6HP26 automatic transmission at each gear can be obtained from the following equation, as shown in Table 6.

[\begin{matrix} U \\ D_{i} \\ I_{i} \end{matrix}] [\begin{matrix} T_{1} \\ T_{2} \\ ⋮ \\ T_{9} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix}] (i = 1, 2, 3, \dots)

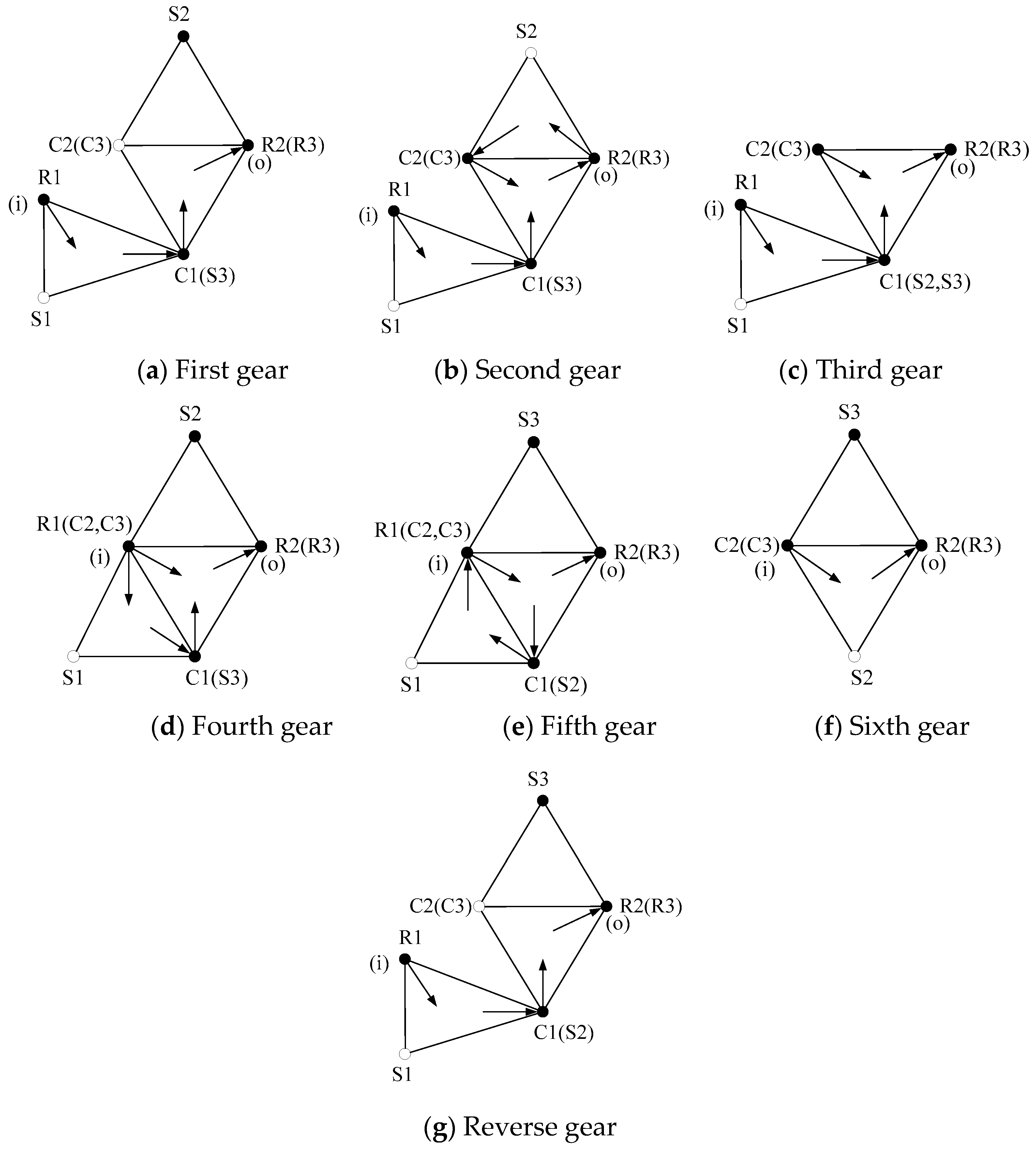
3.3. Power Flow and Efficiency Analysis

From Table 5 and Table 6, component speed and moment can determine the power flow. Power flow diagram of 6HP26 automatic transmission at each gear is shown in Figure 11.

According to the transmission ratio of each gear in Table 4, the efficiency of 6HP26 automatic transmission at each gear can be obtained from Formula (9), as shown in Table 7.

It can be seen that the efficiency is low in the first gear, second gear and reverse gear, because it is series connection in these gears.

4. Conclusion

Multi-speed PGTs improve fuel economy and dynamic performance. Therefore, a novel graph theory method is proposed in this paper for the performance analysis of automatic transmission. Taking 6HP26 automatic transmission as an example, the performance analysis model is established, and the motion, moment, power flow and efficiency analysis are completed.

This method is entirely dependent on the matrices, and performance analysis is performed automatically. In contrast to other analysis methods, this proposed method reduces the dependence on previous design experience and beforehand works of engineers. It also overcomes the disadvantages of using traditional analytical method, such as the need to repeatedly derive formulas and the complexity of calculation. And the automatic analysis of motion, moment, power flow and efficiency is realized by computer, which improves the calculation efficiency and accuracy of planetary transmission performance analysis. Moreover, This method also helps to guide the further design of the PGT, such as the geometrical parameter design of the gears.

Author Contributions

Writing—original draft preparation, H.-L.X.; funding acquisition, L.-J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by National Natural Science Foundation of China(No. 52005158).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Gaertner, L.; Ebenhoch, M. The ZF automatic transmission 9HP48 transmission system, design and mechanical parts. SAE Int. J. Passeng. Cars-Mech. Syst. 2013, 6, 908–917. [Google Scholar] [CrossRef]
Suzuki, T.; Sugiura, H.; Niinomi, A.; Maezuka, S.; Miyazaki, T.; Habata, Y. New RWD 10 speed automatic transmission for passenger vehicles, SAE Int. J. Engines 2017, 10, 695–700. [Google Scholar]
Salgado, D.R.; Del Castillo, J.M. Analysis of the transmission ratio and efficiency ranges of the four-, five-, and six-link planetary gear trains, Mech. Mach. Theory 2014, 73, 218–243. [Google Scholar] [CrossRef]
Hwang, W.M.; Huang, Y.L. , Connecting clutch elements to planetary gear trains for automotive automatic transmissions via coded sketches. Mech. Mach. Theory 2011, 46, 44–52. [Google Scholar] [CrossRef]
Tsai, M.C.; Huang, C.C.; Lin, B.J. Kinematic analysis of planetary gear systems using block diagrams, J. Mech. Des. 2010, 132, 065001. [Google Scholar] [CrossRef]
Geitner, G.H.; Komurgoz, G. Key characteristics of generic bond graphs for planetary gears, Mech. Mach. Theory 2022, 178, 105082. [Google Scholar] [CrossRef]
Dong, P.; Zuo, S.M.; Liu, T.Y.; Xu, X.Y.; Guo, W.; Liu, Y.F.; Wu, H.C.; Wang, S.H. A matrix-based method for searching configurations of planetary gear trains, Mech. Mach. Theory 2023, 180, 105161. [Google Scholar] [CrossRef]
Prikhod’ko, A.A.; Smelyagin, A.I. Kinematics of a planetary train with elliptical gears with internal gearing, J. Mach. Manuf. Reliab. 2021, 50, 412–418. [Google Scholar] [CrossRef]
Chen, H.; Chen, X.A. Recirculation of parallel-connected planetary gear trains, Chin. J. Mech. Eng. 2022, 35, 1–11. [Google Scholar]
Zhang, C.; Dong, H.M.; Dong, B.; Wang, D.L. A bi-directional drive model for lost motion behavior of planetary gear train, Mech. Mach. Theory 2022, 174, 104885. [Google Scholar] [CrossRef]
Yang, W.J.; Ding, H.F.; Zi, B.; Zhang, D. New graph representation for planetary gear trains, J. Mech. Des. 2018, 140, 012303. [Google Scholar] [CrossRef]
Hussen, H.A.; Esmail, E.L. Application of incidence matrix to topological structure and kinematic analysis of multi-planet gear trains. Results Eng. 2021, 12, 100305. [Google Scholar] [CrossRef]
Xie, T.L.; Hu, J.B.; Liu, C.W. Synthesis of seven-speed planetary gear trains for heavy-duty commercial vehicle, Mech. Mach. Theory 2015, 90, 230–239. [Google Scholar] [CrossRef]
Ke, T.; Ding, H.F.; Gong, C.; Geng, M.J. Configuration synthesis of nine-speed automatic transmissions based on structural decomposition, Mech. Mach. Theory 2021, 164, 104421. [Google Scholar] [CrossRef]
Dong, P.; Liu, Y.F.; Tenberge, P.; Xu, X.Y. Design and analysis of a novel multi-speed automatic transmission with four degrees-of-freedom. Mech. Mach. Theory 2017, 108, 83–96. [Google Scholar] [CrossRef]
Esmail, E.L. A matrix-based method for detection of degenerate structures in planetary gear trains, Mech. Mach. Theory 2022, 175, 104925. [Google Scholar] [CrossRef]
Shivam, M.; Arun, D.D.; Karuna, M.; Manjula, D. Efficiency analysis of dual motor powertrain with planetary gear set, Int. J. Emerg. Electr. Power Syst. 2022, 1. [Google Scholar]
Ge, Y.J.; Liu, D.N. Transmission efficiency and optimization of the power-confluence magnet planetary gear, J. Power Electron. 2022, 22, 1–10. [Google Scholar] [CrossRef]
Yang, J.Y.; Ge, Y.J. Transmission performance of planetary permanent magnet gear with few pole difference, J. Mech. Sci. Technol. 2022, 36, 6217–6225. [Google Scholar] [CrossRef]
Mohite, D.D.; Patil, N.R.; Shinde, S.B.; Rade, K.A. Experimental investigation on speed and torque analysis of planetary gearing system, J. Algebr. Stud. 2022, 13, 1439–1446. [Google Scholar]
Ding, H.F.; Cai, C.W.; Chen, Z.M.; Ke, T.; Mao, B.W. Configuration synthesis and performance analysis of 9-speed automatic transmissions. Chin. J. Mech. Eng. 2020, 33, 1–21. [Google Scholar] [CrossRef]
Liao, Y.G.; Chen, M.Y. Analysis of multi-speed transmission and electrically continuous variable transmission using lever analogy method for speed ratio determination. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
Kahraman, A.; Ligata, H.; Kienzle, K.; Zini, D.M. A kinematics and power flow analysis methodology for automatic transmission planetary gear trains. J. Mech. Des. 2004, 126, 1071–1081. [Google Scholar] [CrossRef]
Liu, J.X.; Yu, L.D.; Zeng, Q.L.; Li, Q.Y. Synthesis of multi-row and multi-speed planetary gear mechanism for automatic transmission, Mech. Mach. Theory 2018, 128, 616–627. [Google Scholar] [CrossRef]
Yang, X.D.; Shao, Y.M.; Wang, L.M.; Yu, W.N.; Yue, N.; Du, W.T. Configuration design of dual-input compound power-split mechanism for in-wheel motor-driven electrical vehicles based on an improved lever analogy method, J. Mech. Des. 2021, 143, 1–12. [Google Scholar] [CrossRef]
Deng, T.; Gan, Z.H.; Xu, H.; Wu, C.J.; Zhang, Y.X.; Liu, F.; Ding, Z.T.; Chen, W. Configuration design and screening of multi-mode double-planetary-gears hybrid powertrains, J. Mech. Des. 2022, 144, 073301. [Google Scholar] [CrossRef]
Jiang, X.Y.; Hu, J.J.; Peng, H.; Chen, Z.P. A design methodology for hybrid electric vehicle powertrain configurations with planetary gear sets, J. Mech. Des. 2021, 143, 1–10. [Google Scholar] [CrossRef]
Timofeev, G.A.; Panyukhin, V.V.; Sashchenko, D.V. Studying self-braking planetary gears with single-crown satellites, J. Mach. Manuf. Reliab. 2020, 49, 308–313. [Google Scholar] [CrossRef]
Prikhodko, A. Experimental kinematic analysis of an intermittent motion planetary mechanism with elliptical gears, J. Meas. Eng. 2020, 8, 122–131. [Google Scholar] [CrossRef]
Zanasi, R.; Tebaldi, D. Modeling of complex planetary gear sets using power-oriented graphs, IEEE Trans. Veh. Technol. 2020, 69, 14470–14483. [Google Scholar] [CrossRef]

Figure 1. Automatic transmission performance analysis flow chart.

Figure 2. Three-speed planetary gear transmission and its overall performance analysis model.

Figure 3. Connected branch of overall performance analysis model of three-speed planetary gear transmission.

Figure 4. Performance analysis model of various gears of automatic transmission.

Figure 5. Power flow diagram of a planetary row.

Figure 6. Schematic diagram of 6HP26 automatic transmission.

Figure 7. Transmission diagram of each gear of 6HP26 automatic transmission.

Figure 8. Performance analysis model of 6HP26 automatic transmission.

Figure 9. Connected branch of performance analysis model of 6HP26 automatic transmission.

Figure 10. Performance analysis model of various gears of 6HP26 automatic transmission.

Figure 11. Power flow diagram of 6HP26 automatic transmission at each gear.

Table 1. The state table of control elements.

Gear	C_1,R	C_1,2,3	B_3,R	B₂
First gear	●	●
Second gear		●		●
Third gear		●	●
Reverse gear	●		●

Table 2. The control element status table of 6HP26 automatic transmission.

Gear	C_1,2,3,4	C_4,5,6	C_3,5,R	B_1,R	B_2,6
First gear	●			●
Second gear	●				●
Third gear	●		●
Fourth gear	●	●
Fifth gear		●	●
Sixth gear		●			●
Reverse gear			●	●

Table 3. 6HP26 automatic transmission gear ratio of each gear.

Gear		Gear	Transmission ratio
First gear	$i_{1} = \frac{α_{3} (1 + α_{1})}{α_{1}}$	Second gear	$i_{2} = \frac{(1 + α_{1}) (α_{2} + α_{3})}{α_{1} (1 + α_{2})}$
Third gear	$i_{3} = \frac{1 + α_{1}}{α_{1}}$	Fourth gear	$i_{4} = \frac{α_{3} (1 + α_{1})}{α_{3} (1 + α_{1}) - 1}$
Fifth gear	$i_{5} = \frac{α_{2} (1 + α_{1})}{α_{2} (1 + α_{1}) + 1}$	Sixth gear	$i_{6} = \frac{α_{2}}{1 + α_{2}}$
Reverse gear	$i_{R} = - \frac{α_{2} (1 + α_{1})}{α_{1}}$

Table 4. Transmission ratio of 6HP26 automatic transmission at each gear.

First gear	Second gear	Third gear	Fourth gear	Fifth gear	Sixth gear	Reverse gear
$i_{1} = 4.167$	$i_{2} = 2.338$	$i_{3} = 1.521$	$i_{4} = 1.143$	$i_{5} = 0.867$	$i_{6} = 0.691$	$i_{R} = - 3.407$

Table 5. Component speed of 6HP26 automatic transmission at each gear (r/min).

	R1	C1	S2	R2	C2	S3	R3	C3
First gear	4500	2959	-2419	1080	0	2959	1080	0
Second gear	4500	2959	0	1925	1331	2959	1925	1331
Third gear	4500	2959	2959	2959	2959	2959	2959	2959
Fourth gear	4500	2959	5760	3938	4500	2959	3938	4500
Fifth gear	4500	2959	2959	5188	4500	6385	5188	4500
Sixth gear	4500	2959	0	6509	4500	10004	6509	4500
Reverse gear	4500	2959	2959	-1321	0	-3619	-1321	0

Table 6. Component moment of 6HP26 automatic transmission at each gear (N•m).

	S1	R1	C1	S2	R2	C2	S3	R3	C3
First gear	208.3	400	-608.3	0	0	0	608.3	-1666.8	1058.5
Second gear	208.3	400	-608.3	326.7	731.8	-1058.5	608.3	-1666.8	1058.5
Third gear	208.3	400	-608.3	212.6	476.1	-688.7	395.8	-1084.5	688.7
Fourth gear	57.14	109.7	-166.84	0	0	0	166.84	-457.14	290.3
Fifth gear	-53.04	-101.85	154.89	-154.89	-346.96	501.85	0	0	0
Sixth gear	0	0	0	-123.46	-276.54	400	0	0	0
Reverse gear	208.3	400	-608.3	608.3	1362.7	-1971	0	0	0

Table 7. The efficiency of 6HP26 automatic transmission at each gear.

First gear	Second gear	Third gear	Fourth gear	Fifth gear	Sixth gear	Reverse gear
$η_{1} = 0.9188$	$η_{2} = 0.9407$	$η_{3} = 0.9864$	$η_{4} = 0.9869$	$η_{5} = 0.9909$	$η_{6} = 0.9874$	$η_{R} = 0.9472$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Motion, Static Force and Efficiency Analysis of Planetary Gear Transmission Based on Graph Theory

Abstract

1. Introduction

2. Performance Analysis Model of Automatic Transmission

2.1. Motion Analysis of Automatic Transmission

2.2. Moment Analysis of Automatic Transmission

2.3. Power Flow and Efficiency Analysis of Automatic Transmission

3. Performance Analysis Example of Automatic Transmission

3.1. Motion Analysis

3.2. Moment Analysis

3.3. Power Flow and Efficiency Analysis

4. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe