A Hydro-Powered Climate-Neutral Pump: Full Cycle Simulation and Performance Evaluation

Preprint

Article

A Hydro-Powered Climate-Neutral Pump: Full Cycle Simulation and Performance Evaluation

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

Mansour Al Qubeissi^*

Scott Daniel Beard

Mansour Al Qubeissi^*

Scott Daniel Beard

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

This paper presents a parametric study of the multistorey hydro-powered pump, known as "Bunyip," which has demonstrated significant potential in contributing to rural regions. The study aims to understand the underlying physics of the system and enhance its hydraulic performance. A transient three-dimensional model using the commercial Computational Fluid Dynamics (CFD) tool Ansys-Fluent is utilized to gain insights into the fundamental flow mechanics, operational efficiency, standard capacity, and relative delivery. The investigation involves an initial assessment of performance for three Bunyip devices based on manufacturing data. Parametric analysis is conducted, and a parametric dataset is generated through meticulous application and numerical modelling. The CFD results are validated against experimental data. Three design configurations are considered, and 58 sets of varied input parameters are examined. The best design configuration is evaluated against five cases of conventional hydro-power pump systems. The results indicate that a smaller diameter of the pressure chamber and a higher supply head lead to higher pressure, achieving a target head of 3 m with 15% efficiency and a flowrate of 11.82 l/min.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The escalating climate crisis and the need for sustainable energy solutions have prompted a global push towards renewable energy adoption [1]. As fossil fuel prices continue to rise due to inflation and geopolitical conflicts, the finite nature of these resources poses challenges to their accessibility [2]. In response to these concerns, significant investments have been made in transitioning towards cleaner energy sources, reaching a staggering $1.3 trillion in 2022 [3].

Developing regions, often facing economic vulnerability, bear the brunt of the increasing pressure to afford and access reliable power sources. These regions heavily rely on stable access to power for sustaining growth, productivity, and overall well-being. Among the crucial resources required for development, access to water stands as an indispensable necessity [4]. Whether it is for safe drinking, personal hygiene, agriculture, livestock rearing, or other developmental needs, a stable water supply plays a pivotal role. Traditionally, fossil-fuel or electrically powered systems have been the primary mechanisms used for lifting and transporting water in these regions. However, the detrimental impact of fossil-fuels, including rising prices and environmental concerns, is now driving the need to shift towards alternative renewable mechanisms that can capture and harness the natural energy systems present in the local environment.

The Hydraulic Ram Pump (HRP) is a simple yet effective device that utilizes a paired check-valve mechanism to harness hydro-kinetic energy from a drive volume and convert a fraction of the incoming flow into an elevated head potential. By tapping into the "free" gravitational energy present in natural rivers, springs, or flowing water bodies, the HRP offers a sustainable solution for micro-hydro-power needs [5]. Due to its potential and versatility, the HRP has been actively researched and recognized as a prominent hydro-powered system in current technology reviews [6]. Despite its success, much of the existing research on the HRP, like other pumping technologies, tends to focus on marginal improvements rather than exploring more significant enhancements. This raises questions regarding the feasibility and benefits of introducing additional hydraulic complexity to the system in pursuit of enhanced water head potential.

Over the past decade, research on internal flows has significantly advanced, enabling a more detailed and focused analysis of individual components within hydraulic pumping systems. This progress has led to the discovery of additional capabilities, offering opportunities to enhance the previously established analytical relationships [7]. To serve a valuable resource to observe best practices and methodologies used in HRP system, we have utilized the development of an advanced multi-storey hydraulic pumping system known as "Bunyip [8]." Several studies have been conducted, providing valuable insights into the modelling procedures, validation processes, and overall success of hydraulic pumping systems. Among these studies, two groups of researchers have made notable contributions:

In [9,10], a comprehensive detail on the adopted CFD setup and validation procedure is given. This includes RNG k-ε Turbulence model, suitable for high shear rate flow and separation, the PISO pressure-velocity coupling and the coarse mixed mesh designed within 5 mm – 20 mm size range and 1 million cells. The wall treatment exploits four inflation layers between y+ 17.78 – 442.79, utilising standard wall functions and a roughness of 0.15 mm. Nonetheless, the settings attained an average relative error of 1.9% for head loss and drag coefficients when corroborated with their physical equipment. Thus, despite the criticisms made, the model performed well in application and remains to be some of the most successful validations and hybrid studies published.

In [11,12], a detailed simulation of ram pump is made, including the traditional spring waste valve mechanism, to conclude three optimal designs. The best numerically analysed design reduced waste valve loss by 30%. The latter finding is less extensive than the previous two pieces of research, but still nontrivial, using the realizable k-ε turbulence model, second order spatial, kinetic and turbulence dissipation. However, the latter finding provides little insight into the validation and description, particularly surrounding the mesh and justification for model accuracy.

The critical gap in literature is addressing the motion definition in six degrees of freedom (6DOF). Such set-up requires a time-based User Defined Function (UDF) to establish the relative motion within the domain, favourable for computational speed and control [13]. In Ansys-fluent [14], the excellent capacity of the 6DOF solver enables direct calculation for the motion observed. However, this is computationally expensive and notably sensitive to validate. Therefore, it requires significant input to attain suitable validation [15]. In our analysis, we provide the simulation of the multi-story hydraulic pump (bunyip), considering the 3D and 6DOF effects to provide potential system advancement. In what follows, the system is described in Section 2. The numerical set-ups and modelling are presented in Section 3. In Section 4, we present the results. The key findings are concluded in Section 5.

2. System description

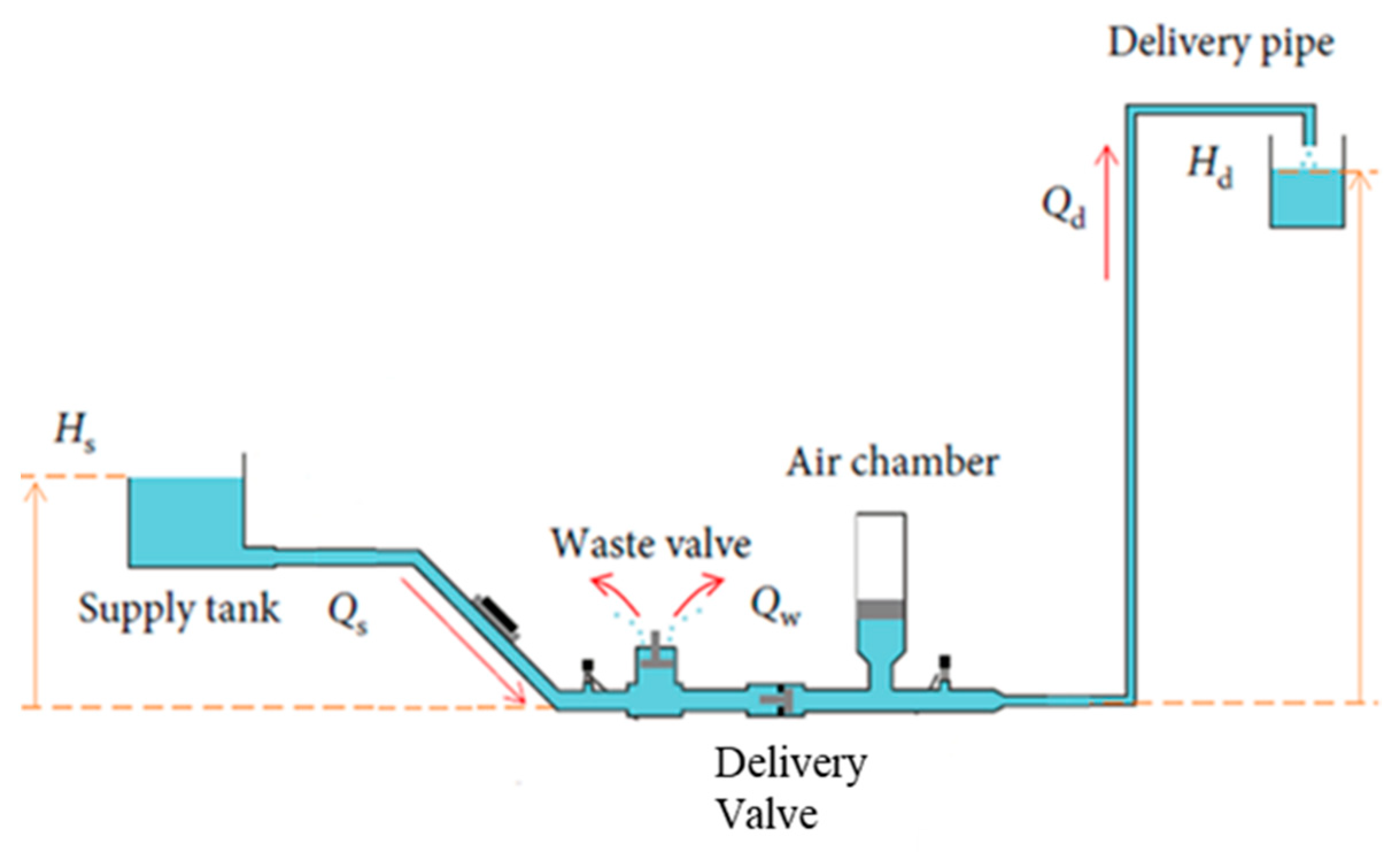
2.1. Conventional hydraulic ram pump

The conventional Hydraulic Ram Pump (HRP) system operates through a series of well-defined phases, each contributing to its efficient and continuous operation. Figure 1 illustrates the fundamental components and arrangement of the conventional HRP system, showcasing the three operational phases: 'acceleration,' 'delivery,' and 'recoil.'

The system includes the supply pipe, installed at a known height, and measured relative to the delivery valve. Water from a higher source flow through the supply pipe and undergoes 'acceleration' as it enters the drive pipe. During this phase, the potential energy of the water is marginally elevated, transforming it into hydro-kinetic energy. Subsequently, the water rapidly discharges through the waste valve. As the water continues to flow, it passes the waste valve at a critical velocity, resulting in a drag force that overcomes the spring mechanism, leading to the abrupt closure of the waste valve. This action traps the high dynamic pressure flow, generating a sharp peak in static pressure known as water hammer. The water hammer phenomenon allows the internal pressure to overcome the elevated head, pre-loading the delivery valve. Consequently, a fraction of the initial flow is rapidly passed to enter the delivery system. The subsequent drop in internal pressure following the peak re-opens the initial waste valve, enabling the flow to recommence its initial flow regime, known as the 'recoil.' The drive flow begins to accelerate once again, initiating a perpetual cycle. The pair of check valves in the system play a crucial role in regulating the flow direction during the operational phases. These check valves ensure that water flows in the desired direction and prevent backflow, contributing to the pump's efficiency.

Over time, auxiliary components have been developed to improve the conventional HRP system's performance [17]. One such component is the air chamber, which dampens the sharp peaks in pressure and results in a more gradual delivery stroke, leading to a more consistent flow [7,18].

2.2. HRP limitations

When discussing the perpetual operation and regulation of the system. It can be recognised that the start of the HRP cycle requires external physical input to prime the system. This initially opens the waste valve to initiate the ‘acceleration’ phase. The supplied partially elevated flow enters the body and at the critical velocity closes the waste valve, inducing a peak in static water hammer as the flow is abruptly brought to ‘rest’. In principle, under consistent flow conditions the pump can be observed and acknowledged to operate independently, though, in application it could be shared that naturally occurring flow variation can impact the pair of valves timing and result in stalled cycles. This is further escalated by the pumps discussed inability to self-start. In remote regions where these systems tend to thrive, it is both time consuming to restart and potentially could go unrecognised for some time, compromising system supplies within the likes of storage vessels [7,19]. One of the greatest distinguishing features for the Bunyip system is the ‘automated’ ability to self-regulate dependent upon the incident flow from the drive supply [8]. In no-flow conditions the pump remains dormant. Once the supply returns with sufficient dynamic pressure, the tyre will begin to inflate and commence the cycle. The ability to manage the complexities of operation is critical for the productivity of the pumping system. Thus, although the output will vary subject to the water available to the system, the Bunyip would likely provide an enhanced degree of flexibility and consistency.

Due to the simple operational principle, manipulated by two isolated components, previous research could be used to highlight the limitations of the arrangement and the risks associated with dependency upon the sprung mechanisms. Harith et al. [11,12] and Li et al. [10] both identified the waste valve as the primary contributor to accessing improved performance of the HRP. Acknowledged to dictate the associated critical velocities, cycle rate sustained, the volume wasted during the acceleration phase and the capacity to overcome or deliver greater quantity to the elevated supply. The process of ‘tuning’ the valve, typically using a threaded travel mechanism, could be described as temperamental and by nature directly tailoring the operation to a singular case, whereby actual flow parameters will change. In their subsequent research, Harith et al. investigated multiple adapted arrangements and recognised that a modified component with height regulation and a more developed sprung mechanism would provide the capacity to increase the associated model operational efficiency by 0-20%. The Bunyip system also utilises a pair of check valves, however, they operate in a significantly different manner. The pair operate across a larger cycle period and do not dictate the critical velocity and the volume of water wasted directly, alternatively managed by the simple tyre seal mechanism. The mechanism utilises a blend of components including the body mass, internal spring tyre stiffness and the dynamic water pressure for example, for a more reliable operation [16].

The conventional HRP principle operates through a rapid and relatively forceful motion to generate sufficient hammer pressure to breach the delivery valve. This could be researched and identified to account for multiple considerations. In [9], the full losses are considered, attributing to abrupt changes in velocity, turbulent flow conditions, geometry, and internal pressure gradients. One can conclude that features should be designed to implement diffuser entry regions and more efficient entry geometry. This was aimed to reduce the head loss coefficients and improve the velocity distribution, described to produce enhanced efficiencies of 50%-70% for their designs.

2.3. System design

The co-founders of Bunyip system (Porta and Trew [8]) provided the requirement for higher-quality rubber seal materials. In the same vein as accessibility, the exerted hammer forces induced within the HRP throughout rapid operation places greater stress upon the system and consumable parts. Thus, increasing maintenance retirements and the likelihood of failure. The advanced models core components may last up to 50 years, conversely, the likely capacity of design made in remote regions could be as little as 10 years using weaker materials and limited facilities [4]. The Bunyip’s smooth and lower velocity flow design requires a reduced complexity manufacture and lighter weight design, components and features, reporting maintenance of the consumable rod and piston seals to last up to three-years without significantly compromising performance. Additionally with low engagement replacement [16].

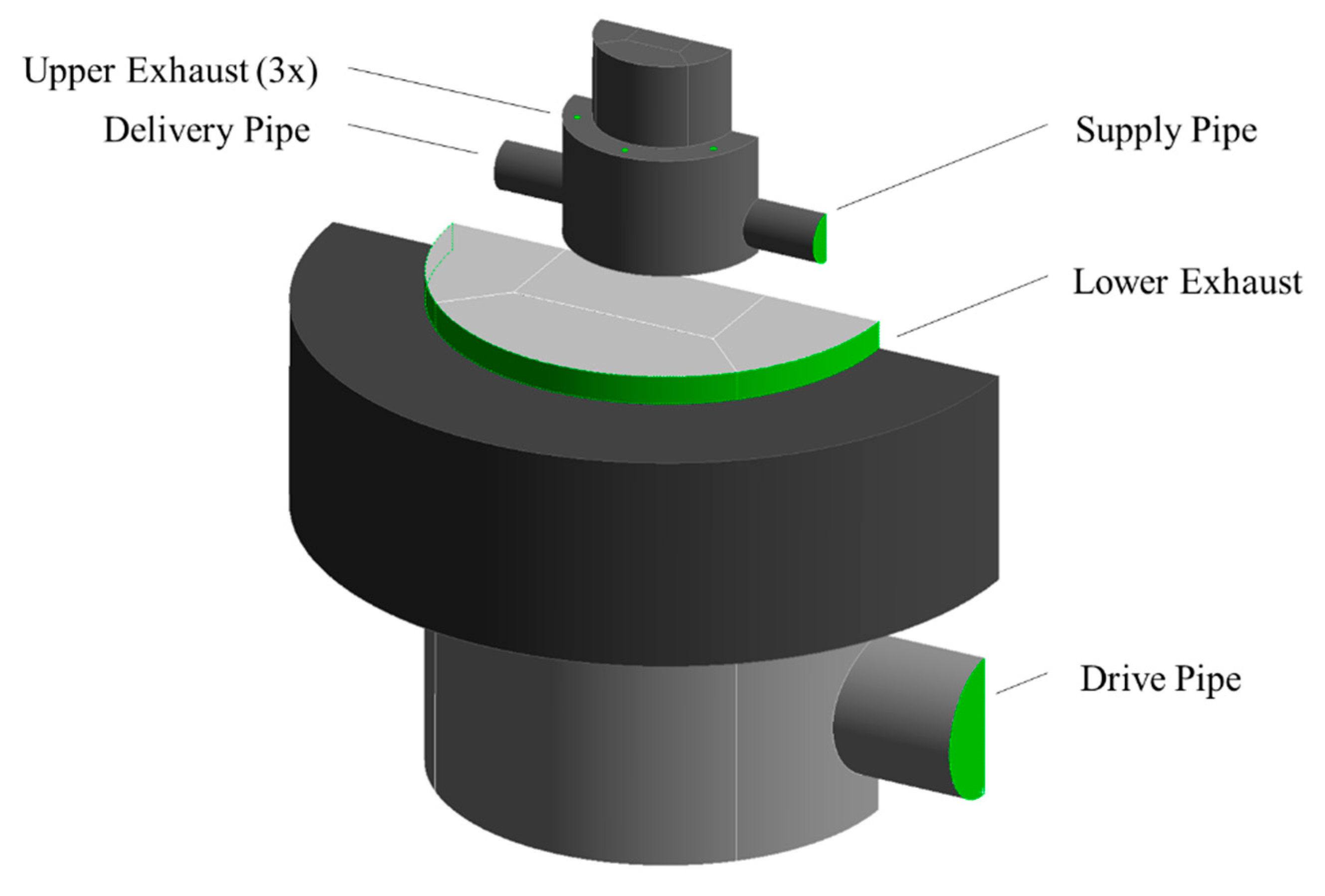
This paper begins to investigate and explore an alternative design, known as the Bunyip, shown in Figure 2. The research inspired by the developed commercial momentum, yet extremely limited presence within academic research. The following study aims to investigate the operational characteristics and performance capacity of the adapted mechanism. This will utilise a combined methodology of secondary performance data and a dedicated numerical model constructed in Ansys-Fluent 2021 R2 [14]. The work facilitates the critical analysis of the internal physics and performance potential using the student constrained discretization capacity and appropriately simplified domain. The design will implement verified methods where possible to quantify and evaluate the domain to support discussion alongside manufacturer provided data and the conventional HRP system.

The introduced Bunyip pump was very much inspired by the HRP previously described. Whereby the inventors (Brett Porta and Ralph Glockemann [16]) recognised that for their specific application, the conventional design failed to manage the fluctuated operating conditions. Disappointed and determined to resolve the issue, a chain of new systems and designs could be developed at a domestic level, incrementally surpassing, and growing in capacity. Focused upon enhancing the resilience in varied operation conditions and to minimise the disruptive hammer noise and forces in HRP for a local installation to their residence. Several designs were produced, namely, the Oasis, Water Dragon and the Glockemann Pump [20,21]. The last of which awarded a Gold Medal at the Geneva 2002 International Exhibition [16] setting a high standard for its successor in the form of the Bunyip invented in 2006 by Bunyip Water Pumps, formally Porta’s Affordable Pumps [8].

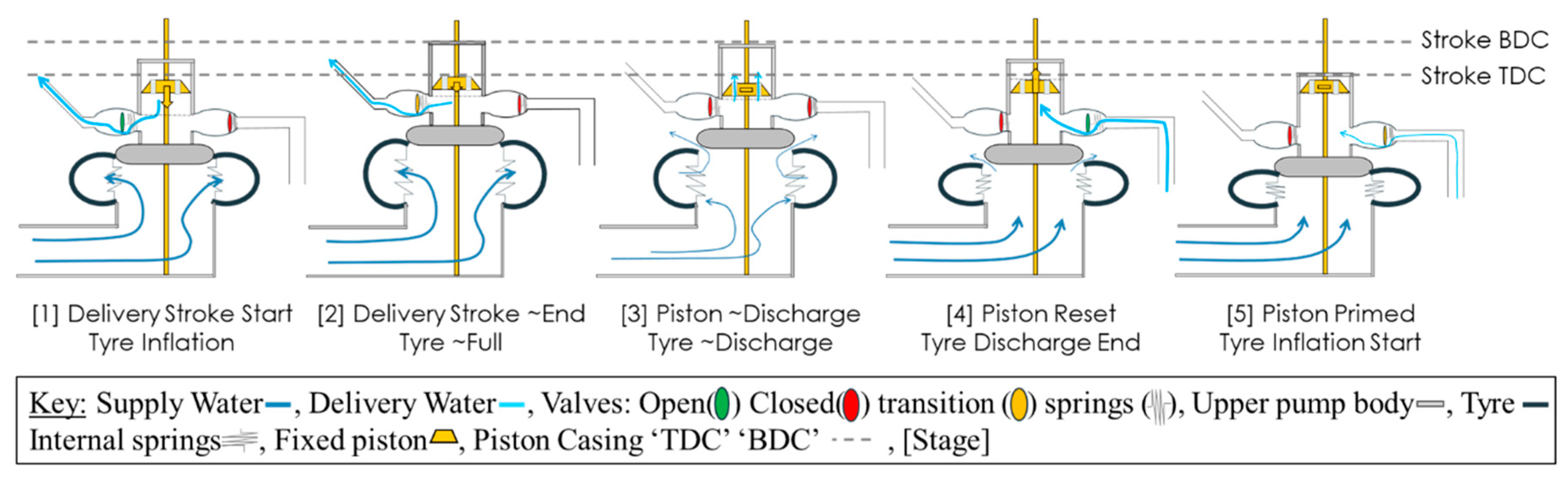
The Bunyip system previously introduced operates using a vastly different principle and cycle depicted in Figure 3. The system utilises a positive displacement piston arrangement, with two separate upper and lower flow volume chambers to transfer and amplify the dynamic tyre pressure into the elevated head pressure. Then, generating a series of relative strokes using a fixed length piston to deliver a secondary supply of water against the elevated head, understood through five operational phases (1-5), as follows [8]:

(1): The incident drive supply inflates the tyre, increasing static pressure resulting in a smooth relative piston stroke. The stroke is resisted by the elevated pressures in the upper system and internal tyre and spring stiffness, resulting in delivery through sufficient pressure to breach the delivery line, and overcome the elevated head for a stroke of delivery.
(2): As the upper body approaches TDC, the delivery stroke output reduces and transitions to close the delivery check-valve as the tyre inflation approaches the limit of its travel.
(3): At TDC the piston travels beyond a series of discharge holes in the walls of the piston housing, resulting in the ‘unlock’ and discharge of the Piston. Meanwhile, the incident internal tyre pressure is sufficient to overcome the tyre seals, detaching and expelling the trapped internal pressure from the domain.
(4): The reduced internal tyre pressure, internal stiffness of the tyre and springs and mass of the upper portion result in the ‘dump’ phase collapse. The upper body and tyre fall, generating a relative suction stroke in the piston, priming the volume for the next cycle.
(5): The piston is now full, the tyre and upper body connected and the drive pipe beginning inflation as the cycle restarts.

A relevant and recent hydro-power review paper by Zambrano et al, 2019 provided an invaluable insight into both the HRP and the Bunyip. Firstly, reinforcing the wealth and depth of research available for the conventional system, despite the discussed initial push for the greater capacities of fossil-fuel systems. On the other hand, the paper recognised the introduction of the Bunyip between 2006-2018. At this stage the Bunyip could only be recognised as present within grey, none-scientific literature. Despite the lack of research, the commercial momentum indicates great promise for the system and its capacity to outperform the conventional system. Thus, the door opens for the current piece of research to conduct a comparative appraisal of performance based upon manufacturer provided data, develop an advanced numerical model to investigate the current operational capacity, examine the internal flow features and characteristics before delivering the first report of its kind within the scientific research field to evaluate and appraise the potential and next steps for research within the field.

2.4. Performance indicators

Upon review of several studies in the field, the primary indicator adopted for performance is the operational efficiency, calculating the ratio of power through the delivered volume (

P_{d}

) relative to the total input quantity supplied (

P_{s}

). The relationship derived below using the Head (

H

) and Flow Rate (

q

) ratio [21,22]. Ultimately, the value quantifies the capacity of the pump to overcome the elevated head and an opportunity to compare the system model and data against alternative pumps. The operational efficiency (

η

) will change dependent upon supply and delivery head ratios, nominally in the range 50% - 60%. For a typical HRP system under 30 m, this can be determined as [9]:

η = \frac{P_{d}}{P_{s}} = \frac{ρ g q_{d} H_{d}}{ρ g q_{s} H_{s}} = \frac{q_{d}}{q_{s}} \frac{H_{d}}{H_{s}} = Q H .

(1)

A secondary method identified was the Standard Capacity (

S_{c}

), a normalised method to standardise a flow rate capacity. This is calculated using the delivery flow rate (

Q_{d}

) and inlet diameter for the pump squared (

D^{2}

) in

{m m}^{- 2}

. Several studies utilise this measure to compare their novel designs against established models in the market, represented in a normalised form, independent of the system size [10], shown in Figure 5. This is known as the standard capacity (

S_{c}

), and used as an indicator of pure delivery capacity [23]:

S_{c} = \frac{q_{d}}{D^{2}} .

(2)

The final measure has been indicated a consideration towards the total percentage of water delivered [11]. This is crucial for remote applications where water scarcity is a challenge. In previous research recognised that the volume of water wasted could outweigh the high other performance indicators for a given Thai application in Ban Ha, Samoeng District, Thailand [19]. This can be facilitated with the Bunyip using multiple inlets/outlets through a total flow rate term (

q_{T})

. The delivery rate is calculated as:

R_{d} = \frac{q_{d}}{q_{T}}

(3)

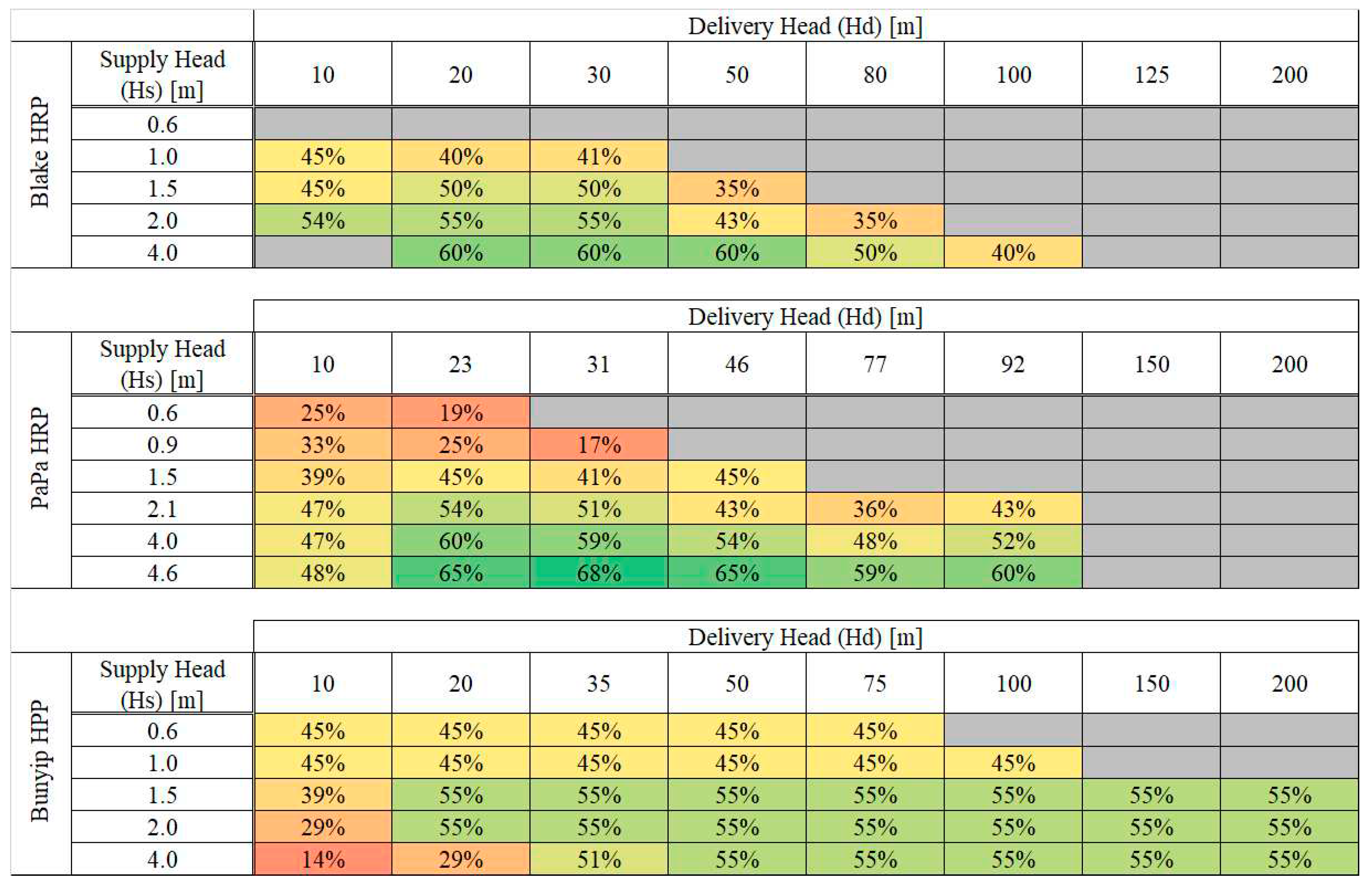
The identified performance criteria enabled manufacturer published output data to be tabulated for comparison in Table 1, including a traditional style Blake’s HRP [24], the recently adapted springless in-line HRP PaPa [25] and the Bunyip plotted in Figure 6.

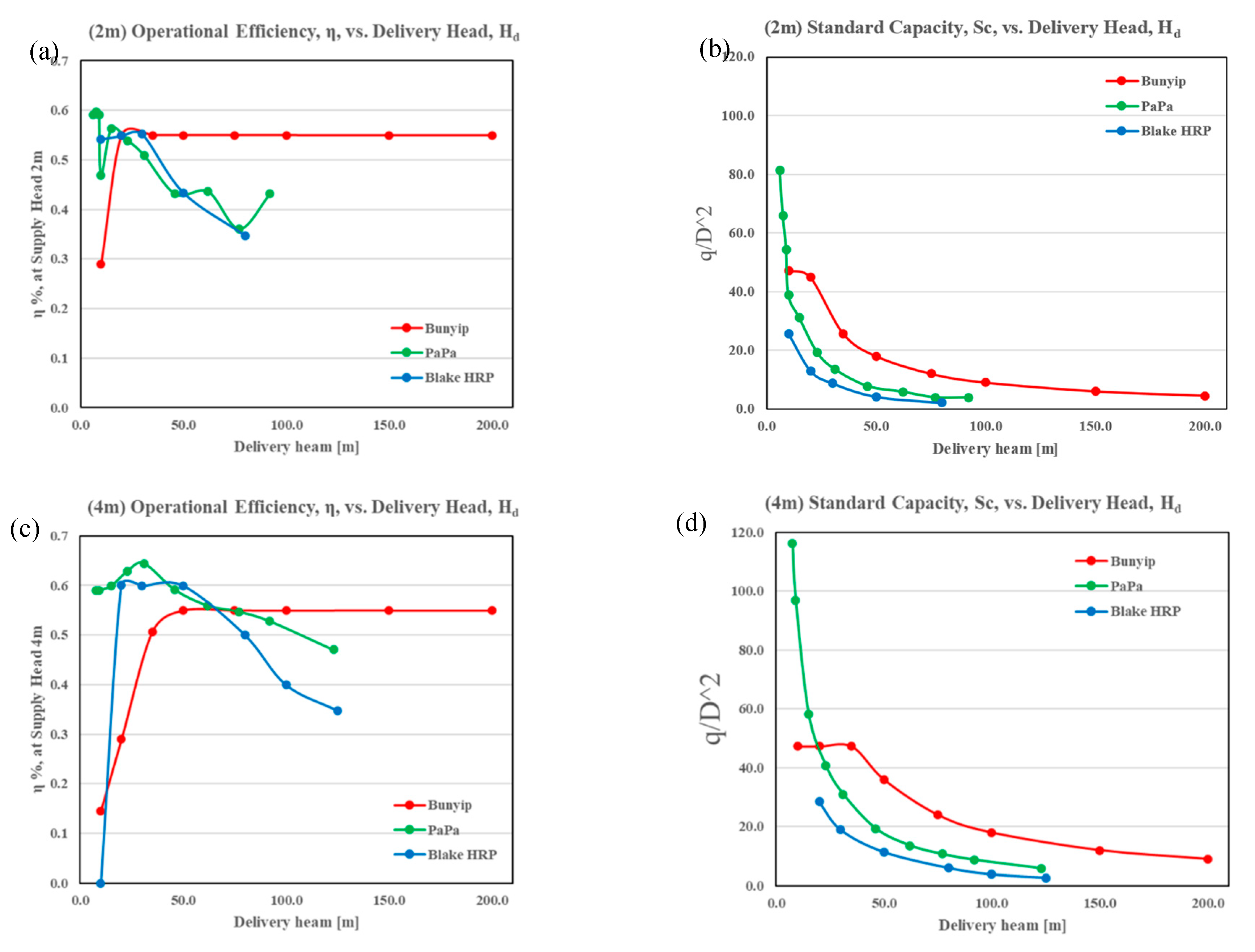
The Bunyip can operate at a reduced supply head, as described in Table 1, whilst additionally requesting to ’consult’ the associated sales teams for application at or less than 1m for the two HRP designs. Additionally, the HRP’s demonstrate a better efficiency than the HRP in the lower region of Figure 4 (a)(c) at approximately 15 m delivery head. The Bunyip in principle provides a significantly greater capacity to deliver to greater ranges for the equivalent supply, illustrated by the extended line lengths in Figure 4, attainable through the of the pressure amplified positive displacement design. Clearly establishing the Bunyip as the only system that can operate to greater heads than 100m and even reported to operate up to 432 m in an adapted reinforced cylinder model currently under development.

Figure 4. Graphical performance evaluation at 60 l/minute and 2 m – 4 m supply heads.

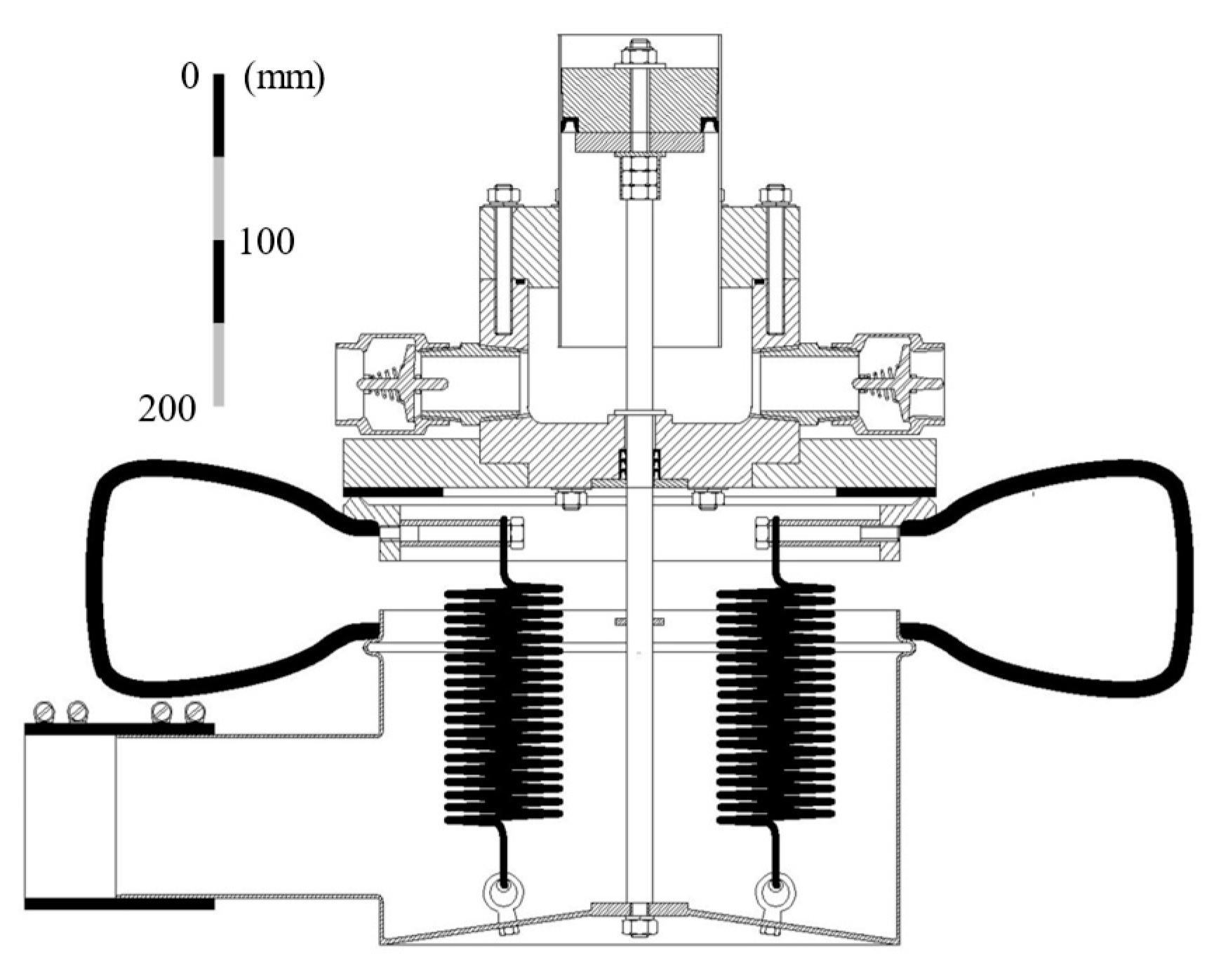
Figure 5. Bunyip PA-13 Technical Drawing, scalable using 100mm drive pipe, inferred from private communication with the manufacturer [16].

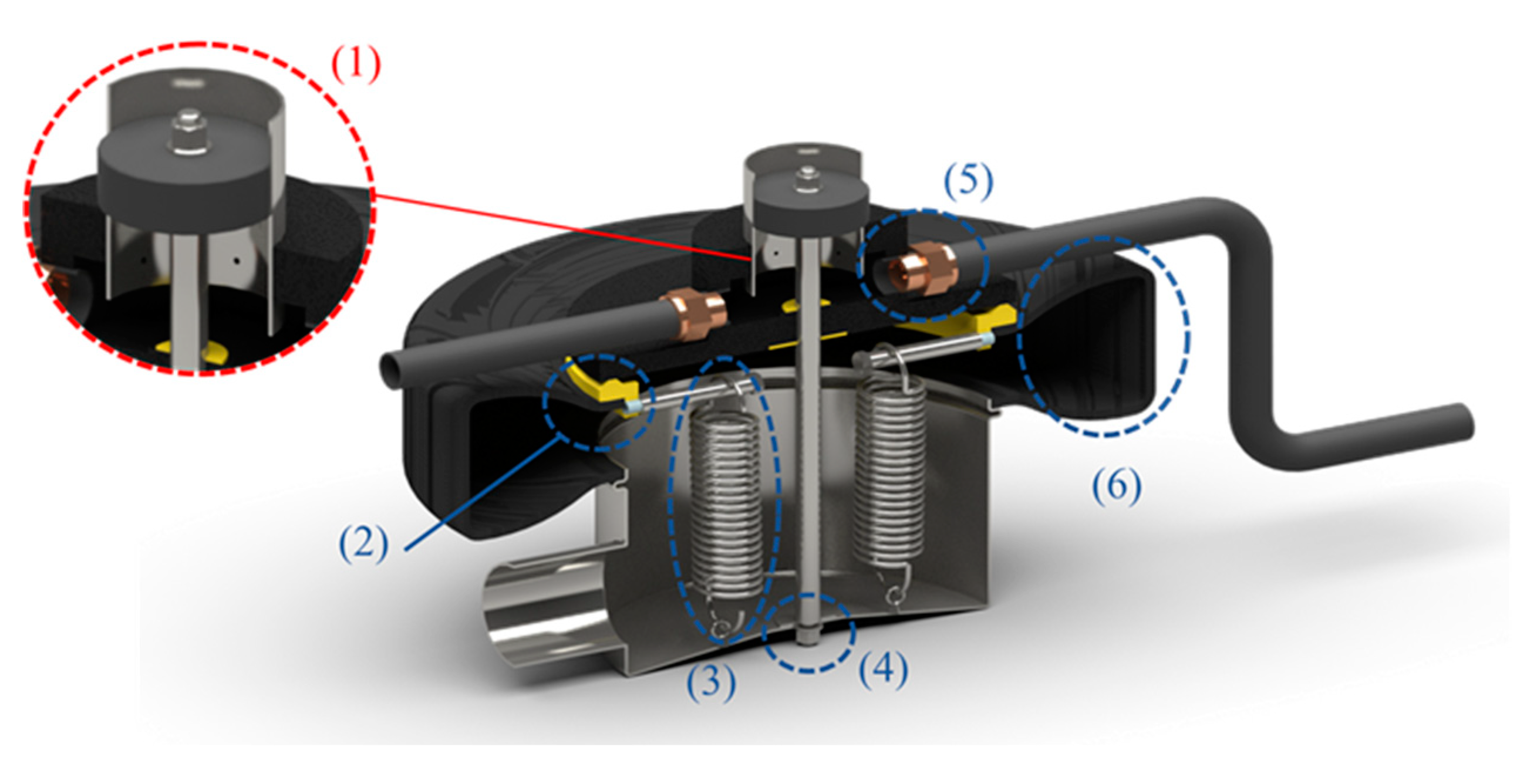
Figure 6. Bunyip 3D internal system render, used in this analysis. Annotations are discussed following this figure.

It can be recognised that when the Bunyip receives a relatively high supply head for delivery to low elevation, the efficiency drops considerably in Figure 6(a)(c), indicating high waste in the cycle is accounted for in the delivery elevation attainable. This is likely due to the mechanisms extended positive displacement travel. In this region the HRP will enable greater volumes to propagate per cycle, increasing operational efficiency and standard capacity. The PaPa pump enables faster manipulation of the low-travel and springless valves to manage internal pressures more efficiently. At a low head ratio, the supply also has a greater ability to overcome a ‘lighter’ elevation head and deliver a greater portion of the flow provided [25]. As such, Bunyip yields the greatest standard capacity, measured relative to the supply pipe diameter. Though, the Bunyip supply is defined at Ø = 35 mm, the definition does not consider the drive pipe at a greater Ø (100 mm). Thus, holds limited insight and could use an alternate pump volume.

3. Set-ups

Numerical methods in recent years continue to drive innovation, routinely integrating advanced features and the identification of further applications that would benefit from the depth of analysis available. The research platform implemented utilises Ansys-Fluent [14], a market leading suite of progressive modelling modules to construct each stage of the model process with unique potential to utilise User-defined-Functions (UDF) to enhance the standard capacity and investigate advanced multi-body physics 6DOF capacity.

3.1. Geometry

To access the most accurate geometry possible, contact made to Bunyip pumps inventor [8,16,20] to receive the scalable technical drawing of their best-selling PA-13 model. This has been used in conjunction with available Bunyip content including the operational calculation tool and charts to describe the typical stroke length (

y_{s l}

) and piston bore, 90 mm and 98 mm, respectively [8]. The procedure followed when analysing the domain is made using a developed 3D CAD render based upon the technical and annotations provided in parallel, shown in Figure 5 and Figure 6.

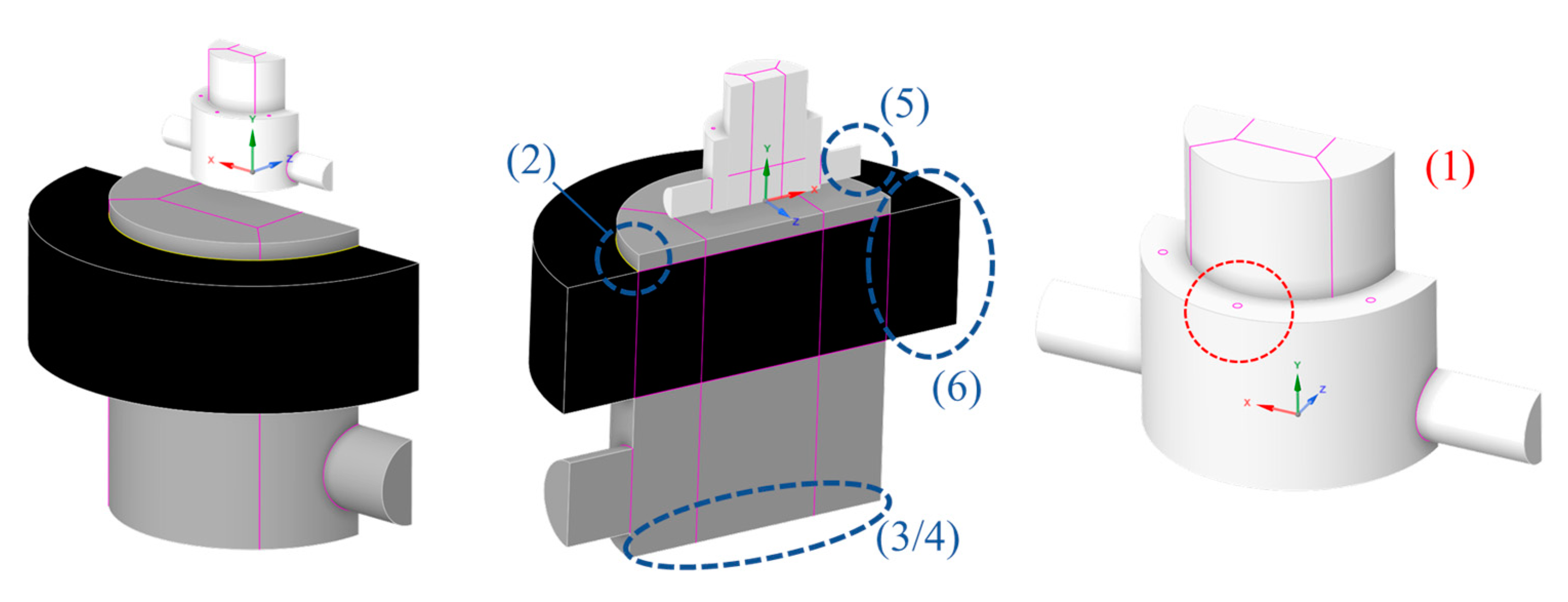
The illustration introduces the decisions made to translate the real-world system into a functional modelling form, considering the reduction in complexity and a reduced cell count and computational requirements. The domain shared in Figure 7, illustrates shared faces that connect adjacent zones are illustrated in pink, enabling separate volumes to facilitate structured meshing strategy to be discussed.

(1). Internal piston discharge holes: to prevent the requirement to place the feature upon a meshing interface and dynamic region, they could be relocated upon the adjacent bore surface as indicated.

(2). Tyre body-seals: indicated in yellow the component could be treated as a raised region to reduce the requirement to model the confined mechanism due to licence limitations. This will also provide limited compromise through a relatively representative entry region and discharge path for internal flow.

(3/4). Internal Spring/Rod: These features were defeatured, assumed to have limited influence upon outlet regions with flow primarily driven by strong pressure gradients, their induced losses acknowledged but removed at this time.

(5). Check-valve mechanisms: Although the features could be dynamically modelled, their operation is less-significant for the study, assumed as idealised changes in boundary inlet to outlet type later discussed.

(6). Tyre deformation: The multi-directional expansion, non-linear rubber material properties and specific deformation pattern surrounding the tyre walls are complex to model. Considered to add limited value, primarily to act as a large piston. Thus, a vertical cylinder defined at an equivalent scaled size to deliver an equivalent stroke rate for the provided flow could be implemented.

3.2. Dynamic meshing

The developed model could now be discretised using the integrated Ansys meshing module. This enables a suite of meshing tools to utilise the previously highlighted edges in fluid zones to assign meshing controls. Namely, the application of edge, face, and body sizing in conjunction with both structured sweep and couple compatibility regions of tetrahedral elements to maintain high mesh quality could facilitate the dynamics of the domain. For the study, a development mesh could be utilised opting for a nominal mesh size of 5 mm across the core areas and 10mm in zones within dynamic regions. This is to compromise within the Ansys licence capacity and trade-off time step size to across relatively extended transient simulations ~2-4 s at 0.005 s. The upper and lower region of the system occupy separate volumes and utilise cylindrical structures comprising of a square face surrounded by an anulus of sections. This can be recognised to maintain quality in central regions particularly to the aspect ratio.

At this stage, due to the meshing constraints associated with the licence, limited traditional inflation and refinement methods could be implemented. Thus, a prospective mesh sensitivity would only indicate that further refinement is required. Additionally, due to the implicit layering approach, to maintain layers successful operation and avoid negative cell volumes, the time step would also need to be adjusted. Thus, further refinement within the licence bounds would likely add limited improvement upon the current grid, whilst inducing a significant jump in computation through element size and the number of total time steps.

The internal motion of the domain could be facilitated using dynamic meshing. Ansys as a platform provides three available methods, including smoothing, layering and remeshing. Upon careful review, the layering method was considered to provide the best functionality for application. The method operates through the construction and destruction of individual layers of the domain using the user defined relative height split and collapse factors defined at 0.4 and 0.2 respectively. This not only provides an advantage of only remeshing the direct group of cells influenced but more importantly ensures the cell quality initially established is maintained. In the case the other methods were used, it would be more difficult to maintain control, whilst the additional computation requirements arguably are only just for multi-dimensional rotations and translations, at this stage not included within the model.

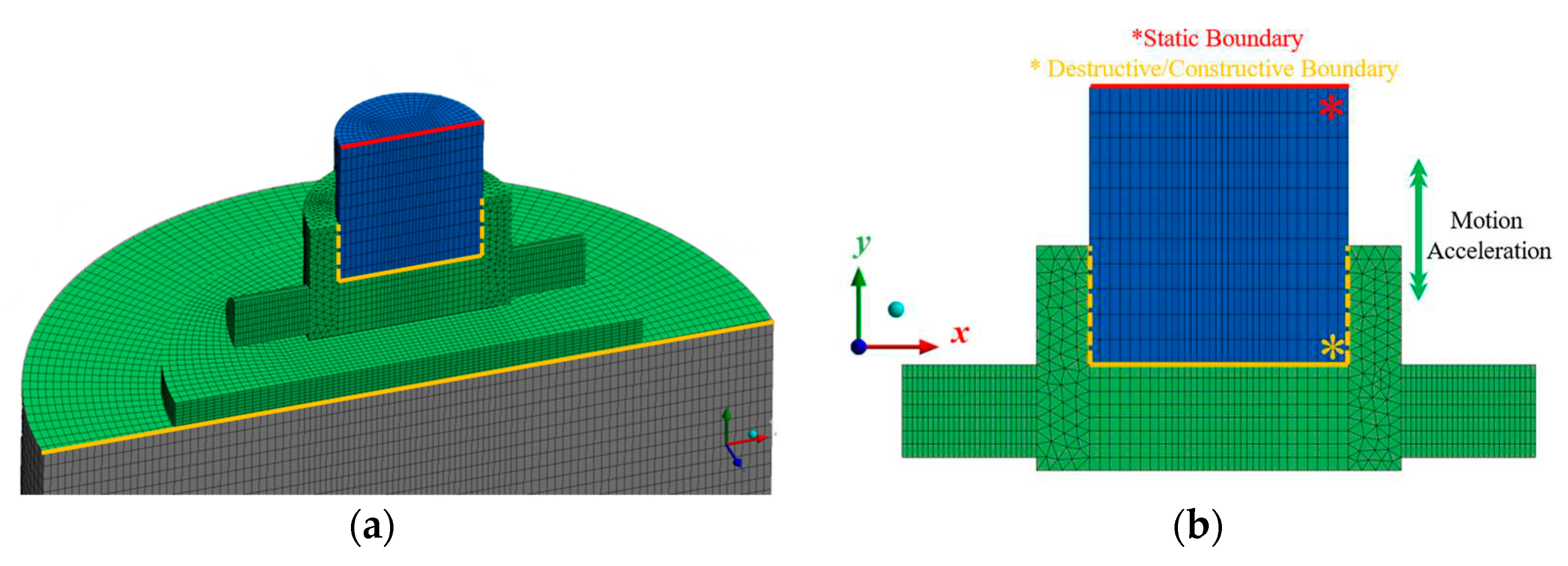
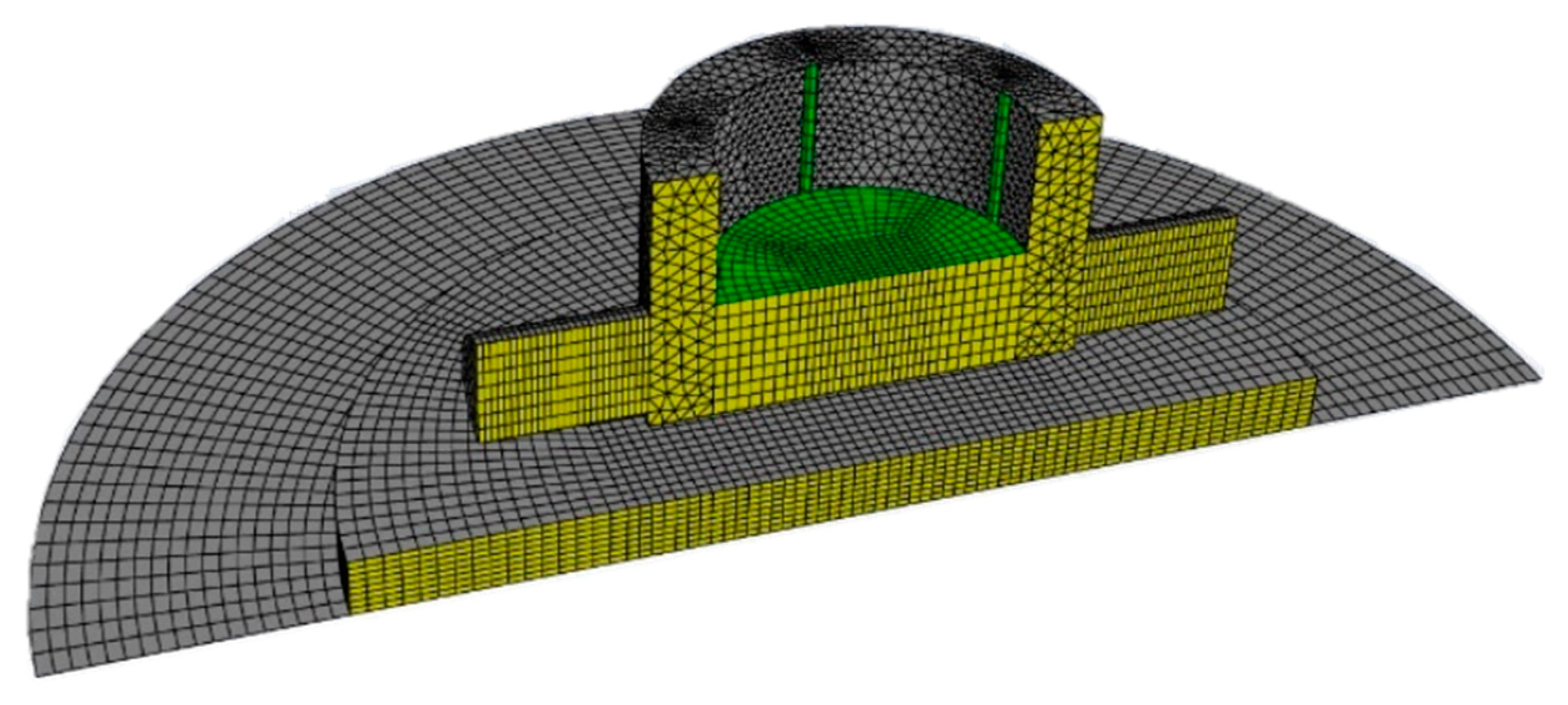
In application, Figure 9 (a)(b) illustrate the dynamic zones established to describe the operation in the upper chamber. In this case the relative power and reset stroke of the piston could be defined by setting the piston as static, depicted in blue. The upper piston surface could be defined as static and the foot set as a Rigid Body (RB) dynamic zone with established solution stabilization and meshing options set for the adjacent boundary indicated in orange. This could be defined in parallel for the lower region upon the lower ‘roof’ of the tyre. The orange and green regions could then be set in RB motion through the application of a designed UDF profile. This enables the internal tyre and piston region to extend and contract to represent the changes in the domain. This required the definition of over 60 dynamic zones including interiors, boundaries, and volumes as depicted in Figure 10.

3.3. Motion methodology

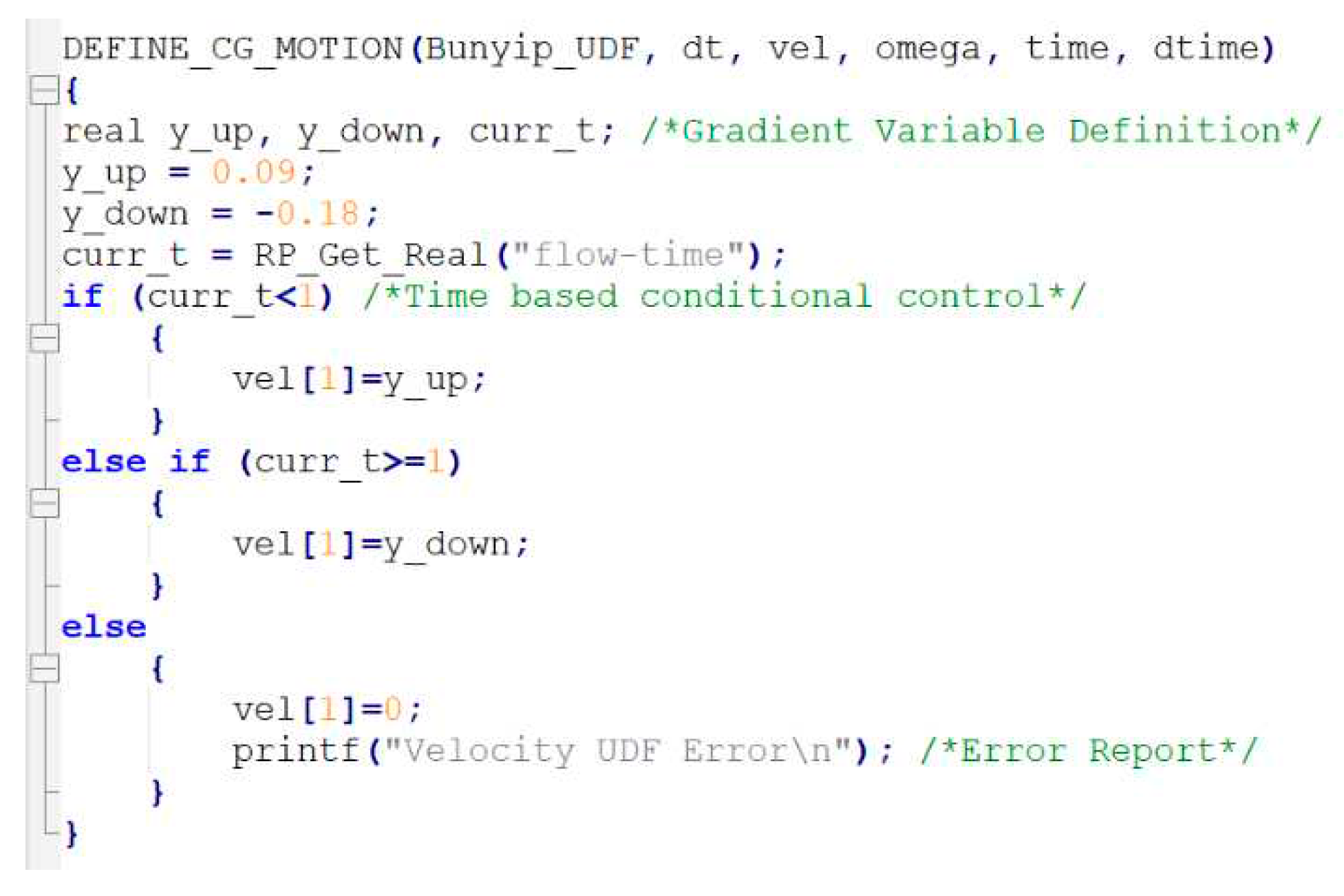
To integrate motion within the domain, the system has two potential options: UDF profiles to determine position based upon time, then, the powerful 6DOF multibody physics solver. Naturally, both methods provide advantages and disadvantages. UDF functionality provides additional computational complexity and the ability for the user to develop bespoke features within the model to enhance its operation. For this application, the ‘DEFINE_CG_MOTION’ function could be implemented to initialise a dynamically set cell velocity across the thread (face ID) defined using the C code , shared in Appendix A.1.

The UDF methods provide an opportunity to utilise the available manufacturer data and video footage to investigate and setup an associated time and position-based profile. The simpler of the two methods can then be compiled into machine code for definition at each time-step. One primary advantage of this method being the simplification of the internal physics to avoid making the specific assumptions in calculation, using data based upon real-world characteristics that could be known and measured in real-world applications. Although by definition a more simplified approach, this has the potential to improve validation and significantly reduces the calculation required. The limitation however is the capacity to directly isolate operational parameters such as the stiffness or components of pressure to directly investigate their influence. This will now be limited to a defined cycle rate, which can be expected to act as a function of flow rate, supply, delivery and drive pressure. Thus, the boundaries will also be required to be fixed at the determined pressure, then, use inlets/outlets to act upon domain changes as opposed to the external pressure driving the system.

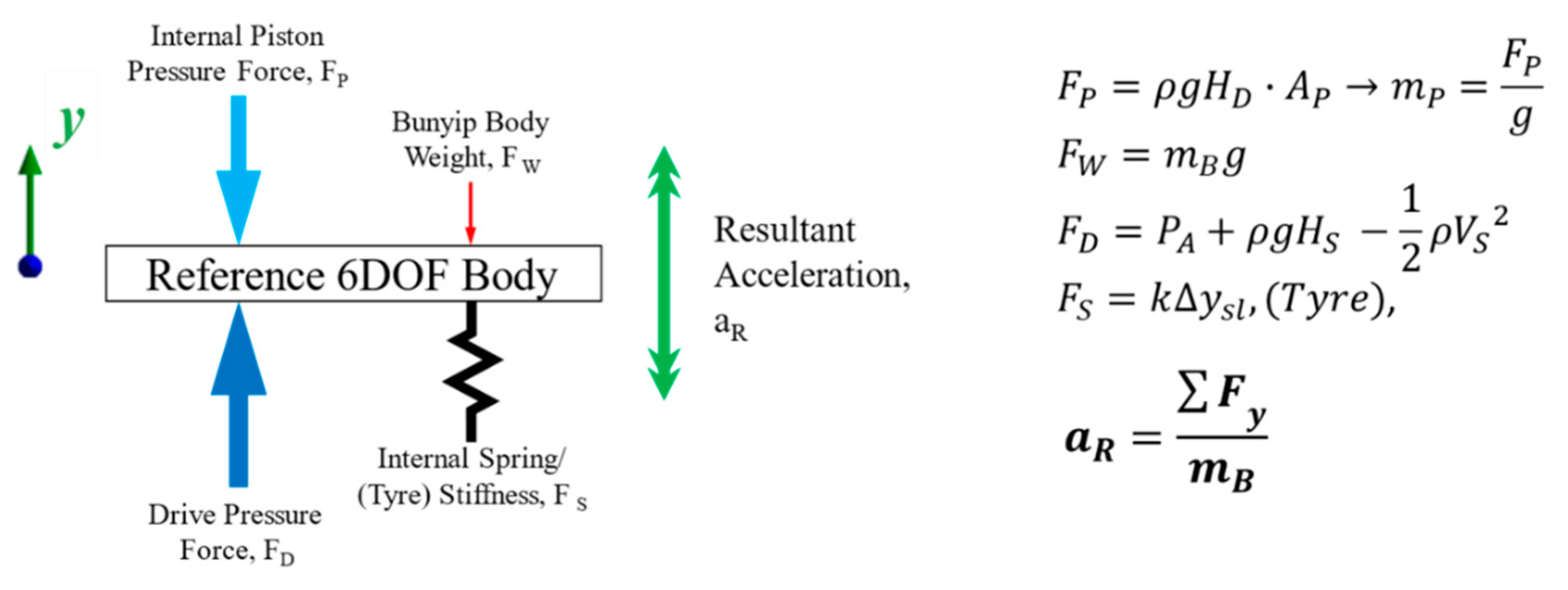
The second method uses the multi-body physics solver with capacity to define the internal physics through the individual definition of mas and stiffness properties of the system. For the Bunyip application, a free-body diagram could be illustrated in Figure 11 to introduce the primary forces considered within operation. For the given case under study, the internal pressure upon the piston could be calculated as an equivalent hydrostatic pressure ‘mass’ and defined through the 6DOF properties in addition to the Bunyip Body mass of 5.6 kg. This could be directly applied during the power stroke and removed using a UDF during the reset phase (Ansys, 2013). In addition, properties could also be defined for internal spring stiffness could be implemented at 700 N/m across a constrained stroke length of 90 mm. At this time, negating the tyre stiffness due to its non-linear properties and multi-dimensional characteristics and additional losses due to friction also. The solver enables the calculation of internal equilibrium equations incident upon the internal flow forces at the base volume of the tyre, referenced centrally to the upper tyre surface. The result, similarly, to the UDF, mapped across the domain relative to the surrounding green cell zones, as illustrated in Figure 9 before.

Time-based velocity UDF has been adopted in this analysis. The 6DOF solver for the limited mesh proved to be unstable, accelerating rapidly, uncharacteristic of the pump. This could significantly influence validation and in retrospect, with very limited presence within research application, it is quite likely the gap previously discussed for motion is primarily developed within the simplified UDF profile definition.

3.4. Boundary method and automation

The domain can now be informed with the appropriate boundary conditions across several inlets and outlets for the operational cycle, as shown in Figure 12. This includes the application of both traditional pressure inlet/outlets and vent types to provide potential functionality to define losses across components such as the check-valves. The associated pressures could be calculated using the standard Bernoulli equation assuming each source of water is static and at atmospheric pressure. Then, calculate the hydrostatic head pressures relative to the delivery valve, demonstrated for an example delivery pressure condition below.

The pressures and outlets for a typical example case are presented in Table 2 at supply head at 4 m, delivery up to 35 m and defined inlet/outlet conditions to observe cycle time dependant flow rates. The ideal represent of the energy balance is Bernolli’s equation:

P_{A} + \frac{1}{2} ρ V^{2} + ρ g h = Constant

(4)

P_{Delivery} = P_{A} + 1000 \cdot 9.81 \cdot 35 = P_{A} + 343.4 (i n k Pa)

(5)

Due to the dynamic nature of the system and incorporation of check-valves and the multiple exhausts, the domain is coupled to integrate the boundary conditions and synchronise the cycle in relation to the defined motion. Again, two options remain for application.

Scheme file methods enable the time-based sequencing of model inputs using the integrated Text-User-Interface (TUI) commands. These definitions make use of conditional sequencing to determine the current phase of the cycle and adjust the boundaries accordingly as depicted in an example script provided in Appendix A.2. The file can be constructed and read to define a new command in the ‘.scm’ format, providing full access to edit and manipulate internal boundary types, values and 6DOF properties. It could be recognised that their limitation appeared to be their dependency upon ‘RP-variables’, such as standard global variables or constants, such as, flowtime and ‘2’ for example. Consequently, the desire to utilise user-defined reports to inform decisions using mesh velocity and co-ordinates did not appear to be possible with this method. As the 6DOF previously discussed was unsuited to stable operation on a limited mesh domain, the scheme file application provides desired flexibility for time-based UDF operation. Thus, could be implemented directly within the model.

When investigating alternative methods for application with time independent solvers such as the 6DOF, an alternative control script could be developed again using the powerful UDF capacity. This could be facilitated utilising the DEFINE_ADJUST and DEFINE_PROFILE functions to directly access the solver to quantify the co-ordinates and velocity of the hooked tyre boundary. Each quantity could be calculated using a surface average for each face in the domain (grid) thread and used again in place with a sequence of conditional statements to define the pump phase and associated pressures at each boundary described in Appendix A.3.

3.5. Pre-processing and modelling

Previous research could be used to identify the most appropriate models to implement. The licence again limits the local processing to 4 cores, activated in parallel with double precision. The pumping system is inherently turbulent, exhibiting flow mixing and chaotic motion due to the sharp changes in pressure gradients and flow direction throughout the geometry. For this reason, the study will employ an appropriate turbulence model. These equations solve the transient 3D incompressible Navier-Stokes equations for the developed model to measure the continuity of various forms within the model. For example, the conservation of momentum and turbulent kinetic energy and dissipation. There is no best fit for selecting the appropriate model and could be best informed through the review of active researchers in the field, previously adopting the use of k-ε models, described to have improved computational speed and mesh sensitivity relative to the default k-ω model [15]. In previously discussed literature, the Realizable model could be recognised to provide strong validation in similar work [10,12]. The basic equations used in computation stated are summarised below, but given in more detail in [15] and ANSYS User Guide [14]:

Turbulent kinetic energy:

\frac{\partial}{\partial t} (ρ k) + \frac{\partial}{\partial x_{j}} (ρ k u_{j}) = \frac{\partial}{\partial x_{j}} ((μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{j}}) + G_{k} + G_{b} - ρ ε

(6)

Turbulent dissipation rate:

\frac{\partial}{\partial t} (ρ ε) + \frac{\partial}{\partial x_{j}} (ρ ε u_{j}) = \frac{\partial}{\partial x_{j}} ((μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{j}}) + ρ C_{1} S ε - ρ C_{2} \frac{ε^{2}}{k + \sqrt{ν ε}} + C_{1 ε} \frac{ε}{k} C_{3 ε} G_{b}

(7)

where

C_{1} = \max [0.43, \frac{χ}{χ + 5}]

χ = S \frac{k}{ε}

S = \sqrt{2 S_{i j}^{2}}

S_{i j} = \frac{1}{2} (\frac{\partial u_{j}}{\partial x_{i}} + \frac{\partial u_{i}}{\partial x_{j}})

, and

μ_{t} = ρ C_{μ} \frac{k^{2}}{ε}

. The default values for model constants are set in Ansys-Fluent as:

C_{1 ε} = 1.44

C_{3 ε} = 1.92

C_{μ} = 0.09

σ_{ε} = 1.3

and

σ_{k} = 1 .

As previously discussed in the meshing strategy, the model developed is not only constrained by the Ansys cell limit but also the extended nature of a relatively long physical simulation time and short time steps of 0.005 s. To resolve near wall treatment, the model implements standard wall functions. If advanced computation and a full academic licence were to be available, further refinement methods including inflation, local refinements, and enhanced wall functions could be used to better resolve near-wall flow. As the model doesn’t include any associated heat transfer or other models, for an initial development method and the default option could be considered sufficient, advised for a broad range of applications. Ansys guidance indicates that it can be utilised when the first node cannot be placed within the viscous sub-layer developed [14].

The coupling scheme used for the pressure-based transient calculations selected the PISO algorithm, typically advised for fully turbulent flow, and described to maintain stability with larger time-steps, relevant when simulating extended physical time associated with a complete cycle (See Ansys guide, Section 26.3.1 [14]). The discretization method could be set as Green-Gauss Node based, calculating the scalar values and gradients using the arithmetic average of the element values surrounding each node. Additionally avoiding the default least squares method observed to require additional calculation when implemented in parallel with PISO (See Ansys guide, Section 18.3.3 [14]).

4. Results

To investigate the model developed, a series of cases could be identified through applied video analysis of Physical Testing (PT) models and installed Bunyip systems. The key operational parameter inputs are listed in Table 3, operating at a delivery flow rate between 5-6 l/s to investigate varied head ratios influence upon performance of the Bunyip system, to undertake an initial parametrised review and support validation. The associated sources provided in Appendix A.4. The following Figures illustrate the operational principle through total pressure and velocity graphics to be discussed in tandem with focused post-processed depictions to aid analysis.

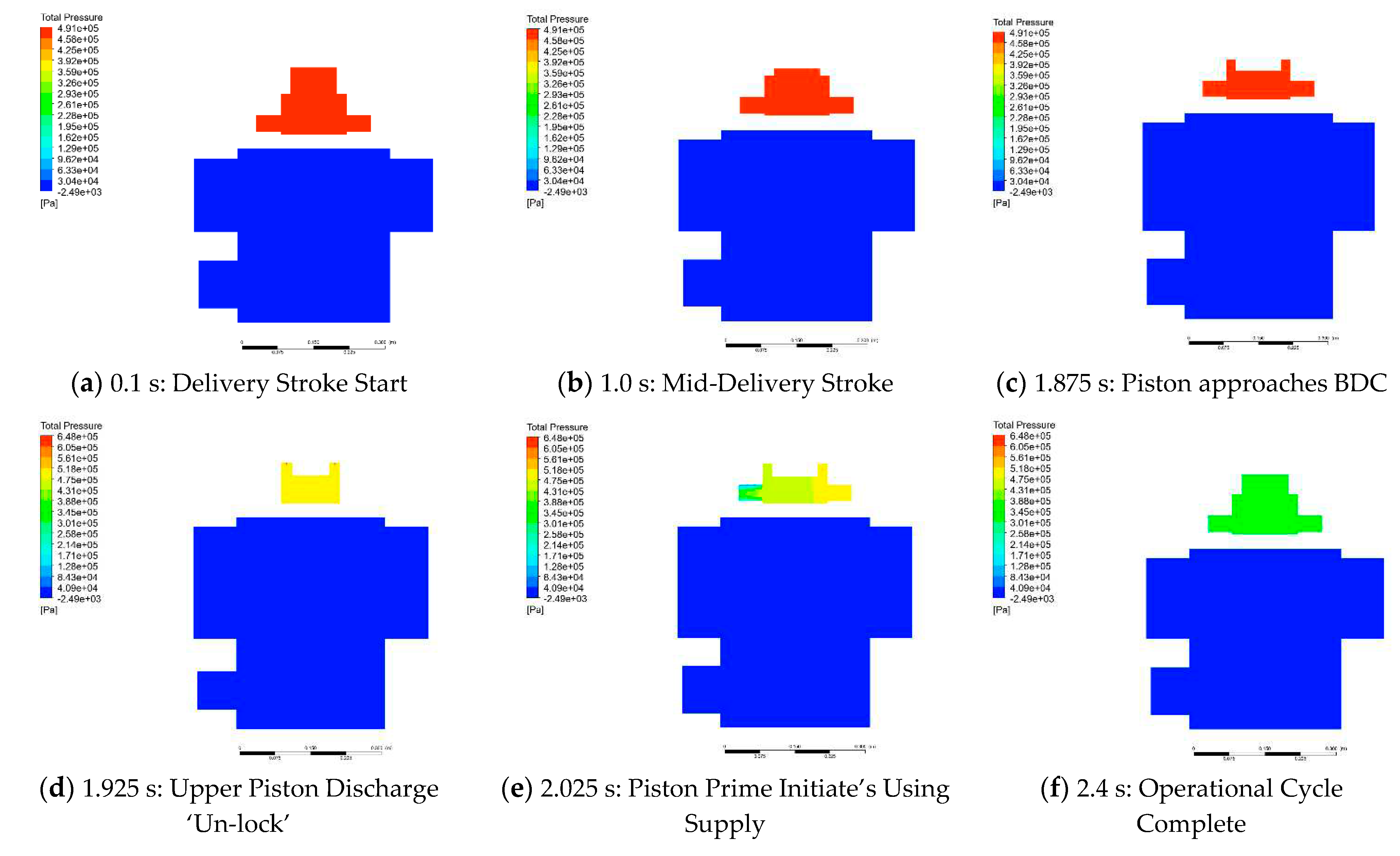
Firstly, to illustrate the ‘free’ hydro-power cycle in principle. The propagation of the total internal pressure within the domain could be plotted globally to indicate the associated values relative to the total cycle. This additionally provides an opportunity to review the initial flow mechanics alongside a series of vector and magnitude illustrations, again using the graphics to aid the internal investigation of the Bunyip mechanism. Figure 13 describes the process from motion initiation, upper piston compression and delivery, then, in (d)(e) the discharge features release the upper piston to a reduced pressure for the motion to reset.

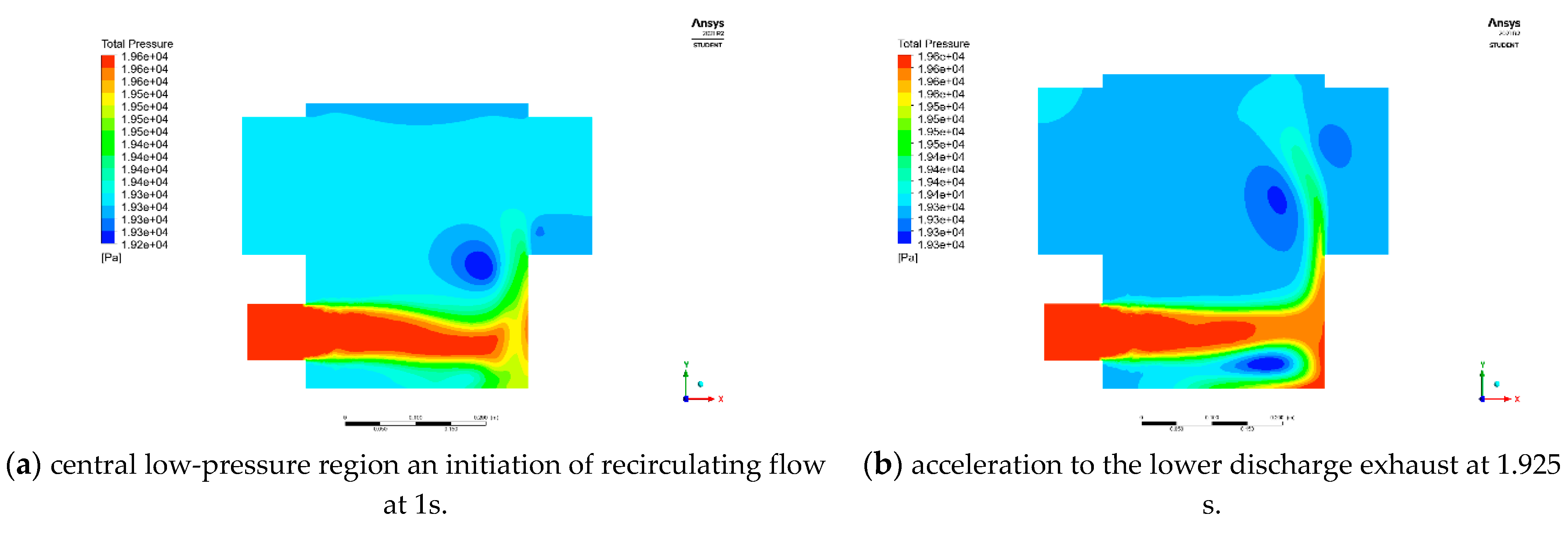
The above operational process visualisation can also be enhanced through the application of the definition of internal planes to enable enhanced visuals of the relative quantities and better illustrate the internal flow, set apart using local and global pressures and velocity scenes. In this case, better describing the rotation and mixing induced by the abrupt changes in inlet geometry in Figure 14a,b. The plots illustrating the complex dynamic nature of the chamber and the turbulent incident flow.

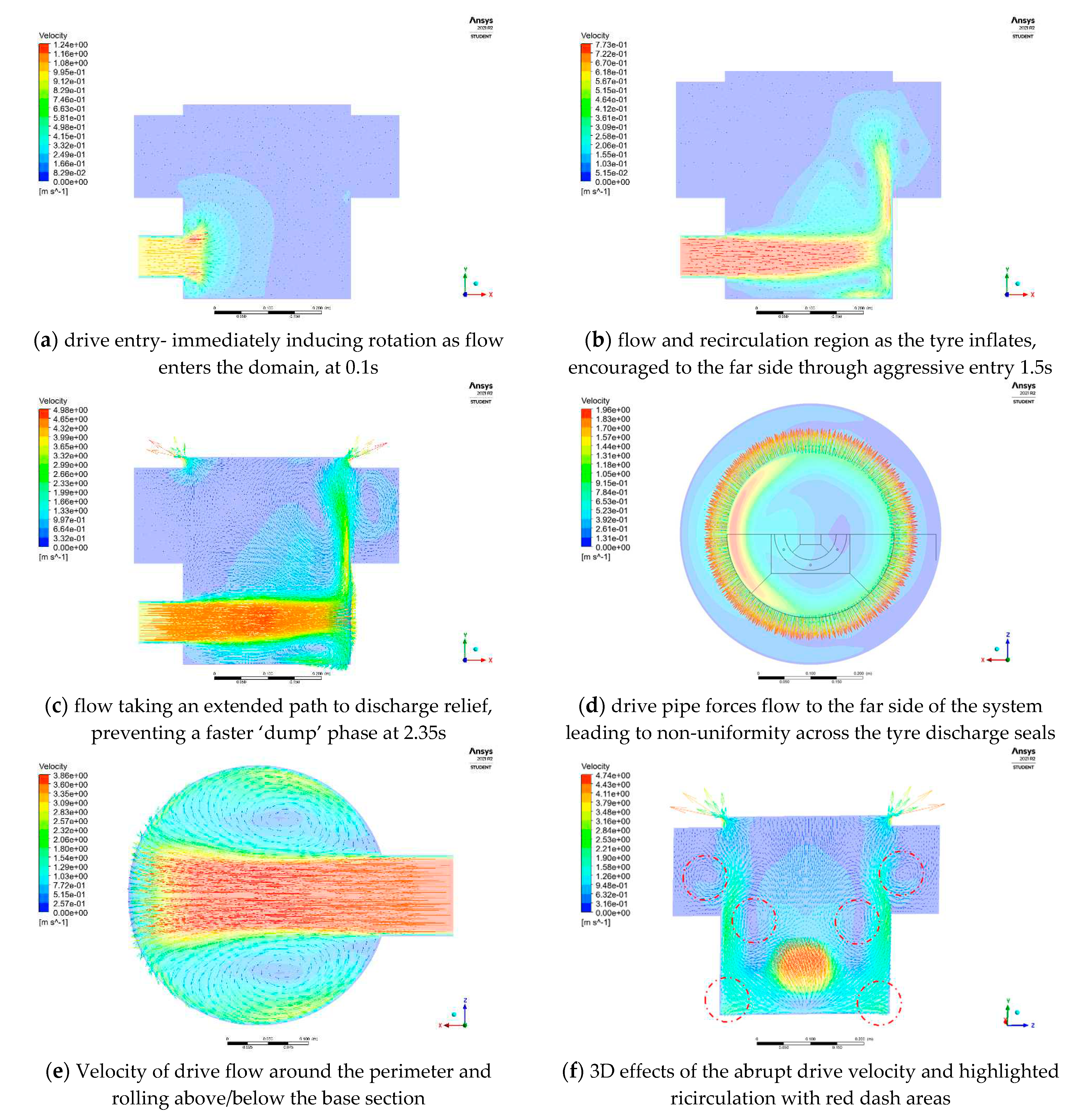
In addition to total pressure, flow velocity could also be used to illustrate the advancement and properties of flow within the volume and construct an improved picture of where energy may be lost and routes for improvement. This could be closely evaluated for the operation of the lower tyre in Figure 15. It can be recognised that the inlet flow generates a catalogue of chained rotational regions that build from entry in the base right up to the filling of the tyre and upper discharge domain. The Figures illustrate the extended path taken by flow, generally associated with greater losses. In this case, forcing the drive flow directly at the far side wall. This results in the rapid deceleration and re-direction of flow and momentum to rotate away from the wall, either rolling under the delivery flow or around and over the drive flow, mixing layers and inducing the rotational effects observed particularly in Figure 15e,f.

Similarly, to the lower system. The upper piston can also be analysed, using the velocity vector and contour plot. In this case, the flow of the piston is very predictable due to the dominant changes in static pressure to drive flow. The upper piston compression and exhaust phase could also be investigated and presented below in the delivery pattern illustrations in Figure 16.

4.1. Operational Observations

The previously conducted analysis provided valuable insight into the flow mechanics of the system in demonstrating the complete operational cycle and enhanced detail upon the dump and discharge of the upper piston. In principle the ‘free’ hydro-kinetic energy principle utilised could be successfully demonstrated across the four cases and the model validated against real-world operational data with moderate corroboration. The study can now use the numerical model and physical data to appreciate and discuss where the system excels and where it may need further development.

The created model could utilise the power of numerical tools to individually measure and monitor quantities throughout the domain. Enabling the associated flow rates at each boundary to be measured under the action of the initialized motion relative to the pump cycle period in application. Of which, the model provided reasonable agreement with the advertised capacity using the modelling method comprehensively discussed. The efficiency maintains to be as anticipated at a respectable value across the three cases, operating within the regions previously shared in the supply head values in Table 1. The initial appraisal indicated the pumps do provide significant potential, however, can be somewhat limited by their mechanism within certain flows. It is important to recognise that in this case the primary driver for the Bunyip would be the significant jump in elevation capacity relative to the HRP. Thus, as expected in the tested regions it may be the case, the HRP is potentially more efficient in the overall hydrokinetic energy transfer at moderate supply and delivery head. Though as discussed at length, performance should also consider sel-regulation amongst other factors as opposed to purely capacity.

As previously hypothesised, to manipulate the pressure amplifier and act upon the large tyre system, the Bunyip would be expected to wate a greater portion of water. Yielding a reduced Relative Delivery in contrast to a conventional HRP, delivering an extremely small 2% of the available water. For water rich regions, this may still be deemed appropriate through the ability to unlock head potential in excess of even reportedly 400m in a recently developed steel piston chamber device for application in the Philippines [20]. Incomparable to the maximum described Blake HRP at 100m, even significantly improved against conventional centrifugal fossil-fuel based pumps, unable to match the potential delivery power of a piston mechanism. Although this naturally opens many doors for operation, the high portion of waste may impede the application of the Bunyip in some regions. Thus, an advised area of research would be to better utilise the supplied water discussed shortly.

4.2. Data Validation

When considering the method to implement the model for validation and analysis. The model could be defined through a defined user input of a known Physical Test cycle-period, directly related to the flow rate and internal pressure of the system. In order to begin investigating a series of initial cases and demonstrating the model’s suitability for analysis, four cases could be extracted from by Bunyip Water Pump’s (Appendix A.4). The content focuses upon installations delivered, sharing an insight into operational parameters, and achieved outputs, paired with the fundamental values to validate the modelling method. A series of four cases could be examined for the PA-13, sharing similar input flow rates to aim to isolate the flow rate and investigate the head ratio’s influence upon the associated performance metrics. Each case could be modelled as per the video parameters and the bespoke UDF files developed for the time-based cycle to facilitate the motion relative to the observed cycle period and established boundary pressures to enable the compilation of a complete summary in Table 4.

Initially focusing upon validation, several values can be contrasted between Physical Testing (PT) data and the Numerical Model (NM). This enabled the fundamental components to be corroborated in addition to the enhanced break down of components in the NM case to appraise the model suitability for application. The cases to investigate operated within the bounds of 5-6 l/s drive supply with varied supply between 1.2-2.2 m. The system maintained to operate within an appropriate magnitude and demonstrate fluctuation both above and below the physical value, additionally feeding into the operational efficiency. Upon installation, certain parameters will be fixed, however, the model additionally enables the individual case stroke length to be tailored to the application and each case assumed to have a standard Ø= 98 mm design. Naturally, in application, the spacers upon the central rod can be used to adapt the system stroke length for its application. This could be assumed at 90mm from the scaled geometry; thus, the PT devices could be expected to induce a degree off variation. Thus, a good indication of suitable validation is the bi-directional variance for similar cases in 2 and 3. This indicates the model values attained still provide a reasonable indicator for the anticipated output capacity. Although, it could be noted that there is potential for both under and overestimates. Due to the enhanced lifting capacity, even a small variance in output paired with can quickly develop into notable variance in the efficiency, emphasised further within the Bunyip. The variance in both output and efficiency remains consistently above or below each PT result and should be considered when extracting data. The model is suitable for the initial analysis and in future should consider further investigation into cases that each system parameter is observed.

4.3. Parametric Analysis

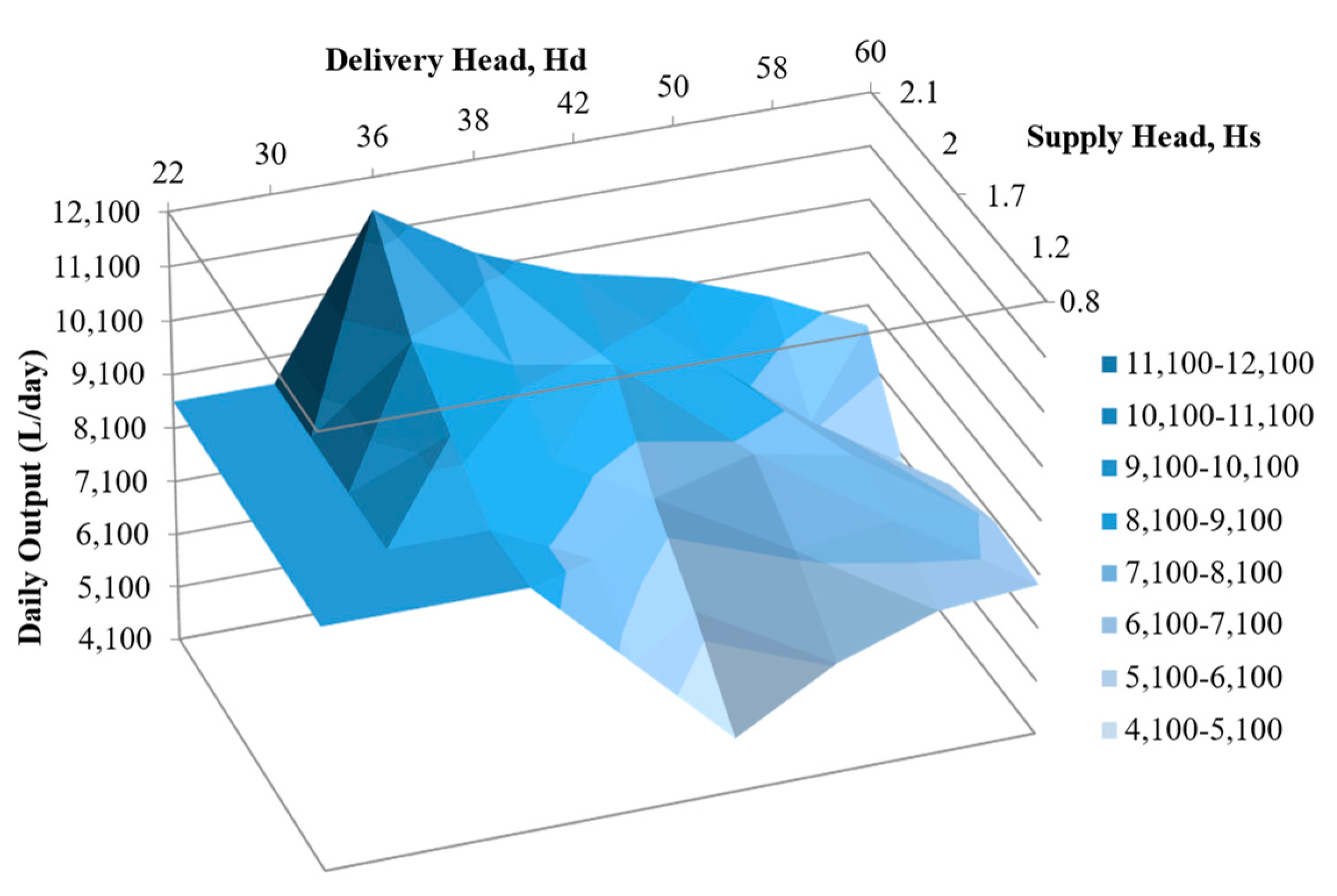
The previously discussed series of real-world systems provide the opportunity to observe the influence of supply and delivery performance. The data collected and calculated using the numerical model could be used to an initial three-dimensional surface plot in Figure 17. This visual representation uses the analysed cases to begin building an indication to how the supply and delivery head in combination may influence the daily output and proportional operational efficiency. Importantly noting that region such as high delivery and high supply head have not been included, thus, assigned an average capacity of 8600 l/day within the lower delivery head regions to illustrate the surface floor average. In many of the cases away from the data point tested, it is recommended to adopt a smaller bunyip PA-8, thus, generally cases were not available in low-low systems either. At the given supply rate, the trend that within the current data set indicates that as expected, with an increased supply head, the Bunyip can access improved daily output. Meanwhile, the ability to connect the two variables again indicates that for the typical 2 m average tested, the greatest accessible performance capacity would be at ~32 m delivery.

It was also recognised that the elevated lifting capacity attained through the positive displacement pump could in fact impede performance at low delivery heads. In this region, the ‘lighter’ pressure upon the conventional HRP delivery valve enables a rapid delivery of increased fractions of delivery. Conversely, the extended travel of the piston mechanism and two stroke process spears to reach a terminal speed, whereby the linear delivery cannot benefit from similar operation. It should also be recognised that the cases available for analysis did not operate at a greater head than 60 m. Thus, expansion to include additional data would enable Figure 20 to become a more powerful tool for parametric assessment. This could be achieved using the implementation of the current or further advanced tool to strategically identify a clear performance ‘surface’ to inform installation and identify the optimal range for operation at varied supply rates available to end users.

5. Conclusion

The results highlight several key findings and potential areas for further research related to the Bunyip micro hydro-power system. The research began with a comprehensive literature review, which provided valuable insights into conventional hydro-ram pump (HRP) systems, their limitations, and micro hydro-power performance indicators. The project aimed to explore the potential of the Bunyip system as a disruptive technology in the hydro-powered pumping field. The initial manufacturer data appraisal revealed that the Bunyip system had significant lifting potential, but its relative delivery was lower than that of the conventional HRP. Despite this limitation, the Bunyip mechanism demonstrated superior reliability and consistency compared to traditional HRPs. The research involved creating a detailed and advanced dynamic model, which required new modelling and programming skills. The use of user-defined functions (UDFs) facilitated a good degree of validation for the initial analysis and provided a clear pathway for future research and model development.

The study acknowledges that the Bunyip system cannot completely replace the HRP, as the latter remains more operationally efficient under moderate supply and moderate delivery conditions. However, the Bunyip's enhanced delivery head capacity and operation under reduced supply head make it a valuable alternative in the field dominated by traditional HRPs. The conclusion also highlights that further research is needed to fully validate a 6DOF (6 degrees of freedom) model capable of isolating each variable within the Bunyip system. The system shows promise in lifting water to significantly greater elevations, surpassing typical HRPs and fossil-fuel centrifugal systems. However, this increased capacity comes at the cost of reduced relative delivery, making it less suitable for water-scarce regions. The results indicate that a smaller diameter of the pressure chamber and a higher supply head lead to higher pressure, achieving a target head of 3 m with 15% efficiency and a flowrate of 11.82 l/min.

To better capture and utilize the lower portion of exhaust flow during the dump phase, submerging this region can help dissipate discharge energy more efficiently. Also, capturing the trapped energy in the wasted water by using a combined large diaphragm valve. This could chain the energy from the initial Bunyip pump cycle into another renewable system for delivering elevated pressure to a secondary location. The conclusion emphasizes that the Bunyip system has the potential to elevate micro hydro-powered systems and calls for further focused research to optimize its design and improve its water delivery capacity.

Author Contributions

Conceptualization, M.A.; methodology, S.B. and M.A.; software, S.B.; validation, S.B.; formal analysis, S.B.; resources, S.B. and M.A.; data curation, M.A. and S.B.; writing—original draft preparation, S.B. and M.A.; writing—review and editing, M.A.; visualization, M.A.; supervision, M.A.; project administration, M.A.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data was created.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

Notation	Description
$g$	Acceleration due to gravity [ $m \cdot s^{- 2}$ ]
$σ_{ε}$	Constant for turbulent energy dissipation rate, 1.2
$σ_{k}$	Constant for turbulent kinetic energy, 1.0
$C_{1}, C_{2}, C_{3}$	Constants in realizable k- ε turbulence model
$ρ$	Density of the fluid [ $kg \cdot s^{- 3}$ ]
$μ, μ_{t}$	Dynamic viscosity, turbulent [ $Pa \cdot s^{- 1}$ ]
$η_{S}$	Operational Efficiency [%]
$G_{b}$	Turbulence kinetic energy, generated due to buoyancy [ $Pa \cdot s^{- 1}$ ]
$G_{k}$	Turbulence kinetic energy, generated due to mean velocity gradient [ $Pa \cdot s^{- 1}$ ]
$H$	Height relative to delivery valve [ $m$ ]
$i, j$	Tensor indices
$t$	Time [ $s$ ]
$ε$	Turbulent energy dissipation rate per unit mass [ $m^{2} \cdot s^{- 3}]$
$k$	Turbulent kinetic energy [ $m^{2} \cdot s^{- 2}$ ]
$K$	Internal spring stiffness [ $N \cdot s^{- 1}]$
$u, ν$ , V	Velocity: x, y, mean flow [ $m \cdot s^{- 1}]$
$p$	Pressure [Pa]
Q	Volumetric flow rate [ $l \cdot s^{- 1}$ ]
$S_{c}$	Standard capacity [ $m \cdot s^{- 2}$ ]
$R_{d}$	Relative delivery
$F$	Force [ $N$ ]
$A$	Area [ $m^{2}]$
$a_{R}$	Resultant acceleration [ $m \cdot s^{- 2}$ ]
$y_{s l}$	Bunyip stroke length [ $m$ ]
$m$	Mass [ $kg$ ]

Appendix A

Appendix A.1. User Defined Function for linear rise-fall velocity profile definition

Appendix A.2. Boundary Manipulation Scheme Functions

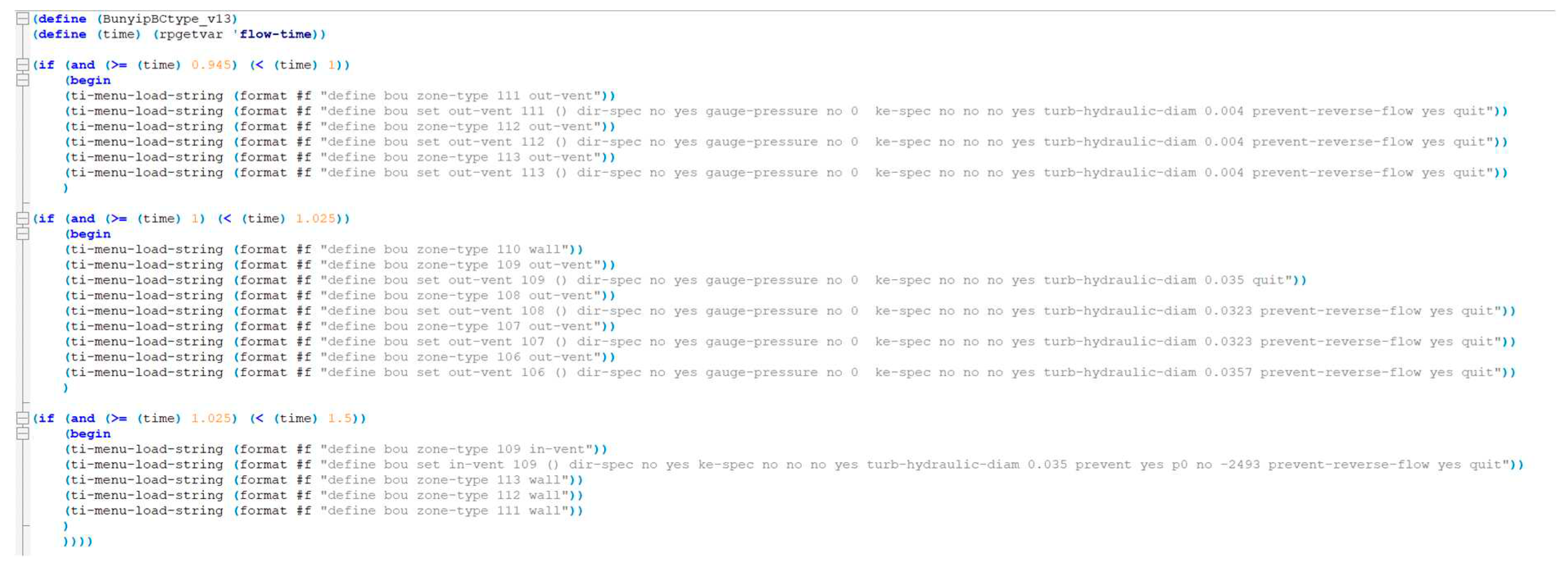
Appendix A.3. Bunyip Automation Script Monitoring Tyre boundary ID To Set Inlet/Outlet profiles

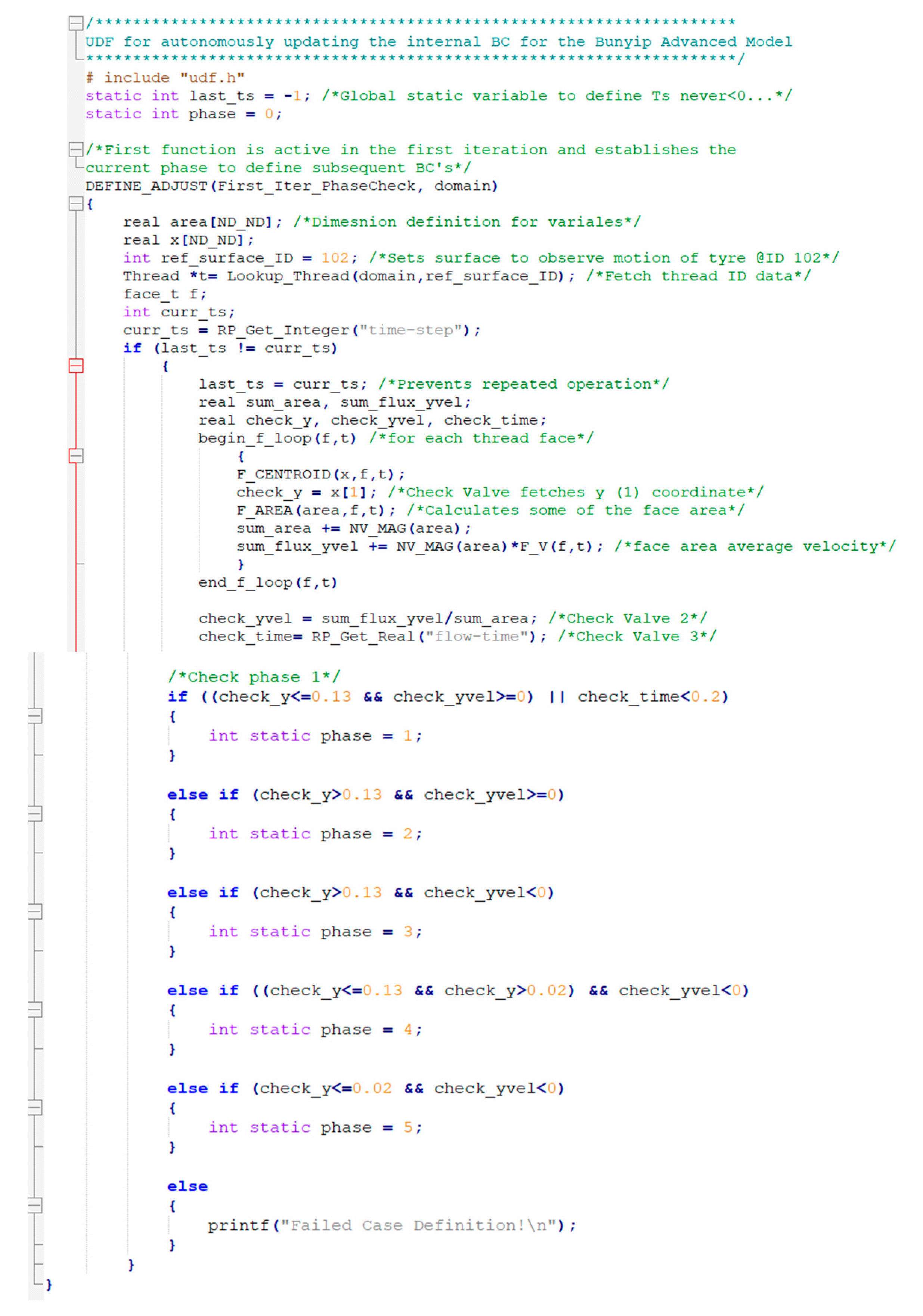
Appendix A.4. Bunyip PA-13 Operational Case Information

Details: Operational with a 98 mm piston without water ballast devices or drive supply connections to the supply piston. The device remains in the conventional position (no submerged tyre valves or out of water installations).

Case 1 - Bunyip PA13 Pump at Misty Mountain Biggs road Nth QLD, Australia. Available at <(86) Bunyip PA13 Pump at Misty Mountain Biggs road Nth QLD, Australia. - YouTube> [14/04/22]

Case 2/ Case 3 - Bunyip Pump(s) on Thiaki Creek, available at < (86) Second Bunyip Pump on Thiaki Creek - YouTube>[14/04/22]

Case 4 - Tableland Bunyip, available at <(86) Another Tableland happy Bunyip - YouTube> [14/04/22]

References

United Nations What Is Renewable Energy? Available online: https://www.un.org/en/climatechange/what-is-renewable-energy (accessed on 2 July 2023).
IEA The Global Energy Crisis Pushed Fossil Fuel Consumption Subsidies to an All-Time High in 2022. Available online: https://www.iea.org/commentaries/the-global-energy-crisis-pushed-fossil-fuel-consumption-subsidies-to-an-all-time-high-in-2022 (accessed on 2 July 2023).
IRENA.; CPI Global Landscape of Renewable Energy Finance 2023.
Karekezi, S.; Kimani, J.; Wambille, A.; Balla, P.; Magessa, F.; Kithyoma, W.; Ochieng, X. The Potential Contribution of Non-Electrical Renewable Energy Technologies (RETs) to Poverty Reduction in East Africa; AFREPREN/FWD: Nairobi, Kenya, 2005. [Google Scholar]
Roberts, A.; Thomas, B.; Sewell, P.; Hoare, E. Generating Renewable Power from Water Hammer Pressure Surges. Renewable Energy 2019, 134, 1392–1399. [Google Scholar] [CrossRef]
Intriago Zambrano, J.C.; Michavila, J.; Arenas Pinilla, E.; Diehl, J.C.; Ertsen, M.W. Water Lifting Water: A Comprehensive Spatiotemporal Review on the Hydro-Powered Water Pumping Technologies. Water 2019, 11, 1677. [Google Scholar] [CrossRef]
Young, B.W. Design of Hydraulic Ram Pump Systems. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy 1995, 209, 313–322. [Google Scholar] [CrossRef]
Porta’s Engineering Home | Bunyip Water Pumps. Available online: https://www.bunyipwaterpumps.com/ (accessed on 16 July 2023).
Guo, X.; Li, J.; Yang, K.; Fu, H.; Wang, T.; Guo, Y.; Xia, Q.; Huang, W. Optimal Design and Performance Analysis of Hydraulic Ram Pump System. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy 2018, 232, 841–855. [Google Scholar] [CrossRef]
Li, J.; Yang, K.; Guo, X.; Huang, W.; Wang, T.; Guo, Y.; Fu, H. Structural Design and Parameter Optimization on a Waste Valve for Hydraulic Ram Pumps. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy 2021, 235, 747–765. [Google Scholar] [CrossRef]
Harith, M.N.; Bakar, R.A.; Ramasamy, D.; Quanjin, M. A Significant Effect on Flow Analysis & Simulation Study of Improve Design Hydraulic Pump. IOP Conf. Ser.: Mater. Sci. Eng. 2017, 257, 012076. [Google Scholar] [CrossRef]
Harith, M.N.; Bakar, R.A.; Ramasamy, D.; Kardigama, K.; Quanjin, M. A Study of Waste and Delivery Valve Design Modification to the Pump Performance. IOP Conf. Ser.: Mater. Sci. Eng. 2018, 342, 012090. [Google Scholar] [CrossRef]
Rybdylova, O.; Al Qubeissi, M.; Braun, M.; Crua, C.; Manin, J.; Pickett, L.M.; Sercey, G. de; Sazhina, E.M.; Sazhin, S.S.; Heikal, M. A Model for Droplet Heating and Its Implementation into ANSYS Fluent. International Communications in Heat and Mass Transfer 2016. [Google Scholar] [CrossRef]
ANSYS, Inc. Ansys® 2022.
Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics - A Practical Approach; Butterworth-Heinemann, 2008. [Google Scholar]
Porta, B.; Glockemann, R.; Beard, S. Bunyip vs. RAM Comparison 2021.
Maratos, D.F. Technical Feasibility of Wavepower for Seawater Desalination Using the Hydro-Ram (Hydram). Desalination 2003, 153, 287–293. [Google Scholar] [CrossRef]
Yussupov, Z.; Yakovlev, A.; Sarkynov, Y.; Zulpykharov, B.; Nietalieva, A. Results of the Study of the Hydraulic Ram Technology of Water Lifting from Watercourses. International Journal of Engineering Science 2022, 177, 103713. [Google Scholar] [CrossRef]
Inthachot, M.; Saehaeng, S.; Max, J.F.J.; Müller, J.; Spreer, W. Hydraulic Ram Pumps for Irrigation in Northern Thailand. Agriculture and Agricultural Science Procedia 2015, 5, 107–114. [Google Scholar] [CrossRef]
Glockemann, R.; Beard, S. Opportunities to Improve the Bunyip System 2022.
Asvapoositkul, W.; Nimitpaitoon, T.; Rattanasuwan, S.; Manakitsirisuthi, P. The Use of Hydraulic Ram Pump for Increasing Pump Head-technical Feasibility. Engineering Reports 2021, 3. [Google Scholar] [CrossRef]
Asvapoositkul, W.; Juruta, J.; Tabtimhin, N.; Limpongsa, Y. Determination of Hydraulic Ram Pump Performance: Experimental Results. Advances in Civil Engineering 2019, 2019, 1–11. [Google Scholar] [CrossRef]
Fatahi-Alkouhi, R.; Lashkar-Ara, B. Experimental Evaluation of Effective Parameters on Characteristic Curves of Hydraulic Ram-Pumps. Scientia Iranica 2017, 0, 0–0. [Google Scholar] [CrossRef]
Blake’s Hydram The Blake Hydram Water Pump - Self Powered - No Fuel - None Polluting. Available online: https://blakeshydram.co.uk/ (accessed on 16 July 2023).
Papa Pump Papa Multi-Pump Systems 2017.

Figure 1. Conventional hydraulic ramp pump (HRP) and associated system diagram, inferred from [8,16] with permission.

Figure 2. Alternative Bunyip system annotated arrangement diagram (a) and photograph (b), inferred from [8] with permission from [16].

Figure 3. Bunyip operational process diagram, inferred from [8] with permission from [16].

Figure 7. Volume of interest modelled in Ansys Space claim, annotated with discussed features.

Figure 8. Illustration of the development mesh employed within the study at 5 mm nominal, 10 mm dynamic.

Figure 9. Illustration of dynamic zone setup. Green regions depicting Rigid Body Motion, Blue active dynamic layering in the upper piston and Grey the interface between the static tyre/base. .

Figure 10. Ansys Fluent dynamic zone mesh preview using default colours.

Figure 11. Free-body diagram and determination of 6DOF properties.

Figure 12. Bunyip named selection annotation for boundary condition definition.

Figure 13. Illustration of Bunyip cycle internal total pressure distribution.

Figure 14. Tyre inflation flow intake at two-time instants (a) 1 s and (b) 1.925 s.

Figure 15. Analysis of the Bunyip lower system using velocity-based vector and contour methods to investigate the internal mixing and energy loss/ unfavourable flow characteristics during the ‘dump’ phase.

Figure 16. Study of the upper piston stroke and discharge using a velocity-based vector and contour method.

Figure 17. A Parametric study graph, showing the delivery head per supply head ratio versus the predicted Bunyip's daily output capacity.

Table 1. Operational Efficiency for common HPP systems at 58 cases of varied Supply and Delivery values, using manufacturer published data of Bunyip pumps [8], Blake’s Hydram [24] and PaPa Pumps [25].

Table 2. Pressure boundary condition types and example case: 4 m supply, 35 m delivery.

Name	Type	$Gauge pressure (k Pa$ )
Drive pipe	Velocity inlet	$39.2$
Supply pipe	Pressure inlet vent	$- 2.9$
Delivery pipe	Pressure outlet vent	$343.4$
Upper/ lower exhaust	Pressure outlet vent	$0$

Table 3. Tabulation of Physical Testing (PT) cases, source in Appendix A.4.

Features	$Drive flowrate (l / s$ )	Supply head (m)	Delivery head (m)	$Daily capacity (l / day$ )	Observed cycle period (s)
Case 1	5	1.2	22	8600	2.06
Case 2	5	2.0	50	8640	2.51
Case 3	5	2.0	60	5800	2.74
Case 4	6	2.2	36	14,400	1.39

Table 4. Summary of operational cases (further detail in Appendix A.4).

Descriptions		Cycle period (s)	Supply head (m)	Delivery head (m)	Flow Components (l/cycle)					Daily capacity (l/day)	% error (NM to PT)	% efficiency	% error (NM to PT)	Standard capacity Sc (m/s)	Relative delivery RD
Descriptions		Cycle period (s)	Supply head (m)	Delivery head (m)	Delivery	Drive flow	L-exhaust	Supply	U-exhaust	Daily capacity (l/day)	% error (NM to PT)	% efficiency	% error (NM to PT)	Standard capacity Sc (m/s)	Relative delivery RD
case 1	PT	2.06	1.2	22	0.205	10.30	-	0.21	-	8600	6	36	5	81.3	2.0
case 1	NM	2.06	1.2	22	0.218	10.38	10.95	0.26	0.04	9125	6	38	5	86.2	2.1
case 2	PT	2.51	2.0	50	0.251	12.55	-	0.25	-	8640	-14	50	-15	81.6	2.0
case 2	NM	2.51	2.0	50	0.216	12.70	13.26	0.27	0.05	7443	-14	43	-15	70.3	1.7
case 3	PT	2.74	2.0	60	0.184	13.70	-	0.18	-	5800	18	40	27	54.8	1.3
case 3	NM	2.74	2.0	60	0.216	12.71	13.25	0.27	0.05	6821	18	51	27	64.4	1.7
case 4	PT	1.39	2.2	36	0.232	12.51	-	0.23	-	14400	-6	30	-11	136.1	1.9
case 4	NM	1.39	2.2	36	0.219	13.28	14.05	0.25	0.03	13594	-6	27	-11	128.4	1.6

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Hydro-Powered Climate-Neutral Pump: Full Cycle Simulation and Performance Evaluation

Abstract

1. Introduction

2. System description

2.1. Conventional hydraulic ram pump

2.2. HRP limitations

2.3. System design

2.4. Performance indicators

3. Set-ups

3.1. Geometry

3.2. Dynamic meshing

3.3. Motion methodology

3.4. Boundary method and automation

3.5. Pre-processing and modelling

4. Results

4.1. Operational Observations

4.2. Data Validation

4.3. Parametric Analysis

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Nomenclature

Appendix A

Appendix A.1. User Defined Function for linear rise-fall velocity profile definition

Appendix A.2. Boundary Manipulation Scheme Functions

Appendix A.3. Bunyip Automation Script Monitoring Tyre boundary ID To Set Inlet/Outlet profiles

Appendix A.4. Bunyip PA-13 Operational Case Information

References

MDPI Initiatives

Important Links

Subscribe