Due to its high power, high efficiency, low pollution, and compact size, permanent magnet synchronous motors (PMSMs) have been widely used in a variety of fields, including electric vehicles, aerospace, wind turbines, and marine devices which are used in renewable, sustainable, and environmentally friendly energy resources. However, in these practical scenarios, the motor operating conditions are complex and variable. Under high temperatures and high current conditions, PMSMs may experience demagnetization failures, not only leading to performance degradation but also inducing unexpected failures of the motors. To reduce the risk of unexpected losses caused by demagnetization faults and improve the safety and reliability of motor systems, it is necessary to apply automated monitoring of the magnet flux of the motor's permanent magnets and achieve real-time diagnosis of early demagnetization faults, ensuring the safe operation of the motor. This review article tries to summarize the current detecting methods of the automated monitoring of demagnetization faults in PMSMs. The main online monitoring technologies from both practical and academic perspectives were summarized and their benefits and challenges have been reviewed. Finally, the research trends and suggestions for future improvements are provided. This review article will not only shed light on the origins of the automated monitoring of demagnetization faults but also help to design highly effective and sustainable permanent magnet synchronous motors.

Keywords:

Subject: Engineering - Automotive Engineering

1. Introduction

In the past decades, as the requirement of sustainable development has become the priority due to the negative environmental impact that has influenced our daily lives, it has placed greater research interests on exploring renewable and environmentally friendly energy resources. In the driving technology area, which is the flag to reduce energy consumption, it is critical to design and develop new materials and new technologies to realize energy-effective motors. With the rapid development of permanent magnet materials, particularly the performance enhancement of neodymium iron boron permanent magnets and the gradual reduction in their prices, the application of highly effective Permanent Magnet Synchronous Machines (PMSM) has been continuously increased [1]. In addition, the PMSM’s advantages such as simple structure, small size, high efficiency, large torque, high energy density, and low noise have made it widely applied in various fields such as electric vehicles, aerospace, and marine industries [2].

However, for the application of electric vehicles, which is the mainstream topic in sustainable energy consumption, the integrated electric drive systems have limited space for installation, and thus face the constraints of heat dissipation, especially when it operates under synergistic service conditions, including startup, braking, acceleration, and deceleration, as well as variable load conditions. As a result, when the motor runs continuously at high speeds, the internal temperature of the system keeps increasing, leading to uniform demagnetization faults in the permanent magnets.

In addition to the demagnetization resulting from the high temperature, due to armature reaction in PMSMs, the direction of the magnetic field generated by the armature current is opposite to that of the permanent magnets. When the motor runs at a high speed or under heavy loads, the transient armature current increases rapidly, enhancing the demagnetizing effect of the armature reaction, which can cause irreversible local demagnetization failure of the permanent magnet materials. A previous study has predicted and tested the rotor demagnetization of a 0.6 kW (cont.), 9-slot/6-pole fractional-slot concentrated winding (FSCW), and interior PM synchronous machine under controlled temperature conditions. The experimental testing results of the rotor demagnetization were compared with the finite element predictions characteristics in a 3-phase symmetrical short-circuit and single-phase asymmetrical short-circuit. These results confirm that the properties of the magnet material, such as the magnet thermal coefficients, have significant impacts on the failure mode of the machine [3].

Another detrimental demagnetization failure originated from the cracks of the permanent magnet materials during the manufacturing or installation process of the PMSM. The randomly distributed cracks can also result in local or uniform demagnetization failure when the motor operates at high speeds or experiences severe collisions [4]. Moreover, the aging phenomenon of the permanent magnet materials is inevitable with the increasing service life of the motor, which also governs the demagnetization failure of the motors [5].

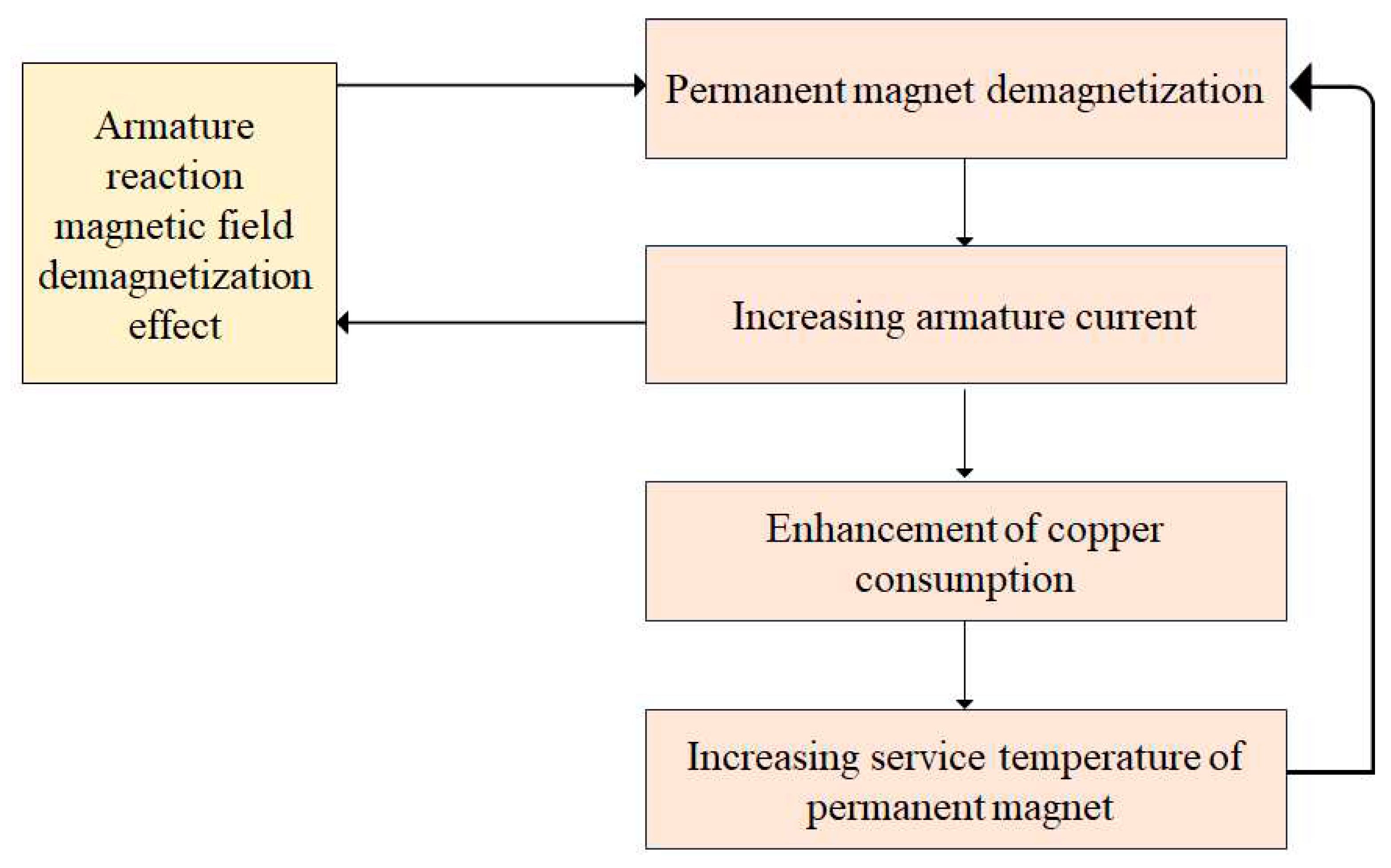
The occurrence of demagnetization failure leads to a reduction in the magnetic flux of the permanent magnet materials, thus decreasing the output electromagnetic torque. Figure 1 illustrates the dynamic demagnetization process of a PMSM. Under the same load torque conditions, the decrease in the magnetic flux of the permanent magnets leads to an increase of the stator current, which induces a higher copper loss in the PMSM, resulting in elevated internal temperatures and further accelerating the demagnetization process of the permanent magnet materials. Furthermore, the increase in stator current enhances the demagnetizing effect of the armature reaction magnetic field, creating a vicious cycle between PMSM demagnetization faults, internal operating temperature, and the demagnetizing effect of the armature reaction magnetic field [6]. Additionally, the occurrence of local demagnetization faults in the permanent magnets of a PMSM introduces non-integer harmonic components in the magnetic flux, which generates corresponding non-integer harmonic currents in the PMSM’s armature. This leads to torque and speed ripples in the motor, directly affecting the control precision of the PMSM. As a result, it is critical to implement the online automated monitoring of demagnetization faults in permanent magnet synchronous motors to avoid severe damage in advance [7].

Therefore, in a practical application, such as electric vehicles, in which safety and reliability are the priority issues, it is necessary to perform real-time online monitoring of the magnetic flux of the PMSM’s permanent magnets, achieving the real-time diagnosis of initial demagnetization faults, and further differentiate the demagnetization fault modes. This ensures the safe, reliable, and efficient operation of electric drive systems in electric vehicles and aerospace motors, reducing the occurrence of accidents and minimizing economic losses. The core of online monitoring for demagnetization faults in PMSMs is to find reliable and unique fault features. Moreover, when applied in scenarios such as electric vehicles and aerospace, it is necessary to identify fault features under non-stationary operating conditions. According to previous research results, the online monitoring methods for demagnetization faults in PMSMs can be categorized into two types: the uniform demagnetization fault monitoring methods and the local demagnetization fault monitoring methods, depending on various demagnetization fault modes [8].

For uniform demagnetization fault monitoring, one approach is to analyze the change in back electromotive force (EMF) characteristics of the PMSMs [9]. The demagnetization fault can cause a decrease in the amplitude and distortion of the back EMF waveform, which can be detected and analyzed to identify the fault condition [10]. Another method involves monitoring the change in the air-gap magnetic field distribution of the PMSMs using magnetic field sensors or Hall effect sensors [11]. The demagnetization fault affects the magnetic field distribution, and deviations from the normal pattern can indicate the occurrence of a fault. On the other hand, for local demagnetization fault monitoring, the focus is on detecting and identifying the specific regions or magnets that have experienced demagnetization [12]. This can be done by analyzing the harmonic components in the stator current or by using additional sensors, such as flux sensors or magnetic field sensors, to measure the magnetic field distribution and identify any deviations from the expected pattern. Additionally, advanced signal processing techniques, such as Fast Fourier Transform (FFT) analysis or wavelet analysis, can be applied to extract fault-related information from the measured signals [13].

It is worth noting that to achieve effective demagnetization fault monitoring in non-stationary operating conditions, advanced signal processing and pattern recognition algorithms are often employed. These algorithms can adaptively adjust their parameters and criteria to account for varying operating conditions and ensure accurate fault detection and identification. Overall, the development of reliable and unique fault feature extraction methods, along with the utilization of advanced signal processing and pattern recognition techniques, is critical for the successful online monitoring of demagnetization faults of the PMSMs in electric vehicles.

2. Automated Monitoring of Uniform Demagnetization Faults in PMSMs

2.1. Background

The online monitoring of uniform demagnetization faults starts by detecting the internal electrical parameters of the motor, such as current, voltage, and magnetic flux, and then establishes a mathematical model for fault monitoring. By analyzing the mathematical model, specific parameters related to the magnetic flux, such as the amplitude and distortion of the back electromotive force (EMF), can be extracted and monitored. The obtained parameter information enables qualitative analysis and quantitative diagnosis of demagnetization faults. Changes in these parameters can indicate the occurrence of demagnetization faults in the permanent magnets [14].

Through qualitative analysis, patterns and trends associated with demagnetization faults can be identified based on the mathematical model. For example, a decrease in the amplitude or distortion of the back EMF waveform may indicate the presence of a uniform demagnetization fault [15]. Quantitative observation and diagnosis involve comparing the extracted parameter values with predefined thresholds or reference values. If the values exceed the specified thresholds or deviate from the expected range, it suggests the presence of a demagnetization fault. To facilitate this process, real-time monitoring of the electrical parameters within the motor is required [16]. This can be achieved by using appropriate sensors to measure the currents and voltages in the motor and employing signal processing techniques to analyze and extract the relevant information. Additionally, advanced data analysis methods, such as model-based estimation or system identification, can be utilized to improve the accuracy and reliability of the monitoring system. By combining the mathematical model of the PMSM with real-time measurements and analysis, it becomes possible to qualitatively and quantitatively analyze and diagnose uniform demagnetization faults in the PMSM’s permanent magnets [17].

2.2. Recursive Least Squares method

In PMSMs, it’s critical to accurately estimate parameters including motor resistance, inductance, and EMF constant, which are governed by manufacturing tolerances or temperature changes. The Recursive Least Squares (RLS) method is a mathematical and computational technique used for parameter estimation and system identification of PMSMs. The RLS method is a valuable tool that enables real-time parameter estimation and adaptation, contributing to the efficiency and reliability of PMSM control systems. Different from traditional least squares methods, which require re-computation of parameters by using all available data points, RLS updates parameter estimates sequentially as new data and ensures particularly suitable for online applications and control systems. In addition, RLS allows prompt alignment in the motor’s behavior by employing a weighted least squares approach, where more recent data points can be given a higher weight in the parameter estimation process. RLS-based parameter estimation has been widely used in PMSM control and fault detection. It helps improve control performance, efficiency, and fault tolerance by ensuring that the control algorithm operates with accurate and up-to-date parameter values [18].

To meet the challenges originating from inaccuracies of modeling, a real-time and data-driven RLS method was used to control the current in a PMSM. The results indicated that the effectiveness of model predictive controllers is strongly depending on the quality of the utilized models. By using an RLS-based model to identify and interlock time compensation, the control system can make more accurate predictions about the system’s behavior. This study suggests that the RLS approach is suitable for self-commissioning applications where the drive system needs to be set up or commissioned automatically without relying on predefined wide-band models. In particular, this study presents an advanced control strategy that combines data-driven model identification, timing compensation, and predictive control to enhance the performance of electric drives, particularly in scenarios where accurate models are not readily available or when system parameters are variable. [19].

A novel online method to estimate the complete set of parameters in PMSMs has been developed by Yu. By introducing an algorithm based on the RLS method, the full range of motor parameters, including stator resistance, d-axis and q-axis inductances, and flux linkage can be estimated in an α-β frame. The simulation and experiment results manifest the effectiveness of the proposed full parameters estimation algorithms in α-β frame during both steady and transient states. Compared with other algorithms, it was claimed that the proposed method has the merits of faster convergence rate, less computational cost, and high accuracy [20].

Most recently, an updated RLS method, named Long-Term Memory Recursive Least Squares current estimation, has been developed for Finite-Control-Set Model Predictive Controllers. This approach can be used to identify the differential inductance and flux linkage maps without additional signal injection for online self-commissioning in seconds. By continuously adapting the flux linkage maps, it ensures precise open-loop torque control by merely using stator resistance as the datasheet. The results prove the accuracy of the identified model and the superior control performance of the Finite-Control-Set Model Predictive Controllers during the transient and steady-state operations [21].

Although RLS is a powerful algorithm for parameter estimation and online monitoring, it has several defects, including computational complexity, memory usage, initialization, sensitivity to outliers, stability, convergence rate, and adaptability, to nonlinear systems. Engineers and practitioners should carefully consider these limitations when choosing RLS for monitoring PMSM and combine them with alternative methods or modifications to address specific application requirements. Future research in this area should be focused on improving control strategies, performance optimization, and fault diagnosis methods for electrical machines. These efforts may contribute to more efficient and reliable systems in various applications, from industrial automation to renewable energy generation. The first suggestion is to explore methods for extracting physical parameters from identified models. These parameters could be essential for various analyses and control strategies. The operating point control could optimize motor performance, energy efficiency, and responsiveness, and the long-term memory models can provide valuable support during transient conditions, where traditional control methods may be less effective. Long-term memory models can capture complex relationships and patterns in data, making them suitable for adaptive and data-driven control strategies.

2.3. Current or voltage injection estimation

Current or voltage injection estimation is a technique used in the control and estimation of PMSMs. In this method, a current signal is injected into the motor windings, and the resulting motor response is analyzed to estimate various parameters, including rotor position, rotor speed, stator resistance, and the states of the motor. In this method, a current waveform with known frequency and amplitude is injected into one or more phases of the motor’s stator windings. This injected current perturbs the motor’s operation and generates a response in the form of back-EMF and variations in current and voltage. After carefully measuring and analyzing the response of the injected current, the current and voltage signal variations and their phase relationships can be obtained. The current injection estimation provides a non-invasive and efficient method for estimating critical motor parameters without the need for additional sensors. It can also be implemented during normal motor operation, making it suitable for online parameter identification and control adjustments. By accurately estimating rotor position and speed, this sensorless control method can operate PMSMs without relying on costly and failure-prone position sensors [22].

Accurate parameter identification is imperative for sensorless field-oriented control, as it enables precise control of the motor. For accurate parameter identification in a high-speed PMSM that can improve the performance of sensorless field-oriented control, a parameter identification method based on current injection, which eliminates the need for a low-pass filter in the current controller, has been developed. This method allows the maintenance of a high control bandwidth for 14,000 rpm high-speed PMSMs. The estimated parameters are shown to enhance the performance at both low and high speeds, highlighting the accuracy of the identification process [23].

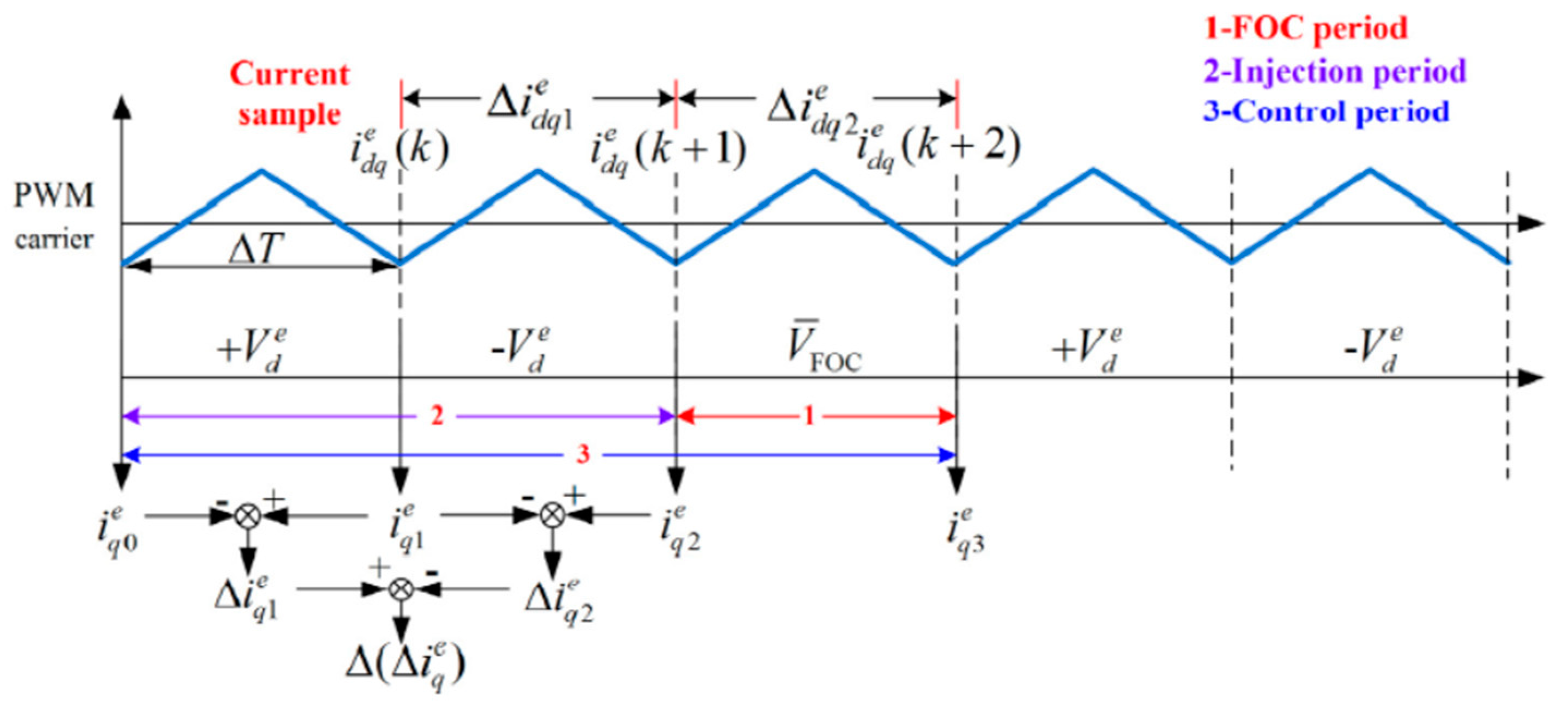
To ensure a reliable startup of the interior PMSM, an innovative method for the initial estimation of rotor position has been developed by combining enhanced high-frequency pulse signal injection with the injection of positive and negative d-axis current biases, shown in Figure 2. Different from previous methods for detecting the initial rotor position, this method divides the injection and the field-oriented control periods to eliminate the filters in the high-frequency response current and fundamental current extracting process. The estimation of magnet polarity has been achieved by the stimulating of positive and negative d-axis currents. In addition, to determine the rotor magnetic polarity, the peak values of the d-axis current during the injection period have been accumulated. The results indicated that the high-frequency pulse voltage signal injection method shows the merit of a high current control loop bandwidth without filters. More importantly, this method is robust in magnetic polarity identification and has a wider applicative situation. The effectiveness of the initial position estimation method is verified on a 1.5 Kw interior PMSM drive platform. It was claimed that this approach is beneficial to enhance the reliability of magnet polarity detection and can be applied to standstill rotors and free-running rotors [24].

Current or voltage injection estimation is a valuable tool for monitoring PMSM, but it has limitations originating from the diagnostic capability, sensitivity to noise, steady-state operation assumptions, and its ability to detect nonlinearities and specific faults. As a result, it is necessary to complement this method with other techniques to ensure a comprehensive view of the motor’s condition and performance. The following items should be considered as the future research challenges:

1. Current and voltage injection estimation may not provide detailed diagnostic information. It is typically used for estimating resistance and inductance, which are essential but may not capture more complex issues or faults.

2. The current or voltage injection estimation deals with a steady-state operation, in which the motors operate under constant speed and load conditions. However, in practical applications, motors are facing transient and dynamic conditions, and the current and voltage injection may not be suitable for capturing variations outside steady-state operation. In addition, the current and voltage injections are sensitive to noise and external disturbances, which can affect the accuracy of parameter estimation. In noisy environments or with significant disturbances, obtaining accurate parameter estimates can be challenging.

3. PMSMs exhibit nonlinear behavior, especially when faults occur. The current or voltage injection methods may not adequately capture these nonlinearities or detect issues related to them. Although current or voltage injection methods can identify changes in motor parameters, it is hard to detect rotor faults or winding faults, which require advanced techniques and additional sensors.

2.4. Nonsingular terminal sliding-mode control algorithm

The nonsingular terminal sliding-mode control algorithm weakens the need for an accurate mathematical model of the PMASMs, making it particularly suitable for systems with uncertain or time-varying parameters. Unlike traditional control methods that rely on accurate motor models, this algorithm doesn’t require precise mathematical models of the motor system. Instead, it employs a sliding-mode control approach with a nonsingular terminal condition, ensuring robust and precise control even in the presence of uncertainties and variations in the motor’s parameters. This makes it an effective method to achieve high-performance control and improve efficiency in PMSM’s various industrial and automotive applications [25].

A nonsingular fast terminal sliding mode control was designed to achieve fast and precise position regulation for a linear PMSM. This mode can achieve a rapid convergence of the position tracking error. To mitigate the problems posed by lumped disturbances and incomplete state information, the authors utilized a high-order super-twisting observer to estimate the missing state variables, thus enhancing the robustness of the control strategy. By using the Lyapunov stability theory, the stability of the system was rigorously analyzed, and the results demonstrated that the system remains stable during operation. Real-time testing results highlight the efficiency of this approach, making it a valuable contribution to the field of motor control. Although this nonsingular sliding mode is effective for position tracking, it faces challenges when dealing with lumped disturbances in the system. These disturbances can result in incomplete system state information and may lead to chattering in the control signal [26].

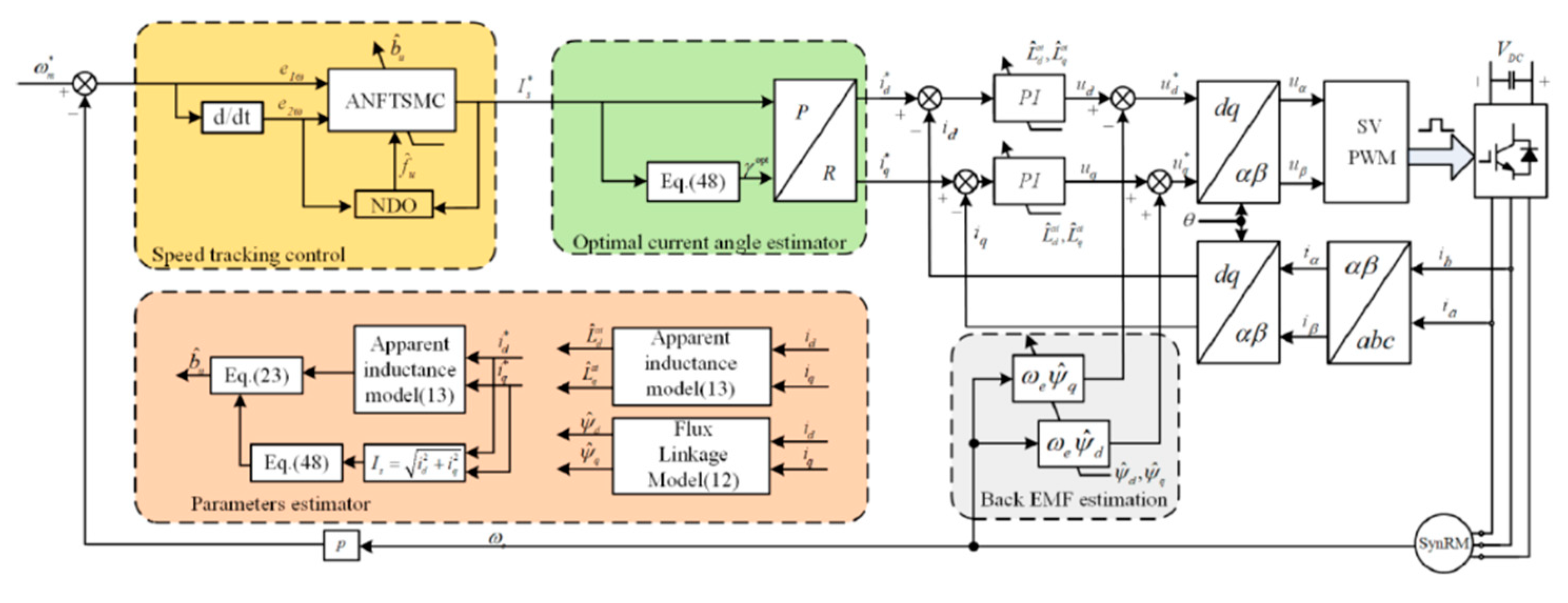
To overcome the challenges posed by magnetic saturation effects and the lack of a maximum torque per ampere control guideline with unmodeled dynamic compensation based on online excitation level calculation in synchronous reluctance motors, an adaptive non-singular terminal sliding mode control scheme was developed to face the highly nonlinear and time-varying parameters. Figure 3 shows the control block diagram of the proposed method. It shows the speed tracking, current regulators, optimal current angle estimator, and parameters estimator. The main contributions of this method can be claimed that it can effectively track MTPA operating points, solve the reference current distribution problem under the influence of nonlinear and time-varying parameters, and reach the goal of shortening the time to reach the sliding mode surface and reducing chatter (undesired high-frequency oscillations) near the surface. The experimental results demonstrated that this control strategy achieves satisfactory dynamic performance and robustness, despite the nonlinearities and time-varying parameters [27].

Although model-free nonsingular terminal sliding-mode control algorithms have potential benefits, they also face problems such as complex implementation, sensitivity to chattering, and measurement noise due to the lack of model-based adaptation. As a result, it is hard for it to deal with the nonlinearities in real-time implementation.

2.5. Sliding mode observer

A sliding mode observer (SMO) combines observer and controller to estimate the critical motor variables or states in real-time of the PMSM system. SMO has been widely used in various PMSMs, including electric vehicle propulsion systems, robotics, and renewable energy systems, where sensorless operation is preferred for higher efficiency and reliability. In this control mode, a robust control technique is used to guarantee the stability and accuracy of the system even with uncertainties and disturbances. The key variables include rotor position, rotor speed, and rotor flux, which are critical for precise motor control, especially in sensorless operations to reduce cost and complexity. SMO continuously updates its estimation to track the actual values. One of the palpable merits of SMO is its robustness to system parameter variations, load disturbances, and sensor inaccuracies. It allows for accurate estimation even under changing operating conditions. SMO not only plays a key role in sensorless control strategies but also provides accurate estimation of essential variables without additional sensors, thus reducing cost and increasing reliability [28].

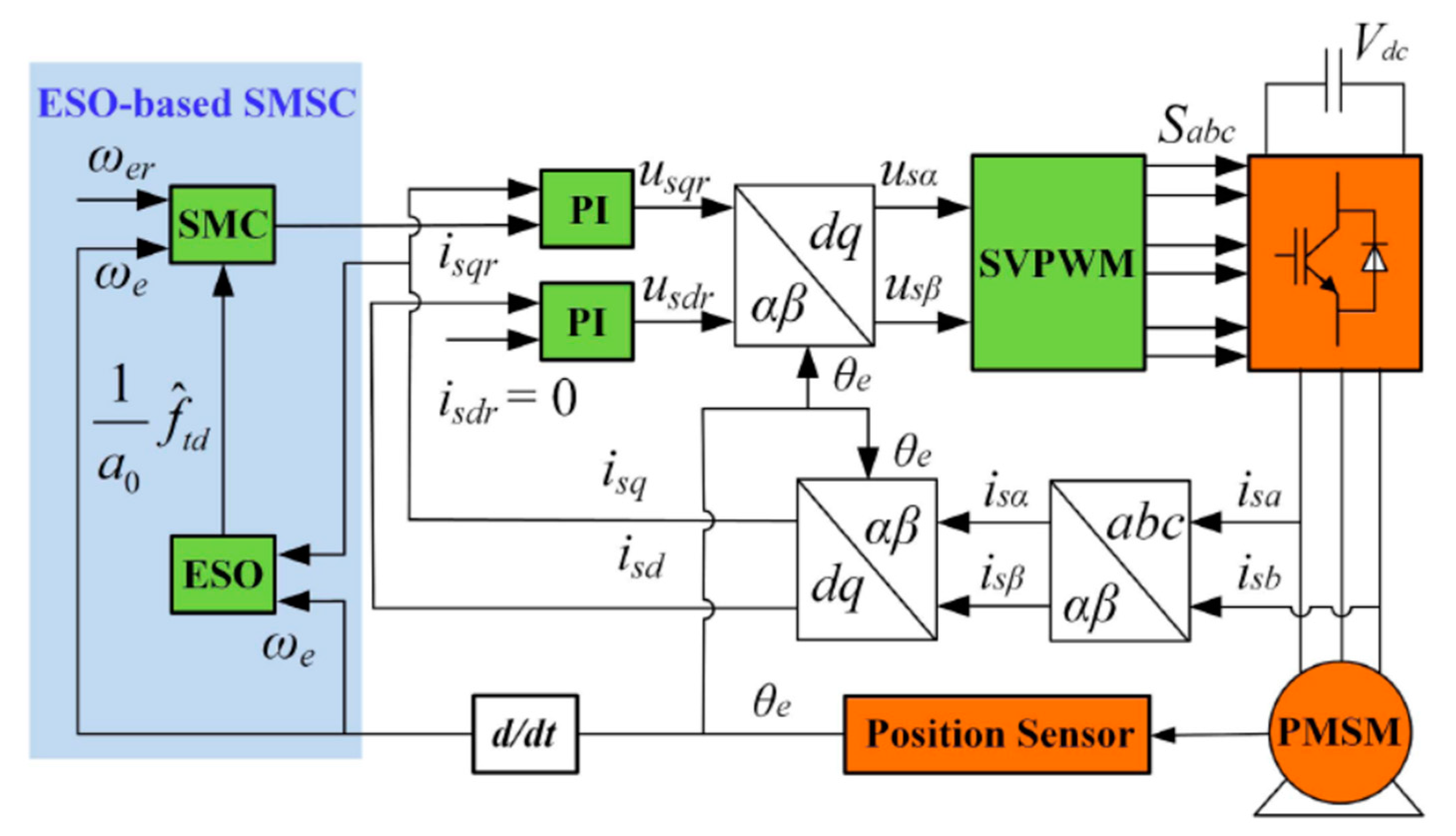
To enhance the tracking performance of speed controllers in PMSM drive systems, an extended state observer-based sliding mode observer was designed to handle various disturbances in real-time, including internal parameter variations and external load changes, based on an upper bound estimate of the total disturbance. Through this method, the extended state observer’s parameters could be configured according to the desired bandwidth of the observer, and the estimated total disturbance obtained from the observer was used to continuously update the control law in real-time. The results indicated an improved speed-tracking performance and robustness against disturbances without sacrificing the fast dynamic response. The stability of the closed-loop PMSM drive system with the proposed control is rigorously demonstrated through the Lyapunov theory. Experimental results from a 200 W salient pole PMSM drive system confirm the practical efficiency of this strategy [29]. Similarly, another study introduces an active disturbance rejection-based sliding-mode current control to enhance the tracking performance of current controllers in PMSM drive systems when facing internal disturbances. The schematic demonstration is shown in Figure 4. The results indicated that the current controller can significantly improve both steady-state and transient current tracking performance, along with reinforcing the robustness to internal disturbances [30].

Apart from the state observer-based sliding mode observer and the active disturbance rejection-based observer, a fuzzy sliding mode observer with a sensorless control strategy was introduced for PMSMs. This approach built a sliding mode observer that adheres to the Lyapunov stability condition. Instead of the traditional sign function, in this study, a sigmoid function was developed as the switching function within the sliding mode observer. The contribution of this study lies in adjusting the parameters of the sigmoid function in real-time through the established fuzzy rules, which effectively modifies the convergence characteristics of the sigmoid function to enhance observation performance. Furthermore, the EMF signals, which were extracted by the sliding mode observer, have been smoothed by using a back EMF adaptive law. This is beneficial to reduce the chatter and observation errors of the system. The proposed fuzzy sliding mode observer has been experimentally verified on a 2kW surface-mounted PMSM vector control platform and validated through a Matlab/Simulink simulation. Both simulation and experimental results have proved the effectiveness of this method in tracking changes in rotor speed and position during motor speed reversals [31].

Even though SMO provides an accurate estimation for the online monitoring of PMSMs, from the perspectives of model mismatch, sensitivity to disturbances and noise, design complexity, limited fault detection capabilities, limited information about mechanical components, computational load, and nonlinearities, it is still facing challenges. First, SMOs significantly depend on a mathematical model of the system to create a sliding surface. If the model used in the observer differs significantly from the actual motor dynamics due to parameter variations, nonlinearities, or modeling inaccuracies, the SMO’s performance can be degraded, thus leading to inaccurate state estimates. In addition, like other nonlinear observers, SMOs are sensitive to disturbances and measurement of noise. External disturbances or noisy sensor measurements can disrupt the sliding mode behavior and affect the quality of state estimation.

2.6. Luenberger observer

Luenberger observer, also called Luenberger state observer, is a control method applied in PMSM to estimate the unmeasurable internal states or variables of PMSM, including rotor position, rotor flux, and rotor speed. These variables are hard to measure directly but extremely critical for motor control. By developing a mathematical model, Luenberger observer can describe the evolution process of the internal states. Subsequently, by combining this model with the available measurements, the states’ current values can be estimated by the Luenberger observer by feeding back into the motor control system, allowing the controller to make real-time adjustments based on the estimated states. Luenberger observers can provide accurate state estimation with the presence of disturbances and inaccuracies. It is robust to measure noise and uncertainties in the motor model and operates in real-time, continuously updating its estimation as new measurements without additional sensors [32].

To overcome the limitations of substantial computational requirements and steady-state current errors in the presence of parameter mismatches, a low-complexity, three-vector-based model predictive current control method with reduced steady-state current errors for the PMSM drive system has been developed. The optimal voltage vector combination is selected to relieve the computational burden associated with the three-vector-based model. To mitigate steady-state current errors stemming from parameter mismatches, a Luenberger observer is incorporated to estimate the collective disturbance caused by parameter mismatches and unmodeled dynamics. The estimated disturbance is then used for compensation within the model. The testing results indicated that the three-vector-based low complexity model predictive current control can reduce the computational complexity without sacrificing the dynamic and static performance. This method not only can reduce the steady-state current error resulting from the parameter mismatch and unmodelled dynamics, but also improve the robustness against parameter variation [33].

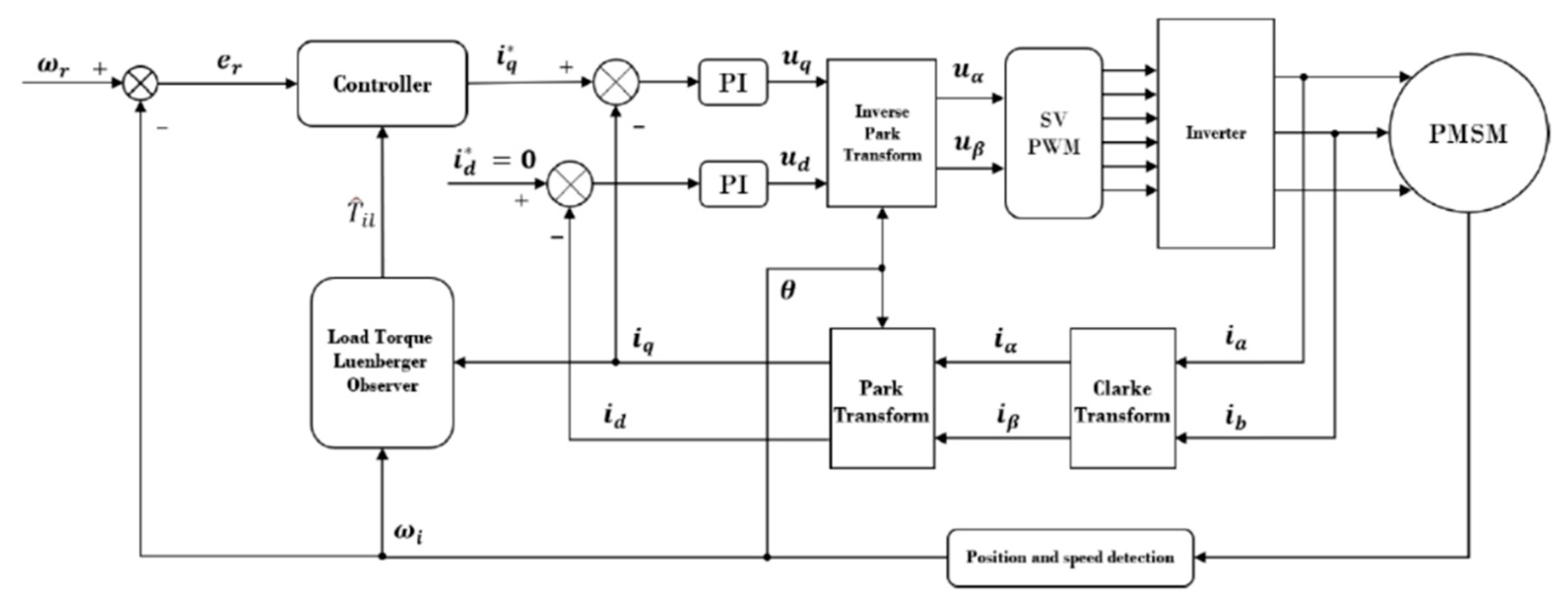
To reduce the impact of external load disturbances, a load torque Luenberger observer is developed to mitigate the slow response speed and the chattering phenomenon in the general sliding mode control of PMSMs. This strategy is designed to enhance the ability to withstand external interference. An experimental platform for a PMSM is established to evaluate the performance of the proposed control strategy and the effectiveness of the observer, and the block diagram of the control system is shown in Figure 5. The experimental results demonstrate that the load torque Luenberger observer excels at accurately estimating the actual load torque and tracking the motor’s real speed. Furthermore, the global fast terminal sliding mode control strategy substantially enhances the motor’s response speed and bolsters the system’s robustness [34].

Although the Luenberger observer is a powerful tool to estimate the states of PMSMs, it has limitations related to model dependency, sensitivity to parameter variations, limited fault detection capabilities, convergence and stability concerns, computational complexity, sensitivity to noise, and limited information about mechanical components.

1. Luenberger observers rely on a mathematical model of the system to estimate the states. For the PMSMs, the accuracy of the observer is highly dependent on the accuracy of the motor model used. Any discrepancies between the model and the actual motor behavior can lead to inaccurate state estimates. PMSMs can experience variations in parameters over time due to factors like temperature changes, aging, and manufacturing tolerances. The Luenberger observer may not adapt well to these parameter variations and can result in inaccurate state estimates if the model parameters are not updated. While the Luenberger observer can estimate the states of a motor, it is primarily a state estimation technique and may not be well-suited for detecting specific motor faults or anomalies. Fault detection typically requires additional techniques and sensors.

2. The Luenberger observer’s convergence and stability depend on the eigenvalues of the system’s dynamic matrix. If the eigenvalues are poorly conditioned or close to the imaginary axis, the observer may converge slowly or exhibit instability, especially in the presence of measurement noise. The Luenberger observer involves solving a set of differential equations in real time, which can be computationally intensive, especially for high-dimensional systems or systems with complex dynamics. This can be a limitation in real-time applications with limited computational resources.

3. Accurate initial state estimates are crucial for the Luenberger observer to provide reliable estimates. If the initial state estimates are far from the true values, it may take some time for the observer to converge to the correct estimates, leading to inaccuracies during the transient phase. Like any state estimation technique, the Luenberger observer is sensitive to measurement noise. In practice, sensor noise can degrade the accuracy of state estimates, particularly when measurements are noisy or corrupted. The Luenberger observer primarily focuses on estimating the electrical states of the motor, such as rotor flux and stator currents. It may not provide detailed information about mechanical components, such as bearings or load-related issues.

2.7. Model reference adaptive system observer

Model Reference Adaptive System (MRAS) observers are suitable for sensorless control of PMSMs in electric vehicles, industrial machinery, robotics, and renewable energy systems. MRAS observers are designed to be robust to disturbances, noise in measurements, and variations in motor parameters. They provide reliable state or parameter estimates under various operating conditions. Similar to the sliding mode observers, the primary purpose of the MRAS observer is to estimate unmeasurable states or parameters, such as rotor position, rotor speed, and rotor flux of the PMSM. MRAS observers can adjust their internal model or reference to minimize the error between the estimated states and the actual measurements. This adaptation enables them to handle varying operating conditions and load changes. MRAS observers use a reference model that represents the expected behavior of the PMSM under nominal conditions. The discrepancies between the model and the actual system are compensated through adaptation, allowing the observer to provide accurate estimates even in the presence of model uncertainties. MRAS observers are less sensitive to variations in motor parameters and load conditions compared to traditional observers, making them well-suited for applications where these factors may change dynamically. The estimated states or parameters generated by the MRAS observer are typically used as feedback in the motor control system. This feedback allows the controller to adjust the control signals in real time based on the estimated states, enabling precise motor control [35].

To monitor the position and speed of a PMSM, an MRAS approach was developed by considering the error between actual and estimated rotor position values. A state equation for the PMSM was formulated within the synchronous d-q reference frame. This frame relies on the estimated speed and the nominal parameters of the PMSM. Figure 6 presents the scheme of the block diagrams of the sensorless control system. The primary contribution of this approach is the MRAS adaptation scheme, which aims to estimate the rotor position and speed while minimizing the errors between the derivatives of d-q axis currents of the real system and the model system. Experimental results demonstrate strong performance and accurate speed-tracking capabilities when compared to the sliding mode observer under various speed and load torque conditions [36].

To enhance the motor’s performance in standstill and low-speed operating regions, a straightforward and robust approach for sensorless control of a surface mount PMSM drive was developed based on an electromagnetic torque-based MRAS speed estimator, combined with a cascaded pseudo derivative feedback controller. In this approach, a small signal model was employed to analyze the stability and sensitivity of the estimator. The testing results indicated that the estimator remains stable in a wide range of speed regions, and exhibits robustness against uncertainties in machine parameters. To further confirm the benefits of this approach, the estimator was implemented on a 1.5-kW laboratory prototype PMSM drive using an ALTERA Cyclone II field programmable gate array (FPGA). The experimental results further affirmed the efficacy of the method under various test conditions in a wide and adjustable speed range, including low-speed regions and standstill conditions [37].

MRAS algorithm faces difficulties in designing the adaptive law to ensure the simultaneous convergence of multiple parameters and determining control parameters. The Extended Kalman Filter algorithm incorporates noise factors and effectively reduces the influence of system noise on identification results, thereby improving identification accuracy.

2.8. Kalman filter

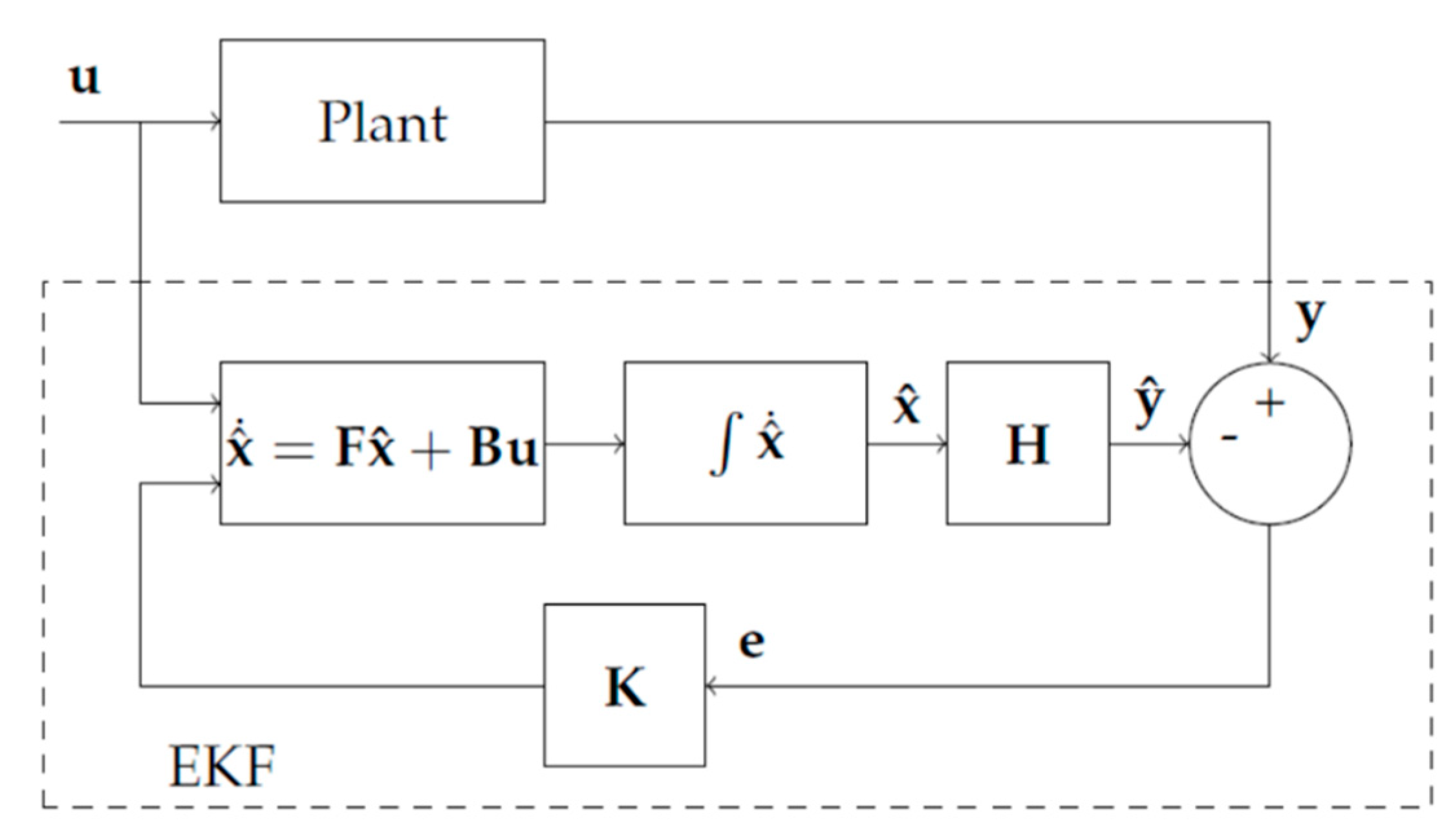
Kalman filter is a recursive algorithm, meaning it continually updates its estimation based on new measurements. It is beneficial to mitigate the defects of the MRAS observer in PMSMs. The block diagram is shown in Figure 7. As can be seen from this figure, the Kalman filter can be used to estimate unmeasurable states or parameters within the motor system, such as rotor position and speed. This adaptability is particularly valuable in real-time applications like motor control. In PMSMs, it can integrate measurements from various sensors, such as encoders, resolvers, and current sensors, to provide a more accurate and robust estimation of motor states. The Kalman Filter leverages a mathematical model, which predicts the expected behavior of the PMSM system, given the current state and control inputs. It minimizes the error between the predicted state (based on the model) and the measured state (based on sensor readings) by adjusting the filter’s gain. This minimization process optimally balances the contributions of the model and measurements to improve estimation accuracy. The filter can account for various sources of noise, including sensor noise and process noise. This makes it suitable for applications where measurements are subject to uncertainty and variability. Kalman Filters are computationally efficient, making them well-suited for embedded systems and applications with limited computational resources [38].

A novel approach was proposed to detect partial demagnetization faults in running PMSMs under nonstationary conditions. This method was developed based on tracking the characteristic orders of the stator current by using the Vold-Kalman Filter, in which the amplitude of these fault characteristic orders was used as an indicator. The proposed method has been experimentally assessed and demonstrated outstanding performance in detecting partial demagnetization faults in PMSMs under various speed and load conditions. [40]:

For diagnosing single and multiple open-switch faults in three-phase PMSM drives, a real-time estimation was tested based on three-phase motor currents with three Kalman filters. In this method, the residual signals were analyzed by comparing the differences between the measured and estimated stator currents for each phase. The averaged normalized residual signals were defined as diagnostic criteria, which were used to identify the presence of open-switch faults, locate the faulty switches, and distinguish open-switch faults from the current sensor, for detecting open-switch faults. The main advantages of this method are the fast detection times, robustness to measurement noises and errors, and the ability to handle load variations. It can be applied in both closed-loop and open-loop PMSM drives, and act as a subroutine in the drive control unit without requiring additional hardware. The effectiveness of the proposed method has been verified through extensive simulations and hardware-in-the-loop experiments by using a 1.5 kW PMSM and a low-cost microprocessor technology. The testing results indicated that, although the execution time is relatively long, this KF-based method can serve as an efficient and reliable approach for diagnosing open-switch faults in PMSM drives, making it a valuable tool for maintenance and fault detection in motor control systems [41].

To reduce the execution time of the Kalman Filter estimator but no sacrificing the accuracy for sensorless control of PMSMs, an Extended Kalman Filter was applied along with an ARM Cortex-M3 microcontroller. This study implemented various optimization levels to relieve the arithmetic calculation burden. Through these optimizations, the execution time of the Extended Kalman Filter estimator was significantly reduced from 260.4 μs to 37.7 μs, while maintaining the accuracy. By exploring the relationship between the frequency of Kalman gain, covariance matrices, and the rotor electrical frequency, the simulations and experimental results confirmed the effectiveness of these techniques in achieving accurate and efficient sensorless real-time control of PMSMs in resource-constrained environments [39].

While Kalman Filter is a powerful tool for state estimation and monitoring, a few concerns, including the model dependency, sensitivity to model errors, initialization challenges, sensitivity to nonlinearities, computational complexity, measurement noise, limited fault detection capabilities, difficulty in handling parameter variability, limited information about mechanical components, and challenges with multimodal noise distributions, should be considered before the practical applications. First, the Kalman filter is significantly dependent on a mathematical model that describes the system’s dynamics. If the model cannot represent the motor’s behavior accurately due to parameter variations, nonlinearities, or modeling inaccuracies, the filter’s performance can be compromised, thus sacrificing the accuracy of the estimation. Second, accurate initialization is critical for the Kalman filter to provide reliable state estimation. If the initial state estimation is far from the actual state, the filter may converge, thus leading to inaccuracies during the transient phase. In addition, the standard Kalman filter is designed for linear systems, it may not perform well when dealing with highly nonlinear motor behaviors or abrupt changes in dynamics. Third, Kalman filters are computationally intensive, especially for high-dimensional systems or systems with complex dynamics. Therefore, in real-time monitoring systems with limited computational resources, it could be confined. Finally, the Kalman filter faces the challenges of rapid or significant changes in motor parameters, such as sudden load variations, especially with the unimodal Gaussian distributions for process and measurement noise, achieving accurate state estimates during such transient conditions can be difficult.

2.9. Adaptive inertia weight particle swarm optimization algorithm

The adaptive inertia weight particle swarm optimization (AIWPSO) algorithm is a specialized optimization technique aimed at enhancing the performance and efficiency of PMSMs. This method extends the conventional Particle Swarm Optimization (PSO) approach to handle the intricate and ever-changing optimization challenges inherent in PMSM control and design. In the realm of PMSMs, AIWPSO is employed to tune a range of factors, including motor parameters, control strategies, and efficiency enhancements. One of its key benefits is its ability to dynamically strike a balance between exploration and exploitation during the optimization process. This adaptability empowers the algorithm to effectively navigate the solution space, rendering it particularly well-suited for optimizing PMSMs operating under variable conditions and system parameters. Consequently, its adaptive nature equips it to address the intricacies of PMSMs, ultimately contributing to superior motor performance and efficiency, even when grappling with dynamic and uncertain factors in motor design and control [42,43,44].

Cheng Yong introduced an approach for the online identification of electrical and mechanical parameters in PMSM by using an adaptive inertia weight particle swarm optimization algorithm based on logical functions. Compared with traditional complex and inefficient methods for parameter identification, the authors leverage a logistic function-based adaptive inertia weight particle swarm optimization algorithm to achieve precise online identification of both electrical and mechanical parameters in PMSMs. The experimental results proved the algorithm’s ability to accurately identify key motor parameters in real time. This approach sheds light on how to realize a faster convergence with improved accuracy [45].

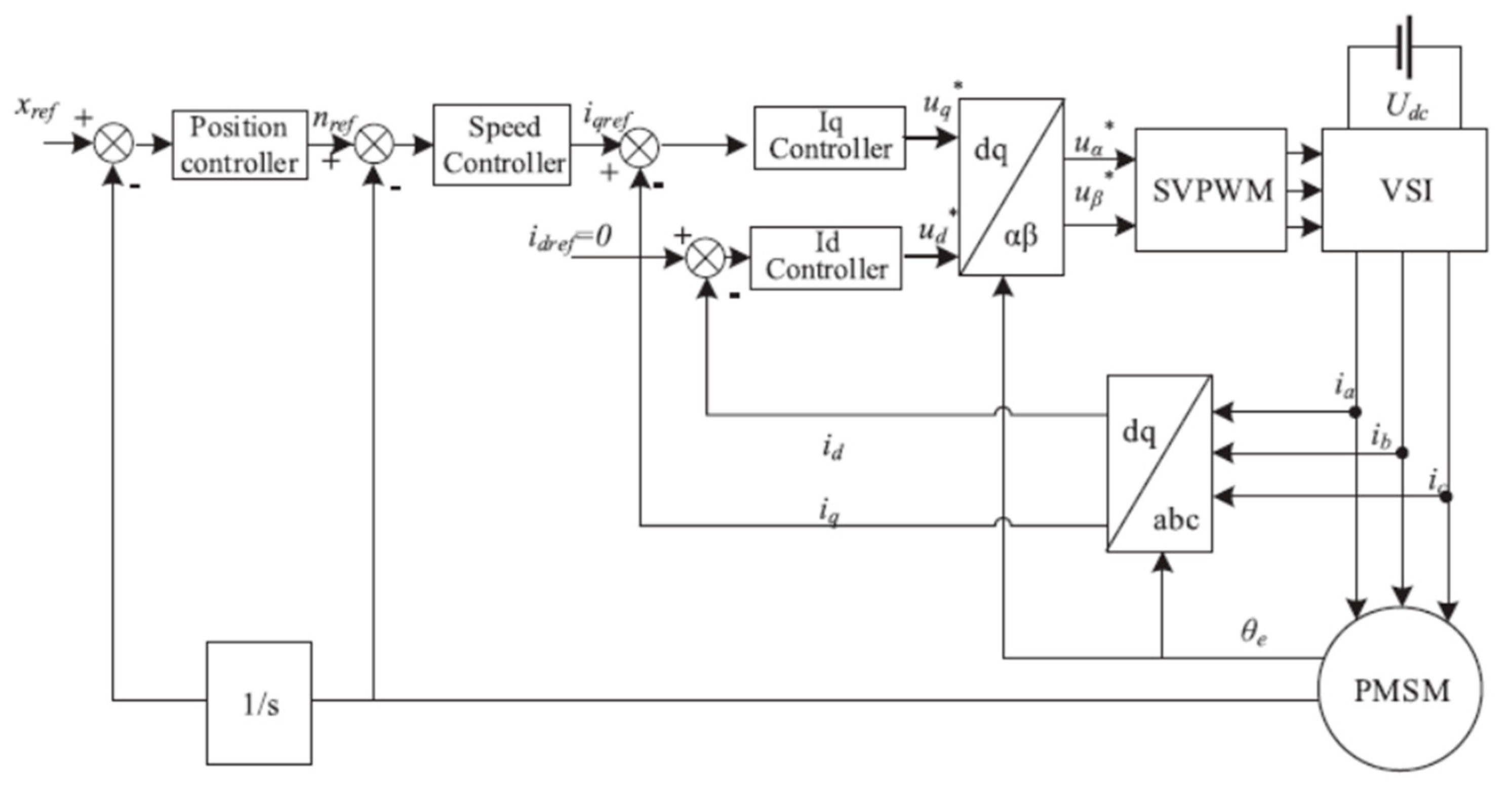
Recently, an enhanced optimization technique, named as hybrid particle swarm optimization algorithm was designed to address the parameter optimization challenges in the development of a servo system in PMSMs. This algorithm incorporates a unique directional mutation operation applied to the particles within the optimization process. This operation involves fixing the positions of specific particles to enhance their search capability in remote regions. To complement the directional mutation operation, the algorithm also refines the formula used for updating particle velocities. The servo system itself features a speed control mechanism based on biological intelligence regulation and a position controller with feedforward compensation. The servo system uses the i_d = 0 strategy in field-oriented control, as shown in Figure 8. The main contribution of this study can be claimed as follows. First, a directional mutation operation was presented to increase the searching ability to select remote regions. Second, a linear decreasing strategy of inertia weight and a modified velocity updating formula were developed to control the convergence process. Third, the biological intelligence controller and the feedforward compensation strategy were implemented in the speed and position servo system to enhance the steady state and dynamic performance. Finally, the algorithm can solve complex parameter setting and coordination problems of the designed controllers [46].

It is no doubt that the AIWPSO has great potential to be used for online monitoring of PMSMs, however, it has defects due to the confinement of computational intensity, search space size, lack of physical insights, constraint handling, initialization sensitivity, handling noisy data, lack of real-time adaptation, limited fault detection capabilities, convergence to local optima, and challenges in handling nonlinearities. The following aspects could be considered as the future research trends:

1. AIWPSO can be computationally intensive, especially when facing a complex optimization process. In real-time monitoring applications, in which quick responses are required, the heavy computational load of AIWPSO is quite challenging, especially when the motor system is high-dimensional or involves complex dynamics. In these high-dimensional parameter spaces, it is hard for the AIWPSO to explore and search such vast parameter spaces efficiently, leading to slow convergence and suboptimal solutions. Furthermore, due to the AIWPSO being a model-free optimization technique, the lack of physical insights is a limitation when compared to model-based techniques that utilize known system dynamics.

2. AIWPSO is primarily an optimization tool and may not inherently provide fault detection capabilities. When facing noise or measurement errors during the online monitoring process, AIWPSO finds it hard to present accurate parameter estimation or control policies without incorporating additional complexity, due to the lack of robust to noisy input, especially the innate nonlinear behaviors when faults occur. Furthermore, AIWPSO is typically not well-suited for real-time adaptation or control adjustments. The optimization process may take considerable time, making AIWPSO less suitable for applications that require rapid responses to changing motor conditions. The accuracy of the AIWPSO can be sensitive to the initial parameter settings. Weak initializations will result in suboptimal or premature convergent solutions.

2.10. Artificial Intelligence Algorithms

The method of online monitoring for uniform demagnetization faults in PMSMs based on artificial intelligence algorithms involves the use of machine learning and data analysis techniques for fault detection and diagnosis. This method utilizes machine learning algorithms and data analysis techniques to learn and recognize the characteristic patterns of demagnetization faults from a large amount of data, enabling real-time monitoring and automatic identification of such faults. In this approach, a significant amount of operational data is collected, including parameters such as current, voltage, speed, and temperature. Appropriate feature extraction techniques, such as spectral features, time-domain features, and statistical features, are applied to extract useful information from the data. Machine learning algorithms such as support vector machines (SVM), neural networks (NN), decision trees (DT), and deep learning are then employed to train and model the extracted features. Once the training is complete, the system can collect real-time data from the PMSM and input it into the trained model for fault detection and diagnosis. The model utilizes the learned patterns to determine the presence of local demagnetization faults and provides corresponding diagnostic results [47,48,49].

An artificial intelligence algorithm for detecting inter-turn short-circuit faults in PMSMs was proposed by using machine learning techniques. In this study, the machine learning technique was leveraged to enable the early detection of minor inter-turn short-circuit faults, facilitating the timely replacement of faulty motors. Additionally, the machine learning technique was applied to distinguish minor, moderate, and severe faults, and thus guide appropriate maintenance actions. By using Support Vector Machines and Convolutional Neural Networks for training the diagnostic model, experimental data were collected from laboratory tests. It was found that the SVMs could optimize training by selecting relevant features based on the PMSM mathematical model, while the CNNs were data-driven and typically required more extensive datasets for effective training. Both methods exhibit impressive accuracy, but the SVMs achieve this accuracy with significantly less data, demonstrating the advantages of a model-aided machine learning approach [50].

Model Predictive Control (MPC) has gained significant popularity as a control technique for motor drives due to its exceptional dynamic performance. Constant Switching Frequency MPC (CSF-MPC) is a variation of MPC that offers the benefits of MPC while maintaining a constant switching frequency. However, selecting the appropriate weighting factors for the cost function in CSF-MPC can be a challenging task. To address this challenge, a specific Artificial Neural Network was optimized by using a genetic algorithm. The objective of this study is to automate and expedite the selection of optimal weighting factors for CSF-MPC in PMSM drives powered by a three-level T-type inverter. The methodology involves gathering key performance metrics such as Total Harmonic Distortion (THD) and switching frequency error through simulation. These data were utilized to train and evaluate the algorithm. It was claimed that the trained model can automatically and accurately select the optimal weighting factors, aiming to minimize the THD and error under various operating conditions [8].

The AI-based approach offers high accuracy and robustness, capable of adapting to different operating conditions and fault modes; however, there are challenges in using AI algorithms for online monitoring of local demagnetization faults. Sufficient training data and appropriate feature selection are necessary to ensure the accuracy and reliability of the model. Additionally, the design and optimization of the algorithm need to consider real-time performance and computational complexity. The robustness and generalizability of the model also require thorough validation and testing. With the continuous development and improvement of AI technology, the AI-based method for online monitoring of local demagnetization faults is expected to find widespread applications in industrial practice, providing more effective solutions for motor fault diagnosis and maintenance. Due to the rapid development and the advantages of artificial intelligence algorithms, as well as their reduced dependency on motor parameters and mathematical-physical models, an increasing number of research studies have focused on fault diagnosis in the field. AI-based diagnostic methods involve the collection and processing of appropriate signals to extract fault feature vectors from the motor. Then, using the autonomous learning and predictive capabilities of artificial intelligence, the methods diagnose and identify the motor fault modes. However, this approach requires extensive training and involves significant computational complexity. Implementing diagnostic methods based on artificial intelligence algorithms can be challenging.

3. Concluding Remarks, challenges, and future trends

Automated monitoring of demagnetization faults in PMSMs is a complex task that involves addressing challenges related to early fault detection, data collection, complexity of data, noise and interference, modeling, temperature effects, complex operating conditions, fault classification, real-time implementation, integration with control systems, maintenance planning, and cost considerations. Successfully overcoming these challenges requires a multidisciplinary approach, combining expertise in electrical engineering, signal processing, data analysis, and industrial maintenance practices. The following areas might be considered as the future research focus to solve the above-mentioned problems.

1. In most cases, demagnetization faults are slowly developed, and their effects may not be immediately apparent in motor performance or monitoring data. As a result, detecting demagnetization faults at an early stage is crucial for preventing further damage and ensuring motor reliability.

2. Gathering the necessary data for monitoring demagnetization faults requires specialized sensors and data acquisition systems capable of measuring magnetic properties and temperature variations within the motor. The data generated by sensors for monitoring demagnetization faults can be complex and high-dimensional. Analyzing and interpreting this data in real-time can be computationally intensive and may require advanced signal-processing techniques.

3. Sensor measurements may be susceptible to noise and electromagnetic interference, which can impact the accuracy of demagnetization fault detection algorithms. Filtering out noise while preserving relevant information is a non-trivial task. Demagnetization faults are often associated with temperature increases in the magnets. Monitoring and interpreting temperature variations within the motor are critical but challenging tasks, as temperature sensors may not be uniformly distributed or easily accessible.

4. Developing accurate models for PMSMs and establishing baseline data for normal operation are essential for detecting deviations caused by demagnetization. Model-based approaches require a thorough understanding of motor behavior and parameter variations.

5. Identifying the specific type and extent of demagnetization (e.g., partial or complete) can be difficult. Developing algorithms capable of classifying and quantifying the severity of demagnetization is essential for maintenance decisions. Real-time monitoring and decision-making are critical for preventing further damage. Implementing real-time demagnetization fault detection algorithms can be resource-intensive and require fast computational platforms.

In conclusion, automated monitoring of uniform demagnetization faults in PMSMs represents a vital component of modern motor maintenance and reliability strategies. Uniform demagnetization faults, which occur due to temperature variations or mechanical stress, gradually weaken the permanent magnet materials in the motors. This degradation will lead to efficiency reduction of motors, increasing energy consumption, and potentially catastrophic failures. To tackle this issue, automated monitoring systems must be developed to continuously assess the health conditions of PMSMs. These systems employ a combination of sensors, data analysis algorithms, and real-time monitoring techniques. In this review article, typical automated monitoring methods, including the recursive least squares method, current or voltage injection estimation, nonsingular terminal sliding-mode control algorithm, sliding mode observer, Luenberger observer, model reference adaptive system observer, Kalman filter, adaptive inertia weight particle swarm optimization algorithm, and artificial intelligence algorithm, were summarized. The main contributions and defects of these methods were analyzed and the future research trends were discussed as well. It is beneficial to manufacture highly effective and sustainable permanent magnet synchronous motors.

Author Contributions

Junxiang Li prepared most of this manuscript. Ziang Li, Feitian Cheng, Chuan Qian, and Xingyu Hu reviewed the manuscript and organized the figures and references. Jian Zhang and Shuyuan Zhao revised the manuscript, and Guoxiang Zhou organized the outline and the whole contents.

Funding

This research was funded by the Jiangsu Industry-University-Research Corporation Program (BY2022254), and LianyungangKey TechniqueCompetition Program (CGIBGS2103), and the Lianyungang Science and Technology TransformationProgram(CA202206).

Conflicts of Interest

The authors declare no conflict of interest.

References

Zhu, Zi-Qiang, Dawei Liang, and Kan Liu. "Online parameter estimation for permanent magnet synchronous machines: An overview." Ieee Access 9 (2021): 59059-59084. [CrossRef]
Moosavi, Seyed Saeid, Abdesslem Djerdir, Y. Ait Amirat, and Davod Arab Khaburi. "Demagnetization fault diagnosis in permanent magnet synchronous motors: A review of the state-of-the-art." Journal of magnetism and magnetic materials 391 (2015): 203-212. [CrossRef]
Choi, G., Y. Zhang and T.M. Jahns, Experimental Verification of Rotor Demagnetization in a Fractional-Slot Concentrated-Winding PM Synchronous Machine under Drive Fault Conditions. IEEE Transactions on Industry Applications, 2017. 53(4): p. 3467-3475. [CrossRef]
Urresty, et al., Influence of the Stator Windings Configuration in the Currents and Zero-Sequence Voltage Harmonics in Permanent Magnet Synchronous Motors With Demagnetization Faults. IEEE Transactions on Magnetics, 2013.
Mahmouditabar, F., A. Vahedi and P. Ojaghlu, Investigation of Demagnetization Phenomenon in Novel Ring Winding AFPM Motor with Modified Algorithm. Journal of Magnetism and Magnetic Materials, 2019. 491: p. 165539. [CrossRef]
Oberretl and K., Losses, torques and magnetic noise in induction motors with static converter supply, taking multiple armature reaction and slot openings into account. Iet Electric Power Applications, 2007. 1(4): p. 517-531.
Urresty, J., et al., Detection of Demagnetization Faults in Surface-Mounted Permanent Magnet Synchronous Motors by Means of the Zero-Sequence Voltage Component. IEEE Transactions on Energy Conversion, 2012. 27(1): p. 42-51. [CrossRef]
Yao, C., et al., Optimal Parameters Design for Model Predictive Control using an Artificial Neural Network Optimized by Genetic Algorithm. 13th International Symposium on Linear Drives for Industry Applications (LDIA), 2021. [CrossRef]
Kondo, S., et al., Analysis about Control Model for Position Sensorless Control of PMSMs based on Expression of Imaginary Electromotive Force. IEEJ Transactions on Industry Applications, 2019. 139(1): p. 1-12. [CrossRef]
Qin, Z., et al., Analysis of Demagnetization Fault for PMSM of Electric Vehicle Based on Back-EMF Mathematical Model. Gaoya Dianqi/High Voltage Apparatus, 2014. 50(9): p. 35-40.
Anders, et al., Experimental comparison of ring and diamond shaped planar Hall effect bridge magnetic field sensors. Journal of Applied Physics, 2015. 118(10): p. 103901-103901. [CrossRef]
Liu, Z., et al., Study on local magnetization of magnetic flux leakage testing for storage tank floors. Insight: Non-Destructive Testing and Condition Monitoring, 2003(5): p. 45.
Choudhury, A., D. Paliwal and T. Govandhan, Identification of faults through wavelet transform vis-a-vis fast Fourier transform of noisy vibration signals emanated from defective rolling element bearings. Frontiers of mechanical engineering, 2014. [CrossRef]
Changfan, Z., et al., Fault-Tolerant Predictive Control for Demagnetization Faults in Permanent Magnet Synchronous Machine. Transactions of China Electrotechnical Society, 2017.
Qin, Z., et al., Analysis of Demagnetization Fault for PMSM of Electric Vehicle Based on Back-EMF Mathematical Model. Gaoya Dianqi/High Voltage Apparatus, 2014. 50(9): p. 35-40.
Medina-García, J., et al., A Wireless Sensor System for Real-Time Monitoring and Fault Detection of Motor Arrays. Sensors, 2017. [CrossRef]
Tudorache, T., et al., Improved Mathematical Model of PMSM Taking Into Account Cogging Torque Oscillations. Advances in Electrical and Computer Engineering, 2012. 12(3): p. 59-64. [CrossRef]
Dwivedi, et al., Fast Block LMS and RLS-Based Parameter Estimation and Two-Dimensional Imaging in Monostatic MIMO RADAR Systems With Multiple Mobile Targets. IEEE Transactions on Signal Processing A Publication of the IEEE Signal Processing Society, 2018.
Brosch, A., et al., Data-Driven Recursive Least Squares Estimation for Model Predictive Current Control of Permanent Magnet Synchronous Motors. IEEE, 2021(2). [CrossRef]
Yu, Y., et al., Full Parameter Estimation for Permanent Magnet Synchronous Motors. IEEE Transactions on Industrial Electronics. 2022. 69(5). [CrossRef]
Anian, B., W. Oliver and B. Joachim, Long-Term Memory Recursive Least Squares Online Identification of Highly Utilized Permanent Magnet Synchronous Motors for Finite-Control-Set Model Predictive Control. IEEE Transactions on Power Electronics, 2023. 38(2).
Li, W. and X. Chen, An Estimating and Controlling Method of Speed and Rotor Position for PMSM. International Journal of Advancements in Computing Technology, 2013.
Z., L., et al., Grid-Side Current Harmonic Suppression and Power Factor Improvement Using q – Axis Damping Current Injection for PMSM Drives Without Electrolytic Capacitor. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023. 11(3): p. 3371-3384.
Wu, X., et al., A reliable initial rotor position estimation method for sensorless control of interior permanent magnet synchronous motors. ISA Transactions, 2020. 97: p. 116-129. [CrossRef]
Ruimin, et al., On-line RNN compensated second order nonsingular terminal sliding mode control for hypersonic vehicle. International Journal of Intelligent Computing and Cybernetics, 2008.
Xu, D., et al., Nonsingular Fast Terminal Sliding Mode Control for Permanent Magnet Linear Synchronous Motor via High-Order Super-Twisting Observer. IEEE/ASME Transactions on Mechatronics, 2022. 27(3). [CrossRef]
Ren, L., et al., Adaptive Nonsingular Finite-Time Terminal Sliding Mode Control for Synchronous Reluctance Motor. IEEE Access, 2021(9). [CrossRef]
Zhang, J., et al., On sliding mode observers for non-infinitely observable descriptor systems. Automatica, 2023. [CrossRef]
Qu, L., W. Qiao and L. Qu, An Extended-State-Observer-Based Sliding-Mode Speed Control for Permanent-Magnet Synchronous Motors. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021. 9(2).
Qu, L., W. Qiao and L. Qu, Active-Disturbance-Rejection-Based Sliding-Mode Current Control for Permanent-Magnet Synchronous Motors. IEEE Transactions on Power Electronics. 36(1).
Ding, H., X. Zou and J. Li, Sensorless Control Strategy of Permanent Magnet Synchronous Motor Based on Fuzzy Sliding Mode Observer. IEEE Access, 2022. 10. [CrossRef]
Jiao, Z., et al., Improved Particle Filter Using Clustering Similarity of the State Trajectory with Application to Nonlinear Estimation: Theory, Modeling, and Applications. Journal of Sensors, 2021. [CrossRef]
Xu, Y., et al., Three-vector-based low-complexity model predictive current control with reduced steady-state current error for permanent magnet synchronous motor. IET Electric Power Application, 2020. 14(2).
Zhu, C., et al., Global fast terminal sliding mode control strategy for permanent magnet synchronous motor based on load torque Luenberger observer. IEICE Electronics Express., 2021. 18(19). [CrossRef]
Gao, W. and Z. Guo, Speed Sensorless Control of PMSM using Model Reference Adaptive System and RBFN. Journal of Networks, 2013. 8(1). [CrossRef]
Abo-Khalil, A.G., et al., Sensorless control for PMSM using model reference adaptive system. ELECTRICAL ENERGY SYSTEMS, 2021(31).
Prabhakaran, K.K. and A. Karthikeyan, Electromagnetic Torque-Based Model Reference Adaptive System Speed Estimator for Sensorless Surface Mount Permanent Magnet Synchronous Motor Drive. 2020. 68(7). [CrossRef]
Dilys, J., V. Stankevič and K. Łuksza., Implementation of Extended Kalman Filter with Optimized Execution Time for Sensorless Control of a PMSM Using ARM Cortex-M3. Energies, 2021. [CrossRef]
Dilys, J., V. Stankevi and K. Uksza, Implementation of Extended Kalman Filter with Optimized Execution Time for Sensorless Control of a PMSM Using ARM Cortex-M3 Microcontroller. Energies, 2021. 14(12): p. 3491.
Wang, C., et al., Detection of Partial Demagnetization Fault in PMSMs Operating under Nonstationary Conditions. IEEE Transactions on Magnetics, 2016. 52(7): p. 1-4. [CrossRef]
Naseri, F., et al., Real-time open-switch fault diagnosis in automotive permanent magnet synchronous motor drives based on Kalman filter. 2020. 13(12).
Mustafa, M.O., Optimal parameter values of PID controller for DC motor based on modified particle swarm optimization with adaptive inertia weight. Eastern-European Journal of Enterprise Technologies, 2021. [CrossRef]
Gupta, I.K. and V. Yadav, Modified Adaptive Inertia Weight Particle Swarm Optimization for Data Clustering. International Journal of Innovative Computing and Applications, 2021. [CrossRef]
Taherkhani, M. and R. Safabakhsh, A novel stability-based adaptive inertia weight for particle swarm optimization. Applied Soft Computing, 2016. 38: p. 281-295. [CrossRef]
Cheng, Y., M. Zhao and Q. Liu, Online Parameter Identification of PMSM Based on LAWPSO. 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), 2020: p. 2188-2192. [CrossRef]
Fang, S., et al., Design of Permanent Magnet Synchronous Motor Servo System Based on Improved Particle Swarm Optimization. IEEE Transactions on Power Electronics, 2022. 37(5). [CrossRef]
Xu, X., et al., Review of intelligent fault diagnosis for permanent magnet synchronous motors in electric vehicles. Advances in Mechanical Engineering, 2020. 12(7): p. 168781402094432. [CrossRef]
Meiring, G. and H. Myburgh, A Review of Intelligent Driving Style Analysis Systems and Related Artificial Intelligence Algorithms. Sensors, 2015. [CrossRef]
Wang, F., et al., ARTIFICIAL INTELLIGENCE AND STOCHASTIC OPTIMIZATION ALGORITHMS FOR THE CHAOTIC DATASETS. Fractals, 2023. 31(06). [CrossRef]
Shih, K., et al., Machine Learning for Inter-Turn Short-Circuit Fault Diagnosis in Permanent Magnet Synchronous Motors. IEEE Transactions on Magnetics, 2022. 5(8). [CrossRef]

Figure 1. Dynamic demagnetization process of a PMSM.

Figure 2. Sequence of improved high-frequency pulse voltage signals injection method with opposite voltage injection [24].

Figure 3. Control block diagram of proposed ANFTSMC system [27].

Figure 4. Schematic illustration of an FOC-based PMSM drive system with an SMO [30].

Figure 5. PMSM control system block diagram [34].

Figure 6. Scheme of the MRAS and the overall block diagrams of the sensorless control system [36].

Figure 7. Block diagram of Kalman filter [39].

Figure 8. Structural diagram of the swarm optimization algorithm [46].

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Submitted:

07 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

Keywords:

Subject: Engineering - Automotive Engineering

1. Introduction