Prerpints.org logo
Preprint
Article

Wind Resistant Performance Assessment of Long-span Cable stayed Bridges Based on Time Varying Reliability Theory

Altmetrics

Downloads

99

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts
Abstract
Long span cable-stayed bridge is the main bridge type with a span of more than 400 meters. It is generally designed as a double tower long-span structure with good spanning capacity and economic performance. Wind resistance safety performance is the main index to control the long-span cable-stayed bridge structure. During the operation of long-span cable-stayed bridge structure, because the service life of the cable is far less than the design life of the structure, the wind resistance performance of the structure will inevitably deteriorate significantly, which will seriously affect the structural service performance of symmetric cable-stayed bridge. Based on symmetric reliability theory, this paper takes flutter and static wind stability of long-span cable-stayed bridge structure as the main design control index, uses positive reliability theory to calculate the reliability index of symmetric cable-stayed bridge structure, uses inverse reliability theory to calculate the safety factor of symmetric cable-stayed bridge structure, and evaluates the wind resistant time-varying performance of long-span cable-stayed bridge structure by comprehensively considering the reliability index and safety factor. Taking a practical project of a long-span cable-stayed bridge as a specific case, the wind resistant time-varying reliability of the bridge during its operation for more than 30 years is analyzed, and the parameter sensitivity is analyzed. The results show that the wind resistance performance of the cable-stayed bridge structure is obviously affected by the cable, and the degradation of the cable performance will have an important impact on the wind resistance time-varying performance of the structure, especially the critical wind speed of the structure has obvious time-varying characteristics. The safety factor and reliability index can objectively evaluate the wind resistance time-varying performance of the long-span cable-stayed bridge structure.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Cable supported bridge is one of the main types of modern long-span bridges. As the lifeline of the cable-supported bridge, the cable is one of the most critical load-bearing components, and also the most vulnerable component to damage in the cable-supported bridge structure. In the operation stage, it is easy to be damaged by various environmental factors or accidents, endangering the service safety of the bridge. Therefore, it is very important to explore the impact of cable damage on the reliability of the overall structure of the bridge.
As China is moving steadily from a large bridge country to a powerful bridge country, more and more long-span cable-supported bridges are being built. As the core load-bearing component, the design life of the cables is far less than the design life of long-span cable-supported bridges. The damage of the cables during the operation period (Figure 1 and Figure 2) will inevitably face the practical problem of cable replacement. The anchorage system is the weak link of cable damage. The complex structure of the cable anchorage system makes the damage location difficult to detect and the damage mechanism unclear, which seriously affects the safety of long-span cable-supported bridges in the operation stage.
The cable body and anchorage system are two main forms of cable damage. The cable body damage will reduce the stress sectional area of the cable, while the cable anchorage system damage has the risk of cable breakage under strong wind. Therefore, once the cable is damaged, the risk of wind instability and collapse of the structure will increase dramatically, which will directly threaten the wind resistance safety of long-span cable-supported bridges in the operation stage. The parts (different cables, anchor heads, cable bodies, etc.) and damage degree (corrosion depth and area, etc.) of cables damaged during operation have strong randomness in different environments. Due to the fabrication error of the stiffening beam and the unsteady flow characteristics of the wind speed, the static three component force coefficient of the stiffening beam has strong uncertainty in the physical wind tunnel test and the virtual wind tunnel test results. In addition, the wind load and structural parameters of long-span cable-supported bridges have significant probability characteristics. Therefore, the wind-induced instability of long-span cable-supported bridges in the state of cable damage is essentially a random event.
As the main load-bearing component of the cable-supported bridge, the cable transfers almost all the loads of the bridge structure. Once the cable and its anchorage structure are damaged or broken, it will inevitably lead to the redistribution of the internal force of the structure, which will have a great impact on the safety and usability of the structure. Therefore, the research on the mechanical properties of cable-supported bridges with cable damage has become a hot topic in recent years. Static and dynamic performance is the focus of attention in the construction and operation stages of cable-supported bridges. A large number of scholars have studied the performance degradation of cable-supported bridges caused by cable damage, mainly involving the stress distribution of cables after wire breakage [1,2], structural mechanical properties after cable breakage [3,4], structural residual bearing capacity after cable damage [5], and cable damage transmission laws [6,7]. By studying the impact of cable damage on cable-supported bridges from the perspective of probability, we can clearly understand the reliability of the structural safety of cable-supported bridges after cable damage, such as the reliability analysis method of time-varying system of cables based on machine learning [8], the reliability analysis method of time-varying system of cable-supported bridges based on support vector regression [9], and the reliability evaluation of time-varying system of cable-supported bridges based on the fatigue test results of steel wires [10]. In addition, some scholars have studied the wind resistance performance of cable-supported bridge structures under cable damage, such as the influence of cable damage on the dynamic performance of long-span cable-supported bridges under automobile and wind loads [11], and the influence of different surface damage (Figure 3) degrees of cables on aerodynamic resistance based on wind tunnel force test [12,13].
Based on previous studies, it is found that the research on the influence of cable damage on the performance of cable-supported bridges mainly focuses on the static and dynamic characteristics and reliability, and only focuses on the aerodynamic shape of cables from the perspective of wind-induced effects, and almost does not involve the influence of cable damage on the wind resistant safety performance of long-span cable-supported bridges. The damage degree of the cable increases with time, leading to the degradation of the structural performance of the cable supported bridge. The damage of the cable anchorage system and its wind resistance safety have strong time-varying statistical characteristics. It is very necessary to use probability method to study the wind resistance safety time-varying regularity of long-span cable supported bridges. Therefore, on the basis of analyzing the wind resistant time-varying performance of long-span cable-supported bridge under cable damage, the risk of wind resistant safety collapse of long-span cable-supported bridge under cable damage is evaluated by comprehensively considering reliability index and probability safety factor, which lays a solid theoretical foundation for the preventive maintenance of cables and the formulation of economic and reasonable cable replacement scheme, and provides technical support for ensuring the wind resistant safety of long-span cable-supported bridge in the operation stage.

2. Wind Resistance Time-Varying Characteristics

At present, the reliability design only considers the random factors of the structure and ignores the time variation of the structure, so its reliability is independent of the time variation. With the development of research on durability and reliability evaluation of engineering structures, considering the structural resistance decaying with time during the service life, the research on the relationship between structural reliability and time variables has become a major topic of reliability research. In addition, the resistance of the structure also has randomness, so it is more appropriate to study its random time-varying reliability with the actual situation.
The dynamic response of time-varying structures is very complex. Because in the structural analysis, its control equation has become the parameter differential equation of stochastic process, and it is generally difficult to solve this kind of equation. Therefore, for the sake of simplification, when establishing the time-varying structural vibration equation under the action of fluctuating wind pressure, it is necessary to make the following assumptions: For a multi degree of freedom structure, its mass is concentrated on several particles and changes with time; The fluctuating wind load is a concentrated load acting on a particle, and is assumed to be a Gauss process; The vibration of the structure is linear in the duration of fluctuating wind, and the damping is Rayleigh complex damping.
After determining the resistance variation law, the corresponding structural safety criteria can be obtained. The resistance safety limit R ( t ) is generally in a state of decay over time, and the safety criterion of structures is defined as τ ， τ + ∆ τ , The resistance S ( t ) of the structure shall not exceed the resistance safety limit R ( t ) , namely
Φ = { S ( t ) < R ( t ) , t ∈ [ τ ， τ + ∆ τ ] }
Generally, R ( t ) and S ( t ) are stochastic processes.
The first passage failure criterion is adopted, the maximum annual average wind speed considering the standard height conforms to Bernoulli experiment, and the basic assumptions such as the random time change of the structure's stiffness and strength. The probability that the structure will not be damaged under the action of wind pressure is
P s = ∫ 0 ∞ P V S ( t ) < R ( t ) F ( V ) d V
where, F V was probability density function of annual maximum average wind speed at standard altitude. P V S ( t ) < R ( t ) was the probability that the structural response S ( t ) will not exceed the limit R ( t ) when the annual average wind speed is V .
According to the analysis of equation (2), the critical wind speed V c r for flutter (or aerostatic wind) stability. The calculation of cr is very important in the wind resistant time-varying safety analysis of long-span cable-supported bridges. Because of flutter (or) static wind stability, the critical wind speed V c r is the implicit expression of its influencing factors. in this paper, the finite element method based on certainty is used to calculate the critical wind speed of flutter (or aerostatic wind) stability.

2.1. Flutter Instability Mechanism

According to the self-excited aerodynamic expression proposed by Professor Scanlan, the aerodynamic lift L a e on the unit length of the structure, aerodynamic resistance D a e and aerodynamic torque M a e can be expressed as vertical displacement h, horizontal displacement p and torsional displacement respectively α function, using dimensionless aerodynamic derivative H i * , P i * , A i * （i=1,2,…,6）.
L a e = 1 2 ρ U 2 ( 2 B ) [ K H 1 * h ˙ U + K H 2 * B α ˙ U + K 2 H 3 * α + K 2 H 4 * h B + K H 5 * p ˙ U + K 2 H 6 * p B ]
D a e = 1 2 ρ U 2 ( 2 B ) [ K P 1 * p ˙ U + K P 2 * B α ˙ U + K 2 P 3 * α + K 2 P 4 * p B + K P 5 * h ˙ U + K 2 P 6 * h B ]
M a e = 1 2 ρ U 2 ( 2 B 2 ) [ K A 1 * h ˙ U + K A 2 * B α ˙ U + K 2 A 3 * α + K 2 A 4 * h B + K A 5 * p ˙ U + K 2 A 6 * p U ]
Eqs. (3-5) are the aerodynamic self-excited force on the unit width of the bridge deck, U was average wind speed of incoming flow， ρ was air density，B was dimension of member section along the main flow direction, K = B ω U was dimensionless frequency, ω was vibrating circular frequency, aerodynamic derivative H i * 、 P i * 、 A i * （i=1,2,…,6）was the function of dimensionless wind speed U ~ = U f B or dimensionless frequency, their values are related to the geometric shape of the bridge section.

2.2. Mechanism of Static Wind Instability

The static wind load acting on the unit length of the stiffening beam of suspension bridge can be divided into horizontal wind load P H , vertical wind load P V and torsional moment M . Under the action of static wind, the attitude of the stiffening beam will change, and the relative wind attack angle of the static wind load and the stiffening beam section will change accordingly. The concept of effective wind attack angle is introduced, and the static wind load is expressed as a function of wind speed, three component coefficient and effective wind attack angle.
P H = ( 1 2 ρ V 2 ) C H ( α ) D P V = ( 1 2 ρ V 2 ) C V ( α ) B M = ( 1 2 ρ V 2 ) C M ( α ) B 2
where, ρ was air density, D was lateral projection height of stiffening beam, B was stiffener width, V was average wind speed, C H was resistance coefficient, C V was lift coefficient, C M was lifting torque coefficient, α was effective angle of attack.

3. Symmetric Reliability Theory

When the overall structure or part of the structure exceeds a certain specific state and cannot meet a certain functional requirement specified by the design, this specific state is the limit state of the function. The limit state of the structure can be described by the limit state equation, which is expressed as:
g=g(R,S)=R-S=0
Where, g(R,S) is the limit state function of the structure; R is the resistance of the structure or structural members; S is the effect of the action.
In general, the design variables in the inverse reliability analysis problem can be deterministic variables or random variables. Let X = X 1 , X 2 , ⋯ , X i , ⋯ , X n be the basic design variables, and let d = d 1 , d 2 , ⋯ , d k , ⋯ , d p be deterministic design variables, let r = r 1 , r 2 , ⋯ , r k , ⋯ , r p be random design variables. It is worth noting that the design parameters of random variables can be mean or variance. For a given target reliability index β T , the inverse reliability problem can be described as calculating d or r according to the given β T that meeting equation (8) and equation (9).
β ( X , d , r ) = β T
G ( X , d , r ) = 0
Where, G ( X , d , r ) is the limit state function.

3.1. Forward Reliability

From the above analysis, it can be seen that the design parameters related to structural wind stability are closely related to the target reliability index. The target reliability index of large-span cable-supported bridges is a non-explicit function of the random variables corresponding to the design parameters, and in this case, the finite element reliability method is very suitable. A very important step in the iterative calculation process of reliability is the structural response and its partial derivatives on the design variables. In finite element reliability, the differential method can be used to numerically simulate the partial derivatives.
The relationship between the load effect S
and the basic random vector X can be expressed as
S = S ( X )
For the finite element first-order reliability method in application of implicit function such as the cable-supported bridges, the limit state function is
g [ s ( x ) , x ] = G ( u )
d i = ∇ u i G T u i − G ( u i ) ∇ u i G 2 ∇ u i G − u i
∇ u i G = ( J u , x − 1 ) T · ∇ x g
∇ x g = ∇ s g · J s , x
∇ u i G = ( J u , x − 1 ) T · ∇ x g · J s , x
Where, ∇ u i G is the gradient of structural effect to the random variables, ∇ s g is the gradient of the limit state function g ( s , x ) to s ; ∇ x g is the gradient of the limit state function g ( s , x ) to x ; J u , x is the Jacobian matrix of probability transformation; J s , x is the Jacobian matrix of mechanical transformation.

3.2. Inverse Reliability

For the relationship of the structural target reliability index β T , the basic random variables of the vector of standard normal distribution u , and the ( u , θ ) is a function of the structure. The inverse problem of structural reliability analysis as follows [14,15]:
u − β T = 0
u + u ∇ u G ( u , θ ) ∇ u G ( u , θ ) = 0
G ( u , θ ) = 0
where G ( u , θ ) is a function of the structure; ∇ u is the gradient operator; and θ is the design parameters to be determined.
In the forward reliability analysis, the iteration of random variable u can be expressed as:
u = [ ( ∇ u G ) T ( ∇ u G ) T u ] ∇ u G
And the target reliability index β T is:
β T = − ( ∇ u G ) T [ ( ∇ u G ) T u 1 / 2                                                                                                              
Using the Taylor expansion, β T at the point β j can be expressed as:
β T = β j + ∂ β ∂ K K j ( K j + 1 − K j )
Where , K is the design parameter, j was the iteration times.
The iterative formula for the design parameter can be expressed as [16]:
K j + 1 = K j + β T − β j ∂ β ∂ K K j
In order to achieve the iteration results for the design parameter. The convergence criterion using ε is as follows:
K j + 1 − K j ≤ ε

4. Evaluation of Wind Resistance Time-Varying Performance of Symmetrical Cable-Supported Bridges

Flutter and static wind instability of long-span cable-supported bridges belong to the limit state of bearing capacity, corresponding to the maximum bearing capacity or the deformation that is not suitable for continuous bearing. The flutter and wind-induced instability limit state of long-span cable-supported bridges can be expressed by a problem of exceeding the limit state. When the expected wind speed (design wind speed) at the bridge site exceeds the critical wind speed for flutter (or wind-induced) instability of the bridge in a given return period, flutter (or wind-induced) instability occurs. Therefore, for flutter and static wind stability of long-span cable-supported bridges, the limit state function can be expressed as:
g = C w ⋅ V c r ( t ) − G s ⋅ V b
Similar to the limit state equation established in the process of flutter and static wind stability reliability analysis of long-span cable-supported bridges, the safety factor evaluation expression of flutter and static wind stability of long-span cable-supported bridges can be expressed as:
g = C w ⋅ V c r ( t ) − K ⋅ G s ⋅ U b
where， K was safety factor， V c r ( t ) was time-dependent flutter (or still wind) stability critical wind speed taking into account uncertainties in structural characteristics, C w was conversion coefficient of critical wind speed considering uncertainty factors in wind field characteristics, G s was gust factor considering the influence of maximum fluctuating wind, V b was the wind speed.

5. Application

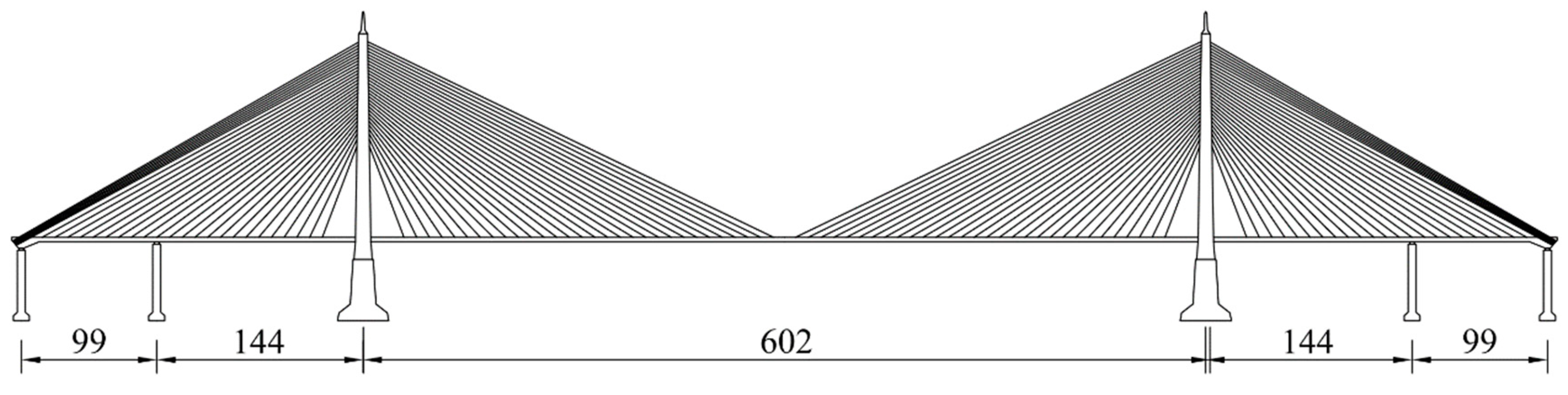
Yangpu Bridge is a river crossing hub on the Inner Ring Viaduct in Shanghai. The total length of the bridge is 7658m. The main bridge is a cable-supported bridge with composite beam, which spans over the river. The main span is 602m. It was completed and opened to traffic in 1993. The general layout is shown in Figure 3.

5.1. Time-Varying Characteristic of Cable Slack

Once the structural system of the cable-supported bridge is determined, the stress state of the completed bridge is mainly determined by the cable force of the cable. However, due to the influence of its own relaxation effect, the cable force will change with time. At this time, the relaxation effect of the cable will affect the stress and strain of the whole bridge. The variation law of the relaxation rate of the cable of this bridge with time is as follows:
μ = 0.6233 + 0.3357 l g t

5.2. Basic Information of Random Variable

According to the statistical characteristics of structural damping ratio of symmetric cable-supported bridges, the damping ratio follows the lognormal distribution which have the mean value 1 and the coefficient of variation 0.4.
In view of the statistical characteristics of flutter derivatives of stiffened beam sections of symmetric cable-supported bridges, it is assumed that each flutter derivative of stiffened beam sections of Yangpu Bridge is independent of each other and follows normal distribution which have the average value 1 and the coefficient of variation 0.2.
For the statistical characteristics of the static three component force coefficients of symmetric cable-supported bridges, for the sake of simplifying the analysis, it is assumed that the drag coefficient, lift coefficient and lifting moment coefficient are independent and obey the normal distribution which have the mean value 1 and the variation coefficient 0.1.
The design wind speed of Yangpu Bridge follows the Gumbel distribution, and its probability distribution function can be expressed as:
F ( V ) = e x p ⁡ [ − e x p ⁡ ( − V − b a ) ]
where, b = 23.7, a = 4.06.

5.3. Safety Assessment of Wind Resistance Time-Varying Characteristics

(1) Critical wind speed
The flutter stability of Yangpu Bridge is calculated by time domain method, and the damping ratio of the first order vertical bending and torsional vibration of the structure at various wind speeds is searched. When the wind speed is less than 62.7 m/s, the torsional damping ratio and vertical bending damping ratio of the system are positive; When the wind speed is 62.7 m/s, the torsional damping ratio of the system is 0, and the vertical bending damping ratio of the system is positive; When the wind speed is greater than 62.7 m/s, the torsional damping ratio of the system is negative, and the vertical bending damping ratio of the system is positive. Therefore, the flutter critical wind speed of Yangpu Bridge is 62.7 m/s. The time variation rule of flutter critical wind speed of Yangpu Bridge under cable relaxation is shown in Table 1.
The numerical analysis of three-dimensional nonlinear static wind stability considers the 0 ° wind attack angle, takes the structure bearing dead load as the initial state, increases the wind speed step by step, and calculates the vertical, lateral and torsional displacement of the bridge structure under the combined action of static wind load and dead load at all wind speeds. When the wind speed is low, the displacement of the stiffening beam in all directions is small. With the increase of the wind speed, the torsional displacement and lateral displacement of the stiffening beam gradually increase, while the increase of the vertical displacement is still very slow; When the wind speed increases to 60m/s, the torsional displacement and vertical displacement begin to accelerate, until the wind degree increases to 80.28m/s, and the torsional displacement and vertical displacement diverge, indicating that the structure has lost stability under static wind load and dead load, and the lateral displacement of the structure also tends to diverge. Therefore, the critical wind speed at 0 ° wind attack angle is 80.28m/s. See Table 2 for the time varying rule of the critical wind speed for static wind instability of Yangpu Bridge under cable relaxation.
From the analysis in Table 1 and Table 2, it can be found that, due to the influence of environmental factors, the cable relaxation will directly affect the structural performance of the structure under the wind load during the operation of the symmetrical cable-supported bridge. With the passage of time, the wind critical wind speed of symmetric cable-supported bridge structure has obviously decreased. Through comprehensive comparison, it can be found that the critical wind speed of aero-static instability of cable-supported bridge structures is generally higher than the critical wind speed of flutter at the same time, although the critical wind speed has a certain degree of decreasing trend.
(2) Reliability index
The time-varying reliability index is used to evaluate the wind resistance safety performance of the symmetric cable-supported bridge structure. The results are shown in Table 3 and Table 4. Through analysis, it can be found that the reliability of the symmetric cable-supported bridge structure will be affected when the critical wind speed of the cable-supported bridge structure decreases due to the degradation of the cable performance during the operation stage. Through the calculation of wind resistance reliability index of symmetric cable-supported bridge structure based on the positive reliability theory, it can be found that the wind resistance reliability index of symmetric cable-supported bridge structure has obviously decreased with the passage of time. It can be seen from comprehensive comparison that the aero-static stability reliability index of symmetric cable-supported bridge structure is generally greater than the flutter stability reliability index at the same time, which indicates that the static wind stability performance of cable-supported bridge structure is higher than the flutter stability performance.
(3) Probabilistic safety factor
Probabilistic safety factor is used to evaluate the wind resistance reliability of symmetric cable-supported bridge structure, which can be seen in Table 5 and Table 6. It can be found from the analysis that the reliability of symmetric cable-supported bridge structure will be affected when the critical wind velocity of cable-supported bridge structure decreases due to the degradation of cable performance during the operation stage. Through the calculation of the wind resistant probability safety factor of symmetric cable-supported bridge structure based on the inverse reliability theory, it can be found that the wind resistant probability safety factor of symmetric cable-supported bridge structure has obviously decreased with the passage of time. Through comprehensive comparison, it can be seen that the probability safety factor of static wind stability of symmetric cable-supported bridge structures is generally greater than the probability safety factor of flutter stability at the same time, indicating that the aero-static stability performance of cable-supported bridge structures is higher than the flutter stability performance.
From the view of above analysis, it can be found that the structural flutter and wind stability and wind resistance safety of cable-supported bridge will be directly affected after the performance degradation of cables, which will lead to the significant reduction of flutter critical wind speed and wind instability critical wind speed of the structure. The wind resistance safety of symmetric cable-supported bridge structure is evaluated from the perspective of probability. The flutter stability reliability index and the static wind stability reliability index decrease with time, and the flutter stability probability safety coefficient and the static wind stability probability safety coefficient decrease with time. Considering the reliability index and probability safety factor, the wind resistance safety performance of symmetric cable-supported bridge decreases with the occurrence of cable relaxation. That is to say, since the degradation of cable performance will directly affect the safety of structural wind resistance performance, it is necessary to comprehensively consider the reliability index and probability safety factor in the operation stage, and establish a safety performance evaluation system of structural wind resistance stability of symmetric cable-supported bridge based on the symmetric reliability theory.

6. Conclusions

Based on symmetric reliability theory, this paper takes flutter and static wind stability of long-span cable-supported bridge structure as the main design control index, uses positive reliability theory to calculate the reliability index of long-span cable-supported bridge structure, uses inverse reliability theory to calculate the safety factor of symmetric cable-supported bridge structure, and evaluates the wind resistant time-varying performance of long-span cable-supported bridge structure by comprehensively considering the reliability index and safety factor. Taking a practical project of a long-span cable-supported bridge as a specific case, this paper analyzes the wind resistant time-varying reliability of the bridge during its more than 30 years of operation, and draws the following conclusions.
(1) As the core force transmission component of symmetric cable-supported bridge structure, the degradation of cable performance will change the stiffness of the structure, thereby reducing the flutter critical wind speed and static wind instability wind speed of symmetric cable-supported bridge structure.
(2) The critical wind speed of long-span cable-supported bridge structure is an implicit function of structural parameters. The critical wind speed of the structure is calculated by using the point element method. Based on the long-span reliability theory, the time-varying reliability index is calculated by using the finite element positive reliability theory, and the time-varying probability safety factor is calculated by using the finite element inverse reliability theory.
(3) With the time-varying degradation of cable performance, the reliability index and probability safety factor of symmetric cable-supported bridge structure also decrease correspondingly, and the time-varying wind resistance performance of cable-supported bridge structure will be significantly reduced.
(4) It can be seen from parameter sensitivity analysis that the variability of parameters will directly affect the reliability index and safety factor of symmetric cable-supported bridge structure. The greater the variability of parameters, the smaller the reliability index and safety factor of structure.
(5) The wind resistance performance evaluation system of symmetric cable-supported bridge structure considering reliability index and probability safety factor is proposed, which can objectively evaluate the wind resistance time-varying performance of long-span cable-supported bridge structure, and provide guarantee for the time-varying safety of symmetric cable-supported bridge structure in the operation stage.

Funding

the Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors wish to express their sincere to the Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Xu, Y.; Li, H.; Li, S.; Guan, X.; Lan, C. 3-D modeling and statistical properties of surface pits of corroded wire based on image processing technique. Corrosion Science 2016, 111, 275–287. [Google Scholar] [CrossRef]
  2. Xu, J.; Chen, W. Behavior of wires in parallel wire supported cable under general corrosion effects. Journal of Constructional Steel Research 2013, 85, 40–47. [Google Scholar] [CrossRef]
  3. Mozos, C.M.; Apaeicio, A.C. Numerical and experimental study on the interaction cable structure during the failure of a stay in a cable supported bridge. Engineering Structures 2011, 33, 2330–2341. [Google Scholar] [CrossRef]
  4. Zhang, Y.; Fang, Z.; Jiang, R.; Xiang, Y.; Long, H.; Lu, J. Static performance of a long-span concrete cable-supported bridge subjected to multiple-cable loss during construction. Journal of Bridge Engineering 2020, 25, 04020002. [Google Scholar] [CrossRef]
  5. Li, S.; Xu, Y.; Zhu, S.; Guan, X.; Bao, Y. Probabilistic deterioration model of high-strength steel wires and its application to bridge cables. Structure and Infrastructure Engineering 2015, 11, 1240–1249. [Google Scholar] [CrossRef]
  6. Aoki, Y.; Valipour, H.; Samali, B.; Saleh, A. A study on potential progressive collapse responses of cable-supported bridges. Advances in Structural Engineering 2013, 16, 689–706. [Google Scholar] [CrossRef]
  7. Lu, N.; Liu, Y.; Xiao, X.; Yin, X. Reliability evaluation of long-span cable-supported bridge system based on joint intelligent algorithm. Chinese Journal of Applied Mechanics 2015, 32, 858–864, 902. [Google Scholar]
  8. Liu, Y.; Wang, Q.; Lu, N. Reliability evaluation of cable-supported bridge system considering cable resistance degradation. Journal of Hunan University (Natural Sciences) 2018, 45, 88–96. [Google Scholar]
  9. Lu, N.; Liu, Y.; Beer, M. System reliability evaluation of in-service cable-supported bridges subjected to cable degradation. Structure and Infrastructure Engineering 2018, 14, 1486–1498. [Google Scholar] [CrossRef]
  10. Yan, D.; Guo, X. Influence of cable damage on the reliability of existing cable-supported bridges. Journal of Central South University (Science and Technology) 2020, 51, 213–220. [Google Scholar]
  11. Zhou, Y.; Chen, S. Numerical investigation of cable breakage events on long-span cable-supported bridges under stochastic traffic and wind. Engineering Structures 2015, 105, 299–315. [Google Scholar] [CrossRef]
  12. Liu, Q.; Zhang, L.; Wang, X.; Jia, Y.; Hu, B.; Ma, W.; Liu, X. Experimental Study on Average Aerodynamic Resistance Characteristics of Cable with Surface Damage. Journal of Vibration and Shock 2020, 39, 140–149. [Google Scholar]
  13. Xiao, B.; Liu, Q.; Zhang, L.; Sun, Y.; Jia, Y. Aerodynamic and Flow Field Analysis of Cable with Surface Damage in Reynolds Number Critical Region. China Journal of Highway and Transport 2019, 32, 210–221. [Google Scholar]
  14. Der Kiureghian, A.; Zhang, Y.; Li, C.C. Inverse reliability problem. Journal of Engineering Mechanics, ASCE 1994, 120, 1154–1159. [Google Scholar] [CrossRef]
  15. Li, H.; Foschi, R.O. An inverse reliability method and application. Structural Safety 1998, 20, 257–270. [Google Scholar] [CrossRef]
Preprints 84599 g001
Figure 1. Corrosion of the cable.
Figure 1. Corrosion of the cable.
Preprints 84599 g001
Preprints 84599 g002
Figure 2. Cable surface damage.
Figure 2. Cable surface damage.
Preprints 84599 g002
Preprints 84599 g003
Figure 3. The layout of the Yangpu Bridge (Unit: m).
Figure 3. The layout of the Yangpu Bridge (Unit: m).
Preprints 84599 g003
Table 1. Time varying law of flutter critical wind speed of Yangpu Bridge.
Table 1. Time varying law of flutter critical wind speed of Yangpu Bridge.
Time
(year)		 Flutter Critical Wind Speed (m/s) Time
(year)		 Flutter Critical Wind Speed (m/s) Time
(year)		 Flutter Critical Wind speed (m/s)
1 62.71 11 60.07 21 55.46
2 62.53 12 59.62 22 54.86
3 62.34 13 59.28 23 54.24
4 62.13 14 58.84 24 53.65
5 61.92 15 58.43 25 53.08
6 61.61 16 57.96 26 52.37
7 61.37 17 57.47 27 51.63
8 61.06 18 56.92 28 50.91
9 60.73 19 56.54 29 50.22
10 60.46 20 56.06 30 49.54
Table 2. Time varying law of critical wind speed for static wind instability of Yangpu Bridge.
Table 2. Time varying law of critical wind speed for static wind instability of Yangpu Bridge.
Time
(year)		 Critical Wind Speed for Static Wind Instability (m/s) Time
(year)		 Critical Wind Speed for Static Wind Instability（m/s） Time
(year)		 Critical Wind Speed for Static Wind Instability (m/s)
1 80.28 11 78.72 21 75.63
2 80.12 12 78.56 22 75.26
3 80.03 13 78.24 23 74.82
4 79.91 14 77.98 24 74.45
5 79.85 15 77.63 25 73.97
6 79.76 16 77.32 26 73.44
7 79.53 17 77.07 27 72.88
8 79.35 18 76.79 28 72.34
9 79.18 19 76.43 29 71.73
10 78.94 20 76.01 30 71.15
Table 3. Time-varying characteristics of flutter stability reliability index of Yangpu bridge.
Table 3. Time-varying characteristics of flutter stability reliability index of Yangpu bridge.
Time (year) Reliability Index Time (year) Reliability Index Time (year) Reliability Index
1 13.512 11 12.875 21 11.898
2 13.487 12 12.798 22 11.798
3 13.412 13 12.623 23 11.673
4 13.362 14 12.547 24 11.524
5 13.237 15 12.389 25 11.362
6 13.141 16 12.253 26 11.121
7 13.105 17 12.187 27 10.887
8 13.076 18 12.102 28 10.673
9 12.975 19 12.003 29 10.446
10 12.927 20 11.954 30 10.216
Table 4. Time varying characteristics of static wind stability reliability index of Yangpu Bridge.
Table 4. Time varying characteristics of static wind stability reliability index of Yangpu Bridge.
Time (year) Reliability Index Time (year) Reliability Index Time (year) Reliability Index
1 15.413 11 14.456 21 13.054
2 15.376 12 14.287 22 12.898
3 15.312 13 14.105 23 12.763
4 15.267 14 13.968 24 12.701
5 15.143 15 13.867 25 12.669
6 14.987 16 13.786 26 12.565
7 14.876 17 13.627 27 12.387
8 14.747 18 13.489 28 12.031
9 14.664 19 13.275 29 11.887
10 14.571 20 13.112 30 11.653
Table 5. Time-varying characteristics of probability safety factor of flutter stability of Yangpu bridge.
Table 5. Time-varying characteristics of probability safety factor of flutter stability of Yangpu bridge.
Time (year) Probabilistic Safety Factor Time (year) Probabilistic Safety Factor Time (year) Probabilistic Safety Factor
1 9.127 11 8.413 21 7.243
2 9.054 12 8.342 22 7.171
3 8.909 13 8.293 23 7.003
4 8.912 14 8.112 24 6.813
5 8.837 15 7.997 25 6.688
6 8.789 16 7.898 26 6.565
7 8.721 17 7.771 27 6.319
8 8.653 18 7.659 28 6.027
9 8.594 19 7.497 29 5.736
10 8.487 20 7.368 30 5.426
Table 6. Time varying characteristics of probability safety factor of static wind stability of Yangpu Bridge.
Table 6. Time varying characteristics of probability safety factor of static wind stability of Yangpu Bridge.
Time (year) Probabilistic Safety Factor Time (year) Probabilistic Safety Factor Time (year) Probabilistic Safety Factor
1 11.312 11 10.569 21 9.587
2 11.276 12 10.512 22 9.431
3 11.231 13 10.462 23 9.289
4 11.185 14 10.341 24 9.135
5 11.113 15 10.161 25 9.021
6 11.076 16 10.023 26 8.889
7 10.972 17 10.872 27 8.687
8 10.868 18 10.763 28 8.472
9 10.763 19 10.701 29 8.213
10 10.654 20 10.643 30 7.988
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated