Target Localization and Grasping of Parallel Robots with Multi-Vision Based on Improved RANSAC Algorithm

Some traditional robots are based on offline programming reciprocal motion, and with the continuous upgrading of vision technology, more and more tasks are replaced by machine vision. For the current problem of insufficient accuracy of robot target localization based on binocular vision, and an improved random sampling consistency algorithm is proposed to complete parallel robot target localization and grasping under the guidance For the current problem of insufficient accuracy of robot target localization based on binocular vision, an improved random sampling consistency algorithm is proposed to complete parallel robot target localization and grasping under the guidance of multi Firstly, the RANSAC algorithm is improved based on the SURF algorithm; then the parallax gradient method is applied to iterate the matched point pairs several times to further optimize the data; then the 3D reconstruction is completed by the program technique; finally the obtained data is finally the obtained data is input into the robot arm and the camera internal and external parameters are obtained by the calibration method so that the robot can accurately locate and The experiments show that the improved algorithm has advantages in recognition accuracy and grasping success rate under multi- The experiments show that the improved algorithm has advantages in recognition accuracy and grasping success rate under multi-vision system.

Keywords:

Subject: Engineering - Control and Systems Engineering

0. Introduction

With the rapid development of the application of stereo vision technology, target recognition and three-dimensional reconstruction technology is also more widely used in a variety of products, significantly improving the production efficiency of assembly-line production industry, the identification and distinction of the target items more intelligent, more detailed detection of defects in the goods, not only to reduce the demand for labor, but also to make people's daily life more convenient.

The accuracy of depth values has a critical impact within high-performance 3D applications, In obtaining depth values, some methods use sensors, LIDAR or structured light cameras[1]. These methods are not only very demanding in terms of the environment in which they are used, but the equipment is also expensive. Most of these direct depth acquisition methods result in a sparse point cloud of depth maps.Therefore, using binocular cameras, it is particularly important to extract various feature values from a 2D image and map these feature values from the image to the depth information to obtain better results.obtaining accurate object depth information from two 2D maps is key to achieving accurate object localization. But the most important step in obtaining depth values is a parallax map with one image as the reference and the other image relative to its complementary information.The relationship between parallax and depth information for corresponding pixels is inversely proportional. Obtaining an accurate parallax map is crucial in stereo vision[2].

When the human eye opens and closes the left and right eyes respectively, it will find that the object is not in the same position, and this phenomenon is parallax. Similarly, when a binocular camera observes the same object at the same time, the difference between the projected points obtained from the phase planes of the left and right eye cameras is parallax. Encoding the difference between the horizontal coordinates of the corresponding image points is an important step in obtaining a parallax map.

In order to obtain better image information, feature-based matching methods are currently popular in the research field[3] . In 1999, David Lowe, a professor at Columbia University, first proposed the SIFT algorithm[4] , which was used in various fields of vision processing at that time because of its good detection results in occlusion and illumination. In 2006, Herbert Bay proposed the SURF[5] algorithm, which significantly reduced the efficiency and improved the robustness by using Haar wavelet[6] transform, Hessian Matrix[7] and integral image[8] . However, due to the possible inaccuracy of the main direction of SURF algorithm[9] , affected by factors such as a large number of similar point features on the edge line[10] , it is slightly less effective in matching accuracy, and the case of mis-matching becomes more and more obvious when the target object has rich texture features. In order to solve the case of mis-matching, based on the SURF algorithm, the improved RANSAC algorithm is fused to extract the target image feature points, and the similar points found by the bidirectional Euclidean distance[11] are judged using the Hessian matrix trace to exclude the feature points that do not meet the requirements. Then the depth map of the target image is compared with the reconstruction map by SGBM[12] stereo matching algorithm, and the object information is reconstructed in 3D according to the machine vision related algorithm. Finally, the robot and the host computer are connected through TCP communication to achieve hand-eye calibration[13] , and complete the project work.

In this paper, we choose to use a trinocular camera to take pictures of the target object, complete the 3D reconstruction by the improved RANSAC algorithm, then apply SGBM to optimize the processing of the image to complete the stereo matching, and finally grasp and place the target object by the robot in the eye-in-hand mode. This experiment completes the camera calibration task by MATLAB2022b and MV viewer image acquisition software under 64-bit Windows 10 system, and the experimental program is run by installing contrib+PCL under VS2017+opencv4.5.1 software.

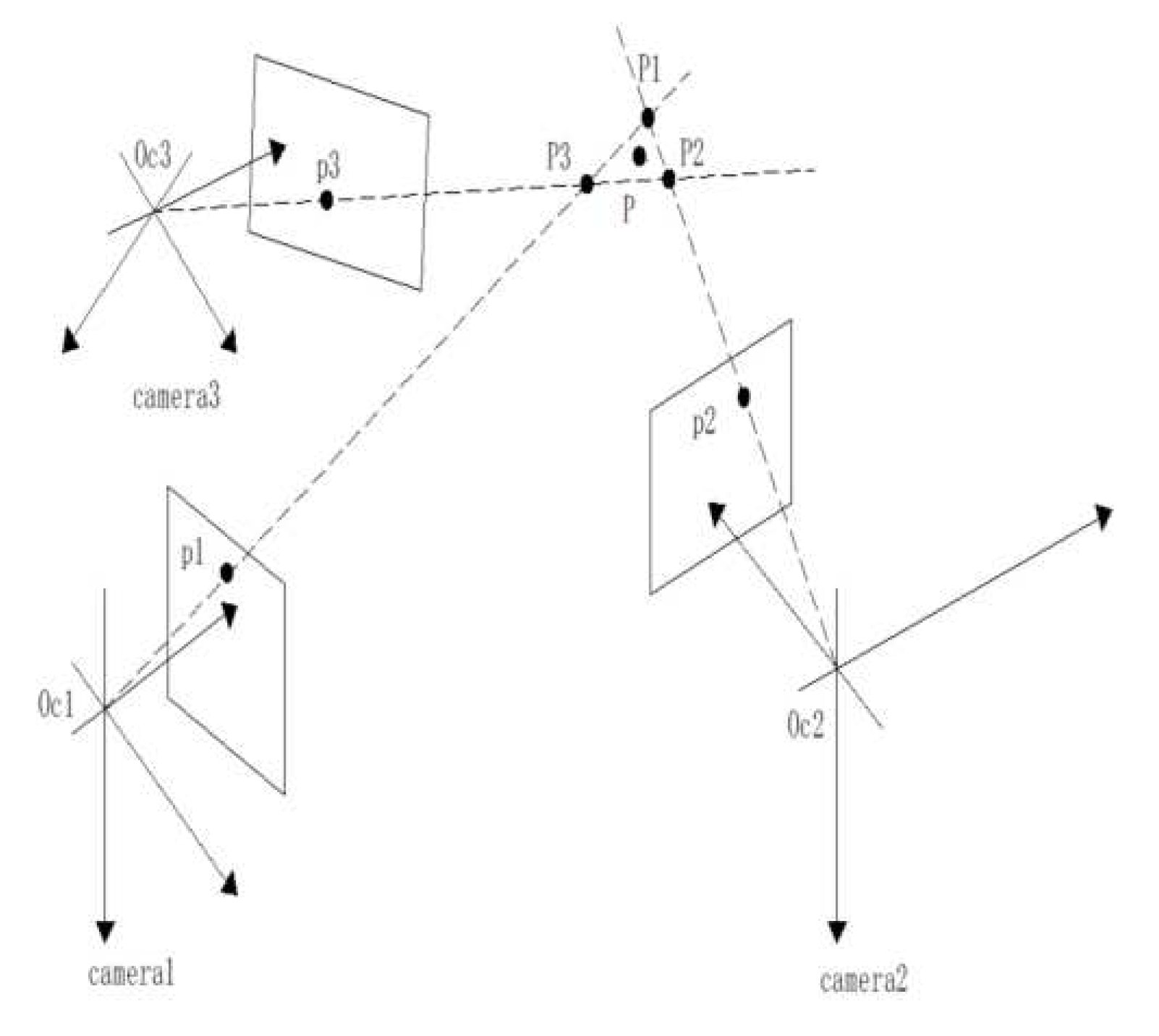
1. Trinocular vision model

1.1. Two-dimensional vision

Machine vision[14] is the intersection of artificial intelligence and computer vision[15], which allows machines to be able to process image information, video information, and a variety of signals like humans, and process these signals accordingly, and make the decisions and actions we expect, assisting humans to complete a variety of tasks, and simulating and expanding the visual ability of humans. Machine vision is of great significance in improving the productivity and efficiency of factories and certain large-scale enterprises.

Binocular stereo vision technology through two cameras to get to the target object of the different viewpoints of the picture, the camera can be based on their own goals to choose the specific function of the model, simulate the human eye, extend the human eye function, access to the target object of the three-dimensional information, and make the corresponding processing and judgment.

In binocular stereo vision, two cameras are generally made to have their camera centers in the same straight line, spaced a certain distance apart from each other, and facing the same direction. Then the internal and external parameters of binocular camera are obtained by Zhang Zhengyou calibration method, after the calibration of the camera, then the two images are processed by the algorithm to get the important information such as parallax map, depth map and so on. However, the depth information acquired by binocular stereo vision is limited, and the acquired depth image will still have a certain error, and there will be a certain degree of mis-matching points when stereo matching.

1.2. Three-dimensional vision

The trinocular camera has a better visual matching effect compared with the binocular camera. Assuming that the object is located at a certain point P, the projection point of the target object on its imaging surface in camera 1 is p₁ , and the camera coordinate origin is O_c1 , similarly, the corresponding points in camera 2 and camera 3 are set to p₂ , O_c2 and p₃ , O_c3 respectively. Due to camera aberrations, as well as the solution error in the least squares[16] calculation and the noise generated during calibration, the line between the origin and the projection point of the three groups of cameras will be slightly shifted the real position P of the target object, resulting in the coordinate position P₁ of the target image captured by the binocular vision system composed of camera 1 and camera 2 inevitably cannot coincide with the display position P of the target object. Similarly, the target image positions P₂ and P₃ captured by camera 2 and camera 3 as well as camera 1 and camera 3 will also fail to coincide with each other and the target object.

In order to reduce the gap between the position of the target image obtained by the binocular vision system composed of each group of cameras and the actual position of the target object in the world coordinate system, reduce the impact of subsequent calculations, and improve the effect of 3D reconstruction, this paper proposes a joint solution algorithm based on trinocular cameras to realize the joint optimization of coordinate points P₁ , P₂ and P₃ , reduce the system error, and make the actual coordinate values of the target object obtained more accurate.

From Figure 1, it can be intuitively seen that the object world coordinate point P is in the middle of P₁ , P₂ and P₃ , so it can be considered that the minimum value of the sum of the relative distances between P and these three points is the more accurate real coordinate point. That is, as shown in Equation (1-1).

F = \min (‖P - P_{1}‖ + ‖P - P_{2}‖ + ‖P - P_{3}‖)

(1-1)

Let camera 1, 2 measured point P₁ coordinates are (X₁ ,Y₁ ,Z₁ ), similarly, the coordinates of point P₂ and point P₃ are (X₂ ,Y₂ ,Z₂ ) and (X₃ ,Y₃ ,Z₃ ), the three coordinate point values are substituted into the formula (1-1) expansion to obtain.

\begin{array}{l} F = \min [{(X - X_{1})}^{2} + {(X - X_{2})}^{2} + {(X - X_{3})}^{2}] \\ + \min [{(Y - Y_{1})}^{2} + {(Y - Y_{2})}^{2} + {(Y - Y_{3})}^{2}] \\ + \min [{(Z - Z_{1})}^{2} + {(Z - Z_{2})}^{2} + {(Z - Z_{3})}^{2}] \end{array}

(1-2)

Thus the true coordinates of the point P can be derived by applying the properties of the arithmetic mean, i.e., as shown in Equation (1-3).

\{\begin{cases} X = \frac{X_{1} + X_{2} + X_{3}}{3} \\ Y = \frac{Y_{1} + Y_{2} + Y_{3}}{3} \\ Z = \frac{Z_{1} + Z_{2} + Z_{3}}{3} \end{cases}

(1-3)

By solving the above equation for the coordinate values of realistic target points, more accurate values can be obtained than those of binocular vision systems.

2. Target image optimization processing

2.1. Image grayscaling

In order to achieve the desired effect in stereo matching, it is necessary to first exclude the interference of noise, illumination, pixels and other factors as much as possible, so the image needs to be grayed out and image enhanced first, which can reduce the computation of the program processing procedure while still retaining the complete two-dimensional information of the image. In the RGB model, if R=G=B, then the color indicates a gray-scale color, where the value of R=G=B is called the gray-scale value, therefore, the grayscale image only one byte per pixel to store the gray-scale value, the gray-scale range of 0-255, when the grayscale is 255, it means the brightest; when the grayscale is 0, it means the darkest.

The benefits of grayscale are: compared to color images grayscale images take up less memory and run faster; after the grayscale image can visually increase the contrast and highlight the target area.

In this paper, the weighted average method is used to weight the R, G and B components according to the more suitable weights, as shown in Equation (2-1).The effect is shown in Figure 2

G r a y = \frac{W_{R} \times R + W_{G} \times G + W_{B} \times B}{3}

(2-1)

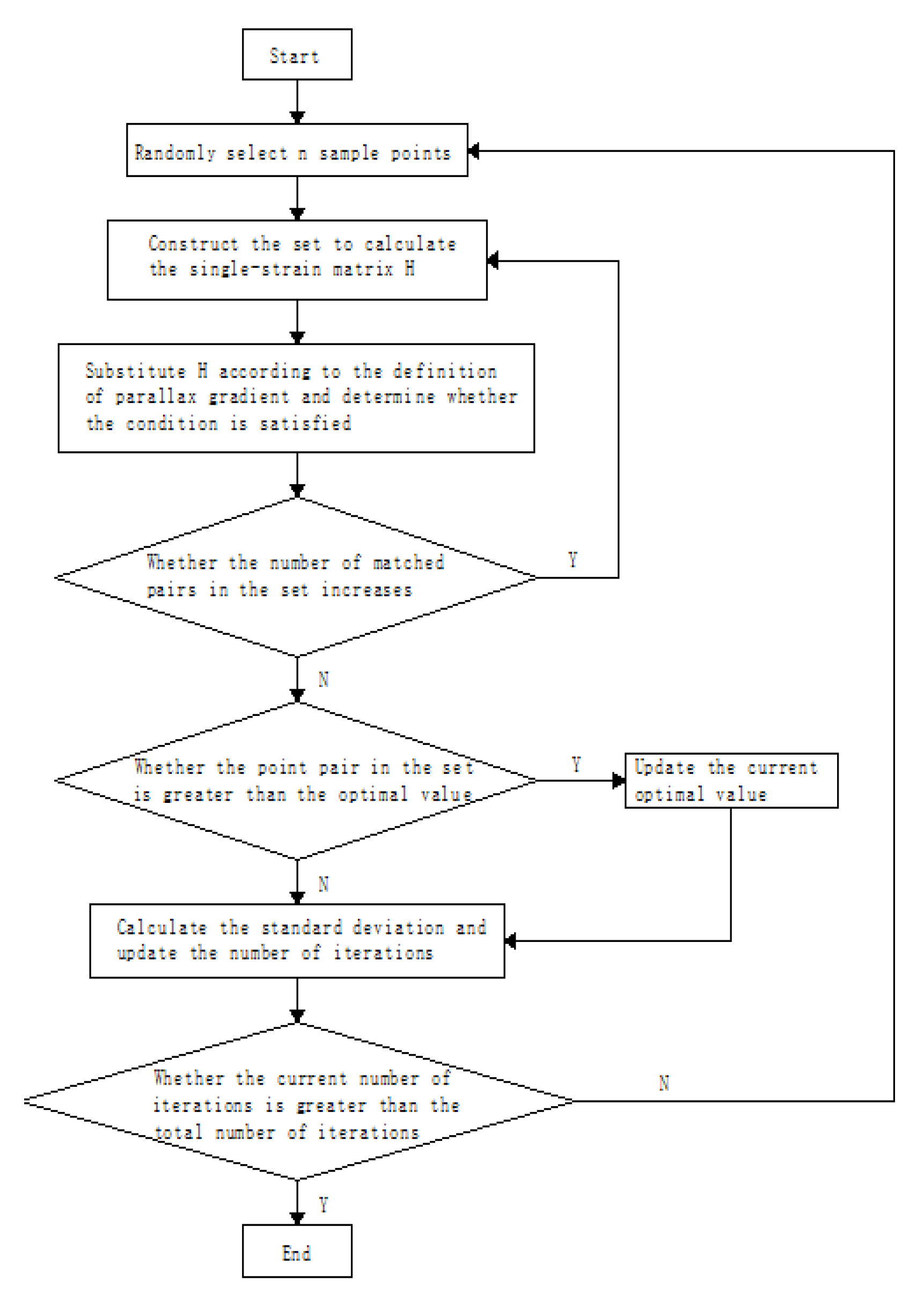
2.2. Improved RANSAC algorithm

(1): Traditional algorithm

First, a matrix H of size three rows and three columns is created, so that the matrix is equal to one making the matrix normalized, and since there are eight unknown parameters, at least four sets of matching point pairs are needed to correspond to the location information.

[\begin{matrix} x_{2} \\ y_{2} \\ z_{2} \end{matrix}] = [\begin{matrix} H_{11} & H_{12} & H_{13} \\ H_{21} & H_{22} & H_{23} \\ H_{31} & H_{32} & H_{33} \end{matrix}] [\begin{matrix} x_{1} \\ y_{1} \\ z_{1} \end{matrix}]

(2-2)

Namely.

X_{2} = H \cdot X_{1}

(2-3)

where the points I₁ and I₂ correspond to the coordinates (x₁ ,y₁ ) and (x₂ ,y₂ ), respectively, while the size of z₁ , which is introduced into the chi-square equation, is 1.

x_{2} = [\frac{H_{11} \cdot x_{1} + H_{12} \cdot y_{1} + H_{13} \cdot z_{1}}{H_{31} \cdot x_{1} + H_{32} \cdot y_{1} + H_{33} \cdot z_{1}}] = [\frac{h_{11} \cdot x_{1} + h_{12} \cdot y_{1} + h_{13}}{H_{31} \cdot x_{1} + H_{32} \cdot y_{1} + 1}]

(2-4)

y_{2} = [\frac{H_{21} \cdot x_{1} + H_{22} \cdot y_{1} + H_{23} \cdot z_{1}}{H_{31} \cdot x_{1} + H_{32} \cdot y_{1} + H_{33} \cdot z_{1}}] = [\frac{h_{21} \cdot x_{1} + h_{22} \cdot y_{1} + h_{23}}{H_{31} \cdot x_{1} + H_{32} \cdot y_{1} + 1}]

(2-5)

The equation containing four matched pairs of points is then solved for.

A \cdot u = ν

(2-6)

Matrix of unknowns.

A = [\begin{matrix} x_{1} & y_{1} & 1 & 0 & 0 & 0 & - x_{1} {x^{'}}_{2} & - {z^{'}}_{1} y_{1} \\ 0 & 0 & 0 & x_{2} & y_{2} & 0 & - x_{1} {y^{'}}_{2} & - y_{1} {y^{'}}_{2} \end{matrix}]

(2-7)

Vector of unknowns.

u = {[\begin{matrix} h_{11} & h_{12} & h_{13} & h_{21} & h_{22} & h_{23} & h_{31} & h_{32} & h_{33} \end{matrix}]}^{T}

(2-8)

Value vectors.

ν = {[{x^{'}}_{2}, {y^{'}}_{2}]}^{T}

(2-9)

The traditional RANSAC algorithm[17] will first extract a part of matching points from the first matching result, and then construct a primary model to calculate the remaining matching points, and will classify the resulting point pairs into two types: matching original model and non-matching original model, where the point pairs matching original model are also called valid data, and the other type of point pairs are invalid data. Then, some matching pairs are extracted from the valid data, and the optimal model is obtained by continuing to distinguish good data from bad data in the above way and iterating continuously. Finally, the data model in the optimal model is solved, and the point pairs that do not meet the matching conditions are excluded to achieve data optimization.

(2): Improved mis-matching algorithm

Before the improvement of RANSAC algorithm, when matching feature points, there is a situation that a feature point is used multiple times to correspond to other points. In this paper, after optimizing the RANSAC algorithm, in order to improve the purification effect and reduce the situation that one point is used more than one time, this paper optimizes the RANSAC algorithm by setting the queue value and solving the single-response matrix. The flow chart of the algorithm is shown in Figure 3.

Assume that the number of samples in the data is K, P is the model probability (confidence probability) of the local points at the iteration, n is the minimum value to successfully solve the formula, N_i is the local points, N_t is the external points, and

ω

is the ratio of the local points to the total number of points in the data, i.e.

ω = \frac{N_{i}}{N_{i} + N_{t}}

(2-10)

The probability that there will always be an outlier during the iteration is

(1 - P^{k})

; the probability that at least one of the n points is an outlier is [19]:

(1 - ω^{n})

Combining the two outlier probabilities yields the formula

P = 1 - {(1 - ω^{n})}^{k}

(2-11)

When k → ∞, P → 1 general P = 0.995.

Sample size:

k = \frac{\log (1 - p)}{\log (1 - ω^{n})}

(2-12)

Among all matching points of the image to be extracted, n are selected as sample points. According to the definition of parallax gradient, two pairs of matching points are selected among all the extracted data points for calculation and comparison, and the model parameters of the data matching points that meet the requirements are selected and the matching points that do not meet the requirements are excluded. The standard deviation of k is then used to calculate the size of the standard deviation and compare the number of better matched points obtained for each group by.

S D (k) \frac{\sqrt{1 - ω^{n}}}{ω^{n}}

(2-13)

The points with the best quality of matched points are then brought into the model parameters, and all outlier points are removed, and the remaining points with higher matching rates are used to calculate the model parameters. Then reverse search is performed to determine the correct rate of point pair matching, set the queue value using Hamming distance as a similarity measure, eliminate the feature points that do not meet the conditions, and then apply single response matrix verification to get more accurate matching points.

Repeat the above steps, and finally get the largest number of pairs of correct matching points in the set.

The image acquisition was performed by the camera in the middle of the trinocular vision system, and the relay was selected as the template reference for the feature matching experiments, and four cases of interference, rotation, interference plus rotation and scale change were designed. The experiments were conducted with the traditional SURF algorithm and the improved feature matching algorithm based on SURF+RANSAC, respectively, and the results are shown in Figure 4. The correct alignment rate is used to indicate the performance of the algorithm feature descriptors. The higher the correct rate, the higher the accuracy of recognizing the target by the algorithm using the template image, using the directional consistency principle to obtain the matching logarithm. The number of correct matching pairs, the total matching pairs and the algorithm matching time for the initial image and the image to be detected with environmental influence in five cases are counted, as shown in Table 2-1.

In Figure 4, (a), (c), (e) and (g) are the matching results under different situations based on the traditional SURF algorithm, where the corresponding lines of left and right image matching are seriously skewed and quite misleading, with "one point corresponds to many points", "point to point cross matching [18]"The matching results based on the improved algorithm of SURF+RANSAC combined with the principle of parallax gradient are shown in Figs. (b), (d), (f) and (h), which can be found intuitively that the feature point pairs of relay interface and label information and other details are more uniform, and there is no " One-to-many" phenomenon, the alignment effect is greatly improved and the robustness is better.

2.33. D reconstruction

Considering the inevitable errors in the actual system, the least squares method is used to obtain Equation (2-14), where

X = {[\begin{matrix} X & Y & Z \end{matrix}]}^{T}

,A,B are known, to find the value of the three-dimensional coordinates of a point in the world.

X = {(A^{T} A)}^{- 1} A^{T} B

(2-14)

Also combining Equation (1-1), the trinocular visual reconstruction coordinates are obtained from the arithmetic mean property.

P^{`} = \frac{P_{1} + P_{2} + P_{3}}{3}

(2-15)

The 3D reconstruction displays the 3D reconstruction of the relay in OpenGL, as shown in Figure 5 for the reconstruction generated by the target object captured by the binocular camera.

3. Parallel robot gripping

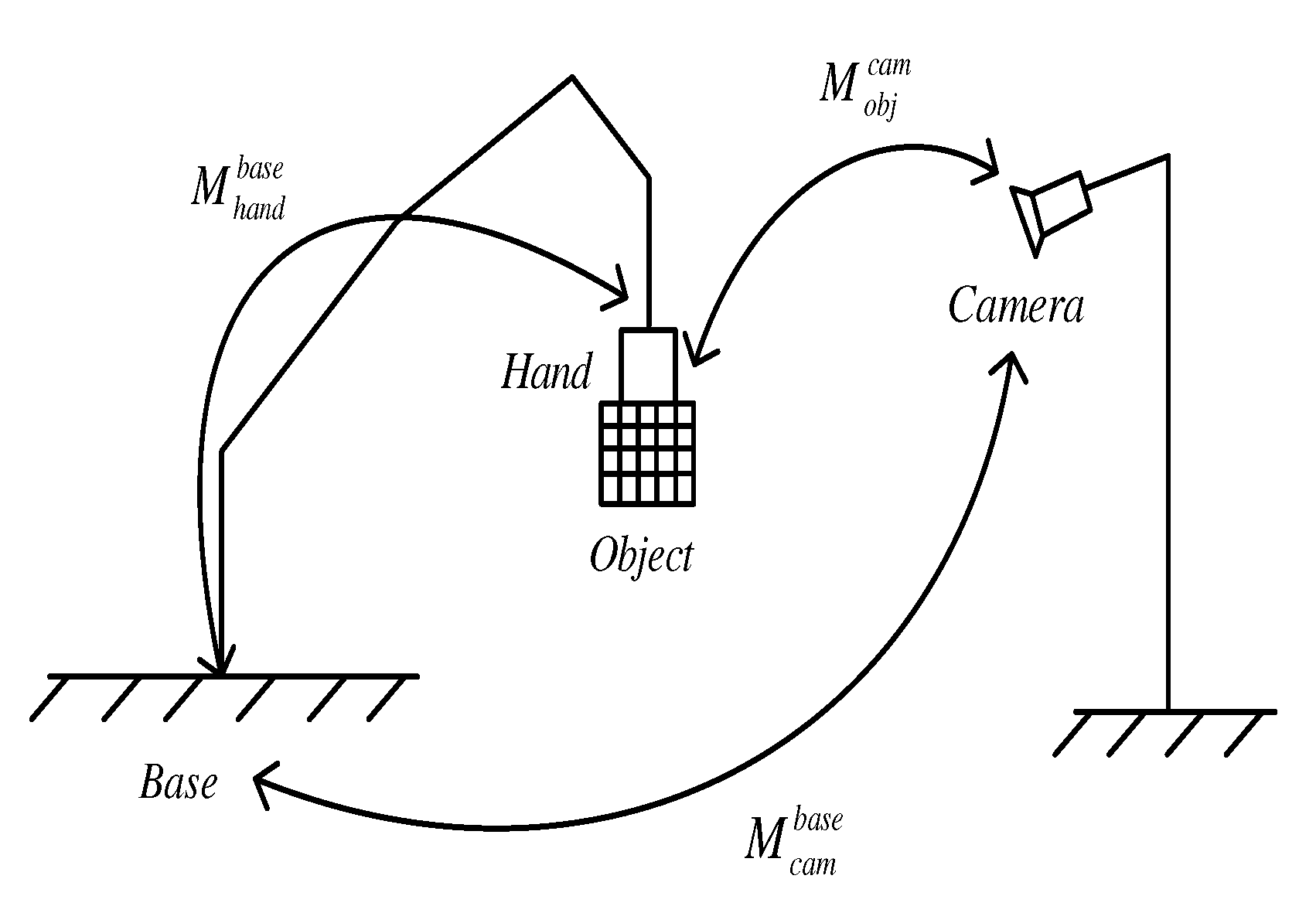
3.1. Hand-eye calibration

What the hand-eye calibration calibrates is the transformation matrix from the camera to the robot coordinate system. For accurate grasping of the target object, it is necessary to know the position of the target object with respect to the orientation in the robot's base coordinate system.

Hand-eye calibration is a kind of eye on the hand, its camera coordinate system and end coordinate system fixed connection, their relative position relationship is fixed, so the calibration is the camera to the end. Another for the eye in the hand outside, because the camera and the robot are fixed, their relative position is unchanged, so this way of calibration is the camera coordinate system and the robot base coordinate system.

In this paper, the eye-to-hand mode (Eye-to-Hand) is used for hand-eye calibration, and the relative position relationship between each coordinate system is shown in Figure 6.

During the calibration process, the calibration plate is fixed to the robot suction cup, and the relationship between the two is always constant regardless of the robot motion, and the positional parameters on the demonstrator are recorded during the calibration process.

Let the relationship between the end-effector and the base coordinates of the robot base when the robot is working to the nth group be

{(M_{b a s e}^{hand})}_{n} = Q_{n}

(3-1)

The relationship of the filming system with respect to the polar coordinate system of the manipulator base is

{(M_{c a m}^{base})}_{n} = W_{n}

(3-2)

The matrix between the calibration plate and the coordinate system of the shooting system is

{(M_{o b j}^{cam})}_{n} = E_{n}

(3-3)

When the table works to group i with group j, there is Equation (3-4) holds.

Q_{i} \cdot W_{i} \cdot E_{i} = Q_{j} \cdot W_{j} \cdot E_{j}

(3-4)

Transforming Equation (3-4) yields

Q_{j}^{- 1} \cdot Q_{i} \cdot W_{i} = W_{j} \cdot Z_{j} \cdot Z_{i}^{- 1}

(3-5)

Order.

A = Q_{j}^{- 1} \cdot Q_{i}, B = E_{j} \cdot E_{i}^{- 1} ， X = W_{i} = W_{j}

(3-6)

Thus, for group i and group j the change in position of the robot as it moves can be reduced to

A X = X B

(3-7)

Among them.

A represents the relationship between the twice displaced robot end-effector and the base coordinates, which can be obtained from the robot system by means of a schematic trainer.

B represents the relationship between the calibration plate and the camera at two displacements, obtained by camera calibration.

X is the final result of the hand-eye calibration, i.e., the mathematical relationship between the camera and the robot arm base.

3.2. Positioning and grasping experiments

The processed images are processed by the stereo matching algorithm to obtain the information of the 3D reconstructed model. The information obtained under the camera coordinate system is converted to the robot coordinate system by using the hand-eye calibration algorithm. In the SGBM algorithm, the camera coordinate values of the target object and the four corner points and the center point on the robot demonstrator are obtained respectively, and then the coordinate values are converted to obtain their corresponding 3D coordinate information according to the above obtained data and the hand-eye calibration algorithm, and the upper computer communication is applied to transmit the object shape center coordinates to the Finally, the identification and grasping of the target object is completed according to the corresponding internal program. Figure 7 shows the establishment of the experimental platform.

By randomly placing 28 target objects, a total of 10 sets of experimental data of accuracy when grasping cylindrical blocks were counted. From the data in Table 3-1, it can be seen that the improved RANSAC algorithm has significantly improved the accuracy of target recognition and grasping compared to the SURF algorithm.

4. Summary

In this paper, the trinocular camera is used to capture and recognize a wider range of data than the binocular camera. The traditional SURF algorithm is integrated with RANSAC algorithm to eliminate the phenomenon of "one-to-many" in feature matching and make the selection of feature points more reasonable, and the matching rate is increased from 60.38% to 93.78% compared with the algorithm before optimization; and the object 3D spatial information can be restored better, which makes the The improved RANSAC algorithm can make the grasping target of multi-vision parallel robot more accurate and improve the working efficiency.

References

Chen W, Luo X, Liang Z, et al. A Unified Framework for Depth Prediction from a Single Image and Binocular Stereo Matching[J]. Remote Sensing, 2020, 12(3): 588. [CrossRef]
Okutomi, M.; Kanade, T. A multiple-baseline stereo. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 353–363. [Google Scholar] [CrossRef]
Jie Yang, Yunsong Hua, A SURF optimization algorithm applied to binocular ranging[J]. Software Guide, 2021, 20(08): 195-199. [CrossRef]
Lowe D G . Lowe, D.G.: Distinctive Image Features from Scale-Invariant Key-points. Int. J. Comput. Vision 60(2), 91-110 [J]. International Journal of Computer Vision, 2004, 60(2). [CrossRef]
BAY H. SURF: Speeded up robust features [J]. Computer Vision & Image Understanding, 2006, 110(3):404-417. [CrossRef]
Kumar Gundugonti Kishore, Shaik Mahammad Firose,kulkarni Vikram, Busi Rambabu. Power and Delay Efficient Haar Wavelet Transform for Image Processing Application[J]. Journal of Circuits, Systems and Computers, 2022, 31(08). [CrossRef]
Lin Psang Dain. Simple and practical approach for computing the ray Hessian matrix in geometrical optics.[J]. Journal of the Optical Society of America. A,Optics,image science,and vision, 2018,35(2). [CrossRef]
Huang Yingqing, Yan Zhan, Jiang Xiaoyu, Jing Tao, Chen Song, Lin Min, Zhang Jinguo, Yan Xingpeng. Performance Enhanced Elemental Array Generation for Integral Image Display Using Pixel Fusion[J]. Frontiers in Physics, 2021,9. [CrossRef]
Jianguo Cui, Changku Sun, Yupeng Li, Luhua Fu, Peng Wang. Improved algorithm for fast image matching based on SURF[J/OL]. Journal of Instrumentation:1-8[2022-10-28].
Yang, Gen-Xin, Wang, You-Kun, Xie, Zheng-Ming. Scene judgment enhanced SURF image matching algorithm[J]. Survey and Mapping Bulletin,2022(S2):233-236+259.
Huang H-B, Nie X-F, Li X-L, et al. Research on bi-directional feature matching algorithm based on normalized Euclidean distance[J]. Computers and Telecommunications, 2018(11):35-40.
Zhao Chengxing, Zhang Xiaoling, Yang Yu, 3D reconstruction based on SGBM semi-global stereo matching algorithm[J]. Laser Journal,2021,42(04):139-143.
Zijian Zhao and Ying Weng. A flexible method combining camera calibration and hand-eye calibration[J]. Robotica. 2013, 31(5):747-756. [CrossRef]
Sonka M,V Hlavác,Boyle R.Image processing,analysis,and machine vision[J].Journal of Electronic Imaging,2014,xix.
.Russakovsky O,Deng J,Su H,et al.ImageNet Large Scale Visual RecognitionChallenge[J].International Journal of Computer Vision,2015,115(3):211-252. [CrossRef]
Deng Gaoxu, Wu Shiqian, Zhou Shiyang, Chen Bin, Liao Yucheng. A Robust Discontinuous Phase Unwrapping Based on Least-Squares Orientation Estimator[J]. Electronics,2021,10(22). [CrossRef]
Martin, A. Fischler and Robert C. Bolles. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Commun. ACM, 1981, 24(6) : 381-395.
Lu, Xianxiao. Research on workpiece positioning technology based on binocular stereo vision[D]. Zhejiang University,2019.
Junhua Kang, Lin Chen, Fei Deng, Christian Heipke. Context pyramidal network for stereo matching regularized by disparity gradients[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2019,157(C). [CrossRef]

Figure 1. Convergent trinocular stereo vision model.

Figure 2. Image pre-processing.

Figure 3. Flowchart of improved mis-matching RANSAC algorithm.

Figure 4. Experimental comparison of two algorithms in different scenarios.

Figure 5. 3D reconstruction point cloud of the relay.

Figure 6. Relationship between the position of the eye in each coordinate outside the hand.

Figure 7. Experimental platform.

Table 2-1. Comparison of the performance data of the two algorithms.

Scenes	Algorithm	Total number of matched pairs	Correctly matching logarithms	Correct match rate/%	Matching time/s
Interference	SURF	123	74	60.38	1.913
Interference	Improvements	96	93	97.32	1.482
Rotation	SURF	138	109	78.75	1.620
Rotation	Improvements	99	92	93.78	1.113
Rotation plus interference	SURF	103	70	67.89	1.749
Rotation plus interference	Improvements	92	89	96.98	0.948
Scale change	SURF	113	87	77.32	1.561
Scale change	Improvements	98	96	97.90	1.215

Table 3. Object data grasped by robots with different algorithms.

Number of experimental groups (groups)	SURF algorithm grabs objects (pcs)	SURF algorithm crawl accuracy (%)	Improvements to RANSACNumber of catches (pcs)	Improvements to RANSACCrawl accuracy (%)
1	20	71.43	25	89.29
2	21	75.00	27	96.43
3	18	64.28	27	96.43
4	22	78.57	26	92.86
5	20	71.43	26	92.86
6	19	67.85	25	89.29
7	22	78.57	26	92.86
8	23	82.14	27	96.43
9	20	71.43	27	96.43
10	22	78.57	25	89.29

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer