A Novel EEG Classification Method for Quantifying Kinematic Parameters

David Collins

doi:10.20944/preprints202308.2103.v1

Preprint

Hypothesis

A Novel EEG Classification Method for Quantifying Kinematic Parameters

This version is not peer-reviewed.

David Collins^*

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

28 August 2023

Posted:

31 August 2023

You are already at the latest version

Abstract

Abstract: In recent years, low frequency (LF) electroencephalogram (EEG) signals have been decoded to obtain kinematic trajectories with the aim of achieving closed loop natural control. However, decoded trajectories suffer variability and low correlation against the measured movement. This paper suggests that if EEG features of motor intents are directly associated with fixed points along a given range of motion, then the natural kinematic parameters can be quantified. A novel classification method is proposed to evaluate this hypothesis along with equations for obtaining the movement parameters (velocity, acceleration). Furthermore, this implies that the force of an end-effector and work done in moving the end-effector may be computed, leading to natural control of EEG-based robotic arms and neuroprostheses. Finally, expectations are that combining the proposed method with existing classification methods will increase the accuracy and scalability of brain-computer interface (BCI) applications.

Keywords:

Keywords: Kinematic trajectories

;

movement parameters

;

natural closed loop control

;

EEG decoding

;

classification method

;

brain-computer interface

;

BCI

Subject:

Engineering - Bioengineering

1. Introduction

Loss of motor function caused by stroke, spinal cord injury or other neurological or neuromuscular diseases generally reduces the quality of life. Researchers continue to push the boundaries of BCI technology as a means to regain control of devices. So far EEG based BCIs have successfully been used to control cursors [1], games [2], spelling applications [3], drones [4]. Researchers have also used EEG based BCIs for continuous control of robotic arms [5,6], and virtual arms [7]. However, these BCIs do not accurately express the natural kinematic parameters (velocity, acceleration) of voluntary movement due to low correlation between the measured movement and decoded trajectories.

Decoding kinematics of natural hand movements from EEG was first reported in [8], three-dimensional (3D) hand velocity was continuously reconstructed from the LF band of the signals. This was further confirmed in several studies using linear regression models [9,10,11], however, only few of these studies report online decoding. Mondini et al [6] performed the first continuous online control of a robotic arm with LF-EEG-based decoded movements, obtaining correlations of 0.32 on average between hand kinematics and decoded trajectories. 3D trajectories of imagined arm movements have also been decoded online, from spectral density of mu, low beta, high beta, and low gamma EEG oscillations [7] using multiple linear regression to control virtual arms. However the real-time control reported was in the range of chance (33.3%).

Recent studies have focused on decoding EEG signals to obtain kinematic trajectories, the performance of decoding is however subject to scaling limitations and there is also variability in the decoded trajectories [10]. Sensorimotor rhythm amplitude has also been used for 2D cursor control [12], robotic arm control [5], however to improve movement, adaptive weights were applied to minimize the difference between actual and predicted target locations during tasks. Molina-Cantero et al. [13] controlled a mouse pointer with a single channel EEG. The speed of the mouse pointer was modulated by users’ attention level, though the minimum and maximum values were pre-defined.

This paper proposes a classification method for quantifying movement parameters (velocity, acceleration) rather than decoding EEG signals. The research focused on the alpha (8Hz – 13Hz) and beta (14Hz – 30Hz) rhythms of the acquired signals. Typical application of the classification method was described for the control of a virtual slider using band power features. To reduce cost a single channel EEG was built to acquire signals between 7Hz and 30Hz. Movement parameters were ultimately controlled by the users’ attention level.

2. Hypothesis and Classification Method

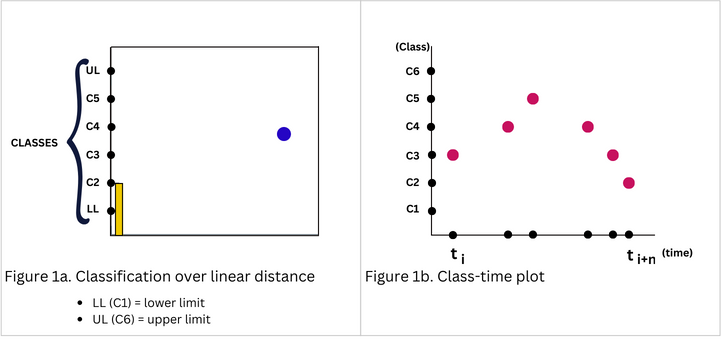
This paper hypothesizes that if the features of motor intents are directly associated with points along a given range of motion, then the natural kinematic parameters of the motor intents can be quantified. The classification method followed the statistical analogy of collection, ordering and analysis of continuous data. Firstly the range of motion of the virtual slider (end-effector) was determined then the upper and lower limits were defined. The latter was divided to create classes, each representing a point along the path (Figure 1a). Extracted features were ordered in the classes after determining class intervals and boundaries of the features.

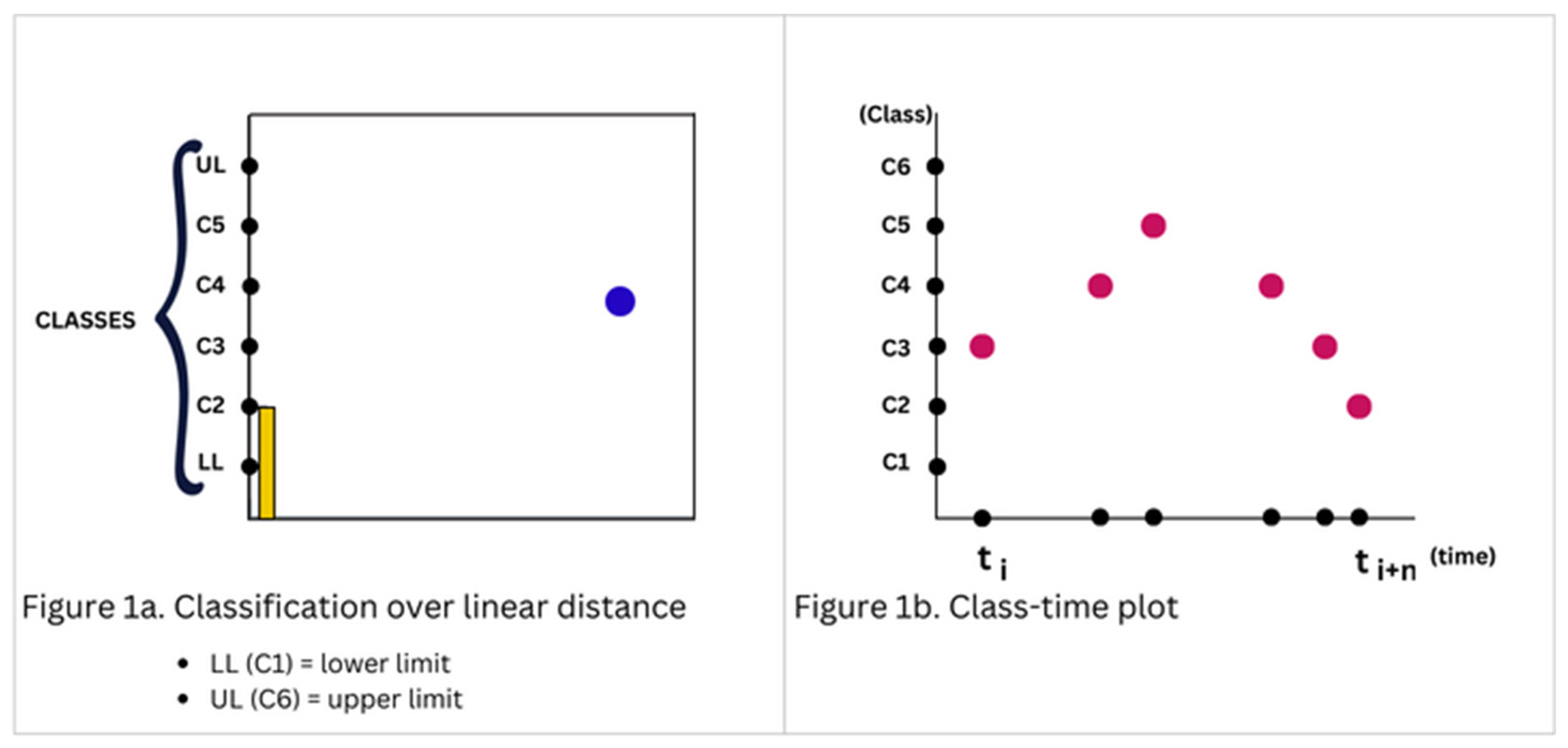
Kinematic parameters were computed by considering displacement as the distance between the current and previous class (points along the range), and the time interval between the said classification. Hence, rather than obtaining kinematic parameters through decoding and reconstruction from LF-EEG, the classification process provides the basis for their computation.

3. Evaluation

3.1. Signal Acquisition

A portable battery powered single channel EEG was built to reduce cost, with cut-off frequencies of 7Hz and 30Hz. Hence attention level was considered between alpha and frequency bands. Wet gold plated electrodes were used, placed at Fp1 and the reference electrode on A1 (left mastoid) considering the international electrode placement 10-20 recommended by the American clinical neurophysiology society [14].

3.2. Feature Extraction

A digital band pass filter was applied to the raw EEG signal with cut-off frequencies 7Hz and 30Hz. The power distribution across the alpha waves frequency band was obtained using Fast Fourier Transform (FFT). Power spectral density (PSD) of frequencies within the frequency bands was calculated by squaring the magnitude of the complex FFT coefficients, and band power was obtained.

3.3. Classification

Classes were created after defining the upper and lower limits of the linear distance. The lower and upper limits represented the first and last classes respectively (Figure 1a). In this study, the frequencies across the alpha and beta bands (8Hz – 30Hz) were ordered evenly in the classes ensuring uniform class intervals.

Kinematic parameters of the virtual slider were computed by first analyzing the frequency band with the higher band power and obtaining the class with the highest PSD within the band. Afterwards, velocity was obtained by considering rate of change of class (Figure 1b), described by Equations (1) and (2). Where

D_{i}

and

V_{i}

are the displacement and velocity intended by the user,

C_{c}

and

C_{i}

are the current class and the intended class (positions), and

t_{c}

and

t_{i}

are the time of classification of

C_{c}

and

C_{i}

respectively.

{D_{i} = | C}_{i} - C_{c} |

(1)

V_{i} = \frac{| C_{i} - C_{c} |}{t_{i} - t_{c}}

(2)

Finally, acceleration was computed as described in Equation (3) as the time rate of change of velocity. Where

A_{i}

is the intended acceleration, and

V_{c}

and

V_{i}

are the current and intended velocities respectively.

A_{i} = \frac{| V_{i} - V_{c} |}{t_{i} - t_{c}}

(3)

3.4. Discussion

The classification method proposed is a working hypothesis for BCI applications involving continuous control over a given range (linear, angular), such as robotic arms and neuroprostheses. The path of the slider represents an approximate attention scale from alpha to beta frequency bands [15]. Hence the BCI expresses attention level as a point along the linear distance (upper-lower limits). However, this paper focuses on the movement parameters (velocity, acceleration) of the end-effector.

More so, the force and work done in moving the end-effector may also be obtained as described in Equations (4) and (5). Where

F_{i}

is the amount of force intended to be exerted,

W_{i}

is the amount of work intended to be done,

m

is the mass of the end-effector,

n

is the number of displacements between the classes and

D_{f}

is the final displacement of the end-effector.

F_{i} = m A_{i}

(4)

W_{i} = \sum_{n = D_{i}}^{D_{f}} [F_{i} D_{i}]

(5)

The performance of a classifier developed from the proposed method, may be evaluated by correlating measured movement against quantified trajectories. Combining a classifier of this sort with existing classification methods may increase accuracy and scalability of BCI applications. Finally, applications involving two or more types of features, present an opportunity to explore Fuzzy logic in the classification process.

4. Conclusion

This paper further pushes the boundaries of noninvasive BCI development by presenting a classification method for quantifying rather than decoding and reconstructing movement parameters. Obtaining accurate movement parameters for BCI applications will increase the general quality of life of people after the loss of motor function. Over the years, decoding EEG signals to obtain kinematic trajectories has been investigated in both offline and online studies, however, decoding performance is subject to scaling limitations and there is also variability in the decoded trajectory [10].

This paper suggests that features be directly associated with fixed points along a linear or angular distance, hence the rate of change of features (class) will imply the rate of change of displacement intended by the user, however, this must be further evaluated. Furthermore, the obtained parameters may be applied to end-effector tracjectories (position, velocity, acceleration) as well as grip force, for natural control of EEG-based robotic arms and neuroprostheses.

Acknowledgements

The author acknowledges the support of the departments of Mechanical & Mechatronics Engineering and Biomedical Engineering at Afe Babalola University (ABUAD).

Conflicts of Interest

The author declares no conflict of interest.

References

Z. Xiaoyuan, G. Cuntai, W. Jiankang, C. Yimin, and W. Yixiao, “Bayesian method for continuous cursor control in EEG-based Brain-Computer Interface,” Annu. Int. Conf. IEEE Eng. Med. Biol. - Proc., vol. 7 VOLS, no. February 2005, pp. 7052–7055, 2005. [CrossRef]
L. De Liao et al., “Gaming control using a wearable and wireless EEG-based brain-computer interface device with novel dry foam-based sensors,” J. Neuroeng. Rehabil., vol. 9, no. 1, 2012. [CrossRef]
F. Gembler, P. Stawicki, and I. Volosyak, “Autonomous parameter adjustment for SSVEP-Based BCIs with a novel BCI wizard,” Front. Neurosci., vol. 9, no. DEC, pp. 1–12, 2015. [CrossRef]
X. Duan, S. Xie, X. Xie, Y. Meng, and Z. Xu, “Quadcopter Flight Control Using a Non-invasive Multi-Modal Brain Computer Interface,” Front. Neurorobot., vol. 13, no. May, pp. 1–11, 2019. [CrossRef]
B. Xu et al., “Continuous Hybrid BCI Control for Robotic Arm Using Noninvasive Electroencephalogram, Computer Vision, and Eye Tracking,” Mathematics, vol. 10, no. 4, 2022. [CrossRef]
V. Mondini, R. J. Kobler, A. I. Sburlea, and G. R. Müller-Putz, “Continuous low-frequency EEG decoding of arm movement for closed-loop, natural control of a robotic arm,” J. Neural Eng., vol. 17, no. 4, 2020. [CrossRef]
A. Korik, R. Sosnik, N. Siddique, and D. Coyle, “Decoding imagined 3D arm movement trajectories from EEG to control two virtual arms-a pilot study,” Front. Neurorobot., vol. 13, no. November, pp. 1–22, 2019. [CrossRef]
T. J. Bradberry, R. J. Gentili, and J. L. Contreras-Vidal, “Reconstructing three-dimensional hand movements from noninvasive electroencephalographic signals,” J. Neurosci., vol. 30, no. 9, pp. 3432–3437, 2010. [CrossRef]
P. Ofner and G. R. Muller-Putz, “Decoding of velocities and positions of 3D arm movement from EEG,” Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. EMBS, pp. 6406–6409, 2012. [CrossRef]
A. Úbeda; J. M. Azorín, R. Chavarriaga, and J. del R Millán, “Classification of upper limb center-out reaching tasks by means of EEG-based continuous decoding techniques,” J. Neuroeng. Rehabil., vol. 14, no. 1, pp. 1–14, 2017. [CrossRef]
N. Robinson and A. P. Vinod, “Noninvasive Brain-Computer Interface: Decoding Arm Movement Kinematics and Motor Control,” IEEE Syst. Man, Cybern. Mag., vol. 2, no. 4, pp. 4–16, 2016. [CrossRef]
J. R. Wolpaw and D. J. McFarland, “Control of a two-dimensional movement signal by a noninvasive brain-computer interface in humans,” Proc. Natl. Acad. Sci. U. S. A., vol. 101, no. 51, pp. 17849–17854, 2004. [CrossRef]
A.J. Molina-Cantero, J. A. Castro-García, F. Gómez-Bravo, R. López-Ahumada, R. Jiménez-Naharro, and S. Berrazueta-Alvarado, “Controlling a mouse pointer with a single-channel eeg sensor,” Sensors, vol. 21, no. 16, pp. 1–31, 2021. [CrossRef]
J. N. Acharya, A. Hani, J. Cheek, P. Thirumala, and T. N. Tsuchida, “American Clinical Neurophysiology Society Guideline 2: Guidelines for Standard Electrode Position Nomenclature,” J. Clin. Neurophysiol., vol. 33, no. 4, pp. 308–311, 2016. [CrossRef]
M. Rodríguez et al., “Playing with your mind,” J. Phys. Conf. Ser., vol. 477, no. 1, pp. 1–10, 2013. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Novel EEG Classification Method for Quantifying Kinematic Parameters

Abstract

Keywords:

Subject:

1. Introduction

2. Hypothesis and Classification Method

3. Evaluation

3.1. Signal Acquisition

3.2. Feature Extraction

3.3. Classification

3.4. Discussion

4. Conclusion

Acknowledgements

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe