1. Introduction
Sea sites identified for potential tidal turbine installations are characterised by complex current conditions including high velocity magnitudes, sheared velocity profiles, turbulent flows and direction variability [
1,
2,
3]. Over that complexity, the presence of surface waves induces velocity fluctuations in the water column that affect the tidal kinetic energy resource [
4,
5] and cause unsteady loads on the tidal turbines. Indeed, numerical models such as the one presented in Perez et al. [
6] find that when Horizontal Axis Tidal Turbines (HATT) operate in large wave conditions at sea, the load cycle is governed by the periodic wave-induced velocity fluctuations while the average power and thrust are barely affected by the presence of waves. Similarly, waves with a significant wave height (
) close from 3 m induced torque and drag standard deviations of the order of 0.7 times the average values for the 1 MW-rated ducted Twin Vertical Axis Tidal Turbine (2-VATT) demonstrator installed by HydroQuest at the Paimpol-Bréhat test site [
7]. Therefore, the accurate prediction of the unsteady loads on tidal turbines induced by the waves is critical for a cost effective structural design while insuring mechanical resistance to extreme events and fatigue stress.
Over the past years, numerous studies have considered the effect of waves on reduced-scale HATT in towing tanks or flumes to better understand the wave-current-turbine interaction [
8] and provide reliable assessment of the unsteady loads endured by the turbine. Among the first, Barltrop et al. [
9] found that the root bending moments of rotor blades fluctuate significantly due to the waves and Gaurier et al. [
10] revealed that the average power and thrust are unaffected by the presence of waves but their standard deviations increase as a peak appears at the wave frequency in the torque and drag spectra. Later, Martinez et al. [
11] showed that the presence of waves propagating collinearly with the current are more detrimental than oblique ones and that they induce torque and thrust standard deviation that are almost double those associated with current only. Ordonez-Sanchez et al. [
12] analysed the performance of a HATT in the presence of both regular and irregular waves of similar characteristic heights and periods. They found no difference on the average power and thrust coefficients between the two wave cases but smaller fluctuation amplitudes with irregular waves than with regular ones. In addition, Martinez et al. [
13] observed a phase difference between the surface elevation and the thrust signals indicating that the turbine senses the waves before they reach the rotor plane. Such phase differences were also observed earlier regarding the forces exerted by surface waves on piles and were explained by the added mass force, which is proportional to the accelerative force exerted on the mass of water displaced by the pile [
14]. Lately, Draycott et al. [
15] offered a new insight into the nature of wave loading on a HATT revealing the rotational sampling of wave-induced velocities, that oscillate at the frequency
, by the blades rotating at the frequency
. As a result, they observed high frequency loading pattern on the blades with dominant frequencies at
(where
m and
k are any integers) whose magnitude decrease with
m and
k.
As opposed to the plentiful studies considering waves effect on HATTs, only a few studies considered the wave influence on VATTs although this type of turbine has several advantages [
16]. Bachant and Wosnik [
17] were the first to address the effect of waves on the average performance of a lift-based vertical axis water turbine. The experimental results showed an increase in power coefficient as well as a shift towards higher tip speed ratios of the whole power curve with waves compared to current only conditions. They suggested that the wave-induced fluid velocity could increase the blade angle of attack beyond its stall angle. Secondly, combining viscous CFD method and linear wave theory, Zhang et al. [
18] found that the instantaneous tip speed ratio of a Darrieus type rotor varies due to the presence of waves, which leads to thrust and power fluctuations. They explained the increase in mean thrust and power with waves by the non-linear relationships of the thrust (quadratic) and of the power (cubic) with the flow speed that induce larger thrust and power increases than decreases. Finally, Lust et al. [
19] tested a 1 m diameter H-Darrieus rotor in a tow tank with three regular surface waves of different height and period. They found, conversely to the two previous studies, that the presence of waves degrades the power production slightly when compared to the current only case, and that the power variation increases with the wave height. In addition, their results show that the waves modify the cyclic signatures in the power measurement depending on the phase difference between the blade angular position and the wave phase.
Several studies reveal that placing two counter-rotating vertical axis turbines side by side improves the power performance significantly and reduces the vertical torque on the turbine base, which is beneficial for the structural design [
20]. With twin vertical axis turbines, the relative counter-rotation direction of the side by side rotors, while not significantly affecting the power production, strongly modifies the two rotors’ wake interactions [
21,
22]. However, to the authors knowledge, apart from the above mentioned in-situ measurements [
7], no study considered the effect of waves on 2-VATTs. The present study aims at filling this gap by testing a 1/20 scale model of the 1 MW-rated 2-VATT demonstrator under several regular and irregular wave conditions in Ifremer’s wave and current flume tank. The
Section 2 describes the turbine model, the experimental setup, the flow conditions in the different wave cases and the data processing carried out for the analysis. Then, the
Section 3.1 presents the effects of the wave amplitude and frequency on the turbine power performance and loads, as well as the difference between regular and irregular waves. The wave-current-turbine interaction is further analysed in the
Section 3.2 focusing on one specific regular and irregular wave cases either with the rotors parked or operating at the optimal tip speed ratio.
2. Materials and Methods
2.1. Turbine model
The 1/20 scale model is a ducted 2-VATT geometrically similar to the 1 MW-rated demonstrator tested by HydroQuest at the Paimpol-Bréhat test site from 2019 to 2021 [
7]. It is composed of two independent counter-rotating vertical axis rotor columns. Each column is made of two levels of H-Darrieus type rotors with a 60° phase difference between them, and each rotor of radius
200 mm is made of
blades that are
190 mm high with a chord
c of 73 mm. Thus, the rotor solidity
is 1.1. The rotors are mounted in a
W = 1.24 m wide structure made of fairings and plates. The turbine height is defined as the distance between the top and the bottom horizontal plates such that
H = 0.45 m; and the 2-VATT capture area is
. For this study, the turbine is fixed on a tripod bottom-mounted base similar to the demonstrator’s one so the whole structure height is
= 0.84 m. The two rotor columns are controlled at a constant rotational speed by two independent
Maxon RE50 DC motors and
Escon 70/10 servo-controllers. The torque
Q of each rotor column is measured using
Scaime DR2112-W torque-meters and the rotational speeds
are measured by the motor encoders. The 6 load components applied between the turbine and the base and those between the base and the tank floor are measured using
SIXAXES 1.5 kN and 20 kN load cells, respectively (
Figure 1). All of these analog signals are acquired at a sampling frequency of 128 Hz using
National Instruments PXI and
LabView systems. The model and its instrumentation are fully described in Moreau et al. [
22].
The base geometry upstream and the relative counter-rotation direction of the two column is different when the flow comes from one side or the other of the device. The two flow directions are referred either to FC, corresponding to the Flood tide Configuration at the Paimpol-Bréhat test site, or to EC for the Ebb tide Configuration (
Figure 1a). The performance and wake differences between these two flow directions is presented in Moreau et al. [
22].
2.2. Experimental setup
The 2-VATT model is tested in the Ifremer wave and current flume tank in Boulogne-sur-mer, France (
Figure 1b), whose depth is
= 2 m and width is 4 m. It is operated at a velocity setpoint of 0.8 m.s
-1 in its low turbulence configuration with the inlet conditioned by a honeycomb structure and a uniform grid [
23]. The 2-VATT is placed in the ebb tide configuration at the centre of the tank
with
x in the main flow direction,
y towards the wall and
z towards the free surface with
at the tank bottom. The 2-Component Laser Doppler Velocimeter (2C-LDV) measures the velocities
along
at
at the centre of the turbine capture area, ie.
m. At this far upstream distance, the flow is not disturbed by the 2-VATT [
22]. The time average of
u at this location is considered as the reference far upstream velocity and is
= 0.825 m.s
.
In addition to the current, waves are generated to propagate against it, like during ebb tides at Paimpol-Bréhat offshore test site [
7]. In that configuration, the wave-current interaction tends to increase the wave height and shorten the wave length compared to waves on still water [
24]. To do so, wave makers are immersed downstream of the test section and a wave absorber is installed upstream [
23]. A servo type wave height meter (
Kenek SHT3-30) measures the free surface elevation (
) right above the 2-VATT at
. Seven wave cases are presented in this study including one irregular wave case noted
and six regular wave cases noted
, which indicates first the wave frequency and then the amplitude level. Three of the cases are regular waves at constant frequency (
= 0.4 Hz) and variable amplitude levels noted
(low),
(medium) and
(high); four cases are regular waves at variable frequencies from 0.2 to 0.5 Hz at the lowest amplitude level
; and one case presents irregular waves with a JONSWAP spectrum (with a peak enhancement factor
, according to Hasselmann et al. [
25]) with similar peak period (
) and significant wave amplitude (
, the average amplitude of the highest third of the waves) as the regular case
(
Table 1). Thus, we can assess the effect of the waves amplitude and their frequency on the 2-VATT response as well as compare the effect of regular and irregular waves.
For all the test cases, the 2C-LDV, the wave gauge and the turbine related signals are acquired simultaneously during 3 minutes to guarantee the time convergence of the average and the standard deviation of the signals. Over this time, the 2-VATT sees between 36 and 89 wave crests when
= 0.2 Hz and 0.5 Hz respectively. In this setup, the blade chord based Reynolds number (
, with
the water kinematic viscosity and
the tip speed ratio - Equation
5) is of the order of 8.5 10
4 which is about 60 times smaller than at full-scale; and the Froude number based on the submergence depth (
, with
g = 9.81 m.s
-2 the gravity constant) is 0.24 against 0.17 at full-scale. Due to the relatively low Reynolds number in the tank, we expect depreciated rotor performance compared to the full-scale 2-VATT [
26] but we expect the effect of the surface waves to be similar given the close Froude numbers.
2.3. Flow conditions
The velocity
, with
along
, can be decomposed such that
with
, the bar above indicating the time average, the prime the overall signal fluctuating part,
the turbulence contribution to the velocity fluctuations and
the waves contribution, called orbital velocity. According to the linear wave theory [
27], the free surface elevation
in presence of regular waves propagating along
x can be defined as a cosine function of the time
t and the space (equation
1 with
the wave number and
the wave pulsation). This surface elevation generates streamwise and vertical orbital velocities (
and
) in the water column. The orbital velocities are defined in equations
2 and
3 as a cosine and a sine function of time and space respectively, with
and
the orbital velocity amplitudes that depend on the depth and the surface wave characteristics. When waves propagate on top of a current, the definitions of
and
as well as the dispersion relation between
and
are modified but the orbital velocities remain defined of the same cosine and sine functions of time and space [
24].
The flow characteristics in presence of waves opposing the current in Ifremer’s tank were first presented in Saouli et al. [
28] and thoroughly described in Magnier [
29].
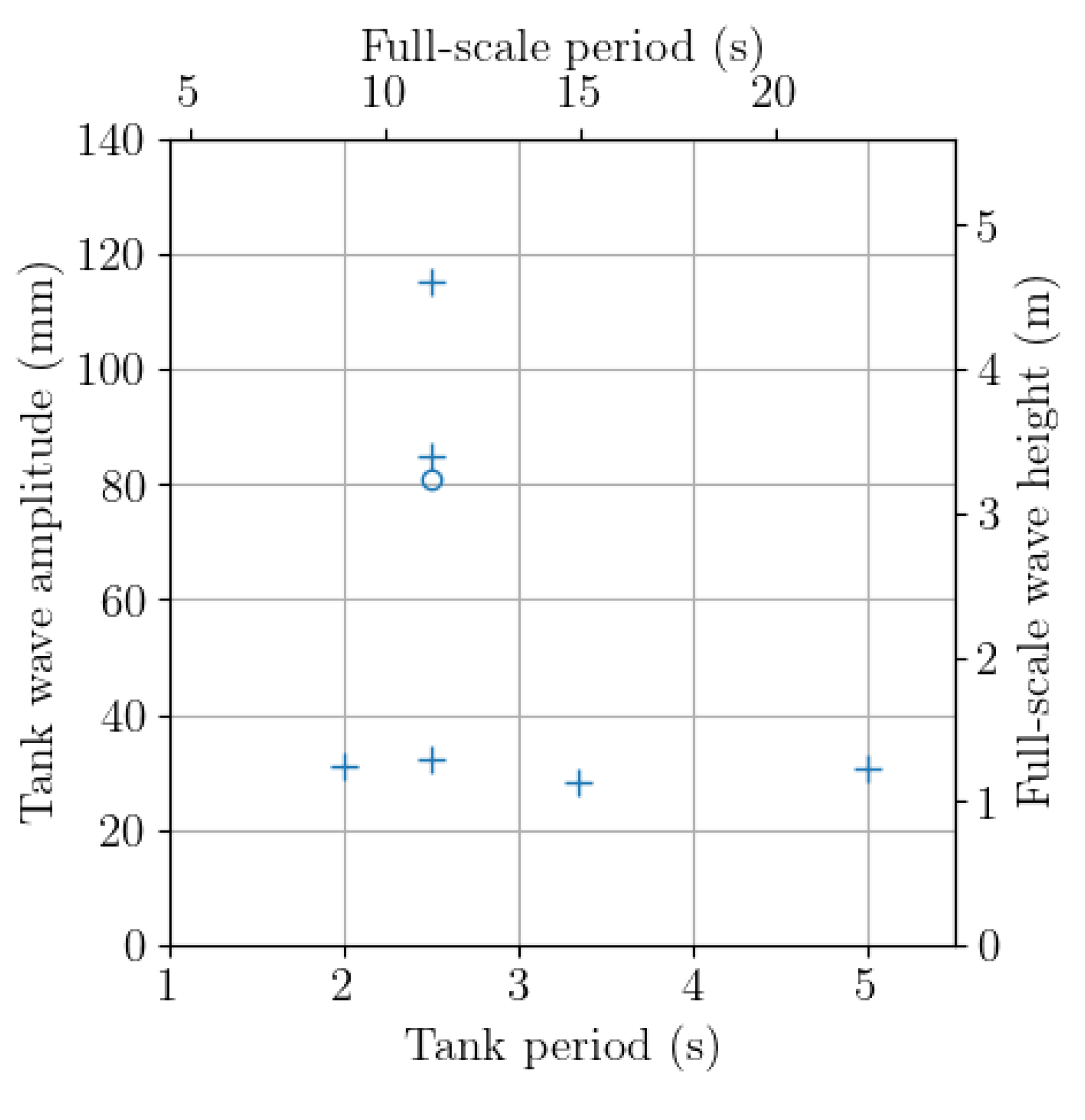
Figure 2 displays the wave amplitude with regard to their period measured in the tank without turbine for the seven wave cases and gives the similar wave height and period at full-scale according to the Froude similitude law. At full-scale, the
(medium) amplitude level was roughly the limit below which the 1 MW-rated demonstrator of the ducted 2-VATT was operating and above which the rotors were parked to avoid extreme loading on the structure. At the first order for regular waves, Saouli et al. [
28] obtain the orbital velocity
by filtering the velocity signal around the wave frequency. Then, the remaining velocity fluctuations are fully attributed to the turbulence
. Defined that way,
Figure 3 presents the streamwise average velocity and turbulence intensity profiles for all the wave cases, with
indicating the standard deviation. The transverse average velocities
are insignificant. The profiles labelled
refer to the tank configuration in current only with the wave makers and absorber out of the water whereas the
profiles refer to the condition in current only with the wave makers and absorber immersed but inactive. It appears that the immersion of the wave makers and absorber in the top 0.5 m of the water column significantly modifies the average velocity and turbulence intensity profiles with a velocity increase in the bottom part of the tank and a turbulence increase in the top part. That being,
and
profiles remain rather homogeneous over the 2-VATT capture height, from
z = 0.28 to 0.73 m. This observation justifies the use of a single velocity measurement point at the centre of the capture area as the reference velocity
. In the following, the
current only case will be the reference when assessing the effect of surface waves. Furthermore,
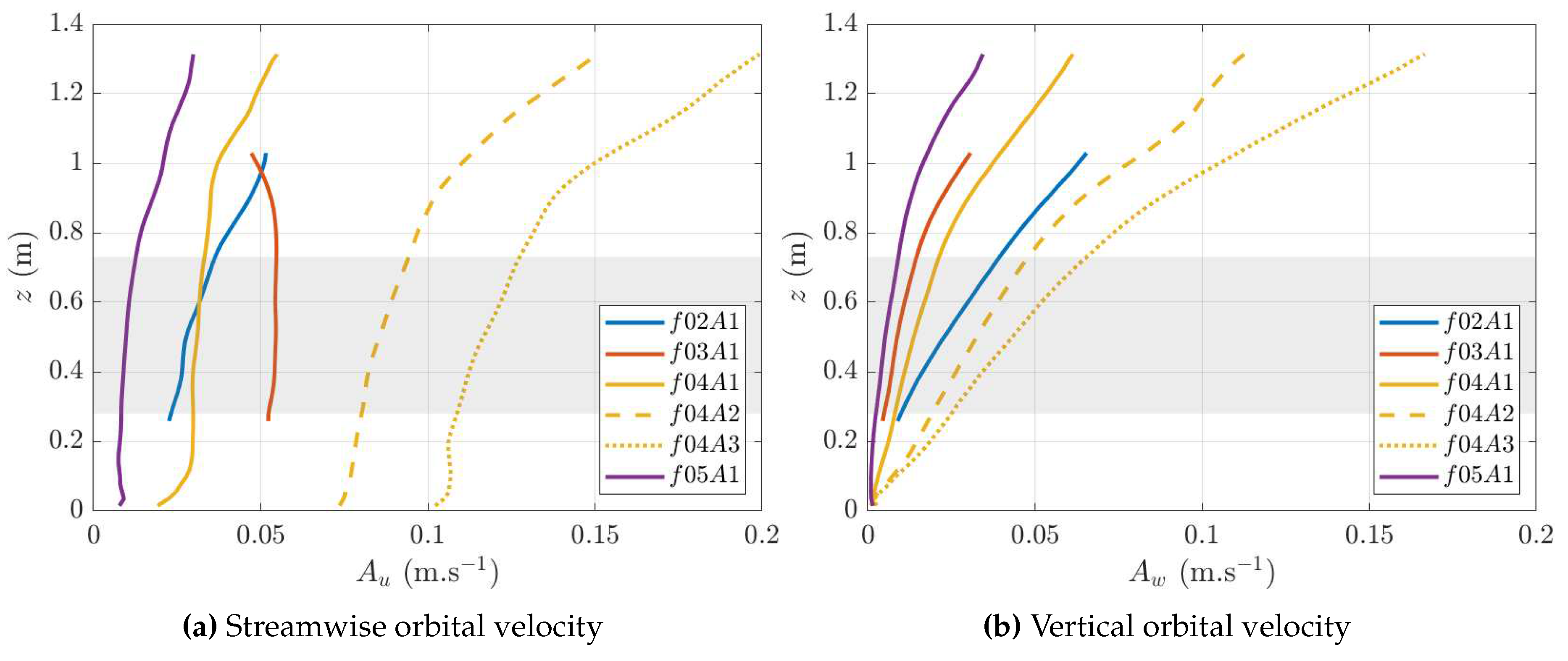
Figure 4 displays the oscillation amplitude of the streamwise and vertical orbital velocities for all the regular wave cases, presented in Magnier [
29]. For the low amplitude case (
), both the streamwise and vertical orbital velocities are less than 0.05 m.s
-1 (0.06
) over the whole 2-VATT height. As predicted by the linear wave theory, the orbital velocity amplitude increases with the wave amplitude such that
in
and
in
at mid-turbine height.
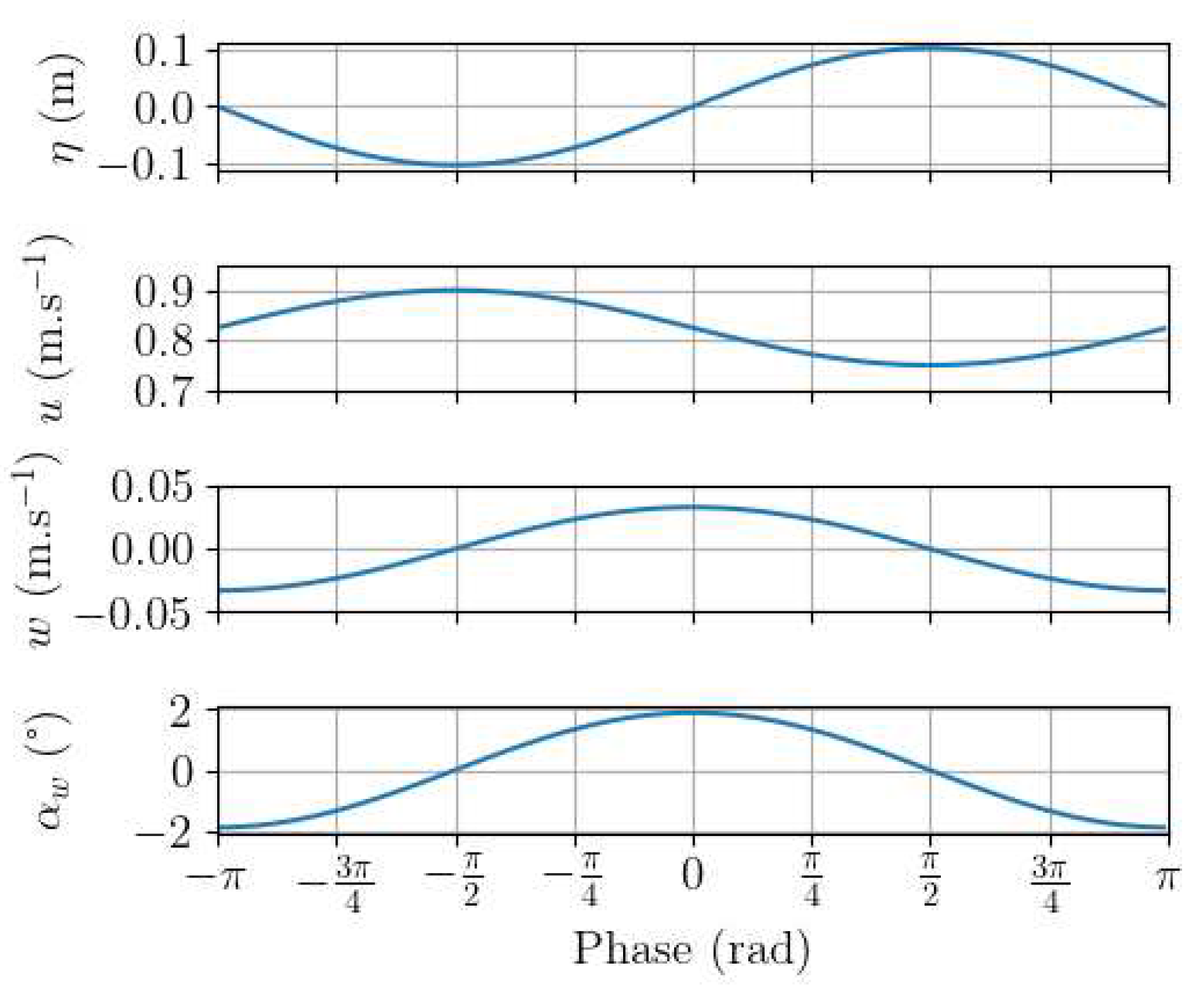
Among the seven wave cases, we will specially focus on the regular wave case
and the irregular wave case compared to the current only case. Using the linear wave theory,
Figure 5 displays one theoretical period of the surface elevation in
along with the streamwise and vertical velocities at mid-turbine depth (
m), where the velocity characteristics are approximately
m.s
,
and
(
Figure 4). The figure also displays the angle
between the total velocity direction and the horizontal direction.
Figure 5 shows that the streamwise velocity fluctuations are in phase opposition with regard to the surface elevation while the vertical orbital velocity is
out of phase. In that wave-current condition, the total velocity direction is in phase with
w and reaches almost ± 2° with regard to the horizontal direction. In addition,
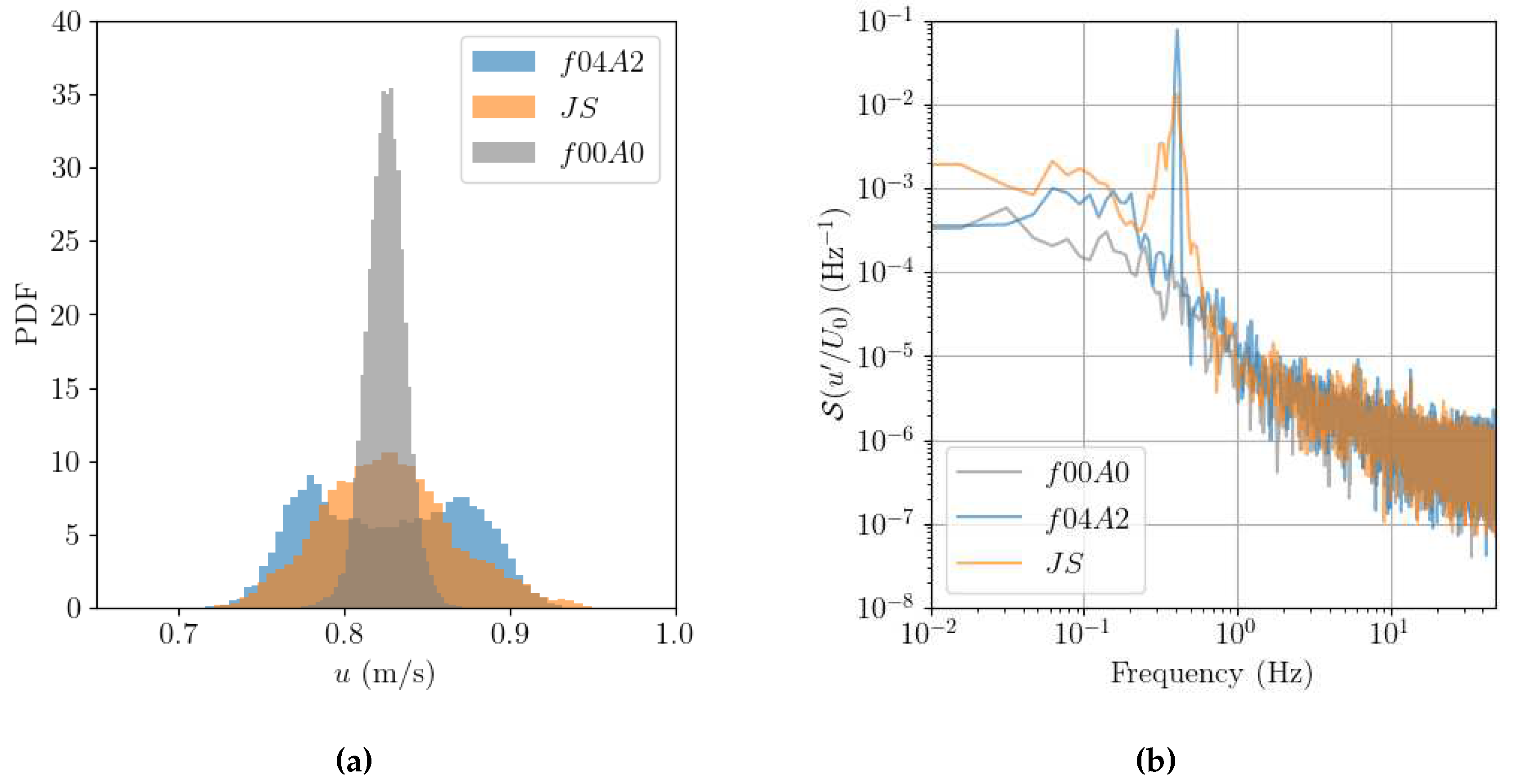
Figure 6a presents the Probability Density Function (PDF) of the streamwise velocity measured with the 2C-LDV upstream of the 2-VATT at
and at the centre of the projected capture area in these three flow conditions. The arithmetic average of the velocity at this position is equal to
in the three cases but the velocity distribution around that average value varies. In presence of waves, the velocity range is extended compared to the current only case, due to the orbital velocities induced by the waves. However, with regular waves the distribution presents two maxima, related to the periodical increase and decrease of the velocity occurring when a wave through and crest passes, respectively; whereas a single PDF maxima is present at the average value in
as the orbital velocities do not have favourite amplitudes with irregular waves. Besides,
Figure 6b presents the power spectral density of the same 2C-LDV streamwise velocity measurements. The power spectral densities of the fluctuating part of
u (
) are computed using Welch’s method with 64 s long windows and 50 % overlap. The spectral analysis reveals a strong energy peak at the wave frequency, as expected, with a sharp peak for the regular wave case and an increased level of energy between about 0.25 and 0.55 Hz in the JONSWAP case.
2.4. Data processing
The power coefficient of each rotor column
is computed as in equation
4 with
and
t the time. The reference surface is that of the rotors projected area (
) and the torque signal considered is corrected by the friction torque induced by the seals and the transmission system for each rotor column [
22]. Then, the overall average power coefficient
is the average of the two
and the power fluctuations are analysed considering the average standard deviation between the two rotor columns, noted
.
The tip speed ratio (
) is defined in equation
5. Thus,
refers to the tests with parked rotors and
refers to the those at the operating point providing the maximal power coefficient. The force and moment coefficients are defined in equations
6 and
7 for the components along
x with the four rotors projected area as a reference surface. They are defined the same way for the loads along
y and
z. The loads measured without current at
are subtracted to consider only the hydrodynamic loads on the device without the gravity. In this study, we consider the forces applied by the turbine on the gravity base, measured by the upper load cell, and the moments applied to the ground, measured by the bottom load cell (
Figure 1(b)). These are the loads to consider for the design of a stable gravity base. For all the hydrodynamic coefficients the reference upstream velocity measurement
is averaged with the appropriate power weighting (power 1 for
, 2 for the load coefficients and 3 for the power) [
30].
In addition to the load coefficients evolution with the tip speed ratio, we also analyse their probability density functions with 50 equal-width bins to consider the load distributions and extrema. The extreme load value is considered as the maximum between the absolute value of the first and the last percentile (max[abs(p01), abs(p99)]) and the load range is considered as the difference between p01 and p99. The correlation between the wave-induced velocity fluctuation and the loads fluctuation is analysed by computing the normalised cross-correlation coefficient
with regard to the time lag (
) between the free surface elevation (
) above the 2-VATT and the loads or the rotor torque (equation
8, with
s indicating the loads or torque signal).
We also study the fluctuations of the rotor torque, the drag and lift coefficients averaged according to the wave phase with 3 degrees phase bins, indicated by a tilde above the symbols. The wave phase is obtained by Hilbert transform of the surface elevation signal filtered at the wave frequency ± 0.1 Hz. Finally, the Fourier transform () of , and are computed as well as their coherence with the upstream velocity measurement using Welch’s method with 32 s long windows and 50 % overlap to analyse the periodical characteristics of the 2-VATT related signals compared to those of the wave-induced flow fluctuations.
3. Effect of surface waves opposing the current on the 2-VATT behaviour
3.1. Wave amplitude and frequency effect
Figure 7 gives an overview of the wave effect on the average and standard deviation of the power performance and on the loads of the ducted 2-VATT with regard to the tip speed ratio. The general trend comparing which ever wave case to the case without waves
is that the average values are barely affected by the presence of surface waves but that the standard deviations are increased, whether the 2-VATT rotors are parked or in operation. In addition, the evolution of the average and the standard deviation with the tip speed ratio is affected by the presence of waves for the power coefficient but not for the loads. More specifically, looking at the effect of the wave amplitude on the evolution of the average performance with the tip speed ratio, we observe an increase of
with
, without changing the maximal
. Regarding the average loads on the 2-VATT, the waves induce a slight increase of their value with less than 5 % difference compared to the case without waves, and without modifying the loads evolution with regard to
.
Conversely, the presence of surface waves strongly affects the standard deviation of the power and loads coefficients. Indeed, the latter increase linearly with the wave amplitude such that an
increase of 0.1 m generates roughly a 2, 3 and 4 times higher
,
and
respectively at
(
Figure 8). As a consequence,
for the wave case with the highest amplitude. Those linear trends between the load standard deviations and the wave amplitude are rather independent of
, which indicates a low interaction between the rotors rotation and the waves on the loadings. We only observe an offset in
and
when comparing between
and
due to the blades passing, but the linear trends with
are unchanged (
Figure 8). Regarding the power coefficient, the impact of waves on
grows with
. Indeed, the slope of the linear fit with
increases with
, which indicates an interaction between the rotors rotation and the waves on the power performance, unlike the loads. To the authors knowledge, such a linear relationship between the surface wave height and the load’s standard deviation of a turbine had never been shown. However, using a theoretical model, Xin et al. [
31] also found a linear relationship between the wave height and the standard deviation of the horizontal force applied to a bottom-fixed vertical slender cylinder subjected to surface waves and a tidal current.
In the design process, under the assumption of a normal law of distribution, the extreme loads to which the turbine can be submitted are estimated combining the average and the standard deviation values. For instance, the extreme drag coefficient value is estimated as
. Here,
at the optimal operating point in the medium wave case
against 1.32 with the rotors parked in the extreme wave case
. This result justifies the choice to park the rotors in presence of extreme wave conditions to limit structural damages and to carry out experiments with the 2-VATT operating in wave conditions to assess the maximal loads for the design process. Following the linear trends in
Figure 8 for regular waves at 0.4 Hz, we find that the extreme loads on the turbine would be greater with the rotors parked compared to the limit case at
with intermediate wave conditions (
) if
m, which gives 7.2 m wave height at full-scale according to Froude similitude law. That wave height at sea is likely to be encountered during winter storms, with about a 5 years return period at the Paimpol-Bréhat tidal turbine test site [
32].
Still looking at
Figure 7, it appears that the irregular wave case
affects the turbine power precisely the same way as the regular wave case
, whose peak period and significant wave amplitude are similar (
Table 1). However, we observe little differences between the regular and irregular cases on the loads as the average loads are equal to the case without waves in
at
while they are slightly higher with regular waves. In addition, with the rotors in operation,
is similar with regular and irregular waves but
and
are a few percent lower in
; while
and
are unchanged but
is 37 % lower in
compared to
.
Beyond the wave amplitude, its frequency is also expected to affect the 2-VATT response. However, the power and drag coefficients evolution with the tip speed ratio are almost the same in the four wave cases at variable frequency (
Figure 9). Due to the wave-current interaction and the wave maker amplitude limits at low frequency, multiple wave frequency cases could only be generated at the amplitude level
. Since the previous results on the effect of the wave amplitude have shown that the 2-VATT response is barely affected by waves of that amplitude level, we assume that the absence of frequency effect observed here is actually due to the smallness of the waves amplitude.
3.2. Wave-current-turbine interaction
To better understand how the surface waves increase the ducted 2-VATT power and loads fluctuations, we focus on the regular wave case and the irregular wave case. The turbine’s response is studied with parked rotors first to look at the wave effects on the static structure before addressing the interaction with the turbine in operation.
3.2.1. Parked turbine
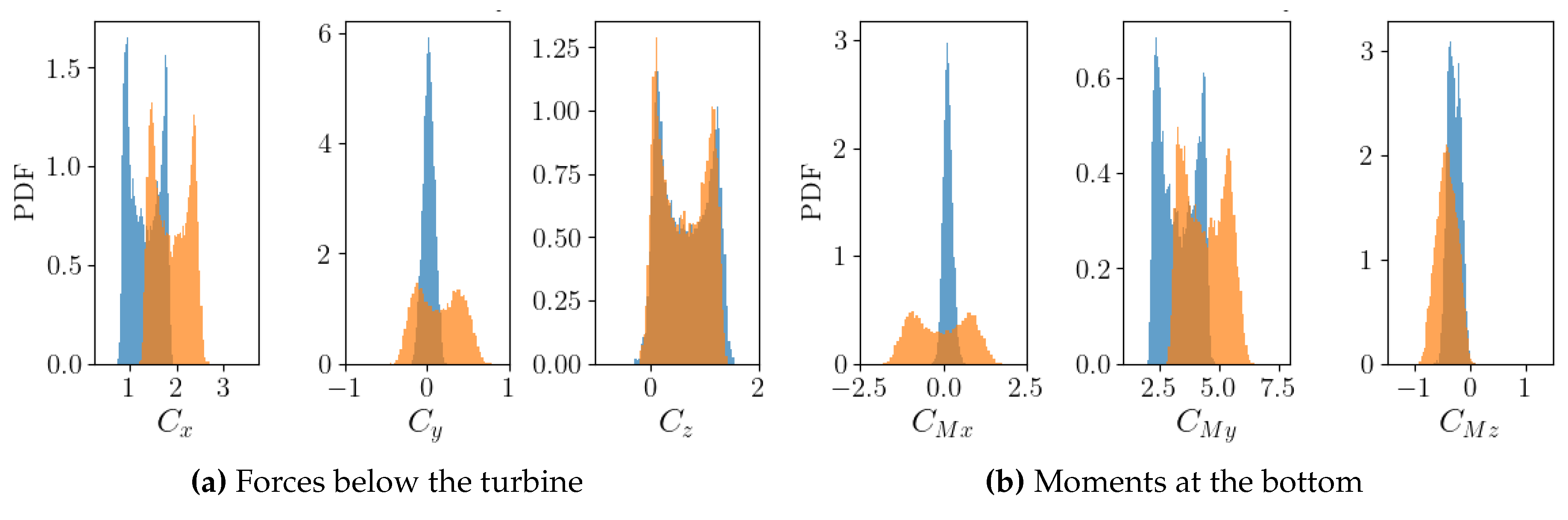
Figure 10 shows the Probability Density Function (PDF) of the forces and the moments on the turbine at
in the two above mentioned wave cases and without waves. As expected, the ranges of
,
and
between the first and the last percentile (p99-p01), that are critical for the fatigue structural design, are strongly extended in presence of surface waves. Indeed, in
, the three load ranges are 5.7 to 6.7 times higher than without waves (
Table 2). That range increase goes along with extreme values breaking by +41 % for
and
and by +87 % for
in
compared to
, which is also critical for the structural design. On the other hand, the 3 other load components are less affected by the presence of surface waves propagating collinearly against the current direction. It is of interest to notice that the
and
ranges are more than 40 % higher in irregular waves than in regular ones, although
Figure 7 revealed higher standard deviations with the regular wave case. That result is due to a difference of load distribution for these three components between the regular wave case, with 2 PDF modes, and the irregular wave case, with a single PDF mode. The difference of load distribution mimics the difference of velocity distribution between the two cases (
Figure 6), which indicates a strong correlation between the wave-induced velocity fluctuations and the load fluctuations.
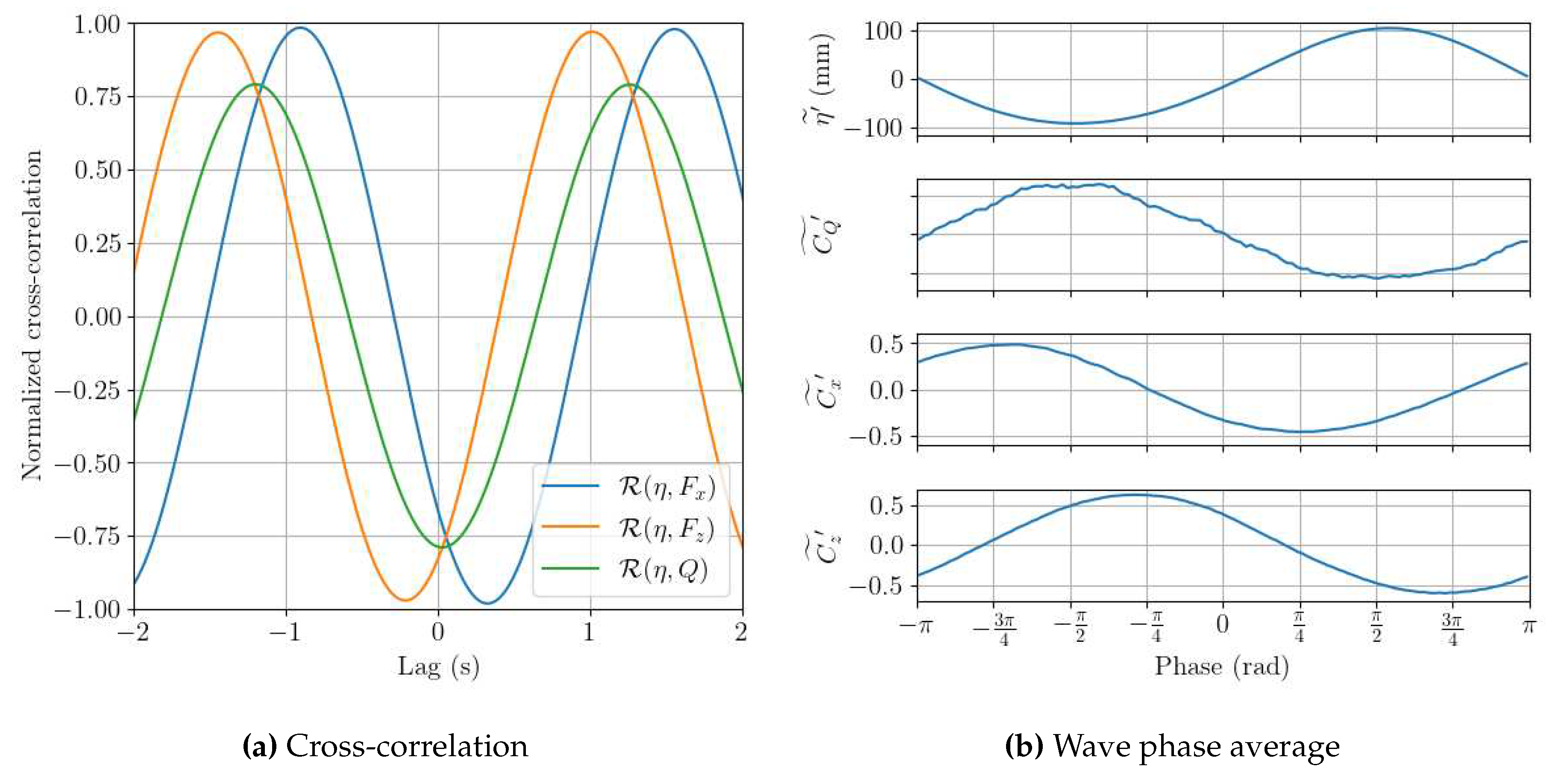
Figure 11a presents the cross-correlation coefficients (
) of the surface elevation measurement above the 2-VATT with a rotor column torque and with the whole 2-VATT drag and lift forces in the
case. The extreme cross-correlation coefficients are almost ±1 for
and
, and
is close from ±0.8 for the torque, which already quantifies the strong impact of the surface waves on the loads and rotor torque fluctuations. The interpretation of the time lags at which
is maximum or minimum is not straightforward however and requires to get back to the linear wave theory. As presented in the
Section 2.3, in this wave against current case, the streamwise orbital velocity (
) is in phase opposition with the surface elevation while the vertical one (
) (and so the pitch angle between the velocity and the turbine) is
out of phase (
Figure 5), ie. a quarter of the wave period (
/4 = 0.625 s in
). Assuming that the fluctuations of the rotor torque
Q and
are mainly caused by the fluctuations of
u and that those of
can be mainly attributed to the fluctuations of
w, we expect
and
Q to be in phase with
(and so in phase opposition with
) while
would be in phase with
(and so
out of phase with
). That assumption is valid for
Q as a minimum of
occurs with zero time lag, meaning that a crest of
generates a trough of
Q without lag, similarly to
. The two maxima at
1.25 s reveal the maxima of
Q generated by the surface elevation trough. That perfect phase opposition between
and
Q is also observed in the wave phase-averaged graphs (
Figure 11b). In contrast, the minimum of
expected with a 0 s lag, and the maximum of
expected with a
/4 = 0.625 s lag, appear with a ∼ 0.35 s lag compared to the expected values. That lag is also observed in
Figure 11b as the wave phase averages of the fluctuating
and
are
= -45° shifted compared to the relative phase of
u and
w with regard to
(
Figure 5). Phase shifts from -5 to -80° between the surface elevation and the drag force were also observed by Martinez et al. [
13] on a HATT. Those results mean that the force extrema (crest or through) occur before the surface elevation extrema and so before the orbital velocity extrema, as it was demonstrated regarding the force exerted by surface waves on piles by Morison et al. [
14]. According to the later, the phase shift increases with the pile diameter relatively to the water depth. Therefore, the small blade size relatively to water depth, by opposition to the large size of the whole 2-VATT, may explain the absence of such a phase shift on the rotor torque
Q while it is observed on the whole turbine loads.
3.2.2. Operating turbine
To look at the combination of the wave-induced loads with the rotors rotation-induced loads,
Figure 12 presents the loads PDF with the turbine operating at
and
when subjected to the regular waves
. The results show that
is unaffected by the rotors rotation as its distribution is the same whether with parked or operating rotors.
and
appear to be shifted in average due to rotors thrust and their distribution are slightly widened but they remain with 2 modes at
like at
. However, the distribution of
and
shows 2 modes at
whereas these were made of a single mode at
. That
and
bimodal distribution was already observed without waves and was found to be due to the asymmetrical thrust of the two rotor columns when their angular position is asymmetrical [
30]. Therefore, the loads PDF at
present a combination of the wave-induced characteristic distribution (on
and
) and of the rotor-induced one (on
and
) without showing clear interaction between the two. Similarly, the cross-correlations of the surface elevation with a rotor column torque and with the turbine drag and lift forces, and their phase average results are barely affected by the rotors operation. We only observe a reduction of
extrema to less than ±0.7 with a slight time lag that could indicate the appearance of some added mass effects on the rotating rotors compared to the case with parked rotors.
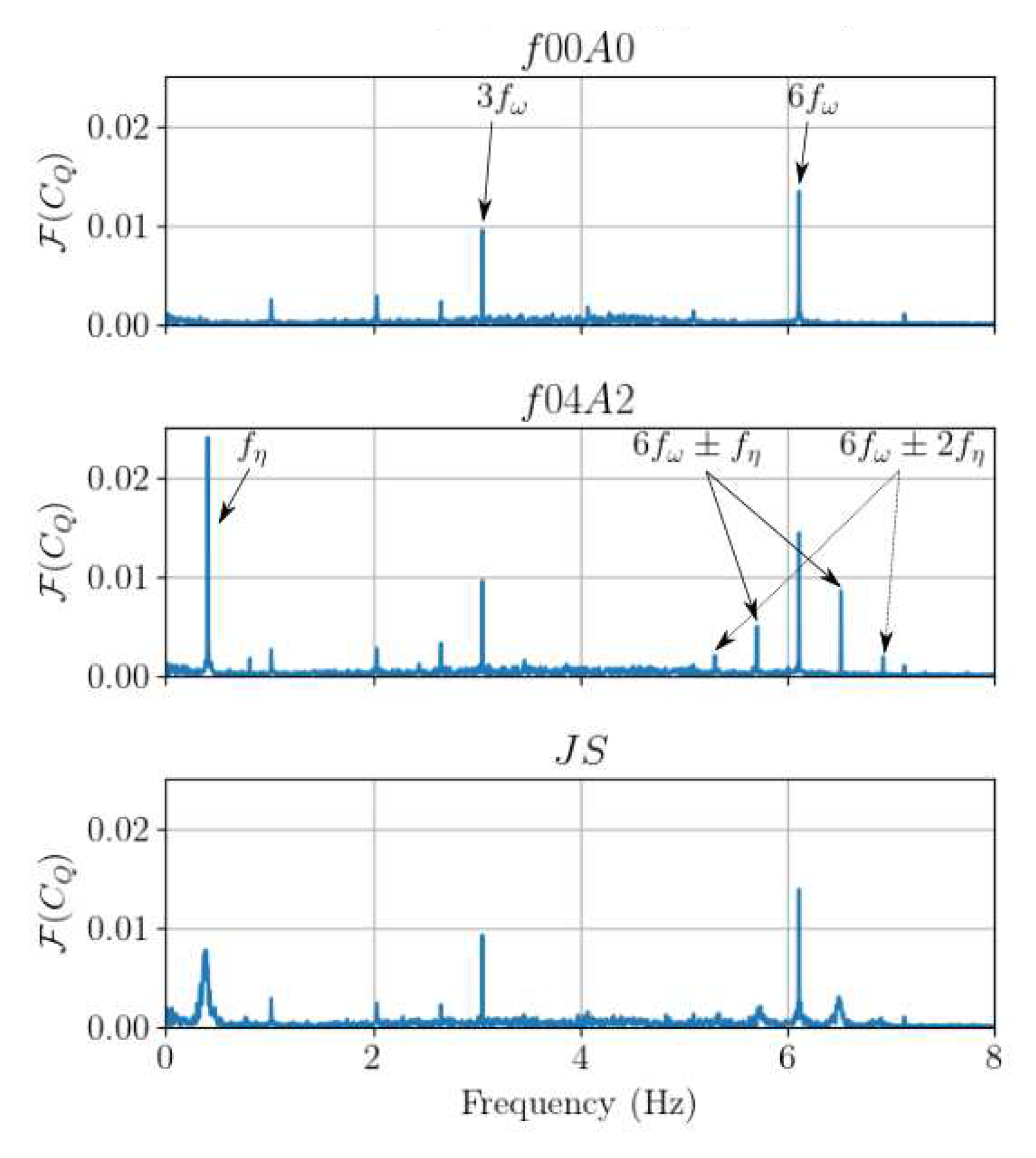
The Fourier transform (
) of one rotor column torque in the case without waves
, with regular waves
and with irregular waves
gives a better insight into the origin of the increased load fluctuations in presence of surface waves and the wave-rotation interaction (
Figure 13). First, without waves, the torque spectral content is mainly located at 3 and 6 times the rotational frequency (
), that corresponds to the blade passing frequency since the rotor columns are made of two levels of out-of-phase 3 bladed rotors. When adding surface waves to the current, those rotor-induced spectral peaks are unchanged but other peaks raise. A strong peak appears at the wave frequency (
) both with regular and irregular waves on the Fourier transform of the torque, as well as on the loads Fourier transform, similarly to the results on HATT [
10,
11,
15]. With regular waves, the peak at
dominates the rotor-induced peaks in
whereas the peaks at 3 and 6
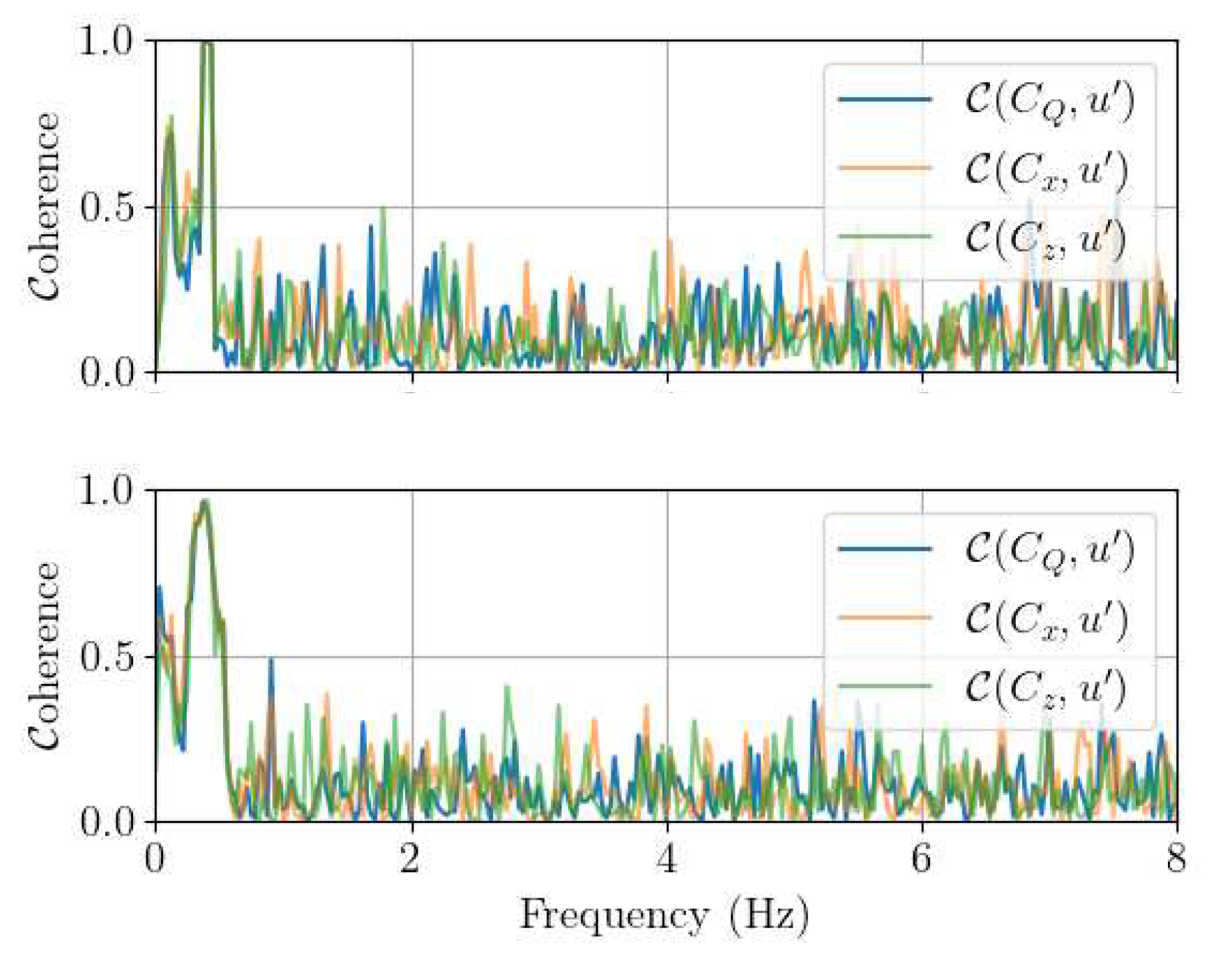
remain the highest with irregular waves. Both in the regular and irregular wave cases, the coherence function between the upstream velocity measurement and the torque, the drag and the lift force reaches almost 1 around
, meaning that the torque and loads spectral content at that frequency is fully due to the wave-induced orbital velocity (
Figure 14). Those coherence functions also reveal that the 2-VATT responds to the whole wave spectrum width in the irregular wave case as the three coherences exceed 0.5 from 0.25 to 0.55 Hz. Finally, in addition to the strong peak at
in the torque Fourier transform, additional peaks appears at
, with
k = 1 and 2, both with regular and irregular waves. Those peaks evidence the interaction between the periodic loadings induced by the surface waves and those induced by the rotor columns rotation. Similar peaks combining the turbine rotational frequency harmonics and the wave frequency have also been observed on horizontal axis tidal turbines by Draycott et al. [
15]. These are explained by a rotational sampling of the waves by the turbine blades that do several rotations during one wave period.
4. Conclusion
While numerous studies analysed experimentally the effect of surface waves on horizontal axis tidal turbines, only a few considered vertical axis ones and none considered twin vertical axis tidal turbines (2-VATT). In this paper, we tested a 1/20 scale bottom mounted and ducted 2-VATT, similar to HydroQuest’s 1 MW-rated demonstrator, in Ifremer’s flume tank with waves propagating against the current. Seven wave conditions are presented to assess independently the effect of the waves amplitude and their frequency as well as to compare the effect of regular and irregular waves on the turbine behaviour.
The results show that the maximal average power coefficient is unaffected by the presence of waves, although the power curve may be slightly shifted towards higher tip speed ratios. The average hydrodynamic loads on the turbine increase with the regular wave amplitude but they remain less than 5 % higher than without waves. The effect of the waves on the power and loads fluctuations is much more important as the standard deviation of the power, the drag and the lift follow a linear trend with a slope of 2, 3 and 4 respectively with regard to the wave amplitude. Those linear trends are unchanged by the tip speed ratio for the loads while the slope increases with the tip speed ratio for the power standard deviation. That result indicates a low interaction between the periodic wave loadings and the periodic rotors loadings considering the turbine loads but a strong interaction considering the power. Furthermore, no effect of the wave frequency is observed on the average and standard deviation of the power and loads, but the waves amplitude level at variable frequencies is probably too low to significantly affect the turbine response, whatever the frequency.
Looking in more details at the effect of the intermediate frequency and amplitude wave cases, we find that the drag, lift and pitching moment distribution ranges are largely extended, up to 6.7 times greater, and that the extreme values are exceeded by 40 to 90 % with the regular waves compared to the condition with current only. Those results must be taken into account for the structural design of such a ducted 2-VATT. Moreover, the rotor torque (and so the power) fluctuations are strongly correlated and in phase with the free surface elevation above the turbine, which, according to the linear wave theory, is also phased with the streamwise orbital velocity. The turbine loads fluctuations are also correlated to the surface elevation but with a phase lag that may indicate added mass effects on the loads applied to the whole structure. In addition, the spectral analysis of a rotor column torque reveals a rotational sampling of the waves by the blades, similarly to horizontal axis turbines, with peaks at frequencies combining the wave frequency and the rotational frequency.
Regarding the difference between regular and irregular waves, apart from the standard deviation of the lift that is lower with irregular waves, the 2-VATT response is similar in terms of average and standard deviation of the power and the loads. However, the load distributions are different between the two cases as they mimic the velocity distribution that presents a single mode with irregular waves against two modes in regular waves. As a result, the streamwise load ranges are 1.4 times larger in irregular waves and the extreme values are exceeded compared to the regular wave case. Thus, testing vertical axis tidal turbine models in regular waves only is insufficient to accurately predict the wave-induced loads for the design of full-scale turbines operating at sea. The spectral signature of the irregular waves on the torque and the loads is similar to that of regular waves, except that the peaks at the wave frequency and its combinations with the rotational frequency are wider. Indeed, the torque and loads spectra are coherent with the velocity spectrum on the whole wave frequency bandwidth.
In the future, tests with several wave directions relatively to the current direction could extend the present study and improve the understanding of the ducted 2-VATT response to surface waves at sea. A dedicated analyse of the added mass coefficients may better explain the correlation lags between the surface elevation and the loads, and could contribute to better predict the wave-induced load fluctuations on such a ducted 2-VATT. Furthermore, beyond the turbine response, studying the effect of the surface waves on the turbine wake would also be of interest in the perspective of tidal turbine farm deployments.
Author Contributions
Conceptualization, G.G. and G.M.; methodology, M.M., G.G., G.M; software, M.M.; validation, G.G. and G.M.; formal analysis, M.M.; investigation, M.M; and G.G.; resources, G.G. and G.M.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, M.M. and G.G.; visualization, M.M.; supervision, G.G. and G.M.; project administration, G.G. and G.M.; funding acquisition, G.G. and G.M.. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported in part by the French Research and Technology National Association (ANRT) under the convention Cifre n°2020/0688.
Data Availability Statement
The research data can be available upon request to the authors.
Acknowledgments
The authors acknowledge Jean-Valéry Facq and Cédric Derveaux for the design of the turbine model as well as Benoît Gomez and Benoît Gaurier for their help during the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sentchev, A.; Nguyen, T.D.; Furgerot, L.; Bailly du Bois, P. Underway velocity measurements in the Alderney Race: towards a three-dimensional representation of tidal motions. Phil. Trans. R. Soc. A 2020, 378. [Google Scholar] [CrossRef]
- Cossu, R.; Penesis, I.; Nader, J.R.; Marsh, P.; Perez, L.; Couzi, C.; Grinham, A.; Osman, P. Tidal energy site characterisation in a large tidal channel in Banks Strait, Tasmania, Australia. Renewable Energy 2021, 177, 859–870. [Google Scholar] [CrossRef]
- Mercier, P.; Guillou, S. The impact of the seabed morphology on turbulence generation in a strong tidal stream. Physics of Fluids 2021, 33, 055125. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G.; Neill, S.P. The influence of waves on the tidal kinetic energy resource at a tidal stream energy site. Applied Energy 2016, 180, 402–415. [Google Scholar] [CrossRef]
- Bennis, A.C.; Furgerot, L.; Bailly Du Bois, P.; Poizot, E.; Méar, Y.; Dumas, F. A winter storm in Alderney Race: Impacts of 3D wave–current interactions on the hydrodynamic and tidal stream energy. Applied Ocean Research 2022, 120, 103009. [Google Scholar] [CrossRef]
- Perez, L.; Cossu, R.; Grinham, A.; Penesis, I. Tidal turbine performance and loads for various hub heights and wave conditions using high-frequency field measurements and Blade Element Momentum theory. Renewable Energy 2022, 200, 1548–1560. [Google Scholar] [CrossRef]
- Moreau, M.; Germain, G.; Maurice, G.; Richard, A. Sea states influence on the behaviour of a bottom mounted full-scale twin vertical axis tidal turbine. Ocean Engineering 2022, 265, 112582. [Google Scholar] [CrossRef]
- Gaurier, B.; Ordonez-Sanchez, S.; Facq, J.V.; Germain, G.; Johnstone, C.; Martinez, R.; Salvatore, F.; Santic, I.; Davey, T.; Old, C.; Sellar, B. MaRINET2 Tidal Energy Round Robin Tests—Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions. Journal of Marine Science and Engineering 2020, 8, 463. [Google Scholar] [CrossRef]
- Barltrop, N.; Varyani, K.S.; Grant, A.; Clelland, D.; Pham, X. Wave-current interactions in marine current turbines. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2006, Vol. 220, pp. 195–203. [CrossRef]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renewable Energy 2013, 59, 1–12. [Google Scholar] [CrossRef]
- Martinez, R.; Payne, G.S.; Bruce, T. The effects of oblique waves and currents on the loadings and performance of tidal turbines. Ocean Engineering 2018, 164, 55–64. [Google Scholar] [CrossRef]
- Ordonez-Sanchez, S.; Allmark, M.; Porter, K.; Ellis, R.; Lloyd, C.; Santic, I.; O’Doherty, T.; Johnstone, C. Analysis of a Horizontal-Axis Tidal Turbine Performance in the Presence of Regular and Irregular Waves Using Two Control Strategies. Energies 2019, 12, 367. [Google Scholar] [CrossRef]
- Martinez, R.; Ordonez-Sanchez, S.; Allmark, M.; Lloyd, C.; O’Doherty, T.; Germain, G.; Gaurier, B.; Johnstone, C. Analysis of the effects of control strategies and wave climates on the loading and performance of a laboratory scale horizontal axis tidal turbine. Ocean Engineering 2020, 212, 107713. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The Force Exerted by Surface Waves on Piles. Journal of Petroleum Technology 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Draycott, S.; Steynor, J.; Nambiar, A.; Sellar, B.; Venugopal, V. Rotational sampling of waves by tidal turbine blades. Renewable Energy 2020, 162, 2197–2209. [Google Scholar] [CrossRef]
- Ouro, P.; Dené, P.; Garcia-Novo, P.; Stallard, T.; Kyozuda, Y.; Stansby, P. Power density capacity of tidal stream turbine arrays with horizontal and vertical axis turbines. Journal of Ocean Engineering and Marine Energy 2022. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Experimental Investigation of Helical Cross-Flow Axis Hydrokinetic Turbines, Including Effects of Waves and Turbulence. ASME-JSME-KSME 2011 Joint Fluids Engineering Conference; ASMEDC: Shizuoka, Japan, 2011; pp. 1895–1906. [Google Scholar] [CrossRef]
- Zhang, X.w.; Zhang, L.; Wang, F.; Zhao, D.y.; Pang, C.y. Research on the unsteady hydrodynamic characteristics of vertical axis tidal turbine. China Ocean Engineering 2014, 28, 95–103. [Google Scholar] [CrossRef]
- Lust, E.E.; Bailin, B.H.; Flack, K.A. Performance characteristics of a cross-flow hydrokinetic turbine in current only and current and wave conditions. Ocean Engineering 2021, 219, 108362. [Google Scholar] [CrossRef]
- Vergaerde, A.; De Troyer, T.; Muggiasca, S.; Bayati, I.; Belloli, M.; Kluczewska-Bordier, J.; Parneix, N.; Silvert, F.; Runacres, M.C. Experimental characterisation of the wake behind paired vertical-axis wind turbines. Journal of Wind Engineering and Industrial Aerodynamics 2020, 206, 104353. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Conversion and Management 2021, 247, 114768. [Google Scholar] [CrossRef]
- Moreau, M.; Germain, G.; Maurice, G. Experimental performance and wake study of a ducted twin vertical axis turbine in ebb and flood tide currents at a 1/20th scale. Renewable Energy 2023, 214, 318–333. [Google Scholar] [CrossRef]
- Gaurier, B.; Germain, G.; Facq, J.V.; Bacchetti, T. Wave and current flume tank of IFREMER at Boulogne-sur-mer. Description of the facility and its equipment. Technical report, IFREMER, 2018. [CrossRef]
- Brevik, I.; Bjørn, A. Flume experiment on waves and currents. I. Rippled bed. Coastal Engineering 1979, 3, 149–177. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Eake, K.; Euring, J.A.; Gicnapp, A.; Hasselmann, D.E.; Kruseman, P.; Meerburg, A.; Mullen, P.; Olbers, D.J.; Richren, K.; Sell, W.; Walden, H. Measurements of wind-wave growth and swell decay during the joint North Sea wave project (JONSWAP). Erganzungsheft zur Deutschen Hydrographischen Zeitschrift, 1973; A(8). [Google Scholar]
- Bachant, P.; Wosnik, M. Effects of Reynolds Number on the Energy Conversion and Near-Wake Dynamics of a High Solidity Vertical-Axis Cross-Flow Turbine. Energies 2016, 9, 73. [Google Scholar] [CrossRef]
- Molin, B. Hydrodynamique des structures offshore; Editions Technip, 2002.
- Saouli, Y.; Magnier, M.; Germain, G.; Gaurier, B.; Druault, P. Experimental characterisation of the waves propagating against current effects on the wake of a wide bathymetric obstacle. 18ème Journées de l’Hydrodynamique;, 2022; Number 1, pp. 1–12.
- Magnier, M. Étude expérimentale des courants de marée et de la houle sur la dynamique tourbillonnaire d’une variation bathymétrique et sur le comportement d’une hydrolienne. PhD thesis, Université de Lille, 2023.
- Moreau, M.; Bloch, N.; Maurice, G.; Germain, G. Experimental study of the upstream bathymetry effects on a ducted twin vertical axis tidal turbine. Renewable Energy (Under review) 2023. [Google Scholar]
- Xin, Z.; Li, X.; Li, Y. Coupled effects of wave and depth-dependent current interaction on loads on a bottom-fixed vertical slender cylinder. Coastal Engineering 2023, 183, 104304. [Google Scholar] [CrossRef]
- EDF.; SEENEOH. Paimpol-Bréhat tidal turbine test site documentation v1.2. Technical report, EDF, 2022.
Figure 1.
(a) Schematic top view of the turbine operating in Ebb tide or Flood tide Configuration (EC or FC respectively). (b) Schematic side view of the experimental setup in Ifremer’s tank with waves opposing the current direction.
Figure 1.
(a) Schematic top view of the turbine operating in Ebb tide or Flood tide Configuration (EC or FC respectively). (b) Schematic side view of the experimental setup in Ifremer’s tank with waves opposing the current direction.
Figure 2.
Amplitude and period of the waves generated in the tank (left and bottom axes). The crosses represent the regular wave cases and the circle is the JONSWAP case. The right and top axes provide the waves period and height at a 20/1 scale according to Froude similitude law.
Figure 2.
Amplitude and period of the waves generated in the tank (left and bottom axes). The crosses represent the regular wave cases and the circle is the JONSWAP case. The right and top axes provide the waves period and height at a 20/1 scale according to Froude similitude law.
Figure 3.
Average
(a) and turbulence intensity
(b) streamwise velocity profiles in the classical current only case (CO), with the damping beach and wave makers immersed (
) and in all the wave cases considered, from Saouli et al. [
28]. The grey area represents the 2-VATT capture height.
Figure 3.
Average
(a) and turbulence intensity
(b) streamwise velocity profiles in the classical current only case (CO), with the damping beach and wave makers immersed (
) and in all the wave cases considered, from Saouli et al. [
28]. The grey area represents the 2-VATT capture height.
Figure 4.
Amplitude of the streamwise
(a) and vertical
(b) orbital velocities along the water depth in the regular wave cases, from Magnier [
29]. The grey area represents the 2-VATT capture height.
Figure 4.
Amplitude of the streamwise
(a) and vertical
(b) orbital velocities along the water depth in the regular wave cases, from Magnier [
29]. The grey area represents the 2-VATT capture height.
Figure 5.
Theoretical period of the surface elevation , the streamwise and the vertical velocities u and w and the angle between the velocity direction and the horizontal direction, with m.s, and . This corresponds approximately to the flow conditions in at m according to the linear wave theory.
Figure 5.
Theoretical period of the surface elevation , the streamwise and the vertical velocities u and w and the angle between the velocity direction and the horizontal direction, with m.s, and . This corresponds approximately to the flow conditions in at m according to the linear wave theory.
Figure 6.
(a) Probability Density Function and (b) Power spectral density of the streamwise velocity measured with the 2C-LDV at upstream of the 2-VATT at the centre of the projected capture area.
Figure 6.
(a) Probability Density Function and (b) Power spectral density of the streamwise velocity measured with the 2C-LDV at upstream of the 2-VATT at the centre of the projected capture area.
Figure 7.
Evolution with the tip speed ratio of the power (a), drag (b), lift (c) and pitch (d) coefficients with the average at the top and standard deviation at the bottom of each sub-figure. The values are normalised by the maximal average value in the case (without waves).
Figure 7.
Evolution with the tip speed ratio of the power (a), drag (b), lift (c) and pitch (d) coefficients with the average at the top and standard deviation at the bottom of each sub-figure. The values are normalised by the maximal average value in the case (without waves).
Figure 8.
Coefficients’ standard deviation with regard to the waves amplitude for = 0.4 Hz, when the turbine is parked or operating at . Dashed lines are linear fits of the data points. The points labelled are the values of .
Figure 8.
Coefficients’ standard deviation with regard to the waves amplitude for = 0.4 Hz, when the turbine is parked or operating at . Dashed lines are linear fits of the data points. The points labelled are the values of .
Figure 9.
Power (a) and drag (b) coefficients with the average at the top and standard deviation at the bottom of each sub-figure. The are normalised by the maximal average value in the case (without waves).
Figure 9.
Power (a) and drag (b) coefficients with the average at the top and standard deviation at the bottom of each sub-figure. The are normalised by the maximal average value in the case (without waves).
Figure 10.
Probability Density Functions of the load coefficients at computed without waves, with regular waves and with irregular waves of the same characteristic amplitude and frequency.
Figure 10.
Probability Density Functions of the load coefficients at computed without waves, with regular waves and with irregular waves of the same characteristic amplitude and frequency.
Figure 11.
In the case with the rotors parked, (a) the cross-correlations of the surface elevation with the torque of a rotor column, the drag and the lift forces on the turbine, and (b) the surface elevation, the torque coefficient of a rotor column, the drag and the lift coefficients averaged according to the surface elevation phase.
Figure 11.
In the case with the rotors parked, (a) the cross-correlations of the surface elevation with the torque of a rotor column, the drag and the lift forces on the turbine, and (b) the surface elevation, the torque coefficient of a rotor column, the drag and the lift coefficients averaged according to the surface elevation phase.
Figure 12.
Probability Density Functions of the load coefficients in when the 2-VATT rotors are parked (blue) against when they operate at (orange).
Figure 12.
Probability Density Functions of the load coefficients in when the 2-VATT rotors are parked (blue) against when they operate at (orange).
Figure 13.
Fourier transform of the torque coefficient of one rotor column without waves (top), with regular waves (middle) and with irregular waves (bottom).
Figure 13.
Fourier transform of the torque coefficient of one rotor column without waves (top), with regular waves (middle) and with irregular waves (bottom).
Figure 14.
Coherence function of the torque coefficient of one rotor column, the drag and lift coefficients of the 2-VATT at with the upstream streamwise velocity measurement at in regular waves (top) and irregular waves (bottom).
Figure 14.
Coherence function of the torque coefficient of one rotor column, the drag and lift coefficients of the 2-VATT at with the upstream streamwise velocity measurement at in regular waves (top) and irregular waves (bottom).
Table 1.
Wave against current cases’ characteristics measured in the tank without turbine.
Table 1.
Wave against current cases’ characteristics measured in the tank without turbine.
| Case |
Wave type |
|
|
|
| (Hz) |
(s) |
(mm) |
|
No wave |
− |
− |
− |
|
Regular |
0.2 |
5.0 |
30 |
|
Regular |
0.3 |
3.3 |
38 |
|
Regular |
0.4 |
2.5 |
37 |
|
Regular |
0.4 |
2.5 |
102 |
|
Regular |
0.4 |
2.5 |
141 |
|
Regular |
0.5 |
2.0 |
42 |
|
JONSWAP |
0.4 |
2.5 |
107 |
Table 2.
Load range (p99-p01) and extreme value (max[abs(p01), abs(p99)]) ratios between the cases with waves and the case without waves at .
Table 2.
Load range (p99-p01) and extreme value (max[abs(p01), abs(p99)]) ratios between the cases with waves and the case without waves at .
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).