Submitted:
29 August 2023
Posted:
30 August 2023
You are already at the latest version
Abstract
Keywords:
MSC: 51N20
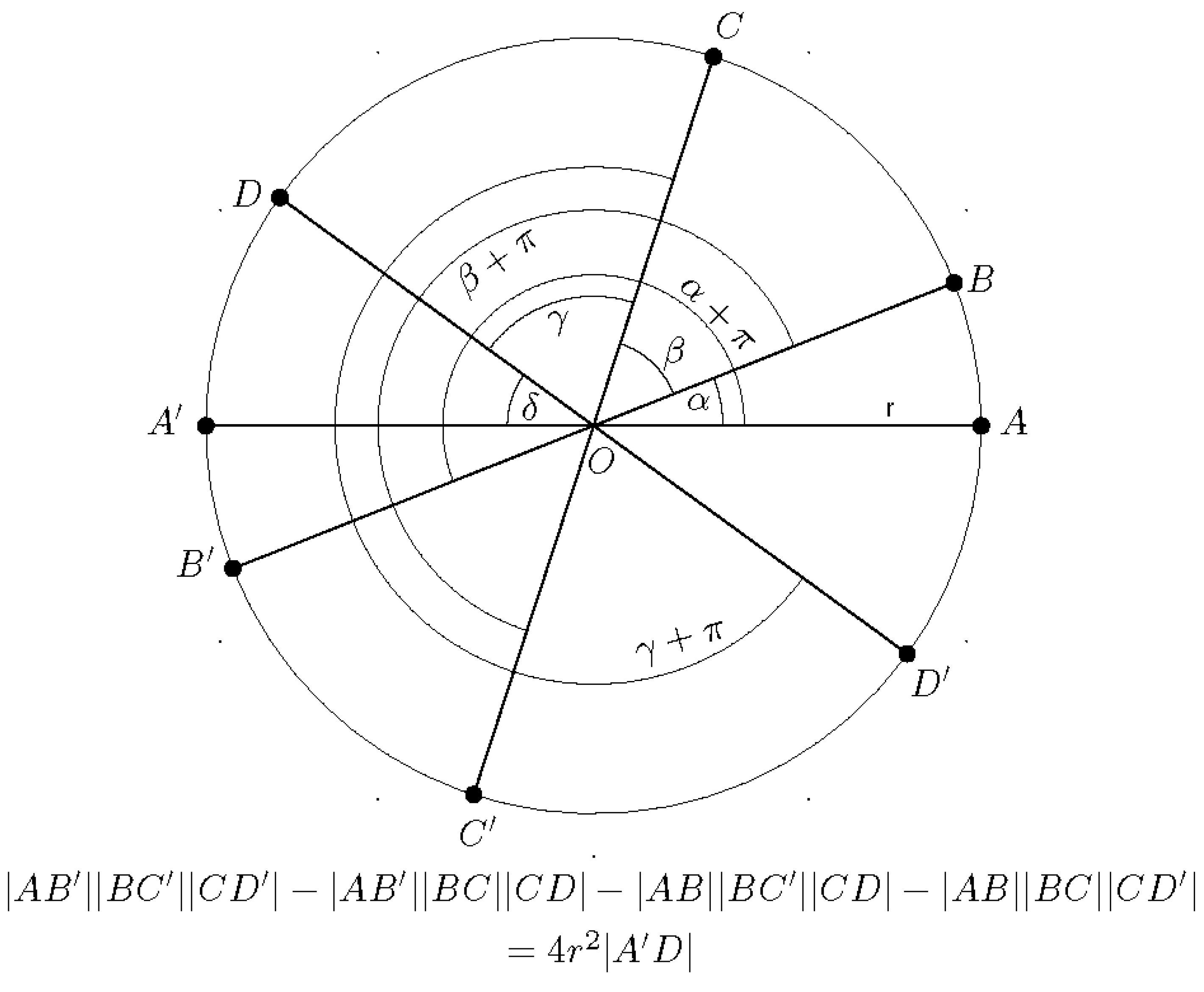
1. Four Cyclic Antipodal Points
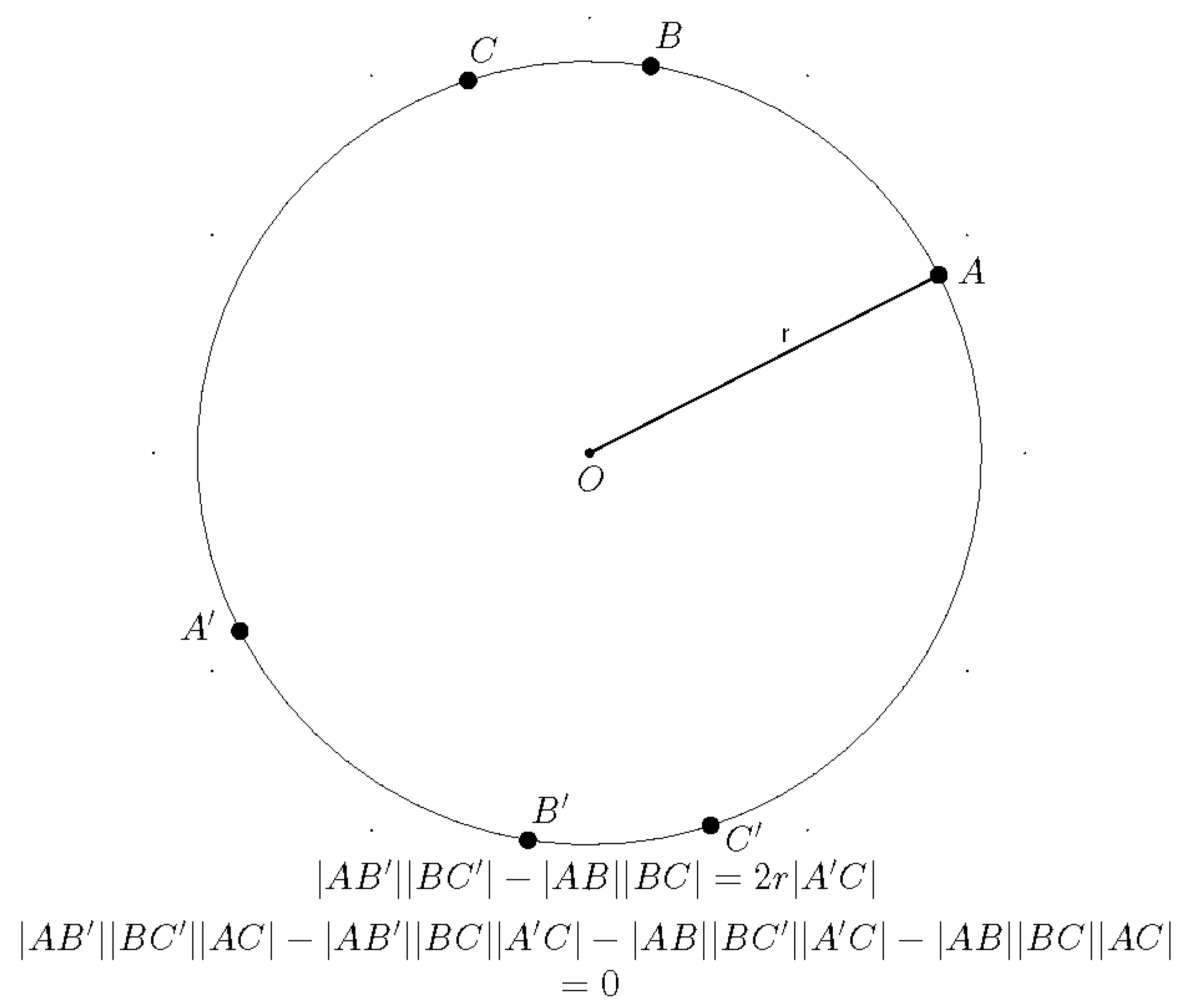
2. Special Cases
References
- Abraham, A. Ungar. Ptolemy’s theorem in the relativistic model of analytic hyperbolic geometry. Symmetry, 2023. [Google Scholar]
- Abraham, A. Ungar. The hyperbolic ptolemy’s theorem in the poincaré ball model of analytic hyperbolic geometry. Symmetry, 1487. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




