Submitted:
23 August 2023
Posted:
24 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- We conduct the first risk-averse, expected utility analysis in the presence of consumption for the non-affine class of SV models known as 4/2, under the preferable setting of MPR proportional to variance (type I). Our closed-form solutions, see Propositions 2, are of a non-affine nature, requiring confluent hypergeometric functions. As a byproduct, we produce the very first closed-form portfolio analysis for the 3/2 model for finite horizons.
- We extend the solutions described above to an ambiguity-averse investor, leading to the very first related analyses for the 4/2 and 3/2 models, see Proposition 3. In all cases, we consider complete markets, providing conditions for well-defined solutions under the assumption of existence, and proper changes of measure.
-
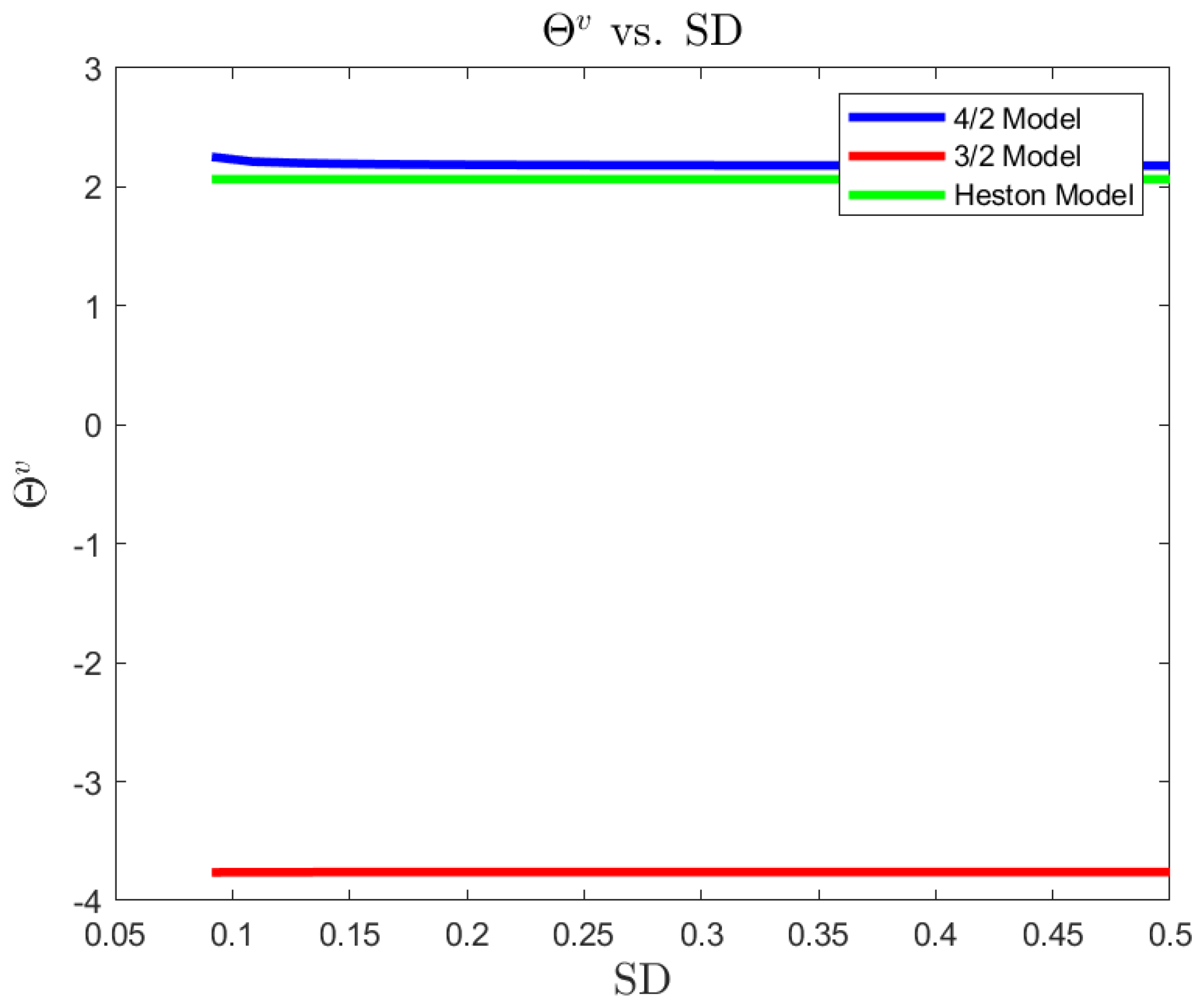
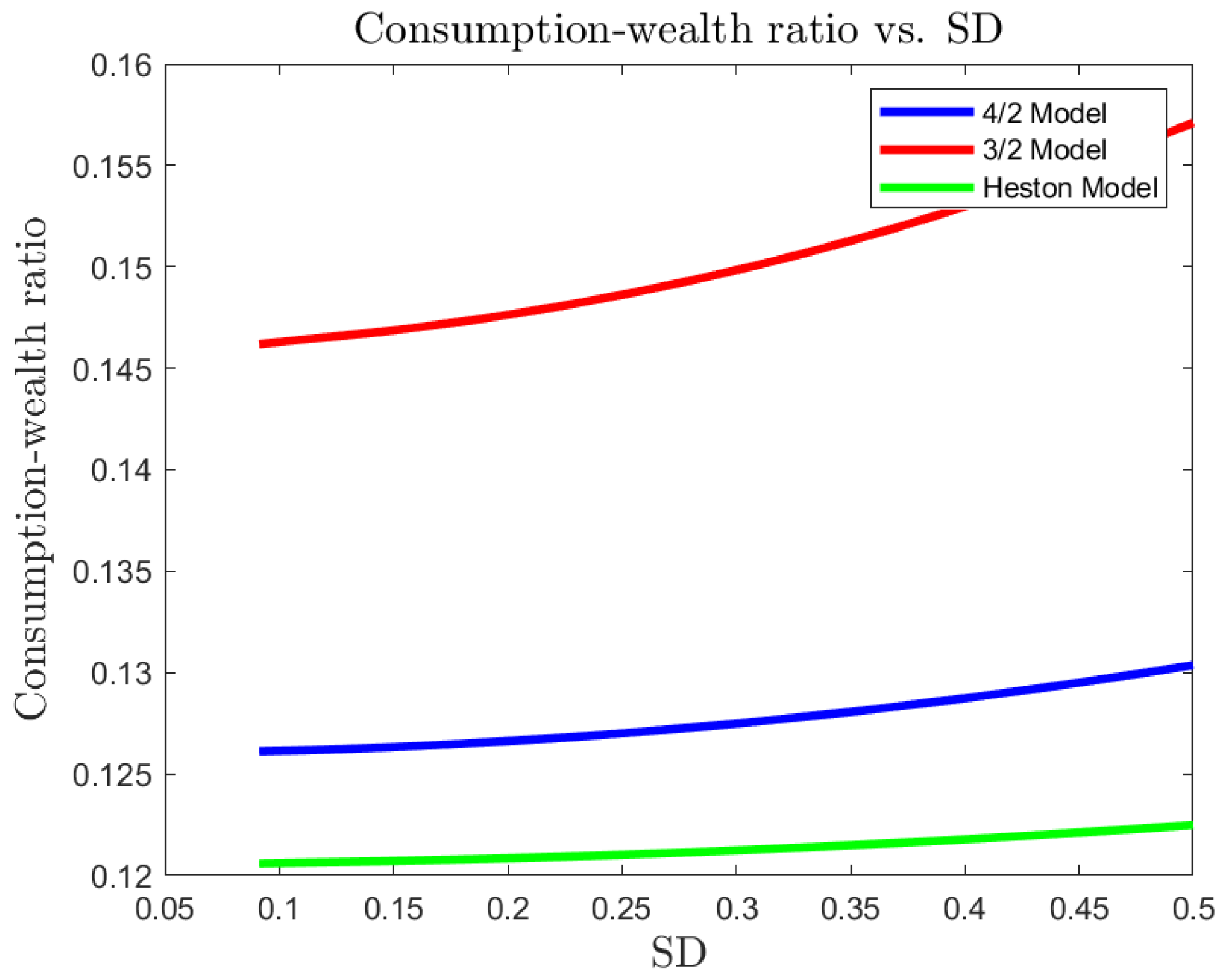
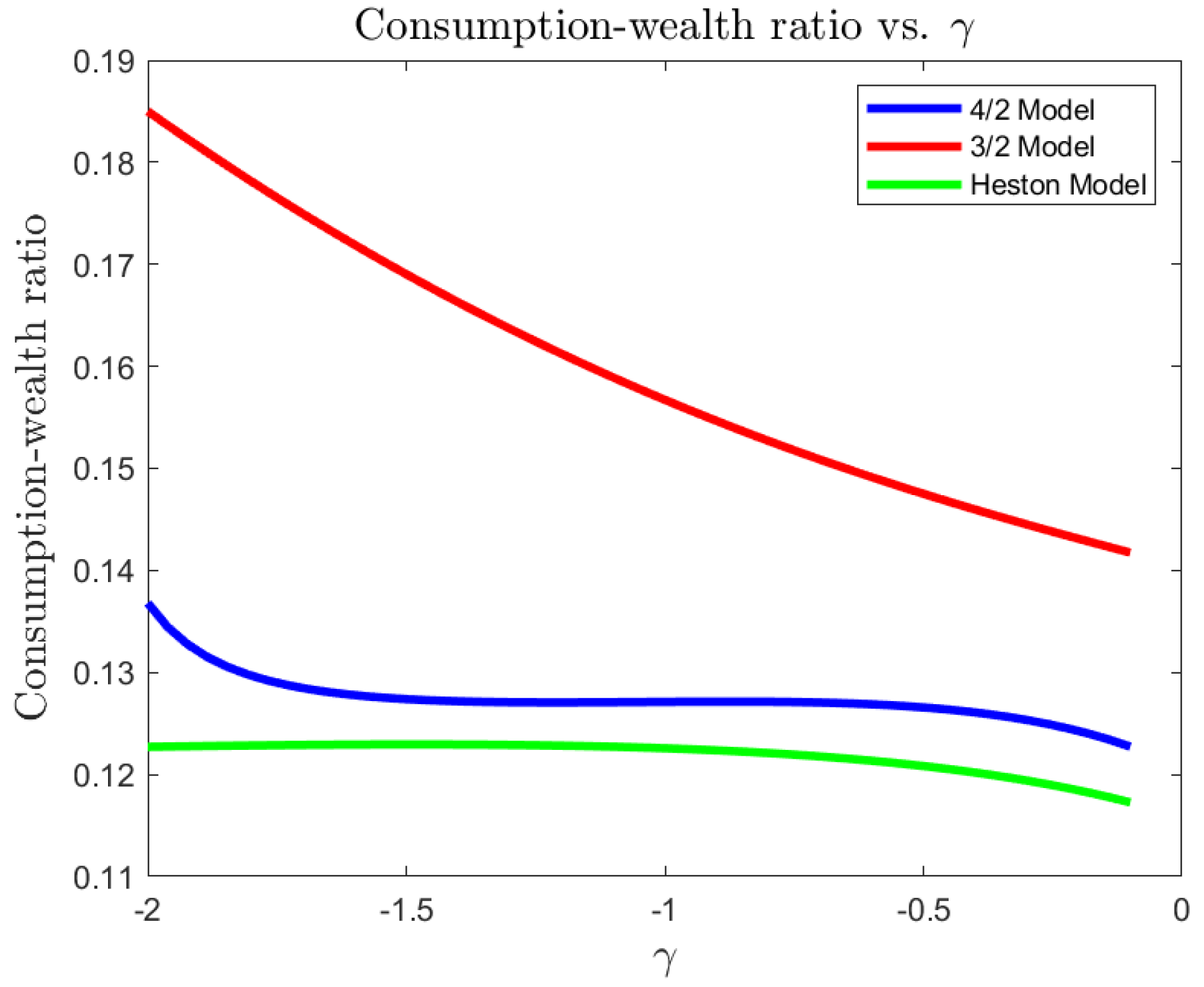
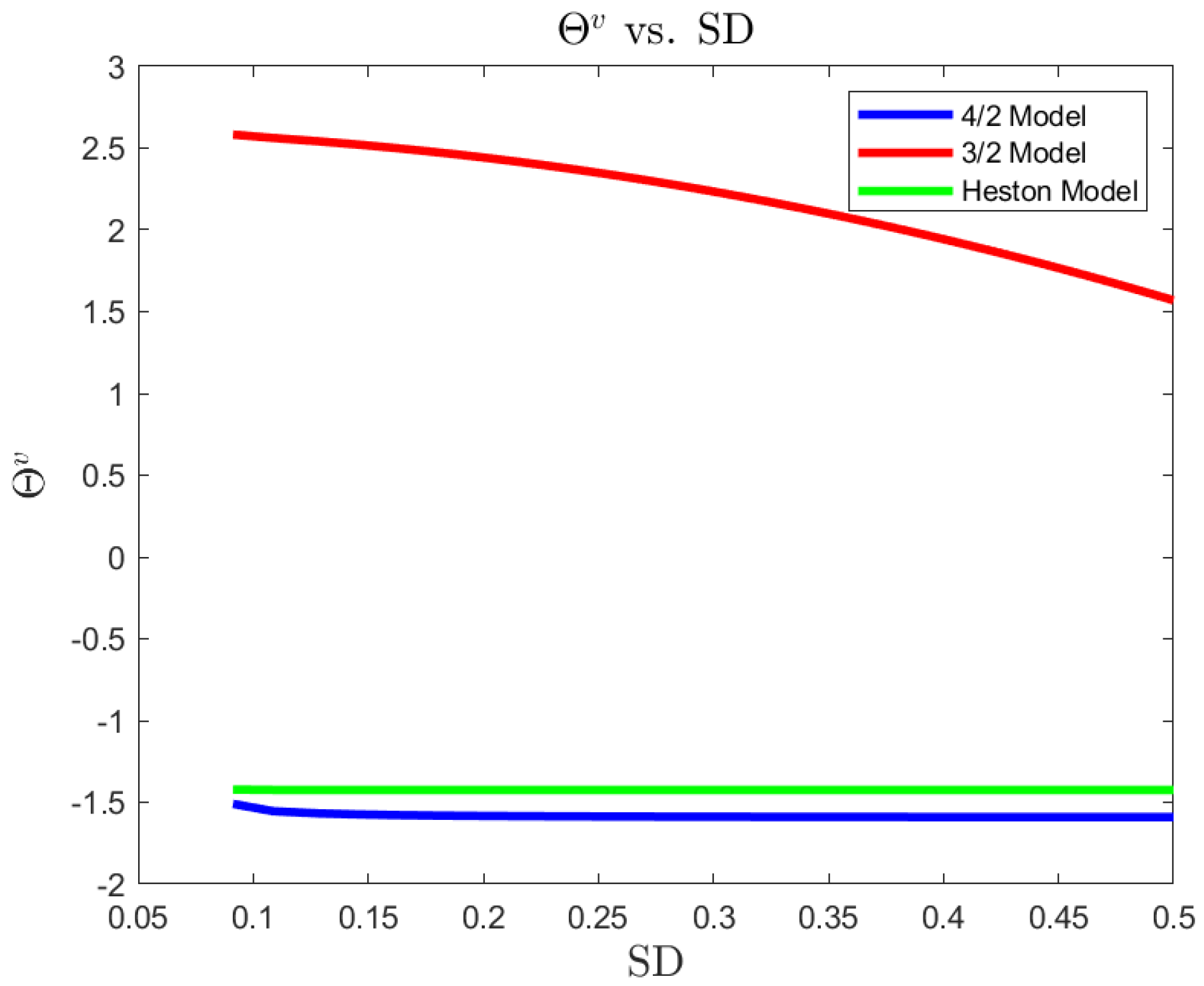
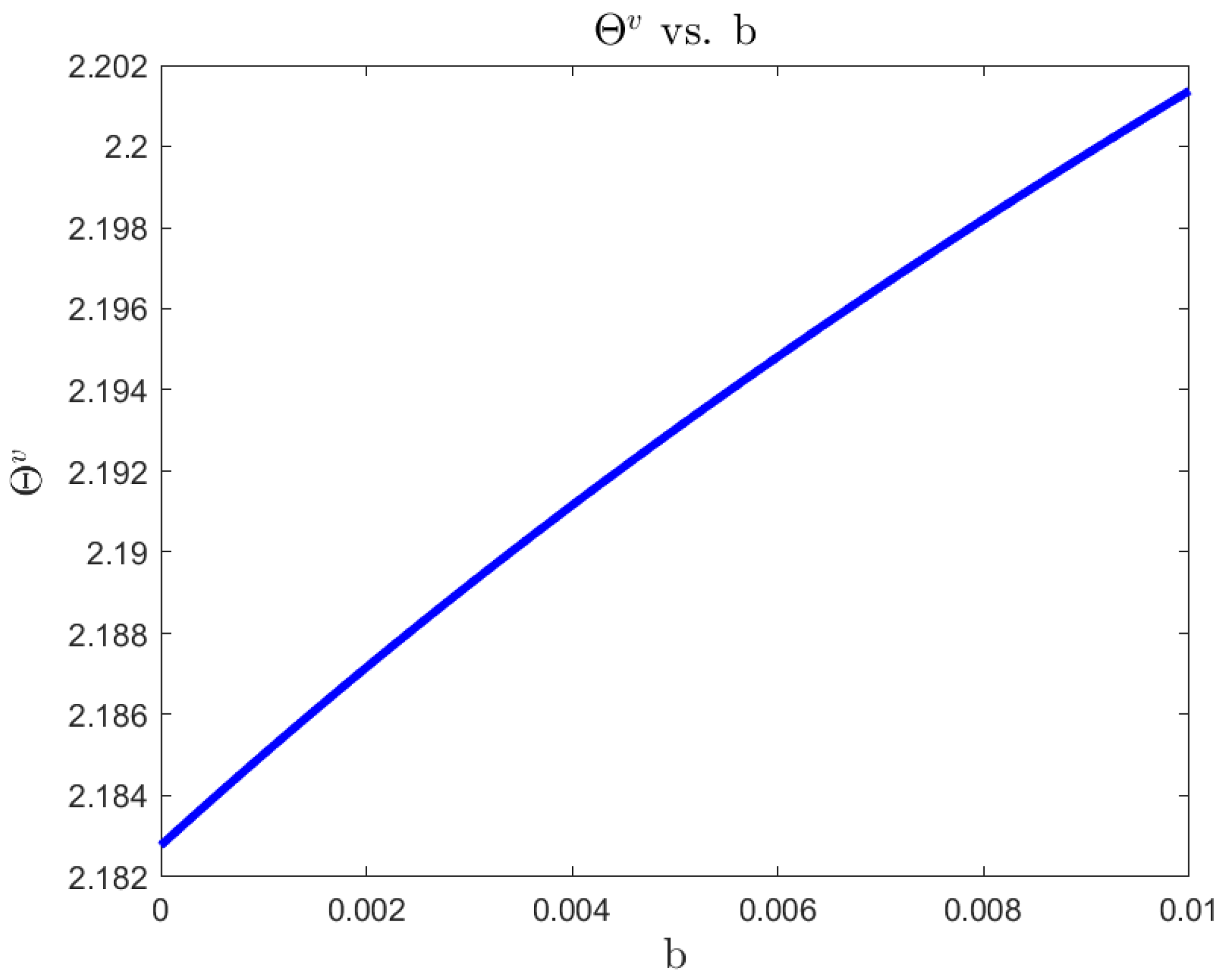
For a risk-averse investor, in a complete market, we illustrate the differences between the 4/2 model and the popular embedded cases of the 1/2 (Heston) and 3/2 models. On the one hand, the 4/2 and 1/2 models recommend similar levels of consumption and exposure. On the other hand, the 3/2 leads to 20% or higher levels of consumption and absolute exposures (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6).The difference in terms of exposures is exacerbated when considering an ambiguity-averse investor in a complete market. In such case, the 3/2 model performance could double absolute exposures compare to the 1/2 and 4/2 models (see Figure 12).
2. Model formulation
3. Portfolio optimization under EUT
3.1. Complete market analysis
4. Robust consumption portfolio optimization under EUT
4.1. Complete market analysis
5. Numerical analysis
5.1. Complete market analysis with consumption
5.2. Complete market analysis without consumption for ambiguity-averse investors
6. Conclusion
Appendix A. Proofs
Appendix A.1. Proof of conditions on change of measure
Appendix A.2. Proof of Proposition 2 (Complete Market, No Robustness, Consumption)
Appendix A.3. Proof of Proposition 3 (Complete Market, Robustness, Consumption)
Appendix A.4. Proof of Proposition 4
Appendix A.5. Proof of Corollary 5 (Complete Market, Robustness, No Consumption)
References
- Merton, R.C. On estimating the expected return on the market: An exploratory investigation. Journal of financial economics 1980, 8, 323–361. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. The review of financial studies 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Bakshi, G.; Cao, C.; Chen, Z. Empirical performance of alternative option pricing models. The Journal of finance 1997, 52, 2003–2049. [Google Scholar] [CrossRef]
- Bates, D.S. Post-’87 crash fears in the S&P 500 futures option market. Journal of econometrics 2000, 94, 181–238. [Google Scholar]
- Kraft, H. Optimal portfolios and Heston’s stochastic volatility model: an explicit solution for power utility. Quantitative Finance 2005, 5, 303–313. [Google Scholar] [CrossRef]
- Chacko, G.; Viceira, L.M. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets. The Review of Financial Studies 2005, 18, 1369–1402. [Google Scholar] [CrossRef]
- Heston, S.L. A simple new formula for options with stochastic volatility 1997.
- Grasselli, M. The 4/2 stochastic volatility model: a unified approach for the Heston and the 3/2 model. Mathematical Finance 2017, 27, 1013–1034. [Google Scholar] [CrossRef]
- Cheng, Y.; Escobar-Anel, M. Optimal investment strategy in the family of 4/2 stochastic volatility models. Quantitative Finance 2021. [Google Scholar] [CrossRef]
- Cheng, Y.; Escobar-Anel, M. Robust portfolio choice under the 4/2 stochastic volatility model. IMA Journal of Management Mathematics 2021, 00, 0–36. [Google Scholar] [CrossRef]
- Lewis, A. Option Valuation under Stochastic Volatility. Technical report, Finance Press, 2000.
- Cheng, Y.; Escobar-Anel, M.; Gong, Z. Generalized Mean-Reverting 4/2 Factor Model. Journal of Risk and Financial Management 2019, 12, 159. [Google Scholar] [CrossRef]
- Escobar, M.; Ferrando, S.; Rubtsov, A. Robust portfolio choice with derivative trading under stochastic volatility. Journal of Banking & Finance 2015, 61, 142–157. [Google Scholar]
- Liu, J.; Pan, J. Dynamic derivative strategies. Journal of Financial Economics 2003, 69, 401–430. [Google Scholar] [CrossRef]
- Maenhout, P.J. Robust portfolio rules and asset pricing. Review of financial studies 2004, 17, 951–983. [Google Scholar] [CrossRef]
- Heath, D.; Schweizer, M. Martingales versus PDEs in finance: an equivalence result with examples. Journal of Applied Probability 2000, 947–957. [Google Scholar] [CrossRef]
| 1 | incomplete market solutions follow trivially from our setting |

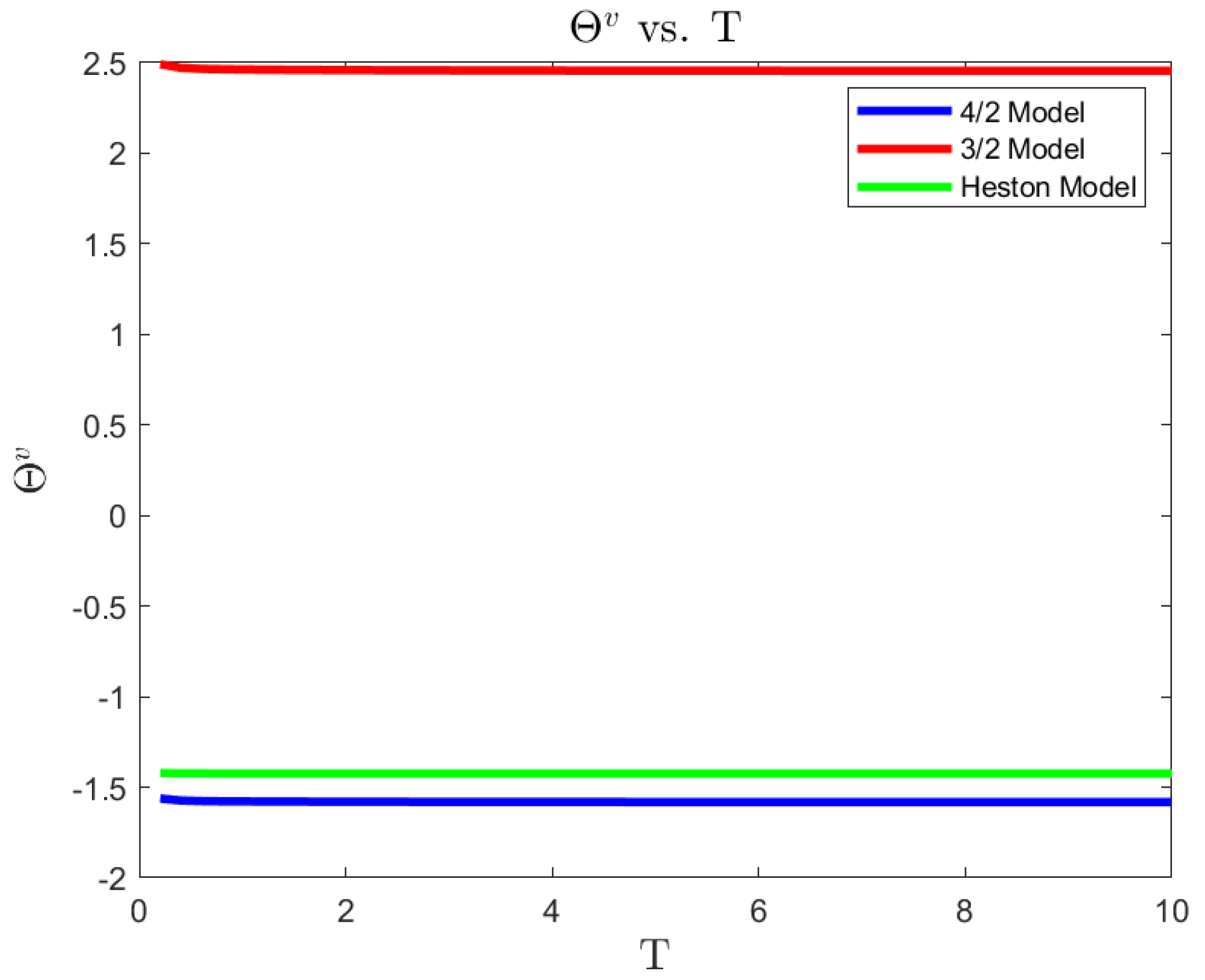
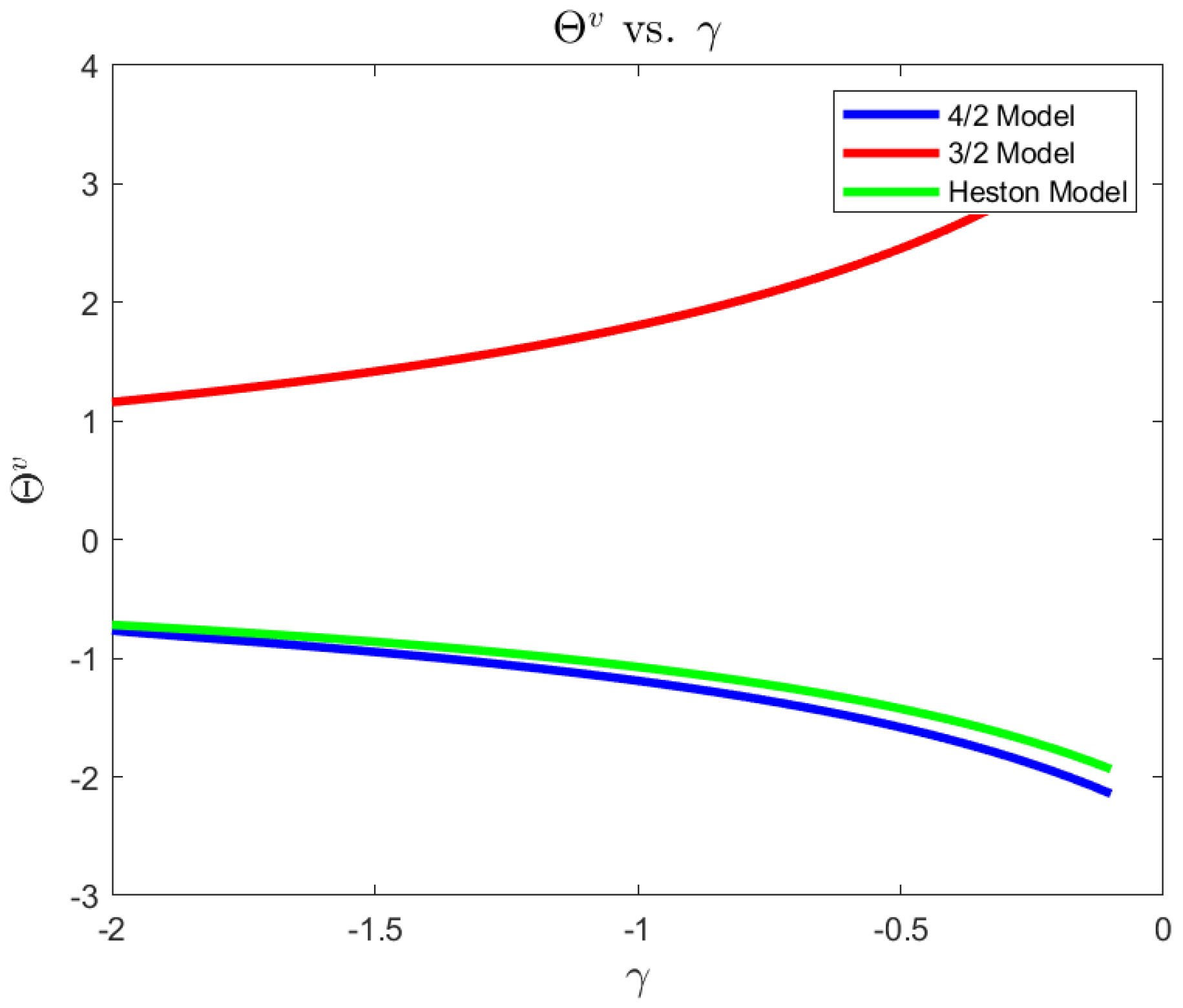
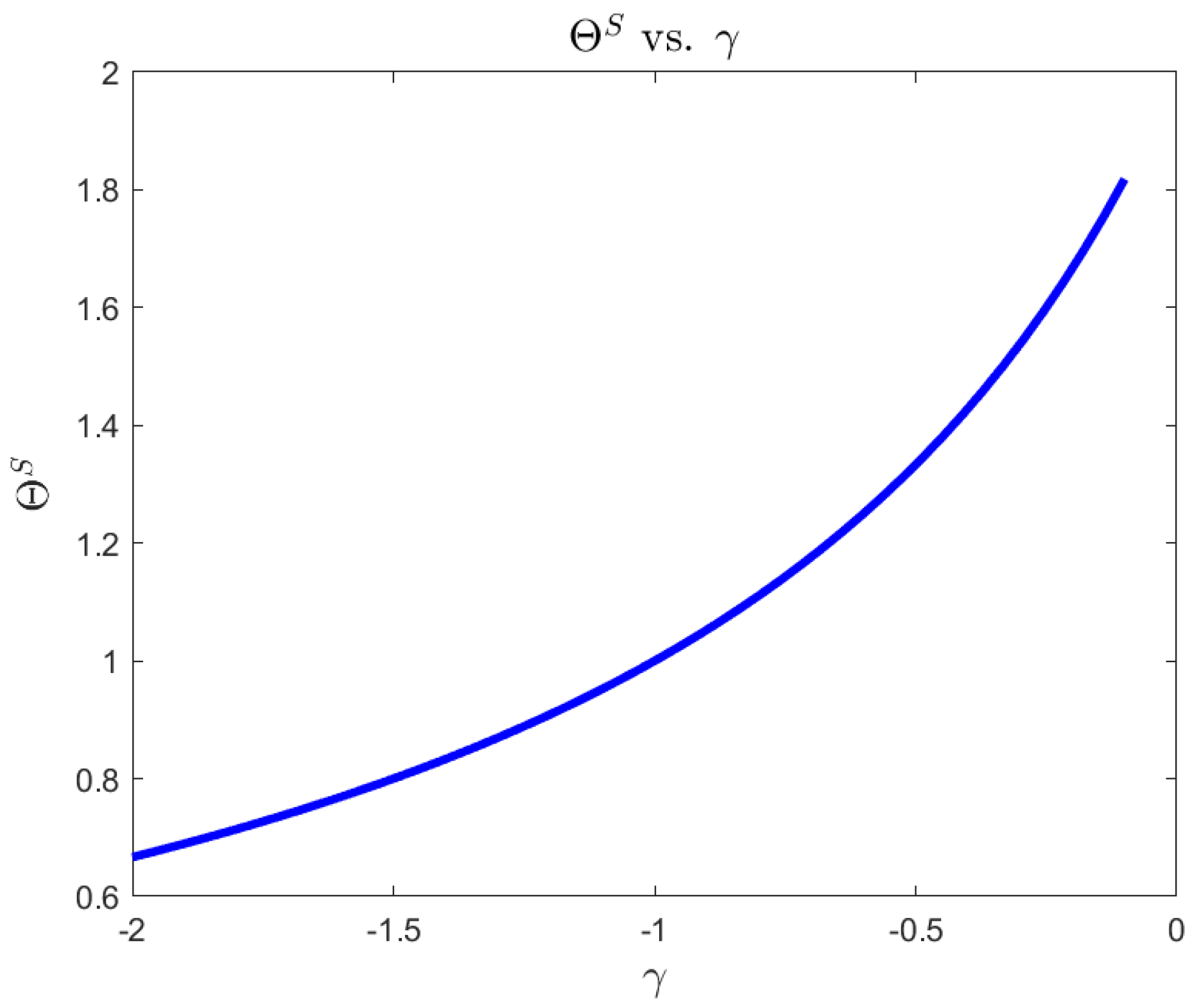
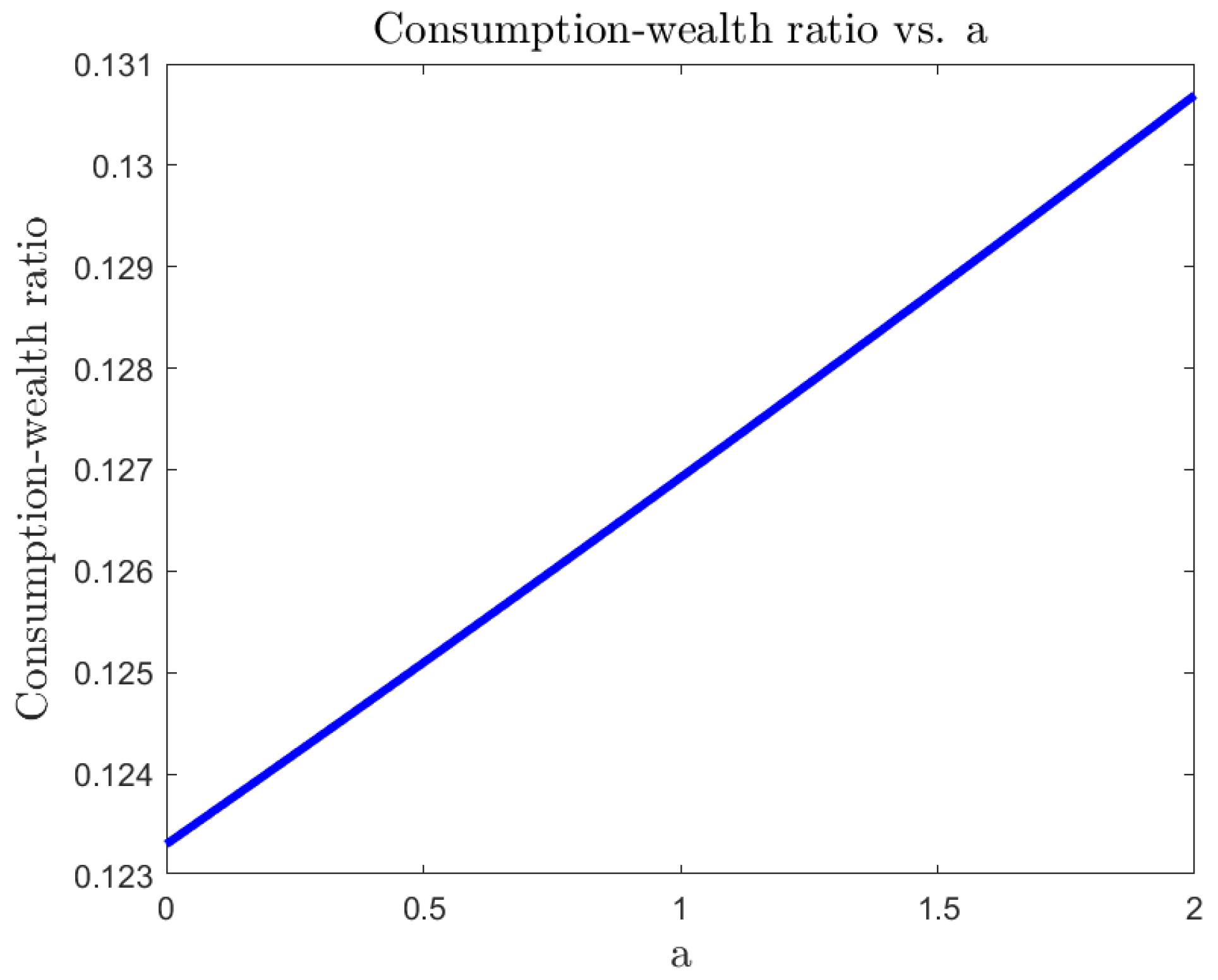
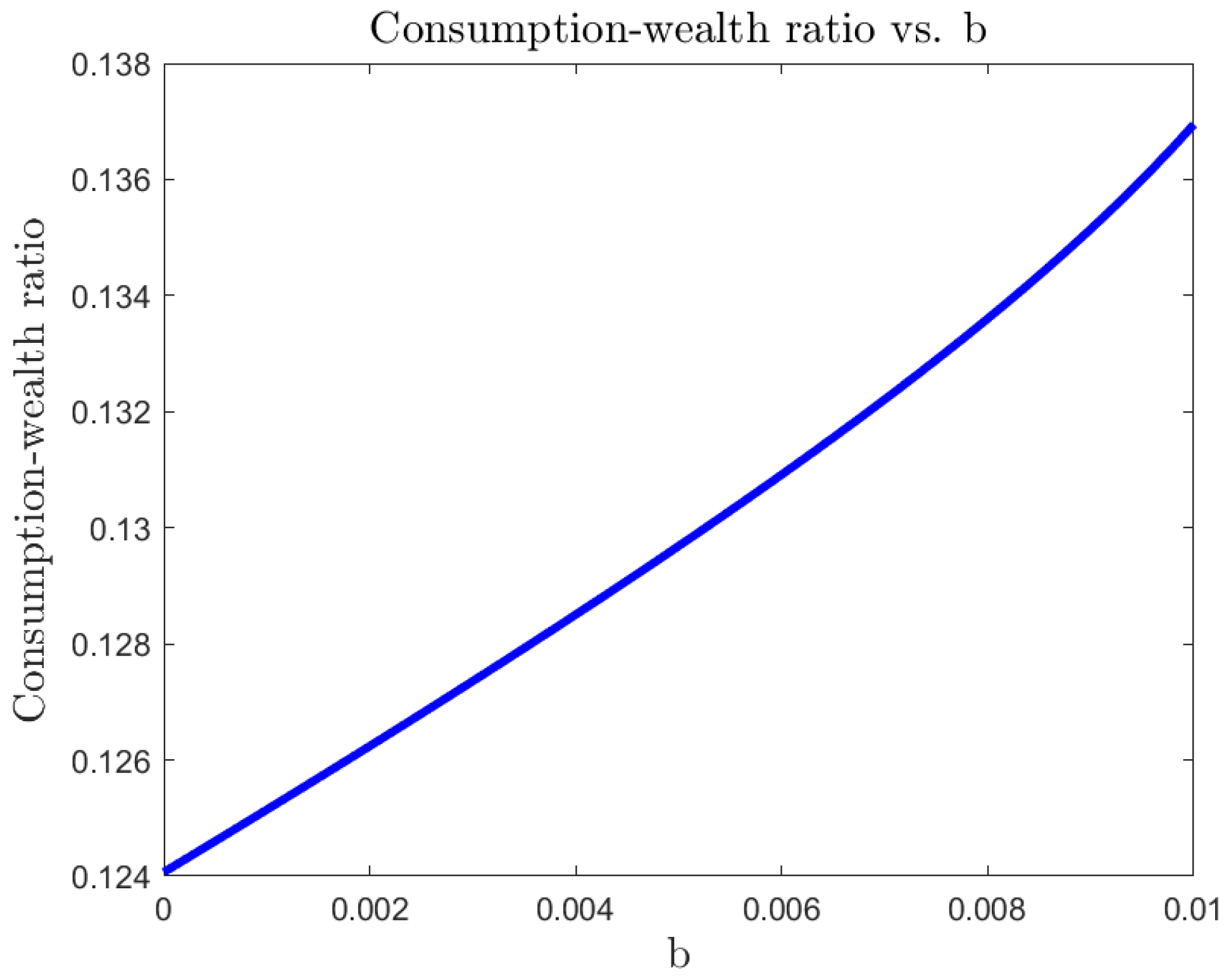
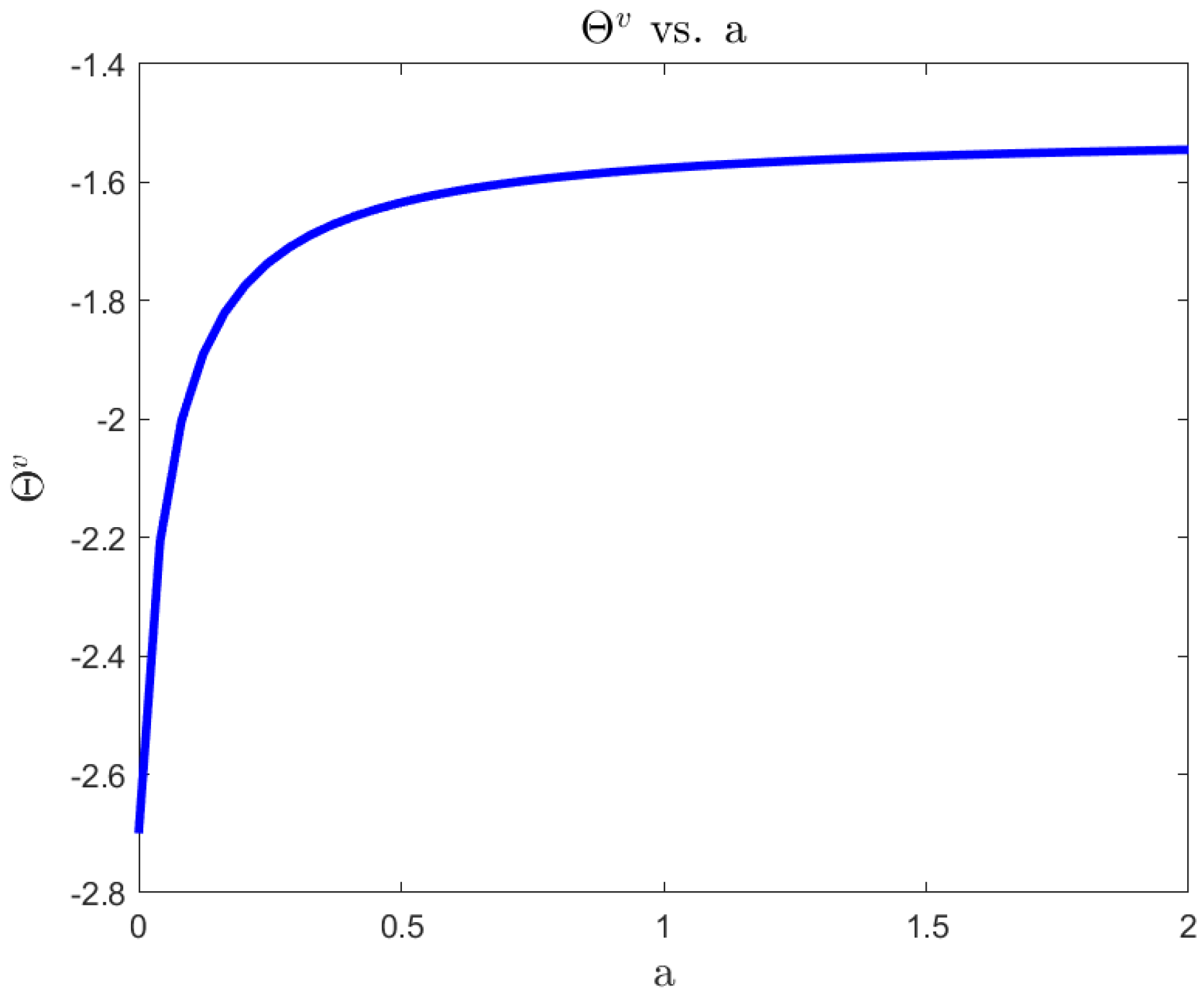
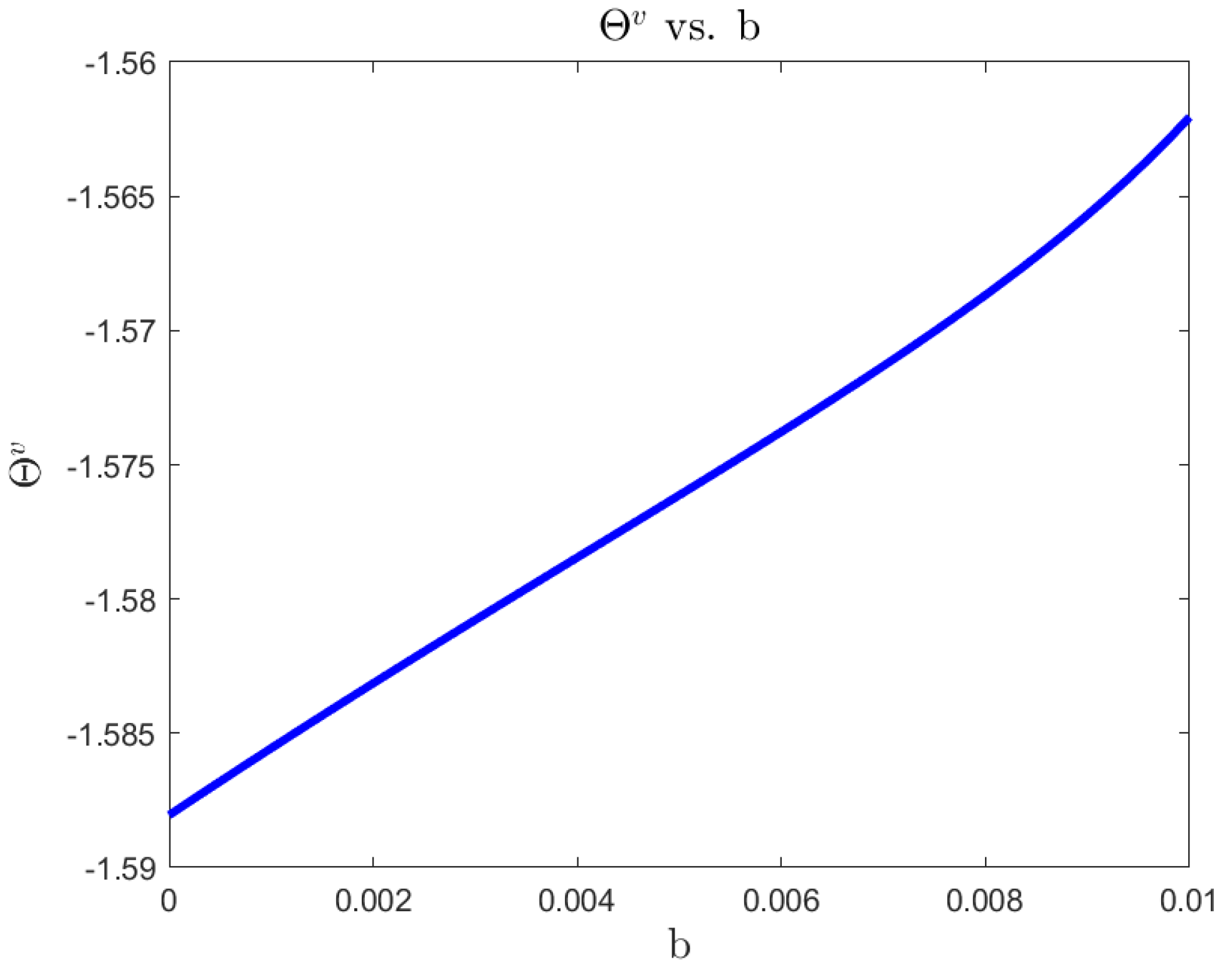

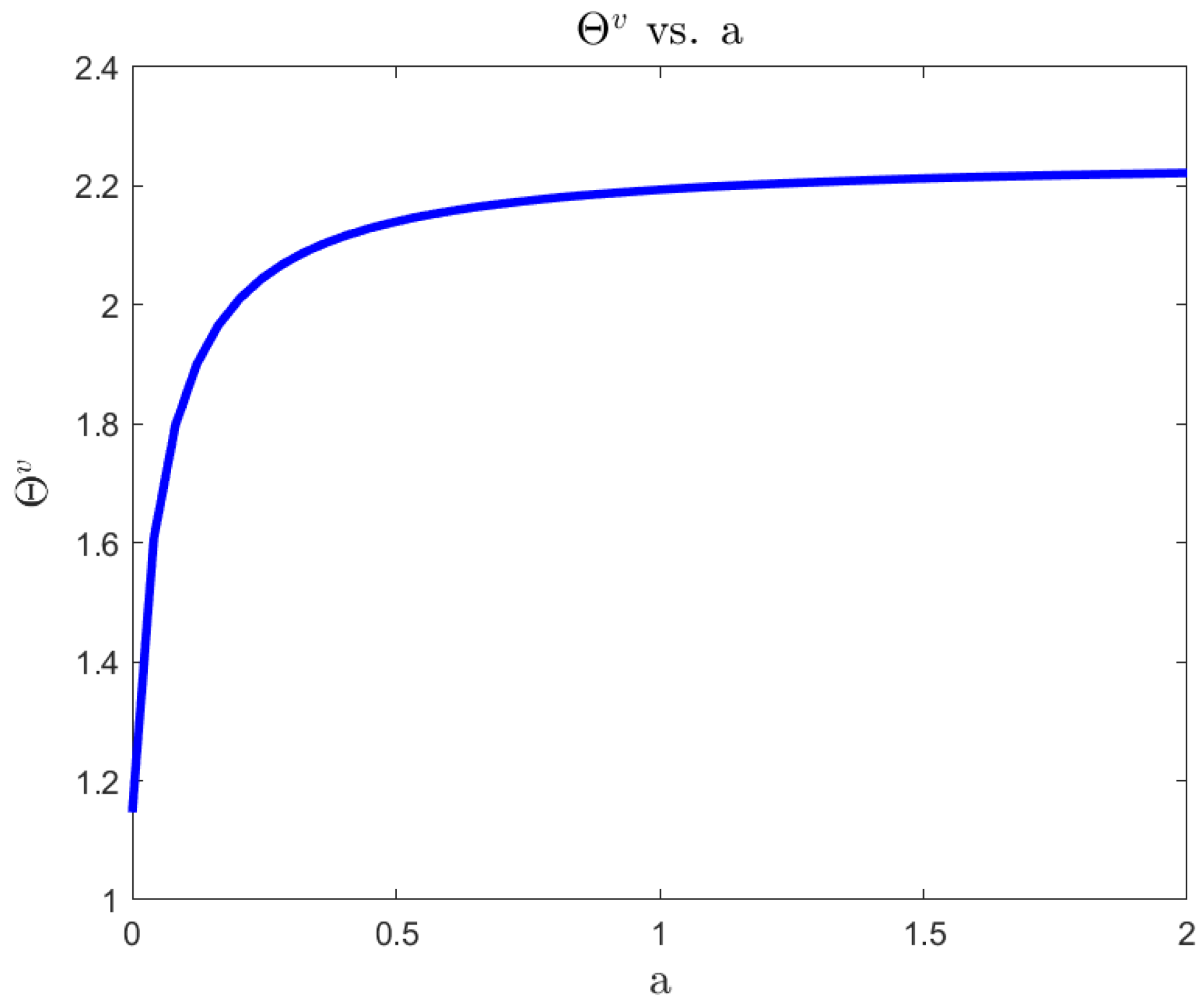
| 4/2 Model | 3/2 Model | Heston | |
|---|---|---|---|
| 7.3479 | 6.9884 | 14.6290 | |
| 0.0328 | 0.0323 | 0.0315 | |
| 0.6612 | 0.3760 | 0.5210 | |
| 0.9051 | 0 | 1 | |
| 0.0023 | 0.0268 | 0 | |
| -0.7689 | 0.7910 | -0.8129 | |
| 3.0176 | 4.2973 | 2.8689 | |
| Theoretical leverage () | -0.7689 | -0.7910 | -0.8129 |
| r | t | T | |||||
|---|---|---|---|---|---|---|---|
| 0.05 | 0.02 | -0.5 | 0.04 | 0 | 10 | 1 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





