With the deepening of the diversification and openness of financial system, financial vulnerability, as an endogenous attribute of financial system, becomes an important measurement of financial security. Based on network analysis, we introduce network curvature indicator improved by Copula entropy as an innovative metric of financial vulnerability. Compared with previous network curvature analysis method, CE-based curvature proposed in this paper can measure market vulnerability and systematic risk with significant advantages.

Keywords:

Subject: Business, Economics and Management - Finance

1. Introduction

As the "blood supply station" of modern economy, finance has become increasingly vulnerable in the face of rising global inflationary pressure and the frequent occurrence of related crises, which gradually endanger the security of real economy. Many countries are increasingly concerned about how to prevent financial risks and measure market vulnerability. Along with the continuous progress of technological tools, new methods of measuring financial vulnerability are urgently needed to enable countries to respond to and prevent crises in a timely manner and ensure smooth economic operation.

Minsky (1982)[1] argues that financial vulnerability is the inherent instability caused by the financial industry's own highly indebted operation. Other scholars have also put forward their own views based on this hypothesis. However, as there are many factors affecting financial vulnerability, the definition has not yet been unified, and the corresponding measurement methods are also different. Some scholars construct financial crisis early warning models to predict the likelihood of a country's crisis in a certain future time frame and thus measure the financial stability state of a country, such as Kaminsky et al. (1998)[2]; other studies focus on constructing measurement indicators, that is, using a certain method to combine multiple core indicators into a composite index, the financial stability index, to reveal the overall status of future financial stability, such as Billio et al. (2016)[3]. Unfortunately, despite the increasing sophistication of models and indicator methods, there are still problems like the inability to dynamically demonstrate changes in market vulnerability and characterize market risk contagion. With the rapid development of complex network analysis methods and tools, newer studies on financial vulnerability measures have started to introduce weighted undirected graph as an abstract model of the financial system[4,5,6,7]. Based on this theory, Sandhu et al. (2015)[8] proposed using curvature index to measure financial vulnerability, but the related research is relatively preliminary and the research field of applying various discrete curvatures to measure market vulnerability still needs to be further studied.

An important drawback of previous network analysis methods is that they often use linear correlation to describe the dependencies and associations between nodes, while ignoring higher-order correlations, and these approaches are often tepid in measuring tail risk. A good example is the 2008 financial crisis, when the Gaussian copula function, which measures linear correlation, was widely used in derivative pricing. However, linear correlation ignores higher- order correlations between variables, especially tail risks. Therefore, when a series of default events broke out collectively, it was finally found that derivatives constructed by linear correlation lost the function of risk hedging. Compared with using traditional methods such as Pearson or Spearman correlation coefficient to measure the correlation between nodes in a network, we attempt to apply the Copula entropy (CE) proposed by Ma J and Sun Z (2008)[9] to network construction. CE can measure the statistical correlation of all orders, which can provide a clearer correlation pattern for the network and show a strong correlation measurement effect, so it is suitable for this study.

The following is the arrangement of each part of this paper: the second part is our method; the third part is about empirical results and analyses; and final part is our conclusions.

2. Copula entropy and Ricci curvature

2.1. Nonlinear causal and information captured with Copula entropy

Usually, the marginal distribution of each variable can be easily determined from the joint distribution of random variables, but it was difficult to determine the joint distribution from the marginal distributions until Sklar proposed the Copula theory in 1959[10]. This theory can decompose a joint distribution into n marginal distributions and a Copula function that describes the correlation between variables, including the magnitude of correlation coefficient and the type of correlation structure.

Suppose the marginal distribution of the joint distribution function is

F_{i} (x_{i}) (i = 1, \dots, n)

, then there exists a Copula function

C

that satisfies Eq. (1).

\begin{matrix} F (x_{1}, \dots, x_{n}) = C (F_{1} (x_{1}), \dots, F_{n} (x_{n})) \end{matrix}

(1)

F_{i} (x_{i}) (i = 1, \dots, n)

is a continuous function, then

C

is uniquely determined; if

F_{i} (x_{i}) (i = 1, \dots, n)

is a one-dimensional distribution function, then

C

is the corresponding Copula function. For any

{(u}_{1}, \dots, u_{n})

in the domain of function

C

, Eq.(2) holds:

C {(u}_{1}, \dots, u_{n}) = F (F_{1}^{- 1} (x_{1}), \dots, F_{n}^{- 1} (x_{n}))

(2)

Among them,

F_{i}^{- 1} (x_{i})

is the pseudo-inverse function of

F_{i} (x_{i})

Taking partial derivatives of both sides of Eq. (1), we obtain the joint probability density function as Eq.(3):

f (x_{1}, \dots, x_{n}) = c (F_{1} (x_{1}), \dots, F_{n} (x_{n})) \prod_{i = 1}^{n} f_{i} (x_{i})

(3)

where

c (u_{1}, \dots, u_{n}) = \frac{\partial^{n} C (u_{1}, \dots, u_{n})}{\partial u_{1} \partial u_{2} \dots \partial u_{n}}

is the Copula density function, and

f_{i} (x_{i})

is the density function of marginal distribution.

Therefore, it can be inferred that the Copula function establishes a mapping relationship between the joint distribution and the marginal distributions. By utilizing the Copula function, it is possible to construct a multidimensional joint distribution using multiple one-dimensional marginal distributions, and this joint distribution is not restricted to specific marginal distributions. Once the type and parameters of the Copula function are determined, the joint probability distribution can be obtained by combining the probability density functions of the marginal distributions.

As we know, previous network analysis methods based on traditional correlation coefficients are only able to describe linear correlations between nodes, which is not sufficient for our study of financial markets with complex tail correlations. Therefore, we introduce Copula entropy to improve the method.

The concept of Copula entropy, defined by the Copula density function, was first proposed by Ma J and Sun Z in 2008[9]. It was proved to be equivalent to mutual information in information theory[11]. Essentially it is a form of Shannon entropy, expressed as

H_{c} (u_{1}, \dots, u_{n}) = - \int_{0}^{1} \dots \int_{0}^{1} c (u_{1}, \dots, u_{n}) \log [c (u_{1}, \dots, u_{n})] d u_{1} \dots d u_{n}

(4)

Considering the case of two variables, Eq.(4) is expressed as

- H_{c} (u_{1}, u_{2}) = H (X_{1}) + H (X_{2}) - H (X_{1}, X_{2})

(5)

Among them,

H (X_{i}) (i = 1,2)

and

H (X_{1}, X_{2})

are the uncertainty degree of random variable

X_{i}

obtained by Shannon information theory and the joint entropy of random variable

X_{1}

and

X_{2}

, which are calculated by Eq.(6) and Eq.(7) respectively.

H (X) = - \sum_{i = 1}^{N} p (x_{i}) l o g p (x_{i})

(6)

H (X, Y) = - \sum_{i = 1}^{N} \sum_{j = 1}^{N} p (x_{i}, y_{i}) l o g p (x_{i}, y_{i})

(7)

In addition, mutual information can be regarded as the amount of information contained in a random variable about another random variable, or the uncertainty of a random variable that is reduced by knowing another random variable, expressed as Eq.(8).

\begin{matrix} M (X, Y) = \sum_{i = 1}^{N} \sum_{j = 1}^{N} p (x_{i}, y_{i}) l o g \frac{p (x_{i}, y_{i})}{p (x_{i}) p (y_{i})} = H (X) + H (Y) - H (X, Y) \end{matrix}

(8)

Obviously,

H_{c} (u_{1}, u_{2}) = - M (X_{1}, X_{2})

, that is, Copula entropy has the same value as interaction entropy with opposite sign[12]. From this, it can be understood that Copula entropy and mutual information share a fundamental unity as they both quantify the amount of information regarding all orders of correlation between random variables.

In the context of correlation becoming an important indicator of financial market risk, the advantages of CE over the traditional Pearson coefficient are as follows: (1) Copula function value can be obtained by non-parametric estimation method, which does not require random variables to conform to or be close to normal distribution, and works well when measuring the correlation of non-elliptic distribution families. (2) Different Copula functions can be selected to portray the correlation between variables according to the focus of the study, including the Gumbel Copula function, which is sensitive to the change of the upper tail of the variable distribution, the Clayton Copula function, which is sensitive to the change of the lower tail, and the Frank Copula function, which is not sensitive to the change of the tail, etc.. (3) It is not limited by dimensions, and can measure the correlation between multidimensional variables, including nonlinear relationships.

In fact, Copula entropy is not the first optimization on Pearson coefficient. In 1904, the British psychologist Spearman proposed the rank correlation coefficient[13]. In the statistical sense, this coefficient can be regarded as a special case of the Pearson correlation coefficient, but the main difference is that it does not require variables to be close to or conform to a normal distribution, and it can measure the nonlinear relationship between two variables. However, the Spearman coefficient also has the disadvantages that it cannot reflect the correlation structure of variables and cannot calculate the correlation of multidimensional variables. Therefore, this paper finally chooses Copula entropy to measure the correlation and correlation structure between variables, and compares the empirical effect of traditional correlation coefficients and CE on the CSI 300 data in 4.1 to verify the above conclusions.

2.2. Market vulnerability measurement with Ricci curvature

Although graphs and networks are composed of discrete objects, they can be considered as metric spaces just like smooth manifolds, where the distance between any two nodes can be specified by the length of the path between them. The classic Ricci curvature is applicable to smooth manifolds and requires tensor and higher order derivatives, and thus cannot be directly applied in discrete graphs or networks. In order to make Ricci curvature applicable to financial vulnerability studies, it is necessary to focus on the quantification of Ricci curvature for two basic geometric properties of manifolds, namely, the bulk growth and divergence of geodesics. In n-dimensional Riemannian manifolds, Ricci curvature controls the n-1 dimensional volume growth of geodesics along a certain vector direction in n-dimensional stereo angles; in addition, Ricci curvature quantifies the dispersion of geodesics with the same initial point in a given stereo angle.

Classic Ricci curvature is related to vectors in smooth manifolds, and extended to network analysis, the notion of discrete Ricci curvature is related to edges rather than vertices or nodes. Since the discretized Ricci curvature does not have all the characteristics of the classic Ricci curvature, different discretization methods can give different interpretations to the graph or network, and then produce different curvature concepts, such as Ollivier-Ricci(OR), Forman-Ricci(FR), Menger-Ricci(MR) , Haantjes-Ricci(HR), etc. OR curvature realizes discretization processing based on classic Ricci curvature by comparing the optimal average distance and Euclidean distance between neighbor nodes, and its core process lies in the solution of the optimal average distance; FR curvature is mainly based on the relationship between Laplacian and Ricci curvature, which is more algebraic in nature and can quantify the amount of information propagated by the end of the edge in the network; the basic principles of HR curvature and MR curvature are relatively similar, both derived from the definition of measuring triangle curvature proposed by Menger. The main difference is that MR curvature only considers triangles or simple paths of length 2 formed between two nodes of an edge, while HR curvature considers longer paths between two nodes.

There are different curvature properties in above four discrete Ricci curvatures due to differences in their principles and metrics. In a discrete network, the Ollivier-Ricci curvature can well explain the volume growth in the classic Ricci curvature; while the Forman-Ricci, Menger-Ricci, and Haantjes-Ricci curvatures describe the divergence of geodesics in the classic Ricci curvature characteristic. The specific introduction of the four curvatures is available in Appendix A.

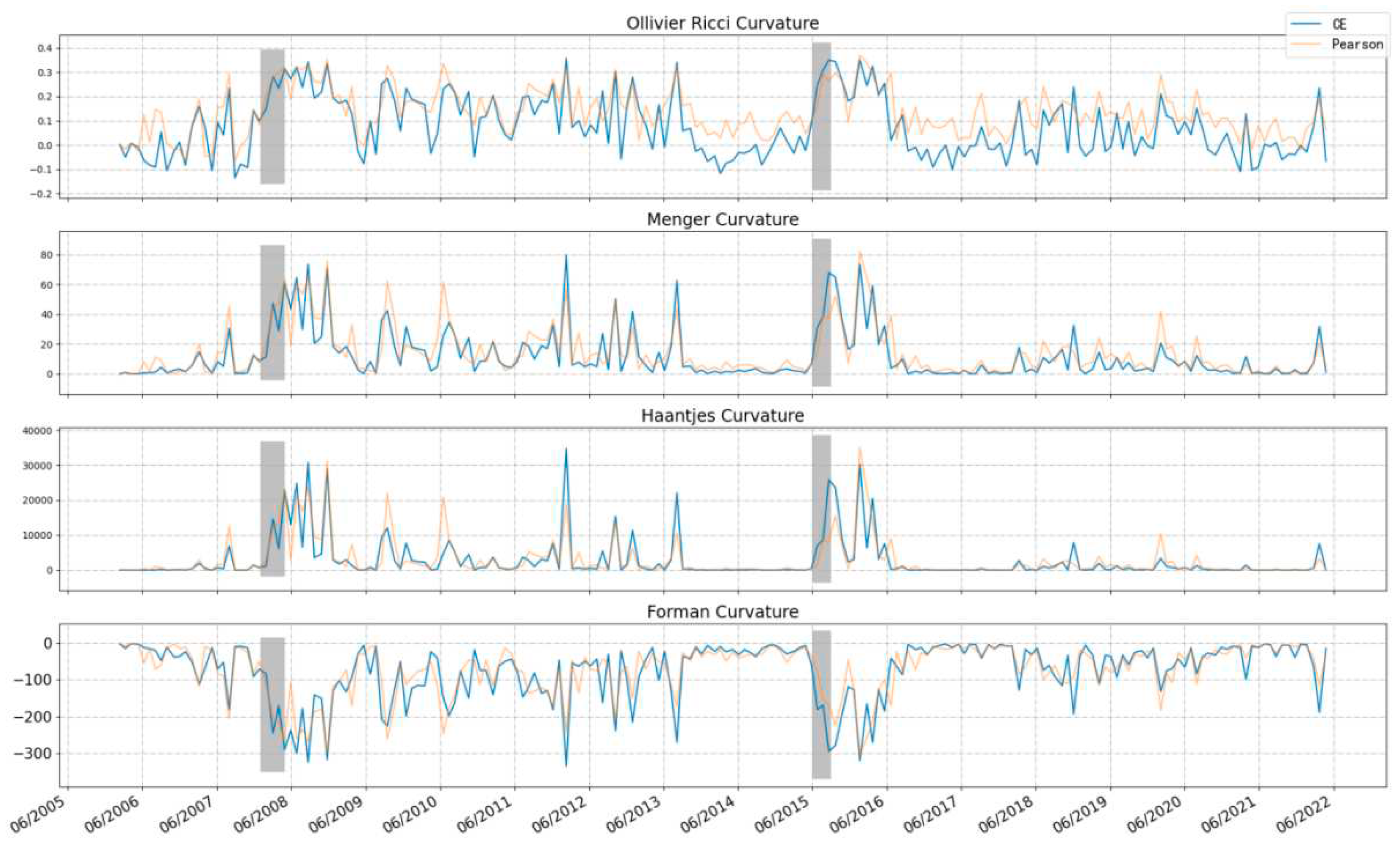
3. The calculation of curvature

In general, our analysis methods are as follows: (1) We calculate CE between assets in the market refer to the method of Ma J and Sun Z(2009)[9]. In this step, we try to account for the superiority of CE compared to the linear correlation coefficients. (2) We add CE into the construction of the market network to get the curvature measure we need.

In the first step, we use the nonparametric CE estimation method. The method consists of two steps: (1) Estimate the empirical Copula density function; (2) Estimate CE with the empirical Copula density function.

Given a set of independent identically distributed samples

{x_{1}, . ., x_{T}}

of random variable X, the empirical Copula density function can be easily estimated by ordinal statistics, as Eq.(9)

F_{i} (x_{i}) = \frac{1}{T} \sum_{t = 1}^{T} 1 (x_{t}^{i} < x_{i})

(9)

Where

1 (\cdot)

represents the indicative function.

After obtaining the empirical Copula density function, we used the K-nearest neighbor method proposed by Kraskov et al.[14] to estimate CE.

In the second step, we don't directly use CE as the edge weight, but we treat it as follows.We take the following processes on the calculated CE according to its distribution: tail the CE of perfectly positive correlated stocks to 2; then, use linear scaling method to transform the scale of CE to [0,1]. The purpose of these processes is to enlarge the difference between CE in the value range, thus constructing a heterogeneous network as much as possible.On this basis, Eq.(10) is used to measure the distance between individual stocks as the weight of the edge.

w = 2 \times \sqrt{1 - a d j_C E}

(10)

In order to extract the main information in the network, a threshold

α = 0.5

is set according to the distribution of CE. All edges with

a d j_C E

below the threshold will be deleted from the network. The setting of the threshold takes into account not only the distribution of CE, but also the computational efficiency and effectiveness.

4. Empirical results and analyses

4.1. CE and correlation coefficient

In order to explain the role of CE in correlation measurement more deeply, in this part we explore the characteristics of CE based on the data of constituent stocks within CSI 300 index. First, we try to compare CE with two common correlation coefficients, Pearson correlation coefficient and Spearman correlation coefficient. The former is usually used to measure linear correlation, while the latter, which is a non-parametric version of the former, can measure partial non-linear relationships.

Therefore, we calculate the correlation coefficients and CE between every two component stocks, and output the matrix as shown in Figure 1. In order to show the correlation between stocks more clearly in the figure, we group the stocks of the same industry together according to Shenwan's industry classification standard. As can be seen from the figure, CE provides a clearer correlation pattern than these two correlation coefficients. In the regions with low correlation, the two correlation coefficient measures will have more noise, resulting in that the correlation of the truly correlated region is not clear in the matrix. This is because CE measures statistical correlations for all orders, whereas correlation coefficients only measure statistical correlations for second orders. In the internal comparison of the two correlation coefficients, the color difference of Spearman's correlation coefficient matrix is slightly more pronounced than that of Pearson's, probably because it is also estimated non-parametrically. However, there is still a big difference between the former and CE. Theoretically, they use different copula functions. CE can describe statistical correlation more clearly than Spearman correlation coefficient.

In addition, there is an obvious difference between CE and normal correlation coefficient, that is, CE measures the correlation strength between variables and does not distinguish between positive and negative, while correlation coefficient measures the positive and negative correlation between variables and takes a value between [-1,1].

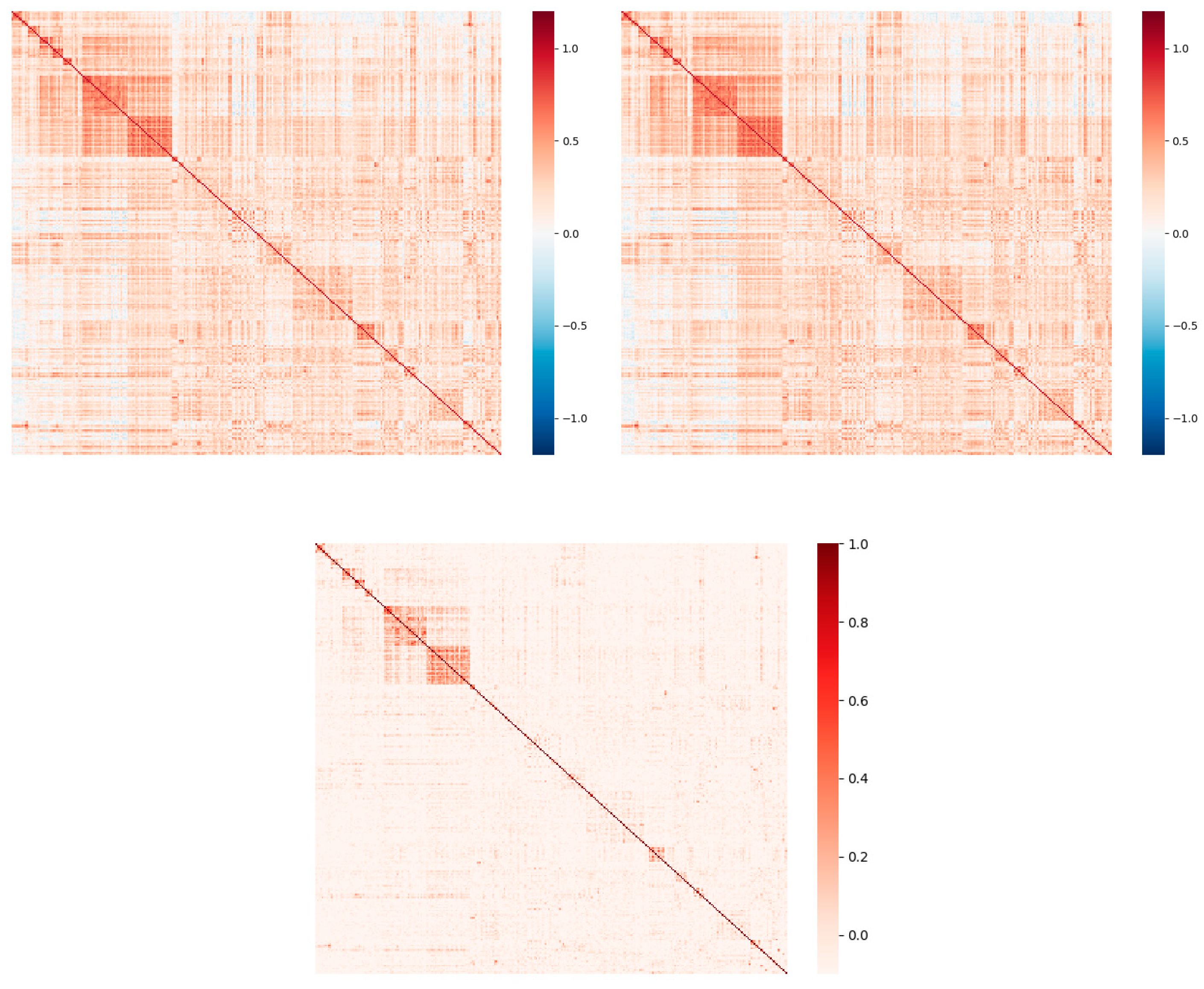
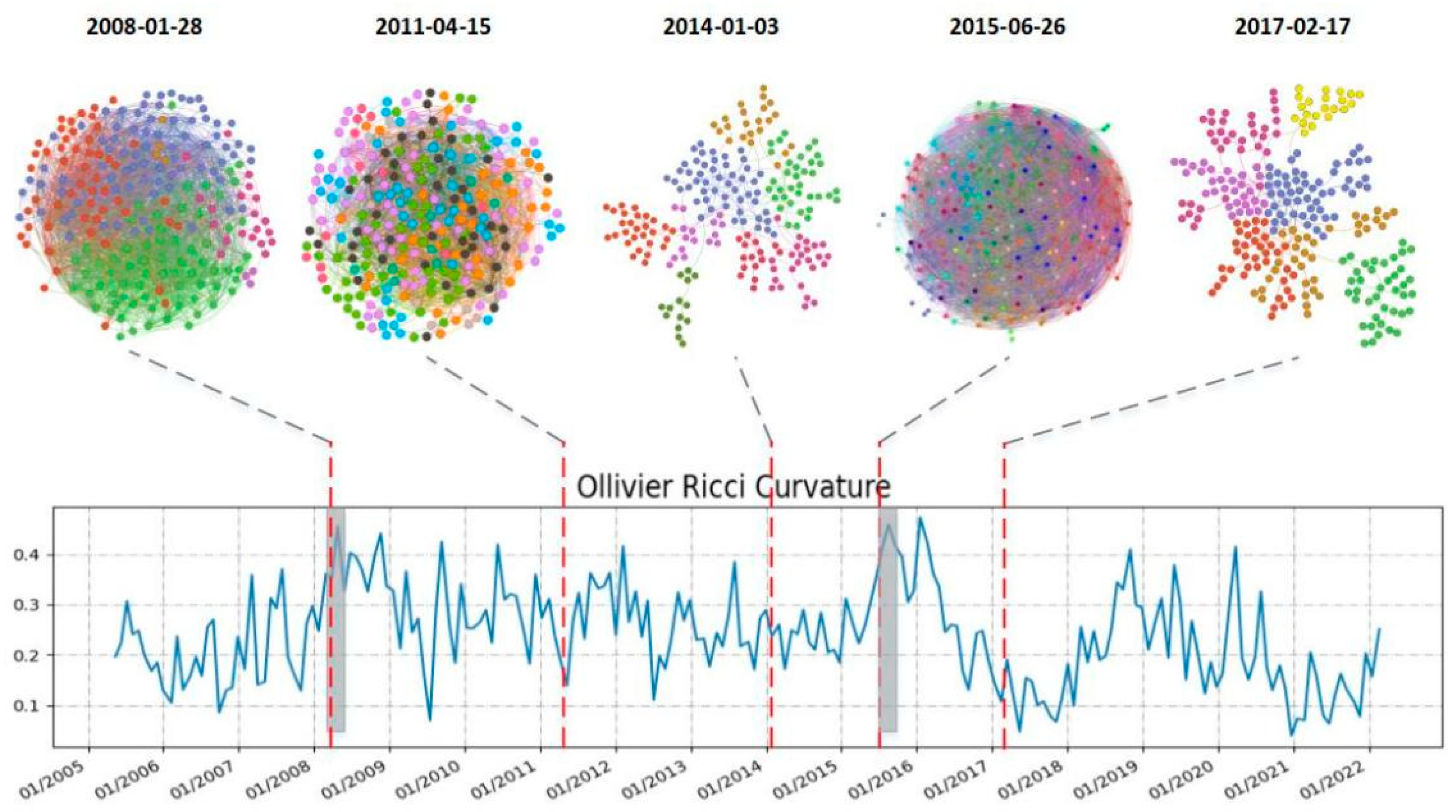
4.2. Network analysis with CSI 300 component stocks

On the basis of exploring the Copula entropy of CSI 300 component stocks in the previous section, referring to the practice of Samal A et al. (2021)[15], we attempt to construct a market network composed of component stocks in CSI 300 from April 2006 to April 2022. Therefore, we calculate the changes of the following four kinds of curvature over time in the network: Ollivier-Ricci curvature, Menger-Ricci curvature, Haantjes-Ricci curvature and Forman-Ricci curvature. The stock data used in this section and subsequent sections are from the CSMAR database.

Figure 2 reports the network curvature based on CE for the period from April 2006 to April 2022. From top to bottom are Ollivier-Ricci curvature, Menger-Ricci curvature, Haantjes-Ricci curvature and Forman-Ricci curvature, respectively. The two shaded sections mark the periods when stock market crashes occurred in 2008 and 2015. In addition, the curvature based on Pearson's coefficient of the network is also reported, which is identified by a light orange curve in the figure.

From the perspective of measuring market vulnerability and systematic risk, the curvature measure undoubtedly fulfilled the task well: all four curvatures remained high for a long period of time after the crisis broke out (Forman curvature is always negative, and the greater the absolute value, the more fragile the network structure). Bearing the bear market is often painful, so the curvature measure gives a "fragile and dangerous" signal for a long time after the crisis. This phenomenon can be explained by the noise trader model which De Long J B et al. (1990)[16] put forward. The model said that the transaction noise brought by extreme emotions is difficult to eliminate, so it often leads to long-term value deviation. In addition, this phenomenon may also be closely related to arbitrage asymmetry proposed by Stambaugh R F et al. (2015)[17]. The wild fluctuations of market lead to the increase of arbitrage risk, so the deviation of value is more serious. In short, the mechanism of " vulnerability " in securities market is not exactly the same as the transmission of risk when a banking crisis occurs. It should be noted that the measurement method proposed in this paper itself cannot predict the arrival of the crisis in a forward-looking way. It is not difficult to see from the figure that the curvature is essentially a signal that exists simultaneously with the crisis and it measures the state of the market. However, after the crisis occurs, this index can indicate when the market comes to normal, which is also quite important.

What's more, Figure 2 also shows the curvature sequence of network constructed by Pearson’s correlation coefficient, which is calculated with the same method as Sandhu R S (2016)[18] and Samal A et al. (2021)[15]. We find that it has a similar trend with CE based method. However, the CE based method provides more pronounced differences between different market environments, indicating its superior ability to capture market vulnerability and differentiate the magnitude of systematic risk. Visually, this feature is represented by higher curvature peaks during crisis periods and comparatively smaller curvature measurements during other stable periods. Additionally, during the crisis period (grey area in Figure 2), the CE-based index rises faster, which indicates that it can better reflect the sharp release of market risk.

In addition to marking the special time period of 2008 and 2015, we further explore the network structure characteristics of five key time nodes: 2008-01-28, 2011-04-15, 2014-01-03, 2015-06-26, 2017-02-17. The community discovery algorithm is used to realize the modularization of the network structure, as shown in Figure 3. The five figures above the curvature diagram respectively represent the graph network model formed by the component stocks of CSI 300 at different time points. After modularization, the color of the nodes represents the module (community) to which they belong.

As Figure 3 shows, during the two stock market crash periods, with four kinds of curvature at a high level, there are significantly more edges in the network. As a whole, the modularity levels of networks are relatively low (the measure of modularity Q^{^[1]} is between 0.1 and 0.2), and we could not distinguish different communities clearly. In contrast, during 2014-01-03 and 2017-02-17 periods with low curvatures, the numbers of edges formed in the network are significantly less than that in other periods. At the same time, there is a higher modularity level (the modularity degree Q is higher than 0.7), and the characteristics of community distribution morphology and scale can be clearly observed from the network. In addition, although 2011-04-15 is not the peak of curvature in the interval, the curvature fluctuates greatly. With the large number of edges and low modularity in the network, at this time, the market usually has high vulnerability and systematic risk. According to the above results and analyses, it can be preliminarily inferred that in general, high curvature is accompanied by low module degree of network structure, large number of edges, close connections between different nodes, and high market risk. Low curvature corresponds to high module degree, fewer edges, less closeness between nodes, and less market risk and vulnerability.

4.3. Comparison with traditional risk metrics

In order to reveal the characteristics of network curvature in measuring financial risk, we select several risk metrics commonly used in finance for comparison, which are the volatility of the optimal portfolio of risky assets, the volatility of the index estimated by GARCH model, and the realized volatility of the index. It should be noted that the above three metrics mainly indicate risk from the market. Market risk is a type of systematic risk, and only in the framework of the CAPM does systematic risk include only the component from the market. But to a certain degree, these metrics are closely related to systemic risk.

In this paper, the optimal risky asset portfolio is computed in Markowitz's framework to maximize the expected utility of an investor with a quadratic utility function. In Markowitz's framework, the optimal risky asset portfolio is the market portfolio with a β of 1, whose volatility measures the magnitude of market risk. In calculating the optimal risky asset portfolio, this paper uses the maximization of the Sharpe ratio, which is maximizing

\frac{r_{p} - r_{f}}{σ_{p}}

. In this formula,

r_{p}

and

σ_{p}

are the portfolio's average daily return and volatility (standard deviation of returns) for the year, and

r_{f}

represents the year's risk-free rate of return.

Index volatility is a good indicator of market risk. As a commonly used regression model to analyze financial data, GARCH can more accurately simulate the volatility changes of time series variables than ARCH. More specifically, the GARCH(1,1) model is the most widely used. This paper takes the daily return data of CSI 300 index as the research sample and establishes GARCH (1,1) model to analyze the return volatility. By drawing the time series chart, it can be seen that the volatility of return in this period of time is large, there is the phenomenon of "volatility aggregation", and the ADF test and correlation test show that the return series is smooth without significant correlation. On this basis, we use ARMA(1,1) to fit the yield series. The residuals passed the ARCH effect test, which is a prerequisite for GARCH modeling.

Realized volatility, which is the historical volatility of an asset, is a commonly used risk measure. Like the index volatility estimated by GARCH model, the realized volatility of an index can be used to measure overall market risk. In this paper, we calculate the realized volatility of CSI 300 index for each month (20 trading days).

Figure 5 illustrates the trend of the four curvature measures and the three commonly used risk metrics above. It shows that the seven risk metrics are extremely similar over time. In addition, Table 1 reports the results of Pearson correlation coefficient tests for the seven risk metrics. From top to bottom, there are the Ollivier-Ricci, Menger-Ricci, Haantjes-Ricci, and Forman-Ricci curvatures as well as the volatility of the optimal risk portfolio, the volatility estimated by the GARCH(1,1) model, and the realized volatility. There are highly significant correlations among the seven metrics, and this result suggests the commonality of the seven risk measures, as well as the robustness of the CE-based network analysis approach.

Since the latter three risk metrics (volatility of the optimal risk portfolio, forecasted volatility of the index, and realized volatility) are all representative of systematic risk from the market, it is feasible to use curvatures to measure the systematic risk empirically.

5. Conclusions

This paper introduces Copula entropy into curvature analysis of the network, and generates some insights in measuring the vulnerability and systematic risk of financial markets. We find that CE provides clearer identification of correlations than Pearson and Spearman correlation coefficients, presenting less noise in the low correlation region. CE shows a better correlation measurement performance and can effectively distinguish different financial sectors. This is due to the fact that CE measures statistical correlations of all orders, while the correlation coefficient measures only the second-order statistical correlations.

Based on the network analysis, the curvature trends are similar for both correlation measurement methods, but the CE approach is relatively more distinct across market states and has a greater ability to characterize market vulnerability and distinguish the magnitude of systematic risk in the market. The figures show that while the curvature metric cannot predict the onset of a crisis in advance, it remains high for a long time after the outbreak of a crisis, giving a signal of vulnerability and danger. Therefore, it can suggest when the market will start to stabilize. In addition, high curvature is often associated with low modularity and high number of edges in the network structure, with close ties among different nodes and high market risk. Accordingly, low curvature corresponds to high modularity and low number of edges in the network structure, with reduced closeness among nodes, moderated market risk and low vulnerability.

Author Contributions

Conceptualization, Ning Zhang and Yichao Zheng; methodology, Ning Zhang; software, Yichao Zheng; validation, Mengyuan Chen, Jilan Liu and Yichao Zheng; formal analysis, Ning Zhang; investigation, Jilan Liu; resources, Ning Zhang; data curation, Mengyuan Chen; writing—original draft preparation, Mengyuan Chen and Jilan Liu; writing—review and editing, Ning Zhang and Yichao Zheng.; visualization, Mengyuan Chen and Jilan Liu; supervision, Ning Zhang; project administration, Yichao Zheng; funding acquisition, Mengyuan Chen, Jilan Liu and Yichao Zheng. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CUFE Postgraduate students support program for the integration of research and teaching(202209).

Data Availability Statement

All data are from the CSMAR database.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

(i) Ollivier-Ricci (OR)

Ollivier's discretization of classical Ricci curvature has been widely used in the analysis of graphs or networks. In spaces of positive curvature, the average distance between balls is smaller than their center distance, while in negative curvature space, the average distance between balls is larger than their center distance. Based on the above principle, Ollivier extends the classical Ricci curvature to graphs and networks. Taking the edge

e

between nodes

u

and

v

as an example, the OR curvature is defined as:

O (e) = 1 - \frac{W_{1} (m_{u}, m_{v})}{d (u, v)}

(1)

In Eq. (1),

m_{u}

and

m_{v}

represent discrete probability distribution functions at nodes

u

and

v

, respectively;

W_{1}

represents the Wasserstein distance between

m_{u}

and

m_{v}

, which is used to measure the transportation cost between them. The specific calculation method is shown in Eq. (2), where

d (u, v)

represents the path distance (Euclidean distance) between nodes

u

and

v

in the graph.

W_{1} (m_{u}, m_{v}) = \underset{μ_{u, v} \in \prod (m_{u}, m_{v})}{i n f} \sum_{(u^{'}, v^{'}) \in V \times V} d (u^{'}, v^{'}) μ_{u, v} (u^{'}, v^{'})

(2)

\sum_{v^{'} \in V} μ_{u, v} (u^{'}, v^{'}) = m_{u} (u^{'}), \sum_{u^{'} \in V} μ_{u, v} (u^{'}, v^{'}) = m_{v} (v^{'})

(3)

Eq. (3) represents all transfer possibilities that transform the discrete probability distribution function

m_{u}

into

m_{v}

, where

V

is the set of all nodes in the graph. For

\forall u \in V

, its probability distribution

m_{u}

must be explicit and consistent with the neighbor nodes.

Ollivier-Ricci curvature realizes discretization based on classical Ricci curvature by comparing the optimal average distance between the neighbor nodes of

u

and

v

(based on edge

e

) and the Euclidean distance between

u

and

v

. During this process, the key is to solve for the optimal average distance, which is regarded as an optimal transportation problem, namely, minimizing the average distance.

(ii) Forman-Ricci (FR)

Forman's Ricci curvature discretization method is mainly based on the relationship between the Laplacian and Ricci curvature, which is more algebraic in nature. This method was originally used for discrete geometric objects much larger than weighted graphs, and was subsequently introduced into undirected networks by Areejit Samal et al.(2016)[19], and further extended to directed networks. To calculate the Forman-Ricci curvature

F (e)

of edge e in an undirected network, it is necessary to determine the weights of all edges and nodes related to the edge

e

in advance, and the specific calculation process is shown in Eq. (4).

F (e) = w_{e} (\frac{w_{v_{1}}}{w_{e}} + \frac{w_{v_{2}}}{w_{e}} - \sum_{e_{v_{1}} \sim e, e_{v_{2}} \sim e} [\frac{w_{v_{1}}}{\sqrt{w_{e} w_{e_{v 1}}}} + \frac{w_{v_{2}}}{\sqrt{w_{e} w_{e_{v_{2}}}}}])

(4)

In Eq. (4),

e

represents the edge connecting nodes

v 1

and

v 2

;

w_{e}

represents the weight of edge

e

;

w_{v 1}

and

w_{v 2}

represent the weights associated with nodes

v 1

and

v 2

respectively;

e_{v_{1}} \sim e

and 和

e_{v_{2}} \sim e

denotes the set of edges incident to nodes

v 1

and

v 2

respectively after excluding edge

e

From a geometric point of view, FR curvature can quantify the amount of information propagated by the ends of edges in the network. The higher the degree of information diffusion at the end of the edge, the greater the absolute value of FR curvature. Specifically, an edge with a high negative FR curvature may have multiple adjacent edges connected to two nodes of the edge, that is, both ends are funnel-shaped and can be connected to a large number of neighbor nodes. This makes it very likely that the shortest paths formed between other nodes (including nodes that are far away in the network) pass through this edge. Therefore, edges with high negative FR curvature have high betweenness centrality.

(iii) Menger-Ricci (MR)

Among the concepts of metric space and discrete curvature, the simplest definition was first proposed by Menger. He defined the curvature of a metric triangle

T

composed of three points in the space as the reciprocal of

R (T)

, which is the circumcircle radius of the triangle

T

, that is,

1 / R (T)

. Areejit Samal et al.[20,21] extended Menger's definition to the network. Let

(M, d)

be a metric space, and

T = T (a, b, c)

represents a triangle that sides are

a ， b ， c

, then the Menger-Ricci curvature of

T

K_{M} (T)

K_{M} (T) = \frac{\sqrt{p (p - a) (p - b) (p - c)}}{a \cdot b \cdot c}

(5)

In Eq. (5),

p = (a + b + c) / 2

, it can be seen from the equation that the MR curvature value is constantly positive. According to the differential geometry method, the MR curvature of edge

e

in the network can be defined as

κ_{M} (e)

κ_{M} (e) = \sum_{T_{e} \sim e} κ_{M} (T_{e})

(6)

In Eq. (6),

T_{e} \sim e

represents the triangle adjacent to side

e

. If an edge is part of several triangles in the network, it will have a high positive MR curvature.

(iv) Haantjes-Ricci (HR)

The basic principle of Haantjes-Ricci curvature is similar to that of Menger-Ricci curvature. The main difference lies in the fact that MR curvature only considers triangles formed by the two nodes of edge

e

or simple paths of length 2, whereas HR curvature takes longer paths between two nodes into account. In special cases, these two curvature concepts can coincide through a universal constant.

Haantjes defined the curvature of a curve as the ratio of the arc length of the curve to its corresponding chord length. Specifically, given a curve

c

in a metric space

(M, d)

, and three points

p, q, r

c

(with

p

located between

q

and

r

), the HR curvature at point

p

is defined as

κ_{H}^{2} (p)

κ_{H}^{2} (p) = 24 \underset{q, r \to p}{l i m} \frac{l (\hat{q r}) - d (q, r)}{(d (q, r))^{3}}

(7)

In Eq. (7),

l (\hat{q r})

represents the length of the arc

\hat{q r}

. In the network,

\hat{q r}

represents the path

π = v 0, v 1, \dots, v n

, and the edge

e = (v 0, v n)

represents the chord corresponding to

\hat{q r}

. On this basis, Areejit Samal et al.[20,21] defined the HR curvature of a simple path

π

κ_{H}^{2} (π)

κ_{H}^{2} (π) = \frac{l (π) - l (v 0, v n)}{(l {(v 0, v n))}^{3}}

(8)

Thus, the HR curvature of edge

e

can be defined as

κ_{H} (e)

κ_{H} (e) = \sum_{π \sim e} κ_{H} (π)

(9)

In Eq. (9),

π \sim e

represents the path connecting two nodes of edge

e

. Due to calculation limitations, we only consider simple paths with length less than or equal to 4 when using this formula to calculate HR curvature in this paper.

References

Minsky Ph D H, P. The financial-instability hypothesis: capitalist processes and the behavior of the economy; 1982.
Kaminsky G; Lizondo S, Reinhart C M. Leading indicators of currency crises. Staff Papers, 1998, 45(1), pp. 1-48.
Billio M, Casarin R; Costola M, et al. An entropy-based early warning indicator for systemic risk. Journal of International Financial Markets, Institutions and Money, 2016, 45, pp. 42-59.
Battiston S; Puliga M; Kaushik R, et al. Debtrank: Too central to fail? financial networks, the fed and systemic risk. Scientific reports, 2012, 2(1), pp. 1-6.
Haldane A G; May R M. Systemic risk in banking ecosystems. Nature, 2011, 469(7330), pp. 351-355.
Mantegna R, N. Hierarchical structure in financial markets. The European Physical Journal B-Condensed Matter and Complex Systems, 1999, 11, pp. 193–197. [Google Scholar] [CrossRef]
Onnela J P; Chakraborti A; Kaski K, et al. Dynamics of market correlations: Taxonomy and portfolio analysis. Physical Review E, 2003, 68(5), pp. 056110.
Sandhu R; Georgiou T; Tannenbaum A. Market fragility, systemic risk, and Ricci curvature. arXiv preprint arXiv:1505.05182, 2015. arXiv:1505.05182, 2015.
Ma, J.; Sun, Z. Dependence Structure Estimation via Copula. CoRR, 2008, abs/0804.4451.
Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. inst. statist. univ. Paris, 1959, 8, pp. 229–231. [Google Scholar]
Ma J; Sun Z. Mutual information is copula entropy. Tsinghua Science & Technology, 2011, 16(1), pp. 51-54.
Li, Y.L.; Gong, Y.J. Research on LSTM drought prediction model based on drive analysis. Journal of Mathematics in Practice and Theory, 2022, pp. 1-11.
Spearman, C. The american journal of psychology. American Journal of Psychology, 1904, 15, pp 88. [Google Scholar]
Kraskov A; Stögbauer H; Grassberger P. Estimating mutual information. Physical review E, 2004, 69(6): 066138.
Samal A; Pharasi H K; Ramaia S J, et al. Network geometry and market instability. Royal Society Open Science, 2021, 8(2), 201734.
De Long J B; Shleifer A; Summers L H, et al. Positive feedback investment strategies and destabilizing rational speculation. The Journal of Finance, 1990, 45(2), pp. 379-395.
Stambaugh R F; Yu J; Yuan Y. Arbitrage asymmetry and the idiosyncratic volatility puzzle. The Journal of Finance, 2015, 70(5), pp. 1903-1948.
Sandhu R S; Georgiou T T; Tannenbaum A R. Ricci curvature: An economic indicator for market fragility and systemic risk. Science advances, 2016, 2(5): e1501495.
Sreejith R P; Mohanraj K; Jost J, et al. Forman curvature for complex networks. Journal of Statistical Mechanics: Theory and Experiment, 2016(6): 063206.
Saucan E; Samal A; Jost J. A simple differential geometry for complex networks. Network Science, 2021, 9(S1), pp. S106-S133.
Saucan E; Samal A; Jost J. A simple differential geometry for networks and its generalizations. Complex Networks and Their Applications VIII: Volume 1 Proceedings of the Eighth International Conference on Complex Networks and Their Applications COMPLEX NETWORKS 2019 8. Springer International Publishing, 2020, pp. 943-954.

Figure 1. Pearson(upper left), Spearman(upper right) correlation coefficient and CE(bottom).

Figure 2. Curvatures of CSI 300 network.

Figure 3. Curvature diagram and modularization of network.

Figure 4. Time series of CSI 300 index returns.

Figure 5. Seven financial risk metric. From top to bottom, there are the Ollivier-Ricci, Menger-Ricci, Haantjes-Ricci, and Forman-Ricci curvatures are shown, as well as the volatility of the optimal risk portfolio, the volatility estimated by the Garch(1,1) model, and the realized volatility.

Table 1. Correlation between seven risk metrics (Pearson).

	OR	MR	HR	FR	ORP	EVOL	VOL
OR	1

MR	0.8840***	1
	(0.0000)
HR	0.7445***	0.9613***	1
	(0.0000)	(0.0000)
FR	-0.9354***	-0.9792***	-0.8936***	1
	(0.0000)	(0.0000)	(0.0000)
ORP	0.5249***	0.5285***	0.4579***	-0.5342***	1
	(0.0000)	(0.0000)	(0.0000)	(0.0000)
EVOL	0.5861***	0.6187***	0.5477***	-0.6376***	0.7975***	1
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)
VOL	0.6215***	0.6596***	0.5939***	-0.6720***	0.8225***	0.9089***	1
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)

¹ * p<0.1, ** p<0.05, *** p<0.01.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Vulnerability Analysis Method Based on Network and Copula Entropy

Abstract