Submitted:
21 August 2023
Posted:
22 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- (1)
- By modeling the three-dimensional attack and defense scene between UAV and interceptor, analyzing terminal and process constraints of UAV, guidance penetration strategy based on DRL is proposed, aiming to solve the optimal solution of maneuvering penetration under constant environment or mission.
- (2)
- Meta learning is used to improve the UAV guidance penetration strategy, to make the UAV learn to learn and improve the autonomous flight penetration ability. Improving generalization performance to time-varying scenarios not encountered in the training process.
- (3)
- Testing the network parameters based on Meta DRL, and analyzing the flight path and state under different attack and defense distances. Besides, analyzing the penetration strategy, and exploring penetration timing and maneuvering overload, and summarizing the penetration tactics.
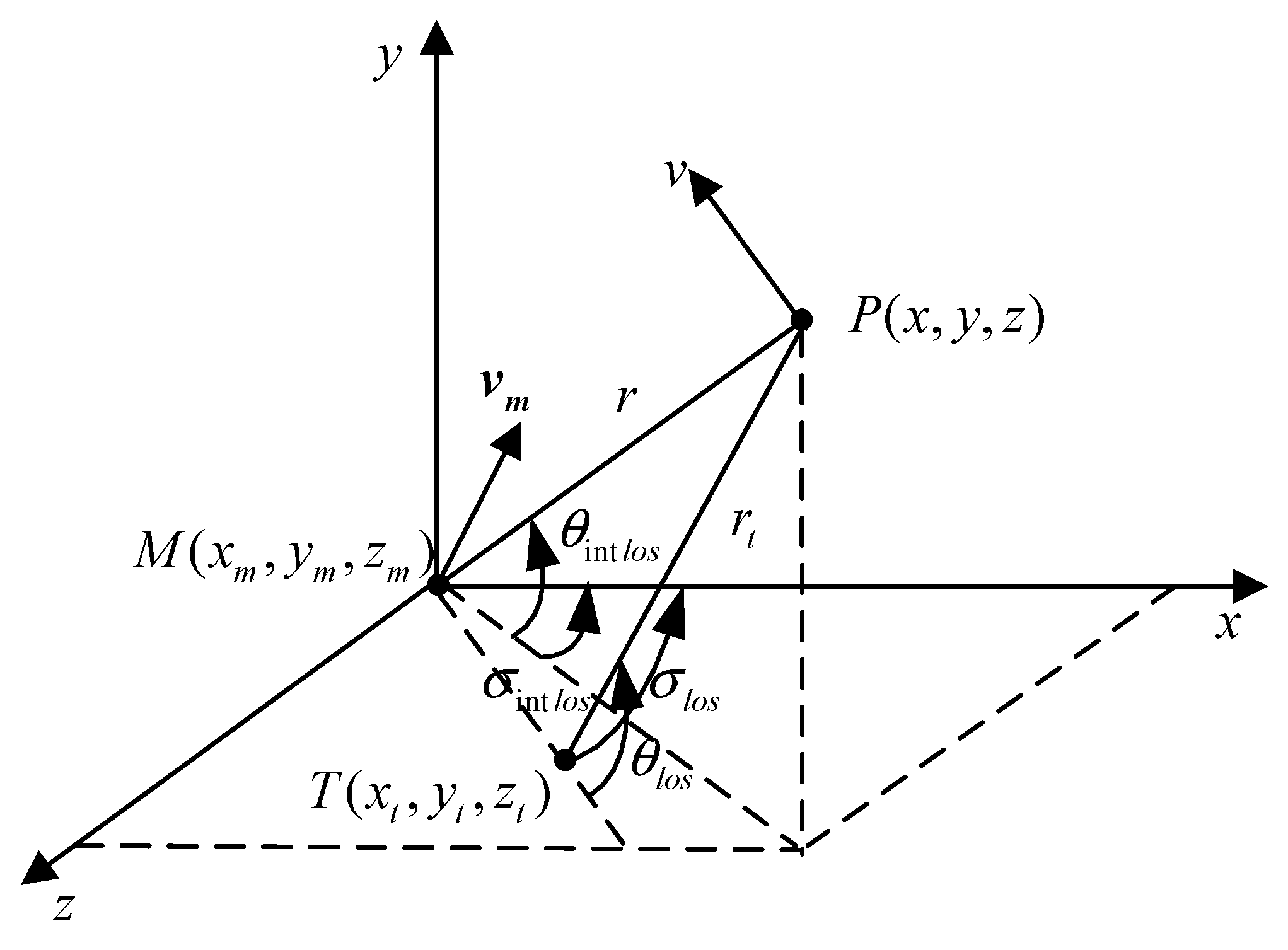
2. Modeling of the Penetration Guidance Problem
2.1. Modeling of UAV Motion
2.2. Description of Flight Missions
2.2.1. Guidance Mission
2.2.2. Penetration Mission
- (1)
- The miss distance with interceptor at the encounter moment.
- (2)
- The overload of interceptor at the last phase.
- (3)
- The line-of-sight (LOS) angular rates and with interceptor at the encounter moment.
2.3. The Guidance Law of Interceptor
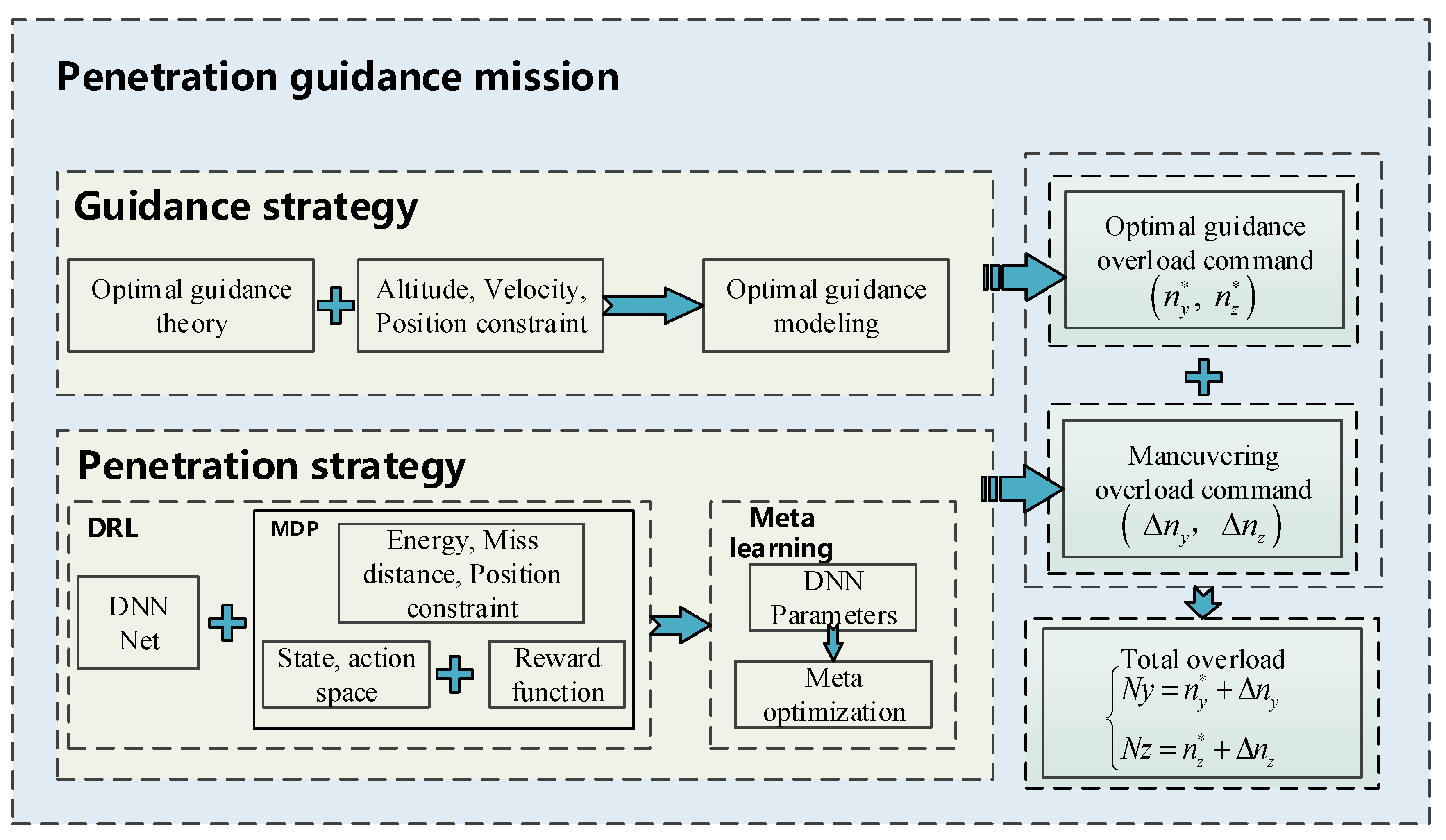
3. Design of Penetration Strategy Considering Guidance
3.1. Guidance Penetration Strategy Analysis
3.2. Energy Optimal Gliding Guidance Method
4. RL Model for Penetration Guidance
4.1. MDP of Penetration Guidance Mission
4.1.1. State Space Design
4.1.2. Action Space Design
4.2. Multi-Missions Reward Function Designing
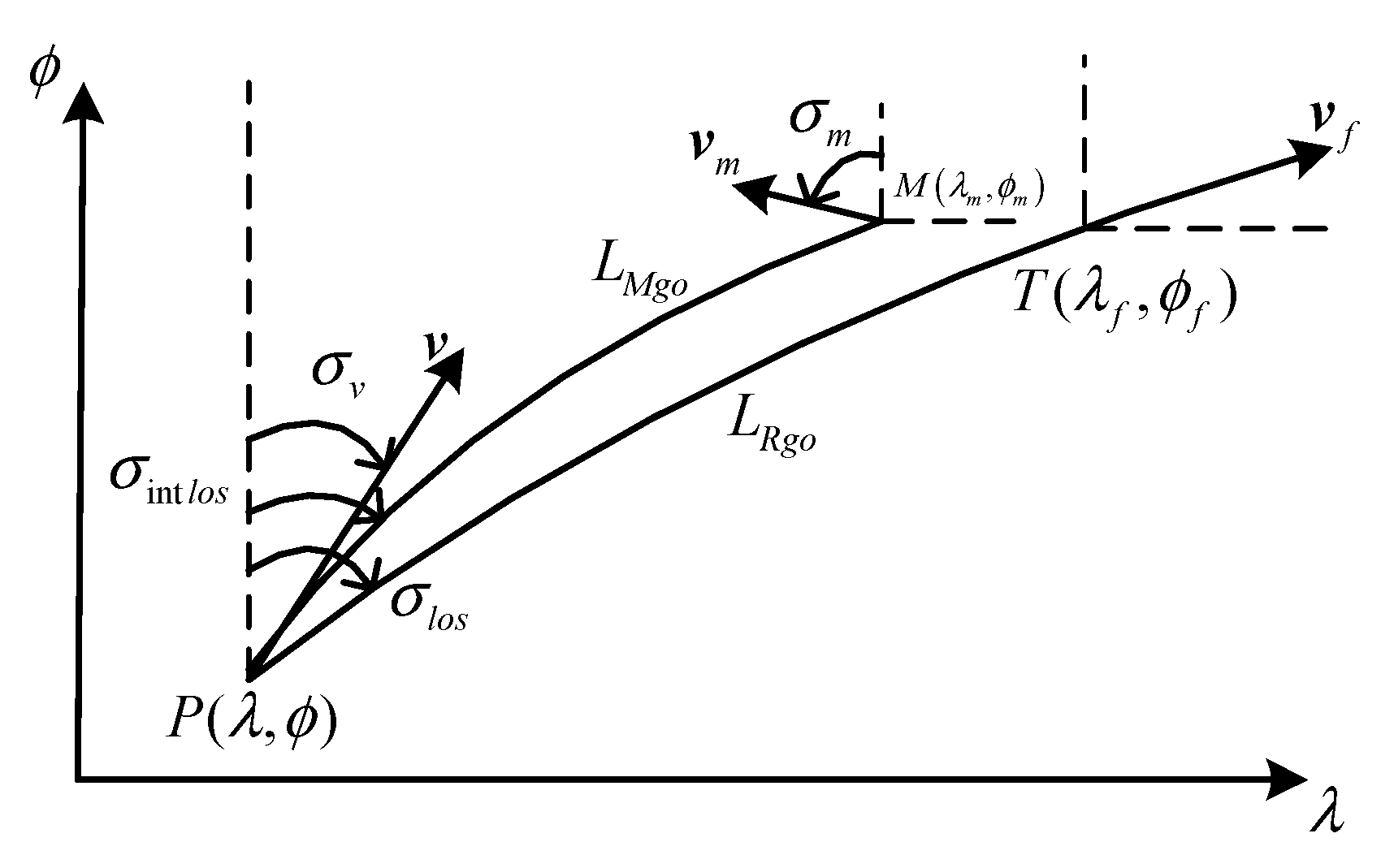
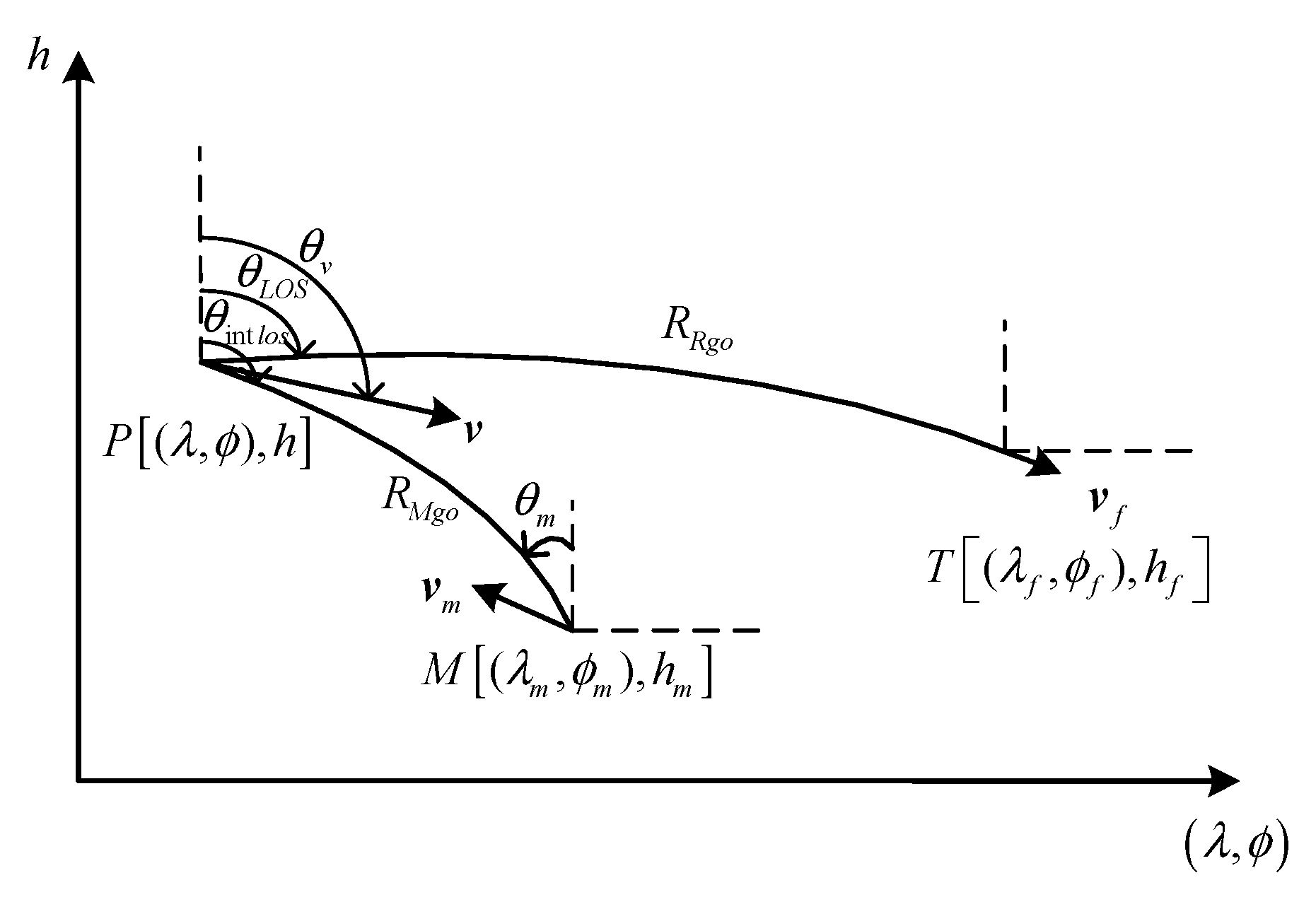
4.2.1. The Solution of LOS Angular Rate in the Lateral Direction
4.2.2. The Solution of LOS Angular Rate in the Longitudinal Direction
5. DRL Penetration Guidance Law
5.1. SAC Training Model
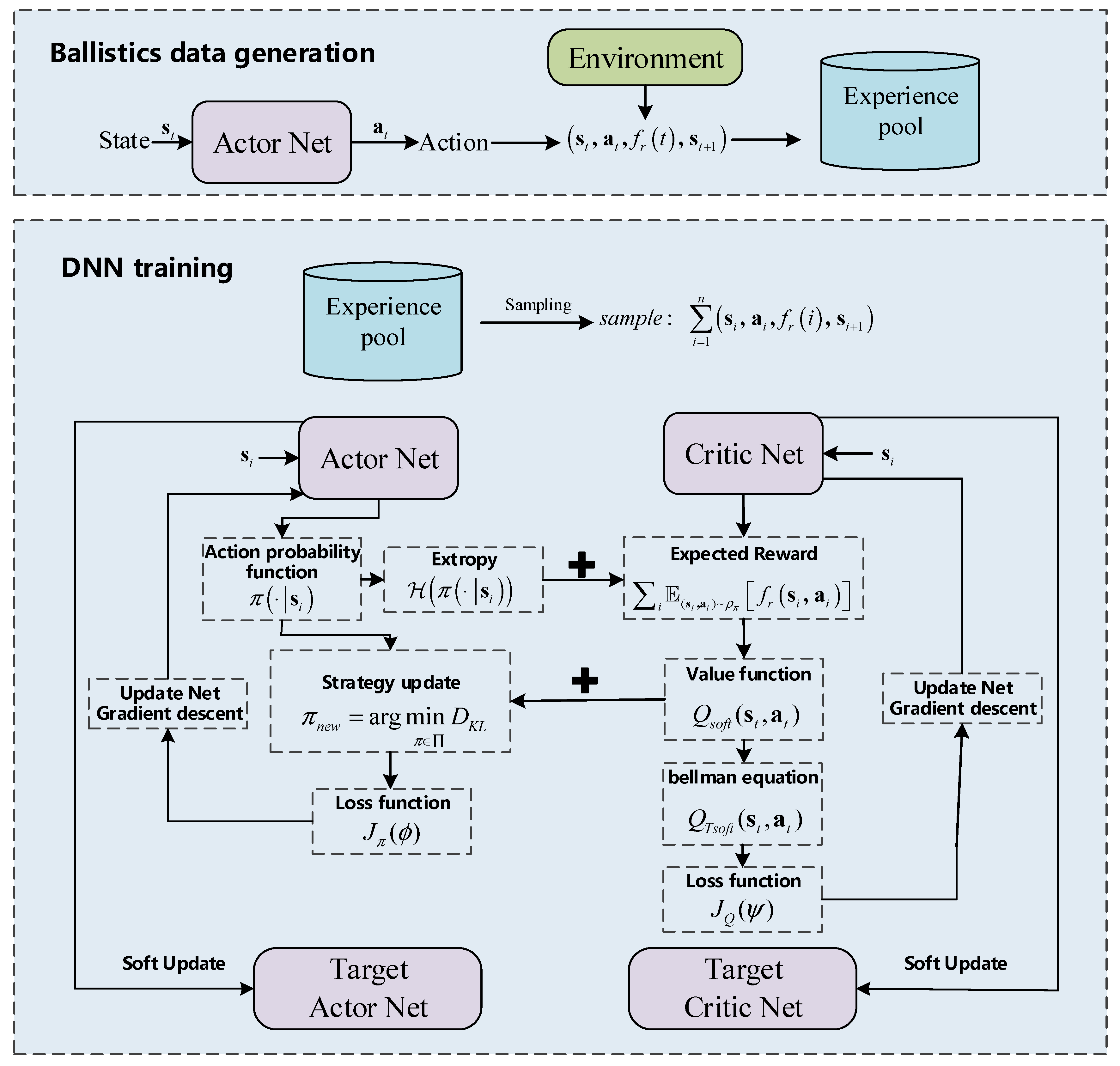
5.2. Meta SAC Optimization Algorithm
| Algorithm 1 Meta SAC |
| 1: Initialize the experience pool ,Storage space N 2: Meta training: 3: Inner loop 4: for iteration k do 5: sample mission(k) from 6: update actor policy to using SAC based on mission(k): 7: . 9: Outer loop 10: 11:Generate from Θ and estimate the reward of Θ. 12: Add a hidden layer feature as a random noise. 13: 14: The meta learning process of different missions is carried out through SGD. 15: for iteration mission(k) do 16: 17: 18: Meta testing 19: Initialize the experience pool ,Storage space N. 20: Load meta training network parameters . 21: Set training parameters. 22: for iteration i do 23: sample mission from 24: End for |
6. Simulation Analysis
6.1. Validity verification on SAC
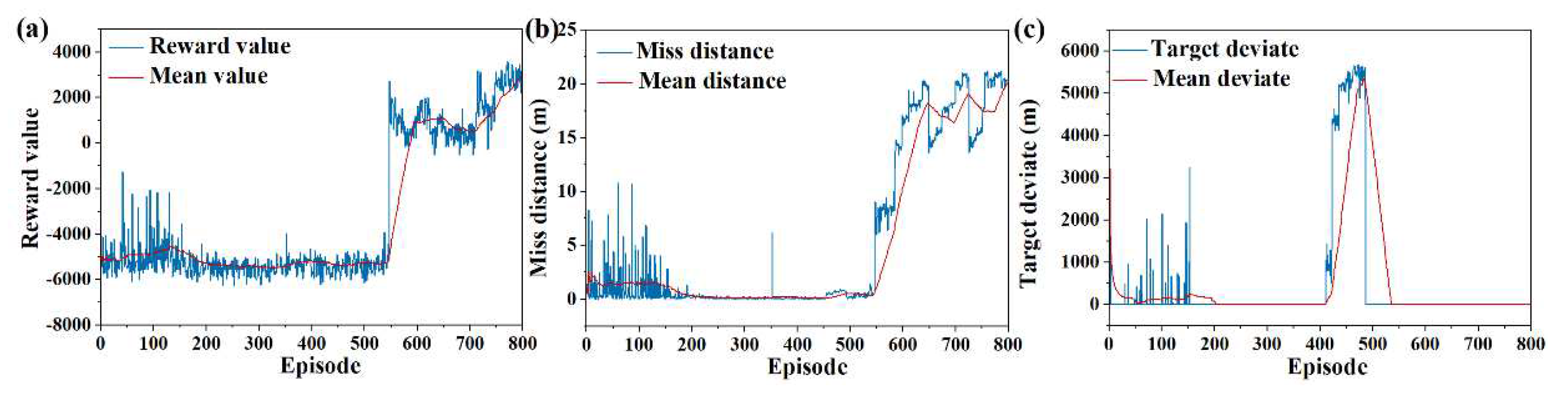
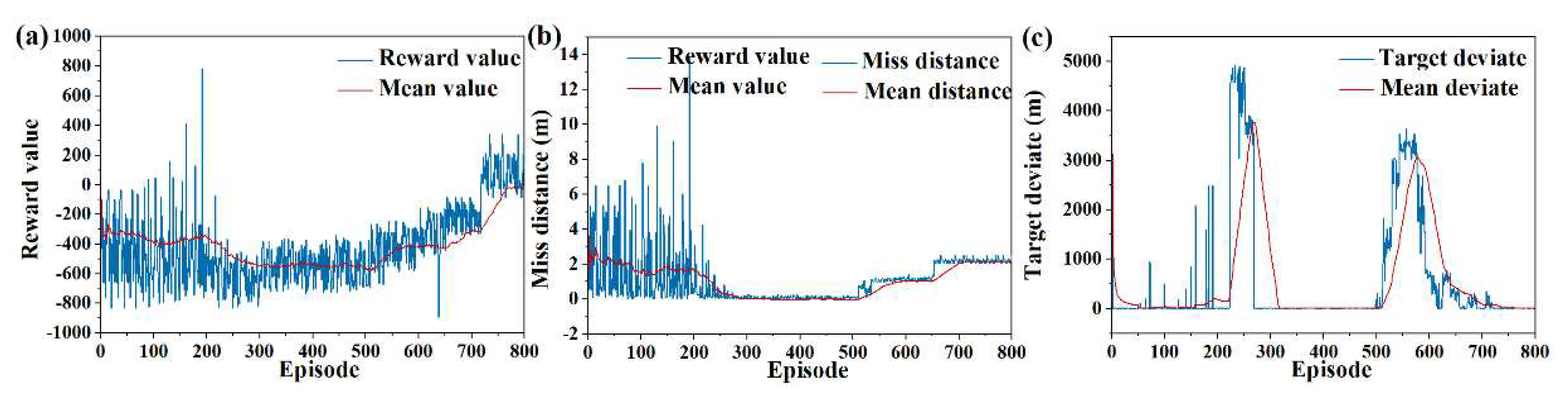
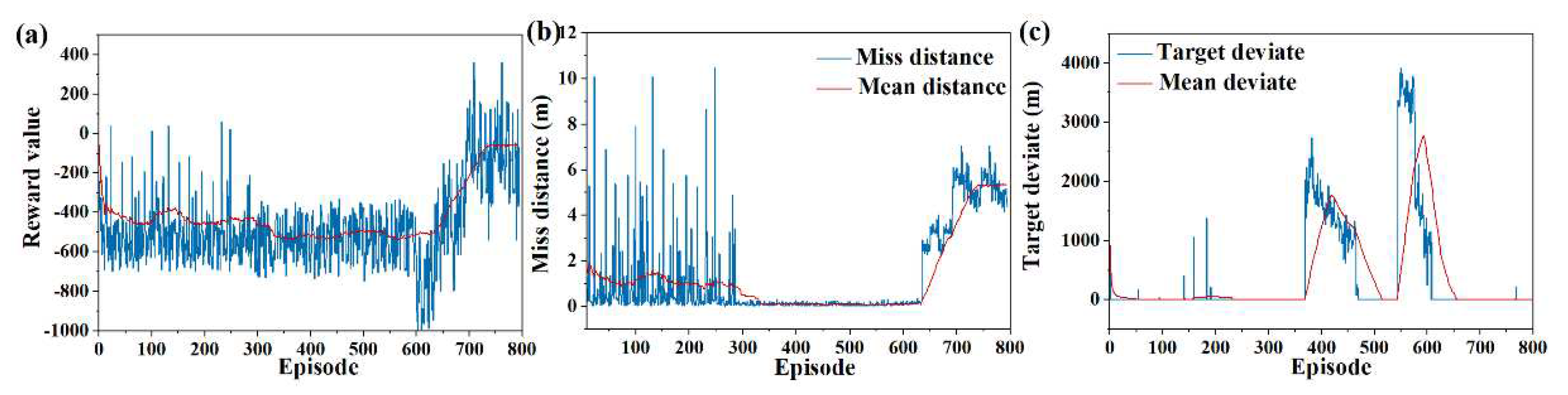
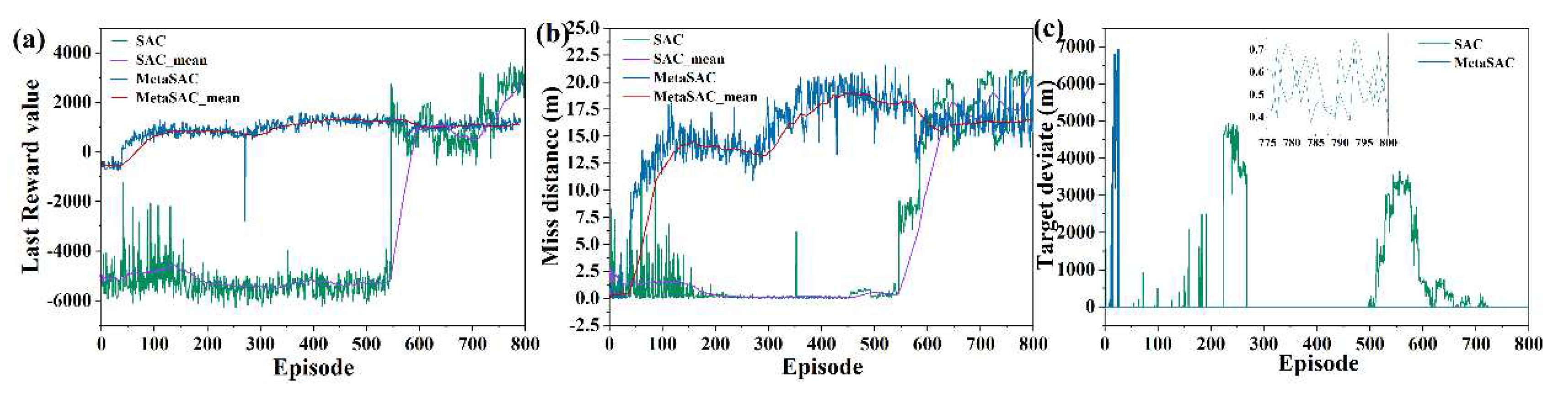
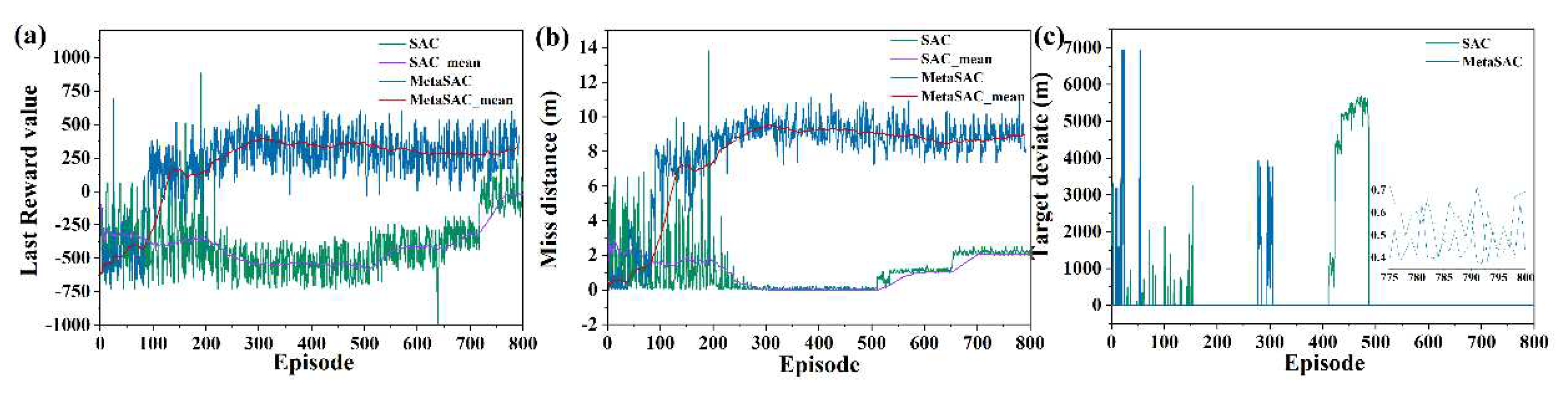
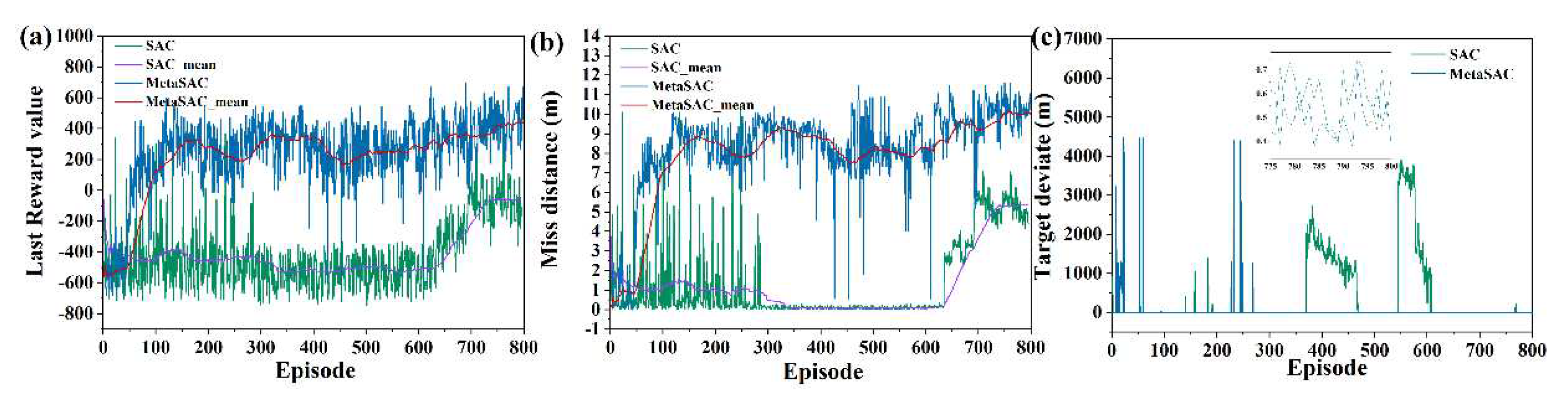
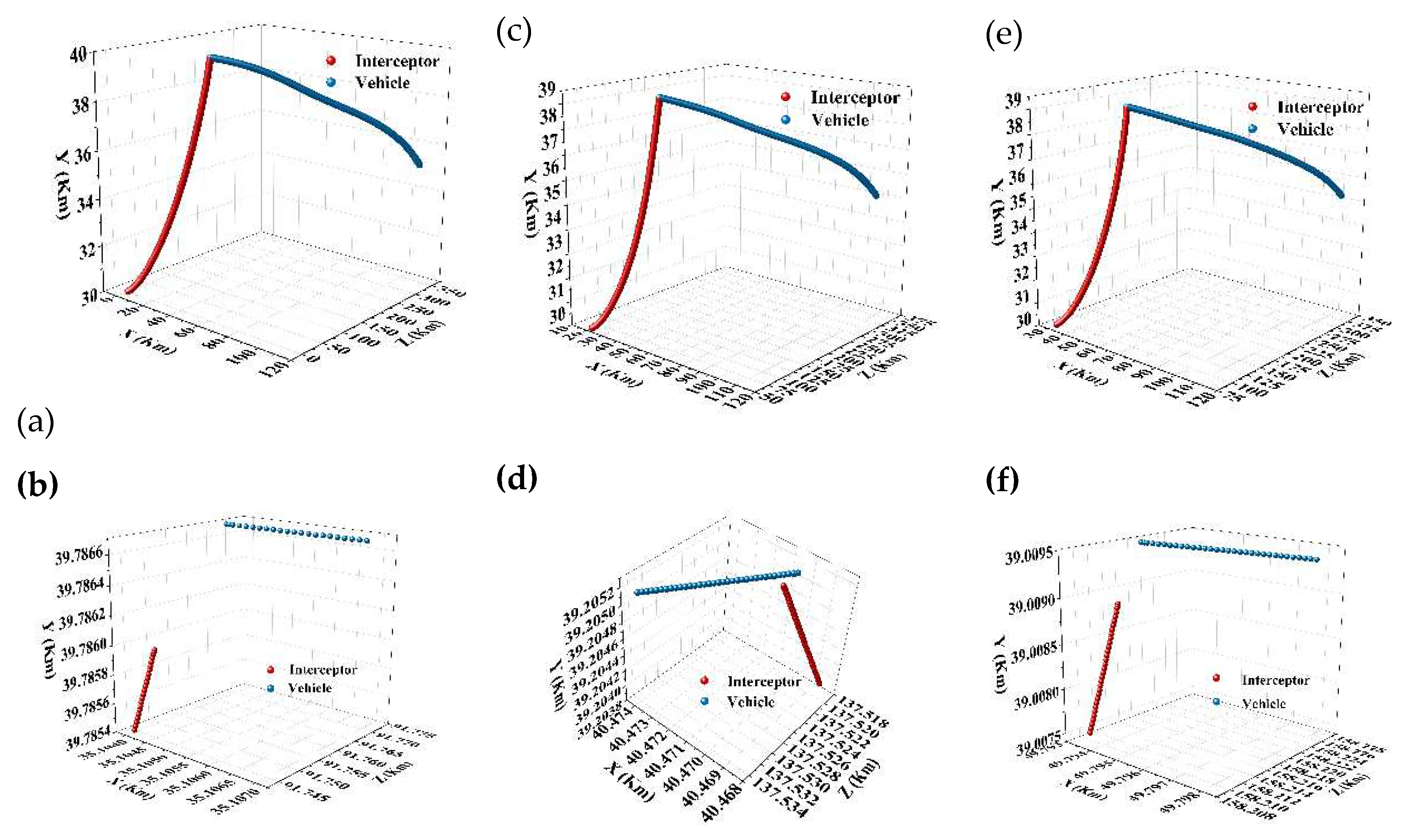
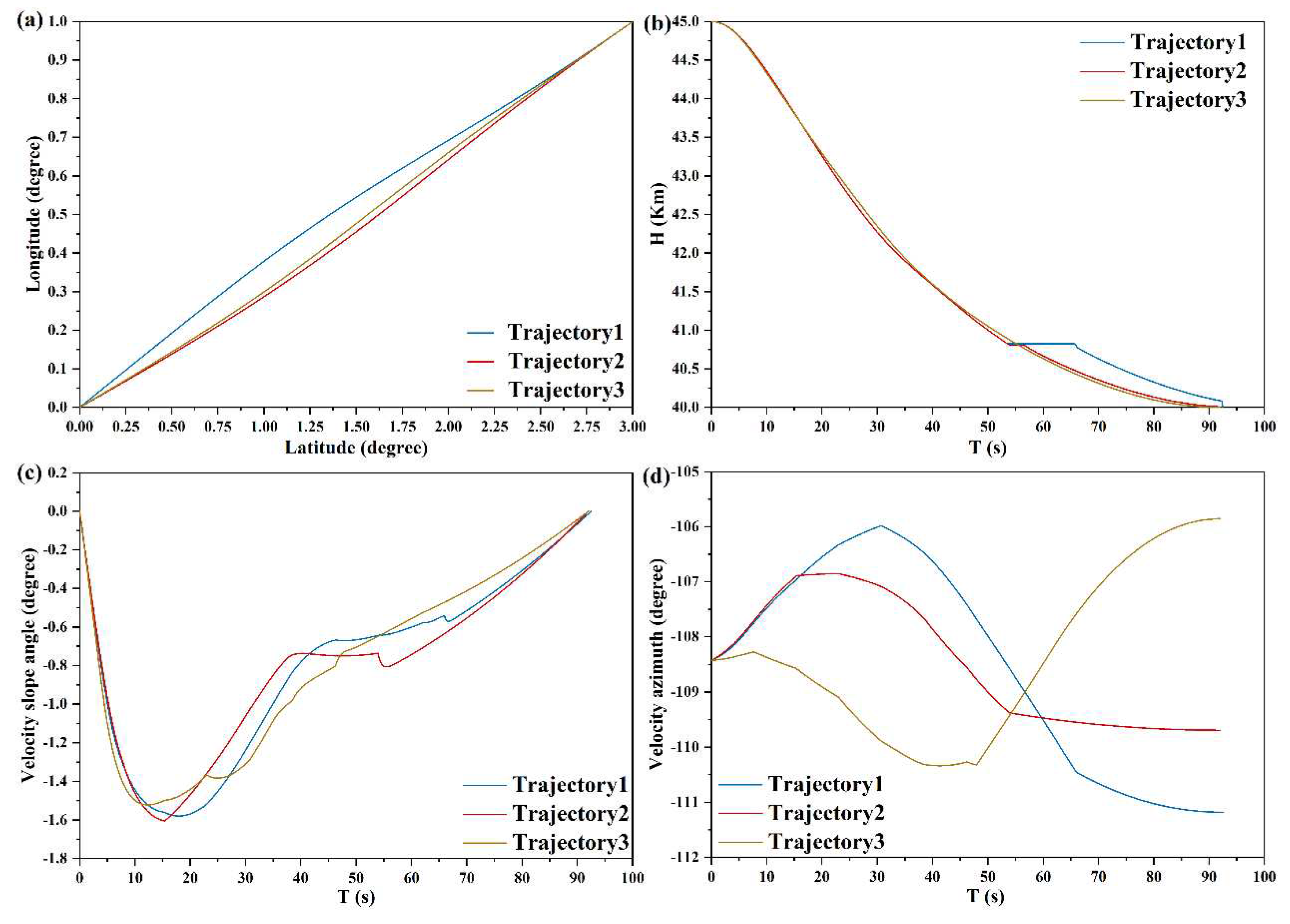
6.2. Validity Verification on Meta SAC
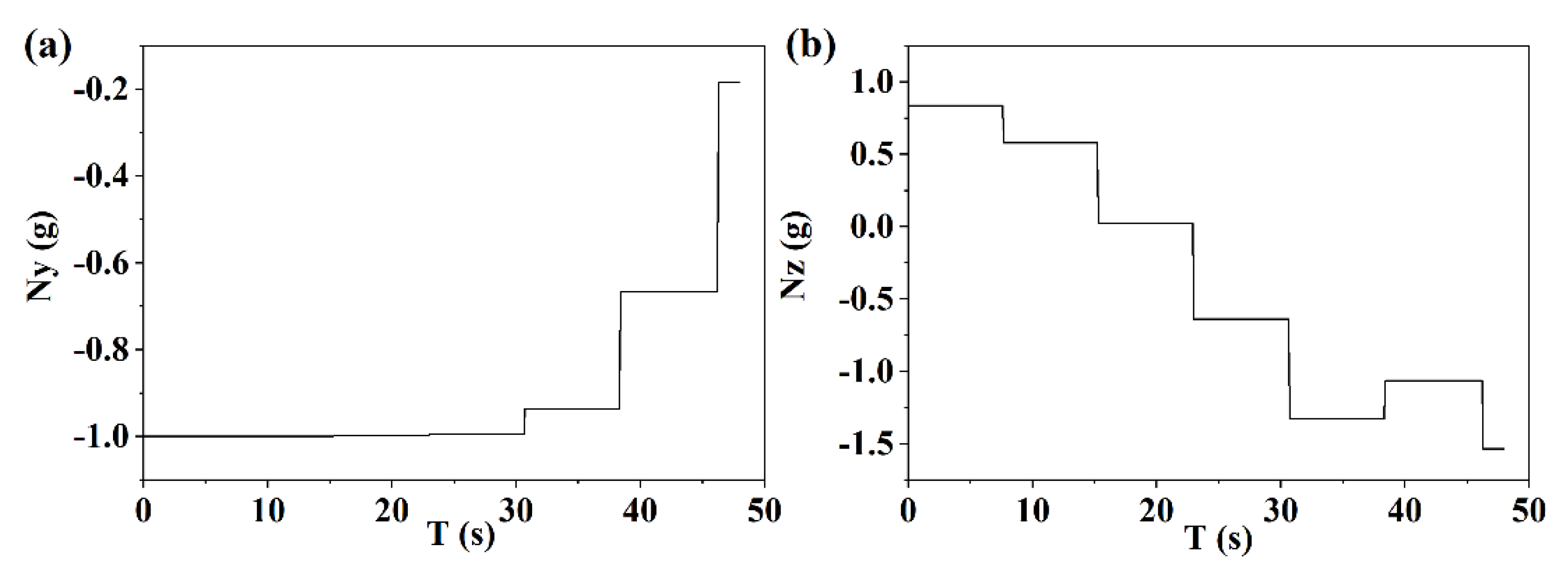
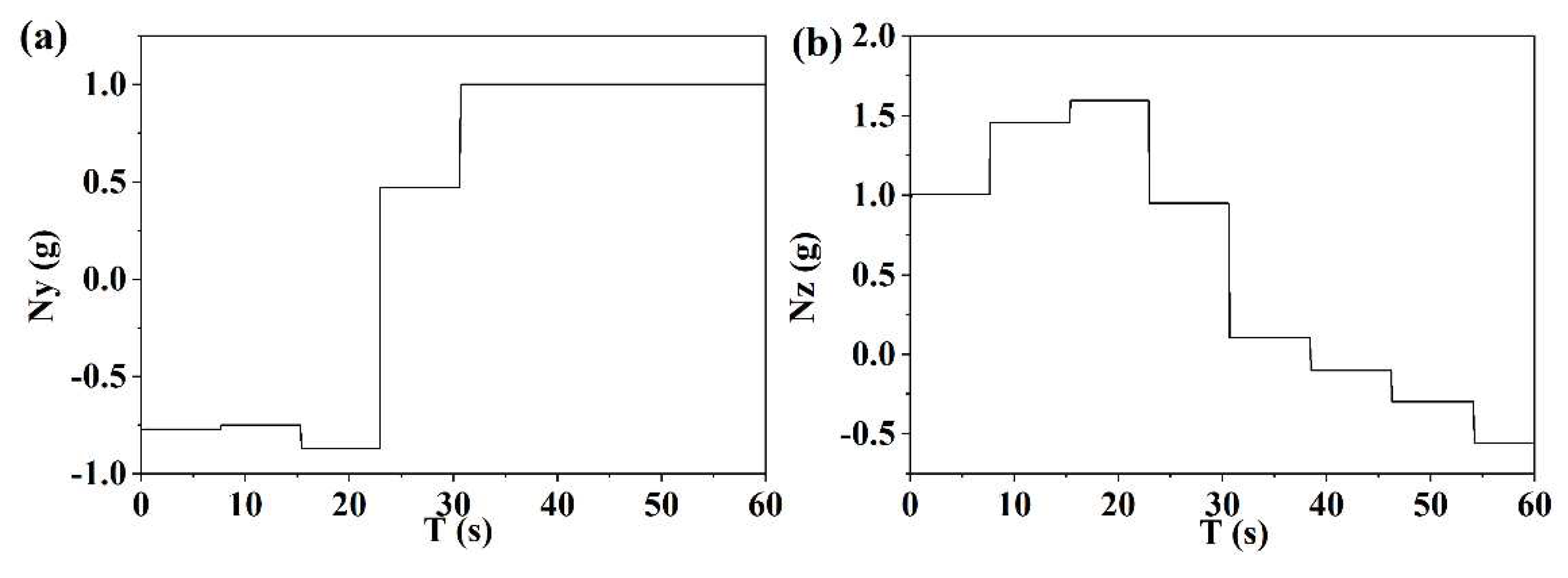
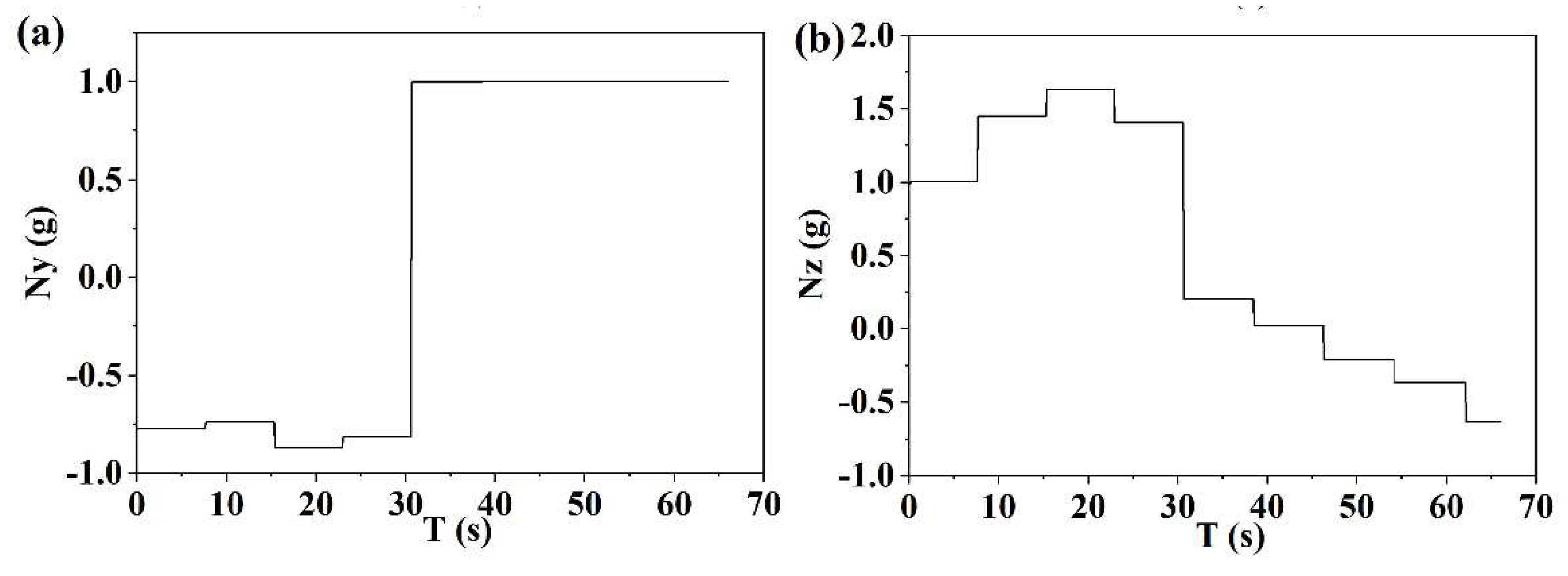
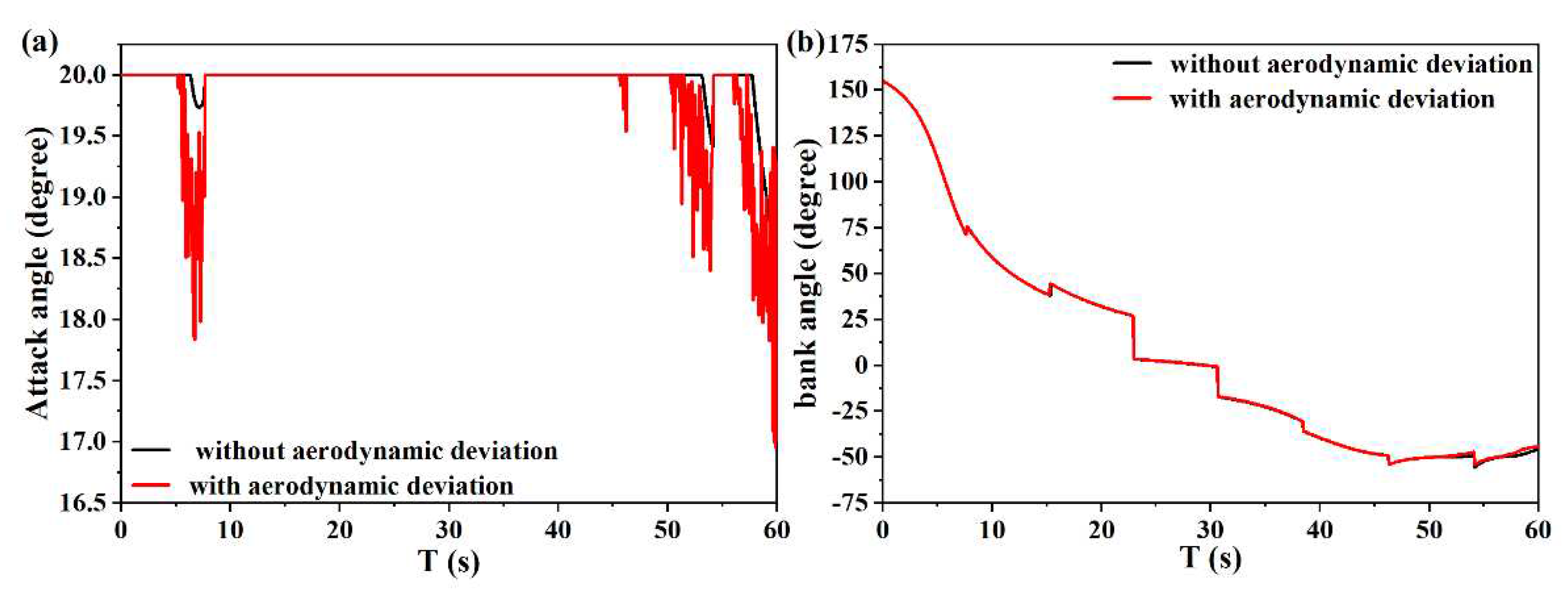
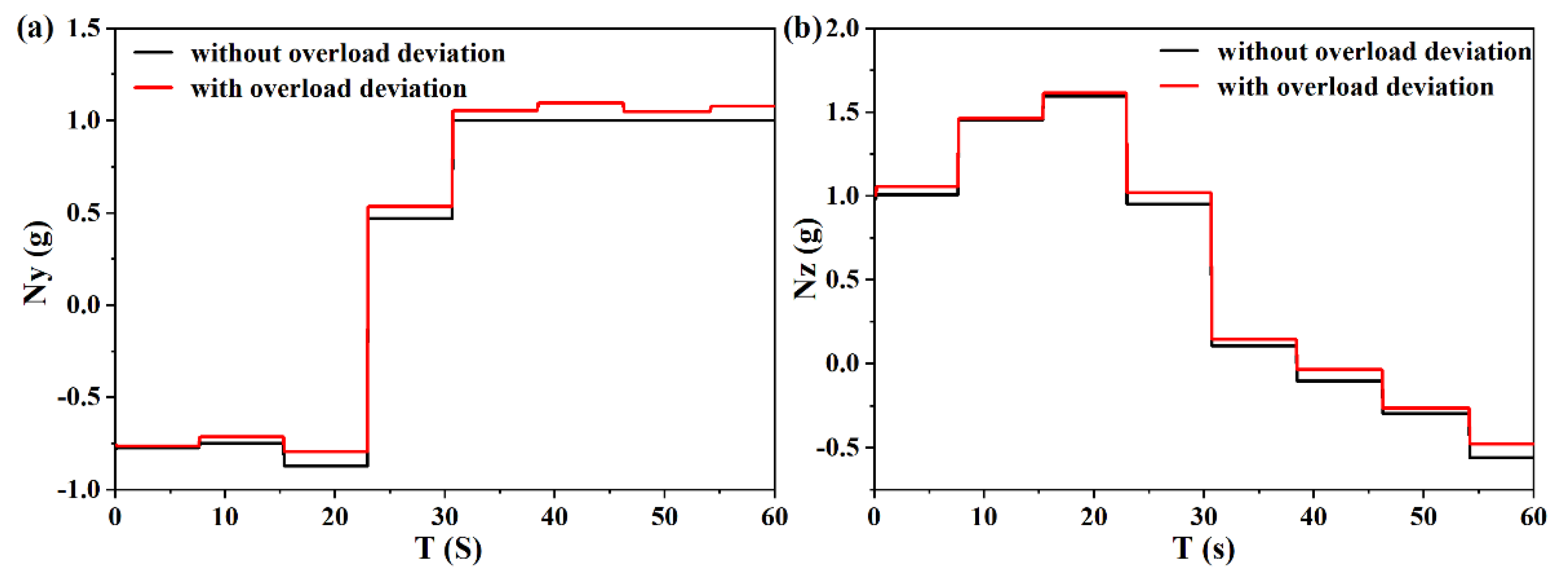
6.3. Strategy Analysis Based on Meta SAC
7. Conclusion
- (1)
- The escape guidance strategy based on SAC is a feasible tactical escape strategy, which can achieve high precision guidance under meeting the escape requirements.
- (2)
- Meta SAC can significantly improve the adaptability of escape strategy. When the escape mission changes, it can fine-tune network parameters to adapt to mission through a small number of training. This method provides a possibility for the UAV to learn while flying.
- (3)
- The strong adaptive escape strategy based on meta SAC can adjust the escape timing and maneuvering overload in real time according to the pursuit evading distance. On the one hand, the overload corresponding to this strategy can confuse the interceptor and cause some interference, on the other hand, it can take into account the guidance mission, correcting the course deviation caused by escape.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- H. W. LI ZB, Z. J. S. ZHANG, and T. n. Review, "Summary of the Hot Spots of Near Space Vehicles in 2018," vol. 37, no. 1, p. 44, 2019. [CrossRef]
- Li, G.; Zhang, H.; Tang, G. Maneuver characteristics analysis for hypersonic glide vehicles. Aerosp. Sci. Technol. 2015, 43, 321–328. [CrossRef]
- Wang, L.; Lan, Y.; Zhang, Y.; Zhang, H.; Tahir, M.N.; Ou, S.; Liu, X.; Chen, P. Applications and Prospects of Agricultural Unmanned Aerial Vehicle Obstacle Avoidance Technology in China. Sensors 2019, 19, 642. [CrossRef]
- Y. WANG, T. ZHOU, W. CHEN, T. J. J. o. B. U. o. A. HE, and Astronautics, "Optimal maneuver penetration strategy based on power series solution of miss distance," vol. 46, no. 1, p. 159. [CrossRef]
- Rim, J.-W.; Koh, I.-S. Survivability Simulation of Airborne Platform With Expendable Active Decoy Countering RF Missile. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 196–207. [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Robust multi-agent differential games with application to cooperative guidance. Aerosp. Sci. Technol. 2021, 111, 106568. [CrossRef]
- E. Garcia, D. W. Casbeer, and M. J. I. T. o. A. C. Pachter, "Design and analysis of state-feedback optimal strategies for the differential game of active defense," vol. 64, no. 2, pp. 553-568, 2018. [CrossRef]
- H. Liang, W. Jianying, W. Yonghai, W. Linlin, and L. J. C. J. o. A. Peng, "Optimal guidance against active defense ballistic missiles via differential game strategies," vol. 33, no. 3, pp. 978-989, 2020. [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [CrossRef]
- Liu, S.; Wang, Y.; Li, Y.; Yan, B.; Zhang, T. Cooperative guidance for active defence based on line-of-sight constraint under a low-speed ratio. Aeronaut. J. 2022, 127, 491–509. [CrossRef]
- D. Zhang, T. Zhang, Y. Lu, Z. Zhu, and B. J. A. i. N. I. P. S. Dong, "You only propagate once: Accelerating adversarial training via maximal principle," vol. 32, 2019.
- Ruthotto, L.; Osher, S.J.; Li, W.; Nurbekyan, L.; Fung, S.W. A machine learning framework for solving high-dimensional mean field game and mean field control problems. Proc. Natl. Acad. Sci. 2020, 117, 9183–9193. [CrossRef]
- Ullah, Z.; Al-Turjman, F.; Mostarda, L.; Gagliardi, R. Applications of Artificial Intelligence and Machine learning in smart cities. Comput. Commun. 2020, 154, 313–323. [CrossRef]
- Song, H.; Bai, J.; Yi, Y.; Wu, J.; Liu, L. Artificial Intelligence Enabled Internet of Things: Network Architecture and Spectrum Access. IEEE Comput. Intell. Mag. 2020, 15, 44–51. [CrossRef]
- Gong, X.; Chen, W.; Chen, Z. All-aspect attack guidance law for agile missiles based on deep reinforcement learning. Aerosp. Sci. Technol. 2022, 127. [CrossRef]
- Furfaro, R.; Scorsoglio, A.; Linares, R.; Massari, M. Adaptive generalized ZEM-ZEV feedback guidance for planetary landing via a deep reinforcement learning approach. Acta Astronaut. 2020, 171, 156–171. [CrossRef]
- Yuan, Y.; Zheng, G.; Wong, K.-K.; Letaief, K.B. Meta-Reinforcement Learning Based Resource Allocation for Dynamic V2X Communications. IEEE Trans. Veh. Technol. 2021, 70, 8964–8977. [CrossRef]
- Zhao, L.-B.; Xu, W.; Dong, C.; Zhu, G.-S.; Zhuang, L. Evasion guidance of re-entry vehicle satisfying no-fly zone constraints based on virtual goals. Sci. Sin. Phys. Mech. Astron. 2021, 51, 104706. [CrossRef]
- Guo, Y.; Li, X.; Zhang, H.; Wang, L.; Cai, M. Entry Guidance With Terminal Time Control Based on Quasi-Equilibrium Glide Condition. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 887–896. [CrossRef]
- Krasner, S.M.; Bruvold, K.; Call, J.A.; Fieseler, P.D.; Klesh, A.T.; Kobayashi, M.M.; Lay, N.E.; Lim, R.S.; Morabito, D.D.; Oudrhiri, K.; et al. Reconstruction of Entry, Descent, and Landing Communications for the InSight Mars Lander. J. Spacecr. Rocket. 2021, 58, 1569–1581. [CrossRef]
- Huang, Z.C.; Zhang, Y.S.; Liu, Y. Research on State Estimation of Hypersonic Glide Vehicle. J. Physics: Conf. Ser. 2018, 1060, 012088. [CrossRef]
- Zhu, J.; Su, D.; Xie, Y.; Sun, H. Impact time and angle control guidance independent of time-to-go prediction. Aerosp. Sci. Technol. 2019, 86, 818–825. [CrossRef]
- Ni, C.; Zhang, A.R.; Duan, Y.; Wang, M. Learning Good State and Action Representations via Tensor Decomposition. 2021, 1682–1687. [CrossRef]
- Ma, Y.; Wang, Z.; Castillo, I.; Rendall, R.; Bindlish, R.; Ashcraft, B.; Bentley, D.; Benton, M.G.; Romagnoli, J.A.; Chiang, L.H. Reinforcement Learning-Based Fed-Batch Optimization with Reaction Surrogate Model. 2021. [CrossRef]
- X. Yang et al., "Learning high-precision bounding box for rotated object detection via kullback-leibler divergence," vol. 34, pp. 18381-18394, 2021.
| Simulation Conditions | Meta SAC Training Parameters | ||
|---|---|---|---|
| UAV initial velocity | 4000m/s | Learning episodes | 1000 |
| Initial velocity Inclination | 0° | Guidance period | 0.1s |
| Initial velocity azimuth | 0° | Data sampling interval | 30Km |
| Initial position | (3°E, 1°N) | Discount factor | = 0.99 |
| Initial altitude | 45km | Soft update tau | 0.001 |
| Terminal altitude | 40km | Learing rate | 0.005 |
| Target position | (0°E, 0°N) | Sampling size for each train | 128 |
| Interceptor Initial velocity | 1500m/s | Net layers | 2 |
| Initial velocity Inclination | longitudinal LOS angle | Net nodes | 256 |
| Initial velocity azimuth | lateral LOS angle | Capacity of experience pool | 20000 |
| Interceptor Initial position (Km) |
Interaction episodes | Miss distance (m) | Terminal deviate (m) | |||
|---|---|---|---|---|---|---|
| SAC | Meta SAC | SAC | Meta SAC | SAC | Meta SAC | |
| (0, 30, 0) | 74 | 1 | 3.78 | 3.29 | 0.56 | 0.61 |
| (2, 30, 6) | 75 | 4 | 2.80 | 2.72 | 0.68 | 0.72 |
| (4, 30, 12) | 59 | 8 | 6.93 | 3.75 | 0.69 | 0.58 |
| (6, 30, 18) | 59 | 1 | 2.71 | 6.82 | 0.68 | 0.72 |
| (8, 30, 24) | 26 | 2 | 3.16 | 3.70 | 0.47 | 0.50 |
| (10, 30, 30) | 58 | 3 | 3.50 | 2.37 | 0.61 | 0.64 |
| (12, 30, 36) | 67 | 1 | 2.86 | 2.21 | 0.68 | 0.45 |
| (14, 30, 42) | 56 | 8 | 2.18 | 2.89 | 0.55 | 0.61 |
| (16, 30, 48) | 69 | 1 | 2.73 | 2.23 | 0.61 | 0.72 |
| (18, 30, 54) | 106 | 1 | 2.45 | 3.71 | 0.56 | 0.63 |
| (20, 30, 60) | 94 | 1 | 2.7 | 2.35 | 0.49 | 0.54 |
| (22, 30, 66) | 59 | 1 | 2.23 | 2.51 | 0.73 | 0.71 |
| (24, 30, 72) | 62 | 1 | 2.11 | 3.47 | 0.48 | 0.67 |
| (26, 30, 78) | 63 | 1 | 2.04 | 4.5 | 0.48 | 0.57 |
| (28, 30, 84) | 63 | 4 | 2.64 | 5.12 | 0.47 | 0.40 |
| (30, 30, 90) | 63 | 9 | 2.95 | 6.05 | 0.68 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




