Submitted:
21 August 2023
Posted:
21 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Proposed Approach
1.2. Related Works
2. Materials and Methods
2.1. Design Data Set
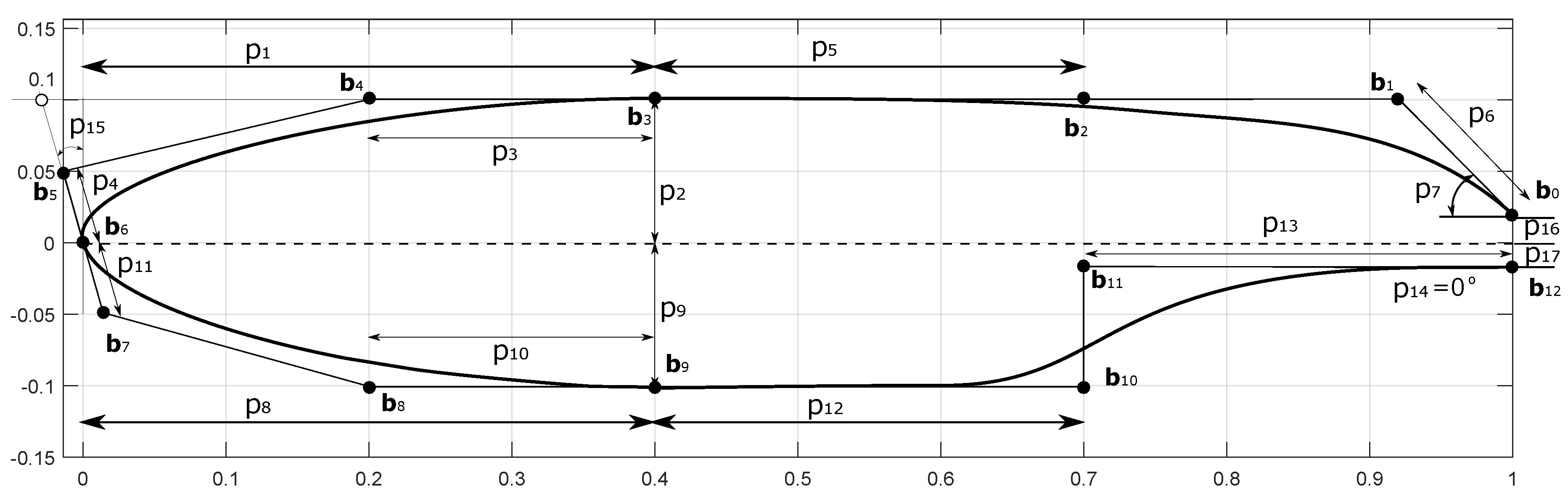
2.1.1. Employed Parametric Model
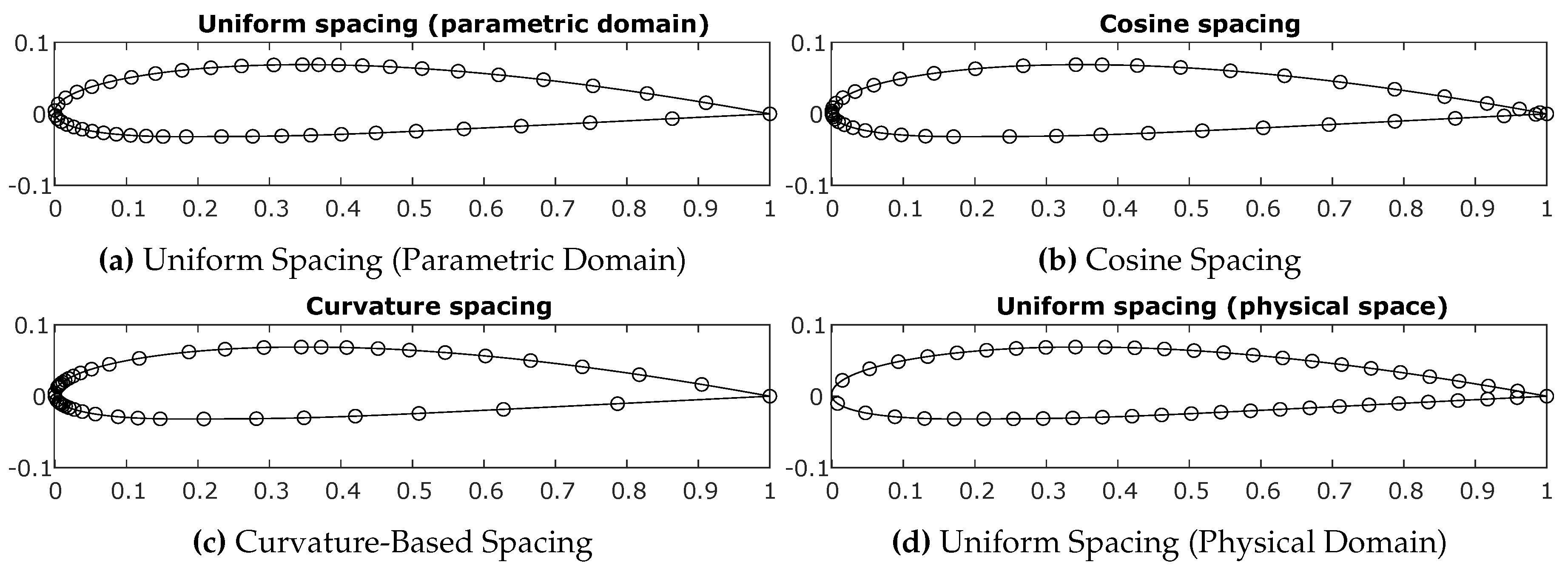
2.1.2. Design Discretization
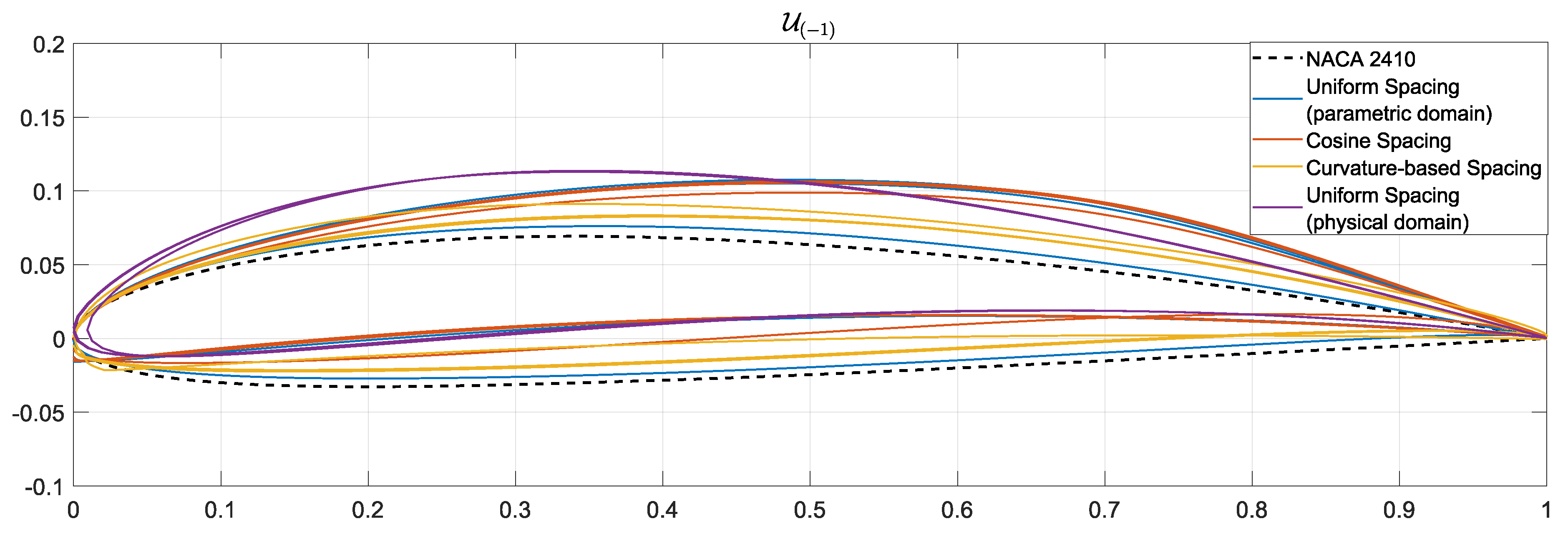
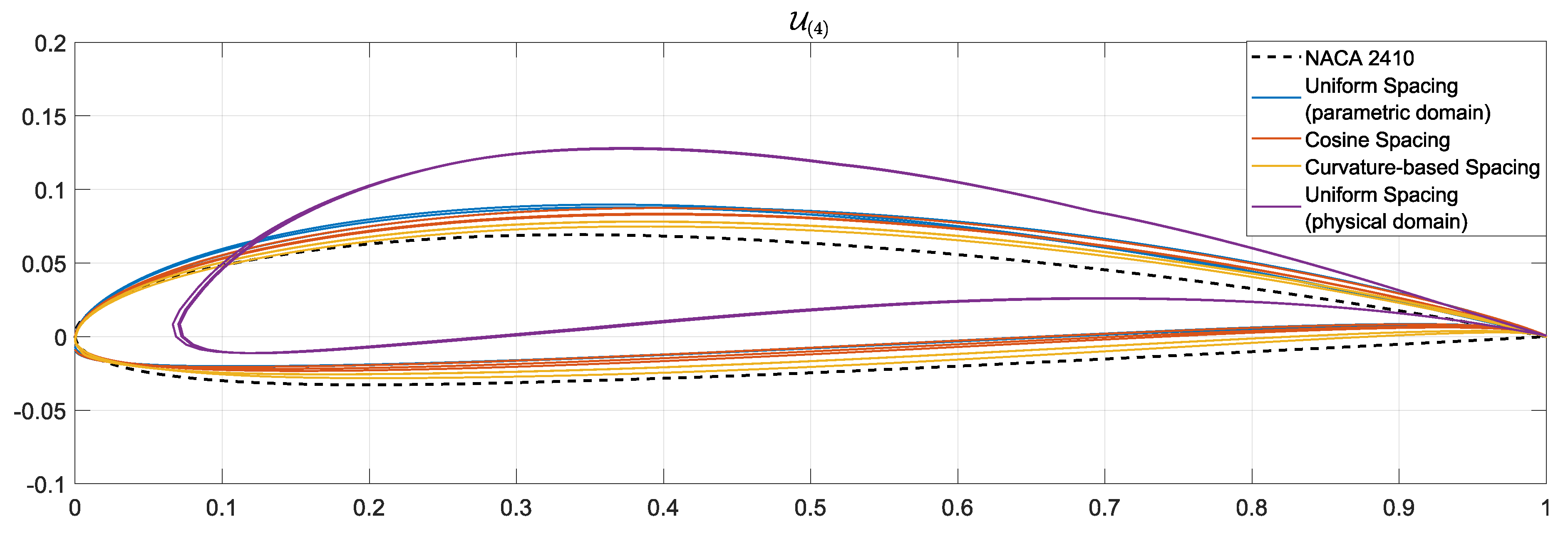
- Uniform spacing over the parametric domain: We consider 200 parametric values, uniformly distributed on the parametric domain, ; see Eq. (2). The corresponding 200 points on the profile are used in this case. Note that these 200 points are generally not uniformly distributed on the profile curve; see Figure 2a.
- Curvature-based spacing: This approach employs the profile’s curvature for calculating the distribution of parametric values. Specifically, parametric points are distributed in a way that guarantees an equal curvature integral for all parametric intervals. This approach results in a large concentration of curve points near the leading edge; see Figure 2c.
- Uniform spacing over the physical domain: This approach discretizes the profile by calculating segments of equal arc-length by dividing the curve length in 199 equal-length curve segments; see Figure 2d.
2.2. Geometric Moments
2.3. Dimension Reduction
2.3.1. Karhunen-Loève Expansion (KLE)
2.4. Latent Space
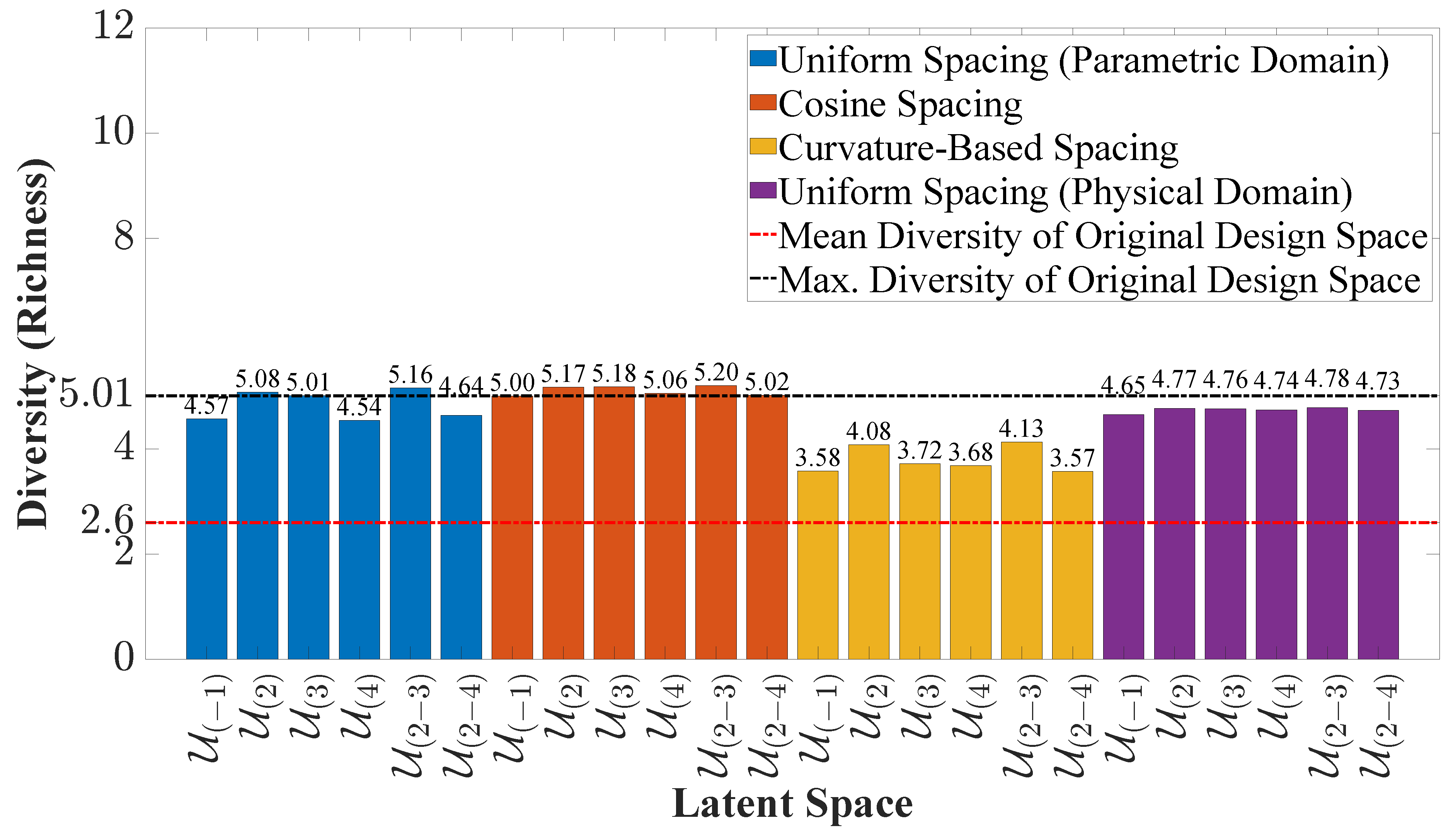
2.4.1. Latent Space Quality Analysis Measures
2.5. Shape Optimization
2.5.1. Jaya Algorithm (JA)
3. Results and Discussion
3.1. Geometric Moment Invariants in SSVs
3.2. Construction of Latent Spaces
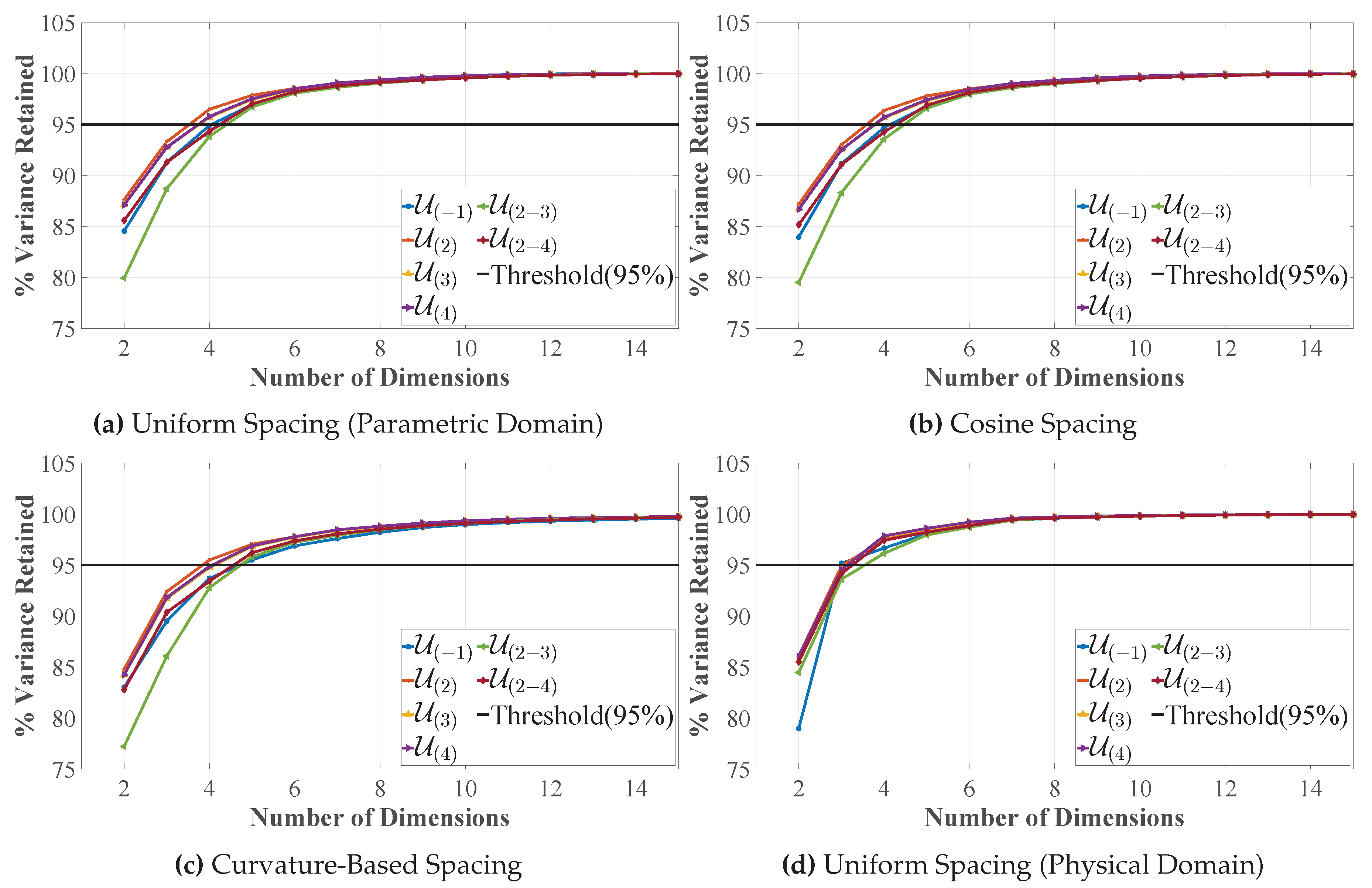
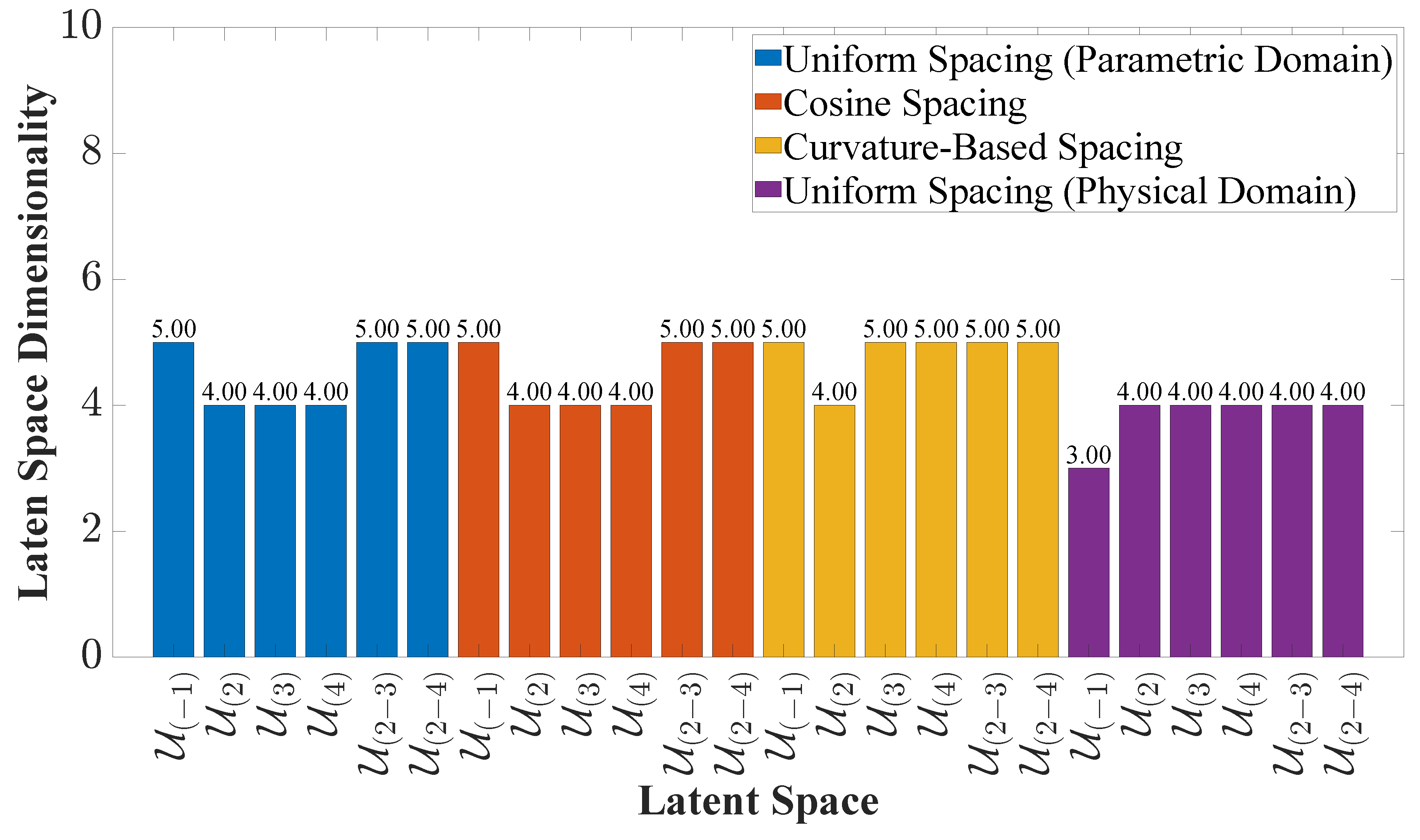
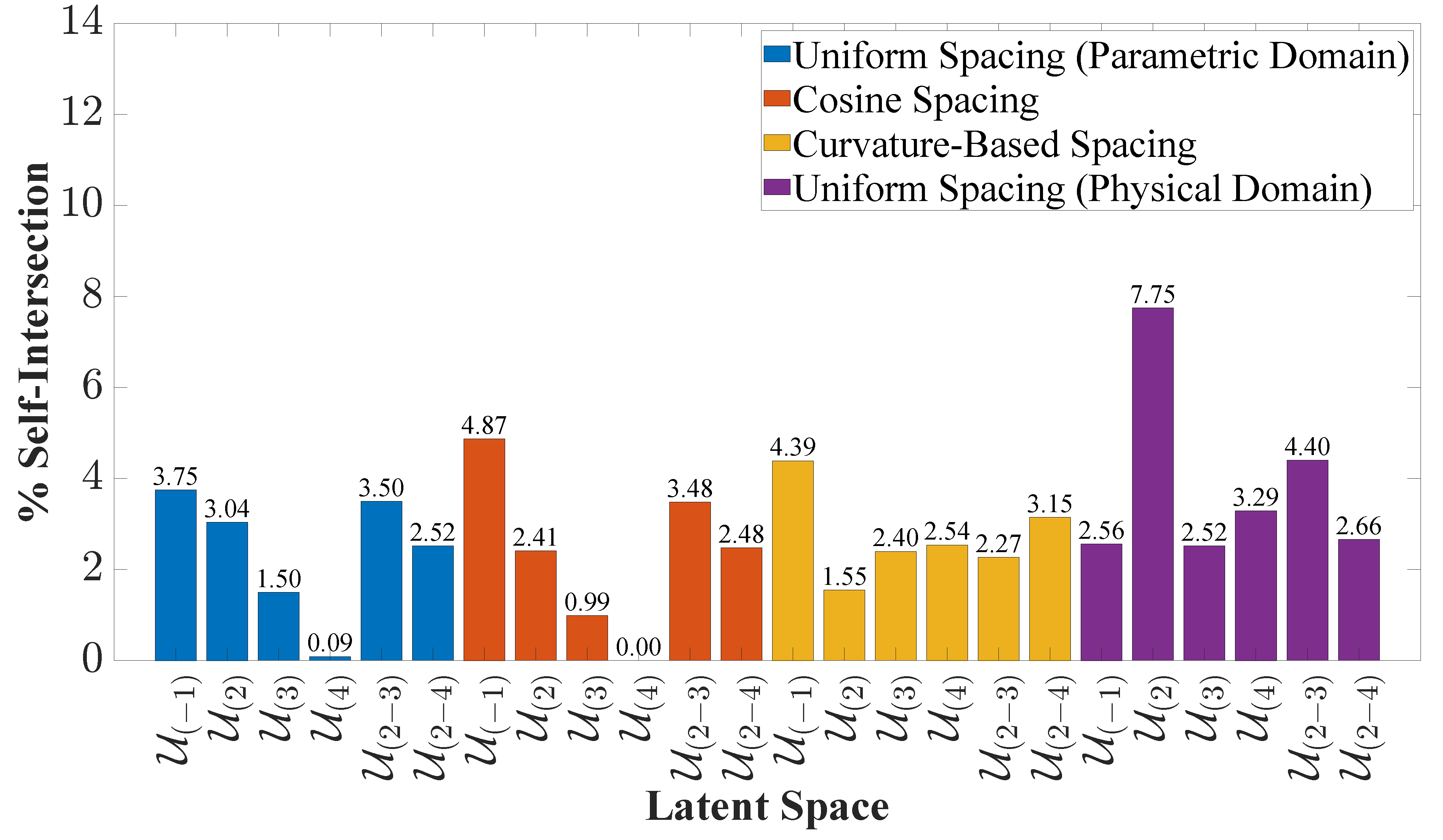
3.3. Latent Space Quality Analysis
3.4. Latent Spaces in Shape Optimization
- The abscissas of the first and last foil profile point were not the same, for some designs, leading to performance inconsistencies when lift coefficient was assessed using XFOIL. In most cases, the problem was a minor difference in the coordinate value which could be easily fixed by equating the abscissas of the two points. In the rare occasion of a big difference, the design was penalized.
- A similar problem was faced with the ordinates of the same pair of points which was handled by penalizing design exhibiting blunt trailing edges with a gap exceeding the maximum gap found in the UIUC database.
- Shape irregularities including self intersections, abrupt shape changes, and lack of abscissa monotonicity along the upper or lower foil side. In all cases, these shape irregularities were monitored and penalized by the employed objective function.
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, S.; Goucher-Lambert, K.; Kostas, K.; Kaklis, P. ShipHullGAN: A generic parametric modeller for ship hull design using deep convolutional generative model. Computer Methods in Applied Mechanics and Engineering 2023, 411, 116051. [Google Scholar] [CrossRef]
- Harries, S.; Abt, C.; Brenner, M. Upfront CAD—Parametric modeling techniques for shape optimization. In Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences; 2019; pp. 191–211. [Google Scholar]
- Khan, S.; Awan, M.J. A generative design technique for exploring shape variations. Advanced Engineering Informatics 2018, 38, 712–724. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic programming; Princeton university press, 2010. [Google Scholar]
- Montgomery, D.C.; Weatherby, G. Factor screening methods in computer simulation experiments; Technical report; Institute of Electrical and Electronics Engineers (IEEE), 1979. [Google Scholar]
- Khan, S.; Kaklis, P. From regional sensitivity to intra-sensitivity for parametric analysis of free-form shapes: Application to ship design. Advanced Engineering Informatics 2021, 49, 101314. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and computers in simulation 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE transactions on pattern analysis and machine intelligence 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Diez, M.; Campana, E.F.; Stern, F. Design-space dimensionality reduction in shape optimization by Karhunen–Loève expansion. Computer Methods in Applied Mechanics and Engineering 2015, 283, 1525–1544. [Google Scholar] [CrossRef]
- Khan, S.; Kaklis, P.; Serani, A.; Diez, M.; Kostas, K. Shape-supervised Dimension Reduction: Extracting Geometry and Physics Associated Features with Geometric Moments. Computer-Aided Design 2022, 150, 103327. [Google Scholar] [CrossRef]
- He, X.; Yan, S.; Hu, Y.; Niyogi, P.; Zhang, H.J. Face recognition using laplacianfaces. IEEE transactions on pattern analysis and machine intelligence 2005, 27, 328–340. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural computation 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Yu, W.; Wang, R.; Nie, F.; Wang, F.; Yu, Q.; Yang, X. An improved locality preserving projection with ℓ1-norm minimization for dimensionality reduction. Neurocomputing 2018, 316, 322–331. [Google Scholar] [CrossRef]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil design parameterization and optimization using Bézier generative adversarial networks. AIAA journal 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R. A B-spline-based generative adversarial network model for fast interactive airfoil aerodynamic optimization. In Proceedings of the AIAA Scitech 2020 Forum; 2020; p. 2128. [Google Scholar]
- Kedward, L.; Allen, C.B.; Rendall, T. Gradient-limiting shape control for efficient aerodynamic optimization. AIAA Journal 2020, 58, 3748–3764. [Google Scholar] [CrossRef]
- Li, J.; Bouhlel, M.A.; Martins, J.R. Data-based approach for fast airfoil analysis and optimization. AIAA Journal 2019, 57, 581–596. [Google Scholar] [CrossRef]
- UIUC Applied Aerodynamics group. UIUC airfoil coordinates database. 2023. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on February 2023).
- Li, J.; Zhang, M.; Martins, J.R.; Shu, C. Efficient aerodynamic shape optimization with deep-learning-based geometric filtering. AIAA Journal 2020, 58, 4243–4259. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. On deep-learning-based geometric filtering in aerodynamic shape optimization. Aerospace Science and Technology 2021, 112, 106603. [Google Scholar] [CrossRef]
- Khan, S.; Goucher-Lambert, K.; Kostas, K.; Kaklis, P. ShipHullGAN: A generic parametric modeller for ship hull design using deep convolutional generative model. Computer Methods in Applied Mechanics and Engineering 2023, 411, 116051. [Google Scholar] [CrossRef]
- Kostas, K.; Ginnis, A.; Politis, C.; Kaklis, P. Shape-optimization of 2D hydrofoils using an Isogeometric BEM solver. Computer-Aided Design 2017, 82, 79–87. [Google Scholar] [CrossRef]
- Kostas, K.; Amiralin, A.; Sagimbayev, S.; Massalov, T.; Kalel, Y.; Politis, C. Parametric model for the reconstruction and representation of hydrofoils and airfoils. Ocean Engineering 2020, 199, 107020. [Google Scholar] [CrossRef]
- Masters, D.A.; Poole, D.J.; Taylor, N.J.; Rendall, T.; Allen, C.B. Impact of Shape Parameterisation on Aerodynamic Optimisation of Benchmark Problem. In Proceedings of the 54th AIAA Aerospace Sciences Meeting; 2016. [Google Scholar] [CrossRef]
- Masters, D.A.; Taylor, N.J.; Rendall, T.C.S.; Allen, C.B.; Poole, D.J. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA Journal 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Kulfan, B.; Bussoletti, J. Fundamental Parametric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference; 2006. [Google Scholar]
- Kulfan, B.M. Universal Parametric Geometry Representation Method. Journal of Aircraft 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The Nurbs Book, 2nd ed.; Springer Verlag, 1997. [Google Scholar]
- Drela, M.; Giles, M. Viscous-inviscid analysis of transonic and low Reynolds number airfoils. AIAA 1987, 25, 1347–1355. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics. Lecture Notes in Engineering; Mueller, T., Ed.; Springer: Berlin, Heidelberg, 1989; Volume 54. [Google Scholar]
- Kostas, K.V.; Manousaridou, M. Machine-Learning-Enabled Foil Design Assistant. Journal of Marine Science and Engineering 2023, 11. [Google Scholar] [CrossRef]
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Numerical geometry of non-rigid shapes; Springer Science & Business Media, 2008. [Google Scholar]
- Xu, D.; Li, H. Geometric moment invariants. Pattern recognition 2008, 41, 240–249. [Google Scholar] [CrossRef]
- Cignoni, P.; Rocchini, C.; Scopigno, R. Metro: Measuring error on simplified surfaces. In Proceedings of the Computer graphics forum; Wiley Online Library, 1998; 17, pp. 167–174. [Google Scholar]
- Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Masood, Z.; Khan, S.; Qian, L. Machine learning-based surrogate model for accelerating simulation-driven optimisation of hydropower Kaplan turbine. Renewable Energy 2021, 173, 827–848. [Google Scholar] [CrossRef]
- Degertekin, S.O.; Lamberti, L.; Ugur, I.B. Sizing, layout and topology design optimization of truss structures using the Jaya algorithm. Applied soft computing 2018, 70, 903–928. [Google Scholar] [CrossRef]
- Degertekin, S.; Yalcin Bayar, G.; Lamberti, L. Parameter free Jaya algorithm for truss sizing-layout optimization under natural frequency constraints. Computers & Structures 2021, 245, 106461. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Yang, P.; Xu, J.; Wang, H. Modeling and optimization of the thermal-hydraulic performance of direct contact heat exchanger using quasi-opposite Jaya algorithm. International Journal of Thermal Sciences 2022, 173, 107421. [Google Scholar] [CrossRef]
- Atrevi, D.F.; Vivet, D.; Duculty, F.; Emile, B. A very simple framework for 3D human poses estimation using a single 2D image: Comparison of geometric moments descriptors. Pattern Recognition 2017, 71, 389–401. [Google Scholar] [CrossRef]
- Jin, P.; Xie, B.; Xiao, F. Multi-moment finite volume method for incompressible flows on unstructured moving grids and its application to fluid-rigid body interactions. Computers & Structures 2019, 221, 91–110. [Google Scholar]
| 1 | After excluding some inappropriate or almost identical designs, a base set with 1263 foil designs was identified. For each of these base designs, 5 random shape perturbations around them were generated, leading to foil designs. |
| 2 | excluding of course the case of a coincident pair of points at the trailing edge. |
| 3 | If we split the foil curve in two parts using the points corresponding to the minimum and maximum coordinate, each part should behave as a graph of function. |
| 4 | |
| 5 | recall that we need to use 17 parameters of the foil parametric model to represent the dataset within Kulfan tolerance; see also Section 2.1.1. |
| 6 | To a lesser extend when only second moments are included. |
| 1 | 0 | 0 | 0.0036 | 7.1537E-04 |
| 0.3260 | 3.2836E-05 | -4.6849E-04 | -0.0036 | 0.0499 |
| 2.6985E-05 | 1.2810E-05 | 7.8598E-04 | -4.0455E-04 | 0.2297 |
| Geometry only | ||
| Geometry and second moments | ||
| Geometry and third moments | ||
| Geometry and fourth moments | ||
| Geometry and second to third moments | ||
| Geometry and second to fourth moments |
| Discretization | Initial | ||||||
|---|---|---|---|---|---|---|---|
| Uniform Spacing (Parametric Domain) | 2.0518 | 1.4176 | 1.6590 | 2.1210 | 2.1494 | 2.5657 | 2.7720 |
| Cosine Spacing | 1.1562 | 1.2220 | 1.5515 | 2.0975 | 1.2719 | 1.4411 | |
| Curvature-Based Spacing | 1.2967 | 1.8346 | 2.8000 | 2.7417 | 2.6835 | 2.2227 | |
| Uniform Spacing (Physical Domain) | 1.1214 | 1.1368 | 1.2826 | 1.2210 | 1.1519 | 1.1816 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





