Prerpints.org logo
Preprint
Review

A Survey of Numerical Simulation Tools for Offshore Wind Turbine Systems

Altmetrics

Downloads

643

Views

149

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 January 2024

Posted:

11 January 2024

You are already at the latest version

Alerts
Abstract
The emerging industry of offshore wind turbines mounted on floating bases has garnered significant attention from both academia and industry. The desire to understand the complex physics of these floating structures has led to the development of numerical and physical modelling techniques. While physical testing has traditionally been employed, there is a growing focus on cost-effective and accurate high-fidelity numerical modelling as a potential alternative or supplement. However, commonly used numerical engineering tools in the offshore industry are considered mid- to low-fidelity and may lack the desired precision for floating offshore wind turbines (FOWTs). Given the complexity of these simulation codes, it is crucial to validate their accuracy. To address this, the International Energy Agency (IEA) Wind Technology Collaboration Programme initiated various research endeavors, including the Offshore Code Comparison Collaboration (OC3), Offshore Code Comparison Collaboration Continuation (OC4), Offshore Code Comparison Collaboration Continuation with Correlation (OC5), and the recent Offshore Code Comparison Collaboration Continued with Correlation and Uncertainty (OC6) projects. This study offers a comprehensive survey of the simulation tools available for FOWTs which were part of OC projects, focusing particularly on horizontal axis wind turbines (HAWTs) and highlighting their capabilities and fundamental theories.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

A rapidly expanding sector of the wind energy industry is floating wind energy devices. Currently, there are relatively few large operational floating offshore wind farms that are connected to the grid: Hywind Tampen (88 MW) wind farm [1], which is located approximately 140 km into the Economic Exclusive Zone of the Norwegian North Sea, Haiyou Guanlan floating wind farm (7.25 MW) located 136 kilometres from Wenchang in Hainan province in China [2], Typhoon-Proof floating wind power project located 72 km (44 miles) off the coast of Guangdong Province in China [2], Block Island Wind Farm (30 MW) off the coast of Rhode Island [3], Hywind (30 MW) and Kincardine (50 MW) in Scotland, and Windfloat Atlantic (25 MW) near Viana de Castelo in Portugal [4]. As of now, despite the rapid growth in this industry, the expenses associated with floating wind turbines are still much greater than those for fixed offshore ones.
The complexity and coupling of floating offshore wind turbine (FOWT) systems, as well as the presence of several excitation sources, make floating wind optimization challenging. As such, advanced modelling and design tools capable of precisely capturing these systems’ physical behavior under realistic conditions are necessary. To this end, it is essential to understand and address the causes of inaccuracies and uncertainties in these tools in order to develop a cost-effective design tool for floating wind turbines. Currently, there are a number of different numerical and physical modelling methods available, both independently and with a cross-validation method [4].
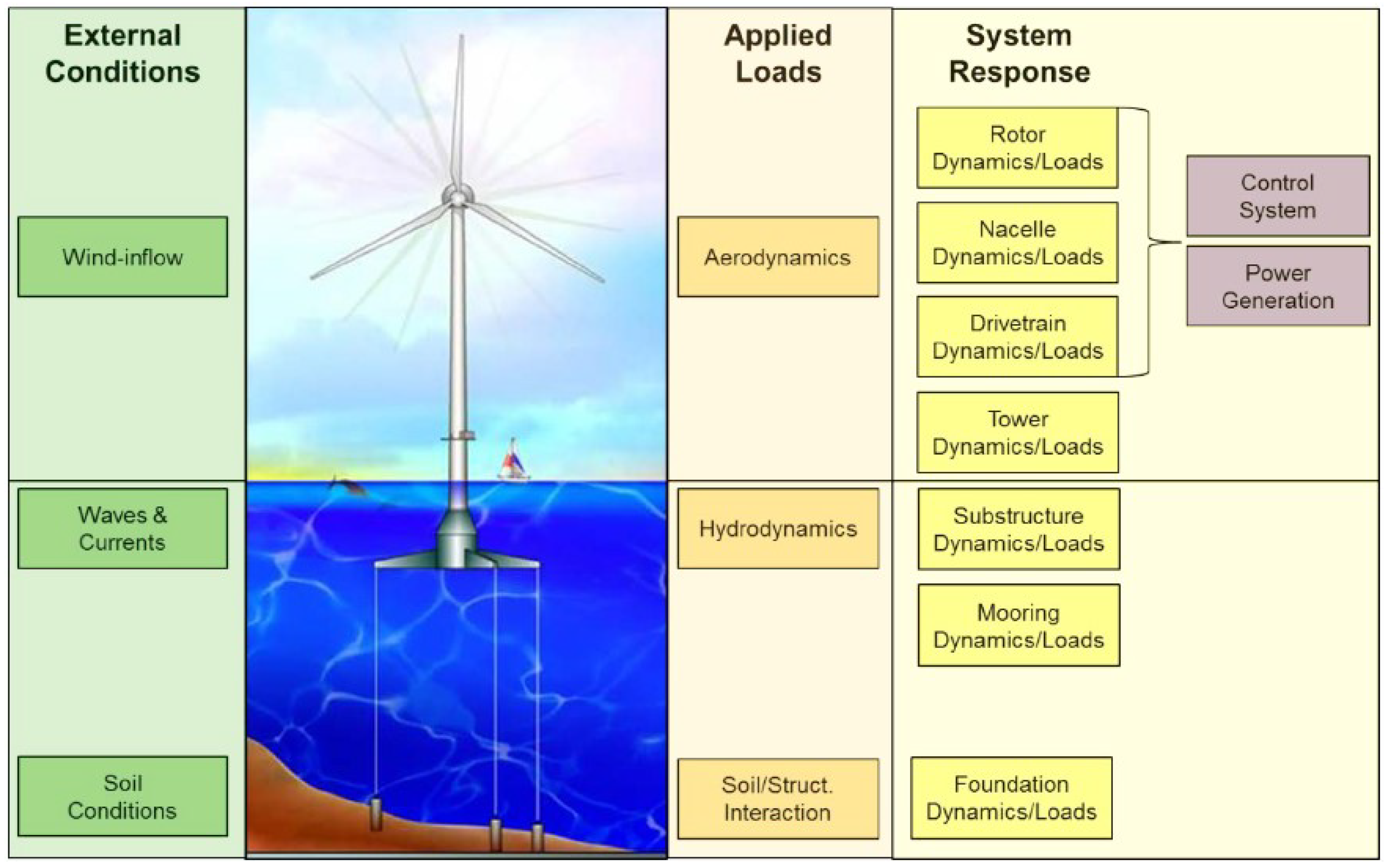
In recent years, a large variety of simulation tools have been developed to examine various structural dynamic, aerodynamic, wind-inflow, and mooring models of wind turbines in the time-domain, as well as to anticipate and assess their response. Fields related to FOWTs have recently received substantial research attention because of the potential benefits of these systems over onshore systems. Waves, sea currents, hydrodynamics, and mooring systems have all been modelled to replicate the additional physical phenomena involved with offshore wind turbines. The various components of offshore wind turbine modelling tools are depicted in Figure 1.
Almost all simulation codes for onshore and offshore wind turbines are based on time-domain solutions that use numerical techniques, like the Fast Fourier Transform (FFT), to simulate a wind turbine’s dynamic behavior. Furthermore, the majority of these aeroelastic modelling codes are based on blade element momentum (BEM) theory and multibody simulation (MBS) techniques, which allow for acceptable modification and prediction of rotor aerodynamics like tip loss correction, turbulent wake state, dynamic inflow, and dynamic stall [6,7,8,9,10].
In order to validate and verify the accuracy of the available simulation codes through code-to-code comparisons, two research tasks have been defined by the International Energy Agency (IEA) within Tasks 23 and 30 [10,11,12]: The Offshore Code Comparison Collaboration (OC3) and the Offshore Code Comparison Collaboration Continuation (OC4) projects. Subsequently, an extension of Task 30, the Offshore Code Comparison Collaboration Continuation with Correlation (OC5) was initiated in three different phases to address the limitation of the previous tasks by comparing the simulated response with physical response data from an experimental test, and identifying which solution is the most accurate [13,14,15]. In 2019, the IEA Wind Task 30 defined the OC6 project (Offshore Code Comparison Collaboration Continued with Correlation and Uncertainty) to improve the overall accuracy and predictive capability of the offshore wind turbine simulation codes [16].
This paper begins by dissecting the numerical modelling of floating offshore wind turbines (FOWTs) into four distinct components: structural dynamics, hydrodynamics, aerodynamics, and mooring. The primary focus of this exploration is an in-depth evaluation and comparison of various simulation tools tailored for FOWTs, particularly emphasizing horizontal axis wind turbines (HAWTs). The central objective of this survey is to provide an extensive overview of the numerical simulation tools and their foundational theories, drawing from their participation in the Offshore Code Comparison (OC) projects. These initiatives have played a pivotal role in scrutinizing the precision of these simulation tools through rigorous code-to-code and code-to-model comparisons, ensuring their reliability and efficacy in FOWT analysis. Moreover, this survey casts a spotlight on the underlying theories, capabilities, and limitations of these tools, offering valuable insights into their applicability for diverse aspects of FOWT simulation. In the subsequent sections, we delve into each of these three critical components, followed by an extensive examination of the individual simulation tools, elucidating their distinct attributes and functionalities.

2. Structural Codes

In the analysis of structural modules, a variety of approaches have been employed, including modal-based, finite element codes, and multibody methods. Some simulations have utilized combinations of these techniques to enhance accuracy. For instance, HAWC2 adopted a comprehensive approach, employing both multibody and linear finite element representations to model the turbine. On the other hand, ADCoS-Offshore opted for a nonlinear finite element system to capture intricate interactions. Codes like FAST, Bladed, and FLEX5 adopted a blend of modal and multibody techniques, incorporating modal elements derived from a finite-element-based preprocessor [10].
It is worth noting that modal-based codes yield slightly different second and higher coupled eigenmodes compared to their higher-fidelity multibody and finite element counterparts which indicates a stiffer behavior of a structure. As a result, variations in dynamic response and energy content are anticipated, particularly in the higher-frequency range. Multibody and FEM codes accommodate more DOF and thus allow for more vibrational modes and higher local vibrational modes. This results in reduced stiffness of the structure, which should better mimic reality. Mode-shape-based tools might not accurately predict these vibrations due to the limited number of mode shapes used for the model. The modal-based codes are categorized into two groups based on their formulation: Euler–Bernoulli and Timoshenko. The former is utilized by Bladed, FLEX5-Poseidon, ADCoS-Offshore, WaveLoads-ANSYS, HAWC2-BE, and ANSYS Beam, while the latter is employed by HAWC2, ANSYS Pipe, and Bladed (Timoshenko) [10,11].
When it comes to predicting natural frequencies of flexible body modes, not all codes exhibit the same level of accuracy. Codes that account for tower and blade bending, along with drivetrain torsion modes, tend to yield similar results with only minor discrepancies. Notably, codes neglecting tower torsion, like FAST, project higher natural frequencies, reflecting the stiffer compliance about the tower centerline. Conversely, codes that consider tower torsion, such as ADAMS and HAWC2, align more closely with each other [10].
In terms of tower fore–aft deflection induced by platform motion, a majority of codes demonstrate reasonable agreement. However, Simo and SESAM predict no deflection due to their rigid tower modelling approach. This underscores the significance of accounting for tower flexibility in accurately capturing such dynamic responses [10].

3. Aerodynamic Codes

In the realm of aerodynamic modelling, a blade-element-momentum-theory-based model was predominantly employed across simulation tools, albeit with variations in corrections and attributes. Some tools went further to encompass a dynamic wake element, which accounts for the time lag in induced velocities created by vorticity shed from the blades. Additionally, unsteady airfoil aerodynamics were integrated to model flow hysteresis, covering aspects like unsteady attached flow, trailing-edge flow separation, dynamic stall, and flow reattachment. Although most participants adhered to a BEM model, a subset incorporated dynamic wake and unsteady airfoil aerodynamics. The inclusion of unsteady airfoil aerodynamics notably led to an augmentation in system-wide broadband frequency excitation, enhancing alignment with experimental data [5,14].
In the domain of floating offshore wind turbine system modelling, various fidelity approaches were adopted, categorized under blade element momentum (BEM) theory, dynamic BEM (DBEM) incorporating dynamic inflow effects, generalized dynamic wake (GDW), free-vortex wake (FVW), and blade-resolved or actuator-line-based computational fluid dynamics (CFD). Several of these approaches, including BEM, DBEM, GDW, select FVW, and actuator-line-based CFD, are rooted in the lifting-line theory. Here, the airfoil polar data serve as a pivotal input, providing insights into lift and drag coefficients as a function of the angle of attack [14,17].
The conventional BEM theory operates on the premise of an instantaneous wake reaction, where induced velocities based on axial and tangential induction factors are quasi-steady. In reality, however, there exists a delay for the wake to respond to shifts in flow conditions arising from changes in wind patterns or turbine responses. To address this, the dynamic inflow model (or dynamic wake) in BEM theory incorporates low-pass filters to rectify the unsteady aerodynamic response from this delayed wake reaction. On the other hand, GDW explicitly calculates dynamic inflow by representing induced velocity through series expansion and accounting for apparent mass. In FVW, dynamic inflow is intrinsically captured, while CFD solves momentum and continuity equations, inherently encompassing this dynamic inflow aspect [14,17].
Most BEM and DBEM models accommodate prevalent aerodynamic corrections, critical in wind turbine design, such as blade-root and blade-tip losses. Tools utilizing FVW or CFD gain valuable insights into wind turbine wake behavior. However, it is important to note that most numerical models exhibit a slight overprediction of wake expansion, potentially influenced by the proximity of the blade tip to the experimental ceiling. Notably, CFD tools incorporating wind tunnel boundaries demonstrated superior agreement with experimental data. FVW models face limitations in accounting for these boundary conditions without implementing additional features [17].
While the motion of the turbine itself does not mandate an unsteady aerodynamic modelling approach for accurate load prediction, a realistic scenario involving generator torque control and blade pitch angle control would necessitate unsteady aerodynamic models—encompassing airfoil unsteady aerodynamics and dynamic inflow models—for precise load projections [17].

4. Hydrodynamic Codes

Hydrodynamic loads on a floating structure encompass the influence of incident waves, the generation of outgoing waves due to platform movement (incorporating added mass and damping effects), and the effects of viscous forces. Typically, modelling these loads relies on two main techniques: potential flow (PF) theory and Morison’s equation (ME). The choice between these theories is contingent on the scale of the structure being simulated and the prevailing water flow conditions. The hydrodynamic approaches used in the simulation tools are based on one of these methods, or a blend of both. For large structures in the water, where their size is significantly greater than the wavelength, the water remains attached as it flows past the structure, making potential flow theory applicable. The most common technique for modelling potential loads is through panel methods. This approach encompasses capturing excitation from waves (including diffraction) and radiation effects (including added mass and damping effects). However, it does not encompass viscous drag resulting from flow separation. Consequently, codes exclusively using this method often apply a global quadratic drag to the structure as an approximation. In the case of smaller structures, where flow separation occurs, Morison’s equation is the typical choice. This equation is an empirically derived model for hydrodynamic loading, encompassing excitation from waves (with a long wavelength approximation), added mass effects, and viscous forces. The theory can be further refined by integrating the Morison forces up to the instantaneous water surface elevation using a wave stretching approach, and/or by applying the forces at the instantaneous position of the displaced body in the water. When exclusively using this method, it is imperative to also account for both the hydrostatic forces and dynamic pressure loads [5,14].

5. Mooring Codes

The numerical techniques for analyzing mooring systems can be broadly categorized into three methods: static, quasi-static, and dynamic [18]. The static method exclusively considers constant loads like gravity, buoyancy, steady currents, wind, and mean wave-drift forces. The quasi-static method is introduced due to the absence of an absolute static state. It assumes that within a given time step, the motion of a system motion is uniform and linear between two static positions, and the system loads remain constant. Typically employed during preliminary design, the quasi-static method assumes that the mooring line is in static equilibrium at each time step, with the body’s position dependent solely on the static restoring force. Quasi-static mooring models range from simple linear stiffness matrices to catenary equations solving Newton’s force equation at each connection node [19].
For greater accuracy in mooring loads, especially during large displacements where inertial effects are more pronounced, dynamic mooring models are utilized. Dynamic models fall into three main types: lumped-mass model, finite element method (FEM), and finite difference (FD) models [18,20]. In dynamic mooring models, the mooring line is discretized into small elements, accounting for hydrodynamic drag and added mass [21]. The lumped-mass model is a simpler numerical approach, assuming the mooring line consists of concentrated masses connected by massless springs. Mooring dynamics are derived by solving a system of equations of motion for each individual mass. FEM and FD provide high-fidelity solutions, treating the mooring line as infinitesimally small differential elements. The key distinction lies in the formulation of the governing equation, which is in a differential and integral form for FEM and FD, respectively [18]. Generally, the lumped-mass method converges to the same solution as FEM and FD with sufficient resolution [22]. Other methods, such as the finite segment scheme involving ball-and-socket connected rigid rods, have also been used to discretize the mooring line [23,24,25,26].

6. Numerical Simulation Tools

6.1. FAST Computer-Aided Engineering Tool

FAST (Fatigue, Aerodynamics, Structures, and Turbulence) is the primary computer-aided engineering (CAE) tool applicable to wind turbines. It was developed by the National Renewable Energy Laboratory (NREL) with support from the United States Department of Energy. It simulates the coupled dynamic response of a variety of wind turbine configurations, including two- and three-bladed horizontal-axis rotors, pitch or stall regulation, rigid or teetering hubs, upwind or downwind rotors, and lattice or tubular towers [27,28,29].
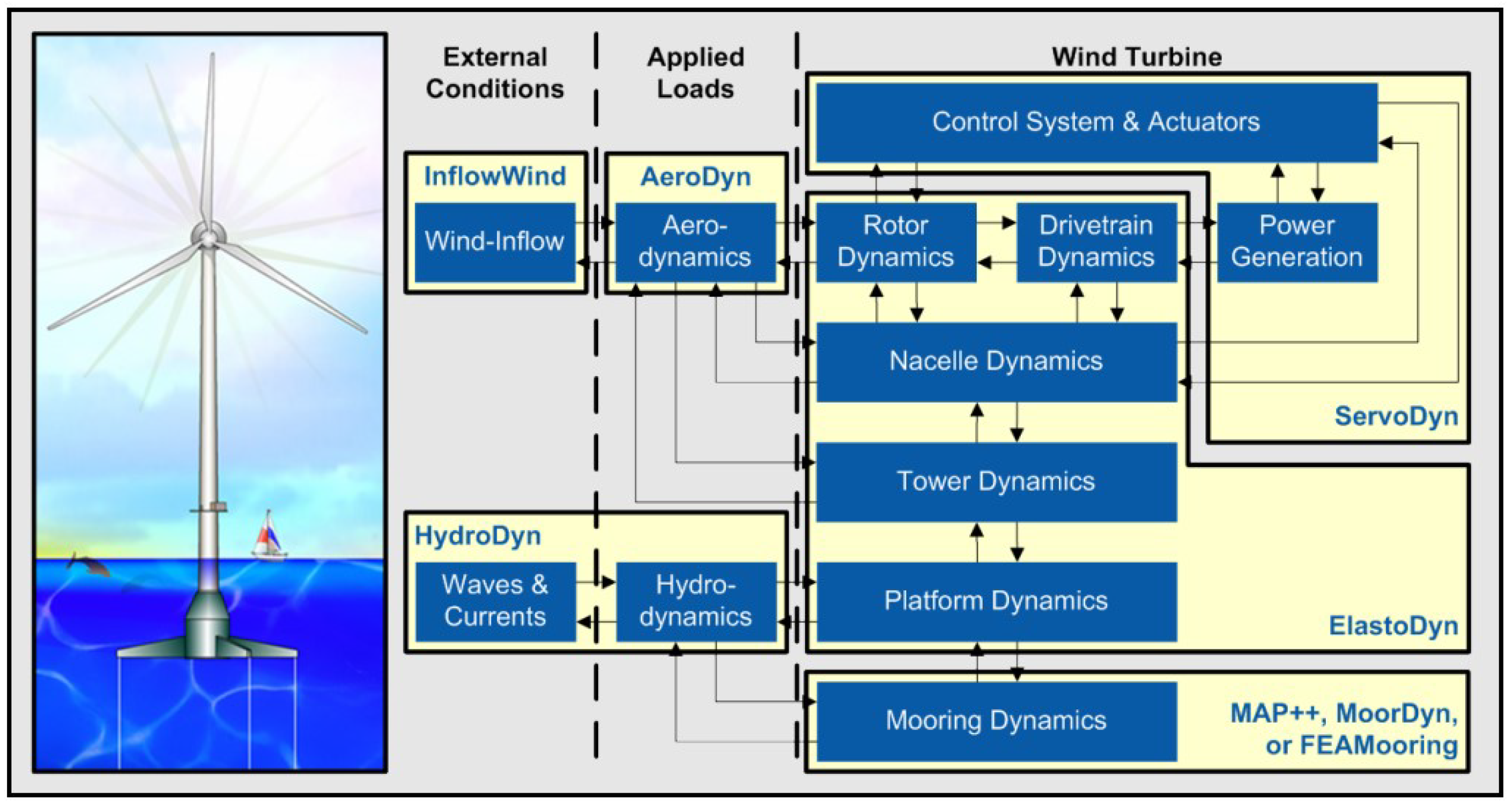
FAST includes a number of modules that use mathematical models to simulate one or more turbine components, such as AeroDyn (aerodynamics), HydroDyn (hydrodynamics of platforms for offshore structures), ServoDyn (control and electrical systems), and BeamDyn or ElastoDyn (structural dynamics). The schematic of various modules available in FAST is depicted in Figure 2. The time-domain simulation and investigation of coupled nonlinear aerohydroservoelastic simulation of onshore or offshore wind turbines on the fixed-bottom or floating substructure is made possible by the assembly of these modules.
FAST was utilized as the principal simulation tool in the OC projects, and its numerical calculations for the OC3- Hywind and DeepCwind semisubmersible platforms were in good agreement with experimental results [9,14].

6.1.1. FAST Modularization Framework

NREL recently released the FAST Modularization Framework in order to improve the modularity of the FAST aerohydroservoelastic simulation tool. As the core of this tool, FAST v8 is a software framework and algorithm for interconnecting modules in the time-domain [30]. Modules can communicate in the FAST Modularization Framework using matching or non-matching spatial meshes with different time steps and time integrators. A predictor–corrector technique can be used to transfer data between modules, allowing for both implicit and explicit time integration within each module [28,30,31,32].

6.1.2. ElastoDyn

ElastoDyn is the main structural dynamics module of FAST, where Kane’s method is used to construct and implement nonlinear equations of motion [29,33]. As a call-able module, it can be called in the framework with separate input files and source codes. ElastoDyn is based on a formulation that combines multibody dynamics (blade and tower) with modal dynamics (platform, nacelle, generator, gears, and hub) [32]. The dominant mode shapes in ElastoDyn are found externally through modal tests or BModes and are represented as sixth-order polynomials [34].
ElastoDyn is based on Euler–Bernoulli beam theory in bending, meaning that no axial or torsional degrees of freedom (DOF) and no shear deformation are considered [30,35,36,37,38]. As a result, the module is better suited to straight beams with isotropic material and no mass or elastic offsets, with small to moderate blade deflections, and some geometric nonlinearities [30,37,38]. This module allows you to model any HAWT with a two- or three-bladed, upwind or downwind rotor, with a rigid or teetering hub.

6.1.3. BeamDyn

NREL recently released BeamDyn, a new time-domain structural dynamics module for modelling slender structures and advanced aeroelastically tailored blades [28,30,37,38,39]. For dynamic simulation of highly flexible composite wind turbine blades with bend–twist coupling, BeamDyn is integrated into the FAST modular framework [30,34,37,38]. BeamDyn substitutes in the place of ElastoDyn’s simplified blade structural model. BeamDyn is based on geometrically exact beam theory and is discretized in the space domain using the Legendre spectral finite element (LSFE) [30,36,37,38]. This new module allows for the modelling of twisted composite blades with significant deformations, including bending, torsion, shear, and extensional DOFs [30,34,36,40]. It may also be used as a standalone high-fidelity beam tool.

6.1.4. AeroDyn

AeroDyn is used to perform the aerodynamic modelling for the FAST simulation tool. AeroDyn is a time-domain wind turbine aerodynamics module that may be used either independently to compute wind turbine aerodynamic response or in conjunction with FAST to enable aeroelastic modelling of wind turbines [31]. AeroDyn solves for rotor-wake effects and blade element aerodynamic loads, including dynamic stall, using wind-inflow data [31]. Rotor Wake/Induction, Blade Airfoil Aerodynamics, Tower Influence on the Blade Nodes, and Tower Drag are the four submodules of AeroDyn [41,42]. The BEM theory and the generalized dynamic-wake (GDW) theory are two models in AeroDyn for calculating the effect of wind turbine wakes. Many wind turbine designers employ BEM theory, whereas GDW theory is a more contemporary development that can be used to simulate skewed and unsteady wake dynamics [31,42,43]. AeroDyn v15.04 is a new NREL release that includes improvements to skewed-wake, dynamic wake, and unsteady airfoil aerodynamics modelling, as well as the ability to model highly flexible and curved or swept blades [31,41,42,43,44].

6.1.5. HydroDyn

The time-domain hydrodynamics module of the NREL simulation tool known as HydroDyn has been integrated with FAST to enable aerohydroservoelastic simulation of offshore wind turbines. This module, however, can also be used to compute hydrodynamic loads as a standalone module. HydroDyn supports both fixed-bottom and floating offshore installations. In HydroDyn, the hydrodynamic loads on a structure are calculated using a potential flow theory solution (radiation/diffraction), a strip-theory solution (via an extension of the Morison equation), or a combination of the two (radiation/diffraction and the drag component of the Morison equation) [29,32,37,43,45].
Linear hydrostatic restoring; nonlinear viscous drag from incident-wave kinematics, sea currents, and platform motion; added mass and damping contributions from linear wave radiation, including free-surface memory effects; and incident-wave excitation from linear diffraction in regular or irregular seas are all features that HydroDyn can account for [29,46].

6.1.6. InflowWind

For processing wind-inflow data, a new module named InflowWind was created, which can also be used independently of FAST. Undisturbed wind inflow such as steady, uniform, and time-varying deterministic-like gusts; full-field (FF) turbulence models like TurbSim and Mann; and a specific user-defined format are among the wind formats supported by the InflowWind module [47,48].

6.1.7. SubDyn

NREL developed SubDyn, a time-domain structural dynamics module for multi-member fixed-support substructures . It can also be used as a standalone code to compute the mode shapes, natural frequencies, and time-domain free vibration response of substructures independently from the rest of the wind turbine system. SubDyn can support a variety of substructure types, including monopiles, tripods, jackets, and other lattice-type substructures widely used for offshore wind turbine installations, as well as lattice support structures for land-based wind turbines [49,50].

6.1.8. MAP++

MAP++ is designed as a library for modelling the steady-state forces on a multi-segmented quasi-static (MSQS) mooring line in conjunction with other CAE tools. The MSQS module in MAP++ solves all algebraic equations for all elements with a resultant of zero at connection points at the same time. Modelling of seabed contact, seabed friction, and externally applied forces is also included in MAP++ [19,51,52,53].

6.1.9. MoorDyn

MoorDyn is a lumped-mass modelling technique that was created in 2015. Its purpose is to use the Morison equation to capture key phenomena linked to FOWT mooring systems, such as mooring stiffness, inertia and damping forces in the axial direction, weight and buoyancy effects, seabed contact forces, and hydrodynamic loads from mooring motion. The MoorDyn module does not take into account bending and torsional cable stiffness, as well as bottom friction [54,55,56].

6.1.10. FEAMooring

FEAMooring is a finite-element-based mooring-dynamics module that, while integrated into FAST, may also be used to compute mooring dynamics as an independent code. Different types of mooring systems, such as catenary mooring, taut mooring, and tendons, can be analyzed using FEAMooring. It calculates mooring line reaction forces at the floating platform’s fairlead positions while taking into consideration mooring dynamics including inertia and drag forces at each line element [53,57,58,59].

6.1.11. IceFloe and IceDyn

IceFloe (Quasi-Steady Ice Loading) and IceDyn (Ice Dynamics) are two modules created by NREL to model ice floe loading on vertical and sloping structures when bottom-fixed offshore wind turbines interact with surface ice [60,61,62].

6.1.12. Transition to OpenFAST

The NREL recently created OpenFAST (previously known as FAST) to model the physical phenomena and dynamic response of the entire wind turbine system (rotor, tower, support structure, nacelle, drivetrain, and controller) to normal and extreme environmental loading conditions (wind, wave, and current). OpenFAST was released to help with the transition to an open-source community-based development of FAST as an aerohydroservoelastic simulation tool, as well as to provide a framework for future development of FAST with features such as automated regression and unit tests, source code documentation, and a compiler built system [28,63].

6.2. OrcaFlex

OrcaFlex is a time-domain, finite element commercial software for dynamic analysis of marine systems developed by Orcina [64]. It is notable for its dynamic mooring line representation and comprehensive hydrodynamic modelling capability [65,66], which allows it to model a multi-member floating support system as discrete elements. Moreover, OrcaFlex is capable of performing a fully coupled analysis of both onshore and offshore wind turbines [64,65]. The long-established hydrodynamic capabilities of OrcaFlex are combined with a built-in aerodynamic turbine model by embedding it into OpenFAST, resulting in a fully coupled dynamic analysis tool applicable for both fixed and floating platform offshore wind turbines. Nonetheless, in FAST v8 there is a module called OrcaFlexInterface that computes all hydrodynamic and mooring loads, while FAST computes the turbine, tower, and floating platform structural dynamics, aerodynamics, and control and electrical-drive dynamics [67].
OrcaFlex supports both frequency-domain and time-domain dynamic analysis. The frequency-domain analysis is a linear procedure. The frequency-domain solver approximates any nonlinearities through the process of linearization. The nonlinearity of time-domain analysis is more comprehensive since at each time step, mass, damping, stiffness, loading, and other parameters are evaluated, taking into consideration the instantaneous, time-varying geometry. OrcaFlex uses a 3-D finite element model to simulate mooring line dynamics. To model the axial, torsional, and bending stiffness and damping of lines, they are discretized as lumped-mass elements connected to visco-elastic spring-damper segments. Moreover, the two types of time-domain integration schemes, implicit and explicit, have been implemented in OrcaFlex and are available to users [68].
The blade modelling is similar to OrcaFlex line objects where each blade is modelled as part of a series of straight massless segments with a node at each end [68].

6.3. OPASS

Offshore Platform Anchorage System Simulator (OPASS), developed by the Spanish National Renewable Energy Center (CENER), is a tool for simulating nonlinear mooring dynamics using a lumped-mass model [69,70]. OPASS is built using the finite element method, with three translational DOF at each node and element mass lumped at nodes. Each element is made up of a slender line with a constant circular section, with the effects of inertia, gravity, hydrodynamic added mass, hydrostatic, wave kinematics, hydrodynamic drag, structural damping, and axial elasticity all taken into account [69]. The code can be used as a standalone tool to simulate mooring lines, or it can be used with FAST to model mooring lines using a quasi-static technique [69,71].
The collaboration between CENER and Norway’s Institute for Energy Technology (IFE) has resulted in various scaled experiments for experimental validation and verification of OPASS. OPASS was initially validated using 3DFloat code computations [72], a dynamic mooring line module based on a finite element formulation [69,73]. Following that, OPASS was combined with FAST V6.02, and the final tool was satisfactorily confirmed as an aerohydroservoelastic simulation code under IEA task 30’s OC4 project [5,69]. Furthermore, OPASS was experimentally confirmed in a tank test at the Ecole Centrale de Nantes (ECN) against a submerged chain. OPASS was recently verified against test data from a submerged chain in which the suspension point was excited with horizontal harmonic motions of various periods in the plane of the catenary [69,70]. By considering the mooring lines as dynamic systems, Azcona et al. combined OPASS and FAST to compute the fatigue and ultimate loads of three distinct platform concepts of FOWTs (The UMaine TLP [74], the OC4 DeepCwind semisubmersible [75], and the UMaine Hywind spar [10]).

6.4. Bladed

Bladed is an integrated aerohydroservoelastic modelling package developed by Det Norske Veritas (Norway) and Germanischer Lloyd (Germany) (DNV GL) which is capable of modelling both onshore and offshore wind turbines. Bottom-fixed offshore structures, such as jackets, can be designed in Bladed with beam components and flexible joints, or imported from third-party offshore design tools like SESAM and SACS [76]. Bladed can also simulate FOWTs using a mooring line system. Bladed models the dynamics of the mooring line as a multibody system in which bar components are linked together with universal joints to form a chain [76].
Bladed uses a flexible multibody dynamics technique in its structural dynamics code. Various flexible and rigid bodies can be linked together to model the entire system in this method. The Craig–Bampton approach is used to calculate the mode shapes and frequencies for each flexible body as a linear finite element body [76,77,78,79]. Each blade splits into several flexible bodies to form a geometrically nonlinear model capable of large deflections, whereas the tower is modelled using modal analysis [76,78,79]. This approach is a key feature of Bladed that allows stability analysis and determining the dynamic response of large modern wind turbine blades. Bladed’s multibody dynamics framework is also used to describe other physical components of wind turbines, such as pitch drives and generators [76].
The Morison equation provides the basis for Bladed’s hydrodynamic module. Since the Morison equation cannot be applied adequately for structures with large members, wave diffraction and radiation terms can be important, and the boundary element approach can be utilized to calculate hydrodynamic loads [5]. Furthermore, Bladed can be linked to a third-party hydrodynamic code like WAMIT, AQWA, or WADAM, and then the hydrodynamic properties imported into Bladed [76].
Bladed uses BEM theory to implement aerodynamic loads, and it can accommodate sophisticated unsteady aerodynamics by using the following models [76,79]:
  • Prandtl’s tip and root loss, to account for the effect of the blade tip vortices on induced velocity;
  • Dynamic wake model;
  • Glauert skew model;
  • Dynamic stall model, including Beddoes–Leishman compressible and incompressible flows and Øye dynamic stall.
Bladed can generate a variety of wind models, including steady and dynamic models, as well as turbulent wind files. It can also provide earthquake acceleration time histories for turbines in seismic zones, which can be used to determine the effects on turbine loads [76].

6.5. HAWC2

The coupled aeroelastic Horizontal Axis Wind Turbine Simulation Code 2nd Generation (HAWC2) was created at Risoe National Laboratory in Denmark between 2003 and 2006 as part of an aeroelastic design research program [80]. The code has been tested both internally against the previous version, HAWC, and empirically against other offshore simulation codes used in OC research projects under IEA Annex 23 and Annex 30 [5,9,10,11,12,13,14,15,16,80]. The HAWCStab2 is another software tool created by Technical University of Denmark (DTU) Wind Energy for computing and analyzing the modal parameters of a wind turbine in both closed- and open-loop operations with or without unsteady aerodynamic loads [81].
HAWC2 is a time-domain tool for analysis of wind turbine dynamic response. Each body is an assembly of Timoshenko beam elements, and the structural module is formulated using a multibody dynamics technique. Modelling and analysis of complicated structures with large deflections and rotations of the bodies are possible with this formulation method. HAWC2 simulates a wind turbine by connecting bodies with constraint equations, with a constraint being a fixed connection to a global point (e.g., tower bottom clamping), a fixed coupling of relative motions (e.g., fixed pitch or yaw), frictionless bearings, and bearings with user-controlled rotation angles [80,82].
The aerodynamic loads are estimated using the conventional BEM approach, which has been extended to account for dynamic stall, skew inflow, dynamic inflow, and shear effects on the induction factor, as well as the effects of modern wind turbine blade deflection. In addition, the new Dynamic Wake Meandering (DWM) model has been included in HAWC2 [81], which is capable of capturing the response of turbines running in the wake of upstream turbines.
In HAWC2, the hydrodynamic load is estimated using the Morison equation. However, wave kinematics are not calculated. Externally defined Dynamic Link Library (DLL) interfaces are used, which contain regular and irregular Airy waves [80]. The wind turbine’s control is planned to be accomplished by coupling one or more external controllers via DLL interfaces [80].

6.6. aNySIM

aNySIM is an in-house time-domain hydrodynamic code developed by the Netherlands’ Maritime Research Institute (MARIN) in 2006. The goal of aNySIM is to simulate the coupled behavior of floating structures, taking into consideration wave, current, and wind loadings, as well as floating body dynamics and mooring dynamics [83].
Offshore oil and gas facilities including one or more vessels in offloading operations, mooring simulations and multibody lifting operations, and dynamic positioning capability investigations are some of the traditional applications of aNySIM [84,85,86]. However, aNySIM has recently been utilized to simulate floating wind turbines [87].
The hydrodynamic loads in aNySIM are calculated using potential flow theory, and the potential damping and added mass of floating bodies are converted into a non-frequency-dependent added mass in the time-domain [83,88].

6.7. PHATAS

The Energy Research Centre of the Netherlands (ECN) developed the computer Program for Horizontal Axis Wind Turbine Analysis and Simulation (PHATAS) tool to determine loads on horizontal axis wind turbines and model their dynamic response in the time-domain. PHATAS is part of the wind turbine design package FOCUS which was developed by the Wind Turbine, Materials and Constructions (WMC) group at Technology Center Netherlands (TCN) [89,90].
In PHATAS, a significant number of structural DOF can be represented [90]:
  • Continuous flapwise blade bending;
  • Continuous edgewise blade bending;
  • Passive or controlled pitch;
  • Blade flapping hinges;
  • Teetered hub;
  • Generator characteristics;
  • Drivetrain;
  • Tower torsion;
  • Tower bending.
The flexibility of the wind turbine blades is calculated using a nonlinear deflection model while following the Craig–Bampton method and a modal approach is used for modelling the tower [91].
The aerodynamic rotor loads in PHATAS are determined based on the BEM theory with the assumption of a stationary (equilibrium) wake. Moreover, the flow around the blade tips is described using the tip loss factor of Prandtl [90].

6.8. 3DFloat

3DFloat is a fully coupled algorithm created by the Wind Energy Department at IFE and is frequently used to simulate the dynamic response of floating wind turbines during the conceptual design stage [92].
IEA has evaluated 3DFloat against various codes as part of OC initiatives. It has also been used to model the OC3-Hywind floating wind turbine for the OC3 project [10], the bottom-fixed (with jacket type) wind turbine for the OC4 project [11], and the semisubmersible platform for the OC4 project [5]. It has also been tested in wave tanks for three different types of tension-leg buoys [93], a semisubmersible platform [94], and the OC5 project [13].
3DFloat is based on a nonlinear co-rotational FEM framework that takes into account geometric nonlinearities and connects computational nodes with elements. Each element is modelled as a 12-DOF Euler–Bernoulli beam. In addition, each element has structural, aerodynamic, and hydrodynamic characteristics in relation to the principal axes of the section and the axial direction. The calculation is done in the time-domain using either implicit methods such as the generalized α method and the Newmark scheme, or explicit methods such as the central difference scheme [95].
Wind, waves, gravity, and buoyancy are all applied as distributed external loads on the structure in 3DFloat. Regular wave kinematics can be defined using either Airy theory or stream functions up to order 12 [72,96]. The Morison equation is used to compute wave and current loads on the wet part of the structure and for slender beams [72]. Furthermore, a third-party module such as WAMIT [97], NEMOH [98], or WADAM [99] can be utilized to compute the frequency-dependent added mass and damping coefficient matrices for a given structural element.
BEM theory is used to determine the aerodynamic loads and induced velocity over the rotors with modification for dynamic inflow and yaw errors. The turbulence model is imported from HAWC or TURBSIM turbulence files [72].
For wind speeds below the rated wind speed, the control system in 3DFloat is designed for a variable speed rotor with constant blade pitch angle. For wind speeds greater than the rated wind speed, proportional integral (PI) control of pitch angle is utilized to control the rotor’s speed and power. The control module of 3DFloat includes a Dynamic Link Library interface [72].

6.9. DeepLines Wind

DeepLines Wind is a comprehensive software developed jointly by Principia and IFP Energies Nouvelles [100] for the dynamic response of fixed-bottom and FOWTs subjected to ultimate and fatigue offshore environmental loadings. Constant winds, unsteady wind gusts, conventional wind spectra, and full-field turbulent wind are all represented as environmental loads in DeepLines Wind using Airy and nonlinear wave theories; user-defined or random wave spectra like JONSWAP; and steady and unsteady current profiles [100,101,102].
The structural dynamics of the blades are characterized using 3D beam dynamic finite elements that account for the structural twist, variable stiffness, structural damping along the blade, as well as in-plane and out-of-plane pre-bends [100,101,102].
The rotor’s aerodynamic loads are computed using BEM theory, which includes improvements for dynamic stall and tower shadow effects [100,101,102].
The hydrodynamic loads are calculated using drag and inertia Morison elements, diffraction and radiation loads, first-order wave loads (based on potential flow), and second-order wave loads (based on Newman or Quadratic Transfer Function (QTF)). Nonlinear hydrostatic loads can alternatively be represented by pressure integrals across the hull surface or by bar elements [100,101,102,103].
The mooring system for floating wind turbines can be modelled either as a solid subjected to hydrodynamic loads using potential flow theory or as deformable assembled elements subjected to hydrodynamic loads using Morison equations [100,101,102].

6.10. SAMCEF

CAESAM, SAMCEF Field, and SAMCEF Mecano [104,105,106] are among the SAMTECH general tools used by S4WT. CAESAM is a general framework for integrating models and computational tools to perform transient, modal, and fatigue analysis of wind turbines. SAMCEF is a graphical preprocessor tool that helps S4WT build wind turbine components. Finally, SAMCEF Mecano is SAMCEF’s implicit nonlinear finite element solver [104,105], which contains multibody simulation elements.
In S4WT, the structural formulation is based on geometrically exact nonlinear beam theory, and the blades are modelled using a nonlinear FEM approach that is suitable for nonlinear modelling and composite blades subjected to large deformation. Furthermore, the blade model can be expressed as super elements or nonlinear beam elements [105,106].
The aerodynamic loads are computed using BEM theory with various corrections and additional models to account for tip and hub losses, the tower shadow effect, dynamic inflow, and dynamic stall. S4WT may import wind loads from external software such as Bladed or Flex 5, or build them using its built-in models [106,107]. To account for structural and hydrodynamic coupling effects, the hydrodynamic formulation is implemented in SAMCEF Mecano and uses the Morison equation [107].

6.11. Sesam

Sesam has been in use since 1969 for hydrodynamic and structural analysis of offshore structures. The key tools in Sesam, including GeniE, Sima, HydroD, and DeepC, are utilized for modelling and simulation programs as entry points for various sectors [108,109,110].
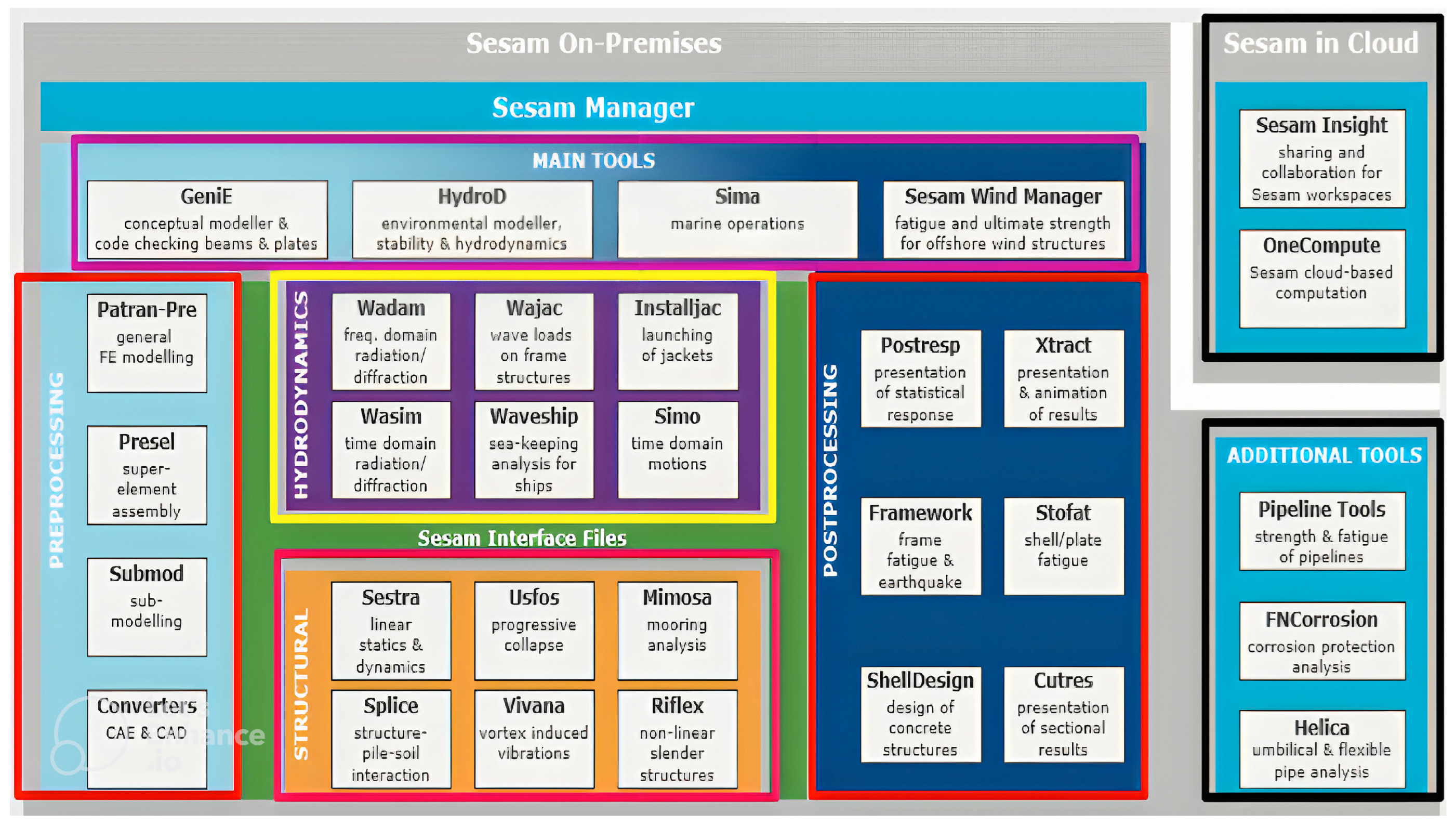
The preprocessor, hydrodynamic analysis programs, structural analysis programs, and postprocessors are the four programs that make up Sesam [108]. An overview of Sesam is presented in Figure 3.
GeniE is the Sesam entry point for designing and evaluating fixed offshore structures as well as offshore wind turbine platforms. It is defined for conceptual modelling of beams, stiffened plates, and shells, as well as code validation. The following packages are available as a result of combining analytic programs with GeniE [108,109,110]:
−
Sestra: a program for static and dynamic structural analysis. The finite element approach was used to formulate it. Sestra may also analyze gap/contact problems and members that are just in tension or compression.
−
Wajac: Wind, wave, and current loads on fixed and rigid frame structures are calculated using this program. In either a frequency- or time-domain simulation, the load is calculated using the Morison equation. Hydrodynamic loads due to irregular, regular, or constrained waves can be computed using time-domain analysis.
−
Splice: nonlinear analysis of the structure–pile–soil interaction problems.
−
Framework: fatigue analysis of structures.
−
Fatigue Manager: time-domain fatigue and ultimate strength analysis under combined wind and wave loads.
In reference to the schematic depicted in Figure 3, the entry points to the package for floating structures are HydroD (modelling and stability analysis module) and GeniE for the following applications [108,109,111]:
−
Wadam: linear frequency-domain hydrodynamics.
The hydrodynamic loads are determined using the Morison equation as well as first- and second-order potential theory. In addition, through frequency-domain simulation analysis, the incident waves are defined as an Airy wave.
−
Wasim: nonlinear time-domain hydrodynamics.
Wasim is based on the Morison equation, which uses the Rankin panel approach to solve the 3D diffraction/radiation problem.
−
Sima: modelling, analysis, control, and results presentation.
This is a time-domain simulation tool that uses a fully coupled technique to simulate a floating wind turbine. The hydrodynamics of the substructure can be estimated using conventional hydrodynamic programs, while the mooring system can be specified in Sima.
−
Simo: simulation of motions.
−
Riflex: analysis of moorings.
Three methods of analysis are available in the Sesam software [109]:
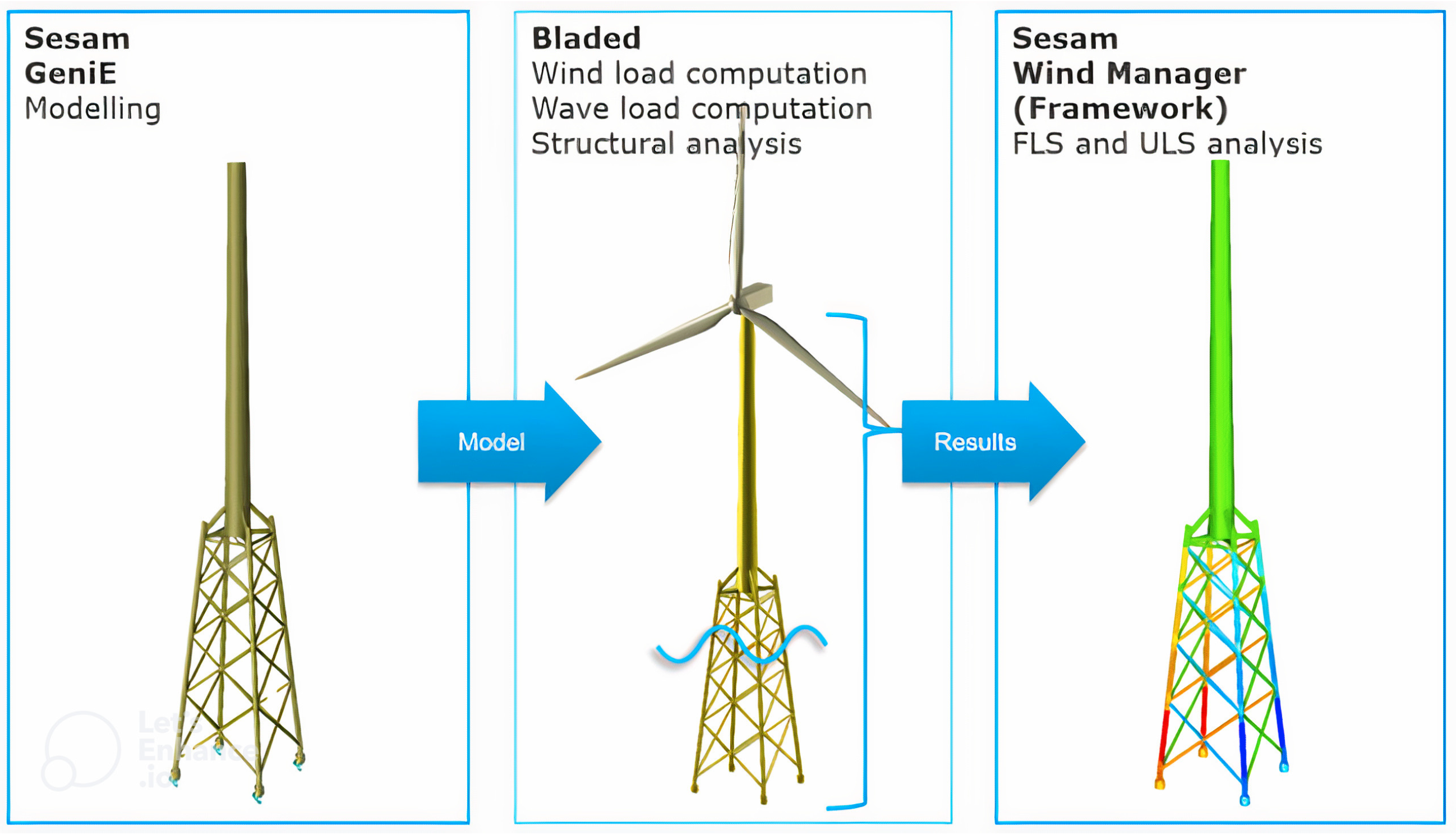
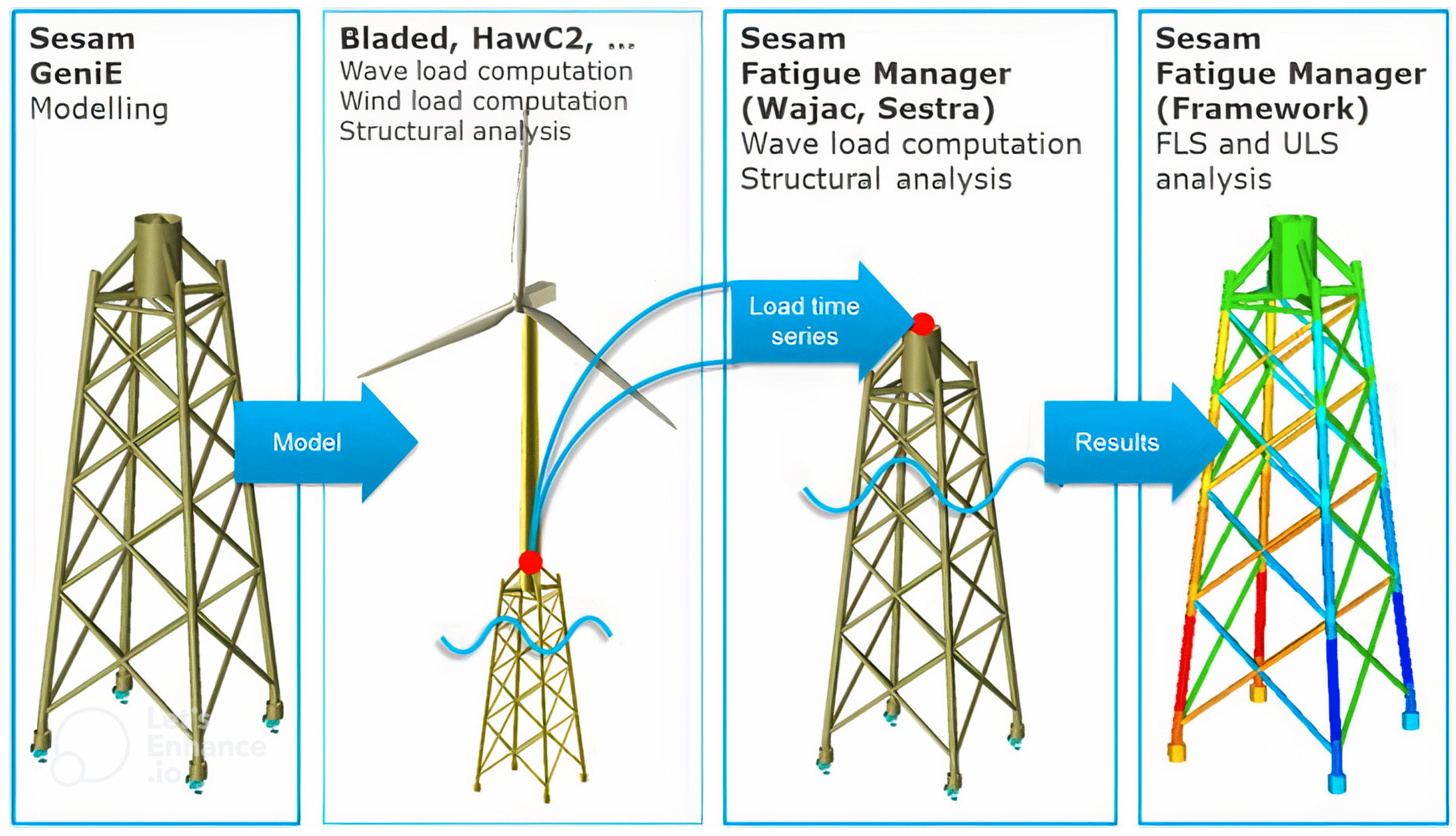
  • Integrated analysis: This method involves modelling in Sesam, which is then imported and coupled to a wind turbine model in a tool like Bladed. After computing the resulting forces and loads for each component, the data are translated into Sesam for postprocessing, which includes fatigue and ultimate analysis, as shown in Figure 4.
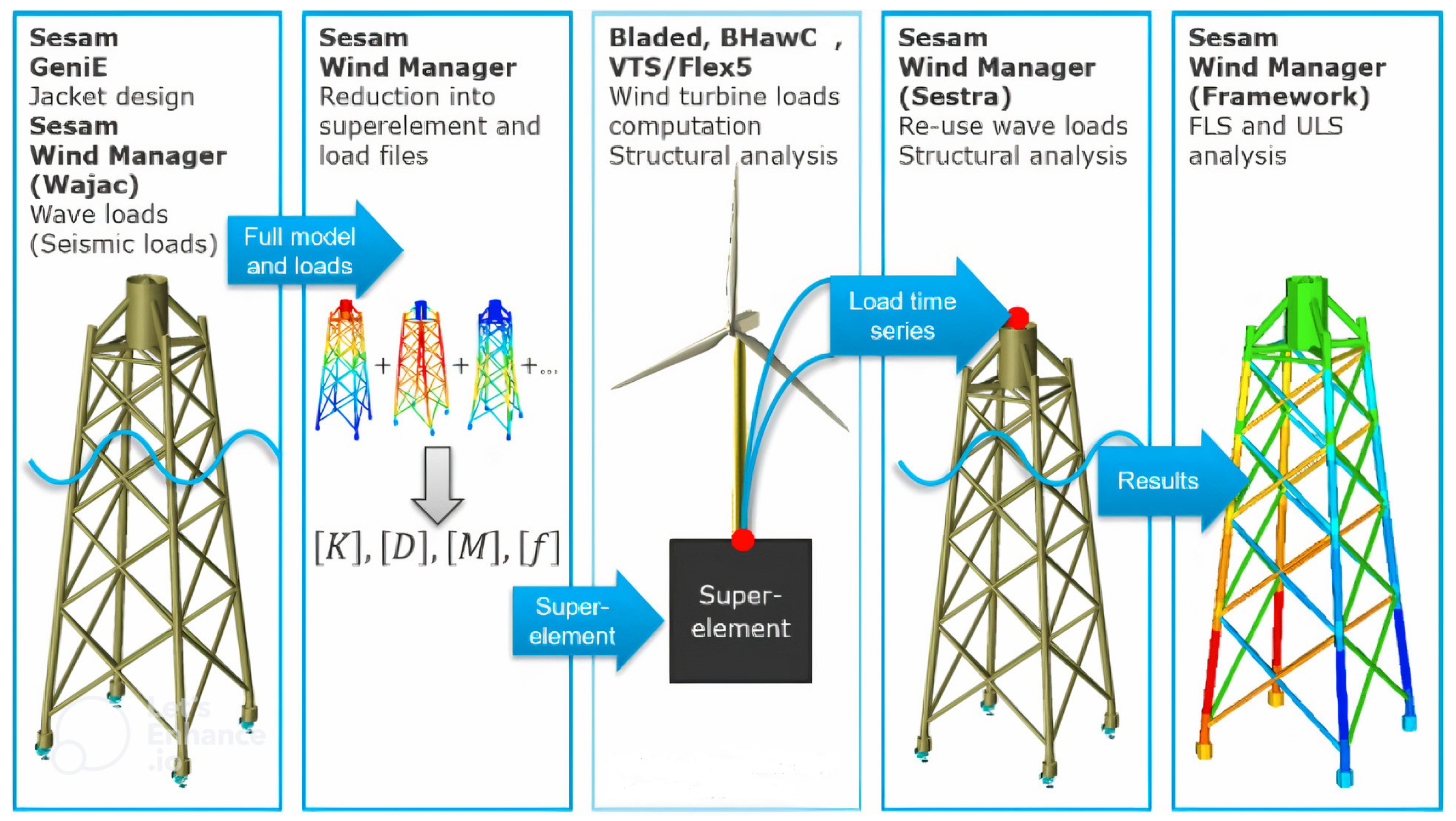
  • Super-element and sequential analysis : Wave loads are generated in Sesam using the super-element technique. The wind turbine is modelled in a separate third-party software package, and the wind turbine loads are extracted at an interface point. Sesam may use wind turbine loads from any third-party wind turbine tool, where converters for Bladed, BHAWC, and HAWC2 are available. These loads are then incorporated into the Sesam analysis, followed by a dynamic analysis to determine the structure’s stress time histories. Following that, the stresses are postprocessed to meet fatigue limit state and/or ultimate limit state criteria [109]. A super-element approach is employed in a special type of sequential analysis, in which the model and wave loads are converted into a super-element file and wave load files from Sesam, which are then used by the turbine load calculation tool. This is mostly used in conjunction with Bladed and Siemens Gamesa’s BHAWC. These approaches are illustrated in Figure 5 and Figure 6.

6.12. UTWind

UTWind is a rotor–floater–mooring coupled analysis code established by the University of Tokyo for a variety of floater platforms used in FOWTs [112,113,114,115]. In a weak coupling algorithm, the coupled motions of the rotor–floater–mooring system are addressed in the time-domain using the Newmark beta time integration approach.
The beam elements are utilized to model the blades and floaters as a frame structure, while the lumped-mass model is used to represent the mooring system. The rotor motion is defined in a fixed rotating coordinate system with Coriolis and centrifugal forces taken into account.
The aerodynamic loads are estimated using the BEM approach, which accounts for tip and hub loss as well as changes in air inflow velocity due to floater motion [112,113]. t’ Hooft’s method [116] has been used in the code for computing the hydrodynamic loads [112,113,114,115]. However, for the cylindrical structure elements, the modified Morison equation is utilized for hydrodynamic load calculation [112].

7. Discussion

The investigation into FOWTs necessitates a comprehensive exploration of aerodynamic, structural, hydrodynamic, and mooring aspects. This intricate analysis aims to unravel the interconnected dynamics of aerodynamic forces, structural responses, hydrodynamic behaviors, and mooring system intricacies. As FOWTs stand at the forefront of renewable energy advancements, understanding the synergies and challenges within each domain becomes imperative. This multifaceted examination is pivotal for optimizing design, enhancing reliability, and maximizing the performance of FOWTs. In the following discussion, we dissect the realms of aerodynamics, structure, hydrodynamics, and mooring systems, providing valuable insights that collectively contribute to the ongoing evolution of floating offshore wind technology.
Aerodynamic loads are conventionally assessed using the BEM theory, a method combining momentum and blade element theories. Despite its efficiency in computation, BEM theory relies on assumptions such as rotor discretization as annuli, neglecting of root and tip losses, and consideration of steady flow. To enhance accuracy, correction models are introduced, addressing issues like hub and root losses. The BEM theory, while widely employed, requires further investigation, especially for FOWTs facing complex inflow wind conditions due to platform motions. Alternatives like the GDW model offer advantages by inherently including dynamic wake effects and addressing issues of the BEM model. However, instabilities at low wind speeds warrant a judicious choice between BEM and GDW. CFD models, though challenging due to complexity, provide detailed flow field information. Actuator models and direct modelling are two approaches within CFD, each with its advantages, but the latter excels in capturing intricate flow details.
The structural integrity of wind turbine blades is modelled using either the 3D FEM or the 1D Equilibrium Beam Model (EBM). While 3D FEM offers precise deformation predictions through shell or solid elements, it incurs high computational costs. The widely used FEM approach discretizes structures into finite elements, applied predominantly to slender bodies using beam theory. The 1D EBM efficiently models wind turbine blade structures, categorized into linear and nonlinear beam models. Nonlinear models, such as the Geometrically Exact Beam Theory (GEBT), address geometrically nonlinear characteristics, ensuring suitability for analyzing large deformations. Discretization methods like modal approach, multibody dynamics (MBD), and 1D FEM provide options, each with its own trade-offs. The choice between them depends on computational efficiency, accuracy, and the specific analysis requirements.
For hydrodynamic performance, FOWTs commonly utilize the ME, the PF method, and CFD. While ME lacks considerations for floating platform effects on incident wave fields, CFD captures more physical flow mechanisms, offering increased accuracy. Hydrodynamic modelling ranges from linear to nonlinear, with nonlinear methods proving more accurate but computationally expensive. Consideration of nonlinear effects is crucial for accurate modelling and involves factors like incoming wave characteristics and the hydrodynamic body. Various methods, including the Froude–Krylov force, quadratic transfer function (QTF), and Newman’s approximation, address nonlinear loads. The choice between frequency-domain and time-domain modelling depends on the trade-off between computational efficiency and accuracy, with the Cummins equation providing a framework for the latter [117].
Mooring systems are analyzed using static, quasi-static, and dynamic methods. Static methods consider constant loads, while quasi-static methods assume uniform and linear motion between static positions. Dynamic methods, including lumped-mass models, FEM, and finite difference (FD) models, account for large displacements and inertial effects. Lumped-mass models are computationally simpler, assuming that mooring lines consist of masses connected by springs. FEM and FD models offer high-fidelity solutions by discretizing the mooring line into small elements. The choice between them depends on computational requirements. Other methods, such as the finite segment scheme, have also been employed for mooring line discretization.
Table 1 gives a thorough summary of the underlying numerical methods for the main FOWT modules for the engineering tools presented in this study.
For the design process of an FOWT prototype at an earlier stage, a variety of numerical approaches and software programs are available. A novel design is often produced as a numerical model, which is subsequently tested in a lab setting at model scales. Designers of FOWT technology may, however, be trying to employ high-fidelity numerical tools in an effort to lessen reliance on expensive and time-consuming physical testing as well as reduce the uncertainty of simpler numerical models. Lower-fidelity models, on the other hand, might be important when taking into account lifetime operations, maintenance issues, and control. In general, accuracy and fidelity as well as computational effectiveness at an acceptable performance level in the phenomena of interest are the major significant factors that differentiate one numerical modelling approach from another. Here, accuracy is defined as the difference between predicted values and observed physical responses. However, fidelity reflects how much the underlying physics or phenomena of interest have been simplified by the numerical model, giving a level of assurance that the accuracy predicted during simulations is indeed attained. On the other hand, the time it takes for a simulation to finish using normal computer hardware is a common way to assess computational efficiency [4].
Overall, numerical models may be divided into three categories [4,117]: low-fidelity, mid-fidelity, and high-fidelity. As fidelity increases, larger computational resources are demanded, thus leading to a reduction in computational efficiency. For sizing analysis and optimization at the first stage of FOWT design, low-fidelity models are typically employed. In order to analyze loads on FOWTs under operational and extreme scenarios, following the original design stage, mid-fidelity models or engineering-level tools are utilized. In the last stages of design, high-fidelity models are frequently utilized for thorough studies, particularly to precisely determine stresses on the structure. Figure 7 outlines the computational efficiency of various modelling approaches commonly applied to FOWTs.
A low-fidelity model involves basic descriptions using a damping matrix for aerodynamic loads, Morison’s equation for hydrodynamics, and a linear stiffness matrix for mooring and structure [117]. However, Morison’s equation is best suited for slender structures, and most FOWT support structures do not fall into this category [117]. Still, there are a few instances where Morison’s equation has been used for FOWT hydrodynamic loads, especially for structures like spar buoys that can be treated as slender cylinders [123]. Another approach is representing the structure as a rigid body, overlooking its flexible behavior. For more accuracy, models like BEMT or GDW are employed for aerodynamics, potential theory for hydrodynamic loads, quasi-static and lumped-mass models for mooring, and modal and multibody approaches for structural dynamics.
Higher-fidelity numerical options are typically chosen for time-domain models, while lower-fidelity models are associated with frequency-domain models. In optimization studies, the goal is to keep computations as minimal as possible. While models like FWV, FE, and CFD provide high fidelity to the real system, they are computationally intensive and not ideal for optimization studies [124]. State-of-the-art numerical tools strike a balance by offering reasonable agreement for normal operating conditions with higher computational efficiency compared to high-fidelity tools. They might introduce modifications to better capture physics related to extreme events, unsteady aerodynamics, substructure flexibility, and viscous hydrodynamic damping. These advanced tools are comprehensive, consider all relevant physics, and find application in preliminary design. However, their use in optimization studies is limited due to their time-domain nature and computational demands. When it comes to the conceptual design of a floating platform, several design parameters come into play, and a frequency-domain model is often deemed the most suitable [117,124].

8. Conclusions

In conclusion, this survey thoroughly examines tools used for simulating floating offshore wind turbines (FOWTs). These tools include both commercial software originally designed for the oil and gas industry, and academic codes. Notable options like OrcaFlex and OpenFAST, known for their reliability, have been extensively tested in experiments. These tools stand out for their efficiency and accuracy. Efficiency means how well a tool can run simulations in a reasonable time with standard computers. However, due to some limitations in the models, there may be small differences compared to real-world tests. Accuracy, on the other hand, refers to how well the tool replicates the real physical phenomena. It is a crucial factor in choosing the right simulation tool.
The survey categorizes simulation methods into two main types: frequency- and time-domain. Time-domain methods are used in later design stages and for comprehensive dynamic analyses. Frequency-domain methods are primarily used in early design phases and for sizing FOWTs. Time-domain models provide more detailed and accurate results, while frequency-domain techniques offer a quicker but less detailed analysis.
In summary, this comprehensive survey of simulation tools for FOWTs has provided valuable insights into their performance across crucial domains: structural dynamics, hydrodynamics, aerodynamics, and mooring. In the structural domain, various approaches have been explored, including modal-based codes, finite element methods, and multibody techniques. These different techniques offer unique insights into dynamic responses, especially in higher-frequency ranges. Hydrodynamic simulations examine how waves interact with floating structures, considering incident and outgoing waves, added mass effects, damping, and viscous forces. The survey thoroughly explains two primary techniques—potential flow theory and Morison’s equation—showing their roles based on the structure’s size and water flow conditions. These simulations form the foundation for understanding hydrodynamic loads on FOWTs. Simulating the mooring system, which is crucial in offshore wind turbine dynamics, involves using either quasi-static or dynamic methods. This includes various models, from simplified representations to complex equations. The choice of model depends on specific simulation requirements. Aerodynamic modelling mainly relies on the blade-element-momentum-theory-based model across simulation tools. These models incorporate adjustments and dynamic elements to improve accuracy in load predictions by accounting for delays in induced velocities and capturing complex flow behavior.

9. Future Work

Considerable efforts are being directed towards exploring the intricacies of fully coupled aerohydroelastics in FOWTs. This represents a complex and challenging task for high-fidelity simulations, integral for understanding aerohydroelastic behaviors. However, there is a notable scarcity of CFD research on the aerohydroelastic performance of FOWTs, resulting in a lack of systematic examination and analysis of their aeroelastic characteristics. It is imperative to shift some of these efforts towards understanding the aerohydroelastic performance of FOWTs, especially concerning large-scale blades and severe sea conditions.
In CFD-related simulations, two predominant approaches exist: actuator models and direct modelling [125]. Actuator models, categorized as actuator disk (AD), actuator line (AL), and actuator surface (AS), offer computational advantages but depend heavily on airfoil data. In contrast, direct blade-resolved modelling excels in capturing intricate flow details on blade surfaces without prior airfoil data requirements, demonstrating excellent potential for designing and developing novel wind turbine blades [126]. Hybrid models, combining actuator disk models with CFD, have been employed to enhance computational efficiency, especially in extensive domains like wind farms. The actuator disk model reasonably approximates the far wake region, while the near wake region benefits from a high-fidelity CFD model [125,126]. In this regard, the 3D FEM integrated with blade-resolved modelling for aerodynamics stands out as the highest-fidelity aeroelastic analysis method, providing detailed stress and strain information for blade structures. However, attention needs to be given to challenges such as mismatches between fluid and structural domain meshes, mesh updates due to blade deformations, and computational costs [124]. Alternatively, the 1D EBM incorporated with blade-resolved modelling offers a compromise to save computational resources. Furthermore, replacing blade-resolved modelling with actuator line (AL) models and combining them with 1D EBM, known as the elastic actuator line (EAL) aeroelastic framework, emerges as the most suitable choice for cost-effective CFD-related simulations of aerohydroelastic behaviors in FOWTs [124]. In the selection of aerodynamic and structural models for constructing the aerohydroelastic framework of FOWTs, achieving desired results within affordable computational costs remains the primary consideration.
The continuous progress of FOWTs towards larger scales introduces more complex atmospheric inflow conditions over the wind turbine rotor. Wind shear, characterized by increasing wind speed with height, is a distinct feature of atmospheric inflow [124]. While some high-fidelity CFD simulations account for wind shear, it is often oversimplified, neglecting the turbulence characteristics of atmospheric inflow that are closely linked to fatigue loads and structural failure of wind turbines. Large-scale atmospheric turbulence, which contributes to wake meandering effects, is frequently absent in these simulations, leading to significant lateral oscillations with noteworthy impacts on downstream wind turbines’ inflow conditions [124].
In reality, FOWTs are deployed as floating wind farms for commercial operation, constrained by sea area and mooring cables. Downstream FOWTs inevitably operate in the wakes of upstream turbines, which are known as wake effects, potentially reducing power outputs and increasing fatigue loads. Additionally, floating wind farms experience more power deficit due to low turbulence intensity in high-quality wind resources compared to onshore wind farms. Therefore, investigating the physical mechanisms underlying wake interactions in multi-FOWT scenarios is essential to mitigate power deficits and reduce fatigue loads in floating wind farms.

Author Contributions

Conceptualization, S.F.; Methodology, S.F.; Resources, S.F.; Data Curation, S.F.; Writing—original draft preparation, S.F.; Writing—review and editing, S.F., F.F.A. and R.G.L.; Visualization, S.F.; Supervision, F.F.A. and R.G.L.; Project Administration, F.F.A. and R.G.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) under grant numbers RGPIN-2015-06335 and RGPIN-2019-07104.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Haghshenas, A.; Hasan, A.; Osen, O.; Mikalsen, E.T. Predictive digital twin for offshore wind farms. Energy Inform. 2023, 6, 1. [Google Scholar] [CrossRef]
  2. Mei, D. A Race to the Top: China 2023; Technical Report; Global Energy Monitor: California, CA, USA, 2023. [Google Scholar]
  3. Christopher, T.R.; Goldstein, M.; Williams, M.; Carter, A. The Road to 30 Gigawatts: Key Actions to Scale an Offshore Wind Industry in the United States; Technical Report; Center for American Progress: Washington, DC, USA, 2022. [Google Scholar]
  4. Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
  5. Robertson, A.; Jonkman, J.; Vorpahl, F.; Popko, W.; Qvist, J.; Frøyd, L.; Chen, X.; Azcona, J.; Uzunoglu, E.; Soares, C.G. Offshore code comparison collaboration continuation within IEA wind task 30: Phase II results regarding a floating semisubmersible wind system. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, San Francisco, CA, USA, 8–13 June 2014; Volume 45547, p. V09BT09A012. [Google Scholar]
  6. Sayed, M.; Klein, L.; Lutz, T.; Krämer, E. The impact of the aerodynamic model fidelity on the aeroelastic response of a multi-megawatt wind turbine. Renew. Energy 2019, 140, 304–318. [Google Scholar] [CrossRef]
  7. Riziotis, V.A.; Voutsinas, S.G.; Politis, E.S.; Chaviaropoulos, P.K.; Hansen, A.M.; Madsen, H.A.; Rasmussen, F. Identification of structural non-linearities due to large deflections on a 5 MW wind turbine blade. In Proceedings of the Scientific Proceedings, Brussels, Belgium, 22–24 September 2008; pp. 9–14. [Google Scholar]
  8. Jeong, M.S.; Yoo, S.J.; Lee, I. Aeroelastic Analysis for Large Wind Turbine Rotor Blades. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011. [CrossRef]. [Google Scholar]
  9. Wang, L.; Liu, X.; Kolios, A. State of the art in the aeroelasticity of wind turbine blades: Aeroelastic modelling. Renew. Sustain. Energy Rev. 2016, 64, 195–210. [Google Scholar] [CrossRef]
  10. Jonkman, J.M.; Musial, W. Offshore Code Comparison Collaboration (OC3) for IEA Wind Task 23 Offshore Wind Technology and Deployment; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
  11. Popko, W.; Vorpahl, F.; Zuga, A.; Kohlmeier, M.; Jonkman, J.; Robertson, A.; Larsen, T.J.; Yde, A.; Sætertrø, K.; Okstad, K.M.; et al. Offshore Code Comparison Collaboration Continuation (OC4), Phase 1—Results of Coupled Simulations of an Offshore Wind Turbine with Jacket Support Structure. In ISOPE International Ocean and Polar Engineering Conference; ISOPE: Rhodes, Greece, 2012. [Google Scholar]
  12. Robertson, A.; Jonkman, J.M.; Musial, W.; Vorphal, F.; Popko, W.; et al. Offshore Code Comparison Collaboration, Continuation: Phase II Results of a Floating Semisubmersible Wind System. In Proceedings of the Roceedings, EWEA Offshore, Frankfurt, Germany, 19–21 November 2013. [Google Scholar]
  13. Robertson, A.N.; Wendt, F.F.; Jonkman, J.M.; Popko, W.; Vorpahl, F.; Stansberg, C.T.; Bachynski, E.E.; Bayati, I.; Beyer, F.; de Vaal, J.B.; et al. OC5 Project Phase I: Validation of Hydrodynamic Loading on a Fixed Cylinder. In ISOPE International Ocean and Polar Engineering Conference; ISOPE: Mountain View, CA, USA, 2015. [Google Scholar]
  14. Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 Project Phase II: Validation of Global Loads of the DeepCwind Floating Semisubmersible Wind Turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
  15. Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Borg, M.; Bredmose, H.; Schlutter, F.; Qvist, J.; Bergua, R.; Harries, R.; et al. OC5 Project Phase Ib: Validation of Hydrodynamic Loading on a Fixed, Flexible Cylinder for Offshore Wind Applications. Energy Procedia 2016, 94, 82–101. [Google Scholar] [CrossRef]
  16. Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcón, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B.; et al. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. J. Phys. Conf. Ser. 2020, 1618, 032033. [Google Scholar] [CrossRef]
  17. Bergua, R.; Robertson, A.; Jonkman, J.; Branlard, E.; Fontanella, A.; Belloli, M.; Schito, P.; Zasso, A.; Persico, G.; Sanvito, A.; et al. OC6 project Phase III: Validation of the aerodynamic loading on a wind turbine rotor undergoing large motion caused by a floating support structure. Wind Energy Sci. 2023, 8, 465–485. [Google Scholar] [CrossRef]
  18. Davidson, J.; Ringwood, J. Mathematical Modelling of Mooring Systems for Wave Energy Converters—A Review. Energies 2017, 10, 666. [Google Scholar] [CrossRef]
  19. Masciola, M.D.; Jonkman, J.M.; Robertson, A. Implementation of a Multisegmented, Quasi-Static Cable Model. In Proceedings of the Twenty-Third (2013) International Offshore and Polar Engineering Conferenc, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
  20. Masciola, M.; Jonkman, J.; Robertson, A. Extending the Capabilities of the Mooring Analysis Program: A Survey of Dynamic Mooring Line Theories for Integration Into FAST. In Proceedings of the Volume 9A: Ocean Renewable Energy, San Francisco, CA, USA, 8–13 June 2014. [CrossRef]. [Google Scholar]
  21. Walton, T.S.; Polachek, H. Calculation of transient motion of submerged cables. Math. Comput. 1960, 14, 27–46. [Google Scholar] [CrossRef]
  22. Leonard, J.W.; Nath, J.H. Comparison of finite element and lumped parameter methods for oceanic cables. Eng. Struct. 1981, 3, 153–167. [Google Scholar] [CrossRef]
  23. Winget, J.; Huston, R. Cable dynamics—A finite segment approach. Comput. Struct. 1976, 6, 475–480. [Google Scholar] [CrossRef]
  24. Kamman, J.W.; Huston, R.L. Modelling of submerged cable dynamics. Comput. Struct. 1985, 20, 623–629. [Google Scholar] [CrossRef]
  25. Nichol, T.; DuBuque, G.; Fabien, B. Dynamic modelling of compliant-moored submerged systems with applications to marine energy converters. In Proceedings of the 2nd Marine Energy Technology Symposium (METS2014), Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
  26. Garrett, D.L. Coupled Analysis of Floating Production Systems. Ocean Eng. 2005, 32, 802–816. [Google Scholar] [CrossRef]
  27. Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
  28. Jonkman, J.M.; Wright, A.D.; Hayman, G.J.; Robertson, A.N. Full-System Linearization for Floating Offshore Wind Turbines in OpenFAST. In Proceedings of the ASME 2018 1st International Offshore Wind Technical Conference, San Francisco, CA, USA, 4–7 November 2018. [CrossRef]. [Google Scholar]
  29. Jonkman, J.M. Dynamics of offshore floating wind turbines-model development and verification. Wind Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
  30. Wang, Q.; Sprague, M.A.; Jonkman, J.; Johnson, N.; Jonkman, B. BeamDyn: A high-fidelity wind turbine blade solver in the FAST modular framework. Wind Energy 2017, 20, 1439–1462. [Google Scholar] [CrossRef]
  31. Ning, A.; Hayman, G.; Damiani, R.; Jonkman, J.M. Development and Validation of a New Blade Element Momentum Skewed-Wake Model within AeroDyn. In Proceedings of the 33rd Wind Energy Symposium, Kissimmee, FL, USA, 5–9 January 2015. [CrossRef]. [Google Scholar]
  32. Wendt, F.F.; Robertson, A.; Jonkman, J.M.; Hayman, G. Verification of New Floating Capabilities in FAST v8. In Proceedings of the 33rd Wind Energy Symposium, Kissimmee, FL, USA, 5–9 January 2015. [CrossRef]. [Google Scholar]
  33. Branlard, E.S.P. Flexible multibody dynamics using joint coordinates and the Rayleigh-Ritz approximation: The general framework behind and beyond Flex. Wind Energy 2019, 22, 877–893. [Google Scholar] [CrossRef]
  34. Saverin, J.; Peukert, J.; Marten, D.; Pechlivanoglou, G.; Paschereit, C.O.; Greenblatt, D. Aeroelastic simulation of multi-MW wind turbines using a free vortex model coupled to a geometrically exact beam model. J. Phys. Conf. Ser. 2016, 753, 082015. [Google Scholar] [CrossRef]
  35. Dose, B.; Rahimi, H.; Stoevesandt, B.; Peinke, J.; Schepers, J. On the effect of blade deformations on the aerodynamic performance of wind turbine rotors subjected to yawed inflow. J. Phys. Conf. Ser. 2018, 1037, 022030. [Google Scholar] [CrossRef]
  36. Qu, X.; Li, Y.; Tang, Y.; Chai, W.; Gao, Z. Comparative study of short-term extreme responses and fatigue damages of a floating wind turbine using two different blade models. Appl. Ocean Res. 2020, 97, 102088. [Google Scholar] [CrossRef]
  37. Wang, Q.; Sprague, M.A.; Jonkman, J.M. Nonlinear Legendre Spectral Finite Elements for Wind Turbine Blade Dynamics. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014. [CrossRef]. [Google Scholar]
  38. Wang, Q.; Sprague, M.A.; Jonkman, J.M. Partitioned nonlinear structural analysis of wind turbines using BeamDyn. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016. [CrossRef]. [Google Scholar]
  39. Jonkman, J.M.; Jonkman, B.J. FAST modularization framework for wind turbine simulation: Full-system linearization. J. Phys. Conf. Ser. 2016, 753, 082010. [Google Scholar] [CrossRef]
  40. Wang, Q.; Jonkman, J.M.; Sprague, M.; Jonkman, B. BeamDyn User’s Guide and Theory Manual; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2016. [Google Scholar]
  41. Damiani, R.R.; Hayman, G. The Unsteady Aerodynamics Module for FAST8; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [Google Scholar]
  42. Karimirad, M.; Bachynski, E.E. Sensitivity Analysis of Limited Actuation for Real-time Hybrid Model Testing of 5 MW Bottom-fixed Offshore Wind Turbine. Energy Procedia 2017, 137, 14–25. [Google Scholar] [CrossRef]
  43. Yang, Y.; Bashir, M.; Michailides, C.; Li, C.; Wang, J. Development and application of an aero-hydro-servo-elastic coupling framework for analysis of floating offshore wind turbines. Renew. Energy 2020, 161, 606–625. [Google Scholar] [CrossRef]
  44. Yang, Y.; Bashir, M.; Wang, J.; Yu, J.; Li, C. Performance evaluation of an integrated floating energy system based on coupled analysis. Energy Convers. Manag. 2020, 223, 113308. [Google Scholar] [CrossRef]
  45. Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A. Validation of Hydrodynamic Load Models Using CFD for the OC4-DeepCwind Semisubmersible. In Volume 9: Ocean Renewable Energy; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
  46. Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts: April 2009; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2010. [Google Scholar]
  47. Guntur, S.; Jonkman, J.M.; Jonkman, B.; Wang, Q.; Sprague, M.A.; Hind, M.; Sievers, R.; Schreck, S.J. FAST v8 Verification and Validation for a Megawatt-Scale Wind Turbine with Aeroelastically Tailored Blades: Preprint. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology Forum and Exposition (SciTech 2016), San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
  48. Jonkman, B.J. Turbsim User’s Guide: Version 1.50; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
  49. Damiani, R.; Jonkman, J.; Hayman, G. SubDyn User’s Guide and Theory Manual; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015. [Google Scholar]
  50. Song, H.; Damiani, R.; Robertson, A.N.; Jonkman, J.M. New Structural-Dynamics Module for Offshore Multimember Substructures within the Wind Turbine Computer-Aided Engineering Tool FAST: Preprint. In Proceedings of the 23rd International Ocean, Offshore and Polar Engineering Conference ISOPE 2013, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
  51. Andersen, M.T.; Wendt, F.F.; Robertson, A.; Jonkman, J.; Hall, M. Verification and Validation of Multisegmented Mooring Capabilities in FAST v8. In Proceedings of the Twenty-Sixth (2016) International Ocean and Polar Engineering Conference (ISOPE), Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
  52. Masciola, M.D. MAP++ Documentation. NREL: Golden, CO, USA, 2018.
  53. Wendt, F.; Robertson, A.; Jonkman, J.; Andersen, M.T. Verification and Validation of the New Dynamic Mooring Modules Available in FAST v8: Preprint. In Proceedings of the Twenty-Sixth (2016) International Ocean and Polar Engineering Conference (ISOPE), Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
  54. Hall, M. Efficient Modelling of Seabed Friction and Multi-Floater Mooring Systems in MoorDyn. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
  55. Pribadi, A.B.K.; Donatini, L.; Lataire, E. Numerical Modelling of a Mussel Line System by Means of Lumped-Mass Approach. J. Mar. Sci. Eng. 2019, 7, 309. [Google Scholar] [CrossRef]
  56. Hall, M. MoorDyn User’s Guide; Technical Report; University of Maine: Orono, ME, USA, 2015. [Google Scholar]
  57. Bae, Y. Development of a Dynamic Mooring Module Feam for Fast v8; Technical Report; Texas A and M University: College Station, TX, USA, 2014. [Google Scholar]
  58. Min, H. Numerical Simulation of Floating Offshore Wind Turbine Dynamic Responses with Experimental Comparison. Doctoral Dissertation, Texas A and M University, College Station, TX, USA, 2018. [Google Scholar]
  59. Andersen, M.T. Floating Foundations for Offshore Wind Turbines. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2016. [Google Scholar]
  60. Yu, B.; Karr, D.G.; Song, H.; Sirnivas, S. A Surface Ice Module for Wind Turbine Dynamic Response Simulation Using FAST. J. Offshore Mech. Arct. Eng. 2016, 138, 051501. [Google Scholar] [CrossRef]
  61. Karr, D.G.; Yu, B.; Sirnivas, S. Bottom Fixed Platform Dynamics Models Assessing Surface Ice Interactions for Transitional Depth Structures in the Great Lakes: FAST8—IceDyn; Technical Report; Golden Field Office: Golden, CO, USA, 2015. [Google Scholar]
  62. Song, Z.; Hu, Y.; Cheng, Y.; Wang, H. Dynamic Ice Load Alleviation of Offshore Wind Turbine via Optimized Pitch Control. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar]
  63. Johnson, N.; Jonkman, J.; Wright, A.; Hayman, G.; Robertson, A. Verification of Floating Offshore Wind Linearization Functionality in OpenFAST. J. Phys. Conf. Ser. 2019, 1356, 012022. [Google Scholar] [CrossRef]
  64. Arramounet, V.; de Winter, C.; Maljaars, N.; Girardin, S.; Robic, H. Development of coupling module between BHawC aeroelastic software and OrcaFlex for coupled dynamic analysis of floating wind turbines. J. Phys. Conf. Ser. 2019, 1356, 012007. [Google Scholar] [CrossRef]
  65. Masciola, M.; Robertson, A.; Jonkman, J.; Coulling, A.; Goupee, A. Assessment of the Importance of Mooring Dynamics on the Global Response of the DeepCwind Floating Semisubmersible Offshore Wind Turbine. In Proceedings of the Twenty-Third International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
  66. Tran, T.T.; Kim, D.H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind. Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
  67. Masciola, M.; Robertson, A.; Jonkman, J.; Driscoll, F. Investigation of a FAST-OrcaFlex Coupling Module for Integrating Turbine and Mooring Dynamics of Offshore Floating Wind Turbines: Preprint. In Proceedings of the 2011 International Conference on Offshore Wind Energy and Ocean Energy, Beijing, China, 31 October–2 November 2011. [Google Scholar]
  68. Ross, A. Orcina Project 1405 Wind Turbine Validation Report; Technical Report; Orcina Ltd.: Ulverston, UK, 2018. [Google Scholar]
  69. Azcona, J.; Munduate, X.; González, L.; Nygaard, T.A. Experimental validation of a dynamic mooring lines code with tension and motion measurements of a submerged chain. Ocean Eng. 2017, 129, 415–427. [Google Scholar] [CrossRef]
  70. Azcona, J.; Palacio, D.; Munduate, X.; González, L.; Nygaard, T.A. Impact of mooring lines dynamics on the fatigue and ultimate loads of three offshore floating wind turbines computed with IEC 61400-3 guideline. Wind Energy 2017, 20, 797–813. [Google Scholar] [CrossRef]
  71. Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; Technical Report; University of Colorado at Boulder: Boulder, CO, USA, 2007. [Google Scholar]
  72. Nygaard, T.A.; De Vaal, J.; Pierella, F.; Oggiano, L.; Stenbro, R. Development, Verification and Validation of 3DFloat; Aero-servo-hydro-elastic Computations of Offshore Structures. Energy Procedia 2016, 94, 425–433. [Google Scholar] [CrossRef]
  73. Armendariz, A.J.; Munduate, X.; Nygaard, T.A.; Hoyos, M.D. Development of OPASS Code for Dynamic Simulation Mooring Lines in Contact with Seabed; In Proceedings of the EWEA Offshore 2011 Conference Proceedings, Amsterdam, Netherland. 29 November – 1 December 2011; pp. 1–9.
  74. Stewart, G. ; Lackner, Matthew Robertson, A.; Jonkman, J.; Goupee, A. Calibration and Validation of a FAST Floating Wind Turbine Model of the DeepCwind Scaled Tension-Leg Platform: Preprint. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17-22 June 2012.
  75. Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2014. [Google Scholar]
  76. Hassan, G. Bladed Theory Manual Version 4.0; Technical Report; DNV Services UK Limited: Bristol, UK, 2010. [Google Scholar]
  77. Craig, R., Jr. Coupling of substructures for dynamic analyses—An overview. In Proceedings of the 41st Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000. [CrossRef]. [Google Scholar]
  78. Beardsell, A.; Collier, W.; Han, T. Effect of linear and non-linear blade modelling techniques on simulated fatigue and extreme loads using Bladed. J. Phys. Conf. Ser. 2016, 753, 042002. [Google Scholar] [CrossRef]
  79. Collier, W.; Milian Sanz, J. Comparison of linear and non-linear blade model predictions in Bladed to measurement data from GE 6MW wind turbine. J. Phys. Conf. Ser. 2016, 753, 082004. [Google Scholar] [CrossRef]
  80. Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the User’s Manual; Technical Report; Risø National Laboratory, Technical University of Denmark: Roskilde, Denmark, 2007. [Google Scholar]
  81. Bellew, S.; Yde, A.; Verelst, D.R. Application of the Aero-Hydro-Elastic Model, HAWC2-WAMIT, to Offshore Data from Floating Power Plants Hybrid Wind- and Wave-Energy Test Platform, P37. In Proceedings of the 5th International Conference on Ocean Energy (ICOE), Halifax, NS, Canada, 4–6 November 2014. [Google Scholar]
  82. Pavese, C.; Wang, Q.; Kim, T.; Jonkman, J.; Sprague, M.A. HAWC2 and BeamDyn: Comparison Between Beam Structural Models for Aero-Servo-Elastic Frameworks. In Proceedings of the European Wind Energy Association Annual Conference and Exhibition 2015 (EWEA 2015), Paris, France, 17–20 November 2015. [Google Scholar]
  83. Gueydon, S.; Lindenburg, K.; Savenije, F. Coupling of Two Tools for the Simulation of Floating Wind Turbines. In Proceedings of the Volume 8: Ocean Renewable Energy, Melbourne, Australia, 11–16 June 2013. [CrossRef]. [Google Scholar]
  84. Naciri, M.; Waals, O.; de Wilde, J. Time Domain Simulations of Side-by-Side Moored Vessels: Lessons Learnt From a Benchmark Test. In Volume 1: Offshore Technology; Special Symposium on Ocean Measurements and Their Influence on Design; ASMEDC: Stamford, CT, USA, 2007; pp. 801–811. [Google Scholar]
  85. de Wilde, J.; van Dijk, A.; van den Berg, J.; Dekker, J. Direct Time Domain Downtime Assessment For LNG Operations Using Computer Cluster. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
  86. Serraris, J.J. Time Domain Analysis for DP Simulations. Int. Conf. Offshore Mech. Arct. Eng. 2009, 43413, 595–605. [Google Scholar]
  87. Gueydon, S.; Weller, S. Study of a Floating Foundation for Wind Turbines. J. Offshore Mech. Arct. Eng. 2013, 135, 031903. [Google Scholar] [CrossRef]
  88. Gueydon, S.; Xu, W. Floating wind turbine motion assessment. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–10. [Google Scholar]
  89. Lindenburg, C. Comparison of Phatas Versions and the Wind turbine Module; Technical Report; ECN: Petten, The Netherlands, 2011. [Google Scholar]
  90. Lindenburg, C. PHATAS Release NOV-2003 and APR-2005 User’s Manual: Program for Horizontal Axis Wind Turbine Analysis and Simulation; Technical Report; ECN: Petten, The Netherlands, 2005. [Google Scholar]
  91. Huijs, F.; de Bruijn, R.; Savenije, F. Concept Design Verification of a Semi-submersible Floating Wind Turbine Using Coupled Simulations. Energy Procedia 2014, 53, 2–12. [Google Scholar] [CrossRef]
  92. Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
  93. Myhr, A.; Nygaard, T.A. Comparison of Experimental Results and Computations for Tension-Leg-Buoy Offshore Wind Turbines. J. Ocean Wind Energy 2015, 2, 12–20. [Google Scholar]
  94. Azcona, J.; Bouchotrouch, F.; González, M.; Garciandía, J.; Munduate, X.; Kelberlau, F.; Nygaard, T.A. Aerodynamic Thrust Modelling in Wave Tank Tests of Offshore Floating Wind Turbines Using a Ducted Fan. J. Phys. Conf. Ser. 2014, 524, 012089. [Google Scholar] [CrossRef]
  95. Pai, P. Highly Flexible Structures: Modeling, Computation, and Experimentation; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
  96. Chaplin, J.R. Developments of stream-function wave theory. Coast. Eng. 1979, 3, 179–205. [Google Scholar] [CrossRef]
  97. Lee, C.H. WAMIT Theory Manual. Technical Report; Massachusetts Institute of Technology, Cambridge, Massachusetts, 1995.
  98. Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]
  99. Det Norske Veritaswadam. SESAM User Manual Developed and Marketed; Technical Report; DNV: Bærum, Norway, 2010. [Google Scholar]
  100. Le Cunff, C.; Heurtier, J.M.; Piriou, L.; Berhault, C.; Perdrizet, T.; Teixeira, D.; Ferrer, G.; Gilloteaux, J.C. Fully Coupled Floating Wind Turbine Simulator Based on Nonlinear Finite Element Method: Part I—Methodology. In Proceedings of the Volume 8: Ocean Renewable Energy, Melbourne, Australia, 11–16 June 2013. [CrossRef]. [Google Scholar]
  101. Perdrizet, T.; Gilloteaux, J.C.; Teixeira, D.; Ferrer, G.; Piriou, L.; Cadiou, D.; Heurtier, J.M.; Le Cunff, C. Fully Coupled Floating Wind Turbine Simulator Based on Nonlinear Finite Element Method: Part II—Validation Results. In Proceedings of the Volume 8: Ocean Renewable Energy, Melbourne, Australia, 11–16 June 2013. [CrossRef]. [Google Scholar]
  102. Leroy, J.M.; Poirette, Y.; Brusselle Dupend, N.; Caleyron, F. Assessing Mechanical Stresses in Dynamic Power Cables for Floating Offshore Wind Farms. In Volume 10: Ocean Renewable Energy; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
  103. Ledru, R.; Le Cunff, C.; Heurtier, J.M.; Perdrizet, T.; Poirette, Y. Influence of Hydrodynamic Modeling Assumptions on Floating Wind Turbine Behaviour. In Volume 9B: Ocean Renewable Energy; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
  104. Evren, S.; Unel, M.; Adak, O.K.; Erbatur, K.; Aksit, M.F. Modeling and simulation of a horizontal axis Wind Turbine using S4WT. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6. [Google Scholar]
  105. Prasad, C.; Chen, Q.Z.; Bruls, O.; D’Ambrosio, F.; Dimitriadis, G. Advanced aeroservoelastic modeling for horizontal axis wind turbines. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014; pp. 3097–3104. [Google Scholar]
  106. Gözcü, M.O.; Kayran, A. Investigation of the effect of bending twisting coupling on the loads in wind turbines with superelement blade definition. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 524, p. 12040. [Google Scholar]
  107. Heege, A.; Gaull, A.; Horcas, S.G.; Bonnet, P.; Defourny, M. Experiences in controller adaptations of floating wind turbines through advanced numerical simulation. In Proceedings of the AWEA WINDPOWER 2013 Conference and Exhibition, Chicago, IL, USA, 21–22 October 2013; pp. 5–8. [Google Scholar]
  108. Digital Solutions at DNV. Sesam Feature Description; Technical Report; DNV: Bærum, Norway, 2022. [Google Scholar]
  109. Alblas, L. Fixed Offshore Wind Structure Design, What Sesam Can Do for Fixed Offshore Wind Turbine Structure Design and Analysis; Technical Report; DNV GL—Digital Solutions: Bærum, Norway, 2018. [Google Scholar]
  110. Barrera, C.; Guanche, R.; Rodríguez, Á.; Armesto, J.A.; Losada, I.J. On the importance of mooring system parametrisation for accurate floating structure designs. Mar. Struct. 2020, 72, 102765. [Google Scholar] [CrossRef]
  111. Lu, H.; Fan, T.; Zhou, L.; Chen, C.; Yu, G.; Li, X.; Hou, F. A rapid response calculation method for symmetrical floating structures based on state–space model solving in hybrid time-Laplace domain. Ocean Eng. 2020, 203, 107227. [Google Scholar] [CrossRef]
  112. Suzuki, H.; Shibata, H.; Fujioka, H.; Hirabayashi, S.; Ishii, K.; Kikuchi, H. Development of an Analysis Code of Rotor-Floater Coupled Response of a Floating Offshore Wind Turbine. In Proceedings of the Volume 8: Ocean Renewable Energy, Melbourne, Australia, 11–16 June 2013. [CrossRef]. [Google Scholar]
  113. Ishii, K.; Suzuki, H.; Hirabayashi, S. 2015S-OS1-7 Improvement of Accuracy of Wave Drift Force of a Floating Offshore Wind Turbine. In Conference Proceedings The Japan Society of Naval Architects and Ocean Engineers 20; The Japan Society of Naval Architects and Ocean Engineers: Tokyo, Japan, 2015; pp. 25–28. [Google Scholar]
  114. Shiohara, H.; Gonçalves, R.T.; Houtani, H.; Suzuki, H.; Schnepf, A.; Hirabayashi, S.; Carmo, L.H.S.; Nihei, Y. Numerical and experimental comparison of the wave response of a very light floating offshore wind turbine with guy wires. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84317, p. V001T01A055. [Google Scholar]
  115. Suzuki, H.; Xiong, J.; do Carmo, L.H.S.; Vieira, D.P.; de Mello, P.C.; Malta, E.B.; Simos, A.N.; Hirabayashi, S.; Gonçalves, R.T. Elastic response of a light-weight floating support structure of FOWT with guywire supported tower. J. Mar. Sci. Technol. 2019, 24, 1015–1028. [Google Scholar] [CrossRef]
  116. Hooft, J.P. Hydrodynamic Aspects of Semi-Submersible Platforms. Ph.D. Thesis, Delft University of Technology, Delft, Netherlands, 1972. [Google Scholar]
  117. Faraggiana, E.; Giorgi, G.; Sirigu, M.; Ghigo, A.; Bracco, G.; Mattiazzo, G. A review of numerical modelling and optimisation of the floating support structure for offshore wind turbines. J. Ocean Eng. Mar. Energy 2022, 8, 433–456. [Google Scholar] [CrossRef]
  118. Gözcü, O.; Kontos, S.; Bredmose, H. Dynamics of two floating wind turbines with shared anchor and mooring lines. J. Phys. Conf. Ser. 2022, 2265, 042026. [Google Scholar] [CrossRef]
  119. Karimirad, M. Modeling aspects of a floating wind turbine for coupled wave–wind-induced dynamic analyses. Renew. Energy 2013, 53, 299–305. [Google Scholar] [CrossRef]
  120. Veldman, P.N. Essentials in Coupled Dynamics of Floating Offshore Wind Turbines. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
  121. Vriends, C. Efficient Long Term CFD Simulation of the Tri-Floater Using ComFLOW. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]
  122. Duarte, T.; Tomas, D.; Matha, D.; Sarmento, A.; Schuon, F. Verification of Engineering Modeling Tools for Floating Offshore Wind Turbines. In Proceedings of the Volume 8: Ocean Renewable Energy, Melbourne, Australia, 11–16 June 2013. [CrossRef]. [Google Scholar]
  123. Utsunomiya, T.; Matsukuma, H.; Minoura, S.; Ko, K.; Hamamura, H.; Kobayashi, O.; Sato, I.; Nomoto, Y.; Yasui, K. At Sea Experiment of a Hybrid Spar for Floating Offshore Wind Turbine Using 1/10-Scale Model. J. Offshore Mech. Arct. Eng. 2013, 135. [Google Scholar] [CrossRef]
  124. Xu, S.; Xue, Y.; Zhao, W.; Wan, D. A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2022, 10, 1357. [Google Scholar] [CrossRef]
  125. Witha, B. CFD-Type Wake Models. In Handbook of Wind Energy Aerodynamics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1001–1038. [Google Scholar]
  126. Amano, R.; Malloy, R. CFD analysis on aerodynamic design optimization of wind turbine rotor blades. World Acad. Sci. Eng. Technol. 2009, 60, 71–75. [Google Scholar]
Preprints 96051 g001
Figure 1. Diagram of the components of offshore wind modelling tools [5].
Figure 1. Diagram of the components of offshore wind modelling tools [5].
Preprints 96051 g001
Preprints 96051 g002
Figure 2. FAST schematic [28].
Figure 2. FAST schematic [28].
Preprints 96051 g002
Preprints 96051 g003
Figure 3. Sesam overview [108].
Figure 3. Sesam overview [108].
Preprints 96051 g003
Preprints 96051 g004
Figure 4. Overview of the integrated approach concept with the help of Sesam package and Bladed [109].
Figure 4. Overview of the integrated approach concept with the help of Sesam package and Bladed [109].
Preprints 96051 g004
Preprints 96051 g005
Figure 5. Overview of the super-element approach concept with the aid of the Sesam package, Bladed, and HAWC2 [109].
Figure 5. Overview of the super-element approach concept with the aid of the Sesam package, Bladed, and HAWC2 [109].
Preprints 96051 g005
Preprints 96051 g006
Figure 6. Overview of the sequential approach concept with the aid of the Sesam package and Bladed [109].
Figure 6. Overview of the sequential approach concept with the aid of the Sesam package and Bladed [109].
Preprints 96051 g006
Preprints 96051 g007
Figure 7. Compromise between fidelity and computational performance for the most popular numerical models used on an FOWT [117].
Figure 7. Compromise between fidelity and computational performance for the most popular numerical models used on an FOWT [117].
Preprints 96051 g007
Table 1. Summary of reviewed numerical simulation tool capabilities used to model an FOWT.
Table 1. Summary of reviewed numerical simulation tool capabilities used to model an FOWT.
Software Structure Aerodynamic Hydrodynamic Mooring Analysis Type
OpenFAST RB + Modal/FEM + Dyn/QS BEM + GDW/FVW PF + ME Lumped-mass + MSQS or with FEAMooring time-domain
OrcaFlex RB + FEM + Dyn With OpenFAST PF + ME 3-D FEM both
OPASS With OpenFAST With OpenFAST With OpenFAST Lumped-mass time-domain [117]
Bladed Modal BEM + GDW ME + third-party code like WAMIT or coupled with SESAM MBD time-domain [117]
HAWC2 FEM + Dyn BEM + GDW ME + external DLL or third-party code like WAMIT Shared mooring line design [118] or with SIMO/RIFLEX [119] time-domain
aNySIM with PHATAS [120] with PHATAS [120] PF Lumped-mass lines [121] time-domain
PHATAS FEM + Modal BEM with aNySIM [120] with aNySIM [120] time-domain
3DFloat FEM BEM ME + third-party code like WAMIT FEM [69] time-domain
DeepLines Wind FEM BEM ME + PF + QTF Solid elements + PF or deformable elements + ME time-domain
SAMCEF FEM + MBD BEM ME FEM + ME [122] time-domain
Sesam FEM With Bladed/HAWC2 ME + PF + Airy wave Panel method + ME [119] both
UTWind BE BEM Hooft’s method + ME Lumped-mass [115] time-domain
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated