Submitted:
11 August 2023
Posted:
14 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doi, M. Soft Matter Physics Oxford University Press: New York, 2017.
- Madras, N.; Slade, G. The Self-Avoiding Walk; Birkhauser: Boston, 1996. [Google Scholar]
- Weiss, G.H.; Rubin, R.J. RANDOM-WALKS - THEORY AND SELECTED APPLICATIONS. Adv. Chem. Phys. 1983, 52, 363–505. [Google Scholar] [CrossRef]
- Webb, B.Z.; Cohen, E.G.D. Self-avoiding modes of motion in a deterministic Lorentz lattice gas. Journal of Physics a-Mathematical and Theoretical 2014, 47. [Google Scholar] [CrossRef]
- Triampo, D.; Shobsngob, S.; Triampo, W.; Pongkitiwanichkul, P. Modified self-avoiding walk in a polymerization process. Journal of the Korean Physical Society 2005, 46, 1429–1432. [Google Scholar]
- Sykes, M.F. SELF-AVOIDING WALKS ON SIMPLE CUBIC LATTICE. J. Chem. Phys. 1963, 39, 410. [Google Scholar] [CrossRef]
- Brydges, D.; Frohlich, J.; Spencer, T. THE RANDOM-WALK REPRESENTATION OF CLASSICAL SPIN SYSTEMS AND CORRELATION INEQUALITIES. Communications in Mathematical Physics 1982, 83, 123–150. [Google Scholar] [CrossRef]
- Alvarez, J.; van Rensburg, E.J.J.; Soteros, C.E.; Whittington, S.G. Self-avoiding polygons and walks in slits. Journal of Physics a-Mathematical and Theoretical 2008, 41. [Google Scholar] [CrossRef]
- Fisher, M.E.; Sykes, M.F. EXCLUDED-VOLUME PROBLEM AND THE ISING MODEL OF FERROMAGNETISM. Physical Review 1959, 114, 45–58. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory: Revised Second Edition; CRC Press: Boca Raton, 2014. [Google Scholar]
- Janse van Rensburg, E.J. The Statistical Mechanics of Interacting Walks, Polygons, Animals and Vesicles, 2nd ed.; Oxford University Press: Oxford, 2015. [Google Scholar]
- Ottinger, H.C. Stochastic Processes in Polymeric Fluids; Springer Science & Business Media: Berlin, 2012. [Google Scholar]
- Rubin, R.J. THE EXCLUDED VOLUME EFFECT IN POLYMER CHAINS AND THE ANALOGOUS RANDOM WALK PROBLEM. J. Chem. Phys. 1952, 20, 1940–1945. [Google Scholar] [CrossRef]
- Rubin, R.J. Random-Walk Model of Chain-Polymer Adsorption at a Surface. J. Chem. Phys. 1965, 43, 2392–2407. [Google Scholar] [CrossRef]
- Fisher, M.E. SHAPE OF A SELF-AVOIDING WALK OR POLYMER CHAIN. J. Chem. Phys. 1966, 44, 616. [Google Scholar] [CrossRef]
- Helfand, E. THEORY OF INHOMOGENEOUS POLYMERS - FUNDAMENTALS OF GAUSSIAN RANDOM-WALK MODEL. J. Chem. Phys. 1975, 62, 999–1005. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics (Chemistry); Oxford University Press: Oxford, 2003. [Google Scholar]
- deGennes, P.G. Scaling Concepts in Polymer physics; Cornell University Press: Ithaca, 1980. [Google Scholar]
- Guyeux, C.; Nicod, J.M.; Philippe, L.; Bahi, J.M. The study of unfoldable self-avoiding walks - Application to protein structure prediction software. Journal of Bioinformatics and Computational Biology 2015, 13. [Google Scholar] [CrossRef] [PubMed]
- Guyeux, C.; Charr, J.C.; Abdo, J.B.; Demerjian, J. Advances in the enumeration of foldable self-avoiding walks. International Journal of Computational Science and Engineering 2020, 22, 365–375. [Google Scholar] [CrossRef]
- Flory, P.J. THE CONFIGURATION OF REAL POLYMER CHAINS. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- Orr, W.J.C. STATISTICAL TREATMENT OF POLYMER SOLUTIONS AT INFINITE DILUTION. Trans. Faraday Soc. 1947, 43, 12–27. [Google Scholar] [CrossRef]
- Janse Van Rensburg, E.J.; Whittington, S.G. Self-avoiding walks adsorbed at a surface and pulled at their mid-point. Journal of Physics a-Mathematical and Theoretical 2017, 50. [Google Scholar] [CrossRef]
- Pereira, G.G. INTERNAL STRUCTURE OF POLYMER-CHAINS. Physica A 1995, 219, 290–304. [Google Scholar] [CrossRef]
- Rosa, A.; Everaers, R. Conformational statistics of randomly branching double-folded ring polymers. European Physical Journal E 2019, 42. [Google Scholar] [CrossRef]
- Bishop, M.; Clarke, J.H.R. INVESTIGATION OF THE END-TO-END DISTANCE DISTRIBUTION FUNCTION FOR RANDOM AND SELF-AVOIDING WALKS IN 2 AND 3 DIMENSIONS. J. Chem. Phys. 1991, 94, 3936–3942. [Google Scholar] [CrossRef]
- Clisby, N.; Conway, A.R.; Guttmann, A.J. Three-dimensional terminally attached self-avoiding walks and bridges. Journal of Physics a-Mathematical and Theoretical 2016, 49. [Google Scholar] [CrossRef]
- Yang, Q.H.; Yang, X.; Luo, M.B. Adsorption of polymer chains on heterogeneous surfaces with random adsorption sites. Polymer 2019, 180. [Google Scholar] [CrossRef]
- Domb, C.; Gillis, J.; Wilmers, G. ON SHAPE AND CONFIGURATION OF POLYMER MOLECULES. Proceedings of the Physical Society of London 1965, 85, 625. [Google Scholar] [CrossRef]
- Beaton, N.R.; Flajolet, P.; Garoni, T.M.; Guttmann, A.J. Some New Self-avoiding Walk and Polygon Models. Fundamenta Informaticae 2012, 117, 19–33. [Google Scholar] [CrossRef]
- Bosi, G.; Campanino, M. Random Walk on a Randomly Oriented Honeycomb Lattice. Markov Processes and Related Fields 2019, 25, 75–99. [Google Scholar]
- Adler, J. THE SELF-AVOIDING WALK ON THE HONEYCOMB LATTICE. Journal of Physics a-Mathematical and General 1983, 16, L515–L517. [Google Scholar] [CrossRef]
- Beaton, N.R.; Guttmann, A.J.; Jensen, I. A numerical adaptation of self-avoiding walk identities from the honeycomb to other 2D lattices. Journal of Physics a-Mathematical and Theoretical 2012, 45. [Google Scholar] [CrossRef]
- Deforcrand, P.; Koukiou, F.; Petritis, D. SELF-AVOIDING RANDOM-WALKS ON THE HEXAGONAL LATTICE. Journal of Statistical Physics 1986, 45, 459–470. [Google Scholar] [CrossRef]
- Guttmann, A.J. ON THE CRITICAL-BEHAVIOR OF SELF-AVOIDING WALKS. Journal of Physics a-Mathematical and General 1987, 20, 1839–1854. [Google Scholar] [CrossRef]
- Macdonald, D.; Hunter, D.L.; Kelly, K.; Jan, N. SELF-AVOIDING WALKS IN 2 TO 5 DIMENSIONS - EXACT ENUMERATIONS AND SERIES STUDY. Journal of Physics a-Mathematical and General 1992, 25, 1429–1440. [Google Scholar] [CrossRef]
- Jensen, I. Self-avoiding walks and polygons on the triangular lattice. Journal of Statistical Mechanics-Theory and Experiment 2004. [Google Scholar] [CrossRef]
- Guttmann, A.J. ON THE CRITICAL-BEHAVIOR OF SELF-AVOIDING WALKS.2. Journal of Physics a-Mathematical and General 1989, 22, 2807–2813. [Google Scholar] [CrossRef]
- MacDonald, D.; Joseph, S.; Hunter, D.L.; Moseley, L.L.; Jan, N.; Guttmann, A.J. Self-avoiding walks on the simple cubic lattice. Journal of Physics a-Mathematical and General 2000, 33, 5973–5983. [Google Scholar] [CrossRef]
- Schram, R.D.; Barkema, G.T.; Bisseling, R.H. Exact enumeration of self-avoiding walks. Journal of Statistical Mechanics-Theory and Experiment 2011. [Google Scholar] [CrossRef]
- Schram, R.D.; Barkema, G.T.; Bisseling, R.H.; Clisby, N. Exact enumeration of self-avoiding walks on BCC and FCC lattices. Journal of Statistical Mechanics-Theory and Experiment 2017. [Google Scholar] [CrossRef]
- McKenzie, D.S. END-TO-END LENGTH DISTRIBUTION OF SELF-AVOIDING WALKS. Journal of Physics a-Mathematical and General 1973, 6, 338–352. [Google Scholar] [CrossRef]
- Bahi, J.M.; Guyeux, C.; Mazouzi, K.; Philippe, L. Computational investigations of folded self-avoiding walks related to protein folding. Comput. Biol. Chem. 2013, 47, 246–256. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Hammond, A. Self-Avoiding Walk is Sub-Ballistic. Communications in Mathematical Physics 2013, 324, 401–423. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Glazman, A.; Hammond, A.; Manolescu, I. ON THE PROBABILITY THAT SELF-AVOIDING WALK ENDS AT A GIVEN POINT. Annals of Probability 2016, 44, 955–983. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Ganguly, S.; Hammond, A.; Manolescu, I. BOUNDING THE NUMBER OF SELF-AVOIDING WALKS: HAMMERSLEY-WELSH WITH POLYGON INSERTION. Annals of Probability 2020, 48, 1644–1692. [Google Scholar] [CrossRef]
- Caracciolo, S.; Pelissetto, A.; Sokal, A.D. DYNAMIC CRITICAL EXPONENT OF THE BFACF ALGORITHM FOR SELF-AVOIDING WALKS. Journal of Statistical Physics 1991, 63, 857–865. [Google Scholar] [CrossRef]
- Caracciolo, S.; Causo, M.S.; Ferraro, G.; Papinutto, M.; Pelissetto, A. Bilocal dynamics for self-avoiding walks. Journal of Statistical Physics 2000, 100, 1111–1145. [Google Scholar] [CrossRef]
- Caracciolo, S.; Gherardi, M.; Papinutto, M.; Pelissetto, A. Geometrical properties of two-dimensional interacting self-avoiding walks at the theta-point. Journal of Physics a-Mathematical and Theoretical 2011, 44. [Google Scholar] [CrossRef]
- Hooper, W.; Klotz, A.R. Trapping in self-avoiding walks with nearest-neighbor attraction. Phys. Rev. E 2020, 102. [Google Scholar] [CrossRef] [PubMed]
- Brydges, D.C.; Imbrie, J.Z. Green's function for a hierarchical self-avoiding walk in four dimensions. Communications in Mathematical Physics 2003, 239, 549–584. [Google Scholar] [CrossRef]
- Gherardi, M. Exact Sampling of Self-avoiding Paths via Discrete Schramm-Loewner Evolution. Journal of Statistical Physics 2010, 140, 1115–1129. [Google Scholar] [CrossRef]
- Grimmett, G.R.; Li, Z.Y. Self-avoiding walks and amenability. Electronic Journal of Combinatorics 2017, 24. [Google Scholar] [CrossRef]
- Lindorfer, C. A general bridge theorem for self-avoiding walks. Discrete Mathematics 2020, 343. [Google Scholar] [CrossRef]
- Zbarsky, S. Asymptotically faster algorithm for counting self-avoiding walks and self-avoiding polygons. Journal of Physics a-Mathematical and Theoretical 2019, 52. [Google Scholar] [CrossRef]
- James, E.W.; Soteros, C.E. New pattern theorems for square lattice self-avoiding walks and self-avoiding polygons. Journal of Physics a-Mathematical and Theoretical 2007, 40, 8621–8634. [Google Scholar] [CrossRef]
- Schram, R.D.; Barkema, G.T.; Bisseling, R.H. SAWdoubler: A program for counting self-avoiding walks. Comput. Phys. Commun. 2013, 184, 891–898. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Smirnov, S. The connective constant of the honeycomb lattice equals root 2+root 2. Annals of Mathematics 2012, 175, 1653–1665. [Google Scholar] [CrossRef]
- Clisby, N.; Dunweg, B. High-precision estimate of the hydrodynamic radius for self-avoiding walks. Phys. Rev. E 2016, 94. [Google Scholar] [CrossRef]
- Clisby, N. Accurate Estimate of the Critical Exponent nu for Self-Avoiding Walks via a Fast Implementation of the Pivot Algorithm. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Conway, A.R.; Enting, I.G.; Guttmann, A.J. ALGEBRAIC TECHNIQUES FOR ENUMERATING SELF-AVOIDING WALKS ON THE SQUARE LATTICE. Journal of Physics a-Mathematical and General 1993, 26, 1519–1534. [Google Scholar] [CrossRef]
- Conway, A.R.; Guttmann, A.J. Square lattice self-avoiding walks and corrections to scaling. Phys. Rev. Lett. 1996, 77, 5284–5287. [Google Scholar] [CrossRef] [PubMed]
- Shukla, P. Physics of disordered solids; Mittal Publications: Delhi, 1982. [Google Scholar]
- Benito, J.; Karayiannis, N.C.; Laso, M. Confined Polymers as Self-Avoiding Random Walks on Restricted Lattices. Polymers 2018, 10. [Google Scholar] [CrossRef]
- Parreno, O.; Miguel Ramos, P.; Karayiannis, N.C.; Laso, M. Self-Avoiding Random Walks as a Model to Study Athermal Linear Polymers under Extreme Plate Confinement. Polymers 2020, 12. [Google Scholar] [CrossRef]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Martinez-Fernandez, D.; Foteinopoulou, K.; Laso, M.; Karayiannis, N.C. Crystallization of Flexible Chains of Tangent Hard Spheres under Full Confinement. J. Phys. Chem. B 2022, 126, 5931–5947. [Google Scholar] [CrossRef]
- Ostwald, W. Studien uber die bildung and umwandlung fester korper. Z. Phys. Chem. 1897, 22, 289–330. [Google Scholar] [CrossRef]
- Herranz, M.; Benito, J.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
- Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers 2022, 14. [Google Scholar] [CrossRef] [PubMed]
- Herranz, M.; Pedrosa, C.; Martínez-Fernández, D.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Fine-tuning of colloidal polymer crystals by molecular simulation. Phys. Rev. E 2023, 107, 064605. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar] [CrossRef]
- Bruce, A.D.; Wilding, N.B.; Ackland, G.J. Free energy of crystalline solids: A lattice-switch Monte Carlo method. Phys. Rev. Lett. 1997, 79, 3002–3005. [Google Scholar] [CrossRef]
- Mau, S.C.; Huse, D.A. Stacking entropy of hard-sphere crystals. Phys. Rev. E 1999, 59, 4396–4401. [Google Scholar] [CrossRef]
- Pronk, S.; Frenkel, D. Can stacking faults in hard-sphere crystals anneal out spontaneously? J. Chem. Phys. 1999, 110, 4589–4592. [Google Scholar] [CrossRef]
- Herranz, M.; Martínez-Fernández, D.; Ramos, P.M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Simu-D: A Simulator-Descriptor Suite for Polymer-Based Systems under Extreme Conditions. Int. J. Mol. Sci. 2021, 22, 12464. [Google Scholar] [CrossRef]
- Herranz, M.; Santiago, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Crystal, Fivefold and Glass Formation in Clusters of Polymers Interacting with the Square Well Potential. Polymers 2020, 12. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, 1987. [Google Scholar]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10. [Google Scholar] [CrossRef]
- Frank, F.C.; Kasper, J.S. COMPLEX ALLOY STRUCTURES REGARDED AS SPHERE PACKINGS.1. DEFINITIONS AND BASIC PRINCIPLES. Acta Crystallogr. 1958, 11, 184–190. [Google Scholar] [CrossRef]
- Frank, F.C.; Kasper, J.S. COMPLEX ALLOY STRUCTURES REGARDED AS SPHERE PACKING.2. ANALYSIS AND CLASSIFICATION OF REPRESENTATIVE STRUCTURES. Acta Crystallogr. 1959, 12, 483–499. [Google Scholar] [CrossRef]
- Serrano-Illán, J.; Navascués, G.; Velasco, E. Noncompact crystalline solids in the square-well potential. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006, 73, 011110. [Google Scholar] [CrossRef]
- Armas-Pérez, J.C.; Quintana-H, J.; Chapela, G.A.; Velasco, E.; Navascués, G. Phase diagram of a square-well model in two dimensions. The Journal of Chemical Physics 2014, 140, 064503. [Google Scholar] [CrossRef]
- Clisby, N. Scale-free Monte Carlo method for calculating the critical exponent. of self-avoiding walks. Journal of Physics a-Mathematical and Theoretical 2017, 50. [Google Scholar] [CrossRef]
- Sykes, M.F.; Watts, M.G.; Roberts, P.D.; Guttmann, A.J. ASYMPTOTIC BEHAVIOR OF SELFAVOIDING WALKS AND RETURNS ON A LATTICE. Journal of Physics Part a General 1972, 5, 653. [Google Scholar] [CrossRef]
- Clisby, N.; Liang, R.; Slade, G. Self-avoiding walk enumeration via the lace expansion. Journal of Physics a-Mathematical and Theoretical 2007, 40, 10973–11017. [Google Scholar] [CrossRef]
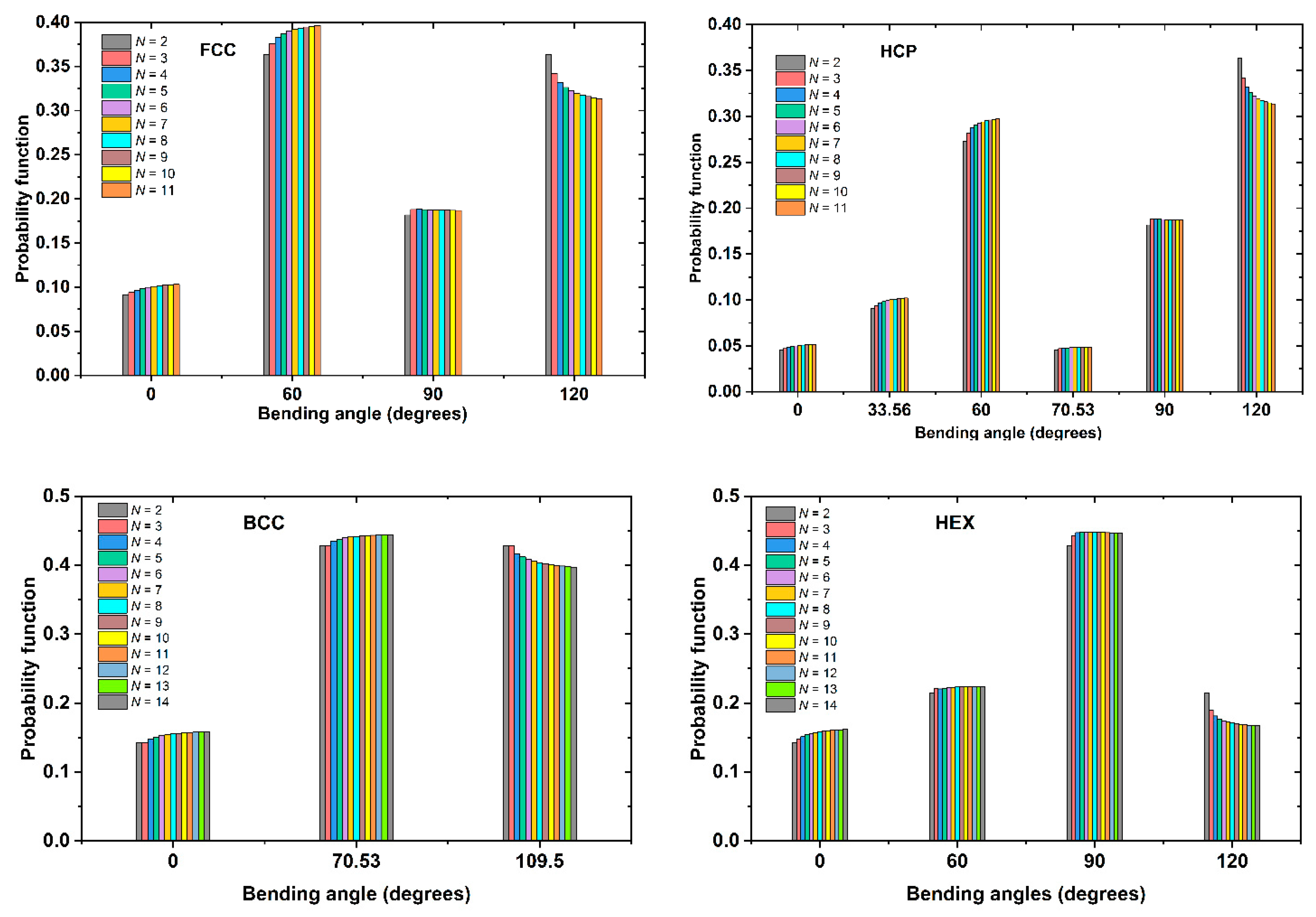
| θ (degrees) | FCC | HCP | BCC | HEX |
|---|---|---|---|---|
| 0.000 | + | + | + | + |
| 33.56 | - | + | - | - |
| 60.00 | + | + | - | + |
| 70.53 | - | + | + | - |
| 90.00 | + | + | - | + |
| 109.47 | - | - | + | - |
| 120.00 | + | + | - | + |
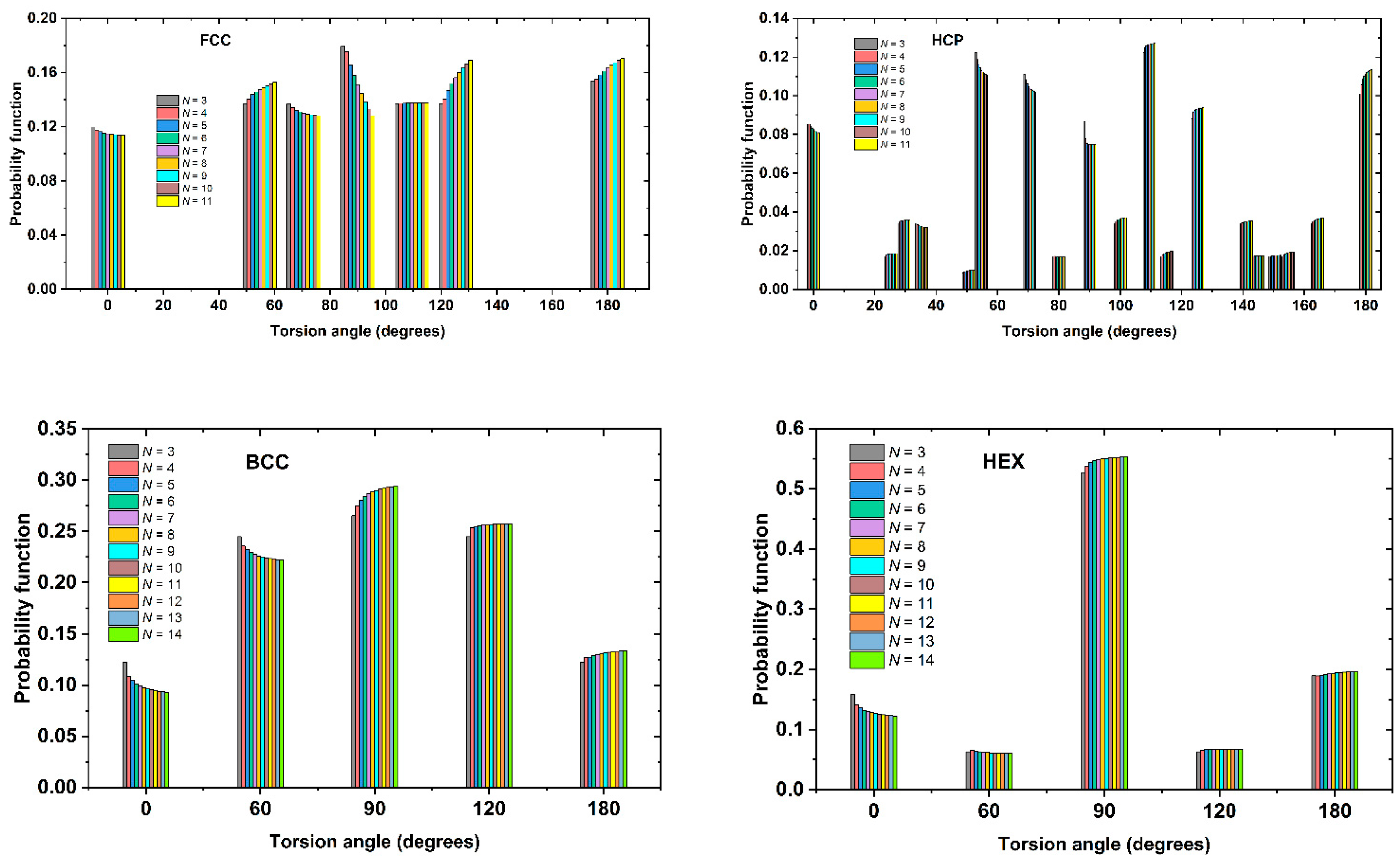
| ϕ | FCC | HCP | BCC | HEX |
|---|---|---|---|---|
| 0.000 | + | + | + | + |
| 25.24 | - | + | - | - |
| 29.50 | - | + | - | - |
| 35.26 | - | + | - | - |
| 50.48 | - | + | - | - |
| 54.74 | + | + | - | - |
| 60.00 | - | - | + | + |
| 70.53 | + | + | - | - |
| 79.98 | - | + | - | - |
| 90.00 | + | + | + | + |
| 100.02 | - | + | - | - |
| 109.47 | + | + | - | - |
| 115.24 | - | + | - | - |
| 120.00 | - | - | + | + |
| 125.26 | + | + | - | - |
| 141.06 | - | + | - | - |
| 144.74 | - | + | - | - |
| 150.50 | - | + | - | - |
| 154.76 | - | + | - | - |
| 164.21 | - | + | - | - |
| 180.00 | + | + | + | + |
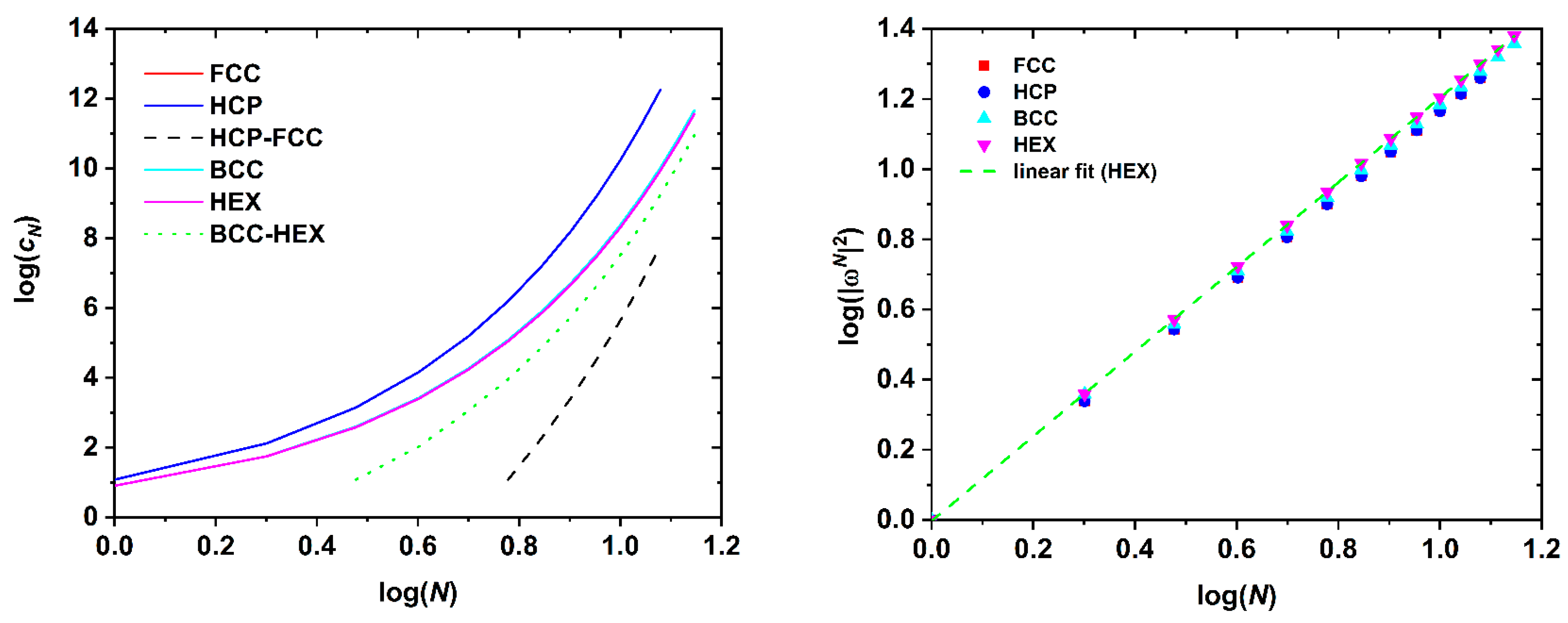
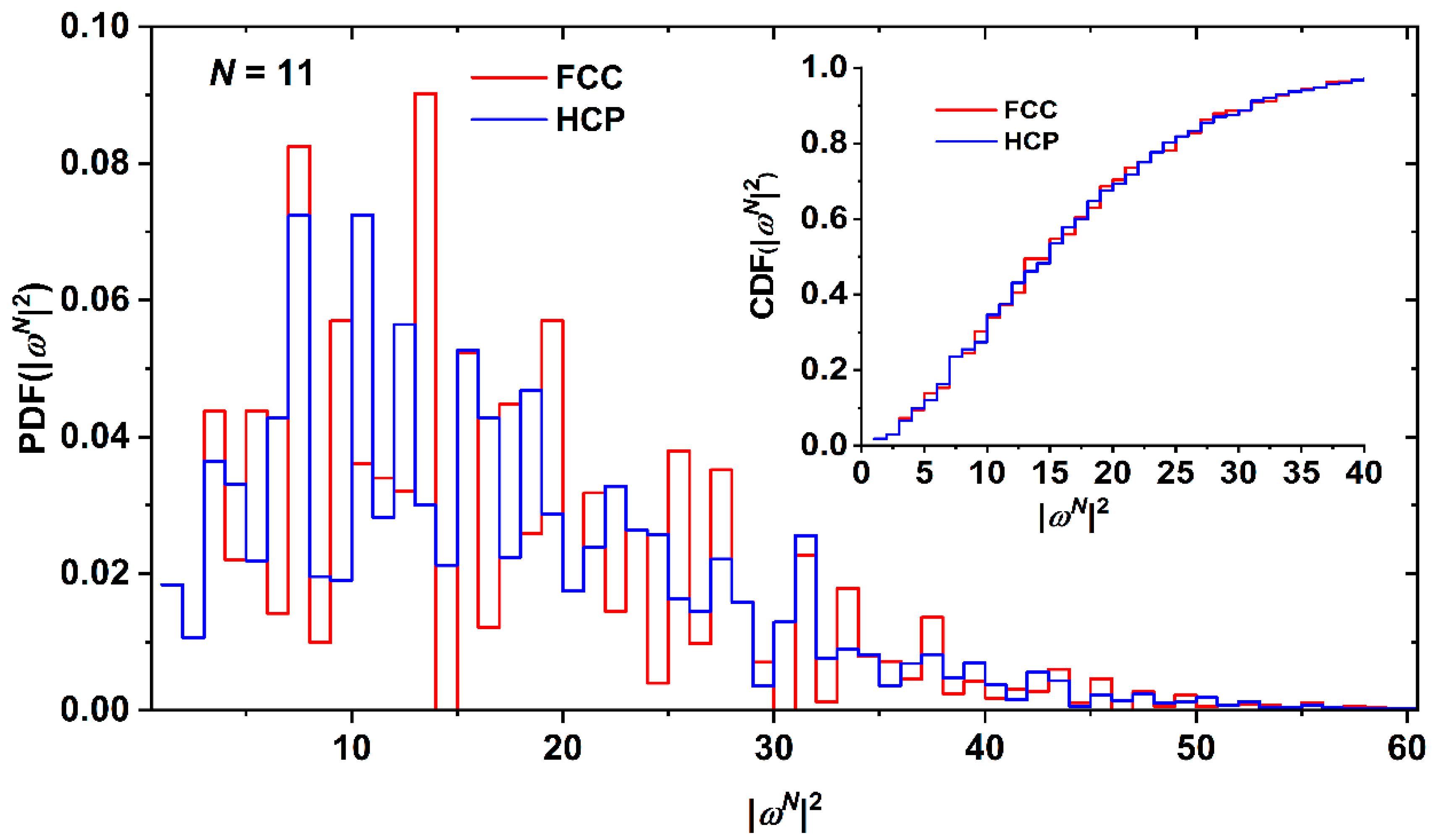
| FCC | HCP | Difference | |||
|---|---|---|---|---|---|
| N | cN | cN | ΔcN | ||
| 1 | 12 | 1.000 | 12 | 1.000 | 0 |
| 2 | 132 | 2.182 | 132 | 2.182 | 0 |
| 3 | 1404 | 3.496 | 1404 | 3.496 | 0 |
| 4 | 14700 | 4.908 | 14700 | 4.908 | 0 |
| 5 | 152532 | 6.397 | 152532 | 6.397 | 0 |
| 6 | 1573716 | 7.950 | 1573728 | 7.950 | 12 |
| 7 | 16172148 | 9.556 | 16172340 | 9.556 | 192 |
| 8 | 165697044 | 11.21 | 165699744 | 11.21 | 2700 |
| 9 | 1693773924 | 12.90 | 1693809348 | 12.90 | 35424 |
| 10 | 17281929564 | 14.64 | 17282367084 | 14.64 | 437520 |
| 11 | 176064704412 | 16.41 | 176069916384 | 16.41 | 5211972 |
| 12 | 1791455071068 | 18.21 | 1791515688168 | 18.21 | 60617100 |
| BCC | HEX | Difference | ||||
|---|---|---|---|---|---|---|
| N | cN | cN | ΔcN | |||
| 1 | 8 | 1.000 | 8 | 1.000 | 0 | 0.000 |
| 2 | 56 | 2.286 | 56 | 2.286 | 0 | 0.000 |
| 3 | 392 | 3.612 | 380 | 3.726 | 12 | -0.114 |
| 4 | 2648 | 5.124 | 2540 | 5.280 | 108 | -0.156 |
| 5 | 17960 | 6.645 | 16844 | 6.918 | 1116 | -0.274 |
| 6 | 120056 | 8.294 | 111068 | 8.628 | 8988 | -0.334 |
| 7 | 804824 | 9.940 | 729524 | 10.40 | 75300 | -0.458 |
| 8 | 5351720 | 11.69 | 4777628 | 12.22 | 574092 | -0.533 |
| 9 | 35652680 | 13.43 | 31217552 | 14.09 | 4435128 | -0.661 |
| 10 | 236291096 | 15.26 | 203608520 | 16.01 | 32682576 | -0.747 |
| 11 | 1568049560 | 17.08 | 1326015428 | 17.96 | 242034132 | -0.879 |
| 12 | 10368669992 | 18.97 | 8625090800 | 19.95 | 1743579192 | -0.973 |
| 13 | 68626647608 | 20.86 | 56043338096 | 21.97 | 12583309512 | -1.11 |
| 14 | 453032542040 | 22.81 | 363826528532 | 24.02 | 89206013508 | -1.21 |
| Lattice | A | μ | γ | D | v |
|---|---|---|---|---|---|
| HCP | 1.19 | 10.07 | 1.134 | 0.977 | 0.587 |
| BCC | 1.21 | 6.565 | 1.124 | 0.995 | 0.593 |
| HEX | 1.24 | 6.436 | 1.129 | 0.994 | 0.603 |
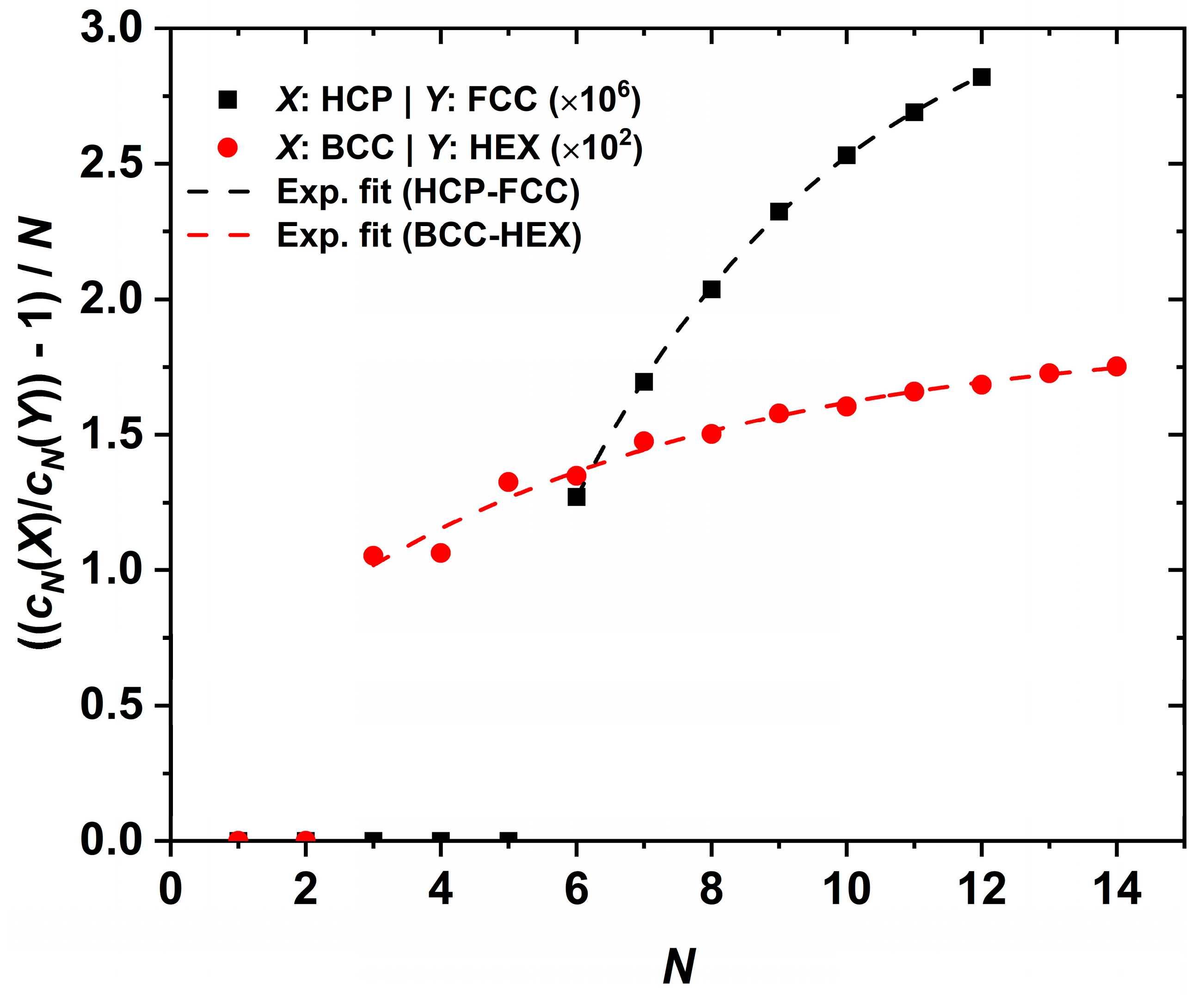
| Pair of Crystals | A | B | d | Range of Validity |
| HCP - FCC | 3.31×10-6 | 8.63×10-6 | 0.24 | N > 5 |
| BCC - HEX | 0.0188 | 0.0144 | 0.17 | N > 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





