1. Introduction
Big data usually have a large number of features, also called predictors or covariates, that are potentially associated with an outcome, so that they require new analysis methods (Engelhard MM et al. 2021). Such big data are specifically called high dimensional data. Machine learning (ML) methods are accredited for prediction of high dimensional data, which is a preferred alternative to traditional statistical methods. Recent feats of ML have held collective attention, and a great amount of literature illustrating its superiority in applied performance has encouraged researchers to exploit ML methods to the great extent. However, it still needs more investigations to recognize their superiority over the standard statistical methods for the analysis of clinical big data. In this paper, we assume that only a small number of candidate features are associated with the outcome.
Least absolute shrinkage and selection operator (LASSO) has been popularly used for prediction model fitting since it can be used for any types of regression models depending on the type of outcome variables. There are some issues with LASSO. LASSO seems to over-select features, so that the selected features with insignificant or no association with the outcome will play the role of noise in the fitted prediction model and lower the prediction accuracy. If a fitted prediction model includes a large number of features, it often incurs excessive cost. For example, suppose that we want to develop a model to predict patients’ outcomes based on gene expression data. At the development stage, we usually use commercial microarray chips with thousands of genes. Once a prediction model is fitted, we usually develop customized chips including only the genes selected for the fitted prediction model to increase the assay accuracy and lower the price of chips. If the number of genes is too large, the decrease in price of the customized chips and the increase in assay accuracy can be minimal while sacrificing prediction performance due to falsely selected genes. As another example, suppose that we want to develop a model to predict the purchase type of customers using big data for a retailer . Once a prediction model is fitted, the retailer using the fitted model will have to collect the features included in the model and manage them to increase the sales volume. In this case, if the number of selected features is too large, these activities can be unnecessarily costly. As in the microarray example, falsely selected features will result in the loss of prediction accuracy too.
Using -norm penalty, LASSO selects features based on the size of regression coefficients, rather than their statistical significance associated with the outcome variable. We standardize feature observations as an effort to make the distributions of features similar and to make the variable selection based on the size of regression coefficients as similar as that based on the statistical significance. However, no known standardization method removes this issue completely, especially when the features have different variable types. For example, if some features are continuous and some are binary, then it is impossible to make the distributions the same by any standardization or transformation, so that the fitted prediction model can include insignificant features while missing some significant ones. Elastic net (EN) uses a combination of -norm and -norm which is less strict than -norm penalty, so that it has more serious problems in these issues.
As an alternative to LASSO and EN, we propose to use a standard (un-penalized) regression method combined with the stepwise variable selection procedure to develop a prediction model using high dimensional data. While the penalized methods provide 0-shrinkage estimators even for a reduced model, regression methods equipped with the stepwise variable selection procedure provide the standard maximum likelihood estimators. Furthermore, unlike LASSO and EN, the standard regression methods provide the statistical significance of the regression coefficients for the features included in fitted prediction models.
There have been numerous literatures comparing the performance between logistic regression and some ML methods and claiming that the latter do not have better prediction performance than the former, e.g. Khera R et al. 2021, Christodoulou E et al. 2019, Jing et al. 2022, Piros et al. 2019, Song et al. 2021, Kuhle et al. 2018, and Stylianou N et al. 2015. However, most of these findings are anecdotal in the sense that their conclusions are based on real data analyses, without any systematic simulation studies. While these publications are limited to classification problems using a binary outcome, Kattan (2003) compared the performance of machine learning methods for survival outcomes with that of Cox’s regression method using three urological data sets. For all of the real data sets, the numbers of cases are large but those of features are not so big that they are not high dimensional data. Although this type of data may have a big size due to the large number of cases, we do not have any difficulty in analyzing them using a standard regression method. Limited to real data analyses only, these studies do not provide systemic evaluation of machine learning methods for high dimensional data.
In this paper, we compare the variable selection performance of LASSO and EN with the standard statistical regression methods combined with a stepwise variable selection procedure. We conduct extensive simulations for binary outcomes using logistic regression and survival outcomes using Cox regression model. The performance of prediction methods are evaluated by mean true selections and mean total selections from training sets, and measures of association between fitted prediction model and observed outcome for both training and validation sets. Through simulations and real data analysis, we find that LASSO and EN tend to over-select features, while prediction accuracy is no better than that of the standard regression methods equipped with stepwise variable selection which selects much smaller number of features.
2. Materials and Methods
The ML methods for comparison include LASSO and EN. The traditional generalized linear model for binary outcomes is logistic regression with stepwise variable selection (L-SVS) and that for time-to-event outcomes is Cox regression with stepwise variable selection (C-SVS). We briefly review these methods and introduce the performance measurements we employ including true selections and total selections, and association between fitted model and outcome data, such as the area under the curve (AUC) of receiver operating characteristic (ROC) curves for binary outcomes, and Harrell’s C-index and negative log p-value for survival outcomes.
Suppose that there are n subjects, and we observe an outcome variable y and m features from each subject. The resulting data will look like . For high dimensional data, m is much bigger than n, while the number of features that are truly associated with the outcome, denoted as , is often small. We will consider a hold-out method to partition the whole data set into a training and a validation sets.
2.1. Traditional Statistical Models
Let denote a subset of the features that are possibly related with an outcome variable, and their regression coefficients.
2.1.1. Logistic Regression
Logistic regression method is popularly used to associate a binary outcome
y taking 0 or 1 (Tolles J and Meurer WJ 2016) with features. For
, a logistic regression model is given as
where
is the intercept term. Noting that, given covariates
, outcomes
are independent Bernoulli random variables, the regression coefficients
are estimated by maximizing the log-likelihood
with respect to
.
2.1.2. Cox Proportional Hazards Model
The Cox proportional hazards model is commonly used to relate a survival outcome with covariates. For subject
, let
denote the minimum of survival time and censoring time, and
the event indicator taking 1 if
is the survival time and 0 if
is the censoring time. A data set will be summarized as
. The basic assumption for survival data is that, for each subject, censoring time is independent of survival time given the covariates. Using a Cox’s proportional hazards regression model, we assume that the hazard function,
, of subject
i’s survival time is expressed as
at time t, where
denotes the baseline hazard. By Cox (Cox, D. R. 1972), the regression coefficients are estimated by maximizing the partial log-likelihood function
where
is the indicator function.
2.1.3. Forward Stepwise Variable Selection
One of the challenges of high dimensional data is that the number of candidate features m is much larger than the sample size n. So, variable selection (or dimension reduction) is a critical procedure in prediction model building using high dimensional data. Popular variable selection methods for standard regression methods include forward stepwise procedure, backward elimination procedure, and all possible combination procedure. For high dimensional data, however, backward elimination and all possible combination procedures do not work because the estimation procedure of regression models with a large number of covariates does not converge. In this case, forward selection procedure is very useful, especially when the number of covariates that are truly associated with the outcome is small. It begins with an empty model (or one with an intercept term only for logistic regression model) and in each step the most significant covariate is added to the model if its p-value is smaller than , and the extraneous covariates are eliminated if they become insignificant by adding a new variable (i.e. if their p-values are larger than ). This procedure continues until no more variables are added to the current model. Before starting an analysis using stepwise procedure, we pre-specify the alpha levels, for insertion and for deletion (usually ). By the selection of alpha levels, we can control the number of selections in prediction model building.
Some existing stepwise programs, including SAS, use penalized likelihood criteria such as Akaike information criterion (AIC) or Bayesian information criterion (BIC) instead of specifying the significance levels. As such, by these methods, we do not know how significant the selected covariates are and we can not control the number of selected covariates.
2.2. Machine Learning Methods
2.2.1. LASSO
LASSO is a regularized regression model which adds an
-norm penalty to the objective function of traditional regression models. For binary outcomes, LASSO adds an
-norm penalty term to the negative log-likelihood function for a logistic regression and estimate the regression parameters by minimizing (Tibshirani R. 1996)
with respect to
.
For time-to-event outcomes, LASSO adds an
-norm penalty to the negative log-partial likelihood function for a proportional hazards model and estimate the regression parameters by minimizing (Tibshirani R. 1997)
with respect to
. In this paper the tuning parameter
is selected to minimize the regularized objective function using an internal cross-validation (Tibshirani R. 1996, Tibshirani R. 1997).
2.2.2. Elastic Net
EN is a generalized regularized model with both
- and
-norm regularization terms added to an objective function. For logistic regression with binary outcomes, the regression parameters are estimated by minimizing (Zou H. and Hastie T. 2005)
with respect to
. And, for Cox regression with time-to-event outcomes, regression parameters are estimated by minimizing (Zou H. and Hastie T. 2005)
with respect to
. As in LASSO, in this paper, the tuning parameters
are obtained by minimizing the regularized objective function using an internal cross-validation.
2.3. Performance Measurements
In our simulation studies, we evaluate the variable selection performance of prediction methods by total selection (i.e. total number of selected covariates) and true selection (i.e. the number of selected covariates that are truly associated with the outcome). Let denote the vector of estimated regression coefficients and Z the vector of corresponding covariates. Then, represents the risk score of a subject with covariate Z. For a data set with a binary outcome, , the precision of a fitted prediction model can be evaluated by the AUC of an ROC curve generated by , where . A large AUC close to 1 means good accuracy of the fitted prediction model. On the other hand, for a data set with a survival outcome, , the precision of a fitted prediction model can be evaluated by calculating Harrell’s concordance C-index between and . For a survival outcome, we also calculate for the univariate Cox proportional hazards model to regress on . A large negative log p-value means a high accuracy of the fitted prediction model.
All modeling and analyses are conducted using open-source R software, version 3.6.0 (R Foundation for Statistical Computing).
3. Results
3.1. Impact of Over-Selection
At first, we investigate the impact of over-selection on prediction accuracy. Since, LASSO and EN do not control the number of selections, we use the standard logistic and Cox regression methods equipped with stepwise variable selection procedure, L-SVS and C-SVS respectively, that can control the number of selections by choosing different alpha levels for insertion and deletion.
We generate samples of candidate predictors from a multivariate Gaussian distribution with means 0 and variances 1, consisting of 10 independent blocks with block size 100. Each block has a compound symmetry correlation structure with a common correlation coefficient . We assume that or 10 true predictors of the candidate predictors are associated with the outcome.
At first, we consider a binary outcome case. For subject
with true predictors
, the binary outcome
is generated from a Bernoulli distribution with the logistic regression model
where
is a vector of regression coefficients corresponding to the true predictors
. We consider two scenarios for choosing true predictors: the first (S1) is to choose all
predictors in the first block and the second (S2) is to choose one predictor from each of
different blocks. The true regression coefficients are set at
and
is the intercept term. We use 50-50 hold out, i.e
samples for training and the remaining
samples for validation.
We apply L-SVS to each training set to fit a prediction model, and count the total selection and the true selection included in the fitted model. Let Z denote the vector of predictors selected for the fitted model and the vector of corresponding regression estimates. We estimate the AUC of the ROC curve using the fitted risk score and binary outcome using training set and validation set. We repeat this simulation times, and calculate mean total selection and true selection for training sets, and the mean AUC for training and validation sets. Note that the AUC for a training set measures how well the estimated prediction model fits the training data. Due to the over-fitting, the estimated model tends to fit the training set better by including more predictors in the model, so that the AUC from a training set does not measure the real prediction accuracy of a fitted model (Simon R et al. 2003). Instead, the true prediction accuracy of a fitted model will be measured by the AUC from an independent validation set. We use the stepwise variable selection procedure with various levels for inclusion by keeping the value for deletion twice the size of , i.e. .
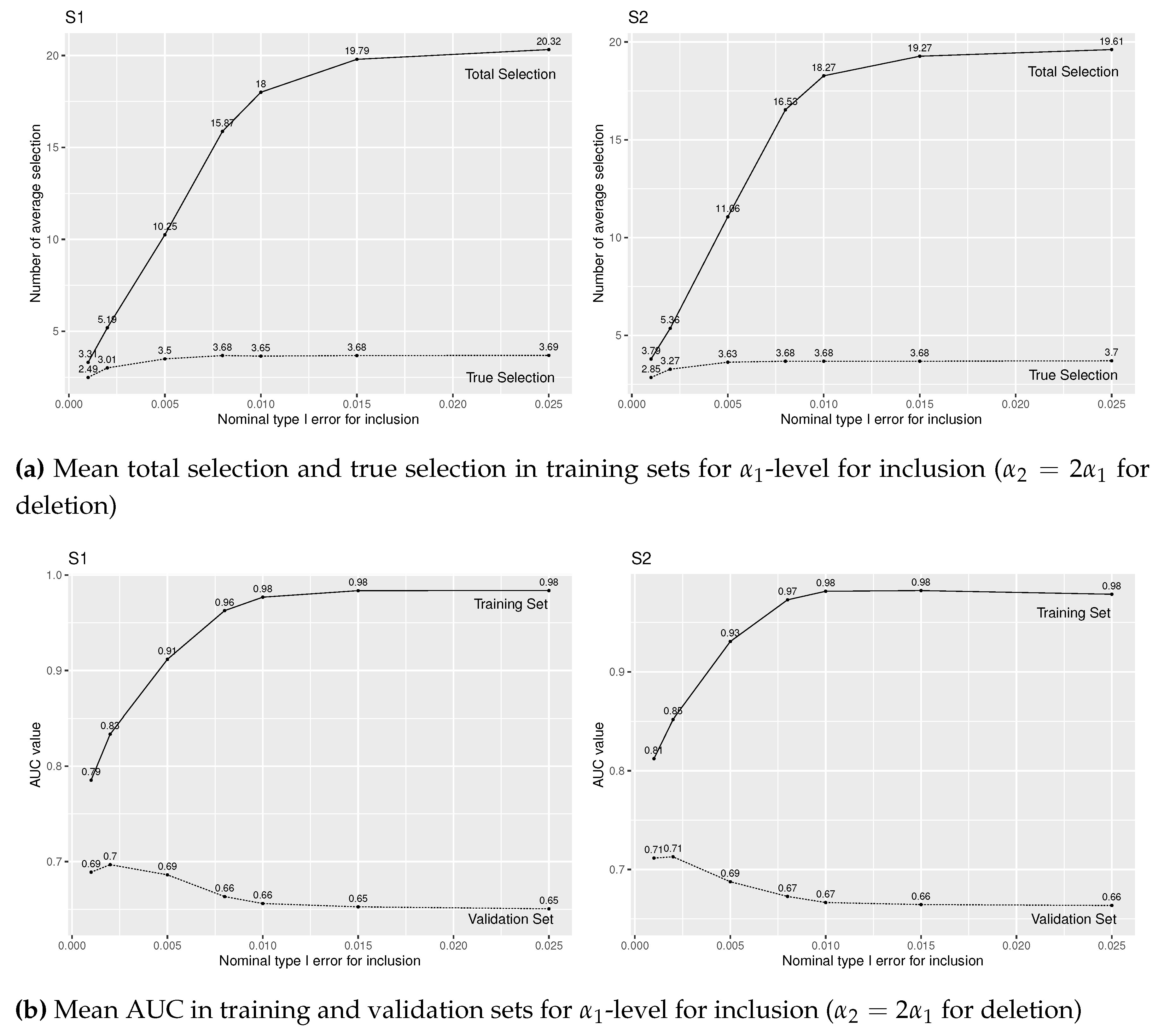
For , Figure 1(a) presents mean true selection (dotted line) and total selection (solid line) from training sets, and Figure 1(b) presents mean AUC for validation sets (dotted line) and training sets (solid line). We find that mean total and true selections quickly increases by increasing level up to 0.01, but becomes stable after that. Even though we increase over 0.01 level, L-SVS will not select much more predictors. On the other hand, from Figure 1(b), the prediction models fit training sets better (i.e. mean AUC increases) by increasing level and the models select more predictors. However, the prediction accuracy (AUC for validation sets) decreases for , probably because of the large number of falsely selected predictors. We observe similar results under (S1) and (S2) settings.
(Figure 1 may be placed around here.)
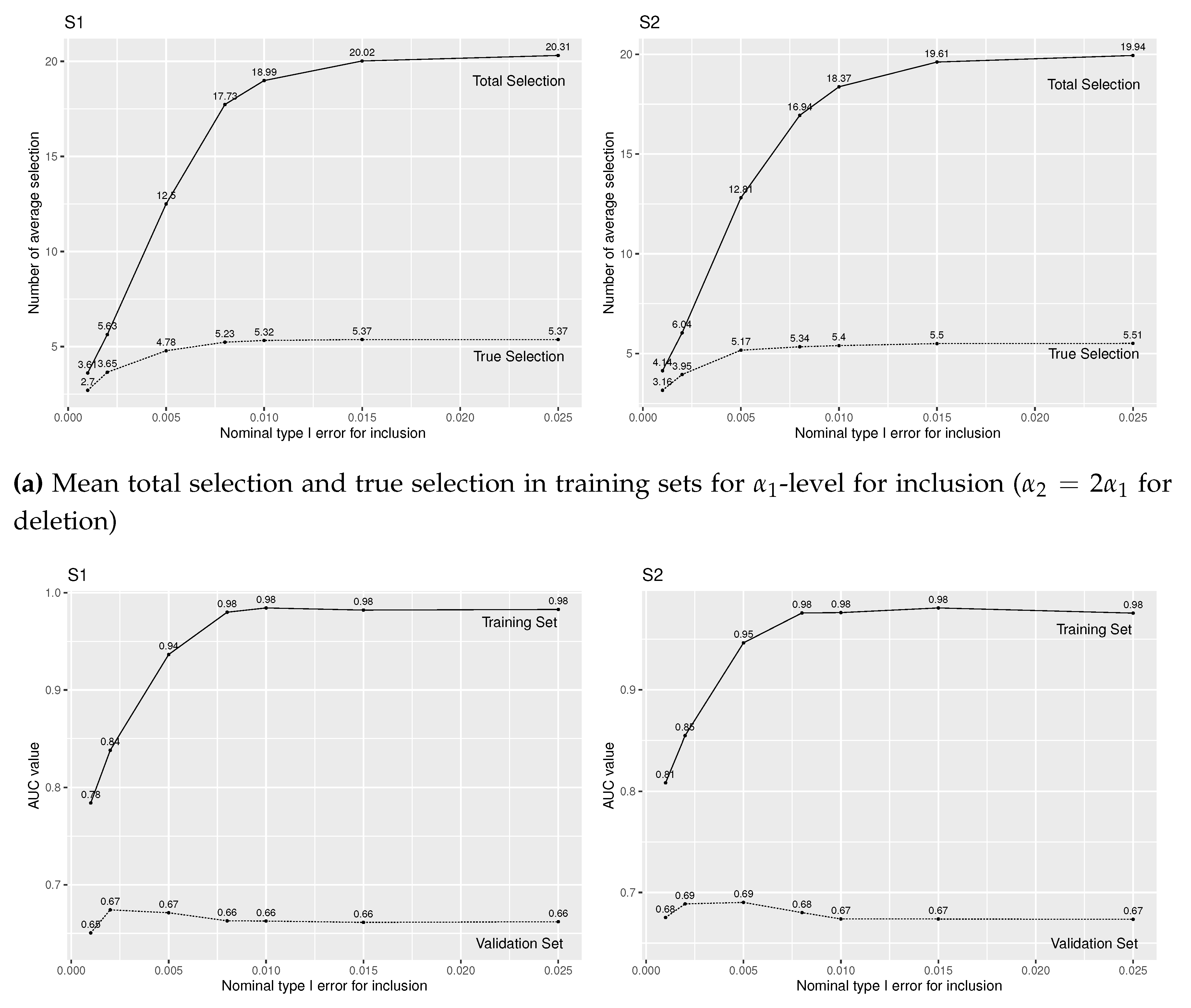
When , we observe similar results from Figure 2. The only difference is that, with a larger number of true predictors, the proportion of false selections is smaller (Figure 2(a)) than when (Figure 1(a)), so that the prediction accuracy decreases rather slowly than when after around (Figure 2(b)).
(Figure 2 may be placed around here.)
For simulations on survival outcomes, we generate covariate vectors as in the binary outcome case. For subject
with true predictors
, the hazard rate of the survival time is given as
where
is a vector of the regression coefficients for the true predictors
.
We set and under both (S1) and (S2). We assume or 10 true predictors. Censoring times are generated from a uniform distribution, for 30% of censoring for a selected accrual period a. With the accrual period a fixed, we also generate 10% of censoring from by a selected additional follow-up period b. We apply C-SVS to each training set. Let Z denote the vector of predictors selected by C-SVS and the vector of their regression estimates. We count the total selections and true selections from the fitted prediction model. We fit a univariate Cox regression of the survival outcome on a covariate using each of training and validation sets, and calculate the p-value. We also estimate the association between the risk score and the outcome by Harrell’s C-index using each of training and validation sets. Note that large p-value and C-index from the training set mean that the prediction model fits the training set well, while those from a validation set mean that the fitted prediction model has a high accuracy. From simulation replications, we calculate the mean total and true selections from training sets, and the mean p-value and C-index from training and validation sets. C-SVS is performed using various values with .
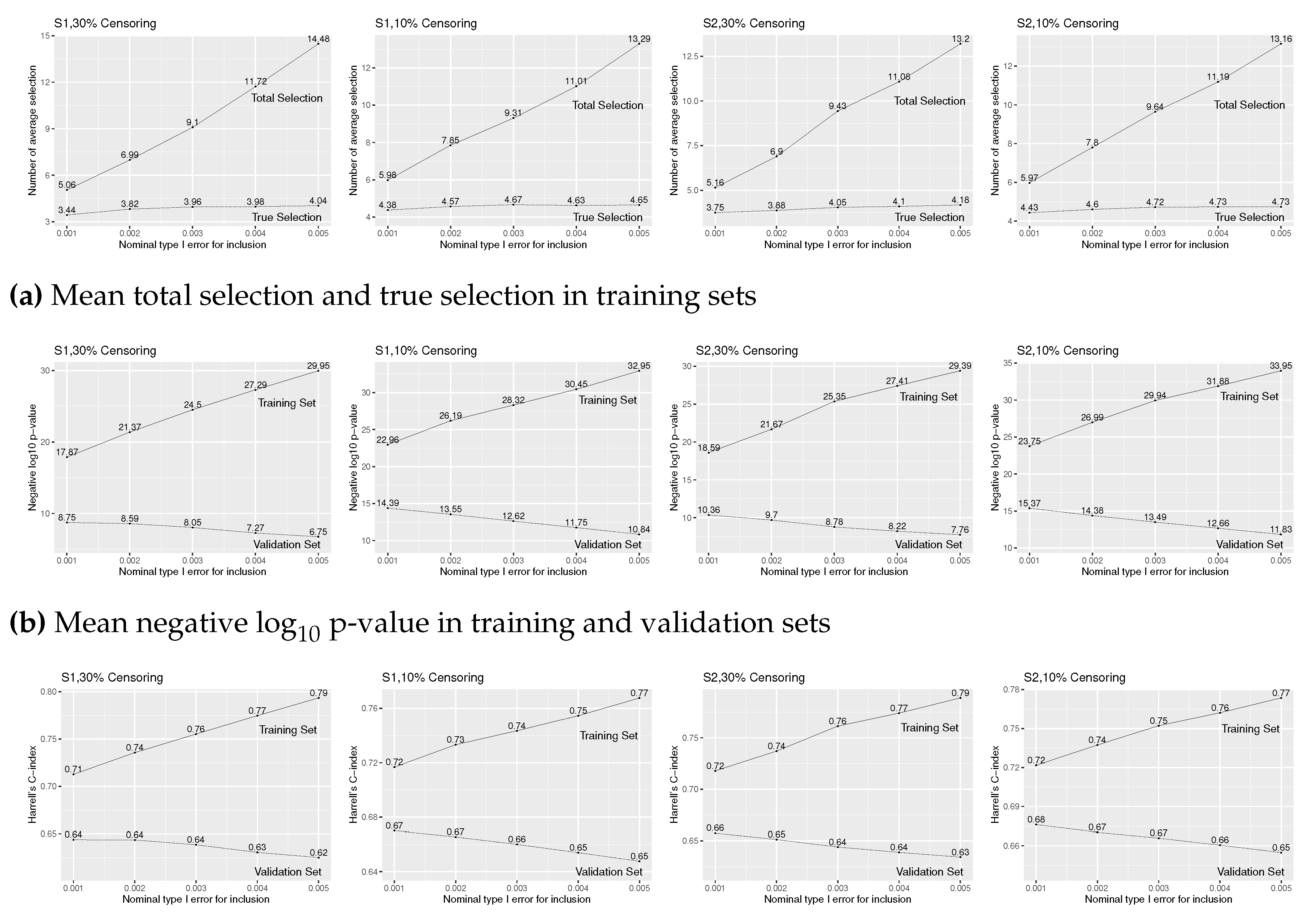
Figure 3 reports the simulation results for for a range of values. From Figure 3(a), we find that the true selection is slightly higher with 10% censoring for both (S1) and (S2) models. For both (S1) and (S2) and both 30% and 10% censoring, mean total and true selections increase in , so that p-value and C-index increase for training sets, the solid lines in Figure 3(b) and (c). By increasing , however, the number of false selections also increases, so that p-value and C-index decrease for validation sets, the dotted lines in Figure 3(b) and 3(c). That is, over-selection lowers the accuracy of fitted prediction models.
(Figure 3 may be placed around here.)
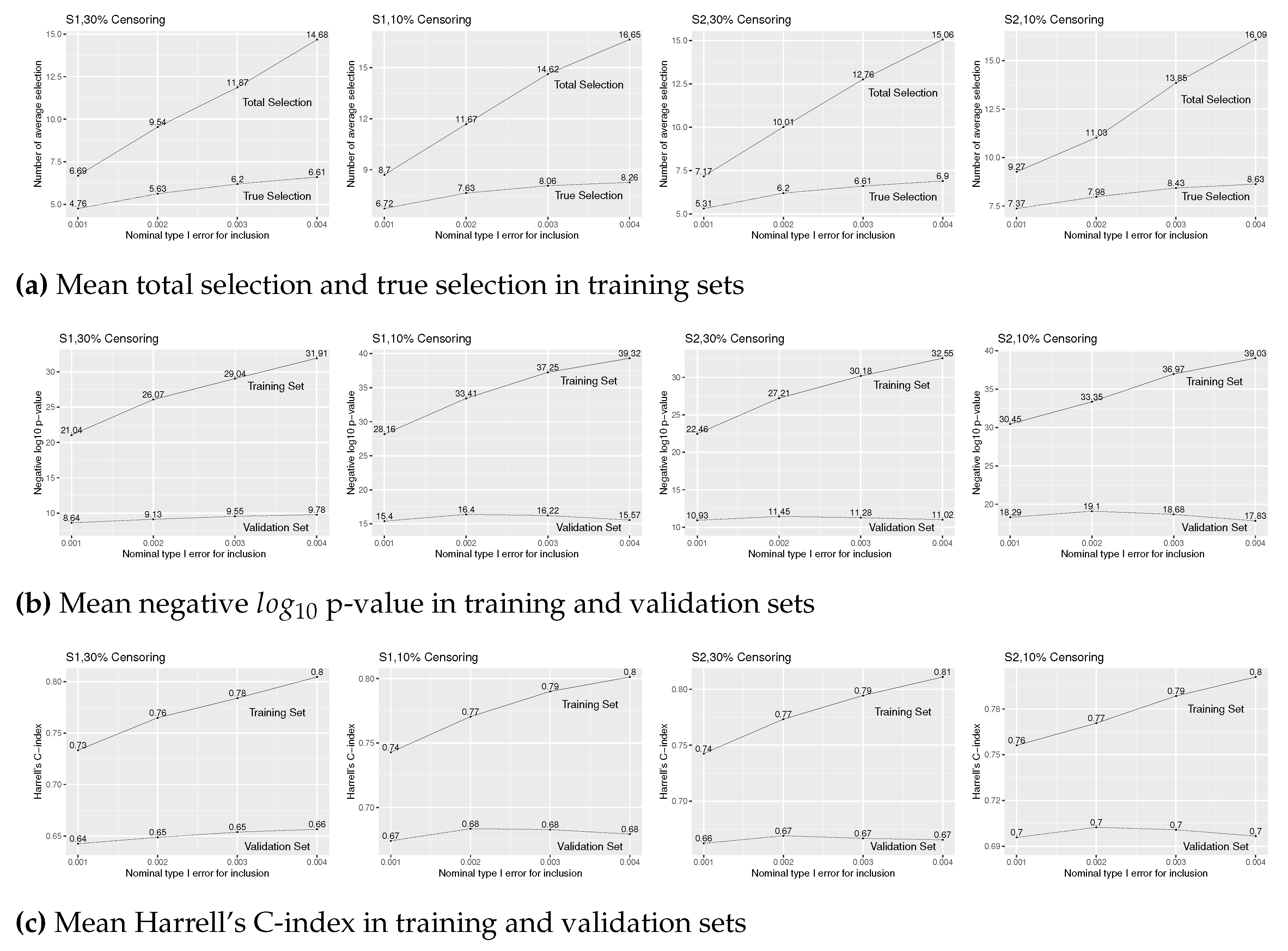
Figure 4 reports the simulation results for . The mean total and true selections (Figure 4(a)), and p-value and C-index for training sets (the solid lines of Figure 4(b) and (c)) increase in as in the case of . With a larger number of true predictors, however, due to the increase in the proportion of false selections, the prediction accuracy, that are measured by p-value and C-index in validation sets (the dotted lines of Figure 4(b) and (c)), decreases after a brief increase up to , except for model (S1) with 10% of censoring.
(Figure 4 may be placed around here.)
3.2. Comparison of Prediction Methods
Using the simulation data sets for Figures 1 and 2, we compare the performance of LASSO, EN, and L-SVS with . By applying each of these prediction methods to each training set, we estimate the same performance measures of Figures 1 and 2. The simulation results are summarized in Table 1. Since -norm penalty is stricter than -norm penalty, LASSO has smaller true selections than EN which employs a combination of - and -norm penalties. Note that LASSO and EN select large number of predictors while L-SVS selects only slightly over 5 predictors in total. By selecting a large number of predictors, the two ML methods have a slightly larger true selection and slightly better fitting (i.e. a larger AUC) than L-SVS for training sets. For validation sets, however, AUCs of the ML methods are no larger than that of L-SVS. We have this kind of results because the large false selections of the ML methods act like error terms and lower the prediction accuracy. L-SVS has better (or comparable under S2) prediction accuracy even with a slightly smaller number of true selections (and much smaller total selections under S2) than LASSO and EN. Overall, we have similar simulation results between (S1) and (S2). In conclusion, we find that good fitting (high AUC) of training sets is not necessarily translated into high prediction accuracy (AUC of validation sets) because of the increased false selections. With a larger number of true predictors (), the mean true selection increases, but the mean false selection increases as well, so that the prediction accuracy is about the same as that for .
(Table 1 may be placed around here.)
Using the simulation data for Figures 3 and 4, we compare the performance of LASSO, EN and C-SVS with for survival outcomes. Table 2 reports the simulation results. As in the binary outcome case, the two ML methods have much larger mean total selection and slightly larger true selection compared to C-SVS. With a lower censoring (10%), each method has larger mean total and true selections, better model fitting (in terms of p-value and C-index for training sets), and higher prediction accuracy (in terms of p-value and C-index for validation sets). Between models (S1) and (S2), with 30% of censoring, the prediction methods tend to have slightly larger mean total and true selections, and larger negative log10(p-value) and C-index for both training and validation sets for model (S2). However, with 10% of censoring, these measures are similar between (S1) and (S2). The mean total and true selections are larger with than with . Between the two ML methods, LASSO has slightly higher prediction accuracy (in terms of p-value and C-index for validation sets) than EN overall, probably due to the higher over-selection. In spite of the slightly lower true selection, C-SVS has higher prediction accuracy than the two ML methods with 10% of censoring or with , (S2), and 30% of censoring. Under the other simulation settings, the three prediction methods have similar prediction accuracy.
(Table 2 may be placed around here.)
3.3. Real Data Analysis
Farrow NE et al. (2021) used the Nanostring nCounter PanCancer Immune Profiling Panel to quantify the expression level of 730 immune-related genes in sentinel lymph node (SLN) specimens from patients (31 positive, 29 negative) from a retrospective melanoma cohort. Since a significant proportion of patients experience recurrence of melanoma after surgery, early detection of poor prognosis and adjuvant therapy may eliminate residual disease and improve the patients’ prognosis. We want to predict SLN positivity and recurrence-free survival (RFS) using the microarray data and baseline characteristics such as gender, age at surgery, and use of additional treatment (add_trt).
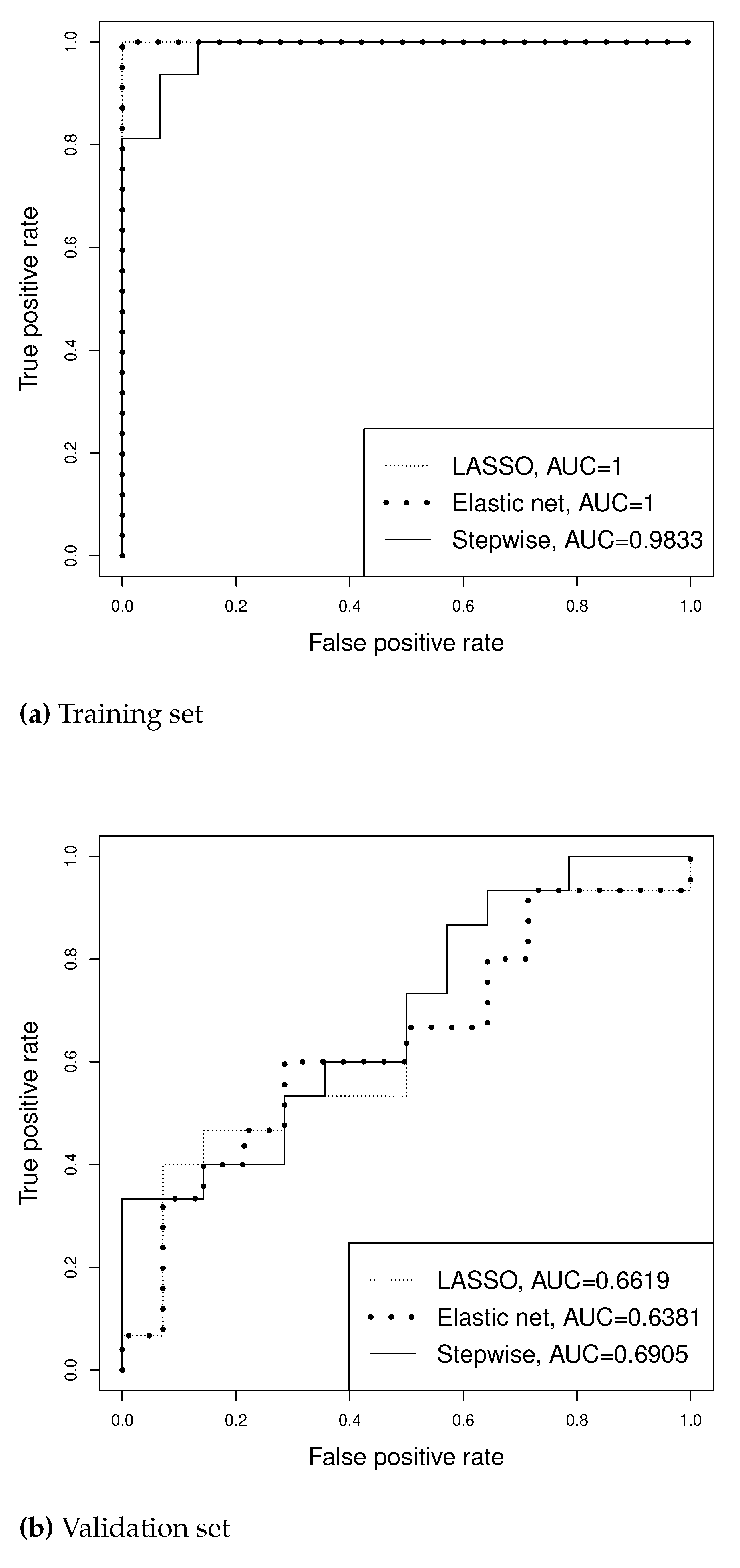
For the binary outcome of SLN positivity, we randomly partition the 60 patients into a training set and a validation set so that the two sets have similar number of SLN positive and negative cases. We apply LASSO, EN and L-SVS with to the training set. Figure 5 reports the ROC curves for the training set and validation set. Due to over-fitting, all three methods have large AUCs for the training set. For the validation set, however, EN has smaller AUC than the other methods, while L-SVS has the largest AUC. Table 3 presents more analysis results. While L-SVS selects only four covariates (two of which are also selected by LASSO and three of which are also selected by EN) as significant predictors, it has the highest prediction accuracy (AUC-validation) among the three prediction methods. Lasso and EN select the same number of predictors, but slightly different sets.
(Figure 5 and Table 3 may be placed around here.)
For the time-to-event endpoint of RFS, we randomly partition the 60 patients into a training set and a validation set so that the two sets have similar number of events and censored cases. We apply EN, LASSO, and C-SVS with to the training set. The analysis results are reported in Table 4. As in the analysis of SLN positivity, C-SVS selects the smallest number of predictors, but it has the highest prediction accuracy in terms of p-value for validation set among the three methods and higher prediction accuracy than EN in terms of C-index for validation set. Both the prediction model by L-SVS and C-SVS selected add_trt and three genes.
(Table 4 may be placed around here.)
In order to see if each prediction method really selects significant features, we fit a multivariate Cox regression model of RFS on the selected features using the training set of Farrow et al. data, and summarize the result in Table 5. Note that add_trt and GE_NEFL are selected by all three methods, but their significance diminishes for EN, probably because their effects are diluted by many of less significant features selected together. While LASSO and EN select many insignificant features, C-SVS selects a set of significant features only by using stepwise variable selection procedure.
(Table 5 may be placed around here.)
4. Discussion
LASSO and EN have been widely used to develop prediction models using high dimensional data. Recent recognition of ML methods prompts collective investment and applications which not only stimulate the development of clinical medicine but also induce potential overuse risk. Systematic reviews have been conducted to show that LASSO and EN tend to over-select predictors for fitted prediction models. This leads some additional costs as discussed in the Introduction section and unfavorable prediction accuracy. As an alternative approach, we have investigated standard regression methods combined with stepwise variable selection procedure (R-SVS) compared with LASSO and EN. Through simulations and real data analysis, we found that the ML methods do over-select predictors, over-fit training sets, and, consequently, lose prediction accuracy. In contrast, R-SVS selects much smaller number of predictors and fitted prediction models have comparable or better accuracy than LASSO and EN.
From this research, we find that R-SVS provides very efficient prediction models with easy and fast computing. SAS provides variable selection procedures for regression methods based on information (such as AIC and BIC) or R-square only, so that they can not control the selection of predictors like LASSO and EN. So, we developed R programs for R-SVS based on the significance level of regression coefficients. Even though standard regression methods are not appropriate for high dimensional data, those combined with stepwise variable selection procedure work perfectly as far as the number of true predictors is much smaller than the sample size. Note that the backward deletion method is not appropriate for high dimensional data because it starts to fit the full model with all candidate predictors. Since regression methods are well developed for any type of outcomes, R-SVS can be used for any type of regression methods. Furthermore, R-SVS is a standard statistical method, so that statisticians without deep knowledge in bioinformatics can use it for prediction model fitting with high dimensional data.
Some may claim that LASSO and EN have computing power which takes less time to train models while step-wise selection takes much longer. Logistic regression or Cox regression with forward stepwise variable selection spends most of running time performing hypothesis testing and the p-value of a potential covariate is the criterion for inclusion or deletion. The reason why LASSO and EN are faster origins from their different variable selection scheme. Instead of conducting hypothesis testing, LASSO and EN select covariates based on the size of regression coefficients. They apply regularization with penalized likelihood to increase prediction performance with the sacrifice of interpretability.
While R-SVS has very few false selections, it has lower true selections than LASSO and EN also, so that its prediction accuracy is not much higher than the latter. It would be challenging to develop a prediction method to increase the true selections while maintaining the false selections low and to drastically improve the prediction accuracy.
We have illustrated the potential drawback and risk of LASSO and EN for clinical projects. However, we are not discouraging the development of ML methods, since they are still trendy and powerful for prediction using high dimensional data. We want to make it clear that the prediction methods we have considered in this paper are appropriate only when the number of true predictors is small and variable selection (or dimension reduction) is one of main goals. In some areas, such as medical image analysis, text mining, and speech recognition, all collected predictors have information on the outcome. In such cases, deep learning method has been one of the most powerful approaches, but those investigated in this paper may not be much useful.
Author Contributions
LL conducted simulation study and data analysis, and wrote the manuscript with SJ. SJ guided LL through the simulation studies and real data analysis. GB provided the real data and helped with the interpretation of analysis results jointly with JG. All authors read and approved the final manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated or analysed during this study are included in this published article [and its supplementary information files].
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest..
Abbreviations
The following abbreviations are used in this manuscript:
| AIC |
Akaike information criterion |
| AUC |
area under the curve |
| BIC |
Bayesian information criterion |
| C-SVS |
Cox regression with forward stepwise selection |
| EN |
elastic net |
| LASSO |
least absolute shrinkage and selection operator |
| L-SVS |
logistic regression with forward stepwise selection |
| ML |
machine learning |
| MLE |
maximu likelihood estimation |
| RF |
random forest |
| ROC |
receiver operating characteristic |
| R-SVS |
regression methods with stepwise selection |
| SLN |
sentinel lymph node |
| SVS |
stepwise variable selection |
Appendix A. Tables
Table A1.
Binary outcome: Simulation results (mean total selections and true selections from training sets, and mean AUC from training and validation sets) of the three prediction methods with true covariates and with S1 and S2 models. L-SVS (logistic regression with stepwise variable selection) uses .
Table A1.
Binary outcome: Simulation results (mean total selections and true selections from training sets, and mean AUC from training and validation sets) of the three prediction methods with true covariates and with S1 and S2 models. L-SVS (logistic regression with stepwise variable selection) uses .
| |
(S1) |
|
(S2) |
| |
LASSO |
EN |
L-SVS |
|
LASSO |
EN |
L-SVS |
| |
(i)
|
| Total Selections |
31.15 |
74.59 |
5.32 |
|
28.59 |
56.61 |
5.32 |
| True Selections |
4.03 |
4.49 |
3.25 |
|
4.28 |
4.60 |
3.25 |
| AUC-Training |
0.92 |
0.95 |
0.84 |
|
0.92 |
0.95 |
0.85 |
| AUC-Validation |
0.70 |
0.69 |
0.71 |
|
0.72 |
0.71 |
0.71 |
| |
(ii)
|
| Total Selections |
34.64 |
101.47 |
5.63 |
|
44.56 |
84.76 |
6.88 |
| True Selections |
6.73 |
7.92 |
3.60 |
|
7.76 |
8.19 |
4.31 |
| AUC-Training |
0.92 |
0.96 |
0.83 |
|
0.96 |
0.97 |
0.87 |
| AUC-Validation |
0.69 |
0.68 |
0.67 |
|
0.73 |
0.72 |
0.70 |
Table A2.
Survival outcome: Simulation results (mean total selections and true selections from training sets, and mean and C-index from both training and validation sets) of the three prediction methods with or 10 true covariates with (S1) and (S2) models. C-SVS (Cox regression with stepwise variable selection) uses .
Table A2.
Survival outcome: Simulation results (mean total selections and true selections from training sets, and mean and C-index from both training and validation sets) of the three prediction methods with or 10 true covariates with (S1) and (S2) models. C-SVS (Cox regression with stepwise variable selection) uses .
| |
(S1) |
|
(S2) |
| |
LASSO |
EN |
C-SVS |
|
LASSO |
EN |
C-SVS |
| |
(i) & 30% Censoring |
| Total Selections |
16.51 |
24.30 |
4.80 |
|
19.28 |
25.89 |
5.37 |
| True Selections |
4.11 |
4.46 |
3.53 |
|
4.45 |
4.53 |
3.78 |
|
(training) |
22.79 |
26.25 |
17.32 |
|
25.76 |
28.24 |
19.68 |
|
(validation) |
9.06 |
8.76 |
9.79 |
|
10.45 |
10.20 |
10.41 |
| C-index (training) |
0.74 |
0.76 |
0.71 |
|
0.76 |
0.77 |
0.73 |
| C-index (validation) |
0.64 |
0.64 |
0.65 |
|
0.66 |
0.66 |
0.66 |
| |
(ii) & 10% Censoring |
| Total Selections |
20.16 |
23.89 |
5.74 |
|
20.96 |
25.00 |
5.86 |
| True Selections |
4.61 |
4.82 |
4.44 |
|
4.78 |
4.82 |
4.43 |
|
(training) |
27.60 |
29.72 |
22.51 |
|
29.73 |
31.61 |
23.83 |
|
(validation) |
12.89 |
12.88 |
14.95 |
|
14.66 |
14.39 |
15.69 |
| C-index (training) |
0.74 |
0.75 |
0.71 |
|
0.75 |
0.76 |
0.72 |
| C-index (validation) |
0.66 |
0.66 |
0.67 |
|
0.67 |
0.67 |
0.68 |
| |
(iii) & 30% Censoring |
| Total Selections |
26.68 |
36.83 |
6.57 |
|
30.35 |
37.73 |
7.85 |
| True Selections |
7.52 |
8.26 |
4.89 |
|
8.44 |
8.61 |
5.69 |
|
(training) |
30.12 |
34.26 |
20.61 |
|
34.18 |
36.50 |
24.90 |
|
(validation) |
9.89 |
9.87 |
9.07 |
|
13.07 |
12.87 |
11.48 |
| C-index (training) |
0.78 |
0.81 |
0.73 |
|
0.81 |
0.82 |
0.76 |
| C-index (validation) |
0.66 |
0.66 |
0.64 |
|
0.69 |
0.69 |
0.67 |
| |
(iv) & 10% Censoring |
| Total Selections |
29.46 |
36.69 |
8.52 |
|
32.47 |
37.53 |
9.65 |
| True Selections |
8.56 |
8.85 |
6.69 |
|
9.10 |
9.32 |
7.71 |
|
(training) |
36.21 |
38.68 |
27.61 |
|
39.76 |
41.38 |
32.14 |
|
(validation) |
14.77 |
14.44 |
15.62 |
|
18.44 |
18.26 |
19.54 |
| C-index (training) |
0.78 |
0.79 |
0.74 |
|
0.80 |
0.80 |
0.76 |
| C-index (validation) |
0.67 |
0.67 |
0.68 |
|
0.70 |
0.70 |
0.70 |
Table A3.
Analysis results of Farrow et al. data on SLN positivity.
Table A3.
Analysis results of Farrow et al. data on SLN positivity.
| |
# Selected |
AUC |
|
| Method |
Features |
Training |
Validation |
Selected Features |
| LASSO |
13 |
1.0000 |
0.6619 |
add_trt, GE_CCL1, GE_CLEC6A, |
| |
|
|
|
GE_HLA_DQA1, GE_IL1RL1, GE_IL25, |
| |
|
|
|
GE_MAGEA12, GE_MASP1, GE_MASP2, |
| |
|
|
|
GE_PRAME, GE_S100B, GE_SAA1, |
| |
|
|
|
GE_USP9Y |
| Elastic Net |
13 |
1.0000 |
0.6381 |
add_trt, GE_CCL1, GE_CLEC6A, |
| |
|
|
|
GE_HLA_DQA1, GE_IL1RL1, GE_IL1RL2, |
| |
|
|
|
GE_IL25, GE_MASP1, GE_MASP2, |
| |
|
|
|
GE_PRAME, GE_S100B, GE_SAA1, |
| |
|
|
|
GE_USP9Y |
| L-SVS |
4 |
0.9833 |
0.6905 |
add_trt, GE_IL1RL1, GE_IL17F, GE_IL1RL2 |
Table A4.
Analysis results of Farrow et al. data on recurrence-free survival.
Table A4.
Analysis results of Farrow et al. data on recurrence-free survival.
| |
# Selected |
p-value |
C-index |
| Method |
Features |
Training |
Validation |
Training |
Validation |
| LASSO |
5 |
3.7153 |
1.3623 |
0.8848 |
0.6959 |
| Elastic Net |
11 |
3.8872 |
1.1965 |
0.9058 |
0.6701 |
| C-SVS |
4 |
3.1182 |
1.4518 |
0.9634 |
0.6907 |
| |
Selected Features |
| LASSO |
add_trt, GE_CCL3, GE_CCL4, GE_IL17A, GE_NEFL |
| Elastic Net |
add_trt, GE_CCL3, GE_CCL4, GE_CRP, GE_CXCL1, |
| |
GE_CXCR4, GE_HLA_DRB4, GE_IL17A, GE_IL8, |
| |
GE_MAGEA12, GE_NEFL |
| C-SVS |
add_trt, GE_NEFL, GE_IFNL1, GE_MAGEC1 |
Table A5.
Multivariate Cox regression on recurrence-free survival using the training set of Farrow et al. data.
Table A5.
Multivariate Cox regression on recurrence-free survival using the training set of Farrow et al. data.
| LASSO |
|
Elastic Net |
|
C-SVS |
| Feature |
Coef. |
p-value |
|
Feature |
Coef. |
p-value |
|
Feature |
Coef. |
p-value |
| add_trt |
4.558 |
0.004 |
|
add_trt |
3.021 |
0.251 |
|
add_trt |
5.352 |
0.001 |
| GE_CCL3 |
3.634 |
0.153 |
|
GE_CCL3 |
0.094 |
0.908 |
|
GE_NEFL |
|
0.006 |
| GE_CCL4 |
1.163 |
0.563 |
|
GE_CCL4 |
6.818 |
0.693 |
|
GE_IFNL1 |
0.146 |
0.003 |
| GE_IL17A |
6.268 |
0.073 |
|
GE_CRP |
|
0.191 |
|
GE_MAGEC1 |
|
0.011 |
| GE_NEFL |
|
0.023 |
|
GE_CXCL1 |
7.499 |
0.164 |
| |
|
|
|
GE_CXCR4 |
|
0.548 |
| |
|
|
|
GE_HLA_DRB4 |
|
0.412 |
| |
|
|
|
GE_IL17A |
5.879 |
0.202 |
| |
|
|
|
GE_IL8 |
|
0.802 |
| |
|
|
|
GE_MAGEA12 |
|
0.846 |
| |
|
|
|
GE_NEFL |
|
0.736 |
|
|
|
|
Appendix B. Figures
Figure A1.
Simulation results of logistic regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), and true covariates
Figure A1.
Simulation results of logistic regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), and true covariates
Figure A2.
Simulation results of logistic regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), and true covariates
Figure A2.
Simulation results of logistic regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), and true covariates
Figure A3.
Simulation results of Cox regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), 30% and 10% censoring, and true covariates
Figure A3.
Simulation results of Cox regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), 30% and 10% censoring, and true covariates
Figure A4.
Simulation results of Cox regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), 30% and 10% censoring, and true covariates
Figure A4.
Simulation results of Cox regression with forward stepwise variable selection for various level for insertion and for deletion under (S1) and (S2), 30% and 10% censoring, and true covariates
Figure A5.
ROC curves from prediction of SLN positivity using different methods for Farrow et al. data
Figure A5.
ROC curves from prediction of SLN positivity using different methods for Farrow et al. data
References
- Christodoulou E et al. (2019) A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J Clin Epidemiol., 110:12-22. [CrossRef]
- Cox, D. R. (1972) Regression Models and Life-Tables. Journal of the Royal Statistical Society. Series B (Methodological), 34(2), 187–220.
- Engelhard MM et al. (2021) Incremental Benefits of Machine Learning—When Do We Need a Better Mousetrap. JAMA Cardiol., 6(6):621–623. [CrossRef]
- Farrow NE et al. (2021) Characterization of Sentinel Lymph Node Immune Signatures and Implications for Risk Stratification for Adjuvant Therapy in Melanoma. Ann Surg Oncol., 28(7):3501-3510. [CrossRef]
- Jing B et al. (2022) Comparing Machine Learning to Regression Methods for Mortality Prediction Using Veterans Affairs Electronic Health Record Clinical Data. Medical Care, 60(6):470-479. [CrossRef]
- Kattan MW. (2003) Comparison of Cox regression with other methods for determining prediction models and nomograms. J Urol., 170(6 Pt 2):S6-10. [CrossRef]
- Khera R et al. (2021) Use of Machine Learning Models to Predict Death After Acute Myocardial Infarction. JAMA Cardiol., 6(6):633–641. [CrossRef]
- Kuhle S et al. (2018) Comparison of logistic regression with machine learning methods for the prediction of fetal growth abnormalities: a retrospective cohort study. BMC Pregnancy Childbirth, 18(1):333. [CrossRef]
- Piros P et al. (2019) Comparing machine learning and regression models for mortality prediction based on the Hungarian Myocardial Infarction Registry. Knowledge-Based Systems, 179(1):1-7. [CrossRef]
- Simon R et al. (2003) Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification. Journal of National Cancer Institute, 95:14–8. [CrossRef]
- Song X et al. (2021) Comparison of machine learning and logistic regression models in predicting acute kidney injury: A systematic review and meta-analysis. International Journal of Medical Informatics, 151:104484. [CrossRef]
- Stylianou N et al. (2015) Mortality risk prediction in burn injury: Comparison of logistic regression with machine learning approaches. Burns, 41(5):925-934. [CrossRef]
- Tibshirani R. (1996) Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1), 267-288.
- Tibshirani R. (1997) The lasso Method for Variable Selection in the Cox Model. Statistics in Medicine, 16 (4): 385–395. [CrossRef]
- ToTolles J and Meurer WJ (2016) Logistic Regression: Relating Patient Characteristics to Outcomes. JAMA, 316(5):533–534. [CrossRef]
- Zou H. and Hastie T. (2005) Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society. Series B (Statistical Methodology), 67(2), 301-320. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).