Prerpints.org logo
Preprint
Article

Assessment of Machine Learning Algorithms in Predicting Air Entrainment Rates in a Confined Plunging Liquid Jet Reactor

Altmetrics

Downloads

113

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 August 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
: The effects of the main parameters on the air entrainment rate, Qa, were investigated experimentally in a confined plunging liquid jet reactor CPLJR. Various downcomer diameters (Dc), jet lengths (Lj), liquid volumetric flow rates (Qj), nozzle diameters (dn), and jet velocity (Vj) were used to measure air entrainment, Qa. The non-linear relationship between the air entrainment ratio and confined plunging jet reactor parameters suggests that applying unconventional regression algorithms to predict the air entrainment ratio is appropriate. This study applied machine learning algorithms to the confined plunging jet reactor parameters to predict Qa. The obtained results showed that K-Nearest Neighbour (KNN) gave the best prediction abilities, R2 = 0.900, RMSE = 0.069, and MAE = 0.052. The sensitivity analysis was applied to determine the most effective predictor. The liquid volumetric flow rate (Qj) and jet velocity (Vj) were the most influential among all the input variables. Our findings support using machine learning algorithms to accurately forecast the CPLJR system’s experimental results.
Keywords: 
Subject: Environmental and Earth Sciences  -   Sustainable Science and Technology

1. Introduction

The aeration procedure is crucial in the treatment of water and wastewater. Diffusers for submerged aeration devices and mechanical surface aerators for the dispersion of atmospheric oxygen into the sewerage water surface are examples of aeration systems for wastewater treatment. Sewage treatment utilizing natural techniques is a perceived strategy where an aeration system distributes oxygen into the wastewater to deliver the oxygen needs of microbes to oxidize the natural matter. In general, the presence of a huge air–water interfacial area results in the absorption of atmospheric oxygen from the air, generating massive instability in the liquid with the emergence of a submerged two-phase zone, and the oxygen is subsequently distributed into the liquid body by diffusion and convection.
A plunging liquid jet can offer robust gas–liquid interaction and distribution of tiny bubbles in the liquid while increasing the mass transfer rate by increasing the gas–liquid interfacial area. As a result, this technique can be used to bring air into a body of water, control the oxygen concentration, and mix the water efficiently at low capital and operating cost [1]. Air entrainment by a plunging water jet is common in both nature and engineering.
Because of their low installation, operating, and maintenance expenses, jet aerators are an effective alternative for processing biological liquid waste [2,3]. The jet is intended to plunge through the headspace and impinge on a pool of receiving water that collects a substantial amount of ambient air. It creates a vast agitation area at the water surface due to its contact, leading to higher oxygen transfer with lower energy consumption. This procedure is recognized as plunging liquid jet reactor (PLJR) aeration.
There have been numerous research studies on the impact of jet variables in plunging jets on water oxygenation effectiveness. Harby et al. (2014), Qu et al. (2011), AL-Anzi (2007), and Van de Sande and Smith (1975) looked at the oxygen transfer from bubbles below the water’s surface caused by the effect of a plunging water jet [4,5,6,2]. Tojo and Miyanami (1982) explained the mass transfer properties of a gas–liquid jet mixer with cylindrical and rectangular tanks by employing a downflow jet or an up-flow jet [7]. Bagatur et al. (2002) tested numerous circular, elliptical, and rectangular nozzle shapes with rounded ends and a 45° penetration angle, finding that the expansion of a water jet with a lesser depth of penetration resulted in significantly greater absorption of air and oxygen transfer ability than other shaped nozzles due to water jet expansion [8]. In the research by Baylar and Emiroglu (2003), Emiroglu and Baylar (2003)m and Ohkawa et al. (1986), the water jet expansion, air entrainment rate, depth of penetration, and oxygen transfer performance of various shaped nozzles with air holes at varied places were examined [8,9,10,11]. S Ranjan (2008) and Subodh Ranjan (2007) conducted research on expansion and hollow jet aerators [12,13]. Deswal (2011) explored the capability of supporting vector machines and Gaussian process regression methods for demonstrating the overall volumetric transfer coefficient of numerous plunging jet frameworks, and He recommended that the supporting vector machines method functions admirably by both exact connections, and a Gaussian process could be utilized efficiently in oxygen transfer modelling[14]. Some studies utilized artificial neural network (ANN) and Gaussian process network (GPN) methods to show air entrainment rates by plunging jets, contrasting these demonstrative strategies, exploratory information, and consequences of multiple linear regression (MLR)/multiple non-linear regression (MNLR) and different conditions existing in previous studies. After sensitivity evaluation, the nozzle diameter was shown to be the most important parameters on the volumetric air entrainment rate with water jet variables [15,16]. The studies show that the reactor parameters affect the aeration performance in the plunging liquid jet reactor (PLJR). Experimental research shows that even if new devices are incorporated into the PLJR, the new device parameters still affect the net air entrainment rate Q a n e t . Al-Anzi and Fernandes (2023) incorporated a newly invented Al-Anzi disentrainment ring (ADR) device with a confined plunging liquid jet reactor (CPLJR) to investigate the net air entrainment rate enhancement [17]. The results showed that the ADR new variables (distance from the end of ADR to the receiving pool d s and ADR length l A D R ) positively impacted the Q a n e t ; for the same ADR device, shorter d s and l A D R   produced higher Q a n e t .
For decades, the plunging jet reactor concept has been used to generate high mass transfer rates by entraining gas bubbles into a liquid while maintaining low capital and operational expenses [1]. The application of machine learning (ML) algorithms in confined plunging liquid jets (CPLJR) remains an interesting part of research due to the gap in the literature concerning the application of ML in CPLJR. Therefore, it is essential to define the most critical plunging jet parameter that influences the final outcome results, enabling designers to choose the best combinations of parameters to provide a high air entrainment rate, and thus enhance the oxygen mass transfer rate at a reasonable power input.
The treatment of wastewater is an important step in reducing aqueous pollution and improving water quality. The configuration of wastewater is extremely diverse, with influent qualities, pollutant concentrations, and treated effluent differing dramatically amongst wastewater treatment plants [18]. Wastewater treatment plants (WWTPs) are complicated, non-linear systems with large swings in flow rate, pollutant load, chemical environment, and hydraulic characteristics. Modelling WWTP procedures is difficult due to these complications and uncertainty [19,20]. Activated sludge models (ASMs) and other biological models have been extensively utilized to evaluate WWTP operations and estimate the behaviour of multiple factors [21,22,23,24].
Nevertheless, mechanistic models require a lot of assumptions and explanations to be workable and consistent; hence, they have a lot of constraints, such as, ASMs are only valid under specified temperature, pH, and alkalinity limits. Furthermore, due to variations in methodologies used to calculate state variables, linking multiple mechanistic models that replicate processes in different units is difficult, for example, Total Suspended Solids (TSS) is calculated and included uniquely in ASMs and second clarifier models [25]. Other inherent flaws of mechanistic models include difficulty in thoroughly replicating multiple processes, significant costs, and poor generalization performance [26]. Because they are entirely dependent on finding correlations between output and input data that allow projections and/or assist decisions, machine learning (ML) models overcome many of these restrictions [27]. The fact that ML models represent real reaction/process conditions rather than mechanisms defined in advance relying on core concepts is a significant advantage. As a result, they’re reliable and thorough, which is significant because many of the processes entangled in wastewater treatment are still unknown [28,29]. As a result, ML modelling of WWTPs is commonly employed as an alternative to mechanistic modelling [26,30,31].
In WWTPs, several researchers have been working on long-term wastewater regulation [32,33,34]. ML technology has the potential to recover clean water, electricity, and different elements from wastewater. Wastewater treatment could enhance environmental quality and offer potential economic advantages while also saving water [35]. The wastewater treatment ability achieved by contact aeration for groundwater recharge was evaluated using a known neural network model [36]. The rainfall index was used as a valuable input in the model to improve the economic viability of wastewater treatment, and decisions were made based on the climatic conditions. Akhoundi and Nazif (2018) selected wastewater treatment applications and treatment technologies using evidence-based argumentation approaches [37]. Agricultural irrigation, artificial groundwater recharge, and industrial applications were the most common uses for wastewater treatment—the evidence-based reasoning strategy allowed for a coordinated and complete assessment of wastewater treatment feasibility.
Artificial neural networks (ANNs) are a popular ML technique that is based on biological neurons [38]. ANNs can tackle multivariate non-linear problems when given a suitable training technique and enough data [39]. ANNs are also widely used in methodological approaches to eliminate pollutants from water and wastewater. To build black-box representations of systems, ANNs use extremely simplified models made from multiple processing elements—artificial neurons—connected by links of variable weight. Each neuron takes input signals from other neurons, analyses them, and gives out the result, which is then passed on to succeeding neurons as an input [40]. ANNs adapt from training data and record data point connections, which can then be utilized for modelling, predicting, and optimization. ANNs are machine learning systems that look like the human brain [41]. They range from simple single-direction logic networks with only one or two layers to complicated multi-input networks with many directional feedback loops and layers. Popular Kernel Function (RBF), Multilayer Perceptron (MLP), Feedforward Neural Network (FNN), Wavelet Neural Network (WNN), Self-organizing Map (SOM), Edited Nearest Neighbour (ENN), Recurrent Neural Network (RNN), and deep learning network are some of the ANNs that can be utilized to create models and evaluate the wastewater treatment procedure.
Federated Learning (FL), genetic algorithm (GA), and Evolution Strategies (ES) are examples of single artificial intelligence (AI) technologies in addition to ANNs. The FL was created to model complicated and uncertain systems, and it is made up of four parts: fuzzification, defuzzification, and fuzzy rules are all terms used to describe the fuzzy information system [42]. Fuzzy Inference System (FIS), which comprises four parts: fuzzifier, inference engine, knowledge base, and defuzzifier, is the most extensively employed [43]. GA, or evolutionary algorithm, models the natural evolutionary procedure to attain the lowest or greatest objective function using Darwin’s theory [44]. Expert System (ES) can replicate the decision-making procedure to resolve complicated problems by combining the skills and knowledge of several experts in a certain sector [45].
Atypical approaches such as Model Tree (MT), clustering algorithm, Batch-Normalization (BN), Particle Swarm Optimization (PSO), and support vector machine (SVM) are included in ML technology. By separating the input into subdomains and using a linear multivariate regression model for those subdomains, the MT model can be utilized to address continuous class problems. It can also generate a structural description of the dataset by approximating a non-linear relationship with a piecewise linear model [46]. Problems are addressed in DM by breaking them down into subproblems (subdomains) and then integrating the results of these subproblems. Clustering is an unsupervised technique of organizing the data based on a similarity metric [42]. As per the concept of aggregation, the clustering method, a quantitative multivariate statistical analysis, arranges the unclassified feature vectors into clusters. A Bayesian belief network (BN) is a directed acyclic graph model with nodes and directed edges between connected nodes [47]. The conditional probability distribution of node association represents each node as a random variable [48]. The PSO is an evolving meta-heuristic algorithm that solves optimization issues by starting with a random solution and iterating until the best answer is found [49]. SVM is a generalized linear classifier that uses the optimal separation concept of classes to solve the binary classification issue [50]. SVMs and associated algorithms have significantly evolved for use in pattern classification [51].
The ANFIS (a hybrid of the neural and fuzzy approaches) was utilized to improve the efficiency of ANNs even further [52,53]. ANFIS adjusts the premise and concluding parameters using a hybrid of backpropagation and least-squares algorithms, and it can produce “If/Then” rules automatically. ANN-GAS employs a genetic algorithm to iteratively refine the parameters of the neural network and improve its problem-solving ability.
The objective of the present investigation is to make use of higher-level machine learning technology as a way of forecasting the gaseous entrapment ratio. The aim of the current study was to evaluate the use of the selected modelling algorithms in predicting the measured air entrainment rates in a CPLJR system. The method is devoid of the costs that would otherwise be associated with laboratory tests. Furthermore, this study explores the use of sensitivity analysis as a method for determining the key variable whose effect has the greatest impact on the results. The results are expected to aid designers in selecting the most appropriate parameters that ultimately lead to enhanced entrapment and improve the oxygen transfer ratio with relatively low-power considerations.

2. Material and Methods

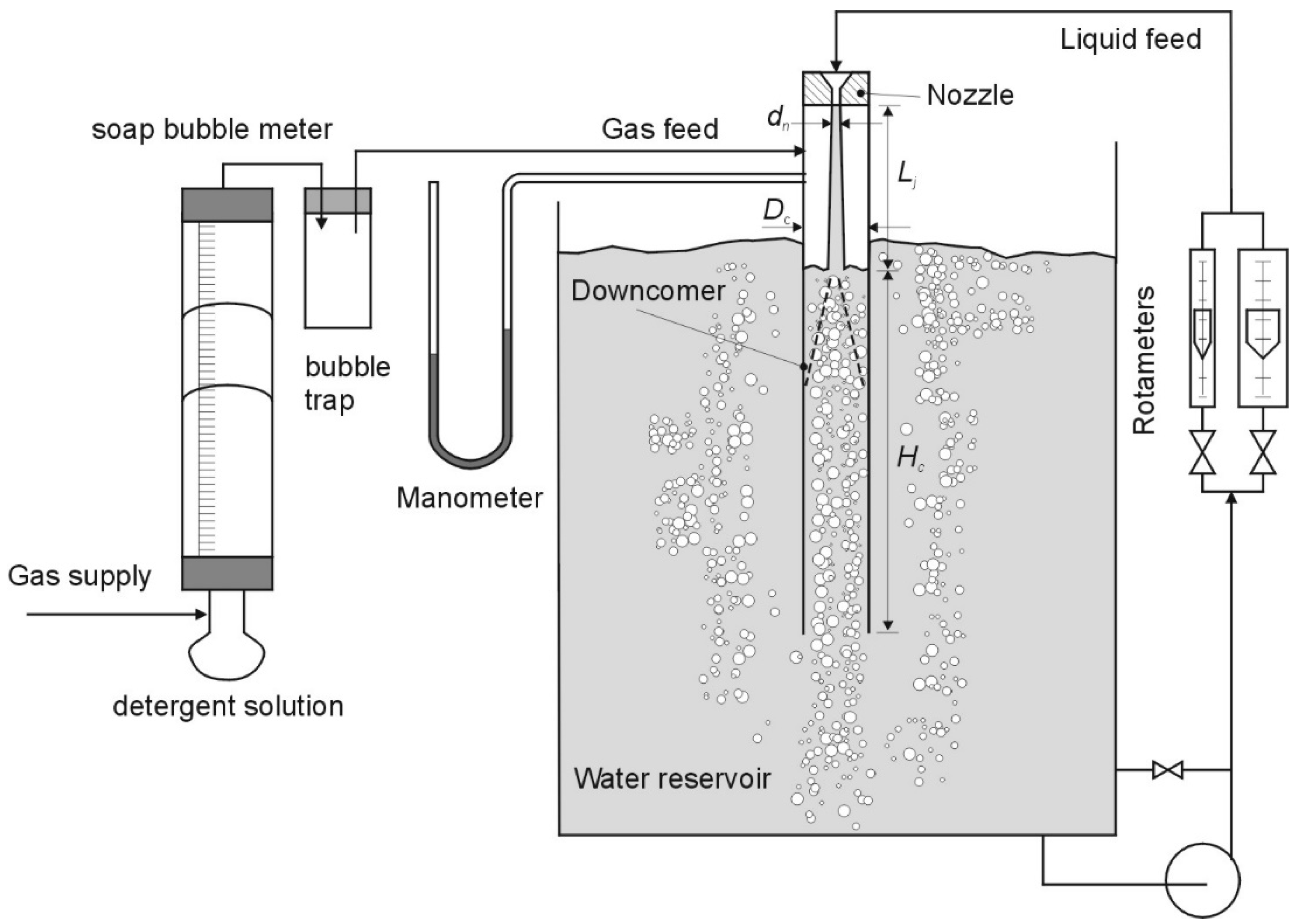
2.1. Experimental Work and Data Collection

The confined plunging liquid jet apparatus utilized to generate the current air entrainment rate (Qa) is shown in Figure 1, which is similar to the apparatuses used by [1,6]. The main operating conditions used to measure Qa are jet length of Lj = 0.3 and 0.4 m, nozzle diameter dn = 0.06, 0.08. 0.012, 0.012 and 0.015 m, downcomer diameter of Dc = 0.023, 0.038, 0.0505. 0.071 and 0.089 m and downcomer submergence length of H = 0.3 and 0.4 m. The nozzle internal design was similar to that used by [9].

2.2. Dataset

In order to run soft computing models, a total of 353 experimental observations of air entrainment rates were measured by employing a confined plunging liquid jet reactor with a variation in jet length (0.3 to 0.4) m, jet velocity (0.9 to 16.3) m/s, jet entrainment rate (1.46 × 10−5–1.91 × 10−3) m3/s, downcomer diameter (0.023–0.089) m and nozzle diameter (0.006–0.015) m. The complete experimental observations were divided into two datasets for the training (67% of the data) and testing (33% of the data) of the modelling procedures.

2.3. Modelling

The data were grouped based on a random sample of the total readings. The hyperparameter was tuned using a grid search to define the optimal one. Then, the optimal hyperparameter was used to build the model. Finally, we applied sensitivity analysis to figure out the most critical plunging jet parameter that effects the air entertainment ratio. We used the permutation importance function from the sklearn library to calculates the variable importance of the machine learning algorithms for our experimental dataset. The permutation feature importance is defined as the drop in model score caused by randomly rearranging a single feature value.

2.4. Results

The various machine learning models were established for unique sets of testing and training data, as illustrated in Figure 2. The plots have been generated plotting the air entrainment ratings versus the predicted ratings. The goodness-of-fit (R2) measure for decision tree, elastic net, Extra tree, Gradient boosting, K-Nearest Neighbour, lasso, random forest, ridge and support vector machine were found to be 0.89, 0.87, 0.87, 0.90, 0.94, 0.83, 0.89, 0.88 and 0.92, respectively. As the R2 value approaches 1, the machine learning algorithms’ predictions of air entrainment, Qa, were efficiently performed when applied to the confined plunging jet reactors parameters.
The produced ML regression model was evaluated using the Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE). These data were used to determine how accurate our predictions are and how they differ from the actual values. The MAE shows how much of an error from the predicted air entertainment rate expected on average, and the RMSE shows the average distance between the predicted air entertainment rates from the model and the actual rates in the experimental dataset. The results are summarized in Table 1.
Table 1 shows that K-Neighbours and random forest are the most accurate models that explain the air entertainment rate by the PLJR variables, R2 = 0.94, RMSE = 0.04, and MAE = 0.0271; R2 = 0.9223, RMSE = 0.0484, and MAE = 0.0381. Granata and de Marinis (2017) developed a method based on machine learning techniques for predicting the air entrainment rate. Three different algorithms were compared in the previous study: M5P, bagging, and random forest. The latter definitively outperformed both M5P and bagging; however, the results were poor, as seen in the assessment metrics (in the case of RF, the R2 value was 0.793, while the MAE and RMSE were 0.1406 and 0.2125, respectively). The ML algorithms used in this research are far more accurate than the prior one since the study compares a number of different algorithms.
The aim of this models is to not only build a model with excellent performance, but also clarify the model input variables and how these variables affect model performance. A powerful way to define the most critical parameters is by performing a sensitivity analysis on our machine learning models, where we examine the impact of each parameter on the model’s prediction. Figure 3 shows the increase in model RMSE when a single plunging jet reactor parameter value is randomly shuffled. This can tell us which parameter has most impact in the air entertainment rate.
Among all the machine learning models, the graph shows that the two most important parameters for the models were liquid volumetric flow rate (Qj) and jet velocity (Vj). The importance of these variables makes sense because when we inverse the jet velocity the ore bubbles were transferred to the system. Our findings are in line with previous research performed by Al-Anzi [1]; through his experiment, he found that when the downcomer diameter to nozzle diameter ratio was greater than 5, the highest gas entrainment rates were attained as long as the liquid’s surface velocity was high enough to propel bubbles downwards. Furthermore, the machine learning graphs in Figure 3 maintain the same two important variables. However, the jet velocity (Vj) effect decreased in some of the algorithms, such as elastic net, ridge and support vector machine. On the other hand, lasso can predict the air entrainment rate when the other variables are shuffled without any root mean square error. The coefficient of determination of the lasso algorithm was 82%. This shows that lasso can build a good model using only the most important variables (Qj and Vj).
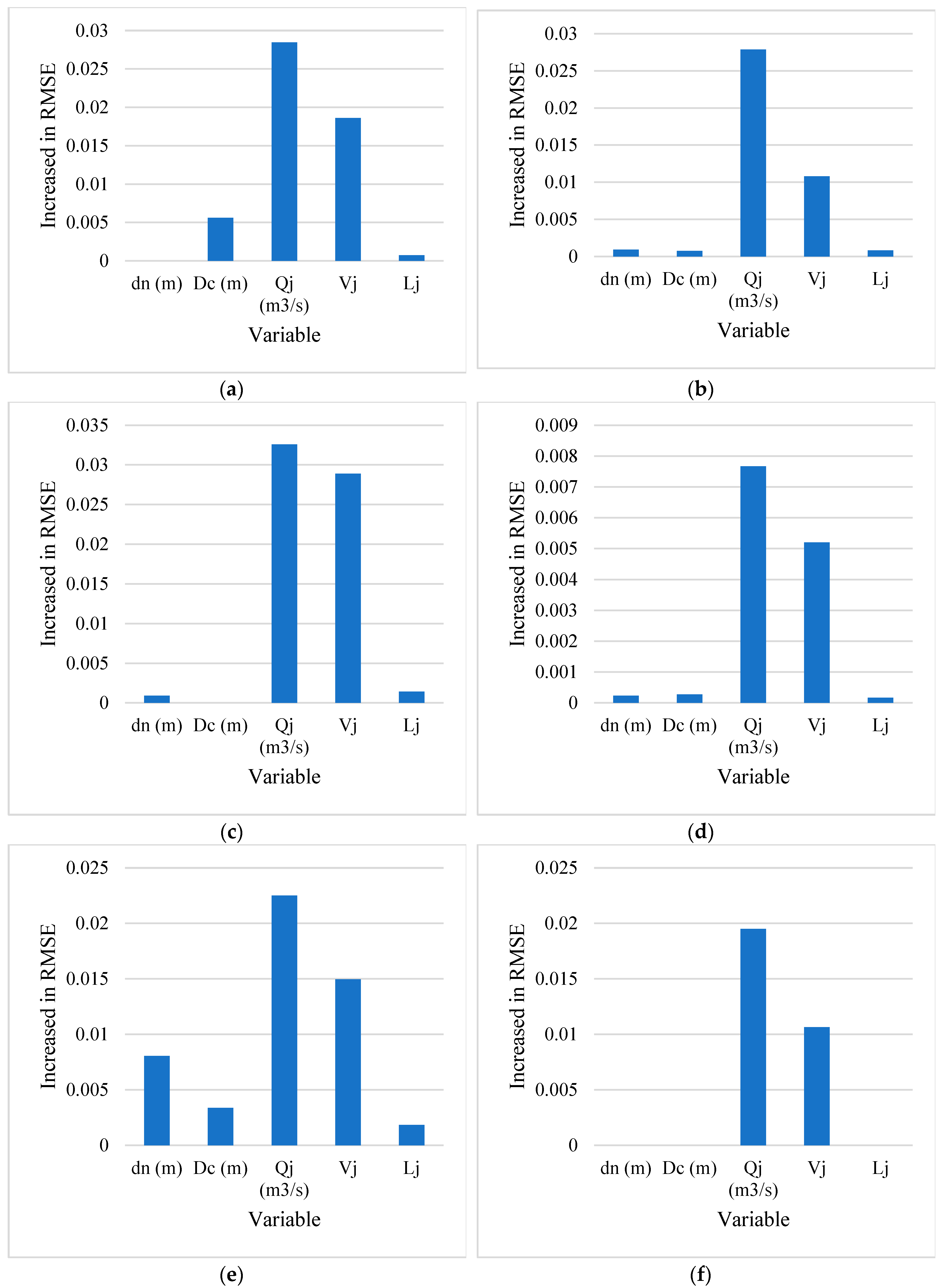
Finally, to obtain a clear overview, we compared the measured, predicted and calculated air entrainments rates. Figure 4 shows that the fit of the best machine learning model (K-Neighbours) is better than the fit of the calculated model. Machine learning successfully predicted the air entertainment rate using the confined plunging jet reactor parameters.

3. Conclusions

A precise prediction of the air entrainment rate in a confined plunging liquid jet reactor is essential to avoid the poor operating conditions related to an insufficient air inlet from the outside. A number of machine learning algorithms were compared in this research. All the studied models showed robustness, reliability, and a high generalization capability. However, with reference to the root mean square error and coefficient of determination R2, KNN and random forest presented better performances than the others in predicting an accurate air entrainment rate. Machine learning algorithms might be additionally helpful for giving an assessment of the qualities to be considered for estimating treatment units, given the attributes of the area, when direct measures are not accessible. The projected method could also be compelling with regard to the continuous administration issues of wastewater treatment plants, and used to address environmental planning issues.

Author Contributions

This work was done by A.A and B.A. and reviewed by B.A. “Conceptualization, A.A. and B.A.; methodology, A.A. and B.A. ; software, A.A.; validation, A.A.; formal analysis, A.A. and B.A.; investigation, B.A.; resources, B.A.; data curation, A.A.; writing—original draft preparation, A.A.; writing—review and editing, B.A.; visualization, A.A.; supervision, B.A.; project administration, A.A.; funding acquisition, B.A. All authors have read and agreed to the published version of the manuscript.”.

Funding

This research received no external funding.

Institutional Review Board Statement

“Not applicable”

Informed Consent Statement

“Not applicable”

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

“The authors declare no conflict of interest.”.

References

  1. Akhoundi, A., & Nazif, S. (2018). Sustainability assessment of wastewater reuse alternatives using the evidential reasoning approach. Journal of Cleaner Production, 195, 1350–1376. [CrossRef]
  2. Al-Anzi, B. S., Cumming, I. W., & Rielly, C. D. (2006). A IR ENTRAINMENT RATES IN A CONFINED PLUNGING LIQUID JET REACTOR. The 10th International Conference on Multiphase Flow in Industrial Plants, 1, 71–82.
  3. Al-Anzi, Bader S. (2020). Effect of Primary Variables on A Confined Plunging liquid jet reactor. Water, 12, 1–13. [CrossRef]
  4. Al-Anzi, Bader S., & Fernandes, J. (2023). Measurement of Total Air Entrainment, Disentrainment and Net Entrainment Flow Rates Utilizing Novel Downcomer Incorporating Al-Anzi’s Disentrainment Ring (ADR) in a Confined Plunging Jet Reactor. Water (Switzerland), 15(5). [CrossRef]
  5. Al Aani, S., Bonny, T., Hasan, S. W., & Hilal, N. (2019). Can machine language and artificial intelligence revolutionize process automation for water treatment and desalination? Desalination, 458, 84–96. [CrossRef]
  6. Bagatur, T., Baylar, A., & Sekerdag, N. (2002). The effect of nozzle type on air entrainment by plunging water jets. Water Quality Research Journal, 37(3), 599–612. [CrossRef]
  7. Bagatur, T., & Onen, F. (2014). A predictive model on air entrainment by plunging water jets using GEP and ANN. KSCE Journal of Civil Engineering, 18(1), 304–314. 1. [CrossRef]
  8. Bagheri, M., Mirbagheri, S. A., Ehteshami, M., & Bagheri, Z. (2015). Modeling of a sequencing batch reactor treating municipal wastewater using multi-layer perceptron and radial basis function artificial neural networks. Process Safety and Environmental Protection, 93, 111–123. [CrossRef]
  9. Baylar, A., & Emiroglu, M. E. (2003). Air entrainment and oxygen transfer in a venturi. Proceedings of the Institution of Civil Engineers-Water and Maritime Engineering, 156(3), 249–255.
  10. Bozkurt, H., van Loosdrecht, M. C. M., Gernaey, K. V, & Sin, G. (2016). Optimal WWTP process selection for treatment of domestic wastewater–A realistic full-scale retrofitting study. Chemical Engineering Journal, 286, 447–458. [CrossRef]
  11. Buaisha, M., Balku, S., & Özalp-Yaman, S. (2020). Heavy metal removal investigation in conventional activated sludge systems. Civil Engineering Journal, 6(3), 470–477. 3. [CrossRef]
  12. Cao, W., & Yang, Q. (2020). Online sequential extreme learning machine based adaptive control for wastewater treatment plant. Neurocomputing, 408, 169–175. [CrossRef]
  13. Chakraborty, T., Chakraborty, A. K., & Chattopadhyay, S. (2019). A novel distribution-free hybrid regression model for manufacturing process efficiency improvement. Journal of Computational and Applied Mathematics, 362, 130–142. [CrossRef]
  14. Chanapathi, T., & Thatikonda, S. (2019). Fuzzy-based regional water quality index for surface water quality assessment. Journal of Hazardous, Toxic, and Radioactive Waste, 23(4), 4019010. [CrossRef]
  15. Chen, J.-C., Chang, N. B., & Shieh, W. K. (2003). Assessing wastewater reclamation potential by neural network model. Engineering Applications of Artificial Intelligence, 16(2), 149–157. [CrossRef]
  16. Deswal, S. (2011a). Modeling oxygen-transfer by multiple plunging jets using support vector machines and Gaussian process regression techniques. International Journal of Civil and Environmental Engineering, 5(1), 1–6.
  17. Deswal, S. (2011b). Modeling oxygen-transfer by multiple plunging jets using support vector machines and Gaussian process regression techniques. World Academy of Science, Engineering and Technology, 73.
  18. Emiroglu, M. E., & Baylar, A. (2003). Role of nozzles with air holes in air entrainment by a water jet. Water Quality Research Journal, 38(4), 785–795. [CrossRef]
  19. Erdirencelebi, D., & Yalpir, S. (2011). Adaptive network fuzzy inference system modeling for the input selection and prediction of anaerobic digestion effluent quality. Applied Mathematical Modelling, 35(8), 3821–3832. [CrossRef]
  20. Fenu, A., Guglielmi, G., Jimenez, J., Sperandio, M., Saroj, D., Lesjean, B., Brepols, C., Thoeye, C., & Nopens, I. (2010). Activated sludge model (ASM) based modelling of membrane bioreactor (MBR) processes: A critical review with special regard to MBR specificities. Water Research, 44(15), 4272–4294. [CrossRef]
  21. Graham, S. E., Chariton, A. A., & Landis, W. G. (2019). Using Bayesian networks to predict risk to estuary water quality and patterns of benthic environmental DNA in Queensland. Integrated Environmental Assessment and Management, 15(1), 93–111. 1. [CrossRef]
  22. Granata, F., & de Marinis, G. (2017). Machine learning methods for wastewater hydraulics. Flow Measurement and Instrumentation, 57, 1–9.
  23. Harby, K., Chiva, S., & Muñoz-Cobo, J.-L. (2014). An experimental study on bubble entrainment and flow characteristics of vertical plunging water jets. Experimental Thermal and Fluid Science, 57, 207–220. [CrossRef]
  24. Jia, X., Li, Z., Tan, R. R., Foo, D. C. Y., Majozi, T., & Wang, F. (2019). Interdisciplinary contributions to sustainable water management for industrial parks. In Resources, Conservation and Recycling (Vol. 149, pp. 646–648). Elsevier. [CrossRef]
  25. Li, D., Yang, H. Z., & Liang, X. F. (2013). Prediction analysis of a wastewater treatment system using a Bayesian network. Environmental Modelling & Software, 40, 140–150.
  26. Liu, H., Zhang, Y., & Zhang, H. (2020). Prediction of effluent quality in papermaking wastewater treatment processes using dynamic kernel-based extreme learning machine. Process Biochemistry, 97, 72–79. [CrossRef]
  27. Long, S., Zhao, L., Liu, H., Li, J., Zhou, X., Liu, Y., Qiao, Z., Zhao, Y., & Yang, Y. (2019). A Monte Carlo-based integrated model to optimize the cost and pollution reduction in wastewater treatment processes in a typical comprehensive industrial park in China. Science of the Total Environment, 647, 1–10. [CrossRef]
  28. López-Morales, C. A., & Rodríguez-Tapia, L. (2019). On the economic analysis of wastewater treatment and reuse for designing strategies for water sustainability: Lessons from the Mexico Valley Basin. Resources, Conservation and Recycling, 140, 1–12. [CrossRef]
  29. López, M. E., Rene, E. R., Boger, Z., Veiga, M. C., & Kennes, C. (2017). Modelling the removal of volatile pollutants under transient conditions in a two-stage bioreactor using artificial neural networks. Journal of Hazardous Materials, 324, 100–109. [CrossRef]
  30. Lu, H., Li, H., Liu, T., Fan, Y., Yuan, Y., Xie, M., & Qian, X. (2019). Simulating heavy metal concentrations in an aquatic environment using artificial intelligence models and physicochemical indexes. Science of the Total Environment, 694, 133591. [CrossRef]
  31. Man, Y., Hu, Y., & Ren, J. (2019). Forecasting COD load in municipal sewage based on ARMA and VAR algorithms. Resources, Conservation and Recycling, 144, 56–64. [CrossRef]
  32. Metcalf, E., Tchobanoglous, G., Stensel, H. D., Tsuchihashi, R., & Burton, F. (2013). Wastewater Engineering: Treatment and Resource Recovery McGraw-Hill. New York, NY, USA.
  33. Mohandes, M., Rehman, S., & Rahman, S. M. (2011). Estimation of wind speed profile using adaptive neuro-fuzzy inference system (ANFIS). Applied Energy, 88(11), 4024–4032. 4032. [CrossRef]
  34. Müller, A. C., & Guido, S. (2016). Introduction to machine learning with Python: a guide for data scientists. “ O’Reilly Media, Inc.”.
  35. Nadiri, A. A., Shokri, S., Tsai, F. T.-C., & Asghari Moghaddam, A. (2018). Prediction of effluent quality parameters of a wastewater treatment plant using a supervised committee fuzzy logic model. Journal of Cleaner Production, 180, 539–549. [CrossRef]
  36. Nopens, I., Batstone, D. J., Copp, J. B., Jeppsson, U., Volcke, E., Alex, J., & Vanrolleghem, P. A. (2009). An ASM/ADM model interface for dynamic plant-wide simulation. Water Research, 43(7), 1913–1923. [CrossRef]
  37. Ohkawa, A., Kusabiraki, D., Shiokawa, Y., Sakai, N., & Fujii, M. (1986). Flow and oxygen transfer in a plunging water jet system using inclined short nozzles and performance characteristics of its system in aerobic treatment of wastewater. Biotechnology and Bioengineering, 28(12), 1845–1856. 12. [CrossRef]
  38. Onen, F. (2014). Prediction of penetration depth in a plunging water jet using soft computing approaches. Neural Computing and Applications, 25(1), 217–227. [CrossRef]
  39. Qiao, Y., Zhang, S., Wu, N., Wang, X., Li, Z., Zhou, M., & Qu, T. (2019). Data-driven approach to optimal control of ACC systems and layout design in large rooms with thermal comfort consideration by using PSO. Journal of Cleaner Production, 236, 117578. [CrossRef]
  40. Qu, X. L., Khezzar, L., Danciu, D., Labois, M., & Lakehal, D. (2011). Characterization of plunging liquid jets: A combined experimental and numerical investigation. International Journal of Multiphase Flow, 37(7), 722–731. [CrossRef]
  41. Ranjan, S. (2008). Hydraulics of jet aerators. Journal of the Institution of Engineers (India): Environmental Engineering Division, 88, 29–32.
  42. Ranjan, Subodh. (2007). Hydraulics of hollow jet aerators. Journal of Indian Water Resources Society, 27(1–2), 27–31.
  43. Rout, P. R., Zhang, T. C., Bhunia, P., & Surampalli, R. Y. (2021). Treatment technologies for emerging contaminants in wastewater treatment plants: A review. Science of the Total Environment, 753, 141990. [CrossRef]
  44. Sattar, A. A., Elhakeem, M., Rezaie-Balf, M., Gharabaghi, B., & Bonakdari, H. (2019). Artificial intelligence models for prediction of the aeration efficiency of the stepped weir. Flow Measurement and Instrumentation, 65, 78–89. [CrossRef]
  45. Shi, S., & Xu, G. (2018). Novel performance prediction model of a biofilm system treating domestic wastewater based on stacked denoising auto-encoders deep learning network. Chemical Engineering Journal, 347, 280–290. [CrossRef]
  46. Sousa, V., Matos, J. P., & Matias, N. (2014). Evaluation of artificial intelligence tool performance and uncertainty for predicting sewer structural condition. Automation in Construction, 44, 84–91. [CrossRef]
  47. Tojo, K., & Miyanami, K. (1982). Oxygen transfer in jet mixers. The Chemical Engineering Journal, 24(1), 89–97. 1.
  48. Van de Sande, E., & Smith, J. M. (1975). Mass transfer from plunging water jets. The Chemical Engineering Journal, 10(3), 225–233. 3.
  49. Vučić, V., Süring, C., Harms, H., Müller, S., & Günther, S. (2021). A framework for P-cycle assessment in wastewater treatment plants. Science of The Total Environment, 760, 143392. [CrossRef]
  50. Wagner, W. P. (2017). Trends in expert system development: A longitudinal content analysis of over thirty years of expert system case studies. Expert Systems with Applications, 76, 85–96.
  51. Wang, J., & Deng, Z. (2016). Modeling and prediction of oyster norovirus outbreaks along Gulf of Mexico coast. Environmental Health Perspectives, 124(5), 627–633. 124, 5, 627–633. [CrossRef]
  52. Wu, X., Yang, Y., Wu, G., Mao, J., & Zhou, T. (2016). Simulation and optimization of a coking wastewater biological treatment process by activated sludge models (ASM). Journal of Environmental Management, 165, 235–242. [CrossRef]
  53. (a)Yang, Z., Liu, Y., & Li, C. (2011). Interpolation of missing wind data based on ANFIS. Renewable Energy, 36(3), 993–998.
  54. Zhang, Y., Gao, X., Smith, K., Inial, G., Liu, S., Conil, L. B., & Pan, B. (2019). Integrating water quality and operation into prediction of water production in drinking water treatment plants by genetic algorithm enhanced artificial neural network. Water Research, 164, 114888. [CrossRef]
Preprints 81211 g001
Figure 1. Schematic diagram of the confined plunging liquid jet experimental apparatus [6].
Figure 1. Schematic diagram of the confined plunging liquid jet experimental apparatus [6].
Preprints 81211 g001
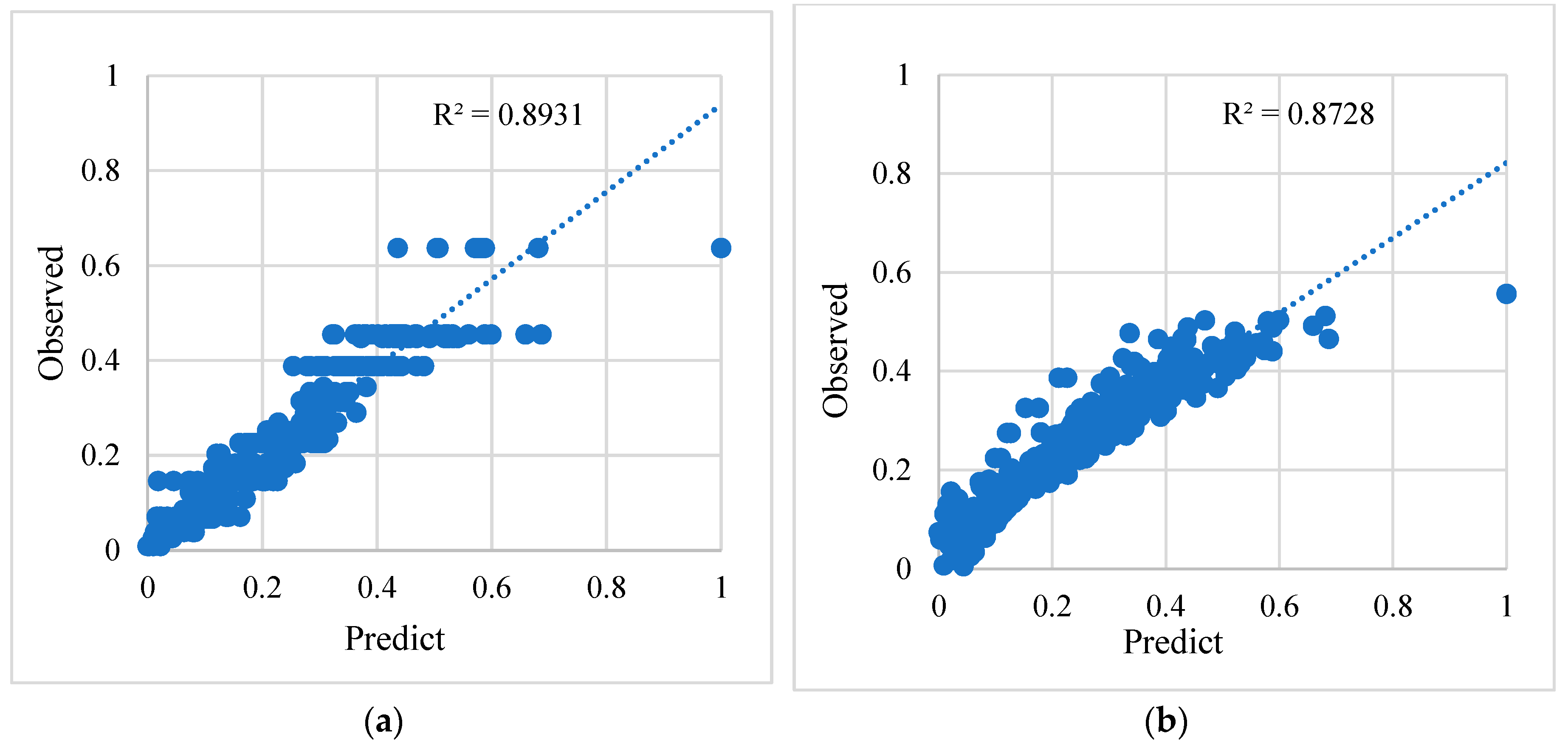
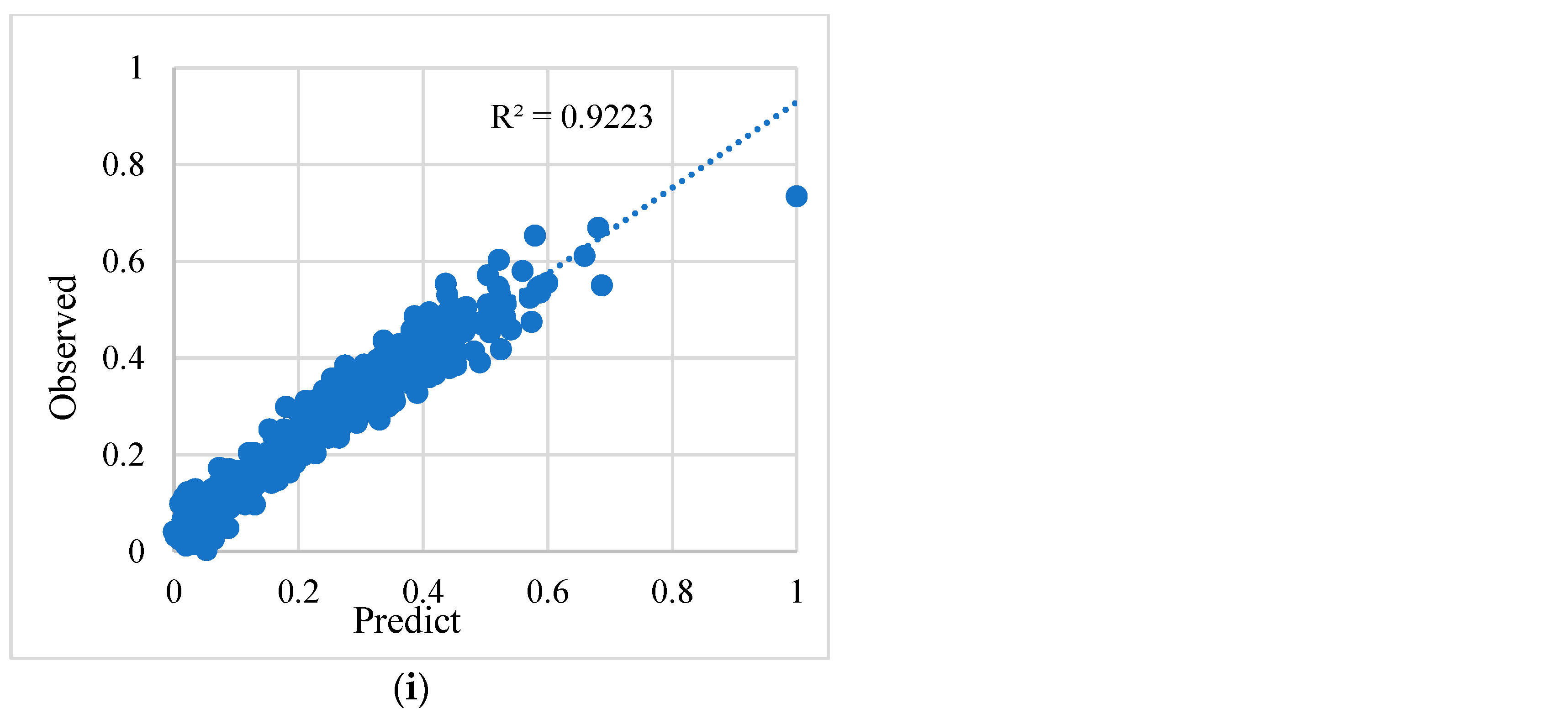
Preprints 81211 g002aPreprints 81211 g002bPreprints 81211 g002c
Figure 2. Scatter plots of normalized air entrainment by normalized predicted ratings of the machine learning models applied. (a) Air entrainment rate predicted by decision tree; (b) air entrainment rate predicted by elastic net; (c) air entrainment rate predicted by Extra tree; (d) air entrainment rate predicted by Gradient boosting; (e) air entrainment rate predicted by K-Neighbours; (f) air entrainment rate predicted by lasso; (g) air entrainment rate predicted by random forest; (h) air entrainment rate predicted by ridge; (i) air entrainment rate predicted by support vector machine.
Figure 2. Scatter plots of normalized air entrainment by normalized predicted ratings of the machine learning models applied. (a) Air entrainment rate predicted by decision tree; (b) air entrainment rate predicted by elastic net; (c) air entrainment rate predicted by Extra tree; (d) air entrainment rate predicted by Gradient boosting; (e) air entrainment rate predicted by K-Neighbours; (f) air entrainment rate predicted by lasso; (g) air entrainment rate predicted by random forest; (h) air entrainment rate predicted by ridge; (i) air entrainment rate predicted by support vector machine.
Preprints 81211 g002aPreprints 81211 g002bPreprints 81211 g002c
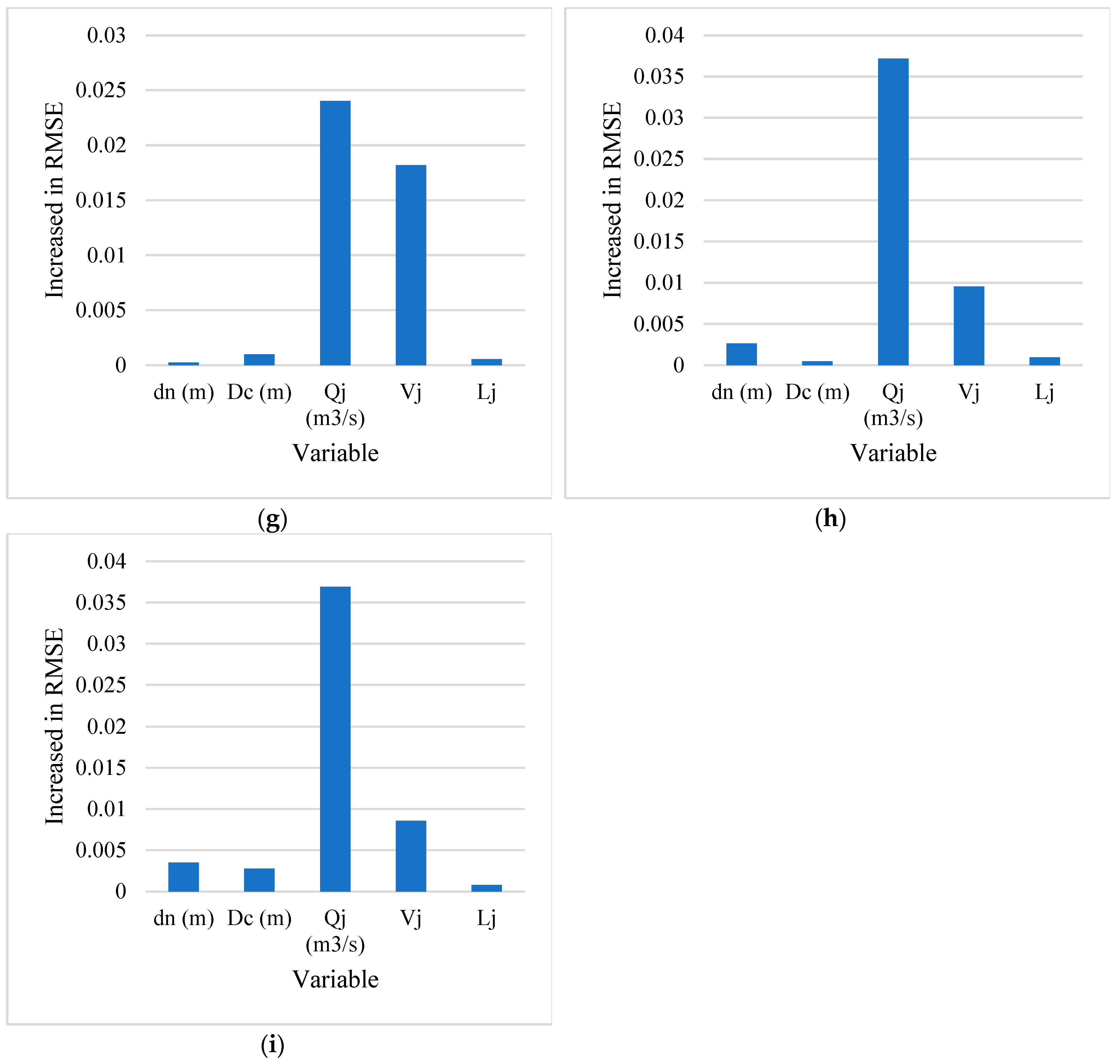
Preprints 81211 g003aPreprints 81211 g003b
Figure 3. Confined plunging jet reactor parameter level sensitivity analysis graphs of the machine learning models. (a) Decision tree sensitivity analysis; (b) elastic net sensitivity analysis; (c) Extra tree sensitivity analysis; (d) Gradient boosting sensitivity analysis; (e) K-neighbours sensitivity analysis; (f) lasso sensitivity analysis; (g) random forest sensitivity analysis; (h) ridge sensitivity analysis; (i) support vector machine sensitivity analysis.
Figure 3. Confined plunging jet reactor parameter level sensitivity analysis graphs of the machine learning models. (a) Decision tree sensitivity analysis; (b) elastic net sensitivity analysis; (c) Extra tree sensitivity analysis; (d) Gradient boosting sensitivity analysis; (e) K-neighbours sensitivity analysis; (f) lasso sensitivity analysis; (g) random forest sensitivity analysis; (h) ridge sensitivity analysis; (i) support vector machine sensitivity analysis.
Preprints 81211 g003aPreprints 81211 g003b
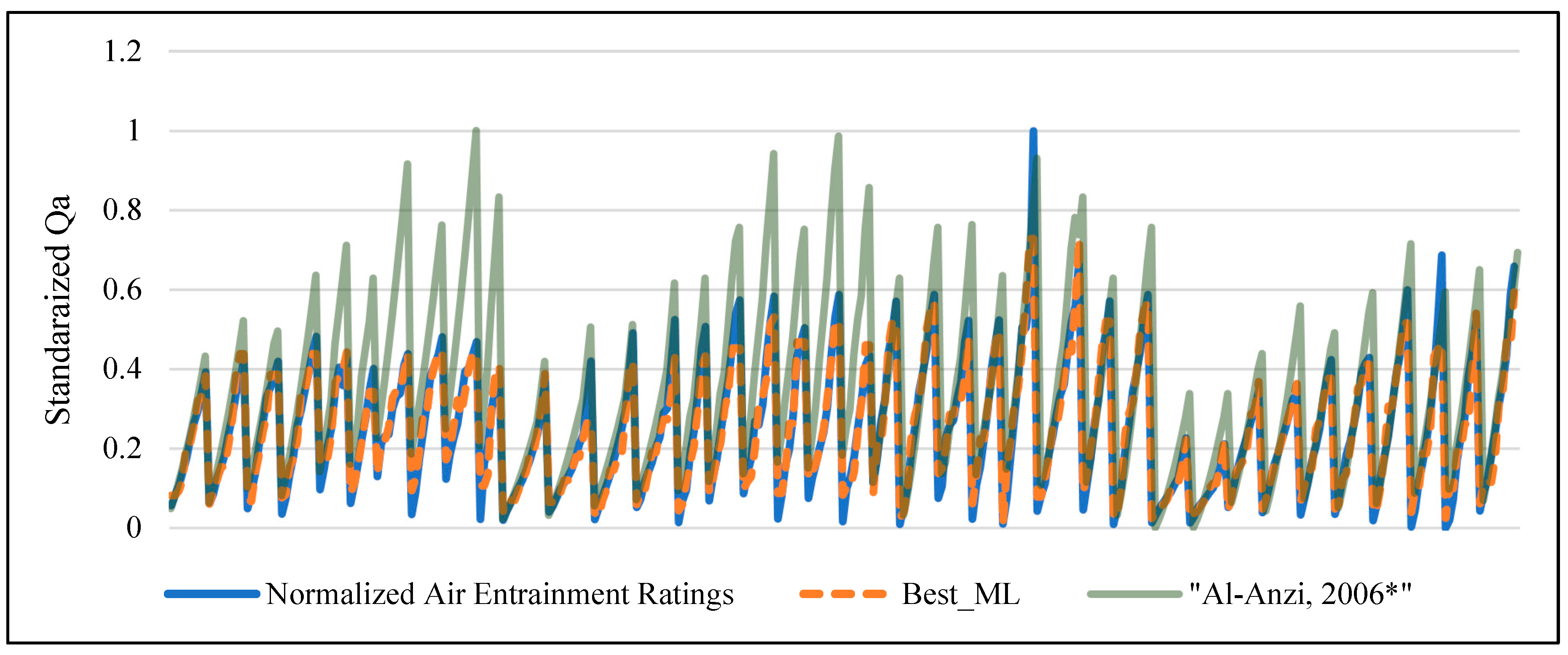
Preprints 81211 g004
Figure 4. Comparative study between the measured, predicted and calculated air entrainments rates [*6]
Figure 4. Comparative study between the measured, predicted and calculated air entrainments rates [*6]
Preprints 81211 g004
Table 1. Summary of results of the different ML models.
Table 1. Summary of results of the different ML models.
Regressor MAE RMSE R2
Decision Tree 0.0387 0.0539 0.8931
Elastic Net 0.0442 0.0618 0.8728
Extra Tree 0.0430 0.0598 0.8685
Gradient Boosting 0.1014 0.1255 0.9027
K-Neighbours 0.0271 0.0403 0.9423
Lasso 0.0656 0.0854 0.8279
Random Forest 0.0371 0.0552 0.8873
Ridge 0.0408 0.0581 0.8753
Support Vector Machine 0.0381 0.0484 0.9223
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated