Graphs Defined on Rings: A Review

1. Introduction

Graph theory and algebra are two disciplines of mathematics which concentrate on building and investigating structures. Algebra is a fundamental branch of mathematics, whose roots are traced back to the early sixteenth century, whereas, graph theory is a flourishing mathematical research ground, which unfolded in the early eighteenth century, as the Swiss mathematician solved the famous Königsberg bridge problem, by representing the structure of the bridge and the landmass surrounding it as a graph. Hence, the subject emerged as a consequence of modeling real-life problems in terms of graphs, as it gives a comprehensive visual representation of the problem, and this aids in obtaining optimal and feasible solutions to the problem. It is interesting to note that, along with the increase in applications of the developed theories, the theory by itself has evolved independently over the period of time and has established itself as a flourishing mathematical discipline.

An algebraic structure is a non-empty set along with one or more operations (usually binary) defined on it and by the very definition of a graph, it can be noticed that a graph can be realised as a structural representation of a relation defined on a (vertex) set. Relating these two structural aspects, a synergy between the algebraic and graphical structures is studied in the field of algebraic graph theory. It has become a stimulating research field, yielding numerous intriguing results as these two disciplines; algebra and graph theory, interact in many ways to mutually extend the tools of one subject for the benefit of the other. In fact, powerful combinatorial methods found in graph theory have been used to prove specific significant and well-known results in group theory. For example, all finite groups can be represented as the automorphism group of a connected graph (c.f.[1]).

Any algebraic structure can be interpreted as a graph, and there are multiple ways of associating an algebraic structure with a graph. In the past few decades, several graphs are being constructed from algebraic structures based on different properties that the algebraic structures posses, and these algebraic graphs have been studied extensively in a motivation to understand the algebraic structure more clearly; thereby making this an enthralling area of research (c.f.[2,3,4]).

This association of an algebraic structure with a graph began in the end of the nineteenth century, when Arthur Cayley connected graph theory and group theory by introducing the Cayley graph of a group (c.f. [5]), which encoded the algebraic information of a group as a graphical structure. The Cayley graph for a group $\mathcal{G}$ is a graph with the vertex set as the elements of the group $\mathcal{G}$, which is invariant under the right translation by elements of $\mathcal{G}$. Cayley graphs are by far the most well-known graph associated with an algebraic structure. They have a massive yet, growing literature to an extent to convince that algebraic graph theory is only the study of Cayley graphs of finite groups (see [6,7,8,9,10,11]).

Another important class of algebraic graph construction is the construction of graphs from rings, as the study of graphs constructed from rings contributes to an interplay between the ring structure and the corresponding graph structure. One can sometimes translate the algebraic properties of the rings in terms of graph-theoretic properties and vice-versa, which can help in exploring some interesting results related to the graphs as well as the rings. Graphs defined on rings either have vertices as the set of elements of the ring or they are intersection graphs such that each vertex represent some subset of the ring, or some well-known sub-structure of the ring like ideals, subring, etc. and the edges are defined with respect to an algebraic condition on the elements of the vertex set.

The study on graph defined from rings began with the introduction of the zero-divisor graphs, which is one of the most well-studied graph defined on commutative rings that have massive and still augmenting literature (see [12,13,14]). Apart from the zero-divisor graphs, there are several other graphs such as the total graphs, annihilating graphs, comaximal graphs, unit graphs, Jacobson graphs, generalized total graphs, etc. They all have substantial and growing literature (c.f. [13,14,15,16,17,18,19]). A few decades back, algebraic graph theory was just a theory that did not apply to ordinary human activities, whereas it has now been successfully used in transmitting encrypted information with high security and privacy through public communication networks (c.f.[20]).

Though Cayley graphs were initially constructed on groups, the graph construction has been extended to rings as well. As rings possess several symmetric subsets like the set of all zero-divisors, units, idempotent, nilpotent elements, etc. many variants of Cayley graphs using these symmetric subsets of the rings were constructed and studied. This literature review intends to present an overview of these variants of Cayley graphs that are defined on rings. That is, the graphs defined such that their vertex sets are the ring elements and their adjacency relation is similar to the adjacency condition given in the Cayley graph, with respect to some symmetric subset of the ring.

It can be seen that there are many survey papers, review papers and books on graphs defined on rings (see [12,16,17]), but many of them cover only several well-studied graphs. Furthermore, review papers that focus on a particular property of the graph defined on rings can also be found in the literature (c.f. [21,22,23]), whereas there was no comprehensive review found on the variants of Cayley graphs defined on rings. This motivated us to create a literature hub on these graphs defined on common grounds, and systematically analyse the study that has been done on these graphs to understand the pattern and dynamics of research in this area. This systematic review also helps to identify unsolved open problems that were proposed in the literature as well as the future scope of study on the topic. Also, this article aims to clear the ambiguity over different graphs with similar names and the same graphs with different names that have been defined and studied independently by different authors, which falls under this criteria.

The outline of the article is as follows. The graph theoretic and algebraic preliminaries that are required to proceed further are given in Section 1.1. A comprehensive review on the unitary Cayley Graph of ${\mathbb{Z}}_n$ and unitary Cayley graph of a ring, where the former is a particular case of the latter is given in Section 2 and Section 3 respectively. This is followed by a review on the unitary addition Cayley graph in Section 4 and the unit graph of a ring in Section 5, where again the first class of graphs forms a subset of the second one. Finally, a review on other variants of Cayley graphs, for which detailed investigations are not yet done, is given in Section 6 and we conclude the article by proposing the research gaps that we have found over the course of the review along with several possible avenues for further research in Section 7.

1.1. Preliminaries

This subsection aims to familiarise the reader with the terminology and notation that are used in the article. It also includes definitions and results which are required to understand the study. Unless otherwise noted, all definitions relating to algebra are from [24], and all definitions relating to graph theory are from [25].

We let $\mathbb{N},\mathbb{Z},\mathbb{R}and\mathbb{C}$ denote the set of positive integers, integers, real numbers and the complex numbers. A non-empty set together with a binary operation termed as addition is called a group if the properties of closure, associativity, existence of a unique identity (additive identity) of the set and a unique inverse for each element in the set, are satisfied. In addition to this, if the group elements commute with each other under the defined binary operation, then the group is said to be an Abelian group.

The structure of a group endowed with another binary operation called the multiplication gave rise to the abstract concept of rings in the mid nineteenth century. A non-empty set R with two binary operations of addition and multiplication, denoted by + and · respectively, is said to be a ring or an associative ring if R is a commutative group under addition and the properties of associativity and distributivity hold for the multiplication.

In general, the binary operation of multiplication need not be commutative and the ring need not have an identity element under multiplication. If the ring is commutative under multiplication, then the ring called a commutative ring and when a ring has an identity element under multiplication, called the multiplicative identity, the ring is termed as a ring with identity, where this multiplicative identity is denoted by 1. Similarly, the existence of a multiplicative inverse for a non-zero element in a ring with identity is not guaranteed. If a non-zero element in a ring has a multiplicative inverse, then it is called a unit element of the ring and the set of all unit elements of the ring R form a group under multiplication and is called the multiplicative group of units. For a ring R, we denote this group of units of R by $R^{*}$. In other words, if R is a ring with identity and $x\in R$, x is a unit of R when there exists a $y\in R$, such that $xy=yx=1$ and $R^{*}=\{x\in R:xy=yx=1,y\in R\}$ is the group of units of R.

An element $x\in R$ in a left (ring) zero-divisor if there exists a $y\in R$ such that $xy=0$ ($yx=0$) and $y\ne 0$. Note that the additive identity 0 of a ring R is a trivial zero-divisor and for a commutative ring, the notions of left and right zero-divisors mean the same and we just say the zero-divisors. An integral domain is a commutative ring with identity such that there are no non-zero zero-divisors and a field is a commutative ring with identity such that every non-zero element is a unit. Therefore, it can be concluded that every integral domain is a field. Also, a field can be interpreted as ring that forms an Abelian group with respect to both addition and multiplication. The characteristic of a ring R, denoted by $char\left(R\right)$, is the smallest integer k such that $\underset{k-times}{\underbrace{1+1+\dots +1}}=0$ in R and if there exists no such k, then R is said to have characteristic 0.

A subring of a ring R is a subset of R, which is a ring by itself, with the operations defined on R. A subset I of a ring R is called a left (right) ideal of R if $(I,+)$ is a subgroup of R and $yx\in I$ ($xy\in I$) for all $x\in I$ and $y\in R$. For an element $x\in R$, the set $\langle x\rangle =Rx=\{yx:y\in R\}$ ($\langle x\rangle =xR=\{xy:y\in R\}$) is an ideal of R called the principal left (right) ideal generated by x. A left (right) ideal I of a ring R is said to be a maximal left (right) ideal of R if whenever $I_1$ is a left (right) ideal of R and $I\subseteq I_1\subseteq R$, then $I_1=I$ or $I_1=R$; that is, the only ideal that properly contains a maximal ideal is the ring itself. Note that the notions of left and right are the same for a commutative ring.

A commutative ring with identity is called a local or quasilocal ring if it has a unique maximal ideal. A division ring is a non-trivial ring in which division by non-zero elements is defined. In other words, a field is a commutative division ring and all division rings that are not fields are non-commutative rings in which the non-zero elements have a multiplicative inverse either with respect to left or right multiplication. The Jacobson radical of a ring R, denoted by $J_R$, is the intersection of all the maximal ideals of R. For a ring R and an ideal I of R, $\frac{R}{I}=\{x+I:x\in R\}$ is called a quotient ring of R by I. For a commutative ring R, $R\left[x\right]=\{{\displaystyle \sum _{i=0}^n}{a}_i{x}^i:a_i\in R,n\in \mathbb{Z}\}$ is called the ring of polynomials over R in the indeterminate x.

A ring R is said to be left (right) Artinian if every strictly descending chain of left (right) ideals in R is finite. The structure theorem for Artinian rings says that an Artinian ring R is uniquely (up to isomorphism) a finite direct product of Artinian local rings, where the direct product $R_1\times R_2\times \dots \times R_k$ of rings $R_1,R_2,\dots ,R_k$ is the set of all ordered pairs $\{(r_1,r_2,\dots ,r_k):r_i\in R_i,1\le i\le k\}$ such that the binary operations of addition and multiplication are defined element-wise. A simple ring is a non-zero ring that has no non-zero proper ideals. By ${\mathbb{Z}}_n$, we denote the ring of integers modulo n with the usual operations of addition modulo n and multiplication modulo n; that is, ${\mathbb{Z}}_n=({\mathbb{Z}}_n,{+}_n,{·}_n)$. The units of the ring ${\mathbb{Z}}_n$, denoted by ${\mathbb{Z}}_n^{*}$ are the set of all integers that are relatively prime to n and are less that n; that is, ${\mathbb{Z}}_n^{*}=\{k\in {\mathbb{Z}}_n:gcd(k,n)=1\}$ and the cardinality of this set is given by the arithmetic function called the Euler’s totient function, denoted by $\varphi \left(n\right)$.

A ring-homomorphism $f:R_1\to R_2$ between two rings $R_1$ and $R_2$ is a mapping that preserves the two ring operations; that is, $f(x+y)=f\left(x\right)+f\left(y\right)$ and $f\left(xy\right)=f\left(x\right)f\left(y\right)$ for all $x,y\in R_1$, where we assume that $f\left(1\right)=1$. A one-to-one and onto ring-homomorphism is a ring-isomorphism and if two rings $R_1$ and $R_2$ are isomorphic, it is denoted by $R_1\cong R_2$. Note that other related definitions are given in the article on the basis of requirement.

For a graph G with the vertex set $V\left(G\right)$ and edge set $E\left(G\right)$, the order and the size of the graph are $\left|V\right(G\left)\right|=n$ and $\left|E\right(G\left)\right|=m$ respectively. A graph in which there exists an edge joining a vertex to itself, called a loop is known as a pseudograph and a graph in which the edges are ordered pairs of vertices is called a directed graph. A subgraph H of a graph G is said to be a spanning subgraph, if with $V\left(H\right)=V\left(G\right)$ and for any subset $S\subseteq V\left(G\right)$, the subgraph induced by S, denoted by $\langle S\rangle$, is the maximal subgraph of G with vertex set S. The complement $\overline{G}$ of a graph G is the graph such that $V\left(\overline{G}\right)=V\left(G\right)$ and $E\left(\overline{G}\right)=\{uv:uv\notin E\left(G\right)\}$.

The set $N\left(v\right)=\{u\in V(G):uv\in E(G\left)\right\}$ is called the open neighborhood of a vertex $v\in V\left(G\right)$ and for each vertex $v\in V\left(G\right)$, the set $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}$ is the closed neighborhood of v. The degree of a vertex $v\in V\left(G\right)$, denoted by $de{g}_G\left(v\right)$ or $d\left(v\right)$, is the number of vertices adjacent with v in G; that is, $deg\left(v\right)=\left|N\right(v\left)\right|$ and $\delta \left(G\right)=sup\left\{\right|N\left(v\right)|:v\in V(G\left)\right\}$ is the maximum degree of a graph G.

A graph G is called connected if there is a path between any two distinct vertices in G; otherwise, G is said to be disconnected. A graph is called Eulerian if it contains a closed trail containing every edge and a graph is Hamiltonian if it contains a spanning cycle. Let G be a connected graph and for two vertices $u,v\in V\left(G\right)$, the length of a shortest path from u to v is denoted by $d(u,v)$ and the diameter of the graph G, $diam\left(G\right)=sup\left\{d\right(u,v):u,v\in V(G\left)\right\}$. The girth of a graph G is the length of the smallest induced cycle in G and if the graph is acyclic, girth of the graph is taken as ∞.

An isomorphism between two graphs G and H is a bijective function $f:V\left(G\right)\to V\left(H\right)$ such that any two vertices u and v of G are adjacent in G if and only if $f\left(u\right)$ and $f\left(v\right)$ are adjacent in H and an isomorphism from a graph G to itself is called an automorphism. The set of all automorphisms of a graph G forms a group called the automorphism group of G, denoted by $Aut\left(G\right)$. Since each graph has a unique automorphism group, it is called the algebraic invariant of the graph.

The adjacency matrix $A\left(G\right)$ of a graph G is a binary matrix of order n such that the $ij$-th entry is 1 if $v_i{v}_j\in E\left(G\right)$ or 0, otherwise. The set of all eigenvalues of this real symmetric adjacency matrix of a graph G, along with their multiplicities is called the spectra of the graph G. A graph G is said to be perfect if the clique number and the chromatic number are equal for all the induced subgraphs of G. A graph is said to be planar is it can be drawn on a surface such that no two edges cross each other. The other graph parameters and concepts that are investigated for different graphs are defined on the basis of requirements.

For more definitions and concepts related to Algebra, see [26,27], and [24] specifically for ring theory. For fundamental concepts in graph theory, we refer to [25], and for algebraic and spectral aspects in graphs, see [20,28]. For the theory of domination in graphs, refer to [29]. For more details on concepts related to the planarity of graphs, see [30] and for all basic definitions and results required to understand the study of graphs defined on rings in both graph theory as well as ring theory, we refer the reader to (Chapter 1, [12]).

As the ring of integers modulo n is a standard ring that has an easily understandable structure, almost all graphs defined on rings are examined on ${\mathbb{Z}}_n$, whose elements are the integers modulo n. Therefore, to examine the graphs defined on ${\mathbb{Z}}_n$ and related rings, proficiency in ring theory, graph theory, as well as elementary number theory is essential. Therefore, for fundamental concepts in number theory, we refer the reader to [31,32].

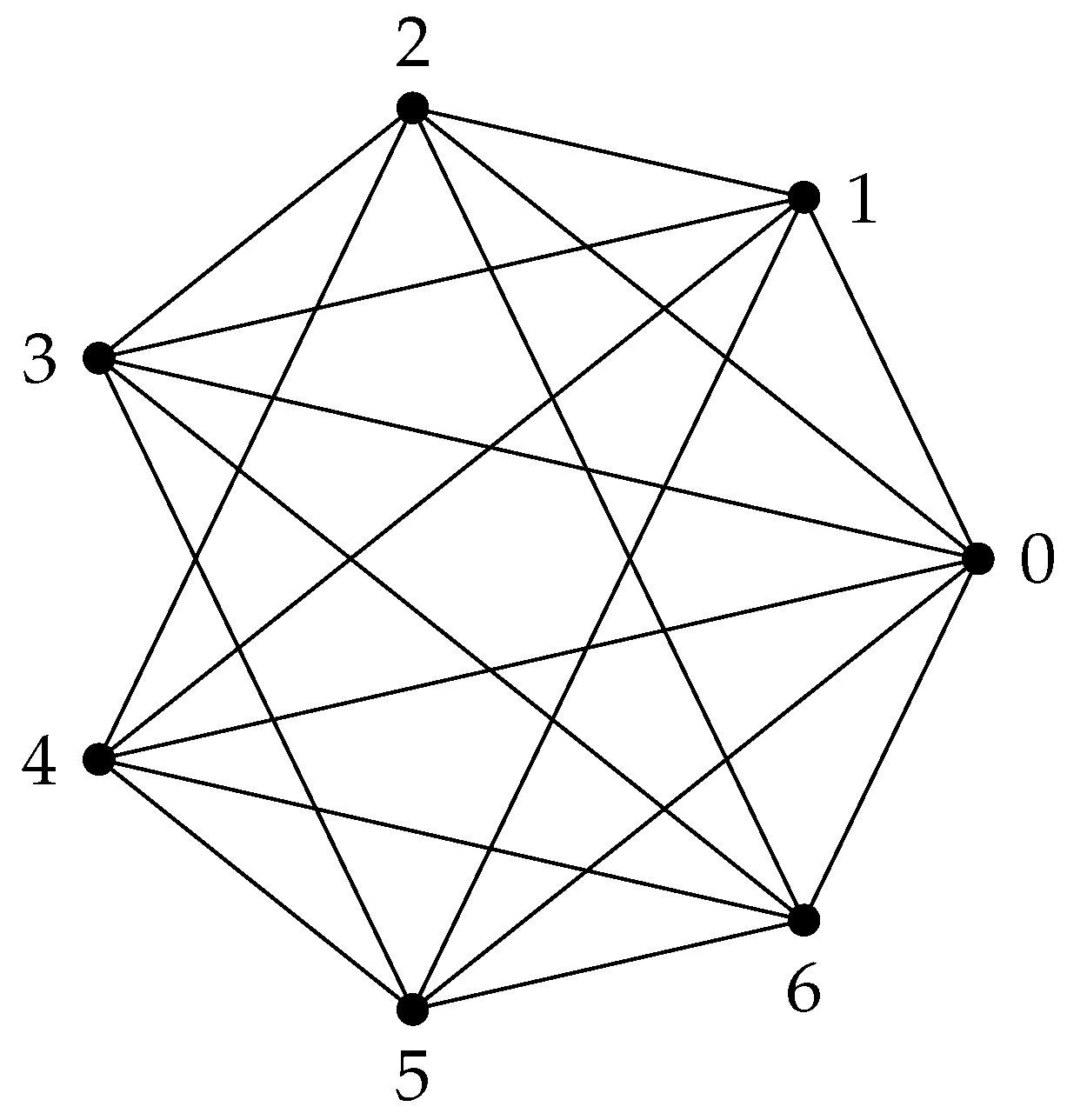
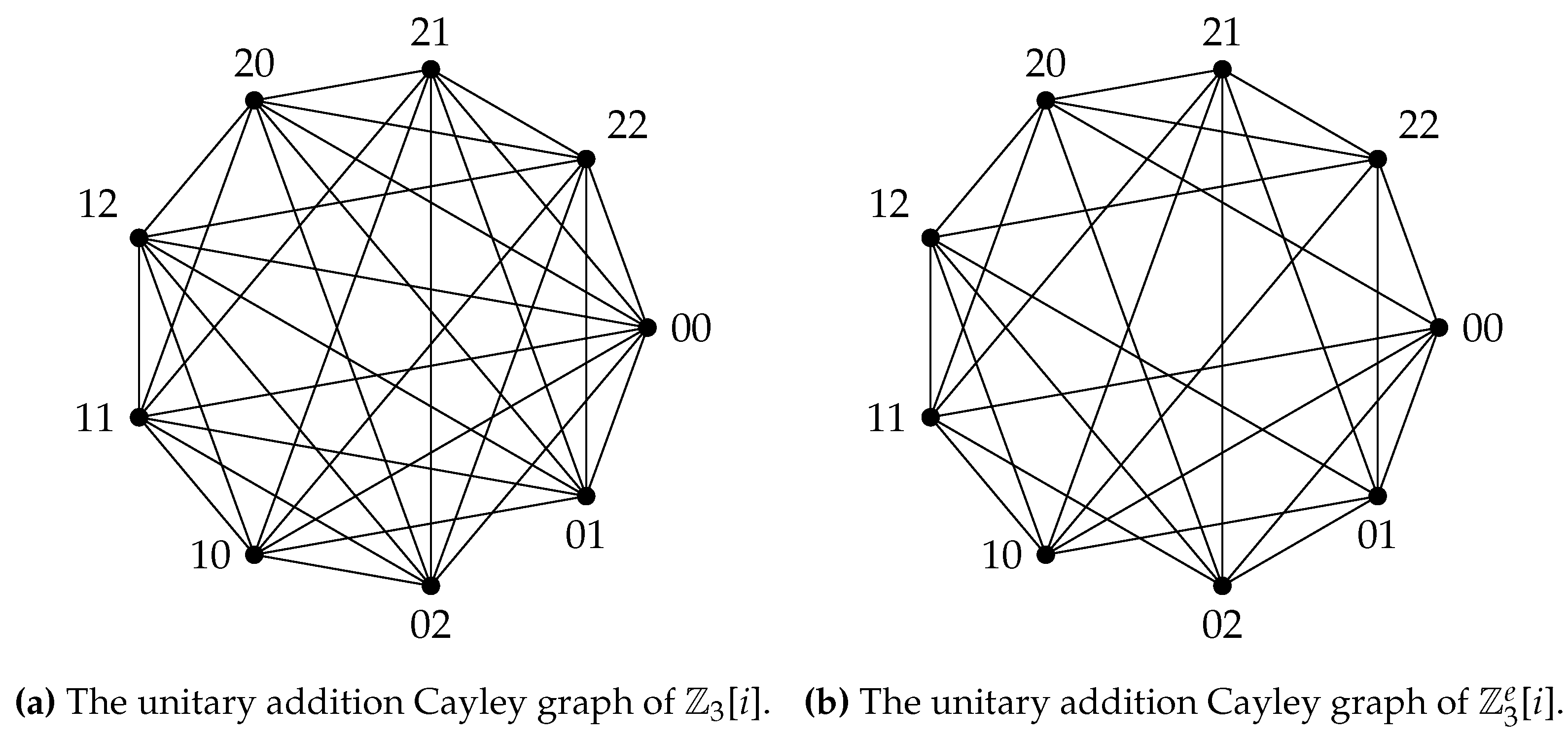
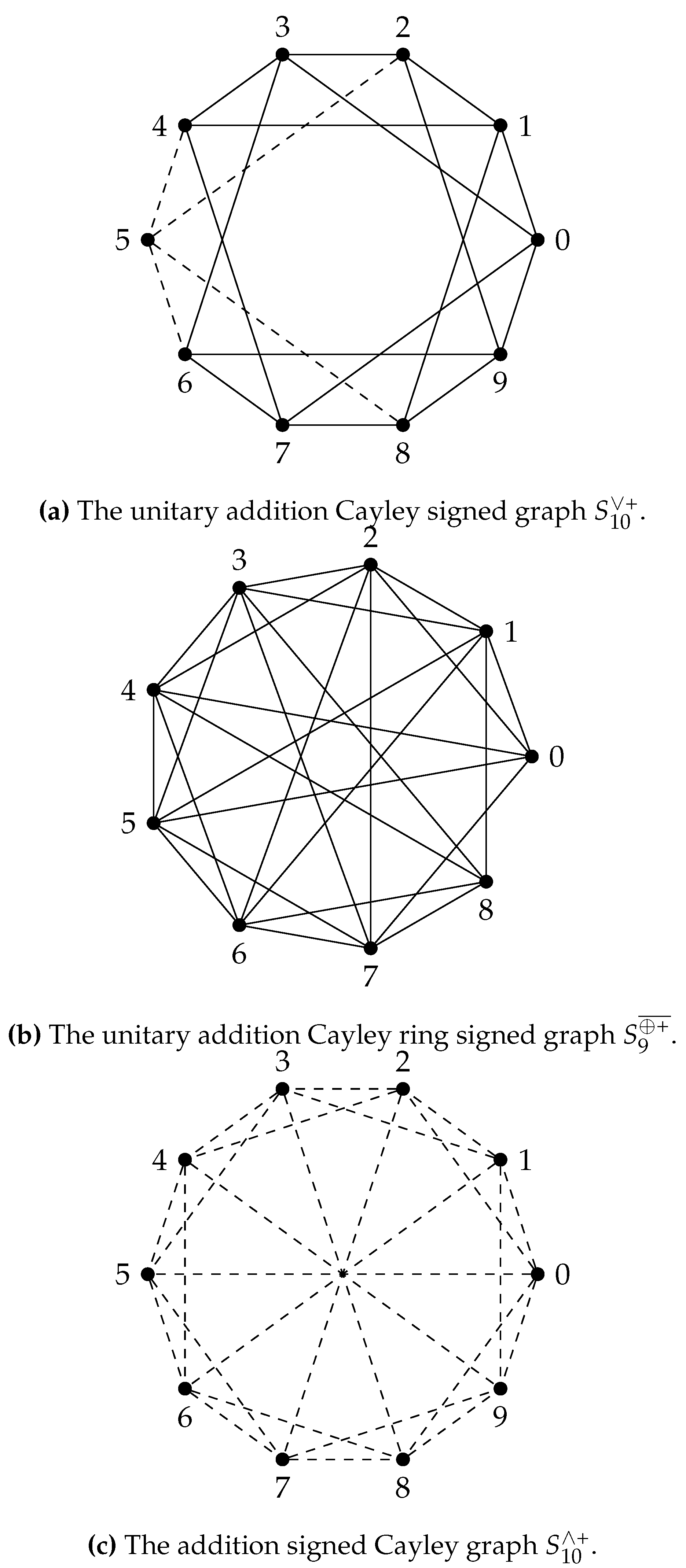
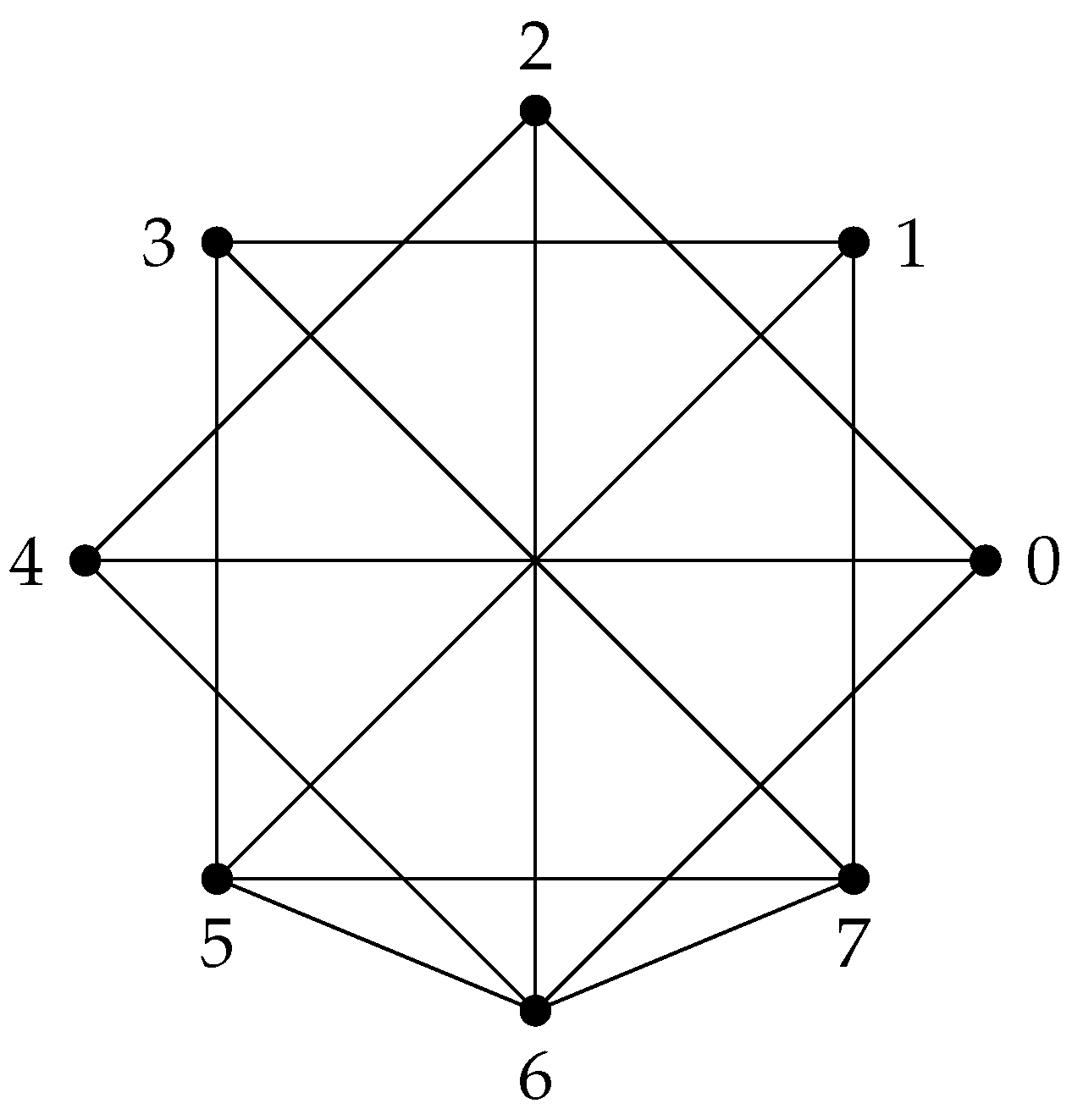
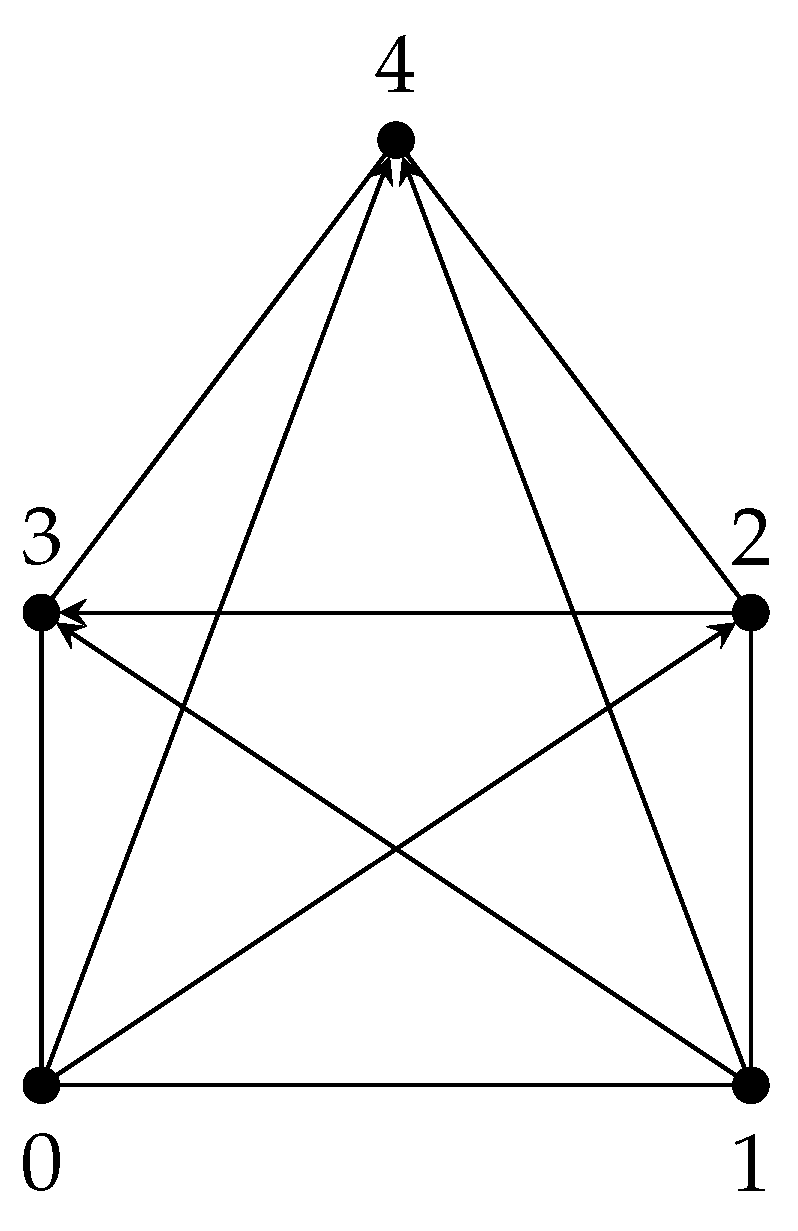
2. Unitary Cayley Graph of ${\mathbb{Z}}_n$

One of the well-studied graphs defined on rings, especially on ${\mathbb{Z}}_n$, is the unitary Cayley graphs. As the name suggests, the unitary Cayley graphs can be seen as a restriction or a variation of the broadly defined Cayley graphs. As this graph is specifically defined on ${\mathbb{Z}}_n$, it can be seen that the number-theoretic definition of the graph leads to several interesting results that are obtained using number-theoretic properties and often the innate structure of the graph gives rise to pleasing combinatorial results.

A graph of order n is said to be representable modulo k if its vertices can be labeled using distinct integers between 0 and k such that the difference of the labels of two vertices are relatively prime to k if and only if the vertices are adjacent and the smallest k for which the graph is representable modulo k is called the representation number of the graph (see [33]). The problem of determining the representation number of a given graph and analysing the property of graphs that have a given representation number, along with its relation between the order of the graph was one of prominent that was put forth as the graph representation problem in the last decade of the twentieth century, as it was proved that every graph is representable modulo for some positive integer (c.f.[33]). 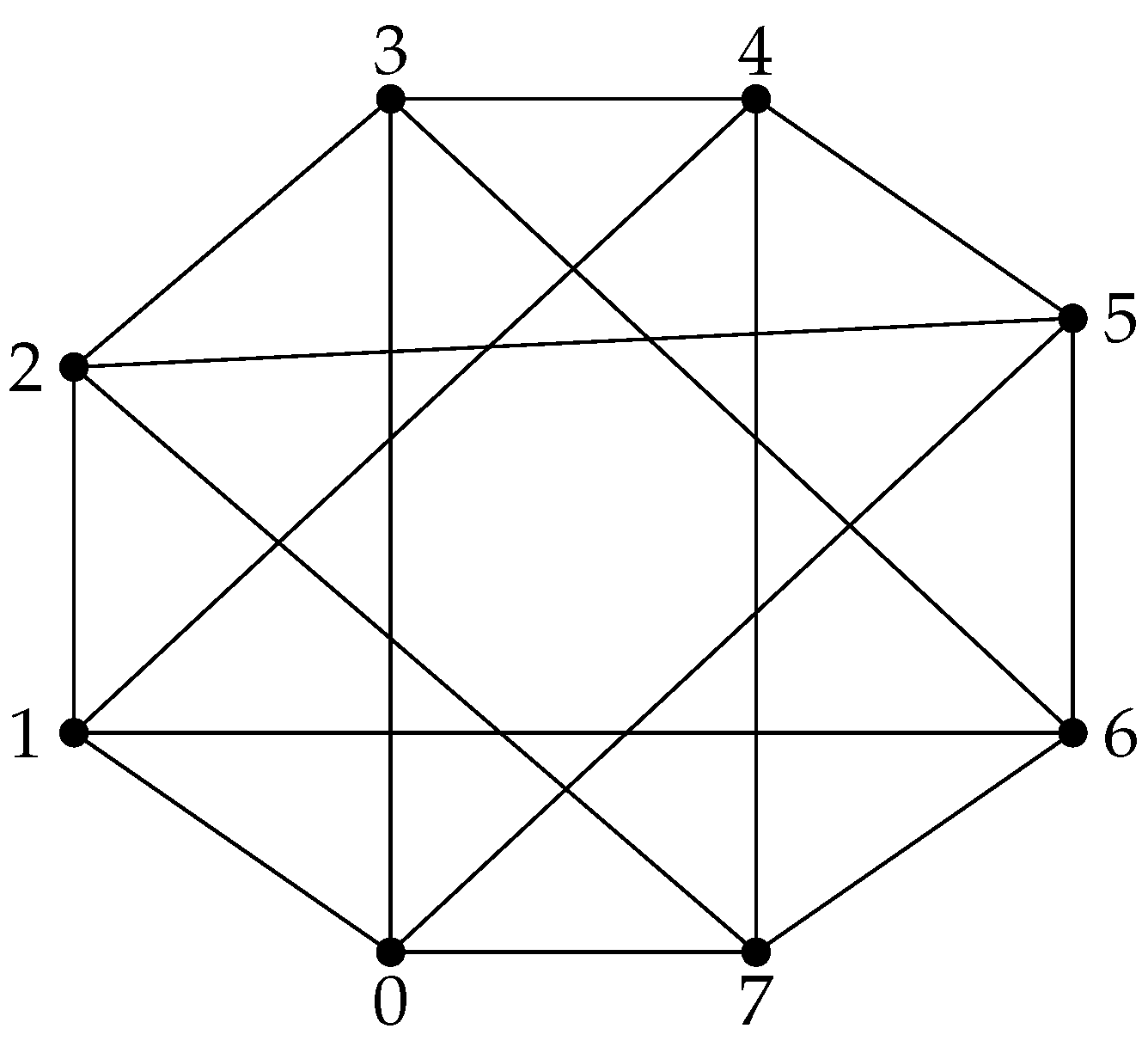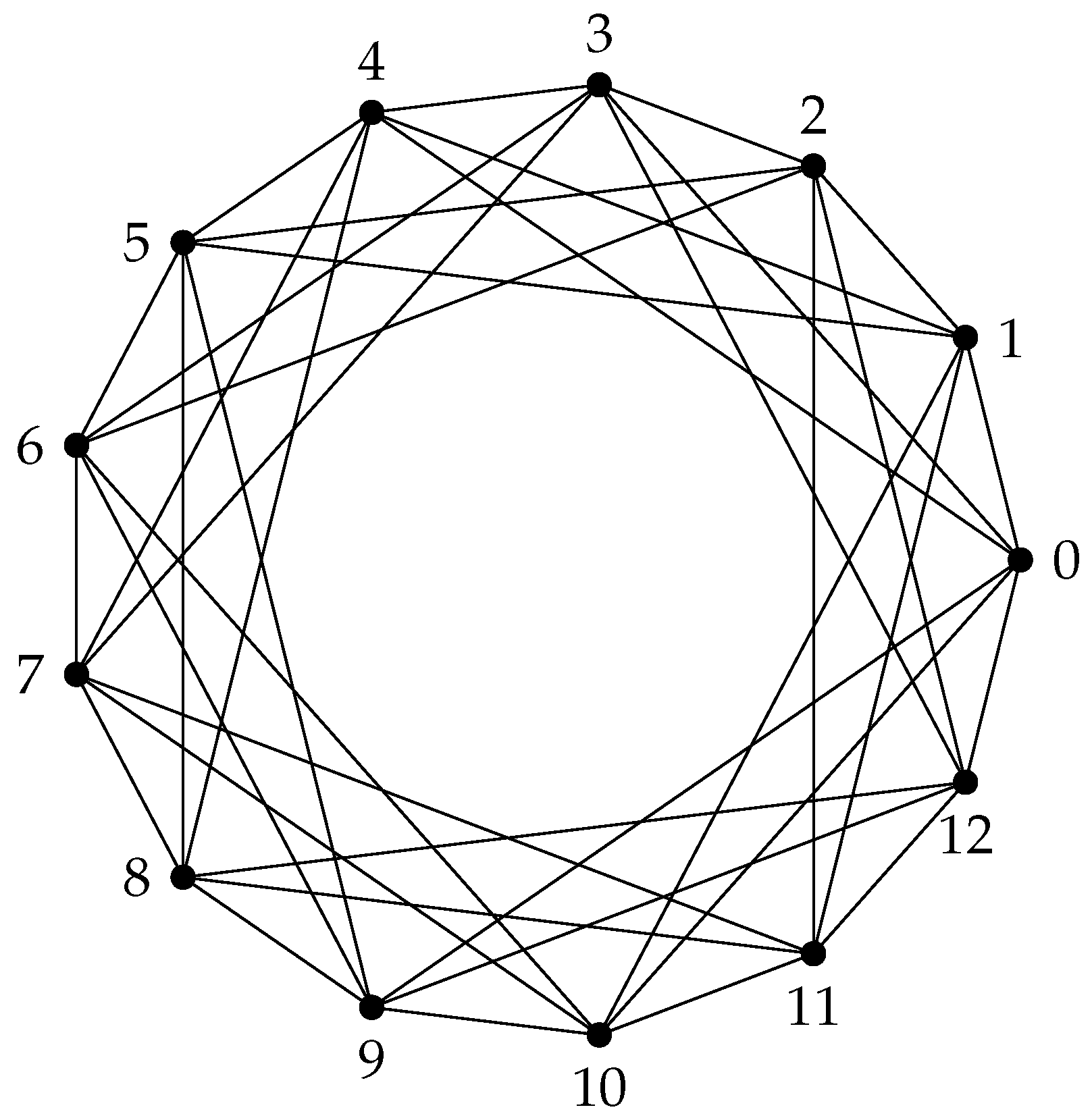The main motivation to study the unitary Cayley graph on ${\mathbb{Z}}_n$ was to investigate the representation problem of graphs, put forth in [33], which is closely related to the definition of the unitary Cayley graph on ${\mathbb{Z}}_n$ given below, following which an example of a unitary Cayley graph is given in Figure 1.

Definition 1 

([34]). Theunitary Cayley graphof the ring ${\mathbb{Z}}_n$, denoted by $X_n=Cay({\mathbb{Z}}_n,{\mathbb{Z}}_n^{*})$, is a graph with vertex set as the elements of the ring; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is a unit of the ring; that is, for all $x,y\in V\left(X_n\right)$, $xy\in E\left(X_n\right)$ when $|x-y|\in {\mathbb{Z}}_n^{*}$, where ${\mathbb{Z}}_n^{*}$ is the set of all relatively prime integers to n, which are units of ${\mathbb{Z}}_n$.

Note that the definition of the unitary Cayley graph of ${\mathbb{Z}}_n$ is closely associated with the definition of a graph to be representation modulo n and therefore, motivated to gain insights on the graph representation problem, the unitary Cayley graphs were investigated. It can be observed that post the introduction of the unitary Cayley graph $X_n$, the definition of a graph to be representable modulo n was given in terms of $X_n$. In other words, a graph is said to be representable modulo k if it is isomorphic to an induced subgraph of $X_n$ (refer to [35]).

Though the representation problem is stated in terms of the unitary Cayley graphs, $X_n$ and the results obtained on the investigation of the representation problem may be related to the graph $X_n$, note that we do not consider them in the review as the results may address only certain induced subgraph structures of the graph $X_n$, which may or may not have all the properties of $X_n$.

The unitary Cayley graph of ${\mathbb{Z}}_n$ was introduced in [34] as a specific case of the Cayley graphs defined using the generating sets of ${\mathbb{Z}}_n$, as the set ${\mathbb{Z}}_n^{*}$ generates ${\mathbb{Z}}_n$. The other variants of Cayley graphs defined based on generating sets in [36] were complete graphs and based on coloring the edges of these complete graphs in a symmetric fashion, the realisation of the induced subgraphs of these complete graphs as totally multicolored (TMC) subgraphs; that is, a subgraph of a graph in which no two edges have the same color, was studied in [36].

Motivated to investigate the possibilities of obtaining totally multicolored Cayley graphs, the unitary Cayley graph was defined on ${\mathbb{Z}}_n$ and its basic properties were investigated in [34]. By Definition 1, it can be seen that the graph $X_n$ is $\varphi \left(n\right)$-regular, where $\varphi \left(n\right)$ is the Euler’s totient function that gives the number of integers less than n that are relatively prime to n. The symmetric nature of the graph can be observed from the adjacency pattern as well as the regularity, as it is closely related to the number theoretic concepts of modular arithmetic (c.f. [37]). This symmetry of the unitary Cayley graphs gives raise to several applications in modelling networks and encourages the investigation on the graph in several directions.

The primary focus of the study in [34] was to examine the existence of triangles and the enumeration of them in the newly defined unitary Cayley graph, as the intended study was to explore the possibilities of obtaining totally multicolored graphs. This study on the triangles present in the graph helps to identify TMC graphs, but it can be seen that the study shall not be significant when the graph turns out to be a complete graph. Therefore, the first result obtained on $X_n$ classifies the values of n for which $X_n$ is a complete graph. Since bipartite graphs are characterised based on the existence of odd cycles, the values of n for which $X_n$ is bipartite and complete bipartite were also obtained as follows.

Theorem 1 

([34]).

(i) 

A unitary Cayley graph $X_n$ is isomorphic to a complete graph $K_n$ and a complete bipartite graph $K_{2^{t-1},2^{t-1}}$, when n is prime and $n=2^t$, $t\ge 1$, respectively.

(ii) 

A unitary Cayley graph $X_n$ is a bipartite graph if n is even.

It can be observed that the graphs $X_{2^t}$, $t\in \mathbb{N}$ are regular, with each vertex having degree equal to half the number of vertices and this makes the size of the graph as the square of the sum of degrees of all vertices in the graph. Since the chromatic uniqueness of complete bipartite graphs was proved in [38], the graphs $X_{2^t}$, $t\in \mathbb{N}$ are called chromatically unique unitary Cayley graphs. Note that for a graph G, the polynomial that gives the number of graph colorings as a function of the number of colors is a chromatic polynomial (see [25]) and two graphs $G_1$ and $G_2$ are chromatically equivalent if they have the same chromatic polynomial; that is, $P_{\alpha }\left(G_1\right)=P_{\alpha }\left(G_2\right)$ and a graph $G_1$ is said to be chromatically unique if $P_{\alpha }\left(G_1\right)=P_{\alpha }\left(G_2\right)$ implies that $G_1\cong G_2$ (see [39]).

As the graph $X_n$ is triangle-free for even n, the enumeration of triangles were restricted to $X_n$, for odd n. As a first step, the number of triangles in $X_n$ with two common vertices were enumerated, following which the total number of triangles in the graph was determined. The number of triangles with two common vertices was obtained as the cardinality of the set $\{u\in {\mathbb{Z}}_n^{*}:(u-1)\in {\mathbb{Z}}_n^{*}\}$. This is because, the vertex set of any triangle in $X_n$ with two common vertices can be taken as $\{0,1,u:u\in {\mathbb{Z}}_n^{*}\}$, owing to the fact that the difference between the vertices of any edge in the graph is a unit. Therefore, the third vertex that differs for the triangles with two common vertices will always be a unit and hence, the number of triangles with two common vertices is obtained as

$$n\prod _{p|n}\left(1-\frac{2}{n}\right),$$

where the product is runs over all the prime factors of n.

To enumerate the number of triangles in the graph $X_n$, the group action of the group, ${\mathbb{Z}}_n^{*}\times {\mathbb{Z}}_n$ on the set of all triangles of the graph; that is, if $(u^{\prime },x)\in {\mathbb{Z}}_n^{*}\times {\mathbb{Z}}_n$, then the action $(u^{\prime },x)\{0,1,u\}=\{u^{\prime }x,u^{\prime }(1+x),u^{\prime }(u+x)\}$ that gives the orbits of the triangles corresponding to different pairs $(u^{\prime },x)\in {\mathbb{Z}}_n^{*}\times {\mathbb{Z}}_n$ was considered. As orbits partition a set, the sum of the cardinalities of these orbits obtained through the given group action aided in determining the total number of triangles in the graph $X_n$. Using the orbits obtained through the group action, the edges of the triangles were also colored to obtain the edge coloring of the graph and this led to the enumeration of triangles having different possible combination of colors; that is, the triangles that have all three edges colored with different colors, all three edges colored with the same color and two edges colored with same color were termed as scalene-color triangles, equilateral-color triangles and isosceles-color triangles and they were enumerated.

The enumeration of triangles in the unitary Cayley graphs gave rise to the problem of counting the number of induced cycles of any given length k. Also, it was seen that to prove the chromatic uniqueness of a graph, it is important to count the number of induced k cycles in the graph, as some of the coefficients in the chromatic polynomials are related with the number of such induced cycles (see [40]). Therefore, this problem of counting the induced k cycles was proposed in [41] and the induced cycles of length 4 were enumerated using the concept of the multiplicative arithmetic property (map) of the graphs $X_n$.

A sequence of Cayley graphs $Cay({\gamma }_t,S_t)$, where ${\gamma }_t$ is an Abelian group and $S_t$ is a symmetric subset of ${\gamma }_t$, is said to have the multiplicative arithmetic property if for each pair of positive relatively prime integers $(n_1,n_2)$, there is a group isomorphism ${\varphi }_{n_1,n_2}$ from ${\gamma }_{n_1{n}_2}$ to ${\gamma }_{n_1}\times {\gamma }_{n_2}$ such that ${\varphi }_{n_1,n_2}$ maps $S_{n_1{n}_2}$ onto $S_{n_1}\times S_{n_2}$ (see [41]). In [41] the multiplicative arithmetic property on all the Cayley graphs defined on Abelian groups were discussed and since ${\mathbb{Z}}_n$ is also an Abelian group and ${\mathbb{Z}}_n^{*}$ is a symmetric subset of ${\mathbb{Z}}_n$, the unitary Cayley graphs were also examined in [41].

In [41], all Cayley graphs defined on Abelian groups were proved to have the multiplicative arithmetic property by obtaining the corresponding multiplicative arithmetic functions. A construction of sequences of Cayley graphs with the multiplicative arithmetic property, based on the number theoretic concepts like the Chinese reminder theorem was also given in the article. As an application of proving the multiplicative arithmetic property of the unitary Cayley graphs, the number of induced cycles of length 3 (triangles) and 4 were enumerated. Though, the formula for the number of triangles had been obtained previously in [34] using the group actions, the same result was deduced in this article using the multiplicative arithmetic property of the graph.

Along with the results obtained, the authors had also posted many open problems, among which the possibility to obtain a generalised expression to find the number of induced k cycles in the graph $X_n$, for any given n and to characterise the chromatic uniqueness in $X_n$ pertains to the unitary Cayley graphs. These open problems were partially addressed by the same authors in [42], by establishing a connection between the existence of an induced k cycle in $X_n$ and the number of prime divisors of n as follows.

Theorem 2 

([42]). Given $r\in \mathbb{N}$, there is a natural number $M\left(r\right)\in \mathbb{N}$, depending only on r, such that the number of induced k cycles in $X_n$ is zero for all $k\ge M\left(r\right)$ and for all n with at most r different prime divisors.

This result was proved based on the results obtained in [41], that established the multiplicative arithmetic property of the unitary Cayley graphs. By Theorem 2, it was deduced that $X_n$ is a complete p-partite graph on n vertices with the maximum number of edges and is chromatically unique, when $n=p^t$, where p is prime and $t\in \mathbb{N}$, with the partitions $P_i=\{x:x\cong imodp,0\le i\le p-1\}$ . In [34], it was obtained that $X_n$ is chromatically unique when $n=2^t$, for some $t\in \mathbb{N}$ based on the structure of the graph, and this result is extends the class of chromatically unique unitary Cayley graphs from n being only $2^t$ to any prime power, $p^t$ and this result was also proved based on the multiplicative arithmetic property. Along with this, the bounds for the value $M\left(r\right)$ are also obtained as follows.

Theorem 3 

([42]). For $r\in \mathbb{N}$, there is a natural number $M\left(r\right)\in \mathbb{N}$, that depends only on r such that $(r-1)ln(r-1)\le M\left(r\right)\le 9r!$

The bounds given in Theorem 3 shows the existence of induced k cycles in $X_n$, for arbitrarily large r, which adds credibility to Theorem 2. Also, a large gap between the bounds of $M\left(r\right)$ opened an avenue to find better estimates, which were computed in [43]. The main problem addressed in [43] was to determine the length of the longest induced cycle in $X_n$ for a given n and to address this problem, a representation of the vertices in $X_n$ based on their residues modulo the prime factors of n, called the residue representation is introduced as follows.

Definition 2 

([43]). For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and ${\alpha }_i\in \mathbb{N}$, if $x\in V\left(X_n\right)$ such that $x\equiv {\alpha }_{i}mod{p}_i$, for $1\le i\le r$ and $0\le {\alpha }_i<p_i$, theresidue representationof x is the unique string ${\alpha }_1{\alpha }_2\dots {\alpha }_r$.

This representation simplifies the problem of finding the induced cycles in the graph to that of checking the similarity conditions between consecutive vertices; that is, to check if any pair of non-consecutive vertices has at least one same index in the representation, as it can be observed that for any $x,y\in V\left(X_n\right)$, $xy\in E\left(X_n\right)$ if and only if $x\equiv ymod{p}_i$ for all $1\le i\le r$. In this article, the number $M\left(r\right)$ defined in [42] is given in terms of $m\left(n\right)$, which denotes the longest induced cycle in $X_n$ as $M\left(r\right)={max}_n\left\{m\left(n\right)\right\}$, where the maximum is taken over all n values with r distinct prime divisors. Since $M\left(r\right)$ was proved to depend only on r in [42], $m\left(n\right)$ was also proved to depend only on r in [43], so that there arises no ambiguity in the given definition of $M\left(r\right)$ in terms of $m\left(n\right)$. Significant questions on the relation between the values $m\left(n\right)$ and $M\left(r\right)$ were also answered in [43], from the conditions under which these values of $m\left(n\right)$ and $M\left(r\right)$ are equal were obtained as given below.

Theorem 4 

([43]). For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and are large, $m\left(n\right)=M\left(r\right)$.

Theorem 5 

([43]). For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$ and $n^{\prime }=p_1{p}_2{p}_3\dots p_r$, where $p_i$, $1\le i\le r$ are distinct primes and $r\ne 1$, $m\left(n\right)=M\left(n^{\prime }\right)$.

Theorem 5 reduces the complexity of calculating $m\left(n\right)$ for large values of n, as it considers only the values of n whose prime powers are square-free. These results aided in improving the tightness of the bounds of $M\left(r\right)$ in [43], which is given below.

Theorem 6 

([43]). For all positive integers n with $r>1$ distinct prime divisors, $2^r+2\le M\left(r\right)\le 6r!$.

To prove Theorem 6, an induced subgraph of $X_n$ with $2^r+2$ vertices was constructed for all n, and it was proved that the construction depends only on the number of prime divisors, r of n and not on the value of the prime divisors, thus providing a lower bound for $m\left(n\right)$. It was natural to examine the properties of $X_n$ that contributed to the results that were obtained and to explore the possibilities of constructing similar graphs. On analysing these properties, it was noted that the above results on the length of the longest cycles can be extended to the direct product of any number of complete k-partite graphs and this extension can be seen as an immediate consequence of the fact that for any $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, $X_n\cong X_{p_1^{{\alpha }_1}}\times X_{p_2^{{\alpha }_2}}\times \dots \times X_{p_r^{{\alpha }_r}}$, as $X_n$ is a complete p-partite graph for $n=p^t$, when p is prime. Note that the unitary Cayley graphs are referred to as the unitary circulant graphs in [43].

A random walk on a finite, connected graph is a Markov chain1 that jumps from a current vertex v to one of its k neighbors, where with a uniform probability (refer to [45]). The hitting time $T_v$ of a vertex v is the minimum number of steps that a random walk takes to reach back the same vertex and the expected value of $T_v$ for a vertex is known as the expected hitting time. The expected hitting times for the random walks in the unitary Cayley graph $X_n$ and the direct product of two unitary Cayley graphs $X_{n_1}$ and $X_{n_2}$, where $n_1=p^{t_1}$ and $n_2=p^{t_2}$,$t_1,t_2\in \mathbb{N}$ were studied in [46] and [47] respectively, as an extension of the study on the expected hitting time of the edge transitive graphs by the same authors in [45]. Though the high symmetry of the graph $X_n$ can be realised from the graph construction, the unitary Cayley graphs were formally proven to be arc-transitive in [46], by obtaining an automorphism of the graph that satisfies the condition of arc transitivity as follows.

Theorem 7 

([46]). The function $\psi \left(x\right)=wx+z$, where $w\in {\mathbb{Z}}_n^{*}$, $z\in {\mathbb{Z}}_n$ and $x\in V\left(X_n\right)$ are fixed, is an automorphism of the graph $X_n$.

A graph G is said to be a vertex-transitive (edge transitive) graph if its automorphism group acts transitively on $V\left(G\right)$ ($E\left(G\right)$). In other words, a graph G is vertex-transitive (edge-transitive), if there exists an automorphism between any two distinct vertices (edges) of G. Similarly, a graph G is arc-transitive if there exists an automorphism between any two distinct edges of G such that the direction of the edges are preserved.

As it can be observed that arc-transitive graph is both vertex transitive and edge transitive, and hence, this automatically proves that the unitary Cayley graphs are both vertex and edge transitive. The main focus of the article [46] was to determine the expected hitting time of the edge transitive graphs, when the diameter of the graphs are 2 and 3, and to tighten the results when the graphs follow certain adjacency patterns. Since Theorem 7 proves the edge transitivity of the unitary Cayley graphs, the expected hitting times of these graphs were explicitly computed in [46] by classifying the graphs that have diameter 2 and 3 as follows.

Theorem 8 

([46]). The diameter of $X_n$,

$$diam\left(X_n\right)=\left\{\begin{array}{cc}2,\hfill & ifn=2ornisoddandcomposite;\hfill \\ 3,\hfill & ifn=2^{l}k,wherel\ge 1andm>1isodd.\hfill \end{array}\right.$$

By the definition of a random walk, it can be noted that the study of random walk in a regular graph tends to give a uniform distribution, as the number of neighbors to which the vertex can jump is equal for all the vertices in the graph. Also, the unitary Cayley graphs considered in the study were the graphs $X_n$, $n=p^k$, where p is a prime which were already proven to be complete k-partite graphs in [42]. To determine the hitting times of these graphs, the degree and distance between each pair of vertices in the graph must be known and therefore, the degree and distance between each pair of vertex in the graph $X_n$, when n is a prime power was determined in [46], and the diameter of the graph $X_{n_1}\times X_{n_2}$, where $n_1=p^{r_1}$ and $n_2=p^{r_2}$; for $r_1,r_2\in \mathbb{N}$, was also determined as 2 in [47]. As the graphs $X_{n_1}\times X_{n_2}$ are of diameter 2, the hitting time of the vertices of these graphs were also computed and are given as follows.

Theorem 9 

([47]).

(i) 

The expected hitting time between the vertices at distance 1 is

$|V(X_{n_1}\times X_{n_2})|-1=p^{n_1+n_2}-1$.

(ii) 

The expected hitting time between the vertices at distance 2 is

(a) 

$|V(X_{n_1}\times X_{n_2})|=p^{n_1+n_2}$, when no pair of vertices are at distance 1 in the graphs $X_{n_1}$ or $X_{n_2}$.

(b) 

$|V(X_{n_1}\times X_{n_2})|+\frac{1}{p-2}=p^{n_1+n_2}+\frac{1}{p-2}$, otherwise.

Though the unitary Cayley graphs were officially introduced in [34] in the year 1995, not many studies had emerged on the unitary Cayley graphs until 2007, before [48] was published. It was the first study that laid a strong foundation to the study on the unitary Cayley graphs, as it had an in-depth investigation on the properties of the unitary Cayley graphs; only after which, a huge growing literature can be found on the topic. The study in [48] begins with a brief review on the previous investigations of the unitary Cayley graphs, following which the chromatic number, clique number, and the vertex connectivity of $X_n$ were computed as follows.

Theorem 10 

([48]). If p is the smallest prime divisor of n, then $\chi \left(X_n\right)=\omega \left(X_n\right)=p$, where χ and ω denote the chromatic and clique number respectively.

Theorem 11 

([48]). The vertex connectivity $\kappa \left(X_n\right)$ of the unitary Cayley graph $X_n$ is $\varphi \left(n\right)$, where $\varphi \left(n\right)$ is the Euler’s totient function.

An arc-transitive graph for which the vertex connectivity being its degree makes the unitary Cayley graphs highly reliable and stable for networks models. Also, the regularity of the graph $X_n$ implies that its complement is also regular and highly symmetric and therefore, using Theorem 10, the chromatic and clique number, $\chi \left({\overline{X}}_n\right)$ and $\omega \left({\overline{X}}_n\right)$ of the complement of $X_n$ were computed as $\frac{n}{p}$, where p is the smallest prime divisor of n. Based on these results on the complement of the unitary Cayley graphs, the following realisation was obtained.

Theorem 12 

([48]). A unitary Cayley graph $X_n$ is self-complementary if and only if $n=1$ or $n=2$. That is, $X_n\cong {\overline{X}}_n$ if and only if $n=1$ or $n=2$.

Based on the investigation of the complement of the graph $X_n$ and its regularity, the number of common neighbors between the vertices were enumerated in [48] by partitioning the vertex based on different conditions for different values of n. On obtaining the chromatic and the clique number of the graphs, perfection in the unitary Cayley graphs was studied by investigating the existence of odd cycles of length 5 or more in the graph $X_n$ and the unitary Cayley graphs that are perfect were characterised as follows.

Theorem 13 

([48]). A unitary Cayley graph $X_n$ is perfect if and only if n is even or n is odd and has at most two distinct prime divisors.

The investigation of the spectral properties of the unitary Cayley graphs began in [48], where the adjacency matrix of the graph $X_n$ was obtained. It is known that there are multiple adjacency matrices for any graph, which are given based on different ordering of the vertices. With the natural order of vertices $0,1,2,\dots ,n-1$, the adjacency matrix of the unitary Cayley graphs were obtained as circulant matrices; that is, matrices in which the entries of its first row generate the entries of the other rows by a cyclic shift, which established that the unitary Cayley graphs are circulant graphs; the graphs with circulant adjacency matrices (c.f. [20]).

Using the explicit formula to obtain the eigenvalues of a circulant matrix given in [49], the eigenvalues of the adjacency matrix of $X_n$ was obtained in terms of an arithmetic function $c(r,n)$ called the Ramanujan sum2, which takes only integral values for the given integers $r,n,n>0$. Therefore, it was concluded that all eigenvalues of unitary Cayley graphs are integers and hence, the unitary Cayley graphs fall under the class of graphs called the integral circulant graphs; circulant graphs whose eigenvalues are integers (see [50]). Further investigation on the eigenvalues of the graph $X_n$, based on their symmetry and the number theoretical properties had led to following interesting results on the eigenvalues of the graphs.

Theorem 14 

([48]). Let $\varphi \left(n\right)$ denote the Euler’s totient function and $\mu \left(n\right)$ denote the Mobiüs function 3.

(i) 

Every non-zero eigenvalue of $X_n$, $n>1$ is a divisor of $\varphi \left(n\right)$.

(ii) 

Let p be the maximal square-free divisor of n. Then, ${\lambda }_{min}=\mu \left(p\right)\frac{\varphi \left(n\right)}{\varphi \left(p\right)}$is a non-zero eigenvalue of $X_n$, $n>1$ of minimal absolute value and multiplicity $\varphi \left(p\right)$.

(iii) 

Every eigenvalue of $X_n$, $n>1$ is a multiple of ${\lambda }_{min}$.

(iv) 

If $n>1$ is odd, then ${\lambda }_{min}$ is the only non-zero eigenvalue of $X_n$ with minimal absolute value.

(v) 

If $n>1$ is even, then $-{\lambda }_{min}$ is also an eigenvalue of $X_n$ with multiplicity $\varphi \left(n\right)$.

Theorem 15 

([48]).

(i) 

There is an eigenvalue $-1$ or 1 of $X_n$, if and only if n is square-free.

(ii) 

If n is square-free, then $X_n$ has the eigenvalue $\mu \left(n\right)$ with multiplicity $\varphi \left(n\right)$.

(iii) 

The unitary Cayley graph $X_n$ has both eigenvalues 1 and $-1$ with multiplicity $\varphi \left(n\right)$ if and only if n is square-free and even.

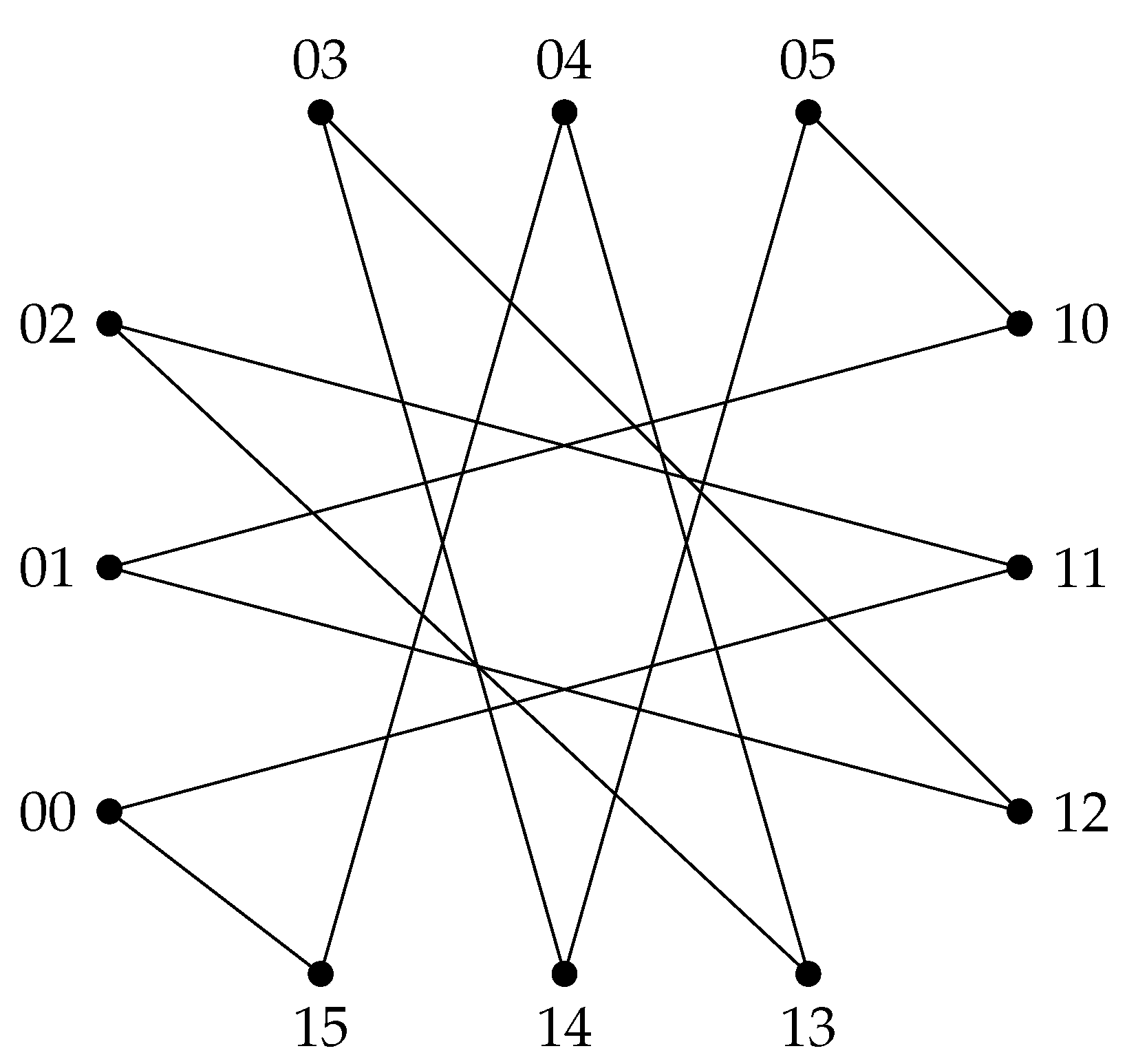
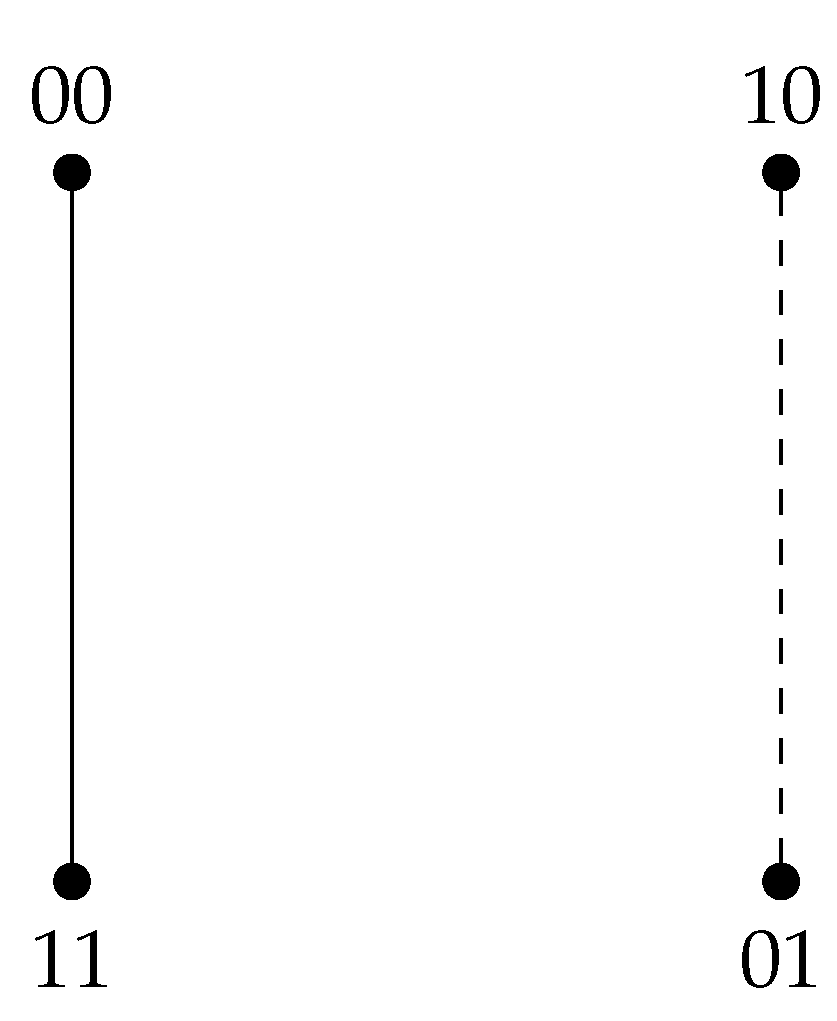
Fascinated by the spectral properties of the unitary Cayley graphs and its close relation with number theory, the authors defined a generalisation of the unitary Cayley graphs, called the $GCD$-graphs, in which the set of all positive, proper divisors of an integer $n>1$ is considered as the symmetric subset, to define the adjacency condition. The formal definition of the graph is given below.

Definition 3 

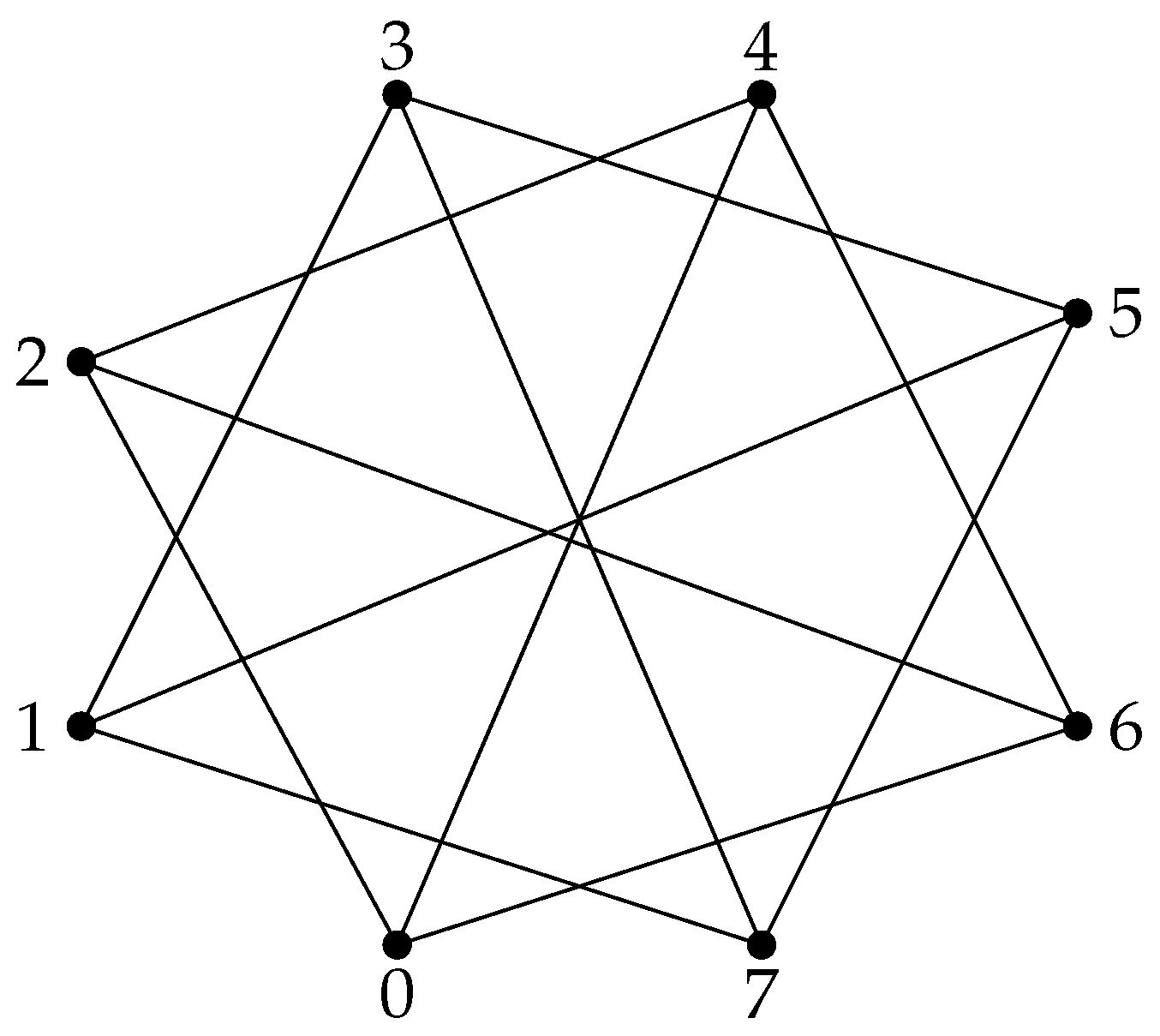
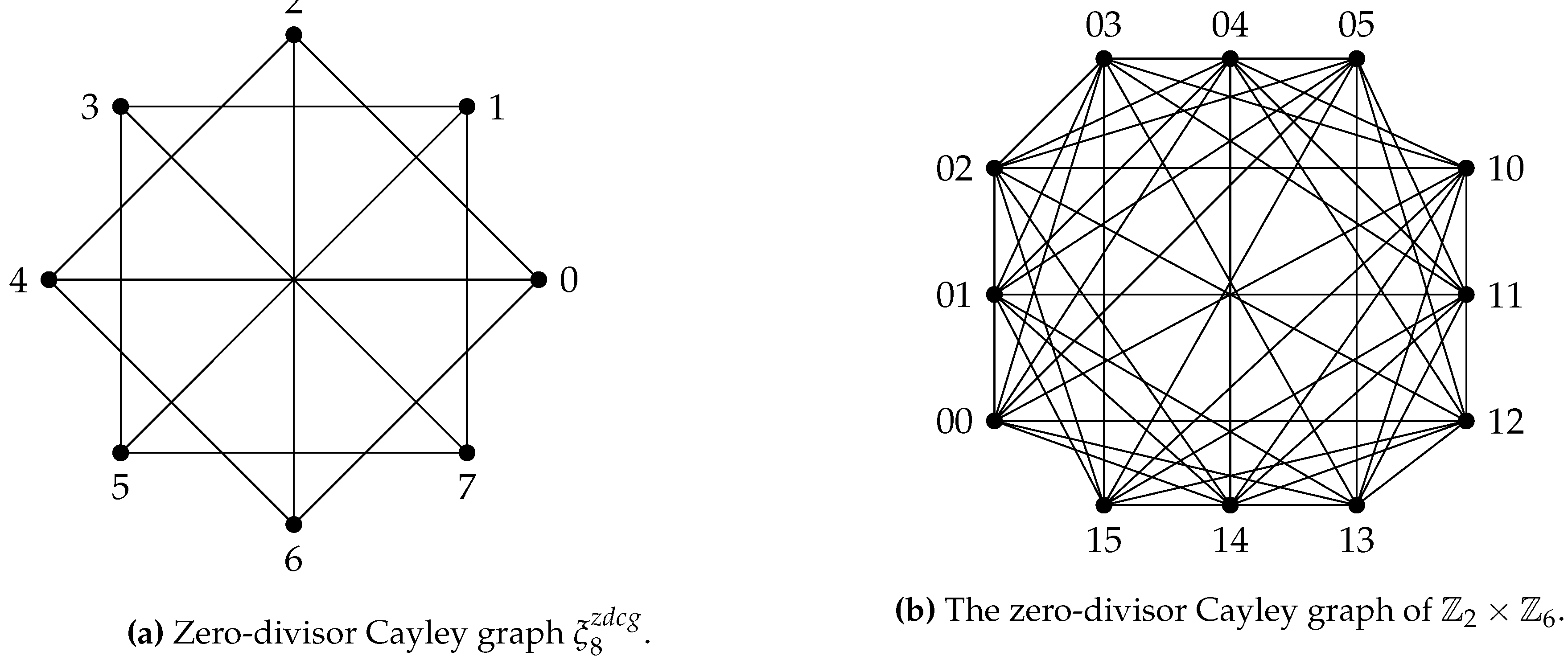
([48]). The $GCD$-graph, denoted by $X_n\left(D_n^{*}\right)$ is a graph with vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots n-1$, and two vertices are adjacent if the gcd of their difference and n is a positive proper divisor of n; that is, for all $x,y\in V\left(X_n\left(D_n^{*}\right)\right)$, $xy\in E\left(X_n\left(D_n^{*}\right)\right)$ when $gcd(x-y,n)\in D_n^{*}$, where $D_n^{*}$ is the set of all positive, proper divisors of the integer $n>1$. An example of a $GCD$-graph is given in Figure 2.

Observe that the set $D_n^{*}$ consists of only all the proper positive divisors because when one is included as a divisor, the graph obtained shall be the complement of $X_n$, for certain values of n. The analysis on the spectra of $GCD$-graphs in [51] proved that the $GCD$-graphs also have integral eigenvalues. On further exploration of the properties of these graphs that have integral spectra, the authors came up with a slightly modified definition of the graphs based on this basic definition of the $GCD$-graphs that was put forth by them in [48], to obtain multiple smaller graphs which fall under this broad category with similar properties as follows.

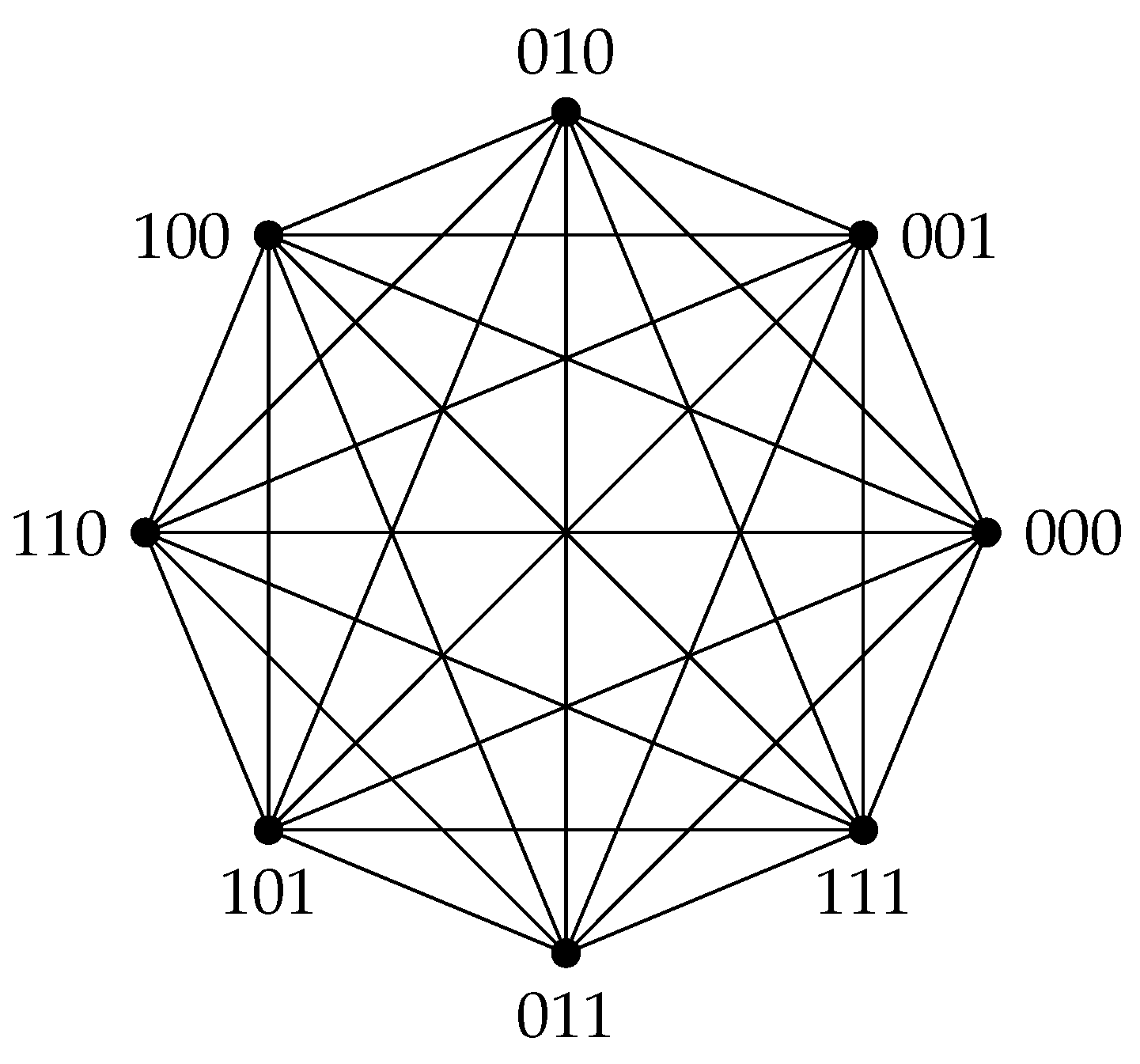
Definition 4 

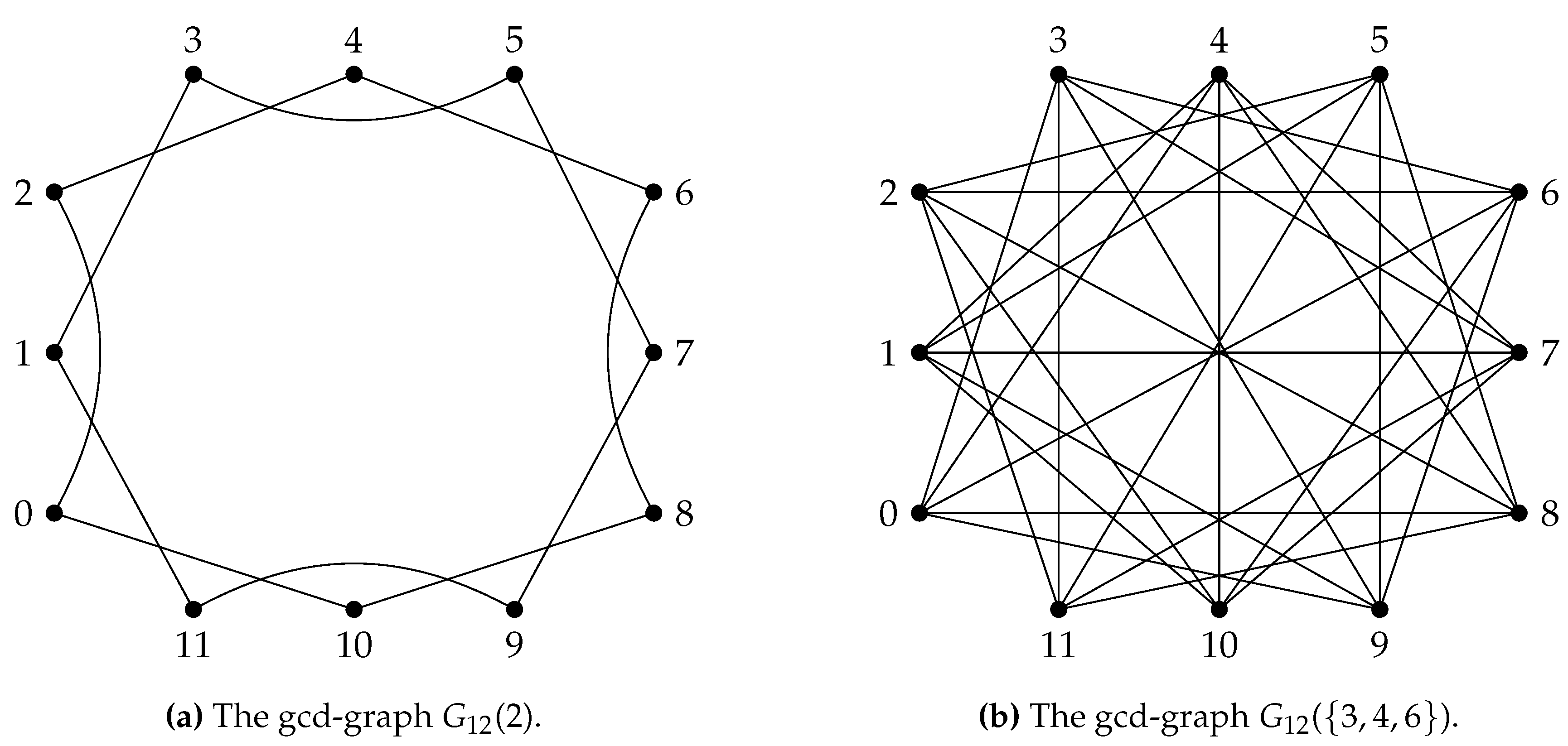
([52]). For a positive integer n, let $D_n$ be the set of all its divisors. Define the graph $G_n\left(d\right)$, where $d\in D_n$, with the vertex set as the elements of the ring ${\mathbb{Z}}_n$ and two vertices $x,y$ in the graph are adjacent when the $gcd(x-y,n)=d$. The graph $G_n\left(d\right)$ is extended by increasing the number of divisors and modifying the adjacency condition of any two vertices $x,y$ to be $gcd(x-y,n)\in D$, where $D\subseteq D_n$ and this graph is represented as $G_n\left(D\right)$. These graphs are known asgcd-graphs.

Note that if $|D_n|=k$, then $2^{k-1}$gcd-graphs $G_n\left(D\right)$ are possible for any integer n,where the graphs $X_n$ and $X_n\left(D_n\right)$ are also one among them. An illustration of some gcd-graphs emerging from ${\mathbb{Z}}_{12}$, for the subsets $D\subset D_n$, apart from $D=\left\{1\right\}$ and $D=D_n$ is given in Figure 3.

This new generalised definition was simultaneously given in [51] in the process of characterising integral circulant graphs and it was proved that a graph is an integral circulant graph if and only if it can be realised as the graph $G_n\left(D\right)$, for some $D\subseteq D_n$. It can be observed that when the set of all proper divisors are considered, the gcd-graphs $G_n$ will be the $GCD$-graph defined in [48] and when $D=\left\{1\right\}$, $G_n\left(1\right)=X_n$.

Therefore, it can be seen that the unitary Cayley graphs can be realised as a special case of $GCD$-graphs as well as the gcd-graphs from their definitions, and any study on gcd-graphs can be considered to obtain results on the the unitary Cayley graphs. Also, based on the characterisation of the integral circulant graphs as gcd-graphs and the fact $G_n\left(1\right)=X_n$, the results established for the integral circulant graphs will also hold for the unitary Cayley graphs. The integral circulant graphs or the graphs $G_n\left(D\right)$ have a huge, growing literature, owing to its spectral properties that have applications in fields like chemistry, quantum physics, radiology, etc (c.f. [50]).

As already seen, the unitary Cayley graph $X_n$ is a special case of the integral circulant or gcd-graphs and hence, all the properties that are investigated for the latter shall hold for $X_n$, but the bounds and results obtained for the unitary Cayley graphs shall be more specific and tight than results obtained for these broader classes of graphs. Therefore, in this article, we present a review of the study which aree specifically made on the Unitary Cayley graphs and the results that were explicitly stated for the graph $X_n$, as an application or a corollary in the articles that study the integral circulant graphs or gcd-graphs.

In [48], an open problem to determine the automorphism group of the unitary Cayley graphs $X_n$, for $n>6$ had been posted by the authors, which led to the investigation on the automorphisms of $X_n$. Though the problem was not fully addressed, a necessary and sufficient condition for a bijective mapping to possess the structure of an automorphism of the graph $X_n$ was given in [53] as follows.

Theorem 16. 

[53] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes, ${\alpha }_i\in \mathbb{N}$, and r is the number of distinct prime divisors of n. Then, a bijective mapping induces an automorphism of the graph $X_n$ if and only if it preserves congruence modulo $p_i$ for all i.

Apart from the above mentioned result that was obtained on the automorphism of $X_n$, a characterisation of planar unitary Cayley graphs was obtained along with the crossing number (The least number of edges that cross in a planar graph drawing.) of $X_n$ for few values of n for which the graph structure is a well-known graph class, using the existing results on the crossing number of these graph classes. The traversal properties of $X_n$ were also discussed in the article along with which the edge chromatic number and the edge connectivity of the graph were also determined as given below, where $\varphi \left(n\right)$ denotes the Euler’s totient function.

Theorem 17. 

[53] The graph $X_n$ is planar if and only if $n\in \{1,2,3,4,6\}$.

Theorem 18. 

[53] The graph $X_n$, $n\ge 3$ is Eulerian as well as Hamiltonian and each such $X_n$ can be decomposed into $\frac{\varphi \left(n\right)}{2}$ edge-disjoint Hamiltonian cycles.

Theorem 19. 

[53] The edge connectivity of the graph $X_n$ is $\varphi \left(n\right)$.

Theorem 20. 

[53] For the graph $X_n$, the edge chromatic number is $\varphi \left(n\right)$ and $\varphi \left(n\right)+1$, when n is even and odd, respectively.

The property of the graph $X_n$ having both its edge and vertex connectivity equal to its degree of regularity and the graph being integral circulant, increases the application of the graphs in the field of networks, especially in areas that require a stable and strong network. This increases the significance of the study on the graph for various purposes and this also gives the researchers the curiosity to investigate other properties of the graphs, and construct similar graphs. Extending the study further, the authors studied the basic graph properties of the unitary Cayley graph of a ring, which is obtained as a finite direct product of the rings ${\mathbb{Z}}_n$, for different values of n. This extension gave rise to the idea of generalising the unitary Cayley graphs of ${\mathbb{Z}}_n$ to any ring R, a detailed review of which is given in Section 3.

The open problem to determine the automorphism group of $X_n$, put forth in [48] was solved in [54] by obtaining the automorphism groups of $X_n$ and their cardinality, for different values of n, as a tool to generalise the automorphism groups of the integral circulant graphs. The results obtained are given below and it shows that the structure of the automorphism groups are highly sophisticated as the value of n increases.

Theorem 21. 

[54] For $n=p^k$, where p is a prime number and $k\ge 1$, the size of the automorphism group of $X_n$, $|Aut\left(X_n\right)|=p!{(\left(p^{k-1}\right)!)}^p$.

Theorem 22. 

[54] For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$, are distinct primes and ${\alpha }_i\in \mathbb{N}$, the size of the automorphism group of $X_n$, $|Aut\left(X_n\right)|={\displaystyle \prod _{i=1}^r}{p}_i!{(\left(\frac{n}{{\displaystyle \prod _{i=1}^r}{p}_i}\right)!)}^{{\displaystyle \prod _{i=1}^r}{p}_i!}$.

The structure of the automorphism group of $X_n$ was proved by partitioning the vertices of $X_n$ based on the residue modulo primes, which is similar to the residue representation introduced in [43] and the permutations on these residue classes were considered to obtain automorphisms of the graph, using the notion of modular arithmetic and the Chinese remainder theorem. According to the construction of automorphisms of $X_n$ in the proof of Theorem 22, it was concluded that the automorphism group is isomorphic to the wreath product of the permutation group (refer to [55]) of the graphs of residue classes modulo r and the permutation groups of vertices in each class, as given below.

Theorem 23. 

[54] For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and ${\alpha }_i\in \mathbb{N}$, the automorphism group of $X_n$, $Aut\left(X_n\right)\cong (S_{p_1}\times S_{p_2}\times \dots \times S_{p_r})\wr S_{\frac{n}{r}}$, where $S_k$ represents the group of permutations on k elements and ≀ denotes the product of groups.

The same problem of determining the automorphism group of the unitary Cayley graph was solved in [56,57], using different approaches. The study in [56] began with a motive to investigate the automorphism group of $X_n$; but the authors on observing the symmetric pattern of $X_n$ in several aspects, extended the concept of unitary Cayley graphs to any ring R and the automorphism groups of the unitary Cayley graphs defined on a ring R were investigated, which on special case of $R={\mathbb{Z}}_n$ gave the automorphism group of $X_n$. The main idea of their algebraic proof, where the dependence of the automorphisms on the underlying algebraic structure of the rings concerned was emphasized, is different from the proof given in [54], which used a number-theoretical approach. The authors of [57] investigated the automorphism group of the rational circulant graphs; circulant graphs with a rational spectra, in which the integral circulant graphs become a subclass, by developing a framework based on Schur rings (For more details, refer to [58,59]). The approach is highly complex as it is built for all rational circulant graphs; but it is claimed in [57] that the automorphism group of $X_n$ could have been traced a few decades ago if the framework of the approach presented in [57] was followed.

The results on the spectra of the unitary Cayley graphs obtained in [48] fascinated the researchers to explore other parameters and properties of the unitary Cayley graph $X_n$ that are closely associated with its adjacency matrix and its eigenvalues. The first of such properties to be investigated was the perfect state transfer in the unitary Cayley graphs. For a graph G with the adjacency matrix A, $H\left(t\right)$ is defined as the operator $e^{\left(itA\right)}$, called the transition operator. A perfect state transfer between the vertices u and v is said to happen at time $\tau$ if the $uv$-entry of ${|H\left(\tau \right)}_{u,v}|=1$. This perfect state transfer is being used in several areas that deals with allocation and assignment factors, especially it has been efficiently applied to key distribution in commercial cryptosystems, and in assignment of objects in quantum spin networks (see [50]). This notion was introduced to circulant graphs in [60] and the perfect state transfer in the integral circulant graphs was studied in [50]. Based on these studies, the class of unitary Cayley graphs that allow perfect state transfer was characterised in [50] as follows.

Theorem 24. 

[50] The only unitary Cayley graphs that allow perfect state transfer are $X_2$ and $X_4$.

Following the study on perfect state transfer in the unitary Cayley graph $X_n$ the properties related to the energy of the graph, which is the sum of the absolute values of the eigenvalues of the adjacency matrix of the graph was determined in [61] and [62] as follows.

Theorem 25. 

[61,62] For $n=p^t$, where p is a prime and $t\in \mathbb{N}$, the energy of $X_n$, $\mathcal{E}\left(X_n\right)=2\varphi \left(n\right)$, where $\varphi \left(n\right)$ represents the Euler’s totient function.

Theorem 26. 

[61,62] For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$ and $n^{\prime }=p_1{p}_2{p}_3\dots p_r$, where $p_i$, $1\le i\le r$ are distinct primes and $r\ne 1$, the energy of $X_n$, $\mathcal{E}\left(X_n\right)=2^r\varphi \left(n\right)$, where $\varphi \left(n\right)$ represents the Euler’s totient function.

Theorem 26 arises as a consequence of Theorem 25 along with the fact that for $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$ and $n^{\prime }=p_1{p}_2{p}_3\dots p_r$, where $p_i$, $1\le i\le r$ are distinct primes and $r\ne 1$, $X_n\cong X_{p_1^{{\alpha }_1}}\times X_{p_2^{{\alpha }_2}}\times \dots \times X_{p_r^{{\alpha }_r}}$. Based on the energy of the graph $X_n$ obtained, the hyperenergetic unitary Cayley graphs along with their complements were characterised in [61,62] as follows. Note that a graph G of order n is called hyperenergetic if its energy, $\mathcal{E}\left(G\right)$ is greater than the energy of the complete graph of order n; that is, $\mathcal{E}\left(G\right)>\mathcal{E}\left(K_n\right)=2(n-1)$ (see [61]).

Theorem 27. 

[61,62] The graph $X_n$ is hyperenergetic if and only if n has at least two prime factors greater than 2 or at least three distinct prime factors.

Theorem 28. 

[61,62] The graph ${\overline{X}}_n$ is hyperenergetic if and only if n has at least two distinct prime factors and $n\ne 2p$, where p is a prime number.

Both [61] and [62] discuss the energy and hyperenergercity of the graphs $X_n$ and ${\overline{X}}_n$ and the same results using similar proof techniques were obtained independently. In addition to these results, the ratio $\frac{\mathcal{E}\left(X_n\right)}{2(n-1)}$ that measures the degree of hyperenergecity of $X_n$, which can be seen to grow exponentially as the number of distinct prime divisors of n increases, was given in [62]. In the process of proving the above results, the nullity of the graph was discussed, which was also independently proven in [63]. After the publication of [62], a comment on the article was released, wherein a one line proof to determine the energy of the unitary Cayley graphs that was determined in Theorem 25 and Theorem 26, using the notion of Ramanujan sums was given.

This was followed by a discussion on the eigenspace of the Unitary Cayley graphs in [64], where a specific case in the class of graphs called the Hamming graphs were proved to be isomorphic to the unitary Cayley graphs and using the results obtained on the spectra of these unitary Cayley graphs, the eigenspace of Hamming graphs were determined. Note that for non-negative integers $k,r,s$, the hamming graph $HG(l_1,l_2,...l_r;s)$ is a graph which is constructed based on the number of words formed by considering r out of a given k letters, which have a hamming distance s. In other words, given k letters, the $k^r$ possible words with $r\le k$ letters are the vertices of a hamming graph and two vertices are joined by an edge if their associated words differ in exactly s positions (see [64]).

Theorem 29. 

[64] For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$ and $n^{\prime }=p_1{p}_2{p}_3\dots p_r$, where $p_i$, $1\le i\le r$ are distinct primes and $r\ne 1$, $X_n\cong HG(p_1,\dots ,p_r;r)$.

A k-regular graph G is said to be a Ramanujan graph if and only if the second largest absolute value of the eigenvalues of the adjacency matrix of G, ${\lambda }_2\left(G\right)\ge 2\sqrt{k-1}$ (c.f. [65]). This idea of realising a graph as a Ramanujan graph was explored in unitary Cayley graphs and its complement, using the spectra of the graphs that were obtained in the previous literature and a complete characterisation of the cases in which the unitary Cayley graph and its complement are Ramanujan graphs was obtained in [65] and [66] respectively as follows.

Theorem 30. 

[65] The graph $X_n$ is a Ramanujan graph if and only if n satisfies one of the following conditions for some distinct odd primes $p_1<p_2$ and for $s\in \mathbb{N}$.

(i) 

$n=2s$, for some $s>2$;

(ii) 

$n=p_1$;

(iii) 

$n=2^{s}p$, where $p>2^{s-3}+1$;

(iv) 

$n=p_1^2$ , $2p_1^2,4p_1^2$;

(v) 

$n=p_1{p}_2$ , $2p_1{p}_2$, where $p-1<p_2\le 4p_1-5$;

(vi) 

$n=4p_1{p}_2$, where $p-1<p_2\le 2p_1-3$.

Theorem 31. 

[66] For $n\ge 2$, the graph ${\overline{X}}_n$ is a Ramanujan graph if and only if n has one of the following forms.

(i) 

n is a prime power;

(ii) 

$n=2^{t_1}{3}^{t_2}$, where $1\le t_1\le 3$ when $t_2=1$, or $t_1=1$, when $t_2=1,2$;

(iii) 

$n=10$ or 30;

(iv) 

$n=p_1{p}_2$, where $p_1=3,5$ and $p_2=5,7$.

Further investigation on some variants of energy, namely the distance energy, color energy, minimum covering Gutman energy, the minimum edge dominating energy and the Seidal Laplacian energy of the unitary Cayley graphs was conducted in [67,68,69,70,71,72] respectively. As already known, energy of a graph is the sum of the absolute values of the eigenvalues of a matrix. Based on the matrix defined, the corresponding spectra and the energies are computed. Therefore, the distance energy is obtained from the distance matrix of the graph, which is a square matrix in which the $ij$-th entry gives the shortest distance between the vertices $v_i$ and $v_j$ in the graph (see [69]). The color energy of a graph G corresponds to the energy of the $A_L$-matrix of G (c.f.[67,71]), whose entries are based on a proper vertex coloring of the graph G, say c, such that

$$a_{L_{ij}}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{v}_i{v}_j\in E\left(G\right)\mathrm{and}c\left(v_i\right)\ne c\left(v_j\right);\hfill \\ -1,\hfill & \mathrm{if}{v}_i{v}_j\notin E\left(G\right)\mathrm{with}c\left(v_i\right)=c\left(v_j\right);\hfill \\ 0,\hfill & \mathrm{if}{v}_i=v_j\mathrm{or}{v}_i{v}_j\notin E\left(G\right)\mathrm{with}c\left(v_i\right)\ne c\left(v_j\right).\hfill \end{array}\right.$$

A emphminimum covering set $C\subseteq V\left(G\right)$ of a graph G is a subset of vertices such that each edge of the graph is incident to at least one vertex in the subset, and the minimum number of vertices in such a set is called the minimum covering number of the graph (c.f.[70]). A minimum covering matrix $M{C}_C\left(G\right)$ of a graph G of order n is a $n\times n$ matrix defined based on the adjacency of the vertices in a minimum covering set C such that the diagonal entries of the adjacency matrix of the graph G is 1 if the corresponding vertex belongs to the minimum covering set considered (see [73]). The Gutman matrix $GM\left(G\right)$ of a graph G of order n is a square matrix of order n, whose entries are 0 and $d_i{d}_j{d}_{ij}$, where $d_i$ and $d_j$ are the degrees of the vertices $v_i$ and $v_j$ and $d_{ij}$ is the shortest distance between $v_i$ and $v_j$; corresponding to the conditions if the vertices $v_i=v_j$ and $v_i\ne v_j$ (c.f. [74]).

The minimum covering Gutman energy of a graph G is computed based on the minimum covering Gutman matrix $MCG\left(G\right)$ defined in [70], which as observed is defined as a combination of the minimum covering matrix and Gutman matrix as follows.

$$mc{g}_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{v}_i{v}_j\in E\left(G\right)\mathrm{and}c\left(v_i\right)\ne c\left(v_j\right);\hfill \\ 0,\hfill & \mathrm{if}i=j\mathrm{and}{v}_i\notin C,\mathrm{where}Cisa\mathrm{minimum}\mathrm{covering}\mathrm{set};\hfill \\ d_i{d}_j{d}_{ij},\hfill & \mathrm{otherwise},\mathrm{where}{d}_{i}and{d}_j\mathrm{are}\mathrm{the}\mathrm{degrees}\mathrm{of}\mathrm{the}\mathrm{vertices}{v}_i\mathrm{and}{v}_j\hfill \\ & \mathrm{and}{d}_{ij}\mathrm{is}\mathrm{the}\mathrm{shortest}\mathrm{distance}\mathrm{between}{v}_i\mathrm{and}{v}_j.\hfill \end{array}\right.$$

Similarly, the minimum edge dominating energy of a graph G is the sum of the absolute values of eigenvalues of the minimum edge dominating matrix of G, which is a binary matrix of order $m\times m$, where m is the size of G in which the entries are based on the adjacency of the edges and the minimum edge dominating set of the graph. A subset $F\subseteq E\left(G\right)$ is an edge dominating set of a graph G if every edge not in F is adjacent to at least one edge in F and an edge dominating set with the least cardinality is called a minimum edge dominating set of the graph and cardinality is the edge domination number of the graph (c.f. [29]).

The study on minimum covering Gutman energy of $X_n$ involved the discussion of this energy for unitary Cayley graph $X_n$, for the values of n for which $X_n$ is a common graph class such as complete graph, complete multipartite graph, etc. A similar situation was encountered on the discussion of the minimum edge dominating energy of the unitary Cayley graphs in [68], except for a few bounds that were deduced instead of the exact values.

The distance spectra along with the corresponding energy of the unitary Cayley graphs was computed in [69], as a part of the study of the same on the integral circulant graphs and it was proved that the integral circulant graphs, including $X_n$, have integral distance spectra. On investigating the distance energies of both these graphs, a construction of infinite families of distance equi-energetic graphs (graphs, possibly isomorphic, that have the same energy) emerged, which were the first ones to be derived without using construction methods by taking graph products nor iterated line graphs (defined in the later part of this section). The results on the distance energy of $X_n$ and the construction obtained in [69] are given below.

Theorem 32. 

[69] The distance energy of $X_n$,

$$DE\left(X_n\right)=\left\{\begin{array}{cc}2(n-1),\hfill & ifnisprime;\hfill \\ 4(n-2),\hfill & ifn=2^t,forsomet\in \mathbb{N}.\hfill \end{array}\right.$$

Theorem 33. 

[69] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and ${\alpha }_i\in \mathbb{N}$, be an odd composite number and $m=p_1{p}_2\dots p_r$ be the maximal square-free divisor of n. The distance energy of $X_n$,

$$DE\left(X_n\right)=2\left[2n+\varphi \left(n\right)(2^{r-1}-1)-m-2+{\displaystyle \prod _{i=1}^k}(2-p_i)\right],$$

where $\varphi \left(n\right)$ is the Euler’s totient function.

Theorem 34. 

[69] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and ${\alpha }_i\in \mathbb{N}$, be an even number with odd prime divisor and $m=p_1{p}_2\dots p_r$ be the maximal square-free divisor of n. The distance energy of $X_n$,

$$DE\left(X_n\right)=\frac{9n}{2}-2m+1+\varphi \left(n\right)(2^{k+1}-6)+|2\varphi \left(n\right)-2-\frac{n}{2}|,$$

where $\varphi \left(n\right)$ is the Euler’s totient function.

In Theorem 34, the value of $|2\varphi \left(n\right)-2-\frac{n}{2}|$ cannot be resolved, since it takes all positive, zero and negative values and on specific n values, the solution of the problem relates to the still open conjecture on the Euler’s totient function (refer to [75]), for which obvious solutions involve prime Fermat numbers4.

Theorem 35. 

[69] Let $n=p_1{p}_2$, where $p_1$ and $p_2$ are odd primes. The unitary Cayley graph $X_n$ is equi-energetic with the gcd-graph $G_n(1,p_1)$; that is, $DE\left(X_n\right)=DE\left(G_n(1,p_1)\right)$.

The color energy of the unitary Cayley graph and its complement was studied in [67,71]. The eigenvalues of the $A_L$ matrix defined with respect to the proper colorings of the graphs were examined and the corresponding energy was obtained in terms of the chromatic number of the graph and the Euler’s totient function, using the notion of Ramanujan Sums. A study on a few other matrices of the unitary Cayley graphs along with their eigenvalues and energy was conducted in [76], where a small-world network depending on the unitary Cayley graph was proposed with an intent to decrease the delay and increase the reliability in data transfer and used to create and analyse network communication.

The Seidal Laplacian energy of the unitary Cayley graph $X_n$ was computed in [72] by obtaining the eigenvalues of the Seidal Laplacian matrix $SL\left(X_n\right)=S\left(X_n\right)-DS\left(X_n\right)$ of $X_n$, where $SL\left(X_n\right)$ is the Seidal Laplacian matrix of $X_n$, $S\left(X_n\right)$ is the Seidal matrix of $X_n$ and $DS\left(X_n\right)$ is an $n\times n$ diagonal matrix of $X_n$ which has its diagonal entries $n-1-2deg\left(v_i\right)$, $1\le i\le n$. The Seidal matrix of a graph G is an $n\times n$ matrix with entries 1, -1 corresponding to whether the vertices $v_i{v}_j\in E\left(G\right)$ or $v_i{v}_j\notin E\left(G\right)$ or 0, otherwise (refer to [72]).

An algebra over a field is an algebraic structure consisting of a set together with the operations of addition, multiplication and scalar multiplication by elements of a field that satisfies the axioms of a vector space with a bilinear operator5; that is, an algebra over a field is a vector space equipped with a bilinear operator (c.f. [77]). For a positive integer n, the set of all $n\times n$ matrices over the field of complex numbers, $\mathbb{C}$ forms an algebra ${\mathbb{M}}_n\left(\mathbb{C}\right)$, with the usual matrix multiplication. As the adjacency matrix of a graph $A\left(G\right)$ is a well-known square matrix, the adjacency algebra of a graph is defined as the subalgebra of ${\mathbb{M}}_n\left(\mathbb{C}\right)$ which consists of all polynomials of $A\left(G\right)$ with coefficients from $\mathbb{C}$, where a subalgebra is a subset of the algebra which is an algebra by itself under the same bilinear operator (refer to [78]).

The adjacency algebra of the unitary Cayley graph $X_n$ was investigated in [77]. Since every element of the adjacency algebra of a graph is a linear combination of the powers of its adjacency matrix, the results on the adjacency algebra of a graph was obtained using the powers of the adjacency matrix. Therefore, using the existing results in on the adjacency matrix of the graph $X_n$, the adjacency algebra of $X_n$ was discussed in [77] and it was proved that the adjacency algebra of unitary Cayley graphs is a coherent algebra; that is, it is a subalgebra of ${\mathbb{M}}_n\left(\mathbb{C}\right)$ containing $I,J$, where I is the identity matrix and J is the matrix with all its entries 1, which is closed under Hadamard product6 and conjugate transposition.

For a graph G with an adjacency matrix $A\left(G\right)$, its coherent closure, denoted by $\mathcal{CC}\left(G\right)$, is the smallest coherent algebra containing $A\left(G\right)$, and a graph G is said to be a pattern polynomial graph if its adjacency algebra is its coherent closure. On proving that the unitary Cayley graphs have a coherent adjacency algebra, the authors proved that every unitary Cayley graph is a pattern polynomial graph and using this, certain properties of the unitary Cayley graphs were derived based on the properties of pattern polynomial graphs, obtained in [79]. To prove that all unitary Cayley graphs are pattern polynomial graphs, the following characterisations on the structure of the graphs were obtained.

Theorem 36. 

[77] The graph $X_n$ is strongly regular graph if and only if n is a prime power.

Recall that a k-regular graph G of order n is strongly regular with parameters $(n,k,r,s)$ if any two adjacent vertices have exactly rcommon neighbours and any two non-adjacent vertices have exactly s common neighbours and a crown graph, $C_{r,r}$ is a bipartite graph with vertex set such that $V\left(C_{r,r}\right)=V_1\cup V_2$ and $|V_1|=|V_2|=r$, with $V_1=\{v_1,v_2,\dots ,v_r\}$ and $V_2=\{u_1,u_2,\dots ,u_r\}$ such that $v_i{u}_j\in E\left(C_{r,r}\right)$ if and only if $i\ne j$.

Theorem 37. 

[77] The graph $X_n$ is crown graph if and only if $n=2p$, where p is an odd prime.

Appropriate representation of the circulant graphs on a Euclidean plane, unveils the rotational symmetry of the graph. As known earlier, unitary Cayley graphs are integral circulant graphs and therefore such a suitable representation or drawing called the unit circle drawing of the unitary Cayley graphs were examined in [80]. The unit circle drawing of the graph $X_n$ is nothing but drawing the graph $X_n$ such that the vertices are placed equi-distantly on a unit circle on the complex plane $\mathbb{C}$ and the edges are drawn as line segments. This representation gives a hole like structure in the middle of the graph, which is called the central hole or the geometric kernel of the graph. Just like how the spectrum of a graph provides vital information on the graph, the size of the geometric kernel in the unit circle drawing of an integral circulant graph, which is measured through the kernel radius also provides the arithmetic properties of the graph.

It was proven in [81] that the central hole in the unit circle drawing of any circulant graph on $n>3$ vertices is a regular n-gon. Therefore, only the size of the geometric kernel for $X_n$, which is already known to be an n-gon had to be determined in [80], by computing the kernel radius, given by the formula $max\{k:1\le k<\frac{n}{2},gcd(k,n)=1\}$. Only integers less than $\frac{n}{2}$ are considered because there shall be no central hole when the edge $(k,\frac{k}{2})$ exists in the unit circle drawing of a graph. It was observed that the kernel radius of $X_n$ is a strictly decreasing function in the range $\left(0,\frac{n}{2}\right]$.

Apart from this, computation of certain graph parameters of the unitary Cayley graph were carried out in [82,83,84,85,86,87,88,89], where certain topological indices of the unitary Cayley graphs were computed in [86,87,88] and few graph polynomials for the unitary Cayley graphs were determined in [82], using the results that were given in [48], as graph polynomials are also graph invariants that codes numerical information about the underlying graph (c.f [90]).

It was already seen that the unitary Cayley graphs are highly reliable networks and can be used in modeling situations which require stable networks. To assert this and to study the degree of reliability of these networks, few vulnerability parameters which measures the vulnerability of a graph were computed for the unitary Cayley graphs in [84] and this study on computing vulnerability parameters paved way to examine the parameters related to graph covering in [89] and [91].

Graph covering problem is one of the most classical topics in graph theory, where the minimum number of the entities of a graph, like vertices, edges, etc. with a particular property having a given graph as their union is determined. One such covering parameter is the tree covering number, which is defined as the minimum cardinality among all tree covers of the graph, where a family of mutually edge disjoint trees in a graph is called a tree cover of the graph if each edge is an edge of a tree in the family. This tree covering number was determined for the unitary Cayley graph $X_n$ and its complement ${\overline{X}}_n$ in [89], from which the Nordhaus-Gaddum type inequalities; that is, bounds on the sum and the product of the invariant for a graph and the its complement, for the tree covering number were obtained. The exact value of the tree covering number of $X_n$ was computed as given in Theorem 38, whereas for the complement ${\overline{X}}_n$ the bounds according to different values of n were obtained. Based on these bounds, the Nordhaus-Gaddum type inequalities were also obtained for different cases of n depending on its prime factorisation.

Theorem 38. 

[89] The tree covering number of a unitary Cayley graph $X_n$ is $\frac{\varphi \left(n\right)}{2}+1$, where $\varphi \left(n\right)$ is the Euler’s totient function.

The other aspect related to covering that was discussed for the unitary Cayley graphs in [91] was the property of the well-coveredness of a graph. A graph G is said to be well-covered if all its maximal independent sets are of the same size. In [91], the well-coveredness of the graphs $X_n$ and ${\overline{X}}_n$, along with its vertex decomposability were examined and the condition under which the graphs are well-covered and vertex decomposable (refer to [92] for more details on vertex decomposable graphs) were given. The number of walks between any pair of two vertices in the unitary Cayley graphs was enumerated in [83] and as an application of this result, it was shown that there exists a bijection between walks in $X_n$ and the ordered sums of units in ${\mathbb{Z}}_n$, using which the number of representations of a fixed residue class mod n as the sum of k units in ${\mathbb{Z}}_n$ was determined.

A function which is defined on the set of positive integers to a subset of the set of complex numbers is an arithmetic function. An arithmetic function h is multiplicative, if it is not identically zero, and for any $r,s\in \mathbb{N},h\left(rs\right)=h\left(r\right)h\left(s\right)$ whenever $gcd(r,s)=1$. For each non-negative integer r and prime p, the r-th Schemmel’s totient function $S{T}_r$ is a multiplicative arithmetic function that satisfies

$$S{T}_r\left(p^{\alpha }\right)=\left\{\begin{array}{cc}{p}^{\alpha -1}(p-r),\hfill & \mathrm{if}p\ge r;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $\alpha$ is a positive integer. From the name Schemmel’s totient function, it can be seen that this function introduced by Schemmel, is a generalisation of the Euler’s totient function $\varphi \left(n\right)$ (c.f.[93]). It can be seen that $S{T}_0\left(n\right)=n$ and $S{T}_1\left(n\right)=\varphi \left(n\right)$, for all integers n. Since most of the graph invariants of the unitary Cayley graph $X_n$ are computed and expressed in terms of $\varphi \left(n\right)$ and $S{T}_r\left(n\right)$ being its generalisation, it opened an avenue to check the possibility of expressing the parameters in terms of $S{T}_r\left(n\right)$ and in [94], a simple formula for the number of cliques of any order in the unitary Cayley graph $X_n$ was obtained as follows.

Theorem 39. 

[94] For a given integer k, the number of cliques of order k in the unitary Cayley graph $X_n$ is given by the expression ${\displaystyle \prod _{i=1}^k}\frac{S{T}_{i-1}\left(n\right)}{k}$, where $S_{i-1}\left(n\right)$ is the Schemmel totient function.

This formula naturally gives the number of triangles in the graph $X_n$ in terms of the Schemmel totient function as $\frac{S{T}_0\left(n\right)}{1}\frac{S{T}_1\left(n\right)}{2}\frac{S{T}_2\left(n\right)}{3}$, which is more generalised and simple than the same expression which was computed independently in [34,41,42,48].

The k-th power $G^{\left(k\right)}$ of a graphG is a graph whose vertex set is the same as the vertex set of G and there is an edge between two vertices in the graph $G^{\left(k\right)}$ if and only if there is a path of length at most k between them in G. The k-th power of the unitary Cayley graphs were examined in [85], where the energies of these graphs were determined and all the powers of unitary Cayley graphs that are Ramanujan graphs were classified. Note that in [85], the k-th powers of a unitary Cayley graph is addressed as the the distance powers of the graph. Using the results obtained on the energies of distance powers of unitary Cayley graphs, infinitely many pairs of non-cospectral equi-energetic graphs were constructed and all the hyperenergetic distance powers of unitary Cayley graph $X_n$ were characterised. It can be noticed that the k-th power of any graph G can be defined for the values $1\le k\le diam\left(G\right)$ and $diam\left(X_n\right)\le 3$. Therefore, the investigation is limited to the unitary Cayley graphs that have diameter 3, in which case there exists only the value $k=2$ for which the discussion of the k-th power of the graph $X_n$ is non-trivial.

Apart from Cayley graphs, the power graphs of groups have a growing literature, giving rise to several survey papers (c.f.[2,95,96,97]). Note that the power graph of a finite group is a graph with the vertex set as the elements of the group, and two vertices are adjacent if one is a power of the other and are not to be confused with the k-th power of a graph, as both the graphs are referred to as the power graphs in the literature. Owing to the huge literature on power graphs of finite groups, an open problem to explore the relation between the power graphs and Cayley graphs was put forth in [95]. This problem was addressed in [98] and it was shown that, for certain values of n, the vertex deleted subgraphs of power graphs of ${\mathbb{Z}}_n$ are spanning subgraphs or the complement of the vertex deleted subgraphs of certain unitary Cayley graphs. Using these relations, the relation between the energy of power graphs and Cayley graphs were also obtained in [98]. The following theorem gives a relation between the power graph $\mathcal{P}\left({\mathbb{Z}}_n\right)$ and unitary Cayley graph $X_n$ of ${\mathbb{Z}}_n$, for some values of n.

Theorem 40 

([98]).

(i) 

For any prime p, $\mathcal{P}\left({\mathbb{Z}}_p\right)\cong X_p\cong K_p$.

(ii) 

If $n=p_1^{{\alpha }_1}$, for a prime $p_1$ and ${\alpha }_1>1$, $X_n$ is a regular spanning subgraph of $\mathcal{P}\left({\mathbb{Z}}_n\right)$.

(iii) 

When $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$, where $p_1,p_2$ are distinct primes, and ${\alpha }_1,{\alpha }_2$ are positive integers, ${\mathcal{P}}^{*}\left({\mathbb{Z}}_n\right)$ is a spanning subgraph of ${\overline{X^{*}}}_n$, where ${\mathcal{P}}^{*}\left({\mathbb{Z}}_n\right)$ is the vertex deleted subgraph, $\mathcal{P}\left({\mathbb{Z}}_n\right)-\{{\mathbb{Z}}_n^{*}\cup 0\}$ and $X_n^{*}$ is the vertex deleted subgraph, $X\left({\mathbb{Z}}_n\right)-\{{\mathbb{Z}}_n^{*}\cup 0\}$. The graphs ${\overline{X^{*}}}_n\cong {\mathcal{P}}^{*}\left({\mathbb{Z}}_n\right)$ if and only if ${\alpha }_1={\alpha }_2=1$.

Recall that the study on unitary Cayley graphs began with the investigation of the edge coloring of the graph, in order to obtain a total multicolored graph. This motivated to study different colorings of the graph and to investigate the related parameters and properties. The total coloring and the strong edge coloring of the unitary Cayley graphs were studied in [99,100,101]. A total coloring of a graph G is a proper coloring on both the edges and vertices such that no two adjacent entities (both vertices and edges) are assigned the same color and the total chromatic number is the minimum number of colors required in the total coloring of the graph (see [101]). The total coloring conjecture given in [102] states that the total chromatic number of a graph G is at most $\delta \left(G\right)+2$, where $\delta \left(G\right)$ is the maximum degree of G and this was proved for the unitary Cayley graphs in [101], as a part of the investigation on the total coloring of some regular graphs. Also, the total chromatic number of the unitary Cayley graphs was determined along with which a pattern to assign colors to obtain an optimal total coloring of unitary Cayley graphs for some values of n was given in [99].

A strong edge coloring of a graph G is a proper edge coloring of G such that every color class induces a matching and the minimum number of colors required is the strong chromatic index. In [100], the strong chromatic index of all unitary Cayley graphs was determined and the coloring technique revealed the underlying product structure from which the unitary Cayley graphs emerge.

Following the notion of coloring, domination in unitary Cayley graphs were investigated in [103,104,105,106]. In [94], the domination number, upper domination number and the total domination number (refer to [29]) of the unitary Cayley graphs were investigated based on the structural property of the unitary Cayley graph $X_n$ to be realised as a direct product of its factor graphs, that are complete. The bounds for these domination parameters were obtained in terms of an arithmetic function called the Jacobsthal function $g\left(n\right)$, that denotes the smallest positive integer r such that every set of r consecutive integers contains an element that is relatively prime to n (see [107]). By the definition of $g\left(n\right)$ and $X_n$, it can be deduced that the set $\{0,1,\dots ,g(n)-1\}$ is a dominating set as well as a total dominating set of $X_n$, the cardinality of which gives a tight bound on the total domination number and the domination number of $X_n$. It was proved that the domination number of $X_n$ necessarily need not be equal to $g\left(n\right)$ by identifying the cases when the equality $\gamma \left(X_n\right)=g\left(n\right)$ does not hold. Also, the rate at which the tightness of the bound decreases as the n value increases was also discussed in [104], as given below.

Theorem 41. 

[104] For each positive integer j, there is an integer n with more than j distinct prime factors such that $\gamma \left(X_n\right)\le {\gamma }_t\left(X_n\right)\le g\left(n\right)$, where $\gamma \left(X_n\right)$, ${\gamma }_t\left(X_n\right)$ and $g\left(n\right)$ denote the domination number of $X_n$, total domination number of $X_n$ and the Jacobsthal’s function.

Theorem 42. 

[104] If $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$ is an integer with a square-free canonical representation (${\alpha }_i<2,forall1\le i\le r$), having less than 3 distinct prime, then the domination number of $X_n$ is at most 4.

Theorem 43. 

[104] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes and ${\alpha }_i\in \mathbb{N}$. If $r\le 3$ and ${\alpha }_j\ge 2$ for some $1\le j\le r$, then the domination number of $X_n$ is at least $\frac{p_1}{p_1-1}$.

Theorem 44. 

[104] If the number of distinct prime factors of n is at most 3 such that n is not square-free, then the domination number of $X_n$ is $g\left(n\right)$, where $g\left(n\right)$ denotes the Jacobsthal’s function.

The proof of Theorem 38 and Theorem 43 establishes that for infinitely many n, the domination number of $X_n$ is strictly less than the Jacobsthal function evaluated at n and this gives rise to a tighter bound on the total domination number (For definition, refer to Section 4) of $X_n$, ${\gamma }_t\left(X_n\right)$; ${\gamma }_t\left(X_n\right)\le g\left(n\right)$, whenever n has at most three distinct prime factors. These results also affirm the fact that as the number of prime factors of n increases, the domination number as well as the total domination number of $X_n$ shall never be equal to the Jacobsthal’s function $g\left(n\right)$, by showing that there exists an integer n with arbitrarily many distinct prime factors such that the bound $\gamma \left(X_n\right)\le {\gamma }_t\left(X_n\right)<g\left(n\right)$ holds.

Also, the possibility of the value $g\left(n\right)-\gamma \left(X_n\right)$ being arbitrarily large was not explored in the article, owing to which the open problems to determine the existence of integers n with arbitrarily large number of distinct prime factors such that $\gamma \left(X_n\right)\le g\left(n\right)-2$ and to find a single integer n such that ${\gamma }_t\left(X_n\right)\le g\left(n\right)-2$ were posted. Apart from this, it was also conjectured that the upper domination number of $X_n$ is $\frac{n}{p_1}$, where $p_1$ is the smallest prime factor of n and the conjecture was proved for certain values of n, based on their number theoretical properties. The approach in [103] to determine the domination parameters of the unitary Cayley graphs were built in order to investigate the solutions of the two open problems posed in [104]. These open problems were solved in [103] by constructing integers n with arbitrarily many distinct prime factors such that the unitary Cayley graph $X_n$ contains a dominating cycle of size $g\left(n\right)-2$; thus answering both questions, because a dominating cycle is a total dominating set.

Recall that a dominating set which is independent is called an independent dominating set and the minimum cardinality of such a set is called the independent domination number. Also, a set $S\subseteq V\left(G\right)$ is called irredundant if for each $v\in S$, either v is isolated in S or v has a neighbor $u\notin S$ such that u is not adjacent to any vertex of $S-\left\{v\right\}$ and the minimum size of a maximal irredundant set is called the irredundance number of the graph G (c.f.[29]). The bounds on other domination parameters like the irredundance number, ($ir\left(X_n\right)$), independent domination number($i\left(X_n\right)$), etc. of the unitary Cayley graphs were determined in [103], as a special case of these bounds obtained for the direct products of complete graphs. This result gave raise to the construction of some infinite families of integers n, where $ir\left(X_n\right)=\gamma \left(X_n\right)=i\left(X_n\right)$ as given below.

Theorem 45. 

For a unitary Cayley graph $X_n$, $ir\left(X_n\right)=i\left(X_n\right)$, when $n=p$, $n=2p$, or $n=3p$, for some prime p, or n is square-free with exactly three prime divisors.

The problem of finding other square-free integers n for which the equality is achieved in the lower portion of the domination chain (see [29]) was posed along with two other open problems similar to the ones posed in [104], to check the existence of infinitely many integers n such that ${\gamma }_c\left(X_n\right)>g\left(n\right)$; if so, to check if such integers can have arbitrarily many distinct prime factors and to check if there exists a single integer n such that ${\gamma }_t\left(X_n\right)\ge g\left(n\right)-3$, where ${\gamma }_c\left(X_n\right)$ and ${\gamma }_t\left(X_n\right)$ are the connected and total domination number of $X_n$, respectively. Note that the connected domination number of a graph is the cardinality of a minimum dominating set whose induced subgraph is connected (refer to [29]).

The study on the domination parameters of the unitary Cayley graph $X_n$ was extended in [106], where the open problem to find an integer n such that ${\gamma }_t\left(X_n\right)\ge g\left(n\right)-3$ was solved, using the updated results on the nature of Jacobsthal’s function in the literature. The problem was solved for not just ${\gamma }_t\left(X_n\right)\ge g\left(n\right)-3$, but the existence of n with arbitrarily many prime factors that satisfy ${\gamma }_t\left(X_n\right)\ge g\left(n\right)-16$ was also proved in [106]. In addition to this, new lower bounds on the domination numbers of direct products of complete graphs were presented in [106], from which new asymptotic lower bounds on the domination number of $X_n$, when n is a product of distinct primes, were obtained by adopting the proof techniques used in [104].

Two variants of domination namely, the closed domination and the inverse closed domination of the unitary Cayley graphs were discussed in [105], by determining the corresponding domination parameters. Given a graph G, choose $v_1\in V\left(G\right)$ and put $S_1=\left\{v_1\right\}$. If $N_G\left[S_1\right]\ne V\left(G\right)$, choose $v_1\in V\left(G\right)-S_1$ and put $S_2=\{v_1,v_2\}$. Where possible, for $\ge 3$, choose $v_k\in V\left(G\right)-N_G\left[S_{k-1}\right]$ and put $S_k=\{v_1,v_2,\dots ,v_k\}$. At some point, we obtain a positive integer k such that $N_G\left[S_k\right]=V\left(G\right)$. A dominating set obtained in the given above method is called a closed dominating set and the smallest cardinality of a closed dominating set is called the closed domination number of G (c.f.[108]). The dominating set $S\subseteq V\left(G\right)-D$ is called an inverse dominating set with respect to D. A closed dominating set $S\subseteq V\left(G\right)-C$ is called an inverse closed dominating set with respect to C and the minimum cardinality of an inverse closed dominating set is the inverse closed domination number of G (c.f.[109]). In the study, the closed and inverse closed domination numbers of the unitary Cayley graphs whose structures are standard graph classes like complete graphs, complete r-partite graphs, etc. were computed based on the existing results for those graph classes and hence, it does not contribute to any dynamic results.

On reviewing the literature on the domination of unitary Cayley graphs, it was seen that the unitary Cayley graphs were independently investigated under the name Euler totient Cayley graph and a review of the studies conducted on the graphs $X_n$ under the name Euler totient Cayley graphs is given in the following subsection.

2.1. Euler Totient Cayley Graphs

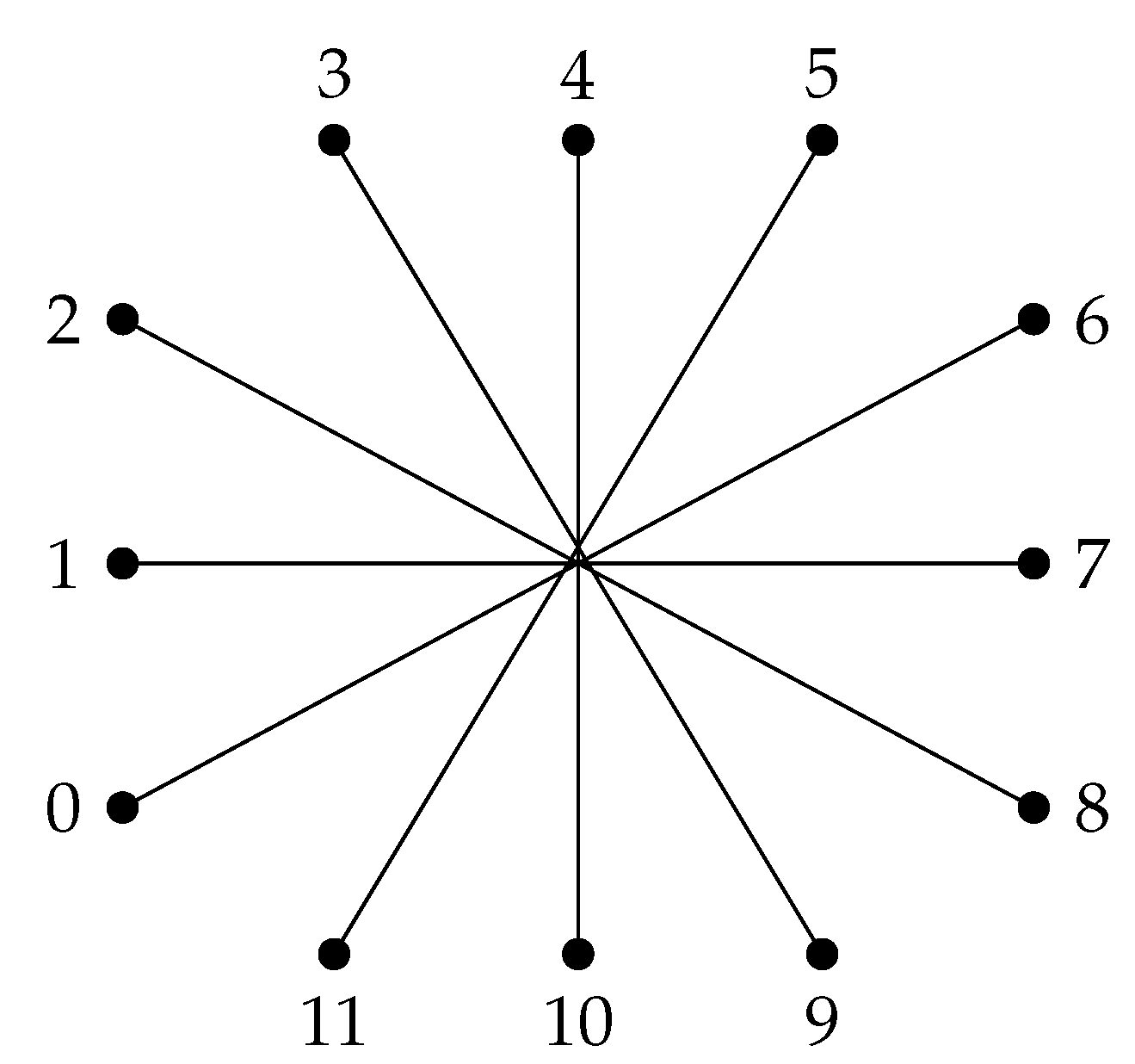
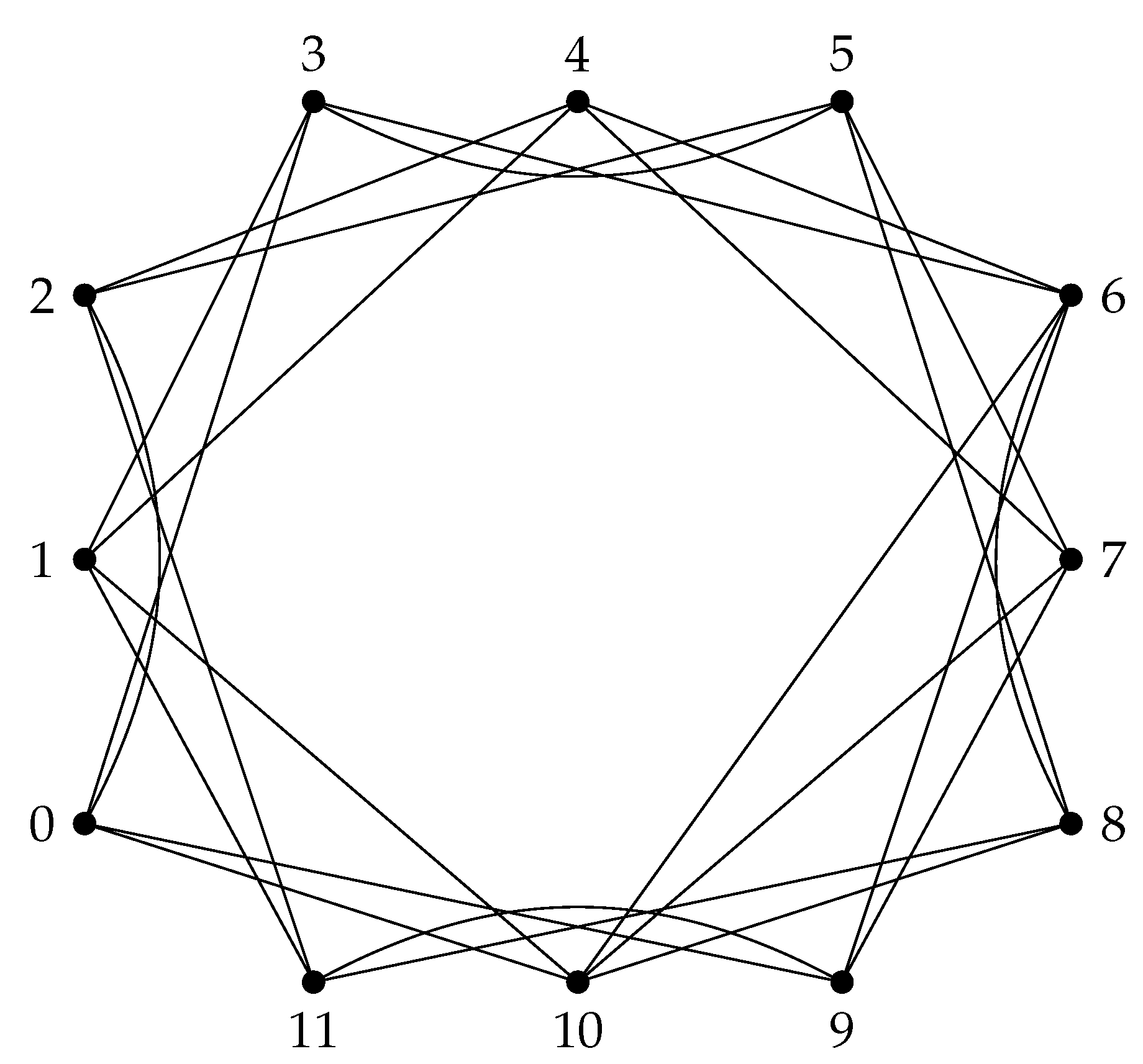
Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}\dots p_r^{{\alpha }_r}$, where $p_i$, $1\le i\le r$ are distinct primes, ${\alpha }_i\in \mathbb{N}$ and r is the number of prime divisors of n. The arithmetic graph ${\mathcal{V}}_n$ is defined as the graph whose vertex set consists of the divisors of n and two vertices are adjacent in the graph if and only if their gcd is a prime divisor of n. In other words, two vertices $u,v\in E\left({\mathcal{V}}_n\right)$, when $gcd(u,v)=p_i$, $1\le i\le r$. An illustration of an arithmetic graph is given in Figure 4.

The Euler totient Cayley graphs were introduced in [110] as a combination of arithmetic graphs and Cayley graphs. As it was a parallel, independent study on the same graph with a different name, various results are repeated in the literature; but the study on the Euler totient Cayley graphs were mainly concentrated on the computation of different domination parameters of the graph. The Euler totient Cayley graphs were introduced in [110] and the basic properties of the graph was studied and the values of n for which the graph is a standard graph class were classified and characterised. Using this study, various types of domination were discussed and the corresponding domination parameters were determined in [111,112,113,114,115,116,117,118].

The results on the domination number of the Euler totient Cayley graph proved in [116] was the motivation to investigate the tightness of the bounds of the domination number in terms of the Jacobsthal’s function as given in [103,104]. Also, on computing the domination parameters of $X_n$ in [103], an error in the bounds obtained in [113] for the independent domination number of the graph was stated and rectified. The independent domination number and the isolate domination number of the Euler totient Cayley graphs were discussed again in [119], in which the bounds obtained in [113] were improved for a few cases and a few counterexamples to disprove the results in [119] were also obtained. Note that a set dominating set of a graph G whose induced subgraph has an isolate vertex is called an isolate dominating set of G and the minimum cardinality of such a set is the isolate domination number of the graph (c.f. [120]).

Apart from this, the energy of the Euler totient Cayley graphs was studied in [119,121], which was a prefatory study when compared to the study on the energy of the unitary Cayley graphs in [61,62]. Also, certain functions defined on the vertex set of a graph like independent function and basic minimal dominating functions (For more details, see SubSection 6.5.2) were discussed for the Euler totient Cayley graphs in [122,123], and the structure and enumeration of cycles in the Euler totient Cayley graphs was discussed in [118,124]. Note that a function $f:V\to [0,1]$ is an independent function if for every vertex v with $f\left(v\right)>0$, ${\displaystyle \sum _{u\in N\left(v\right)}}f\left(u\right)=1$, where $N\left(v\right)$ is the set of all vertices adjacent to v (see [123]).

As the Euler totient Cayley graphs were introduced relating the arithmetic graphs, different domination numbers that were determined for the Euler totient Cayley graphs were also computed for the different graph products of Euler totient Cayley graphs with the arithmetic graphs in [125,126,127,128,129]. This includes the lexicographic product, Cartesian product, direct product and the strong product of the graphs concerned, where the definition of different graph products studied are given as follows.

Definition 5 

([130]). Let $G_1$ and $G_2$ be two simple graphs with vertex sets $V\left(G_1\right)$ and $V(G_2$) respectively. Thelexicographic product$G_1\left[G_2\right]$ of $G_1$ and $G_2$ is a graph with $V\left(G_1\left[G_2\right]\right)=V\left(G_1\right)\times V\left(G_2\right)$ and two vertices $(v_1,u_1)$ and $(v_2,u_2)$ are adjacent in $G_1\left[G_2\right]$ if either $v_1$ is adjacent to $v_2$ in $G_1$ or $u_1$ is adjacent to $u_2$ in $G_2$.

Definition 6 

([130]). For two graphs $G_1$ and $G_2$ with vertex sets $V\left(G_1\right)$ and $V(G_2$), and edge sets $E\left(G_1\right)$ and $E(G_2$), thedirect productof $G_1$ and $G_2$, denoted by $G_1\times G_2$, is a graph with $V(G_1\times G_2)=V\left(G_1\right)\times V\left(G_2\right)$ and two vertices $(v_1,u_1)$ and $(v_2,u_2)$ are adjacent in $G_1\times G_2$ if both $v_1{v}_2\in E\left(G_1\right)$ and $u_1{u}_2\in G_2$.

Definition 7 

([130]). Let $G_1$ and $G_2$ be two graphs with vertex sets $V\left(G_1\right)$ and $V(G_2$) and edge sets $E\left(G_1\right)$ and $E(G_2$). TheCartesian productof $G_1$ and $G_2$, denoted by $G_1\square G_2$, is a graph with the vertex set $V(G_1\square G_2)=V\left(G_1\right)\times V\left(G_2\right)$ and two vertices $(v_1,u_1)$ and $(v_2,u_2)$ are adjacent in $G_1\square G_2$ if either $u_1=u_2$ and $u_1{u}_2\in E\left(G_1\right)$ or $v_1=v_2$ and $u_1{u}_2\in G_2$.

Definition 8 

([130]). Let $G_1$ and $G_2$ be two simple graphs with vertex sets $V\left(G_1\right)$ and $V(G_2$) respectively. Thestrong product$G_1⊠G_2$ of $G_1$ and $G_2$ is a graph with $V(G_1⊠G_2)=V\left(G_1\right)\times V\left(G_2\right)$ and two vertices $(v_1,u_1)$ and $(v_2,u_2)$ are adjacent in $G_1⊠G_2$ if either

• $u_1=u_2$ and $v_1$ is adjacent to $v_2$ in $G_1$ or
• $v_1=v_2$ and $v_1$ is adjacent to $v_2$ in $G_2$ or
• $v_1{v}_2\in E\left(G_1\right)$ and $u_1{u}_2\in E\left(G_2\right)$.

The study in [127,131] focus on the computation of the domination parameters of the Cartesian product of $X_n\square {\mathcal{V}}_n$, and in [125,126,129,132] the domination parameters in the direct product of $X_n$ and ${\mathcal{V}}_n$ are studied. The domination parameters in the lexicographic product of $X_n$ and ${\mathcal{V}}_n$ was discussed in [128,133,134,135] and the matching domination number; the minimum cardinality of a dominating set that induces a matching in a graph, of the strong product of the graphs $X_n$ and ${\mathcal{V}}_n$ was determined in [136].

The different products of the arithmetic graph with the Euler totient Cayley graphs give rise to various graphs with different structural properties, as per the number theoretic properties of the values of n. Based on this, the parameters were computed in multiple cases, where it can be observed the results are mainly obtained for the structure of graph products that are standard graph classes and this makes the study a secondary one. Also, it can be seen that the product structures are complex as the value of n increases and the number of prime factors increase. Therefore, this sets a challenge in studying many other structural parameters, despite the pattern and symmetry of the factor graph.

2.2. Signed Graphs Based on the Unitary Cayley Graphs

A signed graph or a sigraph, $S=(G,\sigma )$ is a graph obtained from G, in which every edge is assigned either a positive or a negative sign by a function $\sigma :E\left(G\right)\to \{+,-\}$. If the signs assigned to the edges depend on some property, the graph is called an induced sign graph. It is very natural to extend the theory of signed graphs into the algebraic graphs by assigning signs to the edges of algebraic graphs and the study on such signed algebraic graphs (algebraic signed graphs) are found to be of much interest (see [137,138]).

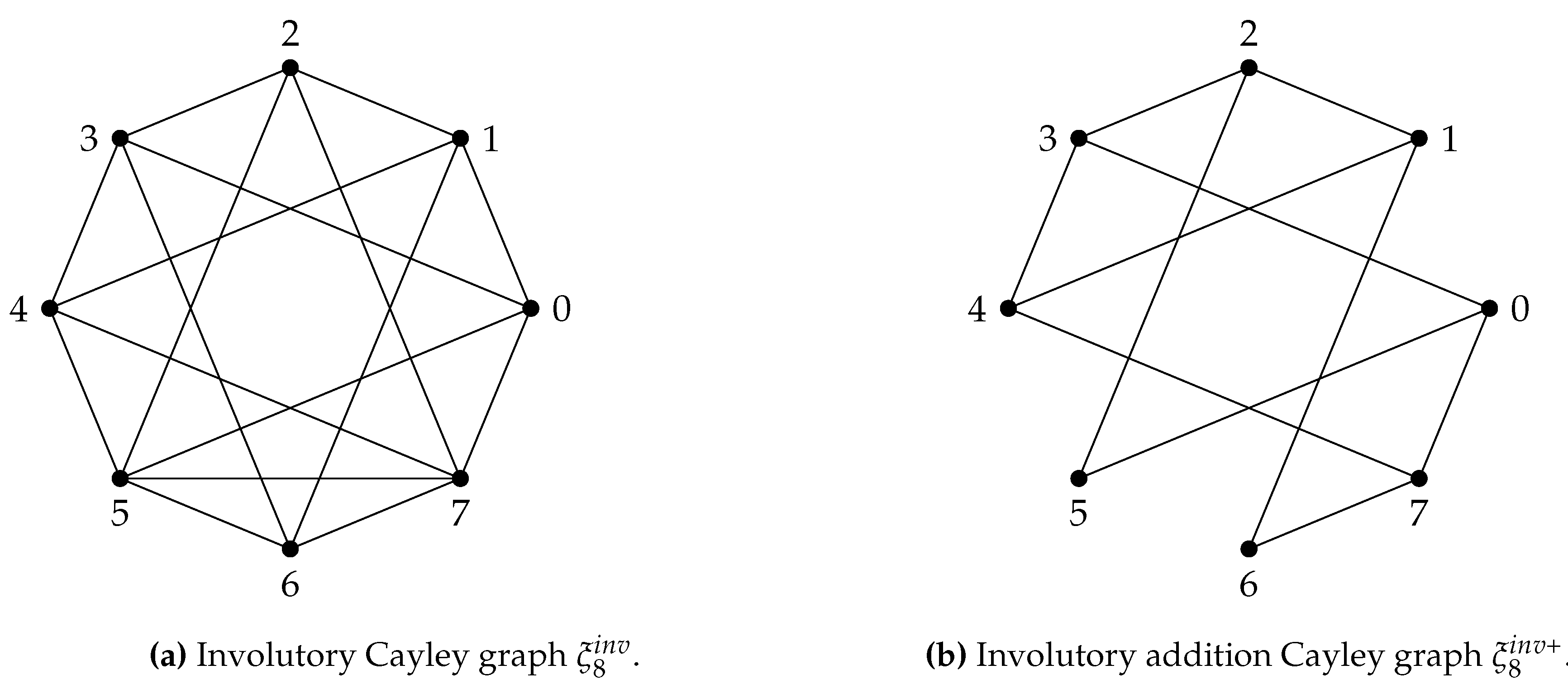
One such signed algebraic graph is the signed unitary Cayley graph. As the assignment of signs can be arbitrary or it can depend on any property, there are possibilities for generating several variations of signed graphs from a single algebraic graph. 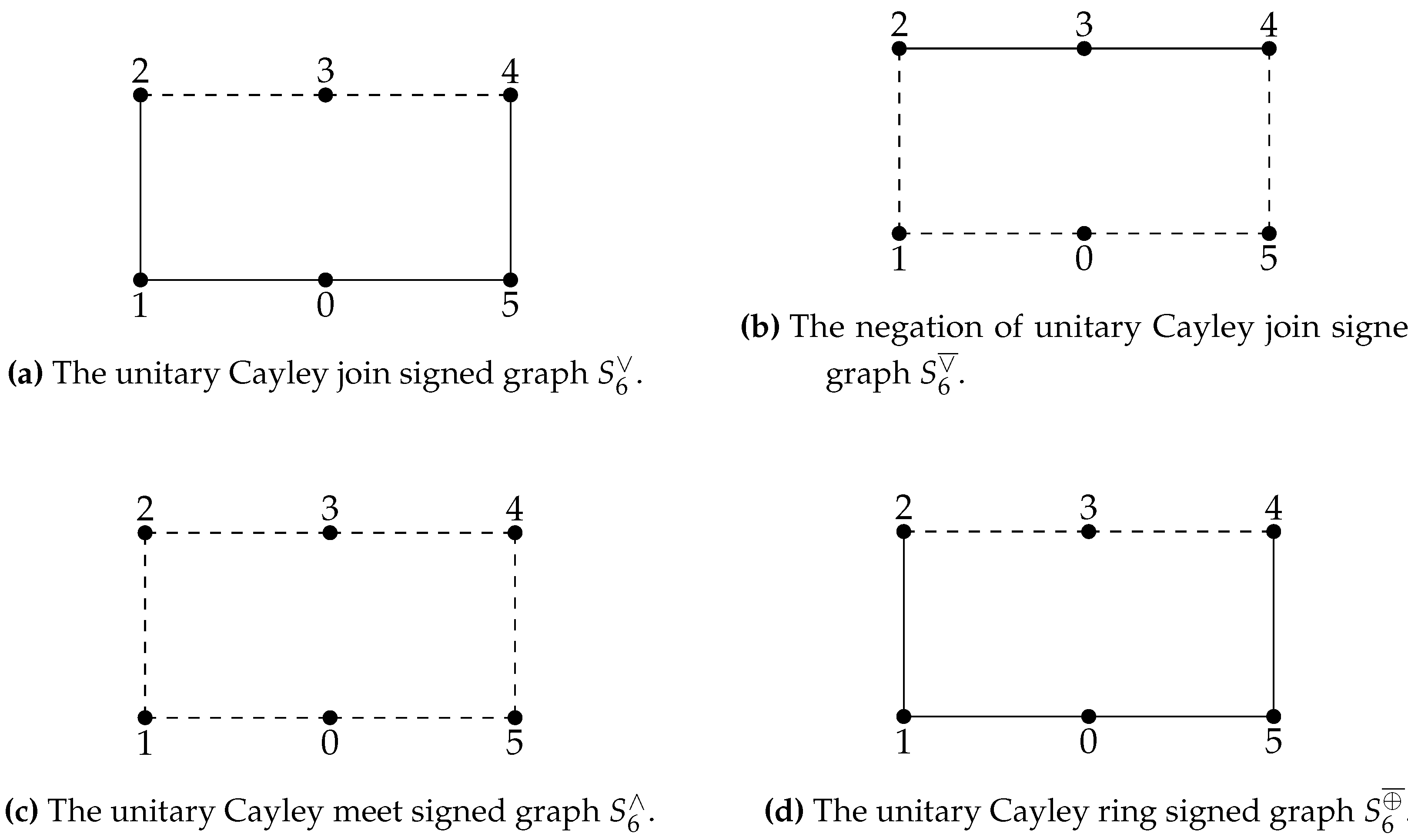Depending on how the signs are assigned to the edges of the graph $X_n$, there are four variations of the signed graphs that have emerged from the unitary Cayley graphs, until now, and the definitions of these graphs are given below, following which the illustration of each of them is given in Figure 5. Note that the dashed edges in the figures represent the negative edges and the other edges are positively signed.

Definition 9 

([139]). Theunitary Cayley join signed graph, denoted by $S_n^{\vee }=(X_n,{\sigma }^{\vee })$, is a signed graph whose underlying graph is the unitary Cayley graph $X_n$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(S_n^{\vee }\right)$ is assigned by the function ${\sigma }^{\vee }:E\left(X_n\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n$,

$${\sigma }^{\vee }\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & if{v}_i\in {\mathbb{Z}}_n^{*}or{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 10 

([139]). Thenegation of the unitary Cayley join signed graph, denoted by $S_n^{\overline{\vee }}=(X_n,{\sigma }^{\overline{\vee }})$, is a signed graph whose underlying graph is the unitary Cayley graph $X_n$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(S_n^{\overline{\vee }}\right)$ is assigned by the function ${\sigma }^{\overline{\vee }}:E\left(X_n\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n$,

$${\sigma }^{\overline{\vee }}\left\{\begin{array}{cc}+,\hfill & ifboth{v}_i\notin {\mathbb{Z}}_n^{*}and{v}_j\notin {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 11 

([139]). Theunitary Cayley meet signed graph, denoted by $S_n^{\wedge }=(X_n,{\sigma }^{\wedge })$, is a signed graph whose underlying graph is the unitary Cayley graph $X_n$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(S_n^{\wedge }\right)$ is assigned by the function ${\sigma }^{\wedge }:E\left(X_n\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n$,

$${\sigma }^{\wedge }\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & ifboth{v}_i\in {\mathbb{Z}}_n^{*}and{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 12 

([139]). Theunitary Cayley ring signed graph, denoted by $S_n^{\oplus }=(X_n,{\sigma }^{\oplus })$, is a signed graph whose underlying graph is the unitary Cayley graph $X_n$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(S_n^{\oplus }\right)$ is assigned by the function ${\sigma }^{\oplus }:E\left(X_n\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n$,

$${\sigma }^{\oplus }\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & ifeither{v}_i\in {\mathbb{Z}}_n^{*}or{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

One of the main properties of a signed graph is its balance and consistence. A signed graph is said to be balanced if every cycle in the graph has an even number of negative edges. A marked sign graph of a graph G is an ordered pair $S_{\mu }=(S,\mu )$, where $S=(G,\sigma )$ is a signed graph and the function $\mu :V\left(S\right)\to \{+,-\}$ is called a marking of the signed graph S. A cycle in $S_{\mu }$ is said to be consistent if it contains an even number of negative vertices and a sign graph S is said to be consistent if every cycle in it is consistent (see [140]). The unique marking ${\mu }_{\sigma }$ induced by the sign function $\sigma :E\left(G\right)\to \{+,-\}$ such that for every vertex $v\in V\left(S\right)$, ${\mu }_{\sigma }\left(v\right)={\displaystyle \prod _{e\in E_v}}\sigma \left(e\right)$, where $E_v$ is the set of all edges incident with v in S, is called the canonical marking and a cycle in S is said to be canonically consistent if it contains an even number of negative vertices and the given sigraph is said be canonically consistent if every cycle in it is canonically consistent. A sigraph S is sign-compatible if there exists a marking of its vertices such that the end vertices of every negative edge receives a negative marking and no positive edge in S has both of its ends assigned a negative sign by the marking, otherwise the graph is sign-incompatible (see [140]).

The above mentioned four variations of the signed unitary Cayley graphs were examined in [139,141,142,143], where the properties of the unitary Cayley join signed graph and its negation were investigated in [142], the unitary Cayley ring signed graph was investigated in [141], the unitary Cayley meet signed graph was explored in [139,143]. In [142], a characterisation of the balanced unitary Cayley join signed graphs and canonically consistent unitary Cayley join signed graphs $S_n^{\vee }$, where n has at most two distinct odd prime factors were obtained as follows.

Theorem 46. 

[142] The unitary join Cayley signed graph $S_n^{\vee }$ is balanced if and only if either n is even or if n is odd and it does not have more than one distinct prime factors.

Theorem 47. 

[142] The negation of a unitary join Cayley sigraph $S_n^{\vee }$ is balanced if and only if n is even.

Theorem 48. 

[142] The unitary join Cayley sigraph $S_n^{\vee }$, where n has at most two distinct odd prime factors is canonically consistent if and only if n is odd, 2, 6 or a multiple of 4.

The unitary Cayley ring signed graphs, which are closely associated with the unitary Cayley join signed graphs were examined in [141]. It can be seen that an edge in unitary Cayley join signed graph is positively signed when at least one of its end vertex is a unit of the ring; that is, either one or both the end vertices can be units for an edge to be positive; whereas, an edge in the unitary Cayley ring signed graph is positively signed only when exactly one of its end vertex is a unit of the ring. Therefore, the difference and the relation between the unitary join Cayley signed graph, the unitary ring Cayley signed graph and the unitary Cayley meet signed graph was given in [141] and the conditions under which they shall be isomorphic were obtained as given in Theorem 49 and Theorem 50.

Theorem 49. 

[141] For a unitary Cayley graph $X_n$, the unitary Cayley join sigraph and unitary Cayley ring sigraph are isomorphic if and only if n is even.

Theorem 50. 

[141] For a unitary Cayley graph $X_n$, the unitary Cayley join sigraph can never be isomorphic to the unitary Cayley meet sigraph.

Along with the above mentioned characterisations of balanced and canonically consistent unitary Cayley ring signed graphs, the characterisations of clusterable and sign-compatible unitary Cayley ring signed graphs were also obtained in [141], as given in Theorem 51 and Theorem 52, based on the results on the property of balance. A signed graph is said to be clusterable if its vertex set can be partitioned into pairwise disjoint subsets, called clusters, such that every negative edge joins vertices in different clusters and every positive edge joins vertices in the same cluster.

Theorem 51. 

[141] For unitary Cayley graph $X_n$, the unitary Cayley ring sigraph is balanced if and only if n is even and is clusterable if and only if the graph is balanced.

Theorem 52. 

[142] The unitary Cayley ring signed graph $S_n^{\vee }$ is sign-compatible if and only if either n is even or if $n=p^t$, where p is an odd prime and $t\in \mathbb{N}$.

The unitary Cayley meet signed graphs in which an edge is positively signed only when both of its end vertices are units was investigated in [139,143], where the graph was characterised based on the similar properties of balance, canonical consistency, sign-compatibility and clusterability as given below.

Theorem 53. 

[139,143] For unitary Cayley graph $X_n$, the unitary Cayley meet sigraph is balanced if and only if n is even or n is a power of an odd prime.

Theorem 54. 

[139,143] The unitary meet Cayley sigraph $S_n^{\wedge }$, where n has two distinct odd prime factors, is canonically consistent if and only if n is even.

Theorem 55. 

[139,143] For unitary Cayley graph $X_n$, the unitary Cayley meet sigraph is always clusterable.

Theorem 56. 

[139,143] For unitary Cayley graph $X_n$, the unitary Cayley meet sigraph is sign-compatible if and only if n is even.

Along with the significant characterisations on the properties of balance, clusterability, etc. of the four different signed graphs defined from the unitary Cayley graphs, a few cursory studies on certain derived signed graphs from the signed graphs corresponding to each of the definitions of the signed graphs were also done in [139,141,142,143], which included the discussions on different variations of the line signed graphs, as the canonical marking serve as the signs of the edges in the line signed graphs and the property of canonical consistency of the signed graph can be used to investigate the properties like balance, clusterability, etc. of the line signed graphs.

3. Unitary Cayley Graph of a Ring

The definition of the unitary Cayley graph $X_n$ of the ring ${\mathbb{Z}}_n$, naturally fostered an extension of the definition to any associative ring R, in order to explore the properties of the ring and to obtain similar graphs to that of $X_n$ with the same properties. It can be seen that all investigations on the unitary Cayley graphs of rings are inspired from the investigations of the same concepts on $X_n$ and a particular case of the study or the results obtained on the unitary Cayley graph of a ring R produces the existing results on the graph $X_n$, which can be seen as a factor of verification of the obtained results on the unitary Cayley graph of any ring, as well as a validation of the existing results on the graphs $X_n$. This definition of the unitary Cayley graph for a ring R, which is mentioned below was first put forth in [144]. Following the definition, an illustration of a unitary Cayley graph of a ring is given in Figure 6.

Definition 13. 

[144] Let R be a ring and $R^{*}$ be the group of units in R. The unitary Cayley graph, denoted by $G\left(R\right)=Cay(R,R^{*})$, is a graph with the vertex set as the elements of the ring and any distinct two vertices u and v are adjacent in the graph if their difference is a unit; that is, for $u,v\in V\left(G\right(R\left)\right)$, $uv\in E\left(G\right(R\left)\right)$ when $u-v\in R^{*}$.

Before the introduction of the graph as the unitary Cayley graphs in [15], a graph that was constructed using the property of the elements of an Artinian ring to be expressed as the sum of two units under certain conditions had the same definition in [144], where a short introductory study on the graph was done to understand the nature of the graph. The two main results obtained in the study was that, for an Artinian ring R, the number of connected components of the constructed graph $G\left(R\right)$ is always a power of 2 and is Hamiltonian. Also, to answer the question of the existence of algebraic graphs possessing certain properties that have their clique and chromatic numbers equal, a graph construction on the Artinian rings was proposed in [145] using the same notion; that is, the nature of the elements to be expressed as the sum of units, which later emerged as the formal definition unitary Cayley graphs of rings in [15].

As we restrict our study to finite graphs, the rings considered shall be taken as finite rings, unless mentioned. In [43], the unitary Cayley graph of a ring was defined with a motive to extend a few results of $X_n$ to the unitary Cayley graph of any ring R, where the result on the number of induced cycles in the graph $X_n$ that was enumerated was extended to the graph $G\left(R\right)$, for some specific rings. To obtain this extension, the rings which were isomorphic to the direct product of local rings were considered first and it was proved that if $R\cong R_1\times R_2\times \dots \times R_t$, where each $R_i$, $1\le i\le t$ is a local ring with $M_i$ as their maximal ideal, called the local factors of R, then $G\left(R\right)$ is a direct product of complete $k_i$-partite graphs, for some $k_i$. As it was also proved in [43] that the result obtained on the length of the longest induced cycle in $X_n$ holds for the direct product of complete $k_i$-partite graphs, for some $k_i$ (which need not be necessarily finite), the longest induced cycles in $G\left(R\right)$, for a ring R which is isomorphic to the direct product of the local rings were investigated in [43].

To prove the structure of the graph $G\left(R\right)$ as the direct product of complete $k_i$-partite graphs when R is the direct product of local rings, the graph $G\left(R_i\right)$ for each local ring $R_i$ was first obtained as a complete $k_i$-partite graph, where $k_i=\left|\frac{R_i}{M_i}\right|$, by partitioning the vertex set of the graph into $k_i$ residue classes modulo. In this partition, two vertices, say $u,v\in V\left(G\left(R_i\right)\right)$, $1\le i\le t$ belong to the same residue class modulo $k_i$, only when $u-v\in M_i$ and hence $u-v\notin R^{*}$. This implies that two vertices $u,v\in V\left(G\left(R_i\right)\right)$ belong to different partite sets, only when they are adjacent and hence, their difference is a unit, according to the definition of the graph. This partition gives a complete $k_i$ partition for the unitary Cayley graph of each of the local rings, such that the partite sets are the cosets of $M_i$ in the additive group R. Following this, the graph $G\left(R\right)$ was proved to be isomorphic to the direct product $G\left(R_1\right)\times G\left(R_2\right)\times \dots \times G\left(R_t\right)$, based on the similar argument. As a corollary of this result, the same direct product structure of the unitary Cayley graphs of a Dedekind ring; that is, the quotient ring of a Dedekind domain, was also discussed, as the Dedekind rings are local rings.

In algebraic graph theory, realisation of an algebraic structure through the structure of the graph defined on the corresponding algebraic structure is a fundamental problem considered for any new algebraic graph defined. That is, to investigate the relation between the isomorphism of the algebraic structure and the corresponding graphs defined, in order to understand the properties of the algebraic structure that induces the properties of the graph. This problem of realising rings through the graph $G\left(R\right)$ was addressed in [146], by proving that the unitary Cayley graphs of rings are isomorphic when the corresponding rings on which they are defined are isomorphic, with respect to certain conditions on the structure of the ring.

A ring $R_1$ is said to be a determined by the unitary Cayley graph $G\left(R_1\right)$ if $R_2$ is also a ring such that $G\left(R_1\right)\cong G\left(R_2\right)$ implies $R_1\cong R_2$. The Jacobson radical of a ring R, denoted by $J_R$, is defined as the intersection of all the maximal ideals of R and a ring R is said to be reduced if it has no non-zero nilpotent elements.

Successively, the unitary Cayley graph of finite rings was investigated in [146], where the study as a whole aims to discuss the unitary Cayley graphs of all finite rings; but, the results obtained were mainly focused on the unitary Cayley graphs of some specific finite rings and finite commutative rings. For these rings, the graph invariants of $G\left(R\right)$ like the clique and the chromatic number were also obtained when $R={\mathbb{M}}_n\left(\mathbb{F}\right)$, where $\mathbb{F}$ is a field. Also, for a ring R, it was proved that the clique and the chromatic number of $G\left(R\right)$ will be equal to the clique and the chromatic number of the graph $G\left(\frac{R}{J_R}\right)$,s the unitary Cayley graph of the ring $\frac{R}{J_R}$. A more stronger result that was proved on the isomorphism of these graphs in [146], as given below.

Theorem 57. 

[146] Let $R_1$ and $R_2$ be finite rings such that $G\left(R_1\right)\cong G\left(R_2\right)$. Then, $G\left(\frac{R_1}{J_{R_1}}\right)\cong G\left(\frac{R_2}{J_{R_2}}\right)$. Also, $|J_{R_1}|=|J_{R_2}|$.

As an application of Theorem 57, a similar result was proved in the case of commutative rings, which aided in proving that a commutative reduced ring can be determined by the unitary Cayley graph. Along with the proof of this theorem, an example of the ring $R={\mathbb{Z}}_4$ was also given to show that not all commutative rings can be determined by the unitary Cayley graphs. Finally, a conjecture on the isomorphism between the reduced rings $\frac{R_1}{J_{R_1}}$ and $\frac{R_2}{J_{R_2}}$, when their unitary Cayley graphs are isomorphic was given in [146].

Followed by this, the diameter of unitary Cayley graphs of rings was investigated in [147] and it was proved that for each integer $n\ge 1$, there exists a ring R such that $diam\left(G\right(R\left)\right)=n$. The proof of this result revealed that the connectedness of the graph $G\left(R\right)$ is closely related to the property of the ring R to be generated additively by its units. The diameter of the unitary Cayley graphs of a few extensions of rings like the power series ring over a ring, polynomial ring over a ring and self injective rings were also investigated based on the main results that were obtained. Note that a ring R is called right (left) self-injective if every homomorphism from a right (left) ideal of R into R can be extended to a homomorphism of R to itself (refer to [148]).

An element of a ring R is said to be k-good if it can be expressed as a sum of k units of the ring R and a ring is said to be k-good if every element is k-good. The unit sum number, $usn\left(R\right)$ of a ring R is the smallest number l such that every element can be written as the sum of at most l units. If some element of R is not k-good for any $k\ge 1$, then $usn\left(R\right)$ is ∞ (c.f. [149]). Few characterisations of rings with their unitary Cayley graphs having different values of diameter was obtained based on the definitions of the unit sum number of a ring, as follows.

Theorem 58. 

[146] Let R be any ring with the unitary Cayley graph $G\left(R\right)$ and unit sum number $usn\left(R\right)$. Then,

(i) 

$diam\left(G\right(R\left)\right)=1$ if and only if R is a division ring.

(ii) 

$diam\left(G\right(R\left)\right)=2$ if and only if $usn\left(R\right)=2$ and R is not a division ring.

(iii) 

$diam\left(G\right(R\left)\right)=k$ if and only if $usn\left(R\right)=k$, for $k\ge 3$.

In [15], the unitary Cayley graph of finite commutative rings with a non-zero unit element was considered for the study, where the properties of the graph $G\left(R\right)$ were investigated in a similar pattern like how the properties of $X_n$ were discussed in [48]; but using an algebraic approach. That is, the proof techniques of the results on the unitary Cayley graph of finite commutative rings emphasize on the algebraic structure of the rings, which in some cases were comparatively simpler and more efficient that the proofs given in [48], for the graphs $X_n$. The structure of the graph $G\left(R\right)$ was first discussed by obtaining results on its regularity, the number of common neighbors between the vertices of the graph, and the basic graph parameters like diameter, girth, the number of triangles, chromatic number, clique number, edge and vertex connectivity, etc. as follows.

Theorem 59. 

[15] For any ring R with the group of units $R^{*}$, $G\left(R\right)$ is a r-regular graph, where $r=|R^{*}|$.

Theorem 60. 

[15] Let R be a local ring with maximal ideal M. Then, $G\left(R\right)$ is a complete graph if and only if R is a field.

Theorem 61. 

[15] Let $G\left(R\right)$ be the unitary Cayley graph of an Artinian ring R. The neighbourhood of two vertices $u,v\in V\left(G\right(R\left)\right)$ are equal if and only if $u-v$ belongs to the ideal of all nilpotent elements of R.

Recall that a finite ring R is Artinian, and the structure theorem of Artinian rings (refer to [26]) that states $R\cong R_1\times R_2\times \dots \times R_t$, where each $R_i$, $1\le i\le t$ is a finite local ring with the corresponding maximal ideal $M_i$, $1\le i\le t$, such that the decomposition is unique up to permutation of factors. Here, the finite residue field is $\frac{R_i}{M_i}$, and the mapping ${\pi }_i:R_i\to \frac{R_i}{M_i}$ is the quotient map. With appropriate permutation of the factors, $f_1\le f_2\le \dots \le f_t$, where $f_i=\left|\frac{R_i}{M_i}\right|$, for $1\le i\le t$ can be obtained. Note that these notations are used in the following Theorems and the notation shall be maintained throughout the paper whenever R is mentioned as a finite or an Artinian ring.

Theorem 62. 

[15] Let $G\left(R\right)$ be the unitary Cayley graph of an Artinian ring $R\cong R_1\times R_2\times \dots \times R_t$. Then, the diameter of $G\left(R\right)$,

$$diam\left(G\left(R\right)\right)=\left\{\begin{array}{cc}1,\hfill & ift=1andRisafield;\hfill \\ 2,\hfill & ift=1andRisnotafield;\hfill \\ 3,\hfill & ift\ge 2,f_1\ge 3ort\ge 2,f_1=2,f_2\ge 3;\hfill \\ \infty ,\hfill & ift\ge 2,f_1=f_2=2.\hfill \end{array}\right.$$

Theorem 63. 

[15] Let $G\left(R\right)$ be the unitary Cayley graph of an Artinian ring $R\cong R_1\times R_2\times \dots \times R_t$. Then, the girth of $G\left(R\right)$,

$$gir\left(G\left(R\right)\right)=\left\{\begin{array}{cc}3,\hfill & if{f}_1\ge 3;\hfill \\ 6,\hfill & ifR\cong {\mathbb{Z}}_2^r\times {\mathbb{Z}}_3,forsomer\ge 1;\hfill \\ \infty ,\hfill & ifR\cong {\mathbb{Z}}_2^r,forsomer\ge 1;\hfill \\ 4,\hfill & otherwise.\hfill \end{array}\right.$$

Theorem 64. 

[15] Let $G\left(R\right)$ be the unitary Cayley graph of an Artinian ring $R\cong R_1\times R_2\times \dots \times R_t$. Then,

(i) 

The clique number, $\omega \left(G\left(R\right)\right)=\chi \left(G\left(R\right)\right)=f_1$, where $\chi \left(G\right(R\left)\right)$ denotes the chromatic number of $G\left(R\right)$.

(ii) 

The independence number, $\alpha \left(G\left(R\right)\right)=\frac{\left|R\right|}{f_1}$.

(iii) 

The edge chromatic number,

$${\chi }^{\prime }\left(G\left(R\right)\right)=\left\{\begin{array}{cc}|R^{*}|+1,\hfill & if\left|R\right|isodd;\hfill \\ |R^{*}|,\hfill & otherwise.\hfill \end{array}\right.$$

(iv) 

The vertex and the edge connectivity of $G\left(R\right)$, $\kappa \left(G\left(R\right)\right)={\kappa }^{\prime }\left(G\left(R\right)\right)=\left|R^{*}\right|$.

Along with the computation of these parameters, the planarity and perfection of the graph $G\left(R\right)$ was also discussed in [15] and a characterisation of planar and perfect unitary Cayley graphs of finite commutative rings were obtained as mentioned in Theorem 66 and Theorem 67. To investigate the perfection of the graph, the clique and the chromatic numbers of the complement $\left(\overline{G\left(R\right)}\right)$ of the graph $G\left(R\right)$ was also determined in [15] as given below.

Theorem 65. 

[15] The clique number of the graph $\overline{G\left(R\right)}$, $\omega \left(\overline{G\left(R\right)}\right)=\chi \left(\overline{G\left(R\right)}\right)=\alpha \left(G\left(R\right)\right)=\frac{\left|R\right|}{f_1}$, where χ and α represent the chromatic and the independence number.

Theorem 66. 

[15] Let R be an Artinian ring. Then, $G\left(R\right)$ is perfect if and only if $f_1=2$, R is local, or R is a product of two local rings.

Theorem 67. 

[15] Let R be a finite ring and s be a non-negative integer. Then, the graph $G\left(R\right)$ is planar if and only if R is one of the following rings.

(i) 

${\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$,

(ii) 

$\frac{\mathbb{Z}}{3\mathbb{Z}}\times {\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$,

(iii) 

$\frac{\mathbb{Z}}{4\mathbb{Z}}\times {\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$,

(iv) 

${\mathbb{F}}_4\times {\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$, where ${\mathbb{F}}_4$ is a field with 4 elements.

Following this, the algebraic properties like the automorphism group and the spectra of the graph $G\left(R\right)$ were obtained using the concept of reduction of a graph, given in [33] as follows.

Two vertices of a graph G are said to be equivalent if their open neighborhoods are equal and this defines an equivalence relation on the vertices of the graph, as two vertices are adjacent only if they are in different equivalence classes, and the induced subgraph of the vertices of two equivalence classes is either a complete bipartite graph or an edgeless graph. The reduction of a graph G is said to be the graph in which vertices are the equivalence classes of G, and two classes are adjacent if and only if their union induces a complete bipartite graph and a graph is said to be reduced if it is isomorphic to its reduction. Recall that a ring is said to be reduced if it has no non-zero nilpotent element and hence a finite commutative reduced ring is a finite product of finite fields.

An interesting relation between the reduction of the unitary Cayley graph $G\left(R\right)$ of a ring R and the structure of the reduced ring R was obtained in [15], which decreases the complexity of answering general questions about unitary Cayley graphs of finite rings to answering the questions for the corresponding finite reduced rings, as follows.

Theorem 68. 

[15] Let R be an Artinian ring. Then, the reduction ${\left(G\left(R\right)\right)}_{red}\cong G\left(R_{red}\right)$, where ${\left(G\left(R\right)\right)}_{red}$ is the reduced graph of $G\left(R\right)$ and $R_{red}\cong \frac{R}{{\mathcal{N}}_R}$, where ${\mathcal{N}}_R$ is the maximal ideal of R containing the nilpotent elements is the reduced ring R and $G\left(R_{red}\right)$ is the unitary Cayley graph of the ring $R_{red}\cong \frac{R}{{\mathcal{N}}_R}$.

The above established relation aids in determining the automorphism group of the graph $G\left(R\right)$, by reducing the problem to determine the automorphism group of the reduced graph of $G\left(R\right)$. In that case, an isomorphism $f:Aut\left(G\left(R\right)\right)\to Aut\left(G\left(R_{red}\right)\right)\times {\left(S_n\right)}^{\frac{R}{{\mathcal{N}}_R}}$ is established between the structures of the automorphism group of the graph $G\left(R\right)$ and its reduced graph, because any $\sigma \in Aut\left(G\right(R\left)\right)$ permutes the cosets of ${\mathcal{N}}_R$ and induces an automorphism $\overline{\sigma }\in Aut\left(G\left(R_{red}\right)\right)$, as a consequence of Theorem 61. As the automorphism group of the reduced graph is known through this process, the automorphism group of the graph was determined using this in [15] as follows.

Theorem 69. 

[15] Let $t\in \mathbb{N}$ and $r_1,r_2,\dots ,r_t$ be prime power integers, such that $2\le r_1<r_2<\dots <r_t$ and $R\cong {\displaystyle \prod _{i=1}^t}{\left(F_i\right)}^{n_i}$, where $F_i$ denotes a field with $r_i$ elements and $n_i\in \mathbb{Z}$, for each $1\le i\le t$. Then, $Aut\left(G\left(R\right)\right)\cong {\displaystyle \prod _{i=1}^t}{S}_{r_i}\times {\displaystyle \prod _{i=1}^t}{S}_{n_i}$.

As mentioned previously, the spectra of the unitary Cayley graph $G\left(R\right)$ of a ring R, was also determined based on the properties of the ring by grouping the rings under three cases. Firstly, the spectra of $G\left(R\right)$ when R is a field was computed as the graph $G\left(R\right)$ is a complete graph in that case. Followed by that, the spectra of $G\left(R\right)$ when R is not a field was computed as follows.

Theorem 70. 

[15] Let R be a finite local ring which is not a field, having a non-zero maximal ideal of size s and $f=\frac{\left|R\right|}{s}$. Then,

$$Spec\left(G\left(R\right)\right)=\left(\begin{array}{cc}-s& 0\\ f& f(s-1)\end{array}\right).$$

Theorem 71. 

[15] Let $R\cong R_1\times R_2\times \dots \times R_t$ be a finite ring having t local factors of which none are fields. Then,

$$Spec\left(G\left(R\right)\right)=\left(\begin{array}{cc}-1^t\left(\right|{\mathcal{N}}_R\left|\right)& 0\\ |R_{red}|& \left|R\right|-|R_{red}|\end{array}\right),$$

where ${\mathcal{N}}_R$ is the maximal ideal of R containing the nilpotent elements and $R_{red}$ is the reduced ring of R.

On computing the eigenvalues of the graph $G\left(R\right)$, the properties related to the spectra like energy, perfect state transfer, etc. of the graph were studied. It could be seen that all these properties that were examined on the unitary Cayley graph of a finite commutative ring was inspired from the study of the same property on the unitary Cayley graph of ${\mathbb{Z}}_n$. The energy of the unitary Cayley graph of finite commutative rings, as well as their complements was determined in [150] and the rings that have hyperenergetic unitary Cayley graphs were characterised as follows.

Theorem 72. 

[150] Let R be a finite commutative ring such that $R\cong R_1\times R_2\times \dots \times R_t$, where each $R_i$, $1\le i\le t$ is a local ring with the corresponding maximal ideal $M_i$.Then, the energy, $\mathcal{E}\left(G\left(R\right)\right)=2^t\left|R^{*}\right|$, where $R^{*}$ is the group of units in R.

Theorem 73. 

[150] Let R be a finite commutative ring such that $R\cong R_1\times R_2\times \dots \times R_t$, where each $R_i$, $1\le i\le t$ is a local ring with the corresponding maximal ideal $M_i$ and assume that $f_1\le f_2\le \dots \le f_t$, where $f_i=\left|\frac{R_i}{M_i}\right|$, for $1\le i\le t$. Then,

(i) 

For $s=1$, $G\left(R\right)$ is not hyperenergetic.

(i) 

For $s=2$, $G\left(R\right)$ is hyperenergetic if and only if $f_1\ge 3$ and $f_2\ge 4$.

(iii) 

For $s\ge 3$, $G\left(R\right)$ is hyperenergetic if and only if $f_{s-2}\ge 3$ or $f_{s-1}\ge 3$ and $f_s\ge 4$.

The Study on the energy of the unitary Cayley graph $G\left(R\right)$ was followed by the characterisation of finite commutative rings R, for which $G\left(R\right)$ and its complement $\overline{G\left(R\right)}$ are Ramanujan graphs in [151] as given in Theorem 74 and Theorem 75. In addition to it, the energy of the line graph $\mathcal{L}\left(G\right(R\left)\right)$ of the unitary Cayley graph $G\left(R\right)$ of a ring R, its hyperenergecity and its spectral moments were also determined in [151]. Note that for an integer $k\ge 0$, the k-th spectral moment of a graph G of order n with eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ is given by the the value, $s{m}_k\left(G\right)={\displaystyle \sum _{i=1}^n}{\lambda }_i^k$, which was found to be related to many combinatorial properties of the graph (see [152]).

Theorem 74. 

[151] Let R be a finite local ring with maximal ideal M of order s. Then, $G\left(R\right)$ is a Ramanujan graph if and only if either $\left|R\right|=2s$ or $\left|R\right|={\left(\frac{m}{2}+1\right)}^2$ and $m\ne 2$.

Theorem 75. 

[151] The complement $\overline{G\left(R\right)}$ of the unitary Cayley graph, $G\left(R\right)$ of a finite local ring R is always a Ramanujan graph.

All the characterisations obtained in [151] were given separately for the cases of R being a local ring and R being a finite product of local rings, where the characterisation on the latter involved the number theoretic properties of the cardinalities of the quotient ring $|\frac{R_i}{M_i}|$. This is mainly because of the variation in the spectra of the unitary Cayley graph of these two types of rings, which reveals the innate algebraic structure of the rings. This could be observed explicitly because, on proving these characterisations, several other results on the structure of the graph which complete rely on the structure of the rings were obtained in the process. For example, it was proved that the graph $G\left(R\right)$ is connected if and only if there is at most one factor $R_i$ such that $\frac{R_i}{M_i}\cong {\mathbb{F}}_2$, a field with 2 elements. This result on the connectedness of the graph can also be seen as a consequence of the well known fact that for an r-regular graph G, the multiplicity of r as an eigenvalue gives the number of connected components of G, and in view of the same it was also concluded that the unitary Cayley graph of a finite local ring R is always connected.

In the sequence of studying the graph properties based on the spectra, the perfect state transfer in the unitary Cayley graphs of rings; that is, the problem of finding if the network admits data transfer without a loss of information, so that the probability of transfer is 1, were investigated in [153] and [154]. The rings were characterised based on the existence of the perfect state transfer in their unitary Cayley graphs, along with which the time of transfer was also obtained for the unitary Cayley graph of finite local ring, as follows.

Theorem 76. 

[153] Let R be a finite local ring with maximal ideal M of size s. Then, $G\left(R\right)$ has a perfect state transfer if and only if $R={\mathbb{F}}_2$ or $s=2$, where ${\mathbb{F}}_2$ is a field with 2 elements. In particular, a perfect state transfer occurs at time $t=\frac{\pi }{2}.$

One of the interesting aspect of research in spectral graph theory is to find non-cospectral (non-isospectral) equi-energetic graphs. One such problem is to find families of regular graphs which are equi-energetic with their own complements. Unitary Cayley graphs being regular, an attempt to obtain such non-cospectral equi-energetic regular graphs was done in [155,156] and it was proven that if $R\cong R_1\times R_2\times \dots \times R_t$ has an even number of local factors, then $G\left(R\right)$ and $\overline{G\left(R\right)}$ are complementary equi-energetic if and only if R is the product of two finite fields and in this case, the graphs are strongly regular. It was also given that the classification of such complementary equi-energetic unitary Cayley graphs for R, when it has odd number of local factors, greater than three remains open.

A similar problem of finding integral equi-energetic non-isospectral graphs was addressed with the properties of unitary Cayley graphs $G\left(R\right)$, their complements $\overline{G\left(R\right)}$ and the unit graphs $G^{+}\left(R\right)$ (refer to Section 5 for details on the Unit graphs of rings) in [155] and [157]. The conditions under which the unit and unitary Cayley graph of a finite commutative ring are equi-energetic were obtained in [157] and in addition to that, using the results on the equi-energetic complements of the unitary Cayley graphs given in [156], all integral equi-energetic non-isospectral triple $\{G\left(R\right),\overline{G\left(R\right)},G^{+}\left(R\right)\}$ such that all three graphs are also Ramanujan graphs was characterised in [155].

It was first proved that for a ring R, $G\left(R\right)$ and $G^{+}\left(R\right)$ were equi-energetic as the group of units considered for the adjacency criteria is a symmetric subset of R. Following this, the conditions on the structure of the ring R, the spectrum of $G\left(R\right)$ and $G^{+}\left(R\right)$, and the corresponding graphs were obtained in order to prove that the unitary Cayley and the unit graphs of the ring concerned are non-isospectral. Using this, it was shown that $G\left(R\right)$ and $G^{+}\left(R\right)$ are integral equi-energetic non-isospectral connected non-bipartite graphs, under certain conditions and as an application, the graphs $G\left(R\right)$ and $G^{+}\left(R\right)$ which are strongly regular were characterised. This characterisation of all finite commutative rings for which its unitary Cayley graph is strongly regular was also obtained independently in [158] as follows.

Theorem 77. 

[155,158] The unitary Cayley graph $G\left(R\right)$ of a finite commutative ring R is strongly regular if and only if R is a local ring or $R\in \{{\mathbb{Z}}_2^k,\mathbb{F}\times \mathbb{F}\}$, where $\mathbb{F}$ is a finite field with $\left|\mathbb{F}\right|\ge 3$.

Another important spectra of the graph that arises from the adjacency and the degree matrices of the graph is the Laplacian and the signless Laplacian spectra. These Laplacian and the signless Laplacian eigenvalues for the unitary Cayley graph of a commutative ring along with their corresponding energies for the graph $G\left(R\right)$ as well as its line graph $\mathcal{L}\left(G\right(R\left)\right)$ was determined in [159].

It can be noticed that the properties of the Laplacian and the signless Laplacian spectra shall be in parallel with the properties of the adjacency spectra, as the Laplacian matrix and the signless Laplacian matrix of a graph G are given by the relation $L\left(G\right)=A\left(G\right)-Deg\left(G\right)$ and $L\left(G\right)=A\left(G\right)+Deg\left(G\right)$, respectively, where $A\left(G\right)$ is the adjacency matrix and $Deg\left(G\right)$ is the degree matrix of the graph G. The degree matrix $Deg\left(G\right)$ of a graph G of order n is a $n\times n$ matrix whose only non-zero entries are the diagonal entries that gives the degree of the vertices.

The study of groups admitting planar Cayley graphs can be traced back over almost 120 years, and there is a long history for studying infinite planar Cayley graphs which satisfy additional special conditions (For example, see [30,160]). Regarding the unitary Cayley graphs of rings, a list of finite commutative rings whose unitary Cayley graphs are planar was given in [15,161]. This result only dealt only with finite graphs, and the main algebraic tool used in its proof was the Wedderburn-Artin Theorem7. In [161,162], the unitary Cayley graph of arbitrary rings was considered for investigation, for which the unitary Cayley graphs are mostly infinite.

Though the list of finite planar unitary Cayley graphs was given in [15], the difference in the technique of investigating the planarity of a finite graph and an infinite graph was visible on observing the proof techniques used to prove the results in [161,162]. One distinguishing example is, for a finite planar graph, the minimal degree of the graph is at most five; whereas it was proved in [163] that there exists a k-regular planar infinite graph for any positive integer k.

A thorough analysis of the group of units of the associated ring structures was conducted in [162] and it was shown that a ring with a planar unitary Cayley graph has either at most 4 units or exactly 6 units. This result served as a key to obtain a complete characterisation of the rings whose unitary Cayley graphs are planar in [162] as given in Theorem 78. Using Theorem 78, the semilocal rings with planar unitary Cayley graphs were completely determined. Note that a semilocal ring is a commutative Noetherian ring with finitely many maximal ideals, where a ring is called Noetherian if every strictly ascending chain of ideals in the ring is finite.

Theorem 78. 

[151,162] Let R be a ring with the group of units $R^{*}$. Then, $G\left(R\right)$ is planar if and only if one of the following holds:

(i) 

$|R^{*}|\le 3$ and $\left|R\right|\le \left|\mathbb{R}\right|$,

(ii) 

$|R^{*}|=4$, $Char\left(R\right)=0$ and $\left|R\right|\le \left|\mathbb{R}\right|$,

(iii) 

$|R^{*}|=6$ and R contains a subring isomorphic to $\frac{\mathbb{Z}\left[t\right]}{(t^2-t+1)}$ with $\left|R\right|\le \left|\mathbb{R}\right|$, where $\mathbb{Z}\left[t\right]$ is the polynomial ring over a ring $\mathbb{Z}$ in the indeterminate t.

An orientable surface is said to be of genus g if it is topologically homeomorphic to a sphere with g handles. The genus of a graph is the minimum number of handles that must be added to a plane to embed the graph without any crossings. A planar graph is a graph with genus zero, and a toroidal graph is a graph with genus one (c.f.[30]). It could be noted that this investigation on the planarity of unitary Cayley graphs of rings was restricted to finite commutative rings owing to the complexity of the structure of the unitary Cayley graphs emerging from finite as well as infinite arbitrary rings due to the diversity in their properties.

As an extension of the characterisation of planar unitary Cayley graphs, the minimal non-planar unitary Cayley graphs were investigated in [162,164]. In [164], the structure of the finite commutative rings whose unitary Cayley graphs have genus at most 3 was examined and it was proven that for any given positive integer g, there are at most finitely many finite commutative rings whose unitary Cayley graphs have genus g.

A graph G is a ring graph if each block of G which is not a bridge or a vertex can be constructed from a cycle by successively adding H-paths of length at least 2, that meets the graph H in two adjacent vertices. Here, given a graph H, we call a path P an H-path if P is non-trivial and meets H exactly in its ends (For more details, refer to [165]). By definition, it is clear that the ring graphs are planar. An outerplanar graph is a graph that has a planar drawing for which all vertices are in the outer face of the drawing.

Based on the characterisations of planar unitary Cayley graphs on rings, the rings for which the unitary Cayley graphs are outerplanar and the ring graphs were also characterised in [166] as follows.

Theorem 79. 

[166] Let R be a finite ring. Then, $G\left(R\right)$ is a ring graph if and only if it is a planar graph.

This gives the same list of rings for which $G\left(R\right)$ is planar as given in Theorem 67. It was proven in [165] that every outerplanar graph is a ring graph. The following theorem on the characterisation of outerplanar unitary Cayley graphs serves as a counterexample for the converse of the theorem, as the existence of a ring R for which $G\left(R\right)$ is a ring graph but not outerplanar could be seen.

Theorem 80. 

[166] Let R be a finite ring and s be a non-negative integer. Then, $G\left(R\right)$ is outerplanar if and only if R is one of the following rings.

(i) 

${\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$,

(ii) 

$\frac{\mathbb{Z}}{3\mathbb{Z}}\times {\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$,

(iii) 

$\frac{\mathbb{Z}}{4\mathbb{Z}}\times {\left(\frac{\mathbb{Z}}{2\mathbb{Z}}\right)}^s$.

The same study of examining the rings for which the line graph of the unitary Cayley graphs are planar, outerplanar and ring graphs was done in [167] and it was proved that $\mathcal{L}\left(G\right(R\left)\right)$ is planar if and only if $G\left(R\right)$ is planar and $\mathcal{L}\left(G\right(R\left)\right)$ is outerplanar if and only if it is a ring graph. Both of these conditions can be found similar to that of the outerplanarity conditions of the unitary Cayley graphs itself.

Following the investigation on the planarity of line graphs of the unitary Cayley graphs, the planarity parameters on the iterated line graphs were investigated in [168]. The k-th iterated line graph of a graph G, denoted by ${\mathcal{L}}^k\left(G\right)$, is defined inductively as ${\mathcal{L}}^0\left(G\right)=G$, ${\mathcal{L}}^1\left(G\right)=\mathcal{L}\left(G\right)$ and ${\mathcal{L}}^k\left(G\right)={\mathcal{L}}^{k-1}\left(\mathcal{L}\left(G\right)\right)$. The planarity (outerplanarity) index of a graph G, denoted by $\zeta \left(G\right)$$\left(\eta \right(G\left)\right)$, is the smallest integer k such that ${\mathcal{L}}^k\left(G\right)$ is non-planar (non-outerplanar). The results obtained on these parameters of the unitary Cayley graph of R is given as follows.

Theorem 81. 

[168] For a finite commutative ring R,

(i) 

$\zeta \left(G\right(R\left)\right)=\infty$ if and only if $G\left(R\right)$ is outerplanar.

(ii) 

$\zeta \left(G\right(R\left)\right)=2$ if and only if $G\left(R\right)$ is a non- outerplanar ring graph.

(iii) 

$\zeta \left(G\right(R\left)\right)=0$, otherwise.

Theorem 82. 

[168] For a finite commutative ring R,

(ii) 

$\eta \left(G\right(R\left)\right)=\infty$ if and only if $G\left(R\right)$ is outerplanar.

(ii) 

$\eta \left(G\right(R\left)\right)=0$, otherwise.

Equivalently, it can also be told as $\eta \left(G\right(R\left)\right)=\infty$ if and only if $\zeta \left(G\right(R\left)\right)=\infty$ and if not $\eta \left(G\right(R\left)\right)=0$, to establish the significance of the relation between the planarity and outerplanarity indices of the graph. Note that we have rephrased the above results from[168] in terms of the planarity and outerplanarity of the unitary Cayley graphs to emphasize the relation and similarity between the concepts. Along with this, the study in [166,167,168] also determined the same properties and parameters related to planarity, outerplanarity of graphs and line graphs for the unit graphs of the rings also, and similar results were obtained as their structures are similar to each other according to the graph construction.

By identifying the vertices of a simple graph G as the variables of the polynomial ring $R=\mathbb{F}[x_1,x_2,\dots ,x_n]$ over a field $\mathbb{F}$, the edge set of the graph becomes an ideal I for the ring R and the quotient ring $\frac{R}{I}$ is called the edge ring of the graph G. A simplicial complex $\omega$ on a vertex set $V=\{x_1,x_2,\dots ,x_n\}$ is a set of subsets of V that satisfies the following conditions, where the elements of $\omega$ are called its faces.

(i)

If $F\in \omega$ and $F_1\subseteq F$, then $F_1\in \omega$;

(ii)

For each $i=1,2,\dots ,n,\left\{x_i\right\}\in \omega$.

Using the above given definitions, the properties of a graph to be Cohen-Macaulay and Gorenstien are defined based on the Cohen-Macaulay and Gorenstien ring structures (refer to [169]). It was already seen that the property of well-coveredness of the graphs $X_n$ was examined in [91]. The same has been extended to the unitary Cayley graphs of finite commutative rings in [170], in which a characterisation of the rings that have well-covered unitary Cayley graphs was obtained in terms of the unitary Cayley graph of its reduced ring as given in Theorem 83, along with an equivalence relation of the properties of Cohen-Macauleyness, Shellability and Gorenstien, which states that that all the Cohen–Macaulay unitary Cayley graphs are shellable and Gorenstein.

Theorem 83. 

[170] Let R be a finite ring. Then, $G\left(R\right)$ is a well-covered graph if and only if $G\left(\frac{R}{J\left(R\right)}\right)$ is well covered.

It was seen that a several variants of domination numbers and other domination related parameters were computed for the graph $X_n$, as the computation of domination parameters for algebraic graphs is a very common study. Interestingly, for the unitary Cayley graphs of rings, the literature has discussions only on the Roman domination number ${\gamma }_{rom}\left(G\left(R\right)\right)$ (refer to [171]) of these graphs in [172], where the following characterisation of the unitary Cayley graphs with Roman domination number at most four was obtained.

Theorem 84. 

[158] Let R be a finite commutative ring with non-zero identity. Then, the following properties are satisfied:

(i) 

For the graph $G\left(R\right)$, ${\gamma }_{rom}\left(G\left(R\right)\right)=2$ if and only if R is a field.

(ii) 

For the graph $G\left(R\right)$, ${\gamma }_{rom}\left(G\left(R\right)\right)=3$ if and only if R is a local ring with the maximal ideal M such that $\left|M\right|=2$.

(iii) 

For the graph $G\left(R\right)$, ${\gamma }_{rom}\left(G\left(R\right)\right)=4$ if and only if either R is a local ring with the maximal ideal M such that $\left|M\right|\ge 3$ or $R\cong {\mathbb{Z}}_2\times \mathbb{F}$, where $\mathbb{F}$ is a field.

In the course of the study on unitary Cayley graph of a ring, the extension of the graph’s definition to an algebraic signed graph was given in [173]. The Unitary Cayley signed graph was defined based on the definition of unitary Cayley graphs on finite commutative rings as given in Definition 14 and the graphs were characterised based on the properties of balance and canonical consistence of the graph.

Definition 14 

([173]). Let R be a finite commutative ring with the group of units $R^{*}$. Theunitary Cayley signed graph, denoted by $S_R=(G\left(R\right),\sigma )$, is a signed graph whose underlying graph is the unitary Cayley graph $G\left(R\right)$, and the sign of an edge $v_i{v}_j\in E(\left(G\left(R\right)\right)$ is assigned by the function ${\sigma }^{:}E\left(G\left(R\right)\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $\left(G\right(R)$,

$$\sigma \left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & if{v}_i\in R^{*}or{v}_j\in R^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

The spectra and energy of the signed graphs and also their corresponding line signed graph was computed and the characterisation of all finite commutative rings for which the graph $S_R$ is hyperenergetic balanced was given. Also, it was obtained in [173] that for a finite local ring, the adjacency matrix of the unitary Cayley graph and the adjacency matrix of the unitary Cayley signed graph coincide. Using this, the perfect state transfer in this signed graph $S_R$ was examined in [154].

It was seen in [174] that the structure of the unitary Cayley graphs were determined by the appropriate reduction structures of the graph as well as the rings. The properties of the graph as well as the ring reduction gives further scope to examine the rings and the unitary Cayley graphs of the rings by studying the properties of the subgraph induced by the unit elements in the unitary Cayley graph; that is, for a finite commutative ring R with the unitary Cayley graph $G\left(R\right)$, the induced subgraph $\gamma \left(G\right(R\left)\right)$ is the graph with $V\left(\gamma \left(G\left(R\right)\right)\right)=R^{*}$ and two vertices are adjacent if their difference is a unit, where $R^{*}$ the group of all units of the ring R. This graph was introduced in [175] and the basic properties of the graph $\gamma \left(G\right(R\left)\right)$ were investigated. Some characterisation results based on the graph invariants like girth, chromatic number, chromatic index (edge chromatic number) and genus were also given in [175].

The main motivation of the study in [175] was to examine the possibility of determining the structure of the reduced ring of a ring R using $\gamma \left(G\right(R\left)\right)$, for which the outcome was positive. This was proved by showing that for two finite commutative rings $R_1$ and $R_2$, $\gamma \left(G\left(R_1\right)\right)\cong \gamma \left(G\left(R_2\right)\right)$ if and only if $\frac{R_1}{J_{R_1}}\cong \frac{R_2}{J_{R_2}}$, where $J_{R_1}$ and $J_{R_2}$ are the Jacobson radical of $R_1$ and $R_2$ respectively, using the algebraic properties of the spectrum of the graph.

In distinction from the extensive studies on the unitary Cayley graphs over commutative rings, it can be seen that not much work was done on unitary Cayley graphs over non-commutative rings, for which a possible reason is the complicated structures of non-commutative rings, compared to the commutative rings. The first class of non-commutative ring that was specifically considered to construct the graph $G\left(R\right)$ and study its properties, is the matrix rings.

The unitary Cayley graphs of the matrix algebras; that is, the set of all square matrices of order n over a finite field $\mathbb{F}$, denoted by ${\mathbb{M}}_n\left(\mathbb{F}\right)$ was studied specially in [176,177,178]. Though, in [15,146], certain properties of the graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ were discussed for these rings as a special case, [176,177,178] re-iterate them and give a broader proof. As known, the unit group of ${\mathbb{M}}_n\left(\mathbb{F}\right)$ is the set of all invertible matrices of order n, which is also called the general linear group, denoted by $G{L}_n\left(\mathbb{F}\right)$. The graph invariants of $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ were already discussed in [146,158], as given below and they can also be deduced as a special case from the existing results of the graphs $G\left(R\right)$.

Theorem 85. 

[146]

(i) 

The clique number of the unitary Cayley graph of ${\mathbb{M}}_n\left(\mathbb{F}\right)$ is ${\left|\mathbb{F}\right|}^n$.

(ii) 

The independence number of the unitary Cayley graph of ${\mathbb{M}}_n\left(\mathbb{F}\right)$ is ${\left|\mathbb{F}\right|}^{n^2-n}$.

(iii) 

The diameter of $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ is 1, when $n=1$ or 2, otherwise.

In [177], an analogous notion to the representation problem of graphs put forth in [33] was given, as the representation of graphs by matrices was defined to investigate if every graph in any family is an induced subgraph of $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ and it was conjectured that there is a graph G such that for each finite field $\mathbb{F}$, the graph G is not an induced subgraph of $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$. Also, the characterisation of the $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ to be strongly regular was obtained in [177] as follows.

Theorem 86. 

[177] The graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ is strongly regular if and only if $n=2$ and ${\mathbb{M}}_2\left(\mathbb{F}\right)$ is strongly regular with the parameters $(q^4,q^4-q^3-q^2+q,q^4-2q^3-q^2+3q,q^4-2q^3+q)$, where $q=\left|\mathbb{F}\right|$.

In [177], Theorem 86 has been proved only by considering two special cases of n, when $n=2,3$ and has failed to cover the other general cases. This was quoted and rectified in [176], and the same result was re-established by proving that the graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ cannot be strongly regular for any $n>2$. Following this, the spectral properties of the graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ was studied in [178], where the three eigenvalues of the graph were determined using the additive property of the ring ${\mathbb{M}}_n\left(\mathbb{F}\right)$, along with its energy and the conditions for hyperenergecity of the graphs, which was determined without explicitly computing the spectrum of the graph. The characterisation of rings ${\mathbb{M}}_n\left(\mathbb{F}\right)$ by determining the value of n for which $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ are Ramanujan graphs were also obtained in [178] as given below.

Theorem 87. 

[178] The graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ is a Ramanujan graph if and only if $n=2$ or $n=3$ and $\mathbb{F}={\mathbb{Z}}_2$.

The study on the unitary Cayley graphs of matrix rings was extended in [179], where explicit formulas for all the eigenvalues of the graphs $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ and $G\left({\mathbb{M}}_n\left(R\right)\right)$, where R is a finite commutative local ring that is not a field, was obtained using an alternate approach to the one that was followed in [174]. Using this, the energy, the Kirchhoff index and the number of spanning trees of the graphs $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ and $G\left({\mathbb{M}}_n\left(R\right)\right)$ were also derived. Note that the Kirchoff index of a graph G of order n is the value $n{\displaystyle \sum _{i=2}^n}\frac{1}{{\lambda }_i}$, where ${\lambda }_i$, $2\le i\le n$ denote the eigenvalues of the Laplacian matrix of the graph (see [300,305]).

For a vertex v in a graph G, its first and the second subconstituent of G at v is the subgraph of G induced by the neighbors and the non-neighbors of v (except v) respectively. The subconstituents of strongly regular graphs are being studied for several graphs, as they have many interesting properties associated with the structure of the graph (see [180]). Moreover, the problem of finding graphs which have strongly regular subconstituents is a problem of interest to the researchers, as several properties including the eigenvalues of these subconstituents were used to prove the uniqueness of the parameters of some strongly regular graphs (c.f.[180]). This notion of subconstituents of the unitary Cayley graphs of the ring $G\left({\mathbb{M}}_n\left(R\right)\right)$ was investigated in [181].

On examining the subconstituents of the unitary Cayley graphs of a finite ring R with identity $1\ne 0$, it can be seen that both the first and the second subconstituent of the additive identity 0, are the graph isomorphisms that maps v to $u-v$, where $u,v\in V\left(G\left({\mathbb{M}}_n\left(R\right)\right)\right)$. Hence, a complete study on the subconstituents of 0 in $G\left({\mathbb{M}}_n\left(\mathbb{R}\right)\right)$ was done, especially when R is a finite field $\mathbb{F}$; that is the subconstituents of the 0 element in the graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ were investigated. It can be observed that the first constituent of the 0 element in the graph $G\left({\mathbb{M}}_n\left(\mathbb{F}\right)\right)$ is nothing but the graph with the vertex set as the group $G\left(G{L}_n\left(\mathbb{F}\right)\right)$ (can be correlated as the graph $\gamma \left(G\left(G{L}_n\left(\mathbb{F}\right)\right)\right)$ and the second constituent is defined on the set of non-zero non-invertible matrices over $\mathbb{F}$. The structure of these subconstituents were determined, from which the spectra, energy and other spectral related properties like hyperenergeticity and Ramanujan property for both graphs were studied. In addition to it, the clique number, chromatic number and the independence number of these subconstituents were also computed in [181].

The next ring for which the unitary Cayley graphs were investigated in [182] is the quotient ring $\frac{R}{I}$, where R is a Dedekind domain and I is an ideal of R, that gives a finite and non-trivial $\frac{R}{I}$. The unitary Cayley graph defined on this Dedekind ring is a very close generalisation to that of the graph $X_n$ and hence, the unitary Cayley graphs of such Dedekind rings $\frac{R}{I}$ is called the generalised totient graphs. Recall that the Schemmel’s totient function $S{T}_r$ is a generalisation of the Euler’s totient function defined for each non-negative integer r and prime p, as a multiplicative arithmetic function that satisfies

$$S{T}_r\left(p^{\alpha }\right)=\left\{\begin{array}{cc}{p}^{\alpha -1}(p-r),\hfill & \mathrm{if}p\ge r;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $\alpha$ is a positive integer (c.f. [31]).

To study the properties of the generalised totient graphs, the Schemmel’s totient function was used, and especially one of the two extensions of the Schemmel’s totient function was used to obtain a formula for the number of cliques of any order k in a given generalised totient graph. This formula had not been used in the literature even for Euler totient Cayley graphs before this article and after a couple of years, the formula to obtain the number of cliques of any order k was given using the Schemmel’s totient functions in [94].

Using this formula of the number of cliques, the clique domination number of the generalised totient graphs was determined, which aided in the correction of an erroneous claim that had been made regarding this topic in [115] and also to provide a counter-example for the result on the strong domination (refer to Section 4 for definition) of the graph $X_n$ that was given in [110]. The study in [182] can be seen to have built on the basis of [48], as similar results and proof techniques have been adopted. The paper concludes by suggesting further scope of research pertaining to the topic, of which some are investigated over the period for all finite commutative rings.

A dual number is a number $x+ϵy$, where $x,y\in \mathbb{R}$ and $ϵ$ is a matrix with the property that ${ϵ}^2=0$ (refer to [183]). As the set of all dual numbers is an Artinian local ring, the unitary Cayley graph associated with ring of dual numbers was investigated in [183], where the exact values of the diameter, chromatic number and chromatic index was determined along with which a classification of all perfect unitary Cayley graphs of this ring was given.

Definition 15 

([184]). The set of all complex numbers $a+ib$, where $a,b\in \mathbb{Z}$, is the ring ofGaussian integers, denoted by $\mathbb{Z}\left[i\right]$. For any $k\in \mathbb{N}$, if $\left[k\right]$ is the principal ideal generated by k in $\mathbb{Z}\left[i\right]$, then the factor ring $\frac{\mathbb{Z}\left[i\right]}{\left[k\right]}$ is isomorphic to ${\mathbb{Z}}_k\left[i\right]$, where ${\mathbb{Z}}_k\left[i\right]$ is the set of all complex numbers $a+ib$, where $a,b\in {\mathbb{Z}}_k$ and the ring ${\mathbb{Z}}_k\left[i\right]$ is called thering of Gaussian integers modulo k.

Definition 16 

([185]). The set of all complex numbers $a+b\omega$, where $a,b\in \mathbb{Z}$ and $\omega =\frac{1}{2}(-1+i\sqrt{(}3))$ is a primitive third root, forms an integral domain called thering of Eisenstein integers, denoted by ${\mathbb{Z}}^e\left[i\right]$. For any $k\in \mathbb{N}$, if $\left[k\right]$ is the principal ideal generated by k in ${\mathbb{Z}}^e\left[i\right]$, then the factor ring $\frac{{\mathbb{Z}}^e\left[i\right]}{\left[k\right]}$ is isomorphic to ${\mathbb{Z}}_k^e\left[i\right]$, where ${\mathbb{Z}}_k^e\left[i\right]$ is the set of all complex numbers $a+b\omega$, where $a,b\in {\mathbb{Z}}_k$ and the ring ${\mathbb{Z}}_k^e\left[i\right]$ is called thering of Einstein integers modulo k.

To understand the unitary Cayley graphs of these rings, the nature of the units of these rings must be known. Both the rings have $n^2$ elements and they form a ring with respect to the operations of usual addition modulo n and multiplication modulo n. The structure of the units of the ring depends on the norm defined and is given below in the following theorems. An illustration of the unitary Cayley graph on both the rings, ${\mathbb{Z}}_k\left[i\right]$ and ${\mathbb{Z}}_k^e\left[i\right]$ is given in Figure 7.

In [186] and [187] the unitary Cayley graphs of the rings ${\mathbb{Z}}_k\left[i\right]$ and ${\mathbb{Z}}_k^e\left[i\right]$ were studied individually, where the basic graph invariants were obtained for the unitary Cayley graphs of these rings. In addition, the traversal properties of these graphs were explored and it was proved that the unitary Cayley graphs of both these rings were Hamiltonian and certain necessary and sufficient conditions for the graph $G\left({\mathbb{Z}}_k\left[i\right]\right)$ to be Eulerian, were obtained in [186].

Theorem 88. 

[184] An element $a+ib\in {\mathbb{Z}}_n$ is a unit in the ring ${\mathbb{Z}}_n$ if and only if $a^2+b^2$ is a unit in ${\mathbb{Z}}_n$.

Theorem 89. 

[185] An element $a+b\omega \in {\mathbb{Z}}_n^e$ is a unit in the ring ${\mathbb{Z}}_n^e$ if and only if $a^2+b^2-ab$ is a unit in ${\mathbb{Z}}_n$.

It can be seen that the properties of the unitary Cayley graph of rings highly depend on the properties of the rings, owing to which not many properties of the graphs were discussed, unlike the ones studied for the graphs $X_n$. This is because the feasibility of condensing all the rings under same roof and investigating many properties is less; however, still, several avenues are open for further research.

4. Unitary Addition Cayley Graph

The conventional definition of a Cayley graph on any algebraic structure, with respect to any of its symmetric subset is a graph with the vertex set as the elements of the algebraic structure and there exists an edge between two vertices in the graph if their difference is an element of the symmetric subset considered. A slight modification on this adjacency condition in the usual Cayley graph to the sum of two elements to belong to the symmetric subset instead of their difference, paved its way to the concept of addition Cayley graphs, also known as the Cayley-sum graphs in [188], which almost have the same properties and symmetric nature as the usual Cayley graphs.

Though these addition Cayley graphs were termed as a twin to the Cayley graphs, it can be seen that they have received very less attention in the literature, when compared to the Cayley graphs. To some extent, this situation can be explained based on the fact that the addition Cayley graphs are comparatively difficult to study than the Cayley graphs. For example, the connectivity of a Cayley graph on a finite Abelian group was a obtained as an immediate consequence of its adjacency pattern, whereas determining the connectivity of an addition Cayley graph was a non-trivial problem that was exclusively solved in [189].

In the literature, though the addition Cayley graph was first defined for groups in [188], it was extended to many algebraic structures. The addition Cayley graph of an algebraic structure $\mathcal{A}$, with a symmetric subset S is given in Definition 17 ensuing which, an Illustration of the same is given in Figure 8.

Definition 17 

([188]). Anaddition Cayley graphof an algebraic structure $\mathcal{A}$ is the graph with the vertex set as the elements of $\mathcal{A}$ and any two vertices u and v in the graph are adjacent when $u+v\in S$, where S is a symmetric subset of $\mathcal{A}$. This addition Cayley graph of $\mathcal{A}$ with respect to its symmetric subset S is usually denoted by $Ca{y}^{+}(\mathcal{A},S)$.

Combining the notions of the addition Cayley graph with the definition of the graph $X_n$; that is, the unitary Cayley graphs of ${\mathbb{Z}}_n$, the unitary addition Cayley graphs was introduced in [190] as given below and an example of a unitary addition Cayley graph is given in Figure 9.

Definition 18 

([190]). Theunitary addition Cayley graph, denoted by $X_n^{+}=Ca{y}^{+}({\mathbb{Z}}_n,{\mathbb{Z}}_n^{*})$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their sum is a unit of the ring; that is, for all $u,v\in V\left(X_n^{+}\right)$, $uv\in E\left(X_n^{+}\right)$ when $|u+v|\in {\mathbb{Z}}_n^{*}$, where ${\mathbb{Z}}_n^{*}$ is the set of all relatively prime integers to n, which are the units of ${\mathbb{Z}}_n$.

Though the graph was defined and introduced officially with the name unitary addition Cayley graph in [190], this graph was already defined by Grimaldi in [18], from which the unit graphs of rings (refer to Section 5) was defined and studied. Since unitary addition Cayley graph is a unit graph of ${\mathbb{Z}}_n$, researchers focused on studying the unit graphs of all rings, rather than a particular one. Over a period of time, as the unitary Cayley graph of ${\mathbb{Z}}_n$ marked its high significance in this area of research, its claimed twin, the unitary addition Cayley graph was defined independently and is being studied.

In [18], the basic results on the regularity of the graph $X_n^{+}$ and the decomposition of the graph into Hamiltonian cycles were given, along with which the challenging nature of investigating different graph properties for the unitary Cayley graphs with odd order, despite a clear understanding of the structure of the graph was discussed.

On re-introducing the unit graph of ${\mathbb{Z}}_n$ as the unitary addition Cayley graph, the basic properties such as the regularity, girth, size, etc. of the graph was investigated in [190], along with their traversal properties, as mentioned in Theorem 90. The structural characterisations of the graph on their k-partiteness, planarity were also obtained, which are given below.

Theorem 90. 

[190] Let $X_n^{+}$ be the unitary addition Cayley graph of the ring ${\mathbb{Z}}_n$ and $\varphi \left(n\right)$ be the Euler’s totient function. Then, the following properties hold.

(i) 

The graph $X_n^{+}$ is $\left(\varphi \right(n),\varphi (n)-1)$- semiregular, when n is odd.

(ii) 

$|E\left(X_n^{+}\right)|=\frac{(n-1)\varphi \left(n\right)}{2}$, when n is odd.

(iii) 

$gir\left(X_n^{+}\right)=3$, for odd $n>3$ and 4 for even $n>2$ and $n\ncong 0mod3$.

Theorem 91. 

[190] The unitary addition Cayley graph is planar if and only if the value of n is 1, 2, 3, 4 or 6 and it is outerplanar if and only if it is planar.

As the graph is obtained from the unitary Cayley graphs, a natural and an important question of the relation between the unitary addition Cayley graph $X_n^{+}$ and its termed to be twin, the unitary Cayley graph $X_n$ had to be answered. This was solved by obtaining the characterisation that $X_n\cong X_n^{+}$ if and only if n is even and this characterisation reduces the problem of investigating the properties and the structure of $X_n^{+}$ for only the odd values of n. Owing to this, the results on the unitary addition Cayley graphs explicitly mentioned in this section are only for odd values of n.

This characterisation naturally motivates the researchers to extend the investigation on all similar problems and properties that were addressed for the unitary Cayley graphs to the unitary addition Cayley graphs, for two different reasons; one is to understand how the structure and properties of the unitary addition Cayley graphs differ for odd values of n and the other reason is to obtain parallel results with the help of a similar methodology existing in the literature, especially in a similar context and which can also be verified without much challenge.

This study in [190] was extended in [191], by more clearly establishing the structure of the unitary addition Cayley graph as a k-partite graph for odd n, as given in Theorem 92, which aided in computing several numerical parameters of the graph in [191]. Note that the parameters of the graph $X_n^{+}$ that were computed in [191] are given below only for odd n.

Theorem 92. 

[191] The unitary addition Cayley graph $X_n^{+}$, for an odd n is a $\frac{\varphi \left(n\right)}{2}+r$-partite graph, where r is the number of distinct prime factors of n.

Theorem 93. 

[191] Let $X_n^{+}$ be the unitary addition Cayley graph of ${\mathbb{Z}}_n$, where $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_r^{{\alpha }_r}$, such that $p_i<p_j$, for $i<j$ and ${\alpha }_i\in \mathbb{N}$, for all $1\le i\le r$. Then,

(i) 

The independence number, $\alpha \left(X_n^{+}\right)=2$, when n is prime and $\alpha \left(X_n^{+}\right)=\frac{n}{p_1}$, when n is an odd composite number.

(ii) 

The vertex covering number, ${\alpha }_0\left(X_n^{+}\right)=n-2$, when n is prime and ${\alpha }_0\left(X_n^{+}\right)=n-\frac{n}{p_1}$, when n is an odd composite number.

(iii) 

The edge covering number, ${\alpha }_1\left(X_n^{+}\right)=\frac{n+1}{2}$, when n is odd.

(iv) 

The matching number, ${\beta }_1\left(X_n^{+}\right)=\frac{n-1}{2}$, when n is odd.

(v) 

The edge connectivity, ${\kappa }_1\left(X_n^{+}\right)=\varphi \left(n\right)-1$, when n is odd.

(vi) 

The edge chromatic number, ${\chi }^{\prime }\left(X_n^{+}\right)=\varphi \left(n\right)$, for all n.

Based on Theorem 92, the bounds for the chromatic number and clique number of the unitary addition Cayley graph was obtained in [191], using which it was obtained that a unitary addition Cayley graph $X_n^{+}$ is perfect if and only if n is even or a prime power. This characterisation was obtained by proving that for all the other values of n, the unitary addition Cayley graph contains an induced cycle of length 5, according to its chromatic partition.

A more detailed study on the chromatic number of the unitary addition Cayley graph was done in [192], where tighter bounds for the clique and the chromatic number of the unitary addition Cayley graph $X_n^{+}$ for different values of n, based on their number theoretic properties was obtained. A coloring pattern that satisfies the bound was also given along with some examples of the unitary addition Cayley graphs to show that the bounds were sharp as well as strict.

This was followed by a study on the achromatic number of the unitary addition Cayley graph in [193], whose relation with the chromatic number of the graph is visible from the definition given as follows. The achromatic number of G, denoted by ${\chi }_{ach}\left(G\right)$, is the maximum number of colors that can be assigned to the vertices of the graph, such that the adjacent vertices are assigned different colors and any two different colors are assigned to some pair of adjacent vertices. It therefore follows that for any graph G, ${\chi }_{ach}\left(G\right)\ge \chi \left(G\right)$ (c.f. [194]).

Though the lower bounds of the chromatic number obtained in [192] can serve as the lower bounds for the achromatic number, better bounds were computed as per the maximisation condition in [193] and in a similar way, coloring patterns were given to establish the bounds as well as its tightness. In certain cases, the exact value of the achromatic number was also determined, as given below.

Theorem 94. 

[193] The achromatic number of a unitary addition Cayley graph,

$${\chi }_{ach}\left(X_n^{+}\right)=\left\{\begin{array}{cc}2,\hfill & ifn=2^k,forsomek\in \mathbb{N};\hfill \\ 1+\frac{\varphi \left(n\right)}{2}\hfill & ifn=p^k,forandoddprimepandk\in \mathbb{N};\hfill \end{array}\right.$$

Ensuing this, the domination parameters of the unitary addition Cayley graph was determined in [195,196]. In [196], the exact values of the domination number of the unitary addition Cayley graph was determined for a few values of n as given in Theorem 95 and in [196], the strong domination and the total strong domination of the graph $X_n^{+}$ was studied, where the parameters were computed for similar cases of n, which also is given in Theorem 95.

For a graph G without isolated vertices, a total dominating set of the graph is a dominating set in which every vertex of the graph is adjacent to at least one vertex in the dominating set (c.f.[29]). A vertex $v\in V\left(G\right)$strong dominates a vertex $u\in V\left(G\right)$ in a graph G, if $uv\in E\left(G\right)$ and $deg\left(u\right)\ge deg\left(v\right)$. A dominating set $S\subseteq V\left(G\right)$ in which every vertex $u\in V-S$ is strongly dominated by some vertex $v\in S$ is said to be a strong dominating set of the graph G and the minimum cardinality of a strong dominating set is the strong domination number ${\gamma }_s\left(G\right)$ of the graph G (see [197]). A total dominating set $S\subseteq V\left(G\right)$ in which every vertex $u\in V-S$ is strongly dominated by some vertex $v\in S$ said to be a total strong dominating set of a graph G and the minimum cardinality of total strong dominating set of G is called the total strong dominating number of the graph, denoted by ${\gamma }_{ts}$ (refer to [197]).

Theorem 95. 

[195,196] Let $X_n^{+}$ be the unitary addition Cayley graph and $\varphi \left(n\right)$ represent the Euler’s totient function. Then,

(i) 

$\gamma \left(X_n^{+}\right)=2$, when $n=2^r$, for some integer $r\ge 2$.

(ii) 

$\gamma \left(X_n^{+}\right)={\gamma }_s\left(X_n^{+}\right)=1$ and ${\gamma }_{ts}\left(X_n^{+}\right)=2$, when n is prime.

(iii) 

$\gamma \left(X_n^{+}\right)={\gamma }_s\left(X_n^{+}\right)=2$, when $n=2k$, where k is an odd prime.

(iv) 

$\gamma \left(X_n^{+}\right)={\gamma }_s\left(X_n^{+}\right)=\lceil \frac{n}{3}\rceil$, when n is even such that $\varphi \left(n\right)=2$.

(v) 

${\gamma }_{ts}\left(X_n^{+}\right)={\gamma }_s\left(X_n^{+}\right)=2$, when n is a prime power.

Proceeding with the study on other computational parameters of the unitary addition Cayley graphs, a few topological indices for the graph was computed in [198,199]. The Wiener index of a graph, which is the sum of shortest paths between all pairs of vertices in the graph and the hyper-Wiener index of a graph, which is the sum of the shortest distance and its square between every pair of vertices in the graph were computed in [199]. The reverse Wiener index of the graph G, given by the value $\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}diam\left(G\right)-d(u,v)$, where $d(u,v)$ is the shortest distance between two distinct vertices u and v in the graph G was computed for the unitary addition Cayley graph in [198].

By the above mentioned definition of the topological indices, it can be seen that the reverse Wiener index of a graph is closely related with the previously computed Wiener and hyper-Wiener indices. As the computation of all these topological indices required the distance between the vertices, the number of common neighbors between any two vertices in the unitary addition Cayley graph was computed in [199]. The values of all three topological indices for the graph $X_n^{+}$ that were obtained in [198,199], based on the values of n is given in Table 1, where $\varphi \left(n\right)$ denotes the Euler’s totient function.

The Wiener index of the graph $X_n^{+}$ was independently computed in [200] using an algorithm and program. Programs to draw the unitary addition Cayley graphs as well as the unitary Cayley graph of the given order and also to find the adjacency matrix and the energy of unitary addition Cayley graph was given in [200]. Also, few other topological indices for the unitary addition Cayley graphs were computed in [201,202], whose values could be derived from the entries of different matrices associated with the graph.

Apart form the study of these computational parameters, the spectra associated with different matrices defined on the graph along with their corresponding spectral properties were investigated in [203,204,205,206]. In [205], the spectral studies related to the adjacency and the Laplacian matrix was conducted, where the eigenvalues and the Laplacian eigenvalues of the unitary addition Cayley graph $X_n^{+}$ and its complement ${\overline{X^{+}}}_n$ were determined. Also, the bounds for the energy and Laplacian energy, for both these graphs were computed and it was proved that the unitary addition Cayley graph is hyperenergetic if and only if n is an odd composite number that is not a power of 3 or n is even and has at least three distinct prime factors. The characterisation for the complement of the unitary addition Cayley graph to be hyperenergetic was also given as follows.

Theorem 96. 

[205] The graph ${\overline{X^{+}}}_n$ is hyperenergetic if and only if n is odd and has at least 2 distinct prime factors.

On comparing the degree of hyperenergeticity of the unitary Cayley graph $X_n$ with the unitary addition Cayley graph $X_n^{+}$, it was seen that $X_n^{+}$ is more hyperenergetic than $X_n$. A high number theoretical approach can be seen in the proof of the results in which both the adjacency and the Laplacian spectra and their corresponding energies were obtained in [205]. This was followed by a discussion on the signless Laplacian spectrum for the graph in [206], where the results obtained can be seen to be closely related to the results in [205].

The signless Laplacian energy of the unitary addition Cayley graph was also independently examined in [204], which again had the same results, with similar proof techniques. In [204], along with the signless Laplacian energy, other derived forms of Laplacian energies such as the distance Laplacian and the signless distance Laplacian energy for the unitary addition Cayley graphs were investigated. The distance Laplacian energy and the signless distance Laplacian energy of a graph are the sum of the absolute values of the eigenvalues of the distance Laplacian and the signless distance Laplacian matrix respectively. The distance Laplacian matrix and the signless distance Laplacian matrix are correspondingly given as $D\left(v\right)-Dis\left(G\right)$ and $D\left(v\right)+Dis\left(G\right)$, where $Dis\left(G\right)$ denotes the distance matrix of the graph G and $D\left(v\right)$ denotes the diagonal matrix in which each diagonal element corresponding to a vertex v is the sum of the shortest distances from the vertex v to all the vertices of the graph (refer to [204]).

These derived Laplacian spectra were computed for the unitary addition Cayley graph $X_n^{+}$ and its complement ${\overline{X^{+}}}_n$ and the bounds for these energy values for different n were also determined. This was followed by the investigation of the $A_{\alpha }$ matrix of the unitary addition Cayley graph in [203]. The $A_{\alpha }$-matrix of a graph G is defined as $A_{\alpha }\left(G\right)=\alpha D\left(G\right)+(1-\alpha )A\left(G\right)$, $\alpha \in [0,1]$, where $D\left(G\right)$ and $A\left(G\right)$ are the degree and the adjacency matrices of G (see [203]).

In [203], the eigenvalues of the $A_{\alpha }$ matrix for the unitary addition Cayley graph $X_n^{+}$ and its complement were computed along with some bounds for these eigenvalues, when n is odd. Consequently, the $A_{\alpha }$-energy of both $X_n^{+}$ and its complement, when n is a prime power and n is even was determined along with some bounds for the $A_{\alpha }$-energy of $X_n^{+}$ and ${\overline{X^{+}}}_n$, when n is odd, from which the $A_{\alpha }$-borderenergetic and $A_{\alpha }$-hyperenergetic graphs were defined as the graphs having their $A_{\alpha }$-energy equal to the $A_{\alpha }$-energy of a complete graph and the graphs having their $A_{\alpha }$ energy greater than the $A_{\alpha }$-energy of a complete graph respectively; following which a few unitary addition Cayley graphs were classified as $A_{\alpha }$-borderenergetic and $A_{\alpha }$-hyperenergetic.

An incidence structure $\mathcal{D}=(P,B,J)$, with a point set P, block set B, and an incidence relation J is a $t-(r,k,s)$-design, where $\left|P\right|=r$, every block in B is incident with precisely k points, and every t distinct points are together incident with precisely s blocks. The code $C_{\mathbb{F}}\left(\mathcal{D}\right)$ of the structure $\mathcal{D}$ over the finite field $\mathbb{F}$ is the space spanned by the incidence vectors of the blocks over F (c.f. [207]). The notion of codes is given in higher design theory to study the relation between the elements in a design; but, this on restriction to the discrete structure of graphs, reduces to the notions related to the incidence and adjacency in a graph, like the adjacency design, incidence design, neighborhood design, etc. (refer to [208]).

If G is a k-regular graph, then the $1-\left(\right|E|,k,2)$ design with the incidence matrix of G is called the incidence design of G, where the incidence matrix, $B\left(G\right)$ of the graph G is a $\left|V\right(G\left)\right|\times \left|E\right(G\left)\right|$ binary matrix, such that the entry $b_{ij}=1$, if $v_i$ is incident with $e_j$ and 0, otherwise. A code $C_{\left|\mathbb{F}\right|}\left(G\right)$ of a graph G over a finite field $\mathbb{F}$ is the row span of the incidence matrix of the graph over $\mathbb{F}$ and the dimension of the code is the rank of the matrix over $\mathbb{F}$.

As the unitary addition Cayley graphs are regular, linear codes from the incidence matrix of the unitary addition Cayley graph $X_n^{+}$ over the field ${\mathbb{Z}}_2$ were determined in [209], by computing the main parameters of the code for the values $n=p,2p$, where p is prime. Since the incidence matrix is a binary matrix, the field considered to determine the linear code is ${\mathbb{Z}}_2$. To determine these binary linear codes, the edge connectivity, regularity and the size of the graphs were taken from the existing results, as it was stated in that the incidence code of a graph G over a field with 2 elements is a $\left[\right|E|,|V|-1,\left({\kappa }_1\left(G\right)\right){]}_2$ code, where the subscript 2 tells that the binary conversions of these integers are to be considered.

In [210,211,212], the properties of the unitary addition Cayley graph of the ring of Gaussian integers modulo n, ${\mathbb{Z}}_n\left[i\right]$ (refer to Definition 15) was investigated, where the exact values and bounds of certain parameters of the graph ${\mathbb{Z}}_n\left[i\right]$ were obtained. Note that the number of elements in the ring ${\mathbb{Z}}_n\left[i\right]$ is $n^2$, as there are n ways to fill both the real and the complex part of the number $a+ib$. Correspondingly, the number of units of the ring differs, based on the value of n.

The degrees of the vertices, the size, diameter and the girth of the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ was given in [210], based on the value of n, as mentioned in Theorem 97, from which it was characterised that the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ is a complete bipartite graph if and only if $n=2^t$, $t\in \mathbb{N}$. The traversal properties of the graph was also investigated in [210] and it was proven that the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ is always Hamiltonian and when n is even, the graph is Eulerian. It was also found that the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ is planar only for $n=1,2$.

Theorem 97 

([210]).

(i) 

The diameter of the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ is 3, if $n=kp$, where k is even and p is an odd prime or 2, otherwise.

(ii) 

The girth of the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ is 3, if n is odd and 2, when n is even.

Adding on to the study, the basic graph invariants for the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ was computed in [211,212]. Some bounds for the chromatic and the clique number of the graph was given in [212] as well as [211], which coincide with each other. In [211], the clique covering number of the unitary addition Cayley graph of ${\mathbb{Z}}_n\left[i\right]$ was determined by determining the independence number of its complement and in [212], the domination number of the graph was obtained as either 1,2 or 3, based on the value of n. A similar study was conducted on the unitary addition Cayley graphs of the ring Einstein integers modulo n, ${\mathbb{Z}}_n^e\left[i\right]$ (refer to Definition 16) in [213], where along with the basic properties and parameters of the unitary addition Cayley graphs of ${\mathbb{Z}}_n^e\left[i\right]$, a comparison between the unitary addition Cayley graphs of the rings ${\mathbb{Z}}_n\left[i\right]$ and ${\mathbb{Z}}_n^e\left[i\right]$ was also given for a better comprehension of the structure of the rings, graphs and its properties. For understanding the structure of the unitary Cayley graphs on the rings ${\mathbb{Z}}_n\left[i\right]$ and ${\mathbb{Z}}_n^e\left[i\right]$, an illustration of the same is given in Figure 10

In the literature, it can be seen that these unitary addition Cayley graphs of the rings ${\mathbb{Z}}_n\left[i\right]$ and ${\mathbb{Z}}_n^e\left[i\right]$ were independently examined in [186] and [187] respectively as the unit graphs of the corresponding rings, where almost the same invariants and the properties were examined in more detail. In the next section (Section 5), it can be seen that the unit graphs are nothing but the extension of the same definition of a unitary addition Cayley graph to a ring R, like how the unitary Cayley graph $X_n$ of ${\mathbb{Z}}_n$ was extended to all the rings R as the graph $G\left(R\right)$.

For a graph G, $S\subseteq V\left(G\right)$ is a perfect code (different from the notions of a code of a graph) of the graph if S is an independent set such that every vertex in $V\left(G\right)-S$ is adjacent to exactly one vertex in S (see [214]). The perfect codes in an induced subgraph of the unitary addition Cayley graph containing the vertices that represent the idempotent elements of the ring ${\mathbb{Z}}_n$ was examined in [215], where the question of when a subset of the idempotent elements of the ring ${\mathbb{Z}}_n$ is a perfect code in this induced subgraph of a unitary addition Cayley graph was answered.

It was shown in [215] that the subgraph of $X_n^{+}$ induced by the idempotent elements of the ring ${\mathbb{Z}}_n$ admits a perfect code of size 2 if n is a product of two prime powers, where one of the prime is even, a perfect code of size 1 if n is the product of k factors of odd prime powers, and a perfect code of size $2^{t-1}$ for the unitary addition Cayley graph on a ring which is the direct product of the factors of ${\mathbb{Z}}_{p^k}$.

Analogous to the previously discussed unitary Cayley graphs, the notion of signed algebraic graphs were investigated for the unitary addition Cayley graphs also. Similar to the case of the unitary Cayley graphs on ${\mathbb{Z}}_n$, multiple signed graphs were defined on the unitary addition Cayley graph in [216,217,218]. These definitions are given below followed by which an example of these graphs are given Figure 11.

Definition 19 

([217]). The unitary addition Cayley signed graph, denoted by $S_n^{\vee +}=(X_n^{+},{\sigma }^{\vee +})$, is a signed graph whose underlying graph is the unitary addition Cayley graph $X_n^{+}$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(X_n^{+}\right)$ is assigned by the function ${\sigma }^{\vee +}:E\left(X_n^{+}\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n^{+}$,

$${\sigma }^{\vee +}\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & if{v}_i\in {\mathbb{Z}}_n^{*}or{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 20 

([216]). The unitary addition Cayley ring signed graph, denoted by $S_n^{\oplus +}=(X_n^{+},{\sigma }^{\oplus +})$, is a signed graph whose underlying graph is the unitary addition Cayley graph $X_n^{+}$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(X_n^{+}\right)$ is assigned by the function ${\sigma }^{\oplus +}:E\left(X_n\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n^{+}$,

$${\sigma }^{\oplus +}\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & ifeither{v}_i\in {\mathbb{Z}}_n^{*}or{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 21 

([218]). The addition signed Cayley graph, denoted by $S_n^{\wedge +}=(X_n,{\sigma }^{\wedge +})$, is a signed graph whose underlying graph is the unitary addition Cayley graph $X_n^{+}$, $n\in \mathbb{N}$ and the sign of an edge $v_i{v}_j\in E\left(X_n^{+}\right)$ is assigned by the function ${\sigma }^{\wedge +}:E\left(X_n^{+}\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $X_n^{+}$,

$${\sigma }^{\wedge +}\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & ifboth{v}_i\in {\mathbb{Z}}_n^{*}and{v}_j\in {\mathbb{Z}}_n^{*};\hfill \\ -,\hfill & otherwise.\hfill \end{array}\right.$$

For all the above defined signed graphs, the properties of balance, clusterability, sign-compatibility and canonical consistence were studied in the corresponding articles. As the the graphs $X_n$ and $X_n^{+}$ coincide when n is even, the corresponding sign graphs also coincide, and so is their properties and characterisations. In [217], the unitary addition Cayley sigraph was introduced and the above mentioned properties were studied and the following characterisations were obtained.

Theorem 98 

([217]).

(i) 

The unitary addition Cayley sigraph $S_n^{\vee +}$ is balanced if and only if either n is even or it does not have more than one distinct prime factor.

(ii) 

The unitary addition Cayley sigraph $S_n^{\vee +}$ is clusterable if and only if it is balanced.

(iii) 

The unitary addition Cayley sigraph $S_n^{\vee +}$, where n has at most two distinct odd prime factors is canonically consistent if and only if n is either odd, or n is 2, 6 or a multiple of 4.

(iv) 

Every unitary addition Cayley sigraph $S_n^{\vee +}$ is sign-compatible.

It has been shown in [219] that all line signed graphs are sign-compatible. Hence, in view of (iv) in Theorem 98, the question of realising a unitary addition Cayley sigraph as a line sigraph had come up and this was answered by characterising all the unitary addition Cayley sigraph that could be realised as a line graph and also line signed graph as given in Theorem 99.

Theorem 99. 

[217] Unitary addition Cayley graph is a line graph if and only if $n\in \{2,3,4,6\}$ and is a line signed graph if and only if it is a line graph.

Similarly, the unitary addition Cayley ring signed graph and the addition signed Cayley graph were introduced and a similar properties were studied in [216] and [218] respectively. Through the results obtained on all these signed graphs defined on the unitary addition Cayley graphs, it can be seen that even though the definitions of the signed graphs differ, the properties are almost similar to each other, except a very few. It can also be noticed that in some cases, the properties of the signed graphs defined on the unitary Cayley graphs coincide with the properties of the corresponding signed graph defined on the unitary addition Cayley graphs. Along with the characterisation of the signed graphs based on the above mentioned four properties, the characterisations of these properties of balance, clusterability, etc. in certain derived signed graphs from the signed graphs like the negation of the signed graph and some variations of line signed graphs were also investigated in [213,216,217].

5. Unit Graph of a Ring

As mentioned earlier, Grimaldi had introduced the unitary addition Cayley graph as the unit graph of ${\mathbb{Z}}_n$ in [18], which remained latent for some years. This definition of the unitary addition Cayley graph of ${\mathbb{Z}}_n$ was generalised to all rings as the unit graph of a ring in [220] as follows. Note that these graphs may be referred to as Grimaldi graphs in the literature by some authors, owing to the fact that the unit graph of rings is generalised based on the graph formerly introduced by Grimaldi in [18]. Following the definition of the unit graph and the closed unit graph of a ring, examples of these graphs are given in Figure 12.

Definition 22 

([18]). The unit graph of a ring R, denoted by $G^{+}\left(R\right)=Ca{y}^{+}(R,R^{*})$, is a graph with the vertex set as the elements of the ring, and two distinct vertices are adjacent if their sum is a unit of the ring; that is, for all $u,v\in V\left(G^{+}\left(R\right)\right)$, $uv\in E\left(G^{+}\left(R\right)\right)$ when $u+v\in R^{*}$, where $R^{*}$ is the group of units of the ring R. If the word“distinct" is omitted from this definition, it gives the definition of theclosed unit graphof a ring R. That is, aclosed unit graphof a ring R is the unit graph of R, where there may be a loop from the vertex to itself in the graph if the sum of an element with itself is a unit.

Though this definition of the unit graphs is given for any associative ring with unity, it can be seen that for most of the studies, only a finite commutative ring with unity is considered, owing to the symmetric structure of these rings. Furthermore, a very limited study on the unit graphs of associative rings can be seen, as the structure of an arbitrary ring is very sophisticated to comprehend. This sophisticated structure of the ring gives rise to highly complex and diverse graphs, whose structure cannot be generalised. Therefore, it can be seen in the literature reviewed in this section that at several instances, different authors have considered rings with specific properties to obtain the results pertaining to the unit graphs of rings in their study.

Note that the unit graphs of rings are the complement of the total graphs defined on rings, which has the vertex set of the graph as the elements of the ring and two vertices are adjacent if their sum is a zero divisor. This relation between the unit and the total graph of a rings is because of the fact that every element in a ring is either a unit or the zero-divisor of the ring. Total graphs have huge literature (c.f. [12,16,221]), where certain properties of the complement of the total graphs have also been investigated. Though the complement of total graphs of rings represent the unit graphs, in this article, we review the literature that has discussed the properties of unit graphs of rings under its name only.

On observing the definition of the unit graph of a ring, it can be noticed that it is a subgraph of the comaximal graph defined on a ring R, in which the vertices are the elements of the ring any two vertices u and v are adjacent in the graph if $Ru+Rv=R$ (refer to [19]). Though certain properties of the comaximal graphs (when restricted to its subgraphs) hold for the unit graphs also, this article focuses only on the results that are specifically obtained for the unit graphs of rings.

In [220], discussions on the unit graph of rings were initiated, where the properties like the regularity, and connectedness were investigated for the unit graphs of all associative rings and some properties like diameter, girth, and planarity were investigated for the unit graphs of finite commutative rings. The unit graph of a ring was found to be either $|R^{*}|$-regular or ($|R^{*}|$,$|R^{*}|-1$)-biregular based on the unit elements of the ring.

Recall that an element of a ring R is said to be k-good if it can be expressed as a sum of k units of the ring R and a ring is said to be k-good if every element is k-good. The connectedness of the graph was characterised based on the unit sum number and the k-goodness property of the ring as given below and this discloses the fact that the unit graphs are generally not connected, as the unit sum number of not all rings are finite. Also, an interesting relation between the dominating set and the connectedness of the unit graph of rings was also obtained in [220], as stated below.

Theorem 100. 

[220] The unit graph $G^{+}\left(R\right)$ of a ring R is connected if and only if the ring is k-good for some integer $k\ge 1$ or the ring R is not k-good but every element of R is k-good, for some $k\ge 1$; that is, the units additively generate R.

Theorem 101. 

[220] If the set of all vertices that corresponds to the units of the ring form a dominating set of the unit graph of the ring, then the unit graph is connected.

The connectedness of the unit graphs of some particular rings were investigated based on the above mentioned characterisation that was obtained on the connectedness of the unit graphs. The chromatic index of the unit graph of an associative ring was also computed as $\delta +1$, where $\delta$ is the maximum degree of the vertices in the unit graph, and certain structural characterisations of the unit graph on when can the unit graph of a ring be a cycle, path, bipartite and complete bipartite graph were obtained in [220], which are given below.

Theorem 102. 

[220] The unit graph $G^{+}\left(R\right)$ of a ring R is a cycle if and only if R is either ${\mathbb{Z}}_4$, ${\mathbb{Z}}_6$ or the set of all $2\times 2$ matrices of the form $\left(\begin{array}{cc}a& b\\ 0& a\end{array}\right)$, where $a,b\in {\mathbb{Z}}_2$.

Theorem 103 

([220]).

(i) 

The unit graph of a ring R is a complete graph if and only if R is a division ring with characteristic 2.

(ii) 

The unit graph of a ring R is a complete bipartite graph if and only if R is a local ring with the maximal ideal M such that $|\frac{R}{M}|=2$.

Following this, the structure of the cliques and co-cliques (independent sets) in the unit graph of a finite commutative ring R was studied in relation with its Jacobson radical $J_R$ and the corresponding quotient ring $\frac{R}{J_R}$. In addition to it, characterisations of finite commutative rings based on their diameter, girth and planarity were also obtained in [220]. Using this structure of cliques and co-cliques and the structural realisations obtained in in [220], the unit graph of a finite commutative ring was proved to be weakly perfect in [222]; that is, for a finite commutative ring R, $\chi \left(G^{+}\left(R\right)\right)=\omega \left(G^{+}\left(R\right)\right)$, where $\chi$ and $\omega$ denote the chromatic and the clique number of the graph.

This was proved by using a series of lemmas, where finite commutative rings having different algebraic properties were considered and the corresponding unit graphs were proved to be weakly perfect by computing their clique and chromatic numbers. Owing to the fact that every finite commutative ring R is isomorphic to the direct product of local rings, and their quotient ring $\frac{R}{J_R}$ is isomorphic to the direct product of fields, the proof of the main theorem was given in two cases, based on the structure of the fields that are present in the direct product of the quotient ring $\frac{R}{J_R}$. That is, the first case was considered as no field in the local factors of $\frac{R}{J_R}$ has its characteristic 2 and the second one was the existence of at least one field in the local factors of $\frac{R}{J_R}$ with characteristic 2 in the direct product.

The structure of the unit graphs of the quotient rings $\frac{R}{J_R}$ in these cases followed the values of the clique and the chromatic number of the unit graph of obtained in [18], which correlates the structure of a ring R and its quotient ring $\frac{R}{J_R}$. Using this result, the parameters were computed and the final result was proved. This discussion of the weak perfect property led to the discussion of the property of perfection in the unit graphs of rings in [223], where the perfection of the unit graphs of finite commutative Artinian rings were examined and the results on classification of rings whose unit graphs are perfect and not-perfect were obtained.

The girth of the unit graph of any finite commutative ring R was proved to be either 3,4,6 or ∞ in [220]. This result was extended in [224] to the unit graph of any arbitrary ring and the same values were obtained as the girth of the corresponding unit graphs. On obtaining these restricted values for the girth of unit graphs, the exact girth values of the unit graph of specific rings were computed and relations between the girth of the unit graph of a ring R and $\frac{R}{J_R}$ were also established. The rings R with semipotent quotient rings $\frac{R}{J_R}$ such that the girth of the unit graph of the ring R is either 6 or ∞ were determined and some necessary conditions on the group of unit elements of a ring were obtained to realise the unit graph of the corresponding ring based on its girth. Note that a semipotent ring is a ring such that every left ideal that is not contained in the Jacobson radical of the ring contains a non-zero idempotent element

In an analogous manner, it was proved that the diameter of the unit graphs of finite commutative ring take the values 1,2,3, or ∞ in [220] and this result was extended to the unit graphs of rings that have a self-injective quotient ring $\frac{R}{J_R}$ in [225]. Recall that a ring is called self-injective if every homomorphism from the principal ideal to the ring extends to a homomorphism of the ring to itself.

As the diameter of a graph is associated with its connectedness, certain discussions on the connectedness of the unit graphs of some rings, based on their unit sum numbers were given, following which all rings that have a self-injective quotient ring $\frac{R}{J_R}$ were classified based on the values of the diameter of their unit graphs. Furthermore, characterisation of rings based on the diameter values of their unit graphs were also obtained as given in Theorem 104 and it was proved that for any integer $n\ge 1$, there exists a ring R such that $n\le diam\left(G^{+}\left(R\right)\right)\le 2n$.

Theorem 104. 

[225] For a ring R with its unit graph $G^{+}\left(R\right)$, $diam\left(G^{+}\left(R\right)\right)=2$ if and only if $usn\left(R\right)=2$ and R is not a division ring with $char\left(R\right)=2$.

As an extension to the discussions on the diameter of the unit graphs of rings, the radius of the unit graphs were investigated in [226]. It can be seen that the studies on the radius of algebraic graphs are rare when compared to the studies on the diameter, though they are closely related. This is because several graphs tend to have the minimum eccentricity one. In [226], the relation between the unit graph of a ring R and its corresponding quotient ring $\frac{R}{J_R}$ was obtained and some characterisations of rings having the radius of their unit graphs 1, 2, 3 and ∞ were given. It was also proved that for every positive integer n, there exists a ring R such that the radius of its unit graph is n. It can be seen that the investigations in [226] on the radius of the unit graphs of rings are made in a similar pattern of discussion as followed in [224,225].

This was followed by a cursory investigation on the connectedness of the complement of unit graphs of finite commutative rings in [227], where the complement of the unit graph was proved to be always connected and the following equivalent statements were obtained by relating connectedness to the dominating set and the number of the maximal ideals of the ring, based on the results obtained in [18], relating the same notions.

Theorem 105. 

For a finite commutative ring R with the set of all maximal ideals of the ring $\mathcal{M}$. Then, the following statements are equivalent.

(i) 

The complement of the unit graph $\overline{G^{+}\left(R\right)}$ is connected.

(ii) 

$\left|\mathcal{M}\right|\ge 2$.

(iii) 

$R-\left\{R^{*}\right\}$ is a dominating set of the graph $\overline{G^{+}\left(R\right)}$.

Note that Theorem 101 states the necessary condition of the set of all units to be just a dominating set, and not a minimal or a minimum dominating set of the unit graph of a ring. This conveys the possibilities of the graph having other minimal dominating sets, which may possibly be a subset of the set of all vertices that represent the units of the ring also and this led to the investigation of the domination numbers in the unit graphs of rings. In [228], the finite commutative rings that have domination number less than 4 were characterised as given in Theorem 106, by studying the domination number of the unit graphs of fields, product of fields, rings, local rings, etc. The unit graphs of the product of local rings were also investigated by considering the cases of certain special rings as local factors, where these special rings have unit graphs with structural properties that shall influence the structure of the overall unit graph of the ring.

Theorem 106. 

[228] Let R be a finite commutative ring with the unit graph $G^{+}\left(R\right)$. Then,

(i) 

$\gamma \left(G^{+}\left(R\right)\right)=1$ if and only if R is a field.

(ii) 

$\gamma \left(G^{+}\left(R\right)\right)=2$ if and only if either R is a local ring that is not a field or R is isomorphic to the product of two fields such that only one of them have characteristic 2 or $R\cong {\mathbb{Z}}_2\times \mathbb{F}$, where $\mathbb{F}$ is a finite field.

(iii) 

$\gamma \left(G^{+}\left(R\right)\right)=3$ if and only if R is not isomorphic to the product of two fields such that only one of them have characteristic 2 and $R\cong R_1\times R_2$, where $R_1$ and $R_2$ are local rings with maximal ideals $M_1$ and $M_2$, respectively such that their quotient rings are not isomorphic to ${\mathbb{Z}}_2$.

The concept of domination in unit graphs was also studied in [229], where the motive of the study was to characterise commutative rings that have the domination number of their unit graphs as half their order; that is, to characterise rings such that $\gamma \left(G^{+}\left(R\right)\right)=\frac{\left|R\right|}{2}$ or $\gamma \left(G^{+}\left(R\right)\right)=\frac{\left|R\right|-1}{2}$. A characterisation of the former one was obtained completely as given in Theorem 107, whereas the latter problem was solved partially, considering only the rings of integer modulo n.

Theorem 107. 

[228] Let R be a finite commutative ring with the unit graph $G^{+}\left(R\right)$. Then, $\gamma \left(G^{+}\left(R\right)\right)=\frac{\left|R\right|}{2}$ if and only if $R\cong \underset{t-times}{\underbrace{{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times \dots \times {\mathbb{Z}}_2}}\times S$, $t\ge 0$, where S is is either ${\mathbb{Z}}_2$, ${\mathbb{Z}}_4$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{\langle x\rangle }$.

An open problem to determine the existence of a ring R such that given an integer n, the unit graph has domination number n was put forth in [229]. Though the question is yet to be fully answered, in the same article, it was concluded that for integers of the form $2^k$, $k\ge 0$, there exists a ring R such that $\gamma \left(G^{+}\left(R\right)\right)=2^k$, using the results obtained in that article. Continuing the investigation on the domination number of the unit graphs of rings, the study in [230] examined the domination number of the unit graph $G^{+}\left(R\right)$ of a ring $R\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\times {\mathbb{Z}}_{p_2^{{\alpha }_2}}\times {\mathbb{Z}}_{p_3^{{\alpha }_3}}$, where $p_i$; $1\le p\le 3$ are primes was computed and the following characterisations were obtained in [230].

Theorem 108. 

[230] Let $R\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\times {\mathbb{Z}}_{p_2^{{\alpha }_2}}\times {\mathbb{Z}}_{p_3^{{\alpha }_3}}$, where $p_i$; $1\le p\le 3$ and $p_1<p_2<p_3$ are primes and $G^{+}\left(R\right)$ be its unit graph having domination number $\gamma \left(G^{+}\left(R\right)\right)$. Then,

(i) 

$4\le \gamma \left(G^{+}\left(R\right)\right)\le 6$.

(ii) 

$\gamma \left(G^{+}\left(R\right)\right)=4$ if and only if ${\alpha }_1={\alpha }_2={\alpha }_3=1$ or $p_1>3$.

(iii) 

$\gamma \left(G^{+}\left(R\right)\right)=5$ if and only if ${\alpha }_1{\alpha }_2{\alpha }_3\ge 2$ or $p_1=3$.

(iv) 

$\gamma \left(G^{+}\left(R\right)\right)=6$ if and only if ${\alpha }_1{\alpha }_2{\alpha }_3\ge 2$ or $p_1=2$.

In [231], a relation between the domination number as well as the total domination number of the unit graph of a ring R and its Ore’s extension $R[x;{\alpha }_1,{\alpha }_2]$; the ring of polynomials over R with usual addition and multiplication defined as the relation $xy={\alpha }_1\left(y\right)x+{\alpha }_2\left(y\right)$, were studied and it was obtained that for all associative rings, ${\gamma }_t\left(G^{+}\left(R\right)\right)={\gamma }_t\left(G^{+}\left(R[x;{\alpha }_1,{\alpha }_2]\right)\right)$, where ${\gamma }_t$ denotes the total domination number of the graph.

Based on this, an open problem to investigate if the same equality holds for the domination number of the unit graphs of all associative rings and their Ore’s extension. That is, to check if $\gamma \left(G^{+}\left(R\right)\right)=\gamma \left(G^{+}\left(R[x;{\alpha }_1,{\alpha }_2]\right)\right)$, for all associative rings, was posed in [231]. Note that in the former study, the rings considered were the general associative ring and were not restricted to the finite commutative rings, whereas several bounds for the domination number of the unit graphs of only the finite commutative rings were obtained in [232], using the existing results on the domination number of the unit graphs of rings.

Examining planarity in algebraic graphs has caught the attention of several researchers, due to which for any new algebraic graph defined, these algebraic structures are characterised based on the planarity of the algebraic graphs introduced. Such characterisations of finite commutative rings for which the unit graph is planar was obtained in [220] (Theorem 109). This was followed by characterising any associative ring whose unit graph is planar in [233], which was determined based on mainly the order of the ring and its unit group, along with the structure of the ring, as given in Theorem 110 and as an application of the obtained result, all semipotent rings whose unit graphs are planar were characterised in [234] and based on this, a list of all semilocal rings with planar unit graphs were obtained. Recall that a semipotent ring is a ring such that every left ideal that is not contained in the Jacobson radical of the ring contains a non-zero idempotent element and a semilocal ring is a commutative Noetherian ring with finitely many maximal ideals, where a ring is called Noetherian if every ideal of the ring is finitely generated.

Theorem 109. 

[220] Let R be a finite commutative ring with the unit graph $G^{+}\left(R\right)$. Then, $G^{+}\left(R\right)$ is planar if and only if R is either ${\mathbb{Z}}_5$, ${\mathbb{Z}}_3\times {\mathbb{Z}}_3$ or S is isomorphic to one of the following rings.

(i) 

${\mathbb{Z}}_2$,

(ii) 

${\mathbb{Z}}_3$,

(iii) 

${\mathbb{Z}}_4$,

(iv) 

${\mathbb{F}}_4$,

(iv) 

The set of all $2\times 2$ matrices of the form $\left(\begin{array}{cc}a& b\\ 0& a\end{array}\right)$, where $a,b\in {\mathbb{Z}}_2$.

Theorem 110. 

[223] Let R be an associative ring with the unit graph $G^{+}\left(R\right)$ and the group of units $R^{*}$. Then, $G^{+}\left(R\right)$ is planar if and only if one of the following holds.

(i) 

$|R^{*}|<4$ and $\left|R\right|\le \left|\mathbb{R}\right|$,

(ii) 

$|R^{*}|=4$ and $char\left(R\right)=0$ with $\left|R\right|\le \left|\mathbb{R}\right|$,

(iii) 

$R\cong {\mathbb{Z}}_5$,

(iv) 

$R\cong {\mathbb{Z}}_3\times {\mathbb{Z}}_3$.

The planarity of the unit graphs of some local and quasilocal rings were examined in [235,236,237], where a commutative ring R which has only a finite number of maximal ideals is referred to as a quasilocal ring and a ring with a unique maximal ideal is a local ring. In [234], a characterisation of finite quasilocal rings that have planar unit graphs was obtained and it was proved that if the unit graph of a quasilocal ring is planar, then the ring is finite. This was proved by considering rings of two cases, where the first one is when the ring has exactly two maximal ideals and the second case is when the quasilocal ring has more than two, but finitely many ideals. These cases were investigated one each in [236,237] respectively.

In succession to the planar unit graphs, the non-planar unit graphs of finite commutative rings that have genus 1 were investigated in [238], where all finite commutative rings with non-zero identity whose unit graphs are toroidal were determined, up to isomorphism and it was proved that for any positive integer k, the are finitely many number of finite commutative rings with non-zero identity such that the genus of their unit graph is k. As a continuation of the study on the unit graphs of finite commutative rings with unit genus, the rings having unit graphs with higher order genus were investigated in [239] and all finite rings with unit graphs having genus 1, 2 and 3 were characterised.

As the spectra of algebraic graphs are another area of keen interest to the researchers, the adjacency spectrum of the closed unit graph was computed in [240], based on the properties of the closed unit graphs obtained in [220]. The cases when the unit and closed unit graphs coincide with each other as well as few structural properties of the closed unit graphs, when they do not coincide with the unit graph of the corresponding ring were determined in [220]. Utilising these results and properties from [220], especially the result that establishes that the closed unit graph of product of two rings is the direct product of the closed unit graphs of the corresponding rings, which arouse as a consequence of the structure theorem (refer to [26]), the spectra of the closed unit graphs of arbitrary finite rings and their quotient rings $\frac{R}{J_R}$ were determined. Using the spectral values, it was shown that the unit graphs $G^{+}\left(R_1\right)$ and $G^{+}\left(R_2\right)$ of two arbitrary finite rings $R_1$ and $R_2$ are isomorphic if and only if the unit graphs of their corresponding quotient rings $G^{+}\left(\frac{R_1}{J_{R_1}}\right)$ and $G^{+}\left(\frac{R_2}{J_{R_2}}\right)$ are isomorphic.

As the closed unit graph and unit graph of rings coincide in a good number of cases, this spectra can also be taken as the spectra of the unit graphs and based on that, the rings whose unit graphs are Ramanujan graphs were determined, using which a necessary and sufficient condition for the unit graph of a ring to be strongly regular was established in [240] as follows

Theorem 111. 

[240] For a ring R with the unit graph $G^{+}\left(R\right)$, the following statements are equivalent.

(i) 

$G^{+}\left(R\right)$ is a strongly regular graph.

(ii) 

R is a local ring with the maximal ideal M such that $Char\left(\frac{R}{M}\right)=2$ or $R\in \{{\mathbb{Z}}_2^t,\mathbb{F}\times \mathbb{F}\}$, where $\mathbb{F}$ is a field with $\left|\mathbb{F}\right|=2^k$, where $t,k\ge 2$.

A biclique is a complete bipartite subgraph of a graph G and a collection of subgraphs of G is called a biclique partition covering of a graph G if every subgraph in the collection is a biclique and for every edge in the graph, there exists exactly one biclique in the collection to which the edge belongs to. The biclique partition number of a graph G, denoted by $bp\left(G\right)$, is the minimum cardinality among the biclique covers of the graph (refer to [241]). There are several applications of this parameter in networks, but one of the main motivation to study this parameter in graphs is to minimise the storage space, as listing the subgraphs in a minimum complete bipartite decomposition of G consumes less space than the adjacency list representation.

If $a_{+}\left(G\right)$ and $a_{-}\left(G\right)$ denote the number of positive and negative eigenvalues in the adjacency spectrum of the graph G, then the graph is said to be eigensharp (almost eigensharp) when $bp\left(G\right)=max\{a_{+}\left(G\right),a_{-}\left(G\right)\}$ ($bp\left(G\right)=max\{a_{+}\left(G\right),a_{-}\left(G\right)\}+1$) (For more details on the eigensharp properties of graphs, c.f.[242]). In [243], the rings that have eigensharp unit graphs were investigated and by computing the adjacency spectrum and the corresponding biclique numbers, using the structural properties of the rings determined in [220], it was found that for prime p, the rings ${\mathbb{Z}}_p$, ${\mathbb{Z}}_{2p}$ and $\frac{{\mathbb{Z}}_p\left[x\right]}{\langle x^2\rangle }$ are eigensharp graphs. The authors had also posted the problem to check if the unit graphs of rings ${\mathbb{Z}}_{p^n}$, ${\mathbb{Z}}_{qp}$ and $\frac{{\mathbb{Z}}_p\left[x\right]}{\langle x^n\rangle }$, for prime p and q are eigensharp, which still remains unsolved.

The other computational parameters that were determined for the unit graph of finite commutative rings are the topological indices namely, the Wiener index and the hyper-Wiener index. These topological indices were computed for the unitary addition Cayley graphs in[199] and in [244] these results were extended to the unit graphs of all finite commutative rings and from these results, the values of these indices for the graph $X_n^{+}$ were computed by considering the finite commutative ring R as ${\mathbb{Z}}_n$.

The other graph properties like the well-coveredness, Hamiltonicity and chordality of the unit graphs of rings were examined in [245,246] and [247], respectively. In [246], a necessary and sufficient condition for the unit graph of a finite commutative ring to be Hamiltonian was derived, by constructing a graph based on the structural properties of the rings whose unit graph is connected as obtained in [220]. As connectedness of the unit graph of a ring was given based on the unit sum number of the ring, a set of equivalent statements involving all these aspects of the ring was given in [246] as follows.

Theorem 112. 

[246] Let R be a finite commutative ring R that is not isomorphic to ${\mathbb{Z}}_2$ and ${\mathbb{Z}}_3$, with unit graph $G^{+}\left(R\right)$. Then, the following statements are equivalent.

(i) 

$G^{+}\left(R\right)$ is Hamiltonian.

(ii) 

The ring R cannot have ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ as a quotient ring.

(iii) 

The R is generated by its units.

(iv) 

$G^{+}\left(R\right)$ is connected.

Followed by the study on Hamiltonicity, the chordality in the unit graphs of finite commutative rings was studied in [247], where the rings having quotient ring $\frac{R}{J_R}$ as a product of fields were characterised based on the chordality of the unit graphs and in [245], a necessary and sufficient condition under which the unit graphs of finite commutative rings are well-covered was deduced, using which the unit graphs whose edge rings are Cohen–Macaulay and Gorenstein were characterised as given in Theorem 113. This characterisation led to the identification of a large class of non-Cohen–Macaulay graphs.

Theorem 113. 

[246] Let R be a finite commutative ring R with unit graph $G^{+}\left(R\right)$. Then,

(i) 

$G^{+}\left(R\right)$ is Cohen-Macaulay if and only if R is a field with characteristic 2 or $R\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times \dots \times {\mathbb{Z}}_2$.

(ii) 

$G^{+}\left(R\right)$ is Gorenstein if and only if $R\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times \dots \times {\mathbb{Z}}_2$.

A graph G is called realisable as an algebraic graph (unit graph) if it is isomorphic to the algebraic graph defined (unit graph $G^{+}\left(R\right)$, for some ring R). As already mentioned, two prominent problems that exists for any algebraic graph introduced are to analyse the graph parameters of the newly introduced graph and to check if any given graph G can be realised as the defined algebraic graph. A partial solution to the second problem of realising the given graph structure as a unit graph of a ring was given in [248], where the classes of graphs which can be realised as a unit graph were determined as given below.

Theorem 114 

([248]).

(i) 

$P_n$ is realisable as a unit graph if and only if $n=2,3$.

(ii) 

$C_n$ is realisable as a unit graph if and only if $n=4,6$.

(iii) 

$K_n$ is realisable as a unit graph if and only if $n=2^k$, for some a positive integer k.

(iv) 

$K_{s_1,s_2}$ is realisable as a unit graph if and only if $s_1=s_2=2^k$, $k\in \mathbb{N}$ or $s_1=1$ and $s_2=3$.

It can be seen that the graph realisations in Theorem 114 is given based on the results obtained in [220], where the rings were characterised based on the unit graph’s structure as given in Theorems 102 and 103. While using Theorem 102 and Theorem 103 for obtaining further realisations of the unit graphs, the authors of [248] observed that the characterisation of rings whose unit graph is complete bipartite was incomplete, as there emerged an ambiguity if authors of [220] have assumed that the ring R as a local ring with or without the condition $|\frac{R}{M}|=2$, where M is the maximal ideal of the local ring. On both the cases of this assumption, counterexamples of rings with the corresponding properties were obtained in [248], which led to a modification of the existing result.

In the case that such a ring for which $|\frac{R}{M}|\ne 2$ was considered in [18] to prove the result that was given in [18], a counterexample of a field with 4 elements, say ${\mathbb{F}}_4$, whose unit graph is $K_4$, which is not complete bipartite was given in [248], and on the other hand, if R was considered as a local ring with condition $|\frac{R}{M}|=2$, the result was proved to be incorrect because, if $R\cong {\mathbb{Z}}_3,$ then $G^{+}\left(R\right)\cong K_{1,2}$, which is a complete bipartite. Based on these observations, the result was modified in [248], by including the condition $|\frac{R}{M}|\ne 2$ or $R\cong {\mathbb{Z}}_3$, along with the existing statement that was given in [220].

Recollect that for a graph G, $S\subseteq V\left(G\right)$ is a perfect code of the graph if S is an independent set such that every vertex in $V\left(G\right)-S$ is adjacent to exactly one vertex in S. A perfect code can also be called as an efficient independent dominating set (c.f.[214]). By the definition of a perfect code, the investigation of perfect codes can be seen as computing a variant of the domination number of a graph and in [249], perfect codes in the unit graphs were examined, where the rings were characterised first based on the existence of a perfect code in their unit graphs or their complements, as finding whether a graph admits perfect code is also a question to be addressed. Following this characterisation of rings, the commutative rings with identity in which their associated unit graphs accept perfect codes of order 1 and 2 were characterised and few results relating the structure of the perfect code and the structure of the rings were obtained.

This study was extended to investigate the perfect codes in the induced subgraph of the unit graph of finite commutative rings in [250], where the subgraph of the unit graph of a ring induced by the set of all vertices that represent the elements of the ring that are not units of the ring was considered. Here, the commutative rings in which their associated induced subgraphs of unit graphs admit the trivial and non-trivial perfect codes were classified and a characterisation of rings that do not admit perfect codes in this induced subgraph of their unit graph was also deduced. Furthermore, it was proved that the complement of this induced subgraph of the unit graph of finite commutative rings admits only the trivial subring perfect code, where a subring perfect code means the perfect code on a subgraph induced by a subring of the ring. A similar investigation on some other induced subgraphs of the unit graph of commutative rings was conducted in [251], whose results are analogous to the ones obtained in [250], even though the vertex set of the subgraphs induced differ. This gives an underlying property of the unit graph of the ring itself rather than the subgraphs.

A Boolean ring is a ring with identity in which every element is idempotent. Perfect codes in the unit graph of Boolean rings were investigated in [252,253], where the existence of a subring perfect code in the unit graphs associated with the finite Boolean rings was proved in [252], along with which a necessary and sufficient condition for a subring of an infinite Boolean ring to admit a perfect code of size infinity in the unit graph was also obtained. In [253], the perfect codes in spanning subgraphs of a unit graph associated with a Boolean ring R of order $2^k$, for some positive integer $k\ge 1$ was determined and as a consequence of it, sharp lower and upper bounds for the cardinality of a subset of the vertex set to be a perfect code in spanning subgraphs of a unit graph was established.

The line graph of a graph is a well-studied derived graph of a graph and as already known, several properties of the line graph of a graph are interrelated with the properties of the graph. In this regard, the line graph of the unit graphs associated with the finite commutative rings was exclusively studied in [254,255,256]. The basic properties of the line graph of the unit graph of finite commutative rings like the diameter, girth, clique, and chromatic number, along with some classifications of rings whose unit graphs are planar and Hamiltonian were given in [255]. Observe that almost all the results in this article [255], are deduced based on the properties of the unit graphs that were discussed in [220].

An extended investigation on the line graph of the unit graph associated with finite commutative rings was done in [254], where characterisations of the line graphs of the unit graphs of rings on the basis of their structural properties like the completeness, bipartiteness, traversability, diameter, girth, and chromatic number were obtained. Also, the domination number of this line graph of the unit graph of rings was computed in [229] along with the domination number of the unit graphs of rings. Significant and curious problems of identifying the structure of the unit graph of a given finite commutative ring as a line graph of some graph, as well as identifying the finite commutative rings for which the complement of the unit graph can be realised as a line graph of a graph was addressed in [256] and the list of rings of order 2, 3, and 4 with these realisation conditions were given.

For better understanding of the structure of the graph based on the structure of the ring, the unit graphs of certain specific rings whose structures are well known were investigated in detail. In [257], the unit graph of the ring ${\mathbb{Z}}_r\times {\mathbb{Z}}_s$, for any $r,s\in \mathbb{N}$, was discussed exclusively, where the basic structural and traversal properties of the graph $G^{+}({\mathbb{Z}}_r\times {\mathbb{Z}}_s)$ and its graph invariants were determined. Similarly, in [258], the rings of polynomials and power series over a ring were examined and all standard properties and invariants of the unit graph of these rings were obtained, along with some results on the planarity of the graph also.

In [259], the unit graphs of group rings were discussed, where if $\mathcal{G}$ is a group and R is a ring, group ring of $\mathcal{G}$ over R, denoted by $R\left[\mathcal{G}\right]$, is a generalisation of a given multiplicative group, by attaching to each element of the group a “weighting factor" from a given ring. It is a set of mappings with certain properties involving module operations. The basic graph invariants and certain structural properties of the unit graph of these rings were deduced in [259]. As a detailed conceptual understanding of the group rings can be obtained, only with the knowledge on the structure of modules, we refer the reader to [260,261], for more details on group rings.

For most of the study on the unit graphs of rings that had been conducted, it can be seen that the unit graphs of finite commutative rings were considered and in few instances, the unit graph of an associative ring was considered. As already mentioned, this is because of the symmetric nature of the commutative rings. In [262], the unit graph of a left Artinian ring was exclusively examined and the connectedness, girth and the diameter of the unit graph of this ring were determined. Also, the conditions under which the unit graph of any finite ring is Hamiltonian was obtained in [262] by providing an algorithm that finds a spanning cycle of the unit graph, which takes the required end points as the input and provides the corresponding Hamiltonian cycle. In [263], a short discussion on the unit graphs of non-commutative rings was given, wherein a very few results of the unit graphs of commutative rings were extended by proving it without using the commutative property of the ring. With this study, the challenge to investigate the unit graphs associated with non-commutative rings was clearly visible.

The signed graph of the unit graph of rings was defined in [306] as given in Definition 23 and an example of the graph is given in Figure 13. The rings for which this signed unit graph is balanced were characterised in [306] and the line signed graphs of these signed unit graphs were investigated in [264], where the commutative rings with unity for which line signed graph of a signed unit graph is balanced and consistent were characterised, by establishing some sufficient conditions for balance and consistency of line signed graph of signed unit graphs.

Definition 23 

([306]). Thesigned unit graph, denoted by $S\left(G^{+}\left(R\right)\right)=(G^{+}\left(R\right),{\sigma }^{+})$, is a signed graph whose underlying graph is the unit graph $G^{+}\left(R\right)$ of the ring R and the sign of an edge $v_i{v}_j\in E\left(G^{+}\left(R\right)\right)$ is assigned by the function ${\sigma }^{+}:E\left(G^{+}\left(R\right)\right)\to \{+,-\}$ as follows. For an edge $v_i{v}_j$ in $G^{+}\left(R\right)$,

$${\sigma }^{+}\left(v_i{v}_j\right)\left\{\begin{array}{cc}+,\hfill & if{v}_i\in R^{*}or{v}_j\in R^{*};\hfill \\ -,\hfill & otherwise,\hfill \end{array}\right.$$

where $R^{*}$ denotes the group of units of the ring.

An independent investigation on the signed unit graphs of the rings of the form ${\mathbb{Z}}_{p_1}\times {\mathbb{Z}}_{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_r^{{\alpha }_r}}$, where $p_i$, $1\le i\le r$ are prime numbers and $r\in \mathbb{N}$, was done in [265]. In this article, the sign compatibility, balance and clusterability of the unit graphs of these rings were discussed and the rings were characterised according to the above mentioned properties.

It can be seen in the literature that several surveys and brief literature reviews of the investigations on the unit graphs of rings had been done periodically from the time of introduction of these graphs (c.f. [162,266,267]), to understand the dynamics of research problems proposed and addressed on the unit graphs of rings. Further, since the unitary addition Cayley graphs also possess the same definition, the unit graphs of some rings are sometimes addressed as the unitary addition Cayley graphs of the respective ring, and are investigated along with the unitary Cayley graphs and such articles, where more than one graph among the graphs given in the review are discussed are included in the section of the first graph that is discussed, with appropriate explanation and cross-referencing. Also, it can be noticed that not several investigations have been done on the closed unit graphs of rings, unlike the unit graphs. This provides an area to explore on this pseudo-graph structure.

6. Other Cayley Graphs Defined on Rings

Towards the end of eighteenth century, the Cayley graph was defined on groups such that the vertex set of the graph is the elements of the group and the adjacency condition was defined with respect to a symmetric subset of the group. This was considered as an underlying principle to define a Cayley graph on any algebraic structure, and multiple variations of Cayley graphs were defined on algebraic structures, based on several of its well-known symmetric subsets. In this article, as we deal with rings, we collect the literature on different Cayley graphs defined on rings, based on various symmetric subsets of the ring and provide a brief review in this section.

As we can observe, ${\mathbb{Z}}_n$ is one of the most comprehend-able ring structure and the properties of any symmetric subset of this ring is related to the number theoretic properties of n. Owing to this, it can be seen that several Cayley graph variations are defined on ${\mathbb{Z}}_n$ and investigated as the first step, following which, the definitions are extended to a general ring, based on the feasibility of investigation. Though almost all the graph definitions on ${\mathbb{Z}}_n$ can be extended to any ring R, the process of investigating these graphs for any general ring is highly challenging as the graph properties depend on the algebraic structure of the ring. Also, even in the articles where the definitions are extended to a general ring R, it can be observed that the commutative ring with unity, local rings, and rings that can be factorised into product of local rings are mainly considered for determining the properties of these graphs.

In this section, we denote the different Cayley graphs graph by the notation $\xi$ with an appropriate suffix, corresponding to the property using which the graph is defined, for brevity and uniformity. Also, the symmetric subset considered are denoted by S is all the subsections, where in each subsection the set S corresponds to the symmetric subset considered to define the corresponding graph in that subsection.

6.1. Absorption Cayley Graphs

The absorption Cayley graph of the ring ${\mathbb{Z}}_n$ was introduced and studied in [268,269]. As the name conveys, this variant of Cayley graph is defined based on the absorption property of the elements in the ring as given below, following which an example of an absorption Cayley graph is given in Figure 14.

Definition 24 

([269]). TheAbsorption Cayley graph, denoted by ${\xi }_n^{acg}=Cay({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their sum is an element of the set S, where $S=\{x\in {\mathbb{Z}}_n:xy=yx=x,andx\ne y,y\in {\mathbb{Z}}_n\}$. That is, for all $u,v\in V\left({\xi }_n^{acg}\right)$, $uv\in E\left({\xi }_n^{acg}\right)$ when $u+v\in S$, where S is the set of all elements in the ring such that it absorbs some element in the ring, except for itself.

As the graph is defined on the subset formed by all the elements of the ring that absorbs some other element of the ring, the properties of this set was first discussed in [269]. The cardinality of this set and the properties of the elements in the set were discussed and it was found that for $n=2k$, where k is odd, this subset $S\subseteq {\mathbb{Z}}_n$ coincides with the set of zero-divisors of the ring. Following this, the subset was proved to be a subgroup of the group ${\mathbb{Z}}_n$, which verified that the graph defined is with respect to a symmetric subset of the ring ${\mathbb{Z}}_n$.

We know that both, the adjacency matrix of a graph as well as the Cayley table of a group are symmetric, such that each entry in a particular row and the corresponding column is unique. An interesting relation was seen between the adjacency matrix of the absorption Cayley graph of ${\mathbb{Z}}_n$ and the Cayley table of ${\mathbb{Z}}_n$. That is, if each element $a\in S$ is replaced with 1 in the Cayley table and all the other elements, including the diagonals are given 0, the adjacency matrix for the absorption Cayley graph of ${\mathbb{Z}}_n$ could be obtained. As the absorption Cayley graph is defined based on the sum of two elements belonging to the symmetric subset, an interesting relation between the unitary addition Cayley graphs and the absorption Cayley graphs was given in [269] as follows.

Theorem 115. 

[268,269] Let k be an odd integer. For $n\ne 2k$, the complement of the unitary addition Cayley graphs ${\overline{X}}_n^{+}$ is isomorphic to the absorption Cayley graphs ${\xi }_n^{acg}$.

Several graph parameters of the graph ${\xi }_n^{acg}$ were computed in [269] as given in Theorem 116, along with the investigation on the connectedness, traversal properties, perfection and planarity of the graph, as given below. Owing to the relation between the unitary addition Cayley graphs and the absorption Cayley graphs, only the results on absorption Cayley graphs, which are not derived exactly from the properties of the unitary addition Cayley graphs are stated in this subsection.

Theorem 116. 

[268,269] Let ${\xi }_{acg}^n=Cay({\mathbb{Z}}_n,S)$ be the absorption Cayley graph of the ring ${\mathbb{Z}}_n$. Then,

(i) 

The graph ${\xi }_n^{acg}$ is either $\left|S\right|-1$-regular or $\left(\right|S|,|S|-1)$-semi regular.

(ii) 

$|E\left({\xi }_n^{acg}\right)|=k\lceil \frac{n-1}{2}\rceil +\left(\right|S|-k)\left(\lceil \frac{n-1}{2}\rceil -1\right)$, where k is the number of odd elements in S.

(iii) 

$diam\left({\xi }_n^{acg}\right)=2$.

(iv) 

The edge connectivity of ${\xi }_n^{acg}$, when connected, is $\left|S\right|-1$.

(v) 

The girth of ${\xi }_n^{acg}$ (when connected) is 4, when $n=6$ or 3, otherwise.

Theorem 117. 

[268,269]

(i) 

An absorption graph ${\xi }_{acg}^n$ is connected if and only if n has at least two distinct prime factors.

(ii) 

An absorption graph ${\xi }_{acg}^n$ is disconnected if and only if $n=p^k$, where p is prime and $k\ge 1$ is an integer.

(iii) 

The number of components in a disconnected absorption Cayley graph ${\xi }_n^{acg}$ is $\frac{n-1}{2}$, when n is prime and 2, otherwise.

Theorem 118. 

[268,269]

(i) 

An absorption Cayley graph is never Eulerian.

(ii) 

An absorption Cayley graph ${\xi }_n^{acg}$ is Hamiltonian if $\left|S\right|>\frac{n}{2}$, where $n\ne 2k$, for some odd integer k.

It can be observed that due to the strong perfect graph theorem that states that a graph is perfect if and only if the graph as well as its complement does not contain any induced cycle of odd length at least 5, and Theorem 115, the conditions for the perfection of the graph ${\xi }_n^{acg}$ coincides with that of the unitary addition Cayley graphs.

Theorem 119. 

[268,269] The absorption Cayley graph of the ring ${\mathbb{Z}}_n$ is planar if and only if $n\in \{2,4,6,8,p\}$, where p is a prime number.

An important question that arises on defining a new algebraic graph is the realisation of a given graph as the defined algebraic graph; that is, in this context, the question will be, when can a graph of order n be realised as an absorption Cayley graph of order n? This was answered in [268,269] as follows.

Theorem 120. 

[268,269] A given graph G of order n is isomorphic to an absorption Cayley graph ${\xi }_n^{acg}$ if and only if there are $\left|S\right|$ edge disjoint subgraphs of the graph G, say $G_1,G_2,\dots ,G_{\left|S\right|}$, whose union is the graph G, such that the following conditions hold.

(i) 

$ab\in E\left(G_i\right)$ if and only if $a+b\equiv imodn.$

(ii) 

$|E\left(G_i\right)|=\lceil \frac{n-1}{2}\rceil -1$, when i is even and $\lceil \frac{n-1}{2}\rceil$, when n is odd.

Owing to Theorem 120 and the fact that the absorption Cayley graph is disconnected, the structure of the components of a disconnected absorption Cayley graphs was also examined in [269] and it was observed that these disconnected components are the union of subgraphs that are generated by the prime factors of n, which are nothing but disjoint cliques. This gave rise to the characterisation that an absorption Cayley graph ${\xi }_n^{acg}$ is bipartite if and only if n is prime, as $S=\left\{0\right\}$, when n is prime.

As the graph coincides with the unitary addition Cayley graph, in some cases and the zero-divisor Cayley graphs (see SubSection 6.6), for some values of n, the existing literature on these graphs determine most of the properties of them, which curtails the scope of unique study on this graph. Also, in the remaining cases, it was seen that the graph was a union of disjoint cliques, which also does not extend much scope for further exploration.

6.2. Nilpotent Cayley Graphs

The nilpotent Cayley graph of the ring ${\mathbb{Z}}_n$ was introduced in [270] and was studied in [270,271]. As the name suggests, this variant of Cayley graph is defined based on the subset of all nilpotent elements of the ring, as given below. Recall that an element x of a ring is said to be nilpotent if there exists a positive integer k, called the index, such that $x^k=0$, where 0 is the additive identity of the ring.

Note that there are different graphs defined as the nilpotent and non-nilpotent graph of a ring having different vertex sets like the set of all nilpotent elements, non-nilpotent elements etc. or they have been defined based on the product operation of the ring. We donot consider them for the review because we restrict ourselves to the graphs defined on rings that are analogous to Cayley graphs. In other words, the vertex set of the graph to be the elements of the rings, where the adjacency condition is defined based on either the sum or the difference of two elements that has to belong to a symmetric subset.

Definition 25 

([270]). Thenilpotent Cayley graphof the ring ${\mathbb{Z}}_n$, denoted by ${\xi }_n^{nil}=Cay({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is an element of the set S, where $S=\{x\ne 0\in {\mathbb{Z}}_n:x^k=0,forsomek\in \mathbb{N}\}$. That is, for all $u,v\in V\left({\xi }_n^{nil}\right)$, $uv\in E\left({\xi }_n^{nil}\right)$, when $u-v\in S$, where S is the set of all non-zero nilpotent elements of the ring. An example of a nilpotent Cayley graph is given in Figure 15.

The properties of the set of all nilpotent elements and the basic graph properties for the nilpotent Cayley graphs of ${\mathbb{Z}}_n$ were studied in [270], where the number of nilpotent elements in the ring ${\mathbb{Z}}_n$ was given, using which the regularity and size of the nilpotent Cayley graph was determined. It was also proved that for any integer which is a product of distinct prime numbers, the nilpotent Cayley graph is a null graph, which gave rise to the problem of investigating the connectedness of the graph. On solving this problem, it was found that the nilpotent Cayley graph is disconnected in some cases, for which the number of components in the graph was determined in [270] and each component was proved to be a clique. This led to the result that the nilpotent Cayley graph of ${\mathbb{Z}}_n$ is a union of k disjoint cliques, where k is the product of all distinct prime factors of n. The number of triangles in this graph was also enumerated in [270] based on the number of nilpotent elements in the ring.

The study on the nilpotent Cayley graph of ${\mathbb{Z}}_n$ was extended in [271], by investigating the neighborhood set and the neighborhood graph of the nilpotent Cayley graph. A subset $S\subseteq V\left(G\right)$ is called a neighborhood set of the graph G, if $G=\bigcup _{v\in S}\langle N\left[v\right]\rangle$, where $\langle N\left[v\right]\rangle$ is the subgraph induced by the closed neighborhood $N\left[v\right]$ of the vertex v, and the cardinality of a minimum neighborhood set is called the neighborhood number of the graph. The neighborhood graph $N\left[G\right]$ of a graph G is a graph with the same vertex as G and two vertices u and v are adjacent in $N\left[G\right]$ if their closed neighborhood does not intersect (see [271]).

The neighborhood number of the graph ${\xi }_n^{nil}$ was determined as the number of distinct prime factors of n in [271] and the structure of the neighborhood graph of the graph ${\xi }_n^{nil}$ along with the properties like regularity, Hamiltonicity of the graph $N\left[{\xi }_n^{nil}\right]$ were also discussed in [271]. It is known that all nilpotent elements are the zero-divisors of the ring and the set of all non-zero nilpotent elements form a symmetric subset of a ring. So, in several cases it can be seen that the nilpotent Cayley graphs coincide with the zero-divisor Cayley graphs defined for a ring (see SubSection 6.6).

Recall that an element x is idempotent when $x^2=x$. Usig this idempotent property of the elements of a ring, the concept of the idempotent graph of a ring R is introduced in [272], whose definition is given below, following which an example of an idempotent graph of a ring is given below in Figure 16.

Definition 26 

([272]). Theidempotent graphof a ring R is defined for all rings R with unity such that the vertex set of the graph is the set of all elements of the ring R and two vertices u and v are adjacent if and only if $u+v$ is an idempotent element of the ring.

It can be seen that a slight modification of the ring considered and the binary operation of addition in the definition makes the graph distinct from being a subgraph of the other Cayley graphs defined of a ring. In [272], the structural properties of the idempotent graph of a finite non-local commutative ring R with unity was investigated and a necessary and sufficient condition on the ring R for its idempotent graph to be planar was obtained. Using this result, it was proven that the idempotent graph of a ring can never be outerplanar. Moreover, on analysing the structure of the idempotent graphs of rings, all the finite non-local commutative rings having their idempotent graph as cograph, split graph and threshold graph respectively were classified.

Note that a graph is said to be a cograph if it has no induced subgraph isomorphic to $P_4$ and a threshold graph if it does not contain an induced subgraph isomorphic to $P_4,C_4$ or $2K_2$. Graphs whose vertex set can be partitioned into a clique and an independent set, where each vertex of the independent set is adjacent to some vertices in the clique is a split graph. As the idempotent graphs are very recently defined, several avenues like to investigate its relation with the other related graphs like nilpotent Cayley graphs, zero-divisor graphs, etc., studying the traversal, structural properties, graph invariants, etc. are open to explore further.

6.3. Mixed Unitary Cayley Graphs

A mixed graph is a graph that contains directed as well as undirected edges. In [273], the mixed adjacency matrix $M\left(G\right)$ of a graph G of order n is defined as an $n\times n$ matrix on the vertex set of the graph such that

$$m_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}(v_i,v_j)\mathrm{is}\mathrm{an}\mathrm{edge}\mathrm{or}\mathrm{arc};\hfill \\ -1,\hfill & \mathrm{if}(v_j,v_i)\mathrm{is}\mathrm{an}\mathrm{arc};\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

From this, the mixed energy of the graph was defined as the sum of the absolute values of eigenvalues of this mixed adjacent matrix. As it was seen that the unitary Cayley graphs have significant spectral properties, investigating the mixed spectra of the unitary Cayley graphs was a curious area to explore. Hence, the mixed Cayley graphs were defined in [273] and its spectra was investigated. The definition of the mixed unitary Cayley followed by an example of the same is given in Definition 27 and Figure 17.

Definition 27 

([273]). The mixed unitary Cayley graph, denoted by ${\xi }_n^{mix}=Cay({\mathbb{Z}}_n,{\mathbb{Z}}_n^{+})$, is a graph whose underlying graph is the unitary Cayley graph $X_n$ and the conditions for an edge $uv$ to be an arc or an edge is defined based on the properties of the end vertices u and v of the edge considered as given below.

(i) 

$uv$ is an edge if $\frac{v-u}{n}=1$,

(ii) 

$(u,v)$ is an arc if $\frac{v-u}{n}=-1$ and $(j-i)<\lceil \frac{n}{2}\rceil$,

(iii) 

$(v,u)$ is an arc if $\frac{v-u}{n}=-1$ and $(j-i)>\lceil \frac{n}{2}\rceil$.

Using these definitions of the mixed unitary Cayley graph and the mixed adjacency matrix, the spectra of the graph and the corresponding energy was determined in [274]. This investigation on the mixed spectra was done for a few values of n, based on their number theoretic properties, because a general structure of this mixed graph is yet to be studied in detail. As the structures are determined more clearly, other studies can be taken up in future.

6.4. Divisor Cayley Graphs

The Cayley graph variation defined on the ring ${\mathbb{Z}}_n$ with respect to the subset of all divisors of n is called the divisor Cayley graphs, which were first introduced in [275]. An example of a divisor Cayley graph following its definition is given in Figure 18.

Definition 28 

([275]). The divisor Cayley graphs, denoted by ${\xi }_n^{div}=Cay({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is an element of the set S, where $S=\{x,n-x:x\in {\mathbb{Z}}_n\}$. That is, for all $u,v\in V\left({\xi }_n^{div+}\right)$, $uv\in E\left({\xi }_n^{div+}\right)$, when $u-v\in S$, where S is the set of all divisors of n and its inverse in ${\mathbb{Z}}_n$.

Note that the definition of the divisor Cayley graphs may seem like it is almost similar to the gcd-graphs defined in Section 2, but the key difference between these graphs is that, in the definition of a gcd-graph, the subset considered was not a symmetric subset, whereas the divisor Cayley graphs are defined with respect to the symmetric subset of divisors and their inverses.

The graph properties of the divisor Cayley graphs like regularity, Eulerianness and Hamiltonicity were examined in [275] and the number of triangles in the divisor Cayley graph was also enumerated. The number of triangles in the divisor Cayley graph was enumerated by partially following the technique that was used for the enumeration of triangles in the unitary Cayley graphs in [34]. Here, the triangles with vertices $\{0,a,b\}$ was given the term fundamental triangles and first, the number of fundamental triangles was calculated as an intermediate step to compute the total number of triangles in the graph. This result was substantiated by several examples, which led to an interesting question to investigate the relationship between the number of divisors of n and the number of triangles in the divisor Cayley graph of the corresponding ${\mathbb{Z}}_n$; which still remains open.

Following this, the problem of enumerating the disjoint Hamiltonian cycles in the divisor Cayley graph was addressed in [276]. Using the previously determined properties of the divisor Cayley graphs in [275], it was proved that a divisor Cayley graph ${\xi }_n^{div}$ can be decomposed into disjoint Hamiltonian cycles if and only if n is odd, and for this case, it was determined that the graph ${\xi }_n^{div}$ can be decomposed into $k+1$ disjoint Hamiltonian cycles, where k is the number of proper divisors of n.

In [276], an algorithm to find disjoint Hamiltonian cycles in the graph according to the values of n and to enumerate them was also given. This was followed by computing the domination number of the divisor Cayley graphs in [277], where an algorithm to construct a minimal dominating set of the graph was given from which the domination number of the graph was determined. Certain topological indices of the divisor Cayley graph was computed in [278]. Note that the divisor Cayley graphs are also known as the unitary divisor Cayley graphs and are different from the difference divisor graphs which appear to be almost similar to these divisor Cayley graphs (see [279]).

Based on the unitary divisor Cayley graph, the unitary divisor addition Cayley graph, denoted by ${\xi }_n^{div+}$ was introduced in [280] by modifying the adjacency relation in the unitary divisor graphs to the sum of the elements to be a divisor. An example of a unitary divisor addition Cayley graph is given in Figure 19, which succeeds the definition of the graph given as follows.

Definition 29 

([280]). The divisor addition Cayley graphs, denoted by ${\xi }_n^{div+}=Ca{y}^{+}({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is an element of the set S, where $S=\{x,n-x:x\in {\mathbb{Z}}_n\}$. That is, for all $u,v\in V\left({\xi }_n^{div}\right)$, $uv\in E\left({\xi }_n^{div}\right)$, when $u+v\in S$, where S is the set of all divisors of n and its inverse in ${\mathbb{Z}}_n$.

The article [280] is the only study available on the unitary divisor addition Cayley graph, where the graph is defined and the basic invariants of the graph like the size, diameter, matching number, and the degree of the vertices were computed. In addition to it, the unitary divisor addition Cayley graphs were characterised based on their traversal properties, such that the graph ${\xi }_n^{div+}$ is Eulerian if and only if $n=2^t$, for some integer $t>1$ and ${\xi }_n^{div+}$ is Hamiltonian if and only if n is even. Several properties of the graph and its association with the other addition Cayley graphs that are defined on ${\mathbb{Z}}_n$, the gcd-graphs,etc. can be explored further.

6.5. Involutory Cayley Graphs

In mathematics, the term involution means an entity which is its own inverse and the elements of any algebraic structure which is its own inverse are called the involutory elements of the structure. This set of all involutory elements of a ring is called the involution set of the ring, which is a symmetric subset. With respect to this involution set, the involutory Cayley graph of the ring ${\mathbb{Z}}_n$, denoted by ${\xi }_n^{inv}$, was defined in [281] as follows.

Definition 30 

([281]). The involutory Cayley graph, denoted by ${\xi }_n^{inv}=Cay({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is an element of the set S, where $S=\{x\ne 0\in {\mathbb{Z}}_n:x^2\equiv 1modn\}$. That is, for all $u,v\in V\left({\xi }_n^{inv}\right)$, $uv\in E\left({\xi }_n^{inv}\right)$, when $u-v\in S$, where S is the set of all involutory elements in the ring.

Similarly, the addition variant of this Cayley graph, called the involutory addition Cayley graph of the ring ${\mathbb{Z}}_n$, denoted by ${\xi }_n^{inv+}$, was defined in [281], as given below. Illustrations of an involutory Cayley graph and an involutory addition Cayley graph are given in Figure 20.

Definition 31 

([282]). The involutory addition Cayley graph, denoted by ${\xi }_n^{inv+}=Ca{y}^{+}({\mathbb{Z}}_n,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_n$; $0,1,\dots ,n-1$, and two vertices are adjacent if their difference is an element of the set S, where $S=\{x\ne 0\in {\mathbb{Z}}_n:x^2\equiv 1modn\}$. That is, for all $u,v\in V\left({\xi }_n^{inv+}\right)$, $uv\in E\left({\xi }_n^{inv+}\right)$, when $u+v\in S$, where S is the set of all involutory elements in the ring.

The basic properties of the graphs ${\xi }_n^{inv}$ and ${\xi }_n^{inv+}$ were discussed in [281] and [282] respectively. On comparing the graph properties that were obtained for both the graphs, the difference as well as the similarities between the graphs and the values of n for which they coincide could be obtained. The involutory Cayley graph is S-regular, where as the involutory addition Cayley graphs can be $\left|S\right|$-regular or $\left(\right|S|,|S|-1)$-semi regular, depending on the value of n. As, the degree of each vertex in the involutory addition Cayley graph and the diameter of the graph depends on the value of n, the degree and the diameter of the graph were only explored in the article [282]; whereas, in [281] the apart from computing the degree of the vertices in the graph, it was proved that the involutory Cayley graphs are connected, Eulerian and Hamiltonian. The domination number and related parameters for the involutory Cayley graph was computed in [283], where the parameters are computed for the involutory Cayley graphs that fall under the standard graph classes using the exact values that had been obtained for these graph classes.

6.5.1. Quadratic Unitary Cayley Graphs

The symmetric subset of the involutory elements of a ring is also called the quadratic units modulo n, as the square of an element becomes the unit of the ring ${\mathbb{Z}}_n$, integers modulo n. So, the involutory Cayley graphs of ${\mathbb{Z}}_n$ were also studied independently in the name quadratic unitary Cayley graphs for the ring ${\mathbb{Z}}_n$ in [284]. For the values of n such that $n\equiv 1mod4$ and is prime, these graphs were found to coincide with a class of graphs called the Paley graphs on n vertices (refer to [285] for more details on Paley graphs). Some structural properties of the quadratic unitary Cayley graphs of ${\mathbb{Z}}_n$ were presented in [284], where the diameter of the graph was determined for odd and even values of n, by analysing the paths of different lengths in the graph. This analysis led to the examination of self-complementary quadratic unitary Cayley graph of ${\mathbb{Z}}_n$, from which the following characterisation of perfect quadratic unitary Cayley graphs was obtained in [284].

Theorem 121. 

[284] The quadratic unitary Cayley graph of ${\mathbb{Z}}_n$ is perfect if and only if n is even or $n=p^k$, for a prime $p\equiv 3mod4$.

The structural analysis of the graph also led to the characterisation of the quadratic unitary Cayley graph of ${\mathbb{Z}}_n$ that are decomposed into direct product of graphs (see Definition 6) over relatively prime factors of n. Based on the proof techniques used to prove the results, a linear operator called the sympletic operator was defined in [284] as a $2k\times 2k$ matrix called the sympletic form (modulo n),

$${\sigma }_{2k}=\left(\begin{array}{cc}{0}_k& -I_k\\ I_k& 0_k\end{array}\right),$$

where $I_k$ and $0_k$ denote the identity matrix and the zero matrix of order k respectively. It was proven in [284] that the set of all these sympletic operators with coefficients in ${\mathbb{Z}}_n$ form the sympletic group modulo n. These sympletic operators were examined in [284] and a corollary regarding the decomposition of sympletic matrices in terms of these row-operations was obtained. This led to the final result that gave a bound on the complexity of decompositions of these sympletic operators modulo n, which followed from the bounds on the diameter of the quadratic unitary Cayley graph of ${\mathbb{Z}}_n$, that was obtained in the same article.

This notion of quadratic unitary Cayley graphs was extended to all finite commutative rings R in [286] as the graph with the vertex set as the elements of the ring R and two vertices are adjacent if their difference is an element of the set S, where $S^{*}=\{x^2:x\in R-\left\{0\right\}\}$ and $S=S^{*}\cup -S^{*}$. In fact, it can be seen that when the ring is a finite field of prime order k such that $k\equiv 1mod4$, the quadratic unitary Cayley graph of that field is a Paley graph, which by definition is the graph with the vertex set as the elements of the field such that the vertices u and v are adjacent if and only if $u-v$ is a non-zero square of the field.

For a finite commutative ring R that is decomposed as $R=R_1\times R_2\times \dots \times R_t$, where each $R_i$, $1\le i\le t$ is a local ring with the maximal ideal $M_i$ and for a local ring $R_0$ with the maximal ideal $M_0$ such that $\frac{|R_0|}{|M_0|}\equiv 3mod4$, the spectra of the quadratic unitary Cayley graphs of the ring $R_0$ and $R_0\times R$, with the condition that $\frac{|R_i|}{|M_i|}\equiv 1mod4$, $1\le i\le t$ were determined along with their energies. The spectral moments of the quadratic unitary Cayley graphs of the above mentioned rings were also computed and the conditions under which these graphs are hyperenergetic or Ramanujan graphs were determined. A prefatory study on the same graphs were done in [287], where only a very few results on the structure of the graph and its eigenvalues were obtained.

6.5.2. Quadratic Residue Cayley Graphs

Another variant of the Cayley graphs similar to the involutory Cayley graphs are the quadratic residue Cayley graphs. It can be seen as an extension of the quadratic residue property to a prime number. So, these graphs are defined on the rings ${\mathbb{Z}}_n$, where n is an odd prime. If p is an odd prime and $n\in \mathbb{N}$, such that p divides n and the quadratic congruence $x^2\equiv nmodp$ has a solution, then n is called a quadratic residue mod p and the set of all quadratic residues mod p along with their inverse is a symmetric subset of ${\mathbb{Z}}_p$. With respect to this symmetric subset, the quadratic residue Cayley graph was defined in [288] exclusively for the rings ${\mathbb{Z}}_p$, where p is an odd prime as given in Definition 32, that is followed an example of a quadratic residue Cayley graph of a ring in Figure 21.

Definition 32 

([288]). For an odd prime integer p, the quadratic residue Cayley graph of ${\mathbb{Z}}_p$, denoted by ${\xi }_n^{qrcg}=Cay({\mathbb{Z}}_p,S)$, is a graph with the vertex set as the elements of the ring ${\mathbb{Z}}_p$; $0,1,2,\dots ,p$, and two vertices u and v are adjacent if their difference $u-v\in S$, where S the set of all quadratic residues mod p along with their inverse elements.

The studies on the quadratic residue Cayley graph of the ring ${\mathbb{Z}}_p$ was mainly focused on finding dominating functions and some variants of it for the graph. The graph was defined and the basic invariants and properties like the degree, regularity, number of triangles, disjoint Hamiltonian cycles were given in [288]. Following this, all the investigations were on different dominating functions on the graph.

A function $f:V\left(G\right)\to [0,1]$ is a dominating function of a graph G, if $f\left(N\left[v\right]\right)={\displaystyle \sum _{u\in N\left[v\right]}}f\left(u\right)\ge 1$, for every vertex $v\in V\left(G\right)$ and the dominating function f is minimal if $f\left(v\right)\ge g\left(v\right)$, for all $v\in V\left(G\right)$, where g is also a dominating function. A minimal dominating function f is a basic minimal dominating function if it cannot be expressed as a proper convex combination of two distinct minimal dominating functions (see [289]). These definitions on replacing the vertex with an edge gives the corresponding definitions of edge dominating functions.

The edge dominating functions, basic minimal edge dominating functions and the basic minimal dominating functions of the quadratic residue Cayley graphs were computed in [289,290,291] respectively. Different functions were proved to be the corresponding dominating functions for the graph and several examples to convey the significance of the functions were also given. Following this, the variations of the total dominating functions for the graph were explored in [292,293] in a similar way.

In [294], the quadratic residue Cayley graph of the ring ${\mathbb{Z}}_{2^k}$ was exclusively studied. Only for integers of the form $2^k$, the quadratic residue Cayley graph was constructed and investigated. This was the earliest attempt known to define a Cayley graph based on quadratic residues. In this article, it was shown that the diameter of these quadratic residue Cayley graphs defined on ${\mathbb{Z}}_{2^k}$ is 2, following which a recursive formula to determine the number of triangles in the graph was obtained. In addition, a small discussion on the number of k residue modulo $p^r$ (prime p) was also given in [294], to extend the defined quadratic residue Cayley graphs on ${\mathbb{Z}}_{2^k}$.

6.6. Zero-Divisor Cayley Graphs

A symmetric subset of a ring which is highly significant in order to understand the structure of the ring, is the set of all zero-divisors. The Cayley graph defined with respect to this symmetric subset of zero-divisors is called the zero-divisor Cayley graphs. This graph was first defined on the finite commutative rings in [158], followed by which it was defined on the rings of integer modulo n, ${\mathbb{Z}}_n$ in [295]. Illustrations of zero-divisor Cayley graphs of the integer modulo ring and that of a ring R is given in Figure 22.

Definition 33 

([295]). The zero-divisor Cayley graph of a ring R, denoted by ${\xi }_R^{zdcg}=Cay(R,Z\left(R\right))$, is defined as the graph whose vertex set is the set of all elements of the ring and two distinct vertices are adjacent if their difference is a non-zero zero-divisor. That is, for all $u,v\in V\left({\xi }_R^{Z\left(R\right)}\right)$, $uv\in E\left({\xi }_R^{Z\left(R\right)}\right)$, when $u-v\in Z\left(R\right)$, where $Z\left(R\right)$ is the set of all non-zero zero-divisors of the ring R. The zero-divisor Cayley graph of the ring ${\mathbb{Z}}_n$ is denoted by ${\xi }_n^{zdcg}$.

In [158], the graph parameters like the clique number, chromatic number, edge chromatic number, domination number, and the girth of the graph ${\xi }_R^{Z\left(R\right)}$ were computed and the rings for which the zero-divisor Cayley graphs are strongly regular and planar were characterised. On restricting this definition to the ring ${\mathbb{Z}}_n$, more properties like the enumeration of triangles, connectivity, etc. were explored in [296].

We know that any element in a ring is either a zero-divisor or a unit and the set of all non-coprime integers to n are the zero-divisors in the ring ${\mathbb{Z}}_n$. Hence, in this zero-divisor Cayley graphs of ${\mathbb{Z}}_n$, two vertices are adjacent if and only if their difference is not relatively prime to n, precisely, it can be seen as the complement of the unitary Cayley graphs $X_n$ defined on ${\mathbb{Z}}_n$. As many properties of the unitary Cayley graphs and their complements are already studied in the literature, only the basic invariants and the basic properties of the graph were studied in [295,296]. The number of triangles in the graph along with the traversal properties were studied in [295] and the connectedness of the graph and the properties of the components when the zero-divisor Cayley graphs are disconnected were investigated in [295].

Note that on modifying the adjacency condition of the zero-divisor Cayley graphs defined on a ring R from the difference to the sum of two elements to be a zero divisor, the definition of a total graph of a ring is obtained. As total graphs have a huge growing literature along with several exclusive and detailed survey and review papers (For example, see [12,16]), we do not include them in this review.

It can be noted that for all the variations of Cayley graphs that have been discussed in this section, only a cursory investigation has been taken place in the literature. This can be seen because of two reasons; one is while investigating the structure of the new graph defined, a high similarity with the properties of an already defined, existing Cayley graphs were observed and sometimes, the graphs may also coincide with them, leaving no scope for further study. The other reason to not proceed further with the problem is because of the ambiguous structure of the symmetric subset that is considered to define the Cayley graph or the realisation that the graph structure might not reflect the important properties or the structure of the ring, failing to serve the main purpose of the study.

7. Conclusions

It can be seen that the introduction of the unitary Cayley graphs of the ring ${\mathbb{Z}}_n$ provided a new direction for research in algebraic graph theory, using the number theoretic properties of the rings and to define variants of Cayley graphs with respect to different symmetric subsets of the group, by considering both the operations of sum and difference, giving rise to twin-type variants of such graphs. Apart from some specific open problems that were discussed in the respective sections of the graphs, there are several other open problems that can be investigated with respect to these algebraic graphs defined on rings that are discussed in the review, among which a few are presented in this section.

It can be observed that there is an overall pattern of the investigations done on a particular graph, when reviewing the literature as well as while reading this article. Before moving to the open problems, it is important that this pattern is explicitly mentioned, for a better understanding. As a new variant of Cayley graph is defined, its first property that is determined is the regularity, the degree of the vertices, from which the size. Following this, the other parameters of diameter, girth, chromatic number, clique number, etc. are computed. Connectedness, traversability, planarity and perfection are significant properties through which characterisations of rings are obtained. Investigating different matrices associated with the graph and their spectra, especially the adjacency spectrum, the eigenvalues, energy of the graph is an inevitable problem. From these spectra, different properties like hyperenergecity, realising the given graphs as Ramanujan graphs, etc. are discussed.

Furthermore, several matrices are associated, corresponding to which the analogous investigations are made. Realisation of the graph based on isomorphism and structural characterisations of the graph are important problems to address. Apart from this, different chromatic numbers, domination numbers, topological indices, centrality measures, covering numbers, vulnerability parameters, etc. can be computed for the graph and the possibility of characterisations of the graphs and the rings based on these parameters are also examined. All possible studies are extended to the complements of these graphs, as they are also regular, in most of the cases.

Moving on to further areas of exploration with respect to the graphs discussed in the review, in most of the graphs that are given, not many studies on different types of domination and coloring parameters are there, except for the unitary Cayley graphs of ${\mathbb{Z}}_n$. Computation of different topological indices and centrality measures and associating different matrices to these graphs and computing their energies, color energies, are also open, especially for the graphs defined in Section 6 and different types of vertex partitioning of the algebraic graphs are also promising problems to work on.

Similarly, several parameters like covering numbers, metric dimension, resolving sets, etc. have not been computed so far for the graphs, computing them and to check the feasibility of obtaining Nordhaus-Gaddum type inequalities is also an open avenue to explore. In terms of signed graphs, the signed graph varieties have not been introduced for many Cayley graph variations, and even for the ones that are introduced, properties apart from the properties of balance, clusterability, sign-compatibilty and canonical consistence, can be studied and induced sign graphs based on other properties of the ring elements can also be introduced, instead of introducing modified definitions based on the existence of the end vertices of an edge in a subset considered.

Based on the definition of the variants of Cayley graphs presented in this review, it can be seen that they are related to each other, in some aspect. Hence, chain-like inequalities of these graphs can be identified for certain rings and characterisations of rings when the graphs are equal or when one is a subgraph of another can also be presented. On the other hand, a similar type of investigation can be done exclusively with respect to the complements of these graphs or by considering both the graphs defined as well as their complements, as the complement of some variants of Cayley graphs discussed in this article coincide with some graphs. Based on the huge literature available on Cayley graphs of groups, power graphs, zero divisor graphs, and other graphs derived from them, certain analogous studies can also be introduced to these types of graphs.