Method of Obtaining the Ancient Egyptian Formula for the Area of a Circle

1. Introduction

Speaking about of ancient Egyptian mathematics, it is impossible to pass by its famous riddle.

The matter of that the Egyptians considered a circle’s area (S) to be equal to the area of the square, the side of which is 8/9 of circle’s diameter (d), i.e. believed in modern designations,

S = (d – ¹/₉ d )² = (⁸/₉ d )².

(1)

Similar calculations are available in Moscow Mathematical Papyrus that dated to around 19th century BC [1] and Rhind Mathematical Papyrus that dated roughly 17th century BC (but it is probably a copy of an older document) [2].

This formula is characterized by amazing accuracy. If to consider that the ratio of a circle’s circumference (L) to its diameter

L/d = 4 ∙ (8/9)² = 3.16049…,

(2)

the result is really very good: it exceeds the exact value (number π) 3.14159..., less than 0.02 (in other words, an error less than 1%) [3]. But the answer to the question of how this result was obtained, has not yet been.

Various hypotheses have been proposed [4,5], but all of them are unconvincing.

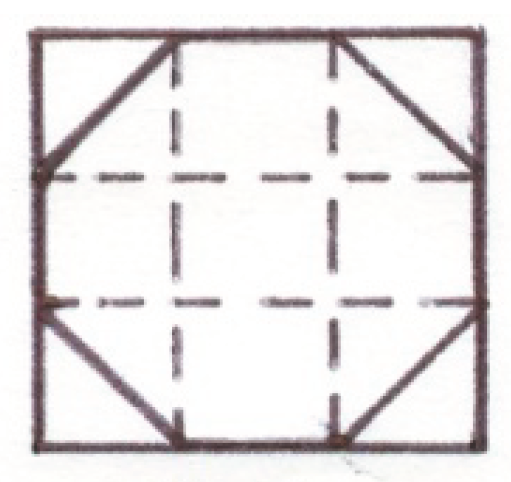
The most reasonable is the assumption (put forward at the beginning of the 20th century) that the Egyptians divided the square into 9 parts, cut corners and get the right octagon the area of which is d² – ²/₉ d², i.e. is 7/9 square area [6], as can be seen in Figure 1.

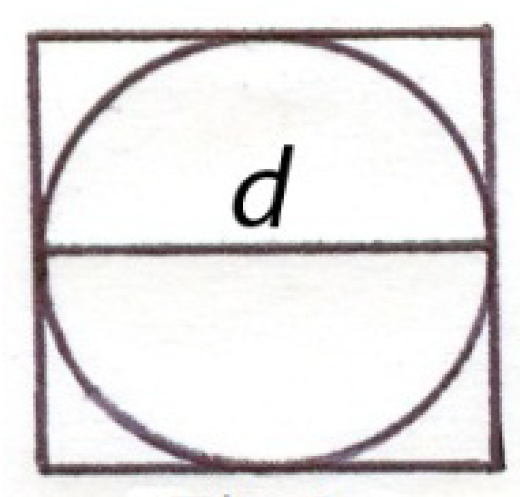
The area of the octagon close to the area of circle inscribed inside a square (Figure 2) and is approximately equal to the area of square with the side 8/9 of the circle’s diameter, because 7/9 = 63/81 ≈ (8/9)². However, the researchers could not understand how the Egyptians came from the expression d² – ²/₉ d² to the expression (d – ¹/₉ d )².

Here we reconstruct the ancient Egyptian method, in modern designations.

2. Method

At first, the Egyptian scientist have determined that an arbitrary square with side d has the area (S_q) is equal to:

S_q = d ∙ d = dP/4,

(3)

where P = 4d is the perimeter of a square.

Then he drawed in the square the circle with a diameter equal to the side of the square (Figure 2) and he found that the circle’s circumference is smaller than the perimeter of the square, and the circle area is smaller than the square area:

L < P, S < S_q.

(4)

Substituting in formula (3) L instead of P, he obtained that the area of the circle

$$S=\frac{Ld}{4}$$

(5)

or

$$S=\frac{L}{d}\frac{d\cdot d}{4}=\frac{L}{d}\frac{1}{4},$$

(6)

where d ∙ d = 1 is the square’s area (in Figure 2).

Hence, the ratio of the circumference to the diameter is equal to:

4S = L/d.

(7)

Thus, to calculate the area of a circle it is necessary to know the ratio of the circumference length to the diameter (L/d). Using a strip of papyrus and a round flat object (such as a disc or wheel), the ancient researcher was able to determine by direct measurement that this relationship lies approximately in the middle between the values 3 + ¹/₄ and 3 + ^l/₉:

3 + ¹/₄ > L /d > 3 + ^l/₉ .

(8)

Substituting in formula (7) the octagon’s area 7/9 instead of the circle’s area S, he obtained 4∙7/9 = 28/9 = 3 + ¹/₉ and made sure that the value of 7/9 for the area of the circle is not suitable.

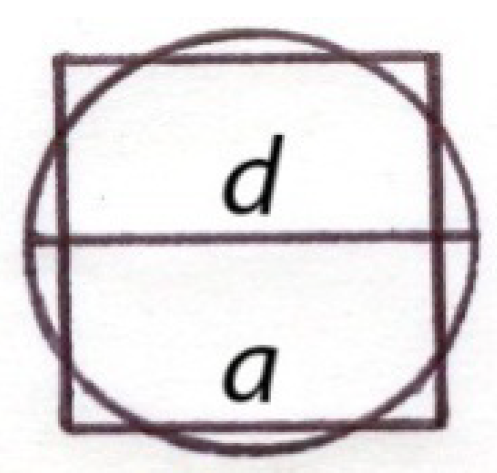
Next, our scientist draws a square with an area equal to a given circle, S_q = S (Figure 3). He sees that the square’s side (а) is slightly smaller than the circle’s diameter (a < d), perhaps, it different from the diameter that is taken as the unit of length (d = 1), at 1/10, or 1/9, or 1/8:

1 – a = (1/10, or 1/9, or 1/8).

(9)

Therefore, the square’s side is one of the following values from the circle’s diameter:

а = (9/10, or 8/9, or 7/8).

(10)

The areas of the circle and the square (in Figure 3) the same, S = a ∙ a, so researcher receives from equation (7):

4a² = L/d.

(11)

Sequentially substituting in the last formula instead of the square’s side a its values (9/10, 8/9, 7/8), he calculates:

4 ∙ (9/10)² = 324 /100 = 3 + ²⁴/₁₀₀ = 3 + ¹/₄ – ¹/₁₀₀ ,

(12)

4 ∙ (8/9)² = 256 /81=3+¹³/₈₁ = 3 + ²⁶/₁₆₂ = 3 + ¹/₆ – ¹/₁₆₂ ,

(13)

4 ∙ (7/8)² = 196 /64 = 3 + ⁴/₆₄ = 3 + ¹/₁₆ .

(14)

Thus, the unknown mathematician came to the conclusion that the empirical condition (8) is satisfied the value L/d = 3 + ¹/₆ , from where a = (8/9)d and the area of the circle is ( ⁸/₉ d )² [7].

3. Conclusion

Ancient Egyptians first proposed a mathematical method for calculating the circle’s area and the ratio of a circumference to diameter. This method is characterized by excellent accuracy, simplicity and elegance.

Footnote: This article is registered as an object of copyright in the Intellectual Property Office of Kyrgyzstan (Kyrgyzpatent) in November 2008 (Certificate № 1162).