1. Introduction
Nowadays, Mueller imaging polarimetry constitutes a mature set of technologies and procedures with an enormous variety of applications that, among many others, covers areas like analysis of biological tissues [
1,
2] and remote sensing [
3,
4,
5].
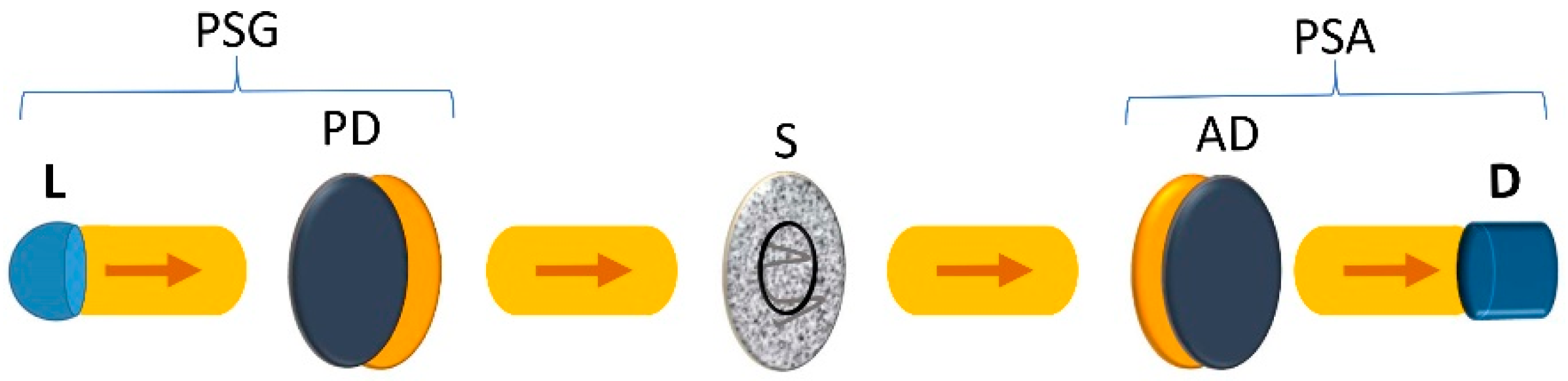
Mueller polarimeters are composed of (see
Figure 1) [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]
A collimated light source with fixed spectral profile.
A polarization state generator (PSG) that modulates the state of polarization incident on the material sample.
A setup for the appropriate placement and relative orientation of the material sample on which the light probe beam impinges.
A polarization state analyzer (PSA) that modulates the state of polarization of the light probe after its interaction with the sample.
A detection, record and processing device that allows for measuring the intensity of the light probe after passing through the PSG, the sample and the PSA
Specific Mueller polarimeters are designed for their operation on samples with a homogeneous behavior over the cross-section covered by the light probe, in which case a single Mueller matrix is obtained for each measurement, while the so-called imaging Mueller polarimeters are designed for the measurement of the point-to-point Mueller matrices covering a certain area of the sample with heterogeneous spatial behavior.
Figure 1.
General structure of an imaging Mueller polarimeter. The polarization state generator (PSG) is constituted by the light source (L), which provides a collimated beam, and a polarizing device (PD). After emerging from the PSG, the light probe is incident on a spatial section of the sample (S), which in general exhibits heterogeneous polarimetric behavior in the area covered by the light probe and whose point-to-point Mueller matrices are under measurement. The polarization state analyzer (PSA) is constituted by an analyzing device (AD), and the detection and processing system (D).
Figure 1.
General structure of an imaging Mueller polarimeter. The polarization state generator (PSG) is constituted by the light source (L), which provides a collimated beam, and a polarizing device (PD). After emerging from the PSG, the light probe is incident on a spatial section of the sample (S), which in general exhibits heterogeneous polarimetric behavior in the area covered by the light probe and whose point-to-point Mueller matrices are under measurement. The polarization state analyzer (PSA) is constituted by an analyzing device (AD), and the detection and processing system (D).
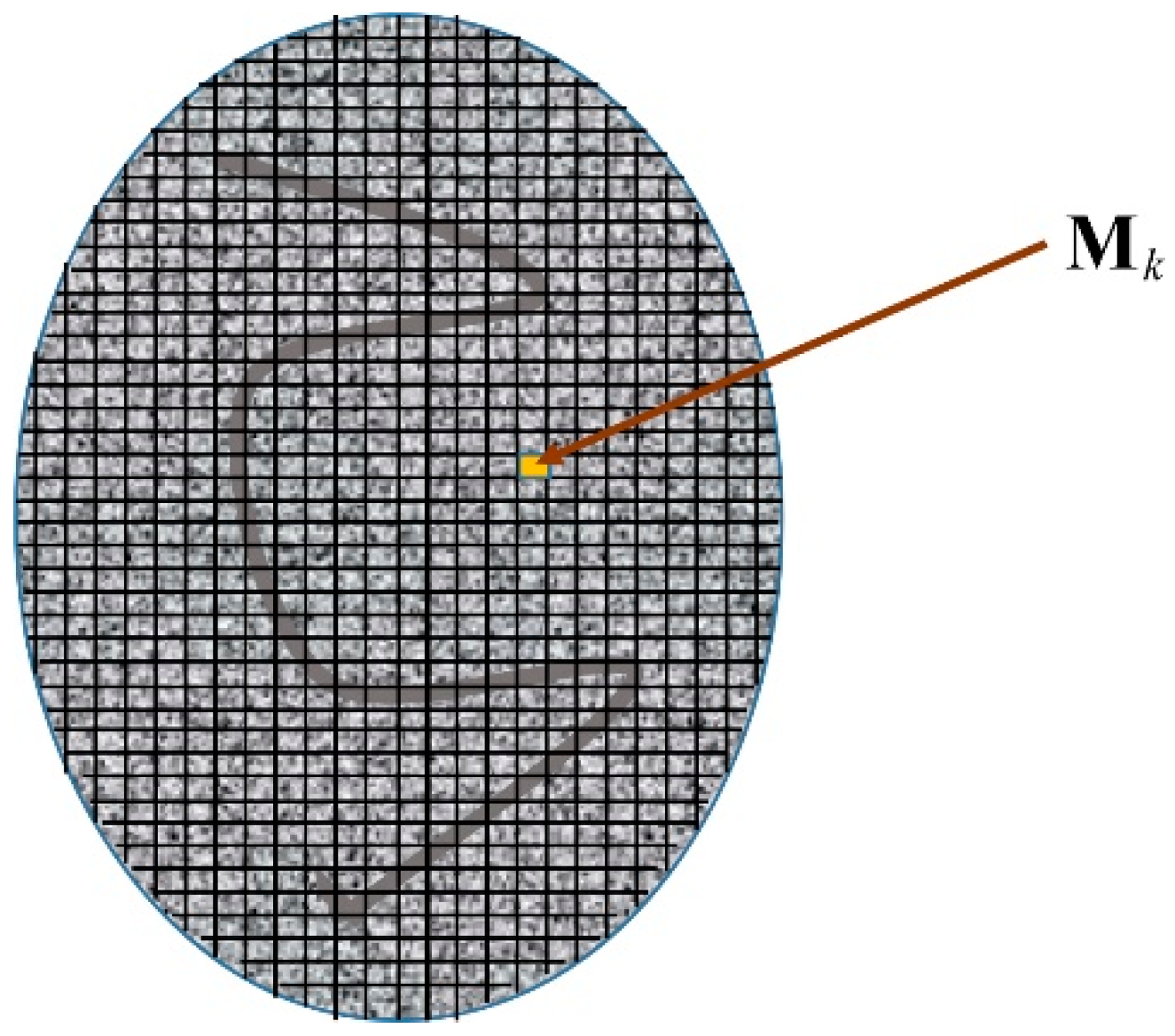
Thus, in Mueller imaging polarimetry, the sample can be considered pixelated, in such a manner that a different Mueller matrix is measured for each pixel (
Figure 2). Note that we are using the term pixels to refer to small areas of the sample, which in general have a common shape and size, so that a number of pixels covers the entire cross-section of the sample under measurement. Thus, each pixel is characterized by a specific and fixed Mueller matrix, which is in general different from those of other pixels. Since, in general, a given Mueller matrix can be parameterized in terms of up to sixteen independent parameters, up to sixteen independent images can be obtained for each complete polarimetric measurement. Nevertheless, when appropriate, additional images can be obtained from specific polarimetric descriptors.
Figure 2.
The area of the sample under measurement impinged by the light probe of the polarimeter is composed of a number m of small parts (pixels) whose respective Mueller matrices are measured. For a particular pixel k, its corresponding Mueller matrix is denoted by , so that the subscript k runs all pixels . When a series of n independent measurements is performed for a fixed sample, the respective Mueller matrices of the pixel k are denoted as, with .
Figure 2.
The area of the sample under measurement impinged by the light probe of the polarimeter is composed of a number m of small parts (pixels) whose respective Mueller matrices are measured. For a particular pixel k, its corresponding Mueller matrix is denoted by , so that the subscript k runs all pixels . When a series of n independent measurements is performed for a fixed sample, the respective Mueller matrices of the pixel k are denoted as, with .
Let us now consider a sequence of
n independent measurements over a given fixed material sample, which are performed with different light probes with respective spectral profiles (
Figure 3), in such a manner that each independent measurement produces a specific set of
m point-to point Mueller matrices, which are denoted as
,
where indices
k,
l refer respectively to the
k pixel and the
l measurement.
Figure 3.
For a given Mueller imaging polarimeter, different complete measurement can be performed by varying the spectral profile of the light probe (L1, L2 and L3 in the figure), leading to respective sets of Mueller matrices associated with the points (pixels) of the sample. The Mueller matrix of a given pixel depends on both the central frequency and the shape of the spectral profile of the light probe. The successive measurements can be performed either with spectral profiles that partially overlap or not. The shaded area represents some overlap of L2 and L3.
Figure 3.
For a given Mueller imaging polarimeter, different complete measurement can be performed by varying the spectral profile of the light probe (L1, L2 and L3 in the figure), leading to respective sets of Mueller matrices associated with the points (pixels) of the sample. The Mueller matrix of a given pixel depends on both the central frequency and the shape of the spectral profile of the light probe. The successive measurements can be performed either with spectral profiles that partially overlap or not. The shaded area represents some overlap of L2 and L3.
Depending on the central frequency, shape and width of the spectral profile used in a given measurement l, the Mueller matrix of the k pixel adopts a specific form , which can be either nondepolarizing (or pure, in the sense that it preserves the degree of polarization of incident totally polarized light), or depolarizing. In general, samples exhibiting inhomogeneous behavior over the cross-section covered by the light probe are considered, and consequently the separate representations of the sixteen elements , where k maps the entire set of m pixels of the sample under measurement, lead to specific images.
It is well known that the elements
of
do not provide a direct and independent information about the polarimetric properties of the sample for the spectral profile of the light probe used in the corresponding measurement, but are related to the enpolarizing (diattenuating and polarizing), retarding and depolarizing properties in an intricate manner. This is the reason why alternative sets of polarimetric descriptors (other than
) are frequently used to generate more significant polarimetric images that describe, in a decoupled manner, the spatial variation of specific properties. A possible parameterization of
in terms of sixteen independent parameters directly related to specific polarimetric features is based on the so-called arrow decomposition of Mueller matrices [
17,
18,
19,
20].
The main argument which will be deal with in this work relies on the fact that, beyond the polarimetric images obtained for each measurement
l, the information obtained through a set of
n independent measurements of
can be used to generate new sets of synthetic images that enhance the contrast or visualization of certain properties or structures of the sample. In particular, for instance, let us build the Mueller matrix
which is directly synthesized from the independent
n measurements but whose associated enpolarizing, retarding and depolarizing properties are different from those of each
. In fact,
carries information on the variation of the polarimetric behavior of the sample as the spectral profile of the probing light is modified. In other words, the set of measured
contains implicit information on certain properties of the sample that only can be represented in the form of polarimetric images obtained from synthetic parallel combinations performed as indicated in Eq. (1).
Thus, the aim of this work is to describe the general theoretical framework for the synthesis of significant polarimetric images based on the parallel composition of the Mueller matrices obtained through a set of
n (with
) independent measurements of a given material sample. To do so, this communication is organized as follows. The main necessary concepts and notations are summarized in
Section 2.
Section 3 is devoted to the general formulation of the synthetic Mueller imaging polarimetry approach, whose nature and scope is discussed in
Section 4. The main conclusions are summarized in
Section 5.
Note that although the term "light" is used in this communication, it should be understood in the wide sense of referring generally to arbitrary frequencies within different areas of the electromagnetic spectrum and not exclusively within the optical range. This is the case, for example, for synthetic aperture radar polarimetry (SAR polarimetry) for which the electromagnetic probe belongs to the microwave range.
2. Theoretical background
The transformation of polarized light by the action of a linear medium (under fixed interaction conditions) can always be represented mathematically as
where
s and
are the Stokes vectors that respectively represent the polarization states of the incident and emerging light beams, and
M is the Mueller matrix that performs the linear transformation, which can be expressed in the partitioned form [
21,
22,
23]
where
denote the elements of
M; superscript T indicates transpose;
represents the mean intensity coefficient (MIC), i.e., the ratio between the intensity of the emerging light and the intensity of incident unpolarized light;
D and
P are the diattenuation and polarizance vectors, with absolute values
D (diattenuation) and
P (polarizance), and
m is the normalized 3×3 submatrix associated with
M.
A proper measure of the ability of
M to preserve the degree of polarization of totally polarized incident light, is given by the
degree of polarimetric purity of
M (also called
depolarization index) [
24],
, which can be expressed as
where
is the
polarimetric dimension index (also called the
degree of spherical purity), defined as
being the Frobenius norm of
m, and
is the so-called degree of polarizance, or
enpolarizance, giving an overall measure of the power of
M to increase the degree of polarization of the interacting light in either forward or reverse interactions [
17,
18,
19].
Maximum degree of polarimetric purity,
, is exhibited uniquely by
nondepolarizing (or
pure) media (i.e., media that do not decrease de degree of polarization of totally polarized incident light), while
corresponds to perfect depolarizers, with associated Mueller matrix
. Maximum
,
, implies
with
(nondepolarizing and nonenpolarizing media), which corresponds uniquely to retarders; minimal
,
, corresponds to media exhibiting
. Maximal enpolarizance,
, implies
and corresponds to perfect polarizers, while the minimal,
, is exhibited by nonenpolarizing interactions (either nondepolarizing or depolarizing) [
18,
19].
In general, two kinds of decompositions of a Mueller matrix can be considered, namely serial decompositions (through product of Mueller matrices) and parallel decompositions (through weighted sums of Mueller matrices) [
25,
26].
Parallel decompositions consist of representing a Mueller matrix as a weighted sum of Mueller matrices. The physical meaning of parallel decompositions is that the incoming electromagnetic wave splits into a set of pencils that interact, without overlapping, with a number of material components that are spatially distributed in the illuminated area, and the emerging pencils are incoherently recombined into the emerging beam.
Thus, the concept of parallel composition of Mueller matrices underlies the very concept of Mueller matrix and obeys the rule that the coefficients of the Mueller components in the sum should be positive and sum to one (convex sum) [
25,
26]. This property is directly linked to the so-called covariance criterion, namely, given a Mueller matrix
M, its associated Hermitian coherency matrix
is positive semidefinite [
27], which is equivalent to the fact that any Mueller matrix can be expressed as a sum of nondepolarizing Mueller matrices [
28]. The explicit expression of
, in terms of the elements
of
M, is given by [
26,
27]
The general formulation for the synthesis of a Mueller matrix associated with a linear polarimetric interaction from the properties of the parallel components of the medium on which the considered light beam interacts has been deal with in [
26,
29,
30,
31,
32,
33,
34].
Since
C is a positive semi-definite Hermitian matrix, it can always be diagonalized through a unitary transformation of the form
where
are the four ordered
nonnegative eigenvalues of
C. The columns
of the
unitary matrix
U are the orthonormal eigenvectors of
C.
Nondepolarizing Mueller matrices have the genuine property that they exhibit a single nonzero eigenvalue (i.e.,
,
) and hereafther, wherever appropriate, we will use the subscript
J to refer to Mueller and coherency matrices associated with nondepolarizing media, which will generically denoted as
and
. The coherency matrix
associated with a nondepolarizing Mueller matrix
can always be expressed as
, where
(called the coherency vector of
) is a unit vector with four complex components [
34].
Complete quantitative information on the structure of polarimetric purity-randomness exhibited by the interaction represented by
M is provided by the set of three indices of polarimetric purity (IPP) [
35]
Given a Mueller matrix
M, it can always be submitted to the so-called arbitrary decomposition [
25,
36]
where
, with
, which coincides with the number of independent nondepolarizing parallel components of
M;
is the pseudoinverse of
, defined as
,
being the diagonal matrix whose
r first diagonal elements are
and whose last
elements are zero [
36].
Consider now the following modified singular value decomposition of the submatrix
m of
M,
where the nonnegative parameters
are the singular values of
m (taken in decreasing order), and
are proper orthogonal
matrices, and consequently the associated
matrices of the form
are orthogonal Mueller matrices (representing respective transparent retarders). The arrow form
of
M is then defined as [
17]
and contains up to ten nonzero elements. The corresponding arrow decomposition of
M is defined as
Note that the diattenuation and polarizance vectors, D and P, of M are recovered from those of through the respective transformations and , which preserve the absolute values of the transformed vectors.
The arrow decomposition allows for the parameterization of
M in terms of the following significant sixteen parameters [
20,
37]:
the three angular parameters determining the entrance retarder, where and are the azimuth and ellipticity of the fast eigenstate and is the retardance;
the three angular parameters determining the exit retarder;
the three parameters determining the diattenuation vector D of M, , where and are the azimuth and ellipticity of the eigenstate with smaller attenuation; or, alternatively, the three parameters determining the diattenuation vector of ;
the three parameters determining the polarizance vector P of M, or, alternatively the three parameters determining the polarizance vector of ;
the three indices of polarimetric purity of M (which coincide with those of ), and
the MIC of M (which coincides with that of ).
Consequently, independent mappings of the above sixteen descriptors provide respective polarimetric images that reflect the variations and associated contrast of each parameter. Obviously, many other parameterizations of M are also possible, but we emphasize the fact that the above one gives separate information on the enpolarizing (D and P vectors), retarding ( and matrices), depolarizing and MIC properties for each spectral profile of the light probe used in the imaging polarimeter.
Furthermore, despite the implicit redundancy of the information held by other descriptors, it can be useful the generation of additional images associated with parameters like, for instance, and .
The parallel composition of Mueller matrices that only differ in their MICs do not produce changes in the fifteen remaining parameters described above. Thus, hereafter the fifteen parameters will be referred to as the polarimetric descriptors of the Mueller matrix to which they correspond.
In the case of nondepolarizing Mueller matrices, the arrow decomposition adopts the symmetric form [
26,
38,
39]
where the central matrix has the general form
so that it represents a horizontal-aligned linear diattenuator, while the set of entrance and exit retarders depends on five parameters through the expressions [
26]
where
,
and
represent respective linear retarders with retardances
,
and
, and whose fast axes are oriented at angles
,
and zero. Recall that diattenuation and polarizance necessarily coincide for nondepolarizing Mueller matrices
.
3. Synthetic Mueller imaging polarimetry
For the sake of clarity, let us first consider a fixed material sample submitted to two independent point-to-point Mueller measurements which only differ in the spectral profile of the light probe, with respective central frequencies denoted as
. and
. It is also assumed that the shift
is big enough for the sample to have different polarimetric behavior, that is to say, some or all of the set of fifteen polarimetric descriptors described in the last paragraph of
Section 2, take different values for both light probes. No particular assumptions are made about the shapes and bandwidths of the spectral profiles, although the implications of their possible partial overlap will be discussed in
Section 4.
Let
,
be the point-to-point Mueller matrices obtained from each independent measurement
corresponding respectively to the light probes with central frequencies
. and
, where we are using the notation introduced in
Section 1.
For a given pixel k, it can always be built the synthetic Mueller matrix
As long as a certain property of the sample behaves differently in both measurements, a respective new polarimetric image associated with arises. Note that other pairs of coefficients (with ) different from can be used, but there is no apparent advantage in straying from the simpler option chosen.
To emphasize the power of this simple procedure, let us consider the special (but common) case where both and are nondepolarizing. Then, provided (that is, proportional Mueller matrices are excluded because of their equivalent polarimetric behavior, which only differ in their respective MICs), is depolarizing, so that its polarimetric descriptors differ from those of both and . In particular, the inequality is necessarily satisfied (recall that nondepolarizing Mueller matrices always satisfy ), and consequently the mapping of associated with each pixel k provides a new and peculiar polarimetric image whose nature is substantially different form the images obtained for and . In fact, it can be said that certain images obtained from the synthetic provide information on the differences on the polarimetric behavior of the sample for both spectral profiles considered.
Obviously, when either or is depolarizing, the polarimetric descriptors of are also genuinely different from those of the sole or .
The power of the synthetic procedure for the generation of images that hold information about the changes in the polarimetric behavior for different spectral profiles of the light probe can be enhanced by using more than two light probes (i.e., ). In general, new point-to-point Mueller matrices can be synthesized through the simple procedure indicated in Eq. (1). The larger n and the larger are (within the range considered: optical, microwave…), the greater polarimetric randomness is generated in , in such a manner that the point-to-point values of the three IPP of decrease correspondingly and move away from unity. In general, up to three new respective images for the three IPP are generated, while the images obtained for the remaining twelve polarimetric descriptors adopt specific new features, which can reflect different aspects of the variation of the polarimetric behavior of the sample as different spectral profiles of the light probe are used.
4. Discussion
Given a point-to-point Mueller matrix measurement on a given material sample with spatially heterogeneous polarimetric behavior (under fixed interaction conditions; i.e. relative orientation of the sample with respect to the direction of the collimated light probe, transmission, reflection or scattering operation mode, angle of observation, etc.), infinite polarimetric images can be generated through the spatial dependence of parameters defined as functions of the sixteen elements of the measured Mueller matrices. Nevertheless, once the spectral profile of the light probe of the imaging polarimeter is fixed, the images obtained for a set of sixteen well suited parameters representing independent and significant properties, like for instance the one derived from the arrow decomposition of the point-to-point Mueller matrix, constitute a reasonable and sufficient framework for inspecting the polarimetric image features of the sample.
Obviously, for each different spectral profile of the light probe used, a new set of images is generated, extending the power to analyze the sample. The changes from a set of images to other one depend on the specific behavior of the sample for each spectral profile, in such a way that both the central frequency and the bandwidth and shape of the profile influence the measurement. In particular, as the bandwidth increases, the more polarimetric randomness is introduced by the interaction with the sample and consequently the lower are the corresponding indices of polarimetric purity. It can be said that, as the bandwidth is reduced, more deterministic the polarimetric behavior of the sample is and vice versa, and that, as the bandwidth is increased, the composition of the polarimetric behaviors of the sample for the different frequencies involved increases the depolarization of the emerging light probe before reaching the polarization state analyzer of the polarimeter.
In addition to the specific images obtained for different spectral profiles of the light probe of the polarimeter, which provide specific information for each corresponding kind of interaction, new sets of images can be generated by the synthetic parallel composition of the point-to-point Mueller matrices obtained in each independent experiment. These new Mueller matrices encompass, in a peculiar manner, information on the differences in the behavior of the sample as the type of the light probe changes.
When two independent measurements are made by using spectral profiles whose frequencies do not overlap, the synthesized Mueller matrices coincide (at least from a theoretical point of view) with those obtained through a simple measurement where both light probes are used simultaneously (provided the relative weights of the Mueller matrices in the convex sum coincide with the relative weights of the intensities used). Nevertheless, when the spectral profiles overlap to some extent, the synthetic matrices differ from those potentially generated experimentally through a simultaneous combination of both light probes. This in no way detracts from interest of the general synthesis of point to point Mueller matrices through parallel composition of the ones obtained in independent measurements. In fact, the synthesis leads to a new arrangement of the polarimetric information already obtained in each measurement, which allows for getting new images that are well defined from an algebraic point of view.
It should be emphasized that the potential improvements in the contrast of images strongly depend on the nature of the material sample and that are not necessarily realized for each independent parameter, but can be made evident for some descriptors, different for each case. Some preliminary analyses of certain samples of biological tissues, allow us to say that the new approach enhances the visualization of certain structures. Specific and comprehensive analyses for certain kinds of material samples require further studies, which will be the subject of future works and fall outside the scope of this communication whose main objective is to present the theoretical approach for synthetic imaging Mueller polarimetry.
In general, all the polarimetric descriptors of the synthetic point-to-point Mueller matrix are different from those of the n measured Mueller matrices used as its parallel components of , while the integer number r of IPP with values below their maximum (with increases as the number of measurements involved increases (recall that ). This property is evident when the measured Mueller matrices are nondepolarizing, thus satisfying , while the synthetic is necessarily depolarizing, with . The specific value of r exhibited by depends strongly on the nature and differences among its components .
5. Conclusions
The sets of point-to-point Mueller matrices associated with a given material sample and obtained by a number n of independent Mueller imaging measurements provide information that, beyond that is held by the measured Mueller matrices themselves, can be rearranged into a set of synthetic point-to-point Mueller matrices whose polarimetric descriptors (enpolarizing, retarding and depolarizing parameters) depend on the changes of the polarimetric behavior of the sample when the spectral profile of the light probe of the polarimeter changes.
The procedure to generate the point-to-point synthetic Mueller matrices is as simple as calculating the respective mean Mueller matrices, which exhibit polarimetric descriptors that, in general, are different from those of the measured Mueller matrices. This allows for generating new polarimetric images of the sample that can enhance the visualization of certain structural properties of the sample.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest
References
- N. Ghosh and I. A. Vitkin, "Tissue polarimetry: concepts, challenges, applications, and outlook,” J. Biomed. Opt. 16, 110801 (2011). [CrossRef]
- D. N. Ignatenko, A.V. Shkirin, Y. P. Lobachevsky, S. V. Gudkov, “Applications of Mueller Matrix Polarimetry to Biological and Agricultural Diagnostics: A Review,” Appl. Sci. 12, 5258 (2022). [CrossRef]
- R. Touzi, W.M. Boerner, J.S. Lee, and E. Lueneburg, “A review of polarimetry in the context of synthetic aperture radar: concepts and information extraction,” Can. J. Remote Sensing, 30, 380–407 (2004). [CrossRef]
- J. S. Tyo, D. L. Goldstein, D. B. Chenault, and J. A. Shaw, “Review of passive imaging polarimetry for remote sensing applications,” Appl. Opt. 45, 5453- 5469 (2006). [CrossRef]
- S. R. Cloude, Polarisation: Applications in Remote Sensing. Oxford University, London, 2009.
- R. M. A. Azzam, “Photopolarimetric measurement of the Mueller matrix by Fourier analysis of a single detected signal,” Opt. Lett. 2, 148–150 1977. [CrossRef]
- P. S. Hauge “Mueller matrix ellipsometry with imperfect compensators,“ J. Opt. Soc. Am. 68, 1519-1528 (1978). [CrossRef]
- J. J. Gil, Metodo dinamico de determinacion de matrices de Mueller por analisis de Fourier, Physics Degree Thesis, 1979. Available in https://www.researchgate.net/publication/235981117_Metodo_dinamico_de_determinacion_de_parametros_de_Stokes_y_matrices_de_Mueller_por_analisis_de_Fourier. Accessed 23/07/2023.
- D. H. Goldstein “Mueller matrix dual-rotating retarder polarimeter,” Appl. Opt. 31, 6676-6683 (1992). [CrossRef]
- J. L. Pezzaniti and R. A. Chipman, “Mueller Matrix Imaging Polarimetry,” Opt. Eng. 34, 1558–1568 (1995). [CrossRef]
- E. Garcia-Caurel, A. De Martina, and B. Drevillon, “Spectroscopic Mueller polarimeter based on liquid crystal devices,” Thin Solid Films 455-456, 120-123 (2004). [CrossRef]
- J. Zallat, S. Ainouz, and M. P. Stoll, “Optimal configurations for imaging polarimeters: impact of image noise and systematic errors,” J. Opt. A: Pure Appl. Opt. 8, 807-814 (2006). [CrossRef]
- Arteaga, J. Freudenthal, B. Wang and B Kahr, "Mueller matrix polarimetry with four photoelastic modulators: theory and calibration," Appl. Opt. 51, 6805-6817 (2012). [CrossRef]
- R. M. A. Azzam, “Stokes-vector and Mueller-matrix polarimetry,” J. Opt. Soc. Am. A 33, 1396-1408 (2016). [CrossRef]
- S. Bian, C. Cui, and O. Arteaga, “Mueller matrix ellipsometer based on discrete-angle rotating Fresnel rhomb compensators,” Appl. Opt. 60, 4964-4971 (2021). [CrossRef]
- J. J. Gil, “Absolute Mueller polarimeters based on dual-rotating imperfect retarders and arbitrary ratio of angular velocities," Dynamics 3, 250-271 (2023). [CrossRef]
- J. J. Gil, “Transmittance constraints in serial decompositions of Mueller matrices. The arrow form of a Mueller matrix,” J. Opt. Soc. Am. A 30, 701-707 (2013). [CrossRef]
- J. J. Gil, “Structure of polarimetric purity of a Mueller matrix and sources of depolarization,” Opt. Commun. 368, 165-173 (2016). [CrossRef]
- J. J. Gil, “Components of purity of a Mueller matrix,” J. Opt. Soc. Am. A 28, 1578-1585 (2011). [CrossRef]
- J. J. Gil, I. San José, M. Canabal-Carbia, I. Estévez, E. González-Arnay, J. Luque, T. Garnatje, J. Campos, and A. Lizana, "Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices," Photonics 10, 669 (2023). [CrossRef]
- B. A. Robson. The Theory of Polarization Phenomena. Clarendon Press, Oxford, 1975.
- Z-F Xing, “On the deterministic and non-deterministic Mueller matrix,” J. Mod Opt. 39, 461-484 (1992). [CrossRef]
- S.-Y. Lu and R. A. Chipman, “Interpretation of Mueller matrices based on polar decomposition,” J. Opt. Soc. Am. A 13, 1106–1113 (1996). [CrossRef]
- J. J. Gil, E. Bernabéu, “Depolarization and polarization indices of an optical system” Opt. Acta 33, 185-189 (1986). [CrossRef]
- J. J. Gil, “Polarimetric characterization of light and media - Physical quantities involved in polarimetric phenomena,” Eur. Phys. J. Appl. Phys. 40, 1–47 (2007).
- J. J. Gil, R. Ossikovski. Polarized light and the Mueller matrix approach, 2nd Ed. CRC Press, 2022. [CrossRef]
- S. R. Cloude, “Group theory and polarisation algebra”, Optik 75, 26-36 (1986).
- J. J. Gil and E. Bernabéu, "A depolarization criterion in Mueller matrices," Optica Acta, 32 259-261 (1985). [CrossRef]
- K. Hingerl and R. Ossikovski, “General approach for modeling partial coherence in spectroscopic Mueller matrix polarimetry,” Opt. Lett. 41, 219-222 (2016). [CrossRef]
- R. Ossikovski and K Hingerl, “General formalism for partial spatial coherence in reflection Mueller matrix polarimetry,” Opt. Lett. 41, 4044-4047 (2016). [CrossRef]
- E. Kuntman, M. A. Kuntman, O. Arteaga, “Vector and matrix states for Mueller matrices of nondepolarizing optical media,” J. Opt. Soc. Am. A 34, 80-86 (2017). [CrossRef]
- E. Kuntman, M. A. Kuntman, J. Sancho-Parramon, O. Arteaga, “Formalism of optical coherence and polarization based on material media states,” Phys. Rev. A 95, 063819 (2017). [CrossRef]
- R. Ossikovski and J. J. Gil, “Basic properties and classification of Mueller matrices derived from their statistical definition,” J. Opt. Soc. Am. A 34, 1727-1737 (2017). [CrossRef]
- San José and J. J. Gil, "Coherency vector formalism for polarimetric transformations," Opt. Commun. 475, 126230 (2020). [CrossRef]
- San José, J. J. Gil, “Invariant indices of polarimetric purity: Generalized indices of purity for n × n covariance matrices,” Opt. Commun. 284, 38-47 (2011). [CrossRef]
- J. J. Gil and I. San José, "Arbitrary decomposition of a Mueller matrix," Opt. Lett. 44, 5715-5718 (2019). [CrossRef]
- J. J. Gil, “Physical Quantities Involved in a Mueller Matrix,” In Proceedings of the SPIE 9853, Baltimore Chenault, MD, USA, 17–21 April 2016; p. 985302. [CrossRef]
- J. J. Gil, Determination of polarization parameters in matricial representation. Theoretical contribution and development of an automatic measurement device. PhD thesis, University of Zaragoza, 1983. Available in http://zaguan.unizar.es/record/10680/files/TESIS-2013-057.pdf.
- R. Ossikovski, "Interpretation of nondepolarizing Mueller matrices based on singular-value decomposition," J. Opt. Soc. Am. A 25, 473-482 (2008). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).