Prerpints.org logo
Preprint
Article

Kernel Geometric Mean Metric Learning

Altmetrics

Downloads

145

Views

41

Comments

1

A peer-reviewed article of this preprint also exists.

Submitted:

29 July 2023

Posted:

01 August 2023

You are already at the latest version

Alerts
Abstract
This paper propose a kernel geometric mean metric learning (KGMML) algorithm. The basic idea is to obtain the closed-form solution of the geometric mean metric learning (GMML) algorithm in the high-dimensional feature space determined by the kernel function. Then, the solution is generalized as a form of kernel matrix by using the integral representation of the weighted geometric mean and the Woodbury matrix in this new feature space. Experimental results on 15 datasets show that the proposed algorithm can effectively improve the accuracy of the GMML algorithm and other metric algorithms.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Analyzing the modeling process of machine learning algorithms, it is clear that the construction of a learning algorithm requires a similarity metric between sample pairs given. It is well known that the distance measure is one of the most commonly used measures to describe the similarity between samples. At present various distance metrics have been proposed such as Euclidean distance and Mahalanobis distance. However, these distance metric expressions are fixed, i.e., there are non-adjustable parameters, which result in different effectiveness of dealing with various problems. Thus, an effective distance metric is proposed by constructing learning from training samples. From the definition of the distance metric, it follows that any binary function d x i , x j defined in the feature space is called a distance function, provided that the four conditions of symmetry, self-similarity, non-negativity, and trigonometric inequality are satisfied simultaneously. Thus any binary function
d M x i , x j = x i − x j T M x i − x j ,
is a distance function determined by any symmetric positive definite (SPD) matrix M, where x i , x j are two samples from the training set X , and usually M is called a metric matrix. The purpose of metric learning is to use training samples to learn a metric matrix M such that the resulting distance function d M x i , x j can improve the performance of the learning algorithm or satisfy some application requirements. Thus, metric learning has wide applications in many fields, such as pattern recognition [1,2], data mining [3,4,5], information security [6,7], bioinformatics [8,9], and medical diagnosis [10,11,12].
Because of the wide application space, metric learning techniques have received a lot of attention and many excellent algorithms have been proposed methods. Xing [13] first proposed a metric learning algorithm. The main idea of the algorithm is to learn a metric matrix so that the distance between similar pairs of samples is small and the distance between dissimilar pairs of samples is large. The algorithm can make the distribution of similar pairs of samples in the new metric space more compact more compact in the new metric space, while the distribution of dissimilar pairs is more discrete. The proposal of this algorithm marked the real development of metric learning, and many subsequent research works were inspired by this algorithm. Davis [14] proposed an information theoretic metric learning algorithm. The basic idea of the algorithm is to assume the existence of an a priori metric matrix M 0 , while ensuring that the distance between similar pairs of samples is less than a threshold and the distance between dissimilar pairs of samples is greater than a threshold. Minimize the relative entropy between the multivariate Gaussian distributions corresponding to M and M 0 . Wang [15] proposed an information geometry metric learning algorithm. The basic idea of the algorithm is to use the category labeling information of the training samples to construct a kernel matrix that can reflect the desired distance between samples. Construct an actual kernel matrix describing the realistic distance relationship between the samples using the eigenvectors of the samples as well as the metric matrix M. The metric matrix M is then solved by minimizing the distance between these two kernel matrices. Weinberger [16] proposed a metric learning algorithm based on maximum margin. The basic idea is to define an interval function between similar samples of each sample and other classes of samples. The metric matrix is then solved by minimizing the distance between similar pairs of samples and maximizing the defined interval.
Geometric mean metric learning algorithm was proposed by Pourya [17] in 2016. The essence of most metric learning algorithms is to minimize the distance between similar pairs of samples rather than maximize the distance between similar pairs of samples, therefore the sign of the term corresponding to the dissimilar pair of samples in the objective function is usually negative, while the strategy of the geometric mean metric learning model is to use the inverse matrix of the metric matrix M to represent the distance between dissimilar pairs of samples. The advantage of this approach is that the sign of the item corresponding to the dissimilar pair of samples in the objective function will become positive, which reduces the difficulty of solving the model. Its objective function is as follows:
min M > 0 ∑ x i , x j ∈ D + d M x i , x j + ∑ x i , x j ∈ D − d M − 1 x i , x j ,
where the similar pair sample set D + and the dissimilar pair sample set D − can be expressed as:.
D + = x i , x j ∣ x i , x j are in the same class , D − = x i , x j ∣ x i , x j are in different class .
Although GMML algorithm has some advantages, such as unconstrained convex objective function, closed form solution and interpretability, and faster calculation speed [18], it is actually a linear learning method and does not work well to address non-linear problems. Kernel methods are key technology for addressing nonlinear problems, and therefore kernel algorithms [19,20,21,22,23] have been proposed. The principle of the kernel method is that the original data transformed from the input space into a higher dimensional feature space by a mapping function. This transformation must be achieved to offer a reliable linear model in the feature space that corresponds to a nonlinear solution in the original data space. Gaussian kernel functions were used to map the data in the feature space. The closed form solution of the GMML algorithm is represented as a kernel matrix by using the integral representation of the weighted geometric mean and the Woodbury matrix. Then the KGMML algorithm is obtained. Thus the nonlinear problem can be handled effectively while retaining the advantages of the GMML algorithm. We define the objective function as the following form:
min M Φ > 0 ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ + d M Φ Φ ( x i ) , Φ ( x j ) + ∑ ( Φ ( x i ) − Φ ( x j ) ∈ D Φ − d M Φ − 1 Φ ( x i ) , Φ ( x j ) ,
where a mapping is Φ : R m ↦ H κ (Hilbert Space), i.e., x ∈ R m → Φ ( x ) ∈ H κ , M Φ is the metric matrix in H κ space, the set of similar pairs D Φ + and the set of dissimilar pairs D Φ − are
D Φ + = Φ ( x i ) , Φ ( x j ) ∣ Φ ( x i ) , Φ ( x j ) are in the same class , D Φ − = Φ ( x i ) , Φ ( x j ) ∣ Φ ( x i ) , Φ ( x j ) are in different class .
The main innovation of the paper is to study kernel geometric mean metric learning algorithm for nonlinear distance using a kernel function. The key idea is to construct kernel matrices based on the distance metric for the given training data. Secondly, the accuracy of the proposed algorithm is superior to GMML algorithm and other metric algorithms. The structure of this paper is organized as follows: In Sect. 2, some lemmas of weighted geometric mean and Woodbury identity are formulated. Then, in Sect. 3, optimization problem and its solution were discuss, then extension to weighted geometric mean is discussed. The steup of the experiment and the analysis of parameter sensitivity are carried out in Sect. 4. Finally, our results are summarized in Sect. 5.

2. Preliminaries

In this section, three lemmas will be given in order to simplify the objective function (4) more clearly.
Lemma 1.
[24] For any t ∈ ( 0 , 1 ) , A is n × n positive definite and B is n × n Hermitian, the following equation holds
A ♯ t B = 2 sin ( π t ) π A ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 ( 1 − s ) I + ( 1 + s ) B − 1 A − 1 d s ,
which is the integral representation of the A , B weighted geometric mean, where I is the identity matrix.
Lemma 2.
[25] If A is a n × n invertible matrix corrected by U C V where U is n × k matrice, C is k × k matrice, V is k × n matrice, then Woodbury identity is
( A + U C V ) − 1 = A − 1 − A − 1 U C − 1 + V A − 1 U − 1 V A − 1 .
Lemma 3.
[24] For any t ∈ ( 0 , 1 ) , A is n × n positive definite and B is n × n Hermitian, the following equation holds
A ♯ t B = A B − 1 A − t .

3. Main results

3.1. Optimization problem and its solution

In the following, the objective function (4) can be simplified in view of Eq.(1), one has
min M Φ > 0 ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ + Φ ( x i ) − Φ ( x j ) T M Φ Φ ( x i ) − Φ ( x j ) + ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ − ( Φ ( x i ) − Φ ( x j ) T M Φ − 1 ( Φ ( x i ) − Φ ( x j ) .
Rewriting the Mahalanobis distance uses traces, Eq.(4) can be turned into the following optimization problem
min M Φ > 0 ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ + tr M Φ Φ ( x i ) − Φ ( x j ) Φ ( x i ) − Φ ( x j ) T + ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ − tr M Φ − 1 Φ ( x i ) − Φ ( x j ) Φ ( x i ) − Φ ( x j ) T = min M Φ > 0 tr ( M Φ S Φ ) + tr M Φ − 1 D Φ = △ min M Φ > 0 h ( M Φ ) ,
where S Φ , D Φ are SPD matrixes, and it is a realistic assumption in many situations [17]. Thus S Φ , D Φ can be expressed as
S Φ = ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ + Φ ( x i ) − Φ ( x j ) Φ ( x i ) − Φ ( x j ) T , D Φ = ∑ Φ ( x i ) , Φ ( x j ) ∈ D Φ − Φ ( x i ) − Φ ( x j ) Φ ( x i ) − Φ ( x j ) T .
Differentiating h ( M Φ ) with respect to M Φ yields
∇ h M Φ = S Φ − M Φ − 1 D Φ M Φ − 1 .
Then, ∇ h ( M ) is set to 0, which implies that
M Φ S Φ M Φ = D Φ ,
it is clear that the above equation is a Riccati equation. Since S Φ and D Φ are positive definite matrices, Eq.(4) has a unique positive solution which is the midpoint of the geodesic joining S Φ − 1 to D Φ [26], that is
M Φ = S Φ − 1 ♯ 1 / 2 D Φ = S Φ − 1 / 2 S Φ 1 / 2 D Φ S Φ 1 / 2 1 / 2 S Φ − 1 / 2 ,
where S Φ − 1 ♯ 1 / 2 D Φ represents the geometric mean of S Φ − 1 and D Φ .

3.2. Extension to weighted geometric mean

In order to incorporate the weighted geometric mean, it is necessary to take into account the determination of weights for the objective function. When assigning linear weights for S Φ − 1 and D Φ , only the metric matrix M Φ can be uniformly scaled by a constant factor. Consequently, it is illogical to assign linear weights to the two components in Eq.(2). Nevertheless, by employing nonlinear weights derived from SPD manifold Riemannian geometry, the weights can be transformed into trade-offs between the two terms. Thus, the Riemann distance δ R is introduced, and the problem of finding the minimum value of h ( M Φ ) is equivalent to solving the minimum value of the following optimization problem
min M Φ ⪰ 0 δ R 2 M Φ , S Φ − 1 + δ R 2 M Φ , D Φ ,
where the Riemannian distance between SPD matrices X and Y is denoted by δ R 2 ( X , Y ) = log Y − 1 / 2 X Y − 1 / 2 F , and . F is the Frobenius norm of a matrix. A linear parameter t ∈ [ 0 , 1 ] is introduced to trade off the relationship of the two terms in the formula
min M Φ ⪰ 0 ( 1 − t ) δ R 2 M Φ , S Φ − 1 + t δ R 2 M Φ , D Φ = △ min M Φ > 0 h t ( M Φ ) .
Because h t ( M Φ ) is still geodesically convex (see [17]), Eq.(13) has a unique positive solution, that is
M Φ = S Φ − 1 ♯ t D Φ .
For the convenience of subsequent calculations, the notations are defined as follow
P Φ = ∑ Φ x i , Φ x j ∈ D Φ + Φ x i − Φ x j , Q Φ = ∑ Φ x i , Φ x j ∈ D Φ − Φ x i − Φ x j .
Theorem 1.
The solution M Φ = S Φ − 1 ♯ t D Φ of the objective function (4) can be rewritten as
M Φ = Q Φ K P Q T K P Q t − 1 Q Φ T ,
where the kernel matrix K P Q = P Φ · Q Φ = P Φ T Q Φ , and · is denoted inner product.
Proof. 
According to Lemma 1
M Φ = S Φ − 1 ♯ t D Φ = 2 s i n ( π t ) π S Φ − 1 ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 ( ( 1 − s ) I + ( 1 + s ) D Φ − 1 S Φ − 1 ) − 1 d s = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 ( ( 1 − s ) S Φ + ( 1 + s ) D Φ − 1 ) − 1 d s .
Substituting S Φ = P Φ P Φ T , D Φ = Q Φ Q Φ T into Eq.(15), it is clearly that
M Φ = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 ( ( 1 − s ) P Φ P Φ T + ( 1 + s ) ( Q Φ Q Φ T ) − 1 ) − 1 d s .
For convenience in the following discussion, we introduce the notation
G : = 1 − s P Φ P Φ T + 1 + s Q Φ Q Φ T − 1 − 1 .
From Lemma 2, it follows that
G = ( A + U C V ) − 1 = A − 1 − A − 1 U C − 1 + V A − 1 U − 1 V A − 1 ,
where A : = 1 + s Q Φ Q Φ T − 1 , U : = P Φ , C : = ( 1 − s ) I , V : = P Φ T . Then, taking it into Eq.(16), one has
M Φ = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 [ Q Φ Q Φ T 1 + s − Q Φ Q Φ T 1 + s · P Φ I − 1 1 − s + P Φ T · Q Φ Q Φ T 1 + s · P Φ − 1 P Φ T Q Φ Q Φ T 1 + s ] d s . = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 [ Q Φ Q Φ T 1 + s − Q Φ 1 + s · K P Q T I − 1 1 − s + K P Q K P Q T 1 + s − 1 K P Q Q Φ T 1 + s ] d s = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 Q Φ [ I 1 + s − K P Q T 1 + s I − 1 1 − s + K P Q K P Q T 1 + s − 1 K P Q 1 + s ] Q Φ T d s ,
where K P Q = P Φ T Q Φ , and set
G : = I 1 + s − K P Q T 1 + s I − 1 1 − s + K P Q K P Q T 1 + s − 1 K P Q 1 + s .
In view of Lemma 2
G = A − 1 − A − 1 U C − 1 + V A − 1 U − 1 V A − 1 = ( A + U C V ) − 1 ,
where A : = [ ( 1 + s ) I ] , U : = K P Q T , C : = ( 1 − s ) I , V : = K P Q . Thus,
M Φ = 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 Q Φ ( ( 1 + s ) I + ( 1 − s ) K P Q T K P Q ) − 1 Q Φ T d s = Q Φ 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 1 + s K P Q T K P Q − 1 K P Q T K P Q + 1 − s K P Q T K P Q − 1 d s Q Φ T = Q Φ K P Q T K P Q − 1 2 s i n ( π t ) π ∫ − 1 1 ( 1 − s ) − t ( 1 + s ) t − 1 1 − s I + 1 + s K P Q T K P Q − 1 − 1 d s Q Φ T = Q Φ K P Q T K P Q − 1 I ♯ t ( K P Q T K P Q ) Q Φ T .
From Lemma 3, it follows that
M Φ = Q Φ K P Q T K P Q − 1 K P Q T K P Q − 1 − t Q Φ T = Q Φ K P Q T K P Q t − 1 Q Φ T .
   □
From the definition of the kernel matrix yields
K i Q = Φ x i · Q Φ , K j Q = Φ x j · Q Φ .
Theorem 2.
The distance d M Φ ( x i , x j ) = Φ x i − Φ x j T M Φ Φ x i − Φ x j can be rewritten as
d M Φ ( x i , x j ) = ( K i Q − K j Q ) K P Q T K P Q t − 1 ( K i Q T − K j Q T ) .
Proof. 
According to Theorem 1
d M Φ ( x i , x j ) = Φ x i − Φ x j T Q Φ K P Q T K P Q t − 1 Q Φ T Φ x i − Φ x j = ( K i Q − K j Q ) K P Q T K P Q t − 1 ( K i Q T − K j Q T ) .
   □
Eq.(23) can be taken as the final result of kernel geometric mean metric learning algorithm. The algorithm is summarized in Algorithm 1.
Algorithm 1 Kernel Geometric Mean Metric Learning Algorithm
Input: Training set S = ( x i , x j ) | x i , x j ∈ X .
Parameter: t: t ∈ [ 0 , 1 ] , the weight coefficient in Eq.(14),
p: kernel parameters of Gaussian kernel function.
Output: d M Φ the distance learned for KGMML,
Step1. According to Eq.(5), construct D Φ + and D Φ − .
Step2. Compute kernel matrices K P Q , K i Q and K j Q according to Theorem 1 and Theorem 2.
Step3. Compute d M Φ ( x i , x j ) = ( K i Q − K j Q ) K P Q T K P Q t − 1 ( K i Q T − K j Q T ) .

4. Experiment

4.1. Experimental setup

To verify the effectiveness of algorithm 1, simulation experiments will be conducted on 15 UCI [27] datasets, where the basic information is shown in Table 1.
Table 1. Characteristics of experimental datasets.
Table 1. Characteristics of experimental datasets.
Data sets Of features Of instances Of classes
1 Pima 8 768 2
2 Vehicle 18 846 4
3 German 24 1000 2
4 Segment 18 2310 7
5 Usps 256 9298 10
6 Mnist 784 4000 10
7 Glasses 9 214 6
8 DNA 180 3186 2
9 Heart-Disease 13 270 2
10 Lymphgraphy 18 148 4
11 Liver-Disorders 6 345 2
12 Hages-Roth 4 160 3
13 Ionosphere 34 351 2
14 Spambase 57 4601 2
15 Balance-Scale 4 625 3
Next, some efficient algorithms are described for distance metric learning, and the proposed method is compared with existing excellent classical algorithms. The specific introduction will be given in Table 2. For the KGMML, the setting of t and p will be given in detail in the next subsection.
Table 2. Briefly describes the distance metric learning method used in this paper
Table 2. Briefly describes the distance metric learning method used in this paper
Name Description
1 Euclidean The Euclidean distance metric [28].
2 DMLMJ Distance metric learning through maximization of the Jeffrey divergence [28].
3 LMNN Large margin nearest neighbor classification [16].
4 GB-LMNN Non-linear Transformations with Gradient Boosting [29].
5 GMML Geometric Mean Metric Learning [17].
6 Low-rank Low-rank geometric mean metric learning [30].
7 KGMML The kernelized version of GMML

4.2. Parameter Sensitivity Analysis

It can be seen from Algorithm1 that the values of t and p are specified before use. To determine the impact of these two parameters on the KGMML algorithm, the experiments are conducted on five datasets selected from 15 datasets. 5-fold cross-validation is used to choose the best t-value, and the two-step method is used to test different t-values. 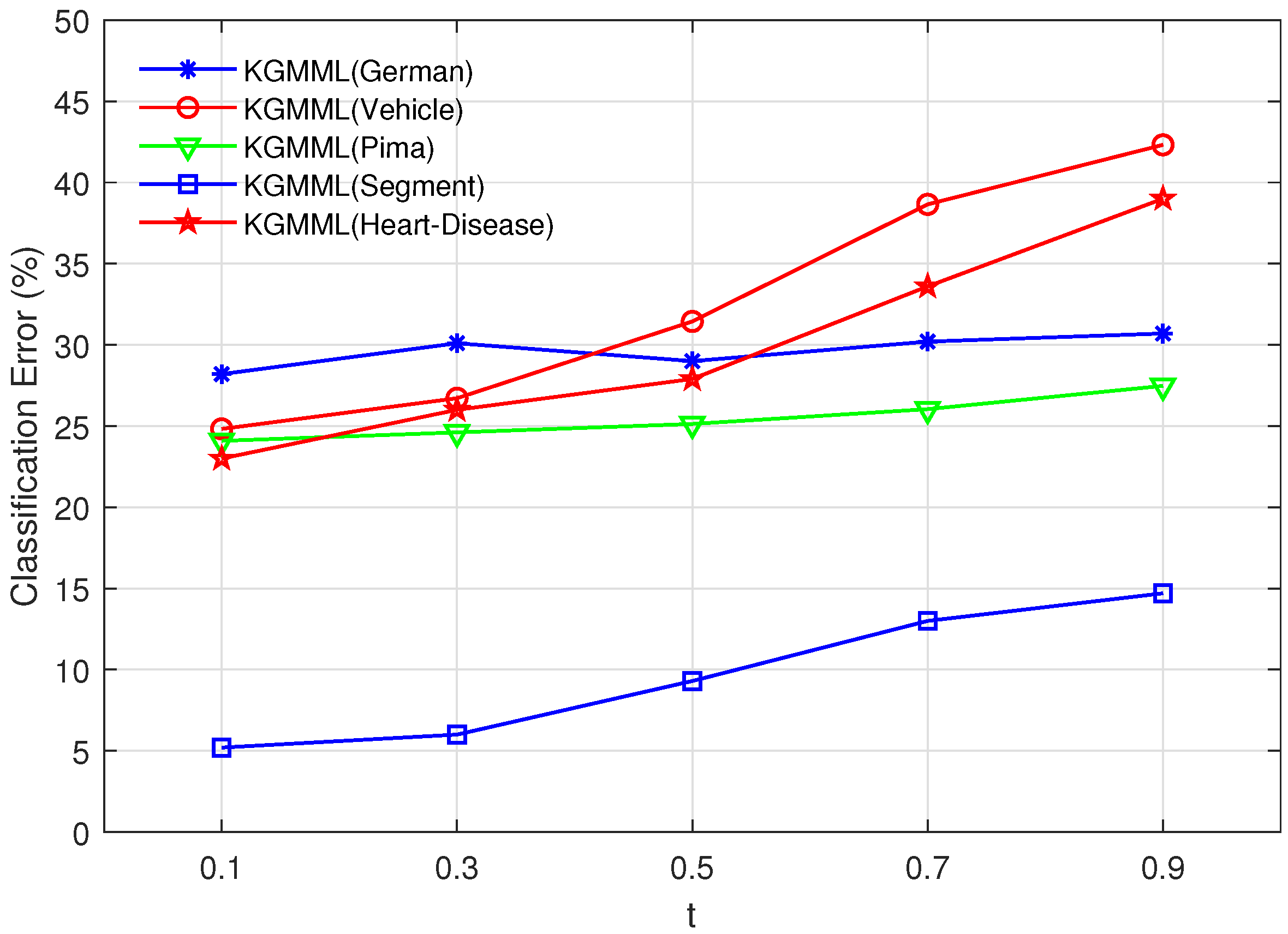The above approach is used to find the best t-value, and its precision can be verified in Figure 1 and Figure 2. Firstly, obtain the optimal t in the set 0 . 1 , 0 . 3 , 0 . 5 , 0 . 7 , 0 . 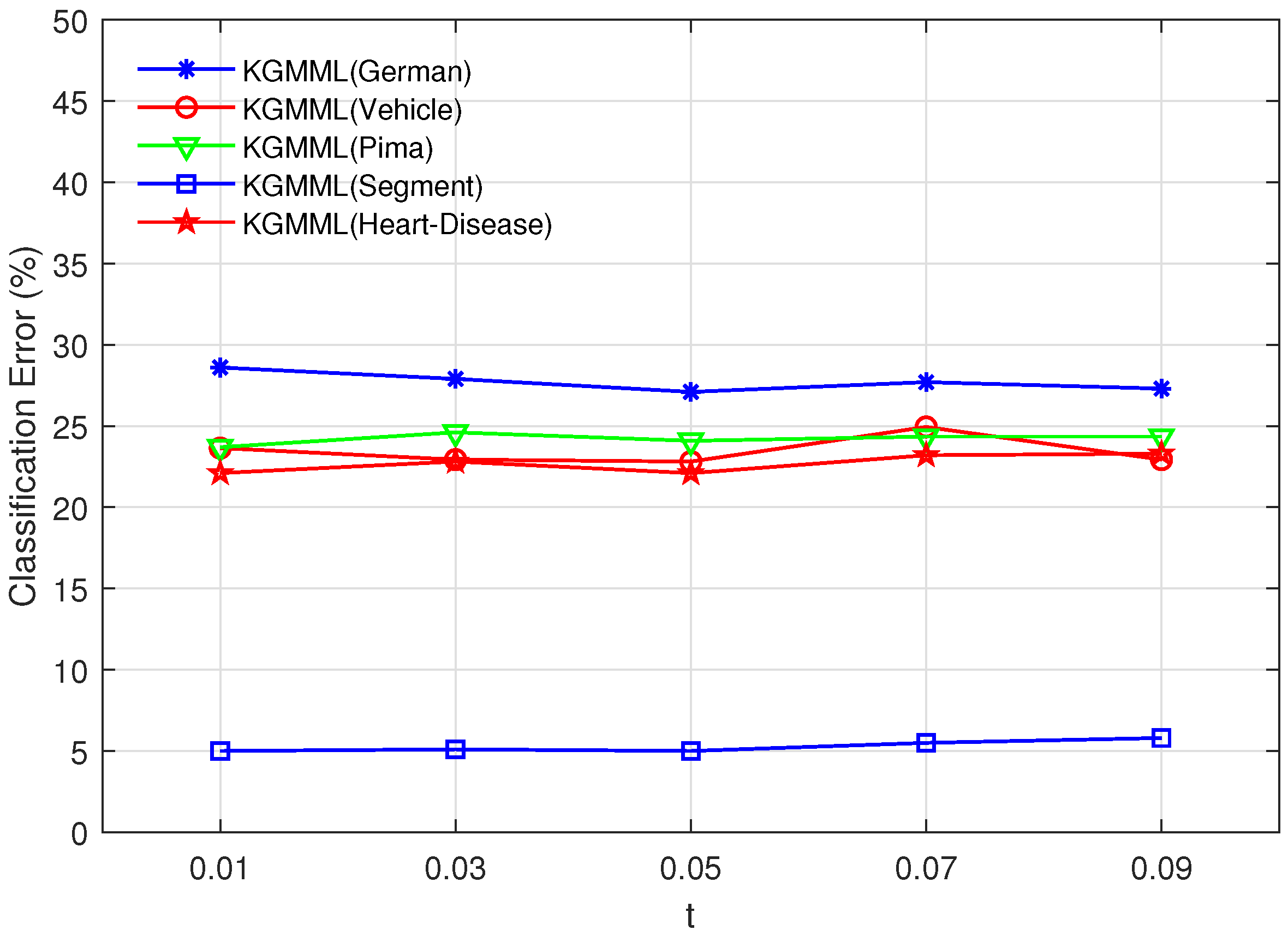9 , and the result is shown in Figure 1. Secondly, test 5 t-values using intervals with a step size of 0.02. As shown in Figure 2, the variation of accuracy in the test interval with a step size of 0.02 is not significant, so we chose the middle t-value of 0.05. 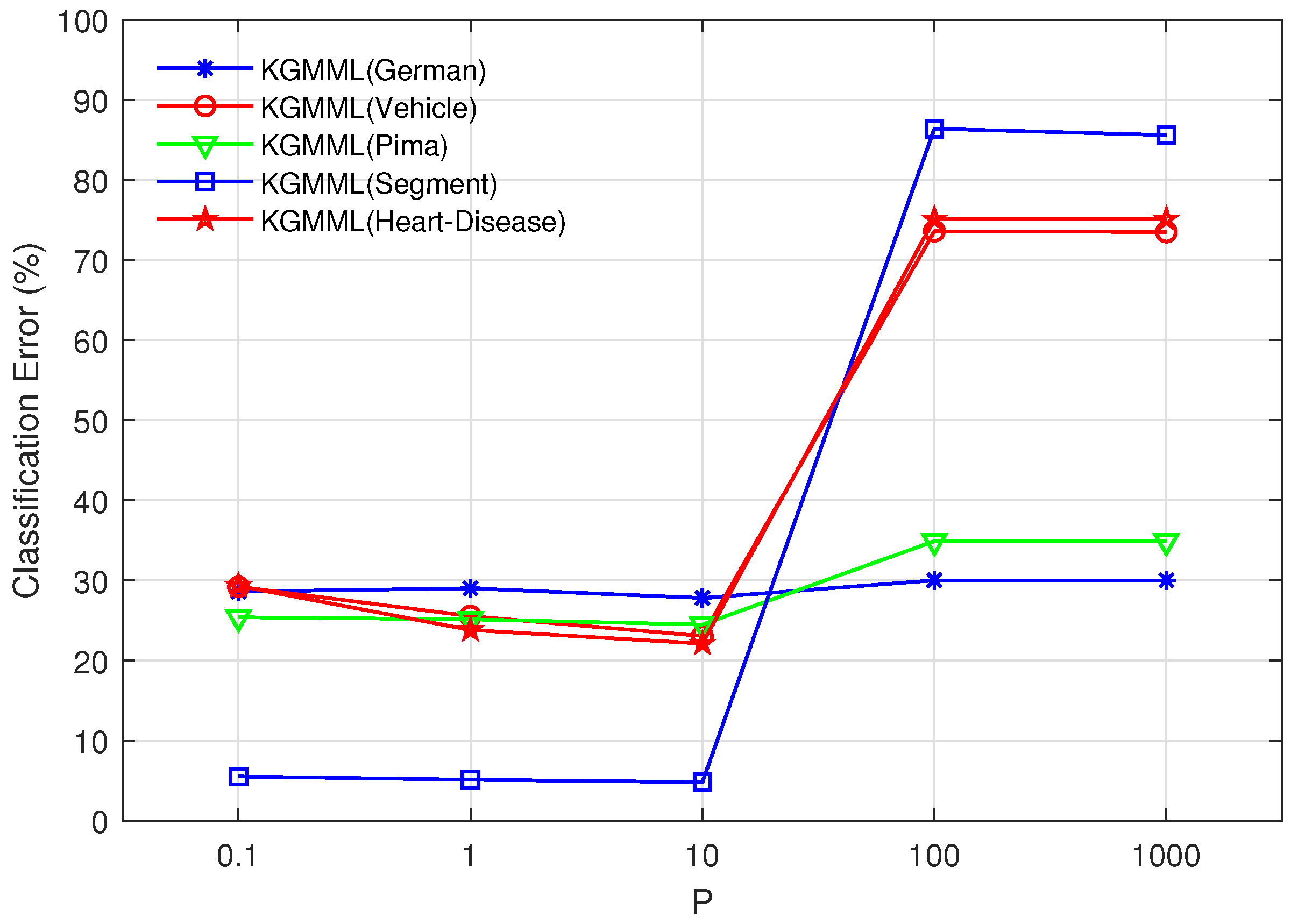When the p-value is 10, the precision has an inflection point in Figure 3, and the precision is higher at the inflection point. Thus, the p- value is chosen as 10. Vary t in the set 0 . 1 , 0 . 3 , 0 . 5 , 0 . 7 , 0 . 9 , and p is fixed.
Preprints 80922 g001
Figure 1. Vary t in the set 0 . 1 , 0 . 3 , 0 . 5 , 0 . 7 , 0 . 9 , and p is fixed.
Figure 1. Vary t in the set 0 . 1 , 0 . 3 , 0 . 5 , 0 . 7 , 0 . 9 , and p is fixed.
Preprints 80922 g001
Preprints 80922 g002
Figure 2. Vary t in the set 0 . 01 , 0 . 03 , 0 . 05 , 0 . 07 , 0 . 09 , and p is fixed
Figure 2. Vary t in the set 0 . 01 , 0 . 03 , 0 . 05 , 0 . 07 , 0 . 09 , and p is fixed
Preprints 80922 g002
Preprints 80922 g003
Figure 3. Vary p in the set 0 . 01 , 1 , 10 , 100 , 1000 , and t is fixed
Figure 3. Vary p in the set 0 . 01 , 1 , 10 , 100 , 1000 , and t is fixed
Preprints 80922 g003

4.3. Experimental Results

The accuracy of each compared algorithm on 15 datasets is shown in Table 3, where the best result on each dataset is shown in boldface. Compared with the other six algorithms, the highest accuracy is achieved from KGMML algorithm on the 8 datasets. All experimental methods are implemented on MATLABR2018b (64-bit), and the simulations are run on a laptop with an Intel Core i5 (2.5GHz) processor.
Table 3. Error rate results are shown on UCI dataset, and the best result is shown in bold.
Table 3. Error rate results are shown on UCI dataset, and the best result is shown in bold.
Data sets GMML DMLMJ LMNN GB-LMNN Educlidean Low-rank KGMML
1 Pima 27.66 30.18 33.82 37.14 27.27 29.58 25.17
2 Vehicle 22.09 25.75 46.53 41.24 33.53 41.32 21.21
3 German 27.41 24.79 30.50 29.32 31.53 26.96 24.40
4 Segment 4.13 3.64 5.19 4.55 6.93 5.59 3.22
5 Usps 3.72 2.88 33.11 10.60 10.55 4.08 2.82
6 Mnist 9.65 16.44 86.80 82.62 17.12 75.34 8.32
7 Glasses 36.96 33.08 30.20 23.30 30.23 33.64 32.47
8 DNA 23.65 21.75 22.32 22.84 27.63 26.24 23.05
9 Heart-Disease 20.82 19.73 31.52 18.51 33.33 22.52 18.97
10 Lymphography 56.88 73.62 70.76 60.21 75.13 57.57 53.75
11 Liver-Disorders 35.00 30.05 30.46 34.88 31.88 41.86 30.17
12 Hages-Roth 37.69 16.84 31.33 31.35 16.67 39.55 19.52
13 Ionosphere 15.34 11.27 5.71 4.29 1.43 17.26 11.54
14 Spambase 19.33 18.27 38.60 15.80 16.09 11.43 11.20
15 Balance-Scale 12.84 8.62 12.80 15.20 14.40 12.31 9.19
In order to show the performance advantages of the KGMML algorithm, a score statistic is performed on the KGMML algorithm and other classic algorithms. The scoring process is as follows: assuming that A is the result of using the KGMML algorithm on a certain data set, and B is the result of uniting the KGMML algorithm on this data set (that is, using other algorithms). Firstly, comparative analysis of A and B is performed by using a 5% significance level t test. In a statistical sense, if A > B , it is considered that the result A obtained by using the KGMML algorithm on this dataset wins the result B using other algorithms. Thus, the statistical result of the score on this data set is recorded as "1/0/0". If A < B , the score statistics result is recorded as "0/0/1". If A = B , it means that A and B are the same in the statistical sense. Thus, it is considered that they are tied and recorded as "0/1/0". It is evident that the notation "5/0/0" signifies that the outcomes achieved by the KGMML algorithm outperform those of other algorithms across five datasets. On each data set and the overall score, the statistical results of the KGMML algorithm are listed in Table 4.
Table 4. The score statistics of the comparison between the results obtained by the KGMML algorithm and other classical algorithms.
Table 4. The score statistics of the comparison between the results obtained by the KGMML algorithm and other classical algorithms.
Datasets KGMML
GMML DMLMJ LMNN GB-LMNN Educlidean Low-rank
Pima 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0
Vehicle 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0
German 1/0/0 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0
Segment 1/0/0 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0
Usps 1/0/0 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0
Mnist 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0
Glasses 1/0/0 0/1/0 0/0/1 0/0/1 0/1/0 1/0/0
DNA 0/1/0 0/0/1 0/0/1 0/1/0 1/0/0 1/0/0
Heart-Disease 1/0/0 0/1/0 1/0/0 0/1/0 1/0/0 1/0/0
Lymphography 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0
Liver-Disorders 1/0/0 0/1/0 0/1/0 1/0/0 0/1/0 1/0/0
Hages-Roth 1/0/0 0/0/1 1/0/0 1/0/0 0/0/1 1/0/0
Ionosphere 1/0/0 0/1/0 0/0/1 0/0/1 0/0/1 1/0/0
Spambase 1/0/0 1/0/0 1/0/0 1/0/0 1/0/0 0/1/0
Balance 1/0/0 0/1/0 1/0/0 1/0/0 1/0/0 1/0/0
Total 12/3/0 5/8/2 11/1/3 9/2/2 11/2/2 14/1/0

5. Conclusions

Kernel geometric mean metric learning is proposed for nonlinear distance metric with the introduction of a kernel function. Traditional metric learning approaches aim to learn a global linear metric, which is not well-suited for nonlinear problems. The experimental results on the UCI dataset show that the algorithm can effectively improve the accuracy of GMML algorithm, and the nonlinear problems can be addressed by the proposed algorithm. In future work, the problem of the inaccurate similarity pair will be tried to improve where it exists in the kernel geometric mean metric learning algorithm. The partial labeling metric learning algorithm has been proposed in recent years, and a partial labeling algorithm based on kernel geometric mean metric learning will be proposed in the future.

Author Contributions

Conceptualization, J.H. and R.Z.; methodology, J.H.; software, Z.F. and T.Y.; validation, Z.F., T.Y. and Y.Z.; formal analysis, Z.F.; investigation, Y.Z.; resources, J.H.; data curation, R.Z.; writing—original draft preparation, Z.F.; writing—review and editing, Z.F.; visualization, Z.F.; supervision, R.Z.; project administration, J.H.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (62102062), the Humanities and Social Science Research Project of Ministry of Education(21YJCZH037), the Natural Science Foundation of Liaoning Province (2020-MS-134, 2020-MZLH-29).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors would like to thank the School of Information and Communication Engineering, Dalian Minzu University for assistance with simulation verifications related to this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lu J, Wang R, Mian A, et al. Distance metric learning for pattern recognition[J]. Pattern recognition, 2018, 75: 1-3. [CrossRef]
  2. Wei Z, Cui Y, Zhou X, et al. A research on metric learning in computer vision and pattern recognition[C]//2018 Tenth International Conference on Advanced Computational Intelligence (ICACI). IEEE, 2018: 254-259. [CrossRef]
  3. Yan Y, Xia J, Sun D, et al. Research on combination evaluation of operational stability of energy industry innovation ecosystem based on machine learning and data mining algorithms[J]. Energy Reports, 2022, 8: 4641-4648. [CrossRef]
  4. Wang F, Sun J. Survey on distance metric learning and dimensionality reduction in data mining[J]. Data mining and knowledge discovery, 2015, 29(2): 534-564. [CrossRef]
  5. Yan M, Zhang Y, Wang H. Tree-Based Metric Learning for Distance Computation in Data Mining[C]//Asia-Pacific Web Conference. Cham: Springer International Publishing, 2015: 377-388. [CrossRef]
  6. Mojisola F O, Misra S, Febisola C F, et al. An improved random bit-stuffing technique with a modified RSA algorithm for resisting attacks in information security (RBMRSA)[J]. Egyptian Informatics Journal, 2022, 23(2): 291-301. [CrossRef]
  7. Kraeva I, Yakhyaeva G. Application of the metric learning for security incident playbook recommendation[C]//2021 IEEE 22nd International Conference of Young Professionals in Electron Devices and Materials (EDM). IEEE, 2021: 475-479. [CrossRef]
  8. Bennett J, Pomaznoy M, Singhania A, et al. A metric for evaluating biological information in gene sets and its application to identify co-expressed gene clusters in PBMC[J]. PLoS Computational Biology, 2021, 17(10): e1009459. [CrossRef]
  9. Makrodimitris S, Reinders M J T, Van Ham R C H J. Metric learning on expression data for gene function prediction[J]. Bioinformatics, 2020, 36(4): 1182-1190. [CrossRef]
  10. Yuan T, Dong L, Liu B, et al. Deep Metric Learning by Exploring Confusing Triplet Embeddings for COVID-19 Medical Images Diagnosis[C]//Workshop on Healthcare AI and COVID-19. PMLR, 2022: 1-10.
  11. Jin Y, Lu H, Li Z, et al. A cross-modal deep metric learning model for disease diagnosis based on chest x-ray images[J]. Multimedia Tools and Applications, 2023: 1-22. [CrossRef]
  12. Xing Y, Meyer B J, Harandi M, et al. Multimorbidity Content-Based Medical Image Retrieval and Disease Recognition Using Multi-label Proxy Metric Learning[J]. IEEE Access, 2023. [CrossRef]
  13. Xing E, Jordan M, Russell S J, et al. Distance metric learning with application to clustering with side-information[J]. Advances in neural information processing systems, 2002, 15.
  14. Davis J V, Kulis B, Jain P, et al. Information-theoretic metric learning[C]//Proceedings of the 24th international conference on Machine learning. 2007: 209-216. [CrossRef]
  15. Wang S, Jin R. An information geometry approach for distance metric learning[C]//Artificial intelligence and statistics. PMLR, 2009: 591-598.
  16. Weinberger K Q, Saul L K. Distance metric learning for large margin nearest neighbor classification[J]. Journal of machine learning research, 2009, 10(2).
  17. Zadeh P, Hosseini R, Sra S. Geometric mean metric learning[C]//International conference on machine learning. PMLR, 2016: 2464-2471.
  18. Zhou Y, Gu H. Geometric mean metric learning for partial label data[J]. Neurocomputing, 2018, 275: 394-402.
  19. Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels[C]//Neural networks for signal processing IX: Proceedings of the 1999 IEEE signal processing society workshop (cat. no. 98th8468). Ieee, 1999: 41-48. [CrossRef]
  20. Li Z, Kruger U, Xie L, et al. Adaptive KPCA modeling of nonlinear systems[J]. IEEE Transactions on Signal Processing, 2015, 63(9): 2364-2376. [CrossRef]
  21. Lee J M, Qin S J, Lee I B. Fault detection of non-linear processes using kernel independent component analysis[J]. The Canadian Journal of Chemical Engineering, 2007, 85(4): 526-536. [CrossRef]
  22. Zhang L, Zhou W D, Jiao L C. Kernel clustering algorithm[J]. CHINESE JOURNAL OF COMPUTERS-CHINESE EDITION-, 2002, 25(6): 587-590.
  23. Choi H, Choi S. Kernel isomap[J]. Electronics letters, 2004, 40(25): 1612-1613. [CrossRef]
  24. Fasi M, Iannazzo B. Computing the weighted geometric mean of two large-scale matrices and its inverse times a vector[J]. SIAM Journal on Matrix Analysis and Applications, 2018, 39(1): 178-203. [CrossRef]
  25. Hager W W. Updating the inverse of a matrix[J]. SIAM review, 1989, 31(2): 221-239. [CrossRef]
  26. Bhatia R. Positive definite matrices[M]. Princeton university press, 2009.
  27. Asuncion A, Newman D. UCI machine learning repository[J]. 2007.
  28. Nguyen B, Morell C, De Baets B. Supervised distance metric learning through maximization of the Jeffrey divergence[J]. Pattern Recognition, 2017, 64: 215-225.
  29. Kedem D, Tyree S, Sha F, et al. Non-linear metric learning[J]. Advances in neural information processing systems, 2012, 25.
  30. Bhutani M, Jawanpuria P, Kasai H, et al. Low-rank geometric mean metric learning[J]. arXiv preprint arXiv:1806.05454, 2018.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated