Submitted:
19 July 2023
Posted:
21 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
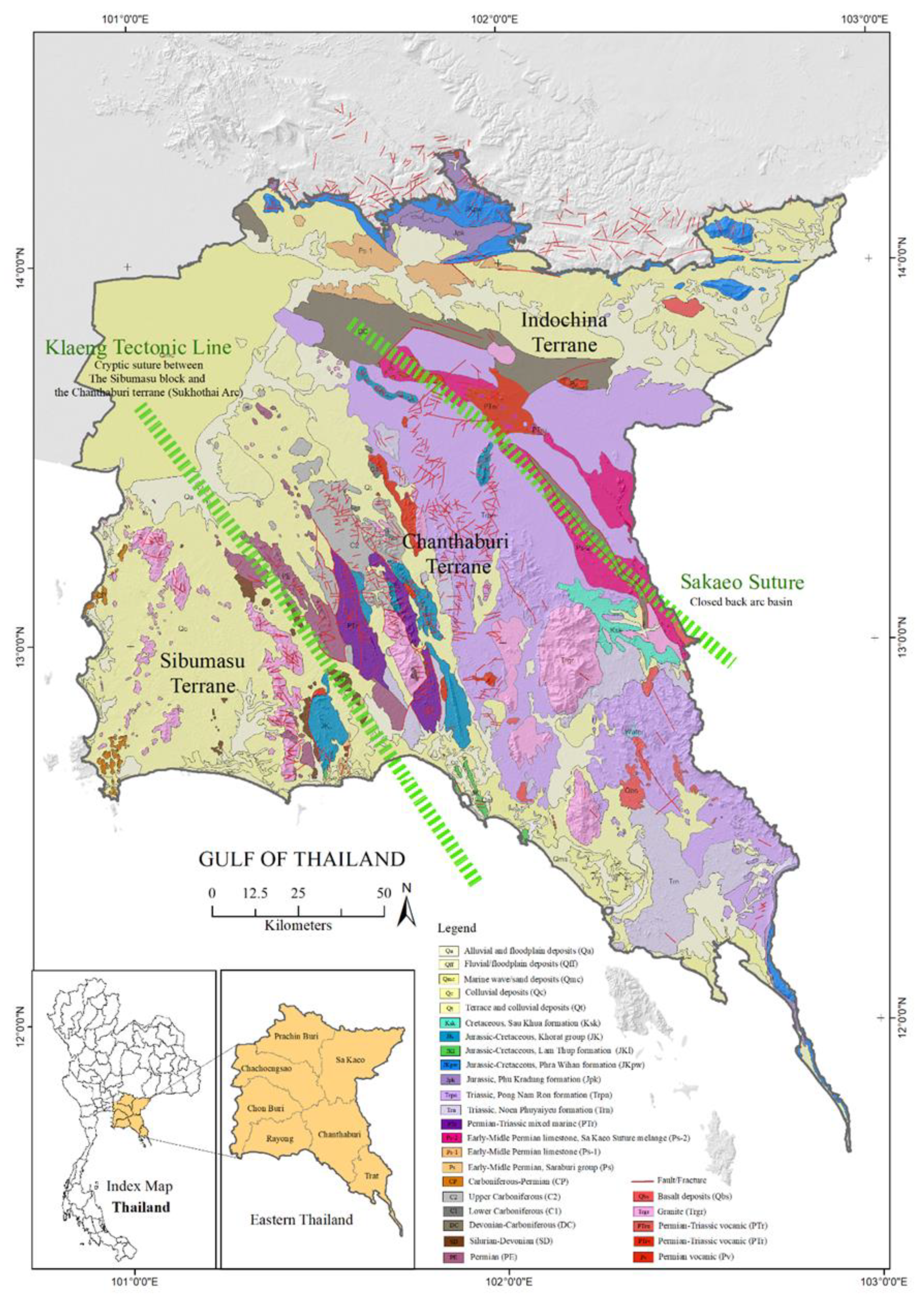
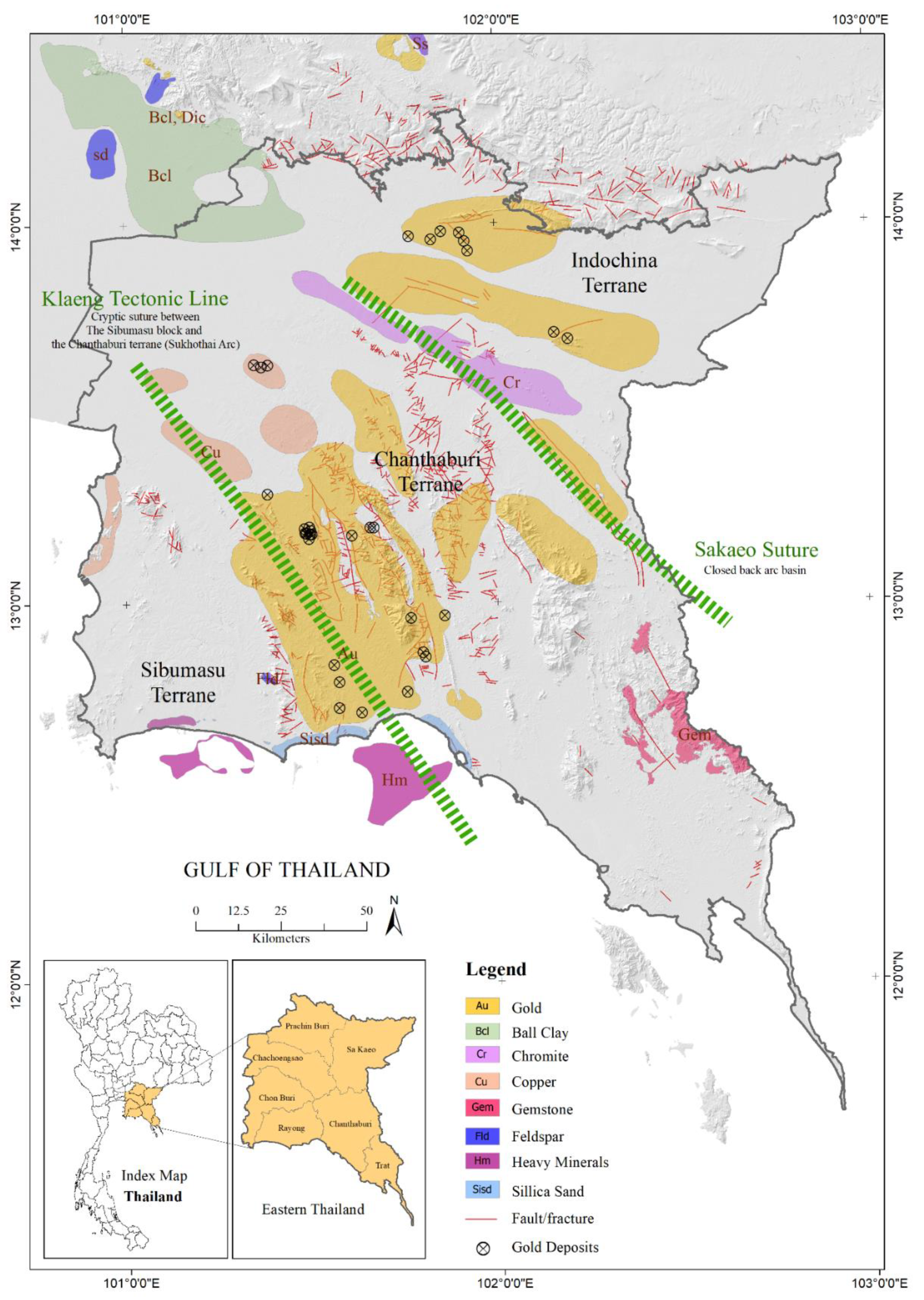
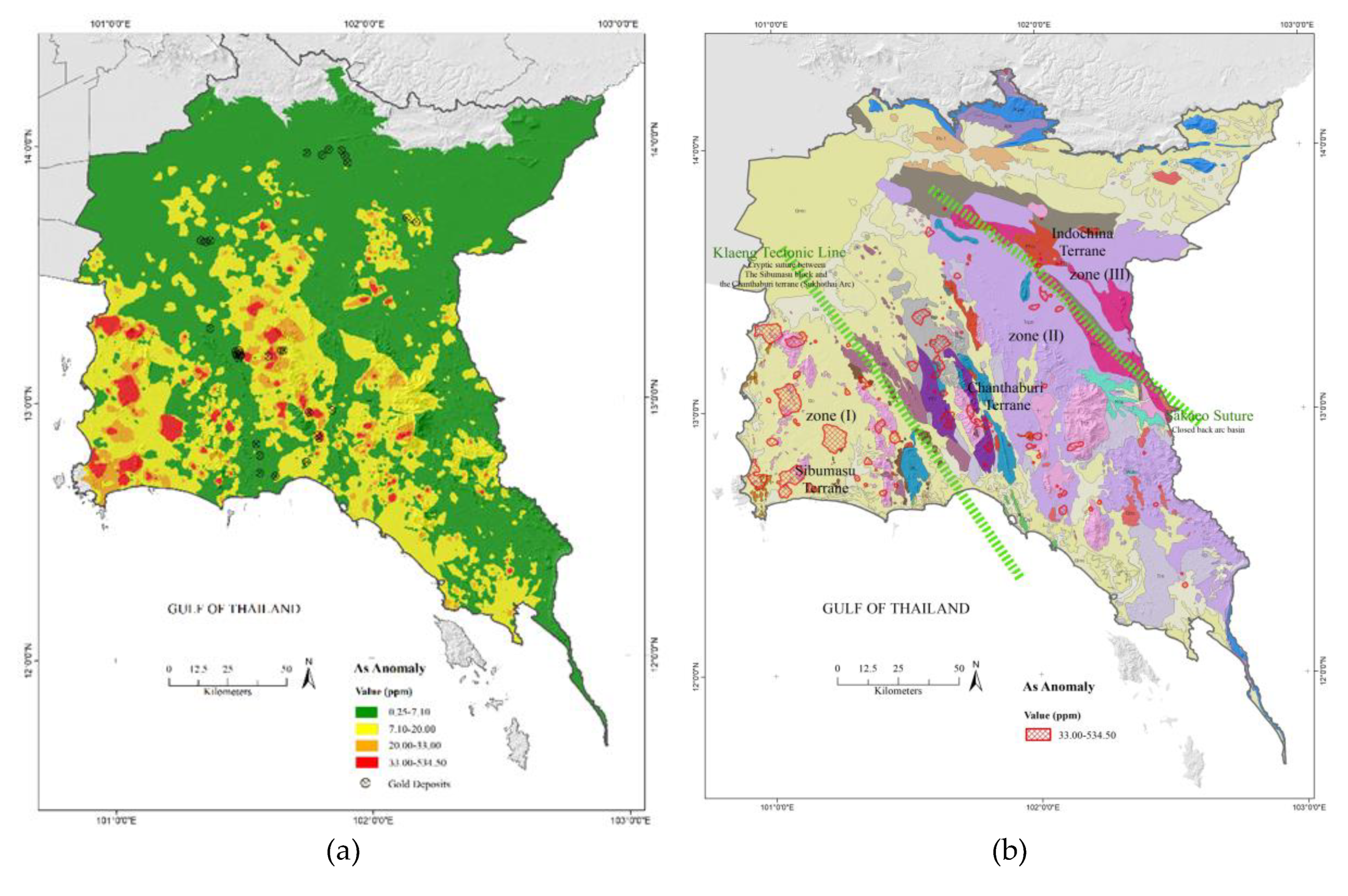
2. Geological Settings
3. Geochemical Data
4. Methodology
4.1. Descriptive Statistics
4.2. The Spectrum-Area (S-A) Multifractal Model
5. Result and Discussion
5.1. Descriptive Statistics
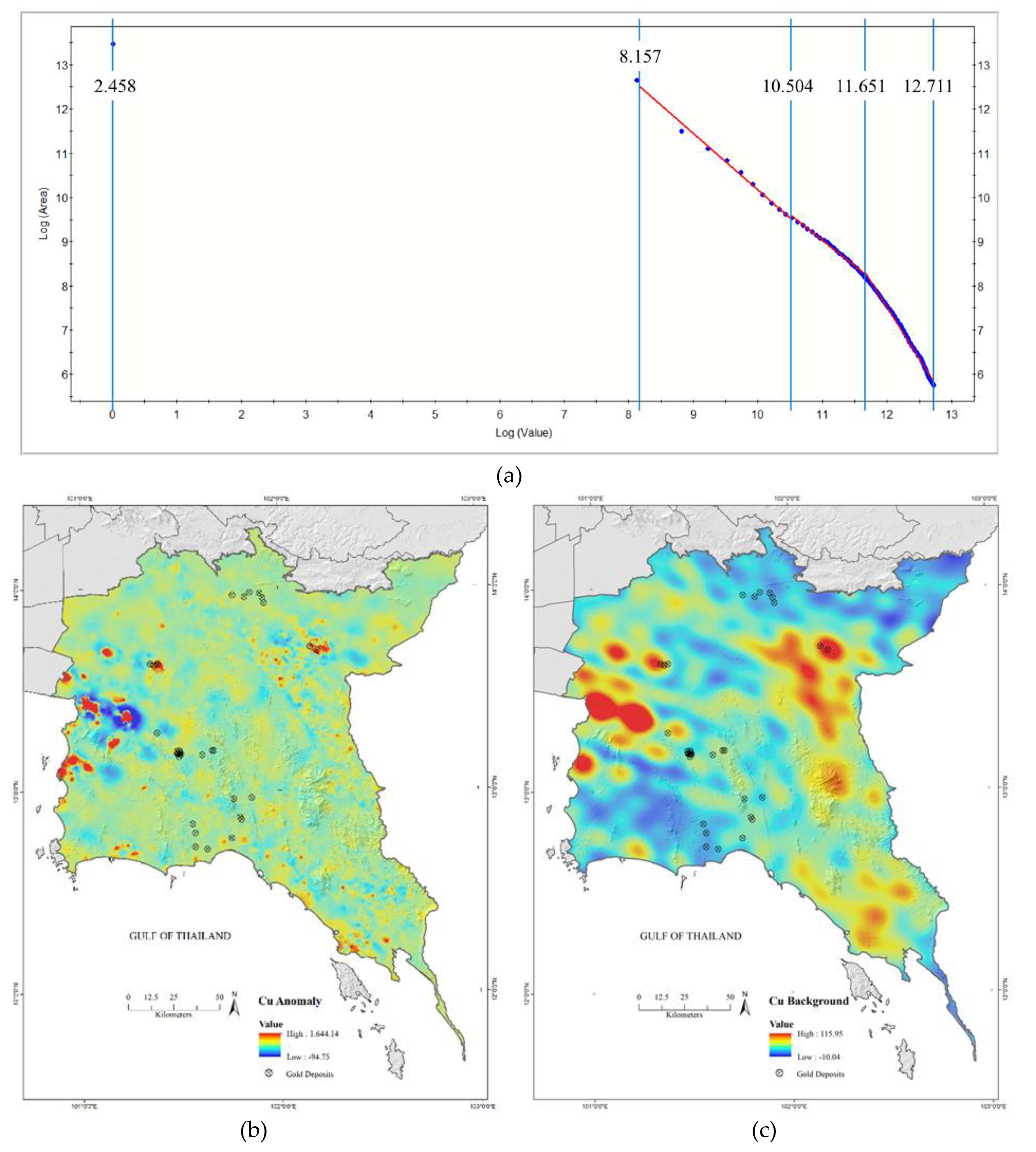
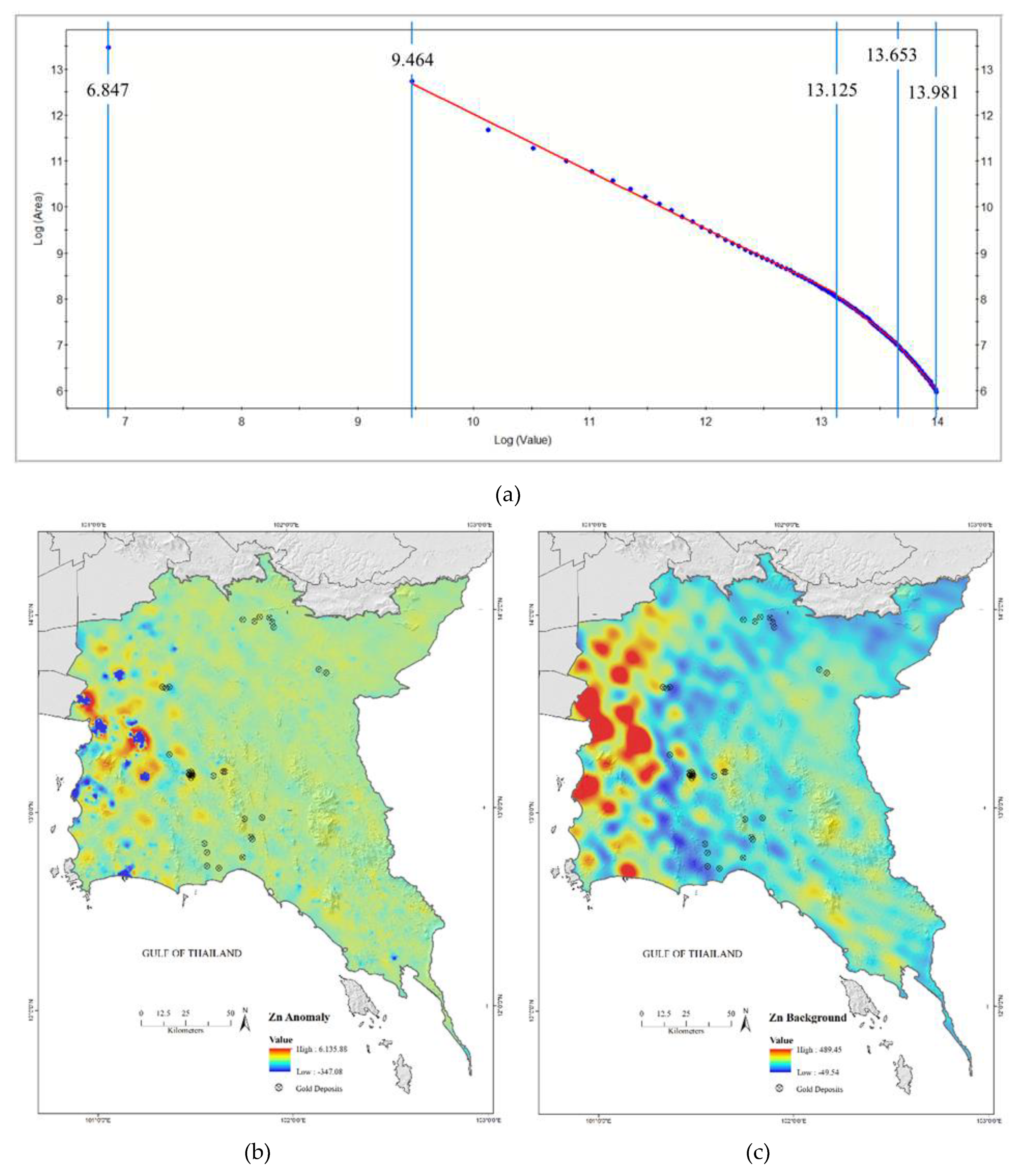
5.2. Spatial Distribution of As, Cu, and Zn
5.3. Determining Thresholds Using the S-A Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Q. , Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. Journal of Geochemical Exploration 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Zuo, R., Q. Cheng, and Q. Xia, Application of fractal models to characterization of vertical distribution of geochemical element concentration. Journal of Geochemical Exploration 2009, 102, 37–43. [Google Scholar] [CrossRef]
- Cheng, Q. , Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geology Reviews 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Parsa, M., A. Maghsoudi, and M. Yousefi, A Receiver Operating Characteristics-Based Geochemical Data Fusion Technique for Targeting Undiscovered Mineral Deposits. Natural Resources Research 2018, 27, 15–28. [Google Scholar] [CrossRef]
- Zuo, R. and Y. Xiong, Geodata science and geochemical mapping. Journal of Geochemical Exploration 2020, 209, 106431. [Google Scholar] [CrossRef]
- Grunsky, E.C. and P.d. Caritat, State-of-the-art analysis of geochemical data for mineral exploration. Geochemistry: Exploration, Environment, Analysis 2020, 20, 217–232. [Google Scholar]
- Zuo, R. , et al., The processing methods of geochemical exploration data: past, present, and future. Applied Geochemistry 2021, 132, 105072. [Google Scholar] [CrossRef]
- Cohen, D. , et al., Major advances in exploration geochemistry, 1998–2007, 2010.
- Winterburn, P.A., R. R. Noble, and D. Lawie, Advances in exploration geochemistry, 2007 to 2017 and beyond. Geochemistry: Exploration, Environment, Analysis 2020, 20, 157–166. [Google Scholar]
- Zuo, R., E. J.M. Carranza, and Q. Cheng, Fractal/multifractal modelling of geochemical exploration data. Journal of Geochemical Exploration 2012, 122, 1–3. [Google Scholar] [CrossRef]
- Xie, S. , et al., Quantitative prediction of potential areas likely to yield Se-rich and Cd-low rice using fuzzy weights-of-evidence method. Science of The Total Environment 2023, 889, 164015. [Google Scholar] [CrossRef]
- Yang, F. , et al., Geochemical quantitative assessment of mineral resource potential in the Da Hinggan Mountains in Inner Mongolia, China. Minerals 2022, 12, 434. [Google Scholar] [CrossRef]
- Cohen, D. and R. Bowell, 13.24-Exploration Geochemistry. Treatise on Geochemistry, 2nd ed.; Holland, HD, Turekian, KK, Eds, 2014, 623-650.
- Xie, S. , et al., Quantitative prediction of prospectivity for Pb–Zn deposits in Guangxi (China) by back-propagation neural network and fuzzy weights-of-evidence modelling. Geochemistry: Exploration, Environment, Analysis 2022, 22, geochem2021–085. [Google Scholar]
- Wang, W., S. Xie, and E.J.M. Carranza, Introduction to the thematic collection: applications of innovations in geochemical data analysis. 2023, The Geological Society of London. p. geochem2022-058. [CrossRef]
- Parsa, M. and E. J.M. Carranza, Modulating the impacts of stochastic uncertainties linked to deposit locations in data-driven predictive mapping of mineral prospectivity. Natural Resources Research 2021, 30, 3081–3097. [Google Scholar]
- Chen, Y., G. Sun, and Q. Zhao, Detection of multivariate geochemical anomalies associated with gold deposits by using distance anomaly factors. Journal of Geochemical exploration 2021, 221, 106704. [Google Scholar] [CrossRef]
- Xie, S. and Z. Bao, Fractal and Multifractal Properties of Geochemical Fields. Mathematical Geology 2004, 36, 847–864. [Google Scholar] [CrossRef]
- Carranza, E.J.M. , Geochemical anomaly and mineral prospectivity mapping in GIS. 2008: Elsevier.
- Harris, D. and G. Pan, Mineral favorability mapping: a comparison of artificial neural networks, logistic regression, and discriminant analysis. Natural Resources Research 1999, 8, 93–109. [Google Scholar] [CrossRef]
- Harris, J., L. Wilkinson, and E. Grunsky, Effective use and interpretation of lithogeochemical data in regional mineral exploration programs: application of Geographic Information Systems (GIS) technology. Ore Geology Reviews 2000, 16, 107–143. [Google Scholar] [CrossRef]
- Hawkes, H. and J. Webb, s., 1962, Geochemistry in mineral exploration. 1962, New York, Harper and Row.
- Sinclair, A. , Selection of threshold values in geochemical data using probability graphs. Journal of geochemical exploration 1974, 3, 129–149. [Google Scholar] [CrossRef]
- Tukey, J.W. , Exploratory data analysis. Vol. 2. 1977: Reading, MA.
- Stanley, C.R. and A.J. Sinclair, Comparison of probability plots and the gap statistic in the selection of thresholds for exploration geochemistry data. journal of Geochemical Exploration 1989, 32, 355–357. [Google Scholar] [CrossRef]
- Matheron, G. , Traité de géostatistique appliquée, Mém BRGM 14. Éditions Technip, Paris, 1962.
- Mandelbrot, B.B. , The fractal geometry of Nature WH Freeman and Company. New York, 1983, 8, 406–406. [Google Scholar]
- Turcotte, D.L. , Fractals in geology and geophysics. Pure and applied Geophysics, 1989, 131, 171–196. [Google Scholar] [CrossRef]
- Cheng, Q. , Multifractality and spatial statistics. Computers & Geosciences 1999, 25, 949–961. [Google Scholar]
- Zhang, Y. , et al., Implication of multifractal analysis for quantitative evaluation of mineral resources in the Central Kunlun area, Xinjiang, China. Geochemistry: Exploration, Environment, Analysis 2022, 22, geochem2021–083. [Google Scholar]
- Cheng, Q., F. P. Agterberg, and S.B. Ballantyne, The separation of geochemical anomalies from background by fractal methods. Journal of Geochemical Exploration 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Behera, S. and M.K. Panigrahi, Mineral prospectivity modelling using singularity mapping and multifractal analysis of stream sediment geochemical data from the auriferous Hutti-Maski schist belt, S. India. Ore Geology Reviews 2021, 131, 104029. [Google Scholar] [CrossRef]
- Cheng, Q. , Spatial and scaling modelling for geochemical anomaly separation. Journal of Geochemical exploration 1999, 65, 175–194. [Google Scholar] [CrossRef]
- Cheng, Q. GeoData Analysis System (GeoDAS) for mineral exploration: User’s guide and exercise manual. in Material for the training workshop on GeoDAS held at York University. 2000.
- Koohzadi, F. , et al., Geochemical exploration for Li in regional scale utilizing Staged Factor Analysis (SFA) and Spectrum-Area (SA) fractal model in north central Iran. Iranian Journal of Earth Sciences 2021, 13, 299–307. [Google Scholar]
- Sadeghi, B. and F. Agterberg, Singularity analysis. Encyclopedia of Mathematical Geosciences 2020, 1–7. [Google Scholar]
- Ali, K., Q. Cheng, and Z. Chen, Multifractal power spectrum and singularity analysis for modelling stream sediment geochemical distribution patterns to identify anomalies related to gold mineralization in Yunnan Province, South China. Geochemistry: Exploration, Environment, Analysis 2007, 7, 293–301. [Google Scholar]
- Cheng, Q. , Multifractal interpolation method for spatial data with singularities. Journal of the Southern African Institute of Mining and Metallurgy 2015, 115, 235–240. [Google Scholar] [CrossRef]
- Zuo, R. and J. Wang, ArcFractal: An ArcGIS add-in for processing geoscience data using fractal/multifractal models. Natural Resources Research 2020, 29, 3–12. [Google Scholar] [CrossRef]
- Song, W. , et al., Genesis, metallogenic model, and prospecting prediction of the Nibao gold deposit in the Guizhou Province, China. Acta Geochimica 2023, 42, 136–152. [Google Scholar] [CrossRef]
- Sunkari, E.D., M. Appiah-Twum, and A. Lermi, Spatial distribution and trace element geochemistry of laterites in Kunche area: Implication for gold exploration targets in NW, Ghana. Journal of African Earth Sciences 2019, 158, 103519. [Google Scholar] [CrossRef]
- Agangi, A. , et al., Antimony in rutile as a pathfinder for orogenic gold deposits. Ore Geology Reviews 2019, 106, 1–11. [Google Scholar] [CrossRef]
- Bayari, E.E., G. Foli, and S.K. Gawu, Geochemical and pathfinder elements assessment in some mineralised regolith profiles in Bole-Nangodi gold belt in north-eastern Ghana. Environmental Earth Sciences 2019, 78, 1–16. [Google Scholar] [CrossRef]
- Arhin, E., S. Boadi, and M.C. Esoah, Identifying pathfinder elements from termite mound samples for gold exploration in regolith complex terrain of the Lawra belt, NW Ghana. Journal of African Earth Sciences 2015, 109, 143–153. [Google Scholar] [CrossRef]
- Anand, R. , et al., Gold and pathfinder elements in ferricrete gold deposits of the Yilgarn Craton of Western Australia: A review with new concepts. Ore Geology Reviews 2019, 104, 294–355. [Google Scholar] [CrossRef]
- Behera, S., M. K. Panigrahi, and A. Pradhan, Identification of geochemical anomaly and gold potential mapping in the Sonakhan Greenstone belt, Central India: An integrated concentration-area fractal and fuzzy AHP approach. Applied Geochemistry 2019, 107, 45–57. [Google Scholar] [CrossRef]
- Mvile, B.N., M. Abu, and J. Kalimenze, Trace elements geochemistry of in situ regolith materials and their implication on gold mineralization and exploration targeting, Dodoma Region, East Africa. Mining, Metallurgy & Exploration 2021, 38, 2075–2087. [Google Scholar]
- Morley, C.K., P. Charusiri, and I.M. Watkinson, Structural geology of Thailand during the Cenozoic. 2011. [CrossRef]
- Ridd, M.F., A.J. Barber, and M.J. Crow, Introduction to the geology of Thailand. 2011.
- Charusiri, P. , Geotectonic evolution of Thailand: a new synthesis. J. Geol. Soc. Thai 2002, 1, 1–20. [Google Scholar]
- Metcalfe, I., C. Henderson, and K. Wakita, Lower Permian conodonts from Palaeo-Tethys ocean plate stratigraphy in the Chiang Mai-Chiang Rai suture zone, northern Thailand. Gondwana Research 2017, 44, 54–66. [Google Scholar] [CrossRef]
- Sone, M., I. Metcalfe, and P. Chaodumrong, The Chanthaburi terrane of southeastern Thailand: Stratigraphic confirmation as a disrupted segment of the Sukhothai Arc. Journal of Asian Earth Sciences 2012, 61, 16–32. [Google Scholar] [CrossRef]
- Hara, H. , et al., Permian–Triassic back-arc basin development in response to Paleo-Tethys subduction, Sa Kaeo–Chanthaburi area in Southeastern Thailand. Gondwana Research 2018, 64, 50–66. [Google Scholar] [CrossRef]
- Saesaengseerung, D. , et al., Discovery of Lower Permian radiolarian and conodont faunas from the bedded chert of the Chanthaburi area along the Sra Kaeo suture zone, eastern Thailand. Paleontological Research 2009, 13, 119–138. [Google Scholar] [CrossRef]
- Fontaine, H. and S. Salyapongse. Unexpected discovery of early Carboniferous (late Visean-Serpukhovian) corals in East Thailand. in Proceedings of the international conference on Stratigraphy and tectonic evolution of Southeast Asia and the South Pacific. 1997.
- Fontaine, H. , et al., Recent biostratigraphic discoveries in Thailand: a preliminary report. CCOP Newsletter 1996, 21, 14–15. [Google Scholar]
- Fontaine, H., S. Salyapongse, and D. Vachard, The Carboniferous of East Thailand—New Information from Microfossils. 1999.
- Sone, M. and I. Metcalfe. Parallel Tethyan sutures and the Sukhothai Island-arc system in Thailand and beyond. in Proceedings of the international symposia on geoscience resources and environments of Asian terranes (GREAT 2008), 4th IGCP. 2008.
- Salyapongse, S. Geology of the Eastern Thailand, Field Excursion Guidebook Route no. 1. in the First International conference on Stratigraphy and Tectonic Evolution of Southeast Asia and the South Pacific. 1997.
- Bunopas, S., Palaeogeographic history of Western Thailand and adjacent parts of Southeast Asia. A plate tectonics interpretation, Geol. Surv. Pap., Dep. Miner. Res. Thailand, 1982.
- Chaodumrong, P., et al. Geology of SW Khorat Plateau and eastern Thailand. in Post-Symposium Excursion Guidebook of Symposium on Geology of Thailand. Department of Mineral Resources Thailand, Bangkok. 2002.
- Chutakositkanon, V. , et al. Tectono-stratigraphy of the Sa Kaeo-Chanthaburi accretionary complex, 4th IGCP. 2008., Eastern Thailand: reconstruction of tectonic evolution of oceanic plate-Indochina collision. in Proceedings of the International Symposia on Geoscience Resources and Environments of Asian Terranes (GREAT 2008). [Google Scholar]
- Crow, M. , Appendix. Radiometric ages of Thailand rocks. The Geology of Thailand. Geological Society, London, 2011, 593-614.
- Palaeozoic–Mesozoic history of SE Asia. Geological Society, London, Special Publications 2011, 355, 7–35.
- DMR, Geologic Map of Thailand 1: 2,500,000: Geological Map of Thailand. 1999, Geological Survey Div., Dept. of Mineral Resources.
- Tansuwan, V. , Geological Map of Changwat Trat 1:250,000. 1997a, Department of Mineral Resources, Thailand, Bangkok.
- Tansuwan, V. , Geology and Mineral Resources Map of Changwat Chanthaburi 1:250,000. 1997b, Department of Mineral Resources Thailand, Bangkok.
- Charusiri, P., et al. Anatomy of Chanthaburi granitoids: geochronology, petrochemistry, tectonics, and associated mineralization. in Proceedings of the National Conference on Geologic Resources of Thailand: Potential for Future Development. Department of Mineral Resources, Ministry of Industry, Bangkok, Thailand. 1992.
- Bunopas, S. and P. Vella. Tectonic and geologic evolution of Thailand. in Proceedings of a workshop on stratigraphic correlation of Thailand and Malaysia. 1983.
- Searle, M. , et al., Tectonic evolution of the Sibumasu–Indochina terrane collision zone in Thailand and Malaysia: constraints from new U–Pb zircon chronology of SE Asian tin granitoids. Journal of the Geological Society 2012, 169, 489–500. [Google Scholar] [CrossRef]
- Cobbing, E. , et al., The granites of the Southeast Asian tin belt. Journal of the Geological Society 1986, 143, 537–550. [Google Scholar] [CrossRef]
- Brown, G.F. , Geologic reconnaissance of the mineral deposits of Thailand. 1951: US Government Printing Office.
- Searle, M.P. and C.K. Morley, Tectonic and thermal evolution of Thailand in the regional context of SE Asia. 2011.
- DMR, Minerals Resources Map of Thailand 1:2,500,00. Bureau of Mineral Resources, Department of Mineral Resources, Thailand, 2006.
- Chen, L. , et al., A multi-convolutional autoencoder approach to multivariate geochemical anomaly recognition. Minerals 2019, 9, 270. [Google Scholar] [CrossRef]
- Xie, S. , et al., Geochemical multifractal distribution patterns in sediments from ordered streams. Geoderma 2010, 160, 36–46. [Google Scholar] [CrossRef]
- Van Loon, J.C. and R. Barefoot, Analytical methods for geochemical exploration. 2013: Elsevier.
- Smith-Forbes, E.V. , et al., Descriptive analysis of common functional limitations identified by patients with shoulder pain. Journal of Sport Rehabilitation 2015, 24, 179–188. [Google Scholar] [CrossRef]
- Xu, Y. and Q. Cheng, A fractal filtering technique for processing regional geochemical maps for mineral exploration. Geochemistry: Exploration, environment, analysis 2001, 1, 147–156. [Google Scholar]
- Zuo, R. and J. Wang, Fractal/multifractal modeling of geochemical data: A review. Journal of Geochemical Exploration 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Darnley, A. , et al., A global geochemical database. Recommendations for international geochemical mapping, 1995.
- Ghezelbash, R., A. Maghsoudi, and M. Daviran, Combination of multifractal geostatistical interpolation and spectrum–area (S–A) fractal model for Cu–Au geochemical prospects in Feizabad district, NE Iran. Arabian Journal of Geosciences 2019, 12, 1–14. [Google Scholar] [CrossRef]
- Xie, X. , et al., Multi-scale geochemical mapping in China. Geochemistry: Exploration, Environment, Analysis 2008, 8, 333–341. [Google Scholar]
- Ke, X. , et al., Multifractal analysis of geochemical stream sediment data in Bange region, northern Tibet. Journal of Earth Science 2015, 26, 317–327. [Google Scholar] [CrossRef]
- Feng, L. , et al., Mapping of geological complexity and analyzing its relationship with the distribution of gold deposits in the Guangxi Gold Ore Province, Southern China. Journal of Geochemical Exploration 2023, 251, 107238. [Google Scholar] [CrossRef]
- Wu, R. , et al., Identifying geochemical anomalies associated with gold mineralization using factor analysis and spectrum–area multifractal model in Laowan District, Qinling-Dabie Metallogenic Belt, Central China. Minerals 2020, 10, 229. [Google Scholar] [CrossRef]
- Farahmandfar, Z. , et al., Description of gold and copper anomalies using fractal and stepwise factor analysis according to stream sediments in NW Iran. Geopersia 2020, 10, 135–148. [Google Scholar]
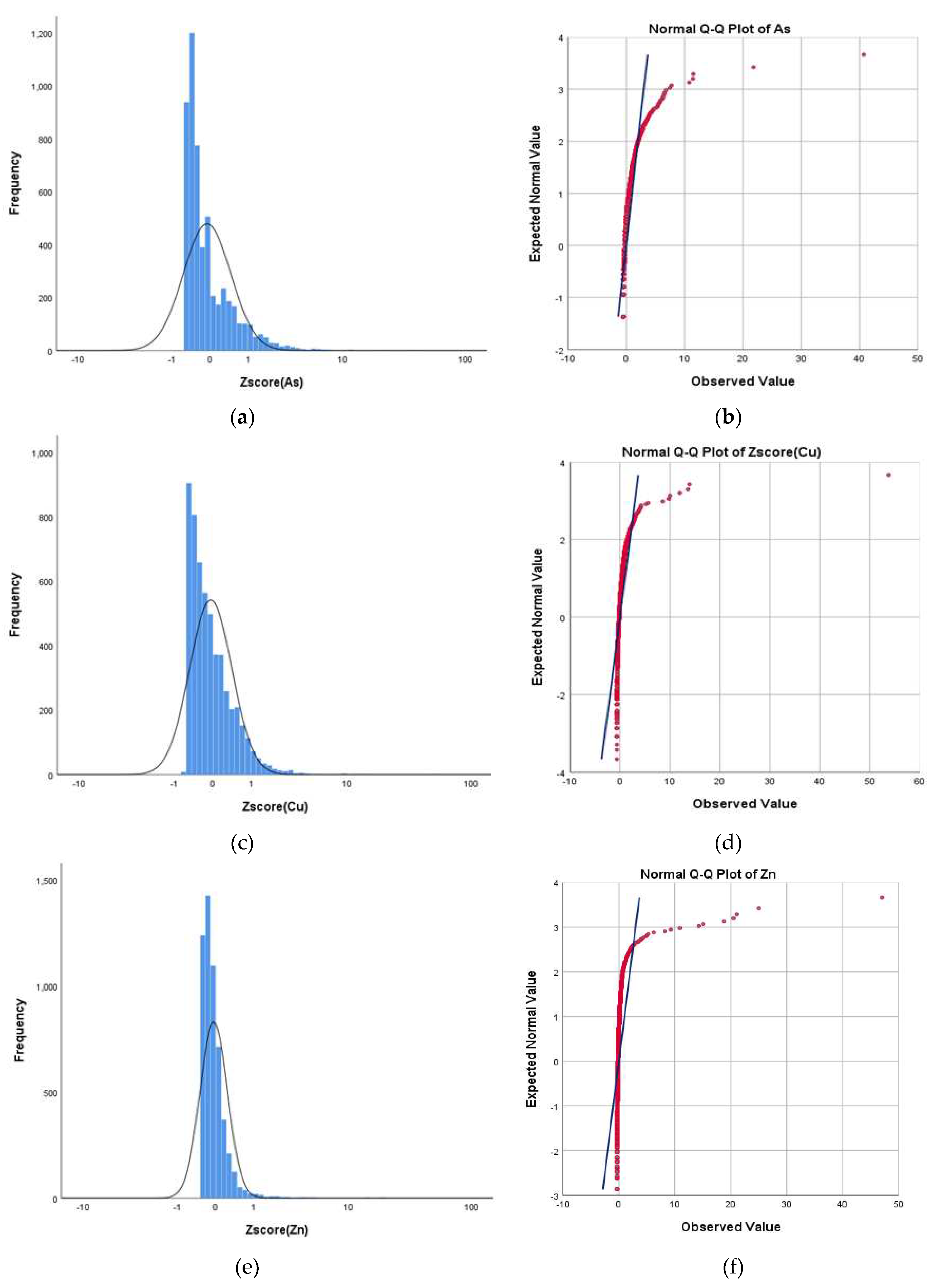

| Elements | N | Max | Min | X | SD | CV% | Skewness |
|---|---|---|---|---|---|---|---|
| As | 5,376 | 534.50 | 0.25 | 7.05 | 12.95 | 183.61 | 16.74 |
| Cu | 5,376 | 1,760.00 | 0.05 | 20.26 | 32.36 | 159.75 | 31.25 |
| Zn | 5,376 | 6,657.00 | 1.00 | 46.45 | 140.53 | 302.55 | 6.86 |
|
Geological unit |
Samples (N) | Elements | |||||||||||
| As | Cu | Zn | |||||||||||
| X | SD | Cv | X | SD | Cv | X | SD | Cv | |||||
| Total | 5,376 | 7.05 | 12.95 | 1.84 | 20.26 | 32.36 | 1.60 | 46.45 | 140.53 | 3.03 | |||
| Q | 2,447 | 7.40 | 15.91 | 2.15 | 16.55 | 43.47 | 2.63 | 57.38 | 206.49 | 3.60 | |||
| Ksk | 32 | 2.83 | 4.38 | 1.55 | 31.12 | 12.62 | 0.41 | 47.47 | 11.23 | 0.24 | |||
| Jk | 132 | 5.94 | 10.82 | 1.82 | 6.61 | 6.24 | 0.94 | 13.83 | 12.16 | 0.88 | |||
| Jkl | 5 | 6.00 | 6.27 | 1.04 | 10.14 | 8.07 | 0.80 | 11.60 | 8.73 | 0.75 | |||
| JKpw | 49 | 2.07 | 1.21 | 0.58 | 6.14 | 4.38 | 0.71 | 23.87 | 14.83 | 0.62 | |||
| Jpk | 60 | 5.94 | 10.82 | 1.82 | 6.61 | 6.24 | 0.94 | 13.83 | 12.16 | 0.88 | |||
| Trpn | 1,207 | 6.16 | 8.97 | 1.46 | 22.37 | 12.45 | 0.56 | 38.89 | 18.35 | 0.47 | |||
| Trn | 313 | 6.73 | 6.86 | 1.02 | 26.10 | 15.82 | 0.61 | 40.16 | 21.93 | 0.55 | |||
| PTr | 100 | 19.74 | 17.35 | 0.88 | 17.32 | 7.69 | 0.44 | 32.79 | 17.32 | 0.53 | |||
| Ps-2 | 201 | 19.74 | 17.35 | 0.88 | 17.32 | 7.69 | 0.44 | 32.79 | 17.32 | 0.53 | |||
| Ps-1 | 37 | 3.50 | 6.21 | 1.78 | 15.30 | 12.10 | 0.79 | 27.05 | 18.32 | 0.68 | |||
| Ps | 3 | 5.11 | 2.80 | 0.55 | 22.29 | 18.69 | 0.84 | 22.48 | 16.95 | 0.75 | |||
| C2 | 67 | 22.33 | 14.80 | 0.66 | 15.40 | 6.35 | 0.41 | 39.62 | 31.68 | 0.80 | |||
| DC | 291 | 4.43 | 6.17 | 1.39 | 30.39 | 29.64 | 0.98 | 33.99 | 19.45 | 0.57 | |||
| SD | 26 | 9.03 | 8.43 | 0.93 | 15.71 | 17.57 | 1.12 | 23.96 | 17.47 | 0.73 | |||
| Qbs | 49 | 5.98 | 6.41 | 1.07 | 29.65 | 11.21 | 0.38 | 61.04 | 33.97 | 0.56 | |||
| Trgr | 153 | 9.24 | 12.49 | 1.35 | 15.20 | 12.79 | 0.84 | 36.71 | 27.80 | 0.76 | |||
| PE | 67 | 7.05 | 12.95 | 1.84 | 20.26 | 32.36 | 1.60 | 46.45 | 140.53 | 3.03 | |||
| PTrv/Ptru | 131 | 8.53 | 11.65 | 1.37 | 41.54 | 22.71 | 0.55 | 45.11 | 20.01 | 0.44 | |||
| Pv | 6 | 7.67 | 2.66 | 0.35 | 108.50 | 27.29 | 0.25 | 69.83 | 10.03 | 0.14 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





