Submitted:
18 July 2023
Posted:
19 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Regional Geology
2.1. Basic geological background
2.2. The tectonic background of the study area
2.2.1. Fold and fracture structure
- (1)
- Lower Carboniferous fold-fault zone of Feiyun Mountain
- (2)
- Pingling-Yinshishan Triassic fault-fold belt
- (3)
- Other large fractures
2.2.2. Structural ophiolitic mélange belt
- (1)
- Hengdiliang complex belt
- (2)
- Feiyunshan ophiolitic mélange belt
2.2.3. Metallogenic belt
- (1)
- Karamiran (compound gully arc belt) Au–Cu–Ag ore belt.
- (2)
- Huangyangling (fold belt) Sb–Hg–Au–Cu ore belt.
- (3)
- Yunwuling (fold belt) Cu–Au ore belt.
2.3. Characteristics of mineral resources
2.3.1. Sedimentary type
2.3.2. Volcanic type
2.3.3. Skarn type
3. Data sources and main research methods
3.1. Data sources and introduction
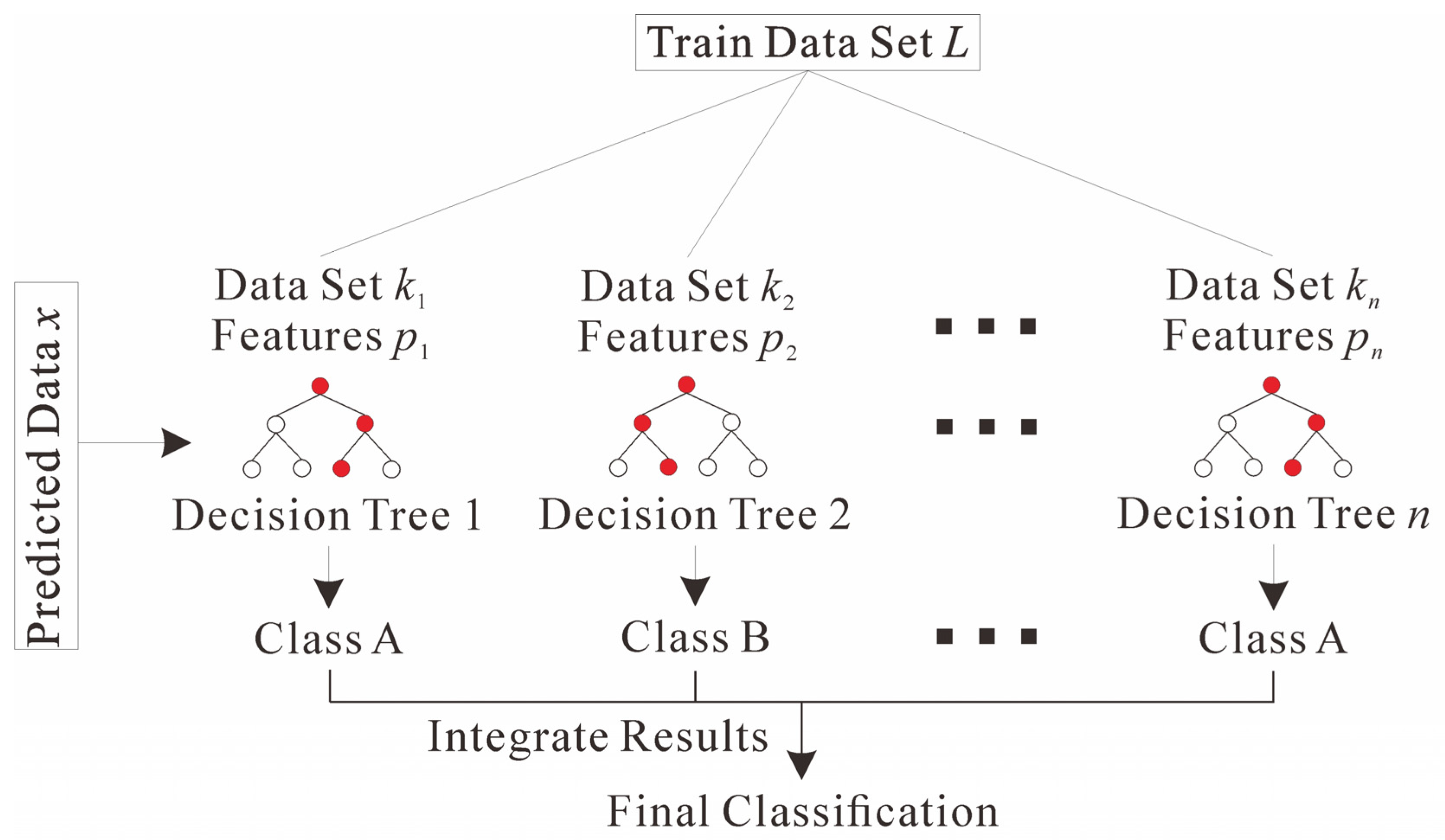
3.2. Random forest algorithm ( RF )
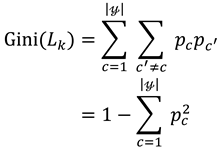

3.2.1. Undersampling method
| Algorithm: Ensemble under-sampling |
| Input: The training sample is the majority class sample, is the minority class sample; |
| Base learner |
| Training rounds T. |
| Output : Integrated model N. |
| Process : |
| 1: for t=1,2,…,T do |
| 2: The subset is randomly selected from , and the size of the subset is consistent with |
| 3: We use the base learner to train a single model on the dataset : |
| 4: end for |
| 5: Integration of results |
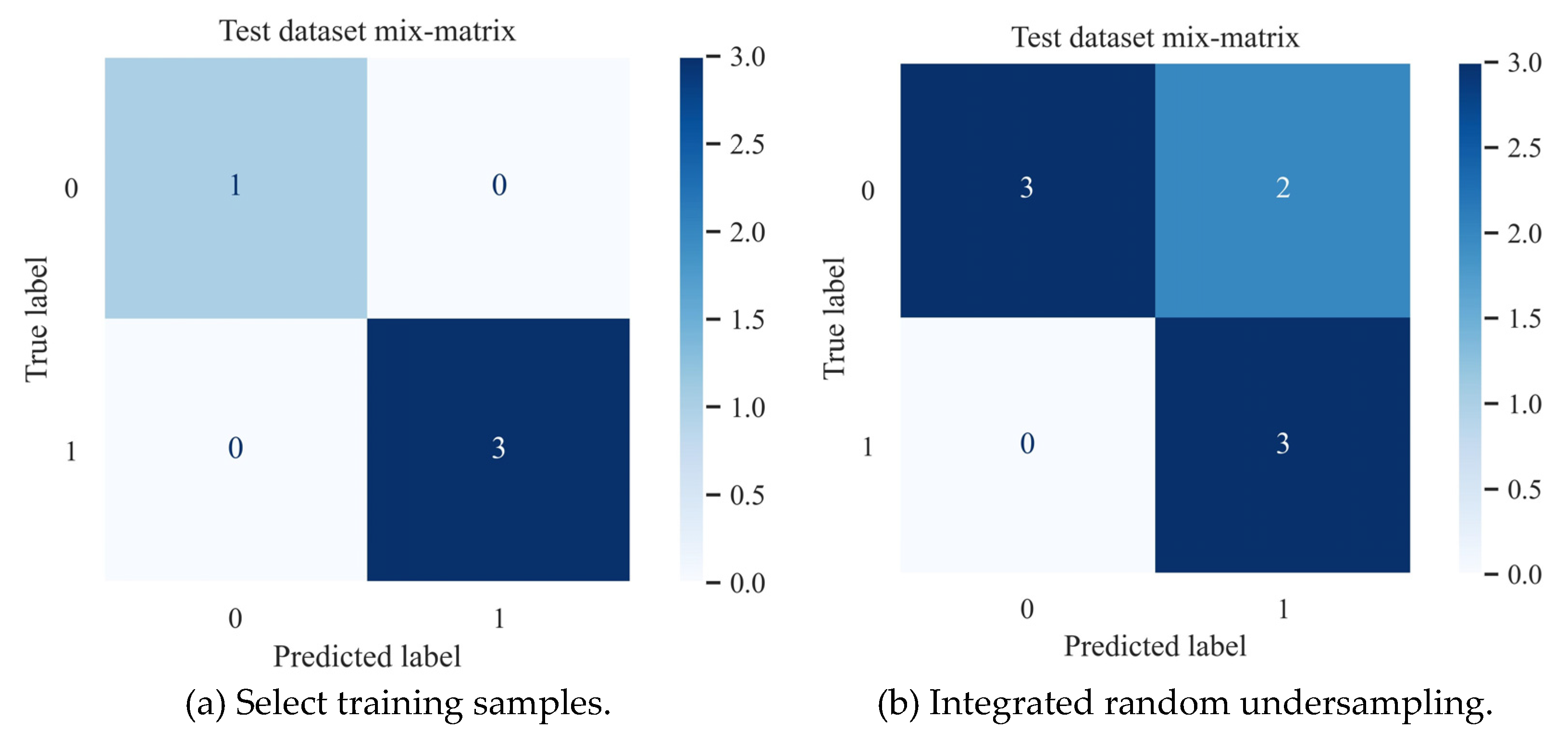
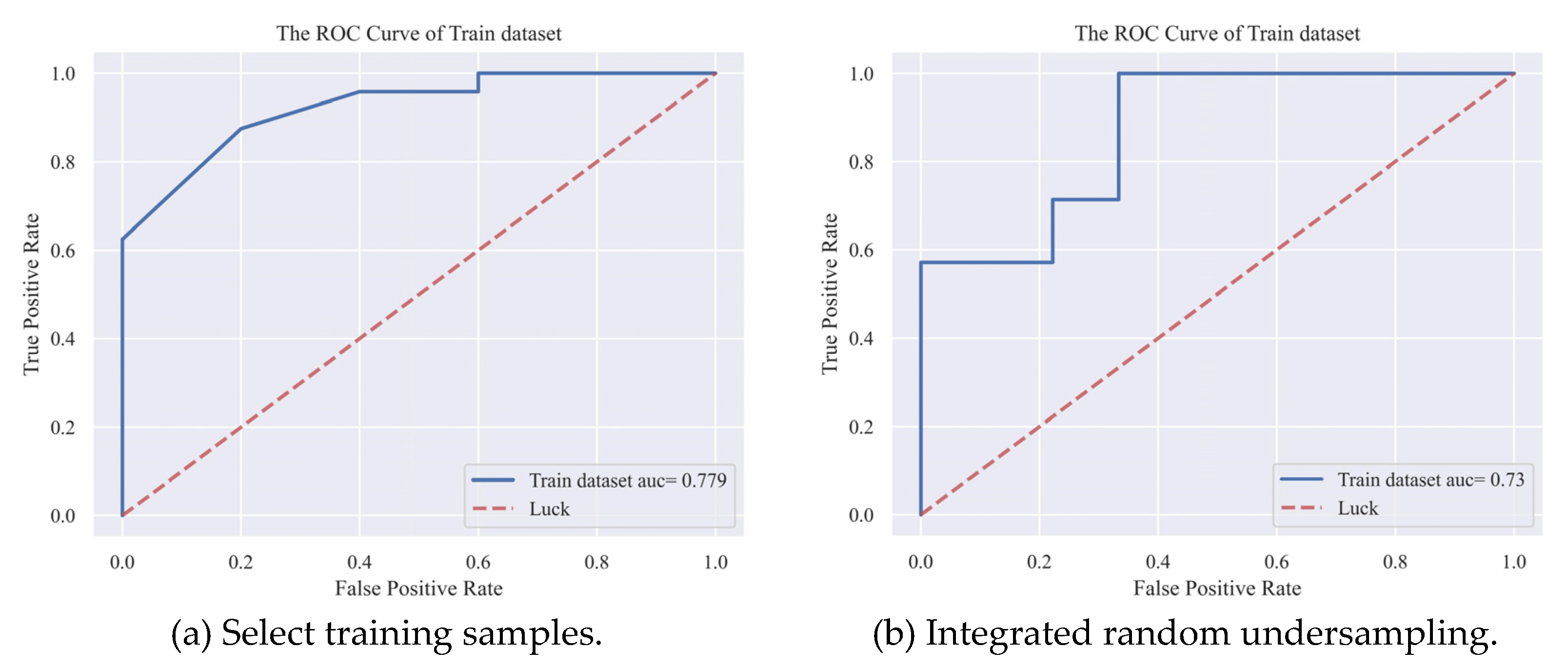
3.2.2. Performance evaluation parameters
3.2.3. Hold-out test
4. Metallogenic prediction and target area delineation of Au polymetallic deposits
4.1. Geochemical characteristics of different geological units
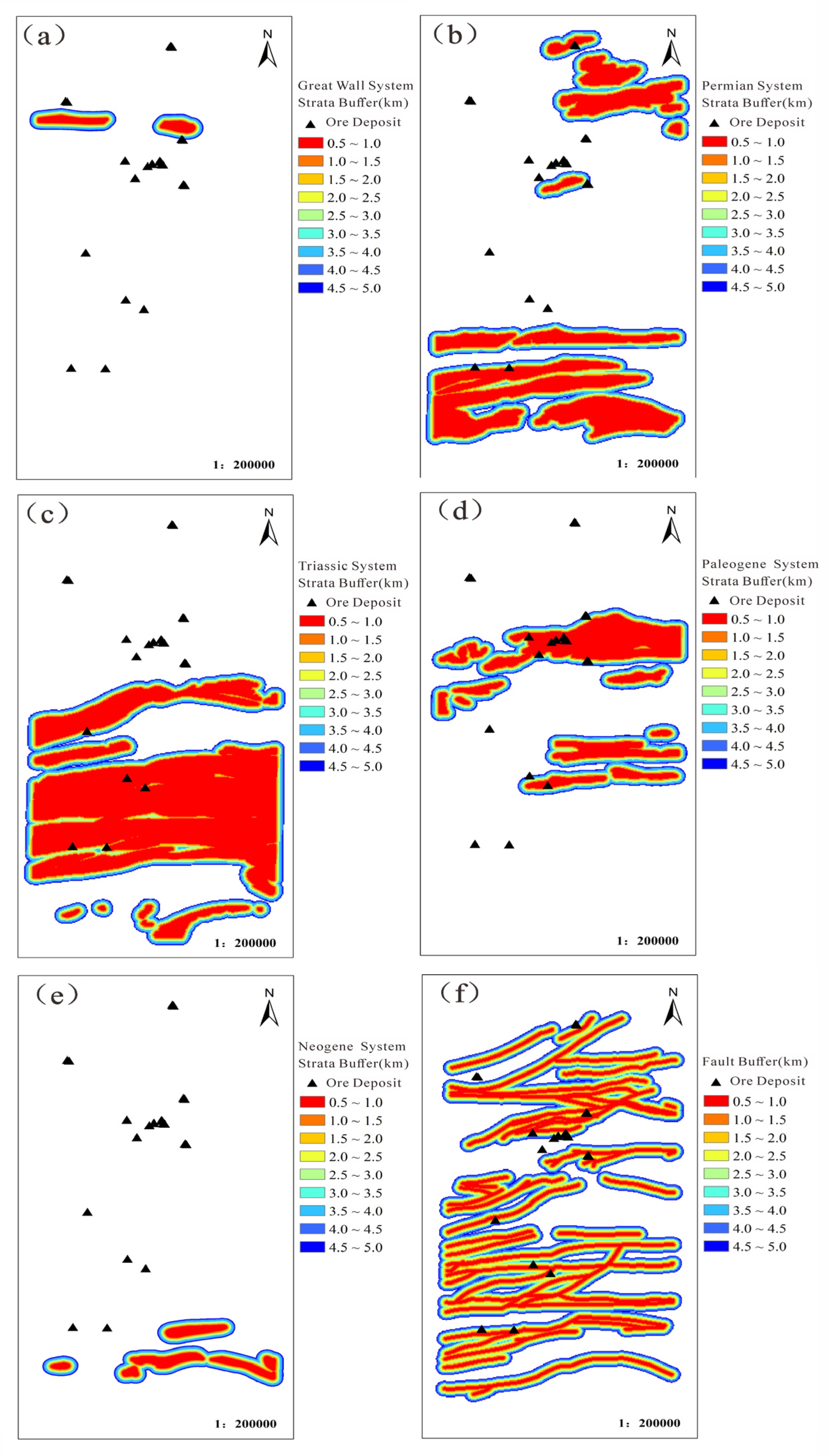
4.1.1. Great Wall System (Ch)
| Geological | N | E | K | J | T | P | C | Ch | Whole Area | |
|---|---|---|---|---|---|---|---|---|---|---|
| Unit Parameter |
||||||||||
| Au | Mean Value | 1.0 | 1.1 | 0.6 | 0.7 | 0.8 | 1.1 | 1.6 | 2.1 | 1.1 |
| Standard Deviation | 0.8 | 1.2 | 0.4 | 0.7 | 0.6 | 2.2 | 1.6 | 2.8 | 1.5 | |
| Coefficient of Cariation | 0.8 | 1.1 | 0.7 | 0.9 | 0.8 | 2.0 | 1.0 | 1.2 | 1.4 | |
| ConcentrationCoefficient | 0.9 | 1.0 | 0.5 | 0.7 | 0.7 | 1.0 | 1.4 | 1.9 | 1.0 | |
| Ba | Mean Value | 639.6 | 756.5 | 677.9 | 1598.3 | 793.9 | 580.1 | 526.3 | 513.9 | 766.7 |
| Standard Deviation | 502.1 | 531.1 | 130.1 | 6135.3 | 1776.1 | 326.5 | 219.6 | 95.3 | 2307.8 | |
| Coefficient of Cariation | 0.8 | 0.7 | 0.2 | 3.8 | 2.2 | 0.5 | 0.4 | 0.1 | 3.0 | |
| ConcentrationCoefficient | 0.8 | 1.0 | 0.9 | 2.0 | 1.0 | 0.7 | 0.6 | 0.6 | 1.0 | |
| Bi | Mean Value | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Standard Deviation | 0.4 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | |
| Coefficient of Cariation | 1.1 | 0.5 | 0.2 | 0.5 | 0.3 | 0.7 | 0.5 | 0.4 | 1.0 | |
| ConcentrationCoefficient | 1.5 | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Co | Mean Value | 11.6 | 9.7 | 7.6 | 8.9 | 12.1 | 10.7 | 10.1 | 7.8 | 10.7 |
| Standard Deviation | 3.0 | 4.5 | 2.2 | 3.9 | 3.1 | 3.6 | 3.6 | 3.3 | 4.3 | |
| Coefficient of Cariation | 0.3 | 0.5 | 0.3 | 0.4 | 0.2 | 0.3 | 0.3 | 0.4 | 0.4 | |
| ConcentrationCoefficient | 1.1 | 0.9 | 0.7 | 0.8 | 1.1 | 0.9 | 0.9 | 0.7 | 1.0 | |
| Cu | Mean Value | 21.5 | 21.5 | 18.7 | 25.2 | 26.6 | 20.7 | 27.6 | 28.2 | 24.4 |
| Standard Deviation | 4.9 | 9.8 | 3.8 | 9.9 | 8.9 | 7.4 | 16.6 | 22.7 | 11.1 | |
| Coefficient of Cariation | 0.2 | 0.5 | 0.2 | 0.3 | 0.3 | 0.3 | 0.6 | 0.7 | 0.4 | |
| ConcentrationCoefficient | 0.9 | 0.9 | 0.8 | 1.0 | 1.1 | 0.8 | 1.1 | 1.1 | 1.0 | |
| Fe | Mean Value | 4.7 | 3.7 | 3.1 | 4.3 | 5.2 | 4.4 | 4.0 | 3.1 | 4.4 |
| Standard Deviation | 1.2 | 1.7 | 0.7 | 1.8 | 1.4 | 1.4 | 1.3 | 1.0 | 1.7 | |
| Coefficient of Cariation | 0.3 | 0.5 | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 0.3 | 0.4 | |
| ConcentrationCoefficient | 1.1 | 0.8 | 0.7 | 0.9 | 1.1 | 1.0 | 0.9 | 0.7 | 1.0 | |
| Mg | Mean Value | 1.3 | 1.6 | 1.2 | 1.4 | 1.7 | 1.6 | 2.0 | 1.6 | 1.7 |
| Standard Deviation | 0.4 | 0.8 | 0.4 | 0.6 | 0.3 | 0.4 | 0.7 | 1.0 | 0.8 | |
| Coefficient of Cariation | 0.3 | 0.5 | 0.3 | 0.4 | 0.2 | 0.3 | 0.3 | 0.6 | 0.5 | |
| ConcentrationCoefficient | 0.8 | 0.9 | 0.7 | 0.8 | 1.0 | 0.9 | 1.1 | 0.9 | 1.0 | |
| Sn | Mean Value | 2.7 | 1.8 | 1.4 | 1.7 | 2.1 | 2.1 | 2.1 | 2.9 | 2.3 |
| Standard Deviation | 1.3 | 0.8 | 0.2 | 0.5 | 0.8 | 1.0 | 0.7 | 1.0 | 2.0 | |
| Coefficient of Cariation | 0.5 | 0.4 | 0.1 | 0.3 | 0.4 | 0.4 | 0.3 | 0.3 | 0.9 | |
| ConcentrationCoefficient | 1.2 | 0.8 | 0.6 | 0.7 | 0.9 | 0.9 | 0.9 | 1.2 | 1.0 | |
| Ti | Mean Value | 3160.2 | 2395.3 | 1861.3 | 1880.9 | 2805.9 | 2515.4 | 2509.1 | 2244.3 | 2574.3 |
| Standard Deviation | 1840.7 | 979.1 | 676.5 | 875.1 | 939.3 | 967.3 | 795.5 | 631.9 | 1162.0 | |
| Coefficient of Cariation | 0.5 | 0.4 | 0.3 | 0.4 | 0.3 | 0.4 | 0.3 | 0.3 | 0.4 | |
| ConcentrationCoefficient | 1.2 | 0.9 | 0.7 | 0.7 | 1.0 | 1.0 | 1.0 | 0.9 | 1.0 |
| Geological | N | E | K | J | T | P | C | Ch | Whole Area | |
|---|---|---|---|---|---|---|---|---|---|---|
| Unit Parameter |
||||||||||
| V | Mean Value | 65.4 | 60.8 | 53.4 | 49.5 | 64.0 | 59.3 | 71.1 | 55.0 | 63.1 |
| Standard Deviation | 19.8 | 25.4 | 22.1 | 18.2 | 17.5 | 22.7 | 26.2 | 32.9 | 25.8 | |
| Coefficient of Cariation | 0.3 | 0.4 | 0.4 | 0.3 | 0.2 | 0.4 | 0.3 | 0.6 | 0.4 | |
| ConcentrationCoefficient | 1.0 | 0.9 | 0.8 | 0.7 | 1.0 | 0.9 | 1.1 | 0.9 | 1.0 | |
| Pb | Mean Value | 20.5 | 15.2 | 14.8 | 17.6 | 21.8 | 19.2 | 15.3 | 15.6 | 18.4 |
| Standard Deviation | 5.6 | 21.3 | 3.4 | 13.5 | 21.9 | 7.6 | 5.4 | 3.2 | 15.1 | |
| Coefficient of Cariation | 0.3 | 1.4 | 0.2 | 0.7 | 1.0 | 0.4 | 0.3 | 0.2 | 0.8 | |
| ConcentrationCoefficient | 1.1 | 0.8 | 0.8 | 0.9 | 1.1 | 1.0 | 0.8 | 0.8 | 1.0 | |
| Zn | Mean Value | 68.9 | 50.1 | 46.1 | 64.6 | 78.3 | 65.5 | 64.8 | 60.0 | 66.0 |
| Standard Deviation | 18.2 | 22.7 | 11.9 | 79.3 | 65.0 | 25.6 | 21.5 | 24.1 | 48.6 | |
| Coefficient of Cariation | 0.3 | 0.4 | 0.2 | 1.2 | 0.8 | 0.4 | 0.3 | 0.4 | 0.7 | |
| ConcentrationCoefficient | 1.0 | 0.7 | 0.7 | 0.9 | 1.1 | 1.0 | 0.9 | 0.9 | 1.0 |
4.1.2. Permian System (P)
4.1.3. Triassic System (T)
4.1.4. Paleogene System (E)
4.1.5. Neogene System (N)
4.2. Data preprocessing and data set establishment
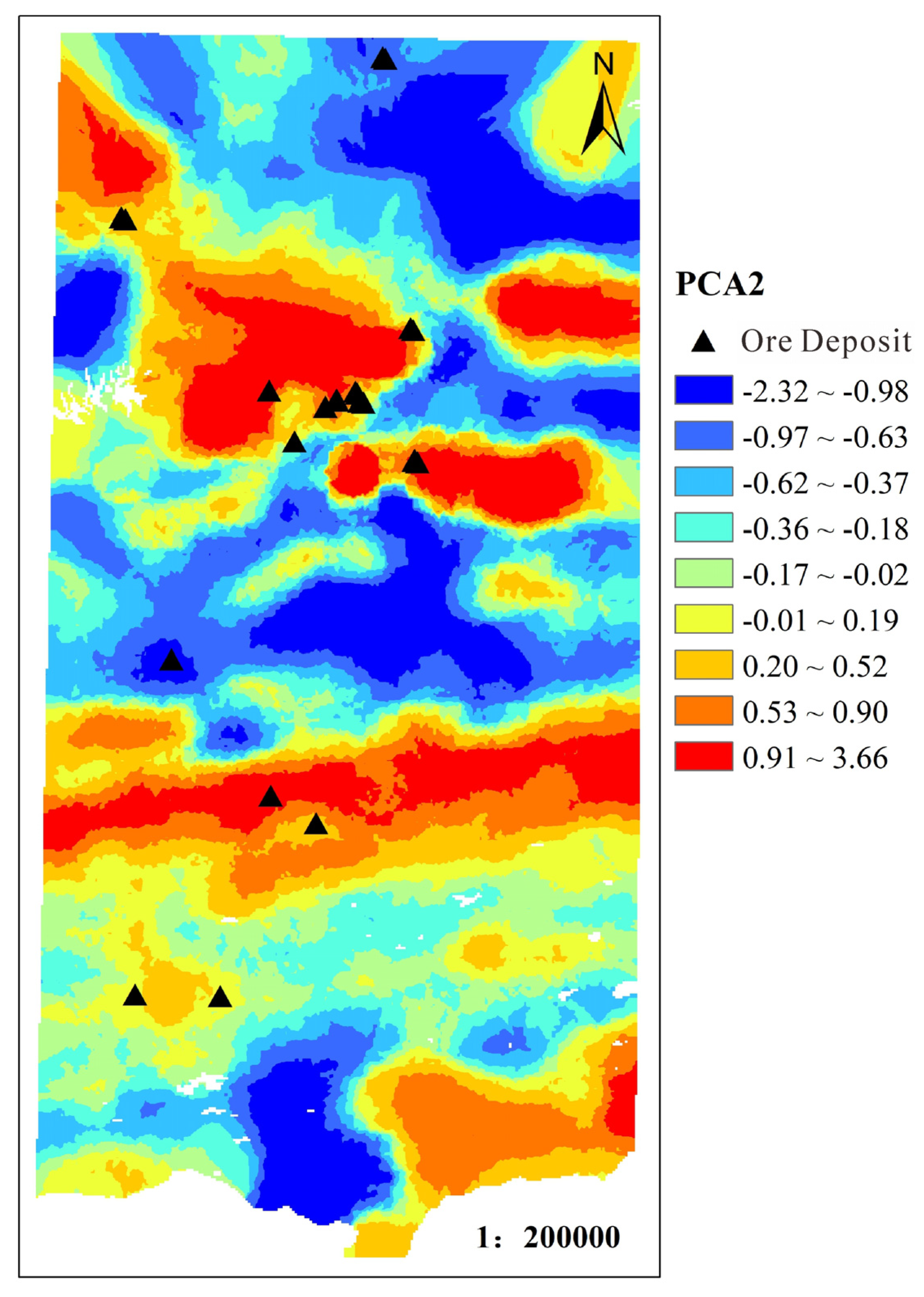
4.2.1. Evidence layer information extraction
4.2.2. Establishment of data sets
4.3. Random forest algorithm implementation
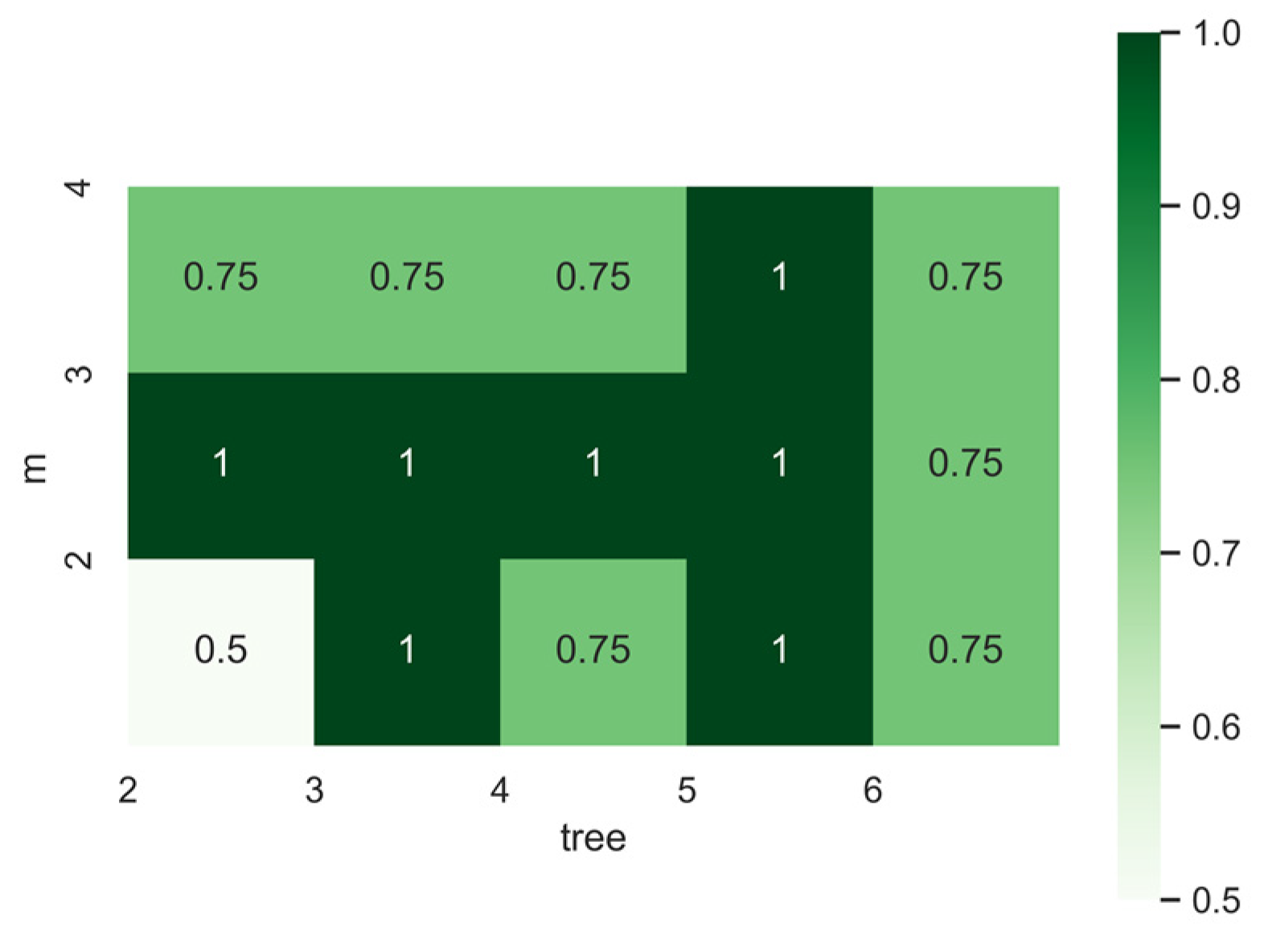
4.3.1. Parameter optimization
4.3.2. Prediction performance assessment
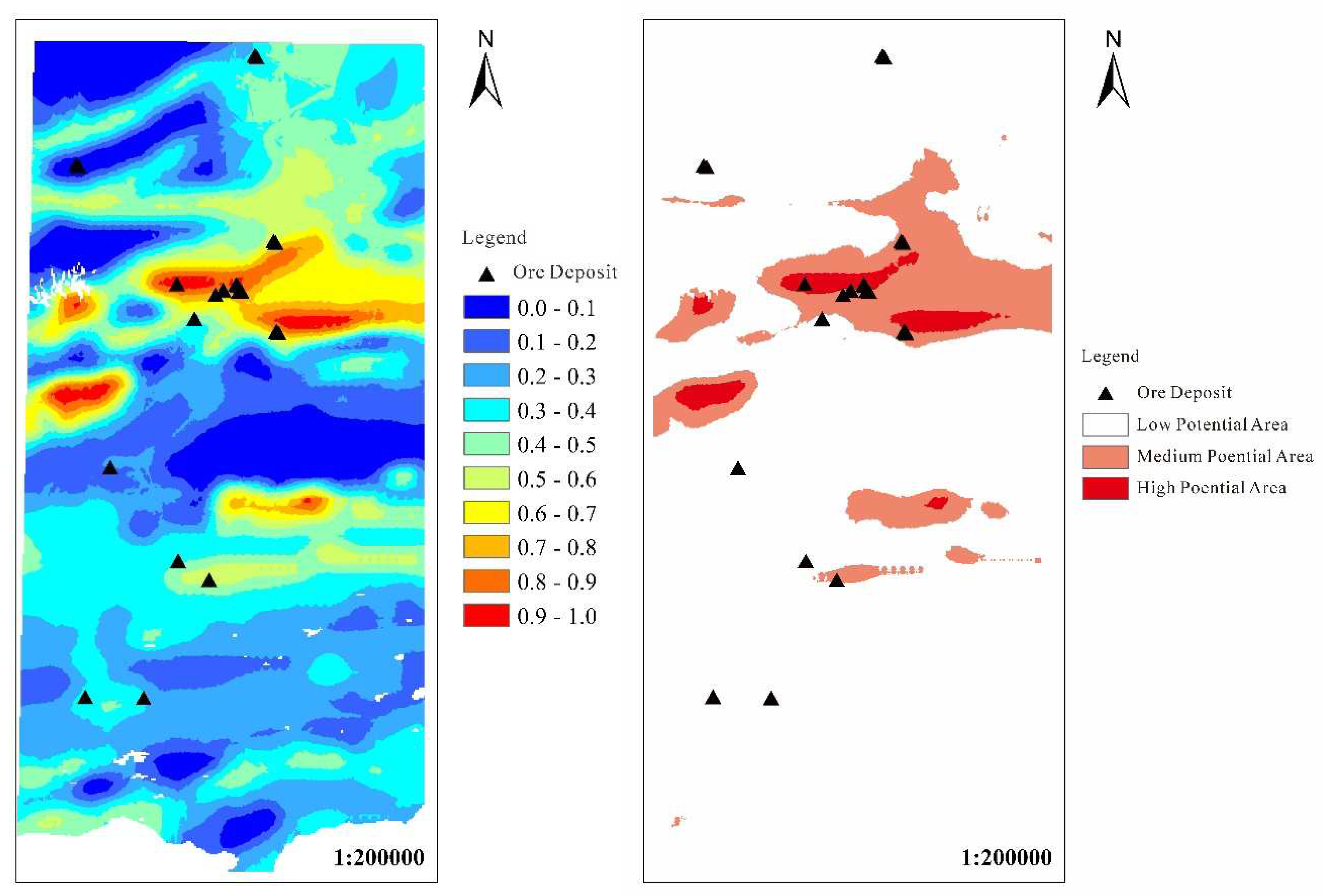
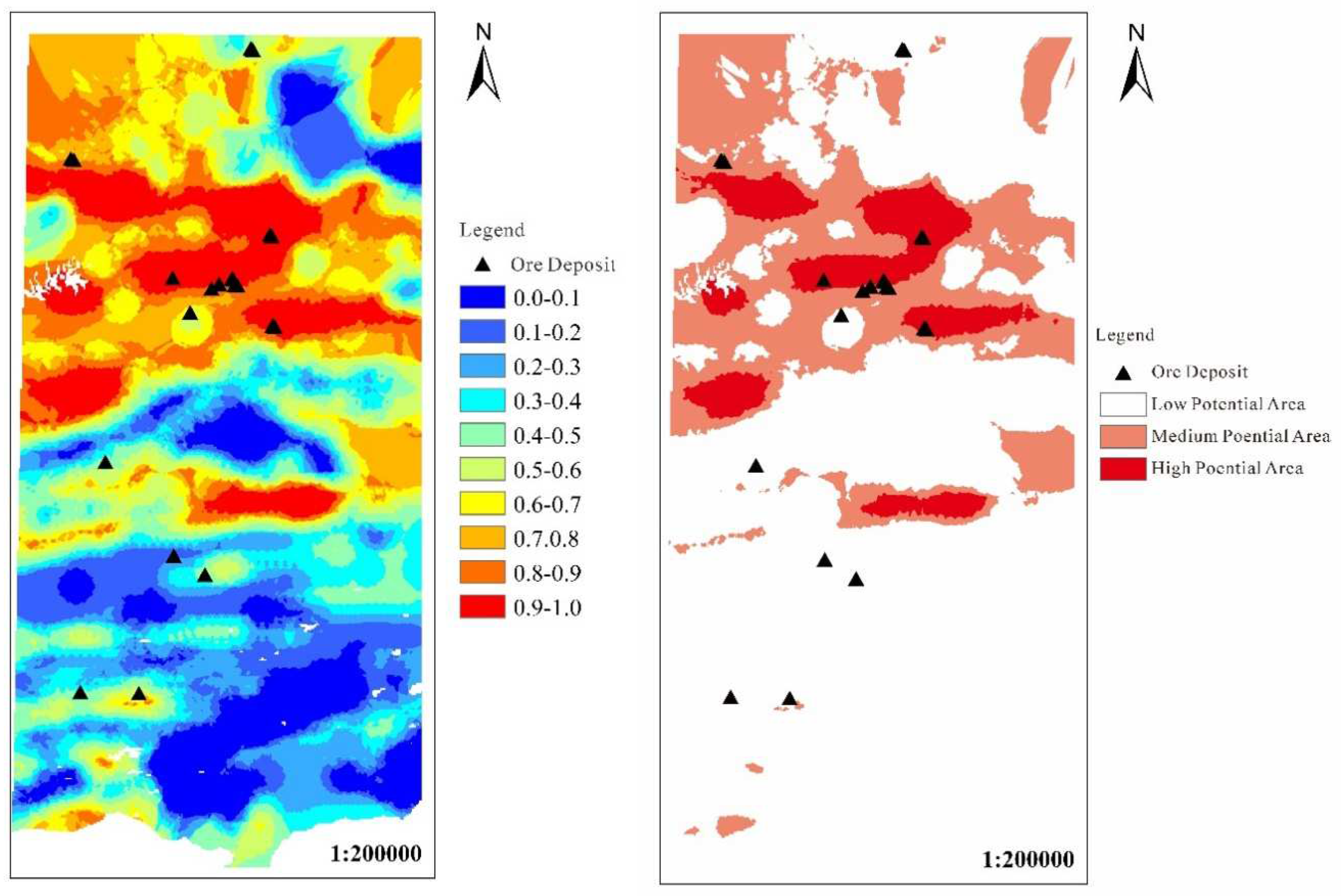
4.3.3. Metallogenic prediction results
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kong, W.H.; Xiao, K.Y.; Chen, J.P.; Sun, L.; Li, N. A combined prediction method for reducing prediction uncertainty in the quantitative mineral resources prediction. Earth Science Frontiers. 2021, 28, 128–138, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Liu, G.; Wang, Y.Z.; Xue, T.; Wu, C.Y.; Xue, B.; Tang, T.T.; Liu, S.M. Mineral Resource Spatial Association Analysis and Prediction: A Case Study in Western China. Geoscience 2019, 33, 751–758, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Agterberg, F.; Kelly, A. Geomathematical methods for use in prospecting. Canadian Mining Journal. 1971, 5, 61–72. [Google Scholar]
- Griffiths, J.; Menzie, D.; Labovitz, M. Exploration for and evaluation of natural resources. AAPG Research Symposium, Probability Methods in Oil Exploration, Aug. 1975, 20-22.
- Singer, D.A. RESIN, a FORTRAN IV program for determining the area of influence of samples or drill holes in resource target search. Computers & Geosciences. 1976, 2, 249–260. [Google Scholar] [CrossRef]
- Singer, D.A. Basic concepts in three-part quantitative assessments of undiscovered mineral resources. Nonrenewable Resources. 1993, 2, 69–81. [Google Scholar] [CrossRef]
- Singer, D.A. Progress in integrated quantitative mineral resource assessments. Ore Geology Reviews. 2010, 3, 242–250. [Google Scholar] [CrossRef]
- Wu, D.C.; Lu, W.Q.; Wang, G.P. 3D geological modeling and metallogenic prediction of Yimaquan M14 magnetic anomaly area in Geermu City of Qinghai. Mineral Resources and Geology 2023, 37, 55–61+71, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Song, W.; Zheng, L.; Liu, J.; Cao, S.; Xie, Z. Genesis, metallogenic model, and prospecting prediction of the Nibao gold deposit in the Guizhou Province, China. Acta Geochimica. 2023, 42, 136–152. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Hale, M. Logistic Regression for Geologically Constrained Mapping of Gold Potential, Baguio District, Philippines. Exploration and Mining Geology. 2001, 3, 165–175. [Google Scholar] [CrossRef]
- Li, W.; Neubauer, F.; Liu, Y.J.; Genser, J.; Ren, S.M.; Han, G.Q.; Liang, C.Y. Paleozoic Evolution of the Qimantage Magmatic Arcs, Eastern Kunlun Mountains : Constraints from Zircon Dating of Granitoids and Modern River Sands. Journal of Asian Earth Sciences. 2013, 77, 183–202. [Google Scholar] [CrossRef]
- Seraj, R.R.R. A hybrid GIS-assisted framework to integrate Dempster-Shafer theory of evidence and fuzzy sets in risk analysis: An application in hydrocarbon exploration. Geocarto international. 2021, 36, 5a8. [Google Scholar] [CrossRef]
- Behera, S.; Panigrahi, M.K. Mineral prospectivity modelling using singularity mapping and multifractal analysis of stream sediment geochemical data from the auriferous Hutti-Maski schist belt, S. India. Ore Geology Reviews. 2021, 131, 104029. [Google Scholar] [CrossRef]
- Koike, K.; Matsuda, S.; Suzuki, T.; Ohmi, M. Neural Network-Based Estimation of Principal Metal Contents in the Hokuroku District, Northern Japan, for Exploring Kuroko-Type Deposits. Natural Resources Research. 2002, 2, 135–156. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M.; Hale, M. Artificial Neural Networks for Mineral-Potential Mapping: A Case Study from Aravalli Province, Western India. Natural Resources Research. 2003, 3, 155–171. [Google Scholar] [CrossRef]
- Choi, S.; Moon, W.M.; Choi, S-G. Fuzzy logic fusion of W-Mo exploration data from Seobyeog-ri, Korea. Geosciences Journal. 2000, 2, 43–52. [Google Scholar] [CrossRef]
- Luo, X.; Dimitrakopoulos, R. Data-driven fuzzy analysis in quantitative mineral resource assessment. Computers & Geosciences. 2003, 1, 3–13. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Q.M.; Xia, Q.L.; Wang, X.Q. Mineral potential mapping for tungsten polymetallic deposits in the Nanling metallogenic belt, South China. Journal of Earth Science. 2014, 4, 689–700. [Google Scholar] [CrossRef]
- Wang, W.L.; Xie, S.Y.; Carranza, E.J.M. Introduction to the thematic collection: Applications of innovations in geochemical data analysis. Geochemistry Exploration Environment Analysis. 2022, 23. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Weights of Evidence Modeling of Mineral Potential: A Case Study Using Small Number of Prospects, Abra, Philippines. Natural Resources Research. 2004, 3, 173–187. [Google Scholar] [CrossRef]
- Yang, F.; Xie, S.Y.; Hao, Z.; Carranza, E.J.M.; Song, Y.; Liu, Q.; Xu, R.; Nie, L.; Han, W.; Wang, C. Geochemical Quantitative Assessment of Mineral Resource Potential in the Da Hinggan Mountains in Inner Mongolia, China. Minerals. 2022, 12, 434. [Google Scholar] [CrossRef]
- Brown, W.; Groves, D.; Gedeon, T. Use of Fuzzy Membership Input Layers to Combine Subjective Geological Knowledge and Empirical Data in a Neural Network Method for Mineral-Potential Mapping. Natural Resources Research. 2003, 3, 183–200. [Google Scholar] [CrossRef]
- Kim, Y.H.; Choe, K.U.; Ri, R.K. Application of fuzzy logic and geometric average: A Cu sulfide deposits potential mapping case study from Kapsan Basin, DPR Korea. Ore Geology Reviews 2019, 107, 239–247. [Google Scholar] [CrossRef]
- Xiao, K.Y.; Zhang, X.H.; Song, G.Y.; Chen, Z.H.; Liu, D.L.; Wang, S.L. Development of GIS-Based Mineral Resources Assessment System. Earth Science. 1999, 5, 525–528, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Cui, C.Q.; Wang, B.; Zhao, Y.X.; Wang, Q.; Sun, Z.M. China's regional sustainability assessment on mineral resources: Results from an improved analytic hierarchy process-based normal cloud model. Journal of Cleaner Production. 2019, 210, 105–120. [Google Scholar] [CrossRef]
- Karapurkar, D.D. RS and GIS based studies on Sediment yield from a tropical watershed: A case study of the Gangolli Catchment, Karnataka. Sedimentation, Tectonics, Mineral Resources and Sustainable Development.
- Xie, S.Y.; Wan, X.; Dong, J.B.; Wan, N.; Jiang, X.N.; Carranza, E.J.M.; Wang, X.Q.; Chang, L.H.; Tian, Y. Quantitative Prediction of Potential Areas Likely to Yield Se-rich and Cd-low Rice using Fuzzy Weights-of-Evidence Method. Science of the Total Environment 2023, 889, 164015. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Transactions on Neural Networks and Learning Systems 2017, 10, 2222–2232. [Google Scholar] [CrossRef]
- Agterberg, F. Geomathematics: Theoretical Foundations, Applications and Future Developments; Springer: Canada, 2014; 552. [Google Scholar]
- Zhou, Y.Z.; Chen, S.; Zhang, Q.; Xiao, F.; Wang, S.G. Advances and Prospects of Big Data and Mathematical Geoscience. Acta Petrologica Sinica. 2018, 2, 255–263. [Google Scholar]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine Learning Predictive Models for Mineral Prospectivity: An Evaluation of Neural Networks, Random Forest, Regression Trees and Support Vector Machines. Ore Geology Reviews. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.X.; Liu, W.M.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geology Reviews. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.H.; Bahroudi, A. Support vector machine for multi-classification of mineral prospectivity areas. Computers & Geosciences. 2012, 46, 272–283. [Google Scholar] [CrossRef]
- Beucher, A.; Siemssen, R.; Fröjdö, S.; Österholm, P.; Martinkauppi, A.; Edén, P. Artificial Neural Network for Mapping and Characterization of Acid Sulfate Soils: Application to Sirppujoki River Catchment, Southwestern Finland. Geoderma 2015, 247-248, 38–50. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. Journal of Hydrology 2010, 1-2, 141–150. [Google Scholar] [CrossRef]
- Xie, S.Y.; Huang, N.; Deng, J.; Wu, S.L.; Zhan, M.G.; Carranza, E.J.M.; Zhang, Y.P.; Meng, F.X. Quantitative Prediction of Prospectivity for Pb–Zn Deposits in Guangxi (China) by Back-propagation Neural Network and Fuzzy Weights-of-Evidence Modeling. Geochemistry: Exploration, Environment, Analysis 2022, 22. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS Journal of Photogrammetry and Remote Sensing. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Dong, L.H.; Zhang, L.C.; Li, W.D. Division and characteristics of geotectonic units in Xinjiang. The 6th Tianshan Geological and Mineral Resources Symposium, Urumqi, Xinjiang, China, 2008; pp. 25–32. (In Chinese). [Google Scholar]
- Pan, Y.S. Formation and Uplifting of the QingHai- Tibet Plateau. Earth Science Frontiers. 1999, 3, 153–163, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Liu, C.Y.; Liu, T. Discovery and Significance of Porphyritic Copper Mineralization in YunwuNing of XinJiang. Xinjiang Geology. 1998, 2, 185–187, (In Chinese with English abstract). [Google Scholar]
- Zhang, Y.P.; Ye, X.F.; Xie, S.Y.; Zhou, X.y.; Awadelseid, S.F.; Yaisamut, O.; Meng, F.X. Implication of multifractal analysis for quantitative evaluation of mineral resources in the Central Kunlun area, Xinjiang, China. Geochemistry: Exploration, Environment, Analysis 2022, 22, geochem2021-083. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Machine learning. 2001, 1, 5–32. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognition Letters 2010, 14, 2225–2236. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In PERNER P. Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin, Heidelberg, 2012; pp. 154–168. [Google Scholar]
- Liu, T.Y. EasyEnsemble and Feature Selection for Imbalance Data Sets. 2009 International Joint Conference on Bioinformatics, Systems Biology and Intelligent Computing, Shanghai, China, 2009; IEEE; pp. 517–520. [Google Scholar]
- Xiong, Y.; Zuo, R. Effects of misclassification costs on mapping mineral prospectivity. Ore Geology Reviews 2017, 82, 1–9. [Google Scholar] [CrossRef]
- Fawcett, T. ROC Graphs: Notes and Practical Considerations for Researchers. Machine Learning 2004, 31, 1–38. https://www.researchgate.net/publication/215992134.
- Kim, E.; Kim, W.; Lee, Y. Combination of multiple classifiers for the customer’s purchase behavior prediction. Decision Support Systems. 2003, 2, 167–175. [Google Scholar] [CrossRef]
- Cui, X.L.; Liu, T.T.; Wang, W.H.; Jing, M.; Bai, Y. Characteristics of geochemistry and prospecting direction of stream sediments in Buqingshan area, East Kunlun Mountains. Geophysical and Geochemical Exploration. 2011, 35, 573–578, (in Chinese with English abstract). [Google Scholar]
- Guo, Y.; Gong, F.Z.; Ning, J.S.; Liu, Y.C.; Liu, Z. Comparative study of the content area fractal method and the traditional statistical method for determining the anomaly lower limit:a case study of Au element of stream sediment survey in Awengcuo area of Tibet. Mineral Resources and Geology. 2018, 4, 736–741, (in Chinese with English abstract). [Google Scholar]
- Thanh, T.N.; Tuyen, D.V. Identification of Multivariate Geochemical Anomalies Using Spatial Autocorrelation Analysis and Robust Statistics. Ore Geology Reviews. 2019, 111, 102985. [Google Scholar] [CrossRef]
- Feng, C.Y.; Wang, S.; Li, G.C.; Ma, S.C.; Li, D.S. Middle to Late Triassic granitoids in the Qimantage area, Qinghai Province, China: Chronology, geochemistry and metallogenic significances. Acta Petrologica Sinica. 2012, 28, 665–678, (in Chinese with English abstract). [Google Scholar]
- Guo, Z.F.; Deng, J.F.; Xu, Z.Q.; Mo, X.X.; Luo, Z.H. Late Palaeozoic-Mesozoic Intracontinental, Orogenic Process and Inter Medate-Acidic Igneous Rocks from the Eastern KunLun Mountains of North Western China. Geoscience 1998, 3, 51–59, (in Chinese with English abstract). [Google Scholar]
- Li, W.; Neubauer, F.; Liu, Y.J.; Genser, J.; Liang, C.Y. Paleozoic Evolution of the Qimantage Magmatic Arcs, Eastern Kunlun Mountains: Constraints from Zircon Dating of Granitoids and Modern River Sands. Journal of Asian Earth Sciences, 2013, 77, 183–202. [Google Scholar] [CrossRef]
- Zheng, M.T.; Zhang, L.C.; Zhu, M.T.; Li, Z.Q.; He, L.D.; Shi, Y.J.; Dong, L.H.; Feng, J. Geological characteristics, formation age and genesis of the Kalaizi Ba-Fe deposit in West Kunlun. Earth Science Frontiers. 2016, 5, 252–265, (in Chinese with English abstract). [Google Scholar] [CrossRef]
- Gribskov, M.; Robinson, N.L. Use of receiver operating characteristic (ROC) analysis to evaluate sequence matching. Computers & Chemistry, 1996, 1, 25–33. [Google Scholar] [CrossRef]
| Predicted Positive(PP) | Predicted Negative(PN) | |
|---|---|---|
| Actual Positive(AP) | TP (True Positive) | FN (False Negative) |
| Actual Negative(AN) | FP (False Positive) | TN (True Negative) |
| Component | Initial Eigenvalues | Rotation Sums of Squared loadings | |||||
|---|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | ||
| 1 | 4.65 | 38.75 | 38.75 | 4.31 | 35.91 | 35.91 | |
| 2 | 1.85 | 15.44 | 54.19 | 1.95 | 16.23 | 52.14 | |
| 3 | 1.56 | 13.01 | 67.19 | 1.80 | 15.00 | 67.14 | |
| 4 | 1.01 | 8.39 | 75.58 | 1.01 | 8.44 | 75.58 | |
| 5 | 0.92 | 7.67 | 83.25 | ||||
| 6 | 0.64 | 5.35 | 88.60 | ||||
| 7 | 0.43 | 3.61 | 92.21 | ||||
| 8 | 0.33 | 2.76 | 94.96 | ||||
| 9 | 0.27 | 2.21 | 97.18 | ||||
| 10 | 0.19 | 1.58 | 98.75 | ||||
| 11 | 0.10 | 0.81 | 99.56 | ||||
| 12 | 0.05 | 0.44 | 100.00 | ||||
| RF | |
|---|---|
| Min | 0.50 |
| Max | 1.00 |
| Mean | 0.85 |
| Std | 0.16 |
| Select training samples | Integrated random undersampling | |
|---|---|---|
| RF | RF | |
| Acc | 1.00 | 0.75 |
| Acc+ | 1.00 | 1.00 |
| Acc- | 1.00 | 0.60 |
| G-mean | 1.00 | 0.87 |
| Integrated random undersampling | Select training samples | ||
|---|---|---|---|
| RF | RF | ||
| Low potential areas | Known number of ore points | 7 | 5 |
| Area (km2) | 11240 | 13768 | |
| Ore-bearing ratio (%) | 0.062 | 0.036 | |
| Mineralization potential area | Known number of ore points | 9 | 10 |
| Area (km2) | 3447 | 1702 | |
| Ore-bearing ratio (%) | 0.261 | 0.588 | |
| High potential areas | Known number of ore points | 11 | 12 |
| Area (km2) | 1068 | 286 | |
| Ore-bearing ratio (%) | 1.030 | 4.196 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




