Prerpints.org logo
Preprint
Article

Evaluating Structural Details Influence on Elastic Wave Propagation for Composite Structures via Ray Tracing

This version is not peer-reviewed.

Submitted:

13 July 2023

Posted:

14 July 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This study presents a novel method based in ray tracing for analyzing wave propagation in composites, specifically tailored for Structural Health Monitoring applications. The method offers distinct advantages over the commonly used Finite Element Method mainly in computational resource utilization, that has become a limiting factor for this kind of analyses. The ray tracing method is evaluated against a number of example cases representing structural details such as thickness changes, stringers or simulated damages and it highlights the significance of ray tracing to study wave propagation under these conditions and how it can serve as a valuable tool for structural health monitoring.
Keywords: 
SHM
;  
wave propagation
;  
composites
;  
ray tracing
Subject: 
Engineering  -   Aerospace Engineering

1. Introduction

Lightweight composite materials have revolutionized various industries by offering superior strength-to-weight ratios, improved mechanical properties, and enhanced design flexibility. Thanks to improvements in the structural analysis discipline, weight reduction in diverse applications such as automobiles or aerospace is achieved either by using less material or by substituting material with a lighter one that could provides more functionality per unit of weight.
The use of lightweight composites, such as carbon fiber-reinforced polymers, has gained significant popularity in aerospace, however, these structures may require some special attention as they could present a much wider range of failure modes, including delamination, fiber breakage, matrix cracking, and impact-induced damage [1,2,3,4]. For this reason, new and affordable systems must be developed to be able to study the performance of these structures in service. Especially in composite materials, where damages such as delaminations or fiber fractures can be difficult to detect visually, but may cause a significant degradation in the strength of the material and if not assessed fast enough, could lead to a structural failure of the component.
This is where SHM plays a vital role. By employing various sensing technologies, data acquisition systems, and signal processing techniques, SHM enables real-time or periodic monitoring of composite structures. It allows for the detection, localization, and quantification of damage, as well as the assessment of its severity and progression over time. From an array of sensors permanently installed in the structure the extraction of damage-sensitive features from these measurements and the analysis of these features can be used to determine the current state of the structure integrity and, additionally, the system could be used to capture events that could possibly damage the structure and assess them in real time [5]. These SHM systems could present many cost advantages when compared with the traditional inspection methods, and could also be used to improve the life prediction of the structure based on its usage [6,7].
Ultrasonic inspections for lightweight structures have historically proven to be a reliable and cheap way of evaluating manufacturing defects or in-service damages. The main advantage of this method is that, in these kind of structures, elastic waves are able to travel large distances with very low attenuation and are are very sensitive to the typical damages that could appear in these kind of components [8] and therefore a significantly complex structure could be inspected with a very small number of sensors [6,9]. Employing elastic waves with a distributed piezoelectric actuator/sensor network based on the pitch-catch method has proven to be very successful for impact damage detection [10,11] and for crack and corrosion localization [12].
Due to the high cost of physical tests, numerical simulation can be especially helpful to predict the elastic wave propagation and may help improve the accuracy of these systems [13]. Computational numerical simulations provide a very effective way to capture and understand the structural behavior in terms of elastic wave response; general purpose computational codes such as time domain spectral finite element methods [14,15] or explicit finite element methods [13,16,17,18] are commonly used to calculate the wave propagation. Numerical methods, however, could present a series of significant disadvantages, such as:
  • Computational Complexity: finite element or finite difference methods, can be computationally intensive, especially for large and complex structures. Long computation times and high memory requirements may limit their efficiency, particularly for real-time or iterative analyses.
  • Grid or Element Discretization: Numerical methods rely on discretizing the structure into grids or elements, which may result in some loss of accuracy, difficulties in capturing fine details or aliasing effects on high frequencies. The choice of grid or element size can impact the accuracy and computational cost of the analysis.
  • Material damping of boundary damping: specifically for the explicit finite element method, introducing damping elements, either as dashpots or material damping, significantly reduces the stable time increment, making it virtually impossible to solve problems where this effect is relevant on the solution.
For these reasons, and also to increase the reliability of the simulations, there exists multiple different attempts of solving the problem without resorting to numerical simulation in the literature, either analytically [19,20,21] or using statistics or artificial intelligence [22,23]; some of these methods are able to achieve very good results, but the algorithms studied may be too complex to generalize or limited in applicability.
A different, very promising idea to solve the problem could be based in the ray tracing method. The ray tracing method is based on the assumption that the particle motion can be modeled as a number of idealized narrow beams (rays) which are advanced through the medium by discrete amounts. By tracing the paths of individual rays, it provides valuable information about wave behavior, including wavefront curvature, mode conversion, reflection, and transmission; as the rays interact with the objects present along their path.
The ray tracing-based approach offers significant advantages over traditional numerical methods in terms of computational efficiency and ease of implementation. It provides a practical tool to analyze wave propagation phenomena and has been widely used in scientific research for many different applications, most notably: astronomy [24], optical design [25], ocean acoustics [26,27] or heat transfer [28]. Specifically it has also been previously used in SHM to solve the guided wave wave propagation problem [29,30,31,32] and it has proven its effectiveness.
The solution presented in this article also applies the ray tracing method to solve the general guided elastic wave propagation problem for an arbitrary shell structure and it aims to provide additional versatility such as accounting for multiple sensors or actuators in the same problem and adjustable boundary parameters in order to accurately match experimental data.
A key point of difference with other methods based on ray tracing is the sensor model, which, instead of using a single spatial point it considers a finite area and integrates the signal on all the rays that intersect the area, being able to take into account all the possible paths that reach the sensor on a desired amount of time, for a sufficiently large number of initial rays.

2. Materials and Methods

2.1. Ray tracing methodology

In general, elastic waves in solid materials are guided by the boundaries of the media in which they propagate. Waves in infinite metallic plates were among the first guided waves to be analyzed in 1917 by Horace Lamb, and have been extensively studied in literature since then for their applications in SHM ([33,34]). They present three distinctive propagation modes: Symmetric ( S 0 ), Anti-symmetric ( A 0 ) and Shear ( S h 0 ). To represent the elastic wave propagation, each propagation mode is modelled with independent rays, and the behavior of the waves in the simulation is considered linear and uncoupled.
Propagation velocities of these modes are dispersive and are calculated by the stiffness transfer matrix method (STMM), described in [35]. This methodology is very convenient for multilayered media, as it condenses the system into four equations, eliminating all other intermediate interfaces. Assuming all composite layers behave as orthotropic media, following Hooke’s law, the layer stiffness matrix in global coordinates C expresses the relation between layer strains and stresses as:
σ 11 σ 22 σ 33 σ 23 σ 13 σ 12 = C 11 C 12 C 13 0 0 C 16 C 12 C 22 C 23 0 0 C 26 C 13 C 23 C 13 0 0 C 36 0 0 0 C 44 C 45 0 0 0 0 C 45 C 55 0 C 16 C 26 C 36 0 0 C 66 ϵ 1 ϵ 2 ϵ 3 γ 23 γ 13 γ 12
applying Newtons second law to the previous equation, considering the small linear strain-displacements approximation: ϵ i , j = 0.5 ∂ u j ∂ x i + ∂ u i ∂ x j , the internal forces can be converted into internal stresses, resulting in ∇ σ ˙ = ρ u ¨ . It is possible to then solve the resulting linear system of equations by imposing a wave solution of the form ( u 1 , u 2 , u 3 ) = ( U 1 , U 2 , U 3 ) e i k x 1 + α x 3 − v p t , being U 1 , U 2 and U 3 the amplitudes of the harmonic motions in time and space. It is then possible to write the equations of motion as:
C 11 − ρ v p 2 + C 55 α 2 C 16 + C 45 α 2 C 13 + C 55 α C 16 + C 45 α 2 C 66 − ρ v p 2 + C 44 α 2 C 36 + C 45 α C 13 + C 55 α C 36 + C 45 α C 55 − ρ v p 2 + C 33 α 2 U 1 U 2 U 3 = 0
The system from 2.1 only presents a non-trivial solution when its determinant has a null value, therefore it can be treated as an eigenvalue problem to obtain the values of α , resulting in a six-order equation with only even coefficients [35,36], therefore:
α 1 = − α 2 , α 3 = − α 4 , α 5 = − α 6
It is then possible to rewrite the expressions for displacements and stresses as follows:
u 1 , u 2 , u 3 = ∑ j = 1 6 1 , V j , W j U 1 e i k x i + α j x 3 − v p t
σ 33 , σ 13 , σ 23 = ∑ j = 1 6 D 1 j , D 2 j , D 3 j U 1 e i k x i + α j x 3 − v p t
values for the parameters V j , W j and D i j can be found in [35]. Defining a stress displacement vector s x 3 = u 1 , u 2 , u 3 , σ 33 , σ 13 , σ 23 the relation for wave propagation in each each layer results:
u 1 u 2 u 3 σ 33 σ 13 σ 23 = 1 1 1 1 1 1 V 1 V 2 V 3 V 4 V 5 V 6 W 1 W 2 W 3 W 4 W 5 W 6 D 11 D 12 D 13 D 14 D 15 D 16 D 21 D 22 D 23 D 24 D 25 D 26 D 31 D 32 D 33 D 34 D 35 D 36 U 11 e k α 1 x 3 U 12 e k α 2 x 3 U 13 e k α 3 x 3 U 14 e k α 4 x 3 U 15 e k α 5 x 3 U 16 e k α 6 x 3 e i k x 1 − v p t
Relating this equation at the top and bottom of each layer, and guaranteeing continuity, it is possible to obtain a relation between the upper and lower surfaces of the plate. Therefore, for a laminate of n layers the expression would be:
{ s t o p } = [ T n ] [ T n − 1 ] . . . [ T 1 ] { s b o t t o m } = ∏ j = 1 n [ T j ] { s b o t t o m } = [ A ] { s b o t t o m }
{ u t o p } { σ t o p } = [ A u u ] [ A u σ ] u σ ] [ A σ σ ] { u b o t t o m } { σ b o t t o m }
Stress free boundary conditions are then guaranteed in the top and bottom layers as { s t o p } = { s b o t t o m } = 0 , hence the dispersion curves can be computed by calculating the determinant | A u σ | = 0
Group velocity, defined as: v g = d ω d k determines the speed at which the wave packet travels, the frequency represents the central frequency of the packet (maximum of the Fourier transform), while phase velocity v p determines the speed at which the ray travels, and the dispersion relation can be obtained via these two values.
The shear wave propagation mode ( S h 0 ) is not accounted for in the model, as its usefulness for SHM applications is negligible compared with the other modes and only the S 0 and A 0 modes are considered and modeled with independent rays.
The ray path along the structure is governed with the Snell’s law, and can be solved incrementally assuming linear propagation:
ξ = cos θ ( z ) c ( z ) = cos θ 0 c 0
Properties of the media are considered uniform until reaching a boundary so rays can travel on a straight line on each time increment, and, therefore, the increment time is only limited by the number and density of boundaries in the simulated component.

2.2. Boundary reflection and transmission

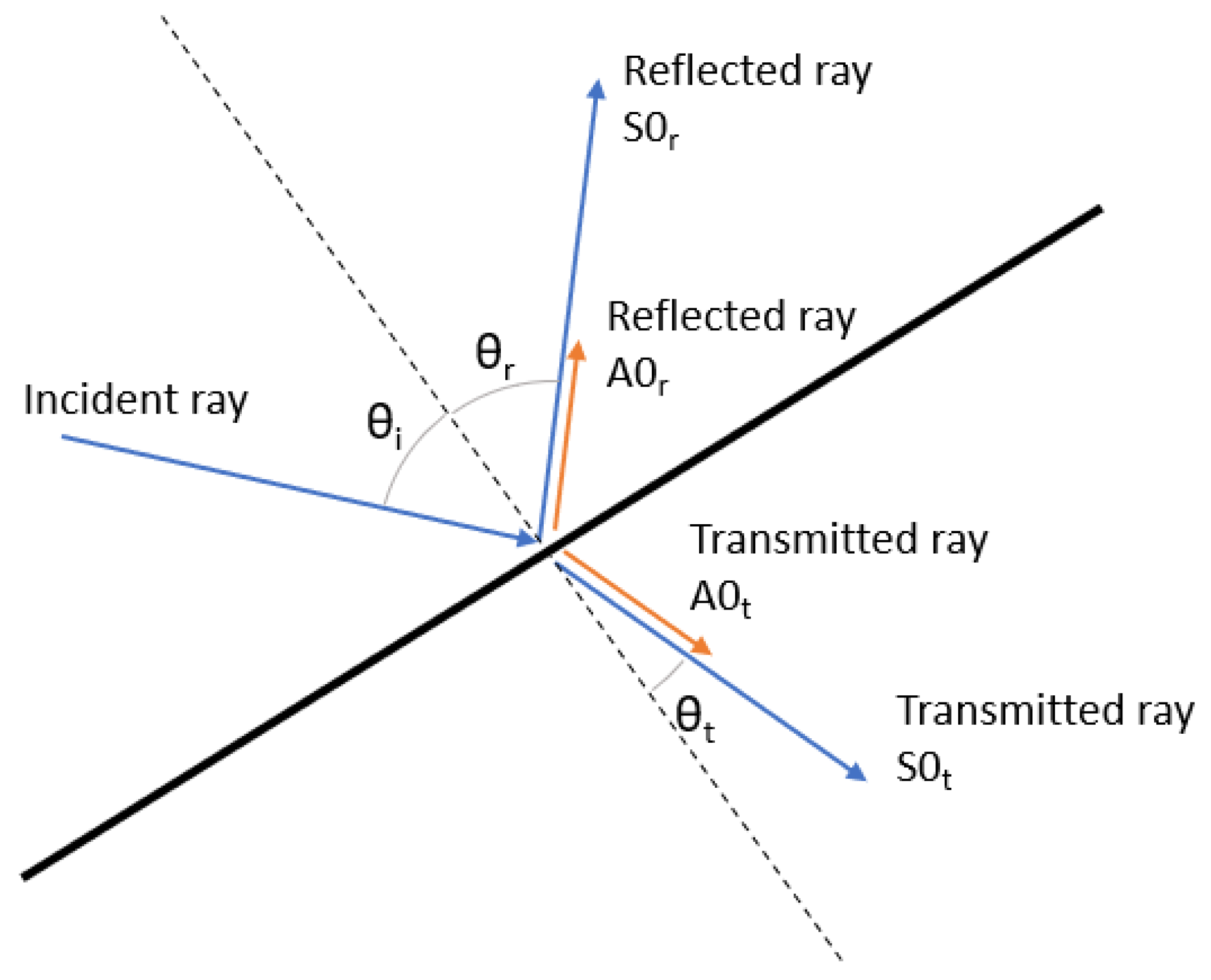
When a ray encounters a boundary a component of the ray energy is reflected and another part is transmitted; the model takes into account the mode conversion phenomena [37,38] at each boundary and therefore, the transmitted and reflected component energy is divided between the different propagation modes. as shown in Figure 1.
The energy of the incident ray E i r a y is divided between the four rays originating at the intersection point and a remnant energy ϵ E that is lost at the boundary, as follows:
E i r a y = f 1 E S 0 r + f 2 E A 0 r + f 3 E S 0 t + f 4 E A 0 t + ϵ E
where E S 0 r and E A 0 r represent the energy of the symmetric and antisymmetric reflected rays, E S 0 t and E A 0 t represent the energy of the symmetric and anti-symmetric transmitted rays and the factors f i represent the wave energy that is distributed between each of the propagation modes, considering f i < 1 . and f 1 + f 2 + f 3 + f 4 < 1 . Both the factors f i and the dissipated energy ϵ E must be adjusted based on the kind of boundary encountered.
For the particular case in which the ray would reach a segment end (ie. a corner) the ray is eliminated from the model. This approach is taken as a simplification to reduce computational effort, as the effect is negligible for a sufficiently large number of rays and can be minimized considering initial rays that wont intersect any corners of the model on their first propagation step, for example: by choosing an odd number of initial rays.

2.3. Ray signal recovery

Typical excitation signals used on active interrogation consist on a tone burst, 50 V peak to peak sine wave modulated by a Hamming window. These signals are named with the convention BURSTn where n represents the width of the window in number of periods. The frequency of these signals is studied in the range of [ 100 , 500 ] kHz.
This signal information is carried independently on each ray in the frequency domain, via a sufficiently large amount of terms of their Fourier transform, and could then be modified as the ray propagates through the model due to different effects, such as the material damping which is considered as a factor over the signal amplitude A, following an exponential law: A = A 0 exp − ω ξ t where ξ is the material damping coefficient.
After considering dispersion and material damping effects, the ray signal can be obtained during its propagation by applying the time shift property of the Fourier transform x t − t 0 ⟷ exp − j ω t 0 X ω therefore being able to recover the time domain signal at any point over the ray path.

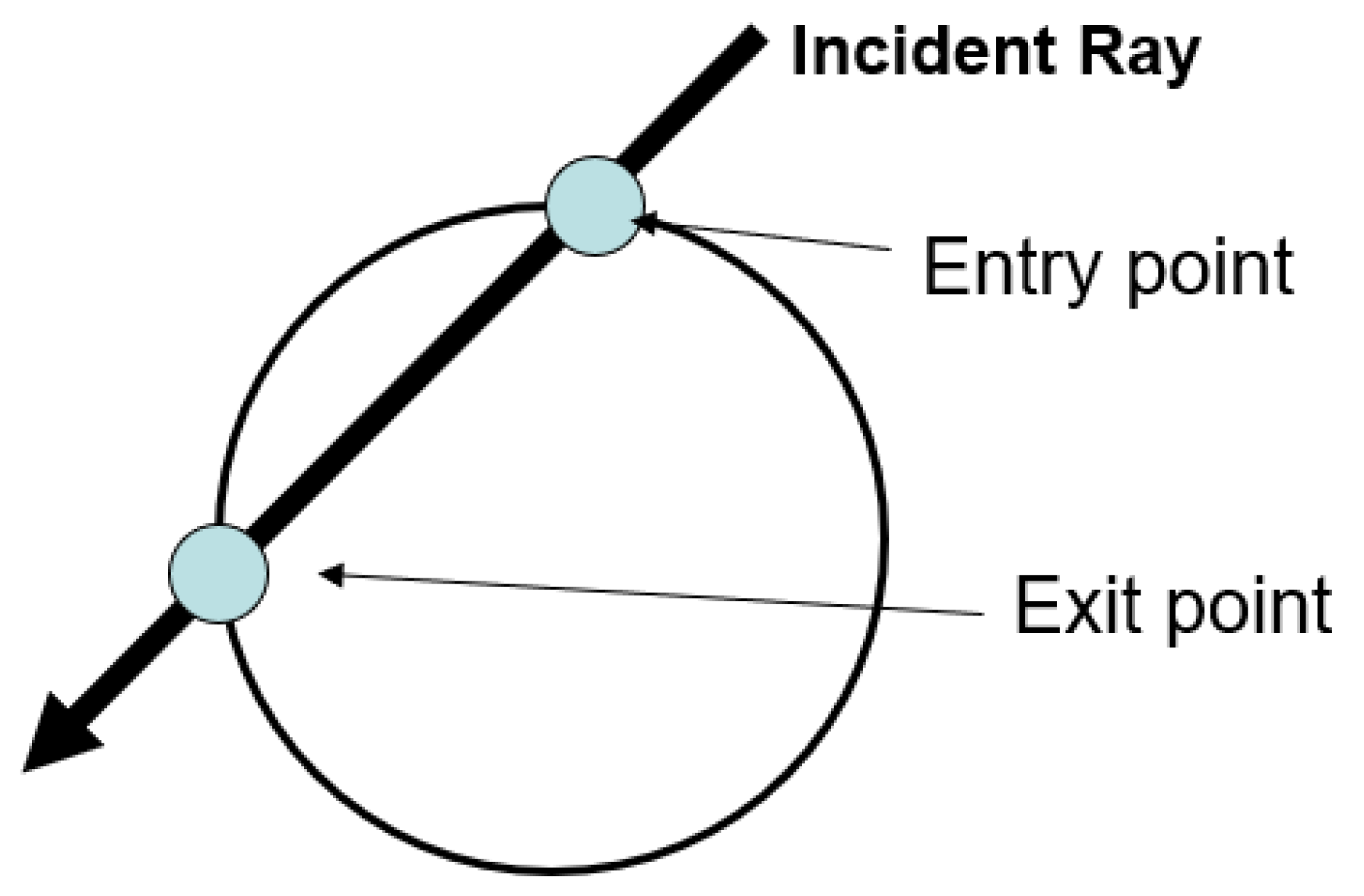
2.4. Piezoelectric sensor model

Due to the piezoelectric sensors low weight, and their ability of both generating and measuring guided elastic waves they are ideal for SHM systems. Signals obtained unavoidably contain multiple modes requiring complex signal processing techniques to extract useful information. Moreover, PZT sensors may also reveal certain nonlinear behavior and hysteresis under large strains/voltages or at high temperature. Brittleness, low fatigue life, etc., may be some other concerns limiting application ([39]).
To include the PZT sensors in the simulation, they are modeled as a circle boundary. This boundary does not interact with the incident rays, however the intersection time points ( t i and t e ) are captured and the ray signal is integrated between the line crossing the sensor area ( s e − s i ), as shown in Figure 2. This way allows the sensor to act as an integrator of the material strain over the area it covers ([40,41]), and the solution is obtained by superimposing the integrated signal of all the incident rays.

3. Damage model evaluation

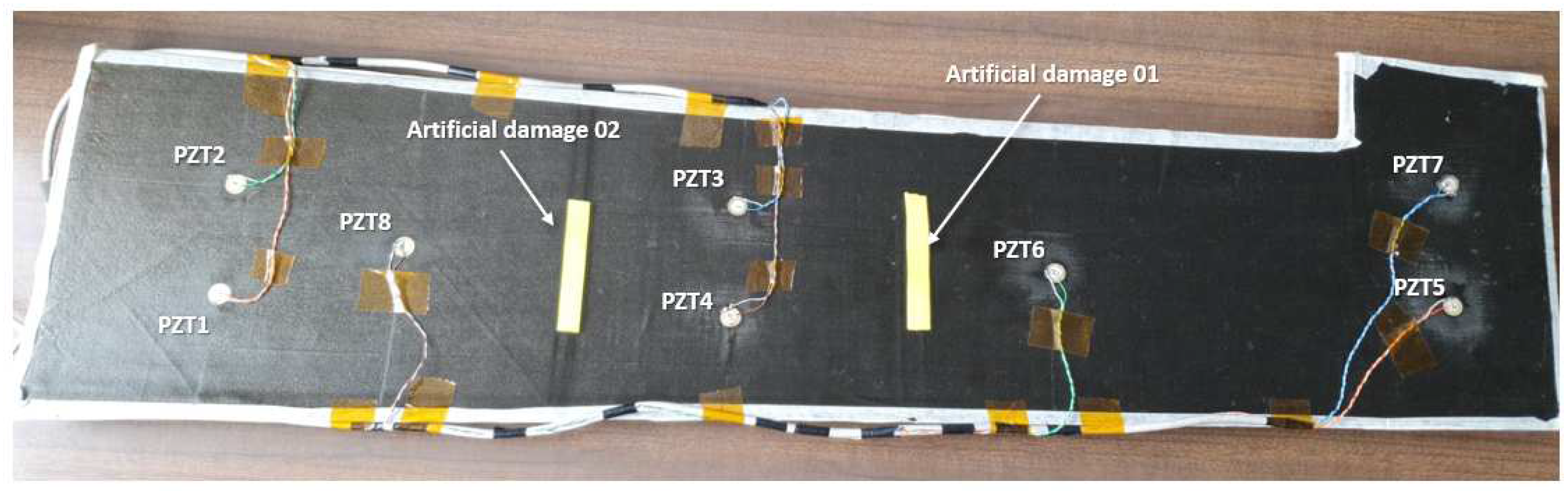
In order to evaluate the simulation behavior in the presence of damage, the methodology is compared against a physical demonstrator of the front left wing lower cover of the remotely piloted aircraft system LIBIS, designed by the Technical University of Madrid.
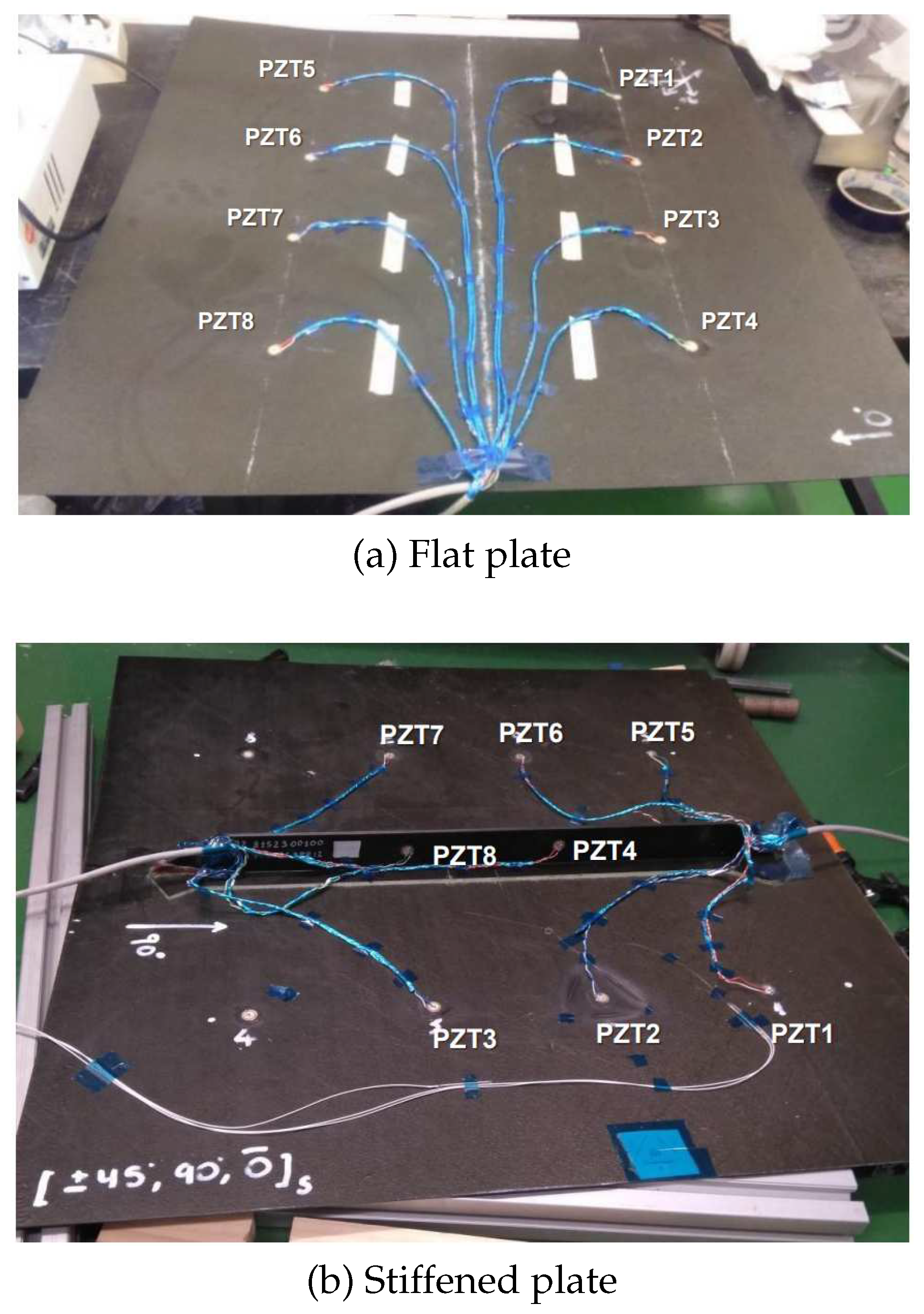
The specimen is instrumented with an array of 8, 12mm piezoelectric (PZT) sensors, as shown in Figure 3, and the data is recorded with an Acellent SCANGENIE system, with a sampling frequency of 48M Hz.
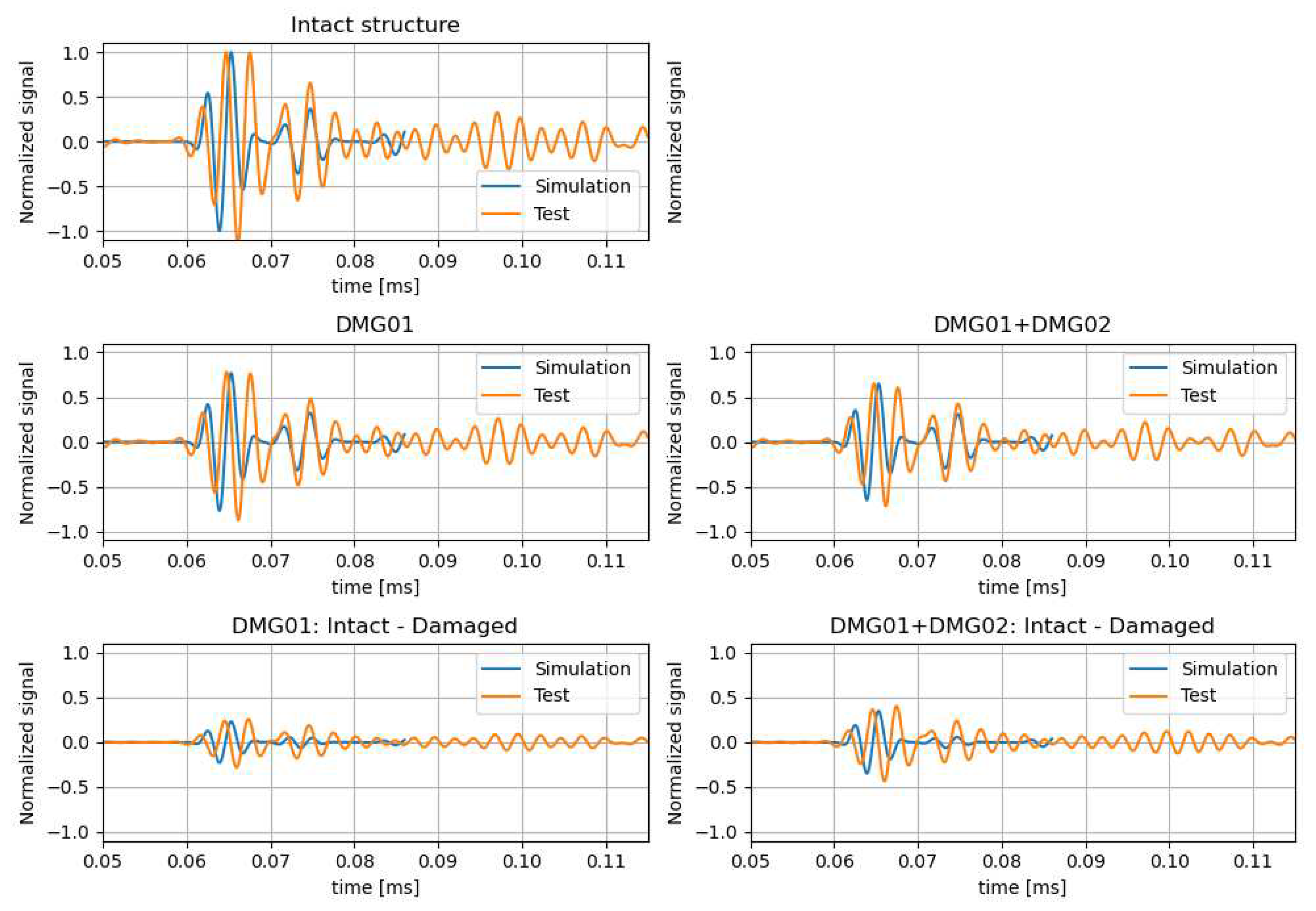
As shown in the figure, artificial damages to emulate the effect of a possible delamination have been introduced in the specimen. Three sets of tests were performed considering the intact structure, the structure with the artificial damage 01 and the structure with both artificial damages. The input signal used consist on a BURST3 at 350kHz; test results are presented as an average of 3 runs.
The simulation is run with 301 initial rays originating from piezo-electric transducer P Z T 8 . To simplify the analysis, the dispersion curves are calculated via the STMM method for one of the sections and then scaled by the thickness on the other two. Damage areas are simulated as linear boundary segments.
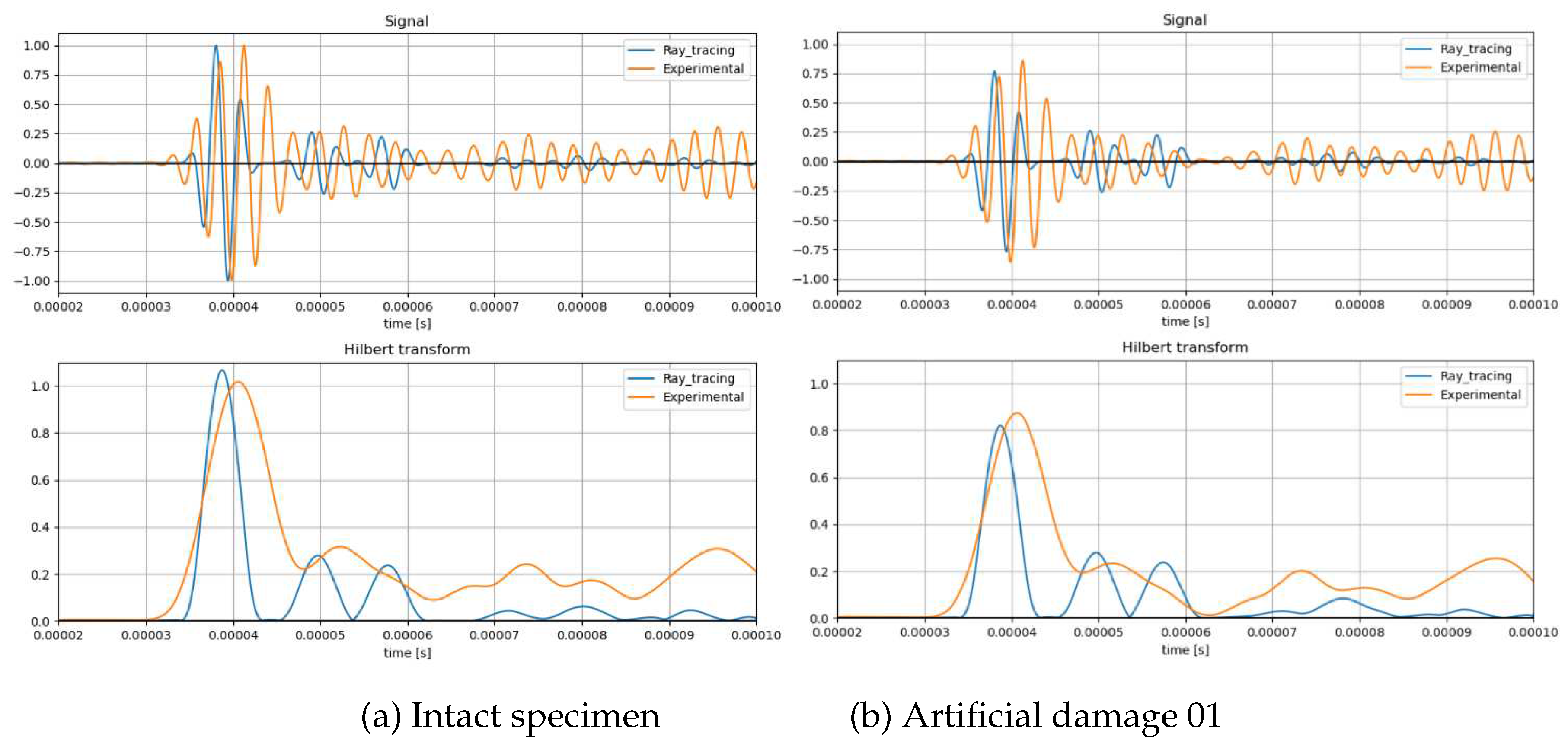
In order to quantify the effect of the damage on the system, both the energy reflected and dissipated in the boundary are adjusted manually based on the shortest linear propagation path, in this case corresponding between sensors P Z T 3 and P Z T 6 . The results compared with the tests after the adjustment are shown in Figure 4. Both intact signals and scatter plots are also shown on the figure.
The values adjusted by a single path are then validate with other paths for the path between transducers P Z T 8 and P Z T 6 . The energy absorption parameters of the damage are adjusted in order to match the amplitude of the first wave package arrival, with this values the results show an acceptable correlation on all sensors studied, as shown in the figure.
The results obtained for the case of artificial damage 1 and 2 are shown in Figure 5. The same parameters adjusted for the artificial damage 1 are applied on the damage 2 and the results still show a similar degree of correlation.
From the figures it can be observed that the results show a very high degree of correlation with the tests.

4. Stiffened composite plates case of study

To validate the simulations and gain a better understanding of the propagation of elastic waves on aeronautic structures, a testing campaign has been designed for two different representative structures: A simple, rectangular composite panel with a quasi-isotropic 7 ply layup and the same panel with a representative T-shape stringer along the center. They are both are instrumented with an array of 8 piezoelectric sensors, as shown in Figure 6, and the data is again recorded with the same DAQ system as in the previous test.
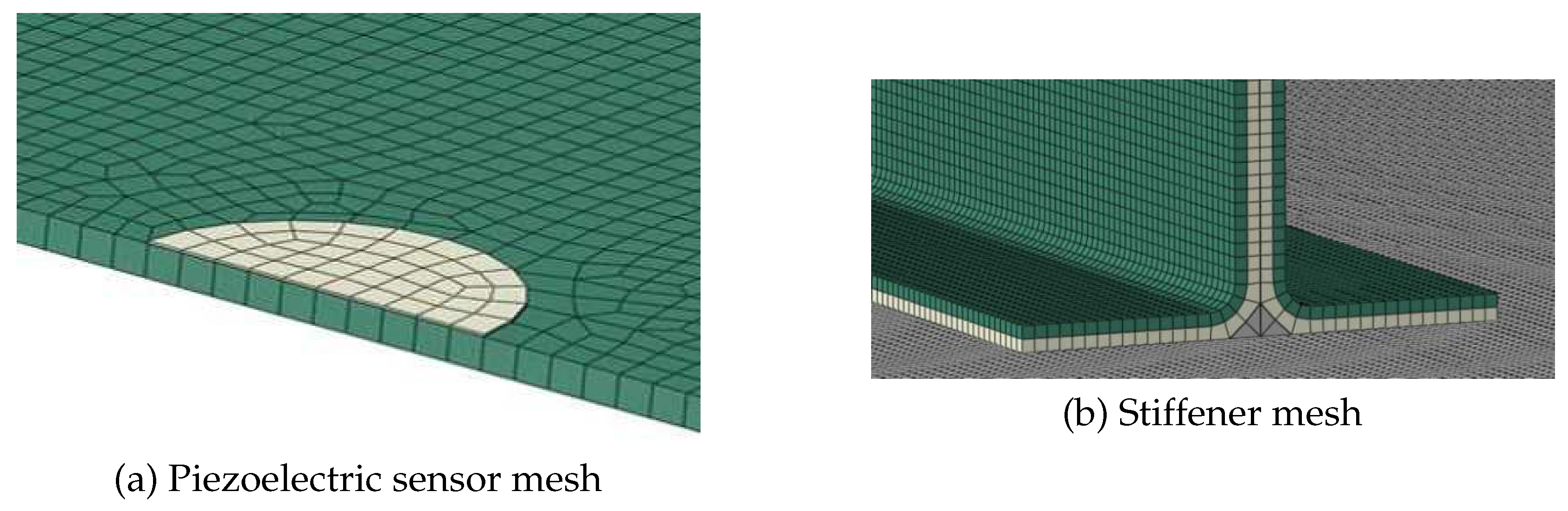
An additional Finite Element Method (FEM) has been developed in parallel to act as a benchmark with the ray tracing simulation ([42]). The analysis is done with Abaqus/Explicit version 2017, the composite solid panel is represented with continuum shell elements (SC8R) and conventional 2D shell elements (S4R) are used for the piezoelectric sensors/actuators. Due to limitations of the FEM code used, the input signal is introduced on the piezoelectric actuator as a temperature variation.
As the simulation must be able to represent the elastic wave behavior as it progresses through the panel an average element length of 1 mm is used in the model; this ensures that an antisymmetric wave up to a frequency of 200 kHz can be captured by the model using at least 10 elements per wavelength. The size limitation to model the elastic wave results in a very large mesh, of around 600000 elements and 1500000 nodes, as shown in Figure 7.
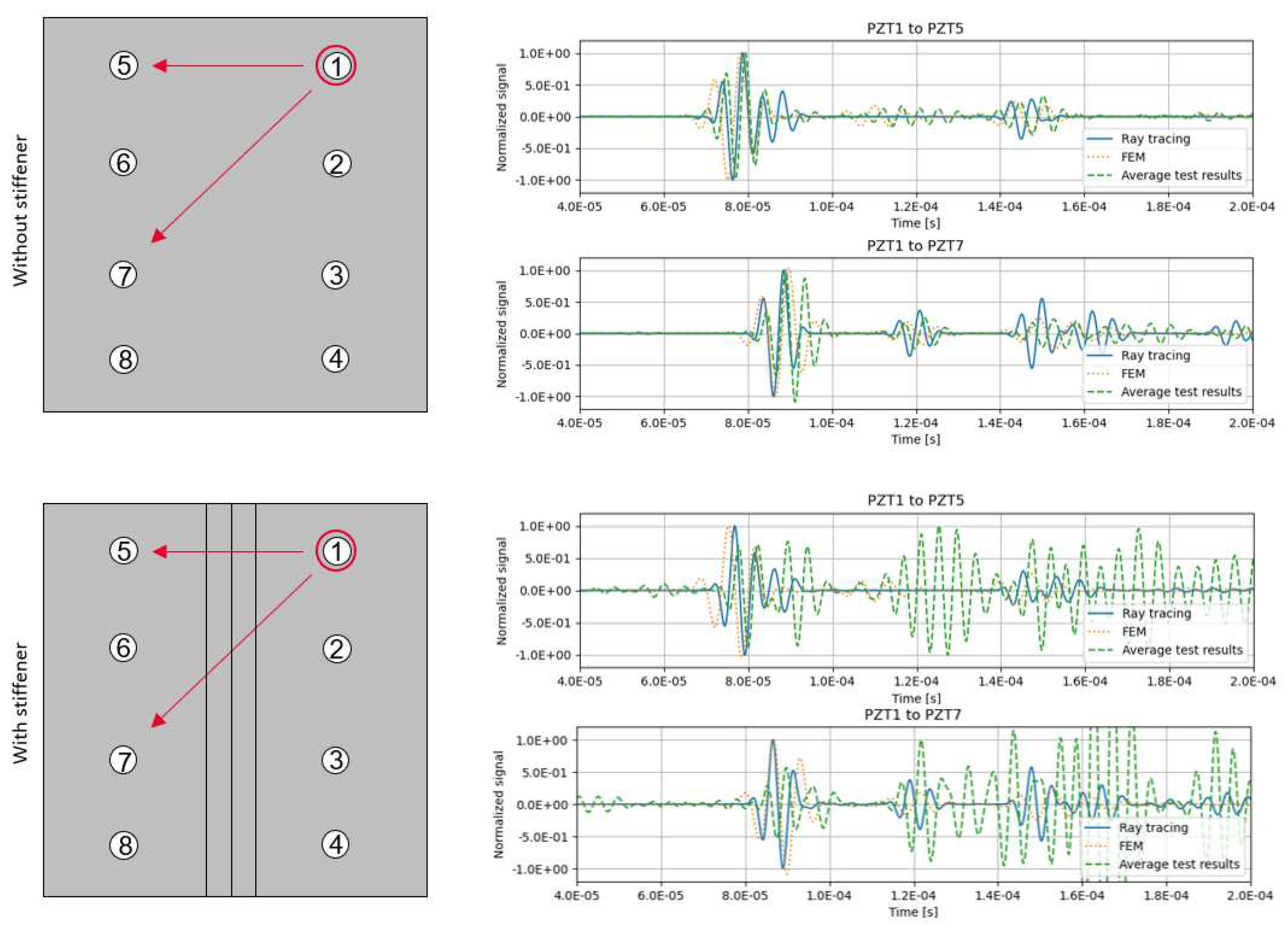
Both the FEM model simulation and the ray tracing model with 600 initial rays are compared against the tests. Signal results at relevant sensors are shown in Figure 8.
Although a computationally costly procedure, mapping the rays signal over a square grid can be useful for visualizing the wave propagation over the plate. This is shown in Figure 9, compared with the FEM model vertical displacement results at t = 0.07 m s . The grid used for the ray tracing model has a side length of 2 m m . The energy absorption caused by the stiffener cohesive bond is not represented in FEM model whereas in the ray tracing model is modelled with a boundary losses factor.

5. Conclusions

This study shows that the ray tracing method has proven to be an efficient way to calculate the guided elastic wave propagation for a general 2D geometry, with an arbitrarily large number of boundaries or sensors. Compared to FEM, the new method exhibits several notable advantages. Firstly, it allows for a higher level of accuracy in capturing wave phenomena; the method can better represent wavefront curvatures, mode conversions, and can trivially represent material or boundary damping.
Secondly, the computational efficiency of the proposed method surpasses that of FEM, making it suitable for real-time SHM applications. The spectral basis functions enable a more concise representation of the wave-field, reducing the computational cost while maintaining high accuracy. This capability facilitates rapid data processing and analysis, enhancing the timeliness of damage detection and localization in composites.
Additionally, the method proposed consists on a computation of the propagation map and the extraction of the signal in the relevant sensors by superimposing all the intersecting rays in the sensors area, as the signal is only evaluated in the sensors, reducing the amount of data and computational time required.
As an example the FEM simulation of the flat composite panel described in this article took an approximate 5h to run on 32 cores in a high performance computing cluster, while the 800 ray model takes approximately 3 minutes to process the result for each sensor.
The implementation shown is able to solve moderately large size problems in a standard laptop without the need of high performance computing resources, which is a significant improvement when compared with other numerical approaches such as the finite element method that could require up to days of computation on specialized equipment.
The methodology has been implemented with scalability in mind, and it is intended to be refined and improved to be used on more complex geometries. Additional benchmarks against both numerical simulations and physical tests could be performed in future research.

Author Contributions

Conceptualization, F.S.I. and A.F.L.; methodology, F.S.I. and A.F.L.; software, F.S.I.; validation, F.S.I.; writing—review and editing, F.S.I. and A.F.L.; supervision, A.F.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The data and algorithms shown in this article have been developed in the framework of the project "Structural health monitoring multisysTem bAsed on FOS/PZT smaRt sensinG Applied to aircrafTs structurEs (STARGATE)".

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

Abbreviations
The following abbreviations are used in this manuscript:
SHM Structural Health Monitoring
FEM Finite Element Method
PZT Lead zirconate titanate
DAQ Data acquisition
HPC High Performance Computing
STMM Stiffness Transfer Matrix Method

References

  1. Tuo, H.; Lu, Z.; Ma, X.; Xing, J.; Zhang, C. Damage and failure mechanism of thin composite laminates under low-velocity impact and compression-after-impact loading conditions. Composites Part B 2019, 163, 642–654. [Google Scholar] [CrossRef]
  2. Li, X.; Ma, D.; Liu, H.; Tan, W.; Gong, X.; Zhang, C.; Li, Y. Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact. Composite structures 2019, 207, 727–739. [Google Scholar] [CrossRef]
  3. Wang, J.; Wang, H.; Chen, B.; Huang, H.; Liu, S. A failure mechanism based model for numerical modeling the compression-after-impact of foam-core sandwich panels. Composites Science and Technology 2017, 151, 258–67. [Google Scholar] [CrossRef]
  4. Guinard, S.; Allix, O.; Guedra-Degeorges, D.; Vinet, A. A 3D damage analysis of low velocity impacts on laminated composites. Composites Science and Technology 2002, 62, 585–9. [Google Scholar] [CrossRef]
  5. Seno, A.H.; Khodaei, Z.S.; Aliabadi, M.F. Passive sensing method for impact localisation in composite plates under simulated environmental and operational conditions. Mechanical Systems and Signal Processing 2019, 129, 20–36. [Google Scholar] [CrossRef]
  6. Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Science 2006, 365. [Google Scholar] [CrossRef]
  7. López, A.F. Detección de daño en estructuras aeronáuticas mediante sensores piezoeléctricos y de fibra óptica. PhD thesis, Technical University of Madrid, 2009. [Google Scholar]
  8. Ostachowicz, W.; Kudela, P.; Malinowski, P.; Wandowski, T. Damage localisation in plate-like structures based on PZT sensors. Mechanical Systems and Signal Processing 2009, 23, 1805–1829. [Google Scholar] [CrossRef]
  9. Qing, X.; Li, W.; Wang, Y.S.; Sun, H. Piezoelectric Transducer-Based Structural Health Monitoring for Aircraft Applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef]
  10. Charles, H. Keilers, J.; Chang, F.K. Identifying Delamination in Composite Beams Using Built-In Piezoelectrics: Part I – Experiments and Analysis. Journal of Intelligent Material Systems and Structures 1995, 6, 649–663. [Google Scholar] [CrossRef]
  11. Lin, M.; Qing, X.; Kumar, A.; Beard, S.J. SMART Layer and SMART Suitcase for structural health monitoring applications. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, June 2001; Vol. 4332, pp. 98–106. [Google Scholar] [CrossRef]
  12. Zhao, X.; Gao, H.; Zhang, G.; Ayhan, B.; F. Yan, C.K.; Rose, J. Yan, C.K.; Rose, J. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization, and growth monitoring. Smart Materials and Structures 2007, 16, 1208–1217. [Google Scholar] [CrossRef]
  13. de Luca, A.; Perfetto, D.; de Fenza, A.; Petrone, G.; Caputo, F. A sensitivity analysis on the damage detection capability of a Lamb waves based SHM system for a composite winglet. In Proceedings of the Proceeding of the AIAS 2018 International Conference on Stress Analysis. Procedia Structural Integrity, December 2018; Vol. 12, pp. 578–588. [Google Scholar]
  14. Kudela, P.; Radzienski, M.; Ostachowicz, W. Impact induced damage assessment by means of Lamb wave image processing. Mechanical Systems and Signal Processing 2018, p. 23–36. [CrossRef]
  15. Kudela, P.; Radzienski, M.; Ostachowicz, W. Wave propagation modeling in composites reinforced by randomly oriented fibers. Journal of Sound and Vibration 2018, 414, 110–125. [Google Scholar] [CrossRef]
  16. Li, F.; Zhao, Y.; Cao, P.; Hu, N. Mixing of ultrasonic Lamb waves in thin plates with quadratic nonlinearity. Ultrasonics 2018, 87, 33–43. [Google Scholar] [CrossRef]
  17. Ong, W.; Rajic, N.; Chiu, W.; Rosalie, C. Adhesive material property evaluation for improved Lamb wave simulation. International Journal of Adhesion & Adhesives 2016, 71, 28–38. [Google Scholar] [CrossRef]
  18. Sánchez Iglesias, F.; Fernández López, A. Rayleigh damping parameters estimation using hammer impact tests. Mechanical Systems and Signal Processing 2020, 135, 106391. [Google Scholar] [CrossRef]
  19. Chiappa, A.; Iakovlev, S.; Marzani, A.; Giorgetti, F.; Groth, C.; Porziani, S.; Biancolini, M. An analytical benchmark for a 2D problem of elastic wave propagation in a solid. Engineering Structures 2021, 229, 111655. [Google Scholar] [CrossRef]
  20. Kim, K.B.; Nah, M.K.; Kim, B.K.; Koo, K.W.; Kang, J.G. The natural frequencies of AISI 316 stainless steel and analytical simulation of a Lamb wave excited by a point source. Wave Motion 2022, p. 103085. [CrossRef]
  21. He, X.J.; Li, J.S.; Huang, X.Y.; Zhou, Y.J. Solving elastic wave equations in 2D transversely isotropic media by a weighted Runge-Kutta discontinuous Galerkin method. Petroleum Science 2022. [Google Scholar] [CrossRef]
  22. Buckley, T.; Ghosh, B.; Pakrashi, V. A Feature Extraction & Selection Benchmark for Structural Health Monitoring. Structural Health Monitoring 2022, 0, 14759217221111141. [Google Scholar] [CrossRef]
  23. Nguyen, A.; Kodikara, K.T.L.; Chan, T.H.; Thambiratnam, D.P. Deterioration assessment of buildings using an improved hybrid model updating approach and long-term health monitoring data. Structural Health Monitoring 2019, 18, 5–19. [Google Scholar] [CrossRef]
  24. Peterson, J.R.; Jernigan, J.G.; Kahn, S.M.; Rasmussen, A.P.; Peng, E.; Ahmad, Z.; Bankert, J.; Chang, C.; Claver, C.; Gilmore, D.K.; et al. SIMULATION OF ASTRONOMICAL IMAGES FROM OPTICAL SURVEY TELESCOPES USING A COMPREHENSIVE PHOTON MONTE CARLO APPROACH. The Astrophysical Journal Supplement Series 2015, 218, 14. [Google Scholar] [CrossRef]
  25. Spencer, G.H.; Murty, M.V.R.K. General Ray-Tracing Procedure†. J. Opt. Soc. Am. 1962, 52, 672–678. [Google Scholar] [CrossRef]
  26. Officer, C.B. Introduction to the Theory of Sound Transmission: with Application to the Ocean.; McGraw-Hill Book Company, Inc., 1958.
  27. Hovem, J. Marine Acoustics-The Physics of Sound in Marine Environments; Peninsula Publishing, Los Altos Hills, CA, USA, 2010.
  28. Piqueras, J.; Pérez-Grande, I.; Sanz-Andres, A.; Torralbo, I. Calculation of linear conductances for thermal lumped models by means of the CMF method. Acta Astronautica 2020, 173, 76–85. [Google Scholar] [CrossRef]
  29. Huang, L.; Zeng, L.; Lin, J.; Zhang, N. Baseline-free damage detection in composite plates using edge-reflected Lamb waves. Composite Structures 2020, 247, 112423. [Google Scholar] [CrossRef]
  30. Malyarenko, E.V.; Hinders, M.K. Ultrasonic Lamb wave diffraction tomography. Ultrasonics 2001, 39, 269–281. [Google Scholar] [CrossRef] [PubMed]
  31. Heinze, C.; Sinapius, M.; Wierach, P. Lamb Wave Propagation in Complex Geometries - Model Reduction with Approximated Stiffeners. In Proceedings of the EWSHM - 7th European Workshop on Structural Health Monitoring; Cam, L.; Vincent.; Mevel.; Laurent.; Schoefs.; Franck., Eds., IFFSTTAR, Inria, Université de Nantes, Nantes, France, July 2014; p. 0.
  32. Shivaprasad, S.B.; Saini1, A.; Purushothaman, P.; Balasubramaniam, K.; Krishnamurthy, C.V. Elastic Wave Propagation in Polycrystalline Materials using Ray Tracing Model. In Proceedings of the 19th World Conference on Non-Destructive Testing (WCNDT 2016). Procedia Structural Integrity, June 2016, Vol. 2016-07, p. 0.
  33. Su, Z.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. Journal of Sound and Vibration 2006, 295, 753–780. [Google Scholar] [CrossRef]
  34. Kessler, S.; Spearing, S.; Atalla, M. In-situ damage detection of composites structures using Lamb wave methods. In Proceedings of the Proceedings of the First European Workshop on Structural Health Monitoring, Paris, France, July 2002; pp. 374–381.
  35. Kamal, A.M.; Gresil, M.; Giurgiutiu, V. Comparative Study of Several Methods for the Calculation of Ultrasonic Guided Waves in Composites. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, April 2013. [CrossRef]
  36. Conry, M.J. Notes on Wave Propagation in Anisotropic Elastic Solids. April 2005.
  37. Gunawan, A.; Hirose, S. Reflection of Obliquely Incident Guided Waves by an Edge of a Plate. MATERIALS TRANSACTIONS 2007, 48, 1236–1243. [Google Scholar] [CrossRef]
  38. Cho, Y.; Rose, J.L. A boundary element solution for a mode conversion study on the edge reflection of Lamb waves. The Journal of the Acoustical Society of America 1996, 99, 2097–2109. [Google Scholar] [CrossRef]
  39. Schulz, M.; Pai, P.; Inman, D. Health monitoring and active control of composite structures using piezoceramic patches. Composites, Part B 1999, 30, 713–725. [Google Scholar] [CrossRef]
  40. Ayers, J.P.; Greve, D.W.; Oppenheim, I.J. Energy scavenging for sensor applications using structural strains. In Proceedings of the Smart Structures and Materials. SPIE, August 2003, Vol. 5057, p. 0. [CrossRef]
  41. Erturk, A.; Inman, D. Piezoelectric Energy Harvesting, 1 ed.; John Wiley & Sons, Ltd., 2011.
  42. Iglesias, F.S.; García, P.B.; Hernanz, R.T.; López, A.F.; Vallejo, M.I. Elastic waves simulation and damping characterization on composite structures for structural health monitoring applications. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences (EUCASS 2019), July 2019. [CrossRef]
Preprints 79407 g001
Figure 1. Ray splitting and mode conversion at a boundary.
Figure 1. Ray splitting and mode conversion at a boundary.
Preprints 79407 g001
Preprints 79407 g002
Figure 2. Schema of the PZT sensors model for the ray tracing algorithm.
Figure 2. Schema of the PZT sensors model for the ray tracing algorithm.
Preprints 79407 g002
Preprints 79407 g003
Figure 3. Case of study specimen used for the simulated damage tests.
Figure 3. Case of study specimen used for the simulated damage tests.
Preprints 79407 g003
Preprints 79407 g004
Figure 4. Result comparison of Path 3-6 with artificial damage 01.
Figure 4. Result comparison of Path 3-6 with artificial damage 01.
Preprints 79407 g004
Preprints 79407 g005
Figure 5. Result comparison of Path 8-6 with artificial damage 01 and 02.
Figure 5. Result comparison of Path 8-6 with artificial damage 01 and 02.
Preprints 79407 g005
Preprints 79407 g006
Figure 6. Test specimens for the composite stiffened plate case study.
Figure 6. Test specimens for the composite stiffened plate case study.
Preprints 79407 g006
Preprints 79407 g007
Figure 7. Detail of the FEM model mesh.
Figure 7. Detail of the FEM model mesh.
Preprints 79407 g007
Preprints 79407 g008
Figure 8. Result comparison of relevant paths from PZT1 for the composite panels.
Figure 8. Result comparison of relevant paths from PZT1 for the composite panels.
Preprints 79407 g008
Preprints 79407 g009
Figure 9. Contour plot comparison at t = 0.07 ms.
Figure 9. Contour plot comparison at t = 0.07 ms.
Preprints 79407 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

83

Views

30

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated